A Group-Theoretic Approach to the Bifurcation Analysis of Spatial Cosserat-Rod Frameworks with Symmetry

Abstract

We present a general approach to the bifurcation analysis of spatial framework structures with symmetry. While group-theoretic methods for bifurcation problems with symmetry are well known, their actual implementation in the context of geometrically exact frameworks is not straightforward. We consider spatial structures comprising assemblages of Cosserat rods; the main difficulty arises from the nonlinear configuration space, due to the presence of (cross-sectional) rotation fields. We avoid this via a single-rod formulation, developed earlier by one of the authors, whereby the governing equations are embedded in a slightly enlarged linear space. The field equations for a framework then comprise the assembly of all such rod equations, supplemented by compatibility and equilibrium conditions at the joints. We demonstrate their equivariance under the natural symmetry group action, and the implementation of group-theoretic methods is now clear within the enlarged linear space. All potential generic, symmetry-breaking bifurcations are predicted a-priori. We then employ an open-source path-following code, which can detect and compute simple, one-dimensional bifurcations; multiple bifurcation points are beyond its capabilities. For the latter, we construct symmetry-reduced problems implemented by appropriate substructures. Multiple bifurcations are rendered simple, and the path-following code is again applicable. We first analyze a simple tripod framework, providing all details of our methodology. We then treat a more complex hexagonal space frame via the same approach. Both structures exhibit simple and double bifurcation points.

Appendices

Appendix 1

Proof of Proposition 1.1

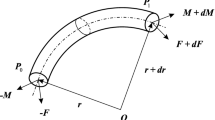
For simplicity, we suppose that the configuration of the rod is prescribed at the two ends, viz. ${\mathbf{r}}(0),{\mathbf{R}}(0),{\mathbf{r}}(L)$ and ${\mathbf{R}}(L)$ are specified. We consider smooth but arbitrary fields ${{\varvec{\upeta}}}(x),{{\varvec{\Theta}}}(x)$ that vanish at the end points with ${{\varvec{\Theta}}}^{T} \equiv - {{\varvec{\Theta}}},$ i.e., ${{\varvec{\Theta}}}$ is a skew-symmetric field. The former is an additive admissible variation for the field ${\mathbf{r}},$ in contrast to the variation in the rotation field ${\mathbf{R}}.$ Rather, a finite perturbation of ${\mathbf{R}}(s)$ reads $\exp [\varepsilon {{\varvec{\Theta}}}(s)]{\mathbf{R}}(s),$ and an admissible first-order variation follows from ${\mathbf{R}} \to$ $\frac{d}{d\varepsilon }\exp [\varepsilon {{\varvec{\Theta}}}]{\mathbf{R}}|_{\varepsilon = 0} = {\varvec{\Theta}}{\mathbf{R}}.$ The first-variation condition for (1.6) then follows from the calculation

$$ \frac{d}{d\varepsilon }{\mathcal{U}}[{\mathbf{r}} + \varepsilon {{\varvec{\upeta}}},{\mathbf{R}} + \varepsilon {\varvec{\Theta}}{\mathbf{R}} + o(\varepsilon )]|_{\varepsilon = 0} = 0{\text{ for all }}{{\varvec{\upeta}}},{{\varvec{\Theta}}} $$

(4.1)

From (1.6), this entails unravelling the pertinent first-order perturbations:

$$ \begin{aligned} [{\bf R} + \varepsilon {\varvec{\Theta}}{\mathbf{R}} + o(\varepsilon )]^{T} ({\dot{\mathbf{r}}} + \varepsilon {\dot{\varvec{\eta }}}) = {\mathbf{R}}^{T} {\dot{\mathbf{r}}} + \varepsilon {\mathbf{R}}^{T} ({\dot{\varvec{\eta }}} - {\varvec{\Theta \dot{r}}}) + o(\varepsilon )\hfill \\ \, = {\mathbf{R}}^{T} {\dot{\mathbf{r}}} + \varepsilon {\mathbf{R}}^{T} ({\dot{\varvec{\eta }}} + {\dot{\mathbf{r}}} \times {{\varvec{\uptheta}}}) + o(\varepsilon ), \end{aligned} $$

where ${{\varvec{\uptheta}}} = axial({{\varvec{\Theta}}}).$ In addition,

$$ \begin{aligned} {[}{\dot{\mathbf{R}}} +\varepsilon ({\dot{\varvec{\Theta }}} {\mathbf{R}}+ {\varvec{\Theta \dot{R}}}) + o(\varepsilon ){]}[{\mathbf{R}} + \varepsilon {\varvec{\Theta R}} + o(\varepsilon )]^{T} \\ = {\mathbf{K}} + \varepsilon ({\dot{\varvec{\Theta }} + {\varvec{\Theta} }{\mathbf{{K}}}} - {\mathbf{{K}}}{\varvec{\Theta} }) + o(\varepsilon ), \\ \end{aligned} $$

$$ axial\{ {\mathbf{K}} + \varepsilon ({\dot{\varvec{\Theta }}} + {\varvec{\Theta}} {{{\rm K}}} - {\mathbf{{\rm K}}}{\varvec{\Theta }}) + o(\varepsilon )\} = {{\varvec{\upkappa}}} + \varepsilon ({\dot{\varvec{\theta }}} + {{\varvec{\uptheta}}} \times {{\varvec{\upkappa}}}) + o(\varepsilon ), $$

and then

$$ \begin{gathered} {[}{\mathbf{R}} + \varepsilon {\varvec{\Theta}} {\mathbf{R}} + o(\varepsilon ){]}^{T} [{{\varvec{\upkappa}}} + \varepsilon ({\dot{\varvec{\theta }}} + {{\varvec{\uptheta}}} \times {{\varvec{\upkappa}}}) + o(\varepsilon )] \hfill \\ \, = {\mathbf{R}}^{T} {{\varvec{\upkappa}}} + \varepsilon {\mathbf{R}}^{T} ({\dot{\varvec{\theta }}} + {{\varvec{\uptheta}}} \times {{\varvec{\upkappa}}} - {\varvec{\Theta \kappa }}) + o(\varepsilon ) \hfill \\ \, = {\mathbf{R}}^{T} {{\varvec{\upkappa}}} + \varepsilon {\mathbf{R}}^{T} {\dot{\varvec{\theta }}} + o(\varepsilon ). \hfill \\ \end{gathered} $$

(4.2)

Returning to (4.1), we now find

$$ \begin{gathered} \left\langle {\delta {\mathcal{U}}[{\mathbf{r}},{\mathbf{R}}],({{\varvec{\upeta}}},{{\varvec{\uptheta}}})} \right\rangle : = \frac{d}{d\varepsilon }{\mathcal{U}}[{\mathbf{r}} + \varepsilon {{\varvec{\upeta}}},{\mathbf{R}} + \varepsilon {\varvec{\Theta}}{\mathbf{ R}} + o(\varepsilon )]|_{\varepsilon = 0} \hfill \\ \, = \frac{d}{d\varepsilon }\int_{0}^{L} {W\left( {{\mathbf{R}}^{T} {\dot{\mathbf{r}}} + \varepsilon {\mathbf{R}}^{T} ({\dot{\varvec{\eta }}} + {\dot{\mathbf{r}}} \times {{\varvec{\uptheta}}}) + o(\varepsilon ),{\mathbf{R}}^{T} {{\varvec{\upkappa}}} + \varepsilon {\mathbf{R}}^{T} {\dot{\varvec{\theta }}} + o(\varepsilon )} \right)} dx|_{\varepsilon = 0} \hfill \\ \, = \int_{0}^{L} {\left\{ {\frac{\partial W}{{\partial{\varvec {\nu}_{i} }}}({\mathbf{R}}^{T} {\dot{\mathbf{r}}},{\mathbf{R}}^{T} {{\varvec{\upkappa}}}){\mathbf{e}}_{i} \cdot [{\mathbf{R}}^{T} ({\dot{\varvec{\eta }}} + {\dot{\mathbf{r}}} \times {{\varvec{\uptheta}}})] + \frac{\partial W}{{\partial \kappa_{i} }}({\mathbf{R}}^{T} {\dot{\mathbf{r}}},{\mathbf{R}}^{T} {{\varvec{\upkappa}}}){\mathbf{e}}_{i} \cdot {\mathbf{R}}^{T} {\dot{\varvec{\theta }}}} \right\}dx} \hfill \\ \, = \int_{0}^{L} {[{\mathbf{n}} \cdot } ({\dot{\varvec{\eta }}} + {\dot{\mathbf{r}}} \times {{\varvec{\uptheta}}}) + {\mathbf{m}} \cdot {\dot{\varvec{\theta }}}]ds = 0{\text{ for all }}{{\varvec{\upeta}}},{{\varvec{\uptheta}}}, \hfill \\ \end{gathered} $$

(4.3)

where the last line follows from the use of (1.1) and (1.5). The first-variation condition (4.3) expresses the weak form of the equilibrium equations; the classical form (1.7) follows from (4.3) via integration by parts and the usual formal arguments of the calculus of variations.$\square$

Proof of Proposition 2.1

We assume the end conditions (2.4), (2.5). In consonance with those, we consider smooth fields ${{\varvec{\upeta}}}^{(j)} (s),_{{}} {{\varvec{\Theta}}}^{(j)} (s)$ satisfying

$$ \begin{gathered} {{\varvec{\upeta}}}^{(j)} (L) = {\mathbf{0}},_{{}} {{\varvec{\Theta}}}^{(j)} (L) = {\mathbf{O}},j = 1,2,3, \hfill \\ {{\varvec{\upeta}}}_{A} : = {{\varvec{\upeta}}}^{(1)} (0) = {{\varvec{\upeta}}}^{(2)} (0) = {{\varvec{\upeta}}}^{(3)} (0), \hfill \\ {{\varvec{\Theta}}}^{(1)} (0) = {{\varvec{\Theta}}}^{(2)} (0) = {{\varvec{\Theta}}}^{(3)} (0), \hfill \\ \end{gathered} $$

(4.4)

which we use to construct admissible variations of $({\mathbf{r}}^{(j)} ,{\mathbf{R}}^{(j)} ),j = 1,2,3,$ respectively, as in (4.2). We express this abstractly via

$$ \begin{gathered} {\tilde{\mathcal{U}}}[{\mathbf{u}};{\mathbf{h}},\varepsilon ]: = {\mathcal{U}}({\mathbf{r}}^{(1)} + \varepsilon {{\varvec{\upeta}}}^{(1)} ,{\mathbf{R}}^{(1)} + \varepsilon {{\varvec{\Theta}}}^{(1)} {\mathbf{R}}^{(1)} ,{\mathbf{r}}^{(2)} + \varepsilon {{\varvec{\upeta}}}^{(2)} ,{\mathbf{R}}^{(2)} + \varepsilon {{\varvec{\Theta}}}^{(2)} {\mathbf{R}}^{(2)} ,{\mathbf{r}}^{(3)} + \varepsilon {{\varvec{\upeta}}}^{(3)} , \hfill \\ \, {\mathbf{R}}^{(3)} + \varepsilon {{\varvec{\Theta}}}^{(3)} {\mathbf{R}}^{(3)} ) + o(\varepsilon ), \hfill \\ \end{gathered} $$

(4.5)

where ${\mathbf{h}}: = ({{\varvec{\upeta}}}^{(1)} ,{{\varvec{\uptheta}}}^{(1)} ,{{\varvec{\upeta}}}^{(2)} ,{{\varvec{\uptheta}}}^{(2)} ,{{\varvec{\upeta}}}^{(3)} ,{{\varvec{\uptheta}}}^{(3)} ),$ with ${{\varvec{\uptheta}}}^{(i)} = axial({{\varvec{\Theta}}}^{(i)} ),$ cf. (2.25).

Then as in (4.3), we compute the first-variation condition:

$$ \begin{gathered} \left\langle {\delta {\mathcal{V}\ominus }[\lambda ,{\mathbf{u}}],{\mathbf{h}}} \right\rangle : = \frac{d}{d\varepsilon }\left\{ {{\tilde{\mathcal{U}}}[{\mathbf{u}};{\mathbf{h}},\varepsilon )] + \lambda ({\mathbf{r}}_{A} + \varepsilon {{\varvec{\upeta}}}_{A} ) \cdot {\mathbf{i}}_{3} } \right\}|_{\varepsilon = 0} = \left\langle {\delta {\mathcal{U}\ominus }[\lambda ,{\mathbf{u}}],{\mathbf{h}}} \right\rangle + \lambda {\mathbf{i}}_{3} \cdot {{\varvec{\upeta}}}_{A} \hfill \\ \, = \sum\limits_{j = 1}^{3} {\{ \frac{d}{d\varepsilon }\int_{0}^{L} {W([{\mathbf{R}}^{(j)} ]^{T} {\dot{\mathbf{r}}}^{(j)} + \varepsilon [{\mathbf{R}}^{(j)} ]^{T} ({\dot{\varvec{\upeta }}}^{(j)} + {\dot{\mathbf{r}}}^{(j)} \times {{\varvec{\uptheta}}}^{(j)} ) + o(\varepsilon ),} } \, [{\mathbf{R}}^{(j)} ]^{T} {{\varvec{\upkappa}}}^{(j)} + \varepsilon [{\mathbf{R}}^{(j)} ]^{T} {\dot{\varvec{\uptheta }}}^{(j)} + o(\varepsilon ))dx{\text{\} }}|_{\varepsilon = 0} \hfill \\ \, \quad+ \lambda {\mathbf{i}}_{3} \cdot {{\varvec{\upeta}}}_{A} \, \hfill \\ \end{gathered} $$

$$ \begin{gathered} = \sum\limits_{j = 1}^{3} {\int_{0}^{L} {\{ \frac{\partial W}{{\partial \nu_{i} }}([{\mathbf{R}}^{(j)} ]^{T} {\dot{\mathbf{r}}}^{(j)} ,[{\mathbf{R}}^{(j)} ]^{T} {{\varvec{\upkappa}}}^{(j)} ){\mathbf{e}}_{i}^{(j)} \cdot [{\mathbf{R}}^{(j)} ]^{T} ({{\dot{\varvec{\upeta}}}}^{(j)} + {\dot{\mathbf{r}}}^{(j)} \times {{{\varvec{\uptheta}}}}^{(j)} )} } \hfill \\ \, \quad+ \frac{\partial W}{{\partial \kappa_{i} }}([{\mathbf{R}}^{(j)} ]^{T} {\dot{\mathbf{r}}}^{(j)} ,[{\mathbf{R}}^{(j)} ]^{T} {{\varvec{\upkappa}}}^{(j)} ){\mathbf{e}}_{i}^{(j)} \cdot [{\mathbf{R}}^{(j)} ]^{T} {{\dot{\varvec{\uptheta}}}}^{(j)} \} dx + \lambda {\mathbf{i}}_{3} \cdot {{\mathbf{\upeta}}}_{A} { = 0} \hfill \\ { = }\sum\limits_{j = 1}^{3} {\int_{0}^{L} {\{ {\mathbf{n}}^{(j)} } } \cdot ({{\dot{\varvec{\upeta}}}}^{(j)} + {\dot{\mathbf{r}}}^{(j)} \times {{\varvec{\uptheta}}}^{(j)} ) + {\mathbf{m}}^{(j)} \cdot \user2{{\dot{\varvec{\uptheta}}}}^{(j)} \} dx + \lambda {\mathbf{i}}_{3} \cdot {{\varvec{\upeta}}}_{A} { = 0}, \hfill \\ \end{gathered} $$

(4.6)

for all admissible fields ${{\varvec{\upeta}}}^{(j)} ,{{\varvec{\uptheta}}}^{(j)} = axial{{\varvec{\Theta}}}^{(j)} ,j = 1,2,3,$ satisfying (4.4); we used (1.1) and (1.4) in going from (4.6)₂ to (4.6)_3. The last line of (4.6) expresses the weak form of the equilibrium equations. Integration by parts yields, use of (4.4), and the usual formal arguments of the calculus of variations then deliver the field Eqs. (2.8).$\hfill\square$

Proof of Proposition 2.3:

First, we note that (2.24) is trivial for the symmetry-preserving loading term: From (4.6)₁, the first variation in the loading potential is simply $\lambda {\mathbf{i}}_{3} \cdot {{\varvec{\upeta}}}_{A} \equiv \lambda {\mathbf{Gi}}_{3} \cdot {{\varvec{\upeta}}}_{A}$ for all ${\mathbf{G}} \in C_{3v} .$ So it’s enough to show the validity of (2.24) for the internal potential energy ${\mathcal{U} }[\lambda ,{\mathbf{u}}].$ Employing (4.5) and (2.26), we compute directional derivative of the invariance conditions (2.15) (ignoring the loading term):

$$ \begin{gathered} \frac{d}{d\varepsilon }{\tilde{\mathcal{U}}}[{\varvec{T}}_{G} {\mathbf{u}};{\mathbf{h}},\varepsilon )]|_{\varepsilon = 0} = \frac{d}{d\varepsilon }{\tilde{\mathcal{U}}}[{\mathbf{u}};{\mathbf{h}},\varepsilon )]|_{\varepsilon = 0} \Rightarrow \hfill \\ \, \left\langle {\delta {\mathcal{U}}[\lambda ,{\varvec{T}}_{G} {\mathbf{u}}],\tilde{\user2{T}}_{G} {\mathbf{h}}} \right\rangle = \left\langle {\delta {\mathcal{U}}[\lambda ,{\mathbf{u}}],{\mathbf{h}}} \right\rangle , \hfill \\ \end{gathered} $$

(4.7)

for all ${\mathbf{G}} \in C_{3v}$ and for all admissible ${\mathbf{h}}.$ The modified action on the space of admissible variations in (4.7)₂ arises as in (4.5)–from the conversion of skew-symmetric-matrix actions to cross products. It is straightforward, if tedious, to verify that the transformations (2.26) generate a faithful representation of $C_{3v} ,$ i.e., the mapping ${\mathbf{G}} \mapsto \tilde{\user2{T}}_{G}$ is one-to-one, and

$$ \tilde{\user2{T}}_{G} \tilde{\user2{T}}_{H} = \tilde{\user2{T}}_{GH} ,_{{}} \tilde{\user2{T}}_{G}^{ - 1} = \tilde{\user2{T}}_{{G^{T} }} ,_{{}} \tilde{\user2{T}}_{I} = {\varvec{I}}{\text{ (identity)}}{.} $$

(4.8)

Moreover, we claim that

$$ \tilde{\user2{T}}_{G}^{*} \equiv \tilde{\user2{T}}_{G}^{ - 1} {\text{ on }}C_{3v} , $$

(4.9)

where $\tilde{\user2{T}}_{G}^{*}$ denotes the adjoint operator of $\tilde{\user2{T}}_{G}$ with respect to the inner-product (2.27). To see this, first note that

$$ \left\langle {\tilde{\user2{T}}_{G}^{*} \tilde{\user2{T}}_{G} {{\varvec{\upsigma}}},{\mathbf{h}}} \right\rangle = \left\langle {\tilde{\user2{T}}_{G} {{\varvec{\upsigma}}},\tilde{\user2{T}}_{G} {\mathbf{h}}} \right\rangle = \left\langle {{{\varvec{\upsigma}}},{\mathbf{h}}} \right\rangle {\text{ on }}C_{3v} , $$

(4.10)

for all smooth fields ${{\varvec{\upsigma}}},{\mathbf{h}},$ the second equality of which is readily verified via (2.26), (2.27). Thus, $\tilde{\user2{T}}_{G}^{*}$ is a left inverse. Now let ${{\varvec{\upsigma}}} = \tilde{\user2{T}}_{G}^{*} {{\varvec{\upmu}}}$ and ${\mathbf{k}} = \tilde{\user2{T}}_{G} {\mathbf{h}}$ in the second part of (4.10), leading to $\left\langle {\tilde{\user2{T}}_{G} \tilde{\user2{T}}_{G}^{*} {{\varvec{\upmu}}},{\mathbf{k}}} \right\rangle = \left\langle {\tilde{\user2{T}}_{G}^{*} {{\varvec{\upmu}}},{\mathbf{h}}} \right\rangle { = }$ $\left\langle {{{\varvec{\upmu}}},{\mathbf{k}}} \right\rangle {\text{ on }}C_{3v} ,$ for all ${{\varvec{\upmu}}},{\mathbf{k}},$ i.e., $\tilde{\user2{T}}_{G}^{*}$ is also a right inverse. Finally, we choose ${\mathbf{h}} = \tilde{\user2{T}}_{G}^{*} {\mathbf{k}}$ in (4.7)₂ and employ (4.9) to deduce

$$ \begin{gathered} \left\langle {\delta {\mathcal{U} }[\lambda ,{\varvec{T}}_{G} {\mathbf{u}}],{\mathbf{k}}} \right\rangle = \left\langle {\delta {\mathcal{U} }[\lambda ,{\mathbf{u}}],\tilde{\user2{T}}_{G}^{*} {\mathbf{k}}} \right\rangle \hfill \\ \, = \left\langle {\tilde{\user2{T}}_{G} \delta {\mathcal{U} }[\lambda ,{\mathbf{u}}],{\mathbf{k}}} \right\rangle , \hfill \\ \end{gathered} $$

for all ${\mathbf{G}} \in C_{3v}$ and for all admissible ${\mathbf{k}}.$ This completes the proof.$\square$

Appendix 2

Here we discuss the $C_{2v} { - }$ symmetry of the transcritical bifurcation, depicted in Fig. 13, associated with irrep $\gamma^{(5)} .$ As noted in Sect. 3, (2.33)₃ and (3.12)₅ reveal that $\gamma^{(5)}$ is associated (faithfully) with $D_{3} { - }$ symmetry on ${\mathbb{R}}^{2} ,$ but with each element appearing twice. Hence, the maximal isotropy subgroup of the fixed-point space $span\{ {\mathbf{i}}_{1} \}$ is actually $\Sigma = \{ \gamma_{I}^{(5)} ,\gamma_{E}^{(5)} ,\gamma_{I}^{(5)} ,\gamma_{E}^{(5)} \} ,$ which is a representation of $D_{2} : = \{ \gamma_{I}^{(6)} ,\gamma_{E}^{(6)} ,\gamma_{{R_{\pi } }}^{(6)} ,\gamma_{{ER_{\pi } }}^{(6)} \} \subset D_{6} .$ Accordingly, we can build a projection operator on configuration space with the symmetry of $\Sigma$ via

$$ {\varvec{P}}_{\Sigma } = \frac{1}{4}[{\varvec{T}}_{I} + {\varvec{T}}_{E} + {\varvec{T}}_{{R_{\pi } }} + {\varvec{T}}_{{ER_{\pi } }} ], $$

where we use the []₁₁ entries of the matrices comprising $\Sigma$ for weights (McWeeny 2002), each of which equals 1 in this case. The operators ${\varvec{T}}_{G}$ are defined via the generators (3.8). Then ${\varvec{P}}_{\Sigma } {\varvec{u}} \in {\mathcal{X}}_{o}^{\Sigma } ,$ for any configuration ${\varvec{u}} \in {\mathcal{X}}_{o} ,$ cf. (2.31), (3.2). We now observe that

$$ \begin{gathered} {\varvec{T}}_{E} {\varvec{P}}_{\Sigma } = {\varvec{T}}_{E} [{\varvec{T}}_{I} + {\varvec{T}}_{E} + {\varvec{T}}_{{R_{\pi } }} + {\varvec{T}}_{{ER_{\pi } }} ]/4 = [{\varvec{T}}_{E} + {\varvec{T}}_{I} + {\varvec{T}}_{{ER_{\pi } }} + {\varvec{T}}_{{R_{\pi } }} ]/4 = {\varvec{P}}_{\Sigma } , \hfill \\ {\varvec{T}}_{{ER_{\pi } }} {\varvec{P}}_{\Sigma } = {\varvec{T}}_{{ER_{\pi } }} [{\varvec{T}}_{I} + {\varvec{T}}_{E} + {\varvec{T}}_{{R_{\pi } }} + {\varvec{T}}_{{ER_{\pi } }} ]/4 = [{\varvec{T}}_{{ER_{\pi } }} + {\varvec{T}}_{{R_{\pi } }} + {\varvec{T}}_{E} + {\varvec{T}}_{I} ]/4 \hfill \\ \quad\quad\quad\quad = {\varvec{P}}_{\Sigma } . \hfill \\ \end{gathered} $$

(5.1)

Above we have used the fact that ${\varvec{T}}_{G} {\varvec{T}}_{H} = {\varvec{T}}_{GH}$ for all $G,H \in C_{6v} \cong D_{6} .$ Finally, for any ${\varvec{v}} = {\varvec{P}}_{\Sigma } {\varvec{u}} \in {\mathcal{X}}_{o}^{\Sigma } ,$ (5.1) implies ${\varvec{T}}_{{R_{\pi } }} {\varvec{v}} = \user2{v,}_{{}} {\varvec{T}}_{E} {\varvec{v}} = \user2{v,}$ and ${\varvec{T}}_{{ER_{\pi } }} {\varvec{v}} = {\varvec{v}},$ i.e., the configuration possesses $C_{2v}$ symmetry.