Discretized Fast–Slow Systems with Canards in Two Dimensions

Abstract

We study the problem of preservation of maximal canards for time discretized fast–slow systems with canard fold points. In order to ensure such preservation, certain favorable structure-preserving properties of the discretization scheme are required. Conventional schemes do not possess such properties. We perform a detailed analysis for an unconventional discretization scheme due to Kahan. The analysis uses the blow-up method to deal with the loss of normal hyperbolicity at the canard point. We show that the structure-preserving properties of the Kahan discretization for quadratic vector fields imply a similar result as in continuous time, guaranteeing the occurrence of maximal canards between attracting and repelling slow manifolds upon variation of a bifurcation parameter. The proof is based on a Melnikov computation along an invariant separating curve, which organizes the dynamics of the map similarly to the ODE problem.

1 Introduction

In this paper, we study the effect of the time discretization upon systems of ordinary differential equations (ODEs) which exhibit the phenomenon called “canards.” It takes place, under certain conditions, in singularly perturbed (slow–fast) systems exhibiting fold points. The simplest form of such a system is

$$\begin{aligned} \begin{array}{l} x' = f(x,y,\lambda ,\varepsilon ), \\ y' = \varepsilon g(x ,y,\lambda ,\varepsilon ), \end{array} \end{aligned}$$

(1.1)

where we interpret $\varepsilon >0$ as a small time scale parameter, separating between the fast variable x and the slow variable y. For $\lambda =0$, the origin is assumed to be a non-hyperbolic fold point, possessing an attracting slow manifold and a repelling slow manifold. One says that the system admits a maximal canard if there are trajectories connecting the attracting and the repelling slow manifolds (Benoît et al. 1981; Dumortier and Roussarie 1996; Krupa and Szmolyan 2001c). This is a non-generic phenomenon which only becomes generic upon including an additional parameter $\lambda$, for the region of $\lambda$’s which is exponentially narrow as $\varepsilon \rightarrow 0$. This makes the study of maximal canards especially challenging.

Krupa and Szmolyan (2001a) have analyzed maximal canards for Eq. (1.1) by using the blow-up method which allows to effectively handle the non-hyperbolic singularity at the origin. The key idea to use the blow-up method (Dumortier 1978, 1993) for fast–slow systems goes back to Dumortier and Roussarie (1996). They observed that non-hyperbolic singularities can be converted into partially hyperbolic one by means of an insertion of a suitable manifold, e.g., a sphere, at such a singularity. The dynamics on this inserted manifold are partially hyperbolic, and truly hyperbolic in its neighborhood. The dynamics on the manifold are usually analyzed in different charts. See, e.g., (Kuehn 2015, Chapter 7) for an introduction into this technique. A non-exhaustive list of different applications to planar fast–slow systems includes (De Maesschalck and Dumortier 2010, 2005; De Maesschalck and Wechselberger 2015; Gucwa and Szmolyan 2009; Krupa and Szmolyan 2001a; Kuehn 2014, 2016).

The main ingredient for a proof of maximal canards in Krupa and Szmolyan (2001a) is the existence of a constant of motion for the dynamics in the rescaling chart in the blown-up space. This constant of motion can be used for a Melnikov method to compute the separation of the attracting and repelling manifold under perturbations, in particular to find relations between parameters $\varepsilon$ and $\lambda$ under which the manifolds intersect, leading to a maximal canard. The role of this constant of motion suggests that, in order to retain the existence of maximal canards, the right choice of the time discretization scheme becomes of a crucial importance. Indeed, one can show that conventional discretization schemes like the Euler method do not preserve maximal canards. The concept of a structure-preserving discretization method is necessary. We investigate time discretization of the ODE (1.1) via the Kahan method which has been shown to preserve various integrability attributes in many examples (and known also as Hirota–Kimura method in the context of integrable systems, see, e.g., Kahan 1993; Petrera and Suris 2019). We apply the blow-up method, which so far has been mainly used for flows, to the discrete-time fast–slow dynamical systems induced by the Kahan discretization procedure. We show that these dynamical systems exhibit maximal canards for $\lambda$ and $\varepsilon$ related by a certain a functional relation existing in a region which exponentially narrow with $\varepsilon \rightarrow 0$. Thus, we extend to the discrete-time context the previously known feature of the continuous time systems, provided an intelligent choice of the discretization scheme. We would like to stress that, despite the similarity of results to the continuous-time case, the techniques of the proofs for the discrete time had to be substantially modified. In particular, the arguments based on the conserved quantity cannot be directly transferred into the discrete-time context, since the conserved quantities there are only formal (divergent asymptotic series). Thus, it turned out to be necessary to use more general arguments based on the existence of an invariant measure and an invariant separating curve characterized as a singular curve of an invariant measure. We use also a more general version of the Melnikov method, similar to the one presented in Wechselberger (2002).

Note that the application of the blow-up method to the discrete-time problem of folded canards is a considerable extension compared to the Euler discretizations for transcritical singularities, as studied in Engel and Kuehn (2019). The folded canard case has specific dynamic structure, as explained above, such that a structure-preserving discretization method is needed, now performing the blow-up for the rational Kahan mapping. Compared to Engel and Kuehn (2019), the kind of map is different, the structure in the singular limit is richer, there is an additional parameter $\lambda$, also rescaled in the blow-up, and the type of result, namely a continuation of the critical object along a two-parameter curve, is new.

Based on observations of this paper, the employment of Kahan’s method for a treatment of canards can also be found in Engel and Jardón-Kojakhmetov (2020). There, the simplest canonical form for folded, pitchfork and transcritical canards is studied and the focus lies on the linearization along trajectories. While it is demonstrated that explicit Runge–Kutta methods cannot provide symmetry of entry–exit relations, the linearization along the Kahan scheme and similar symmetric, A-stable methods are shown to preserve the typical continuous-time behavior. Hence, the discussion of symmetry and linear stability in Engel and Jardón-Kojakhmetov (2020) supplements the paper at hand; here, we establish the existence and extension of maximal canards along parameter combinations for the nonlinear problem of folded canards with additional quadratic perturbation terms, in particular using the blow-up technique.

The paper is organized as follows. Section 2 recalls the setting of fast–slow systems in continuous time and summarizes the main result on maximal canards, Theorem 2.2, with a short sketch of the proof, as given in Krupa and Szmolyan (2001a). In Sect. 3, we study the problem of a maximal canard for systems with folds in discrete time. We establish the Kahan discretization of the canard problem in Sect. 3.1 and discuss the reduced subsystem of the slow time scale in Sect. 3.2. In Sect. 3.3, we introduce the blow-up transformation for the discretized problem. We discuss the dynamics for the entering and exiting chart in Sect. 3.4, and for the rescaling chart in Sect. 3.5. In Sect. 3.6, we explore the dynamical properties of the Kahan map in the rescaling chart, including a formal conserved quantity, an invariant measure and an invariant separating curve. Following this, we conduct the Melnikov computation along the invariant curve in Sect. 3.7, leading to the proof of the main Theorem 3.11, which is the discrete-time analogue to Theorem 2.2. Finally, we provide various numerical illustrations in Sect. 3.8 and conclude with an outlook in Sect. 4.

Thus, we succeeded in adding the problem of maximal canards to the recent list of results, where a geometric analysis shows that certain features of fast–slow systems with non-hyperbolic singularities can be preserved via a suitable discretization, including the cases of the fold singularity (Nipp and Stoffer 2013), the transcritical singularity (Engel and Kuehn 2019) and the pitchfork singularity (Arcidiacono et al. 2019). More broadly viewed, our results also provide a continuation of a line of research on discrete-time fast–slow dynamical systems, which includes the study of canard/delay behavior in iterated maps via normal form transformations (Neishtadt 2009), non-standard analysis (Fruchard 1991, 1992), renormalization (Baesens 1991), Gevrey series (Baesens 1995), complex-analytic methods (Fruchard and Schäfke 2003) and phase plane partitioning (Mira and Shilnikov 2005).

2 Maximal Canard Through a Fold in Continuous Time

2.1 Fast–Slow Systems

We start with a brief review and notation for continuous-time fast–slow systems. Consider a system of singularly perturbed ordinary differential equations (ODEs) of the form

$$\begin{aligned} \begin{array}{rcrcl} \varepsilon \dfrac{\mathrm {d}x}{\mathrm {d}\tau } &{}=&{} \varepsilon {\dot{x}} &{}=&{} f(x,y,\varepsilon ), \\ \dfrac{\mathrm {d}y}{\mathrm {d}\tau }&{}=&{}{\dot{y}} &{}=&{} g(x,y,\varepsilon ), \quad \ x \in \mathbb {R}^m, \quad y \in {\mathbb {R}}^n, \quad 0 < \varepsilon \ll 1\,, \end{array} \end{aligned}$$

(2.1)

where f, g,  are $C^k$-functions with $k \ge 3$. Since $\varepsilon$ is a small parameter, the variables x and y are often called the fast and the slow variables, respectively. The time variable $\tau$ in (2.1) is termed the slow time scale. The change of variables to the fast time scale $t:= \tau / \varepsilon$ transforms the system (2.1) into ODEs

$$\begin{aligned} \begin{array}{l} x' = f(x,y,\varepsilon ), \\ y' = \varepsilon g(x,y,\varepsilon ). \end{array} \end{aligned}$$

(2.2)

To both systems (2.1) and (2.2), there correspond respective limiting problems for $\varepsilon = 0$: The reduced problem (or slow subsystem) is given by

$$\begin{aligned} \begin{array}{l} 0 = f(x,y,0), \\ \dot{y} = g(x,y,0), \end{array} \end{aligned}$$

(2.3)

and the layer problem (or fast subsystem) is

$$\begin{aligned} \begin{array}{l} x' = f(x,y,0), \\ y' = 0. \end{array} \end{aligned}$$

(2.4)

The reduced problem (2.3) can be understood as a dynamical system on the critical manifold

$$\begin{aligned} S_0= \{(x,y) \in \mathbb {R}^{m+n} \,:\, f(x,y,0) = 0 \}\,. \end{aligned}$$

Observe that the manifold $S_0$ consists of equilibria of the layer problem (2.4). $S_0$ is called normally hyperbolic if for all $p\in S_0$ the matrix $\text {D}_xf(p)\in \mathbb {R}^{m\times m}$ has no eigenvalues on the imaginary axis. For a normally hyperbolic $S_0$, Fenichel theory (Fenichel 1979; Jones 1995; Kuehn 2015; Wiggins 1994) implies that, for sufficiently small $\varepsilon$, there is a locally invariant slow manifold $S_{\varepsilon }$ such that the restriction of (2.1) to $S_{\varepsilon }$ is a regular perturbation of the reduced problem (2.3). Furthermore, it follows from Fenichel’s perturbation results that $S_{\varepsilon }$ possesses an invariant stable and unstable foliation, where the dynamics behave as a small perturbation of the layer problem (2.4).

2.2 Main Result on Maximal Canards in Slow–Fast Systems with a Fold

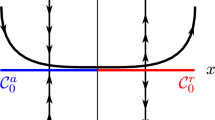
A challenging phenomenon is the breakdown of normal hyperbolicity of $S_0$ such that Fenichel theory cannot be applied. Typical examples of such a breakdown are found at bifurcation points $p\in S_0$, where the Jacobi matrix $\mathrm {D}_x f(p)$ has at least one eigenvalue with zero real part. The simplest examples are folds in planar systems ($m=n=1$), i.e., points $p=(x_0,y_0)\in {\mathbb {R}}^2$ (without loss of generality $p=(x_0,y_0)=(0,0)$) where $\partial f/\partial x$ vanishes and in whose neighborhood $S_0$ looks like a parabola. The left part of $S_0$ (with $x<0$) is denoted by $S_a$ (a for “attractive”), while its right part (with $x>0$) is denoted by $S_r$ (r for “repelling”). These notations refer to the properties of dynamics of the layer problem in the region $y>0$ (see, e.g., Kuehn 2015, Figure 8.1). By standard Fenichel theory, for sufficiently small $\varepsilon > 0$, outside of an arbitrarily small neighborhood of p, the manifolds $S_a$ and $S_r$ perturb smoothly to invariant manifolds $S_{a, \varepsilon }$ and $S_{r, \varepsilon }$.

In the following, we focus on the particularly challenging problem of fold points admitting maximal canards. In this case, the critical curve $S_0=\{f(x,y,0)=0\}$ can be locally parameterized as $y=\varphi (x)$ such that the reduced dynamics on $S_0$ are given by

$$\begin{aligned} \dot{x} = \frac{g(x, \varphi (x),0)}{\varphi '(x)}. \end{aligned}$$

(2.5)

In our setting, the function at the right-hand side is smooth at the origin, so that the reduced flow goes through the origin via a maximal solution $x_0(t)$ of (2.5) with $x_0(0) =0$. The solution $(x_0(t),y_0(t))$ with $y_0(t)=\varphi (x_0(t))$ connects both parts $S_a$ and $S_r$ of $S_0$. However, there is no reason to expect that for $\varepsilon >0$, the (extension of the) solution parameterizing $S_{a, \varepsilon }$ will coincide with the (extension of the) solution parameterizing $S_{r, \varepsilon }$, unless there are some special reasons, like symmetry, forcing such a coincidence.

Definition 2.1

We say that a planar slow–fast system admits a maximal canard, if the extension of the attracting slow manifold $S_{a,\varepsilon }$ coincides with the extension of a repelling slow manifold $S_{r,\varepsilon }$.

Example

Consider the system

$$\begin{aligned} \begin{array}{l} \varepsilon \dot{x} = - y + x^2 , \\ \dot{y} = x, \end{array} \end{aligned}$$

(2.6)

corresponding to $f(x,y,\varepsilon )=x^2-y$ and $g(x,y,\varepsilon )=x$. For the reduced system ($\varepsilon =0$), we obtain $y=\varphi (x)=x^2$ and $2x\dot{x} = x$; hence, $\dot{x} = 1/2$ (regular at $x=0$). The solution $x_0(t)$ is given by $x_0(t)=\tau /2$ so that

$$\begin{aligned} (x_0(\tau ),y_0(\tau ))=\Big (\frac{\tau }{2},\frac{\tau ^2}{4}\Big ). \end{aligned}$$

Observe that the system is symmetric with respect to the reversion of time $\tau \mapsto -\tau$ simultaneously with $x\mapsto -x$. This ensures the existence of the maximal canard also for any $\varepsilon >0$. In this particular example, one can easily find the maximal canard explicitly. Indeed, one can easily check that, for any $\varepsilon >0$,

$$\begin{aligned} (x_{0,\varepsilon }(\tau ),y_{0,\varepsilon }(\tau ))=\Big (\frac{\tau }{2},\frac{\tau ^2}{4}-\frac{\varepsilon }{2}\Big ) \end{aligned}$$

is a solution of (2.6) which parameterizes the invariant set

$$\begin{aligned} S_{\varepsilon } = \left\{ (x,y) \in \mathbb {R}^2 \, : \, y = x^2 - \frac{\varepsilon }{2} \right\} , \end{aligned}$$

(2.7)

which consists precisely of the attracting branch $S_{a, \varepsilon } = \left\{ (x,y) \in S_{\varepsilon } \, : \, x < 0 \right\}$ and the repelling branch $S_{r, \varepsilon } = \left\{ (x,y) \in S_{\varepsilon } \, : \, x > 0 \right\}$, such that trajectories on $S_{\varepsilon }$ go through $x=0$ with the speed $\dot{x} = \varepsilon /2$. However, any generic perturbation of this example, e.g., with $g(x,y,\varepsilon )=x+x^2$, will destroy its peculiarity and will not display a maximal canard.

Thus, maximal canards are not a generic phenomenon in the above setting. In order to find a context where they become generic, we have to consider families depending on an additional parameter $\lambda$:

$$\begin{aligned} \begin{array}{l} x' = f(x,y,\lambda , \varepsilon ), \\ y' = \varepsilon g(x,y,\lambda , \varepsilon ). \end{array} \end{aligned}$$

(2.8)

We assume that at $\lambda = \varepsilon = 0$, the vector fields f and g satisfy the above conditions. By a local change of coordinates, the problem can be brought into the canonical form

$$\begin{aligned} x'&= - y k_1(x,y, \lambda , \varepsilon ) + x^2 k_2(x,y, \lambda , \varepsilon ) + \varepsilon k_3(x,y, \lambda , \varepsilon ),\nonumber \\ y'&= \varepsilon (x k_4(x,y, \lambda , \varepsilon ) - \lambda k_5(x,y,\lambda , \varepsilon ) + y k_6(x,y, \lambda , \varepsilon )), \end{aligned}$$

(2.9)

where

$$\begin{aligned} \begin{array}{l} k_i(x,y, \lambda , \varepsilon ) = 1 + \mathcal {O}(x,y, \lambda , \varepsilon )\,, \quad i=1,2,4,5,\\ k_i(x,y, \lambda , \varepsilon ) = \mathcal {O}(x,y, \lambda , \varepsilon )\,, \quad i=3,6. \end{array} \end{aligned}$$

(2.10)

The main result on existence of maximal canards, as given in (Krupa and Szmolyan 2001a, Theorem 3.1), can be summarized as follows. Set

$$\begin{aligned} \begin{array}{l} a_1 = \frac{\partial k_3}{\partial x}(0,0,0,0), \ a_2 = \frac{\partial k_1}{\partial x}(0,0,0,0), \ a_3 = \frac{\partial k_2}{\partial x}(0,0,0,0), \\ a_4 = \frac{\partial k_4}{\partial x}(0,0,0,0), \ a_5 = k_6(0,0,0,0), \end{array} \end{aligned}$$

(2.11)

and

$$\begin{aligned} C = \frac{1}{8} ( 4 a_1 - a_2 + 3 a_3 - 2 a_4 + 2 a_5). \end{aligned}$$

(2.12)

Theorem 3.11

Consider system (2.9) such that the solution $(x_0(t),y_0(t))$ of the reduced problem for $\varepsilon =0$, $\lambda =0$ connects $S_a$ and $S_r$. Assume that $C\ne 0$. Then, there exist $\varepsilon _0 > 0$ and a smooth function

$$\begin{aligned} \lambda _c(\sqrt{\varepsilon })= - C \varepsilon + \mathcal {O}(\varepsilon ^{3/2}), \end{aligned}$$

defined on $[0, \varepsilon _0]$ such that for $\varepsilon \in [0, \varepsilon _0]$ there is a maximal canard; that is, the extended attracting slow manifold $S_{a, \varepsilon }$ coincides with the extended repelling slow manifold $S_{r,\varepsilon }$, if and only if $\lambda = \lambda _c(\sqrt{\varepsilon })$.

The main result of this paper will be a discretized version of Theorem 2.2 restricted to quadratic vector fields, proving for Kahan maps the extension of canards along a parameter curve, as opposed to Engel and Jardón-Kojakhmetov (2020) where only Example (2.6) and its linearization are studied.

The proof of Theorem 2.2 is based on the blow-up technique, transforming the singular problem to a manifold where the dynamics can be desingularized and studied in two different charts. The crucial step in the second chart $K_2$ is the continuation of center manifold connections via a Melnikov method based on an integral of motion H. In “Appendix A,” we summarize this procedure from Krupa and Szmolyan (2001a), adding several observations on the dynamics, its separatrix, its invariant measure and an alternative non-Hamiltonian expression that relates to the discrete-time proof we will provide in the following.

3 Maximal Canard for a System with a Fold in Discrete Time

3.1 Kahan Discretization of Canard Problem

We discretize system (2.9) with the Kahan method. It was introduced in Kahan (1993) as an unconventional discretization scheme applicable to arbitrary ODEs with quadratic vector fields. It was demonstrated in Petrera et al. (2009, 2011), Petrera and Suris (2019) and in Celledoni et al. (2013) that this scheme tends to preserve integrals of motion and invariant volume forms. There are few general results available to support this claim, in particular, two general cases of preservation of invariant volume forms in (Petrera et al. (2011), Section 2) and a similar result for Hamiltonian systems with a cubic Hamilton function in Celledoni et al. (2013). However, the number of particular results not covered by any general theory and reviewed in the above references is quite impressive. Our study here will contribute an additional evidence, as the result of Sect. 3.6.2 also belongs to this category, i.e., not covered by known general statements.

Consider an ODE with a quadratic vector field:

$$\begin{aligned} z' = f(z) = Q(z) + B z + c, \end{aligned}$$

(3.1)

where each component of $Q: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ is a quadratic form, $B \in {\mathbb {R}}^{n \times n}$ and $c \in {\mathbb {R}}^n$. The Kahan discretization of this system reads as

$$\begin{aligned} \frac{{\tilde{z}} - z}{h} = {\bar{Q}}(z, {\tilde{z}}) + \frac{1}{2} B( z + {\tilde{z}}) + c, \end{aligned}$$

(3.2)

where

$$\begin{aligned} {\bar{Q}}(z, {\tilde{z}}) = \frac{1}{2} ( Q(z +{\tilde{z}}) - Q(z) - Q({\tilde{z}})) \end{aligned}$$

is the symmetric bilinear form such that ${\bar{Q}}(z,z) = Q(z)$. Note that Eq. (3.2) is linear with respect to ${\tilde{z}}$ and therefore defines a rational map ${\tilde{z}} = F_f (z, h)$, which approximates the time h shift along the solutions of the ODE (3.1). Further note that $F_f^{-1}(z,h) = F_f (z, - h)$ and, hence, the map is birational. An explicit form of the map $F_f$ defined by Eq. (3.2) is given by

$$\begin{aligned} {\tilde{z}} = F_f (z, h) = z + h\Big ({{\,\mathrm{Id}\,}}- \frac{h}{2} \mathrm {D}f(z)\Big )^{-1} f(z). \end{aligned}$$

(3.3)

In order to be able to apply the Kahan discretization scheme, we restrict ourselves to systems (2.1), (2.2) which are quadratic, that is, to

$$\begin{aligned} \begin{array}{l} \varepsilon \dot{x} = - y + x^2 + \varepsilon a_1 x - a_2 x y, \\ \dot{y} = x - \lambda + a_5 y + a_4 x^2, \end{array} \end{aligned}$$

(3.4)

resp.

$$\begin{aligned} \begin{array}{l} x' = - y + x^2 + \varepsilon a_1 x - a_2 x y, \\ y' = \varepsilon (x - \lambda ) + \varepsilon a_5 y + \varepsilon a_4 x^2, \end{array} \end{aligned}$$

(3.5)

which corresponds to normal forms (2.9) with $k_1=1+a_2x$, $k_2=1$, $k_3=a_1x$, $k_4=1+a_4x$, $k_5=1$, and $k_6=a_5$.

Remark 3.1

It was demonstrated in (Celledoni et al. 2013, Proposition 1) that Kahan map (3.3) coincides with the map produced by the following implicit Runge–Kutta scheme, when the latter is applied to a quadratic vector field f:

$$\begin{aligned} \frac{{\tilde{z}} - z}{h} = - \frac{1}{2} f(z) + 2f\left( \frac{z+{\tilde{z}}}{2} \right) - \frac{1}{2} f({\tilde{z}}). \end{aligned}$$

(3.6)

This opens the way of extending our present results for more general (not necessarily quadratic) systems (2.9). In the present paper, we restrict ourselves to the case (3.5), since the algebraic structure keeps the calculations clear and explicit and demonstrates the central methodological aspects of our proofs. However, we additionally apply the scheme (3.6) to the folded canard problem with cubic nonlinearity in Sect. 3.8, illustrating its numerical capacity beyond the quadratic case. A proof of maximal canards for the non-quadratic case remains an open problem for future work.

3.2 Reduced Subsystem of the Slow Flow

Kahan discretization of (3.4) reads:

$$\begin{aligned} \begin{array}{l} \dfrac{\varepsilon }{h}({\tilde{x}} - x) = - \dfrac{1}{2}(y +{\tilde{y}})+x{\tilde{x}} + \dfrac{\varepsilon a_1}{2}(x+{\tilde{x}}) - \dfrac{a_2}{2}({\tilde{x}} y+x{\tilde{y}}), \\ \dfrac{1}{h}({\tilde{y}} - y) = \dfrac{1}{2}(x +{\tilde{x}}) -\lambda + \dfrac{a_5}{2} (y+{\tilde{y}}) + a_4 x{\tilde{x}}. \end{array} \end{aligned}$$

(3.7)

Proposition 3.2

The reduced system (3.7) with $\varepsilon =0$ defines an evolution on a curve

$$\begin{aligned} S_{0,h}=\big \{(x,y)\in {\mathbb {R}}^2: y=\varphi _{0,h}(x)\big \} \end{aligned}$$

which supports a one-parameter family of solutions $x_h(n;x_0)$ with $x_h(0;x_0)=x_0$. For small $\varepsilon >0$, this curve is perturbed to normally hyperbolic invariant curves $S_{a,h,\varepsilon }$ resp. $S_{r,h,\varepsilon }$ of the slow flow (3.8) for $x<0$, resp. for $x>0$.

For the simplest case $a_1=a_2=a_4=a_5=0$ and $\lambda =0$,

$$\begin{aligned} \begin{array}{l} \dfrac{\varepsilon }{h}({\tilde{x}} - x) = - \dfrac{1}{2}(y +{\tilde{y}})+x{\tilde{x}}, \\ \dfrac{1}{h}({\tilde{y}} - y) = \dfrac{1}{2}(x +{\tilde{x}}). \end{array} \end{aligned}$$

(3.8)

Everything can be done explicitly. Straightforward computations lead to the following results.

The reduced system

$$\begin{aligned} \begin{array}{l} 0 = - \dfrac{1}{2}({\tilde{y}} + y)+{\tilde{x}} x, \\ \dfrac{1}{h}({\tilde{y}} - y) = \dfrac{1}{2}({\tilde{x}} + x) \end{array} \end{aligned}$$

(3.9)

has an invariant critical curve

$$\begin{aligned} S_{0,h}=\Big \{ (x,y)\in {\mathbb {R}}^2: y=x^2-\frac{h^2}{8}\Big \}. \end{aligned}$$

(3.10)

The evolution on this curve is given by ${\tilde{x}}=x+\frac{h}{2}$, so that $x_h(n;x_0)=x_0+\frac{nh}{2}$.

For the full system (3.8), the symmetry $x\mapsto -x$, $h\rightarrow -h$ ensures the existence of an invariant curve

$$\begin{aligned} S_{\varepsilon ,h}=\Big \{ (x,y)\in {\mathbb {R}}^2: y=x^2-\frac{\varepsilon }{2}-\frac{h^2}{8}\Big \}, \end{aligned}$$

(3.11)

whose parts with $x<0$, resp. $x>0$ are the invariant curves $S_{a,h,\varepsilon }$ resp. $S_{r,h,\varepsilon }$. This curve supports solutions with $x(n)=x_0+\frac{nh}{2}$. Thus, system (3.8) exhibits a maximal canard. Our goal is to establish the existence of a maximal canard for system (3.7).

3.3 Blow-up of the Fast Flow

Kahan discretization of the fast flow (3.5) is the system (3.7) with $h\mapsto h\varepsilon$:

$$\begin{aligned} \begin{array}{l} \dfrac{1}{h}({\tilde{x}} - x) = - \dfrac{1}{2}({\tilde{y}} + y)+{\tilde{x}} x + \dfrac{\varepsilon a_1}{2}({\tilde{x}}+x) - \dfrac{a_2}{2}({\tilde{x}} y+x{\tilde{y}}), \\ \dfrac{1}{h}({\tilde{y}} - y) = \dfrac{\varepsilon }{2}({\tilde{x}} + x) -\varepsilon \lambda + \dfrac{\varepsilon a_5}{2} ({\tilde{y}} +y) + \varepsilon a_4 {\tilde{x}}x. \end{array} \end{aligned}$$

(3.12)

We introduce a quasi-homogeneous blow-up transformation for the discrete-time system, interpreting the step size h as a variable in the full system. Similarly to the continuous-time situation, the transformation reads

$$\begin{aligned} x = r {\bar{x}}, \quad y = r^2 {\bar{y}}, \quad \varepsilon = r^2 {\bar{\varepsilon }}, \quad \lambda = r {\bar{\lambda }}, \quad h = {\bar{h}}/r\,, \end{aligned}$$

where $({\bar{x}}, {\bar{y}}, {\bar{\varepsilon }}, {\bar{\lambda }}, r, {\bar{h}}) \in B := S^2 \times [-\kappa , \kappa ] \times [0, \rho ] \times [0, h_0]$ for some $h_0, \rho , \kappa > 0$. The change of variables in h is chosen such that the map is desingularized in the relevant charts.

This transformation is a map $\Phi : B \rightarrow {\mathbb {R}}^5$. If F denotes the map obtained from the time discretization, the map $\Phi$ induces a map $\overline{F}$ on B by $\Phi \circ \overline{F} \circ \Phi ^{-1} = F$. Analogously to the continuous time case, we are using the charts $K_i$, $i=1,2$, to describe the dynamics. The chart $K_1$ (setting ${\bar{y}} =1$) focuses on the entry and exit of trajectories and is given by

$$\begin{aligned} x = r_1 x_1, \quad y = r_1^2, \quad \varepsilon = r_1^2 \varepsilon _1, \quad \lambda = r_1 \lambda _1, \quad h = h_1/r_1\,. \end{aligned}$$

(3.13)

In the scaling chart $K_2$ (setting ${\bar{\varepsilon }} =1$), the dynamics arbitrarily close to the origin are analyzed. It is given via the mapping

$$\begin{aligned} x = r_2 x_2, \quad y = r_2^2 y_2, \quad \varepsilon = r_2^2 , \quad \lambda = r_2 \lambda _2, \quad h = h_2/r_2\,. \end{aligned}$$

(3.14)

The change of coordinates from $K_1$ to $K_2$ is denoted by $\kappa _{12}$ and, for $\varepsilon _1 > 0$, is given by

$$\begin{aligned} x_2 = \varepsilon _1^{-1/2} x_1, \quad y_2 = \varepsilon _1^{-1}, \quad r _2= r_1 \varepsilon _1^{1/2}, \quad \lambda _2 = \varepsilon _1^{-1/2} \lambda _1, \quad h_2 = h_1 \varepsilon _1^{1/2}.\nonumber \\ \end{aligned}$$

(3.15)

Similarly, for $y > 0$, the map $\kappa _{21} = \kappa _{12}^{-1}$ is given by

$$\begin{aligned} x_1 = y_2^{-1/2} x_2, \quad r_1 = y_2^{1/2} r_2, \quad \varepsilon _1 = y_2^{-1}, \quad \lambda _1 = y_2^{-1/2} \lambda _2, \quad h_1 = h_2 y_2^{1/2}.\nonumber \\ \end{aligned}$$

(3.16)

3.4 Dynamics in the Entering and Exiting Chart $K_1$

Here, we extend the dynamical Eqs. (3.12) by

$$\begin{aligned} {{\tilde{\varepsilon }}}=\varepsilon , \quad {\tilde{\lambda }}=\lambda , \quad {\tilde{h}}=h, \end{aligned}$$

(3.17)

and then introduce the coordinate chart $K_1$ by (3.13):

$$\begin{aligned} x = r_1 x_1, \quad y = r_1^2, \quad \varepsilon = r_1^2 \varepsilon _1, \quad \lambda = r_1 \lambda _1, \quad h = h_1/r_1 \end{aligned}$$

(3.18)

defined on the domain

$$\begin{aligned} D_1 = \left\{ (x_1, r_1, \varepsilon _1, \lambda _1, h_1) \in \mathbb {R}^5 : 0 \le r_1 \le \rho , \;\; 0 \le \varepsilon _1 \le \delta , \;\; 0 \le h_1 \le \nu \right\} .\nonumber \\ \end{aligned}$$

(3.19)

where $\rho , \delta ,\nu > 0$ are sufficiently small.

To transform the map (3.12) into the coordinates of $K_1$, we start with the particular case $a_1=a_2=a_4=a_5=0$, generated by difference equations

$$\begin{aligned} \frac{1}{h} ({\tilde{x}} - x)= {\tilde{x}} x - \frac{1}{2}({\tilde{y}} + y), \quad \frac{1}{h}({\tilde{y}} - y) = \frac{\varepsilon }{2}({\tilde{x}} + x) - \varepsilon \lambda , \end{aligned}$$

(3.20)

supplied, as usual, by (3.17). Written explicitly, this is the map

$$\begin{aligned} \tilde{x}= \frac{P(x,y,\varepsilon ,\lambda ,h)}{R(x,\varepsilon ,h)}, \quad \tilde{y}= \frac{Q(x,y,\varepsilon ,\lambda ,h)}{R(x,\varepsilon ,h)}, \quad {\tilde{\varepsilon }}=\varepsilon , \quad {\tilde{\lambda }}=\lambda , \quad {\tilde{h}}=h,\nonumber \\ \end{aligned}$$

(3.21)

where

$$\begin{aligned} P(x,y,\varepsilon ,\lambda ,h)= & {} x - hy - \tfrac{h^2}{4} \varepsilon x + \tfrac{h^2}{2}\lambda \varepsilon , \end{aligned}$$

(3.22)

$$\begin{aligned} Q(x,y,\varepsilon ,\lambda ,h)= & {} y - hyx - \tfrac{h^2}{2} \varepsilon x^2 - h\lambda \varepsilon + h^2 x \lambda \varepsilon + h \varepsilon x - \tfrac{h^2}{4} \varepsilon y, \end{aligned}$$

(3.23)

$$\begin{aligned} R(x,\varepsilon ,h)= & {} 1- hx + \tfrac{h^2}{4} \varepsilon . \end{aligned}$$

(3.24)

Upon substitution $K_1$, we have:

$$\begin{aligned} P(x,y,\varepsilon ,\lambda ,h)= & {} r_1P_1(x_1,\varepsilon _1,\lambda _1,h_1), \end{aligned}$$

(3.25)

$$\begin{aligned} Q(x,y,\varepsilon ,\lambda ,h)= & {} r_1^2Q_1(x_1,\varepsilon _1,\lambda _1,h_1), \end{aligned}$$

(3.26)

$$\begin{aligned} R(x,\varepsilon ,h)= & {} R_1(x_1,\varepsilon _1,\lambda _1,h_1), \end{aligned}$$

(3.27)

where

$$\begin{aligned} P_1(x_1,\varepsilon _1,\lambda _1,h_1)= & {} x_1 - h_1 - \tfrac{h_1^2}{4} \varepsilon _1 x_1 + \tfrac{h_1^2}{2}\lambda _1 \varepsilon _1, \end{aligned}$$

(3.28)

$$\begin{aligned} Q_1(x_1,\varepsilon _1,\lambda _1,h_1)= & {} 1 - h_1x_1 - \tfrac{h_1^2}{2} \varepsilon _1 x_1^2 - h_1\lambda _1 \varepsilon _1 + h_1^2 x_1 \lambda _1 \varepsilon _1 + h_1 \varepsilon _1 x_1 - \tfrac{h_1^2}{4} \varepsilon _1, \end{aligned}$$

(3.29)

$$\begin{aligned} R_1(x_1,\varepsilon _1,h_1)= & {} 1- h_1x_1 + \tfrac{h_1^2}{4} \varepsilon _1. \end{aligned}$$

(3.30)

Setting

$$\begin{aligned}&Y_1(x_1,\varepsilon _1,\lambda _1,h_1)=\frac{Q_1(x_1,\varepsilon _1,\lambda _1,h_1)}{R_1(x_1,\varepsilon _1,h_1)}, \end{aligned}$$

(3.31)

$$\begin{aligned}&X_1(x_1,\varepsilon _1,\lambda _1,h_1)=\frac{P_1(x_1,\varepsilon _1,\lambda _1,h_1)}{Q_1(x_1,\varepsilon _1,\lambda _1,h_1)^{1/2}R_1(x_1,\varepsilon _1,h_1)^{1/2}}, \end{aligned}$$

(3.32)

we come to the following expression for the map (3.21) in the chart $K_1$:

$$\begin{aligned} \begin{array}{l} {\tilde{x}}_1 = X_1(x_1,\varepsilon _1,\lambda _1,h_1), \\ \tilde{r}_1 = r_1 (Y_1(x_1, \varepsilon _1, \lambda _1, h_1))^{1/2}, \\ {\tilde{\varepsilon }}_1 = \varepsilon _1 (Y_1(x_1, \varepsilon _1, \lambda _1, h_1))^{-1}, \\ {\tilde{\lambda }}_1 = \lambda _1 (Y_1(x_1, \varepsilon _1, \lambda _1, h_1))^{-1/2}, \\ \tilde{h}_1 = h_1 (Y_1(x_1, \varepsilon _1, \lambda _1, h_1))^{1/2}. \end{array} \end{aligned}$$

(3.33)

Now, it is straightforward to extend these results to the general case of the map (3.12) with arbitrary constants $a_i$. For this, we observe:

• In the first equation, the terms y and $x^2$ on the right-hand side scale as $r_1^2$ and $r_1^2x_1^2$, while the terms $\varepsilon x$ and xy scale as $r_1^3\varepsilon _1x_1$ and $r_1^3x_1$, respectively;

• In the second equation, the terms $\varepsilon x$ and $\varepsilon \lambda$ on the right-hand side scale as $r_1^3\varepsilon _1x_1$ and $r_1^3\varepsilon _1\lambda _1$, while the terms $\varepsilon y$ and $\varepsilon x^2$ scale as $r_1^4\varepsilon _1$ and $r_1^4\varepsilon _1x_1^2$, respectively.

Therefore, we can treat all terms involving $a_1, a_2, a_4, a_5$ as $\mathcal {O}( r_1)$. The resulting map is given by formulas analogous to (3.33), with $X_1(x_1,\varepsilon _1,\lambda _1,h_1)$, $Y_1(x_1,\varepsilon _1,\lambda _1,h_1)$ replaced by certain functions

$$\begin{aligned} X_1(x_1,\varepsilon _1,\lambda _1,h_1)+{\mathcal {O}}(r_1)\quad \mathrm{and} \quad Y_1(x_1,\varepsilon _1,\lambda _1,h_1)+{\mathcal {O}}(\varepsilon _1r_1). \end{aligned}$$

We now analyze the dynamics of this map.

• The subset $\{r_1 = 0, \;\varepsilon _1 = 0, \;\lambda _1 = 0\} \cap D_1$ is invariant, and on this subset, we have $Y_1(x_1,r_1,\varepsilon _1, \lambda _1, h_1) =1$, so that

  $$\begin{aligned} {\tilde{x}}_1 = \frac{x_1 - h_1}{1 - h_1 x_1}, \quad {\tilde{h}}_1 = h_1. \end{aligned}$$

  Hence, it contains two curves of fixed points

  $$\begin{aligned} p_{a,1}(h_1) = (-1,0,0,0, h_1) \quad \text {and} \ p_{r,1}(h_1) = (1,0,0,0, h_1). \end{aligned}$$

  We have:

  $$\begin{aligned} \left| \frac{\partial {\tilde{x}}_1}{\partial x_1} (p_{a,1}(h_1)) \right| = \left| \frac{1 - h_1}{1 + h_1} \right| <1, \quad \left| \frac{\partial {\tilde{x}}_1}{\partial x_1} (p_{r,1}(h_1)) \right| = \left| \frac{1 + h_1}{ 1 - h_1 } \right| >1 \end{aligned}$$

  for $h_1 \le \nu < 1$; hence, the point $p_{a,1}(h_1)$ is attracting in the $x_1$-direction and the point $p_{r,1}(h_1)$ is repelling in the $x_1$-direction. In all other directions, the multipliers of these fixed points are equal to 1.

• Similarly, we have on $\{\varepsilon _1 = 0, \lambda _1 = 0\} \cap D_1$ for small $r_1 > 0$:

  $$\begin{aligned} {\tilde{x}}_1 = \frac{x_1 - h_1}{1 - h_1 x_1} + \mathcal {O}(r_1), \quad {\tilde{h}}_1 = h_1, \quad {\tilde{r}}_1 = r_1. \end{aligned}$$

  By the implicit function theorem, we can conclude that on $\{\varepsilon _1 = 0, \; \lambda _1 = 0\} \cap D_1$, there exist two families of normally hyperbolic (for $h_1>0$) curves of fixed points denoted as $S_{a,1}(h_1)$ and $S_{r,1}(h_1)$, parameterized by $r_1\in [0,\rho ]$ and ending for $r_1 = 0$ at $p_{a,1}(h_1)$ and $p_{r,1}(h_1)$, respectively. For the map (3.21), corresponding to difference Eq. (3.20) (that is, to (3.12) with all $a_i=0$), the $\mathcal {O}(r_1)$-term vanishes, and the above families are simply given by

  $$\begin{aligned} S_{a,1}(h_1)= & {} \{(-1,r_1,0,0, h_1): 0 \le r_1 \le \rho \} \cap D_1, \\ S_{r,1}(h_1)= & {} \{(1,r_1,0,0, h_1) : 0 \le r_1 \le \rho \} \cap D_1. \end{aligned}$$

• On the invariant set $\{r_1 = 0, \lambda _1 = 0\} \cap D_1$, the dynamics of $x_1$, $\varepsilon _1$ and $h_1$ are given by

  $$\begin{aligned} \begin{array}{l} {\tilde{x}}_1 = X_1(x_1,\varepsilon _1,0,h_1), \\ {\tilde{\varepsilon }}_1 = \varepsilon _1 (Y_1(x_1, \varepsilon _1, 0, h_1))^{-1}, \\ {\tilde{h}}_1 = h_1 (Y_1(x_1, \varepsilon _1,0, h_1))^{1/2}. \end{array} \end{aligned}$$

  (3.34)

  We compute the Jacobi matrices of the map (3.34) at $p_{a,1}(h_1)$ and $p_{r,1}(h_1)$, restricting to the invariant set $\{r_1 = 0, \lambda _1 = 0\} \subset D_1$,

  $$\begin{aligned}&A_{a}:=\frac{\partial ({\tilde{x}}_1, {\tilde{\varepsilon }}_1, {\tilde{h}}_1)}{\partial (x_1, \varepsilon _1, h_1)} (p_{a,1}(h_1)) = \begin{pmatrix} \frac{1-h_1}{1 + h_1} &{} \frac{-h_1}{2(1+h_1)} &{} 0\\ 0 &{} 1 &{} 0 \\ 0 &{} - \frac{h_1^2}{2} &{} 1 \end{pmatrix}, \\&A_{r}:=\frac{\partial ({\tilde{x}}_1, {\tilde{\varepsilon }}_1, {\tilde{h}}_1)}{\partial (x_1, \varepsilon _1, h_1)} (p_{r,1}(h_1)) = \begin{pmatrix} \frac{1+h_1}{1 - h_1} &{} \frac{-h_1}{2(1-h_1)} &{} 0\\ 0 &{} 1 &{} 0 \\ 0 &{} \frac{h_1^2}{2} &{} 1 \end{pmatrix} \,. \end{aligned}$$

  The matrix $A_{a}$ has a two-dimensional invariant space corresponding to the eigenvalue 1, spanned by the vectors $v_{a}^{(1)}=(0,0,1)^\top$ and $v_{a}^{(2)} = (-1,4,0)^{\top }$, such that

  $$\begin{aligned} (A_a-I)v_{a}^{(1)}=0, \quad (A_a-I)v_{a}^{(2)}=-2h_1^2v_{a}^{(1)}. \end{aligned}$$

  Similarly, the matrix $A_{r}$ has a two-dimensional invariant space corresponding to the eigenvalue 1, spanned by the vectors $v_{r}^{(1)}=(0,0,1)^\top$ and $v_{r}^{(2)} = (1,4,0)^{\top }$, such that

  $$\begin{aligned} (A_r-I)v_{r}^{(1)}=0, \quad (A_r-I)v_{a}^{(2)}=-2h_1^2v_{r}^{(1)}. \end{aligned}$$

  It is instructive to compare this with the continuous-time case $h_1\rightarrow 0$ (see, e.g., Krupa and Szmolyan 2001a, Lemma 2.5), where both vectors $v_{a}^{(1)}$ and $v_{a}^{(2)}$ are eigenvectors of the corresponding linearized system, with $v_{a}^{(1)}$ being tangent to $S_{a,1}$ and $v_{a}^{(2)}$ corresponding to the center direction in the invariant plane $r_1=0$ (and similarly for $v_{r}^{(1)}$ and $v_{r}^{(2)}$).

We summarize these observations into the following statement.

Proposition 3.3

For system (3.33), there exist a center-stable manifold ${\widehat{M}}_{a,1}$ and a center-unstable manifold ${\widehat{M}}_{r,1}$, with the following properties:

• 1. For $i = a, r$, the manifold ${\widehat{M}}_{i,1}$ contains the curve of fixed points $S_{i,1}(h_1)$ on $\{\varepsilon _1 = 0, \ \lambda _1 = 0\} \subset D_1$, parameterized by $r_1$, and the center manifold $N_{i,1}$ whose branch for $\varepsilon _1, h_1 > 0$ is unique (see Fig. 3b). In $D_1$, the manifold ${\widehat{M}}_{i,1}$ is given as a graph $x_1 = {\hat{g}}_i (r_1, \varepsilon _1, \lambda _1,h_1)$.

• 2. For $i = a, r$, there exist two-dimensional invariant manifolds $M_{i,1}$ which are given as graphs $x_1 = g_i (r_1, \varepsilon _1)$.

Proof

The first part follows by standard center manifold theory (see, e.g., Hirsch et al. 1977). There exist two-dimensional center manifolds $N_{a,1}$ and $N_{r,1}$, parameterized by $h_1, \varepsilon _1$, which at $\varepsilon _1 =0$ coincide with the sets of fixed points

$$\begin{aligned} P_{a,1} = \{p_{a,1}(h_1)\,:\, 0 \le h_1 \le \nu \} \quad \text {and} \quad P_{r,1} = \{p_{r,1}(h_1)\,:\, 0 \le h_1 \le \nu \},\nonumber \\ \end{aligned}$$

(3.35)

respectively (see Fig. 3b). Note that, by (3.34), on $\{r_1 = 0, \ \lambda _1 = 0, \ h_1 > 0\} \cap D_1$ we have ${\tilde{\varepsilon }}_1 > \varepsilon _1$ and ${\tilde{h}}_1 < h_1$ for $x_1 \le 0$. Hence, for $\delta$ small enough, the branch of the manifold $N_{a,1}$ on $\{r_1 = 0, \varepsilon _1> 0, \lambda _1 = 0, h_1 > 0\} \cap D_1$ is unique. On the other hand, we observe that for $x_1\ge \frac{1}{K}$ with a constant $K> 1$, we have ${\tilde{\varepsilon }}_1 < \varepsilon _1$ and ${\tilde{h}}_1 > h_1$, if and only if $h_1 < \frac{2K}{1+K^2}$. Thus, for $x_1$ from a neighborhood of 1, we see that $\nu<\frac{2K}{1+K^2} < 1$ guarantees that, for $\delta$ small enough depending on K, the branch of the manifold $N_{r,1}$ on $\{r_1 = 0, \ \varepsilon _1> 0,\ \lambda _1 = 0, \ h_1 > 0\} \cap D_1$ is unique.

The second part follows from the invariances ${\tilde{r}}_1 {\tilde{\lambda }}_1 = r_1 \lambda _1$ and ${\tilde{h}}_1/{\tilde{r}}_1 = h_1 / r_1$, compare (Engel and Kuehn (2019), Proposition 3.3 and Figure 2) for details. $\square$

3.5 Dynamics in the Scaling Chart $K_2$

Next, we investigate the dynamics in the scaling chart $K_2$, in order to find a trajectory connecting ${\widehat{M}}_{a,1}$ with ${\widehat{M}}_{r,1}$, or $M_{a,1}$ with $M_{r,1}$, respectively. Recall from (3.14) that in chart $K_2$ we have

$$\begin{aligned} x = r_2 x_2, \quad y = r_2^2 y_2, \quad \varepsilon = r_2^2 , \quad \lambda = r_2 \lambda _2, \quad h = h_2/r_2\,. \end{aligned}$$

(3.36)

In this chart and upon the time rescaling $t=t_2/r_2$, Eq. (3.5) takes the form

$$\begin{aligned} \begin{array}{l} x'_2 = - y_2 + x_2^2 + r_2 (a_1 x_2 -a_2x_2y_2), \\ y'_2 = x_2 - \lambda _2 + r_2 (a_4x_2^2 + a_5y_2), \end{array} \end{aligned}$$

(3.37)

where the prime now denotes the derivative with respect to $t_2$, compare (A.4). Since in this chart $r_2=\sqrt{\varepsilon }$ is not a dynamical variable (remains fixed in time), we will not write down explicitly differential, resp. difference evolution equations for $\lambda _2=\lambda /\sqrt{\varepsilon }$ and for $h_2=h\sqrt{\varepsilon }$. We will restore these variables as we come to the matching with the chart $K_1$. The Kahan discretization of Eq. (3.37) with the time step $h_2$ can be written as

$$\begin{aligned} \begin{array}{l} {\tilde{x}}_2 = F_{1}(x_2, y_2, h_2) + r_2 {\hat{G}}_1(x_2, y_2, h_2) + \lambda _2 {\hat{J}}_1(x_2, h_2), \\ {\tilde{y}}_2 = F_{2}(x_2, y_2, h_2) + r_2 {\hat{G}}_2(x_2, y_2, h_2) + \lambda _2 {\hat{J}}_2(x_2, h_2),\end{array} \end{aligned}$$

(3.38)

On the blow-up manifold $r_2=0$, we are dealing with the simple model system

$$\begin{aligned} \frac{1}{h_2} ({\tilde{x}}_2 - x_2)= x_2{\tilde{x}}_2 - \frac{1}{2}(y_2 + {\tilde{y}}_2), \quad \frac{1}{h_2}({\tilde{y}}_2 - y_2) = \frac{1}{2}(x_2 +{\tilde{x}}_2) - \lambda _2. \end{aligned}$$

(3.39)

This yields the birational map

$$\begin{aligned} \begin{array}{l} {\tilde{x}}_2 = \dfrac{x_2 - h_2y_2 - \frac{h_2^2}{4} x_2 + \frac{h_2^2}{2}\lambda _2}{ 1- h_2x_2 + \frac{h_2^2}{4}} , \\ {\tilde{y}}_2 = \dfrac{y_2 + h_2 x_2- h_2 x_2 y_2- h_2 \lambda _2- \frac{h_2^2}{2} x_2^2 + h_2^2\lambda _2 x_2 - \frac{h_2^2}{4} y_2}{ 1- h_2x_2 + \frac{h_2^2}{4}} . \end{array} \end{aligned}$$

(3.40)

This gives the following expressions for the map $F =(F_1, F_2)$ and ${\hat{J}} =({\hat{J}}_1, {\hat{J}}_2)$ in (3.38):

$$\begin{aligned} \begin{array}{l} {\tilde{x}}_2 = F_1(x_2,y_2,h_2)= \dfrac{x_2 - h_2y_2 - \frac{h_2^2}{4} x_2}{ 1- h_2x_2 + \frac{h_2^2}{4}}, \\ {\tilde{y}}_2 = F_2(x_2,y_2,h_2)=\dfrac{y_2 + h_2 x_2- h_2x_2 y_2- \frac{h_2^2}{2} x_2^2 - \frac{h_2^2}{4} y_2}{ 1- h_2x_2 + \frac{h_2^2}{4}}, \end{array} \end{aligned}$$

(3.41)

and

$$\begin{aligned} \begin{array}{l} {\hat{J}}_1(x_2, h_2) = \dfrac{\frac{h_2^2}{2}}{1 - h_2 x_2 + \frac{h_2^2}{4}}, \\ {\hat{J}}_2(x_2, h_2) = \dfrac{-h_2+h_2^2 x_2}{1 - h_2 x_2 + \frac{h_2^2}{4}}. \end{array} \end{aligned}$$

(3.42)

Explicit expressions for the functions ${\hat{G}}_1$ and ${\hat{G}}_2$ can be easily obtained, as well, but are omitted here due to their length.

3.6 Dynamical Properties of the Model Map in the Scaling Chart

For a better readability, we omit index “2” referring to the chart $K_2$ starting from here. In particular, we write x, y, r, $\lambda$, h for $x_2$, $y_2$, $r_2$, $\lambda _2$, $h_2$ rather than for the original variables (before rescaling). Similarly to the continuous-time case, we start the analysis in $K_2$ with the case $\lambda =0$, $r = 0$ for $h > 0$ fixed. This means that we study the dynamics of the map given by F (3.41),

$$\begin{aligned} F: \quad \left\{ \begin{array}{l} {\tilde{x}} = \dfrac{x - hy - \frac{h^2}{4} x}{ 1- hx + \frac{h^2}{4}}, \\ {\tilde{y}} = \dfrac{y + h x- hxy - \frac{h^2}{2} x^2 - \frac{h^2}{4} y}{ 1- hx + \frac{h^2}{4}}, \end{array} \right. \end{aligned}$$

(3.43)

which comes as the solution of the difference equation

$$\begin{aligned} \frac{1}{h} ({\tilde{x}} - x)= x{\tilde{x}} - \frac{1}{2}(y+ {\tilde{y}}), \quad \frac{1}{h}({\tilde{y}} - y) = \frac{1}{2}(x +{\tilde{x}}). \end{aligned}$$

(3.44)

We discuss in detail the most important properties of the model map (3.43).

3.6.1 Formal Integral of Motion

Recall that, for $r = \lambda = 0$, the ODE system (A.6) in the chart $K_2$ has a conserved quantity (A.7). Its level set $H(x,y)=0$ supports the special canard solution (A.11),

$$\begin{aligned} \gamma _{0,2}(t_2) = \Big (\frac{1}{2} t_2, \frac{1}{4} t_2^2 - \frac{1}{2}\Big )^\top . \end{aligned}$$

In general, Kahan discretization has a distinguished property of possessing a conserved quantity for unusually numerous instances of quadratic vector fields. For (A.6), it turns out to possess a formal conserved quantity in the form of an asymptotic power series in h. However, there are indications that this power series is divergent, so that map F (3.43) does not possess a true integral of motion. Nevertheless, it possesses all nice properties of symplectic or Poisson integrators; in particular, a truncated formal integral is very well preserved on very long intervals of time. Moreover, as we will now demonstrate, the zero level set of the formal conserved quantity supports the special family of solutions of the discrete-time system crucial for our main results.

We recall a method for constructing a formal conserved quantity

$$\begin{aligned} {\bar{H}}( z, h) = H(z) + h^2 H_2(z) + h^4 H_4(z) + h^6 H_6(z) + \cdots \end{aligned}$$

(3.45)

for the Kahan discretization $F_f$ (3.3) for an ODE of the form (3.1) admitting a smooth conserved quantity $H: \mathbb {R}^n \rightarrow \mathbb {R}$. The latter means that

$$\begin{aligned} \sum _{i=1}^n \frac{\partial H(z)}{\partial z_i} f_i(z) = 0. \end{aligned}$$

(3.46)

The ansatz (3.45) containing only even powers of h is justified by the fact that the Kahan method is a symmetric linear discretization scheme. Writing ${\tilde{z}} =F_f(z,h)$, we formulate our requirement of ${\bar{H}}$ being an integral of motion for $F_f$ as ${\bar{H}}(z,h)={\bar{H}}( {\tilde{z}}, h)$ on $\mathbb {R}^n \times [0,h_0]$, i.e., up to terms $\mathcal {O}(h^4)$,

$$\begin{aligned} H({\tilde{z}}) + h^2 H_2({\tilde{z}}) = H(z) + h^2 H_2(z) + \mathcal {O}(h^4). \end{aligned}$$

(3.47)

To compute the Taylor expansion of the left-hand side, we observe:

$$\begin{aligned} H({\tilde{z}})&= H\left( z + h f(z) + \frac{h^2}{2} f(z)\mathrm {D}f(z) + \mathcal {O}(h^3)\right) \\&= H(z) + h \sum _{i=1}^n \frac{\partial H(z)}{\partial z_i} f_i(z) \\&\qquad + \frac{h^2}{2} \left( \sum _{i,j=1}^n \frac{\partial ^2 H(z)}{\partial z_i \partial z_j} f_i(z) f_j(z) + \sum _{i,j=1}^n \frac{\partial H(z)}{\partial z_i} \frac{\partial f_i(z)}{\partial z_j} f_j(z) \right) + \mathcal {O}(h^3). \end{aligned}$$

Here, the h and the $h^2$ terms vanish, as follows from (3.46) and its Lie derivative:

$$\begin{aligned} 0= & {} \sum _{j=1}^n \frac{\partial }{\partial z_j}\left( \sum _{i=1}^n \frac{\partial H(z)}{\partial z_i} f_i(z)\right) f_j(z) = \sum _{i,j=1}^n \frac{\partial ^2 H(z)}{\partial z_i \partial z_j} f_i(z) f_j(z)\nonumber \\&+ \sum _{i,j=1}^n \frac{\partial H(z)}{\partial z_i} \frac{\partial f_i(z)}{\partial z_j} f_j(z). \end{aligned}$$

(3.48)

Thus, we find: $H({\tilde{z}}) = H(z) + \mathcal {O}(h^3)$, or, more precisely,

$$\begin{aligned} H({\tilde{z}}) = H(z) + h^3 G_3(z) + h^4 G_4(z) + h^5 G_5(z) + \cdots . \end{aligned}$$

(3.49)

Plugging this, as well as a Taylor expansion of $H_2({\tilde{z}})$ similar to $H({\tilde{z}})$, into (3.47), we see that vanishing of the $h^3$ terms is equivalent to

$$\begin{aligned} \sum _{i=1}^n\frac{\partial H_2(z)}{\partial z_i} f_i(z) = -G_3(z). \end{aligned}$$

(3.50)

This is a linear PDE defining $H_2$ up to an additive term which is an arbitrary function of H.

The following terms $H_4, H_6, \ldots$ can be determined in a similar manner, from linear PDEs like (3.50) with recursively determined functions on the right-hand side.

We now apply this scheme to obtain (the first terms of) the formal conserved quantity ${\bar{H}}(x,y,h)$ for (3.41). It turns out to be possible to find it in the form

$$\begin{aligned} {\bar{H}}(x,y, h) \approx H(x,y) + \sum _{k=1}^\infty h^{2k} H_{2k}(x,y), \end{aligned}$$

(3.51)

where

$$\begin{aligned} H(x, y) = e^{-2 y} \big ( y - x^2 + \frac{1}{2} \big )\quad \mathrm{and} \quad H_{2k}(x,y)=e^{-2y}{\bar{H}}_{2k}(x,y), \end{aligned}$$

(3.52)

with ${\bar{H}}_{2k}(x,y)$ being polynomials of degree $2k+2$. The symbol $\approx$ reminds that this is only a formal asymptotic series which does not converge to a smooth conserved quantity. A Taylor expansion of $H({\tilde{x}}, {\tilde{y}})$ as in (3.49) gives

$$\begin{aligned} H({\tilde{x}}, {\tilde{y}}) = H( x, y) + h^3 G_3(x,y) + \mathcal {O}(h^4), \end{aligned}$$

with

$$\begin{aligned} G_3(x,y) = \frac{1}{3} e^{-2 y} (x^3 + x^5 - 4 x^3 y + 3 xy^2). \end{aligned}$$

The differential Eq. (3.50) reads in the present case:

$$\begin{aligned} (x^2 - y)\frac{\partial }{\partial x}\big (e^{-2 y} {\bar{H}}_2(x,y)\big ) + x\frac{\partial }{\partial y} \big (e^{-2 y} {\bar{H}}_2(x,y)\big )=-G_3(x,y). \end{aligned}$$

(3.53)

A solution for ${\bar{H}}_2$ which is a polynomial of degree 4 reads:

$$\begin{aligned} {\bar{H}}_2(x,y) = \frac{1}{3} \big (x^2-\frac{x^4}{2} + (y- x^2)(y -y^2)\big ). \end{aligned}$$

(3.54)

Hence, we obtain the approximation

$$\begin{aligned} {\bar{H}}(x,y, h) =e^{-2 y} \big ( y - x^2 + \frac{1}{2} \big ) + \frac{h^2}{3} e^{-2y} \big (x^2-\frac{x^4}{2} + (y- x^2)(y -y^2)\big ) + \mathcal {O}(h^4).\nonumber \\ \end{aligned}$$

(3.55)

A straightforward computation shows that on the curve $y-x^2+\frac{1}{2}=0$ (the level set $H(x,y)=0$), the function ${\bar{H}}_2(x,y)$ takes a constant value $\frac{1}{8}$. Therefore, the level set ${\bar{H}}(x,y,h)=0$ is given, up to $\mathcal {O}(h^4)$, by

$$\begin{aligned} \varphi _{h}(x,y)=y - x^2 + \frac{1}{2}+\frac{h^2}{8} =0. \end{aligned}$$

(3.56)

Remarkably, we have the following statement.

Proposition 3.4

The curve (3.56) represents a zero level set of the (divergent) formal integral ${\bar{H}}(x,y,h)$. More precisely, on this curve

$$\begin{aligned} H(x,y)+\sum _{k=1}^n h^{2k} H_{2k}(x,y)={\mathcal {O}}(h^{2n+2}). \end{aligned}$$

We will not prove this statement, but rather derive a different dynamical characterization of the curve (3.56).

3.6.2 Invariant Measure

Proposition 3.5

The map F given by (3.43) admits an invariant measure

$$\begin{aligned} \mu _{h} = \frac{\mathrm {d}x \wedge \mathrm {d}y}{|\varphi _{h}(x,y)|} \end{aligned}$$

(3.57)

with $\varphi _{h}(x,y)$ given in (3.56). This measure $\mu _h$ is singular on the curve $\varphi _h(x,y)=0$.

Proof

Difference Eqs. (3.44) can be written as a linear system for $({\tilde{x}},{\tilde{y}})$:

$$\begin{aligned} \begin{pmatrix} 1 - h x &{} \frac{h}{2} \\ -\frac{h}{2} &{} 1 \end{pmatrix} \begin{pmatrix} {\tilde{x}} \\ {\tilde{y}} \end{pmatrix} = \begin{pmatrix} x - \frac{h}{2}y \\ y + \frac{h}{2}x \end{pmatrix}. \end{aligned}$$

Differentiating with respect to x, y, we obtain:

$$\begin{aligned} \begin{pmatrix} 1 - h x &{} \frac{h}{2} \\ -\frac{h}{2} &{} 1 \end{pmatrix} \begin{pmatrix} \frac{\partial {\tilde{x}}}{\partial x} &{} \frac{\partial {\tilde{x}}}{\partial y} \\ \frac{\partial {\tilde{y}}}{\partial x} &{} \frac{\partial {\tilde{y}}}{\partial y} \end{pmatrix} = \begin{pmatrix} 1 + h {\tilde{x}} &{} - \frac{h}{2} \\ \frac{h}{2} &{} 1 \end{pmatrix}. \end{aligned}$$

Computing determinants, we find:

$$\begin{aligned} \det \frac{\partial ({\tilde{x}}, {\tilde{y}})}{\partial (x,y)} = \frac{1 + h {\tilde{x}} + \frac{h^2}{4}}{1 - h x + \frac{h^2}{4}}. \end{aligned}$$

(3.58)

Next, we derive from the first equation in (3.43):

$$\begin{aligned} {\tilde{x}}-x=\frac{-hy+hx^2-\frac{h^2}{2}x}{1-hx+\frac{h^2}{4}}. \end{aligned}$$

Since the system (3.44) is symmetric with respect to interchanging $(x,y)\leftrightarrow ({\tilde{x}}, {\tilde{y}})$ with the simultaneous change $h\mapsto -h$, we can perform this operation in the latter equation, resulting in

$$\begin{aligned} x-{\tilde{x}}=\frac{h{\tilde{y}}-h{\tilde{x}}^2-\frac{h^2}{2}{\tilde{x}}}{1+h{\tilde{x}}+\frac{h^2}{4}}. \end{aligned}$$

Comparing the last two formulas, we obtain:

$$\begin{aligned} \frac{y-x^2+\frac{h}{2}x}{1-hx+\frac{h^2}{4}}=\frac{{\tilde{y}}-{\tilde{x}}^2-\frac{h}{2}{\tilde{x}}}{1+h{\tilde{x}}+\frac{h^2}{4}}, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{y-x^2+\frac{1}{2}+\frac{h^2}{4}}{1-hx+\frac{h^2}{4}}=\frac{{\tilde{y}}-{\tilde{x}}^2+\frac{1}{2}+\frac{h^2}{4}}{1+h{\tilde{x}}+\frac{h^2}{4}}. \end{aligned}$$

(3.59)

Together with (3.58), this results in

$$\begin{aligned} \det \frac{\partial ({\tilde{x}}, {\tilde{y}})}{\partial (x,y)} = \frac{\varphi _{h}({\tilde{x}}, {\tilde{y}})}{\varphi _{h}(x,y)}, \end{aligned}$$

(3.60)

which is equivalent to the statement of proposition. $\square$

3.6.3 Invariant Separating Curve

It turns out that the singular curve of the invariant measure $\mu _h$ is an invariant curve under the map (3.43).

Proposition 3.6

The parabola

$$\begin{aligned} S_{h} : = \left\{ (x,y) \in \mathbb {R}^2 \, : \, y = x^2 - \frac{1}{2} - \frac{h^2}{8} \right\} \end{aligned}$$

(3.61)

is invariant under the map F given by (3.43). Solutions on $S_{h}$ are given by

$$\begin{aligned} \gamma _{h, x_0}(n) = \left( \begin{array}{llll} x_0+ \dfrac{hn}{2} \\ x_0^2+hnx_0+ \dfrac{h^2n^2}{4} - \dfrac{1}{2} - \dfrac{h^2}{8} \end{array}\right) , \quad n \in \mathbb {Z}. \end{aligned}$$

(3.62)

For $(x,y)\in S_h$, we have:

$$\begin{aligned} \left| \frac{\partial {\tilde{x}}}{\partial x}\right| \quad \left\{ \begin{array}{ll}< 1 &{} \mathrm {for\;\;} x < 0, \\ =1 &{} \mathrm { for \;\;}x=0,\\>1 &{} \mathrm {for\;\;} x>0. \end{array}\right. \end{aligned}$$

(3.63)

Proof

Plugging $y= x^2 - \frac{1}{2} - \frac{h^2}{8}$ into formulas (3.43), we obtain upon a straightforward computation:

$$\begin{aligned} {\tilde{x}}=x+\frac{h}{2}, \quad {\tilde{y}}= \Big (x+\frac{h}{2}\Big )^2-\frac{1}{2}-\frac{h^2}{8}. \end{aligned}$$

This proves the first two claims.

As for the last claim, we compute by differentiating the first equation in (3.43):

$$\begin{aligned} \frac{\partial {\tilde{x}}}{\partial x} = \frac{1-h^2y - \frac{h^4}{16}}{\left( 1-hx+\frac{h^2}{4} \right) ^2}. \end{aligned}$$

(3.64)

For $(x,y)\in S_h$, this gives:

$$\begin{aligned} \frac{\partial {\tilde{x}}}{\partial x} = \dfrac{\left( 1+\frac{h^2}{4} \right) ^2- h^2 x^2 }{ \left( 1-hx+\frac{h^2}{4} \right) ^2} = \dfrac{1+hx + \frac{h^2}{4}}{1- hx +\frac{h^2}{4}}, \end{aligned}$$

which implies inequalities (3.63). (We remark that the right-hand side tends to infinity as $x\rightarrow (1+\frac{h^2}{4})/h$.) $\square$

The invariant set $S_h$ (3.61) plays the role of a separatrix for F (3.41): Bounded orbits of F lie above $S_h$, while unbounded orbits of F lie below $S_h$, as illustrated in Figs. 1, 2.

Fig. 1

Trajectories for the Kahan map F in chart $K_2$ (3.41) with $h = 0.01$ for different initial points $(x_{2,0},y_{2,0})$ (black dots): three bounded orbits above the separatrix $S_{h}$ and three unbounded orbits below the separatrix $S_h$

Fig. 2

Approximation of ${\bar{H}}$ along the corresponding trajectories $\gamma _1, \gamma _3, \gamma _4$ from Fig. 1, showing the levels of ${\bar{H}}\simeq H+h^2H_2$ (a) which are then compared with H for $\gamma _1$ (b), $\gamma _3$ (c) and $\gamma _4$ (d)

We can show the following connection to the chart $K_1$:

Lemma 3.7

The trajectory $\gamma _{h}(n)$, transformed into the chart $K_1$ via

$$\begin{aligned} \gamma _{h}^1(n) = \kappa _{21} (\gamma _{h}(n), h) \end{aligned}$$

for large $\left| n \right|$, lies in ${\widehat{M}}_{a,1}$ as well as in ${\widehat{M}}_{r,1}$.

Proof

From (3.16), there follows that for sufficiently large $\left| n\right|$, the component $\varepsilon _1(n)$ of $\gamma _{h}^1(n)$ is sufficiently small such that $\gamma _{h}^1$, which lies on the invariant manifold $\kappa _{21}(S_{h},h)$, has to be in $N_{a,1}$ for $n <0$, and in $N_{r,1}$ for $n > 0$, respectively, due to the uniqueness of the invariant center manifolds (see Proposition 3.3). In particular, observe that if h is small enough, $\gamma _{h}^1$ reaches an arbitrarily close vicinity of some $p_{a,1}(h_1^*)$ for sufficiently large $n <0$ and of some $p_{r,1}(h_1^*)$ for sufficiently large $n >0$, within $N_{a,1} \subset {\widehat{M}}_{a,1}$ and $N_{r,1} \subset {\widehat{M}}_{r,1}$, respectively (see also Fig. 3b). This finishes the proof. $\square$

The trajectory $\gamma _{h}$ is shown in global blow-up coordinates as $\gamma _{{\bar{h}}}$ in Fig. 3a, in comparison with the ODE trajectory ${\bar{\gamma }}_0$ corresponding to $\gamma _{0, 2}$ in $K_2$.

Fig. 3

The trajectory $\gamma _{{\bar{h}}}$ in global blow-up coordinates for $r = \bar{\lambda } = 0$ and a fixed ${\bar{h}} > 0$ (a), and as $\gamma _{h}^1$ in $K_1$ for $r_1=\lambda _1 = 0$ (b). The figures also show the special ODE solution ${\bar{\gamma }}_0$ connecting ${\bar{p}}_{r}({\bar{h}})$ and ${\bar{p}}_{a}({\bar{h}})$ (a), and $\gamma _{0,1}$ connecting $p_{r,1}(h_1^*)$ and $p_{a,1}(h_1^*)$ for fixed $h_1^* > 0$ (b), respectively. In (a), the fixed points ${\bar{q}}^{\text {in}}({\bar{h}})$ and ${\bar{q}}^{\text {out}}({\bar{h}})$, for ${\bar{\varepsilon }} = 0$, are added, whose existence can be seen in an extra chart (similarly to Krupa and Szmolyan (2001a)). In (b), the trajectory $\gamma _{h}^1$ is shown on the attracting center manifold $N_{a,1} \subset {\widehat{M}}_{a,1}$ and on the repelling center manifold $N_{r,1} \subset {\widehat{M}}_{r,1}$ (see Sect. 3.4 and Lemma 3.7)

3.7 Melnikov Computation Along the Invariant Curve

We consider a Melnikov-type computation for the distance between invariant manifolds, which is a discrete-time analogue of continuous time results in Krupa and Szmolyan (2001b) and, for a more general framework, in Wechselberger (2002).

Consider an invertible map depending on a parameter $\mu$:

$$\begin{aligned} \begin{array}{l} {\tilde{x}} = F_1(x,y) + \mu G_1(x,y,\mu ),\\ {\tilde{y}} = F_2(x,y) + \mu G_2(x,y,\mu ),\\ {\tilde{\mu }} = \mu , \end{array} \end{aligned}$$

(3.65)

where $(x,y) \in \mathbb {R}^2$, and $F=(F_1,F_2)^{\top }$ , $G=(G_1,G_2)^{\top }$ are $C^k$, vector-valued maps, $k\ge 1$. The following theory can be easily extended to $\mu \in \mathbb {R}^m$, like in Wechselberger (2002), but for reasons of clarity we formulate it for $\mu \in \mathbb {R}$.

We formulate the following Assumptions:

• (A1) There exist invariant center manifolds $M_\pm$ of the dynamical system (3.65), given as graphs of $C^k$-functions $y = g_\pm (x, \mu )$ and intersecting at $\mu = 0$ along the smooth curve

  $$\begin{aligned} S=\{(x,y)\in \mathbb {R}^2:y=g(x,0)\}, \end{aligned}$$

  where $g_\pm (x,0)=g(x,0)$.

• (A2) Orbits of the map (3.65) with $\mu =0$ passing through a point $(x_0,g(x_0,0))$ on the invariant curve are given by a one-parameter family of solutions $(\gamma _{x_0}(n),0)^\top$ of dynamical system (3.65) with $\mu =0$, such that $\gamma _{x_0}(n)$ and $G(\gamma _{x_0}(n),0)$ are of a moderate growth when $n\rightarrow \pm \infty$ (to be specified later).

• (A3) There exist solutions $\phi _\pm (n)=(w_{\pm }(n),1)^\top$ of the linearization of (3.65) along $(\gamma _{x_0}(n),0)^\top$,

  $$\begin{aligned} \phi (n+1) = \begin{pmatrix} \mathrm {D}F(\gamma _{x_0}(n)) &{} G(\gamma _{x_0}(n),0) \\ 0 &{} 1 \end{pmatrix} \phi (n), \end{aligned}$$

  (3.66)

  such that

  $$\begin{aligned} T_{(\gamma _{x_0}(n),0)^\top } M_\pm = {{\,\mathrm{span}\,}}\left\{ \begin{pmatrix}\partial _{x_0} \gamma _{x_0}(n) \\ 0\end{pmatrix}, \begin{pmatrix} w_\pm (n)\\ 1\end{pmatrix} \right\} , \end{aligned}$$

  and $w_\pm (n)$ are of a moderate growth (to be specified later) when $n \rightarrow \pm \infty$, respectively.

• (A4) The solutions $\psi _{x_0}(n)$ of the adjoint difference equation

  $$\begin{aligned} \psi (n+1) = \left( \mathrm {D}F(\gamma _{x_0}(n))^{\top }\right) ^{-1} \psi (n) \end{aligned}$$

  (3.67)

  with initial vectors $\psi _{x_0}$ satisfying $\langle \psi _{x_0}(0),\partial _{x_0}\gamma _{x_0}(0)\rangle = 0$ rapidly decay at $\pm \infty$ (the rate of decay to be specified later).

For a given $x_0$, we define $\psi _{x_0}(0)$ to be a unit vector in ${\mathbb {R}}^2$ orthogonal to $\partial _{x_0}\gamma _{x_0}(0)$, and set

$$\begin{aligned} \Sigma = \{(x,y, \mu ): (x,y) \in {{\,\mathrm{span}\,}}\{\psi _{x_0}(0)\},\; \mu \in {\mathbb {R}} \}; \end{aligned}$$

the intersections $M_{\pm } \cap \Sigma$ are then given by $(\Delta _{\pm }(\mu ) \psi _{x_0}(0), \mu )$, where $\Delta _{\pm }$ are $C^k$-functions.

The following proposition is a discrete-time analogue of (Krupa and Szmolyan 2001b, Proposition 3.1).

Proposition 3.8

The first-order separation between $M_+$ and $M_-$ at the section $\Sigma$ is given by

$$\begin{aligned} d_{\mu } = -\sum _{n=-\infty }^{\infty } \langle \psi _{x_0}(n+1), G(\gamma _{x_0}(n),0) \rangle . \end{aligned}$$

(3.68)

Proof

Equations (3.66) and (3.67) read:

$$\begin{aligned} \psi _{x_0}(n+1)&= \left( \mathrm {D}F(\gamma _{x_0}(n))^{\top }\right) ^{-1} \psi _{x_0}(n),\\ w_+(n+1)&= \mathrm {D}F(\gamma _{x_0}(n)) w_+(n) + G(\gamma _{x_0}(n) ,0), \\ w_-(n+1)&= \mathrm {D}F(\gamma _{x_0}(n)) w_-(n) + G(\gamma _{x_0}(n) ,0). \end{aligned}$$

There follows:

$$\begin{aligned}&\langle \psi _{x_0}(n+1), w_\pm (n+1) \rangle - \langle \psi _{x_0}(n), w_\pm (n) \rangle \\&\quad = \left\langle \left( \mathrm {D}F(\gamma _{x_0}(n))^{-1}\right) ^{\top } \psi _{x_0}(n), \mathrm {D}F(\gamma _{x_0}(n)) w_\pm (n) + G(\gamma _{x_0}(n) ,0) \right\rangle \\&\qquad - \langle \psi _{x_0}(n), w_\pm (n) \rangle \\&\quad = \langle \psi _{x_0}(n+1), G(\gamma _{x_0}(n),0) \rangle \,. \end{aligned}$$

Choose initial data $w_\pm (0)=\frac{\mathrm {d}\Delta _\pm }{\mathrm {d}\mu }(0)\psi _{x_0}(0)$. Assuming that the growth of $w_\pm (n)$ and the decay of $\psi _{x_0}(n)$ at $n\rightarrow \pm \infty$, mentioned in (A3) and (A4), are such that

$$\begin{aligned} \lim _{n\rightarrow -\infty } \langle \psi _{x_0}(n), w_-(n) \rangle =0, \quad \lim _{n\rightarrow +\infty } \langle \psi _{x_0}(n), w_+(n) \rangle =0, \end{aligned}$$

we derive:

$$\begin{aligned} \frac{\mathrm {d}\Delta _-}{\mathrm {d}\mu } (0) = \langle \psi _{x_0}(0), w_-(0)\rangle = \sum _{n=-\infty }^{-1} \langle \psi _{x_0}(n+1), G(\gamma _{x_0}(n),0) \rangle , \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm {d}\Delta _+}{\mathrm {d}\mu } (0) = \langle \psi _{x_0}(0), w_+(0)\rangle = - \sum _{n=0}^{\infty } \langle \psi _{x_0}(n+1), G(\gamma _{x_0}(n),0) \rangle . \end{aligned}$$

From this formula (3.68), it follows immediately. $\square$

We now apply Proposition 3.8 (or, better to say, its generalization for the case of two parameters $\mu =(r_2,\lambda _2)$) to the Kahan map (3.38) in the rescaling chart $K_2$. First of all, we have to justify Assumptions (A1)–(A4) for this case. Assumption (A1) follows from the fact that for $\mu =(r,\lambda )=0$, the center manifolds ${\widehat{M}}_{a,2}$ and ${\widehat{M}}_{r,2}$ intersect along the curve $S_h$ given in (3.61). Assumption (A2) follows from the explicit formula (3.62) for the solution $\gamma _{h,x_0}$, as well as from formulas (3.42) for the functions ${\hat{J}}$ and similar formulas for the functions ${\hat{G}}$. Assumption (A3) follows from the existence of the center manifolds away from $\mu =(r,\lambda )=0$, established in Proposition 3.3. Turning to the Assumption (A4), we have the following results.

Proposition 3.9

For problem (3.38), the adjoint linear system (3.67),

$$\begin{aligned} \psi (n+1) = \left( \mathrm {D}F(\gamma _{h,x_0}(n), h)^{\top }\right) ^{-1} \psi (n), \end{aligned}$$

(3.69)

has the decaying solution

$$\begin{aligned} \psi _{h, x_0}(n) = \frac{1}{X(n)} \begin{pmatrix} -2x_0 - hn \\ 1 \end{pmatrix}, \ n \in \mathbb {Z}, \end{aligned}$$

(3.70)

where

$$\begin{aligned} X(n) = \prod _{k=0}^{n-1} a(k), \quad X(-n) = \prod _{k=1}^n (a(-k))^{-1} \;\;\mathrm{for}\;\; n>0, \end{aligned}$$

(3.71)

and

$$\begin{aligned} a(k) = \frac{1 + h\left( x_0 + \frac{h}{2}(k+1)\right) + \frac{h^2}{4}}{1 - h\left( x_0 + \frac{h}{2}k\right) + \frac{h^2}{4}}. \end{aligned}$$

(3.72)

We have:

$$\begin{aligned} \left| X(n)\right| \approx |n|^{4/h^2 + 2}, \ \text { as } n \rightarrow \pm \infty . \end{aligned}$$

(3.73)

Here, the symbol $\approx$ relates quantities whose quotient has a limit as $n\rightarrow \pm \infty$.

Proof

Fix $x_0 \in \mathbb {R}$, and set

$$\begin{aligned} A(n)= \mathrm {D}F(\gamma _{h, x_0}(n), h). \end{aligned}$$

Let

$$\begin{aligned} \Phi (n) = \begin{pmatrix} \phi _{1,1}(n) &{} \phi _{1,2}(n) \\ \phi _{2,1}(n) &{} \phi _{2,2}(n) \end{pmatrix} \end{aligned}$$

be a fundamental matrix solution of the linear difference equation

$$\begin{aligned} \phi (n+1) = A(n) \phi (n) \end{aligned}$$

with $\det \Phi (0)=1$. The first column of the fundamental matrix solution $\Phi (n)$ can be found as $\partial _{x_0} \gamma _{h,x_0}$. Using formula (3.62) for $\gamma _{h, x_0}$, we have:

$$\begin{aligned} \begin{pmatrix} \phi _{1,1}(n) \\ \phi _{2,1}(n) \end{pmatrix} = \begin{pmatrix} 1 \\ 2x_0 + hn \end{pmatrix}. \end{aligned}$$

A fundamental solution of the adjoint difference equation

$$\begin{aligned} \psi (n+1) =( A^\top (n))^{-1} \psi (n) \end{aligned}$$

is given by

$$\begin{aligned} \Psi (n) = (\Phi ^{\top }(n))^{-1} = \frac{1}{\det \Phi (n)} \begin{pmatrix} \phi _{2,2}(n) &{} -\phi _{2,1}(n) \\ -\phi _{1,2}(n) &{} \phi _{1,1}(n) \end{pmatrix}. \end{aligned}$$

Its second column is a solution of the adjoint system as given in (3.70), with $X(n)=\det \Phi (n)$. To compute X(n), we observe that from

$$\begin{aligned} \Phi (n)= & {} A(n-1)A(n-2)\ldots A(0)\Phi (0) \quad \mathrm{for} \quad n>0,\\ \Phi (0)= & {} A(-1)A(-2)\ldots A(-n)\Phi (-n) \quad \mathrm{for} \quad n>0, \end{aligned}$$

and from $\det \Phi (0)=1$, there follows a discrete analogue of Liouville’s formula: for $n>0$,

$$\begin{aligned} \det \Phi (n) = \prod _{k=0}^{n-1} \det A(k), \quad \det \Phi (-n) = \prod _{k=1}^{n}(\det A(-k))^{-1}, \end{aligned}$$

which coincides with (3.71) with $a(k)=\det A(k)$. Expression (3.72) for these quantities follows from (3.58).

To prove the estimate (3.73), we observe:

$$\begin{aligned} a(k) = - \frac{k + \beta }{k - \alpha }\quad \mathrm{with} \quad \alpha = \frac{2}{h^2} \left( 1 - hx_0 + \frac{h^2}{4}\right) , \quad \beta = \frac{2}{h^2} \left( 1 + hx_0 + \frac{3 h^2}{4} \right) . \end{aligned}$$

Therefore, for $n>0$,

$$\begin{aligned} X(n)= & {} (-1)^n\prod _{k=0}^{n-1} \frac{k+\beta }{k-\alpha } = (-1)^n\ \frac{\Gamma (n+\beta )}{\Gamma (n-\alpha )}\ \frac{\Gamma (-\alpha )}{\Gamma (\beta )},\\ X(-n)= & {} (-1)^n\prod _{k=1}^{n} \frac{k+\alpha }{k-\beta } =(-1)^n\ \frac{\Gamma (n+\alpha )}{\Gamma (n-\beta )}\ \frac{\Gamma (-\beta )}{\Gamma (\alpha )}. \end{aligned}$$

Using the formula $\Gamma (n+c)\sim n^c \Gamma (n)$ by $n\rightarrow +\infty$ (in the sense that the quotient of the both expressions tends to 1), we obtain for $n\rightarrow +\infty$:

$$\begin{aligned} |X(n)|, \, |X(-n)| \approx n^{\alpha +\beta }= n^{4/h^2 +2}. \end{aligned}$$

(3.74)

This completes the proof. $\square$

With the help of estimates of Proposition 3.9, we derive from Proposition 3.8 the following statement:

Proposition 3.10

For the separation of the center manifolds ${\widehat{M}}_{a,2}$ and ${\widehat{M}}_{r,2}$, and for sufficiently small h, we have the first-order expansion

$$\begin{aligned} D_{h,x_0}(r, \lambda ) = d_{h,x_0,\lambda } \lambda + d_{h,x_0,r}r + \mathcal {O}(2), \end{aligned}$$

(3.75)

where $\mathcal {O}(2)$ denotes terms of order $\ge 2$ with respect to $\lambda ,r$, and

$$\begin{aligned}&d_{h,x_0,\lambda }=-\sum _{n=-\infty }^{\infty } \langle \psi _{h,x_0}(n+1), {\hat{J}}(\gamma _{h,x_0}(n),h) \rangle , \end{aligned}$$

(3.76)

$$\begin{aligned}&d_{h,x_0,r}=-\sum _{n=-\infty }^{\infty } \langle \psi _{h,x_0}(n+1), {\hat{G}}(\gamma _{h,x_0}(n),h) \rangle . \end{aligned}$$

(3.77)

In particular, convergence of the series in Eq. (3.76) is obtained for any $h>0$ and convergence of the series in equation (3.77) is obtained for $0< h < \sqrt{4/3}$.

Proof

The form of the first-order separation follows from Proposition 3.8. Furthermore, recall from equation (3.42) that

$$\begin{aligned} {\hat{J}}(\gamma _h(n),h) = \left( \frac{h^2}{2} \frac{1}{1-\frac{h^2 n}{2}+\frac{h^2}{4}}, - h \frac{1-\frac{h^2 n}{2}}{1-\frac{h^2 n}{2} + \frac{h^2}{4}}\right) \xrightarrow {n \rightarrow \pm \infty } (0, -h). \end{aligned}$$

Using Proposition 3.9, this yields (3.76) for any $h > 0$. Note from Eq. (3.5) that the highest order $n^{\kappa }$ we can obtain in the terms ${\hat{G}}(\gamma _{h}(n),h)$ is $\kappa = 3$ (coming from the term with factor $a_2$) such that for large $\left| n\right|$ we have

$$\begin{aligned} \langle \psi _{h}(n+1), {\hat{G}}(\gamma _{h}(n),h) \rangle = \mathcal {O}\left( n^{-4/h^2-2}n n^3 \right) = \mathcal {O}\left( n^{-4/h^2+2}\right) . \end{aligned}$$

This means that the convergence in (3.77) is given for $-4/h^2+2 < -1$ such that the claim follows. $\square$

We are now prepared to show our main result.

Theorem 1.13 Consider the Kahan discretization for system (3.5). Then, there exist $\varepsilon _0, h_0 > 0$ and a smooth function $\lambda _c^h(\sqrt{\varepsilon })$ defined on $[0, \varepsilon _0]$ such that for $\varepsilon \in [0, \varepsilon _0]$ and $h \in (0, h_0]$ the following holds:

• 1. The attracting slow manifold $S_{a, \varepsilon ,h}$ and the repelling slow manifold $S_{r, \varepsilon ,h}$ intersect, i.e., it exhibits a maximal canard, if and only if $\lambda = \lambda _c^h(\sqrt{\varepsilon })$.

• 2. The function $\lambda _c^h$ has the expansion

  $$\begin{aligned} \lambda _c^h(\sqrt{\varepsilon })= - C \varepsilon + \mathcal {O}( \varepsilon ^{3/2}h), \end{aligned}$$

  where C is given as in (2.12) (for $a_3 =0$).

Proof

First, we will work in chart $K_2$ and show that the quantities $d_{h,x_0,\lambda }$, $d_{h,x_0,r}$ in (3.76), (3.77) with $x_0=0$ approximate the quantities $d_{\lambda }$, $d_{r}$ in (A.13), (A.14)(up to change of sign). We prove:

$$\begin{aligned} \sum _{n=-\infty }^{\infty } \langle \psi _{h,0}(n+1), {\hat{G}}(\gamma _{h,0}(n),h) \rangle&= \int _{-\infty }^{\infty } \big \langle \psi (t_2), G(\gamma _{0,2}(t_2)) \big \rangle \, \mathrm {d}t_2+{\mathcal {O}}(h), \end{aligned}$$

(3.78)

$$\begin{aligned} \sum _{n=-\infty }^{\infty } \langle \psi _{h,0}(n+1), {\hat{J}}(\gamma _{h,0}(n),h) \rangle&= \int _{-\infty }^{\infty } \big \langle \psi (t_2),\begin{pmatrix} 0 \\ -1 \end{pmatrix} \big \rangle \, \mathrm {d}t_2+{\mathcal {O}}(h), \end{aligned}$$

(3.79)

where, recall,

$$\begin{aligned}&\psi _{h, 0}(n) = \frac{1}{X(n)} \begin{pmatrix} - hn \\ 1 \end{pmatrix}, \quad \psi (t_2)=\frac{1}{\mathrm{e}^{t_2^2/2}} \begin{pmatrix} -t_2 \\ 1 \end{pmatrix}, \end{aligned}$$

(3.80)

$$\begin{aligned}&\gamma _{h, 0}(n) = \begin{pmatrix} \dfrac{hn}{2} \\ \dfrac{(hn)^2}{4} - \dfrac{1}{2} - \dfrac{h^2}{8} \end{pmatrix}, \quad \gamma _{0,2}(t_2) = \begin{pmatrix} \dfrac{t_2}{2} \\ \dfrac{t_2^2}{4} - \dfrac{1}{2}\end{pmatrix}, \end{aligned}$$

(3.81)

the function ${\hat{J}}$ is defined as in (3.42), and similar formulas hold true also for the function ${\hat{G}}$. Further recall that the Melnikov integrals can be solved explicitly, yielding

$$\begin{aligned} \int _{-\infty }^{\infty } \langle \psi (t_2), J(\gamma _{0,2}(t_2) \rangle \, \mathrm {d}t_2&= -\int _{-\infty }^{\infty } e^{-t_2^2/2} \, \mathrm {d}t_2 = - \sqrt{2\pi }\,,\\ \int _{-\infty }^{\infty } \langle \psi (t_2), G(\gamma _{0,2}(t) \rangle \, \mathrm {d}t&= \frac{1}{8}\int _{-\infty }^{\infty } (-4 a_5 -(4 a_1 + 2a_2 -2a_4-2a_5 )t_2^2 +a_2 t_2^4) e^{-t_2^2/2} \, \mathrm {d}t_2 \\&= -C\sqrt{2\pi }\,, \end{aligned}$$

where $a_i$ and C are as introduced in Sect. 2.2 (for $a_3=0$, see (3.4) and (3.5)).

We show (3.78)—the simpler case (3.79) then follows similarly. We observe:

• 1. The remainder of the integral satisfies

  $$\begin{aligned} S(t) := \left( \int _{-\infty }^{-T}+\int _T^{\infty }\right) \langle \psi (t_2),G(\gamma _{0,2}(t_2)\rangle \, \mathrm {d}t_2={\mathcal {O}}(T^Me^{-T^2/2}), \end{aligned}$$

  for $T >0$ and some $M \in \mathbb {N}$. Hence, we can keep $S(T) = {\mathcal {O}}(h^{2-c})$ for any $c>0$ with the choice $T\ge (4 \ln \frac{1}{h})^{1/2}$.

• 2. For $N=T/h$, we turn to estimate

  $$\begin{aligned} {\hat{S}}(N) := \left( \sum _{n=-\infty }^{-N}+\sum _{n=N}^{\infty }\right) \langle \psi _{h,0}(n+1), {\hat{G}}(\gamma _{h,0}(n),h) \rangle . \end{aligned}$$

  We denote by $n^*$ the closest integer to $\alpha = 2/h^2 + 1/2$ and recall that $\beta = 2/h^2 + 3/2$. Since

  $$\begin{aligned} \left| \frac{n^* + \beta }{n^*-\alpha } \right| \ge n^* + \beta \ge 4/h^2, \end{aligned}$$

  we can write, for all $n \ge 2/h^2 + 3/2$,

  $$\begin{aligned} \left| X(n+1) \right| \ge \frac{4}{h^2} \prod _{k=0, k\ne n^*}^n \left| \frac{k+ \beta }{k-\alpha } \right| . \end{aligned}$$

  Since with Proposition 3.9 the summands of ${\hat{S}}(N)$ converge to zero even faster for smaller h, we obtain by choosing $N\ge \left\lceil {2/h^2 + 3/2}\right\rceil$, and hence $T \ge 2/h + 5h/2$, that

  $$\begin{aligned} \left( \sum _{n=-\infty }^{-N}+\sum _{n=N}^{\infty }\right) \langle \psi _{h,0}(n+1), {\hat{G}}(\gamma _{h,0}(n),h) \rangle = {\mathcal {O}}(h^2). \end{aligned}$$

• 3. For $T=3/h$, we get by the standard methods the estimate

  $$\begin{aligned} \sum _{n=-N}^{N} \langle \psi _{h,0}(n+1), {\hat{G}}(\gamma _{h,0}(n),h) \rangle - \int _{-T}^{T} \big \langle \psi (t_2), G(\gamma _{0,2}(t_2)) \big \rangle \, \mathrm {d}t_2= {\mathcal {O}}(Th^2) = {\mathcal {O}}(h). \end{aligned}$$

Hence, we can conclude that Eqs. (3.78) and (3.79) hold, and, in particular, that $d_{h,0,\lambda }$ and $d_{h,0,r}$ are bounded away from zero for sufficiently small h. Recall from (3.75) that

$$\begin{aligned} D_{h,0}(r, \lambda ) = d_{h,0,\lambda } \lambda + d_{h,0,r}r + \mathcal {O}(2), \,, \end{aligned}$$

where $D_{h,0}(0,0) = 0$. Hence, the fact that $d_{h,0,\lambda }$ and $d_{h,r}$ are not zero implies, by the implicit function theorem, that there is a smooth function $\lambda ^{h}(r)$ such that

$$\begin{aligned} D_{h,0}(r, \lambda ^{h}(r)) = 0 \end{aligned}$$

in a small neighborhood of (0, 0). Transforming back from $K_2$ into original coordinates then proves the first claim.

Fig. 4

The integral errors (a) $\left| d_{h,\lambda }(N) - d_{\lambda } \right|$ and (b) $\left| d_{h, r}(N) - d_{r} \right|$ for different values of h and $N \in \mathbb {N}$

Furthermore, we obtain

$$\begin{aligned} \lambda ^{h}(r) = - \frac{d_{h,0,r}}{d_{h,0,\lambda }}r + \mathcal {O}(2) = - C r + \mathcal {O}(r h)\,. \end{aligned}$$

Transformation into original coordinates gives

$$\begin{aligned} \lambda _c^{h}(\sqrt{\varepsilon }) = - C\varepsilon + \mathcal {O}\left( \varepsilon ^{3/2} h \right) \,. \end{aligned}$$

Hence, the second claim follows. $\square$

Numerical computations show that $h_0$ in Theorem 3.11 does not have to be extremely small but that our results are quite robust for different step sizes. In Fig. 4, we display such computations for the case $a_1 =1$, $a_2=a_4 = a_5 =0$. In this case, the rescaled Kahan discretization in chart $K_2$ is given by

$$\begin{aligned} \begin{array}{l} {\tilde{x}} = \dfrac{x - hy + \frac{h}{2} x r - \frac{h^2}{4} x + \frac{h^2}{2}\lambda }{ 1- hx - \frac{h}{2} r + \frac{h^2}{4}} , \\ {\tilde{y}} = \dfrac{y - h yx - \frac{h}{2} y r - \frac{h^2}{2} x^2 - h \lambda + h^2 x \lambda + h x + \frac{h^2}{2} \lambda r - \frac{h^2}{4} y}{ 1- hx - \frac{h}{2} r + \frac{h^2}{4}}. \end{array} \end{aligned}$$

(3.82)

Hence, we obtain

$$\begin{aligned} {\hat{G}}_1(x, y, h) = \frac{h x- \frac{h^2}{2}y - \frac{h^2}{2}x^2}{\left( 1 - h x + \frac{h^2}{4}\right) ^2}, \quad {\hat{G}}_2(x, y, h) = \frac{\frac{h^2}{2}x - \frac{h^3}{4}y - \frac{h^3}{4}x^2}{\left( 1 - h x + \frac{h^2}{4}\right) ^2}.\nonumber \\ \end{aligned}$$

(3.83)

For different values of h and N, we calculate

$$\begin{aligned} d_{h,\lambda }(N) :=\sum _{n=-N}^{N-1} \langle \psi _{h}(n+1), {\hat{J}}(\gamma _{h}(n),h) \rangle \approx - d_{h, 0, \lambda }\,, \end{aligned}$$

and, for the situation of (3.82) with ${\hat{G}}$ as in (3.83),

$$\begin{aligned} d_{h,r}(N) :=\sum _{n=-N}^{N-1} \langle \psi _{h}(n+1), {\hat{G}}(\gamma _{h}(n),h) \rangle \approx -d_{h,0,r}\,, \end{aligned}$$

We compare these quantities with the values of the respective continuous-time integrals $d_{\lambda } = - \sqrt{2 \pi }$ and $d_{r} = - \sqrt{2 \pi }/2$. (We have $C=1/2$ in this case.)

We observe in Fig. 4 that the sums converge very fast for relatively small hN in both cases. Additionally, we see that $\left| d_{h,\lambda }(N) - d_{\lambda } \right|$ is significantly smaller than $\left| d_{h,r}(N) - d_{r} \right|$ for the same values of h. Note that the computations indicate that Theorem 3.11 holds for the chosen values of h since $d_{h,0,\lambda } \approx \sqrt{2 \pi } + \left( d_{\lambda } - d_{h,\lambda }(N) \right)$ is clearly distant from 0.

3.8 Numerical Illustrations for $\varepsilon > 0$

We illustrate the results by some additional numerics for $\varepsilon > 0$, supplementing the illustrations of the dynamics in the rescaling chart $K_2$, as given in Figs. 1 and 2 . Firstly, we consider the simplest case where $a_i =0$ for all i, i.e., situation (3.8) with invariant curve $S_{\varepsilon , h}$ (3.11). Figure 5 shows different trajectories of the map (3.8) for $\varepsilon =0.1$ and $h=0.02$, illustrating the organization of dynamics around $S_{\varepsilon , h}$ analogously to the dynamics of (3.44) around $S_{h}$ (3.61) (see Fig. 1).

Secondly, we consider the map (3.12) with $a_1=1$, i.e., a small additional perturbation of the canonical form, similarly to the end of the previous section. We take $\varepsilon =0.1$, $h=0.02$ and $\lambda = - (a_1/2) \varepsilon$, as a leading-order approximation of $\lambda _c^h(\sqrt{\varepsilon })$ (see Theorem 3.11). In Fig. 6, we observe that the numerics given by the Kahan discretization approximate very well the maximal canard, which slightly deviates from $S_{\varepsilon ,h}$, again illustrating the organization of dynamics into bounded and unbounded trajectories separated by the maximal canard. Note that we have chosen $\varepsilon =0.1$ to demonstrate the extension up to a relatively large $\varepsilon$.

In addition, we consider a model with cubic nonlinearity in order to demonstrate the application of the Kahan method beyond the purely quadratic case. Consider the Eq.

$$\begin{aligned} \begin{array}{l} x' = - y + x^2 \left( 1 + \dfrac{x}{3}\right) , \\ y' = \varepsilon (x - \lambda ), \end{array} \end{aligned}$$

(3.84)

as an example of Eq. (2.9), i.e., $a_3 =1/3$ and $a_i =0, i=1,2,4,5$. Equation (3.84) is the van der Pol equation with constant forcing after transformation around one of the fold points (see Kuehn 2015, Example 8.1.6). The Kahan discretization (3.6) of this equation yields

$$\begin{aligned} \begin{array}{l} \dfrac{1}{h}({\tilde{x}} - x) = - \dfrac{1}{2}(y +{\tilde{y}})+x{\tilde{x}} - \dfrac{x^3+{\tilde{x}}^3}{12}(x+{\tilde{x}}) + \dfrac{x^2 {\tilde{x}} + {\tilde{x}}^2 x}{4}, \\ \dfrac{1}{h}({\tilde{y}} - y) = \dfrac{\varepsilon }{2}(x +{\tilde{x}}) -\varepsilon \lambda , \end{array} \end{aligned}$$

(3.85)

such that the cubic nonlinearity does not vanish and we do not directly obtain an explicit form. However, we can use (3.85) as a numerical scheme by always taking the unique real solution $\tilde{x}$, closest to x in absolute value, of the cubic polynomial.

Fig. 5

Trajectories for the Kahan map (3.12), when $a_i =0$ for $i=1,2,4,5$, with $\varepsilon =0.1$, $h = 0.02$ and $\lambda =0$, for different initial points: three bounded orbits above the separatrix $S_{\varepsilon , h}$ and three unbounded orbits below the separatrix $S_{\varepsilon , h}$

Fig. 6

Trajectories for the Kahan map (3.12), when $a_1=1$ and $a_i =0$ for $i=2,4,5$, around maximal canard, taking $\varepsilon =0.1$, $h=0.02$ and $\lambda = -(a_1/2)\varepsilon$, $a_1=1$: a in comparison with symmetric, unperturbed separatrix $S_{\varepsilon ,h}$, and b showing movement along and away from maximal canard

Fig. 7

Trajectories for the Kahan discretization (3.85) of the transformed van der Pol Eq. (3.84) with $h = 0.02$ and $\varepsilon =0.1$, taking $\lambda = -(3 a_3/8) \varepsilon$, $a_3 =1/3$: The orbits $\gamma _1$ and $\gamma _2$ are bounded with initial points $(x_{0},y_{0})$ (black dots) closely above the origin. The other orbits seem to lie beneath a separatrix that would have the role of a maximal canard

In Fig. 7, we illustrate the results of the Kahan discretization (3.85) of the van der Pol Eq. (3.84), again for $\varepsilon =0.1$ and $h=0.02$, taking $\lambda = - (3 a_3/8) \varepsilon$, as a leading-order approximation of $\lambda _c(\sqrt{\varepsilon })$ (see Theorem 2.2). Observe that the numerics indicate the existence of a maximal canard, also in this situation, separating bounded, now spiralling, orbits and unbounded orbits. Note that the implementation is based on the fact that the cubic polynomial in ${\tilde{x}}$ always has exactly one real solution, which we take as the next value, plus a complex conjugate pair with non-trivial imaginary part. A more general, algebraic analysis extends beyond the scope of this work and is left for additional research.

Fig. 8

Trajectories for the Kahan discretization (3.85) of the transformed van der Pol equation (3.84) with $h = 0.02$ and $\varepsilon =0.1$, taking a $\lambda = -(3 a_3/8) \varepsilon$, $a_3 =1/3$, such that spiralling toward an attractive equilibrium is indicated, and b $\lambda = -(3 a_3/8) \varepsilon + 0.15 \varepsilon ^{3/2}$, $a_3 =1/3$, such that a periodic orbit occurs

Note that the results on maximal canards for perturbations of the canonical form are local and do not make statements on the global stability. The preservation of canards for the van der Pol equation as depicted in Fig. 7 is apparently also of predominantly local nature. Hence, we take a closer look in Fig. 8, zooming into a neighborhood of the inward-spiralling orbits from Fig. 7. Here, we observe that the Kahan discretization even seems to capture the occurrence of a Hopf bifurcation in a neighborhood of the maximal canard, as we slightly vary the parameter $\lambda$. Furthermore, the scheme seems to avoid crossing trajectories near the fold, which do occur as spurious solutions for some forward numerical methods near maximal canards. Indeed, there are also robust methods from boundary value problems (BVPs) (Desroches et al. 2010; Guckenheimer et al. 2000) and control theory (Durham and Moehlis 2008; Jardón-Kojakhmetov and Kuehn 2021) to track canards for the van der Pol equation. However, these approaches do not take direct advantage of the polynomial structure, nor of the particular locally approximately integrable or symmetry structures of the van der Pol equation. Hence, building on the presented insights for the Kahan method, we consider an analytical treatment of the discretized cubic canard problem an intriguing direction for future work.

4 Conclusion

Our results show the importance of combining geometric invariants or integrable structures hidden in blow-up coordinates with suitable discretization schemes. Although we have just treated a very low-dimensional fast–slow fold case, one anticipates similar results also to be relevant for various other higher-dimensional singularities and bifurcation points, where blow-up is a standard tool. For example, it is well known that in the Bogdanov–Takens unfolding one obtains small homoclinic orbits via a hidden integrable structure visible only after rescaling. A thorough discretization analysis of higher-dimensional canards, similarly to the one at hand, would also deserve further investigation.

From a numerical perspective, forward integration schemes often provide an exploratory perspective to actually detect interesting dynamics or find a suitable invariant solution for fixed parameter values. In several cases, these particular forward solutions are then used as starting conditions in numerical continuation techniques (Dhooge et al. 2008; Doedel et al. 2007) to study parametric dependence in a setting of BVPs. BVPs have also been successfully adapted to parametrically continue canard-type solutions (Desroches et al. 2008, 2010; Guckenheimer and Kuehn 2009; Kuehn 2010). In particular, BVPs for canards turn out to be well-posed with a small numerical error, yet to set up the problem purely by continuation one already needs a very good understanding of phase space for the initial canard orbits. Therefore, a direct numerical integration scheme can be very helpful to automatically yield suitable starting solutions close to a maximal canard.

The Kahan method has mainly turned out to be favorable, since explicit, for quadratic vector fields; hence, in our analysis we have focused on this situation. However, we have seen in the numerical investigations in Sect. 3.8 that, by using its implicit form, also non-quadratic problems can be tackled, at least numerically. A further investigation into the dynamical and algebraic properties of the scheme, in particular for cubic nonlinearities, is a highly intriguing research question for the future, in general, and also in particular with respect to geometric multiscale problems as the one presented in this work.

Appendix A Existence of Maximal Canards for ODEs

In order to use specific geometric methods in singular perturbation theory, we consider $\varepsilon$ and $\lambda$ as variables, writing Eq. (2.8) as

$$\begin{aligned} \begin{array}{l} x' = f(x,y, \lambda , \varepsilon ), \\ y' = \varepsilon g(x,y, \lambda , \varepsilon ), \\ \varepsilon ' = 0, \\ \lambda ' = 0. \end{array} \end{aligned}$$

(A.1)

Note that in Eq. (2.9) the Jacobi matrix of the vector field in $(x,y, \lambda , \varepsilon )$ has a quadruple zero eigenvalue at the origin. A well-established way to gain (partial) hyperbolicity at such a singularity is the blow-up technique which replaces the singularity by a manifold on which the dynamics can be desingularized. An important technical assumption for this technique is quasi-homogeneity of the vector field $f: \mathbb {R}^n \rightarrow \mathbb {R}^n$ of the ODE (cf. Kuehn 2015, Definition 7.3.2), which means that there are $(a_1, \dots , a_n) \in \mathbb {N}^n$ and $k \in \mathbb {N}$ such that for every $r \in \mathbb {R}$ and each component $f_j:\mathbb {R}^n \rightarrow \mathbb {R}$ of f we have

$$\begin{aligned} f_j(r^{a_1} z_1, \dots , r^{a_n} z_n) = r^{k+a_j} f_j(z_1, \dots , z_n). \end{aligned}$$

The proof of Theorem 2.2 in Krupa and Szmolyan (2001a) uses the quasi-homogeneous blow-up transformation $\Phi : B \rightarrow {\mathbb {R}}^4$,

$$\begin{aligned} x = r {\bar{x}}, \quad y = r^2 {\bar{y}}, \quad \varepsilon = r^2 {\bar{\varepsilon }}, \quad \lambda = r {\bar{\lambda }}, \end{aligned}$$

where $({\bar{x}}, {\bar{y}}, \bar{\varepsilon },{\bar{\lambda }}, r) \in B = S^2 \times [- \kappa , \kappa ] \times [0, \rho ]$, where $S^2 = \{({\bar{x}}, {\bar{y}}, {\bar{\varepsilon }}) \, : \, {\bar{x}}^2 + {\bar{y}}^2 + {\bar{\varepsilon }}^2 = 1 \}$, with some $\kappa , \rho > 0$. We assume that $\rho$ and $\kappa$ sufficiently small, so that the dynamics on $\Phi (B)$ can be described by the normal form approximation. Let $\overline{X}=\Phi ^*(X)$ be the pullback of the vector field X to B. The dynamics of $\overline{X}$ on B are analyzed in two charts $K_1$, $K_2$:

• The entering and exiting chart $K_1$ projecting the neighborhood of (0, 1, 0) on $S^2$ to the plane ${\bar{y}} = 1$:

  $$\begin{aligned} K_1 : \quad x = r_1 x_1, \quad y = r_1^2, \quad \varepsilon = r_1^2 \varepsilon _1, \quad \lambda = r_1 \lambda _1, \end{aligned}$$

  (A.2)

• and the scaling chart $K_2$ projecting the neighborhood of (0, 0, 1) on $S^2$ to the plane ${\bar{\varepsilon }} = 1$:

  $$\begin{aligned} K_2 : \quad x = r_2 x_2, \quad y = r_2^2 y_2, \quad \varepsilon = r_2^2, \quad \lambda = r_2 \lambda _2. \end{aligned}$$

  (A.3)

The dynamics in the chart $K_2$ is of a primary interest. Here, the transformed equations admit a time rescaling allowing to divide out a factor $r_2$, which is possible due to the quasi-homogeneity of the leading part of the vector field X (the new time being denoted by $t_2=r_2t$). Upon this operation, equations of motion take the form

$$\begin{aligned} \begin{array}{l} x_2' = - y_2 + x_2^2 + r_2 G_1(x_2, y_2) + \mathcal {O}(r_2(\lambda _2 + r_2)), \\ y_2' = x_2 - \lambda _2 + r_2G_2(x_2, y_2) + \mathcal {O}(r_2(\lambda _2 + r_2)), \\ r_2' = 0, \\ \lambda _2' = 0, \end{array} \end{aligned}$$

(A.4)

where $G =(G_1, G_2)$ can be written explicitly as

$$\begin{aligned} G(x_2, y_2) = \begin{pmatrix} G_1(x_2, y_2) \\ G_2(x_2,y_2) \end{pmatrix} = \begin{pmatrix} a_1 x_2 - a_2 x_2 y_2 + a_3 x_2^3 \\ a_4 x_2^2 + a_5 y_2 \end{pmatrix} . \end{aligned}$$

(A.5)

On the invariant set $\{r_2 = 0, \lambda _2=0\}$, we have

$$\begin{aligned} \begin{pmatrix} x_2' \\ y_2' \end{pmatrix} = f(x_2,y_2)= \begin{pmatrix} - y_2 + x_2^2 \\ x_2 \end{pmatrix}. \end{aligned}$$

(A.6)

Let us list some crucially important qualitative features of system (A.6).

• As pointed out in (Krupa and Szmolyan 2001a, Lemma 3.3), system (A.6) possesses an integral of motion

  $$\begin{aligned} H(x_2, y_2) = \text {e}^{-2 y_2} \left( y_2 - x_2^2 + \frac{1}{2} \right) . \end{aligned}$$

  (A.7)

• Moreover, one can put (A.6) as a generalized Hamiltonian system

  $$\begin{aligned} \begin{pmatrix} x_2' \\ y_2' \end{pmatrix}=\frac{1}{2}\text {e}^{2y_2}\begin{pmatrix} 0 &{} 1 \\ -1 &{} 0\end{pmatrix} {{\,\mathrm{grad}\,}}H(x_2,y_2). \end{aligned}$$

  (A.8)

• As a generalized Hamiltonian system, (A.6) preserves the measure $\text {e}^{-2y_2}\mathrm {d}x_2\wedge \mathrm {d}y_2$. Since the density of an invariant measure is defined up to a multiplication by an integral of motion, the following is an alternative invariant measure:

  $$\begin{aligned} \mu = \frac{\mathrm {d}x \wedge \mathrm {d}y}{|y_2 - x_2^2 + \frac{1}{2}|} . \end{aligned}$$

  (A.9)

• System (A.6) has an equilibrium of center type at (0, 0), surrounded by a family of periodic orbits coinciding with the level curves $\{H(x_2, y_2)=c\}$ for $0<c< \frac{1}{2}$. The level curves for $c<0$ correspond to unbounded solutions. These two regions of the phase plane are separated by the invariant curve $\{H(x_2, y_2)=0\}$, or

  $$\begin{aligned} y_2=x_2^2-\frac{1}{2}. \end{aligned}$$

  (A.10)

  Thus, we have two alternative characterizations of the separatrix (A.10): On the one hand, it is the level set $\{H(x_2, y_2)=0\}$, and on the other hand, it is the singular curve of the invariant measure (A.9).

• Separatrix (A.10) supports a special solution of (A.6):

  $$\begin{aligned} \gamma _{0,2}(t_2) =\begin{pmatrix} x_{0,2}(t_2)\\ y_{0,2}(t_2)\end{pmatrix} = \begin{pmatrix} \dfrac{1}{2} t_2\\ \dfrac{1}{4} t_2^2 - \dfrac{1}{2} \end{pmatrix}, \quad t_2 \in \mathbb {R}. \end{aligned}$$

  (A.11)

Pulled back to the manifold B, the special solution ${\bar{\gamma }}_0$ connects the endpoint $p_a$ of the critical attracting manifold $S_a$ across the sphere $S^2$ to the endpoint $p_r$ of the critical repelling manifold $S_r$ (see, e.g., Kuehn 2015, Figure 8.2). In other words, the center manifolds $\overline{M}_a$ and $\overline{M}_r$, corresponding to $p_a$ and $p_r$, respectively, and written in chart $K_2$ as $M_{a,2}$ and $M_{r,2}$, intersect along $\gamma _{0,2}$ for $r_2=\lambda _2=0$.

The difference between $M_{a,2}$ and $M_{r,2}$ for $(r_2,\lambda _2)\ne (0,0)$ is measured by the difference $y_{a,2}(0) - y_{r,2}(0)$, where $\gamma _{a,2}(t) = (x_{a,2}(t), y_{a,2}(t))$ and $\gamma _{r,2}(t) = (x_{r,2}(t), y_{r,2}(t))$ are the trajectories in $M_{a,2}$ and $M_{r,2}$, respectively, for given $r_2,\lambda _2$ with the initial data $x_{a,2}(0) = x_{r,2}(0) = 0$. This distance can be expressed as (Krupa and Szmolyan 2001a, Proposition 3.5)

$$\begin{aligned} D(r_2, \lambda _2) = H(0,y_{a,2}(0)) - H(0,y_{r,2}(0)) = d_{r} r_2 + d_{\lambda } \lambda _2 + \mathcal {O}(2)\,, \end{aligned}$$

(A.12)

where

$$\begin{aligned} d_{r}&= \int _{-\infty }^{\infty } \big \langle {{\,\mathrm{grad}\,}}H(\gamma _{0,2}(t_2)), G(\gamma _{0,2}(t_2)) \big \rangle \, \mathrm {d}t_2, \end{aligned}$$

(A.13)

$$\begin{aligned} d_{\lambda }&= \int _{-\infty }^{\infty } \big \langle {{\,\mathrm{grad}\,}}H(\gamma _{0,2}(t_2)),\begin{pmatrix} 0 \\ -1 \end{pmatrix} \big \rangle \, \mathrm {d}t_2 \end{aligned}$$

(A.14)

are the respective Melnikov integrals. Since $d_{\lambda } \ne 0$, one concludes by the implicit function theorem that for sufficiently small $r_2$ there exists $\lambda _2$ such that the manifolds $M_{a,2}$ and $M_{r,2}$ intersect. Transforming back into the original variables yields Theorem 2.2.

It will be important for us that formulas (A.13), (A.14) admit also a non-Hamiltonian expression given in Wechselberger (2002), where ${{\,\mathrm{grad}\,}}H(\gamma _{0,2}(t_2))$ is replaced by

$$\begin{aligned} \psi (t_2)=2\text {e}^{-2y_{0,2}(t_2)}\begin{pmatrix} -y_{0,2}'(t_2) \\ x_{0,2}'(t_2) \end{pmatrix}=\text {e}^{-2y_{0,2}(t_2)}\begin{pmatrix} -t_2 \\ 1 \end{pmatrix}. \end{aligned}$$

(A.15)

The function $\psi (t_2)$ admits a more intrinsic interpretation as the only exponentially decaying solution of the adjoint system for the system (A.6) linearized along the solution $\gamma _{0,2}(t_2)$,

$$\begin{aligned} \psi ' = -\mathrm {D}f (\gamma _{0,2}(t_2))^{\top } \psi , \end{aligned}$$

(A.16)

while the expression $2y_{0,2}(t_2)=t_2^2/2$ in the exponent is interpreted as

$$\begin{aligned} \frac{t_2^2}{2}=\int _0^{t_2} {{\,\mathrm{tr}\,}}\mathrm {D}f(\gamma _{0,2}(\tau ))\mathrm {d}\tau , \end{aligned}$$

(A.17)

the matrix of the system (A.6) linearized along the solution $\gamma _{0,2}(t_2)$ being given by

$$\begin{aligned} \mathrm {D}f(\gamma _{0,2}(t_2)) = \begin{pmatrix} 2x_{0,2}(t_2) &{} -1 \\ 1 &{} 0 \end{pmatrix} = \begin{pmatrix} t_2 &{} -1 \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

(A.18)