On Fast–Slow Consensus Networks with a Dynamic Weight

Abstract

We study dynamic networks under an undirected consensus communication protocol and with one state-dependent weighted edge. We assume that the aforementioned dynamic edge can take values over the whole real numbers, and that its behaviour depends on the nodes it connects and on an extrinsic slow variable. We show that, under mild conditions on the weight, there exists a reduction such that the dynamics of the network are organized by a transcritical singularity. As such, we detail a slow passage through a transcritical singularity for a simple network, and we observe that an exchange between consensus and clustering of the nodes is possible. In contrast to the classical planar fast–slow transcritical singularity, the network structure of the system under consideration induces the presence of a maximal canard. Our main tool of analysis is the blow-up method. Thus, we also focus on tracking the effects of the blow-up transformation on the network’s structure. We show that on each blow-up chart one recovers a particular dynamic network related to the original one. We further indicate a numerical issue produced by the slow passage through the transcritical singularity.

1 Introduction

A wide range of scientific disciplines, such as biochemistry (Aral et al. 2009; Xia et al. 2004), economics (Schweitzer et al. 2009), social sciences (Moreno 1934; Proskurnikov and Tempo 2017, 2018), epidemiology (Barabási 2016; Pastor-Satorras and Vespignani 2001), among many others, benefit from the progress in network theory. Network science represents an important paradigm for modelling and analysis of complex systems. In network theory, individuals are represented as vertices on a graph. These individuals, or agents, can be persons in a community, robots working in an assembly line, computers in an office building, particles of a chemical substance, etc. The interactions between such individuals are then represented as edges or links of the graph. For example, if two persons talk to each other, and one influences the other, we then associate an edge on the graph to such an activity. Similarly, interactions can be identified with edges in all other aforementioned examples. Thus, the individual’s own dynamics (the nodes’ dynamics) and the interaction it has with other individuals of the network (the topology of the network) will not only determine its own fate, but that of the entire group of individuals. This rather convenient way of describing complicated dynamic behaviour is quite powerful and has attracted an enormous scientific interest (Albert and Barabási 2002; Barrat et al. 2004; Boccaletti et al. 2006; Strogatz 2001).

From an applied mathematical perspective, topics such as stability, convergence rates, synchronization, connectivity, robustness, and many others can all be formally described and have important implications in other sciences. In a large part of the mathematical studies of networks, one considers that the interactions between the agents are fixed (Barrat et al. 2008); see also Sect. 2. In another large part of the theory one frequently assumes that the network structure evolves without dynamics at the nodes (van den Hofstad 2016). In most cases, these assumptions are a simplification since it may be expected that there is coupled dynamics of and on the network, i.e. one has to deal with adaptive (or co-evolutionary) networks (Gross et al. 2009). A crucial assumption to approximate an adaptive network by a partially static one with either just dynamics on or dynamics of the network is timescale separation (Kuehn 2015). Yet, if one assumes that either the dynamics on the nodes or the dynamics of the edges are infinitely slow, static leads to a singular limit description. This limit is known to miss adaptive network dynamics effects induced by the interaction of dynamical variables for finite timescale separation (Kuehn 2012). Also from the viewpoint of applications, a finite but large timescale separation is far more reasonable. As an example, consider a group of people that communicate with each other daily but whose mutual influences shape the way they handle elections. One of such activities occurs in time scales of minutes or hours, while the other in timescales of years, yet both are interrelated in a complex manner. Similar examples where different sorts of relations occur at distinct timescales can be found in population dynamics, telecommunication networks, power grids, etc. So, although timescales add an extra level of difficulty to the analysis of networks, they may be useful for a more accurate representation of certain phenomenon. On the other hand, dynamical systems with two or more timescales have also been of interest from many perspectives, particularly in applied mathematics. The overall idea is to distinguish slow from fast subprocesses, analyze them separately, and then come up with an appropriate description of the problem (Jones 1995; Kaper 1999; Kuehn 2015; O’Malley 1991; Verhulst 2005). This basic idea can be made rigorous and has proven to be powerful. However, there are generic complex systems in which the timescale separation can no longer be clearly distinguished. Thus more advanced mathematical techniques are required to analyze multi-scale adaptive networks.

In this article we bring together network and multi-scale theories to study a class of adaptive networks. We are interested in networks whose agents communicate in a rather simple way, known as linear average consensus protocol (see the details in Sect. 2.2). This type of communication has been largely studied due to its relevance in all kinds of sciences (Mesbahi and Egerstedt 2010; Ren et al. 2005). On this class of networks we assume that there is one interaction or communication link that slowly changes over time and investigate the implications of it. We shall see that the aforementioned setting leads to a nontrivial problem from both, network and multi-scale, contexts. As a result we describe the overall behaviour of the network by adequately incorporating techniques from consensus dynamics and geometric singular perturbation theory.

The forthcoming parts of this work are arranged as follows: in Sect. 2 we provide a short technical introduction to the main topics of this paper, namely fast–slow systems and consensus networks. In Sect. 3 we present our main contribution, which consists in the analysis of a simple network that has a dynamic weight and whose overall dynamics evolve in two timescales. Next, in Sect. 4 we show that, in qualitative terms, the analysis performed for the aforementioned simple network can be extended to arbitrary networks with one dynamic edge. We finish in Sect. 5 with concluding remarks and an outlook on future research.

2 Preliminaries

In this section we provide a brief recollection of the two mathematical areas that come together in this paper. We first state what a fast–slow system formally is, the concept of normal hyperbolicity, and two relevant geometric techniques of analysis. Afterwards, to place our work into context, we recall and provide appropriate references to some of the relevant results on dynamic networks.

2.1 Fast–Slow Systems

A fast–slow system is a singularly perturbed ordinary differential equation (ODE) of the form

$$\begin{aligned} \begin{aligned} \varepsilon \dot{x}&= f(x,y,\varepsilon )\\ \dot{y}&= g(x,y,\varepsilon ), \end{aligned} \end{aligned}$$

(1)

where $x\in \mathbb {R}^m$ and $y\in \mathbb {R}^n$ are, respectively, the fast and slow variables, and where $0<\varepsilon \ll 1$ is a small parameter accounting for the timescale difference between the variables. The overdot denotes derivative with respect to the slow time $\tau$. By defining the fast time $t=\tau /\varepsilon$, one can rewrite (1) as

$$\begin{aligned} \begin{aligned} x'&= f(x,y,\varepsilon )\\ y'&= \varepsilon g(x,y,\varepsilon ), \end{aligned} \end{aligned}$$

(2)

where the prime denotes the derivative with respect to the fast time t. Observe that, for $\varepsilon >0$, the only difference between (1) and (2) is their time parametrization. Therefore, we say that (1) and (2) are equivalent.

Although there are several approaches to the analysis of fast–slow systems, e.g. classical asymptotics (Eckhaus 2011a, b; O’Malley 1991; Verhulst 2005), here we take a geometric approach (Fenichel 1979; Jones 1995), which is called geometric singular perturbation theory. The overall idea is to consider (1) and (2) restricted to $\varepsilon =0$, understand the resulting systems, and then use perturbation results to obtain a description of (1) and (2) for $\varepsilon >0$ sufficiently small. Therefore, two important subsystems to be considered are

$$\begin{aligned} \begin{aligned} 0&= f(x,y,0)\\ \dot{y}&= g(x,y,0), \end{aligned}\quad \quad \begin{aligned} x'&= f(x,y,0)\\ y'&= 0, \end{aligned} \end{aligned}$$

(3)

which are called the constraint equation (Takens 1976) (or slow subsystem or reduced system) and the layer equation (or fast subsystem), respectively. It is important to note that the constraint and layer equations are not equivalent any more, there are even different classes of differential equations as the constraint equation is a differential-algebraic equation (Kunkel and Mehrmann 2006), while the layer equation is an ODE, where the slow variables y can be viewed as parameters. In some sense the timescale separation is infinitely large between two singular limit systems (3). However, a geometric object that relates the two is the critical manifold.

Definition 1

The critical manifold of a fast–slow system is defined by

$$\begin{aligned} \mathcal {C}_0=\left\{ (x,y)\in \mathbb {R}^m\times \mathbb {R}^n\,|\, f(x,y,0)=0 \right\} . \end{aligned}$$

(4)

The critical manifold is, on the one hand, the set of solutions of the algebraic equation in the constraint equation, and on the other hand, the set of equilibrium points of the layer equation. There is an important property that critical manifolds may have, called normal hyperbolicity.

Definition 2

A point $p\in \mathcal {C}_0$ is called hyperbolic if the eigenvalues of the matrix $\text{ D }_xf(p,0)$, where $\text{ D }_x$ denotes the total derivative with respect to x, have nonzero real part. The critical manifold $\mathcal {C}_0$ is called normally hyperbolic if every point $p\in \mathcal {C}_0$ is hyperbolic. On the contrary, if for a point $p\in \mathcal {C}_0$ we have that $\text{ D }_xf(p,0)$ has at least one eigenvalue on the imaginary axis, we then call p nonhyperbolic.

In a general sense, whether a critical manifold has nonhyperbolic points or not, dictates the type of mathematical techniques that are suitable for analysis. For the case when the critical manifold is normally hyperbolic, Fenichel’s theory (Fenichel 1979) (see also Tikhonov 1952; Kuehn and Szmolyan 2015, Chapter 3) asserts that, under compactness of the critical manifold, the constraint and the layer equations give a good enough approximation of the dynamics near $\mathcal {C}_0$ of the fast–slow system for $\varepsilon >0$ sufficiently small. In the normally hyperbolic case for $0<\varepsilon \ll 1$, there exists a slow manifold $\mathcal {C}_\varepsilon$, which can be viewed as a perturbation of $\mathcal {C}_0$; see also Fenichel (1979) and Kuehn and Szmolyan (2015).

The case when the critical manifold has nonhyperbolic points is considerably more difficult. One mathematical technique that has proven highly useful for the analysis in such a scenario is the blow-up method (Dumortier et al. 1996). Briefly speaking, the blow-up method consists on a well-suited generalized polar change of coordinates. What one aims to gain with such a coordinate transformation is enough hyperbolicity so that the dynamics can be analyzed using standard techniques of dynamical systems. Nowadays, the blow-up method is widely used to analyze the dynamics of fast–slow systems having nonhyperbolic points in a broad range of theoretical contexts and applications. For detailed information on the blow-up technique the reader may refer to Dumortier et al. (1996), Jardón-Kojakhmetov and Kuehn (2019), Krupa and Szmolyan (2001a), Kuehn and Szmolyan (2015, Chapter 7), and references therein.

2.2 Consensus Networks

In this section we formally introduce the type of consensus problems on an adaptive network which we are concerned with in this work. Let us start by introducing some notation: we denote by $\mathcal {G}=\left\{ \mathcal {V},\mathcal {E},\mathcal {W}\right\}$ an undirected weighted graph where $\mathcal {V}=\left\{ 1,\ldots ,m \right\}$ denotes the set of vertices, $\mathcal {E}=\left\{ e_{ij}\right\}$ the set of edges and $\mathcal {W}=\left\{ w_{ij}\right\}$ the set of weights. We assume that the graph is undirected, that there are only simple edges, and that there are no self-loops, that is $e_{ij}=e_{ji}$ and $e_{ii}\notin \mathcal {E}$. To each edge $e_{ij}$ we assign a weight $w_{ij}\in \mathbb {R}$ and thus we identify the presence (resp. absence) of an edge with a nonzero (resp. zero) weight. Moreover, we shall say that a graph is unweighted if all the nonzero weights are equal to one. The Laplacian (Merris 1994) of the graph $\mathcal {G}$ is denoted by $L=[l_{ij}]$ and is defined by

$$\begin{aligned} l_{ij}={\left\{ \begin{array}{ll} -w_{ij}, &{}\quad i\ne j\\ \sum _{j=1}^m w_{ij}, &{}\quad i=j. \end{array}\right. } \end{aligned}$$

(5)

Remark 1

The majority of the scientific work regarding adaptive/dynamic networks considers nonnegative weights. One of the reasons for such consideration is that the spectrum of the Laplacian matrix is well identified (Barrat et al. 2004; Mohar 1991; Olfati-Saber et al. 2007), which simplifies the analysis. When the weights are allowed to be positive and negative one usually refers to L as a signed Laplacian. Difficulties arise due to the fact that many of the convenient properties of nonnegatively weighted Laplacians do not hold for signed Laplacians. In some part of the literature, see for example Altafini (2013) and Proskurnikov et al. (2016), the diagonal entries of the Laplacian matrix are rather defined by $\sum _{j=1}^m |w_{ij}|$. In this case, however, the Laplacian matrix is positive semi-definite and the potential loss of stability due to dynamic weights (the main topic of this paper) is not possible. One the other hand, Laplacian matrices defined by (5) are relevant in many applications. For example, in Bronski and DeVille (2014), Knyazev (2017), Pan et al. (2016) problems like agent clustering are studied, while the stability of networks under uncertain perturbations is considered in Chen et al. (2016), Zelazo and Bürger (2017).

We identify each vertex i of the graph $\mathcal {G}$ with the state of an agent $x_i$. Here we are interested on scalar agents, that is $x_i\in \mathbb {R}$ for all $i=1,\ldots ,m$. We now have a couple of important definitions.

Definition 3

• We say that the agents $x_i$ and $x_j$ agree if and only if $x_i=x_j$.

• Consider a continuous-time dynamical system defined by

  $$\begin{aligned} \dot{x} =f(x), \end{aligned}$$

  (6)

  where $x=(x_1,\ldots ,x_m)\in \mathbb {R}^m$ is the vector of agents’ states. Let x(0) denote initial conditions and $\chi :\mathbb {R}^m\rightarrow \mathbb {R}$ be a smooth function. We say that the graph $\mathcal {G}$ reaches consensus with respect to $\chi$ if and only if all the agents agree and $x_i=\chi (x(0))$ for all $i\in \mathcal {V}$.

• We say that f(x) defines a consensus communication protocol over $\mathcal {G}$ if the solutions of (6) reach consensus.

We note that the above definition of consensus is rather general, in the sense that there can be “discrete consensus” if all agents only agree at discrete time points; “finite time consensus” if $x_i(T)=\chi (x(0))$ for all $i\in \mathcal {V}$ and $t>T$ with $0\le T<\infty$; “asymptotic consensus” if $\lim _{t\rightarrow \infty } x_i(t)=\chi (x(0))$ for all $i\in \mathcal {V}$; and so on. Similarly, several consensus protocols can be classified with respect to the function $\chi$, see, e.g. Olfati-Saber et al. (2007), Olfati-Saber and Murray (2004) and Saber and Murray (2003).

The appeal in studying consensus problems and protocols is due to their wide range of applications in, for example, computer science (Thomas 1979), formation control of autonomous vehicles (Fax and Murray 2004; Jadbabaie and Morse 2003; Ren et al. 2007), biochemistry (Chen et al. 2013; Holland et al. 2004), sensor networks (Olfati-Saber 2005), social networks (Alves 2007; Xie et al. 2011), among many others. A simple example of consensus would be a group of people in which all agree to vote for the same candidate in an election. Another example would be a group of autonomous vehicles that are set to move with the same velocity.

In this paper we are interested in one of the simplest consensus protocols that leads to average consensus, that is $\chi (x(0))=\frac{1}{m}\sum _{i=1}^m x_i(0)$ with the protocol defined by

$$\begin{aligned} f_i(x)=\sum _{j=1}^m w_{ij} (x_j-x_i). \end{aligned}$$

(7)

This communication protocol is particularly interesting since it is an instance of a distributed protocol. In other words, the time evolution of $x_i$ is solely determined by its interaction with other agents directly connected to it. This type of protocols is widely investigated in engineering applications, for example to design controllers that only require local information in order to achieve their tasks (Lynch 1996; Moreau 2004; Ren and Beard 2008; Xiao et al. 2007). Alternatively, this linear average consensus protocol can be written as

$$\begin{aligned} \dot{x} =-Lx, \end{aligned}$$

(8)

where L denotes the Laplacian of $\mathcal {G}$ as defined by (5). It is then clear that the behaviour of the agents is determined by the spectral properties of the Laplacian matrix (Merris 1994; Mohar 1991; Zelazo and Bürger 2014). One of the most relevant results for systems defined by (8) is that, if the graph is connected and all the weights are positive, then (8) reaches average consensus asymptotically (Olfati-Saber et al. 2007). Although most of the scientific work has been focused on consensus protocols over unweighted graphs and with fixed topology, there is an increased interest in investigating dynamical systems defined on weighted graphs with varying and/or switching topologies (Casteigts et al. 2012; Mesbahi 2005; Moreau 2005; Olfati-Saber and Murray 2004; Proskurnikov 2013; Tanner et al. 2007).

In the main part of this article, Sects. 3 and 4, we are going to consider linear average consensus protocols with a dynamic weight. This dynamic weight is assumed to have a slower timescale than that of the nodes. Therefore, it makes sense to approach the problem from a singular perturbation perspective. We will see that under generic conditions on the weight, the fact that the dynamics are defined on a network, induces the presence of a nonhyperbolic point. As we have described in Sect. 2.1, one suitable technique of analysis to describe the system is then the blow-up method. Since the blow-up method is a coordinate transformation, one should check whether such a transformation preserves the network structure or not. For general networks, this is a classical problem and it is known that for certain coordinate changes, network structure is not preserved (Field 2004; Golubitsky and Stewart 2017). Yet, sometimes symmetries help to gain a better understanding for certain classes such as coupled cell network dynamics (Nijholt et al. 2017). As we will show, the blow-up method not only preserves the network structure for our consensus problem but also the blown-up networks in different coordinate charts also have natural dynamical and network interpretations. In qualitative terms this tells us that the blow-up method is a suitable technique for the analysis of adaptive networks with multiple timescales.

Before proceeding to our main contribution, in the next section we present a first interconnection between the topics discussed above. We show that Fenichel’s theory suffices to analyze state-dependent linear consensus networks with two timescales, and for which the Laplacian matrix has just a simple zero eigenvalue.

2.3 State-Dependent Fast–Slow Consensus Networks with a Simple Zero Eigenvalue

In this section we show that Fenichel’s theorem is enough to describe the dynamics of arbitrary fast–slow consensus networks with state-dependent Laplacian as long as $\lambda _1=0$ is a simple eigenvalue, i.e. we are going to show that the zero eigenvalue corresponds to a trivial parametrized direction and that for each parameter we have a normally hyperbolic structure. The result presented below is motivated by a similar claim that appears in Awad et al. (2018, Section B). However, here we are not concerned with the stability of the fast nor the slow dynamics, and the use of Fenichel’s theorem appears more aligned to the contents of this paper. Let us then consider the fast–slow system

$$\begin{aligned} \begin{aligned} x'&= -L(x,y,\varepsilon )x\\ y'&= \varepsilon g(x,y,\varepsilon ), \end{aligned} \end{aligned}$$

(9)

where $x\in \mathbb {R}^m$, $y\in \mathbb {R}^n$, $\varepsilon >0$ is a small parameter, and $L(x,y,\varepsilon )$ is a state-dependent Laplacian matrix.

Theorem 1

Consider (9) and a compact region $U_x\times U_y\subseteq \mathbb {R}^m\times \mathbb {R}^n$. Let $\varvec{1}_m:=(1,1,\ldots ,1)^\top \in U_x$. If for all $(x,y)\in U_x\times U_y$ one has that $\ker L(x,y,0)={{\,\mathrm{span}\,}}\left\{ \varvec{1}_m\right\}$, then the set

$$\begin{aligned} \mathcal {S}_0=\left\{ (x,y)\in U_x\times U_y \, | \, x_i=\frac{1}{m}\varvec{1}_m^\top x(0) ~\forall i\right\} \end{aligned}$$

(10)

is a normally hyperbolic family of critical manifolds of (9).

Proof

Let $X=({\bar{X}},{\hat{X}})\in \mathbb {R}\times \mathbb {R}^{m-1}$ be new coordinates defined by

$$\begin{aligned} X=\begin{bmatrix} {\bar{X}} \\ {\hat{X}} \end{bmatrix}=Px=\begin{bmatrix} \frac{1}{m}\varvec{1}_m^\top \\ Q \end{bmatrix}x, \end{aligned}$$

(11)

where the matrix Q is found via the Gram–Schmidt process after selecting the first component as indicated in (11). Although L(x, y, 0) cannot really be regarded as a fixed linear operator acting on $\mathbb {R}^m$ as it depends upon (x, y), the choice of the eigenvector $\varvec{1}_m$ is justified due to the fact that $\lambda _1=0$ is a simple zero eigenvalue of the Laplacian matrix L(x, y, 0) if and only if $L(x,y,0)\varvec{1}_m=0$ for all $(x,y)\in U_x\times U_y$. Note then that ${\bar{X}}$ denotes the average of the nodes’ states. It now follows that from the equation of $x'$ we have

$$\begin{aligned} \begin{aligned} \begin{bmatrix} {\bar{X}}' \\ {\hat{X}}' \end{bmatrix} = \begin{bmatrix} \frac{1}{m}\varvec{1}_m^\top \\ Q \end{bmatrix}x' = - \begin{bmatrix} \frac{1}{m}\varvec{1}_m^\top L \varvec{1}_m {\bar{X}} + \frac{1}{m}\varvec{1}_m^\top LQ^\top {\hat{X}}\\ QL\varvec{1}_m {\bar{X}} + QLQ^\top {\hat{X}} \end{bmatrix}=\begin{bmatrix} 0\\ QLQ^\top {\hat{X}} \end{bmatrix}. \end{aligned} \end{aligned}$$

(12)

Therefore we have that (9) is conjugate to

$$\begin{aligned} \begin{aligned} {\bar{X}}'&=0\\ {\hat{X}}'&= -{\hat{L}}({\bar{X}},{\hat{X}},y,\varepsilon ) {\hat{X}}\\ y'&= \varepsilon {\hat{g}}({\bar{X}},{\hat{X}},y,\varepsilon ), \end{aligned} \end{aligned}$$

(13)

where ${\hat{L}}({\bar{X}},{\hat{X}},y,\varepsilon ) = QL(P^{-1}X,y,\varepsilon )Q^\top$ and ${\hat{g}}({\bar{X}},{\hat{X}},y,\varepsilon )=g(P^{-1}X,y,\varepsilon )$. One observes that, as expected, ${\bar{X}}$ has the role of a parameter. Furthermore, due to our hypothesis and definition of ${\hat{L}}$, we have that the matrix ${\hat{L}}({\bar{X}},{\hat{X}},y,0)$ is invertible within the compact region of interest. Therefore, the corresponding critical manifold is given by ${\hat{\mathcal {S}}}_0 =\left\{ {\hat{X}}=0 \right\}$. Denoting $f({\bar{X}},{\hat{X}},y,\varepsilon ) =-{\hat{L}}({\bar{X}},{\hat{X}},y,\varepsilon ) {\hat{X}}$ we have that $\frac{\partial f}{\partial {\hat{X}}}({\bar{X}},0,y,0)=-\hat{L}({\bar{X}},0,y,0)$, which is invertible, implying that ${\hat{\mathcal {S}}}_0$ is normally hyperbolic. The proof is finalized by returning to the original coordinates leading to (10). $\square$

Next we are going to consider a case study in which Fenichel’s theory is not enough to describe the dynamics of a fast–slow network.

3 A Triangle Motif

In this section we study a motif (Milo et al. 2002). Motifs can be seen as building blocks of more general and complex networks. Indeed, as we describe throughout this article, all the dynamic traits and properties that the triangle motif exhibits can be extended to arbitrary networks, see Sect. 4.

Let us consider the following network

To each node $i=1,2,3$ we assign a state $x_i=x_i(t)\in \mathbb {R}$. We assume that the dynamics of each node are defined only by diffusive coupling. Moreover, we assume that $w\in \mathbb {R}$ is a dynamic weight depending on the vertices it connects and on an external state $y\in \mathbb {R}$, which is assumed to have much slower time evolution than that of the nodes. Hence, we study the fast–slow system

$$\begin{aligned} \begin{aligned} x'&= -L(x,y,\varepsilon )x,\\ y'&= \varepsilon g(x,y,\varepsilon ), \end{aligned}\qquad \qquad L=\begin{bmatrix} w + 1 &{}\quad -w &{}\quad -1\\ -w &{}\quad w+1 &{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}, \end{aligned}$$

(14)

where $w=w(x_1,x_2,y,\varepsilon )$ is a smooth function of its arguments and $0<\varepsilon \ll 1$ is a small parameter. In this section we shall consider the simple case in which w is affine in the state variables, that is

$$\begin{aligned} w = \alpha _0 + \alpha _1x_1 + \alpha _2x_2 + \alpha _3y, \end{aligned}$$

(15)

with $\alpha _0,\alpha _1,\alpha _2,\alpha _3$ real constants. We further assume the nondegeneracy condition $\alpha _3\ne 0$ to ensure coupling between the slow and fast variables. By shifting and rescaling $y\mapsto \alpha _0+\alpha _3y$, and a possible a change of signs of the variables, we may also assume

$$\begin{aligned} w = y + \alpha _1x_1 + \alpha _2x_2, \end{aligned}$$

(16)

with $\alpha _1\ge 0$ and $\alpha _2\ge 0$.

3.1 Preliminary Analysis (the Singular Limit)

The following transformation, which is simple to obtain, will be useful throughout this work.

Lemma 1

Consider the symmetric matrix L defined in (14). Then the orthogonal matrix

$$\begin{aligned} T = \begin{bmatrix} \frac{\sqrt{3}}{3} &{}\quad -\frac{\sqrt{6}}{6} &{}\quad -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{3}}{3} &{}\quad -\frac{\sqrt{6}}{6} &{}\quad \frac{\sqrt{2}}{2}\\ \frac{\sqrt{3}}{3} &{}\quad \frac{\sqrt{6}}{3} &{}\quad 0 \end{bmatrix} \end{aligned}$$

(17)

diagonalizes L as $D=T^\top L T={{\,\mathrm{diag}\,}}\left\{ 0,3,2w+1 \right\}$.

Thus, applying the coordinate transformation defined by $(X,Y)=(T^\top x,y)$ one obtains the conjugate diagonalized system

$$\begin{aligned} \begin{aligned} X'&= - D(X,Y)X\\ Y'&= \varepsilon G(X,Y,\varepsilon ), \end{aligned} \end{aligned}$$

(18)

where $D(X,Y)={{\,\mathrm{diag}\,}}\left\{ 0,3,2W+1\right\}$ and

$$\begin{aligned} \begin{aligned} W&= Y + \underbrace{\frac{\sqrt{3}}{3}(\alpha _1+\alpha _2)}_{=:\beta _1}X_1 - \underbrace{\frac{\sqrt{6}}{6}(\alpha _1+\alpha _2)}_{=:\beta _2}X_2 + \underbrace{\frac{\sqrt{2}}{2}(\alpha _2-\alpha _1)}_{=:\beta _3}X_3\\&=Y+\beta _1 X_1 + \beta _2 X_2 + \beta _3 X_3\\ G(X,Y,\varepsilon )&=g(TX,Y,\varepsilon ). \end{aligned} \end{aligned}$$

(19)

Observe that fast–slow system (18) has a conserved quantity given by $X_1'=0$, which arises due the zero eigenvalue of the Laplacian matrix L of (14). Since this is a trivial eigenvalue, that is, independent of the dynamics, we shall assume that $X_1$ is a coordinate on the critical manifold and not in the fast foliation, see also Sect. 2.3.

Remark 2

Due to $X_2'=-3X_2$, the set $\mathcal {A}=\left\{ (X_1,X_2,X_3,Y)=(X_1,0,X_3,Y) \right\}$ is uniformly globally exponentially stable. On the other hand, the local stability properties of $\left\{ X_3=0 \right\}$ are dictated by the sign of $2W+1$.

The previous observations allow us to reduce the analysis of (18) to that of the planar fast–slow system

$$\begin{aligned} \begin{aligned} X_3'&= -(2{\tilde{W}}+1)X_3\\ Y'&= \varepsilon {\tilde{G}}(X_1,0,X_3,Y,\varepsilon ) \end{aligned}, \qquad {\tilde{W}} = W|_{\mathcal {A}}=Y + \beta _1 X_1 + \beta _3 X_3, \end{aligned}$$

(20)

where $X_1$ is regarded as a parameter. It follows that the corresponding critical manifold is

$$\begin{aligned} {\tilde{\mathcal {C}}}_0 = \left\{ (X_3,Y)\in \mathbb {R}^2\, |\, (2{\tilde{W}}+1)X_3=0 \right\} . \end{aligned}$$

(21)

It is now straightforward to see that, for fixed $X_1$, ${\tilde{p}} = \left\{ (X_3,Y)=\left( 0,-\frac{1}{2}-\beta _1X_1\right) \right\}$ is a nonhyperbolic point of the critical manifold.

Remark 3

Our goal will be to describe the dynamics of the network shown in Fig. 1 as trajectories pass through the nonhyperbolic point ${\tilde{p}}$. The reason to consider this will become clear below when we give an interpretation of the singular dynamics in terms of the network. Thus, we assume that $\tilde{G}(X_1,0,0,-\frac{1}{2}-\beta _1X_1,0)<0$.

Fig. 1

Triangle motif: a network of three nodes connected on a cycle

Singular dynamics in terms of the network From the definition $X=T^\top x$ we have

$$\begin{aligned} (X_1,X_2,X_3)=\left( \frac{\sqrt{3}}{3}(x_1+x_2+x_3),\, \frac{\sqrt{6}}{6}(2x_3-x_1-x_2),\, \frac{\sqrt{2}}{2}(x_2-x_1) \right) . \end{aligned}$$

So, first of all, we have that the uniformly globally exponentially stable set $\mathcal {A}$, previously defined by $\mathcal {A}=\left\{ (X_1,X_2,X_3,Y)\in \mathbb {R}^4\,|\, X_2=0 \right\}$ (see Remark 2), is equivalently given by

$$\begin{aligned} \mathcal {A}= \left\{ (x_1,x_2,x_3,y)\in \mathbb {R}^4\,|\, x_3=\frac{x_1+x_2}{2} \right\} . \end{aligned}$$

(22)

Naturally, the uniform global stability of $\mathcal {A}$ is still valid. Next, if we restrict (14) to $\mathcal {A}$ we obtain

$$\begin{aligned} \begin{aligned} x_1'&= \left( w+\frac{1}{2}\right) (x_2-x_1)\\ x_2'&= \left( w+\frac{1}{2}\right) (x_1-x_2)\\ y'&= \varepsilon g\left( x_1,x_2,\frac{x_1+x_2}{2},y,\varepsilon \right) , \end{aligned} \end{aligned}$$

(23)

which is the model of a 2-node 1-edge fast–slow network as shown in Fig. 2.

Fig. 2

Reduced graph corresponding to (23). The dynamics of the triangle motif converge exponentially to the dynamics of this simpler graph

Next, we note in (23) that $x_1'+x_2'=0$, which implies that $x_1(t)+x_2(t)=x_1(0)+x_2(0)=:\sigma _0$ for all $t\ge 0$. Therefore, just as in the diagonalized system above, we can reduce the analysis of the triangle motif to the analysis of the planar fast–slow system

$$\begin{aligned} \begin{aligned} x_1'&= \left( \frac{1}{2}+ \underbrace{y +(\alpha _1-\alpha _2)x_1+\alpha _2\sigma _0}_{=:{\tilde{w}}}\right) (-2x_1+\sigma _0)\\ y'&= \varepsilon g(x_1,-x_1+\sigma _0,\frac{\sigma _0}{2},y,\varepsilon ), \end{aligned} \end{aligned}$$

(24)

Now, it is straightforward to see that the critical manifold is given by

$$\begin{aligned} \mathcal {C}_0 = \left\{ (x_1,y)\in \mathbb {R}^2\, | \, \left( \tilde{w}+\frac{1}{2}\right) (-2x_1+\sigma _0) = 0\right\} . \end{aligned}$$

(25)

Let us consider the lines

$$\begin{aligned} \begin{aligned} \mathcal {M}_0&= \left\{ (x_1,y)\in \mathbb {R}^2\, | \, {\tilde{w}}+\frac{1}{2}= 0\right\} \\ \mathcal {N}_0&= \left\{ (x_1,y)\in \mathbb {R}^2\, | \, -2x_1+\sigma _0 = 0\right\} , \end{aligned} \end{aligned}$$

(26)

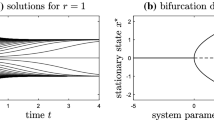
which are subsets of the critical manifold since $\mathcal {C}_0=\mathcal {M}_0\cup \mathcal {N}_0$. It is clear that the intersection $p=\mathcal {M}_0\cap \mathcal {N}_0=\left\{ (x_1,y)=\left( \frac{\sigma _0}{2},-\frac{1+\sigma _0(\alpha _1+\alpha _2)}{2}\right) \right\}$ is the only nonhyperbolic point of the layer equation of (24), and that the stability properties of $\mathcal {C}_0$ are as shown in Fig. 3. For brevity let $q=-\frac{1+\sigma _0(\alpha _1+\alpha _2)}{2}$.

Fig. 3

Left: stability properties of the critical manifold $\mathcal {C}_0$, where we partition the sets $\mathcal {M}_0$ and $\mathcal {N}_0$ into their attracting and repelling parts, and where $p=\left( \frac{\sigma _0}{2},-\frac{1+\sigma _0(\alpha _1+\alpha _2)}{2}\right)$ is a nonhyperbolic point of the fast dynamics. The case $\alpha _1-\alpha _2=0$ is degenerate and corresponds to the case where $\mathcal {M}_0$ is aligned with the fast foliation. Right: blow-up of the nonhyperbolic point p, where $\gamma _c$ is a (singular) maximal canard. The details of the blow-up analysis are given in Sect. 3.3

Next, suppose trajectories converge to $\mathcal {N}_0^\text {a}$. This means that $(x_1(t),x_2(t),x_3(t))\rightarrow \frac{\sigma _0}{2}(1,1,1)$ as $t\rightarrow \infty$. That is, the agents reach consensus; hence, we call $\mathcal {N}_0$ the consensus manifold. On the other hand, assume trajectories converge to $\mathcal {M}_0^\text {a}$. For this it is necessary that $\alpha _1-\alpha _2\ne 0$; otherwise, $\mathcal {M}_0$ is tangent to the fast foliation. Then $(x_1(t),x_2(t),x_3(t))\rightarrow \left( -\frac{\frac{1}{2}+\alpha _2\sigma _0+y}{\alpha _1-\alpha _2}, \frac{\frac{1}{2}+\alpha _1\sigma _0+y}{\alpha _1-\alpha _2},\frac{\sigma _0}{2} \right)$ as $t\rightarrow \infty$. That is, for fixed values of y, agents converge to different values depending on their initial conditions. Therefore, we call $\mathcal {M}_0$ the clustering manifold. Our goal will be to describe the dynamics of the network as agents transition from consensus into clustering. Thus, we also assume that $g(p,0)<0$.

Remark 4

Note that the sign of $(\alpha _1-\alpha _2)$ only changes the orientation of $\mathcal {M}_0$. In fact, if we denote (24) by $X(x_1,y,\varepsilon ,\rho )$ with $\rho =\alpha _1-\alpha _2\ge 0$, one can show that $X(x_1,y,\varepsilon ,-\rho )=-X(-x_1,y,\varepsilon ,\rho )$. From this we shall further assume that $\alpha _1-\alpha _2\ge 0$. For completeness we show the singular limit for the case $(\alpha _1-\alpha _2)<0$ in Fig. 4, but shall not be further discussed.

Fig. 4

Singular limit for the case $(\alpha _1-\alpha _2)<0$, compared with Fig. 3

It should be clear up to this point that the main difficulty for the analysis of fast–slow system (24) is given by the transition across a transcritical singularity (De Maesschalck 2015; Krupa and Szmolyan 2001b). Our goal is not to present a new analysis of this phenomenon but rather to study the effects of the blow-up transformation in a network. We shall show below that on each chart of the blow-up space, the resulting blow-up system can also be interpreted as a particular adaptive network. More importantly, it turns out that via the blow-up transformation one gains a clear distinction between the dynamics occurring at the different timescales. On a more technical matter, we will also show that the fact that the problem under study is defined on a graph results on a maximal canard, which in De Maesschalck (2015), Krupa and Szmolyan (2001b) is nongeneric.

3.2 Main Result

Since p is nonhyperbolic, the classical Fenichel theorem is not enough to conclude that for $\varepsilon >0$ sufficiently small we have a qualitatively equivalent behaviour to the one in the limit $\varepsilon =0$ described above. Therefore, a more detailed analysis is needed for our purposes. To state our main result, and for the analysis to be performed later, it will be convenient to move the origin of the coordinate system to the nonhyperbolic point p and to relabel the coordinates of the nodes. So, let us perform the following steps

• 1. Relabel the fast coordinates as $x=(x_1,x_2,x_3)=(a,b,c)$. This will make our notations across the blow-up charts simpler.

• 2. Translate coordinates according to $(a,b,c,y)\mapsto ((a,b,c)+\frac{\sigma _0}{2}\varvec{1}_3,y-q)$, where $\varvec{1}_m=(1,\ldots ,1)\in \mathbb {R}^m$ and we recall that $\sigma _0=\frac{2}{3}(a(0)+b(0)+c(0))$ and $q=-\frac{1+\sigma _0(\alpha _1+\alpha _2)}{2}$. Note that this translation depends on the initial conditions, but has the convenient implication $a(t)+b(t)+c(t)=0$ for all $t\ge 0$.

• 3. Rescale the parameter $\varepsilon$ by $\varepsilon \mapsto \frac{\varepsilon }{|g(0)|}$. Thus, we may assume that $g(0)=-1$.

With the above we now consider

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a'\\ b'\\ c' \end{bmatrix}&=-\begin{bmatrix} w + 1 &{}\quad -w &{}\quad -1\\ -w &{}\quad w+1 &{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}\begin{bmatrix} a \\ b\\ c\\ \end{bmatrix}\\ y'&=\varepsilon (-1+\mathcal {O}(a,b,c,y,\varepsilon )) \end{aligned} \end{aligned}$$

(27)

where $w=-\frac{1}{2} + y + \alpha _1 a + \alpha _2 b$. Next, let us define the sections

$$\begin{aligned} \begin{aligned} \Sigma ^{\text {en}}&= \left\{ (a,b,c,y)\in \mathbb {R}^4\,|\, y=\delta \right\} ,\\ \Sigma ^{\text {ex}}&= \left\{ (a,b,c,y)\in \mathbb {R}^4\,|\, y=-\delta \right\} ,\\ \end{aligned} \end{aligned}$$

(28)

where $\delta >0$ is of order $\mathcal {O}(1)$. We further define the map

$$\begin{aligned} \begin{aligned} \Pi&:\Sigma ^{\text {en}} \rightarrow \Sigma ^{\text {ex}}, \end{aligned} \end{aligned}$$

(29)

which is induced by the flow of (27). We prove the following.

Theorem 2

Consider fast–slow system (27), where $\alpha _1-\alpha _2\ge 0$. Then

• (T1) The set $\mathcal {A}=\left\{ (a,b,c,y)\in \mathbb {R}^4\,|\, c=\frac{a+b}{2}\right\}$ is globally attracting.

• (T2) The critical manifold of (27) is contained in $\mathcal {A}$ and is given by the union

  $$\begin{aligned} \mathcal {C}_0=\mathcal {N}_0^\text {a}\cup \mathcal {N}_0^\text {r}\cup \mathcal {M}_0^\text {a}\cup \mathcal {M}_0^\text {r}\cup \left\{ 0 \right\} , \end{aligned}$$

  (30)

  where

  $$\begin{aligned} \begin{aligned} \mathcal {N}_0^\text {a}&= \left\{ (a,b,c,y)\in \mathbb {R}^4 \, | \, a=b=c=0, \, y>0 \right\} ,\\ \mathcal {N}_0^\text {r}&= \left\{ (a,b,c,y)\in \mathbb {R}^4 \, | \, a=b=c=0, \, y<0 \right\} ,\\ \mathcal {M}_0^\text {a}&= \left\{ (a,b,c,y)\in \mathbb {R}^4 \, | \, y+\alpha _1 a + \alpha _2 b = 0, \, y<0, \, \alpha _1-\alpha _2>0 \right\} \\ \mathcal {M}_0^\text {r}&= \left\{ (a,b,c,y)\in \mathbb {R}^4 \, | \, y+\alpha _1 a + \alpha _2 b = 0, \, y>0, \, \alpha _1-\alpha _2>0 \right\} . \end{aligned} \end{aligned}$$

  (31)

• (T3) Restriction to $\mathcal {A}$ is equivalent to the restriction to $\left\{ b=-a, \; c=0 \right\}$.

Restricted to $\mathcal {A}$ and for $\varepsilon >0$ sufficiently small:

• (T4) There exists a slow manifold $\mathcal {N}_\varepsilon =\left\{ (a,y)\in \mathbb {R}^2\, | \, a=0 \right\}$ that is a maximal canard. Moreover, $\mathcal {N}_\varepsilon$ is attracting for $y>0$ and repelling for $y<0$.

• (T5) If $\alpha _1=\alpha _2$ then $\Pi |_{\mathcal {A}}(a,b,c,y)=\Pi (a,-a,0,y)=(a,-a,0,-y)$. Moreover, every trajectory with initial condition in $\Sigma ^\text {en}$ with $a\ne 0$ diverges from $\mathcal {N}_\varepsilon$ exponentially fast as $t\rightarrow \infty$.

• (T6) If $\alpha _1-\alpha _2>0$, there exist slow manifolds $\mathcal {M}_\varepsilon ^\text {a}$ and $\mathcal {M}_\varepsilon ^\text {r}$ given by

  $$\begin{aligned} \begin{aligned} \mathcal {M}_\varepsilon ^\text {a}&= \left\{ (a,y)\in \mathbb {R}^2\, | \, a=H(y,\varepsilon )+\mathcal {O}(\varepsilon ^{1/2}), \, y<0 \right\} \\ \mathcal {M}_\varepsilon ^\text {r}&= \left\{ (a,y)\in \mathbb {R}^2\, | \, a=H(y,\varepsilon )+\mathcal {O}(\varepsilon ^{1/2}), \, y>0 \right\} , \end{aligned} \end{aligned}$$

  (32)

  where

  $$\begin{aligned} H(y,\varepsilon )=-\frac{\varepsilon ^{1/2}}{2(\alpha _1-\alpha _2)D_+(\varepsilon ^{-1/2}y)}, \end{aligned}$$

  (33)

  with $D_+$ denoting the Dawson function (Abramowitz and Stegun 1972, pp. 219 and 235). In this case, if $(a-b)|_{\Sigma ^\text {en}}>0$ then the map $\Pi$ is well-defined and the corresponding trajectories converge towards $\mathcal {M}_\varepsilon ^\text {a}$ as $t\rightarrow \infty$. On the contrary, if $(a-b)|_{\Sigma ^\text {en}}<0$, then the corresponding trajectories diverge exponentially fast as $t\rightarrow \infty$.

Proof

Items (T1) and (T2) have already been proven in our preliminary analysis of Sect. 3.1. Item (T3) readily follows from the relations $a+b+c=0$ and $c=\frac{a+b}{2}$, which are simultaneously satisfied on $\mathcal {A}$. The proof of items (T3)–(T6) is given in Sect. 3.3.4. $\square$

The claims of Theorem 2 are sketched in Fig. 5.

Fig. 5

Schematic representation of the dynamics of (27) in $\mathcal {A}$ and for $\varepsilon >0$ sufficiently small, compared with Fig. 3

Interpretation In terms of the network, Theorem 2 tells us that:

• The time evolution of the node c (the node that is not connected by the dynamic weight) can always be described as a combination of the dynamics of the nodes (a, b) (those connected to the dynamic weight).

• The parameters $\alpha _1,\alpha _2$ in the definition of the weight $w=-\frac{1}{2}+y+\alpha _1 a + \alpha _2 b$, play an essential role: (i) if $\alpha _1=\alpha _2$, then there is no “clustering manifold”. Another way to interpret this degenerate case is that the nodes (or agents) have an equal contribution towards the value of the weight. This results in a zero net contribution of the nodes towards the dynamics of the weight. This is already noticeable in (24), where $\alpha _1=\alpha _2$ results in ${\tilde{w}}$ being independent on the nodes’ state. In this case the dynamics are rather simple, trajectories are attracted towards consensus for $y>0$ and repelled from consensus for $y<0$; (ii) if $\alpha _1\ne \alpha _2$, then the clustering manifold exists. For suitable initial conditions, the nodes first approach consensus, but then, when $y<0$, the nodes tend towards a clustered state in which $b=-a$ and $c=0$.

• The consensus manifold $\mathcal {N}_\varepsilon$ is a maximal canard, which implies that one observes a delayed loss of stability of $\mathcal {N}_\varepsilon$. In other words, one expects that trajectories exponentially near $\mathcal {N}_\varepsilon$ stay close to it for time of order $\mathcal {O}(1)$ after they cross the transcritical singularity before being repelled from it. See also “Appendix A”.

3.3 Blow-Up Analysis

In this section we are going to study the trajectories of (27) in a small neighbourhood of the origin. To do this we employ the blow-up method (Dumortier et al. 1996; Jardón-Kojakhmetov and Kuehn 2019; Krupa and Szmolyan 2001a; Kuehn 2015).

Remark 5

We could naturally perform the blow-up analysis restricted to the invariant and attracting subset $\mathcal {A}$. However, since one of our goals is to investigate the effects of the blow-up on network dynamics, we shall proceed by blowing up (27) and track, on each chart, the resulting “blown-up network dynamics”.

Let the blow-up map be defined by

$$\begin{aligned} a=\bar{r}\bar{a}, \; b=\bar{r}\bar{b}, \; c=\bar{r}\bar{c}, \; y=\bar{r}\bar{y}, \; \varepsilon =\bar{r}^2\bar{\varepsilon }, \end{aligned}$$

(34)

where $\bar{a}^2+\bar{b}^2+\bar{c}^2+\bar{y}^2+\bar{\varepsilon }^2=1$ and $\bar{r}\ge 0$.

We define the charts

$$\begin{aligned} \begin{aligned} K_1 = \left\{ \bar{y}= 1 \right\} , \; K_2 = \left\{ \bar{\varepsilon }=1 \right\} , K_3 = \left\{ \bar{y}= -1 \right\} . \end{aligned} \end{aligned}$$

(35)

Accordingly we define local coordinates on each chart by

$$\begin{aligned} \begin{array}{llllll} K_1 : &{}a=r_1a_1,&{} b=r_1b_1,&{} c=r_1c_1,&{} y=r_1,&{} \varepsilon =r_1^2\varepsilon _1,\\ K_2 : &{}a=r_2a_2,&{} b=r_2b_2,&{} c=r_2c_2,&{} y=r_2y_2,&{} \varepsilon =r_2^2,\\ K_3 : &{}a=r_3a_3,&{} b=r_3b_3,&{} c=r_3c_3,&{} y=-r_3,&{} \varepsilon =r_3^2\varepsilon _3.\\ \end{array} \end{aligned}$$

(36)

The following relationship between the local blow-up coordinates will be used throughout our analysis.

Lemma 2

Let $\kappa _{ij}$ denote the transformation map between charts $K_i$ and $K_j$. Then

$$\begin{aligned} \begin{array}{llllllll} \kappa _{12} : &{}r_2 = r_1\varepsilon _1^{1/2},\, &{}a_2 = \varepsilon _1^{-1/2}a_1,\, &{}b_2 = \varepsilon _1^{-1/2}b_1,\, &{}c_2 = \varepsilon _1^{-1/2}c_1,\, &{}y_2 = \varepsilon _1^{-1/2},\\ \kappa _{21} : &{}r_1=r_2y_2, \, &{}a_1=y_2^{-1}a_2,\, &{}b_1=y_2^{-1}b_2,\, &{}c_1=y_2^{-1}c_2,\, &{}\varepsilon _1=y_2^{-2}, \\ \kappa _{32} : &{}r_2 = r_3\varepsilon _3^{1/2},\, &{}a_2 = \varepsilon _3^{-1/2}a_3,\, &{}b_2 = \varepsilon _3^{-1/2}b_3,\, &{}c_2 = \varepsilon _3^{-1/2}c_3,\, &{}y_2 = -\varepsilon _3^{-1/2},\\ \kappa _{23} : &{}r_3=-r_2y_2, \, &{}a_3=-y_2^{-1}a_2,\, &{}b_3=-y_2^{-1}b_2,\, &{}c_3=-y_2^{-1}c_2,\, &{}\varepsilon _3=y_2^{-2}. \end{array}\nonumber \\ \end{aligned}$$

(37)

Note that $\kappa _{ij}^{-1}=\kappa _{ji}$.

Let us now proceed with the blow-up analysis on each of the charts. We recall that on $K_1$ one studies orbits of (27) as they approach the origin, on $K_2$ orbits within a small neighbourhood of the origin, and finally on $K_3$ orbits as they leave a small neighbourhood of the origin.

3.3.1 Analysis in the Entry Chart $K_1$

In this chart the blow-up map is given by

$$\begin{aligned} a=r_1a_1, \; b=r_1b_1, \; c=r_1c_1,\; y = r_1,\; \varepsilon =r_1^2\varepsilon _1. \end{aligned}$$

(38)

We then obtain the blown-up vector field

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a_1' \\ b_1' \\ c_1' \end{bmatrix}&= -\begin{bmatrix} \frac{1}{2}&{}\quad \frac{1}{2}&{}\quad -1 \\ \frac{1}{2}&{}\quad \frac{1}{2}&{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}\begin{bmatrix} a_1\\ b_1\\ c_1\end{bmatrix}+r_1f_1(a_1,b_1,c_1,r_1,\varepsilon _1)\\ r_1'&= r_1^2\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2r_1\varepsilon _1^2(-1+\mathcal {O}(r_1)), \end{aligned} \end{aligned}$$

(39)

where $f_1(a_1,b_1,c_1,r_1,\varepsilon _1)$ reads as

$$\begin{aligned} f_1 = \left( (1+\alpha _1a_1+\alpha _2b_1) \begin{bmatrix} -1 &{}\quad 1 &{}\quad 0 \\ 1 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} - \varepsilon _1(-1+\mathcal {O}(r_1)) \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 \end{bmatrix} \right) \begin{bmatrix} a_1\\ b_1\\ c_1\end{bmatrix}.\nonumber \\ \end{aligned}$$

(40)

Remark 6

In (39) and (40) the term $-1+\mathcal {O}(r_1)$ stands for exactly the same function.

Let us interpret the equations in the first chart from a network dynamics perspective. We are interested in the dynamics of (39) for $\varepsilon _1$ small and with $r_1\rightarrow 0$. This is because $r_1\rightarrow 0$ is equivalent to y(t) approaching the origin in (27). Thus, we may regard (39) as a perturbation of a network with fixed weights as shown in Fig. 6.

Fig. 6

Network interpretation corresponding to (39). The order $\mathcal {O}(1)$ terms in (39) correspond to a triangle motif with fixed weights. The particular values of the weights make such a network degenerate in the sense that the corresponding Laplacian has a kernel of dimension two. Next, the order $\mathcal {O}(r_1)$ terms in (39) correspond to two nodes connected by a dynamic weight. Finally, the $\mathcal {O}(r_1\varepsilon _1)$ correspond to internal node dynamics

The order $\mathcal {O}(r_1)$ terms can be seen as a smaller network, only involving the nodes $(a_1,b_1)$ and with dynamic edge with weight $r_1(1+\alpha _1a_1+\alpha _2b_1)$. The order $\mathcal {O}(r_1\varepsilon _1)$ can be interpreted as internal dynamics on each node.

Continuing with the analysis, it is straightforward to check (with the help of (17)) that for $r_1=0$ we have $c_1(t_1)\rightarrow \frac{a_1(t_1)+b_1(t_1)}{2}$ as $t_1\rightarrow \infty$, where $t_1$ denotes the time parameter of (39). We now proceed with a more detailed analysis of (39) as follows.

Proposition 1

System (39) has the following sets of equilibrium points.

$$\begin{aligned} \begin{aligned} S_{1,0}&= \left\{ (a_1,b_1,c_1,r_1,\varepsilon _1)\in \mathbb {R}^5\,|\, r_1= 0, \, c_1= \frac{a_1+b_1}{2} \right\} ,\\ N_{1,0}&= \left\{ (a_1,b_1,c_1,r_1,\varepsilon _1)\in \mathbb {R}^5\,|\, \varepsilon _1= 0, \, c_1= \frac{a_1+b_1}{2}, \, a_1=b_1\right\} ,\\ M_{1,0}&= \left\{ (a_1,b_1,c_1,r_1,\varepsilon _1)\in \mathbb {R}^5\,|\, \varepsilon _1= 0, \, c_1= \frac{a_1+b_1}{2}, \, 1+\alpha _1a_1+\alpha _2b_1=0 \right\} .\\ \end{aligned} \end{aligned}$$

(41)

Proof

Straightforward computations. $\square$

Next, we show that the set defined by $c_1= \frac{a_1+b_1}{2}$ is an attracting centre manifold.

Proposition 2

The system given by (39) has a local 4-dimensional centre manifold $\mathcal {W}_1^\text {c}$ and a local 1-dimensional stable manifold $\mathcal {W}_1^\text {s}$. The centre manifold $\mathcal {W}_1^\text {c}$ contains the sets of Proposition 1. Furthermore, $\mathcal {W}_1^\text {c}$ is given by $c_1=\frac{a_1+b_1}{2}$, and the flow along it reads as

$$\begin{aligned} \begin{aligned} a_1'&= r_1(1+\alpha _1a_1+\alpha _2b_1)(b_1-a_1) - r_1\varepsilon _1(-1+\mathcal {O}(r_1))a_1\\ b_1'&= r_1(1+\alpha _1a_1+\alpha _2b_1)(a_1-b_1) - r_1\varepsilon _1(-1+\mathcal {O}(r_1))b_1\\ r_1'&= r_1^2\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2r_1\varepsilon _1^2(-1+\mathcal {O}(r_1)). \end{aligned} \end{aligned}$$

(42)

Proof

We start by using the similarity transformation $\begin{bmatrix} A_1&B_1&C_1\end{bmatrix}^\top =T^\top \begin{bmatrix} a_1&b_1&c_1\end{bmatrix}^\top$, where T is defined in (17). Under such a transformation one rewrites (39) as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} A_1' \\ B_1' \\ C_1' \end{bmatrix}&= - \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 3 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \begin{bmatrix} A_1\\ B_1\\ C_1\end{bmatrix} + r_1F_1(A_1,B_1,C_1,r_1,\varepsilon _1)\\ r_1'&= r_1^2\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2r_1\varepsilon _1^2(-1+\mathcal {O}(r_1)), \end{aligned} \end{aligned}$$

(43)

where

$$\begin{aligned} \begin{aligned} F_1 =&\left( \underbrace{\left( 1+\frac{\sqrt{3}}{3}(\alpha _1+\alpha _2)A_1-\frac{\sqrt{6}}{6}(\alpha _1+\alpha _2)B_1+\frac{\sqrt{2}}{2}(\alpha _2-\alpha _1)C_1\right) }_{=:{\bar{W}}} \right. \\&\begin{bmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -2 \end{bmatrix}-\left. \varepsilon _1(-1+\mathcal {O}(r_1)) \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 \end{bmatrix}\right) \begin{bmatrix} A_1\\ B_1\\ C_1\end{bmatrix}. \end{aligned} \end{aligned}$$

(44)

It is now straightforward to see that there is a 1-dimensional stable manifold $\mathcal {W}_1^s$ tangent to the $B_1$-axis and a 4-dimensional centre manifold $\mathcal {W}_1^c$ containing the set of equilibrium points $\left\{ (A_1,B_1,C_1,r_1,\varepsilon _1)\in \mathbb {R}^5\,|\, r_1=B_1=0 \right\}$. $\square$

Remark 7

Observe that, due to the term $(-1+\mathcal {O}(r_1))$, the vector field corresponding to $B_1'$ is not decoupled from the centre directions. However, we show below that $\mathcal {W}_1^c$ is indeed given by $B_1=0$.

The centre manifold $\mathcal {W}_1^c$ can be expressed by $B_1=h_1(r_1,A_1,C_1,\varepsilon _1)$ satisfying $h_1(0)=0$, $\text {D}h_1(0)=0$, where $\text {D}h_1$ denotes the Jacobian of $h_1$. Let $h_1$ be given as

$$\begin{aligned} h_1 = \sum _{\begin{array}{c} i,j,k,l\ge 0\\ i+j+k+l\ge 2 \end{array}}\sigma _{ijkl}A_1^iC_1^jr_1^k\varepsilon _1^l, \end{aligned}$$

(45)

where $\sigma _{ijkl}$ denotes scalar coefficients. Substituting (45) into the equation for $B_1'$ we get

$$\begin{aligned} -3h_1= & {} r_1\varepsilon _1(-1+\mathcal {O}(r_1))\left( -h_1 + A_1\frac{\partial h_1}{\partial A_1}+C_1\frac{\partial h_1}{\partial C_1}+r_1\frac{\partial h_1}{\partial r_1} \right. \nonumber \\&\left. -2\varepsilon _1\frac{\partial h_1}{\partial \varepsilon _1} \right) -2r_1{\bar{W}}C_1\frac{\partial h_1}{\partial C_1}. \end{aligned}$$

(46)

We now have the following observations:

• 1. All the monomials in the right-hand side of (46) are of degree at least 3, therefore, all coefficients $\sigma _{ijkl}$ with $i+j+k+l=2$ are zero.

• 2. Since the right-hand side of (46) is of order $\mathcal {O}(r_1)$ we have that all coefficients $\sigma _{ij0l}$ are zero for all $i+j+l\ge 3$. Naturally, we then have that $h_1\in \mathcal {O}(r_1)$ and thus $k\ge 1$.

• 3. The coefficients $\sigma _{ijk0}$, $k\ge 1$, are computed from the equality

  $$\begin{aligned} \begin{aligned} -3h_1&= -2r_1{\bar{W}}C_1\frac{\partial h_1}{\partial C_1}\\&=-2r_1\left( 1+\frac{\sqrt{3}}{3}(\alpha _1+\alpha _2)A_1-\frac{\sqrt{6}}{6}(\alpha _1+\alpha _2)h_1+\frac{\sqrt{2}}{2}(\alpha _2-\alpha _1)C_1\right) C_1\frac{\partial h_1}{\partial C_1}\\&=-2r_1(1+\eta _1A_1- \eta _2 h_1 + \eta _3C_1)C_1\frac{\partial h_1}{\partial C_1}, \end{aligned}\nonumber \\ \end{aligned}$$

  (47)

  where the last equation is introduced for simplicity. We readily see that all coefficients $\sigma _{i0k0}$ with $i+k\ge 3$ are zero. Next, for $i+j+k=3$, the term $h_1C_1\frac{\partial h_1}{\partial C_1}$ does not play a role because its degree is at least 4. It follows from the first item that $\sigma _{ijk0}=0$ for $i+j+k=3$. Next, let us write (47) in a simplified form by (i) expanding it, (ii) writing all monomials in the exact same form $A_1^iC_1^jr_1^k$, (iii) by omitting the monomial, and (iv) omitting the 0 of the superscript $\sigma _{ijk0}$. We get

  $$\begin{aligned} \begin{aligned} -3\sum \sigma _{ijk}&= -2\sum j\sigma _{ij(k-1)} -2\eta _1\sum j \sigma _{(i-1)j(k-1)}\\&\quad -2\eta _3\sum j\sigma _{i(j-1)(k-1)}+2\eta _2\sum \sigma _{ijk}\sum j\sigma _{ij(k-1)} \end{aligned} \end{aligned}$$

  (48)

  Now, it suffices to note that for each monomial, the coefficient $\sigma _{ijk}$, with $i+j+k=n$ and $n>3$, of the left-hand side depends exclusively on coefficients $\sigma _{ijk}$ with $i+j+k<n$. From the previous items, and by progressing at each degree n, it follows that $\sigma _{ijk0}=0$ for all $i+j+k\ge 2$.

• 4. The exact same argument as in item 3 applies for $l\ge 1$.

The expression of the centre manifold in the original coordinates is obtained by noting that $B_1=\frac{\sqrt{6}}{6}(2c_1-a_1-b_1)$, implying that $c_1= \frac{a_1+b_1}{2}$ as stated. Finally, the flow along the centre manifold is obtained by taking into account the restriction $c_1= \frac{a_1+b_1}{2}$. $\square$

Remark 8

$\mathcal {W}_1^\text {c}$ is the blow-up of $\mathcal {A}$.

Before proceeding with the analysis on $\mathcal {W}_1^\text {c}$, we have the next observation.

Proposition 3

Let $(a_1(0),b_1(0),c_1(0))$ denote initial conditions of (39) and let $\varepsilon _1=0$. Then ${{\,\mathrm{sign}\,}}(a_1)\rightarrow {{\,\mathrm{sign}\,}}(a_1(0)-b_1(0))$ as $t\rightarrow \infty$.

Proof

It is easier to see the claim in (43) with $\varepsilon _1=0$, and where $A_1=\frac{\sqrt{3}}{3}(a_1+b_1+c_1)=0$, ${{\,\mathrm{sign}\,}}(B_1)={{\,\mathrm{sign}\,}}(2c_1-a_1-b_1)$ and ${{\,\mathrm{sign}\,}}(C_1)={{\,\mathrm{sign}\,}}(b_1-a_1)$. We note in (43) that ${{\,\mathrm{sign}\,}}(B_1)$ and ${{\,\mathrm{sign}\,}}(C_1)$ are invariant. Therefore as $B_1\rightarrow 0$ (equivalently $2c_1\rightarrow a_1+b_1$) we have $a_1+b_1\rightarrow 0$ and therefore ${{\,\mathrm{sign}\,}}(b_1-a_1)\rightarrow {{\,\mathrm{sign}\,}}(-2a_1)$ from which the claim immediately follows. $\square$

The previous observation is important since, as we will see, in $\mathcal {W}_1^\text {c}$ the set $\left\{ a_1=0\right\}$ is invariant. Note that we can now desingularize the dynamics restricted to $\mathcal {W}_1^\text {c}$ by dividing by $r_1$ in (42), as is usually the case when blowing up, to obtain

$$\begin{aligned} \begin{aligned} a_1'&= (1+\alpha _1a_1+\alpha _2b_1)(b_1-a_1) - \varepsilon _1(-1+\mathcal {O}(r_1))a_1\\ b_1'&= (1+\alpha _1a_1+\alpha _2b_1)(a_1-b_1) - \varepsilon _1(-1+\mathcal {O}(r_1))b_1\\ r_1'&= r_1\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2\varepsilon _1^2(-1+\mathcal {O}(r_1)). \end{aligned} \end{aligned}$$

(49)

Remark 9

Recall that $a_1(t_1)+b_1(t_1)+c_1(t_1)=0$ for all $t_1\ge 0$. Moreover, since in $\mathcal {W}_1^c$ we have $c_1=\frac{a_1+b_1}{2}$ we further have $a_1(t_1)+b_1(t_1)=0$ for all $t_1\ge 0$. Therefore, we can consider instead of (49) the 3-dimensional system

$$\begin{aligned} \begin{aligned} a_1'&= -2(1+(\alpha _1-\alpha _2)a_1)a_1- \varepsilon _1(-1+\mathcal {O}(r_1))a_1\\ r_1'&= r_1\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2\varepsilon _1^2(-1+\mathcal {O}(r_1)). \end{aligned} \end{aligned}$$

(50)

Naturally, solutions of (50) give solutions of (49) by adding $b_1(t_1)=-a_1(t_1)$. Therefore we proceed by studying (50). It is worth noting that on $\mathcal {W}_1^\text {c}$, the set $\left\{ (a_1,r_1,\varepsilon _1)\in \mathbb {R}^3\,|\,a_1=0\right\}$ is invariant. Therefore, it is important to keep track of the sign of $a_1$ as it approaches $\mathcal {W}_1^\text {c}$. Such sign is given by Proposition 3. That is, if $a_1(0)-b_1(0)>0$ (resp. $a_1(0)-b_1(0)<0$), then $a_1>0$ (resp. $a_1<0$) on $\mathcal {W}_1^\text {c}$. Similarly, if $a_1(0)-b_1(0)=0$, then $a_1=0$ on $\mathcal {W}_1^\text {c}$. Finally, we recall that $\mathcal {W}_1^\text {c}$ coincides precisely with the invariant set $\mathcal {A}$ written in the coordinates of this chart (see the statement of Theorem 2).

To study the dynamics in this chart, we are going to be interested in the properties of the flow between the sections

$$\begin{aligned} \begin{aligned} \Delta _1^\text {en}&= \left\{ (a_1,r_1,\varepsilon _1)\in \mathbb {R}^3\, | \, r_1=\delta _1,\, \varepsilon _1<\mu _1 \right\} \\ \Delta _1^\text {ex}&= \left\{ (a_1,r_1,\varepsilon _1)\in \mathbb {R}^3\, | \, r_1<\delta _1,\, \varepsilon _1=\mu _1 \right\} , \end{aligned} \end{aligned}$$

(51)

where $\delta _1>0$, and $\mu _1>0$ is sufficiently small. The precise meaning of these sections becomes clear in Sect. 3.3.4 where we compute a transition map through a whole neighbourhood of the origin of(27). For now it shall be enough to mention that the definition $\Delta _1^\text {en}$ is motivated by the entry section $\Sigma ^\text {en}$ (recall (28)), while $\Delta _1^\text {ex}$ is a convenient section allowing us to transition towards the central chart $K_2$.

We observe that the subspaces $\left\{ a_1=0\right\}$, $\left\{ r_1=\varepsilon _1=0\right\}$, $\left\{ r_1=0\right\}$, and $\left\{ \varepsilon _1=0\right\}$ are all invariant and thus are helpful to describe overall dynamics (50). So, we proceed as follows.

• In $\left\{ a_1=0 \right\}$ we have the planar system

  $$\begin{aligned} \begin{aligned} r_1'&= r_1\varepsilon _1(-1+\mathcal {O}(r_1))\\ \varepsilon _1'&= -2\varepsilon _1^2(-1+\mathcal {O}(r_1)). \end{aligned} \end{aligned}$$

  (52)

  which has a line of zeros $(r_1,\varepsilon _1)=(r_1,0)$ and an unstable invariant manifold $(r_1,\varepsilon _1)=(0,\varepsilon _1)$. Note that away from $\left\{ \varepsilon _1=0\right\}$ the flow of (52) is equivalent to that of a planar saddle. Next, we want to compute the time it takes to travel from $\Delta _1^\text {en}$ to $\Delta _1^\text {ex}$. Therefore, assume initial conditions $(r_1,\varepsilon _1)=(\delta _1,\varepsilon _1^*)$ and boundary conditions $(r_1,\varepsilon _1)=(r_1(T_1),\mu _1)$. From (52) we find that

  $$\begin{aligned} r_1(T_1) = \delta _1\left( \frac{\varepsilon _1^*}{\mu _1}\right) ^{1/2}. \end{aligned}$$

  (53)

  Then, one can estimate the transition time $T_1$ by integrating the equation for $\varepsilon _1'$, so that we get

  $$\begin{aligned} T_1=\frac{1}{2}\left( \frac{1}{\varepsilon _1^*}-\frac{1}{\mu _1} \right) (1+\mathcal {O}(\delta _1)), \qquad 0<\varepsilon _1^*\le \mu _1. \end{aligned}$$

  (54)

• In $\left\{ r_1=\varepsilon _1=0 \right\}$ we have the 1-dimensional system

  $$\begin{aligned} a_1' = -2(1+(\alpha _1-\alpha _2)a_1)a_1, \end{aligned}$$

  (55)

  where we recall that $\alpha _1-\alpha _2\ge 0$. In this case we have, generically, two hyperbolic equilibrium points: one stable at $a_1=0$ and one unstable at $a_1=\frac{1}{\alpha _2-\alpha _1}$. If $\alpha _1=\alpha _2$ then only the stable equilibrium at the origin exists. It will be useful to integrate (55), that is

  $$\begin{aligned} a_1(t_1)=-\frac{a_1^*}{(\alpha _1-\alpha _2)a_1^* - ((\alpha _1-\alpha _2)a_1^*+1)\exp (2t_1)}, \end{aligned}$$

  (56)

  where $a_1^*$ denotes an initial condition for (55).

• In $\left\{ r_1=0 \right\}$ we have

  $$\begin{aligned} \begin{aligned} a_1'&= -2(1+(\alpha _1-\alpha _2)a_1)a_1+ \varepsilon _1a_1\\ \varepsilon _1'&= 2\varepsilon _1^2. \end{aligned} \end{aligned}$$

  (57)

  Then, we have two 1-dimensional centre manifolds: $\mathcal {E}_1^\text {a}$ is a centre manifold to the equilibrium point $(a_1,\varepsilon _1)=(0,0)$ and $\mathcal {E}_1^\text {r}$ to $(a_1,\varepsilon _1)=\left( \frac{1}{\alpha _2-\alpha _1},0\right)$. The flow on both centre manifolds is given by $\varepsilon _1' = 2\varepsilon _1^2$, and we have that $\mathcal {E}_1^\text {a}$ is tangent to the $\varepsilon _1$-axis, while $\mathcal {E}_1^\text {r}$ is tangent to the vector $\begin{bmatrix} 1&-2(\alpha _2-\alpha _1)\end{bmatrix}^\top$. In fact, one can show that $\mathcal {E}_1^\text {a}$ is actually given by $a_1=0$ and that it is unique. On the other hand $\mathcal {E}_1^\text {r}$ is not unique and has the expansion $a_1=\frac{1}{\alpha _2-\alpha _1}+\frac{1}{2(\alpha _1-\alpha _2)}\varepsilon _1+\mathcal {O}(\varepsilon _1^2)$. Since $\varepsilon _1\ge 0$, we have that in a small neighbourhood of $(a_1,\varepsilon _1)=(0,0)$ the flow is equivalent to that of a saddle, while in a small neighbourhood of $(a_1,\varepsilon _1)=(\frac{1}{\alpha _2-\alpha _1},0)$ the flow is equivalent to that of a source. From this analysis we conclude that the flow of (57) is as sketched in Fig. 7.

Fig. 7

Schematic of the flow of (57) for $\alpha _2-\alpha _1>0$ and $\varepsilon _1$ small

Remark 10

The orbit $\mathcal {E}_1^\text {r}$ can be identified with the critical manifold $\mathcal {M}_0^\text {r}$ as it goes up on the blow-up sphere. The same correspondence holds for $\mathcal {E}_1^\text {a}$ and $\mathcal {N}_0$. Compare Figs. 7 and 3.

• In $\left\{ \varepsilon _1=0 \right\}$ we have

  $$\begin{aligned} \begin{aligned} a_1'&= -2(1+(\alpha _1-\alpha _2)a_1)a_1\\ r_1'&= 0. \end{aligned} \end{aligned}$$

  (58)

  Therefore, the $(a_1,r_1)$-plane is foliated by lines parallel to the $r_1$-axis. Along each leaf the flow is given by (55).

We can now summarize the previous analysis in the following proposition, which completely characterizes the dynamics of (39).

Proposition 4

The following statements hold for (39).

• 1. There exist a 1-dimensional local stable manifold $\mathcal {W}_1^\text {s}$ and a 4-dimensional local centre-stable manifold $\mathcal {W}_1^\text {c}$, which is given by the graph of $c_1=\frac{a_1+b_1}{2}$.

Restricted to $\mathcal {W}_1^\text {c}$ one has $b_1=-a_1$, which implies $c_1=0$, and:

• 2. There is an attracting 2-dimensional centre manifold $\mathcal {C}_1^\text {a}$. The manifold $\mathcal {C}_1^\text {a}$ contains a line of zeros $\ell _1^\text {a}=\left\{ (r_1,a_1,\varepsilon _1)\in \mathbb {R}^3\, | \, a_1=\varepsilon _1=0 \right\}$ and a 1-dimensional centre manifold $\mathcal {E}_1^\text {a}=\left\{ (r_1,a_1,\varepsilon _1)\in \mathbb {R}^3\, | \, r_1=a_1=0\right\}$. On the plane $\left\{ r_1=0 \right\}$, the centre manifold $\mathcal {E}_1^\text {a}$ is unique. The flow along $\mathcal {E}_1^\text {a}$ is unstable, that is, it diverges from the origin, while the flow on $\mathcal {C}_1^\text {a}$ away from $\ell _1^\text {a}$ is locally equivalent to that of a saddle.

• 3. There is a repelling 2-dimensional centre manifold $\mathcal {C}_1^\text {r}$. The manifold $\mathcal {C}_1^\text {r}$ contains a line of zeros $\ell _1^\text {r}=\left\{ (r_1,a_1,\varepsilon _1)\in \mathbb {R}^3\, | \, a_1=\frac{1}{\alpha _2-\alpha _1},\,\varepsilon _1=0 \right\}$ and a 1-dimensional centre manifold $\mathcal {E}_1^\text {r}=\left\{ (r_1,a_1,\varepsilon _1)\in \mathbb {R}^3\, | \, r_1=0, a_1=\frac{1}{\alpha _2-\alpha _1}+\mathcal {O}(\varepsilon _1)\right\}$. The flow along $\mathcal {E}_1^\text {r}$ is unstable, that is, it diverges from the equilibrium point $(a_1,\varepsilon _1)=\left( \frac{1}{\alpha _2-\alpha _1},0\right)$, while the flow on $\mathcal {C}_1^\text {r}$ away from $\ell _1^\text {r}$ is locally equivalent to that of a saddle.

Proof

The existence, graph representation and dimension of $\mathcal {W}_1^\text {c}$ are already proven in Proposition 2. The existence and dimension of $\mathcal {C}_1^\text {a}$ and of $\mathcal {C}_1^\text {r}$ follow from the linearization of (50). The flow on $\mathcal {C}_1^\text {a}$ and on $\mathcal {C}_1^\text {r}$ follows from (50) by noting that, up to leading-order terms, the vector field restricted to either of the centre manifolds is given by

$$\begin{aligned} \begin{aligned} r_1'&= -r_1\varepsilon _1\\ \varepsilon _1'&= 2\varepsilon _1^2. \end{aligned} \end{aligned}$$

$\square$

We are now ready to describe the flow of (50). Let $\Pi _1:\Delta _1^\text {en}\rightarrow \Delta _1^\text {ex}$ be a map defined by the flow of (50).

Theorem 3

The image $\Pi _1(\Delta _1^\text {en})$ in $\Delta _1^\text {ex}$ is of the form

$$\begin{aligned} \Pi _1\left( \begin{matrix} a_1\\ \delta _1 \\ \varepsilon _1\end{matrix}\right) =\left( \begin{matrix} h_{a_1} + O (a_1\varepsilon _1^2) \\ \delta _1\left( \frac{\varepsilon _1}{\mu _1} \right) ^{1/2}\\ \mu _1 \end{matrix} \right) , \end{aligned}$$

(59)

where the function $h_{a_1}=h_{a_1}(a_1,\delta _1,\varepsilon _1)$ is given by

$$\begin{aligned} h_{a_1}= & {} -\frac{a_1}{(\alpha _1-\alpha _2)a_1- ((\alpha _1-\alpha _2)a_1+1)\exp (2T_1)}, \nonumber \\ T_{1}= & {} \frac{1}{2}\left( \frac{1}{\varepsilon _1}-\frac{1}{\mu _1} \right) (1+\mathcal {O}(\delta _1)). \end{aligned}$$

(60)

Proof

The proof follows our previous analysis. The term $h_{a_1}$ is obtained from (56) and evaluating transition time (54). The higher-order terms $\mathcal {O}(a_1\varepsilon _1^2)$ follow from (57) with $\varepsilon _1>0$ small. For the expression of $h_{a_1}$ it is important to recall Proposition 3. This means that the initial condition $a_1^*$ in (56) has the same sign as $a_1(0)-b_1(0)$, and where $a_1(0),b_1(0)$ are initial conditions of (39). $\square$

Remark 11

• If $\alpha _1-\alpha _2=0$ then $h_{a_1}= a_1\exp (-2T_1)$.

• If $a_1>\frac{1}{\alpha _1-\alpha _2}$, then the function $h_{a_1}$ is well-defined for any point $(a_1,\delta _1,\varepsilon _1)\in \Delta _1^\text {en}$. If $a_1\le \frac{1}{\alpha _1-\alpha _2}$, then $h_{a_1}$ is well-defined only for $T_1<\frac{1}{2}\ln \left( \frac{(\alpha _1-\alpha _2)a_1}{(\alpha _1-\alpha _2)a_1+1} \right)$. In such a case we choose suitably $0<\varepsilon _1<\mu _1\ll \delta _1$ so that the function $h_{a_1}$ is well-defined.

The analysis in this chart is sketched in Fig. 8.

Fig. 8

Schematic representation of the flow of (39) restricted to the attracting centre manifold $\mathcal {W}_1^\text {c}$. The wegde-like shape of the image of $\Pi _1(\Delta _1^{\text {en}})$ (shaded in $\Delta _1^{\text {ex}}$) is due to the contraction towards $\mathcal {C}_1^\text {a}$

3.3.2 Analysis in the Rescaling Chart $K_2$

In this chart we study the dynamics of (27) within a small neighbourhood of the origin. The corresponding blow-up map reads as

$$\begin{aligned} a=r_2a_2, \; b=r_2b_2, \; c=r_2c_2,\; y = r_2y_2,\; \varepsilon =r_2^2. \end{aligned}$$

(61)

The blown-up vector field reads as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a_2'\\ b_2' \\ c_2' \end{bmatrix}&=-( {\bar{L}}_0 + r_2\bar{w}{\bar{L}}_1) \begin{bmatrix} a_2\\ b_2\\ c_2\end{bmatrix}\\ y_2'&= r_2(-1+\mathcal {O}(r_2)),\\ r_2'&=0 \end{aligned} \end{aligned}$$

(62)

where

$$\begin{aligned} \begin{aligned} {\bar{L}}_0=\begin{bmatrix} \frac{1}{2}&{}\quad \frac{1}{2}&{} \quad -1 \\ \frac{1}{2}&{}\quad \frac{1}{2}&{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}, \end{aligned}\qquad \qquad {\bar{L}}_1 = \begin{bmatrix} 1 &{}\quad -1 &{}\quad 0\\ -1 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \end{aligned}$$

(63)

with $\bar{w}= y_2+\alpha _1a_2+\alpha _2b_2$. In the rest of this section we omit the equation $r_2'=0$ and just keep in mind that $r_2$ is a parameter in this chart.

Before proceeding with the analysis, it is again very helpful to study the effect that the blow-up map has on the network’s topology. Note that (62) can be regarded as the model of an $\mathcal {O}(r_2)$ graph preserving perturbation of a static network as shown in Fig. 9.

Fig. 9

Graph representation of (62)

Roughly speaking, the blow-up separates two types of dynamics: the dynamics of order $\mathcal {O}(1)$ correspond to a consensus protocol on a degenerate static network. Here by degenerating we mean that the Laplacian of the static network has a kernel of dimension 2, as can be easily seen in (62)–(63) with $r_2=0$. Next, the dynamics of order $\mathcal {O}(r_2)$ occur in a slower timescale and correspond to the slowly varying edge with weight $r_2\bar{w}$.

We proceed with the description of the flow of (62).

Proposition 5

For $r_2\ge 0$ sufficiently small, the equilibrium points of (62) are given by

$$\begin{aligned} \left\{ (a_2,b_2,c_2,y_2,r_2)\in \mathbb {R}^5\,|\, r_2=0,\, (a_2,b_2,c_2)\in \ker ({\bar{L}}_0) \right\} . \end{aligned}$$

(64)

Proof

Straightforward computations. $\square$

Next we show that (62) has an attracting 4-dimensional centre manifold $\mathcal {W}_2^\text {c}$ and a 1-dimensional stable manifold $\mathcal {W}_2^s$. These objects, in fact, correspond, respectively, to $\mathcal {W}_1^\text {c}$ and $\mathcal {W}_1^\text {s}$ found in chart $K_1$. In qualitative terms, reduction to $\mathcal {W}_2^\text {c}$ will correspond to representing the behaviour of the third node, with state $c_2$, in terms of the other two nodes.

Proposition 6

System (62) has a 4-dimensional local centre manifold $\mathcal {W}_2^\text {c}$ and a 1-dimensional local stable manifold $\mathcal {W}_2^s$ that intersect at $\left\{ r_2=0\right\} \cap \left\{ c_2=\frac{a_2+b_2}{2}\right\}$. The centre manifold $\mathcal {W}_2^\text {c}$ is given by the graph of $c_2= \frac{a_2+b_2}{2}$, and it holds that $\kappa _{12}(\mathcal {W}_1^\text {c})=\mathcal {W}_2^\text {c}$.

Proof

The proof follows the same reasoning (and in fact it is simpler than) the proof of Proposition 2. The relation $\kappa _{12}(\mathcal {W}_1^\text {c})=\mathcal {W}_2^\text {c}$ is straightforward from (37). $\square$

Since the centre manifold $\mathcal {W}_2^c$ is attracting, and of codimension 1, the next step is to restrict the dynamics to it. However, the next observation is important (recall Proposition 3).

Lemma 3

The trajectories of (62) restricted to $\left\{ r_2=0 \right\}$ have the asymptotic behaviour

$$\begin{aligned} \lim _{t_2\rightarrow \infty }\left( a_2(t_2),b_2(t_2),c_2(t_2) \right) =\frac{1}{2}\left( a_2(0)-b_2(0),b_2(0)-a_2(0),0 \right) . \end{aligned}$$

(65)

As it was the case in chart $K_1$ the previous lemma gives us the relevant sign of $a_2$ on the centre manifold $\mathcal {W}_2^\text {c}$.

The restriction of (62) to $\mathcal {W}_2^\text {c}$ results on a vector field of order $\mathcal {O}(r_2)$, which can be desingularized as is usual in the blow-up method by dividing by $r_2$. By performing the aforementioned steps we obtain

$$\begin{aligned} \begin{aligned} a_2'&= \bar{w}(b_2-a_2),\\ b_2'&= \bar{w}(a_2-b_2),\\ y_2'&= -1+\mathcal {O}(r_2), \end{aligned} \end{aligned}$$

(66)

where we recall that $\bar{w}=y_2+\alpha _1a_2+\alpha _2b_2$. From the fact that $a+b+c=r_2(a_2+b_2+c_2)=0$ for all $r_2\ge 0$ and due to the restriction to $\mathcal {W}_2^\text {c}$, that is $c_2=\frac{a_2+b_2}{2}$, we further have that $a_2+b_2=0$. Therefore, the analysis of (62) is reduced to the analysis of the planar system

$$\begin{aligned} \begin{aligned} a_2'&= -2(y_2+\underbrace{(\alpha _1-\alpha _2)}_{=:\nu \ge 0}a_2)a_2,\\ y_2'&= -1+\mathcal {O}(r_2). \end{aligned} \end{aligned}$$

(67)

Note that in the restriction of (67) to $\left\{ r_2=0\right\}$, one has that $y_2$ is essentially time in the reverse direction. To describe the flow of (67), let $\delta _2>0$ and define the sections

$$\begin{aligned} \begin{aligned} \Delta _{2}^\text {en}&= \left\{ (r_2,a_2,y_2)\in \mathbb {R}^3\, | \, y_2=\delta _2 \right\} ,\\ \Delta _{2}^\text {ex}&= \left\{ (r_2,a_2,y_2)\in \mathbb {R}^3\, | \, y_2=-\delta _2 \right\} . \end{aligned} \end{aligned}$$

(68)

Accordingly, let $\Pi _{2}:\Delta _{2}^\text {en}\rightarrow \Delta _{2}^\text {ex}$ be the map defined by the flow of (67). We now show the following.

Proposition 7

Consider (67). Then the following hold.

• 1. There exists a trajectory $\gamma _c$ given by

  $$\begin{aligned} \gamma _c(t_2)=\left( a_2(t_2),y_2(t_2) \right) =(0,-t_2)\, \qquad t_2\in \mathbb {R}. \end{aligned}$$

  (69)

  No other trajectory of (67) converges to the $y_2$-axis as $t_2\rightarrow \pm \infty$.

• 2. There exist orbits $\gamma _2^\text {r}$ and $\gamma _2^\text {a}$ that are defined, respectively, in the quadrants $\left\{ a_2<0,y_2>0\right\}$ and $\left\{ a_2>0,y_2<0\right\}$ and are given by

  $$\begin{aligned} \begin{aligned} \gamma _2^\text {r}&= \left\{ (a_2,y_2)\in \mathbb {R}^2\,|\, a_2=-\frac{1}{2\nu D_+(y_2)}, \, a_2<0 \right\} ,\\ \gamma _2^\text {a}&= \left\{ (a_2,y_2)\in \mathbb {R}^2\,|\, a_2=-\frac{1}{2\nu D_+(y_2)}, \, a_2>0 \right\} , \end{aligned} \end{aligned}$$

  (70)

  where $D_+(y_2)$ stands for the Dawson function (Abramowitz and Stegun 1972, pp. 219 and 235). Furthermore, since $y_2$ is essentially time, the trajectory $\gamma _2^j$, $j=\text {r},\text {a}$, has asymptotic expansions

  $$\begin{aligned} \begin{aligned} \gamma _2^j&= -\frac{1}{2\nu y_2} + \mathcal {O}(y_2^{-3}),&\qquad y_2\rightarrow 0\\ \gamma _2^j&= -\frac{1}{\nu }y_2+ \frac{1}{2\nu y_2} + \mathcal {O}(y_2^{-3}),&\qquad |y_2|\rightarrow \infty . \end{aligned} \end{aligned}$$

  (71)

  All trajectories of (67) with initial condition $a_2^*>0$ and $y_2^*>0$ are asymptotic to $\gamma _2^\text {a}$ as $t_2\rightarrow \infty$.

• 3. The transition map $\Pi _{2}:\Delta _{2}^\text {en}\rightarrow \Delta _{2}^\text {ex}$ is well-defined if and only if

  $$\begin{aligned} a_2|_{\Delta _{2}^\text {en}}>-\frac{1}{4D_+(\delta _2)}, \end{aligned}$$

  (72)

  and given by

  $$\begin{aligned} \Pi _{2}\left( \begin{matrix} r_2\\ a_2\\ \delta _2 \end{matrix}\right) = \left( \begin{matrix} r_2\\ \frac{a_2}{1+4a_2\nu D_+(\delta _2)} +\mathcal {O}(r_2)\\ -\delta _2 \end{matrix}\right) . \end{aligned}$$

  (73)

• 4. If $a_2|_{\Delta _{2}^\text {en}}\le -\frac{1}{4D_+(\delta _2)}$ then the corresponding orbit has asymptote $y_2=\Gamma _2$ which is implicitly given by

  $$\begin{aligned} \exp (\Gamma _2^2)D_+(\Gamma _2) = \exp (\delta _2^2)\left( \frac{1}{2a_2^*\nu }+D(\delta _2) \right) . \end{aligned}$$

  (74)

Proof

The first item follows from the invariance of $a_2=0$ and linear analysis along the $y_2$-axis. For the second item, no distinction between the orbits is needed, one only needs to check that $\gamma _2^j$ satisfies (67), for which (Abramowitz and Stegun 1972) $D_+'(y_2)=1-2y_2D_+(y_2)$ is useful. More precisely, from the expression $\gamma _2^j=\left\{ a_2=-\frac{1}{2\nu D_+(y_2)} \right\}$, one has

$$\begin{aligned} \begin{aligned} a_2'&= \frac{D_+'(y_2)y_2'}{2\nu D_+^2(y_2)}=\frac{2y_2D_+(y_2)-1}{2\nu D_+^2(y_2)} = \frac{1}{\nu D_+(y_2)}\left( y_2- \frac{1}{2D_+(y_2)}\right) \\&=-2(y_2+\nu a_2)a_2. \end{aligned} \end{aligned}$$

(75)

Next, the asymptotic expansions for $\gamma _2^j$ follow directly from Abramowitz and Stegun (1972), where one finds

$$\begin{aligned} \begin{aligned} D_+(\xi )&= \xi +\mathcal {O}(\xi ^3), \qquad&\xi \rightarrow 0\\ D_+(\xi )&= \frac{1}{2\xi }+\mathcal {O}(\xi ^{-3}), \qquad&\xi \rightarrow \infty . \end{aligned} \end{aligned}$$

(76)

The fact that $\gamma _2^\text {a}$ attracts all trajectories with the given initial conditions follows from: i) $a_2=0$ is invariant, ii) in the limit $|y_2|\rightarrow \infty$ the curve $\gamma _2^\text {a}$ is asymptotic to $y_2+\nu a_2=0$, and iii) the set $\left\{ y_2+\nu a_2=0\right\}$ is attracting in the quadrant $a_2>0$, $y_2<0$.

For the transition map we have that (67) has an explicit solution given by

$$\begin{aligned} a_2(y_2) = \frac{a_2^*}{\exp ((y_2^*)^2-y_2^2)(1+2a_2^*\nu D_+(y_2^*))-2a_2^*\nu D_+(y_2)}, \end{aligned}$$

(77)

where $(a_2^*,y_2^*)$ denotes an initial condition. Thus, for the map $\Pi _{2}$ to be well-defined we need to ensure that the denominator in (77) does not vanish. Let us substitute $(a_2^*,y_2^*)=(a_2^*,\delta _2)$ with $\delta _2>0$, and compute $a_2(-\delta _2)$. For this it is useful to recall that $D_+$ is an odd function. So we get

$$\begin{aligned} a_2(-\delta _2) = \frac{a_2^*}{1+4a_2^*\nu D_+(\delta _2)}, \end{aligned}$$

(78)

which indeed leads to (72) and the form of $\Pi _{2}$ also follows. Finally, the expression of the asymptote $\Gamma _2$ is obtained by solving the denominator of (77) equal to 0 and with initial condition $(a_2^*,y_2^*)=(a_2^*,\delta _2)$. $\square$

Remark 12

• In particular, it follows from the third item of Proposition 7 that the map $\Pi _2(r_2,a_2,\delta _2)$ is well defined for all $a_2\ge 0$.

• For $\delta _2>0$ sufficiently large and $a_2^*$ sufficiently small one has that $a_2(-\delta _2)\approx a_2^*$.

• If $\alpha _1-\alpha _2=0$ then $\Pi (a_2,\delta _2)=(a_2,-\delta _2)$.

We now relate the curves $\gamma _2$ and $\gamma _c$ with centre manifolds found in chart $K_1$.

Proposition 8

The curves $\gamma _2^\text {r}$ and $\gamma _c$ correspond, respectively, to the centre manifolds $\mathcal {E}_1^\text {r}$ and $\mathcal {E}_1^\text {a}$ of chart $K_1$.

Proof

We detail the relation between $\gamma _2$ and $\mathcal {E}_1^\text {r}$, the correspondence between $\gamma _c$ and $\mathcal {E}_1^\text {a}$ is trivial since they are given by $\left\{ a_2=0\right\}$ and $\left\{ a_1=0\right\}$, respectively. We can transform $\gamma _2$ into the coordinates of chart $K_1$ via the map $\kappa _{21}$, which gives

$$\begin{aligned} \varepsilon _1^{-1/2}a_1=-\frac{1}{2\nu D_+(\varepsilon _1^{-1/2})}. \end{aligned}$$

(79)

Taking the limit $\varepsilon _1\rightarrow 0$ in (79) one gets $a_1=-\frac{1}{\nu }=\frac{1}{\alpha _2-\alpha _1}$. Thus the claim follows from the analysis performed in chart $K_1$ particularly for $r_1=0$. $\square$

Remark 13

The trajectory $\gamma _c$ corresponds to a singular maximal canard of (27), while $\gamma _2^\text {r}$ and $\gamma _2^\text {a}$ correspond to the manifolds $\mathcal {M}_0^\text {r}$ and $\mathcal {M}_0^\text {a}$. Accordingly, $\mathcal {O}(r_2)$-small perturbation of such orbits corresponds to $\mathcal {N}_\varepsilon$, $\mathcal {M}_\varepsilon ^\text {r}$, and $\mathcal {M}_\varepsilon ^\text {a}$ for $\varepsilon >0$ sufficiently small.

The analysis performed in this chart is sketched in Fig. 10.

Fig. 10

Flow of (62) along $\mathcal {W}_2^\text {c}$. This flow is equivalent to that of (27) within a small neighbourhood of the origin and for $\varepsilon >0$ sufficiently small. We observe that trajectories starting at $\Delta _2^\text {en}$ are first attracted to the invariant set $\left\{ a_2=0 \right\}$, which in terms of the network means consensus. Then, once the trajectories pass through the origin, they are repelled from consensus. All trajectories with initial condition $a_2^*>0$ are eventually attracted towards $\gamma _2^\text {a}$, which in terms of the original coordinates corresponds to the clustering manifold

3.3.3 Analysis in the Exit Chart $K_3$

The analysis in this chart is similar to that in chart $K_1$ performed in Sect. 3.3.1. Therefore, we shall only point out the main information required from this chart and omit the proofs.

In this chart the blow-up map is given by

$$\begin{aligned} a=r_3a_3, \; b=r_3b_3, \; c=r_3c_3,\; y = -r_3,\; \varepsilon =r_3^2\varepsilon _3. \end{aligned}$$

(80)

We then obtain the blown-up vector field

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a_3' \\ b_3' \\ c_3' \end{bmatrix}&= -\begin{bmatrix} \frac{1}{2}&{}\quad \frac{1}{2}&{}\quad -1 \\ \frac{1}{2}&{}\quad \frac{1}{2}&{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}\begin{bmatrix} a_3\\ b_3\\ c_3\end{bmatrix} + r_3f_3(a_3,b_3,c_3,r_3,\varepsilon _3)\\ r_3'&= -r_3^2\varepsilon _3(-1+\mathcal {O}(r_3))\\ \varepsilon _3'&= 2r_3\varepsilon _3^2(-1+\mathcal {O}(r_3)), \end{aligned} \end{aligned}$$

(81)

where $f_3(a_3,b_3,c_3,r_3,\varepsilon _3)$ reads as

$$\begin{aligned} f_3 = \left( (-1+\alpha _1a_3+\alpha _2b_3) \begin{bmatrix} -1 &{}\quad 1 &{}\quad 0 \\ 1 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} + \varepsilon _3(-1+\mathcal {O}(r_3)) \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0\\ 0 &{} \quad 0 &{}\quad 1 \end{bmatrix} \right) \begin{bmatrix} a_3\\ b_3\\ c_3\end{bmatrix}.\nonumber \\ \end{aligned}$$

(82)

The flow of (81) is described as follows.

Proposition 9

The following claims hold for (81).

• 1. There exist a 1-dimensional local stable manifold $\mathcal {W}_3^\text {s}$ and a 4-dimensional local centre-stable manifold $\mathcal {W}_3^\text {c}$. The centre manifold is given by the graph of $c_3=\frac{a_3+b_3}{2}$.

Restricted to $\mathcal {W}_3^\text {c}$ one has $b_3=-a_3$, $c_3=0$, and:

• 2. There is a repelling 2-dimensional centre manifold $\mathcal {C}_3^\text {r}$. The manifold $\mathcal {C}_3^\text {r}$ contains a line of zeros $\ell _3^\text {r}=\left\{ (r_3,a_3,\varepsilon _3)\in \mathbb {R}^3\, | \, a_3=\varepsilon _3=0 \right\}$ and a 1-dimensional centre manifold $\mathcal {E}_3^\text {r}=\left\{ (r_3,a_3,\varepsilon _3)\in \mathbb {R}^3\, | \, r_3=a_3=0\right\}$. On the plane $\left\{ r_3=0 \right\}$, the centre manifold $\mathcal {E}_3^\text {r}$ is unique. The flow along $\mathcal {E}_3^\text {r}$ is stable, that is, it converges to the origin, while the flow on $\mathcal {C}_3^\text {r}$ away from $\ell _3^\text {r}$ is locally equivalent to that of a saddle.

• 3. There is an attracting 2-dimensional centre manifold $\mathcal {C}_3^\text {a}$. The manifold $\mathcal {C}_3^\text {a}$ contains a line of zeros $\ell _3^\text {a}=\left\{ (r_3,a_3,\varepsilon _3)\in \mathbb {R}^3\, | \, a_3=\frac{1}{\alpha _1-\alpha _2},\,\varepsilon _3=0 \right\}$ and a 1-dimensional centre manifold $\mathcal {E}_3^\text {a}=\left\{ (r_3,a_3,\varepsilon _3)\in \mathbb {R}^3\, | \, r_3=0, a_3=\frac{1}{\alpha _1-\alpha _2}+\mathcal {O}(\varepsilon _3)\right\}$. The flow along $\mathcal {E}_3^\text {a}$ is stable, that is, it converges to the equilibrium point $(a_3,\varepsilon _3)=\left( \frac{1}{\alpha _1-\alpha _2},0\right)$, while the flow on $\mathcal {C}_3^\text {a}$ away from $\ell _3^\text {a}$ is locally equivalent to that of a saddle.

Define the sections

$$\begin{aligned} \begin{aligned} \Delta _3^\text {en}&= \left\{ (a_3,r_3,\varepsilon _3)\in \mathbb {R}^3\, | \, r_3<\delta _3,\, \varepsilon _3=\mu _3 \right\} \\ \Delta _3^\text {ex}&= \left\{ (a_3,r_3,\varepsilon _3)\in \mathbb {R}^3\, | \, r_3=\delta _3,\, \varepsilon _3<\mu _3 \right\} , \end{aligned} \end{aligned}$$

(83)

where $\delta _3>0$, and $\mu _3>0$ is sufficiently small. Let $\Pi _3:\Delta _3^\text {en}\rightarrow \Delta _3^\text {ex}$ denote the map induced by the flow of (81) restricted to $\mathcal {W}_3^c$. Then $\Pi _3$ has the form

$$\begin{aligned} \Pi _3\left( \begin{matrix} a_3\\ r_3\\ \mu _3 \end{matrix}\right) =\left( \begin{matrix} h_{a_3} +\mathcal {O}(a_3\mu _3^2)\\ \delta _3\\ \mu _3\left( \frac{r_3}{\delta _3}\right) ^2 \end{matrix} \right) , \end{aligned}$$

(84)

where the function $h_{a_3}=h_{a_3}(a_3,\delta _3,\varepsilon _3)$ reads as

$$\begin{aligned} h_{a_3} = \frac{a_3\exp (2T_3)}{(\alpha _1-\alpha _2)a_3(\exp (2T_3)-1)+1},\qquad T_3=\frac{1}{2\mu _3}\left( \left( \frac{\delta _3}{r_3}\right) ^2-1 \right) . \end{aligned}$$

(85)

Remark 14

• If $a_3\ge 0$, then the function $h_{a_3}$ is well-defined for any point $(a_3,r_3,\mu _3)\in \Delta _3^\text {en}$. If $a_3<0$, the function $h_{a_3}$ is well-defined only for $T_3<\frac{1}{2}\ln \left( 1+\frac{1}{(\alpha _1-\alpha _2)|a_3|} \right)$. In such a case, we choose suitably $0<r_3<\delta _3$ so that the function $h_{a_3}$ is well-defined.

• For $a_3>0$, and $T_3>0$ sufficiently large, one has $h_{a_3}\approx \frac{1}{\alpha _1-\alpha _2}$.

• If $\alpha _1-\alpha _2=0$ then $h_{a_3}\approx a_3\exp (2T_3)$.

• $\kappa _{23}(\gamma _2^\text {c})=\mathcal {E}_3^\text {r}$ and $\kappa _{23}(\gamma _2^\text {a})=\mathcal {E}_3^\text {a}$.

The flow in this chart is as depicted in Fig. 11.

Fig. 11

Schematic representation of the flow of (81) restricted to the attracting centre manifold $\mathcal {W}_3^\text {c}$. The wegde-like shape of the image of $\Pi _3(\Delta _3^{\text {en}})$ (shaded in $\Delta _1^{\text {ex}}$) is due to the contraction towards $\mathcal {C}_3^\text {a}$

3.3.4 Full Transition and Proof of Main Result

In this section we prove items (T4)–(T6) of Theorem 2. First of all note that if we choose $\delta _1=\delta _3=\delta$, then the sections $\Delta _1^\text {en}$ and $\Delta _3^\text {ex}$ are precisely the sections $\Sigma ^\text {en}|_\mathcal {A}$ and $\Sigma ^\text {ex}|_\mathcal {A}$ in the blow-up coordinates. Moreover, the set $\mathcal {A}$ corresponds, in each chart, to the centre manifold $\mathcal {W}_1^\text {a}$, $\mathcal {W}_2^\text {a}$, and $\mathcal {W}_3^\text {a}$, respectively. Thus it will suffice to consider the transition map ${\bar{\Pi }}:\Delta _1^\text {en}\rightarrow \Delta _3^\text {ex}$ in the blow-up space (or equivalently $\Pi |_\mathcal {A}$).

The map ${\bar{\Pi }}(\Delta _1^\text {en})$ is then given as

$$\begin{aligned} {\bar{\Pi }}(\Delta _1^\text {en}) = \Pi _3\circ \kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en}), \end{aligned}$$

(86)

where the maps $\Pi _1$, $\Pi _2$, and $\Pi _3$ are given in Sects. 3.3.1, 3.3.2, and 3.3.3, respectively, and where the maps $\kappa _{12}$ and $\kappa _{23}$ are defined in Lemma 2. We compute ${\bar{\Pi }}(\Delta _1^\text {en})$ as follows. For brevity we disregard the higher-order terms in the chart maps.

• 1. We start from $\Delta _1^\text {en}=(a_1,\delta ,\varepsilon )$ and compute $\Pi _1(\Delta _1^\text {en})=(h_{a_1},\delta \varepsilon _1^{1/2}\mu ^{-1/2},\mu )$, where $h_{a_1}$ is as in (60) and we let $\mu _1=\mu$.

• 2. Next we compute $\kappa _{12}\circ \Pi _1(\Delta _1^\text {en})$ from (37), obtaining

  $$\begin{aligned} \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})=\left( \delta \varepsilon ^{1/2},\mu ^{-1/2}h_{a_1},\mu ^{-1/2} \right) . \end{aligned}$$

  (87)

  By defining $\mu ^{1/2}=\delta _2$ we have from (68) that $\kappa _{12}\circ \Pi _1(\Delta _1^\text {en})\subset \Delta _2^\text {en}$.

• 3. Next we can compute $\Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})$ using Proposition 7. We get

  $$\begin{aligned} \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en}) = \left( \delta \varepsilon _1^{1/2}, \underbrace{\frac{\mu ^{-1/2}h_{a_1}}{1+4\mu ^{-1/2}h_{a_1}(\alpha _1-\alpha _2)D_+(\mu ^{-1/2})} }_{h_{a_2}},{-}\mu ^{-1/2} \right) .\nonumber \\ \end{aligned}$$

  (88)

• 4. Next we compute $\kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})$ again using (37), obtaining

  $$\begin{aligned} \kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})=\left( \mu ^{1/2}h_{a_2},\delta \varepsilon _1^{1/2}\mu ^{-1/2},\mu \right) . \end{aligned}$$

  (89)

  By defining $\mu _3=\mu$ we have from (83) that $\kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})\subset \Delta _3^\text {en}$.

• 5. Finally we compute $\Pi _3\circ \kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en})$ from (84), obtaining

  $$\begin{aligned} \Pi _3\circ \kappa _{23}\circ \Pi _2\circ \kappa _{12}\circ \Pi _1(\Delta _1^\text {en}) = \left( h_{a_3},\delta , \varepsilon _1\right) , \end{aligned}$$

  (90)

  where $h_{a_3}= \frac{ \mu ^{1/2}h_{a_2}\exp (2T_3)}{(\alpha _1-\alpha _2) \mu ^{1/2}h_{a_2}(\exp (2T_3)-1)+1}$ reads, after substitutions, as

  $$\begin{aligned} h_{a_3}=\frac{a_1\exp (2 T)}{ (\alpha _1-\alpha _2)a_1\left( 2\exp (2 T)-2+4\mu ^{-1/2}D_+(\mu ^{-1/2}) \right) +\exp (2T)} \end{aligned}$$

  (91)

  where $T=T_1=\frac{1}{2}\left( \frac{1}{\varepsilon _1}-\frac{1}{\mu } \right) (1+\mathcal {O}(\delta ))$. We see that, as it was already evident in each chart, the function $h_{a_3}$ is well-defined for $a_1\ge 0$, while for $a_1<0$ the function $h_{a_3}$ is well-defined only for finite time T. We thus assume that, in either case, we choose appropriate constants $\delta >0$, and $\mu >0$ sufficiently small, such that $h_{a_3}$ is well-defined.

Note that, restricted to $\mathcal {W}_j^\text {c}$, all the sets $\left\{ a_j=0\right\}$, $j=1,2,3$, are invariant along the blow-up space. In other words, if $(\bar{a},\bar{b},\bar{c},\bar{y},{\bar{\varepsilon }},r)$ denote the global blow-up coordinates as in (34), then we have that $\left\{ a_3=0\right\}$ is invariant on the set $\left\{ {\bar{c}}=\frac{\bar{a}+{\bar{b}}}{2}\right\}$. We now proceed with proving each item (T4)–(T6) of Theorem 2.

• (T4) Indeed, we have that ${\bar{\Pi }}(0,\delta ,\varepsilon _1)=(0,\delta ,\varepsilon _1)$. Moreover, it follows from item 1 of Proposition 7 and Sect. 3.3.3 that the curve $\gamma _c$ connects the point $(a_1,r_1,\varepsilon _1)=(0,0,0)$ in chart $K_1$ with the point $(a_3,r_3,\varepsilon _3)=(0,0,0)$ in chart $K_3$. Therefore, the centre manifolds $\mathcal {C}_1^\text {a}$ and $\mathcal {C}_3^\text {r}$ are also connected in the central chart $K_2$ via the map $\Pi _2$ for $r_2\ge 0$ sufficiently small. It is then clear that, since we can identify $\mathcal {C}_1^\text {a}$ with $\mathcal {N}_\varepsilon ^\text {a}$ and $\mathcal {C}_1^\text {r}$ with $\mathcal {N}_\varepsilon ^\text {r}$, the manifolds $\mathcal {N}_\varepsilon ^\text {a}$ and $\mathcal {N}_1^\text {r}$ are also connected for $\varepsilon \ge 0$ sufficiently small. The stability of $\mathcal {N}_\varepsilon$ follows from $\mathcal {C}_1^\text {a}$ being attracting in chart $K_1$ and $\mathcal {C}_3^\text {r}$ being repelling in chart $K_3$.

• (T5) If $\alpha _1-\alpha _2=0$ we have that $h_{a_3}(a_1,\delta _1,\varepsilon _1)=a_1$. Since $\Delta _3^\text {ex}$ is sufficiently away from the origin, the claim for $a\ne 0$ follows from Fenichel’s theory and the stability properties of $\mathcal {N}_0$.

• (T6) The expression of $\mathcal {M}_\varepsilon ^\text {a}$ and $\mathcal {M}_\varepsilon ^\text {r}$ is obtained from blowing down $\gamma _2^\text {a}$ and $\gamma _2^\text {r}$ given in (70). Accordingly the fact that $\mathcal {M}_\varepsilon ^\text {a}$ attracts all trajectories with initial condition $a_1|_{\Delta _1^\text {en}}>0$ follows equivalent arguments as those for the second item in Proposition 7. On the contrary, when we have $a_1|_{\Delta _1^\text {en}}<0$ we see from the expression of $h_{a_3}$ that the trajectories become unbounded in finite time T, see also the remark at the end of Sect. 3.3.3. The proof is finalized by recalling the relationship between the signs of initial conditions in $\Sigma ^\text {en}$ and the corresponding sign of $a_j$ in $\mathcal {W}_j^\text {c}$ given at the beginning of the proof.

4 Some Generalizations

Here we develop a couple of generalizations for the results presented in Sect. 3. The first one is concerned with triangle motifs with one dynamic weight, while the other two weights are fixed and positive, but not necessarily equal. The second generalization deals with consensus protocols defined on arbitrary graphs, where just one weight is dynamic.

4.1 The Nonsymmetric Triangle Motif

In Sect. 3 we studied a triangle motif with the fixed weights equal to 1. In this section we show that the nonsymmetric case is topologically equivalent to the symmetric one. Let us start by considering the fast–slow system

$$\begin{aligned} \begin{aligned} x'&= -L(x,y,\varepsilon )x\\ y'&= \varepsilon g(x,y,\varepsilon ), \end{aligned}\qquad \qquad L=\begin{bmatrix} w + w_{13} &{}\quad -w &{}\quad -w_{13}\\ -w &{}\quad w+w_{23} &{}\quad -w_{23}\\ -w_{13} &{}\quad -w_{23} &{}\quad w_{13}+w_{23} \end{bmatrix}, \end{aligned}$$

(92)

where $w=w^*+y+\alpha _1x_1+\alpha _2x_2$, the weights $w_{13}$ and $w_{23}$ are fixed and positive, and $w^*\in \mathbb {R}$ is such that $\dim \ker L|_{\left\{ w=w^*\right\} }=2$, see more details below. We recall that, from the arguments at the beginning of Sect. 3.2, we may consider that, after a translation depending on initial conditions, we have $x_1+x_2+x_3=0$. System (92) corresponds to the network shown in Fig. 12.

Fig. 12

Triangle motif: a network of three nodes connected on a cycle. The weights $w_{13}$ and $w_{23}$ are fixed and positive

Remark 15

If $w_{13}=w_{23}={\tilde{w}}>0$, one can show, for example using the exact same transformation T of Lemma 1, that the eigenvalues of L are $\left\{ 0,3{\tilde{w}}, 2 w+ {\tilde{w}} \right\}$. Thus, the analysis in this case is completely equivalent to the one already performed in Sect. 3. The only difference would be the rate of convergence towards the set $\left\{ x_3=\frac{x_1+x_2}{2}\right\}$. Therefore, in this section we rather assume $w_{13}\ne w_{23}$.

It is straightforward to show that the spectrum of L is given by

$$\begin{aligned} {{\,\mathrm{spec}\,}}L= & {} \left\{ 0,\lambda _2,\lambda _3\right\} \nonumber \\= & {} \left\{ 0, w+w_{13}+w_{23} \pm \sqrt{w^2+w_{13}^2+w_{23}^2 - ww_{13} - ww_{23}- w_{13}w_{23}} \right\} .\nonumber \\ \end{aligned}$$

(93)

We note the following:

• If $ww_{13} + ww_{23}+ w_{13}w_{23}>0$ then $\lambda _2>0$, $\lambda _3>0$,

• If $ww_{13} + ww_{23}+ w_{13}w_{23}=0$ then $\lambda _2>0$, $\lambda _3=0$,

• If $ww_{13} + ww_{23}+ w_{13}w_{23}<0$ then $\lambda _2>0$, $\lambda _3<0$.

This means that, as in the symmetric case, the Laplacian matrix has always a positive eigenvalue $\lambda _2(w)$, and another $\lambda _3(w)$ whose sign depends on w.

Proposition 10

Let $\varepsilon =0$. Then the equilibrium points of (92) are given by

• $x_1=x_2=x_3=0$, that is consensus.

• $w=-\frac{w_{13}w_{23}}{w_{13}+w_{23}}=:w^*$ and $x_3=\frac{w_{13}x_1+w_{23}x_2}{w_{13}+w_{23}}$, which from the invariant $x_1+x_2+x_3=0$ results in $x_2=-\frac{2w_{13}+w_{23}}{w_{13}+2w_{23}}x_1$. That is (generically) clustering.

• The equilibrium point $p=(x_1,x_2,x_3)$ defined by $p=\left\{ w=w^*\, | \, x_1=x_2= x_3=0 \right\}$ is nonhyperbolic.

Proof

Straightforward computations. $\square$

We emphasize that, just as in the symmetric case, the previous proposition provides the characterization of the critical manifold of (92) given as the union of “the consensus” and the “the clustering” manifolds.

Proposition 11

The layer equation of (92) has a transcritical bifurcation at p.

Proof

We shall compute the eigenvalues associated with the equilibrium points of Proposition 10. We start by substituting $x_3=\frac{w_{13}x_1+w_{23}x_2}{w_{13}+w_{23}}$, and afterwards $x_2=-\frac{2w_{13}+w_{23}}{w_{13}+2w_{23}}x_1$. Naturally, both relations hold at all the equilibrium points. In particular, the equilibrium points along the consensus manifold are given by $x_1=0$, while those along the clustering manifold are given by $x_1=\frac{-(w_{13}+2w_{23})y}{ \alpha _1(w_{13}+2w_{23})-\alpha _2(2w_{13}+w_{23}) }$. By doing so we rewrite (92) in the limit $\varepsilon \rightarrow 0$ as

$$\begin{aligned} \begin{aligned} x_1'&= \frac{-3x_1(w_{13}+w_{13})( (w_{13}+2w_{23})y+x_1(\alpha _1(w_{13}+2w_{23})-\alpha _2(2w_{13}+w_{23})) )}{(w_{13}+2w_{23})^2}, \end{aligned}\nonumber \\ \end{aligned}$$

(94)

where y is considered as a parameter. Let $x_1'=\lambda _Nx_1$ denote the linearization of (94) at $x_1=0$, and $x_1'=\lambda _Mx_1$ denote the linearization of (94) at $x_1=\frac{-(w_{13}+2w_{23})y}{ \alpha _1(w_{13}+2w_{23})-\alpha _2(2w_{13}+w_{23}) }$. We have

$$\begin{aligned} \begin{aligned} \lambda _N&= -3\frac{w_{13}+w_{23}}{w_{13}+2w_{23}}y=-\lambda _M. \end{aligned} \end{aligned}$$

(95)

It is then clear that the eigenvalues along the consensus and the clustering manifolds ($\lambda _N$ and $\lambda _M$, respectively) have opposite signs and that there is an exchange in their signs at $y=0$. Finally we note that $y=0$ precisely corresponds to the point p, completing the proof. $\square$

With the previous analysis we have shown that, at the singular level, the dynamics of the symmetric and the nonsymmetric graphs are topologically equivalent. The reasons for this are: a) the uniform positive eigenvalue of the Laplacian matrix L and b) that the dynamics of both systems are organized by a transcritical singularity corresponding to the intersection of the consensus and of the clustering manifolds. It remains to show that the passage through the transcritical singularity is also equivalent in both cases. We shall show this in the central chart $K_2$. We recall the the blow-up in the central chart is given by

$$\begin{aligned} x_1=r_2a_2, \; x_2=r_2b_2, \;x_3=r_2c_2, \; y=r_2y_2, \; \varepsilon =r_2^2. \end{aligned}$$

(96)

Accordingly, the blown-up vector field reads as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a_2'\\ b_2'\\ c_2' \end{bmatrix}&=-\left( \begin{bmatrix} w^*+w_{13} &{}\quad -w^* &{}\quad -w_{13}\\ -w^* &{}\quad w^*+w_{23} &{}\quad w_{23} \\ -w_{13} &{}\quad -w_{23} &{}\quad w_{13} +w_{23} \end{bmatrix}\right. \\&\quad \left. +r_2(y_2+\alpha _1a_2+\alpha _2b_2)\begin{bmatrix} 1 &{}\quad -1 &{}\quad 0 \\ -1 &{}\quad 1 &{} \quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{bmatrix}\right) \begin{bmatrix} a_2\\ b_2\\ c_2\end{bmatrix}\\ y_2&= -r_2(1+\mathcal {O}(r_2)) \end{aligned} \end{aligned}$$

(97)

For $r_2=0$ we get the linear system

$$\begin{aligned} \begin{bmatrix} a_2'\\ b_2'\\ c_2' \end{bmatrix} =-\underbrace{\begin{bmatrix} w^*+w_{13} &{}\quad -w^* &{}\quad -w_{13}\\ -w^* &{}\quad w^*+w_{23} &{}\quad -w_{23} \\ -w_{13} &{}\quad -w_{23} &{}\quad w_{13} +w_{23} \end{bmatrix}}_{L_0}\begin{bmatrix} a_2\\ b_2\\ c_2\end{bmatrix} \end{aligned}$$

(98)

Using similar arguments as in Sect. 3 we can show that $\mathcal {W}_2^\text {c}= \left\{ c_2= \frac{w_{13}a_2+w_{23}b_2}{w_{13}+w_{23}} \right\}$ is an attracting centre manifold. Restriction to $\mathcal {W}_2^\text {c}$ and division of the vector field by $r_2$ result in

$$\begin{aligned} \begin{aligned} a_2'&= (y_2+\alpha _1a_2+\alpha _2b_2)(b_2-a_2)\\ b_2'&= (y_2+\alpha _1a_2+\alpha _2b_2)(a_2-a_2)\\ y_2'&= -1. \end{aligned} \end{aligned}$$

(99)

Note that (99) is exact same equation (67) that we obtained in the symmetric case. This means that in both cases (symmetric and nonsymmetric), the restriction to the centre manifold $\mathcal {W}_2^\text {c}$ coincides. With the above analysis we have shown the following:

Proposition 12

Fast–slow system (92) with $w_{13}>0$ and $w_{23}>0$ is topologically equivalent to the case $w_{13}=w_{23}=1$.

In qualitative terms, the only difference between the symmetric and the nonsymmetric cases is the convergence rate towards the invariant set $\mathcal {A}$. Once trajectories have converged to $\mathcal {A}$, the dynamics are organized by the same transcritical singularity.

4.2 Arbitrary Graphs

A natural question that arises is whether the analysis we have performed in Sect. 3, particularly in Sect. 3.3, has any relevance for consensus dynamics on arbitrary weighted graphs. In this section we argue that indeed, given some natural assumptions, generic consensus dynamics with one slowly varying weight behave essentially as the triangle motif.

Let us consider an undirected weighted graph $\mathcal {G}=\left\{ \mathcal {V},\mathcal {E},\mathcal {W}\right\}$. We assume that there are no self-loops, i.e. $w_{ii}=0$ for all $i\in 1,\ldots ,m$ and that there is at most one edge connecting two nodes. Next, without loss of generality, let us assume that $w_{12}=w\in \mathbb {R}$ is dynamic, while the rest of the weights $w_{ij}$, $(i,j)\in \mathcal {E}$ and $(i,j)\ne (1,2)$, are fixed and positive. Denote by L(w) the Laplacian matrix corresponding to the graphs we have defined so far. As in the analysis of the triangle motif we assume that the dynamic weight w depends smoothly on the nodes it connects (namely $(x_1,x_2)$) and on an extrinsic slow variable $y\in \mathbb {R}$. Thus we consider the fast–slow system

$$\begin{aligned} \begin{aligned} x'&=-L(w)x,\\ y'&= \varepsilon g(x,y,\varepsilon ), \end{aligned}\qquad w=w(x_1,x_2,y,\varepsilon ), \end{aligned}$$

(100)

where $x\in \mathbb {R}^m$, $y\in \mathbb {R}$ and L is a Laplacian matrix. Recall from the rescaling we performed in Sect. 3.3 that it suffices to consider trajectories such that $\sum _{i=0}^m x_i(0)=0$, and to set $w=w^*+y+a_1 x_1+\alpha _2 x_2 +\mathcal {O}(2)$, where by $\mathcal {O}(2)$ we denote monomials of degree at least 2. Moreover $w^*$ is a particular value at which $\dim (\ker L(w^*))>1$.

Lemma 4

Consider consensus protocol (100) as defined above. Then, the following hold.

• 1. Generically, if $\dim \ker (L(w))>1$, then $\dim \ker (L(w))=2$.

• 2. Suppose that L(w) is analytic in w, and that $\dim \ker (L(w))=2$ at points (x, y) defined by $w=w^*$. Then consensus protocol (100) undergoes a (singular) transcritical bifurcation at $\left\{ w=w^* \right\} \cap \left\{ x=0\right\}$.

Proof

Recall that 0 is a trivial eigenvalue with eigenvector $\varvec{1}_n$. Therefore, $\dim \ker L(w)$ increases its dimension whenever an eigenvalue crosses 0. Next, we note that smooth one parameter families of symmetric matrices have generically simple eigenvalues (Jonker et al. 1993). This means that, generically, only one of the nontrivial eigenvalues of L(w) can vanish for a certain value of w. Thus, the first item in the lemma follows.

Next, assuming analytic dependence of L(w) on w and according to (Kato 2013, II.6.2), the matrix L(w) can be orthogonally diagonalized as $L(w)=Q^\top (w)D(w)Q(w)$, where Q(w) and D(w) are also analytic in w. This means that the layer equation of (100) is conjugate to

$$\begin{aligned} \begin{aligned} z_1'&=0\\ z_j'&=\lambda _j({\tilde{w}})z_j\\ y'&=0, \end{aligned}\quad j=2,\ldots ,m, \end{aligned}$$

(101)

where ${\tilde{w}} = {\tilde{w}}(z,y)= w^*+y+A(z)+\mathcal {O}(2)$, where A is a linear function with $A(0)=0$. We know from our previous arguments that there is a $k\in [2,3,\ldots ,m]$ such that $\lambda _k(w^*)=0$ while $\lambda _j(w^*)\ne 0$ for all $j\ne k$. Thus, we note that $z_k$ undergoes an exchange of stability if $\lambda _k$ crosses transversally the origin. But note that $\frac{\partial \lambda _k}{\partial y}(0)=\frac{\partial \lambda _k}{\partial \tilde{w}}\frac{\partial {\tilde{w}}}{\partial y}(0)$. Since we have that $\lambda _k$ depends analytically on ${\tilde{w}}$, we expect that $\frac{\partial \lambda _k}{\partial {\tilde{w}}}(0)$ is, generically, nonzero. Thus, we conclude that in a generic setting, whenever eigenvalues cross the origin, they do it transversally and thus a typical exchange of stability (transcritical bifurcation) occurs. $\square$

Remark 16

We note that singular pitchfork bifurcations can also occur, but this requires extra conditions on w, namely $w=y+\alpha _1x_1^2+\alpha _2 x_2^2$. In that case one can follow a similar analysis as that performed here; see also Krupa and Szmolyan (2001b).

To finalize this section, we want to emphasize the relevance of the blow-up method to study singularities of dynamic adaptive networks defined on arbitrary graphs. First, we recall that nowadays, the blow-up method is an essential part of geometric singular perturbation theory (GSPT). Thus, it is to be expected that GSPT will be used to analyze the dynamics of adaptive networks with multiple timescales near singularities. Next, we point out that motifs can be regarded as the most basic and simple structures in a network. Motifs can serve as building blocks to model complex phenomena, yet they carry essential properties of the network. In particular, the triangle motif studied in this paper is fairly common in larger networks. Thus, as we have shown in this section for consensus protocols, if the topological changes are due to one dynamic edge, then generically the transcritical singularity is the organizing centre. Here by generic we mean that the dynamic weight is affine on the nodes and on the extrinsic variable y. The fact that the transcritical singularity organizes the dynamic implies that for any communication protocol whose linearization is a consensus protocol, the same transcritical singularity describes the local properties of the dynamics. See also the simulations in “Appendix A”.

The second important observation derived from our analysis is that the blow-up transformation preserves the network structure. This means that after blow-up, in each chart, one obtains local vector fields that inherit network properties of the original problem. Moreover, after blowing-up, the effects of the timescale separation are also clearly visible in terms of the network topology. There is in principle no reason to a priori (or before this paper) expect the aforementioned holds, especially because the blow-up transformation is singular. Therefore, we have also shown that the blow-up method remains a suitable tool of analysis in the context of dynamic networks. Furthermore, although here we have shown the suitability of the blow-up method for fairly simple network dynamics, it is a promising preamble and extensions to more general dynamic networks are currently under development.

5 Summary and Outlook

We have studied a class of adaptive networks under a linear average consensus protocol. The main property of the networks we studied here is that one of the edges is slowly varying and can take values over the whole reals. The fact that the dynamic weight can be negative implies that the Laplacian of the graph may not be positive semi-definite, as is the case of nonnegative weights. We have shown that the dynamics of the network are organized by a transcritical singularity. Interestingly, the network structure induces a generic maximal canard [unlike the fast–slow transcritical singularity of Krupa and Szmolyan (2001b)]. Moreover, we have shown that the blow-up method preserves the network structure. That is, on each of the blow-up charts we have found a related network but whose analysis is simpler compared to the full fast–slow one. Overall we have provided a case study in which centre manifold reduction and tools of geometric singular perturbation theory, in particular the blow-up method, have been successfully used to describe the dynamics of a class of two timescale networks with a dynamic weight.

As we have considered one of the simplest network communication protocols, we conjecture that similar and more complicated problems are to be encountered when one studies general complex networks. For example, already assuming two slow weights presents new mathematical challenges: on the one hand the critical manifold is potentially more complicated leading to more complex singular dynamics; on the other hand, it does not necessarily hold that the nonzero eigenvalues of the Laplacian are simple, and that they cross zero transversally. These two obstacles imply that, probably, one needs to desingularize higher codimension singularities and that generic results would be harder to obtain. Furthermore, although in this paper we have studied continuous-time and continuous state-space network dynamics, we expect that analogous multiscale phenomena can be found in discrete systems. Similar relevance can be expected in more general adaptive network scenarios including directed networks or those incorporating stochastic phenomena. Beyond our work here, there are currently relatively few works linking techniques between multiple timescale dynamical systems and network science (Ashwin et al. 2017; Cappelletti and Wiuf 2017; Kuehn 2012, 2019). Yet, we conjecture that the inclusion of multiscale dynamics into network science will have far-reaching consequences and will have a high impact in better modelling, analysis, and understanding complex phenomena.

Numerical Analysis and Simulations

In this section we briefly discuss a numerical issue that may appear when simulating a fast–slow consensus network. This numerical issue is related to the presence of a maximal canard and yields trajectories not diverging when they should. Accordingly, we present an algorithm that overcomes, to some extent, such an issue. Afterwards, since the main part of the analysis of this paper concerns the triangle motif of Sect. 3, we present some numerical examples of larger networks showcasing a transition through a transcritical singularity. In this way, we also present numerical evidence of the generalizations presented in Sect. 4.2. At the end of this appendix, motivated by the fact that a dynamic weight in the consensus protocol opens up the possibility for more complicated dynamics rather than simple average consensus, we numerically investigate the existence of periodic solutions. Although we do not rigorously study such a problem here, the geometric understanding of the way the dynamics are organized allows us to conjecture situations in which periodic solutions indeed appear.

1.1 An Issue with Numerical Integration

Due to the equivalences shown in Sect. 4, we shall restrict ourselves in this section to the triangle motif with $w_{13}=w_{23}=1$. For convenience we recall that the model reads as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a'\\ b'\\ c' \end{bmatrix}&=-\underbrace{\begin{bmatrix} w + 1 &{}\quad -w &{}\quad -1\\ -w &{}\quad w+1 &{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}}_{L(a,b,y)}\begin{bmatrix} a \\ b\\ c\\ \end{bmatrix}\\ y'&=\varepsilon (-1+\mathcal {O}(a,b,c,y,\varepsilon )) \end{aligned} \end{aligned}$$

(102)

where $w=-\frac{1}{2} + y + \alpha _1 a + \alpha _2 b$ and $a(t)+b(t)+c(t)=0$ for all $t\ge 0$. We know that L(a, b, y) has eigenvalues $\lambda _1=0$, $\lambda _2=3$, $\lambda _3=\lambda _3(a,b,y)$. Thus, roughly speaking, the numerical issue we present below has to do with which nontrivial eigenvalue dominates at $t=0$. Recall that the smallest nontrivial eigenvalue of the Laplacian, called in some instances “spectral gap” or “algebraic connectivity”, bounds the rate of convergence towards consensus.

Let us discretize (102) using the forward Euler approximation method $x'\approx \frac{x_{k+1}-x_k}{\Delta t}$, where $x_k=x(k\Delta t)$ with $k\in {\mathbb {N}}_0$. This discretization preserves the invariant $a(t)+b(t)+c(t)=0$ for all $t\ge 0$, resulting in $a_k+b_k+c_k=0$ for all $k\ge 0$. Taking into account that $c_k=-a_k-b_k$, and disregarding the higher-order terms in $y'$, we write the discretized version of (102) as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a_{k+1} \\ b_{k+1} \end{bmatrix}&= \underbrace{\begin{bmatrix} 1-\Delta t(w_k+2) &{}\quad \Delta t(w_k-1) \\ \Delta t(w_k-1) &{}\quad 1-\Delta t(w_k+2) \end{bmatrix}}_{A_k(a_k,b_k,y_k)}\begin{bmatrix} a_k \\ b_k \end{bmatrix}\\{} y_{k+1}&= y_k-\varepsilon \Delta t, \end{aligned} \end{aligned}$$

(103)

where $w_k=-\frac{1}{2} + y_k + \alpha _1 a_k + \alpha _2 b_k$. The matrix $A_k$ has spectrum ${{\,\mathrm{spec}\,}}A_k=\left\{ \lambda _2, \lambda _3(k) \right\} =\left\{ 1-3\Delta t, 1-(2w_k+1)\Delta t \right\}$. From Sect. 3.1, we further know that the eigenvalue $\lambda _2$ is related to the convergence rate towards $\left\{ c_k=\frac{a_k+b_k}{2}\right\}$, which together with the invariant $a_k+b_k+c_k=0$ is equivalent to the convergence towards $\left\{ a_k=-b_k\right\}$. On the other hand, the eigenvalue $\lambda _3(k)$ is related to the stability of the consensus manifold, that is $\left\{ a_k=b_k\right\}$. Since the aforementioned convergence rates are both exponential, and for meaningful¹ initial conditions both eigenvalues are within the unit circle for $k=0$, the relationship between the two eigenvalues plays an important role in the numerical integration.

Suppose that $|\lambda _3(0)|>M|\lambda _2|$, for some $M>0$. Then, up to truncation and computer precision errors, the relation $a_k=b_k$ dominates over $a_k=-b_k$ for some $k>K>0$. Substitution of $a_k=b_k$ in (103) implies that the governing difference equation is

$$\begin{aligned} a_{k+1} = (1-3\Delta t)a_k, \end{aligned}$$

(104)

where we observe that the weight $w_k$ does not play a role any more, and that $a_k=0$ is invariant. This means that, again disregarding numerical errors and approximations due to computer precision, $a_k=0$ is in this case a unique equilibrium point, independent of the value of the weight $w_k$. In essence, this means that a computer algorithm may not recognize the instability of the consensus manifold; we note that this mechanism of “over-stabilization” induced by conserved quantities due to the network structure, is in principle different from recently discovered extended stabilization by the Euler method near transcritical and pitchfork singularities (Arcidiacono et al. 2019; Engel and Jardón-Kojakhmetov 2019; Engel and Kuehn 2018).

On the contrary case, if $|\lambda _3(0)|<M|\lambda _2|$ for some $M>0$, then the relation $a_k=-b_k$ dominates and the governing difference equation is

$$\begin{aligned} a_{k+1} = (1-(2w_k+1)\Delta t)a_k, \end{aligned}$$

(105)

where the transition through a transcritical singularity, depending on the value of $w_k$, is present. Therefore, as expected from our analysis, there is a typical exchange of stability through a transcritical singularity for some negative values of $w_k$.

With the above-simplified analysis we have argued that numerical integration of (102) may not be correct when $|2w(0)+1|>3M$ for some $M>0$. To prevent the aforementioned issue, one may adapt the analysis presented in Sect. 3.3 as shown in Algorithm 1 and Fig. 13.

Fig. 13

Numerical simulation of (102) realized in MATLAB 2017b. The values of the parameters are $(\alpha _1,\alpha _2,\varepsilon )=(2,1,0.05)$, and the initial conditions of the nodes are $(a(0),b(0),c(0))=(1.5,1,-2.5)$. The plots on the left are for $y(0)=1.9$, while the plots on the right for $y(0)=2$. In both figures we show: a integration via forward Euler on the first row; b integration via ode15s on the second row; and c integration via the proposed algorithm in the third row, where we set $e_\mathcal {A}=1\times 10^{-9}$. The Euler integrations are performed with $\Delta t=1\times 10^{-3}$, while for the ode15s we set the MaxStep to $1\times 10^{-3}$. We observe that for $y(0)=1.9$ the three algorithms provide similar outcome, namely the trajectories first approach consensus and then, when the weight is sufficiently negative, they transition towards clustering. The delay on the transition towards clustering is due to the trajectories being exponentially close to the maximal canard. However, for the case $y(0)=2$, only our proposed method provides a result aligned with the qualitative analysis of Sect. 3. Note that the simulation for $y(0)=2$ falls under the case where after sometimes the dynamics are governed by (104), explaining the observation of the trajectories remaining at (or close to) consensus even though the weight is largely negative. We recall that a negative weight means that the consensus manifold is unstable, yet trajectories remain close to it. In conclusion, our conjecture is that, in general, numerical algorithms for fast–slow consensus networks in the context of this paper work well when initial conditions are near the invariant set $\mathcal {A}$ and y(0) is not too large. Otherwise, numerical integration methods may require careful set-up in order to guarantee correct simulations

1.2 Ring, Complete, and Star Networks

To complement the analysis performed in Sect. 4, we present here a couple of numerical simulations of fast–slow consensus protocols defined on ring, complete, and star networks with more than 3 nodes. In all the simulations shown in Fig. 14 we keep the dynamic weight $w=y+\alpha _1x_1+\alpha _2x_2$ between nodes $x_1$ and $x_2$, while all other edges are fixed to 1. We note that we produce simulations for initial conditions that lead to exchange between consensus and clustering. We observe that in all cases of Fig. 14, we have a qualitative behaviour similar to the one analyzed in the triangle motif, thus validating the arguments of Sect. 4.

Fig. 14

Simulation of fast–slow consensus protocol (100) under several graph topologies. For all these simulations we consider the dynamic weight $w=y+2x_1+x_2$ on the edge $\left\{ 1,2 \right\}$ and all other weights fixed to 1. We also set $\varepsilon =0.05$ and $y(0)=0.5$. We observe in all cases that the trajectories first converge towards the origin (average consensus), and then, when w reaches some negative value, the trajectories leave a small vicinity of the consensus manifold and approach a clustering state. The actual convergence rate in each case is given by the so-called spectral gap, or the smallest nontrivial eigenvalue

1.3 Periodic Orbits on the Triangle Motif

Commonly, and historically, one considers consensus protocols seeking consensus among the nodes. This behaviour is the only possible one if the weights of the graph are nonnegative. However, as we have seen in the main part of this paper, introducing negative weights enriches the dynamics. In this section we want to provide numerical evidence on the existence of periodic orbits in consensus networks. We do not attempt to give a full treatment of the problem. Rather, we present two instances that are constructed from the geometric description we developed in Sect. 3.

Let us then consider triangle motif (102) and let us consider initial conditions with $y(0)>0$. In order to produce periodic orbits one must introduce a return mechanism that allows trajectories to return to $y>0$ after they have crossed the origin. Since we already know that the dynamics are organized as sketched in Fig. 3, we propose two return mechanisms.

• 1. The first natural way to introduce a return mechanism is to add a drift on the slow variable y that acts away from the consensus manifold $\mathcal {N}_\varepsilon$. For this strategy to result in periodic orbits, one further requires that the clustering manifold $\mathcal {M}_0$ is aligned with the fast foliation, that is $\alpha _1-\alpha _2=0$. For this example we them propose

  $$\begin{aligned}&\begin{bmatrix} a'\\ b'\\ c' \end{bmatrix} =-\begin{bmatrix} w + 1 &{}\quad -w &{}\quad -1\\ -w &{}\quad w+1 &{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}\begin{bmatrix} a \\ b\\ c\\ \end{bmatrix},\qquad w=-\frac{1}{2} + y + \alpha (a+b),\nonumber \\&\quad y' =\varepsilon (-1 +k_1a_1^2 ) \end{aligned}$$

  (106)

  We emphasize that in this case, the existence of periodic solutions does not follow from the singular limit. However, we know from our geometric analysis, especially in the chart $K_2$, that this model indeed has periodic solutions. We show in Fig. 15 a simulation of (106).

• 2. Another way to produce a return mechanism is to add higher-order terms to the dynamic weight. Based on the singular limit sketched in Fig. 3, the idea is to achieve a singular limit as depicted in Fig. 16.

Fig. 15

Simulation of (106) with $(y(0),\alpha ,k_1,\varepsilon )=(0.5,1,1,0.05)$. From left to right, the first two plots are the time series for the nodes and the weight, while the third plot depicts the corresponding phase portrait

Fig. 16

Singular limit for a return mechanism via higher-order terms in the weight w

Fig. 17

An example of periodic orbits on the triangle motif due to a cubic weight. We have used parameters $(\alpha _1,\alpha _2,\alpha _3,\alpha _4,\beta ,\varepsilon )=(2,1,1,1.01,-.5,.05)$

We note that near the origin, the singular limit is just as in Fig. 3. Furthermore, by inspecting Fig. 16 we observe that returning on the left side of $\mathcal {M}_0$ is “easier” than on the right, because, to produce a return mechanism on the right side we would actually require to generate a canard cycle. So, for the purposes of this example we shall concentrate on the case where the dynamics with $a_2<0$ exhibit periodic solutions. Following Fig. 16 we propose the weight

$$\begin{aligned} w=-\frac{1}{2} + \alpha _1 a + \alpha _2 b + \alpha _3 a^3 + \alpha _4 b^3, \end{aligned}$$

(107)

with $\alpha _1-\alpha _2>0$ and $\alpha _3-\alpha _4<0$. Next, we must introduce a new slow vector field so that trajectories can travel back along the left branch of the cubic critical manifold. Naturally there are many ways to achieve this. For example:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} a'\\ b'\\ c' \end{bmatrix}&=-\begin{bmatrix} w + 1 &{}\quad -w &{}\quad -1\\ -w &{}\quad w+1 &{}\quad -1\\ -1 &{}\quad -1 &{}\quad 2 \end{bmatrix}\begin{bmatrix} a \\ b\\ c\\ \end{bmatrix},\qquad w=-\frac{1}{2} + \alpha _1 a + \alpha _2 b + \alpha _3 a^3 + \alpha _4 b^3,\\ y'&=\varepsilon (-1 + \beta _1 a), \end{aligned} \end{aligned}$$

(108)

for some $\beta _1<0$. Figure 17 shows a corresponding simulation.