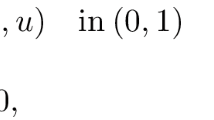Abstract
Motivated by the oscillations that were seen at the Tacoma Narrows Bridge, we introduce the notion of solutions with a prevailing mode for the nonlinear evolution beam equation
in bounded space–time intervals. We give a new definition of instability for these particular solutions, based on the loss of energy concentration on their prevailing mode. We distinguish between two different forms of energy transfer, one physiological (unavoidable and depending on the nonlinearity) and one due to the insurgence of instability. We then prove a theoretical result allowing to reduce the study of this kind of infinite-dimensional stability to that of a finite-dimensional approximation. With this background, we study the occurrence of instability for three different kinds of nonlinearities f and for some forcing terms g, highlighting some of their structural properties and performing some numerical simulations.













Similar content being viewed by others
References
Abramian, A.K., van Horssen, W.T., Vakulenko, S.A.: On oscillations of a beam with a small rigidity and a time-varying mass. Nonlinear Dyn. 78, 449–459 (2014)
Alonso, J.M., Ortega, R.: Roots of unity and unbounded motions of an asymmetric oscillator. J. Differ. Equ. 143, 201–220 (1998)
Ammann, O.H., von Kármán, T., Woodruff, G.B.: The failure of the Tacoma Narrows Bridge. Federal Works Agency, USA (1941)
Arioli, G., Gazzola, F.: A new mathematical explanation of what triggered the catastrophic torsional mode of the Tacoma Narrows Bridge collapse. Appl. Math. Model. 39, 901–912 (2015)
Augusti, G., Sepe, V.: A “deformable section” model for the dynamics of suspension bridges. Part I: model and linear response. Wind Struct. 4, 1–18 (2001)
Bartoli, G., Spinelli, P.: The stochastic differential calculus for the determination of structural response under wind. J. Wind Eng. Ind. Aerodyn. 48, 175–188 (1993)
Battisti, U., Berchio, E., Ferrero, A., Gazzola, F.: Energy transfer between modes in a nonlinear beam equation. J. Math. Pures. Appl. (2017). arXiv:1703.06502v1
Berchio, E., Ferrero, A., Gazzola, F.: Structural instability of nonlinear plates modelling suspension bridges: mathematical answers to some long-standing questions. Nonlinear Anal. Real World Appl. 28, 91–125 (2016)
Berchio, E., Gazzola, F.: A qualitative explanation of the origin of torsional instability in suspension bridges. Nonlinear Anal. Theory Methods Appl. 121, 54–72 (2015)
Berchio, E., Gazzola, F., Zanini, C.: Which residual mode captures the energy of the dominating mode in second order Hamiltonian systems? SIAM J. Appl. Dyn. Syst. 15, 338–355 (2016)
Berkovits, J., Drábek, P., Leinfelder, H., Mustonen, V., Tajčová, G.: Time-periodic oscillations in suspension bridges: existence of unique solutions. Nonlinear Anal. Real World Appl. 1, 345–362 (2000)
Bochicchio, I., Giorgi, C., Vuk, E.: On some nonlinear models for suspension bridges. In: D. Andreucci, S. Carillo, M. Fabrizio, P. Loreti, D. Sforza (eds.) Proceedings of the Conference Evolution Equations and Materials with Memory, Rome, 12–14 July 2010 (2011)
Bochicchio, I., Giorgi, C., Vuk, E.: Asymptotic dynamics of nonlinear coupled suspension bridge equations. J. Math. Anal. Appl. 402, 319–333 (2013)
Bochicchio, I., Giorgi, C., Vuk, E.: On the viscoelastic coupled suspension bridge. Evol. Equ. Control Theory 3, 373–397 (2014)
Boertjens, G.J., van Horssen, W.T.: On mode interactions for a weakly nonlinear beam equation. Nonlinear Dyn. 17, 23–40 (1998)
Boertjens, G.J., van Horssen, W.T.: An asymptotic theory for a weakly nonlinear beam equation with a quadratic perturbation. SIAM J. Appl. Math. 60, 602–632 (2000)
Boertjens, G.J., van Horssen, W.T.: On interactions of oscillation modes for a weakly non-linear undamped elastic beam with an external force. J. Sound Vib. 235, 201–217 (2000)
Brownjohn, J.M.W.: Observations on non-linear dynamic characteristics of suspension bridges. Earthq. Eng. Struct. Dyn. 23, 1351–1367 (1994)
Buitelaar, R.P.: On the averaging method for rod equations with quadratic nonlinearity. Math. Methods. Appl. Sci. 17, 209–228 (1994)
Cazenave, T., Weissler, F.B.: Asymptotically periodic solutions for a class of nonlinear coupled oscillators. Portugal. Math. 52, 109–123 (1995)
Cazenave, T., Weissler, F.B.: Unstable simple modes of the nonlinear string. Q. Appl. Math. 54, 287–305 (1996)
Dancer, E.N.: Boundary-value problems for weakly nonlinear ordinary differential equations. Bull. Aust. Math. Soc. 15, 321–328 (1976)
Drábek, P., Holubová, G., Matas, A., Nečesal, P.: Nonlinear models of suspension bridges: discussion of the results. Appl. Math. 48, 497–514 (2003)
Drábek, P., Leinfelder, H., Tajčová, G.: Coupled string-beam equations as a model of suspension bridges. Appl. Math. 44, 97–142 (1999)
Fabry, C.: Behavior of forced asymmetric oscillators at resonance. Electron. J. Differ. Equ. 74, 1–15 (2000)
Fabry, C., Fonda, A.: Nonlinear resonance in asymmetric oscillators. J. Differ. Equ. 147, 58–78 (1998)
Gazzola, F.: Mathematical Models for Suspension Bridges, vol. 15. MS&A Springer, Berlin (2015)
Gazzola, F., Wang, Y.: Modeling suspension bridges through the von Kármán quasilinear plate equations, progress in nonlinear differential equations and their applications. In: Contributions to Nonlinear Differential Equations and Systems, a Tribute to Djairo Guedes de Figueiredo on Occasion of his 80th Birthday, pp. 269–297 (2015)
Holubová, G., Matas, A.: Initial-boundary value problem for the nonlinear string-beam system. J. Math. Anal. Appl. 288, 784–802 (2003)
Jacover, D., McKenna, P.J.: Nonlinear torsional flexings in a periodically forced suspended beam. J. Comput. Appl. Math. 52, 241–265 (1994)
Krol, M.S.: On a Galerkin-averaging method for weakly non-linear wave equations. Math. Methods Appl. Sci. 11, 649–664 (1989)
Lazer, A.C., McKenna, P.J.: Large-amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis. SIAM Rev. 32, 537–578 (1990)
Mawhin, J.: Resonance and nonlinearity: a survey. Ukr. Math. J. 59, 197–214 (2007)
McKenna, P.J., Walter, W.: Nonlinear oscillations in a suspension bridge. Arch. Rat. Mech. Anal. 98, 167–177 (1987)
Ortega, R.: Periodic perturbations of an isochronous center. Qual. Theory Dyn. Syst. 3, 83–91 (2002)
Plaut, R.H., Davis, F.M.: Sudden lateral asymmetry and torsional oscillations of section models of suspension bridges. J. Sound Vib. 307, 894–905 (2007)
Sweers, G.: A survey on boundary conditions for the biharmonic. Complex Var. Elliptic Equ. 54, 79–93 (2009)
Temam, R.: Infinite Dimensional Dynamical Systems in Mechanics and Physics, vol. 68. AMS Springer, Berlin (1997)
Wagner, H.: Über die entstehung des dynamischen auftriebes von tragflügeln. Z. Angew. Math. Mech. 5, 17–35 (1925)
Weisstein, E.W.: Multiple-Angle Formulas, From MathWorld, A Wolfram Web Resource, http://mathworld.wolfram.com/Multiple-AngleFormulas.html
Acknowledgements
The second author is partially supported by the PRIN project Equazioni alle derivate parziali di tipo ellittico e parabolico: aspetti geometrici, disuguaglianze collegate, e applicazioni. Both authors are members of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). The authors are grateful to the anonymous referees, whose valuable comments allowed to considerably improve the paper and its readability.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gabor Stepan.
Appendix
Appendix
We state here the result that we have used in Sect. 6 for the computation of some integral terms when dealing with the nonlinearity \(f(u)=u^3\). The proof follows from the prosthaphaeresis formulas.
Lemma 16
For all \(p\in {\mathbb {N}}\), we have
For all \(p,q\in {\mathbb {N}}\) (\(q\ne p\)), we have
For all \(p,q\in {\mathbb {N}}\) (\(q\ne p\)), we have
For all \(p,q,r\in {\mathbb {N}}\) (all different and \(q<r\)), we have
For all \(p,q,r,s\in {\mathbb {N}}\) (all different and \(p<q\), \(r<s\)), we have
Rights and permissions
About this article
Cite this article
Garrione, M., Gazzola, F. Loss of Energy Concentration in Nonlinear Evolution Beam Equations. J Nonlinear Sci 27, 1789–1827 (2017). https://doi.org/10.1007/s00332-017-9386-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-017-9386-1