Coordinated Speed Oscillations in Schooling Killifish Enrich Social Communication

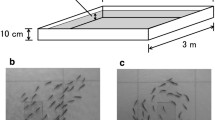
Abstract

We examine the spatial dynamics of individuals in small schools of banded killifish (Fundulus diaphanus) that exhibit rhythmic, oscillating speed, typically with sustained, coordinated, out-of-phase speed oscillations as they move around a shallow water tank. We show that the relative motion among the fish yields a periodically time-varying network of social interactions that enriches visually driven social communication. The oscillations lead to the regular making and breaking of occlusions, which we term “switching.” We show that the rate of convergence to consensus (biologically, the capacity for individuals in groups to achieve effective coordinated motion) governed by the switching outperforms static alternatives, and performs as well as the less practical case of every fish sensing every other fish. We show further that the oscillations in speed yield oscillations in relative bearing between fish over a range that includes the angles previously predicted to be optimal for a fish to detect changes in heading and speed of its neighbors. To investigate systematically, we derive and analyze a dynamic model of interacting agents that move with oscillatory speed. We show that coordinated circular motion of the school leads to systematic cycling of spatial ordering of agents and possibilities for enriched spatial density of measurements of the external environment. Our results highlight the potential benefits of dynamic communication topologies in collective animal behavior, and suggest new, useful control laws for the distributed coordination of mobile robotic networks.

Appendix

1.1 Appendix 1: Experiments and Trajectory Data

Groups of two and three killifish, collected from Silver Lake, Sackville, New Brunswick, Canada, were among the small schools filmed by IDC in September 2000, while they swam in a 155-cm square tank in shallow water (2.5 cm). The smallest of the fish were on average 3 cm long, and the largest were on average 4 cm long. The video was recorded from 190 cm above the tank on a Sony DVCAM at 31.2 frames per second and was later transferred to DV-format video files. Custom tracking software (Swain 2011; Swain et al. 2012) was used to extract raw trajectory data from the video files of the groups of two and three killifish. The output of the tracking software is one trajectory time series for each fish in each video. That is, for each fish in each video with $N_t$ frames we have

$$\begin{aligned} \mathbf {r}(t) = \left[ \begin{array}{c} x(t) \\ y(t) \end{array}\right] ,\ t = \left\{ 0,\ 1,\ \ldots , N_{t}-1\right\} \end{aligned}$$

where (x(t), y(t)) are the coordinates, in meters, of the centroid of the fish relative to the bottom left corner of the video frame at time $t T_s$, and $T_s = 32.1$ ms is the time between video frames.

From these data we calculate positions in meters by multiplying image coordinates in pixels by a scaling factor, that is, the ratio of the known width of the tank in meters to the width of its image in pixels. This scaling conversion is sufficient because there was very little lens distortion and because the camera was mounted such that the image plane was aligned with the plane of the bottom of the tank (i.e., there was negligible rotation between the image coordinate system and the tank coordinate system).

A subset of the trajectory time series data is used for the analysis of speed oscillations (see Sect. 2). To select this subset, a set of candidate data sequences is determined by rejecting time samples for which either a) one or more fish is not visible in the video frame or b) the fastest-swimming fish has a speed of less than 4 cm/s (i.e., the fish were idle). Any of these candidate segments that is less than 2.0 s in duration is rejected. A subset of the remaining sequences is selected in order to balance the number of time sample contributions from each experimental group. First, the group with the smallest total number of candidate time samples is rejected. Sequences were then selected from each of the remaining groups, one group at a time and in the order in which they were recorded, until the number of samples for that group exceeds the number of samples from the second smallest group. This method produces a similar number of samples from each group. It is applied separately to the two-fish data and the three-fish data.

For the analysis of speed oscillations in two-fish schools, the method provides 15 groups of fish (after the group with the fewest available samples was removed) with a total of 130 time segments and a total duration of 1343.40 s (22.39 min). The time contribution per group ranges from 89.94 to 110.51 s with shortest segment 2.08 s, longest segment 40.26 s, and average segment 10.33 s. For the analysis of speed oscillations in three-fish schools, the method provides 11 groups of fish (after the group with the fewest available samples is removed) with a total of 63 time segments and a total duration of 912.63 s (15.21 min). The time contribution per group ranges from 82.95 to 108.14 s with shortest segment 2.08 s, longest segment 61.31 s, and average segment 14.49 s.

A subset of the trajectory time series three-fish data is used for analysis of configurations (see Sect. 3). This subset is determined in a manner similar to that described above with the same constraints on visibility and minimum speed. In addition, segments during which any fish is within three body lengths (12.0 cm) of the edge of the tank or with duration less than 2.0 s are rejected. Of the remaining segments, only those during which at least two of the fish engage in coordinated speed oscillations are kept. These segments are determined according to the algorithm described in Sect. 2.1 for isolating oscillatory segments in a time series using the instantaneous phase of the relative speed between a pair of fish. The number of time samples from each experimental group is balanced using the procedure described above.

For the analysis of configurations in three-fish schools, the method provided 11 groups of fish (after the group with the fewest available samples was removed) with a total of 246 segments and a total duration of 1086.76 s (18.11 min). The time contributed per group ranges from 105.83 to 115.03 s with shortest segment 1.12 s, longest segment 15.45 s, and average segment 4.42 s.

1.2 Appendix 2: Velocity Estimation

We describe the method we use to estimate the velocity, $\mathbf {v}(t)$, and the nominal speed, $\bar{s}(t)$, of each fish at time t during each segment of the trajectory data for the two-fish and three-fish groups.

The velocity, $\mathbf {v}(t)$, is estimated by filtering the “raw” velocity $\bar{\mathbf {v}}(t)$ computed from the forward differences in position as

$$\begin{aligned} \bar{\mathbf {v}}(t) = \frac{1}{T_s}\left( \mathbf {r}(t + 1) - \mathbf {r}(t)\right) . \end{aligned}$$

Filtering is achieved by convolving $\bar{\mathbf {v}}(t)$ with a truncated sinc kernel that approximates an ideal low-pass filter in the frequency domain [(see for example Proakis and Manolakis (1996)]. The filter kernel, $K(\tau )$, is the sequence

$$\begin{aligned} K(\tau ) = \bar{K}\ \frac{\sin 2\pi \tau T_s f_c}{2\pi \tau T_s f_c},\ \;\;\;\; -\frac{L_K-1}{2} \le \tau \le \frac{L_K-1}{2} \end{aligned}$$

(16)

where $f_c = 2.0$ Hz is the cutoff frequency, $L_K=201$ is an odd integer equal to the number of samples in the kernel, and $\bar{K}$ is a constant that satisfies $\sum _{\tau = -\frac{L_K-1}{2}}^{\frac{L_K-1}{2}}K(\tau ) = 1$. The cutoff frequency $f_c$ is chosen to eliminate as much noise as possible from the sample speed sequences without over-smoothing the estimate.

The convolution operation is undefined for the first and last $(L_K-1)/2$ samples of the raw velocity sequence. To avoid losing these samples, the raw velocity sequence is extended beyond its original length, $N_t$. The extended raw velocity is defined as

$$\begin{aligned} \bar{\mathbf {v}}_e(t) = \left\{ \begin{array}{ll} \bar{\mathbf {v}}(-t),&{} -\frac{L_K - 1}{2} \le t < 0 \\ \bar{\mathbf {v}}(t),&{} 0 \le t < N_t \\ \bar{\mathbf {v}}(2 N_t - t),&{} N_t \le t < N_t + \frac{L_K - 1}{2}. \end{array}\right. \end{aligned}$$

(17)

The convolution of the extended raw velocity sequence with the kernel sequence is taken as the estimate of the velocity:

$$\begin{aligned} \mathbf {v}(t) = \sum _{\tau = -\frac{L_K-1}{2}}^{\frac{L_K-1}{2}} \bar{\mathbf {v}}_e(\tau -t) K(\tau ),\ 0 \le t < N_t. \end{aligned}$$

The speed is $s(t) = \Vert \mathbf {v}(t) \Vert$ and the heading is $\theta (t) = \angle \left\{ \mathbf {v}(t) \right\}$. The nominal speed, $\bar{s}(t)$, is calculated by applying a low-pass filter with bandwidth 0.375 Hz to the raw velocity and taking the Euclidean norm of the resulting vector. A sinc kernel of the form (16) is used with $f_c = 0.375$ Hz and $L_K = 1067$ samples. Sequences are extended as in (17) prior to filtering.

1.3 Appendix 3: Metric for Speed Oscillation Phase Difference

The mean sign product (MSP) is derived to provide a measure of coordination of speed oscillations between a pair of fish that is not so sensitive to amplitude fluctuations and noise in the speed variation signals. The MSP is computed as a function of the relative speed variation $\delta s_{ij}$ for the pair of fish i and j, where $\delta s_{ij}(t) = \delta s_i(t) - \delta s_j(t)$. We define

$$\begin{aligned} \mathrm {MSP}(i,j) = \frac{1}{N_t} \sum _{t = 1}^{N_t} \mathrm {sign}\left\{ \left( \delta s_i(t) - \delta \bar{s}_i\right) \left( \delta s_j(t) - \delta \bar{s}_j\right) \right\} , \end{aligned}$$

(18)

where $\delta \bar{s}_i$ ($\delta \bar{s}_j$) is the average value of $\delta s_i(t)$ ($\delta s_j(t)$) over the segment.

When fish i and fish j have speed oscillations that differ in phase by 180$^\circ$, then $\mathrm {MSP}(i,j) = -1$, and we say that their speeds are anti-synchronized. When fish i and fish j have speed oscillations that differ in phase by 0$^\circ$, then $\mathrm {MSP}(i,j) = 1$, and we say that their speeds are synchronized.

For perfect sinusoids, the MSP varies linearly with the phase difference, $\Delta \phi$, modulo $360^{\circ }$, as $\mathrm {MSP} = 1 - 2\left| \frac{\Delta \phi }{180^{\circ }}\right|$. Noise tends to compress the estimate away from the $\pm 1$ extremes. $\mathrm {MSP}(i,j) < 0$ indicates that the speed oscillations of fish i and fish j are more anti-synchronized than they are synchronized. Likewise, $\mathrm {MSP}(i,j) >0$ indicates that the speed oscillations of fish i and fish j are more synchronized than they are anti-synchronized. $\mathrm {MSP}(i,j) = 0$ corresponds to a phase difference of $\pm$90$^\circ$. The variance of the MSP, calculated across subsegments of equal length, is an indication of the uniformity of phase differences. If there is no uniformity, then the mean MSP tends toward zero and the variance tends toward 1/3 (i.e., the variance of a uniform distribution over the range $-1$ to 1). If there is a high degree of uniformity in phase difference, then the variance will be low.

1.4 Appendix 4: Uniform Connectedness of a Periodically Time-Varying Graph

Consider a time-varying graph ${\mathcal {G}}(t)$ defined by a node set ${\mathcal {V}} = \left\{ 1,\ldots , N\right\}$ and an edge set ${\mathcal {E}}(t) \subseteq {\mathcal {V}} \times {\mathcal {V}}$. A node i is said to be connected to node j at time t if there is a path in ${\mathcal {G}}(t)$ from i to j that respects edge directions, i.e., there is a set of nodes $k_1, \ldots , k_n \in {\mathcal {V}}$, $n \le N - 2$, such that $(i,k_1),\, (k_1, k_2),\, \ldots ,\, (k_n,j)$ are all in ${\mathcal {E}}(t)$. The graph ${\mathcal {G}}(t)$ is defined to be connected at time t if there is a node $k \in {\mathcal {V}}$ that is connected to all other nodes at time t. For a time-varying graph ${\mathcal {G}}(t)$ and any time interval I, we may construct a graph ${\mathcal {G}}_I$, where ${\mathcal {G}}_I$ has the same node set, ${\mathcal {V}}$, as ${\mathcal {G}}(t)$ and an edge set ${\mathcal {E}}_I$ defined such that $(i,j) \in {\mathcal {E}}_I$ if and only if $(i, j) \in {\mathcal {E}}(t)$ for some $t \in I$. We say that node i is connected over time interval I to node j if there is a path from i to j in ${\mathcal {G}}_I$ that respects edge directions. A graph ${\mathcal {G}}(t)$ is said to be uniformly connected if there is a node $k \in {\mathcal {V}}$ and a time horizon $\tau > 0$ such that, for all $t \ge 0$, node k is connected to all other nodes over the interval $I = [t, t + \tau ]$. If the graph is periodically time varying with period T, i.e., ${\mathcal {G}}(t) = {\mathcal {G}}(t + T)$, then ${\mathcal {G}}(t)$ is uniformly connected if the graph ${\mathcal {G}}_I$ is connected for $I = [t, t + T]$ for any $t \ge 0$.