Introduction

Diffusion-weighted magnetic resonance imaging (DW-MRI) depicts solid tumours with high contrast because they exhibit increased restriction of water diffusion compared with many normal tissues. DW-MRI has been used in patients with ovarian cancer for localisation of disease, monitoring response to treatment, and in the investigation of recurrence [1–6]. DW-MRI may also provide a quantitative assessment of response to chemotherapy because an increase in the apparent diffusion coefficient (ADC) after chemotherapy, measured over the entire disease burden, has been shown to be indicative of response to treatment [7, 8]. Estimates of ADC are derived from fitting a mono-exponential function to the signal (S) as described by Eq. 1.

$$ S(b)={S}_0 \exp \left(-b.ADC\right) $$
(1)

DW-MRI may be valuable in assessing inter-lesion heterogeneity, for example, lower baseline ADCs have been reported in peritoneal deposits when compared with ovarian or omental lesions [8] and post-treatment changes may also vary by disease site [9]. However, it has previously been shown that the DW-MRI signal in primary and metastatic lesions in ovarian cancer is not fully described by a mono-exponential function [10] and more advanced models potentially provide a better description of the data, which would enable more detailed investigation of differences between tumour sites. A good fit to the data using a minimum number of parameters and good repeatability are key requirements of such models.

An example of a model with a minimum number of additional parameters is the stretched exponential model, which only utilises one additional parameter (α), to describe the deviation of the decay curve from a mono-exponential curve (Eq. 2). The distributed diffusion coefficient (DDC) is conventionally used in the exponent [11].

$$ S(b)={S}_0 \exp \left(-{(b.DDC)}^{\alpha}\right) $$
(2)

The stretched exponential model has been used pre-clinically in healthy rat brains [11] and a rat model of glioma [12] and has also been applied clinically in high-grade glioma [13] and prostate cancer [14]. Stretched exponential behaviour may arise from a distribution of mono-exponential decay processes, for example, multiple pools of water molecules, with different diffusion coefficients within each voxel [11]. A stretched exponential description of the DW-MRI signal can also be derived from a generalisation of the Bloch-Torrey equation using fractional order space and time derivatives to describe a distribution of jump lengths or jump waiting-times in a random walk [15].

Another model, the bi-exponential model, also called intravoxel incoherent motion (IVIM), describes two distinct components in the signal decay (Eq. 3) [16]. The bi-exponential model has been shown to describe the DW-MRI signal in prostate [17], liver [18], and kidneys [19]. The fast component (D*) is associated with the signal decay due to perfusion and the slow component (D) is associated with diffusion processes in the sample. The perfusion fraction is described by the parameter f in Eq. 3.

$$ S(b)={S}_0\left(f \exp \left(-b{D}^{*}\right)+\left(1-f\right) \exp \left(-bD\right)\right) $$
(3)

We therefore aimed to assess repeatability and goodness-of-fit of parameters measured from mono-exponential (ADC), stretched exponential (DDC, α), and bi-exponential (D, f, D*) models in data from ovarian cancer localised in ovary, omentum, peritoneum, and lymph nodes, before and after treatment, in order to determine the best model for future treatment response trials using DW-MRI in this disease. A formal evaluation of response is outside the remit of the current work, which only seeks to establish the optimal model for analysis of pre-treatment and post-treatment data at multiple metastatic sites in ovarian cancer.

Materials and methods

Patients

Patients with high-grade ovarian cancer (primary n = 17, relapsed n = 14) with at least one lesion larger than 2 cm recruited from two institutions as part of an ongoing prospective multicentre clinical trial (DISCOVAR, CCR3694) were studied. Patients with primary disease were scanned twice before starting chemotherapy while those with relapsed disease were scanned only once. The median interval between two pre-treatment scans was 3 days (range 0 days to 7 days). All patients had a scan after three cycles of platinum-based chemotherapy.

Imaging protocol

Hyoscine butylbromide (20 mg) i.m. was administered before scanning to reduce image artefacts due to peristalsis. T1-weighted and T2-weighted images were acquired in order to provide anatomical information. A DW sequence with ten diffusion-weightings (0, 50, 100, 150, 200, 250, 300, 500, 700, 900 s mm-2) was acquired for comprehensive analysis of non-mono-exponential models at a single station as time constraints prevented full volume coverage. The imaging volume for this sequence was positioned on the largest lesion on the baseline examination and copied to the same position on subsequent examinations. The protocols for the DW-MRI sequences are described in Table 1. Stacked DW sequences using four b-values (0, 100, 500, 900 s mm-2) acquired in three stations covering the abdomen and pelvis from the symphysis pubis to the top of the diaphragm for response assessment within the trial did not form part of this study.

Table 1 Protocols used for DW-MRI on two scanners
Full size table

Analysis

Diffusion-weighted images from the additional station (ten b-values between 0 and 900 s mm-2), positioned on the largest lesion, were analysed in this methodological study. Smaller lesions encompassed by this station were also included in the analysis. Regions of interest (ROIs) were drawn by region growing on computed DW images (b = 1000 s mm-2) using in-house software (Adept, Institute of Cancer Research, London) [20]. Computed DW images with high b-values have been shown to have better signal-to-noise ratio (SNR) than acquired images at the same b-value and provide improved conspicuity of lesions compared with acquired images at lower b-values [20]. The use of computed DW images also ensures that the effects of motion between images of different b-values are taken into account in the ROI. In all cases the ROIs were drawn with reference to the anatomical T1-weighted and T2-weighted images. ROIs were drawn on every slice on which the lesion appeared (between two and 23 slices). Mono-exponential, stretched exponential and bi-exponential curves (Eqs. 1, 2, and 3, respectively) were fitted to all ten b-values for each pixel in the lesion using a least-squares fit (trust-region-reflective algorithm, Matlab 2013, MathWorks Inc., Natick, MA). When fitting the bi-exponential curves, starting values of D, f, and D* were determined from a least-squares fit of a mono-exponential curve to the signal at the lowest five b-values and another mono-exponential curve fitted to the remaining signal at the higher b-values. These starting values were used for the least-squares fit of the bi-exponential curve to the data at all ten b-values. The goodness-of-fit of the mono-exponential, stretched exponential, and bi-exponential models were compared using the Akaike information criterion (AIC), which imposes a penalty for additional parameters in the model [21]. In order to reduce the sensitivity to outlier values, the median value of each fitted parameter from all pixels in the lesion was used for analysis of repeatability.

The repeatability of estimates of ADC, DDC, α, D, f, and D* were assessed using pairs of pre-treatment measurements from 22 lesions from patients with primary disease using the method of Bland and Altman [22]. Bland-Altman plots of untransformed data showed a relationship between the differences in the repeated measurements and their means that was improved by using the natural logarithm of the data [22]. The coefficient of variation (CV) of the log-transformed data was used to describe the repeatability of the fitted parameters (CV = √[exp(Σd2/2N)-1], where Σd2 is the sum of squared differences between pairs of measurements and N is the number of lesions).

Results

Thirty-nine lesions were evaluated prior to treatment in newly diagnosed or relapsed ovarian cancer, comprising nine ovarian lesions, 11 omental lesions, 16 peritoneal lesions, and three lymph nodes. Additionally, 31 lesions imaged after three cycles of treatment (seven ovarian lesions, eight omental lesions, 14 peritoneal lesions, and two lymph nodes) were included in the statistical evaluation to assess goodness-of-fit of the model post-treatment. Eight lesions were only included in pre-treatment analysis as three patients (a total of five lesions) withdrew from the study before post-treatment scans and a further three lesions were not visible on post-treatment scans. The numbers of pixels per lesion ranged from 42 to 136,924 (median 4580, interquartile range 21,340).

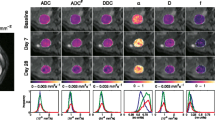
Tumours exhibited high signal intensities on trace diffusion-weighted images (Fig. 1a) and low values on corresponding ADC, DDC, and D maps (Fig. 1b–g). Lesions from all tumour sites (ovarian lesions, omental lesions, peritoneal lesions, and lymph nodes) were well depicted on high b-value images, as described in previous studies, which showed that DW-MRI aids detection and delineation of lesions [4].

Fig. 1
figure 1

(a) Diffusion-weighted trace image (b = 900 s mm-2) of the central slice of an ovarian lesion. (b) ADC estimates from fitting mono-exponential model in ROI. (c, d) DDC and α from the stretched exponential model. (e, f, g) D, f, and D* from the bi-exponential model

Full size image

An example of mono-exponential, stretched exponential, and bi-exponential curves fitted to the data from one pixel in an ovarian lesion in a pre-treatment scan is illustrated in Fig. 2. The fitted parameters for the lesion were: ADC = 1.35 × 10-3 mm2 s-1, DDC = 1.33 × 10-3 mm2 s-1, α = 0.76, D = 1.14 × 10-3 mm2 s-1, f = 0.14, and D* = 1.41 × 10-2 mm2 s-1. The values of AIC were 29.5, 1.6, and 10.2 for the mono-exponential, stretched exponential, and bi-exponential models, respectively, indicating that the stretched exponential model is the preferred model in this instance.

Fig. 2
figure 2

Mono-exponential, stretched exponential and bi-exponential curves fitted to one pixel in an ovarian lesion measured in a pre-treatment scan

Full size image

Repeatability estimates for each of the models from repeated baseline measurements indicated CVs in the range 3 % to 4 % for ADC and DDC, rising to 7 % for α, with very large CVs for D, f, and D*. These data are listed in Table 2 and illustrated with Bland-Altman plots (Fig. 3). After excluding seven lesions which, by inspection of the Bland-Altman plot, were considered to be outliers due to very large differences (>50 %) in D* between baseline measurements, the CV of D, f, and D* were reduced to 6.4 %, 18.2 %, and 13.6 %, respectively.

Table 2 Coefficients of Variation of parameters derived from mono-exponential (ADC), stretched exponential (DDC, α) and bi-exponential (D, f, D*) models in pre-treatment data in patients with primary disease
Full size table
Fig. 3
figure 3

Bland-Altman plots on log-log scale (a) ADC from the mono-exponential model, (b, c) DDC and α from the stretched exponential model (d, e, f) D, f, and D* from the bi-exponential model. Solid lines show mean difference between two estimates. Dashed lines show 95 % Limits of Agreement. The same scales have been used on the y-axes of graphs (a–d) and (e–f) to aid comparison

Full size image

Owing to the poor repeatability of f and D*, the bi-exponential model was excluded from the AIC analysis. The percentages of lesions where the AIC indicated the mono-exponential and stretched exponential models were preferred by the largest number of pixels in the lesion in pre-treatment measurements were 18 % and 64 %, respectively (Table 3). In the remaining 18 % of lesions, the majority of pixels preferred a mono-exponential curve on one pre-treatment scan but a stretched exponential curve on the other scan.

Table 3 Percentage of lesions where mono-exponential and stretched exponential models were preferred by the largest numbers of pixels, as a percentage of all lesions studied at the relevant time-points. Figures in brackets show the numbers of lesions where each model was preferred
Full size table

When separated by tumour site (ovarian, omental, peritoneal, and lymph node), the stretched exponential model provided the better fit to the majority of pixels in the largest number of lesions in all sites (Table 4). In seven lesions in patients with primary disease (three ovarian, four omental) the majority of pixels was on a mono-exponential curve on one pre-treatment scan but a stretched exponential curve on the other scan.

Table 4 Percentage of lesions where mono-exponential and stretched exponential models had the largest numbers of pixels, grouped by tumour site (ovarian, omental, peritoneal, and lymph node). Figures in brackets show the numbers of lesions where each model was preferred
Full size table

Correlation of pre-treatment estimates of DDC with ADC and α with DDC for all 39 lesions studied showed that the estimates of ADC and DDC lay close to the line of identity (solid line) for all lesions (r 2 = 0.997) (Fig. 4a). However, there was no correlation between α and DDC (r 2 = 0.003) (Fig. 4b).

Fig. 4
figure 4

Plots of pre-treatment estimates of (a) DDC against ADC and (b) α against DDC for all lesions. Solid line in (a) shows line of identity

Full size image

Discussion

This study shows that the stretched exponential model provides a better characterisation of DW-MRI data from primary and metastatic ovarian cancer than a mono-exponential or bi-exponential model. Also, as indicated by the AIC statistics, the preference for the stretched exponential model held true for lesions from different sites (ovarian lesions, omental lesions, peritoneal lesions, and lymph nodes) regardless of whether or not treatment had been given. In addition, the repeatability of the stretched-exponential parameters at baseline was good, whereas that for the bi-exponential was poor. This is a key consideration when applying advanced models that provide a better description of the experimental data because their utility in the investigation of treatment effects or inter-lesion heterogeneity may be undermined if they have poor repeatability. The very good repeatability (3.1 %) of the ADC estimates from the mono-exponential model is in agreement with results of other studies [7, 23–25]. The stretched exponential model has comparable repeatability to the mono-exponential model (4.3 % for DDC; 7.0 % for α) indicating that use of this model does not compromise measurement repeatability. The bi-exponential model was unsuitable for analysis of these data owing to its poor repeatability, particularly for f and D*. The poor repeatability of f and D* indicate that the bi-exponential model may be more sensitive to noise in the data than the other models as has been indicated by previous studies [14, 26, 27] with similarly poor repeatability of f and D* [25]. The outliers, defined here as differences larger than 50 % between two baseline measurements of D*, may also reflect the sensitivity of the bi-exponential model to noise in the data. Although the repeatability can be improved by excluding outliers, this was only possible in this study because repeat baseline measurements were acquired. Where a treatment effect is being studied, it may be impossible to distinguish between an outlier and a large treatment effect for a given individual.

The stretched exponential model was the most efficient of the non-mono-exponential models as it only involves estimation of one additional parameter. As demonstrated by the repeatability of D, f, and D*, more advanced diffusion models risk over-fitting the data and increasing the sensitivity to noise, particularly in extra-cranial applications. There is also a practical argument for choosing an efficient model because the number of b-values acquired must be at least as large as the number of parameters in the model, potentially leading to very long acquisition times for the data required to support more advanced models. Moreover, since α is not correlated with DDC any information it provides will be complementary to DDC, and so it may provide a means of assessing inter-lesion heterogeneity at baseline or differential response to treatment in a larger cohort of patients. The strong correlation of DDC with ADC indicates that DDC provides similar information to ADC.

An apparent limitation of this study was that the lower b-values used in this sequence (lower four b-values 0, 50, 100, 150 s mm-2) may not provide sufficient data to support estimation of the fast component of a bi-exponential model, in particular D*. The number of b-values and their values at low diffusion-weightings was limited by the requirement for a common sequence across a wide range of clinical platforms for implementation in a multicentre trial. However, the bi-exponential model is typically used to characterise data which exhibit a steep deviation from mono-exponential behaviour at low diffusion-weightings, which is not the case in these data where the deviation from mono-exponential behaviour is observed at all diffusion-weightings (Fig. 2).

In summary, a stretched exponential model provides a good fit to DW-MRI data from ovarian lesions, omental lesions, peritoneal lesions, and lymph nodes in pre-treatment and post-treatment measurements. It has comparable repeatability to the mono-exponential model and provides a better description of the data in the majority of lesions both before and after treatment. The extra parameter from the stretched exponential model provides scope for further investigation of inter-lesion heterogeneity or response to treatment.