Decision support for prioritizing critical societal services in optimal post-disaster critical lifeline recovery

Abstract

Critical societal services, such as health care, education, law enforcement, and emergency response, are key to societal well-being and safety. Disruption to these services may arise from direct damage to the buildings from which the services are provided, or indirectly as a consequence of damage to supporting lifelines. The order in which lifeline elements are restored post-disaster affects not only the timing for restoring the lifeline services to its customers, but also the timing for restoring critical services that rely on these lifelines. In this paper, a mathematical formulation of the problem of prioritizing critical societal services in lifeline service restoration treated by multiple, specialized crews and exact algorithmic approach for its solution are proposed. Two approaches to accelerate the solution algorithm for use in realistic settings, where efficiency and scalability are essential, are presented. The developed techniques can be embedded in a decision support tool for real-time application with real-time information. To illustrate the proposed modeling and solution methodology and assess its efficiency for large, complex multi-lifeline applications, numerical experiments were run on a synthetic yet real-world network involving three key lifelines, including power, water, and transportation, as well as two hospitals that rely on them. The analysis of this case study shows that cross-lifeline collaboration in prioritization and scheduling in restoration action affects not only the return of services from the individual lifelines, but also of critical services on which, particularly in disaster settings, lives may depend.

1 Introduction

Critical societal services, such as health care, education, law enforcement, and emergency response, are key to societal well-being and safety. Disruption to these services may arise from direct damage to the buildings from which the services are provided or indirectly as a consequence of damage to supporting lifelines. For example, without power and water, a hospital cannot serve its patients. Likewise, without functioning roadways, access to functioning hospital services may be prevented.

The order in which lifeline elements are restored affects not only the timing for restoring the lifeline services to its customers, but also the timing for restoring critical services that rely on these lifelines. Typically, restoration schedules are created for individual lifelines in silos, each using specialized crews. Sometimes, the restoration of two lifelines is coordinated, such as where roadway crews may work jointly with power crews, prioritizing the opening of roadways that most aid the speed of power restoration. This need for coordinated action is primarily due to dependencies and interdependencies in functionality between lifelines.

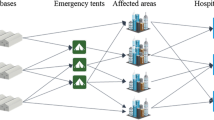
Interdependencies between lifelines can also arise directly or indirectly. For example, a water pump in the water lifeline may need power and the power network may need water. Indirectly, roadways support restoration to other lifelines. With no open pathways to access lifeline elements needing repair, restoration actions may be precluded. How to exploit coordination across lifelines to aid in speeding up time to bring back services to a community impacted by a disaster event was addressed in Shahverdi and Miller-Hooks (2023). Herein, restoring service capability of the key buildings that provide critical societal services is prioritized over full lifeline recovery. A schematic illustrating the reliance of critical societal services on interdependent lifelines, here including power, water and transportation, is given in Fig. 1.

Fig. 1

Interdependent lifelines and the critical societal facilities they support

The power plants generate electricity, which is transmitted to the transformers through switching stations along electricity supply line, and ultimately to the end users (here, the hospitals) via additional supply lines. (U.S. Energy Administration). Transformers increase or decrease voltage in response to power demand. The water network begins with the production of water from a water well source. This is pumped and transferred from the wells to storage tanks from which it is distributed to the end users (here, again, the hospitals). This structure of the power and water lifelines is modeled herein, and is depicted in Fig. 1.

In the immediate aftermath of a disaster event, information on lifeline conditions may be lacking, making the planning of restoration actions challenging. The issue of obtaining updated condition information can persist as the disaster could disrupt communication lines and travel across the region may be obstructed. This suggests that many possible condition state scenarios may need to be considered when initiating restoration actions. Over time situational awareness improves as information is obtained from responders, repair crews, inspection, drones, remote sensing, and other sources, or as power is restored, and hazard impact scenarios that were previously possible may no longer be a threat. Thus, both uncertainty in condition state and decisions will need to be updated as new information is received.

In this paper, the problem of prioritizing critical societal services in lifeline service restoration using multiple, specialized crews with appropriate skills for the lifeline elements they service is conceptualized as a multi-stage stochastic program, where the uncertainty arises in the damage status of the lifeline elements. Interdependencies between lifelines are captured through the model constraints.

A dynamic solution framework is proposed in which a series of interrelated two-stage stochastic programs, approximating the multi-stage stochastic problem, are solved in a rolling horizon setting over a diminishing planning horizon. Exact solution is obtained at each epoch within the horizon through a progressive hedging (PH) algorithm. The PH algorithm decomposes the two-stage stochastic program by scenario. The proposed solution framework exploits real-time information on lifeline element states, creating a monotonically decreasing number of relevant scenarios. Thus, solution speed improves over time with the diminishing scenario set. Additionally, this use of decomposition by scenario further supports parallelization of the PH algorithm, further improving the run times. Time is of the essence when critical operations need to be planned in real-time. The use of these acceleration methods to enable problem scale and simultaneously reduce run time is crucial, especially in the early stages of the restoration period when limited information is available on the condition of lifeline elements. Embedding the solution framework with scenario reduction approach and parallel implementation in a decision support tool can, thus, aid a community in prioritizing critical societal services in optimal post-disaster critical lifeline recovery.

The contributions of this paper given the state-of-the-art are established in the next section (Sect. 2), in which related literature is reviewed. This is followed by the mathematical formulation in Sect. 3 and the solution framework in Sect. 4. The proposed methodology is illustrated in Sect. 5 with a case study developed from a real-world application that includes power (power plants, switching stations, transformers and electricity supply lines), water (water well, water tanks, water pumps and water supply lines), transportation (junctions, interchanges, bridges and roadways) and the health services (hospitals and clinics) that rely on them. Results are analyzed in the same section. Conclusions are drawn in Sect. 6.

2 Literature review

Numerous works have considered the post-disaster restoration of infrastructure lifelines. The vast majority of these works focus on the restoration of only a single lifeline (e.g. Duque and Sörensen 2011; García-Alviz et al. 2021; Akbari and Salman 2017). There are some works, though, that consider more than one lifeline (e.g. Fotouhi et al. 2017; Tariverdi et al. 2019; Kong et al. 2021; Karakoc et al. 2019). These works mostly seek to quantify or enhance resilience, where multiple, interconnected lifelines may be impacted by a disaster event These resilience works, however, do not provide detailed, post-disaster schedules for restoration actions across lifelines. Shahverdi and Miller-Hooks (2023) proposed a stochastic optimization methodology with endogenous uncertainty to support post-disaster repair crew deployment across multiple infrastructure lifelines. The optimization aims to minimize roadway downtime, as well as ensure the timely completion of restoration to other lifelines that rely on the roadways, through coordination in inspection and restoration activities across lifelines. An extensive review of this literature can be found in Shahverdi and Miller-Hooks (2023).

Deshmukh and Hastak (2014) suggest that infrastructure not only involves civil infrastructure (e.g., water, power and transportation), but also civic (e.g., emergency centers, hospitals, police), and social (homes, religious centers) infrastructure, among other categories. The vast majority of the abovementioned works focus on the civil infrastructure category alone. There are some works that consider the reliance of important community services, such as healthcare, on the civil lifelines, but most of these works are qualitative and merely mention the need to develop tools for assessing their resilience. Among these works only five works are quantitative: Tariverdi et al. (2019), Choi et al. (2019), Yuan et al. (2021), Almaleh et al. (2022) and Ojha et al. (2021).

Tariverdi et al. (2019) developed a stochastic optimization approach with an embedded metamodel from simulation runs of a sophisticated hospital model for assessing and optimizing the resilience of healthcare services that are provided from buildings (e.g. hospitals) that rely on interdependent transportation, water and power networks. Choi et al. (2019) developed a stress–strain based methodology with simulation to assess the resilience to disaster events of interdependent, broadly defined infrastructure. They applied their method to analyze the effectiveness of capacity building strategies that can increase the performance of hospitals post-disaster. They specifically consider that the hospitals rely on water and power lifelines. Tariverdi et al. and Choi et al. both focused primarily on system evaluation and evaluating strategy effectiveness in offline settings. Tariverdi et al. account for recourse actions that can be taken in future stages as information about the disaster scene is revealed, but the multi-stage formulation is not designed for real-time decision support. Yuan et al. (2021) explicitly recognized the need for access to hospitals in post-disaster roadway resilience quantification.

Almaleh et al. (2022) proposed a deterministic model to identify the best location for installing a microgrid to support other lifelines and societal services (e.g. healthcare, cellular network, water system). Ideally, the location will be chosen to minimize the microgrid cost given the reliance of other lifelines on microgrids. They explicitly considered the effects of installing a microgrid in a location that might support a hospital given the hospital’s reliance on power. Ojha et al. (2021) proposed a dynamic mathematical model to optimally allocate resources (fuel, potable water, storage space and more) to personnel, lifelines and societal services (e.g. healthcare, fire and police response). All societal services were treated mathematically as a single facility. The reliance of the critical services on the civil lifelines is not modeled. These models are all intended for planning purposes.

There are several studies that have considered a real-time framework for post-disaster restoration scheduling, examples of which include: Akbari et al. (2021), Zhang and Wei (2021), Chang and Li (2010), Zografos et al. (2002), Sayarshad et al. (2020), Chen et al. (2011), Chang et al. (2023), Sun and Zhang (2020), and Yuan et al. (2021). These studies mostly focused on roadway networks alone. Sun and Zhang (2020) considered more than one type of lifeline. Specifically, they proposed a methodological framework to optimize the allocation of repair crew’s post-disaster considering multiple interdependent infrastructure lifelines (power plants, wastewater treatment plants, and bridges) in a real-time framework. Yuan et al. (2021) analyzed the post-disaster resilience of a roadway network using real-time data from tweets made in social networks about affected roadways. They apply their model to study access to four hospitals that are treated as travel destinations. Restoration scheduling is not considered in their work. None of these works consider the restoration of critical societal services, as is the focus herein.

A synthesis of the most relevant studies and some of their features is provided in Table 1. This paper adds to the literature through the development of a scalable modeling and solution methodology for determining an optimal restoration schedule that coordinates actions across multiple lifelines, with the aim of not only returning lifeline services to the community, but also prioritizing the restoration of critical services that are delivered from buildings and are affected by the restoration of lifeline supports.

Table 1 Literature review table

3 Modeling the problem of prioritizing critical societal services in the restoration of lifeline services

3.1 Problem context

The problem of prioritizing critical societal services in lifeline service restoration can be conceptualized as a multi-stage, stochastic program, where the damage state of each network element under each lifeline is known with uncertainty. Specialized repair crews with skills pertaining to the specific components of the lifeline they service are deployed beginning from a depot or set of depots. Due to interdependencies between lifelines, deployment decisions may be restricted. For example, a crew that services switching stations in the power network cannot be deployed to a location that is not reachable via the roadway. Once passage is created between their location and that of the switching station in need of repair, they can be deployed to it.

At each stage over a time horizon, repair crew deployment decisions across lifelines are taken and repairs are completed. These crews observe the condition of nearby lifeline elements. Additional condition state information may be received from exogenous sources, such as sensors or rescue personnel working in the region, over the disaster restoration period. Thus, information on the state of repaired and observed lifeline elements is received over time. The multi-stage stochastic optimization seeks the best set of restoration actions across lifelines accounting for next stage crew deployment actions as future recourse. Note that as observations depend on repair crew deployment decisions, the problem involves decision-dependent or endogenous uncertainty.

This paper aims to aid decision makers in repair crew deployment decisions for a real-time setting in which time is of the essence. A multistage stochastic optimization formulation folds in recourse decisions at all future stages, making a solution of such a model formidable and not well suited for the real-time operations for which it is intended. To address these real-time considerations, the multi-stage stochastic program is split into two-stage, multi-period stochastic problems in a shrinking time horizon as depicted in Fig. 2.

Fig. 2

Multi-stage stochastic program versus two-stage stochastic program in a rolling horizon

Figure 2 shows how information is rolled out over a decision horizon of four time increments under both a multi-stage stochastic programming formulation and an approach that uses a series of interrelated two-stage stochastic programs. In the former (the left-hand side of the figure), decisions in an earlier stage account for all the possible decisions and random variable realizations over all future stages. As the crews observe conditions as they are deployed to service system components, deployment decisions taken by the model affect the realization of random variables within the model. This creates a decision-dependent stochastic model setting. As such, non-anticaptivity constraints (NACs) that ensure that the same decisions will be enforced when scenarios are indistinguishable (that have the same revealed values to this point), are needed (Apap and Grossman 2017). In the latter (the right-hand side of the figure), an approach that reduces the multi-stage program to a series of two-stage stochastic programs with interrelated information (i.e. the outputs of one are the inputs for the next). These programs are rolled out using a rolling horizon framework. With this latter approach, the later stage (conditional) NACs can be eliminated, greatly reducing the computational complexity of solution. More details of the NACs and why they can be eliminated using the latter rolling horizon concept are given in Sect. 3. As shown by Pantuso and Boomsma (2020), increasing the number of stages to more than two does not necessarily result in an improved solution in approximating a multi-stage problem.

This solution framework is designed for decision support as opposed to decision proclamations. That is, it is intended to enable improved decision-making by an informed decision maker who may take only a subset of the actions suggested by the optimization tool. Ultimately, the methodological framework must be designed to take these considerations into account.

3.2 Problem formulation

The two-stage, binary-integer, stochastic program is presented next. Key variables and parameters used in its formulation are provided in Tables 2, 3, 4 and 5. The formulation is given in terms of three key lifelines: power, water and transportation. It can be readily expanded to incorporate additional lifelines and their interconnections to other lifelines. It presumes an underlying multi-lifeline network representation. Here, the nodes represent: power plants, switching stations and transformers in the power network; water wells, water tanks and water pumps in the water network; interchanges in the roadway network; and hospitals.

Table 2 Set and damage-status notation

Table 3 Incidence matrix

Table 4 Decision variables

Table 5 Cross-network variables

Electricity supply lines, water supply lines, and roadways (including pavements and bridges) are modeled as links. Incidence matrices and constraints that rely on them within the model capture the dependencies within each lifeline (e.g. a water pump needs water from a water well to function) and across lifelines (a water pump requires power). Bidirectional flows between lifelines are also captured within the matrices. A disaster event is presumed to affect lifeline elements and these elements are presumed to be either up or down post-disaster. Note that for simplicity, it is assumed that the hospital itself and roadway interchanges will not incur damage. Hospitals are also presumed to function immediately upon receiving lifeline services. The formulation can be extended to incorporate additional condition states and damage to these elements.

Objective function (1) has two components: the first associated with current time 0 and the second with all future time intervals t. The objective seeks to maximize the expected number of time intervals for which critical facilities (first term of each portion of the equation) and lifeline services (specified for power and water in the second and third terms of each portion) are functioning over a short-term, post-disaster time horizon. It rewards early return of service in each system, as opposed to minimizing the time by which the last element is restored. It does this by counting up the number of time intervals over the disaster time horizon for which the services are up (i.e., the related variable = 1). The objective recognizes that there are benefits to society in restoring subsystems and not only the entire system or the system of systems. The objective function can also be restructured to reward the earlier return of services that aid the most people. Each term is weighted by a term $w$ that captures its importance. ${w}_{1}+{w}_{2}+{w}_{3}=1$

$$\begin{aligned}& Max\; Z=\left({w}_{1}\sum_{\varnothing }{cf}_{\varnothing }+{w}_{2}\sum_{l}{s\mu }_{l}+{w}_{3}\sum_{o}{s\beta }_{o}\right)\\&\quad+\sum_{s}{p}_{s}. \left({w}_{1}\sum_{t}\sum_{\varnothing }{cf}_{\varnothing t}\left(s\right) +{w}_{2}\sum_{t} \sum_{l}{s\mu }_{lt}\left(s\right)+{w}_{3} \sum_{t} \sum_{o}{s\beta }_{ot}(s)\right) \end{aligned}$$

(1)

The stochastic program contains 84 sets of constraints. The first 24 (constraints (2)-(25)) are restoration crew-related constraint sets. Without loss of generality, a single specialized repair crew is presumed for each element class of each lifeline (e.g. one for bridges, one for interchanges, etc.). Half of the constraints ensure that each repair crew can only repair one element in the current time period and the other half of the constraints ensure that each repair crew can only plan for repairing one element per time increment in future stages.

Power network	Water network	Roadway network
Network restoration
$\mathop \sum \limits_{i} \sigma_{i} \le 1$	(2)	$\mathop \sum \limits_{v} \rho_{v} \le 1$	(10)	$\mathop \sum \limits_{a} \varrho_{a} \le 1$	(18)
$\mathop \sum \limits_{j} \gamma_{j} \le 1$	(3)	$\mathop \sum \limits_{w} \delta_{w} \le 1$	(11)	$\mathop \sum \limits_{u} \varsigma_{u} \le 1$	(19)
$\mathop \sum \limits_{k} \varphi_{k} \le 1$	(4)	$\mathop \sum \limits_{p} \tau_{p} \le 1$	(12)	$\mathop \sum \limits_{r} \lambda_{r} \le 1$	(20)
$\mathop \sum \limits_{l} \mu_{l} \le 1$	(5)	$\mathop \sum \limits_{p} \tau_{p} \le 1$	(13)	$\mathop \sum \limits_{m} \pi_{m} \le 1$	(21)
$\mathop \sum \limits_{i} \sigma_{it} \left( s \right) \le 1$	(6)	$\mathop \sum \limits_{v} \rho_{vt} \left( s \right) \le 1$	(14)	$\mathop \sum \limits_{a} \varrho_{at} \left( s \right) \le 1$	(22)
$\mathop \sum \limits_{j} \gamma_{jt} \left( s \right) \le 1$	(7)	$\mathop \sum \limits_{w} \delta_{wt} \left( s \right) \le 1$	(15)	$\mathop \sum \limits_{u} \varsigma_{ut} \left( s \right) \le 1$	(23)
$\mathop \sum \limits_{k} \varphi_{kt} \left( s \right) \le 1$	(8)	$\mathop \sum \limits_{p} \tau_{pt} \left( s \right) \le 1$	(16)	$\mathop \sum \limits_{r} \lambda_{rt} \left( s \right) \le 1$	(24)
$\mathop \sum \limits_{l} \mu_{lt} \left( s \right) \le 1$	(9)	$\mathop \sum \limits_{o} \beta_{ot} \left( s \right) \le 1$	(17)	$\mathop \sum \limits_{m} \pi_{mt} \left( s \right) \le 1$	(25)

It is also assumed that each repair job takes exactly one time increment, i.e., is completed in one stage of the multi-stage stochastic program, as captured in constraint sets (26)-(37). If repair jobs may require more than one time increment as a function of the hazard event impact, repair times would need to be modeled and would be scenario-dependent.

Power network	Water network	Roadway network
Network status
$\sum_{t}{\sigma }_{it}(s)\le 1$	(26)	$\sum_{t}{\rho }_{vt}(s)\le 1$	(30)	$\sum_{t}{\varrho }_{at}(s)\le 1$	(34)
$\sum_{t}{\gamma }_{jt}(s)\le 1$	(27)	$\sum_{t}{\delta }_{wt}(s)\le 1$	(31)	$\sum_{t}{\varsigma }_{ut}(s)\le 1$	(35)
$\sum_{t}{\varphi }_{kt}(s)\le 1$	(28)	$\sum_{t}{\tau }_{pt}(s)\le 1$	(32)	$\sum_{t}{\lambda }_{rt}(s)\le 1$	(36)
$\sum_{t}{\mu }_{lt}(s)\le 1$	(29)	$\sum_{t}{\beta }_{ot}(s)\le 1$	(33)	$\sum_{t}{\pi }_{mt}(t)\le 1$	(37)

For water and power lifelines, 12 sets of lifeline structure constraints capture the connection between each lifeline’s elements and, thus, are devised for both current and future stages. For example, switching stations rely on power plants to function. Constraints (38)-(43) model the structure of the power network. For example, constraints (38) ensure that each switching station is up only if its upstream, supporting power plant is up. Constraints (44)-(49) do the same for the water network. Constraints (45) and (48) also capture dependencies (or interdependencies) between the power and water networks. Specifically, constraints (45) and (48) ensure that the water pump is up if both its supporting water well is up, and it receives power from a functioning transformer in the power network.

Power network		Water network
Network connections
$s{\gamma }_{j}\le \sum_{j}{I}_{ij}.s{\sigma }_{i}, \forall j$	(38)	$s{\beta }_{o}\le \sum_{p}{I}_{po}.s{\tau }_{p}, \forall o$	(44)
$s{\varphi }_{k}\le \sum_{j}{I}_{jk}.s{\gamma }_{j}, \forall k$	(39)	$s{\tau }_{p}\le \frac{1}{2}(\sum_{w}{I}_{wp}.s{\delta }_{w}+\sum_{k}{I}_{kl}.s{\varphi }_{k}),\forall p$	(45)
$s{\mu }_{l}\le \sum_{k}{I}_{kl}.s{\varphi }_{k}, \forall l$	(40)	${s\delta }_{w}\le \sum_{v}{I}_{vw}.s{\rho }_{v}, \forall w$	(46)
${s\mu }_{lt}\left(s\right)\le \sum_{k}{I}_{kl}.{s\varphi }_{kt}\left(s\right), \forall l,t,s$	(41)	${s\beta }_{ot}\left(s\right)\le \sum_{p}{I}_{po}.{s\tau }_{pt}\left(S\right), \forall o,t,s$	(47)
${s\varphi }_{kt}\left(s\right)\le \sum_{j}{I}_{jk}.{s\gamma }_{jt}\left(s\right), \forall k,t,s$	(42)	${s\tau }_{pt}(s)\le \frac{1}{2}(\sum_{w}{I}_{wp}.{s\delta }_{wt}\left(s\right)+\sum_{k}{I}_{kl}.s{\varphi }_{kt}(s)),, \forall p,t,s$	(48)
${s\gamma }_{jt}\left(s\right)\le \sum_{j}{I}_{ij}.s{{\sigma }{\prime}}_{it}\left(s\right), \forall j,t,s$	(43)	${s\delta }_{wt}(s)\le \sum_{v}{I}_{vw}.{s\rho }_{vt}\left(s\right), \forall w,t,s$	(49)

16 additional sets of constraints relate to accessibility to lifeline elements. Constraints (50)-(57) ensure that power network elements can only be restored if there exists at least one open pathway to them, while Constraints (58)-(65) guarantee the same for the water network.

Power network		Water network
Network accessibility
${\sigma }_{i}\le \sum_{\alpha }{I}_{in}.{p}_{n\alpha },\forall i$	(50)	${\rho }_{v}\le \sum_{\alpha }{I}_{vn}.{p}_{n\alpha },\forall v$	(58)
${\gamma }_{j}\le \sum_{\alpha }{I}_{jn}.{p}_{n\alpha },\forall j$	(51)	${\delta }_{w}\le \sum_{\alpha }{I}_{wn}.{p}_{n\alpha },\forall w$	(59)
${\varphi }_{k}\le \sum_{\alpha }{I}_{kn}.{p}_{n\alpha },\forall k$	(52)	${\tau }_{p}\le \sum_{\alpha }{I}_{pn}.{p}_{n\alpha },\forall p$	(60)
${\mu }_{l}\le \sum_{\alpha }{I}_{ln}.{p}_{n\alpha },\forall l$	(53)	${\beta }_{o}\le \sum_{\alpha }{I}_{on}.{p}_{n\alpha },\forall o$	(61)
${\sigma }_{it}\left(S\right)\le \sum_{\alpha }{I}_{in}.{p}_{n\alpha t}\left(s\right),\forall i,s,t$	(54)	${\rho }_{vt}\left(s\right)\le \sum_{\alpha }{I}_{vn}.{p}_{n\alpha t}\left(s\right),\forall v,s,t$	(62)
${\gamma }_{jt}(s)\le \sum_{\alpha }{I}_{jn}.{p}_{n\alpha t}\left(s\right),\forall j,s,t$	(55)	${\delta }_{wt}(s)\le \sum_{\alpha }{I}_{wn}.{p}_{n\alpha t}\left(s\right),\forall w,s,t$	(63)
${\varphi }_{kt}(s)\le \sum_{\alpha }{I}_{kn}.{p}_{n\alpha t}\left(s\right),\forall k,s,t$	(56)	${\tau }_{pt}(s)\le \sum_{\alpha }{I}_{pn}.{p}_{n\alpha t}\left(s\right),\forall p,s,t$	(64)
${\mu }_{lt}(s)\le \sum_{\alpha }{I}_{ln}.{p}_{n\alpha t}\left(s\right),\forall l,s,t$	(57)	${\beta }_{ot}\left(s\right)\le \sum_{\alpha }{I}_{on}.{p}_{n\alpha t}\left(s\right),\forall o,s,t$	(65)

12 sets of constraints ensure that the status of any element is up if the element was previously observed to be up or a restoration action was previously taken on that element. This is captured through Constraints (66)-(69) for the power, (70)-(73) for the water, and (74)-(77) roadway networks.

Power network status
$s\sigma_{it} \left( s \right) = d_{i} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \sigma_{{it^{\prime}}} \left( s \right), \forall i$	(66)
$s\gamma_{jt} \left( s \right) = d_{j} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \Upsilon_{{jt^{\prime}}} \left( s \right),\forall j$	(67)
$s\varphi_{kt} \left( s \right) = d_{k} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \varphi_{{kt^{\prime}}} \left( s \right), \forall k$	(68)
$s\mu_{lt} \left( s \right) = d_{l} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \mu_{{lt^{\prime}}} \left( s \right), \forall l$	(69)

Water network status
$s\rho_{vt} \left( s \right) = d_{v} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \rho_{{vt^{\prime}}} \left( s \right),\forall v$	(70)
$s\delta_{wt} \left( s \right) = d_{w} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \delta_{wt^{\prime}} \left( s \right),\forall w$	(71)
$s\tau_{pt} \left( s \right) = d_{p} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \tau_{pt^{\prime}} \left( s \right),\forall p$	(72)
$s\beta_{ot} \left( s \right) = d_{o} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \beta_{{ot^{\prime}}} \left( s \right),\forall o$	(73)

Roadway network status
$s\varrho_{at} \left( s \right) = d_{a} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \varrho_{{at^{\prime}}} \left( s \right),{ }\forall a$	(74)
$s\varsigma_{ut} \left( S \right) = d_{u} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \varsigma_{{ut^{\prime}}} \left( s \right),\forall u$	(75)
$s\lambda_{rt} \left( s \right) = d_{r} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \lambda_{{rt^{\prime}}} \left( S \right),\forall r$	(76)
$s\pi_{mt} \left( s \right) = d_{m} \left( s \right) + \mathop \sum \limits_{{t^{\prime} = 0}}^{t - 1} \pi_{{mt^{\prime}}} \left( s \right),\forall m$	(77)

Two sets of constraints, Constraints (78) and (79), create the connections between the buildings from which critical societal services are provided and which receive services from supporting lifelines. These constraints ensure that societal services are only offered if the facility from which they are provided is functioning, and the facility is functioning only if its supporting lifelines provide services (here, power and water).

Critical societal service connection
$cf_{\phi } \le \frac{1}{2}\left( {\mathop \sum \limits_{l} I_{l\phi } . s\mu_{l} + \mathop \sum \limits_{o} I_{o\phi } . \beta_{o} } \right), \forall \emptyset$	(78)
$cf_{\phi t} \left( s \right) \le \frac{1}{2}\left( {\mathop \sum \limits_{l} I_{l\phi } . s\mu_{lt} \left( S \right) + \mathop \sum \limits_{o} I_{o\phi } . \beta_{ot} \left( s \right)} \right), \forall \emptyset$	(79)

Two additional sets of constraints, Constraints (80) and (81), ensure that a path is “up” and provides access to the element or facility only if roadway links forming a path from the depot are functioning. Binary and integrality constraints are included in constraints (82)-(85).

Path accessibility
$\frac{{\mathop \sum \nolimits_{{a^{\prime} \in A_{\alpha } }} d_{a^{\prime}} }}{{\left| {m_{\alpha } } \right|}} \ge p_{n\alpha } , \forall n,\alpha$	(80)
$\frac{{\mathop \sum \nolimits_{{a{^{\prime}} \in A_{\alpha } }} s\varrho_{{a{^{\prime}}t}} \left( s \right)}}{{\left| {m_{\alpha } } \right|}} \ge p_{n\alpha t} \left( s \right),{ }\forall t,s,n,\alpha$	(81)

Binary and integrality
Power network	$\begin{aligned} & \sigma_{{i{ }}} ,\gamma_{j} ,\varphi_{k} ,\mu_{l} ,s\sigma_{{i{ }}} ,s\gamma_{j} ,s\varphi_{k} ,s\mu_{l} ,\sigma_{{it{ }}} \left( s \right),\gamma_{jt} \left( s \right), \\ & \varphi_{kt} \left( s \right),\mu_{lt} \left( s \right),s\sigma_{{it{ }}} \left( s \right),s\gamma_{jt} \left( t \right),s\varphi_{kt} \left( s \right),s\mu_{lt} \left( s \right) \\ & \in \left\{ {0,1} \right\} \\ \end{aligned}$	(82)
Water network	$\begin{aligned} & \rho_{v} ,{ }\delta_{w} ,\tau_{p} ,\beta_{o} ,s\rho_{v} ,{ }s\delta_{w} ,s\tau_{p} ,s\beta_{o} ,\rho_{vt} \left( s \right){ },{ }\delta_{wt} \left( s \right), \\ & \tau_{pt} \left( s \right),\beta_{ot} \left( s \right),s\rho_{vt} \left( s \right),{ }s\delta_{wt} \left( s \right),s\tau_{pt} \left( s \right),s\beta_{ot} \left( s \right) \\ & \in \left\{ {0,1} \right\} \\ \end{aligned}$	(83)
Roadway network	$\begin{aligned} & \varrho_{a} ,\varsigma_{u} ,\lambda_{r} ,\pi_{m} ,s\varrho_{a} ,s\varsigma_{u} ,s\lambda_{r} ,s\pi_{{m,{ }}} \varrho_{at} \left( s \right),\varsigma_{ut} \left( s \right), \\ & \lambda_{rt} \left( s \right),\pi_{mt} \left( s \right),s\varrho_{at} \left( s \right),s\varsigma_{ut} \left( s \right),s\lambda_{rt} \left( s \right),s\pi_{mt} \left( s \right) \\ & \in \left\{ {0,1} \right\} \\ \end{aligned}$	(84)
Critical service	$cf_{\phi } ,cf{^{\prime}}_{\phi t} \left( s \right){ } \in \left\{ {0,1} \right\}$	(85)

3.3 Extension to multiple crews and depots

The model was presented assuming only a single depot and one crew of each type. To model multiple crews from each lifeline or lifeline component type and each with their own depot, the following modifications would be required.

For all variables related to crew assignment, a second index for crew number would be incorporated in the notation. For example,

${\sigma }_{i}$ = 1 if power repair crew repairs power plant i, = 0 otherwise

would be replaced by the following.

${\sigma }_{ix}$ = 1 if power repair crew x repairs power plant i, = 0 otherwise

Relevant constraints would either be repeated for each crew x or would be incorporated in a second summation. For example, Eqs. (2) and (50) would be replaced by Eqs. (2’) and (50’).

$$\sum_{x}{\sigma }_{ix}\le 1$$

(2’)

$${\sigma }_{ix}\le \sum_{\alpha }{I}_{in}.{p}_{n\alpha },\forall i,x$$

(50')

To model depot locations for each component type, ${p}_{n\alpha }$ would be replaced by ${p}_{n\alpha y}$, for y a chosen depot location, and relevant constraints (50)-(65), (80), (81) would be extended to account for d in the summation or number of needed constraints similar to the extensions for constraints (2) and (50) to (2’) and (50’), respectively. Notation would also be required to demarcate the set of depots and number of crews available under each component type in Table 2.

3.4 Problem considerations

Condition states of the system elements due to the impact of the hazard-event are captured through scenarios. Information on the scenario realization is obtained over the restoration period. This information comes from two sources: (1) exogenously provided information from, for example, observations made by emergency crews, data shared through social media, sensor data, and other surveillance systems and (2) information from repair crews as they move between tasks based on job assignments (i.e., decisions suggested by the optimization model). The latter information is, thus, endogenously discovered. That is, the timing of the realization of the state of those network elements to which crews are sent depends on the decisions suggested by the model itself. This creates a source of endogenous or decision-dependent uncertainty.

Stochastic programs with endogenous uncertainty require the use of first-stage non-anticaptivity constraints (NACs) and second-stage conditional NACs (Apap and Grossman, 2017). These NACs ensure that two scenarios are indistinguishable at stage $h$ if and only if they have the same realizations for all revealed random variables through that stage. For example, for a given scenario pair S and S’, $\emptyset \left( {s,s^{\prime}} \right)$ is defined as the set of elements that make these two scenarios distinguishable. Scenario pairs S and S will remain indistinguishable until a stage where the state of an element that makes the two scenarios distinguishable is realized. In the context of a multi-stage stochastic program with endogenous uncertainty, the first-stage NACs and later-stage conditional NACs for roadway links, for example, can be written as in Constraints $\left(86\right)-\left(87\right)$, respectively, where $\varrho_{ah} \left( s \right)$ indicates whether a transportation repair crew repairs roadway link $a$ at time $t$ under scenario $s$. Constraints (86) ensure that at stage 0, the same decisions are taken under all future scenarios. With information received in future stages, Constraints (87) guarantee that for later stages, the same decisions are taken under all future scenarios pairs until information is received in a stage that reveals the status of one or more elements in these scenarios that makes these scenarios distinguishable.

$$\varrho_{a0} \left( s \right) = \varrho_{a0} \left( {s^{\prime}} \right),{ }\forall \left( {s,s^{\prime}} \right) \in S,{ }a \in A$$

(86)

$$\begin{aligned} \varrho_{ah} \left( s \right) - \varrho_{ah} \left( {s{^{\prime}}} \right) \le \mathop \sum \limits_{{h^{\prime} < h}} \mathop \sum \limits_{{a{^{\prime}} \in \Phi \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}h{^{\prime}}}} \left( s \right) \\ & + \mathop \sum \limits_{{h^{\prime} < h}} \mathop \sum \limits_{{a{^{\prime}} \in \Phi \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}h^{\prime}}} \left( {s^{\prime}} \right),\forall \left( {s,s^{\prime}} \right) \in S,{ }a \in A,{ }h \in \left\{ {H - \left( 0 \right)} \right\} \\ \end{aligned}$$

(87)

By reframing the multi-stage stochastic program as a set of interrelated two-stage stochastic programs, each program capturing decisions of future stages through time-dependent variables in the second stage as proposed herein, it can be shown that the conditional NACs of the second stage can be disregarded. For clarity, $\varrho_{ah} \left( s \right)$ is revised to $\varrho_{aht} \left( s \right)$ within Lemma 1 to differentiate between stage h and time t.

Lemma 1

The conditional NACs of the second stage of the two-stage program are redundant.

Proof

$h\in${0, 1} for the stochastic program with only 2 stages. To capture deployment decisions in future stages, decisions of the second stage are time-dependent. Moreover, only $h=$ 1 applies. As solution of the first stage is time-invariant, Constraints (87) can be written as Constraints (88)$.$

$$\begin{aligned} \varrho_{a1t} \left( s \right) - \varrho_{a1t} \left( {s^{\prime}} \right)& \le \mathop \sum \limits_{{a^{\prime} \in \emptyset \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}00}} \left( s \right)\\ & \quad+ \mathop \sum \limits_{{a^{\prime} \in \emptyset \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}00}} \left( {s^{\prime}} \right), \forall \left( {s,s^{\prime}} \right) \in S, a \in A,t \in \left\{ {T - \left( 0 \right)} \right\} \\ \end{aligned}$$

The two-stage reformulation assumes that all condition states will be realized in stage 1 and all future decisions are set (see Fig. 2). Consequently, Constraints (88) can be replaced by Constraints (89).

$$\begin{aligned} \varrho_{a11} \left( s \right) - \varrho_{a11} \left( s \right)& \le \mathop \sum \limits_{{a^{\prime} \in \emptyset \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}00}} \left( s \right) \\ & \quad + \mathop \sum \limits_{{a^{\prime} \in \emptyset \left( {s,s^{\prime}} \right)}} \varrho_{{a^{\prime}00}} \left( {s^{\prime}} \right), \forall \left( {s,s^{\prime}} \right) \in S, a \in A \\ \end{aligned}$$

As the lefthand side is zero and all terms on the righthand side are nonnegative, this constraint is redundant and can be dropped. Q.E.D.

4 Solution methodology

4.1 An overview of the solution framework

The proposed solution methodology (Fig. 3) is applied in the multi-lifeline network representation over a rolling and diminishing horizon. The procedure begins with information on the status of the lifeline elements as observed by repair crews who can assess the condition states of all links that connect directly to their current locations, as well as elements to which these links connect. Additional condition-state information from alternative sources may also be received over the disaster restoration period.

Fig. 3

General solution methodology (icons from flaticon.com)

With both endogenous and exogenous sources of condition-state information, the scenario set under consideration can be reduced. Details of this reduction are given in Sub Sect. 4.2. The PH algorithm is applied on the reduced scenario set, results of which give updated optimal schedules for deploying the repair crews across their lifelines in future stages. With this schedule, the crews are redeployed from their current locations to elements that are accessible given the state of the roadway network. The scenario set is updated based on this deployment to capture that some elements will be repaired, further reducing the scenario set. If this framework is employed with a human in the loop, the human can choose to use or not use the suggested deployment instructions, and any deployment strategy that is implemented can inform this step. Algorithmically, this merely entails fixing decision variables of the mathematical formulation used in the next time increment. Crew locations are updated and this process is continued until the end of a predesignated planning horizon or once all lifelines and selected critical societal services are restored.

4.2 PH algorithm

The concept of progressive hedging was first introduced by Rockefellar and Wets (1991). The procedure decomposes a two-stage stochastic program by scenario, reducing the optimization to solution of a set of deterministic programs, one for each scenario.

The solution of each deterministic program will likely result in differing optimal first-stage decisions across scenarios, yet only one set of first-stage decisions can be applied. To encourage their decisions to converge on a common first-stage solution, at each iteration, the average of all objective function values is taken and any differences between objective function values from this average are penalized. The penalty is applied through a modified objective function as in Eq. (1').

$$Max\; Z = \mathop \sum \limits_{v} cf_{v} + \mathop \sum \limits_{s} p_{s} .\mathop \sum \limits_{t} \mathop \sum \limits_{v} cf_{vt} \left( s \right) + \mathop \sum \limits_{i} \mathop \sum \limits_{k} \mathop \sum \limits_{s} \omega_{k,s}^{\left( i \right)} + \ldots$$

where penalty term $\omega_{k,s}^{\left( i \right)} = \rho \left( {\sigma_{i} \left( s \right) - \overline{\sigma }_{i} } \right) + \omega_{k - 1,s}^{\left( i \right)}$ for $\omega_{0,s}^{\left( i \right)} = 0$, power plant i, scenario s and iteration k, $\rho$ is a second penalty factor, and $\overline{{\sigma_{i} }}$ is the difference in objective function values from the average associated with the restoration of power plant i. To encourage convergence despite the existence of binary variables, $\rho$ is progressively reduced over the iterations of the PH algorithm. For this purpose, $\rho$ was decremented by 0.5 in each iteration of the experiments of Sect. 5.

The algorithm terminates when first-stage decision variable values across the deterministic programs converge. Upon termination, the PH algorithm gives the restoration schedules for the lifeline elements in current and future time increments in a diminishing planning horizon. The steps of the PH algorithm as applied in this context are given in Fig. 4. The procedure can be readily extended to include additional lifelines and elements.

Fig. 4

Progressive hedging overview

4.3 Acceleration methods for faster execution

Two approaches are applied to accelerate the solution algorithm and allow its use in realistic settings, where efficiency and scalability are important: (1) scenario reduction and (2) parallelization of the PH algorithm.

The scenario reduction technique designed herein was inspired by the treatment of scenarios in (Vatenmacher et al. 2022). Vatenmacher et al. (2022) analyzed the vulnerability of lifelines in disasters to support the planning of preparedness actions for a disaster event. Their method identifies the critical components of the lifelines on which to focus the analysis to ensure that services will be given for specific essential end-users, such as hospitals. They show how a reduction in the number of scenarios allowed the consideration of important information that is otherwise ignored to avoid excessive computational loads. This included specific geological and seismological features that needed to be considered to avoid dangerous risks, which were not identified with conventional probabilistic methods.

Herein, with each stage in the restoration period, as elements are restored and information about lifeline components are revealed, some scenarios in the considered scenario set can be permanently eliminated. It is assumed that any element that is up immediately post-event or that is restored in a prior time increment will remain up and related scenarios can be permanently removed from the consideration set.

There is an additional set of scenarios that can be temporarily removed from consideration. These scenarios will have elements in the up condition state, when at the beginning of the stage the element is known to be down. These scenarios need not be considered in the current stage, but may be relevant in future stages, where restoration actions create such future up condition states. These scenarios can only be temporarily removed, i.e., for the solution in the current time increment.

The PH algorithm can be parallelized by solving each subproblem, one deterministic binary integer program for each scenario, on a different thread in a computer with multi-core processors. In Step 3, solutions from all subproblems are aggregated. The time to completion of Step 3 is reduced to the solution time of the most difficult subproblem (or scenario), thus, reducing the needed computation time for each cycle (or call to Step 6) of the algorithm at any stage. The savings in run time from such parallelization will be most significant in the early stages of the restoration period, where the largest number of scenarios must be considered and repair decisions are most crucial. (Fig. 5).

Fig. 5

A depiction of the benefits of sequential versus parallel implementations of the PH algorithm

5 Case study

5.1 Experimental design

To illustrate the proposed modeling and solution methodology and assess its efficiency for large, complex multi-lifeline applications, numerical experiments were run on the synthetic yet real-world network given in (Vatenmacher et al. 2022) as shown in Fig. 6. The network involves three key lifelines, including power, water and transportation, as well as two hospitals that rely on them. The study area covers nearly 6,000 square km (2,300 square miles), including several urban centers and a network of highways and local roadways. The network consists of 182 lifeline elements and two hospitals in total. The number of elements by lifeline is given in Fig. 7.

Fig. 6

Case study area

Fig. 7

Overview of network elements for the case study

There are dependencies among elements within each lifeline that control the order in which restoration actions must take place if any elements are down. These dependencies can be direct or indirect. Figure 8 illustrates direct and indirect dependencies between the elements in the considered network. Direct dependencies are shown with solid lines, while indirect dependencies are shown with dashed lines. For example, water pump 3 (WP3) relies directly on power from transformer 4 (TS4). Electricity supply line 20 (EL 20) indirectly relies on the functionality of switching station 4 (SS4), which relies on a functioning TS4. As can be seen in the figure, hospitals receive electricity from power supply lines and, thus, directly depend on these lifelines. The hospitals also indirectly rely on power plants, switching stations and the transformers that support the power supply lines. Similarly, hospitals rely directly on water supply lines and indirectly on water wells, water tanks and water pumps.

Fig. 8

Direct and indirect dependencies between lifeline components within and across lifelines

Numerical experiments were run over scenario sets of varying sizes, ranging from 20 to 1,500 initial scenarios that give a realization of the hazard impact in terms of whether elements are up or down. Scenarios were randomly generated by conversion to either 0 or 1 (with a probability of 0.5) from a random number generator. One sequence of randomly generated numbers launched by a single seed value was used to create all scenarios in a scenario set. Thus, only one seed that launches the random number sequence was employed in creating each scenario set.

The experiments were run on a high-end desktop platform (HEDT) with an AMD 1950xthreadripper (3.2 GHz, 16 cores), 32 GB of RAM, and default speed of the CPU is 32 GHz.

6 Results

Figures 9 through 13 give results of the numerical experiments. All results are given as averages over all scenarios in a scenario set. When multiple seeds are employed, results are further averaged over multiple scenarios sets.

Fig. 9

Time increment by which services are functioning for different prioritization options

By varying the weights $w$ on the terms of the objective function, the impacts of prioritizing one system over another or hospital recovery over the recovery of the roadway, water and power lifelines (i.e. the whole system) can be investigated. Results from giving the full weight to all lifelines (whole system), the full water or power system, or to the hospitals are given in Fig. 9. The results show that services are restored to the hospitals earlier (by 11 instead of 13 time increments) when the hospitals are prioritized, and with no impact on the overall time to complete restoration of all services. As illustrated in the figure, whether or not the hospitals are prioritized, 57 time increments are required to return services to all lifelines and to open the hospitals. It appears to be only by chance that the power subnetwork that supports the hospitals is restored earlier even when the hospitals are not prioritized.

Additional analyses were completed, where the objective function weights were evenly distributed across the lifelines and the two hospitals, as well as giving 80% to the lifelines and 20% to the hospitals (creating a final set of 5 cases: 20/80, 80/20, 50/50, 100/0, 0/100). Additional cases were run, with changing priority for each of the two hospitals under both the 80/20 and 20/80 weighting schemes between lifelines and hospitals. Figure 10 show results from the relevant experiments.

Fig. 10

Time increment by which each hospital is fully restored under changing priorities between hospitals 1 and 2 assuming an objective function weight of 80% given to the hospitals and 20% given to the lifelines

Figure 10 shows that the best solution is achieved, where the two hospitals are equally prioritized under the 80/20 weighting scheme between lifelines and hospitals. If all priority is given to one hospital, the non-prioritized hospital will come up 2 time increments later. In the case of hospital 1, this is a 20% increase in time.

Figure 11 indicates the time increment by which each lifeline is fully restored for varying priority schemes between hospitals and lifelines. The values were obtained with priority assigned to hospitals 1 and 2 each at 50%. With 100% weight given to the hospitals over the lifelines, full functionality is restored to the hospitals 15% faster than when 100% weight is given to the lifelines. As the weights shift from 100% given to the hospitals to 100% given to the lifelines, roadway restoration times have the greatest improvement, with as much as 22% quicker restoration. Note, however, that the power network is restored faster when hospitals are prioritized. This shows the importance of accounting for the hospitals’ reliance on other lifelines in restoring health care services to the public.

Fig. 11

Time increment by which each lifeline is fully restored under changing priorities between hospitals and the lifelines with equal priority for each hospital

Additional analyses were completed, where the objective function weights were evenly distributed across the lifelines and the two hospitals, as well as giving 80% to the lifelines and 20% to the hospitals (creating a final set of 5 cases: 20/80, 80/20, 50/50, 100/0, 0/100). Additional cases were run, with changing priority for each of the two hospitals under both the 80/20 and 20/80 weighting schemes between lifelines and hospitals. Figure 10 show results from the relevant experiments.

The impact of prioritizing critical societal services, e.g. hospitals, on the time required to reach full functionality of these services is illustrated in Fig. 12. A key path is defined as the path that includes roadways that create access to elements of the water and power subnetworks that support the hospitals. This key path is shown in Fig. 10 by a solid bold line. Prioritizing hospitals will lead to earlier restoration of roadway network elements that support faster, restored access to the hospitals and needed elements of supporting lifelines.

Fig. 12

Pathway topology created from the depot to the hospitals (roadway link restoration times under different prioritization schemes noted

In Fig. 13, the effects of the location of the depot can be noted. Two possible locations with differing proximity to the hospitals were studied for the depot as depicted by a star at the bottom of the figure. As expected, the closer the depot is to the hospitals, the faster the hospitals can be brought back into service. Note that even with a depot much further away, the benefits of prioritizing the hospitals remain.

Fig. 13

Time by which services are restored with different depot options

In another set of experiments, the effectiveness of scenario reduction and parallelization for runs with scenario sets of between 20 and 1500 scenarios, each run for one seed value, was evaluated. As shown in Fig. 14, applying both acceleration procedures reduced the average run time by 58% for the 500 scenario case. Beyond 500 scenarios, the algorithm could not obtain a solution without the aid of the acceleration methods. The scenario reduction technique accounts for nearly all of the speedup; however, if run on a more sophisticated computer with more CPU cores and threads, or on a larger network, parallelization is likely to be substantially more effective.

Fig. 14

Run time in minutes for different scenario numbers

To demonstrate the potential of the scenario reduction technique to reduce the problem size over the restoration period, Fig. 15 shows the number of scenarios that were permanently or temporarily eliminated in each time increment for scenario sets of 500 to 1500 scenarios. As shown in the figure, by using this technique, scenarios were rapidly eliminated from consideration under all scenario set sizes.

Fig. 15

Number of permanently and temporarily eliminated scenarios by scenario set size

Table 6 shows that there is variability in the number of eliminated scenarios over the restoration period when different seed values were used in the creation of the randomly generated scenario sets of 100 scenarios assuming the depot to be located at node 22. Generally, the vast majority of scenarios are permanently eliminated within the first few time increments, but the specific time increment by which this occurs varies with the generated scenario set and initial observations. Unusual results from seed 25 are noted, where no scenarios can be permanently eliminated from consideration in the first time increment, but 86 are temporarily eliminated. This is because elements 0, 1 and 46 were all observed to be down. 14 of the scenarios replicated the situation where all three elements are down. These scenarios cannot be eliminated at this point in time. In the remaining 86 scenarios, at least one of these three links is up. As links will be repaired over time, these scenarios may need to be considered at a future point in time in the restoration period and cannot be permanently eliminated.

Table 6 Number of remaining scenarios for consideration over time for a scenario set of 100, where each set is created with different seed values- permanently (temporarily) eliminated

7 Conclusions

The problem of determining a best post-disaster restoration schedule across infrastructure lifelines to prioritize the restoration of critical societal services is conceptualized in this paper as multi-stage stochastic program. To support the application of the model for real-world, post-disaster application, the problem is reframed as a series of two-stage stochastic programs that arise over a rolling horizon. Information on the post-disaster condition state arrives over time from observations by the repair crews that are sent out to repair the various lifeline elements and other exogenous sources. The two-stage programs are solved through an exact progressive hedging algorithm. To support its real-world application, techniques of scenario reduction and parallelization are introduced to accelerate solution times. The proposed model and solution technique are designed to support decision-makers in the field who may wish to reject some suggested actions over the course of the restoration period and inject their own decisions. Solutions obtained with the proposed exact technique can also provide a benchmark for assessing alternative, simpler heuristics.

The outcomes of this work show the importance of both collaboration in the restoration of lifelines for returning critical services to a community after a disaster, and the benefits of prioritizing key societal services, such as emergency hospital care, during the restoration phase. The tools developed in this paper can aid regional decision makers in scheduling post-disaster restoration actions to better support a community in need of healthcare services without posing delays in restoring functionality to key lifelines. Typically, specialized crews will be deployed to their respective lifelines independently. The results from the case study illustrate the value of coordinating the activities of the crews across lifelines in restoring both lifeline and critical societal services to the region. That is, this work quantified the gains from collaboration over typically, highly stovepiped activities. Additionally, in post-disaster circumstances, society may be better served by prioritizing the recovery of critical societal services (e.g., health care delivered from hospitals) or other key community assets, such as fueling stations, especially where demand for such services is increased as a consequence of the event.

While hospitals are the focus herein, any facility(ies) can be prioritized using the same methodology. For example, in the case of a blizzard that closes roadways and damages powerlines during school hours, children and teachers may be trapped at schools. In such as case, this model could support prioritizing the opening of roadways and the restoration of power to these school facilities. The methodology could thus be applied directly to ensure access to and prioritize the functioning of other key facilities that provide critical services in post-disaster circumstances, such as grocery stores and fueling stations.

Several assumptions were made throughout this paper. It is assumed that each decision is taken at the beginning of each time interval, and lifeline elements requiring repair are not functional until completion of the repair activity, which is assumed to take exactly one time increment. More realistic models with partial restoration benefits and longer durations for more complicated restoration actions may be useful. For applications with long-term repair needs, e.g. reconstruction of an asset, more accurate modeling of the repair times will be required. The authors are working on an extension for the case where external resources may be required to make larger repairs or to complete full-scale rehabilitation work. To extend this work for these applications, a change in the mathematical model, including decision variables and constraints will be required. Additionally, the restoration activity durations are presumed to be known perfectly; however, in reality, restoration durations depend on many factors that cannot be known in advance. Also, travel times are assumed to be trivial in comparison to the restoration times as modeled. The model can be extended to capture the travel durations more accurately if they are meaningful. While only three lifelines are explicitly incorporated in the model, additional lifelines can be readily added. Alternative formulations might consider the optimal location of one or more depots to pre-position resources immediately before a disaster. This is not considered herein.

Appendix

This appendix provides an illustrative example application to show some of the steps of the algorithm. This example includes a single hospital that is supported by power, water and roadway networks. The roadway network also supports access to the power and water network elements when repairs are required. Power and water networks are interconnected, wherein the water pump in the water network requires power, which is shown through a link between the water pump and a transformer in the power network. The hospital requires access by at least one roadway link, power and water to function. The water is supplied to the hospital from the water pump via a water line. Power is supplied to the hospital via a power line from a switching station in the power network. Power and water networks can only supply power and water, respectively, if all elements of these systems are functioning. The network with these details is portrayed in Fig. 16

Fig.16

Illustrative network

.

Four disaster scenarios, whose impacts are depicted in Table 7, are considered in this example. Impacted elements are presumed to in a “down” state, i.e. not functioning, until they are repaired, at which time they are considered to be in an “up” state, or functioning. It is assumed that there is one crew per element type (or 7 crews), all beginning at the depot located at node 2.

Table 7 State of each network element under four scenarios

The proposed algorithm was applied to the network in Fig. 16 with objective function weights at 80 and 20% for the hospital and other lifelines, respectively. The algorithm when applied to this small example completes with three calls to the optimization.

At the start of the first iteration (iteration 1), with the vantage point of node 2, the crews observe the immediately adjacent infrastructure elements and determine the state of roadway links 1 and 2. Based on a simulation of real-world conditions, the crews can see that roadway links 1 and 2 are down. This suggests that scenarios 0, 1, and 2 are relevant. Additionally, scenario 3 could be relevant in a future iteration, once link 2 is repaired and functioning. Solution of the multi-stage stochastic integer model suggests repair of roadway link 1, opening a path for all crews to access the hospital, power network elements and roadway link 0. Table 8 shows the updated scenarios at the end of iteration 1 or time increment 0.

Table 8 State of each network element under updated scenario set after iteration 0 (or time increment 0)

All crews are assumed to move to node 1 by the start of iteration 2 (time increment 1). At node 1, they observe roadway links 0, 4, 5 and 6 as well as electricity supply line 0. Based on simulated realization, they observe these roadways to be up, down, down and up, respectively, and the electricity supply line to be down. Only scenario 0 is relevant to this realization of states. That is, scenarios 1, 2 and 3 can never be realized. Table 9 shows the state of each network element under the updated scenario set after iteration 1 (or time increment 2).

Table 9 State of each network element under updated scenario set after iteration 1 (or time increment 2)

With only one scenario to consider, the remaining problem is deterministic, although time-dependent. Results are obtained from one last run of the model under the updated scenario 0. The results over all iterations are given in Table 10.

Table 10 Restoration timing