Consistent routing for local same-day delivery via micro-hubs

Abstract

An increasing number of local shops offer same-day delivery in order to compete with the online giants. However, the distribution of parcels from individual shops to customers reduces the rare consolidation opportunities in the last mile even further. Thus, shops start collaborating on urban same-day delivery by using shared vehicles and micro-depots for consolidated transportation of parcels. At this, many stakeholders (storekeepers, drivers, and customers) need to be coordinated. Consistent routes between micro-hubs simplify the distribution process and increase reliability for all stakeholders involved. The shared vehicles thus conduct consistent daily routes between micro-hubs in the city, serving as transshipment and consolidation centres. This allows stores to bring orders to the next micro-hub, where the parcel is picked up by a vehicle and delivered to the micro-hub closest to its destination—if it is feasible with respect to the vehicle’s consistent daily schedule. Creating effective schedules is therefore very important. The difficulty of finding an effective consistent route is amplified by the daily uncertainty in order placements. We model the problem as a two-stage stochastic program. While the first stage determines the vehicle schedules, the second stage optimises the flow of realised orders. The goal is to satisfy as many orders per day as possible with the shared vehicles. We propose a time-expanded network formulation of the problem which is solved to optimality using commercial MIP-software. We assess our model against a non-consistent upper bound and a practically-inspired heuristic to evaluate the cost of consistency and the consolidation of goods. We analyse the performance of our method for a variety of instance settings. We observe that collaborative delivery via micro-hubs is worthwhile for delivery time promises of two hours or more. Noticeably, for these service promises, the costs of consistency are surprisingly low.

1 Introduction

Urban areas are facing an increasing amount of parcel transportations. This is reinforced by various factors, first and foremost the expanding e-commerce. In 2020, about 4.05 billion courier, express, and parcel deliveries were made in Germany according to the German Federal Association of Parcel and Express Logistics (Bundesverband Paket und Expresslogistik e.V. (BIEK) 2021). These numbers indicate that customer behaviour is shifting more and more towards online shopping. Purchasing online from the comfort of one’s own home is more convenient and saves customers the inconvenience of a trip to the crowded and congested city centre as well as from queuing in shops. At the same time, online shopping shows disadvantages. Conventional next-day delivery requires waiting for the customers. According to the Ecommerce Delivery Benchmark Report 2022, 37.5% of UK shoppers see the speed of delivery as the most important incentive to purchase online (Metapack 2022). Seeking an instant gratification of their orders, customers hence prefer a same-day or even instant delivery, if available. However, same-day delivery is usually only offered for a small range of products. Local shops can close the gap, offering a large variety of goods relatively close to the customers. To participate in the e-commerce boom, many local businesses thus start to offer fast same-day delivery. Often, they promise to deliver orders within a few hours. Operating an own delivery fleet however, is very cost- and time-intensive for local retailers as additional expenses for staff and vehicles are incurred. Especially for small shops, owning a fleet is usually not worthwhile, as delivery volumes are relatively small. To overcome these problems, local shops start collaborating for joint delivery, allowing them to offer a fast delivery service to customers, while improving low vehicle fill rates and driving down transportation costs (Datex 2021). In a local collaborative distribution network, goods of local shops can be purchased via an online platform and shipment is organised through the collaborative network.

Visiting the individual shops for every order is very time-consuming. Moreover, shops are often located in clusters within the city. Therefore, local delivery models make use of transshipment centres within the city to bundle orders of different stores (Burns et al. 2022). A number of services working with a similar strategy can be found in various places, e.g., in several Dutch, Scandinavian and German cities (Cameron 2022; velove 2022; Kiezbote 2021). Such transshipment centres—from now on called micro-hubs—increase consolidation opportunities in the joint delivery process even further. In the local collaborative distribution network, they are used as drop-off and pickup points for online orders. Shops can bring their goods to the closest micro-hub and customers can pick them up a short time later at a nearby micro-hub. Between the micro-hubs, low-emission vehicles such as cargo-bikes perform tours to transport the orders within the network. Organising delivery through micro-hubs offers benefits for storekeepers, drivers, and customers. Storekeepers can participate easily by bringing batches of orders to the nearby micro-hubs a few times per day. Drivers do not need to visit individual stores and customers in unfamiliar and crowded streets anymore. Moreover, customers are no longer constrained to remain at home and wait for their deliveries but have high flexibility concerning the pickup of their parcels.

In the local collaborative distribution network, many stakeholders are involved: different storekeepers, drivers, and customers all need to be coordinated. For this reason, the collaborative system must be error-resistant, transparent, and reliable. Consistency in the vehicle tours meets these requirements. Consistent tours in which vehicles follow a predefined daily schedule visiting micro-hubs at predefined times and in a predefined order help to simplify the distribution process and provide reliability to all stakeholders. For storekeepers, consistent routes between micro-hubs offer a reliable structure and planning stability because they can prepare and collect all orders and organise delivery to the next micro-hub at fixed hours every day. Consistent tours are also desirable for drivers. They do not only like to be familiar with facilities, but also with their routes (Wang et al. 2021; Smilowitz et al. 2013; Lian 2017). Fixed consistent routes provide operational stability for drivers which improves their satisfaction and hence their productivity (Kovacs et al. 2014a). Besides this, a consistent schedule is also less error-prone. Since consistent schedules offer reliable arrival times, they also increase customers’ satisfaction and trust as well as their attitude towards the supplier (Mancini et al. 2021; Wang et al. 2021; Zhen et al. 2020). This shows positive effects on the overall business and hence can be a significant competitive advantage for the supplier (Subramanyam and Gounaris 2018; Groër et al. 2009). Nahata (2022) argue that the constant online availability of products has raised the expectation that purchases are to be delivered fast and as accurately as promised. Consistent schedules between micro-hubs allow to successfully satisfy these delivery promises without the need of timely re-scheduling calculations.

In this paper, we aim to investigate how local collaborative delivery can be performed in a consistent way while using micro-hubs as consolidation centres. Particularly, we are interested in how to design effective consistent routes. We aim to analyse the cost to which consistent tours can be implemented if compared to a non-consistent routing, and to detect the conditions under which consolidation at micro-hubs is beneficial. While consistent routes bring many advantages for shops, customers and drivers, finding effective tours is very challenging given the differences in day-to-day orders. Consistent tours need to ensure high service-availability every day, regardless the realised demand. Customers that cannot be served have to be outsourced or served the next day, which is expensive or may lead to dissatisfaction, respectively. Thus, the goal is to find a consistent tour between micro-hubs that maximises the expected amount of delivered parcels per day. In order to provide effective schedules, it is important that they are robust to demand variations in time, respect the pickup and delivery sequence of parcels, and capture the expected daily demand pattern.

We formulate the problem as a two-stage stochastic program. The first stage of the model aims to find a consistent routing schedule for the delivery vehicle between micro-hubs without the exact demand being known. Given this schedule, the second stage determines the flow of realised parcel orders for a specific day. We model the problem over a discrete time horizon using a time-expanded network formulation. Our formulation allows solving realistically-sized instances with commercial MIP-solvers. To determine a solution for the first stage of the problem, several potential future demand scenarios are sampled, which are considered simultaneously in the extended form of the two-stage stochastic model. The extended form is then solved with Gurobi (Gurobi Optimization 2021). In a computational study, we assess the exact solution against a number of benchmarks with respect to solution quality and total runtime. To evaluate the cost of consistency, we use a solution without consistency constraints, i.e. a daily re-optimised solution, as an upper bound. We further implement a scenario-decomposition approach as well as a practically-inspired heuristic solution as benchmarks. In our computational study, we observe that optimisation is very valuable compared to the practically-inspired heuristic. Even the scenario-decomposition approach leads to substantial improvements. We further show that the costs of consistency for same-day delivery are rather negligible if compared to a daily re-optimised, non-consistent routing policy. If delivery time promises get tighter however (e.g. 2 h), the costs of consistency become noticeable. Moreover, we find that consolidation of parcels at micro-hubs may be worthwhile only for delivery promises of two hours or more. We further evaluate the solutions determined by our model in a dynamic simulation and find that they are quite effective for the large majority of instances.

The contributions of this paper are as follows. We are among the first to investigate how micro-hubs can be utilised for collaborative same-day delivery of local shops and for what type of delivery promise they are effective. We further analyse at which cost consistent routes can be implemented between micro-hubs in this delivery system. We present a stochastic two-stage integer program that finds a consistent tour between micro-hubs for pickup and delivery of parcels in a collaborative local delivery system. We provide a formulation that allows us to solve realistically-sized instances to optimality. We perform a targeted analysis and identify important managerial insights.

The remaining part of this paper is structured as follows. In Sect. 2, we present related literature. In Sect. 3, we define the model for consistent pickup and delivery routing. In Sect. 4, we present setup and results of the computational experiments. We finish our paper with a conclusion and outlook in Sect. 5.

2 Literature review on consistent vehicle routing

Several aspects have to be considered when planning consistent schedules in local delivery services: pickup and delivery needs to be organised through a two-echelon transportation system with transshipment facilities, while consistency in vehicle’s routes is to be maintained. This problem of picking up and delivering parcels during one route is denoted as the vehicle routing problem (VRP) with simultaneous pickup and delivery; a review on such problems can be found in Koç et al. (2020). Introducing transshipment facilities to a pickup and delivery problem leads to a two-echelon logistic system which is usually operated by two fleets of vehicles. In general, this is denoted as the two-echelon vehicle routing problem (2E-VRP). A literature review on such problems is presented by Cuda et al. (2015) and more recently by Jiang and Li (2021) and Sluijk et al. (2022). However, most papers focus on delivery only, assume demand to be deterministic, and consequently route first and second fleet at the same time. In contrast, our model aims to determine a routing schedule for the first fleet only in order to provide consistent pickup and delivery service despite daily varying demand. We hence seek to find consistent tours for the fleet serving micro-hubs. We therefore refer to different concepts of consistency in the following.

Kovacs et al. (2014a) provide a survey on consistency in VRPs. They distinguish arrival time, person-oriented, and delivery quantity consistency, and provide modelling concepts and solution methodology for each type. In our context, we require the even stronger concept of routing consistency: vehicles should always conduct the very same tour, i.e. visit the same micro-hubs at the same times each day. This captures the pickup and delivery dimension of our problem and allows storekeepers to organise transportation of their orders to corresponding micro-hubs in time for further shipment. Literature on this concept of routing consistency is very scarce. A close concept is presented by Wang et al. (2021) who develop a VRP for simultaneous distribution and collection of packages over several days with generalised consistency requirements. In their paper, schedules are called consistent if they satisfy consistency in three dimensions: the arrival time at customer locations should not vary more than a number of L time units (time consistency), customers should not be served with more than a number E of different drivers (driver consistency), and vehicle routes should not vary by more than F different arcs (route consistency). The authors propose an exact solution method to deal with the generalised consistency constraints. Our understanding of route consistency corresponds to the special case of Wang et al. (2021) with $L=0$, $E=1$, and $F=\nicefrac {1}{D}$, where D is the number of days in the planning horizon. However, the problem studied by Wang et al. (2021) addresses deterministic demand, whereas demand is considered to be stochastic in our problem setting.

Besides this, arrival time consistency is the closest concept to route consistency in literature and common modelling approaches are imposing hard or soft constraints, previously assigning time windows to customers or determining routes a-priori. We emphasize here that arrival time consistency is not sufficient in our context. For a parcel request to be fulfilled, pickup and delivery micro-hub need to visited after each other, otherwise the order cannot be fulfilled. The sequence of stops thus plays a major role for the success of the system, consequently consistency should be interpreted in terms of entire routes. Exemplary publications and different approaches on arrival time consistency can be found in Kovacs et al. (2014a) and more recently in Song et al. (2020). Most relevant to our work are consistent VRPs including pickup and delivery. Zhen et al. (2020) propose a consistent VRP for simultaneous distribution and collection in reverse logistics. Emadikhiav et al. (2020) address the simultaneous pickup and delivery of orders of an instrument-calibration company. The goal is to minimise transportation costs while limiting late deliveries and enforcing consistent arrival times. A prominent technique to maintain time consistency is bounding the variation in arrival times at customer locations over the planning horizon, which usually consists of several days. Among others, this approach is applied by Groër et al. (2009) who introduce the consistent VRP (ConVRP) for serving customers repeatedly over a given planning horizon. They present a mixed-integer formulation and a solution approach based on a record-to-record travel algorithm. Tarantilis et al. (2012) and Kovacs et al. (2014b) develop further solution approaches to the same problem. Extending this problem, Subramanyam and Gounaris (2018) suggest a TSP with arrival time consistency where waiting at customer locations is allowed. They further present an exact branch-and-bound-search procedure. Some works combine arrival time and driver consistency. Lian (2017) for example, investigates the trade-off between travel costs and service consistency through a multi-objective ConVRP. Mancini et al. (2021) introduce a ConVRP with time and driver consistency, as well as workload balance in collaborative logistics. They apply a matheuristic and an iterated local search algorithm to solve their problem. All ConVRP-variants deal with serving known customers over a number of periods and are therefore, in contrast to our work, deterministic. Still, our solution method samples a set of scenarios to cope for the uncertainty in demand and solves the corresponding deterministic problem. Thus, there are some similarities to the ConVRP, but also significant differences, since we consider pickup and delivery as well as repeated visits of the same micro-hub locations over the course of day.

Two other prominent consistency concepts are assigning time windows to customers previously or determining tours a-priori which are possibly adapted later to the realised demand through recourse actions. The latter can be applied for stochastic customers as well as stochastic demand while the former is applicable only if customer locations are known in advance and only demand volumes vary from day to day. Assigning time windows is often modelled by a two-stage stochastic programming formulation. Spliet and Gabor (2015) for example assign time windows to each customer at the first stage. They formulate a MIP for this stage with the objective to minimise expected travel costs. Once demand volumes are revealed, a VRP has to be solved meeting the previously determined time windows. Dalmeijer and Spliet (2018) and Dalmeijer and Desaulniers (2021) can improve the computational performance of this problem by strengthening the problem formulation through valid inequalities and by developing symmetry breaking strategies. A discrete variant of the above problem is presented by Spliet and Desaulniers (2015). They also propose an exact branch-price-and-cut algorithm. Spliet et al. (2018) extend the problem to time-dependent travel times and develop a branch-price-and-cut algorithm to solve the problem to optimality. A similar problem of previously assigning time windows to customers on first and routing vehicles on second stage is proposed by Subramanyam et al. (2018). They additionally consider stochastic travel times and propose a scenario decomposition algorithm to solve the problem.

Precedently assigning time windows is not enough for our pickup and delivery routing problem as we look for a schedule with exact time synchronisation. We are facing stochastic demand and need to determine routes before demand becomes known, e.g. based on stochastic information. This concept of time consistency is called a priori routing or finding master tours. When demand is revealed, these routes are commonly updated using recourse actions, such as skipping customers or restocking at the depot for example. Some common recourse strategies are explained in Kovacs et al. (2014a). Often, such problems are modelled as a two-stage stochastic program: at the first stage, an a-priori routing is determined under uncertain demand. At the second stage, uncertainty is revealed and corresponding recourse actions are selected. Reviews on a-priori routing problems and corresponding solution methods can be found in Bertsimas et al. (1990); Campbell and Thomas (2008) and Kovacs et al. (2014a). We concentrate on the most relevant work for our context in the following. Hvattum et al. (2006) use a multistage stochastic programming formulation to model a VRP with both deterministic and stochastic customers. Recourse strategies are applied repetitively based on a sample scenarios heuristic approach. Sungur et al. (2010) describe a courier delivery problem with stochastic customers and uncertain service times. They offer a multi-objective two-stage program for a variant of the ConVRP with time windows to develop a-priori master tours using a scenario-based solution approach. Uncertain travel times and stochastic customers are also considered in Sampaio et al. (2019), who propose a VRP with roaming delivery locations which they solve with a scenario-based sample average approximation. Angelelli et al. (2017) solve a probabilistic team orienteering problem through a two-stage stochastic program that maximises the expected profit of visited customers. They solve their problem applying a branch-and-cut approach as well as different heuristic methods. There is some recent work on two-stage stochastic programs for VRPs with stochastic demands and recourse actions. Lagos et al. (2019) suggest such a model minimising the expected travel costs. The models proposed by Bernardo and Pannek (2018); Salavati-Khoshghalb et al. (2019) and Florio et al. (2022) additionally aim to minimise the expected costs of recourse actions. Similar to our problem, Crainic et al. (2016) suggest a two-stage stochastic programming formulation for the 2E-VRP with stochastic demand. At the first stage, an urban-vehicle service network design model routes the first fleet and determines the general load of micro-hubs, using an approximation of the routing cost from micro-hubs to customers. The second stage concerns the routing of second fleet vehicles and possible recourse actions for the first fleet. The authors evaluate different recourse strategies through repetitively applying the adjusted plan for each planning period. Their work differs from ours as determining loads of hubs is not part of our problem, further we do not apply recourse strategies since we seek a consistent routing between micro-hubs. Consistent master routes are also determined in the work of Visser and Savelsbergh (2019). They investigate a strategic time slot management problem where master tours and time windows at customer locations are determined simultaneously on first stage, facing uncertain demand. In difference to our problem, assigning time slots instead of precise arrival times is sufficient. Further, recourse actions may be applied after demand realisation in the sense that customers may be skipped if they cannot be served within their time window. A different approach for consistent vehicle tours is used by Orenstein and Raviv (2022). The authors propose an urban parcel pickup and delivery system including so called service points that can serve as consolidation, transshipment, and pickup point for customers or drivers. Customers may be served from several service points, what further increases flexibility in the delivery process. They develop a myopic policy to route stochastically arriving parcels based on given vehicle routes. Vehicle routes are determined a-priori using a math heuristic. The mentioned papers suggest how to derive consistent tours with later recourse actions for different problem settings. Here, skipping customer nodes or returning to the depot preemptively are the most prominent recourse actions. In our context however, skipping micro-hubs might prevent some parcels to be delivered, others to be picked up, eventually leading to a lower total delivery volume. Because of the consolidation of parcels at micro-hubs, it is highly unlikely that a micro-hub shows no demand. Note that this is a significant difference to the traditional ConVRP literature, where usually one node corresponds to a single customer, making the presence of demand more volatile. To this end, we do not include recourse actions in our model.

Table 1 Related literature on two-stage stochastic routing problems

We summarise related literature on two-stage stochastic routing problems in Table 1. For each paper, we classify the type of route consistency, the source of uncertainty, the decisions taken on first and second stage, the objective, as well as the solution method. By master tours (with recourse) we refer to those papers that address routing consistency via finding master tours on first stage. However, recourse actions on second stage lead to changes in these master tours. This is why we place brackets around the check mark in columns “M” (Consistency/1st stage) if recourse actions are applied. Brackets in the “routing” column of the 2nd stage indicate that re-routing decisions are taken for recourse. No brackets here mean solving an entire routing problem. Finally, some papers consider stochastic customers for pickup and/or delivery. If only one of the two is addressed, this is also indicated by brackets in column “pickup/delivery”.

In Table 1, we see that all revised papers finding master tours on first stage later apply recourse strategies. This is fundamentally different from our problem where routing schedules between micro-hubs need to be fixed for any demand realisation. Vehicles between micro-hubs stick to their routes regardless of the daily varying customer orders. Different to any other publication, we determine the flow of realised parcel orders on second stage. Further, none of the presented papers on two-stage stochastic routing problems includes both pickup and delivery customers. We hence propose a novel two-stage stochastic program for consistent pickup and delivery at micro-hubs with stochastic customer demand, but without recourse actions. To the best of our knowledge, this problem has not been studied in literature yet.

3 Model

In this section, we give a detailed description of the consistent pickup and delivery problem with micro-hubs and stochastic customer demand. To that end, we first state the problem in Sect. 3.1 and highlight the two stages with an illustrative example in Sect. 3.2. In Sect. 3.3, we provide the mathematical framework for the model.

3.1 Problem statement

We propose a model to determine a consistent routing schedule for shared vehicles in collaborative urban delivery. The use of shared vehicles increases consolidation opportunities since parcels from different stores can be bundled for joint delivery to the same region.

To pickup and deliver parcels, shared vehicles conduct service between micro-hubs that are placed at fixed locations in the city. Micro-hubs may either be located in selected stores, or close to customer’s locations or shopping areas. The schedule at micro-hubs must be known previously so that stores can organise transport to the micro-hub accordingly. In our system, we use a fixed number of vehicles with a given, finite capacity each. While operating, vehicles are allowed to wait at micro-hubs in order to include later parcels. Also, vehicles are allowed to perform pickup and delivery on the same route and simultaneously during one stop. Moreover, we consider a limited planning horizon within which service is operated. We call this the service time horizon. At the beginning of the service time horizon, all vehicles are located at a depot at the outskirts of the city. We consider a transfer time at each micro-hub a vehicle visits on its itinerary to load and unload parcels. For simplicity, the transfer times are incorporated in the travel times.

We assume that each parcel order consists of a pickup location (store) with a release time, a delivery location (customer), and a homogeneous parcel volume. We further assume that storekeepers promise to complete deliveries within a certain time window of fixed length. As soon as the order comes in, the corresponding store brings the parcel to its closest micro-hub. Since the distance between the store and its closest micro-hub is relatively short, for simplicity, we therefore assume that the time window only concerns the transportation between micro-hubs. The release time of a parcel hence indicates the earliest time it can be picked up at the close-by micro-hub. At the end of the delivery time promise, customers pick up the parcels at the micro-hub next to them. To represent this in our model, pickup and delivery locations are mapped to their closest micro-hubs such that each parcel has a pickup micro-hub and a delivery micro-hub. We do not have to serve all orders placed, but aim to pickup and deliver as many parcels as possible. Each parcel that is picked up must also be delivered in time.

We model this problem as a two-stage program. The first stage develops the consistent routing schedule for the vehicles, i.e. a sequence of stops at micro-hubs with corresponding departure times. Once this routing is fixed, realised parcel orders are routed according to the given schedule at the second stage. At this, parcels cannot move independently in the network, but must be transported by a vehicle. The goal of the model is to find a routing schedule that maximises the expected amount of daily delivered parcels.

We note that our tactical model assumes the information of the second stage to be revealed at once. In operations, demand reveals over time. Thus, the second stage objective is an upper bound for the operational implementation. In Sect. 4.5, we show that this upper bound is mostly very close to the actual objective value when the second-stage orders are handled dynamically.

3.2 Example

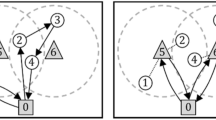
We illustrate our problem setting in a short example. Assume there are one shared vehicle, a depot and two micro-hubs in the city, as displayed in Fig. 1. Moreover, suppose shops promise to deliver any orders within a four hour time window. We further assume that the vehicle has the following first-stage schedule. It leaves the depot at 12:30 and reaches micro-hub 1 at 13:00. After a transfer time of ten minutes it continues to micro-hub 2 where it arrives at 13:50. Again, ten minutes are needed for transfer such that the vehicle leaves micro-hub 2 at 14:00 and reaches the depot at 14:35. This routing schedule is shown in Fig. 1. Now, suppose in scenario 1 there are two parcels which both have to be transported from micro-hub 1 to micro-hub 2, indicated by the plus for pickup, and the minus for delivery. The release times are 11:00 for parcel 1 and 13:00 for parcel 2. With the given schedule and assuming that capacity constraints are satisfied, both parcels can be picked up and delivered in time (Fig. 1).

Fig. 1

Scenario 1: all parcels can be transported

Fig. 2

Scenario 2: no parcel can be transported

Fig. 3

Combined routing schedule

However, in a different demand scenario, this schedule might be inefficient. For instance, suppose that in a second scenario 2 again two orders are placed, differing in release time, pickup and delivery location: parcels 1 and 2 have to be picked up at micro-hub 2, and brought to micro-hub 1, having release times 11:00 and 10:00, respectively. Note that in this scenario no order can be fulfilled using the given routing schedule (see Fig. 2). This small example shows that the performance of our proposed pickup and delivery service highly depends on the shared vehicle’s routing schedule. To transport as many orders as possible, it thus is very important to create effective schedules that are flexible with respect to order uncertainty in time and space. For the example at hand, a routing schedule allowing to meet the demand in both scenario is presented in Fig. 3. The vehicle visits micro-hub 2 first, then continues to micro-hub 1. Instead of returning to the depot directly, it waits there for further parcels to be picked up and then goes back to micro-hub 2. This way, parcels can be transported from micro-hub 1 to micro-hub 2 and vice versa.

3.3 Mathematical formulation

In this section, we first introduce the required notation in Sect. 3.3.1, and then present the stochastic two-stage model in Sect. 3.3.2. The corresponding deterministic second-stage model is stated in Sect. 3.3.3. Note that we focus on the single-vehicle case in our computational study, while in this section we present the more general model allowing for a fleet of vehicles.

3.3.1 Notation

In the following, we introduce the notation of our model, also summarised in Table 2. Parcel orders are placed on a daily basis. We hence consider a set of several daily scenarios denoted by S. We assign a certain probability of occurrence to each scenario $s\in S$. The set of parcel orders placed on scenario $s\in S$ is denoted by $P_s$. We refer to an element $p\in P_s$ as parcel or order equivalently. For our model, we consider a set of physical nodes $V=V_0\cup V_H$, where $V_0=\lbrace v_0\rbrace$ denotes the depot and $V_H$ represents the set of micro-hubs. The pickup hub (origin) of a parcel $p\in P_s$ is represented by node $o_p\in V_H$, the delivery hub (destination) by node $d_p\in V_H$. The parcel’s release time is denoted by $r_p$ for every $p\in P_s$ and indicates the start of a time window of length $T_P\in {{\,\mathrm{{\mathbb {N}}}\,}}$, within which a parcel $p\in P_s$ must be picked up at micro-hub $o_p$ and delivered to micro-hub $d_p$ in order to fulfil the order. Otherwise, we say that the parcel is not served or that the order is not fulfilled by our system, but must be outsourced. For simplicity we assume that each parcel has a homogeneous volume of 1. Service is operated by a homogeneous fleet of vehicles K. Each vehicle has the same velocity $v_K$ and maximum capacity $C_K$. Also, micro-hubs have a limited storage capacity $C_H$. In this section, we present the general model for several vehicles. In our computational study in Sect. 4, we focus on one vehicle only.

We model our problem over a discrete time horizon $T=\lbrace 0, 1, \ldots ,T_{\text {max}}\rbrace$ representing one working day. Service time of the vehicle starts at time step 0 and ends at $T_{\text {max}}\in {{\,\mathrm{{\mathbb {N}}}\,}}$. Inspired by the work of Neumann-Saavedra et al. (2016), we make use of a time extended network for the formulation of our problem. In such, nodes are duplicated per time step and arcs are constructed correspondingly. For this, we first define $t_{i,j}\in {{\,\mathrm{{\mathbb {N}}}\,}}$, $t_{i,j} > 0$, as the integer travel time between two nodes i, $j\in V_0\cup V_H$, $i\ne j$. If a vehicle or a parcel stays at a location $i\in V_0\cup V_H$, we set the travel time to $t_{i,i}:= 1$. This represents waiting at node i until the next discrete time step. Then, we extend the set of physical nodes in the following way: For each node $i\in V_0\cup V_H$ we create one duplicate per time step $t\in T$ and denote this node as (i, t), $\forall i\in V_0\cup V_H$, $\forall t\in T$. This is illustrated in Fig. 4. The exemplary network consists of one depot (node D) and two micro-hubs (nodes A and B). The left hand side of the figure shows the physical network with travel times on the arcs. The right hand side depicts its corresponding time expanded version on a time horizon of 40 min, in discrete time steps of 10 min. The construction of arcs in the time expanded network has to be adapted correspondingly. Grey arcs represent waiting at the respective nodes, while the coloured arcs correspond to the ones of the physical network.

Table 2 Parameters and sets for the model

Fig. 4

Construction of a time expanded network for an exemplary network

Since the number of decision variables and constraints affects whether the model is solvable with commercial solvers, we exclude infeasible arcs from the definition. More precisely, any vehicle must start its tour in the depot. For this reason, vehicle arcs starting at time step 0 in a location different from the depot are not feasible. They are hence not included in the set of arcs. In Fig. 4, this affects all arcs leaving node (A, 0) or node (B, 0). We thus define the set of arcs on which any vehicle $k\in K$ is allowed to travel as:

This set contains all arcs connecting any two physical nodes with each other as long as the itinerary starts later than $t=0$ and ends until $T_{\text {max}}$. At the beginning of the time horizon, vehicles must start their tour at the depot. Thus, the set also contains any arcs starting from the depot at time $t=0$.

Besides the vehicle arc set, we define the set of arcs on which in a given scenario $s\in S$ a particular parcel $p\in P_s$ is allowed to travel as:

This set reflects that parcel $p\in P_s$ can be transported between any pair of micro-hubs after it was released (i.e. from $t=r_p$) and until its delivery time window ends (i.e. until $u =r_p + T_P$). Outside this time window, a parcel is not available in the system, i.e. it cannot be moved. Since each parcel $p\in P_s$ has its own release time, we define $A_{p,s}$ for any $p\in P_s$ for any $s\in S$. Note here that parcels are not allowed to enter the depot.

In the problem formulation below we will need to explicitly refer to those arcs linking the same micro-hub between two following time steps, which represents waiting at the respective micro-hub. We call this the set of waiting arcs for parcel $p\in P_s$ in scenario $s\in S$, defined as:

We remark here that $A_{W_{p,s}}\subset A_{p,s}\subset A_K$ for any $p\in P_s$ for any $s\in S$. Finally, the set of waiting arcs at the depot is defined by:

Again, $A_{V_0}\subset A_K$. Note that in any of the above definitions, arcs only go forward in time by construction. Additional to the different sets of arcs we further define:

as the set of parcels that can feasibly move along arc $a\in \bigcup _{p\in P_s} A_{p,s}$ in scenario $s\in S$. We will later need this for the capacity constraints in the model.

Decisions are made on two stages. The first stage concerns the long-term planning of vehicle routes. Although demand varies from day to day, vehicles are to follow a fixed, consistent schedule. For this, we introduce the first stage decision variables $x^k_{(i,t),(j,u)}$ for each $k\in K$ and for each $(i,t),(j,u)\in A_K$. It is defined as:

$$\begin{aligned} x^k_{(i,t),(j,u)}:={\left\{ \begin{array}{ll} 1, &{} \text {if vehicle }k\text { travels directly from node }(i,t)\text { to node }(j,u),\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

The second stage concerns the operational daily planning of which parcels to serve. Therefore, we use a binary second stage decision variable $y_{p,s}$ for all $p\in P_s$ to decide whether parcel p is served in scenario $s\in S$ or not:

$$\begin{aligned} y_{p,s}:={\left\{ \begin{array}{ll} 1, &{} \text {parcel }p\text { is served in scenario }s\in S,\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

We further consider binary second stage decision variables for parcels to decide which arcs they use on their itineraries. For each scenario $s\in S$, each parcel $p\in P_s$, and each arc $(i,t),(j,u)\in A_{p,s}$ we hence define:

$$\begin{aligned} z^p_{(i,t),(j,u), s}:={\left\{ \begin{array}{ll} 1, &{} \text {if parcel }p\in P_s\text { travels directly from node }(i,t)\text { to node }(j,u)\text { in scenario }s\in S,\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

The objective of the model is to maximise the expected number of delivered parcels.

3.3.2 The stochastic two-stage model

With the notation above we now state the two-stage stochastic integer program for consistent routing in collaborative urban delivery as follows. Let x, $y_s$, and $z_s$ be the vectors with entries defined as above. Then we are looking for a solution of the form $\left( x, \left( y_s, z_s \right) _{s\in S}\right)$ to the two-stage stochastic program:

where $C_s$ represents the feasible set corresponding to scenario s defined by Constraints (1) to (15) following below. The objective of (2-${\mathcal{S}\mathcal{P}}$) maximises the expected amount of parcels that can be served, according to the probability of occurrence of each scenario. Note that the first-stage decision variable x is invariant with regard to the resulting scenario. Thus, the following constraints ensure a feasible routing for the vehicles for any demand realisation. Constraints (1) and (2) ensure that each vehicle starts and ends its tour at the depot. Through Constraints (3) each vehicle leaves the depot at most once, i.e. vehicles do not return to the depot during their route. Together with the flow conservation constraints in Constraints (4), this prohibits vehicles to visit the depot during service.

$$\begin{aligned} \sum _{\left( (0,0),(j,u)\right) \in A_K} x^k_{(0,0),(j,u)}&=1 \quad \forall k\in K, \end{aligned}$$

(1)

$$\begin{aligned} \sum _{\left( (i,t),(0,T_{\text {max}})\right) \in A_K} x^k_{(i,t),(0,T_{\text {max}})}&= 1 \quad \forall k\in K, \end{aligned}$$

(2)

$$\begin{aligned} \sum _{\left( (0,t),(j,u)\right) \in A_K \backslash A_{V_0}} x^k_{(0,t),(j,u)}&\le 1 \quad \forall k\in K, \end{aligned}$$

(3)

$$\begin{aligned} \sum _{\left( (i,t),(j,u)\right) \in A_K} x^k_{(i,t),(j,u)}&= \sum _{\left( (j,u),(i,t)\right) \in A_K} x^k_{(j,u),(i,t)} \quad \forall j\in V_H\cup V_0, \forall k\in K,\nonumber \\&\quad \forall u\in T\backslash \lbrace 0,T_{\text {max}}\rbrace . \end{aligned}$$

(4)

The following Constraints (5) to (8) are concerned with the routing of parcels, that does depend on the resulting scenario. For this reason, all following constraints must be kept for any demand realisation $s\in S$. Constraints (5) ensure that each parcel $p\in P_s$ has to start its itinerary at its pickup micro-hub $o_p$ at its release time $r_p$. In the case where pickup and delivery customer are mapped to the same micro-hub, no transportation by vehicle is needed. This is captured by Constraints (6). Constraints (7) and (8) state that each parcel that is served must leave its pickup hub and enter its delivery hub. Note that with this formulation parcels must leave their pickup hub at time $t=r_p$ and enter their delivery hub at time $t=r_p + T_P$. However, this may be satisfied via waiting arcs such that physical leaving and entering may happen later and earlier, respectively. Parcels hence are present in the system between their release time $r_p$ and the end of their delivery promise $r_p + T_P$, which is when the customer picks up the order. Within this time, flow conservation of parcels at micro-hubs is required, guaranteed by Constraints (9).

$$\begin{aligned} \sum _{\left( (i,r_p),(j,u)\right) \in A_{p,s}, i\ne o_p} z^p_{(i,r_p),(j,u),s}&= 0 \quad \forall p\in P_s, \forall s\in S, \end{aligned}$$

(5)

$$\begin{aligned} z^p_{(i,t),(j,u),s}&= 0 \quad \forall (i,t),(j,u)\in A_{p,s}\backslash A_{W_{p,s}}, \nonumber \\&\quad \forall p\in P_s: o_p = d_p, \forall s\in S, \end{aligned}$$

(6)

$$\begin{aligned} \sum _{\left( (o_p,r_p),(j,u)\right) \in A_{p,s}} z^p_{(o_p,r_p),(j,u),s}&= y_{p,s} \quad \forall p\in P_s, \forall s\in S, \end{aligned}$$

(7)

$$\begin{aligned} \sum _{\left( (i,t),(d_p,r_p + T_P)\right) \in A_{p,s}} z^p_{(i,t),(d_p,r_p + T_P),s}&= y_{p,s} \quad \forall p\in P_s, \forall s\in S, \end{aligned}$$

(8)

$$\begin{aligned} \sum _{\left( (i,t),(j,u)\right) \in A_{p,s}} z^p_{(i,t),(j,u),s}&= \sum _{\left( (j,u),(i,t)\right) \in A_{p,s}} z^p_{(j,u),(i,t),s} \quad \forall j\in V_H, \nonumber \\&\quad \forall t\in T: r_p< t < r_p + T_P. \nonumber \\&\quad \forall p\in P_s, \forall s\in S. \end{aligned}$$

(9)

Parcels cannot move independently in the network but have to be transported by vehicles. To this end, Constraints (10) link the routes of parcels to those of vehicles. More precisely, Constraints (10) make sure a parcel can move along an arc only if transported by a vehicle on that arc. With this formulation, parcels may change vehicles (at micro-hubs) on their route.

$$\begin{aligned}&z^p_{(i,t),(j,u),s} \le \sum _{k\in K} x^k_{(i,t),(j,u)} \quad \forall \left( (i,t),(j,u)\right) \in A_{p,s} \backslash A_{W_{p,s}}, \nonumber \\&\quad \forall p\in P_s, \forall s\in S. \end{aligned}$$

(10)

To not exceed vehicle capacity constraints, we have to control the maximum load capacity on vehicle arcs, which is done with Constraints (11). Note here that the homogeneous parcel volume of 1 is important so that Constraints (11) are meaningfully defined. Otherwise, if the parcel volume is not an integer divisor of the vehicle capacity $C_K$, this formulation might cause split deliveries, which is not allowed. Limited micro-hub capacity is controlled via restricting the load on waiting arcs through Constraints (12).

$$\begin{aligned} \sum _{p\in {\mathcal {P}}_{((i,t), (j,u),s)}} z^p_{(i,t),(j,u),s}&\le C_K\cdot \sum _{k\in K} x^k_{(i,t),(j,u)} \quad \forall \left( (i,t),(j,u)\right) \in \bigcup _{p\in P_s} A_{p,s} \backslash A_{W_{p,s}},\forall s\in S, \end{aligned}$$

(11)

$$\begin{aligned} \sum _{p\in {\mathcal {P}}_{((i,t), (j,u),s)}} z^p_{(i,t),(j,u),s}&\le C_H \quad \forall \left( (i,t),(j,u)\right) \in \bigcup _{p\in P_s} A_{W_{p,s}}, \forall s\in S. \end{aligned}$$

(12)

Finally, Constraints (13) to (15) state the domain of the decision variables.

$$\begin{aligned} x^k_{(i,t),(j,u)}&\in \lbrace 0,1\rbrace \quad \forall ((i,t),(j,u)) \in A_K, \nonumber \\&\quad \forall k\in K, \end{aligned}$$

(13)

$$\begin{aligned} z^p_{(i,t),(j,u),s}&\in \lbrace 0,1\rbrace \quad \forall ((i,t),(j,u)) \in A_{p,s}, \nonumber \\&\quad \forall p\in P_s, \forall s\in S, \end{aligned}$$

(14)

$$\begin{aligned} y_{p,s}&\in \lbrace 0,1\rbrace \quad \forall p\in P_s, \forall s\in S. \end{aligned}$$

(15)

Note that for our computational study the decision variables $y_{p,s}$, $p\in P_s$, $s\in S$, are relaxed to be continuous, i.e. $y_{p,s}\in \left[ 0,1\right]$ $\forall p\in P_s$ $\forall s\in S$. This is computationally advantageous (see Appendix A.2 for details), and integrality is implied by Constraints (7), (8), and (14).

3.3.3 The deterministic second-stage and single-stage model

Although demand is not known at the first stage, the two-stage program allows us to find a vehicle routing schedule that maximises the expected number of fulfilled orders. Based on this schedule $\varvec{{\widehat{x}}}$, the actual flow of parcels can be planned at the second stage once demand is revealed. For this, we define the deterministic second-stage model for a given vehicle routing $\varvec{{\widehat{x}}}$ and a realised demand scenario s as follows:

The feasible set $C_s$ is defined as above, Constraints (1) to (15), with the only difference that $\varvec{{\widehat{x}}}$ is treated like a given value instead of a decision variable. The objective of model (2nd-${\mathcal{S}\mathcal{P}}$) is to serve as many parcel requests as possible.

In our computational study we use a scenario decomposition heuristic (see Sect. 4.2) which requires solving the routing of vehicles and the flow of parcels simultaneously for a given realised demand scenario. To that end, we define the deterministic single-stage problem for a specific scenario $s\in S$ similar to Model (2nd-${\mathcal{S}\mathcal{P}}$) as:

where now $x_s$ constitutes a scenario-dependent decision variable.

4 Computational study

In this section we present the experimental setup and results of our computational study. In Sect. 4.1, we explain how instances are generated. In Sect. 4.2, we introduce benchmark policies to assess the solutions obtained by our approach. In Sect. 4.4, present our computational results.

4.1 Instance generation

The following explains how we generate different possible demand scenarios. We assume demand to be distributed over a square city area with a radius of $r=10$ (km). We motivate our instances by the city structure of Braunschweig, Germany, see Ulmer and Streng (2019). Braunschweig shows the classical European city structure with a city centre and several ring roads. Several parcel locker stations of the German post service DHL are placed on the main ring road in Braunschweig. Inspired by this, we place 5 micro-hubs equidistantly on a circle with a radius of 5 (km), which is half of the city radius. Moreover, with such a circular structure the micro-hubs are evenly spread over the city area. The depot is located at the middle of the upper edge of town. Figure 5 gives an illustration of the circular location of five micro-hubs and the depot in a square city. We assume that each micro-hub has a maximum capacity of 20 parcels. One delivery vehicle conducts service between micro-hubs. In our computational study, we assume the vehicle to be a large cargo bike with a speed of 25 () and maximum capacity of 20 parcels.

For our experiments, we test different delivery promises and service time horizons. We investigate three service designs: “instant”—instant delivery (60 min) in a short horizon (240 min.); “fast”—fast delivery (120 min) in a medium horizon (360 min); and “same-day”—delivery on the same day (480 min) in a large horizon (480 min). The latter is equivalent to not imposing customer time windows. We use a discrete step size of $\delta := 10$ minutes in the time expanded network. The travel time $t_{i,j}$ between two locations $i, j \in V_H \cap V_0$ is computed via the Euclidean distance between i and j divided by the vehicle’s velocity and is then rounded up to the next multiple of $\delta$.

For each service design, we run our experiments with a varying number of parcels, $|P|\in \lbrace 40, 80, [1] 120\rbrace$. For each parcel request we sample a release time, a pickup store and a delivery customer location within the city area. All parcels have a homogeneous volume of one. The release time of a parcel is drawn uniformly over the time horizon $T = \lbrace 0,10, \ldots ,T_{\text {max}}-120\rbrace$.

Pickup micro-hub (origin) and delivery micro-hub (destination) of a parcel are the micro-hub closest to the corresponding pickup store and delivery customer, respectively. For spatial distribution of stores and customers we consider two different demand patterns:

Fig. 5

Example of demand structure uniform (left) and clustered (right)

• uniform: Stores and customers are uniformly distributed over the entire city area. An example of this customer distribution is shown on the left-hand side of Fig. 5. This is inspired by the city structure of Göttingen, Germany, where stores can be found over the entire city area and inhabitants live both inside and outside the city centre.

• clustered: Stores and customers are clustered within the city. Inspired by the city structure of Braunschweig, we designate the inner part of the city as city centre, the south-western part as industrial area, and northern as well as eastern part as residential area. The exact layout is shown on the right-hand side of Fig. 5. Stores are located in the city centre and industrial area; customers mostly in residential, but also in the industrial area. More details are presented in Appendix A.1.

In Table 3 we summarise the parameter values used for scenario generation in the computational experiments.

Table 3 Parameter values used in computational experiments

4.2 Benchmarks

In our computational study, we solve the extended form of the two-stage model (2-${\mathcal{S}\mathcal{P}}$) for a sampled set of scenarios, which are generated as described in Sect. 4.1. We refer to this approach as the EXACT method or policy. In our computational analysis, we compare this policy to several benchmark policies, which we introduce below.

• DAILY: First, we use a policy in which routing consistency constraints are relaxed. To this end, we solve the deterministic single-stage model (1-${\mathcal{S}\mathcal{P}}$) separately for each scenario. As this is done scenario-dependent, we can determine vehicle routing and parcel flow simultaneously on one stage. Given the optimal solution for this deterministic “daily” problem, this constitutes a non-consistent upper bound to the stochastic two-stage problem. Since this policy requires re-planning on a daily basis, we refer to this as the DAILY policy.

• DECOMPOSITION: Next, we present a scenario decomposition method. For a given set of sampled scenarios and their solutions, we choose the scenario solution with best expected performance. For this, each scenario-dependent solution is evaluated on a number of new scenarios using the deterministic second-stage model (2nd-${\mathcal{S}\mathcal{P}}$) and its corresponding objective value is computed. Finally, the scenario solution with best average objective value is selected, as this one is expected to perform best regardless of the true future demand scenario.

• FIXED: Last, we implement a practically-inspired FIXED policy that aims on a high flexibility and reachability among micro-hubs. The policy should allow to reach all micro-hubs from any micro-hub and further should not loose too much time between any two visits. Therefore, we suggest a circular route. The vehicle leaves the depot and visits each micro-hub, in ascending order. When the last micro-hub is reached, the vehicle continues to micro-hub 1 to close the circle. Instead of traversing the same circle again, the vehicle turns and takes the same route back to the depot, visiting all micro-hubs again, but in descending order. This guarantees that not too much time is needed for delivery between two micro-hubs. If the service time horizon is longer than the total tour length, the vehicle starts its tour such that the tour finishes at $T_{\text {max}}$. This is motivated by the idea to increase consolidation opportunities: visiting micro-hubs at a later point in time may allow to transport more parcels, as more demand will arise during the course of the day. In Fig. 6, we provide an illustration of the FIXED policy for $T_{\textrm{max}}=360$.

Fig. 6

FIXED policy for $T_{\text {max}} = 360$, in minutes after the start of the service horizon

4.3 Implementation

In this section, we comment on the implementation of the models (1-${\mathcal{S}\mathcal{P}}$) and (2-${\mathcal{S}\mathcal{P}}$) and describe how the different benchmarks are evaluated. Both models (1-${\mathcal{S}\mathcal{P}}$) and (2-${\mathcal{S}\mathcal{P}}$) are implemented in Gurobi 9.1. (Gurobi Optimization 2021). For optimisation in Gurobi, we set a time limit of 24 h per instance. We further provide a feasible starting solution in which the vehicle stays in the depot and hence no parcels are transported. If the problem cannot be solved to optimality within this time, the current best solution and relative MIP optimality gap are recorded. Based on preliminary experiments, we set the number of scenarios to 15 (in-sample). This number is used for the EXACT and the DECOMPOSITION policies. The FIXED policy is rule-based and does not require any scenarios, while the DAILY policy is calculated independently for every scenario. For final evaluation of the different benchmarks, the solutions obtained by each policy are evaluated on a set of 100 new generated scenarios (out-of-sample), using the deterministic second-stage model (2nd-${\mathcal{S}\mathcal{P}}$), and average objective values are computed for final comparison.

4.4 Computational results

We present our computational results in the following. In Sect. 4.4.1, we conduct a method analysis investigating the runtime and the performance of the extended two-stage model and benchmark policies. In Sect. 4.4.2, we then analyse the effect of different service designs and demand patterns and assess the value of consolidation at micro-hubs as well as the cost of consistent routing, In Sect. 4.4.3, we examine the structure of the consistent routes in more detail.

4.4.1 Method analysis

In this section, we first analyse the runtime needed for the different policies and then investigate the resulting objective values and their gap to the DAILY policy.

Runtime Analysis. In this section, we analyse the different consistent policies with respect to their total runtime. Table 4 shows the total runtime of the EXACT and the DECOMPOSITION policy on each instance in seconds. As the route of the FIXED policy is given beforehand, only arrival times of the predefined sequence of stops have to be computed. This requires less than 0.0001 s per instance, thus it is not included in the table.

Recall that the time limit for the EXACT policy was set to 24 h, i.e. 86400 s. If the optimal solution is not found within this time limit, this is indicated by “>86400” in the table. In this case, the current best solution x and objective upper bound UB are recorded. With this, we compute the relative MIP optimality gap as $\nicefrac {(\textit{UB}-x)}{\textit{UB}}$. As the problem at hand is an maximisation problem, this gives an estimate about the quality of the solution found so far. The table displays the gap of each solution determined via the EXACT method in brackets behind its runtime.

Table 4 Total runtime in seconds for the EXACT and the DECOMPOSITION policy on all instances, with relative MIP optimality gap for the EXACT policy

From the table, we deduce the following main observations. First, the total runtime of the extended two-stage model increases as the number of parcels increases and as the service time horizon gets larger. Both factors raise the complexity of the combinatorial optimisation problem, thus making it harder to solve. Instances with 120 parcels can only be solved to optimality on the instant service design. On the fast and same-day service design, the time limit is hit without finding the optimal solution. However, in case of the fast service design, the solutions found within the time limit have a relatively small optimality gap of 1.34% and 5.31% for uniform and clustered demand, respectively. On the same-day service design in contrast, the optimality gap for 120 parcels is above 40% on both demand patterns. We also see that an increase in the number of parcels has a greater effect on the increase in runtime than an increase in the service time horizon.

The second observation we make is that the solutions for the DECOMPOSITION policy are computed in much shorter time than the EXACT solution. While the DECOMPOSITION policy requires about the same runtime on instances with the instant service design, on the fast service design it requires only 0.84–6.47% of the runtime that is needed to determine the EXACT solution. On the same-day service design, it requires at most 2.93% of the runtime of the EXACT method (on those instances that were solved to optimality). Computation time of the DECOMPOSITION policy is thus significantly lower than for the EXACT method. While the EXACT method cannot solve instances with 120 parcels on the fast and same-day service design to optimality, the DECOMPOSITION policy can treat those instances within less than 5 h.

Fig. 7

Average service rates on uniform demand

Objective Values. After analysing the runtime of the different policies, we investigate their average performance in this section. Figure 7 and Fig. 8 show the average service rates that are obtained by the different policies for each combination of parcel requests (columns) and service designs (rows). As explained in Sect. 4.3, each policy is evaluated on a set of 100 out-of-sample scenarios. On instances where the extended two-stage model is not solved to optimality within the time limit, this is highlighted by dashes on the corresponding bar.

We see that the EXACT method outperforms the remaining consistent benchmarks on all instances where it is solved to optimality (except the DAILY policy, which represents an upper bound). Even when not solved to optimality, it exceeds the remaining policies slightly except on instances with the same-day service design and 120 parcels (where the MIP optimality gap is above 45%). In particular, the EXACT method reaches average service rates that are very close to the DAILY upper-bound policy on the same-day service design. With clustered demand and 40 parcels for example, it allows to fulfil 39.77 parcel requests on average which is only little behind the upper bound of 39.99 parcel requests.

We further observe that the FIXED benchmark performs worst on almost all instances. Since this policy does not incorporate any knowledge about potential demand scenarios, it is not capable to adapt to the corresponding demand setting. It behaves particularly bad on the fast service design. Here, delivery time promises are set to two hours, making the delivery options more restrictive than on the same-day design, where requests have to be fulfilled in eight hours. The latter thus has more flexibility in when to deliver parcels which compensates for the inflexibility of the FIXED policy. In constrast, the methods considering potential demand scenarios are superior. The DECOMPOSITION policy yields better results than the FIXED, but worse results than the EXACT method.

Fig. 8

Average service rates on clustered demand

We conclude this section by shedding a light on the performance of the different policies depending on the service design. For this, we also assess the cost of consistency as the relative gap of the consistent policies (DECOMPOSITION, FIXED, EXACT) to the non-consistent DAILY policy. Let $z_{\textit{DAILY}}$ and $z_p$ denote the objective value of the DAILY policy and the policy $p\in \lbrace \text {DECOMPOSITION, }\text {FIXED, EXACT}\rbrace$, respectively. Then the relative gap of policy p to the DAILY policy is given by

$$\begin{aligned} \frac{z_\textit{DAILY}-z_p}{z_\textit{DAILY}}. \end{aligned}$$

(16)

In Fig. 9 we display the relative gaps of the non-consistent policies for uniform (left) and clustered demand (right), averaged over all instances. As before, bars are dashed if the EXACT policy is not solved to optimality on all instances.

On the instant service design, all policies but the fixed one show a worse performance than with larger delivery time promises. Even the DAILY upper bound policy permits to serve only 47.33% (on uniform demand) and 53.57% (on clustered demand) of all parcel orders on average, respectively. The relative gap to the DAILY policy is clearly above 20% for all consistent policies.

In the service design of fast delivery, more time is available, resulting in approximately 89.96% parcels being served with the DAILY method on uniform demand and 90.47% parcels on clustered demand. Although not all instances are solved optimally with the EXACT method, it has the lowest gap to the DAILY policy on the fast service design, see Fig. 9. On both demand patterns it is about 10% worse than the non-consistent policy. The DECOMPOSITION policy follows with a gap of 14–18%. With a gap of more than 40%, the fixed policy leads to a very high loss in service quality on the fast service design.

While we see the greatest differences of the different policies on the fast service design, all policies perform particularly well on the same-day service design due to the high flexibility in time. If the EXACT method is solved to optimality, we reach nearly day-optimal solutions with this policy: it deviates by 1.52% from the DAILY policy on uniform demand and by 0.57% on clustered demand on the corresponding instances. The average service rates for these instances are also very high: For 40 and 80 parcels, the EXACT method yields average service rates between 96.85% and 99.43% for the same-day service design. Even if not solved to optimality, the EXACT policy yields an average service rate of 97.33% for 80 parcels, clustered demand and the same-day design. On the remaining instances that are not solved to optimality, we can still obtain high service rates with the heuristic approaches. Here, the DECOMPOSITION policy yields average service rates that are close to the non-consistent DAILY upper bound. While it differs by 6.11% (uniform) to 10.45% (clustered) on the fast service design and 120 parcels, it deviates by less than 0.6% from the upper bound on the same-day service design and 120 parcels.

Fig. 9

Average gap to DAILY policy on uniform (left) and clustered demand (right)

4.4.2 Analysis

In this section, we analyse the results from Sect. 4.4.1 with respect to the effect of different service designs and demand patterns on the cost of consistency and the value of consolidation at micro-hubs.

First, we observe that the integration of demand distributions when determining consistent tours is valuable, especially, if demand is heterogeneously distributed. While the FIXED policy, which is invariant with respect to the demand structure, performs relatively well for the uniform distribution, it behaves more poorly on clustered demand. This does not hold true for the remaining policies, see Figs. 7 and 8. They incorporate knowledge about the underlying demand pattern and hence can adapt their routes accordingly.

While including demand distributions in the calculation of consistent routes is beneficial, we observe that the values of consolidation and consistency themselves do not depend on the demand structure. For both investigated demand patterns, consolidation at micro-hubs and consistent tours work similarly well under the same conditions, as we can see in Fig. 7 and Fig. 8.

Next, we find that consolidation at micro-hubs is not worthwhile for an instant delivery model. The low service rates in the instant service design (see Figs. 7 and 8) indicate that it is difficult to use micro-hubs for serving a high number of parcels within a short delivery time promise, even without consistent routes. For such instant delivery business models, the gain in consolidation is limited due to narrow delivery deadlines and direct transportation may be the more suitable choice. Consolidation at micro-hubs becomes more valuable the more delivery time promises are extended. Figures 7 and 8 show that service rates are significantly higher for fast and same-day delivery than on the instant service design. Because of the increased flexibility in time, there is more time available to consolidate orders at micro-hubs.

Regarding consistency, we see that it comes at a certain cost in the fast service design, as indicated by the larger gaps in Fig. 9. For such types of fast same-day delivery, providers therefore must carefully weight the benefits of consistency with its costs. Our results further show that with a same-day delivery promise, consistency can be implemented at a very small loss in service quality. Due to the temporal flexibility of this service design, high amounts of parcels can be delivered with both consistent and non-consistent tours. With the right strategy, it is therefore possible to achieve consistency without compromising service quality when offering same-day delivery.

4.4.3 Routing structure

To conclude our computational analysis, we examine the structure of the consistent routes in more detail. We investigate the structural differences between the routes obtained by the EXACT policy for the instant, the fast, and the same-day service design, 40 parcels, and both demand distributions. The resulting routes are displayed in Fig. 10. Micro-hubs are represented by two half circles. The left-hand side illustrates the relative amount of pickup requests that originates from that specific micro-hub on average over 200 instances. Analogously, the right-hand side illustrates the relative average amount of delivery requests destined to this micro-hub. The upper part of the figure shows the routes for the two demand patterns on the instant service design, the middle part for the fast service design and the lower part for the same-day service design.

First, we analyse the differences between the demand patterns. In the tours of uniform demand, we see that—as demand is uniformly distributed—all micro-hubs have approximately the same amount of parcels that have to be picked up there and delivered to this destination. We further observe that on uniform demand, the vehicle conducts an almost circular route: starting in a certain node, it travels a clockwise or anti-clockwise circle several times, with a few exceptions only, before going back to the depot. Since pickup and delivery locations are uniformly spread, such a circular structure provides a time-efficient route visiting many micro-hubs and thus allowing to deliver many of the unknown parcel requests.

Fig. 10

Routes obtained by the EXACT policy for instances with 40 parcels on the instant (top), fast (middle) and same-day (bottom) service design, for uniform and clustered demand

On clustered demand, we clearly see the structured demand pattern: Most parcels originate from micro-hub 3, some from micro-hub 2 and even fewer from micro-hub 1. Those micro-hubs are located in the city centre or industrial zone and hence are mainly used as pickup locations, see Fig. 5. Micro-hubs 4 and 5 are located within or close to residential areas and consequently barely have pickup requests (4.40% and 2.39% of all parcel requests, respectively). Parcels’ destinations are spread more evenly among micro-hubs. Most parcels are destined to micro-hubs 2, 3, or 5 respectively, serving the industrial zone, the north-western and eastern residential areas. Each of those micro-hubs has a share of 22.21–24.07% of all delivery requests. The route obtained by the EXACT policy captures this demand pattern: in any service design, the vehicle visits micro-hubs with most pickup demand (micro-hubs 3 and 2) in the beginning of the time horizon and then delivers the collected parcels to their destinations. After that, it comes back to micro-hubs 3 and 2, to collect more parcels, which are again delivered. This process of collection and delivery of parcels is repeated until the service time horizon ends.

Concerning the different service designs, we observe the following differences. As the service time horizon gets larger, more time is available, thus vehicles repeat the routing scheme (circles on uniform and “first collect, then deliver” on clustered) more often. Also, in some settings it is beneficial for the vehicle to wait at a certain micro-hub for more orders to arrive before continuing its tour. This happens more often when delivery time promises are longer since they allow a higher temporal flexibility. With the instant service design, we have to collect as much as possible at the beginning of the time horizon and then deliver it promptly because of the short delivery time promise. This is particularly noticeable in the clustered demand pattern. With a fast and same-day service design, on the other hand, we can pick up a lot later in the day and still make a successful delivery.

4.5 Dynamic evaluation of the second stage

The two-stage stochastic program developed in this work assumes the total demand to be revealed at once before taking decisions at the second stage. As mentioned in Sect. 3.1, in operations we do not have perfect information, but parcel requests are placed dynamically over time. Thus, the static second stage objective constitutes an upper bound to a dynamic evaluation of the problem. In this section we shed a light on the tightness of this upper bound. To this end, we evaluate the solutions obtained from the first stage of (2-${\mathcal{S}\mathcal{P}}$) in a dynamic rolling horizon framework. Each time a new order arrives, we re-solve the second stage (2nd-${\mathcal{S}\mathcal{P}}$) to check if the new request can feasibly be served given the vehicle’s route and available capacities. This is a myopic policy, adding all orders that can be feasibly served in every state. The exact procedure of the dynamic evaluation is described in Appendix A.3.

We compare the objective values obtained with the static second stage to the dynamic evaluation of it. In our numerical experiments, we focus on instances with 80 parcel requests only. For 40 parcels, capacity constraints are usually not a problem. For 120 parcels, the exact solution of the two-stage model can not always be determined within the given time limit and the optimality gap is quite large for the same-day service design (see Table 4 for details). For these reasons, we limit our study on the 80 parcels instances. For each service design, we sample 100 instances and solve the static and the dynamic second stage for each of them.

We find that solutions and objective values are exactly the same for the instant and the fast service design. Due to the narrow time windows, parcels stay in the vehicle rather shortly (or are not served), and time constraints are the limiting factor. Capacity constraints play a minor role only such that exactly the same parcels can be served in the static as well as in the dynamic approach. This changes for the same-day design, where time constraints are not an issue anymore. Now, capacity restrictions come into play. For instances with uniform demand, the gap between the static and the dynamic second stage is 5.39% on average. On clustered demand, the average gap is 27.01%. Recall here that on clustered demand and same-day delivery the first stage is not solved to optimality but has an optimality gap of 4.55%. Moreover, requests are heterogeneously distributed on the clustered demand pattern. Figure 10 shows that some micro-hubs have clearly more pickup requests than others. This might cause capacity problems in the micro-hubs with high demand. As another consequence, the length of parcels’ itineraries varies much more on the clustered than on the uniform demand pattern. While the static model under perfect information rather selects those requests with short itineraries, the dynamic implementation accepts requests in a myopic manner. With this, capacities are blocked by parcels with long itineraries, preventing the fulfillment of additional requests in the future. In essence, while the static approximation of the dynamic process in our two-stage stochastic program works well for the majority of cases, there is room for improvement for the case where static and dynamic solutions differ. Here, anticipatory dynamic policies might be developed to increase the performance.

5 Conclusion

In this paper, we have analysed the value and functionality of consistent collaborative delivery with micro-hubs for a local market. We have proposed a novel model formulation, a two-stage stochastic integer program where on the first stage vehicle tours are determined and on the second stage parcels flows are optimised. We have solved the extended form of the two-stage stochastic program using a set of sampled scenarios. The performance of the exact method, and three benchmark policies have been evaluated in a computational study. Our results show when and how consistent tours for local same-day delivery can be beneficial. They further demonstrate that our two-stage stochastic model allows to derive a consistent tour performing not much worse than a daily re-optimised one, and additionally shows the advantage of computing the master tour only once. We also show that employing a static second stage proves to be a good approximation to the dynamic evaluation of the problem. However, there are situations where dynamic decision-making can offer significant value and benefits. As we delve into future research, we aim to explore the advantages of incorporating a dynamic second fleet organising the transportation from stores to micro-hubs and from micro-hubs to customer locations as well as delivering orders that cannot be served within the micro-hub framework. This would lead to a third decision dimension about the routing of the courier bikes. Delivery time promises are then to be implemented in a door-to-door policy to ensure that the local collaborative system is prompt, reliable, and tailored to meet customers’ needs.

There are several avenues for future research. We have seen that micro-hubs can be very valuable for deliveries within two hours. Future work may further investigate what deliveries are suitable for consolidated shipping and which should be shipped directly. In our research, we have focused on the single-vehicle case for moderately sized cities to analyse the functionality of the two-stage model and the impact of consistent routes. Future work may extend the computational study to larger cities and fleets. While the proposed model is already designed to capture multiple vehicles, it is very likely that the second stage problems cannot be solved with standard methodology. Instead, metaheuristics might be developed. Our model further is restricted to one micro-hub per shop and per customer. To increase the flexibility of stores and customers, several close-by micro-hubs may be used for drop-off and pickup, respectively. This would require a reformulation of the model, explicitly deciding about the origin and destination of each parcel. Furthermore, recourse actions such as skipping hubs may become useful in this case. Further, in this research we have assumed that all parcels become known at once during the day. As suggested above, future work may model the arrival of parcels dynamically every day. This would replace the second stage of our model with a stochastic dynamic process, for which anticipatory dynamic policies for the parcel flow decisions may be developed. Determining the consistent tour from a dynamic routing policy of the vehicles would be another, currently unexplored, research opportunity.

Appendix

In this appendix we provide background information on some parts of our work. In Appendix A.1, we explain the distribution of shops and customers in the clustered demand pattern. In Appendix A.2, we present a brief runtime comparison of the single stage model (1-${\mathcal{S}\mathcal{P}}$) when decision variables $y_p$, $p\in P_s$, $s\in S$ are defined to be binary or continuous, respectively. In Appendix A.3, we state the pseudo-code for the dynamic evaluation of the second stage.

1.1 Clustered demand pattern

In this section we explain in more detail the clustered demand pattern. As shown in Fig. 5, the city is divided into city centre, industrial area, and residential areas. Pickup and delivery customer locations are sampled as follows. Half of the pickup customer locations are generated uniformly over the city centre, the other half is generated uniformly over the industrial zone. This is motivated by shops and companies being located in these areas usually. As companies also might order goods or people might order parcels to their work place instead of their home, a fourth of the delivery customer locations is sampled uniformly within the industrial zone. Still, the majority of parcels is ordered to private households. Therefore the remaining four quarters of delivery customer locations are distributed uniformly in the residential areas.

1.2 Runtime comparison for relaxed decision variables $y_{p,s}$

In this section we make a runtime comparison to evaluate the model (1-${\mathcal{S}\mathcal{P}}$) with the decision variables $y_{p,s}$ $\in \lbrace 0,1\rbrace$ $\forall p\in P_s$ $\forall s\in S$ against the model with $y_{p,s}$ $\in \left[ 0,1\right]$ $\forall p\in P_s$ $\forall s\in S$. We create instances with uniform or clustered demand and 100 parcels. For each service design (instant, fast and same-day), we run the model on 100 different instances. Table 5 shows the average runtimes of both versions in seconds.

Table 5 Average runtime (in seconds) for the model with binary or continuous decision variables $y_{p,s}$, $p\in P_s$, $s\in S$

From Table 5 we see that on uniform demand with instant service, both models run equally long on average. On uniform demand with same-day service and on clustered demand with fast service the model with binary decision variables $y_{p,s}$ is slightly faster. On the remaining instances, the model with continuous decision variables $y_{p,s}$ is solved within a shorter time. It is remarkable that instances with fast service require significant more time to be solved than the rest of the instances. Also, the runtime reduction on these instances is larger than the runtime growth on other instances. We hence conclude that relaxing the decision variables $y_{p,s}$ to be continuous is generally beneficial, although this should be checked for different instances.

1.3 Implementation of the dynamic second stage evaluation

Algorithm 1 states the pseudo code for the dynamic evaluation of the second stage. In short, the algorithm re-solves the second stage each time a new order arrives. For this, the algorithm requires a first stage solution x and a set of parcel requests P as an input. To each parcel request, a corresponding release time, pickup, and delivery location is given. To initialise the algorithm, the parcel requests are sorted by their release time in ascending order. Moreover, an empty set of available parcels and of already checked parcels are created. Within the algorithm, they will help to keep track of which parcels are to be investigated and for which parcels a solution has already been determined.

Every time a new parcel request p is placed, the algorithm adds this parcel to the list of available parcels. Then, the deterministic second stage model (2nd-${\mathcal{S}\mathcal{P}}$) is solved where only the set of available parcels is considered. In (2nd-${\mathcal{S}\mathcal{P}}$), the first stage decision variables x, i.e. the consistent tour of the vehicle, are fixed. Further, the decision variables of all parcels whose solution has already been determined in a previous iteration are fixed as well. This way, the solution of one more parcel is fixed in each iteration. In other words, only the decision variables concerning parcel p are to be determined by the model. Given the vehicle tour and the parcel flow of earlier orders, the model hence determines whether the new parcel can be transported with the given schedule and availabe capacities, or not. After a solution has been found, parcel p is added to the list of checked parcels and a new iteration starts.

In each iteration k, the current objective value $\sum _{p\in P_k} y_{p}^k$ specifies the number of parcels that can be transported by the shared vehicle so far. After the last iteration, this is the total number of delivered parcels.

Algorithm 1

Dynamic Evaluation of the Second Stage