The last-mile vehicle routing problem with delivery options

Abstract

The ongoing rise in e-commerce comes along with an increasing number of first-time delivery failures due to the absence of the customer at the delivery location. Failed deliveries result in rework which in turn has a large impact on the carriers’ delivery cost. In the classical vehicle routing problem (VRP) with time windows, each customer request has only one location and one time window describing where and when shipments need to be delivered. In contrast, we introduce and analyze the vehicle routing problem with delivery options (VRPDO), in which some requests can be shipped to alternative locations with possibly different time windows. Furthermore, customers may prefer some delivery options. The carrier must then select, for each request, one delivery option such that the carriers’ overall cost is minimized and a given service level regarding customer preferences is achieved. Moreover, when delivery options share a common location, e.g., a locker, capacities must be respected when assigning shipments. To solve the VRPDO exactly, we present a new branch-price-and-cut algorithm. The associated pricing subproblem is a shortest-path problem with resource constraints that we solve with a bidirectional labeling algorithm on an auxiliary network. We focus on the comparison of two alternative modeling approaches for the auxiliary network and present optimal solutions for instances with up to 100 delivery options. Moreover, we provide 17 new optimal solutions for the benchmark set for the VRP with roaming delivery locations.

1 Introduction

Over the past decade, mail-order trade has shown a strong compound annual growth rate, e.g., of 9.6 % in Germany with an overall revenue of 68.1 billion euros in 2018 (Furchheim et al. 2020). Due to the increasing e-commerce, over 3.5 billion deliveries had to be handled in Germany in 2018 resulting in 12 million deliveries per operations day on average (BIEK 2019). These considerable numbers raise the question of how to cope with the strongly growing demand and general challenges in last-mile logistics. While minimizing logistic costs, operators are also faced with issues such as the trend of smaller and smaller truckloads, restrictions imposed by urban development and environmental policies, and operational issues like traffic congestion and strict parking regulation (Zhou et al. 2018). Furthermore, new challenges arise from logsumers (DHL 2014) who are allowed to individualize their orders by choosing a preferred price, quality, time window, and options for environmental friendliness. Consequently, last-mile logistic has been referred to as “the bottleneck of e-commerce” (Wang et al. 2014) and “the logistic service providers’ nightmare(s)” (Savelsbergh and Van Woensel 2016).

The paper at hand introduces the vehicle routing problem with delivery options (VRPDO) which captures one of the most recent trends in last-mile package delivery related to the introduction of delivery options. The VRPDO is obviously a generalization of the vehicle routing problem with time windows (VRPTW, Costa et al. 2019) and the generalized vehicle routing problem with time windows (GVRPTW, Moccia et al. 2012) in which each customer request is represented by one or several delivery options. The delivery options of a customer differ within the designated location and delivery time window. Exactly one delivery option of each customer has to be selected.

The VRPDO extends the GVRPTW by two important real-world aspects: First, customers can individually prioritize their different delivery options beforehand, and the overall customer satisfaction level is taken into account by a given service level that must be achieved. Second, some delivery options may share a common location, e.g., pick-up points or postal boxes (Janjevic et al. 2019). The capacity of these locations is limited, in particular in densely populated areas of cities where space is scarce and expensive. For finding an optimal set of routes, both extensions lead to a nontrivial interdependence problem, where modifying one route can make another route infeasible regarding location capacities or required service level (Drexl 2012). The objective of the VRPDO is to minimize the overall cost while ensuring a minimum customer satisfaction level as well as not violating location-capacity restrictions.

The main contributions of this work are the following: We introduce the VRPDO and present a branch-price-and-cut (BPC, Costa et al. 2019) algorithm for its solution. In particular, we present a set-partitioning problem for the VRPDO, develop and analyze two different network structures for the solution of the pricing problem, and adapt cutting planes and branching rules. Our extensive computational study includes three parts: First, we evaluate the performance of our algorithm for the two different network structures on a newly introduced benchmark instance set. Second, we compare our BPC with the state-of-the-art algorithm from the literature on benchmark instances for the VRPHRDL and VRPRDL. Last, we conduct a sensitivity analysis to determine the impact of varying service levels and location capacities on routing costs and solution times.

The remainder of the paper is structured as follows: Sect. 2 reviews the pertinent literature. Sect. 3 introduces the VRPDO and all necessary notation. Section 4 describes the BPC algorithm with subsections on the set partitioning formulation, the pricing subproblem, valid inequalities, and branching. In Sect. 5, the results of the computational study are shown and discussed. Final conclusions are drawn in Sect. 6.

2 Literature

To the best of our knowledge, the first basic version of the VRPDO with alternative delivery locations for each customer was proposed in the dissertation of Cardeneo (2005). Service levels and customer preferences together with location selection were considered in the generalized pickup and delivery problem with time windows and preferences proposed by Los et al. (2018).

Shared delivery locations such as delivery to parcel lockers and shops have recently started to gain attention (Savelsbergh and Van Woensel 2016), as offering these in addition to traditional home delivery can significantly alleviate the burden of last-mile urban deliveries on both couriers and customers (Zhang and Lee 2016). Most customers are satisfied with collecting their delivery from established parcel lockers and shops, while others are open for other innovative last-mile delivery concepts such as the use of a reception box, controlled access systems, and trunk delivery (Felch et al. 2019). The VRPDO can easily represent all these options. Mancini and Gansterer (2020) assume that each customer can either chose home delivery, or delivery to one of the shared delivery locations, or allow both. Here, customers receive a monetarily compensation if assigned to a shared delivery location. Home deliveries have a time window, while shared delivery locations are restricted by a location capacity. This problem is refined in (Grabenschweiger et al. 2021) by considering different sizes of parcels and slots of the parcel lockers. Other recent contributions on shared delivery locations are (Zhou et al. 2018; He et al. 2019; Janjevic et al. 2019; Orenstein et al. 2019; Sitek and Wikarek 2019; Enthoven et al. 2020; Schwerdfeger and Boysen 2020). We refer to (Mancini and Gansterer 2020) and (Grabenschweiger et al. 2021) for a more detailed discussion on shared delivery locations. Recently, Jungwirth et al. (2020b) introduce the VRP with time windows and flexible delivery locations which also considers capacitated shared delivery locations and a location cost that can be used to model that customers have preferences for certain locations. Jungwirth et al. (2020a) discuss a similar problem arising in hospitals when physical therapists have to be scheduled to treat their patients at alternative service locations.

Ghoniem et al. (2013) and Reihaneh and Ghoniem (2017, 2019) consider a joint routing and allocation problem that arises in the food delivery context. From a food bank, pallets are first shipped to intermediate delivery sites, from where nonprofit organizations pick up the food and bring it to remote places. The delivery option lies in the selection of the intermediate delivery sites with the objective to minimize the total logistics cost that comprise vehicle routing costs of the food bank and travel costs of the nonprofit organization.

The VRPDO also generalizes some other vehicle routing problems. In the VRP with multiple time windows (Doerner et al. 2008), the delivery options of a customer have an identical location. The multiple-vehicle traveling purchaser problem (Manerba et al. 2017) can be modeled as a VRPDO by considering products as customer requests, the suppliers of a certain product as the delivery options, and the purchasers as the different vehicles. Moreover, the multi-vehicle covering tour problem (Hachicha et al. 2000) can be modeled by introducing one delivery option for each customer and each service point covering that customer. Note that none of these problems considers location capacities or service-level constraints.

The vehicle routing problem with (home and) roaming delivery locations (VRP(H)RDL, Ozbaygin et al. 2017; Reyes et al. 2017) is an application-specific variant of the GVRPTW and therefore also a special case of the VRPDO. The VRP(H)RDL with stochastic travel times has been considered by Lombard et al. (2018); Sampaio Oliveira et al. (2019); He et al. (2020). However, customer’s acceptance for roaming deliveries seems to be limited, since they have to reveal sensitive information (e.g., tracking data) and trust in the carrier is required (Felch et al. 2019).

3 Definition of the VRPDO

In the VRPDO, each customer a priori offers one or several delivery options that specify a delivery location and a priority. We use priorities that indicate how much the customer prioritizes this option, i.e., smaller numbers indicate higher customer satisfaction. In addition, shared delivery locations have a limited capacity in terms of the number of customers that can be served. Given a set of delivery options for each customer request, the VRPDO is the problem of selecting exactly one delivery option for each customer and determining a cost-minimal set of feasible routes that serve the selected delivery options while respecting the time windows of the delivery locations and the vehicle capacity. Moreover, the set of routes must respect all location capacities and all service-level constraints which require a minimum number of customers to be served with an option of the respective service level.

The VRPDO can be formalized as follows: Let $N$ denote the set of all (customer) requests, $L$ the set of all locations, and $P=\{1,\dots , p^{\max }\}$ the set of $p^{\max }\ge 1$ different (delivery) priorities. A delivery option is a triplet $o=(n,\ell ,p)\in N\times L\times P$ and let $O\subset N\times L\times P$ denote the set of all delivery options. In order to identify for an option $o\in O$ the associated request, location, and priority, we write $o=(n_o,\ell _o,p_o)$. A request $n\in N$ is fulfilled by selecting exactly one of the options $O^N_n= \{(n_o,\ell _o,p_o)\in O: n_o= n\}$. For a feasible VRPDO instance, there must exist at least one option per request, i.e., $|O^N_n|\ge 1$ for all $n\in N$. Similarly, we define $O^L_\ell = \{(n_o,\ell _o,p_o)\in O: \ell _o= \ell \}$ as the set of options belonging to location $\ell \in L$ and $O^P_p= \{(n_o,\ell _o,p_o)\in O: p_o\le p\}$ as the set of options with priority level $p\in P$ or smaller (=better). Moreover, each option $o\in O$ has a nonnegative service time $s_o$.

For each location $\ell \in L$, a time window $[a_\ell , b_\ell ]$ represents the time period in which all deliveries to this location must take place. Additionally, the capacity $C_\ell$ limits the number of shipments that can be delivered to that location. A location with exactly one associated delivery option is called individual delivery location (individual delivery is a.k.a. home or private delivery), all other locations are called shared delivery locations and denoted by $L^{\text {shrd}}= \{ \ell \in L: |O^L_\ell | > 1 \}$.

A fleet of $K$ homogeneous vehicles is housed at the depot $0$ for which $\ell _0\in L$ denotes the depot location. A vehicle has a capacity $Q$ to serve the demands $q_n$ of the requests $n\in N$ and fixed cost $c^{f}$ when used. We assume the time window $[a_{\ell _0}, b_{\ell _0}]$ of the depot location to span the whole planning horizon. Traveling between location $\ell$ and $\ell ' \in L$ consumes a travel time of $t_{\ell \ell '}$ and a travel cost of $c_{\ell \ell '}$. The travel time $t_{\ell \ell '}$ also includes a required access time needed, e.g., for parking a vehicle at $\ell '$ before the actual service (=delivery) at $\ell '$ can start.

Each priority level $p\in P$ can be characterized by a percentage $\beta _p$ that indicates that at least $\lceil \beta _p|N|\rceil$ delivery requests must be served with priority level p or smaller (=better). For this purpose, we assume that priorities are nested and the set $O_p^P$ contains all options $o$ with $p_o\le p$. Note that the percentage $\beta _{p^{\max }}$ refers to the set $O^P_{p^{\max }} = O$ and is therefore irrelevant.

Fig. 1

Example of a VRPDO instance and a solution

Example 1

Figure 1 shows an example of a VRPDO instance with five customers and eleven options as well as a solution utilizing two vehicles which (together) serve exactly one delivery option of each customer. Each customer and her/his options are depicted in the same color, e.g., the blue customer can be served either at the individual delivery location in the upper left part of the figure or at a shared delivery location at the bottom left. Note that different customers can have a different number of delivery options. The priority level of each delivery option is depicted next to it, e.g., the individual delivery location of the green customer has the highest priority 1 while his two other green options have a lower priority of 2. Note that not all customers must prioritize individual delivery locations over shared delivery locations (a counterexample is the red customer). Each shared delivery location is depicted as a dotted ellipse around its associated options together with its location index ($\ell \in \{\ell _1,\ell _2,\ell _3\}$).

Next, we briefly discuss the role of the location capacities and service-level constraints. Regarding location capacities, we can see that location $\ell _1$ is used to serve two customers, location $\ell _2$ serves one, and no customer is served at location $\ell _3$. Hence, the solution can only be feasible if $C_{\ell _1} \ge 2$ and $C_{\ell _2} \ge 1$. Regarding the service-level constraints, three options with priority 1 are selected and served and two options with priority 2. Hence, the solution is feasible if $\beta _1\le 60\,\%$.

A (vehicle) route $r=(0,o_1,\dots ,o_{h},0')$ is as sequence of options in which the artificial options $o_0=0$ and $o_{h+1}=0'$ represent the visit of the depot location $\ell _0$ at the start and end of the route, respectively. A route $r$ is feasible if it fulfils the capacity and time-window constraints that we define as follows. The demand served by route $r$ is $q(r)=\sum _{j=1}^{h} q_{n_{o_j}}$, so that $r$ is capacity-feasible if $q(r)\le Q$ holds true. A route is time-window feasible if there exists a schedule $(T_0,T_1,\dots ,T_{h},T_{h+1})\in \mathbb {R}^{h+2}$ which complies with the option service times, travel times, and time windows, i.e., if $T_{j-1} + t_{\ell _{o_{j-1}},\ell _{o_{j} }} + s_{o_{j-1}} \le T_{j}$ for all $1 \le j \le h+1$ (assuming $s_{o_0}=0$) and $[T_j,T_j+s_{o_{j}} ] \subseteq [a_{\ell _{o_j}}, b_{\ell _{o_j}}]$ for all $0 \le j \le h+1$. This definition has the following consequences: a subsequence $o_i,\dots ,o_j$ of options with identical locations $\ell =\ell _{o_{i}}=\cdots =\ell _{o_{j}}$ models a single physical stop of a vehicle at this location. The above time-window feasibility conditions impose that (i) $T_{i},\dots ,T_{j}$ can be considered as the start times when the associated requests are served, (ii) $T_{i}+s_{o_{i}},\ldots ,T_{j}+s_{o_{j}}$ are the respective service end times, and (iii) the time window $[a_{\ell }, b_{\ell }]$ of location $\ell$ must cover all service times entirely. We stress that we have chosen this definition of the time windows (diverging from the standard definition for the VRPTW referring to possible service start times) because in the VRPDO the total service time at a location is a variable. It results from the selection of options that are together served during the one stop of a vehicle at the location.

The cost $c_r$ of a route $r$ is the sum of the fixed cost and the travel costs between the visited locations, i.e., $c_r= c^{f}+ \sum _{j=1}^{h+1} c_{\ell _{o_{j-1}},\ell _{o_{j}}}$. The objective of the VRPDO is to find a least-cost set of feasible routes together covering exactly one option of $O_n^N$ for all customers $n\in N$ respecting the fleet size and location capacities as well as achieving the required service level.

4 Branch-price-and-cut

We use a BPC algorithm in order to solve the VRPDO exactly. According to the recent survey by Costa et al. (2019), BPC is the leading exact methodology for solving many types of vehicle routing problems. Section 4.1 presents the extensive formulation of the VRPDO and Sect. 4.2 the pricing subproblem and approaches for its resolution. In particular, we describe two competing approaches for modeling the underlying network including a discussion of expected pros and cons and a summary of their properties. Section 4.3 then briefly describes known valid inequalities for strengthening the linear relaxation, their adaption for the VRPDO, and separation algorithms. The branching scheme developed in Sect. 4.4 finally ensures integer solutions.

4.1 Extensive formulation

Let $\Omega$ denote the set of all feasible routes. The following extensive formulation of the VRPDO comprises one binary variables $\lambda _r$ per possible route $r\in \Omega$ indicating whether $r$ is part of the solution ($\lambda _r=1$) or not (=0). The binary coefficients $\alpha _{or}$ indicate whether route $r\in \Omega$ serves option $o\in O$. The model is an extended set-partitioning formulation and reads as follows:

$$\begin{aligned} \min \quad&\sum \limits _{r\in \Omega } c_r\lambda _r\end{aligned}$$

(1a)

$$\begin{aligned} \text {subject to} \quad&\sum \limits _{r\in \Omega } \sum \limits _{o\in O^N_n} \alpha _{or} \lambda _r= 1&\forall n\in N\end{aligned}$$

(1b)

$$\begin{aligned}&\sum \limits _{r\in \Omega } \sum \limits _{o\in O^L_\ell } \alpha _{or}\lambda _r\le C_\ell&\forall \ell \in L^{\text {shrd}}\end{aligned}$$

(1c)

$$\begin{aligned}&\sum \limits _{r\in \Omega } \sum \limits _{o\in O^P_{p}} \alpha _{or} \lambda _r\ge \lceil \beta _p|N| \rceil&\forall p \in P \end{aligned}$$

(1d)

$$\begin{aligned}&\sum \limits _{r\in \Omega } \lambda _r\le K\end{aligned}$$

(1e)

$$\begin{aligned}&\lambda _r\in \{0,1\}&\forall r\in \Omega \end{aligned}$$

(1f)

The objective (1a) minimizes the overall costs of the routes that are selected and performed. Constraints (1b) ensure that each request is served exactly once. For each shared delivery location, the number of shipments to this location is bounded by constraints (1c). The required service level per priority level is enforced by constraints (1d). Finally, constraint (1e) restricts the number of employed vehicles.

For solving the linear relaxation of (1), a column-generation algorithm is used (Desaulniers et al. 2005). In the following, the linear relaxation of formulation (1) in which the set of all feasible routes $\Omega$ is replaced by a subset $\bar{\Omega }\subset \Omega$ is denoted as restricted master program (RMP). Column generation alternates between the reoptimization of the RMP and the solution of the pricing subproblem that either generates new negative reduced-cost variables (=routes) to be added to $\bar{\Omega }$, or proves that none exists. In the latter case, the column-generation process terminates with a solution to the linear relaxation of the extensive formulation.

4.2 Column generation

Let $(\pi _{n})_{n\in N}$ denote the dual prices of the constraints (1b), $(\rho _{\ell })_{\ell \in L^{\text {shrd}}}$ of the constraints (1c), $(\nu _{p})_{p\in P}$ of constraints (1d), and $\mu$ of the fleet-size constraint (1e). Then, the reduced cost $\bar{c}_r$ of a route $r\in \Omega$ is given by

$$\begin{aligned} \bar{c}_r= c_r- \mu - \sum _{n\in N} \sum _{o\in O^N_n} \alpha _{or}\pi _{n} - \sum _{\ell \in L^{\text {shrd}}} \sum _{o\in O^L_\ell } \alpha _{or}\rho _{\ell } - \sum _{p\in P} \sum _{o\in O^P_p} \alpha _{or}\nu _{p}. \end{aligned}$$

(2)

The pricing problem asks for a feasible route with minimal reduced cost. We show in the following that it is a variant of the shortest path problem with resource constraints (SPPRC, Irnich and Desaulniers 2005). SPPRCs can be solved with a dynamic-programming labeling algorithm that creates partial paths starting from an origin vertex moving forward to a destination vertex of the network.

Next, we present two different possibilities to model the underlying network. A unified labeling algorithm for both networks is described in Sect. 4.2.2. Standard acceleration techniques are presented in Sect. 4.2.3.

4.2.1 Network modeling

An important characteristic of the VRPDO is that in many realistic instances several options share the same physical delivery location. This happens, e.g., when different customers choose the same delivery locker or the same shop as a potential option. Moreover, customers living together in the same apartment building and allowing home delivery is another case of identical locations.

One of our leading questions was whether these identical locations can be exploited so that a tailored solution approach works better than one that does not anticipate the identical locations. The commodity-constrained split delivery vehicle routing problem (C-SDVRP, Archetti et al. 2016) is an example of a VRP in which the solution approach can be tailored to exploit identical locations. In this problem, the total demand of a customer can be split into given smaller demands (the different commodities requested) which can be served by one or several visits to the customer. A straightforward approach for modeling and solving the C-SDVRP is to reduce it to a standard CVRP, as done in (Archetti et al. 2016), where each customer vertex is duplicated as many times as the number of commodities requested by the customer. Each duplicated vertex has a demand given by the weight of the corresponding commodity. A solution approach may either disregard or exploit the fact that this new CVRP instance has customers with identical locations. The recently presented approach of Gschwind et al. (2019) is of the latter type and heavily benefits from working on a transformed underlying graph with a macroscopic level considering locations and a microscopic level considering the commodities of each customer separately.

In the same spirit, we present two modeling approaches for the underlying network. The first one uses an option-based network $G^{\text {opt}}=(V^{\text {opt}},A^{\text {opt}})$. In $G^{\text {opt}}$, all vertices represent either options or the depot. No information about identical locations is exploited. Using options as vertices emphasizes that they are the basic objects that can be served. In Fig. 1, each depicted package and house represents one option so that the routes directly connect two options (or the depot with an option in either direction). Formally, the vertex set $V^{\text {opt}}$ of the option-based network is given by $\{0,0'\} \cup O$. The arc set $A^{\text {opt}}$ contains all feasible direct connections between vertices, i.e., $A^{\text {opt}} \subset V^{\text {opt}} \times V^{\text {opt}}$.

The second network, the location-based network $G^{\text {loc}}=(V^{\text {loc}},A^{\text {loc}})$, is more sophisticated as it makes use of the location information of options. All options are grouped according to their respective location. The idea of the location-based network is to significantly reduce the number of arcs at the cost of adding two artificial vertices $e_\ell$ and $f_\ell$ for each shared delivery location $\ell \in L^{\text {shrd}}$ modeling the entry and exit point of that location, respectively.

Formally,

$$\begin{aligned} E=\{e_\ell : \ell \in L^{\text {shrd}}\} \qquad \text {and}\qquad F=\{f_\ell : \ell \in L^{\text {shrd}}\} \end{aligned}$$

denote the sets of all entry and exit vertices, respectively. (Conversely, to refer to an entry or exit’s location, we write $\ell _e=\ell _f=\ell$ for $\ell \in L^{\text {shrd}}$.) Then, the vertex set is given by $V^{\text {loc}} = \{0,0'\} \cup O\cup E\cup F= V^{\text {opt}} \cup E\cup F$. Entering (exiting) a shared delivery location is only possible by using the entry (exit) vertex of that location. Thus, the arc set can be characterized by

$$\begin{aligned} A^{\text {loc}}\subseteq & {} \{(i,j) \in A^{\text {opt}}: \ell _i, \ell _j \notin L^{\text {shrd}}\} \\&\cup \, \{(e_\ell ,j) \in E\times V^{\text {opt}}: \ell _j = \ell \} \quad \cup \quad \{(i,f_\ell ) \in V^{\text {opt}} \times F: \ell _i = \ell \} \\&\cup \, \{(f_\ell ,j) \in F\times V^{\text {opt}}: \ell _j \notin L^{\text {shrd}}, j\ne 0\} \quad \\&\cup \quad \{(i,e_\ell ) \in V^{\text {opt}} \times E: i\ne 0', \ell _i \notin L^{\text {shrd}}\} \\&\cup \, \{(f_\ell ,e_\ell ') \in F\times E: \ell \ne \ell ' \}, \end{aligned}$$

where the first row refers direct connections between options at individual delivery locations, the second row internal connections of a shared delivery location, the third row connections between exit/entry vertices and individual delivery locations, and the last row connections between exit and entry vertices. For the sake of clarity, all arcs of the location-based network are summarized in Table 1. Note that typically time-window constraints and demands allow to eliminate infeasible arcs so that $A^{\text {loc}}$ is a proper subset of the indicated arc set (this is also the reason why we write $A^{\text {loc}} \subseteq \dots$).

Table 1 Arcs in the location-based network; entry “–” if no such arc exists, entry “$\checkmark$” if all such arcs exist, and a condition under which some of the arcs exist

Example 2

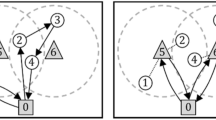
We consider the situation that a route serves six options $o_1, o_2, o_3, o_4, o_5, o_6$ in the given order. Associated with these options are four different locations $\ell _{o_1}$, $\ell _{o_2}=\ell _{o_3}=\ell _{o_4}$, $\ell _{o_5}$, and $\ell _{o_6}$. Moreover, we assume that the second and penultimate location, i.e., $\ell =\ell _{o_2}$ and $\ell '=\ell _{o_5}$, are the only shared delivery locations in this example.

In the option-based network, the resulting route is represented by the path ${{\mathcal {P}}}^{\text {opt}}= (0, o_1, o_2, o_3, o_4, o_5, o_6,0')$.

In the location-based network, the path is ${{\mathcal {P}}}^{\text {loc}}=(0,o_1,e_{\ell },o_2, o_3, o_4, f_{\ell }, e_{\ell '}, o_5, f_{\ell '}, o_6, 0')$.

Table 2 Comparison of the option-based network and the location-based network

Table 2 compares the option-based and location-based networks regarding the sizes of the vertex and arc sets as well as regarding the strength of the dominance that is used in the dynamic-programming labeling algorithm for solving the pricing problem. The following example explains what is meant by strength of dominance:

Example 3

We consider two feasible routes that have no options in common. Moreover, option $o_1$ is served by the first route while option $o_2$ is served by the second route. In addition, we assume that the options have the identical delivery location $\ell =\ell _{o_1}=\ell _{o_2}$.

Then, in the option-based network, the paths ${{\mathcal {P}}}_1$ and ${{\mathcal {P}}}_2$ representing the two routes are vertex disjoint, except for the two depot vertices $0$ and $0'$. As a consequence, no dominance can occur between labels associated with proper partial paths that occur when constructing the two paths.

In contrast, in the location-based network, the two paths are

$$\begin{aligned} (0,\dots ,e_{\ell },\dots ,o_1,\dots ,f_{\ell },\dots ,0') \end{aligned}$$

and

$$\begin{aligned} (0,\dots ,e_{\ell },\dots ,o_2,\dots ,f_{\ell },\dots ,0'), \end{aligned}$$

i.e., they have at least the additional entry and exit vertices is common. At these vertices $e_{\ell }$ and $f_{\ell }$, partial paths associated with the two routes are compared by the dominance algorithm.

We can summarize that, in the location-based network, more partial paths are supposed to meet at the entry and exit vertices of their common shared delivery locations. Consequently, there are more possibilities that labels dominate each other so that the dominance is stronger.

Moreover, the main driver for the computational effort of a labeling algorithm is the network size, because it impacts the number of labels that are generated and compared against each other using the dominance algorithm. Since labels are extended along arcs, also the two last points in combination with Table 2 speak in favor of the location-based network. Therefore, we initially expected that a BPC algorithm with pricing over the location-based network would clearly outperform the other BPC algorithm using the option-based network. The later computational experiments presented in Sect. 5.2 will, however, show that results are less clear cut. This came very unexpectedly for us.

4.2.2 Unified labeling algorithm

We now present the labeling algorithm in a unified way so that the description is correct for both networks. To this end, let $G=(V,A) \in \{G^{\text {opt}},G^{\text {loc}} \}$ be the option-based or location-based digraph.

It is helpful to first introduce the dual price of a vertex $i \in V$ that we defined as

$$\begin{aligned}&\mathrm{dual(i)}= {\left\{ \begin{array}{ll}\pi _{n_i}+\rho _{\ell _i}+ \sum \limits _{p\le p_i} \nu _{p}, &{} \text {if}~i=(n_i,\ell _i,p_i) \in O\\ 0, &\quad{} \text {otherwise} \end{array}\right. } \quad \nonumber \\&\qquad + {\left\{ \begin{array}{ll} \mu -c^{f}, &{} \text {if}~i=0\,\text {or}\, i=0'\\ 0, &{} \text {otherwise} \end{array}\right. } . \end{aligned}$$

(3)

Then, the travel time and reduced cost of an arc $(i,j) \in A$ are defined as

$$\begin{aligned}&\bar{t}_{ij} = t_{\ell _i,\ell _j} + {\left\{ \begin{array}{ll} s_i, &{} \text {if}~i=(n_i,\ell _i,p_i) \in O\\ 0, &{} \text {otherwise} \end{array}\right. } \qquad \text {and}\qquad \nonumber \\&\bar{c}_{ij}=c_{\ell _i,\ell _j} - \frac{1}{2}\,(\mathrm{dual}(i) + \mathrm{dual}(j)), \end{aligned}$$

(4)

respectively.

As in all VRPTW variants, we can remove infeasible arcs. Regarding the time-window constraints, we can remove all arcs $(i,j) \in A$ with $a_{\ell _i} + \bar{t}_{ij} > b_{\ell _j}$. Moreover, for $(i,j) \in O\times O$ the arcs with $q_{n_i}+q_{n_j} > Q$ can be eliminated. Note that the conditions in Table 1 already ensure that $n_i \ne n_j$ holds.

Since the routing cost between two options of the same shared delivery location is 0, the order in which these options are served does not matter. In the following, we therefore reduce the symmetry of the network by eliminating the arcs in one direction. Let a total ordering < of all options be given, i.e., either $i<j$ or $j< i$ holds for all $i,j\in O, i\ne j$. The arcs of set $(i,j) \in O\times O$ with $\ell _i=\ell _j$ and $i > j$ can be removed from $A$. Note that with this symmetry reduction we partially exploit location-specific information also in the option-based network.

A partial path $P_i=(0,\dots ,i)$ starts at the depot $0$ and ends at some vertex $i \in V$. The associated label $L_i=(i, C_i, Q_i, T_i, S_i)$ comprises the attributes

i::

the last visited vertex,

$C_i$::

the accumulated reduced cost,

$Q_i$::

the accumulated load,

$T_i$::

the earliest arrival time at i, and

$S_i$::

the set of the requests served along the partial path $P_i$.

For the trivial partial path $(0)$, the initial label is given by $L_0=(0, C_0, Q_0, T_0, S_0) = (0, 0, 0, a_{\ell _0}, \emptyset )$. Labels are propagated over arcs toward the destination vertex with the help of so-called resource extension functions (REFs, Irnich and Desaulniers 2005). An arbitrary label $L_i=(i,C_i, Q_i, T_i, S_i)$ is extended along an arc $(i,j) \in A$ creating a new label $(j,C_j, Q_j, T_j, S_j)$ using the following REFs:

$$\begin{aligned} C_j&= C_i + \bar{c}_{ij} \end{aligned}$$

(5a)

$$\begin{aligned} Q_j&= {\left\{ \begin{array}{ll} Q_i + q_{n_j}, &{} \text {if }j=(n_j,\ell _j,p_j) \in O\\ Q_i, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5b)

$$\begin{aligned} T_j&= \max \{a_{\ell _j}, T_i + \bar{t}_{ij} \} \end{aligned}$$

(5c)

$$\begin{aligned} S_j&= {\left\{ \begin{array}{ll} S_i \cup \{n_j\}, &{} \text {if }j =(n_j,\ell _j,p_j) \in O\\ S_i, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5d)

The extended partial path $P_j = (0,\dots ,i,j)$ is feasible if the following constraints are fulfilled:

$$\begin{aligned}&Q_j \le Q\\&T_j \le b_j\\&n_j \notin S_i, \text {if }j =(n_j,\ell _j,p_j) \in O\end{aligned}$$

To avoid the enumeration of all feasible paths, provable redundant labels are eliminated through a dominance criterion. Let two labels $L_i=(i,C_i, Q_i, T_i, S_i)$ and $L'_{i}=(i,C'_i, {Q_i'}, {T_i'}, {S_i'})$ of two different partial paths ending at the same vertex $i\in V$ be given. Label $L_i$ dominates $L'_i$ if $C_i \le C_i'$, $Q_i \le Q_i'$, $T_i \le T_i'$, and $S_i \subseteq S_i'$ holds. A dominated label can be discarded as long as a dominating label is kept.

Note that the use of a dominance rule always plays with the tradeoff between the effort resulting from less labels to be generated and further extended and the effort from applying the dominance algorithm itself. For the location-based network, we will investigate different dominance strategies varying the vertices at which the dominance is applied. Dominance can be checked at every vertex (full dominance) or only at some vertices (reduced dominance). Examples for the latter are dominance only at option vertices or dominance at all vertices but not at the option vertices of shared delivery locations. These three strategies are computationally evaluated in Sect. 5.2.

4.2.3 Acceleration of the labeling

We apply bidirectional labeling which has become a quasi-standard for accelerating the solution of SPPRC labeling algorithms (Righini and Salani 2006). In a bidirectional labeling algorithm, forward and backward labels are only extended up to a half-way point that splits the domain of a monotone resource into two intervals, one for extension of forward and one for the extension of backward labeling.

Backward labels refer to backward partial paths $(j,\dots ,0')$ staring at a vertex $j\in V$ and ending at the destination depot $0'$. For the trivial backward partial path $(0')$, the initial label is $B_{0'}=(0', C_{0'}, Q_{0'}, T_{0'}, S_{0'}) = (0', 0, 0, b_{\ell _0}, \emptyset )$. Note that the time attribute in the backward case represents an as-late-as-possible schedule. Backward labels are propagated against the arc direction toward the source vertex. An arbitrary label $B_j=(j,C_j, Q_j, T_j, S_j)$ is extended backward over an arc $(i,j) \in A$ creating a new label $B_i=(i,C_i, Q_i, T_i, S_i)$ defined by:

$$\begin{aligned} C_i&= C_j + \bar{c}_{ij} \end{aligned}$$

(6a)

$$\begin{aligned} Q_i&={\left\{ \begin{array}{ll} Q_j + q_{n_i}, &{} \text {if }i=(n_i,\ell _i,p_i) \in O\\ Q_j, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(6b)

$$\begin{aligned} T_i&= \min \{b_{\ell _i}, T_j - \bar{t}_{ij} \} \end{aligned}$$

(6c)

$$\begin{aligned} S_i&= {\left\{ \begin{array}{ll} S_j \cup \{n_i\}, &{} \text {if }i=(n_i,\ell _i,p_i) \in O\\ S_j, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(6d)

The extended partial path $P_i = (i,j,\dots ,0')$ is feasible if $Q_i \le Q$, $T_i \ge a_i$, and $n_i\notin S_j$ if $i \in O$.

Let two backward labels $B_j=(j,C_j, Q_j, T_j, S_j)$ and $B'_j=(j,C'_j, {Q_j'}, {T_j'}, {S_j'})$ of two different backward partial paths starting at the same vertex $j\in V$ be given. Label $L_j$ dominates $L'_j$ if $C_j \le C_j'$, $Q_j \le Q_j'$, $T_j \ge T_j'$, and $S_j \subseteq S_j'$ holds.

The acceleration of a bidirectional labeling approach results from the consideration of a monotone resource, the time attribute here, for which a half-way point H is defined: Forward labels with a time attribute $T> H$ as well as backward labels with a time attribute $T\le H$ are not further extended. This mitigates the often observed combinatorial explosion that happens when partial paths with many arcs are generated. We use a dynamic half-way point as defined in (Tilk et al. 2017) to balance the labels generated in forward and backward labeling.

The merge step considers a forward label $L_i = (i,C_i, Q_i, T_i, S_i)$ for a partial path $(0,\dots ,i)$ and a backward label $B_i = (i,C_i^{bw}, Q_i^{bw}, T_i^{bw}, S_i^{bw})$ for a backward partial path $(i,\dots ,0')$. The two labels can be merged, i.e., the concatenation $(0,\dots ,i,\dots ,0')$ represents a feasible VRPDO route $r$ if the following conditions hold:

$$\begin{aligned}&Q_i+Q_i^{bw} \le {\left\{ \begin{array}{ll} Q- q_{n_i}, &{} \text {if } i =(n_i,\ell _i,p_i)\in O\\ Q, &{} \text {otherwise} \end{array}\right. }\\&T_i \le T_i^{bw}\\&S_i \cap S_i^{bw} = {\left\{ \begin{array}{ll} \{n_i\}, &{} \text {if } i=(n_i,\ell _i,p_i) \in O\\ \emptyset , &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

The conditions take into account that both (5) and (6) model the operations at the merge point i so that correction terms are needed to not double count. The reduced cost of the route $r$ is $\bar{c}_r = C_i + C_i^{bw}$.

The bidirectional labeling takes by far the largest portion of the computation time in the overall BPC algorithm. To further speed up the solution process, two additional techniques are used. First, we adapt the ng-path relaxation (Baldacci et al. 2011) with a more powerful dominance rule that comes at the cost of introducing nonelementary routes as solutions to the pricing subproblem leading to a weaker linear relaxation bound. We adopt the ng-path relaxation as follows: For each location $\ell$, we define a neighborhood $N_\ell \subset N$ that contains the $\kappa$ closest requests to $\ell$ (ties are broken arbitrarily). We define the distance of a request $n$ to a location $\ell$ as $\min \{c_{\ell , \ell _o}: o\in O_{n}^{N}\}$.

Second, the labeling is solved heuristically but typically faster using a limited discrepancy search (Feillet et al. 2007). In the heuristic labeling algorithm, the set of outgoing arcs of each vertex is partitioned in good and bad arcs. Then the total number of bad arcs that can be traversed in a route is limited by some upper bound. Section 5 provides further details.

4.3 Valid inequalities

To strengthen the linear relaxation of (1), two classes of valid inequalities for the VRPTW are adapted: k-path inequalities (KPIs, Kohl et al. 1999) and limited memory subset-row inequalities (LmSRIs, Pecin et al. 2017). We briefly describe them in the following.

Let $S \subseteq V$ be a subset of vertices. We say that S contains a request $n\in N$ if it contains all options associated with $n$, i.e., $O_n\subseteq S$. The KPI for S is given by

$$\begin{aligned} \sum _{r\in \Omega } \sum _{(i,j) \in \delta ^-(S)} e_{ij}^r \lambda _r \ge k(S), \end{aligned}$$

(7)

where $\delta ^-(S)$ is the set of all in-going arcs into vertex set S, $e_{ij}^r$ an integer coefficient counting how often arc $(i,j) \in A$ is used by route r, and k(S) the minimum number of vehicles need to serve all requests contained in S. KPIs are robust, meaning they do not change the structure of the pricing problem: the dual price of the KPI for S must simply be subtracted from the reduced cost of the arcs in $\delta ^-(S)$. The minimum number k(S) of vehicles can be substituted by any lower bound. This lower bound can be determined either considering the demand or time-window constraints. In the first case, we separate the KPIs by applying two shrinking heuristics presented by Belenguer et al. (2000) and Ralphs et al. (2003), the extended shrinking heuristic and the greedy shrinking heuristic, respectively. In the second case, we restrict ourselves to the case $k(S) = 2$ and use the heuristic proposed by Kohl et al. (1999) to generate candidate sets S.

SRIs were first introduced for the VRPTW by Jepsen et al. (2008). Let $S \subset N$ be any subset of requests and let $h_r^S$ be the number of times the route r serves a request in S. As proposed by Jepsen et al. (2008), we restrict ourselves to SRIs defined on three requests, i.e., $|S|= 3$, because violated SRIs of this type can be separated by straightforward enumeration. The corresponding SRI for S is then given by

$$\begin{aligned} \sum _{r\in \Omega } \left\lfloor \frac{h_r^S}{2} \right\rfloor \lambda _r \le 1 . \end{aligned}$$

(8)

SRIs comprise a family of nonrobust cuts meaning that for each SRI with a positive dual value an additional binary attribute has to be added in the labeling algorithm. Moreover, the standard dominance rule of Sect. 4.2.2 has to be modified to effectively cope with the additional attributes (we refer to, Jepsen et al. 2008, for details).

The presence of many SRIs often drastically increases the practical difficulty of the pricing problem. To alleviate these negative effects, Pecin et al. (2017) introduced LmSRIs that use an S-specific memory for the associated binary attribute. The role of the memory is very similar to the neighborhoods in the ng-path relaxation. With a complete memory, LmSRIs are identical to standard SRIs. However, with a S-specific memory, the difficulty of the pricing subproblem is typically reduced. We use the same separation algorithm and vertex memory as described by Pecin et al. .

4.4 Branching

To finally compute integer solutions for (1), branching may be necessary. We use a hierarchical four-level branching scheme and apply a best-first search to determine the next branch-and-bound node to process. Let $( \bar{\lambda } _r)$ be the current solution of the RMP.

First, we branch on the total number of vehicles used, whenever $\bar{F}=\sum _{r\in \Omega } \bar{\lambda } _r$ is fractional. We create two branches enforcing either $\sum _{r\in \Omega } \lambda _r\le \lfloor \bar{F} \rfloor$ or $\sum _{r\in \Omega } \lambda _r\ge \lceil \bar{F} \rceil$.

At the second level, we branch on whether an option is used to fulfill a customer request. We select an option $o^*\in O$ for which the value $\sum _{r\in \Omega } \alpha _{o^* r} \bar{\lambda } _r$ is fractional and closest to 0.5 (ties are broken arbitrarily). Instead of adding a constraint, we directly implement the branching decision by manipulating the vertex set V of the underlying network. In the first branch, option $o^*$ is removed from $V$. In the second branch, all options $\{o\in O: o\ne o^*, n_o=n_{o^*}\}$ are removed from $V$. Moreover, all route variables that do not comply with the branching decision are removed from the RMP.

The third level decides on the integer flow over arcs $(i,j) \in A$. For all arcs $(i,j) \in A$, we compute the value $\bar{e}_{ij} = \sum _{r\in \Omega } e^{r}_{ij} \bar{\lambda } _r$ and select the arc $(i^*, j^*)$ for which the value $\bar{e}_{i^*j^*} - \lfloor \bar{e}_{i^*j^*} \rfloor$ is fractional and closest to 0.5. Two branches are created by adding the constraint $\sum _{r\in \Omega } e^{r}_{i^* j^*}\lambda _r\le \lfloor \bar{e}_{ij} \rfloor$ and $\sum _{r\in \Omega } e^{r}_{i^* j^*}\lambda _r\ge \lceil \bar{e}_{ij} \rceil$ to the RMP, respectively. Note that this branching rule reduces to standard binary arc branching in the option-based network where it can be enforced directly on the underlying network by removing arcs. Note also that, for the option-based network, this branching rule guarantees integer route variables.

For the VRPDO and the location-based network, integer flows on arcs do not guarantee that the route variables are integer. Therefore, the fourth level applies the additional branching rule based on the flow-splitting method proposed by Feillet et al. (2005). Given a subpath $(i,f,e,j)$ with $f\in F$ and $e\in E$, we branch on the flow induced by all routes that exactly traverse this subpath. This flow value must either be zero or one, which can be seen as follows. The flow on the two arcs $(i,f)$ and $(e,j)$ is necessarily binary, because the network structure ensures that i and j are option vertices, i.e., $i,j\in O$. If the two arcs are traversed by a route in this order, the flow on the subpath is one. Otherwise, the two arcs are traversed by different routes or not in the given order so that the flow on the subpath is zero. We always select a subpath $(i^*,f^*,e^*,j^*)$ with flow closest to 0.5. These branching decisions change the structure of the pricing problem and a new resource for each of these branching decision has to be added to the label. It is worth mentioning that, in our computational experiments, it was never necessary to apply the fourth branching rule (for a more detailed discussion, we refer to Desaulniers et al. 1998; Jans 2010).

5 Computational results

The BPC algorithm is implemented in C++ and compiled with MS Visual Studio 2015 into 64-bit single-thread code. The callable library of CPLEX 12.9.0 was used for (re)optimizing the RMPs and to determine an integer solution based on the columns generated so far when reaching the time limit. All results were obtained using a standard PC with an $\hbox {Intel}^\circledR$ Core™ i7-5930K processor clocked at 3.5 GHz and 64 GB RAM running Microsoft Windows 10 Education.

This Computational results section is structured as follows: In Sect. 5.1, we introduce the considered benchmark instances. Section 5.2 compares the results obtained with the two networks used for solving the subproblem. To evaluate the performance of our algorithm, we also solve benchmark instances of the VRPRDL and the VRPHRDL and compare our results with those using the current state-of-the-art algorithm from the literature in Sect. 5.3. Finally, we explore the impact of different service levels and location capacities on total costs, computation times, and number of optimally solved instances in Sect. 5.4.

5.1 Benchmark instances

We test our BPC algorithm described in Sect. 4 on two benchmark sets. The first set is specifically generated for this study, since the VRPDO is a new problem. The instance set is divided into twelve instance classes with ten instances each differing in the number of requests (25 or 50), the number of options (on average 1.5 options per request in class $V$ and two options in class $U$), and the time-window widths (small, medium, or large). Priorities between 1 and 3 are uniformly distributed over the options of a request. All instances have a planning horizon of 12 hours (=720 minutes) and the average time-window width for individual delivery and shared delivery locations is either 60 and 240 (small), 120 and 480 (medium), or 240 and 600 (large) minutes, respectively. Locations are randomly placed in a 50 times 50 grid. Travel costs and times are computed as Euclidean distances, multiplied by 10 and rounded up.

Travel times include a location preparation time, e.g., for parking, which is 6 minutes for individual delivery locations and 4 minutes for shared delivery locations. Note that shared delivery locations such as shops and locker are usually faster accessible. The number of shared delivery locations is $|N|/5$, each location has a capacity of between three and five requests. Options at shared delivery locations have a service time of 2 minutes, while options at individual delivery locations have a service time of 5 minutes. This reflects that usually deliveries to a shop or a locker can be processed faster than those to private homes. The vehicle capacity is 150 and demands are drawn uniformly at random from the interval [10, 20]. We assume that there is a sufficient number of vehicles available at the depot. The fixed costs of a vehicle are set to 100 000 so that they are dominating the travel costs. As a result, we model the hierarchical objective of minimizing the number of vehicles first and the total travel cost second. Note that the service-level parameters ($\beta _p$ for $p=1,2$) are not part of the instance data. The benchmark set is available at https://logistik.bwl.uni-mainz.de/research/benchmarks.

The second benchmark set has been introduced by Reyes et al. (2017) and is divided into 60 instances for the VRPRDL and 60 instances for the VRPHRDL. All 120 instances are randomly generated with a size ranging from 15 to 120 requests clustered to a maximum of six options per request. We adjust the data of this benchmark set as suggested by Ozbaygin et al. (2017) such that the triangle inequality for travel cost and travel times holds.

5.2 Comparison of the option-based and location-based networks

Recall from Sect. 4.2.1 that the pricing problem can be modeled and solved on two different networks, the option-based network and the location-based network. The consideration of the network size (number of arcs) and of potential dominance between labels suggested that the location-based network may be superior over the option-based network.

However, the following experiments are designed with the intention to make the comparison as fair and clear as possible. To this end, we separately analyze the solution of the linear relaxation of the master problem (1) (Sect. 5.2.1) and the behavior in the branch-and-bound tree when cutting and branching take place (Sect. 5.2.2). One point is that results for the linear relaxation are significantly less scattered regarding computation times, because slightly different trajectories of the column-generation processes often lead to completely different branching decisions and hereby to strongly varying branch-and-bound trees.

Moreover, for the linear relaxation, the two networks can be used interchangeably. In contrast, the possibilities of making cutting and branching decisions differ in the two networks. For every arc $a\in A^{\text {loc}}$ in the location-based network, there is a corresponding set $B\subset A^{\text {opt}}$ of arcs in the option-based network so that any constraint considering the flow over a can also be formulated as a flow constraint over B. This correspondence is detailed in Table 3. As a result, any cutting and branching decision formulated as a flow constraint in the location-based network can also be formulated as a flow constraint in the option-based network. However, the reverse is not true, because arcs in the option-based network may refer to subpaths in the location-based network. For example, an option-based arc $(i,j) \in A^{\text {opt}}$ with $\ell _i, \ell _j \in L^{\text {shrd}}$ and $\ell _i \ne \ell _j$ refers to the subpath (i,$f_{\ell _i}$,$e_{\ell _j}$,j) in the location-based network. The use of such a subpath cannot be formulated directly with arc-flow variables of the location-based network. The experiments for producing integer solutions must therefore be designed so that results are still comparable.

Table 3 Correspondence between arcs of the location-based network and arc sets in the option-based network

5.2.1 Linear relaxation results

In the first experiment, we compare the linear-relaxation solutions when either the option-based or the location-based network is used in the pricing problem. We use the first benchmark, i.e., the self-generated VRPDO instances with the service levels of $\beta _1= 0.8$ and $\beta _2 = 0.9$. Pretests have shown that 10 is a reasonable ng-neighborhood size. Furthermore, for the limited discrepancy search, good arcs are determined in each pricing iteration according to the current reduced cost of the arcs. Only one bad arc per path is admissible.

We use four pricing heuristics, where the maximum number of outgoing good arcs per vertex is 2, 4, 8, and 14, respectively. Note that a reduced option-based network and a reduced location-based network are not at all equivalent. In order to eliminate the impact of the heuristical network reduction, all four pricing heuristics use the option-based network. The exact pricing is then performed with the two different networks. Note that typically the exact solution of the pricing problems consumes more than 25 % of the total computation time. This implies that with this setup any substantial impact of the underlying network should become observable.

Finally, the RMP is initialized with one big-M variable that covers all requests, fulfills all priority constraints, and has no impact on other constraints. The time limit is two hours.

Table 4 Aggregated linear relaxation results for the VRPDO benchmark

Table 4 displays aggregated results of the experiments grouped by classes of instances. Columns “#sol” give the number of solved linear relaxations per group of ten instances and “Time (s)” the average consumed computation time in seconds (unsolved instances are considered with 7200 seconds). For the setup described above, the comparison of the option-based network and the location-based network can be found in the columns headlined “Option-based network” and “Location-based network, default strategy.” The same 114 of 120 VRPDO instances are solved. Moreover, the computation times per class and in total are very similar.

We have carefully checked and analyzed the results and have found out the following: The majority of the computation time is spent in the dominance algorithm. Neither the creation of new labels in the extension step, nor the merge procedure of the bidirectional labeling account for a considerable share of the computation time. Moreover, the computation time of the dominance algorithm differs for different types of vertices. For example, in the location-based network, the dominance on average consumes more time at entry and exit vertices than at option vertices.

We have designed a second experiment in order to highlight the impact that the dominance algorithm has on the overall performance. Recall that the default strategy is to apply dominance at every vertex. We define two alternative dominance strategies, one unwise and one clever.

In the unwise strategy, the dominance algorithm is only applied at option vertices. This eliminates the potentially superior possibility of the location-based network to compare paths not comparable in the option-based network (see Example 3). We can expect a worse performance compared to the default strategy.

In the clever strategy, the dominance algorithm is omitted at option vertices of shared delivery locations. The reasoning behind this strategy is that already the initial and inevitable dominance performed at the entry vertex of a shared delivery location eliminates most of the labels that are discarded at an associated option vertex when the default strategy was used. Moreover, the dominance at the exit vertex of a shared delivery location actually ensures the elimination of all extensions of labels that were eliminated at option vertices of the same location in the default strategy. Hence, the clever strategy can only extend useless labels internally at a shared delivery location.

The last two blocks of Table 4 contain aggregated results for the unwise and the clever strategy. These results confirm the expectations, i.e., the column-generation algorithm on the location-based network using the clever strategy is superior to the one using the default strategy and, in turn, the latter is superior to the one using the unwise strategy. The differences are, however, not really large, the average computation times are 695.3 , 701.7 , and 754.8 seconds, respectively. It is more important that even with the clever strategy, the difference to the approach using the option-based network is minor.

5.2.2 Integer results

For the full BPC algorithm, we rely on the clever strategy when using the location-based network. Moreover, the following reasonable parameters have been identified during pretests: A maximum of ten SRIs in total and 5 per cutting iteration are allowed, since pricing problems rapidly become harder after adding SRIs. For KPIs, only sets S that contain not more than 20 requests are allowed. All valid inequalities are separated up to the second level of the branch-and-bound tree. For all branching and cutting constraints, we use the location-based network as a basis since each arc of the location-based network corresponds to a set of arcs in the option-based network as summarized in Table 3. Hence, in that direction all dual prices of arcs can be transferred in a straightforward way.

Table 5 summarizes in aggregated form the results for the integer problem (1). As additional information, columns headlined with “#BB” give the average number of branch-and-bound nodes solved and columns “#SRIs” and “#KPIs” the number of separated valid inequalities of the respective type. The average number of branch-and-bound nodes solved is computed only over those instances that are solved to proven optimality.

As for the linear relaxation, results do not differ significantly for the two network types. In both cases, the BPC algorithm solves 78 instances to optimality in less than 40 minutes on average.

Table 5 Aggregated integer results for the VRPDO benchmark

The integer results, compared over the different classes of instances, reveal the normal behavior of a BPC approach applied to a VRPTW variant: With increasing time-window widths and number of requests, the computation times grow even stronger. While all instances with small time windows and 25 options can be solved exactly within the time limit, medium and large time windows in combination with more options provide more challenging instances. At the end, only three of 20 instances with large time windows and 50 options are solved to optimality. Detailed results for all 120 VRPDO instances can be found in the Appendix in A.

5.3 Results for the VRP with roaming delivery locations

We now report the results we obtained by applying our BPC algorithm to the VRPRDL and VRPHRDL benchmarks. The current state of the art for exactly solving these problems is the branch-and-price algorithm of Ozbaygin et al. (2017).

These benchmarks differ significantly from the VRPDO benchmark, because time windows are more narrow so that instances require less computational effort. Therefore, we adjust our branching and cutting strategies in the following way: First, we allow up to 200 SRIs in total and 10 per round of separation. Second, we do not use the second-level branching rules (deciding whether a specific option is used), since there are many more options per request on average compared to the VRPDO instances making these branching decision less effective. Third, we apply strong branching with up to ten branching candidates (Achterberg 2007). For each candidate, a heuristic evaluation of the lower bound of the child node is performed by using only the first two pricing heuristics to generate routes. We then choose the branching decision that maximizes the minimum of the lower bounds of its children.

Table 6 Comparison with results of Ozbaygin et al. (2017) on VRPRDL and VRPHRDL benchmarks

As done in (Ozbaygin et al. 2017), we set the computation time limit to 2 hours for the instance with up to 60 requests and 6 hours for the 120-request instances. Table 6 shows aggregated results comparing the two solution approaches. The column entries have the same meaning as in the sections before. For the VRPRDL, our BPC solves all instances with an average computation time less than 15 minutes while Ozbaygin et al. (2017) solved 52 of the 60 instances where the largest class however requires more than 4 hours on average. For the VRPHRDL, Ozbaygin et al. (2017) did not report solution times for the 40-request instances. Their branch-and-price algorithm solves 24 of the 40 remaining VRPHRDL instances, while our BPC solves 33 of them and all 40-request instances. Summarizing, we find eight optimal solutions for previously unsolved VRPRDL instances and nine for the VRPHRDL. In comparison over all instances solved by both algorithms, ours is on average more than 20 times faster than the one of Ozbaygin et al. (2017).

5.4 Sensitivity analysis

During the experiments, we observed that the presence of service-level and location-capacity constraints often makes VRPDO instances practically more difficult to solve. Therefore, we perform and present a sensitivity analysis to more precisely explore the impact of different service levels and location capacities on total costs, computation times, and number of optimally solved instances.

Regarding the service-level constraints (1d), we vary the required service level for the first priority between 60 % and 100 % in steps of 4 %, i.e., $\beta _1 \in \{0.6, 0.64, 0.68, \dots , 0.96, 1.0\}$. Note that an increase of 4 % means that one more customer has to be served with first priority for the 25-customer instances and two more for the 50-customer instances. In order to keep the scenarios simple, the second priorities are set to $\beta _2=0$. Regarding the location-capacity constraints (1c), we only consider two scenarios where either capacities remain as given or are completely disregarded. The latter scenario assumes that location capacity is always sufficient. With these parameter variations, we create 22 scenarios for each original VRPDO instance. The one with $\beta _1=1.0$ and without location capacities leads to a standard VRPTW in which all first-priority options are the customers.

To limit the computational burden, we a priori restrict ourselves to those VRPDO instances solved in less than 3600 seconds when setting the service levels to $\beta _1= 0.8$ and $\beta _2 = 0.9$. This results in 69 instances for each scenario. For all scenarios, we set the computation time limit to 3600 seconds.

Fig. 2

Sensitivity analysis, impact of service-level and location-capacity constraints

Figure 2 summarizes the results of the sensitivity analysis. For each scenario, the figure shows the number of instances solved to optimality (in red), the average solution cost (in green), and the average computation time (in blue). Averages over total costs and computation times are computed only over those 41 VRPDO instances that have been solved to optimality in all scenarios. (This avoids a bias toward more difficult instances.) Moreover, the solid curves depict the scenarios with location capacities and the dashed curves those without.

We can see that between 50 and 65 instances per scenario can be solved to optimality (#sol). The trend is that the number of optima computed increases for higher service levels. Moreover, consistently more instances can be solved when locations have restricting capacities. The curve showing average computation times confirms that the (practical) difficulty decreases when the service level increases. For example, the average run times decrease by around 75 % over the 60–100 % service-level interval for the scenarios without capacity. Moreover, the runtime per service level is on average 25 % higher when location capacities are disregarded.

Note also that for average computation times and number of solved instances (#sol), the impact of the service level is strongest, i.e., the absolute slope of the curves is highest, for values of $\beta _1$ between 0.7 and 0.85, both in the capacitated and uncapacitated case in our benchmark.

Regarding the average routing costs, we can see, as expected, that, increasing the service level leads to an increase in total costs (around 22 % higher for $\beta _1=1.0$ than for $\beta _1=0.6$ with location-capacity constraints). With uncapacitated locations, the average cost decreases by around 7 %.

In summary, the practical difficulty of the VRPDO increases when constraints are relaxed. This is true for service-level requirements as well as location-capacity constraints. We interpret these observations in the following way: the possibility to really choose between more options is the main driver of the computation time and therefore also for the capability to actually solve VRPDO instances.

6 Conclusions and outlook

In this paper, we have introduced the vehicle routing problem with delivery options (VRPDO) as an extension of the generalized VRPTW. The extension consists of service-level constraints that consider the given priorities for the different options of fulfilling a delivery request. Moreover, subsets of options may refer to the same physical location for which capacity constraints can be specified. Both service-level and location-capacity constraints are inter-route constraints as defined in (Hempsch and Irnich 2008) and (Irnich et al. 2014, Sect. 1.3.5) making VRPDOs much more difficult than VRPTWs.

This statement is supported by the comprehensive sensitivity analysis that we performed. In a nutshell, the possibility to choose between options is the main driver of the practical difficulty of the VRPDO. We found also that more binding service-level and location-capacity constraints make instances less difficult, i.e., average computation times decrease and within a given time limit relatively more instances can be solved.

Additionally, we applied a sensitivity analysis of the effects of using different service levels and restricting or nonrestricting location capacities. We have seen that otherwise identical instances tend to become easier when location capacities are restricted. Analyzing costs, we conclude that offering customers the choice of different delivery options can reduce routing costs while a reasonable service level can be provided.

We see an important value in the fact that the VRPDO model allows us to quantify the impact that service-level and location-capacity constraints have on the routing costs. Service levels are typically not naturally given, but the result of negotiations between the carrier and its partners or found by trading costs against customer expectations. In this spirit, the new model allows us to more deeply study independencies and to finally make cost-based decisions.

The exact solution approach we propose for solving VRPDO instances is based on branch-price-and-cut (BPC). It utilizes a route-based extended set-partitioning formulation. For generating routes in the pricing subproblem, we proposed a unified labeling algorithm and offered two alternative networks. On the one hand, the option-based network is straightforward because only options and depots are represented by vertices. On the other hand, the location-based network makes use of the fact that often different options share the same physical location. It has the superficial advantages of having fewer arcs and allowing for a stronger dominance than the location-based network. Surprisingly, the use of the location-based network does not pay off in the BPC algorithm, since both networks perform equally well when used for pricing. Our experiments revealed that the computational effort of the dominance algorithm is the key factor in the performance comparison. In the location-based network, the additional effort of checking dominance at the extra entry and exit vertices of each shared delivery location is not overcompensated by the above-named advantages. We suspect another factor to diminish the otherwise positive effects of grouping options of a location. In the VRPDO, one cannot perform the effective preprocessing on the arcs inside the same location as done in (Archetti et al. 2015; Gschwind et al. 2019) for the commodity-constrained split delivery VRP.

The computational experiments have shown that the BPC algorithm is highly competitive. For the comparison of the pricing networks and the sensitivity analysis, we introduced 120 new benchmark instances of the VRPDO with a variety of characteristics such as different number of requests, number of options per request, and time-window widths. We were able to compute provably optimal solutions for 78 of the 120 instances. To compare our BPC algorithm against the only other exact approach for a slightly simpler problem, we solved the benchmark sets for the VRP with roaming delivery locations. On this benchmark, we computed 17 new optimal solutions with an average computation time that is approximately 20 times faster than the former state of the art.

We see several interesting paths for future research extending the here studied VRPDO. First, revenue related aspects could be integrated in the sense that customers may pay for preferred options or carriers may give a discount or bonus when customers accept lower-prioritized delivery options. Second, we have introduced the VRPDO as a static and deterministic problem. However, in reality, location capacities, e.g., at lockers, are not completely known in advance. Over the day, customers retrieve their deliveries from lockers making the capacity time-dependent and stochastic. Third, we have observed that integrality gaps of the VRPDO instances are larger compared, e.g., to those of typical VRPTW instances. Therefore, research on finding tighter formulations with the help of problem-specific valid inequalities is worthwhile.