The spatio-temporal dynamics of interacting genetic incompatibilities. Part I: the case of stacked underdominant clines

Abstract

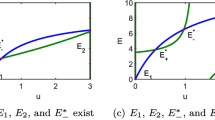
We explore the interaction between two genetic incompatibilities (underdominant loci in diploid organisms) in a population occupying a one-dimensional space. We derive a system of partial differential equations describing the dynamics of allele frequencies and linkage disequilibrium between the two loci, and use a quasi-linkage equilibrium approximation in order to reduce the number of variables. We investigate the solutions of this system and demonstrate the existence of a solution in which the two clines in allele frequency remain stacked together. In the case of asymmetric incompatibilities (i.e. when one homozygote is favored over the other at each locus), these stacked clines propagate in the form of a traveling wave. We obtain an approximation for the speed of this wave which, in particular, is decreased by recombination between the two loci but is always larger than the speed of “one cline alone”.

A Some useful results and tools

We recall the Implicit Function Theorem, see Zeidler (1986, Theorem 4.B) for instance.

Theorem A.1

(Implicit Function Theorem) Let X, Y and Z be three Banach spaces. Suppose that:

• (i) The mapping ${\mathcal {F}}:U\subset X\times Y\rightarrow Z$ is defined on an open neighbourhood U of $(x_0, y_0)\in X\times Y$ and ${\mathcal {F}}(x_0, y_0)=0$.

• (ii) The partial Fréchet derivative of ${\mathcal {F}}$ with respect to y exists on U and

  $$\begin{aligned} {\mathcal {F}}_y(x_0, y_0):Y\rightarrow Z \text { is bijective}. \end{aligned}$$

• (iii) ${\mathcal {F}}$ and ${\mathcal {F}}_y$ are continuous at $(x_0,y_0)$.

Then, the following properties hold:

• (a) Existence and uniqueness. There exist $r_0>0$ and $r>0$ such that, for every $x\in X$ satisfying $\Vert x-x_0\Vert \le r_0$, there exists a unique $y(x)\in Y$ such that $\Vert y-y_0\Vert \le r$ and ${\mathcal {F}}(x, y(x))=0$.

• (b) Continuity. If ${\mathcal {F}}$ is continuous in a neighbourhood of $(x_0,y_0)$, then the mapping $x\mapsto y(x)$ is continuous in a neighbourhood of $x_0$.

• (c) Higher regularity. If ${\mathcal {F}}$ is of the class $C^m$, $1\le m\le \infty$, on a neighbourhood of $(x_0, y_0)$, then $x\mapsto y(x)$ is also of the class $C^m$ in a neighbourhood of $x_0$.

In Sect. 4 we apply Theorem A.1 to the operator ${\mathcal {F}}$ defined in (26), with $X=\mathbb R$, $x=\varepsilon$, $x_0=0$, $Y=\mathbb R\times C^{2,\alpha }_\mu (\mathbb R)$, $y=(c,h)$, $y_0=(0,0)$, and $Z=C^{0,\alpha }_\mu (\mathbb R)$.

Next, we quote some results on Fredholm operators. Let us recall that the operator L has the Fredholm property with index 0 if $\ker L$ has a finite dimension, $\mathrm{rg}\,L$ is closed and has finite codimension and

$$\begin{aligned} \text { ind } L:=\dim \ker L-\mathrm{codim}\,\mathrm{rg}\,L=0. \end{aligned}$$

In particular, since its range is closed, such an operator is normally solvable:

$$\begin{aligned} \exists u\ne 0, Lu=f \quad \Leftrightarrow \quad \forall \phi \in (\mathrm{rg}\,L)^\perp , \phi (f)=0, \end{aligned}$$

and remark that $(\mathrm{rg}\,L)^\perp = \ker L^*$.

We recall below a theorem from Volpert et al. (1999, Theorem 2.1 and Remark p787).

Theorem A.2

(Fredholm property on the line) For $0<\alpha <1$, consider the operator $L:C^{2,\alpha }(\mathbb R)\rightarrow C^\alpha ({\mathbb {R}})$ defined by

$$\begin{aligned} Lu:=a(x)u''+b(x)u'+c(x)u, \end{aligned}$$

where the coefficients a(x), b(x), c(x) are smooth, and $a(x)\ge a_0$ for some $a_0>0$. Assume further that the coefficients a(x), b(x), and c(x) have finite limits as $x\rightarrow \pm \infty$ and denote

$$\begin{aligned} a^\pm :=\lim _{x\rightarrow \pm \infty }a(x), \qquad b^\pm :=\lim _{x\rightarrow \pm \infty }b(x), \qquad c^\pm :=\lim _{x\rightarrow \pm \infty }c(x). \end{aligned}$$

Finally, let us define the limiting operators

$$\begin{aligned} L^\pm u:=a^\pm u''+b^\pm u'+c^\pm u, \end{aligned}$$

and assume that for any $\lambda \ge 0$, the equation

$$\begin{aligned} L^\pm u-\lambda u=0 \end{aligned}$$

has no nontrivial solution in $C^{2,\alpha }({\mathbb {R}})$.

Then L is Fredholm with index 0.

Let us also recall a Fredholm property result for second-order ordinary differential equations, see the monograph of Volpert (2011, Chapter 9, Theorem 2.4 p. 366).

Theorem A.3

(Fredholm property for second-order ODEs) With the notations of Theorem A.2, the operator L is Fredholm provided the two equations

$$\begin{aligned} -a^\pm \xi ^2 + b^\pm i\xi + c^\pm =0 \end{aligned}$$

(39)

has no real solution $\xi \in {\mathbb {R}}$. In this case the index of L is given by the formula

$$\begin{aligned} \text { ind } L=\kappa ^+-\kappa ^-, \end{aligned}$$

where $\kappa ^\pm$ is the number of complex solutions to the characteristic equation

$$\begin{aligned} a^\pm X^2-b^\pm X+c^\pm =0 \end{aligned}$$

(40)

which have a positive real part.

Remark A.4

(Fredholm property in weighted Hölder spaces) We cannot directly apply Theorems A.2 and A.3 to our situation since we consider the operator L acting from $C^{2, \alpha }_\mu (\mathbb R)$ into $C^\alpha _\mu (\mathbb R)$, and not from $C^{2,\alpha }(\mathbb R)$ into $C^{0,\alpha }(\mathbb R)$. To circumvent this, we consider the operator $L^\mu :C^{2, \alpha }({\mathbb {R}})\rightarrow C^\alpha ({\mathbb {R}})$ defined by:

$$\begin{aligned} L^\mu (u)&:=e^{\mu \sqrt{1+x^2}}L\left( ue^{-\mu \sqrt{1+x^2}}\right) \nonumber \\&=a(x)u'' + \left[ \frac{-2\mu x}{\sqrt{1+x^2}}a(x)+b(x)\right] u'\nonumber \\&\quad + \left[ \left( \frac{\mu ^2 x^2}{1+x^2}+ \frac{\mu x^2}{(1+x^2)^{\frac{3}{2}}}-\frac{\mu }{\sqrt{1+x^2}} \right) a(x)- \frac{\mu x}{\sqrt{1+x^{2}}}b(x)+c(x)\right] u. \end{aligned}$$

(41)

Since $T_\mu :u\in C^{2, \alpha }_\mu ({\mathbb {R}}) \mapsto e^{\mu \sqrt{1+x^2}}u\in C^{2, \alpha }({\mathbb {R}})$ is continuously invertible, and $T_\mu ^{-1}:u\in C^{0, \alpha }({\mathbb {R}}) \mapsto e^{-\mu \sqrt{1+x^2}}u\in C^{0, \alpha }_\mu ({\mathbb {R}})$ is continuously invertible, the map $L=T_\mu ^{-1}L^\mu T_\mu$ shares the same Fredholm property and index as $L^\mu$. As a result, if $L^\mu$ satisfies the assumptions of Theorem A.2, or Theorem A.3, then L is a Fredholm operator with the same index as that of $L^\mu$.