Skip to main content
SpringerLink
Log in

Modelling diapause in mosquito population growth

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

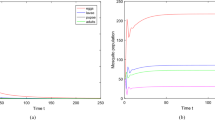
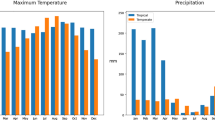
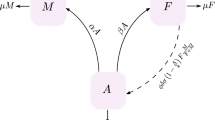
Diapause, a period of arrested development caused by adverse environmental conditions, serves as a key survival mechanism for insects and other invertebrate organisms in temperate and subtropical areas. In this paper, a novel modelling framework, motivated by mosquito species, is proposed to investigate the effects of diapause on seasonal population growth, where the diapause period is taken as an independent growth process, during which the population dynamics are completely different from that in the normal developmental and post-diapause periods. More specifically, the annual growth period is divided into three intervals, and the population dynamics during each interval are described by different sets of equations. We formulate two models of delay differential equations (DDE) to explicitly describe mosquito population growth with a single diapausing stage, either immature or adult. These two models can be further unified into one DDE model, on which the well-posedness of the solutions and the global stability of the trivial and positive periodic solutions in terms of an index \({\mathcal {R}}\) are analysed. The seasonal population abundances of two temperate mosquito species with different diapausing stages are simulated to identify the essential role on population persistence that diapause plays and predict that killing mosquitoes during the diapause period can lower but fail to prevent the occurrence of peak abundance in the following season. Instead, culling mosquitoes during the normal growth period is much more efficient to decrease the outbreak size. Our modelling framework may shed light on the diapause-induced variations in spatiotemporal distributions of different mosquito species.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Alekseev VR, De Stasio B, Gilbert JJ (2007) Diapause in aquatic invertebrates: theory and human use. Springer, New York

    Book  Google Scholar 

  • Beck-Johnson LM, Nelson WA, Paaijmans KP, Read AF, Thomas MB, Bjrnstad ON (2013) The effect of temperature on Anopheles mosquito population dynamics and the potential for malaria transmission. PLoS One 8(11):e79276

    Article  Google Scholar 

  • Belozerov VN (1982) Diapause and biological rhythms in ticks. In: Obenchain FD, Galun R (eds) Physiology of ticks: current themes in tropical science. Pergamon Press, Oxford, pp 469–500

    Chapter  Google Scholar 

  • Beverton RJ, Holt SJ (2012) On the dynamics of exploited fish populations. Springer, New York

    Google Scholar 

  • Bradshaw ME, Holzapfel CM (1990) Resource limitation, habitat segregation, and species interactions of British tree-hole mosquitoes in nature. Oecologia 90(2):227–237

    Article  Google Scholar 

  • Bradshaw WE (1976) Geography of photoperiodic response in diapausing mosquito. Nature 262:384–386

    Article  Google Scholar 

  • Brauer F, Castillo-Chavez C (2001) Mathematical models in population biology and epidemiology. Springer, New York

    Book  MATH  Google Scholar 

  • Buth JL, Brust RA, Ellis RA (1990) Development time, oviposition activity and onset of diapause in Culex tarsalis, Culex restuans and Culiseta inornata in southern Manitoba. J Am Mosq Control Assoc 6(1):55–63

    Google Scholar 

  • Cailly P, Tran A, Balenghien T, L’Ambert G, Toty C, Ezanno P (2012) A climate-driven abundance model to assess mosquito control strategies. Ecol Model 227:7–17

    Article  Google Scholar 

  • Cruz-Pacheco G, Esteva L, Montaõ-Hirose JA, Vargas C (2005) Modelling the dynamics of West Nile virus. Bull Math Biol 67(6):1157–1172

    Article  MathSciNet  MATH  Google Scholar 

  • Cushing JM (1998) An introduction to structured population dynamics. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  • Daszak P, Cunningham AA, Hyatt AD (2000) Emerging infectious diseases of wildlife-threats to biodiversity and human health. Science 287(5452):443–449

    Article  Google Scholar 

  • Denlinger DL (2002) Regulation of diapause. Annu Rev Entomol 47(1):93–122

    Article  Google Scholar 

  • Denlinger DL, Armbruster PA (2014) Mosquito diapause. Annu Rev Entomol 59:73–93

    Article  Google Scholar 

  • Denlinger DL, Lee RE Jr (2010) Low temperature biology of insects. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Denlinger DL, Yocum GD, Rinehart JP, Gilbert LI (2004) Hormonal control of diapause. In: Gilbert LI (ed) Insect endocrinology. Academic, San Diego, CA, pp 430–463

    Google Scholar 

  • Ewing DA, Cobbold CA, Purse BV, Nunn MA, White SM (2016) Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J Theor Biol 400:65–79

    Article  MathSciNet  MATH  Google Scholar 

  • Fang J, Gourley SA, Lou Y (2016) Stage-structured models of intra- and inter-specific competition within age classes. J Differ Equ 260(2):1918–1953

    Article  MathSciNet  MATH  Google Scholar 

  • Flannagan RD, Tammariello SP, Joplin KH, Cikra-Ireland RA, Yocum GD, Denlinger DL (1998) Diapause-specific gene expression in pupae of the flesh fly Sarcophaga crassipalpis. Proc Natl Acad Sci USA 95(10):5616–5620

    Article  Google Scholar 

  • Gong H, DeGaetano AT, Harrington LC (2011) Climate-based models for West Nile Culex mosquito vectors in the Northeastern US. Int J Biometeorol 55(3):435–446

    Article  Google Scholar 

  • Gourley SA, Wu J (2006) Delayed non-local diffusive systems in biological invasion and disease spread. In: Nonlinear dynamics and evolution equations, American Mathematical Society, pp 137–200

  • Gurney W, Nisbet RM, Lawton JH (1983) The systematic formulation of tractable single-species models incorporating age structure. J Anim Ecol 52(2):479–495

    Article  Google Scholar 

  • Hahn DA, Denlinger DL (2011) Energetics of insect diapause. Annu Rev Entomol 56:103–121

    Article  Google Scholar 

  • Hanson SM (1995) Field overwinter survivorship of Aedes albopictus eggs in Japan. J Am Mosq Control Assoc 11(3):354–357

    Google Scholar 

  • Hanson SM, Craig GB Jr (1994) Cold acclimation, diapause, and geographic origin affect cold hardiness in eggs of Aedes albopictus (Diptera: Culicidae). J Med Entomol 31(2):192–201

    Article  Google Scholar 

  • Hasegawa K (1957) The diapause hormone of the silkworm. Bombyx mori. Nature 179(4573):1300–1301

    Article  Google Scholar 

  • Hodek I, van Emden HF, Honek A (2012) Ecology and behaviour of the ladybird beetles (Coccinellidae). Wiley, Chichester

    Book  Google Scholar 

  • Jia P, Lu L, Chen X, Chen J, Guo L, Yu X, Liu Q (2016) A climate-driven mechanistic population model of Aedes albopictus with diapause. Parasit Vectors 9(1):175

    Article  Google Scholar 

  • Koštál V (2006) Eco-physiological phases of insect diapause. J Insect Physiol 52(2):113–127

    Article  MathSciNet  Google Scholar 

  • Lakovic M, Poethke HJ, Hovestadt T (2015) Dispersal timing: emigration of insects living in patchy environments. PLoS One 10(7):e0128672

    Article  Google Scholar 

  • Laing JE, Corrigan JE (1995) Diapause induction and post-diapause emergence in Trichogramma minutum Riley (Hymenoptera: Trichogrammatidae): the role of host species, temperature, and photoperiod. Can Entomol 127(1):103–110

    Article  Google Scholar 

  • Leisnham PT, Sala LM, Juliano SA (2008) Geographic variation in adult survival and reproductive tactics of the mosquito Aedes albopictus. J Med Entomol 45(2):210–221

    Article  Google Scholar 

  • Liang X, Zhang L, Zhao X-Q, Basic reproduction ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease), J Dyn Diff Equat.https://doi.org/10.1007/s10884-017-9601-7

  • Liu K, Lou Y, Wu J (2017) Analysis of an age structured model for tick populations subject to seasonal effects. J Diff Equ 263:2078–2112

    Article  MathSciNet  MATH  Google Scholar 

  • Lou Y, Zhao X-Q (2010) A climate-based malaria transmission model with structured vector population. SIAM J Appl Math 70(6):2023–2044

    Article  MathSciNet  MATH  Google Scholar 

  • Lou Y, Zhao X-Q (2017) A theoretical approach to understanding population dynamics with seasonal developmental durations. J Nonlinear Sci 27(2):573–603

    Article  MathSciNet  MATH  Google Scholar 

  • Martin RH (1976) Nonlinear operators and differential equations in Banach spaces. Wiley, New York

    Google Scholar 

  • Metz JA, Diekmann O (1986) The dynamics of physiologically structured populations. Springer, Berlin, Germany

    Book  MATH  Google Scholar 

  • Marini G, Guzzetta G, Baldacchino F, Arnoldi D, Montarsi F, Capelli G, Rizzoli A, Merler S, Rosà R (2017) The effect of interspecific competition on the temporal dynamics of Aedes albopictus and Culex pipiens. Parasit Vectors 10(1):102

    Article  Google Scholar 

  • Pawelek KA, Niehaus P, Salmeron C, Hager EJ, Hunt GJ (2014) Modelling dynamics of Culex pipiens complex populations and assessing abatement strategies for West Nile Virus. PLoS One 9(9):e108452

    Article  Google Scholar 

  • Pritchard G (1989) The roles of temperature and diapause in the life history of a temperate-zone dragonfly: Argia vivida (Odonata: Coenagrionidae). Ecol Entomol 14(1):99–108

    Article  Google Scholar 

  • Ragland GJ, Denlinger DL, Hahn DA (2010) Mechanisms of suspended animation are revealed by transcript profiling of diapause in the flesh fly. Proc Natl Acad Sci USA 107:14909–14914

    Article  Google Scholar 

  • Rinehart JP, Robich RM, Denlinger DL (2006) Enhanced cold and desiccation tolerance in diapausing adults of Culex pipiens, and a role for Hsp70 in response to cold shock but not as a component of the diapause program. J Med Entomol 43(4):713–722

    Article  Google Scholar 

  • Silver JB (2007) Mosquito ecology: field sampling methods. Springer, New York

    Google Scholar 

  • Sim C, Denlinger DL (2008) Insulin signalling and FOXO regulate the overwintering diapause of the mosquito Culex pipiens. Proc Natl Acad Sci USA 105(18):6777–6781

    Article  Google Scholar 

  • Spielman A (2001) Structure and seasonality of nearctic Culex pipiens populations. Ann NY Acad Sci 951(1):220–234

    Article  Google Scholar 

  • Smith DL, Perkins TA, Reiner RC Jr, Barker CM, Niu T, Chaves LF, Ellis AM, George DB, Le Menach A, Pulliam J et al (2014) Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans R Soc Trop Med Hyg 108(4):185–197

    Article  Google Scholar 

  • Smith HL (1993) Reduction of structured population models to threshold-type delay equations and functional differential equations: a case study. Math Biosci 113(1):1–23

    Article  MathSciNet  MATH  Google Scholar 

  • Smith HL (2010) An introduction to delay differential equations with applications to the life sciences. Springer, New York

    Google Scholar 

  • Tauber MJ, Tauber CA (1976) Insect seasonality: diapause maintenance, termination, and postdiapause development. Annu Rev Entomol 21(1):81–107

    Article  Google Scholar 

  • Tauber MJ, Tauber CA, Masaki S (1986) Seasonal adaptations of insects. Oxford University Press, Oxford

    Google Scholar 

  • Toma L, Severini F, Di Luca M, Bella A, Romi R (2003) Seasonal patterns of oviposition and egg hatching rate of Aedes albopictus in Rome. J Am Mosq Control Assoc 19(1):19–22

    Google Scholar 

  • Tran A, L’Ambert G, Lacour G, Benoît R, Demarchi M, Cros M, Cailly P, Aubry-Kientz M, Balenghien T, Ezanno P (2013) A rainfall-and temperature-driven abundance model for Aedes albopictus populations. Int J Environ Res Public Health 10(5):1698–1719

    Article  Google Scholar 

  • Tsurim I, Silberbush A, Ovadia O, Blaustein L, Margalith Y (2013) Inter-and intra-specific density-dependent effects on life history and development strategies of larval mosquitoes. PLoS ONE 8(3):e57875

    Article  Google Scholar 

  • Vinogradova EB (2007) Diapause in aquatic insects, with emphasis on mosquitoes. In: Alekseev VR, De Stasio B, Gilbert JJ (eds) Diapause in aquatic invertebrates. Springer, London, pp 83–113

    Chapter  Google Scholar 

  • Wang X, Zhao X-Q (2017) A malaria transmission model with temperature-dependent incubation period. Bull Math Biol 79(5):1155–1182

    Article  MathSciNet  MATH  Google Scholar 

  • Wang X, Zou X (2018) Threshold dynamics of a temperature-dependent stage-structured mosquito population model with nested delays. Bull Math Biol 80(7):1962–1987

    Article  MathSciNet  MATH  Google Scholar 

  • Wu X, Magpantay FMG, Wu J, Zou X (2015) Stage-structured population systems with temporally periodic delay. Math Methods Appl Sci 38:3464–3481

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang X, Wu X, Wu J (2017) Critical contact rate for vector-host-pathogen oscillation involving co-feeding and diapause. J Biol Syst 25:657–675

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao X-Q (2017) Basic reproduction ratios for periodic compartmental models with time delay. J Dyn Diff Equat 29:67–82

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao X-Q (2017) Dynamical systems in population biology. Springer, New York

    Book  MATH  Google Scholar 

  • Zhao X-Q, Jing ZJ (1996) Global asymptotic behaviour in some cooperative systems of functional differential equations. Can Appl Math Q 4(4):421–444

    MATH  Google Scholar 

Download references

Acknowledgements

The work of Y. L. and K. L. was supported in part by the Research Grants Council (PolyU 153277/16P) of Hong Kong. D. G. was supported by NSFC (11601336), Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning (TP2015050), and Shanghai Gaofeng Project for University Academic Development Program. S. R. was supported by National Science Foundation (DMS-1853622) and Centre for Disease Control and Prevention “Southeastern Regional Centre of Excellence in Vector-Borne Diseases: The Gateway Program” (U01CK000510). The authors would like to thank Dr. Hongying Shu for helpful discussions on this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong

    Yijun Lou, Kaihui Liu & Daihai He

  2. Mathematics and Science College, Shanghai Normal University, Shanghai, 200234, China

    Daozhou Gao

  3. Department of Mathematics, University of Miami, Coral Gables, FL, 33146, USA

    Shigui Ruan

Authors
  1. Yijun Lou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kaihui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Daihai He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daozhou Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shigui Ruan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yijun Lou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lou, Y., Liu, K., He, D. et al. Modelling diapause in mosquito population growth. J. Math. Biol. 78, 2259–2288 (2019). https://doi.org/10.1007/s00285-019-01343-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-019-01343-6

Keywords

Mathematics Subject Classification

Search

Navigation