Intermediates, catalysts, persistence, and boundary steady states

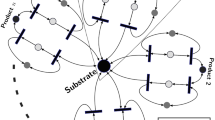
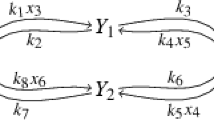
Abstract

For dynamical systems arising from chemical reaction networks, persistence is the property that each species concentration remains positively bounded away from zero, as long as species concentrations were all positive in the beginning. We describe two graphical procedures for simplifying reaction networks without breaking known necessary or sufficient conditions for persistence, by iteratively removing so-called intermediates and catalysts from the network. The procedures are easy to apply and, in many cases, lead to highly simplified network structures, such as monomolecular networks. For specific classes of reaction networks, we show that these conditions for persistence are equivalent to one another. Furthermore, they can also be characterized by easily checkable strong connectivity properties of a related graph. In particular, this is the case for (conservative) monomolecular networks, as well as cascades of a large class of post-translational modification systems (of which the MAPK cascade and the n-site futile cycle are prominent examples). Since one of the aforementioned sufficient conditions for persistence precludes the existence of boundary steady states, our method also provides a graphical tool to check for that.

Appendix: Technical results

1.1 Proof of Proposition 2

Proposition 2(i). We prove that if G is persistent, then it is bounded-persistent. Take any $s_0 \gg 0$. If $\omega (s_0) = \varnothing$, then we have nothing to prove. So, suppose $\omega (s_0) \ne \varnothing$. Choose any $s \in \omega (s_0)$, and a sequence $(t_k)_{k \in {\mathbb {N}}}$ going to infinity in ${\mathbb {R}}_{\geqslant 0}$ such that

$$\begin{aligned} \lim _{k \rightarrow \infty } \sigma (t_k, s_0) = s. \end{aligned}$$

Then

$$\begin{aligned} s_i = \displaystyle \liminf _{k \rightarrow \infty } \sigma _i(t_k, s_0) \geqslant \displaystyle \liminf _{t \rightarrow \infty } \sigma _i(t, s_0) > 0, \quad \forall i \in [n]. \end{aligned}$$

In particular, $s \notin \partial {\mathbb {R}}_{\geqslant 0}^n$. Thus, $\omega (s_0) \cap \partial {\mathbb {R}}_{\geqslant 0}^n = \varnothing$. $\square$

Proposition 2(ii). The converse of Proposition 2(i) is not true. However, (4) holds for bounded trajectories of bounded-persistent networks—hence the terminology.

Since each stoichiometric compatibility class of a conservative network is compact (Horn and Jackson 1972, Appendix 1), every solution of (3) is bounded. The proof of Proposition 2(ii) then follows from the next lemma.

Lemma 17

Suppose a solution $\sigma (\cdot , s_0):{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}^n$ of a bounded-persistent reaction network is bounded. Then

$$\begin{aligned} \liminf _{t \rightarrow \infty } \sigma _i(t, s_0) > 0, \quad \forall i \in [n]. \end{aligned}$$

(26)

Proof

Suppose on contrary that

$$\begin{aligned} \liminf _{t \rightarrow \infty } \sigma _{i_0}(t, s_0) = 0 \end{aligned}$$

for some $i_0 \in [n]$. Then

$$\begin{aligned} \lim _{k \rightarrow \infty } \sigma _{i_0}(t_k, s_0) = 0 \end{aligned}$$

along some sequence $(t_k)_{k \in {\mathbb {N}}}$ going to infinity in ${\mathbb {R}}_{\geqslant 0}$. In virtue of boundedness, by passing into a subsequence, if necessary, we may assume without loss of generality that $(\sigma (t_k, s_0))_{k \in {\mathbb {N}}}$ converges, say,

$$\begin{aligned} \lim _{k \rightarrow \infty } \sigma (t_k, s_0) = s_\infty . \end{aligned}$$

We have $s_\infty \in \omega (s_0)$ by definition. But since the $i_0^{th}$ coordinate of $s_\infty$ is zero, we conclude that $s_\infty \in \partial {\mathbb {R}}_{\geqslant 0}^n$ also. This contradicts the bounded-persistence hypothesis that $\omega (s_0) \cap \partial {\mathbb {R}}_{\geqslant 0}^n = \varnothing$. Thus, (26) must hold. $\square$

Proposition 2(iii). See (Angeli et al. 2007, Theorem 1). $\square$

Proposition 2(iv). The same argument as in Deshpande and Gopalkrishnan (2014), Theorem  6.2 works under our weaker assumptions on the reaction rates. $\square$

Proposition 2(v). We define the zero coordinate set of a point $s \in {\mathbb {R}}_{\geqslant 0}^n$, with respect to some given reaction network G, as the set

$$\begin{aligned} Z(s) := \{S_i \in \mathcal{S}\, | \ s_i = 0\} = \mathcal{S}\backslash {{\mathrm{supp}}}\, s. \end{aligned}$$

Thus, a point $s \in {\mathbb {R}}_{\geqslant 0}^n$ is a boundary steady state if, and only if $Z(s) \ne \varnothing$.

Let $s_0$ be a boundary steady state of G. By Lemma 18 below and our hypothesis, the zero coordinate set $Z(s_0)$ of $s_0$ is a noncritical siphon. It follows by the equivalence between items 1 and 3 in Deshpande and Gopalkrishnan (2014), Theorem  3.7 that $(s_0 + S) \cap {\mathbb {R}}_{\geqslant 0}^n\ne \varnothing$.

The next lemma was proved in Shiu and Sturmfels (2010) for mass-action kinetics. The same argument holds under (r2), and we provide the details for the sake of completeness.

Lemma 18

Let G be a reaction network. If $s_0$ is a boundary steady state, then $Z(s_0)$ is a siphon.

Proof

Pick any $S_{i} \in Z(s_0)$. Consider the set $\mathcal{J}_{i}$ of indices $j \in [m]$ such that $R_j$ is a reaction having $S_{i}$ as one of its products, but not one of its reactants; that is,

$$\begin{aligned} \mathcal{J}_{i} := \{j \in [m]\,|\ \alpha '_{ij} > 0 \quad \text {and} \quad \alpha _{ij} = 0\}. \end{aligned}$$

If $\mathcal{J}_i \ne \varnothing$, we need to show that $Z(s_0)$ contains some species in the reactant of each $R_j$ such that $j\in \mathcal{J}_{i}$. Since $s_0$ is a steady state, we have

$$\begin{aligned} \sum _{j = 1}^m (\alpha '_{ij} - \alpha _{ij}) r_j(s_0) = 0. \end{aligned}$$

(27)

For each $j \notin \mathcal{J}_{i}$, we either have $\alpha _{ij} > 0$ (in which case $r_j(s_0) = 0$ by (r2) since $(s_0)_i=0$) or $\alpha '_{ij} = \alpha _{ij}=0$. Hence the sum in (27) can be simplified as

$$\begin{aligned} \sum _{j \in \mathcal{J}_{i}} \alpha '_{ij} r_j(s_0) = 0. \end{aligned}$$

Since $\alpha '_{ij} > 0$ for every $j \in \mathcal{J}_i$ by construction, we conclude that $r_j(s_0) = 0$ for all $j \in \mathcal{J}_{i}$. It then follows from (r2) that $\alpha _{i(j)j} > 0$ for some $i(j) \in [n]$ such that $S_{i(j)} \in Z(s_0)$, that is, one of the reactants of $R_j$ belongs to $Z(s_0)$ for each $j \in \mathcal{J}_{i}$. This completes the proof that $Z(s_0)$ is a siphon. $\square$

1.2 Drainable and self-replicable siphons

The next result shows that the concepts of drainable and self-replicable sets in Definition 5 are, respectively, equivalent to the concepts of drainable and self-replicable sets in Deshpande and Gopalkrishnan (2014), Definition 3.1 (called here DG-drainable and DG-self-replicable).

Given a reaction network $G = (\mathcal{S}, \mathcal{C}, \mathcal{R})$, we define a G-reaction pathway to be any sequence $y(0), y(1), \ldots , y(k) \in {\mathbb {R}}_{\geqslant 0}^n$ such that

$$\begin{aligned} y(0)&= y_1 + w_1, \nonumber \\ y(j)&= y_j' + w_j = y_{j+1} + w_{j+1}, \quad j = 1, \ldots , k-1, \nonumber \\ y(k)&= y_k' + w_k, \end{aligned}$$

(28)

for some $y_1, y_1', w_1, \ldots , y_k, y_k', w_k \in {\mathbb {R}}_{\geqslant 0}^n$ such that $y_1 \rightarrow y_1, \ldots , y_k \rightarrow y_k' \in \mathcal{R}$. Note that

$$\begin{aligned} y(k) - y(0) = \sum _{j=1}^k \big ( y(j) - y(j-1) \big ) = \sum _{j=1}^k (y_j' + w_j - y_j - w_j) = \sum _{j=1}^k (y_j' - y_j). \end{aligned}$$

(29)

A nonempty subset $\varSigma \subseteq \mathcal{S}$ is said to be DG-drainable (respectively, DG-self-replicable) if there exists a G-reaction pathway $y(0), y(1), \ldots , y(k)$ such that $\big (y(k) - y(0) \big )_i < 0$ (respectively, $\big (y(k) - y(0) \big )_i > 0$), for every $i \in [n]$ such that $S_i \in \varSigma$.

Proposition 6

Let $G = (\mathcal{S}, \mathcal{C}, \mathcal{R})$ be a reaction network. A subset of $\mathcal{S}$ is drainable (respectively, self-replicable) if, and only if it is DG-drainable (respectively, DG-self-replicable).

Proof

$(\Leftarrow )$ Follows from (29) and Definition 5.

$(\Rightarrow )$ Let $y_1 \rightarrow y_1', \ldots , y_k \rightarrow y_k' \in \mathcal{R}$ be any sequence of reactions. Define, iteratively,

$$\begin{aligned} w_1 := y_2+\dots +y_k, \quad \text {and}\quad w_{j+1} := y_j' + w_j - y_{j+1}, \quad j=1,\dots ,k-1. \end{aligned}$$

By construction, $\omega _j\in {\mathbb {R}}_{\geqslant 0}^n$ for all $j=1,\dots ,k$, and $y_{j+1}+w_{j+1} = y'_j + w_j$ for all $j=1,\dots ,k-1$. We can construct a G-reaction pathway $y(0), y(1), \ldots , y(k) \in {\mathbb {R}}_{\geqslant 0}^n$ from $y_1, y_1', w_1, \ldots , y_k, y_k', w_k$ using (28). The implication now follows again from (29) and Definition 5. $\square$