Some Inequalities Involving Perimeter and Torsional Rigidity

Abstract

We consider shape functionals of the form $F_q(\Omega )=P(\Omega )T^q(\Omega )$ on the class of open sets of prescribed Lebesgue measure. Here $q>0$ is fixed, $P(\Omega )$ denotes the perimeter of $\Omega$ and $T(\Omega )$ is the torsional rigidity of $\Omega$. The minimization and maximization of $F_q(\Omega )$ is considered on various classes of admissible domains $\Omega$: in the class $\mathcal {A}_{all}$ of all domains, in the class $\mathcal {A}_{convex}$ of convex domains, and in the class $\mathcal {A}_{thin}$ of thin domains.

1 Introduction

In this paper, given an open set $\Omega \subset \mathbb {R}^d$ with finite Lebesgue measure, we consider the quantities

$$\begin{aligned} \begin{aligned}&P(\Omega )=\text {perimeter of }\Omega ;\\&T(\Omega )=\text {torsional rigidity of }\Omega . \end{aligned} \end{aligned}$$

The perimeter $P(\Omega )$ is defined according to the De Giorgi formula

$$\begin{aligned} P(\Omega )=\sup \left\{ \int _\Omega {{\,\mathrm{div}\,}}\phi \,dx\ :\ \phi \in C^1_c(\mathbb {R}^d;\mathbb {R}^d),\ \Vert \phi \Vert _{L^\infty (\mathbb {R}^d)}\le 1\right\} . \end{aligned}$$

The scaling property of the perimeter is

$$\begin{aligned} P(t\Omega )=t^{d-1}P(\Omega )\qquad \text {for every }t>0 \end{aligned}$$

and the relation between $P(\Omega )$ and the Lebesgue measure $|\Omega |$ is the well-known isoperimetric inequality:

$$\begin{aligned} \frac{P(\Omega )}{|\Omega |^{(d-1)/d}}\ge \frac{P(B)}{|B|^{(d-1)/d}} \end{aligned}$$

(1.1)

where B is any ball in $\mathbb {R}^d$. In addition, the inequality above becomes an equality if and only if $\Omega$ is a ball (up to sets of Lebesgue measure zero).

The torsional rigidity $T(\Omega )$ is defined as

$$\begin{aligned} T(\Omega )=\int _\Omega u\,dx \end{aligned}$$

where u is the unique solution of the PDE

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u=1&{}\text {in }\Omega ,\\ u\in H^1_0(\Omega ). \end{array}\right. } \end{aligned}$$

(1.2)

Equivalently, $T(\Omega )$ can be characterized through the maximization problem

$$\begin{aligned} T(\Omega )=\max \Big \{\Big [\int _\Omega u\,dx\Big ]^2\Big [\int _\Omega |\nabla u|^2\,dx\Big ]^{-1}\ :\ u\in H^1_0(\Omega )\setminus \{0\}\Big \}. \end{aligned}$$

Moreover T is increasing with respect to the set inclusion, that is

$$\begin{aligned} \Omega _1\subset \Omega _2\Longrightarrow T(\Omega _1)\le T(\Omega _2) \end{aligned}$$

and T is additive on disjoint families of open sets. The scaling property of the torsional rigidity is

$$\begin{aligned} T(t\Omega )=t^{d+2}T(\Omega ),\qquad \text {for every }t>0, \end{aligned}$$

and the relation between $T(\Omega )$ and the Lebesgue measure $|\Omega |$ is the well-known Saint-Venant inequality (see for instance [16, 17]):

$$\begin{aligned} \frac{T(\Omega )}{|\Omega |^{(d+2)/d}}\le \frac{T(B)}{|B|^{(d+2)/d}}. \end{aligned}$$

(1.3)

Again, the inequality above becomes an equality if and only if $\Omega$ is a ball (up to sets of capacity zero). If we denote by $B_1$ the unitary ball of $\mathbb {R}^d$ and by $\omega _d$ its Lebesgue measure, then the solution of (1.2), with $\Omega =B_1$, is

$$\begin{aligned} u(x)=\frac{1-|x|^2}{2d} \end{aligned}$$

which provides

$$\begin{aligned} T(B_1)=\frac{\omega _d}{d(d+2)}. \end{aligned}$$

(1.4)

We are interested in the problem of minimizing or maximizing quantities of the form

$$\begin{aligned} P^\alpha (\Omega )T^\beta (\Omega ) \end{aligned}$$

on some given class of open sets $\Omega \subset \mathbb {R}^d$ having a prescribed Lebesgue measure $|\Omega |$, where $\alpha ,\beta$ are two given exponents. Similar problems have been considered for shape functionals involving:

• the torsional rigidity and the first eigenvalue of the Laplacian in [2, 3, 6, 8, 11, 19, 20, 22];

• the torsional rigidity and the Newtonian capacity in [1];

• the perimeter and the first eigenvalue of the Laplacian in [14];

• the perimeter and the Newtonian capacity in [9, 13].

The case $\beta =0$ reduces to the isoperimetric inequality, and we have, denoting by $\Omega ^*_m$ a ball of measure m,

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \big \{P(\Omega )\ :\ |\Omega |=m\big \}=P(\Omega ^*_m)\\ \sup \big \{P(\Omega )\ :\ |\Omega |=m\big \}=+\infty . \end{array}\right. } \end{aligned}$$

Similarly, in the case $\alpha =0$, the Saint Venant inequality yields

$$\begin{aligned} \max \big \{T(\Omega )\ :\ |\Omega |=m\big \}=T(\Omega ^*_m)=\frac{m}{d(d+2)}\Big (\frac{m}{\omega _d}\Big )^{2/d} \end{aligned}$$

while

$$\begin{aligned} \inf \big \{T(\Omega )\ :\ |\Omega |=m\big \}=0. \end{aligned}$$

Indeed if we choose $\Omega _n=\cup _{k=1}^n B_{n,k}$ where $B_{n,k}$ are disjoint balls of measure m/n each, we get for every $n\in \mathbb {N}$

$$\begin{aligned} \inf \big \{T(\Omega )\ :\ |\Omega |=m\big \}\le T(\Omega _n)=\frac{m^{(d+2)/d}}{d(d+2)\omega _d^{2/d}}\,n^{-2/d}\rightarrow 0. \end{aligned}$$

The case when $\alpha$ and $\beta$ have a different sign is also immediate; for instance, if $\alpha >0$ and $\beta <0$ we have from (1.1) and (1.3)

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \big \{P^\alpha (\Omega )T^\beta (\Omega )\ :\ |\Omega |=m\big \}=P^\alpha (\Omega ^*_m)T^\beta (\Omega ^*_m)\\ \sup \big \{P^\alpha (\Omega )T^\beta (\Omega )\ :\ |\Omega |=m\big \}=+\infty , \end{array}\right. } \end{aligned}$$

and similarly, if $\alpha <0$ and $\beta >0$ we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \inf \big \{P^\alpha (\Omega )T^\beta (\Omega )\ :\ |\Omega |=m\big \}=0\\ \max \big \{P^\alpha (\Omega )T^\beta (\Omega )\ :\ |\Omega |=m\big \}=P^\alpha (\Omega ^*_m)T^\beta (\Omega ^*_m). \end{array}\right. } \end{aligned}$$

The cases we will investigate are the remaining ones; with no loss of generality we may assume $\alpha =1$, so that the optimization problems we consider are for the quantities

$$\begin{aligned} P(\Omega )T^q(\Omega ),\qquad \text {with }q>0. \end{aligned}$$

In order to remove the Lebesgue measure constraint $|\Omega |=m$ we consider the scaling free functionals

$$\begin{aligned} F_q(\Omega )=\frac{P(\Omega )T^q(\Omega )}{|\Omega |^{\alpha _q}}\qquad \text {with }\alpha _q=1+q+\frac{2q-1}{d}. \end{aligned}$$

In the following sections we study the minimization and the maximization problems for the shape functionals $F_q$ on various classes of domains. More precisely we consider the cases below.

The class of all domains $\Omega$ (nonempty)

$$\begin{aligned} \mathcal {A}_{all}=\big \{\Omega \subset \mathbb {R}^d\ :\ \Omega \ne \emptyset \big \} \end{aligned}$$

will be considered in Sect. 2; we show that for every $q>0$ both the maximization and the minimization problems for $F_q$ on $\mathcal {A}_{all}$ are ill posed.

The class of convex domains $\Omega$

$$\begin{aligned} \mathcal {A}_{convex}=\big \{\Omega \subset \mathbb {R}^d\ :\ \Omega \ne \emptyset ,\ \Omega \text { convex}\big \} \end{aligned}$$

will be considered in Sect. 3; we show that for $0<q<1/2$ the maximization problem for $F_q$ on $\mathcal {A}_{convex}$ is ill posed, whereas the minimization problem is well posed. On the contrary, when $q>1/2$ the minimization problem for $F_q$ on $\mathcal {A}_{convex}$ is ill posed, whereas the maximization problem is well posed. In the threshold case $q=1/2$ the precise value of the infimum of $F_{1/2}$ is provided; concerning the precise value of the supremum of $F_{1/2}$ an interesting conjecture is stated. At present, the conjecture has been shown to be true in the case $d=2$, while the question is open in higher dimensions.

The class of thin domains $\mathcal {A}_{thin}$, suitably defined, will be considered in Sect. 4. If h(s) represents the asymptotical local thickness of the thin domain as s varies in a $d-1$ dimensional domain A, the maximization of the functional $F_{1/2}$ on $\mathcal {A}_{thin}$ reduces to the maximization of a functional defined on nonnegative functions h defined on A; this allows us to prove the conjecture for any dimension d on the class of thin convex domains.

2 Optimization in the Class of All Domains

In this section we show that the minimization and the maximization problems for the shape functionals $F_q$ are both ill posed, for every $q>0$.

Theorem 2.1

There exist two sequences $(\Omega _{1,n})$ and $(\Omega _{2,n})$ of smooth domains such that for every $q>0$ we have

$$\begin{aligned} F_q(\Omega _{1,n})\rightarrow 0\qquad \text {and}\qquad F_q(\Omega _{2,n})\rightarrow +\infty . \end{aligned}$$

In particular, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \inf \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{all},\ \Omega \text { smooth}\big \}=0\\ \sup \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{all},\ \Omega \text { smooth}\big \}=+\infty . \end{array}\right. } \end{aligned}$$

Proof

In order to show the $\sup$ equality it is enough to take as $\Omega _{2,n}$ a perturbation of the unit ball $B_1$ such that

$$\begin{aligned} B_{1/2}\subset \Omega _{2,n}\subset B_2\qquad \text {and}\qquad P(\Omega _{2,n})\rightarrow +\infty . \end{aligned}$$

Then we have

$$\begin{aligned} |\Omega _{2,n}|\le |B_2|,\qquad T(\Omega _{2,n})\ge T(B_{1/2}), \end{aligned}$$

where we used the monotonicity of the torsional rigidity. Then

$$\begin{aligned} F_q(\Omega _{2,n})\ge \frac{P(\Omega _{2,n})T^q(B_{1/2})}{|B_2|^{\alpha _q}}\rightarrow +\infty . \end{aligned}$$

In order to prove the $\inf$ equality we take as $\Omega _{c,{\varepsilon }}$ the unit ball $B_1$ from which we remove a periodic array of holes; the centers of two adjacent holes are at distance ${\varepsilon }$ and the radii of the holes are

$$\begin{aligned} r_{c,{\varepsilon }}={\left\{ \begin{array}{ll} e^{-1/(c{\varepsilon }^2)}&{}\text {if }d=2\\ c{\varepsilon }^{d/(d-2)}&{}\text {if }d>2, \end{array}\right. } \end{aligned}$$

where c is a positive constant. It is easy to see that, as ${\varepsilon }\rightarrow 0$, we have

$$\begin{aligned} |\Omega _{c,{\varepsilon }}|\rightarrow |B_1|\qquad \text {and}\qquad P(\Omega _{c,{\varepsilon }})\rightarrow P(B_1). \end{aligned}$$

Concerning the torsion $T(\Omega _{c,{\varepsilon }})$, we have (see [10])

$$\begin{aligned} T(\Omega _{c,{\varepsilon }})\rightarrow \int _{B_1} u_c\,dx \end{aligned}$$

where $u_c$ is the nonnegative function which solves

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u_c+K_cu_c=1&{}\text {in }B_1\\ u_c\in H^1_0(B_1), \end{array}\right. } \end{aligned}$$

being $K_c$ the constant

$$\begin{aligned} K_c={\left\{ \begin{array}{ll} c\pi /2&{}\text {if }d=2\\ d(d-2)2^{-d}\omega _d c^{d-2}&{}\text {if }d>2. \end{array}\right. } \end{aligned}$$

Since for every $c>0$ we have that

$$\begin{aligned} \int _{B_1}|\nabla u_c(x)|^2+K_c u^2_c(x)\,dx=\int _{B_1} u_c\,dx \end{aligned}$$

we get that

$$\begin{aligned} \int _{B_1}u_c\,dx\le \frac{\omega _d}{K_c}. \end{aligned}$$

Therefore, a diagonal argument allows us to construct a sequence $(\Omega _{1,n})$ such that

$$\begin{aligned} |\Omega _{1,n}|\rightarrow |B_1|,\qquad P(\Omega _{1,n})\rightarrow P(B_1),\qquad T(\Omega _{1,n})\rightarrow 0, \end{aligned}$$

which concludes the proof. $\square$

3 Optimization in the Class of Convex Domains

In this section we consider only domains $\Omega$ which are convex. A first remark is in the proposition below and shows that in some cases the optimization problems for the shape functional $F_q$ is still ill posed.

Proposition 3.1

We have

$$\begin{aligned} {\left\{ \begin{array}{ll} \inf \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}=0&{}\text {for every }q>1/2;\\ \sup \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}=+\infty &{}\text {for every }q<1/2. \end{array}\right. } \end{aligned}$$

Proof

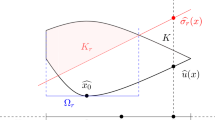
Let A be a smooth convex $d-1$ dimensional set and for every ${\varepsilon }>0$ consider the domain $\Omega _{\varepsilon }\in \mathcal {A}_{convex}$ given by

$$\begin{aligned} \Omega _{\varepsilon }=A\times ]-{\varepsilon }/2,{\varepsilon }/2[. \end{aligned}$$

We have (for the torsion asymptotics see for instance [2])

$$\begin{aligned} \begin{aligned}&P(\Omega _{\varepsilon })\approx 2\mathcal {H}^{d-1}(A),\\&T(\Omega _{\varepsilon })\approx \frac{{\varepsilon }^3}{12}\mathcal {H}^{d-1}(A),\\&|\Omega _{\varepsilon }|={\varepsilon }\mathcal {H}^{d-1}(A), \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} F_q(\Omega _{\varepsilon })\approx \frac{2}{12^q\big (\mathcal {H}^{d-1}(A)\big )^{(2q-1)/d}}\,{\varepsilon }^{(2q-1)(d-1)/d}. \end{aligned}$$

(3.1)

Letting ${\varepsilon }\rightarrow 0$ achieves the proof. $\square$

We show now that in some other cases the optimization problems for the shape functional $F_q$ is well posed. Let us begin to consider the case $q=1/2$.

Proposition 3.2

We have

$$\begin{aligned} \inf \big \{F_{1/2}(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}=3^{-1/2} \end{aligned}$$

(3.2)

and the infimum is asymptotically reached by domains of the form

$$\begin{aligned} \Omega _{\varepsilon }=A\times ]-{\varepsilon }/2,{\varepsilon }/2[ \end{aligned}$$

as ${\varepsilon }\rightarrow 0$, where A is any $d-1$ dimensional convex set.

Proof

Thanks to a classical result by Polya ( [21], see also Theorem 5.1 of [11]) it holds

$$\begin{aligned} T(\Omega )\ge \frac{1}{3}\frac{|\Omega |^{3}}{(P(\Omega ))^2}. \end{aligned}$$

Then

$$\begin{aligned} F_{1/2}(\Omega )=\frac{P(\Omega )(T(\Omega ))^{1/2}}{|\Omega |^{3/2}}\ge 3^{-1/2} \end{aligned}$$

for any bounded open convex set. Taking into account (3.1), we get (3.2). $\square$

Concerning the supremum of $F_{1/2}(\Omega )$ in the class $\mathcal {A}_{convex}$ we can only show that it is finite.

Proposition 3.3

For every $\Omega \in \mathcal {A}_{convex}$ we have

$$\begin{aligned} F_{1/2}(\Omega )\le \frac{2^d d^{3d/2}}{\omega _d}\sqrt{\frac{d}{d+2}}\,. \end{aligned}$$

(3.3)

Proof

By the John’s ellipsoid Theorem [18], there exists an ellipsoid that, without loss of generality, we may assume centered at the origin,

$$\begin{aligned} E_a=\bigg \{x\in \mathbb {R}^d\ :\ \sum _{i=1}^d\frac{x_i^2}{a_i^2}<1\bigg \},\qquad a=(a_1,\dots ,a_d),\text { with }a_i>0 \end{aligned}$$

such that $E_a\subset \Omega \subset dE_a$. Then we have

$$\begin{aligned} F_{1/2}(\Omega )\le \frac{P(dE_a)\big (T(dE_a)\big )^{1/2}}{|E_a|^{3/2}}. \end{aligned}$$

(3.4)

Since the solution of (1.2) for $E_a$ is given by

$$\begin{aligned} u(x)=\frac{1}{2}\bigg (\sum _{i=1}^d a_i^{-2}\bigg )^{-1}\bigg (1-\sum _{i=1}^{d}\frac{x_i^2}{a_i^2}\bigg ), \end{aligned}$$

we obtain

$$\begin{aligned} T(E_a)=\frac{\omega _d}{d+2}\bigg (\sum _{i=1}^d a_i^{-2}\bigg )^{-1}\prod _{i=1}^d a_i, \end{aligned}$$

while

$$\begin{aligned} |E_a|=\omega _d\prod _{i=1}^d a_i. \end{aligned}$$

To estimate $P(E_a)$ we notice that $E_a$ is contained in the cuboid $Q_a=\prod _1^d]-a_i,a_i[$, so that

$$\begin{aligned} P(E_a)\le P(Q_a)=2\sum _{i=1}^d\prod _{j\ne i}(2a_j)=2^d\bigg (\sum _{i=1}^d\frac{1}{a_i}\bigg )\prod _{i=1}^d a_i. \end{aligned}$$

Combining these formulas we have from (3.4)

$$\begin{aligned} F_{1/2}(\Omega )\le \frac{2^d d^{3d/2}}{\omega _d(d+2)^{1/2}}\bigg (\sum _{i=1}^d\frac{1}{a_i}\bigg )\bigg (\sum _{i=1}^d\frac{1}{a_i^2}\bigg )^{-1/2} \end{aligned}$$

and finally, by Jensen inequality,

$$\begin{aligned} F_{1/2}(\Omega )\le \frac{2^d d^{3d/2}}{\omega _d}\sqrt{\frac{d}{d+2}}\;, \end{aligned}$$

as required. $\square$

On the precise value of $\sup \big \{F_{1/2}(\Omega ):\Omega \in \mathcal {A}_{convex}\big \}$ we make the following conjecture.

Conjecture 3.4

We have

$$\begin{aligned} \sup \big \{F_{1/2}(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}=d\Big (\frac{2}{(d+1)(d+2)}\Big )^{1/2} \end{aligned}$$

and it is asymptotically reached by taking for instance

$$\begin{aligned} \Omega _{\varepsilon }=\big \{(s,t)\ :\ s\in A,\ 0<t<{\varepsilon }(1-|s|)\big \} \end{aligned}$$

as ${\varepsilon }\rightarrow 0$, where A is the unit ball in $\mathbb {R}^{d-1}$.

Remark 3.5

We recall that Conjecture 3.4 has been shown to be true in the case $d=2$ (see [21, 23], and the more recent paper [12]). In Sect. 4 we prove the conjecture above for every $d\ge 2$ in the class of convex thin domains.

We show now that for $F_q$ in the class $\mathcal {A}_{convex}$ the minimization problem is well posed when $q<1/2$ and the maximization problem is well posed when $q>1/2$. From the bounds obtained in Propositions 3.2 and 3.3 we can prove the following results.

Proposition 3.6

We have

$$\begin{aligned} {\left\{ \begin{array}{ll} \inf \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}\ge 3^{-1/2}\big (d(d+2)\big )^{1/2-q}\omega _d^{(1-2q)/d}&{}\text {for every }q\le 1/2\\ \sup \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}\le \displaystyle \frac{2^d d^{3d/2-q+1}}{(d+2)^q\omega _d^{1+(2q-1)/d}}&{}\text {for every }q\ge 1/2. \end{array}\right. } \end{aligned}$$

Proof

We have

$$\begin{aligned} F_q(\Omega )=F_{1/2}(\Omega )\left( \frac{T(\Omega )}{|\Omega |^{(d+2)/d}}\right) ^{q-1/2}. \end{aligned}$$

Hence it is enough to apply the bounds (3.2) and (3.3), together with the Saint-Venant inequality (1.3) to get that for every $\Omega \in \mathcal {A}_{convex}$

$$\begin{aligned} \begin{aligned}&\inf \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}\ge 3^{-1/2}\left( \frac{T(B)}{B^{(d+2)/d}}\right) ^{q-1/2}\qquad \text {if }q\le 1/2\\&\sup \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}< \frac{2^d d^{3d/2}}{\omega _d}\sqrt{\frac{d}{d+2}}\left( \frac{T(B)}{B^{(d+2)/d}}\right) ^{q-1/2}\qquad \text {if }q\ge 1/2. \end{aligned} \end{aligned}$$

By the expression (1.4) for T(B) we conclude the proof. $\square$

We now prove the existence of a convex minimizer when $q<1/2$ and of a convex maximizer when $q>1/2$.

Theorem 3.7

There exists a solution for the following optimization problems:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}&{}\text {for every }q<1/2;\\ \max \big \{F_q(\Omega )\ :\ \Omega \in \mathcal {A}_{convex}\big \}&{}\text {for every }q>1/2. \end{array}\right. } \end{aligned}$$

Proof

Suppose $q<1/2$ and consider $(\Omega _n)$ a minimizing sequence for $F_q(\Omega )$. By the John’s ellipsoid Theorem we can assume that there exists a sequence of ellipsoids $E_{a_n}$ such that

$$\begin{aligned} E_{a_n}\subset \Omega _n\subset dE_{a_n}. \end{aligned}$$

By rotations, translations and scaling invariance of $F_q$ we can assume without loss of generality that

$$\begin{aligned} E_{a_n}=\bigg \{x\in \mathbb {R}^d\ :\ \sum _{i=1}^d\frac{x_{i}^{2}}{a_{in}^{2}}< 1\bigg \},\quad a_n=(a_{1n},\dots ,a_{dn}),\ 0<a_{1n}\le \dots \le a_{dn}=1. \end{aligned}$$

Observe that this implies that the diameter of $\Omega _n$ is uniformly bounded in n. We claim that

$$\begin{aligned} a_{1n}\ge c\qquad \text {for every }n\in \mathbb {N}\end{aligned}$$

where c is a positive constant. Then the proof is achieved by extracting a subsequence $(\Omega _{n_k})$ which converges both in the sense of characteristic functions and in the co-Hausdorff metric to some open, non empty, convex, bounded set $\Omega ^-$ and by using the continuity properties of torsional rigidity, perimeter and volume (see for instance, [7, 17]).

To prove the claim we use a strategy similar to the one already used in the proof of Proposition 3.3. Let $Q_{a_n}$ be the cuboid $\prod _{i=1}^d]-a_{in},a_{in}[$. Since

$$\begin{aligned} d^{-1/2}Q_{a_n}\subset E_{a_n} \end{aligned}$$

we have, for n large enough,

$$\begin{aligned} F_q(B_1)\ge F_q(\Omega _n)\ge \frac{1}{d^{(d-1)/2}d^{d\alpha _q}}\frac{T^q(E_{a_n})P(Q_{a_n})}{|E_{a_n}|^{\alpha _q}}. \end{aligned}$$

(3.5)

An explicit computation shows

$$\begin{aligned} \frac{T^q(E_{a_n})P(Q_{a_n})}{|E_{a_n}|^{\alpha _q}} =\frac{2^d\omega _d^{q-\alpha _q}}{(d+2)^q}\left( \frac{\sum _{i=1}^d a_{in}^{-1}}{\big (\sum _{i=1}^d a_{in}^{-2}\big )^{1/2}}\right) \left( \frac{\big (\sum _{i=1}^d a_{in}^{-2}\big )^{1/2}}{(\prod _{i=1}^d a_{in}^{-1})^{1/d}}\right) ^{1-2q}. \end{aligned}$$

Observe that, by Cauchy–Schwarz inequality,

$$\begin{aligned} 1\le \frac{\sum _{i=1}^d a_{in}^{-1}}{\left( \sum _{i=1}^d a_{in}^{-2}\right) ^{1/2}}\le \sqrt{d}, \end{aligned}$$

(3.6)

while for the last term it holds

$$\begin{aligned} \frac{\left( \sum _{i=1}^d a_{in}^{-2}\right) ^{1/2}}{\left( \prod _{i=1}^d a_{in}^{-1}\right) ^{1/d}} =\frac{\left( \sum _{i=1}^d a_{in}^{-2}\right) ^{1/2}}{\left( \prod _{i=1}^{d-1} a_{in}^{-1}\right) ^{1/d}} \ge \frac{a_{1n}^{-1}}{\left( a_{1n}^{-1}\right) ^{(d-1)/d}}=\left( \frac{1}{a_{1n}}\right) ^{1/d} \end{aligned}$$

(3.7)

Therefore, putting together (3.5)–(3.7) and using the fact that $q<1/2$ we obtain that, if n is large enough, the sequence $a_{1n}$ must be greater than some positive constant c, which proves the claim.

The case $q>1/2$ can be proved in a similar way. If $(\Omega _n)$ is a maximizing sequence for $F_q(\Omega )$ and $E_{a_n}$ are ellipsoids such that $E_{a_n}\subset \Omega _n\subset dE_{a_n}$, we have

$$\begin{aligned} F_q(B_1)\le F_q(\Omega _n)\le \frac{P(dE_{a_n})T^q(dE_{a_n})}{|E_{a_n}|^{\alpha _q}}=d^{d-1+q(d+2)}\frac{P(E_{a_n})T^q(E_{a_n})}{|E_{a_n}|^{\alpha _q}}\;.\nonumber \\ \end{aligned}$$

(3.8)

If $Q_{a_n}$ is the cuboid $\prod _{i=1}^d]-a_{in},a_{in}[$ we have $E_{a_n}\subset Q_{a_n}$, so that

$$\begin{aligned} P(E_{a_n})\le P(Q_{a_n})=2^d\left( \sum _{i=1}^d a_{in}^{-1}\right) \prod _{i=1}^d a_{in}\;. \end{aligned}$$

Hence (3.8) implies, for a suitable constant $C_{q,d}$ depending only on q and on d,

$$\begin{aligned} F_q(B_1)\le C_{q,d}\frac{\sum _{i=1}^d a_{in}^{-1}}{\big (\sum _{i=1}^d a_{in}^{-2}\big )^q\big (\prod _{i=1}^d a_{in}\big )^{(2q-1)/d}} \le d^qC_{q,d}\bigg (\frac{\big (\prod _{i=1}^d a_{in}^{-1}\big )^{1/d}}{\sum _{i=1}^d a_{in}^{-1}}\bigg )^{2q-1}, \end{aligned}$$

where in the last inequality we used the Cauchy–Schwarz inequality (3.6). Finally, since $a_{in}\le a_{dn}=1$, we obtain

$$\begin{aligned} F_q(B_1)\le d^q C_{q,d}\left( a_{in}^{-1}\right) ^{(2q-1)/d} \end{aligned}$$

and, since $q>1/2$, the conclusion follows as in the previous case. $\square$

4 Optimization in the Class of Thin Domains

In this section we consider the class of thin domains, that we define below through the families of domains

$$\begin{aligned} \Omega _{\varepsilon }=\big \{(s,t)\ :\ s\in A,\ {\varepsilon }h_-(s)<t<{\varepsilon }h_+(s)\big \} \end{aligned}$$

(4.1)

where ${\varepsilon }$ is a small positive parameter, A is a (smooth) domain of $\mathbb {R}^{d-1}$, and $h_-,h_+$ are two given (smooth) functions. We denote by h(s) the local thickness

$$\begin{aligned} h(s)=h_+(s)-h_-(s), \end{aligned}$$

and we assume that $h(s)\ge 0$. More precisely, we call thin domain a family $(\Omega _{\varepsilon })_{{\varepsilon }>0}$ as above; in other words a thin domain is characterized by the $d-1$ dimensional domain A and by the local thickness function h.

The following asymptotics hold for the quantities we are interested to (for the torsional rigidity we refer to [5]):

$$\begin{aligned} \begin{aligned}&P(\Omega _{\varepsilon })\approx 2\mathcal {H}^{d-1}(A),\\&T(\Omega _{\varepsilon })\approx \frac{{\varepsilon }^3}{12}\int _A h^3(s)\,ds,\\&|\Omega _{\varepsilon }|={\varepsilon }\int _A h(s)\,ds, \end{aligned} \end{aligned}$$

which together give the asymptotic formula when $q=1/2$

(4.2)

where we use the notation

We then define the functional $F_{1/2}$ on the thin domain $(\Omega _{\varepsilon })_{{\varepsilon }>0}$ associated with the $d-1$ dimensional domain A and the local thickness function h by

By Hölder inequality we have

$$\begin{aligned} F_{1/2}(A,h)\ge 3^{-1/2} \end{aligned}$$

and the value $3^{-1/2}$ is actually reached by taking the local thickness function h constant, which corresponds to $\Omega _{\varepsilon }$ a thin slab.

A sharp inequality from above is also possible for $F_{1/2}(A,h)$, if we restrict the analysis to convex domains, that is to local thickness functions h which are concave. The following result will be used, for which we refer to [4, 15].

Theorem 4.1

Let $1\le p\le q$. Then for every convex set A of $\mathbb {R}^N$ $(N\ge 1)$ and every nonnegative concave function f on A we have

where the constant $C_{p,q}$ is given by

$$\begin{aligned} C_{p,q}=\left( {\begin{array}{c}N+p\\ N\end{array}}\right) ^{1/p}\left( {\begin{array}{c}N+q\\ N\end{array}}\right) ^{-1/q}. \end{aligned}$$

In addition, the inequality above becomes an equality when A is a ball of radius 1 and $f(x)=1-|x|$.

We are now in a position to prove the Conjecture 3.4 for convex thin domains.

Theorem 4.2

If $(\Omega _{\varepsilon })_{{\varepsilon }>0}$ is a thin convex domains given by (4.1), we have

$$\begin{aligned} F_{1/2}(A,h)\le d\Big (\frac{2}{(d+1)(d+2)}\Big )^{1/2}. \end{aligned}$$

(4.3)

In addition, the inequality above becomes an equality taking for instance as A the unit ball of $\mathbb {R}^{d-1}$ and as the local thickness h(s) the function $1-|s|$.

Proof

Since the local thickness function h is concave, by Theorem 4.1 with $N=d-1$, $q=3$, $p=1$, we obtain

so that

$$\begin{aligned} F_{1/2}(A,h)\le 3^{-1/2}C_{1,3}^{3/2}=d\Big (\frac{2}{(d+1)(d+2)}\Big )^{1/2} \end{aligned}$$

as required. Finally, an easy computation shows that in (4.3) the inequality becomes an equality if A is the unit ball of $\mathbb {R}^{d-1}$ and $h(s)=1-|s|$. $\square$