1 Introduction

Radiation acting as a heat transfer mechanism as so-called thermal radiation is important in many applications. Such applications include the fields of industrial furnaces, climate modelling, solar power, thermal building design and so on. For example, the radiation exchange of surfaces inside high temperature furnaces significantly determines the process and thus the final quality of the treated products. Models for calculating radiation heat exchange are therefore necessary to map the radiation exchange as accurately as possible while still showing short computation times.

Considering the radiation exchange between surfaces, a surface-to-surface approach using view factors, also known as form factors, based on the geometry of the problem, leads to a solution with high accuracy. A view factor is used as basis to determine the diffuse radiation exchange between a pair of surfaces respectively areas. A view factor \({F}_{ij}\) between two areas \({A}_{i}\) and \({A}_{j}\) is defined as the ratio of the radiation which area \({A}_{j}\) receives from area \({A}_{i}\) to the radiation absolutely emitted by area \({A}_{i}\). The view factor between two areas can be calculated using Eq. (1) [1].

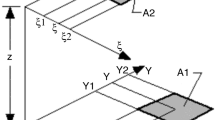
$${F}_{ij}={F}_{{A}_{i}\to {A}_{j}}=\frac{1}{{A}_{i}}\underset{{A}_{i}}{\overset{ }{\int }}\underset{{A}_{j}}{\overset{ }{\int }}\frac{\mathrm{cos}({\theta }_{i})\mathrm{cos}({\theta }_{j})}{\pi {S}^{2}}\cdot {\mathrm{d}A}_{j}{\mathrm{d}A}_{i}$$
(1)

The relative position between the areas is determined by the length of the connecting vector \(S\) and their orientation towards each other, characterized by the angles \({\theta }_{i}\) and \({\theta }_{j}\), which are spanned between the normal vectors \({n}_{i}\) respectively \({n}_{j}\) and \(S\), Fig. 1.

Fig. 1
figure 1

Radiation exchange between two areas according to [1]

Full size image

One way of calculating view factors is solving Eq. (1) directly. This can be done if area integration is analytically possible. Using this approach, many libraries have been build up, describing view factor formulas of two exchanging areas for many variations of different areas [2]. However, those equations are mostly derived for the view factor calculation between simple geometries such as rectangles or circles. As soon as the geometries become more complex, this solution is no longer applicable. If the radiation exchange needs to be resolved locally on the areas, because of different radiation properties or arbitrary geometries are given, the analytical integration or predeveloped solutions are impractical.

Based on a numerical discretization of the problem, various numerical methods are available for calculating radiation exchange. It is possible to calculate the view factors by numerical integration over the areas [1] or to use ray tracing algorithms [3]. In ray tracing, many different methods are used with two common ones shortly presented. The Monte Carlo method uses randomly angled rays emitted from the respective area with their path and thus their impact on other areas being tracked [4, 5]. With the Hemicube method, half a cube is placed over each area, structured into pixels. The surroundings can be projected onto the hemicube’s pixels or rays can be emitted by the source running through each pixel, hitting other areas. This is taken as the basis for the calculation of the view factors [2, 6].

The accuracy of the numerical area integration and ray tracing methods are highly dependent on the discretization of the areas or number of rays emitted. In contrast to ray tracing methods, the area integration method provides a more complete description of the radiation exchange. Since each area is totally checked with all other areas, statistics, geometrical features or other parameters than area discretization are not relevant for calculating the view factors. This makes this method very suitable for the accurate determination of view factors, which can be guaranteed using simple mesh convergence studies. Nevertheless, this comes with a bit of a downside, since this method does not inherently differentiate between “seen” or “unseen” areas unlike the ray tracing methods. Therefore, this approach has to be extended with appropriate blocking detection methods, to account for so called shadowing effects.

In this paper a radiation exchange model is developed using view factors to determine the radiation heat fluxes between arbitrary areas. The model is based on a numerical discretization of the areas, calculating the view factors with area integration, using the so called crossed strings method for two-dimensional problems, developed by Hottel [7]. In addition, a blocking algorithm is developed for differentiating between “seen” and “unseen” (blocked) areas forming the integral and innovating part of the model. To complete the calculation, a heat flux solver is used. The model is written in the Julia programming language [8].

2 Surface-to-surface radiation

In a radiation problem, which is purely a matter of surface exchange (no fluid radiation, scattering or absorption effects), surface-to-surface modelling is used. Here, view factors are the essential basis of description. This is usually done under the following assumptions [9]:

  • Solid state radiation is the primary and only heat transfer mechanism.

  • The radiation chamber respectively enclosure is either filled with an optically transparent, non-radiating medium or there is a vacuum.

  • The individual surfaces are assumed to be diffuse grey or black radiators with constant radiation and irradiation characteristics over the surface.

  • The surfaces themselves or their subdivisions are modelled as isothermal zones.

2.1 View factors

In general, view factor calculation is based on Eq. (1). Nonetheless, when considering view factors, different relations are given, also known as view factor algebra. One important theorem is reciprocity. Having calculated the view factor \({F}_{ij}\) of the two areas \({A}_{i}\) and \({A}_{j}\), the view factor \({F}_{ji}\) can be derived indirectly. For this purpose, the proportion of radiation emitted by area \({A}_{j}\) on \({A}_{i}\) is calculated in relation to the total radiation emission of area \({A}_{j}\), Eq. (2) [1].

$${A}_{i}{F}_{ij}={A}_{j}{F}_{ji}$$
(2)

For an enclosed radiation problem, the total emitted radiation of an area \({A}_{i}\) is equal to the sum of the absorbed radiation of area \({A}_{j}\) for all \(n\) participating areas. This is represented by the summation relation, Eq. (3) [1].

$$\textstyle\sum_{j=1}^{n}{F}_{ij}=1$$
(3)

The third basic equation for calculating view factors is the superposition rule applicable to areas, Eq. (4). The view factor \({F}_{ij}\) of an area \({A}_{i}\) on an area \({A}_{j}\) can also be determined via the summation of the partial view factors \({F}_{ik}\), if area \({A}_{k}\) is part of area \({A}_{j}\) and \(K\) being the number of total subareas [1]. This is only advisable for areas with the same radiation properties or boundary conditions (emissivity, temperature, etc.).

$${F}_{ij}=\textstyle\sum_{k=1}^{K}{F}_{ik}\ with\ {A}_{j}=\textstyle\sum_{k=1}^{K}{A}_{k}$$
(4)

When combining Eq. (2) and (4), the summation rule can be expanded, Eq. (5).

$${F}_{ij}=\frac{\textstyle\sum_{k=1}^{K}{A}_{k}{F}_{kj}}{\textstyle\sum_{k=1}^{K}{A}_{k}}\ with\ {A}_{i}=\textstyle\sum_{k=1}^{K}{A}_{k}$$
(5)

In an enclosure, for every area \({A}_{i}\) to every other area \({A}_{j}\) where \(j\) is part of the total number of areas \(n\), there is a view factor \({F}_{ij}\) including the view factor \({F}_{ii}\) of area \({A}_{i}\) to itself. With the help of the summation relation, Eq. (3), it becomes clear that a view factor can be in the interval between 0 and 1. Figure 2a shows a two-dimensional enclosure with eight areas. For area \({A}_{1}\), all existing view factors towards all other areas are indicated by arrows. The view factors of all areas of the enclosure are summarized in the so-called view factor matrix, Eq. (6) [10].

Fig. 2
figure 2

Radiation exchange of several areas in two-dimensional enclosure: a) all view factors of area \({A}_{1}\) to areas \({A}_{2}\) – \({A}_{8}\) according to [10]; b) Hottel's crossed strings method applied to any two areas in two-dimensional enclosure according to [1]; c) view factors \({F}_{15}\) and \({F}_{17}\), affected by blocking

Full size image
$$\left[\begin{array}{ccc}{F}_{11}& \cdots & {F}_{1n}\\ \vdots & \ddots & \vdots \\ {F}_{n1}& \cdots & {F}_{nn}\end{array}\right]=\left[\begin{array}{ccc}{F}_{11}& \cdots & {F}_{18}\\ \vdots & \ddots & \vdots \\ {F}_{81}& \cdots & {F}_{88}\end{array}\right]$$
(6)

In a nutshell, the view factors of any two finite areas can be determined with Eq. (1) and the associated integration of the areas. For an easy calculation of the view factors, mathematical analytical solutions have been developed, applicable for a large number of simple cases of area pairs [11]. A special method for determining the view factors for two-dimensional problems is Hottel's crossed strings method [7]. It can be applied to pairs of areas, whose propagation into the third dimension can be regarded as infinite and their normal vectors being perpendicular to this third dimension, Fig. 2b. The corner points \(a\), \(b\), \(c\) and \(d\) of both areas \({A}_{i}\) and \({A}_{j}\), are connected with each other so that two crossing (\({A}_{ac}\), \({A}_{bd}\)) and two non-intersecting areas (\({A}_{ad}\), \({A}_{bc}\)) are created. Equation (7) can be used to calculate the view factor \({F}_{ij}\) of the two areas in relation to each other. Equation (2) and (7) result in Eq. (8) for calculating view factor \({F}_{ji}\).

$${F}_{ij}=\frac{\left({A}_{ac}+{A}_{bd}\right)-\left({A}_{ad}+{A}_{bc}\right)}{2{A}_{i}}$$
(7)
$${F}_{ji}=\frac{\left({A}_{ac}+{A}_{bd}\right)-\left({A}_{ad}+{A}_{bc}\right)}{2{A}_{j}}$$
(8)

One point that was omitted from the method presented is another blocking area between two areas and thus an impairment of their view factor. Figure 2c shows two different cases, one with a blocking area and one without. Using the calculation options presented, a view factor would be calculated for both area combinations \({A}_{15}\) and \({A}_{17}\). By including the other areas, however, it becomes clear that the view factor \({F}_{17}\), in contrast to \({F}_{15}\), is not correct, since the areas \({A}_{1}\) and \({A}_{7}\) cannot "see" each other directly. This phenomenon is called blocking or shadowing. A third area, here area \({A}_{9}\), is blocking the view between \({A}_{1}\) and \({A}_{7}\). In order to determine the complete view factor matrix representing the radiation exchange within the enclosure, a blocking check for each area pair needs to be conducted.

2.2 Determination of heat fluxes

Using the view factor matrix, the heat fluxes exchanged between all areas can be calculated. For this purpose, the net radiation method is used [10]. Therefore, it applies that each area must have a homogeneous emissivity \(\varepsilon\), as well as a homogeneous temperature \(T\). Since all areas are assumed to be grey or black radiators, the emissivity of an area is referred to as the area’s emitting radiation divided by the theoretical emitting radiation of a black body area with the same temperature \(T\). Furthermore, the chosen area’s disrectization size should be small enough to accurately map reflection effects, since emissivity \(\varepsilon\) and reflectivity \(\rho\) are coupled via Eq. (9) [2].

$$\varepsilon +\rho =1$$
(9)

For each area \(i\), the net heat flow \({Q}_{i}\) is calculated, which is composed of the outgoing radiation \({J}_{i}\) and the incoming radiation \({G}_{i}\), Eq. (10) [10].

$${Q}_{i}=\left({J}_{i}-{G}_{i}\right){\cdot A}_{i}$$
(10)

The outgoing radiation \(J\) is defined by Eq. (11) [10] and the incoming radiation \(G\) by Eq. (12) [10]. \({\sigma }_{S}\) is the Stefan-Boltzmann constant.

$${J}_{i}={\varepsilon }_{i}{\sigma }_{S}{T}_{i}^{4}+\left(1-{\varepsilon }_{i}\right){G}_{i}$$
(11)
$${G_i}=\sum^{n}_{j}{J_j}{F_{ij}}$$
(12)

A linear system of equations is set up for the solution, see Eq. (13) [2]. Using the temperatures \(T\) of the different areas, the view factor matrix and the Kronecker delta \(\delta_{ij}\), the outgoing radiation \(J\) can be calculated.

$$\left[\textstyle\sum_{j}^{n}\left({\varepsilon }_{i}-1\right){F}_{ij}+{\delta }_{ij}\right]\cdot \left[{J}_{i}\right]=\left[{\varepsilon }_{i}{\sigma }_{S}{T}_{i}^{4}\right]$$
(13)

3 Two-dimensional radiation model

The theoretical consideration of the view factor calculation leads to the following specifications of the developed two-dimensional radiation model:

  1. 1.

    The surfaces of the geometry must be discretized. Therewith, two-dimensional line elements are created which numerically approximate the surfaces. Thus, Hottel's crossed strings method can be used for integration. The normal vectors of the surfaces indicate the direction of the radiation exchange.

  2. 2.

    Each surface element combination then has to be checked for blocking with third elements.

  3. 3.

    The view factor matrix is used as a basis for the radiation exchange of the two-dimensional problem, while applying the net radiation method on the discretized geometry will allow calculating the heat flux exchanges regarding the surface temperatures.

3.1 Discretization

The implementation of the developed radiation model, which is shown in this paper, includes the possibility to create and discretize simple two-dimensional geometries. These geometries include lines, circles, arcs and cosine shapes. The geometries are then discretized into straight-line (linear) elements. More complex geometries can be discretized externally and then be transferred to the developed mesh format. In general, the mesh format consists of nodes and elements. Those elements can be grouped into parts. Those parts, as a group of elements, represent parts of the geometry and simplify mapping the elements. A line element is defined by its boundary nodes, its center, a normal vector and the length further referred to as the element’s area or size. For the discretization of a geometry the element size was given and equidistant throughout the meshed parts. The normal vector indicates the direction of the possible radiation exchange of an individual element. An example problem with two concentric, infinitely extended cylinders, represented by two concentric circles, is shown in Fig. 3. The normal vectors are represented by lines perpendicular to the elements, originating at their center. In the following, this example is used to briefly explain how the developed radiation model works. In this example the element size may vary between \(e = 0.05\, \mathrm{m}\) and \(e = 0.1\, \mathrm{m}\) for a better visualization of the different aspects of the presented model.

Fig. 3
figure 3

Two-dimensional mesh of two concentric infinitely extended cylinders: normal vectors indicating the radiation exchange direction; part 1: cylinder with diameter \(d = 0.8\, \mathrm{m}\); part 2: cylinder with \(d = 1.6\, \mathrm{m}\)

Full size image

The calculated view factors are stored in a corresponding \(n \times n\) matrix with \(n\) being the number of elements. The view factor calculation is split into three parts: First, all element combinations are checked for alignment with each other (3.2), then the blocking check is performed (3.3) for all remaining element combinations and last the actual view factor calculation is done (3.4).

3.2 Element alignment check

The view factor between two elements is greater zero (\({F}_{ij}\ne 0\)), if both angles \({\theta }_{i}\) and \({\theta }_{j}\) between the normal vectors \({n}_{i}\) and \({n}_{j}\) and the connection vector \(S\) are smaller than \(\varphi =\pi /2\), geometric positions in Fig. 1. The two elements cannot “see” each other, if one of the two angles \({\theta }_{i}\) or \({\theta }_{j}\) is greater than or equal to \(\varphi\). In this case, no radiation can directly be exchanged between the elements, i.e., the view factor can be set to \({F}_{ij}=0\). Figure 4 shows an element combination where the two elements “see” each other (solid line) and one where the elements do not “see” each other (dashed line). Checking this geometrical topology between the elements is much faster than the actual view factor calculation itself. Therefore, all element combinations with \({F}_{ij}\ne 0\), or \({F}_{ji}\ne 0\) get marked in the view factor matrix aforehand, so that the following view factor determination only has to be carried out for those marked element combinations, saving computational time.

Fig. 4
figure 4

Two element combinations are shown: one where the elements can “see” each other (solid line) and another one where they cannot “see” each other (dashed line)

Full size image

3.3 Blocking

The sole consideration of an elements pair geometric relationship does not yet guarantee a view factor \({F}_{ij}>0\), Fig. 5a. It is possible that one or more third elements lay in between two facing elements. As a result, the radiation would be intercepted by this third element and is therefore blocking or shadowing this element combination. A naive or brute force blocking algorithm, which checks each possible element combination for intersection with all other elements is of a time complexity of \(O({n}^{3})\) for \(n\) elements, which limits the applicability of such an approach even to small numbers of elements. For this reason, an algorithm was developed which can achieve a reduced time complexity. The detailed speedup analysis is shown in the results. This more efficient blocking algorithm for recognizing the blocked element combinations is a core part of the developed model.

Fig. 5
figure 5

Originating at one specific element, all “seen” elements (\({F}_{ij}>0\)) before (a) and after (b) the blocking analysis are shown; a connection vector (red) indicates a view factor \({F}_{ij}>0\)

Full size image

The result of the blocking analysis of the given example is shown in Fig. 5b. If two elements are blocked by a third one, the view factor between these two elements is zero (\({F}_{ij}=0\), \({F}_{ji}=0\)).

The algorithm developed is based on ray tracing techniques from the field of computer graphics. One way of reducing the number of intersection checks of a ray with its surroundings is to divide the space into smaller areas or volumes dependent of the problem’s dimensions. In three dimensional problems the volumes are called “voxels” (volume elements). Since the developed model is used for two dimensional problems the term “tiles” as a name for these smaller areas is introduced. A tile grid is generated. Then, for each ray all traversed tiles are determined from the ray’s origin to its end point. Afterwards, only the content of the traversed tiles is evaluated, starting with the tile closest to the origin. In this way, the intersection is only checked within a selected area of the entire space. This significantly reduces the total number of intersection checks [12, 13]. Using this approach as the basis of a blocking algorithm in the developed radiation model leads to the following procedure: All elements are pooled into tiles using a sorting algorithm. For each connection vector of an element combination, the traversed tiles are determined. The traversed tiles’ elements are checked for intersection with the vector’s base element pair. As a results, the number of checks for possible blocking elements is usually significantly less than (\(n-2\)). Of course, this totally depends on the size of the tiles used. In the following, the developed algorithm for two-dimensional blocking detection is described in more detail.

Basis of the blocking algorithm is a superimposed structured grid of quadrilateral elements, forming the so-called tiles, which are numbered in x- and y-direction and thus can be uniquely addressed. A sorting algorithm assigns the elements into the individual tiles. Even if an element is located only partially in a tile, it is assigned to this tile. This can lead to multiple assignments of elements to tiles. For each occupied tile, there is a list of its containing elements. Figure 6 shows the discretized example case overlaid with \(15 \times 15\) tiles; in addition the occupied tiles are marked in red.

Fig. 6
figure 6

Discretized geometry of the exemplary two-dimensional problem with superimposed \(15 \times 15\) tiles; tiles containing elements are marked in red

Full size image

Once all elements are assigned to the tiles, the yet unfinished view factor matrix can be checked for blocking between elements. Each line element combination is only checked for blocking in one direction of their line center connecting vector, since blocking from one element \(i\) to another one \(j\) is equivalent to blocking from \(j\) to \(i\). For this purpose, all traversed tiles of the connection vector are determined in one of the two directions, see Fig. 7. In the following the connection vector between element \(i\) and \(j\) is used as an example. The result of the traversed tile detection is a list of tiles that are intersected by this connection vector, see Fig. 7a. Subsequently, the closest occupied tile to element \(i\) is determined from this list. The connection vector is now checked for intersection with the elements contained by this first tile, using a line intersection check according to [14]. If an intersection is found, further consideration of the element combination is immediately terminated and an occurring blocking is noted by setting \({F}_{ij}=0\) and \({F}_{ji}=0\). In Fig. 7b intersection is found in the sixth traversed (third occupied) tile with the impinged element marked in green whereas the elements of the tile, which are not struck, are marked in orange. If no intersection of any third element with the connecting vector of the element combination is found during the check of all traversed tiles, the view factor can be calculated accordingly. Since the check for blocking with the tiles’ elements takes the most time, creating the tile list up front makes no difference to directly checking the traversed tile. Partial blocking approaches are not implemented, as sufficient discretezation in two-dimensional problems is expected to be possible in the very most cases.

Fig. 7
figure 7

Specific element combination and connection vector: in (a) all traversed tiles between two elements \(i\) and \(j\) (blue) are marked in grey; in (b) occupied tiles check—element (green) in sixth tile (third occupied one) blocks element combination whereas other elements of tile (orange) are checked with no intersection

Full size image

3.4 View factor calculation

Until now, all element combinations with view factors of \({F}_{ij}=0\) and \({F}_{ji}=0\) have been detected. To calculate all remaining view factors with \(F\ne 0\), Hottel's crossed strings method is applied, Eq. (7) and Eq. (8). After this, the view factor matrix is complete. For control purposes, the sum of the view factors of a surface can be formed, see Eq. (4) and (5), and thus the error can be determined comparing those results to analytical solutions. Using the matrix to calculate the heat fluxes due to the radiation exchange requires each areas’ view factor sum to match the summation relation, Eq. (3); otherwise it must be normalized.

The reduced view factor matrix of the exemplary case of two concentric, infinitely extended cylinders, Fig. 3, is shown in Eq. (14); part 1 being the inner cylinder and part 2 being the outer one. The discretization was carried out with an element size of \(e = 0.05\, \mathrm{m}\); resulting in an element number of \(n = 151\).

$$\left[\begin{array}{cc}{F}_{11}& {F}_{12}\\ {F}_{21}& {F}_{22}\end{array}\right]=\left[\begin{array}{cc}0& 0.999838\\ 0.499671& 0.495456\end{array}\right]$$
(14)

3.5 Radiation heat transfer

For the calculation of the heat fluxes exchanged by radiation of the individual elements a linear system is set up using the Eqs. (10)-(13). For each surface or element, the emissivity and temperature boundary conditions are required in addition to the view factor matrix. Their values need to be assigned for each element, since it is treated as an individual area within the net radiation method. Figure 8a shows the initial temperature field with different temperatures set throughout the elements. The calculated heat flux densities between the two cylinders are shown in Fig. 8b. Here, a positive heat flux density means an outgoing heat flux and according to that a negative heat flux density is set for incoming heat fluxes. The emissivity of the inner cylinder is \(\varepsilon = 0.9\), that of the outer cylinder \(\varepsilon = 0.5\).

Fig. 8
figure 8

Temperature field (a) and resulting heat flux density (b) of the exemplary cylinder configuration

Full size image

4 Results

4.1 Validation case 1: cylinder in cylinder

Analytical solutions of the described problem of two concentric, infinitely extended cylinders can be found in [15]. Comparing the analytical results, Eq. (15), to the view factor matrices reduced to the two parts calculated with the developed numerical method in Table 1, the results show good agreement and rapid convergence with increasing number of elements.

$$\left[\begin{array}{cc}{F}_{11}& {F}_{12}\\ {F}_{21}& {F}_{22}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ \frac{{r}_{1}}{{r}_{2}}& 1-\frac{{r}_{1}}{{r}_{2}}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0.5& 0.5\end{array}\right]$$
(15)
Table 1 Results of the view factor calculation accumulated into parts for different number of elements of two concentric, infinitely extended cylinders
Full size table

4.2 Validation case 2: emissivity

For validating the model’s capability of calculating heat fluxes exchanged by radiation the effective emissivity is used. Effective emissivities are applied in applications with hollow radiators, i.e. a hollow sphere. With a homogenuous temperature on all surfaces of the hollow radiator, the opening area can be used as a substitute radiator with an effective emissivity higher than the emissivities of the hollow radiator’s surfaces itself [16, 17]. A collection of common two- and three-dimensional cases is given in [18]. For comparison purposes, an infinitely long round groove characterised by \(\beta\) (Eq. (16)) is used, see Fig. 9. The groove characterization factor \(\beta\) indicates the opening length divided by the remaining circumfence. The effective emissivities of this infinitely long round groove presented in [18] and calculated with the developed model are shown in Fig. 10. The results show very good agreement using sufficient discretization.

Fig. 9
figure 9

Infinitely long round groove with opening angle \(\alpha\) according to [18]

Full size image
Fig. 10
figure 10

Effective emissivities for an infinitely long round groove: solid lines calculated with developed model; dotted lines according to [18]

Full size image
$$\beta =\frac{\mathrm{sin}(\alpha) }{\pi -\alpha }$$
(16)

4.3 Runtime comparison: Brute Force vs. developed blocking algorithm

The developed blocking algorithm saves operations compared to the brute force method described earlier, thus leading to shorter computation times. Both blocking methods are compared using an example of infinitely extended cylinders. Four cases with 17 small cylinders (\(d = 0.1\, \mathrm{m}\)) in a big cylinder (\(d = 1.8\, \mathrm{m}\)) at different positions are used for comparing both algorithms. The different positions of the small cylinders create four different blocking situations, Fig. 11. In case a), all small cylinders are positioned randomly within the big cylinder. Case b) only allows positioning the small cylinders randomly in one half. Analogously, in case c) all cylinders were positioned randomly in only one quarter of the big cylinder. Case d) aligns all small cylinders as a cross within the big one. Each case is investigated using different element sizes and tile numbers. Since the computation time is highly dependent on the number of tiles, the term maximum speedup is introduced and determined for each element size. It is used to compare the developed algorithm to the brute force method pointing out how many times faster the developed algorithm finishes. These maximum speedups dependent on the element size are shown in Fig. 12.

Fig. 11
figure 11

Four different arrangements of 17 cylinders in a big cylinder: randomly distributed (a), randomly distributed within one half (b), randomly distributed within one quarter (c) and aligned in a cross shape (d)

Full size image
Fig. 12
figure 12

Maximum speedups in computation time of developed blocking algorithm compared to brute force algorithm for all four investigated cases

Full size image

A solid reduction of computation time is achieved using the developed blocking algorithm. The maximum speedups are achieved with an average ratio of element to tile size of 0.06, meaning that for each discretized case an optimal number of tiles per dimension respectively tile size can be determined. Further, the maximum speedup increases with more elements, respectively a higher number of elements. This relationship has a logarithmic course. If this is put in relation to the time complexity described earlier for the brute force algorithm, the developed algorithm scales with \(O({n}^{3}/\mathrm{log}(n))\). The speedup can be reproduced with other geometries, showing the same logarithmic behavior.

4.4 Reflection case pinhole

The model’s capability to simulate the influence of different emissivities will be shown using a simple example. Here, two neighboring rectangles are connected to each other via a pinhole, Fig. 13. A temperature of \(T = 400\, \mathrm{K}\) is assumed for all surfaces, except for the surface of the smaller rectangle opposite the pinhole, which is set to a temperature \(T = 600\, \mathrm{K}\). Direct radiation exchange between both rectangles is only possible for both surfaces opposite the pinhole, since their temperature difference leads to heat fluxes. The other surfaces inside the bigger rectangle besides the one opposite the pinhole cannot directly “see” the surface with \(T = 600\, \mathrm{K}\) and therefore no direct radiation exchange is possible.

Fig. 13
figure 13

Comparison of two heat flux calculations: Emissivity of all surfaces \(\varepsilon = 1.0\) (a); emissivity of larger rectangle’s surface opposite of the pinhole \(\varepsilon = 0.5\), rest \(\varepsilon = 1.0\) (b)

Full size image

Figure 13 shows the incoming heat flux densities calculated with different emissivities. An emissivity of \(\varepsilon = 1.0\) for all surfaces (a) leads to heat fluxes only on the surface opposite the pinhole in the bigger rectangle. This is due to reflection, which does not take place with an emissivity of \(\varepsilon = 1.0\). As soon as the emissivity of the larger rectangle’s surface opposite of the pinhole is \(\varepsilon < 1.0\) (here \(\varepsilon = 0.5\)(b)), reflection can take place causing all surfaces of the larger rectangle to register an incoming heat flux. The surface opposite the pinhole reflects part of its incoming heat flux towards the other surfaces inside the bigger rectangle.

4.5 Reflection case corridor

The influence of the emissivity can also be seen by surface radiation entering a long two-dimensional corridor. The corridor is investigated at different emissivities reaching from \(\varepsilon = 0.0001\) to \(\varepsilon = 1.0\). The emissivity of both the starting area (source) and the end area (target) is held constant at \(\varepsilon = 1.0\). All areas except the starting one are set to temperatures of \(T = 400\, \mathrm{K}\). With a temperature of \(T = 600\, \mathrm{K}\) the starting area is radiating into the long corridor. The heat flux density is calculated. Figure 14 shows the heat flux densities for three different emissivities of the corridor’s walls.

Fig. 14
figure 14

Comparison of incoming heat flux densities with different emissivities in a two-dimensional corridor; the source and target area at start and end of the corridor are marked

Full size image

It is evident, that with lower emissivities a higher heat flux is reaching the end of the long corridor, Fig. 15. This is due to higher reflectivities coming along with lower emissivities, Eq. (9). The incoming and outgoing heat fluxes of source and target are calculated by taken the heat flux densities on the surfaces and their area into account. With an emissivity close to \(\varepsilon = 1.0\) nearly no reflection takes place and therefore radiation exchange is limited to the beginning of the corridor. With low emissivities close to zero, the radiation exchange between the start and the end of the long corridor, here source and target, is occurring.

Fig. 15
figure 15

Absolute outgoing and incoming heat flows of start (source) and end area (target) of corridor compared at different emissivities

Full size image

5 Conclusion

To conclude, a radiation model based on a surface-to-surface approach was developed working with arbitrary two-dimensional geometries for a calculation of heat fluxes due to thermal radiation exchange. The model includes an accurate view factor calculation with the extension of a fast blocking algorithm to distinguish between “seen” and “unseen” surfaces. The view factor calculation is based on numerical area integration using Hottel’s crossed strings method. The heat flux solver uses the net radiation method assuming all surfaces are grey and diffuse radiators.

The model delivers plausible results, successfully validated against available analytical view factor calculation methods for simple geometries. Good accuracy is achieved through a complete blocking analysis, checking each view factor. The developed blocking algorithm can yield to a significant decrease of computation time compared to a standard blocking determination approach. The advantage of the developed model is the applicability to any set of arbitrary geometries. A benefit of this model compared to most statistical approaches as the Monte-Carlo or Hemicube method, is the sole mesh dependency of this model. There are no second or third factors other than mesh size, influencing the convergence against analytically accurate results, which makes it easy to estimate the accuracy of the given results. Therefore, for many applications it is not necessary to work out an appropriate analytical solution for different cases anymore. To add to this, since the geometries get discretized, the boundary conditions regarding material properties and temperatures can be set element wise, which usually is necessary for a more accurate description of the radiation problem.