Abstract
We introduce a new probabilistic model of the primes consisting of integers that survive the sieving process when a random residue class is selected for every prime modulus below a specific bound. From a rigorous analysis of this model, we obtain heuristic upper and lower bounds for the size of the largest prime gap in the interval \([1,x]\). Our results are stated in terms of the extremal bounds in the interval sieve problem. The same methods also allow us to rigorously relate the validity of the Hardy-Littlewood conjectures for an arbitrary set (such as the actual primes) to lower bounds for the largest gaps within that set.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we introduce a new probabilistic model  for the primes
for the primes  which can be analyzed rigorously to make a variety of heuristic predictions. In contrast to the well known prime model
which can be analyzed rigorously to make a variety of heuristic predictions. In contrast to the well known prime model  of Cramér [6] and the subsequent refinement
of Cramér [6] and the subsequent refinement  of Granville [16], in which random sets are formed by including positive integers with specific probabilities, the model
of Granville [16], in which random sets are formed by including positive integers with specific probabilities, the model  proposed here is comprised of integers that survive the sieve when a random residue class is selected for every prime modulus below a specific bound. We determine the asymptotic behavior of the largest gap function,
proposed here is comprised of integers that survive the sieve when a random residue class is selected for every prime modulus below a specific bound. We determine the asymptotic behavior of the largest gap function,  , for the set
, for the set  , where for any subset
, where for any subset  we denote
we denote

We conjecture that the primes  have similar behavior. Our bounds, given in Theorem 1.1 below, are stated in terms of the extremal bounds in the interval sieve problem.
have similar behavior. Our bounds, given in Theorem 1.1 below, are stated in terms of the extremal bounds in the interval sieve problem.
At present, the strongest unconditional lower bound on  is due to Ford, Green, Konyagin, Maynard, and Tao [11], who have shown thatFootnote 1
is due to Ford, Green, Konyagin, Maynard, and Tao [11], who have shown thatFootnote 1

for sufficiently large \(x\), with \(\log _{k} x\) the \(k\)-fold iterated natural logarithm of \(x\), whereas the strongest unconditional upper bound is

a result due to Baker, Harman, and Pintz [2]. Assuming the Riemann Hypothesis, Cramér [5] showed that

1.1 Cramér’s random model
In 1936, Cramér [6] introduced a probabilistic model  of primes, where each natural number \(n\geqslant 3\) is selected for inclusion in
of primes, where each natural number \(n\geqslant 3\) is selected for inclusion in  with probability \(1/\log n\), the events
with probability \(1/\log n\), the events  being jointly independent in \(n\). By Hoeffding’s inequality (or Lemma 3.3 below), for any fixed \(\varepsilon >0\) one has
being jointly independent in \(n\). By Hoeffding’s inequality (or Lemma 3.3 below), for any fixed \(\varepsilon >0\) one has

with probability one.Footnote 2 The analogous statement for primes is equivalent to the Riemann Hypothesis. In 1936, Cramér [6] proved that  almost surely, and remarked: “Obviously we may take this as a suggestion that, for the particular sequence of ordinary prime numbers \(p_{n}\), some similar relation may hold.” Later, Shanks [40] conjectured the stronger bound
almost surely, and remarked: “Obviously we may take this as a suggestion that, for the particular sequence of ordinary prime numbers \(p_{n}\), some similar relation may hold.” Later, Shanks [40] conjectured the stronger bound  , also based on the analysis of a random model very similar to Cramér’s model. This is a natural conjecture in light of the fact that
, also based on the analysis of a random model very similar to Cramér’s model. This is a natural conjecture in light of the fact that

holds with probability one (although (1.2) doesn’t appear to have been observed before). In the literature, the statements  and
and  are sometimes referred to as “Cramér’s conjecture.” Several people have made refined conjectures, e.g., Cadwell [4] has suggested that
are sometimes referred to as “Cramér’s conjecture.” Several people have made refined conjectures, e.g., Cadwell [4] has suggested that  is well-approximated by \((\log x)(\log x-\log _{2} x)\), a conjecture which is strongly supported by numerical calculations of gaps. We refer the reader to Granville [16] or Soundararajan [41] for additional information about the Cramer model and subsequent developments.
is well-approximated by \((\log x)(\log x-\log _{2} x)\), a conjecture which is strongly supported by numerical calculations of gaps. We refer the reader to Granville [16] or Soundararajan [41] for additional information about the Cramer model and subsequent developments.
Tables of prime gaps have been computed up to \(10^{18}\) and beyond (see [35]), thus

a consequence of the gap of size 1132 following the prime 1693182318746371. See also Fig. 1 for a plot of \(G(x)\) versus various approximations.
Despite its utility, the Cramér model has several well-documented weaknesses, the most dramatic one being that the model does not predict the expected asymptotics for prime \(k\)-tuples. Indeed, for any finite set \(\mathcal{H}\subset \mathbb{Z} \), Cramér’s model gives

with probability one, whereas the analogous assertion for prime numbers is false in general (for example, there is no integer \(n\) such that \(n+h\) is prime for all \(h\in \{0,1,2\}\)). The reason for the disparity is simple: for any prime \(p\), every prime other than \(p\) must lie in one of the residue classes \(\{1,\ldots ,p-1\}\) modulo \(p\) (we refer to this as the bias of the primes modulo \(p\)), whereas  is equidistributed over all residue classes modulo \(p\).
is equidistributed over all residue classes modulo \(p\).
See Pintz [36] and Sect. 2.5 below, for further discussion of flaws in the Cramér model.
1.2 Granville’s random model
To correct this flaw in the Cramér model  , Granville [16] altered the model, constructing a random set
, Granville [16] altered the model, constructing a random set  as follows. For each interval \((x,2x]\) (with \(x\) being a power of two, say), let \(A\) be a parameter such that \(A=\log ^{1-o(1)}x\) as \(x\to \infty \), and put \(Q:=\prod _{p\leqslant A} p\). Discard those \(n\) for which \((n,Q)>1\), and select for inclusion in
as follows. For each interval \((x,2x]\) (with \(x\) being a power of two, say), let \(A\) be a parameter such that \(A=\log ^{1-o(1)}x\) as \(x\to \infty \), and put \(Q:=\prod _{p\leqslant A} p\). Discard those \(n\) for which \((n,Q)>1\), and select for inclusion in  each of the remaining integers \(n\in (x,2x]\) with probability \(\frac{Q/\phi (Q)}{\log n}\), where \(\phi \) is the Euler totient function, the events
each of the remaining integers \(n\in (x,2x]\) with probability \(\frac{Q/\phi (Q)}{\log n}\), where \(\phi \) is the Euler totient function, the events  being jointly independent in \(n\). Since \(\phi (Q)/Q\) is the density in ℤ of the set of integers coprime to \(Q\), this model captures the correct global distribution of primes; that is, an analog of (1.1) holds with
being jointly independent in \(n\). Since \(\phi (Q)/Q\) is the density in ℤ of the set of integers coprime to \(Q\), this model captures the correct global distribution of primes; that is, an analog of (1.1) holds with  replaced by
replaced by  . Unlike Cramér’s model, however, Granville’s model also captures the bias of primes in residue classes modulo the primes \(p\leqslant A\). In particular, for any finite set ℋ of integers, Granville’s set satisfies the appropriate analog of the Hardy-Littlewood conjectures for counts of prime \(k\)-tuples (see (1.4) below).
. Unlike Cramér’s model, however, Granville’s model also captures the bias of primes in residue classes modulo the primes \(p\leqslant A\). In particular, for any finite set ℋ of integers, Granville’s set satisfies the appropriate analog of the Hardy-Littlewood conjectures for counts of prime \(k\)-tuples (see (1.4) below).
In contrast with the Cramér model, Granville’s random set  satisfies
satisfies

with probability one. Granville establishes (1.3) by choosing starting points \(a\) with \(Q\mid a\). If \(y\asymp \log ^{2} x\), then there are about \(y/\log y\) numbers \(n\in [a,a+y]\) that are coprime to every \(p\leqslant A\); this is a factor \(\xi \) smaller than the corresponding quantity for a random starting point \(a\), and it accounts for the difference between (1.2) and (1.3). We elaborate on this idea in our analysis of  .
.
1.3 A new probabilistic model for primes
Hardy and Littlewood [19] conjectured that the asymptotic relation

holds for any finite set \(\mathcal{H}\subset \mathbb{Z} \), where \(\mathfrak{S} (\mathcal{H})\) is the singular series given by
Note that the left side of (1.4) is bounded if \(|\mathcal{H}\bmod p|=p\) for some prime \(p\), since then for every integer \(n\), one has \(p\,\mid \,n+h\) for some \(h\in \mathcal{H}\). In this case, \(\mathfrak{S} (\mathcal{H})=0\). We say that ℋ is admissible if \(|\mathcal{H}\bmod p|< p\) for every prime \(p\).
To motivate our model set  , we first reinterpret (1.4) probabilistically. The rapid convergence of the product (1.5) implies that \(\mathfrak{S} (\mathcal{H})\) is well approximated by the truncation
, we first reinterpret (1.4) probabilistically. The rapid convergence of the product (1.5) implies that \(\mathfrak{S} (\mathcal{H})\) is well approximated by the truncation
where
We interpret \(V_{\mathcal{H}}(z)\) as a product of local densities, and \(\Theta _{z}\) as a kind of global density. In order to match the global density of primes as closely as possible, we take \(z=z(t)\) be the largest prime number for which \(1/\Theta _{z(t)} \leqslant \log t\); this is well-defined for \(t \geqslant e^{2}\), and by the prime number theorem we have
It follows that the right side of (1.4) is
On the other hand, the quantity \(V_{\mathcal{H}}(z)\) can be written probabilistically as
where ℙ denotes probability over a uniform choice of residue classes \(a_{p}\bmod p\), for every prime \(p\), with the random variables \(a_{p} \bmod p\) being jointly independent in \(p\), and \(\mathcal{S} _{z}\) is the random set
Thus, \(\mathcal{H}\subset \mathcal{S} _{z}\) is the event that ℋ survives sieving by random residue classes modulo primes \(p\leqslant z\). Consequently, for admissible ℋ, (1.4) takes the form

Thus, (1.4) asserts that the probability that a random shift of ℋ lies in  is asymptotically the same as the probability that ℋ lies in a randomly sifted set.
is asymptotically the same as the probability that ℋ lies in a randomly sifted set.
Motivated by this probabilistic interpretation of (1.4), we now define

as our random set of integers. Note that the number of primes being sieved out increases as \(n\) increases in order to mimic the slowly decreasing density of the primes. This can be compared with the description of  using the sieve of Eratosthenes, in which \(z(n)\) is replaced by \(n^{1/2}\) and the \(a_{p}\) are replaced by 0.
using the sieve of Eratosthenes, in which \(z(n)\) is replaced by \(n^{1/2}\) and the \(a_{p}\) are replaced by 0.
We believe that the random set  is a useful model for primes, especially for studying local statistics such as gaps. On the other hand, the analysis of
is a useful model for primes, especially for studying local statistics such as gaps. On the other hand, the analysis of  presents more difficulties than the analysis of
presents more difficulties than the analysis of  or
or  , owing to the more complicated coupling between events such as
, owing to the more complicated coupling between events such as  and
and  for \(n_{1} \neq n_{2}\).
for \(n_{1} \neq n_{2}\).
1.4 Large gaps from the model
The behavior of  is intimately tied to extremal properties of the interval sieve. To describe this connection, for any \(y \geqslant 2\) let \(W_{y}\) denote the (deterministic) quantity
is intimately tied to extremal properties of the interval sieve. To describe this connection, for any \(y \geqslant 2\) let \(W_{y}\) denote the (deterministic) quantity
where \(\mathcal{S} _{z}\) is defined in (1.9) and the minimum in (1.11) is taken over all choices of the residue classes \(\{a_{p}\bmod p: p\leqslant (y/\log y)^{1/2}\}\). At present, the sharpest known bounds on \(W_{y}\) are
the lower bound being a consequence of Iwaniec’s theory (see [12, Theorem 12.14] or [21]) of the linear sieve, and the upper bound resulting from the particular choice \(a_{p}:=0\bmod p\) for all primes \(p\leqslant (y/\log y)^{1/2}\). There is a folklore conjecture that the upper bound in (1.12) is closer to the truth. The problem of bounding \(W_{y}\) belongs to a circle of problems centered on the question about the maximum number of primes in some interval of length \(x\); see e.g., [20] and [9].
Theorem 1.1
Asymptotic for largest gap in the random model
Put
and define \(\xi :=2e^{-\gamma}=1.1229\ldots \). For any \(\varepsilon >0\), with probability one, we have

for all large \(x\).
The function \(g(u)\) is evidently increasing, and by (1.12) we see that
and so Theorem 1.1 implies that for every \(\varepsilon >0\), almost surely we have

for all large \(x\).
It seems likely that \(g((\xi \pm \varepsilon (x))\log ^{2} x)\sim g(\xi \log ^{2} x)\) whenever \(\varepsilon (x)\) goes to zero as \(x \to \infty \), although we cannot prove this. Assuming this, Theorem 1.1 leads us to the following prediction for gaps between primes:
Conjecture 1.2
Asymptotic for largest gap in the primes
We have

Assuming the previously mentioned folklore conjecture that the lower bound in (1.14) is asymptotically tight in the sense that \(g(u)\sim u\) as \(u\to \infty \), we are then led to the prediction that

This matches the lower bound (1.3) for the gap in the Granville model  .
.
1.5 Hardy-Littlewood from the model
It has been conjectured that a much more precise version of (1.4) holds (see, e.g., Montgomery and Soundararajan [28]), namely:

There is some computational evidence for this strong estimate for certain small sets ℋ; see Sect. 2.1. Granville’s model set  , by contrast, satisfies the analogous relation with an error term that cannot be made smaller than \(O(x/\log ^{|\mathcal{H}|+1} x)\). This occurs because
, by contrast, satisfies the analogous relation with an error term that cannot be made smaller than \(O(x/\log ^{|\mathcal{H}|+1} x)\). This occurs because  is only capturing the bias of
is only capturing the bias of  modulo primes \(p\leqslant A\); that is, the set
modulo primes \(p\leqslant A\); that is, the set  satisfies the analog of (1.16) with \(\mathfrak{S} (\mathcal{H})\) replaced by \(\mathfrak{S} _{A}(\mathcal{H})\).
satisfies the analog of (1.16) with \(\mathfrak{S} (\mathcal{H})\) replaced by \(\mathfrak{S} _{A}(\mathcal{H})\).
The model set  given by (1.10) has been designed with the Hardy-Littlewood conjectures in mind. We establish a uniform analog of (1.16) that holds in a wide range of ℋ.
given by (1.10) has been designed with the Hardy-Littlewood conjectures in mind. We establish a uniform analog of (1.16) that holds in a wide range of ℋ.
Theorem 1.3
Hardy-Littlewood conjecture for the random model
Fix \(c\in [1/2,1)\) and \(\varepsilon >0\). Almost surely, we have

uniformly for all admissible tuples ℋ satisfying \(|\mathcal{H}| \leqslant \log ^{c} x\) and in the range \(\mathcal{H}\subset [0,\exp ( \frac{\log ^{1-c} x}{\log _{2} x} )]\).
In particular, when \(c=\frac{1}{2}\) the error term is \(O(x^{1/2+o(1)})\), which matches (1.16) provided that \(\mathcal{H}\subseteq [0,\exp \{\frac{\log ^{1/2} x}{\log _{2} x} \}]\) and \(|\mathcal{H}|\leqslant \log ^{1/2} x\). As we will invoke the Borel-Cantelli lemma in the proof, the constant implied by the \(O\)-symbol exists almost surely, but we cannot give any uniform bound on it. This remark applies to the next result as well.
For the special case \(\mathcal{H}=\{0\}\) we have the following more precise statement.
Theorem 1.4
Riemann hypothesis for the random model
Fix \(c>3/2\). Almost surely, we have

Similar results can be obtained for any fixed tuple ℋ; we leave this to the interested reader.
1.6 Large gaps from Hardy-Littlewood
The results stated above have a partial deterministic converse. We show that any set of integers that satisfies a uniform analogue of the Hardy-Littlewood conjecture (1.16) has large gaps. The maximal length of the gaps depends on the range of uniformity of (1.16), and comes close to order \(\log ^{2} x\) with a strong uniformity assumption. Our result extends a theorem of Gallagher [14], who showed that if, for every fixed \(k\in \mathbb{N} \) and real \(c>1\), the primes obey the Hardy-Littlewood conjectures uniformly for every admissible \(k\)-tuple \(\mathcal{H}\subset [0,c\log x]\), then the gaps normalized by \(\frac{1}{\log x}\) enjoy an exponential distribution asymptotically. His approach applies to any set  in place of the primes
in place of the primes  .
.
Theorem 1.5
Hardy-Littlewood implies large gaps
Assume \(\frac{2\log _{2} x}{\log x} \leqslant \kappa \leqslant 1/2\) and that  satisfies the Hardy-Littlewood type conjecture
satisfies the Hardy-Littlewood type conjecture

uniformly over all tuples \(\mathcal{H}\subset [0,\log ^{2} x]\) with \(|\mathcal{H}| \leqslant \frac{\kappa \log x}{2\log _{2} x}\). Then

for all large \(x\), where the implied constant is absolute.
We also have the following variant of Theorem 1.5, which has a stronger conclusion but requires a uniform Hardy-Littlewood conjecture for larger tuples (of cardinality as large as \(\log x \log _{2} x\)); on the other hand, this conjecture is only needed in a certain averaged sense.
Theorem 1.6
Averaged Hardy-Littlewood implies large gaps
Fix \(0< c<1\). Suppose that  satisfies the averaged Hardy-Littlewood type conjecture
satisfies the averaged Hardy-Littlewood type conjecture

uniformly for \(k \leqslant \frac{Cy}{\log x}\) and \(\log x \leqslant y \leqslant (\log ^{2} x) \log _{2} x\), where \(C\) is a sufficiently large absolute constant. Then

where \(g\) is defined in (1.13).
One could combine Theorem 1.3 with Theorem 1.5 (taking \(\kappa :=(\log x)^{c-1+\varepsilon }\) with fixed \(c<1\), say) to obtain results similar to Theorem 1.1. However, the conclusion is considerably weaker than that of Theorem 1.1, and it does not appear that this approach is going to come close to recovering the bounds we obtain using a direct argument.
Below we summarize, in rough form, the various results and conjectures for the primes  , the various random models
, the various random models  for the primes, and for arbitrary sets
for the primes, and for arbitrary sets  obeying a Hardy-Littlewood type conjecture:
obeying a Hardy-Littlewood type conjecture:
Set | Hardy-Littlewood conjecture? | Asymptotic largest gap up to x |
|---|---|---|
| No (singular series is missing) | ∼log2x |
| Yes (with weak error term) | g((ξ ± o(1))log2x) |
| Yes (with error \(O(x^{1-c})\)) | g((ξ ± o(1))log2x) |
| Yes (conjecturally) | ∼ξlog2x (conjecturally) |
| Assumed (error \(O(x^{1-c})\)) | \(\gg c \frac{\log ^{2} x}{\log _{2} x}\) |
| Assumed on average (error \(O(x^{1-c})\)) for tuples of size up to (logx)log2x | ≳g((c ξ − o(1))log2x) |
Of course, one can combine this table’s conclusions with the unconditional bounds in (1.14), or the conjecture \(g(u) \sim u\), to obtain further rigorous or predicted upper and lower bounds for the largest gap.
1.7 Open problems
-
(1)
Improve upon the bounds (1.12); alternatively, give some heuristic reason for why the upper bound in (1.12) should be closer to the truth.
-
(2)
Show that \(g(a)\sim g(b)\) whenever \(a\sim b\). This will clean up the statement of Theorem 1.1.
-
(3)
Analyze the distribution of large gaps between special elements of
 . For example, what is the largest gap between elements of
. For example, what is the largest gap between elements of  below \(x\)? This should be a good predictor for the maximal gap between pairs of twin primes and likely will involve a different extremal sieve problem.
below \(x\)? This should be a good predictor for the maximal gap between pairs of twin primes and likely will involve a different extremal sieve problem.
1.8 Plan of the paper
Following further remarks and background inequalities in Sects. 2 and 3, we prove Theorems 1.3 and 1.4 in Sect. 4 using first and second moment bounds. Section 5 and 6 contain probability estimates on \(|[0,y] \cap \mathcal{S} _{w}|\) for various ranges of \(w\). These are then used to prove Theorem 1.1 in Sect. 7 and Theorems 1.5 and 1.6 in Sect. 8. In Sect. 2.4, we connect the interval sieve problem to the problem of “exceptional zeros,” made explicit in Theorem 2.2; this is proved in Sect. 9.
2 Background and further remarks
The discussion here is not needed for the proofs of the main theorems and may be omitted on the first reading.
2.1 Remarks on the Hardy-Littlewood conjectures
For any \(\mathcal{H}\subseteq [0,y]\), we have \(\mathfrak{S} (\mathcal{H}) \leqslant e^{O(|\mathcal{H}| \log _{2} y)}\) (see Lemma 3.4 below), and thus when \(y \leqslant (\log x)^{O(1)}\), the main terms in (1.16) and (1.17) are smaller than one for \(c_{1} \frac{\log x}{\log _{2} x} \leqslant |\mathcal{H}| \leqslant \exp \{ (\log x)^{c_{2}} \}\), where \(c_{1},c_{2}>0\) are appropriate constants. Therefore, we cannot have a genuine asymptotic when \(|\mathcal{H}| > c_{1} \frac{\log x}{\log _{2} x}\).
In the case of primes, it may be the case that (1.16) fails when \(|\mathcal{H}|> \frac{\log x}{\log _{2} x}\) owing to potentially large fluctuations in both the size of \(\mathfrak{S} (\mathcal{H})\) and in the prime counts themselves. We note that Elsholtz [8] has shown that for any \(c>0\), the left side of (1.16) is bounded by
when \(|\mathcal{H}|\geqslant c\log x\), where the implied function \(o(1)\) depends on \(c\). On the other hand, there are admissible tuples with \(|\mathcal{H}|\ll \log x\) for which the left side of (1.16) is zero (see [8] for a construction of such ℋ).
Our assumption in Theorem 1.6 is more speculative, in light of the above remarks, since we need to deal with tuples ℋ satisfying \(k=|\mathcal{H}| > \log x\). Also, simply considering subsets ℋ of the primes in \((y/2,y]\) (which are automatically admissible), we see that there are at least \((\frac{y}{k\log y})^{k}>(\log x)^{k/2}\) tuples ℋ in the summation, and this means that when \(k>\log x\), (1.18) implies a great deal of cancellation in the error terms of (1.17) over tuples ℋ.
In a few special cases, e.g., \(\mathcal{H}=\{0,2\}\), \(\mathcal{H}=\{0,2,6\}\), and \(\mathcal{H}=\{0,4,6\}\), there is extensive numerical evidence (cf. [19, pp. 43–44, 62–64], [32], [24], [33], [34]) in support of the conjecture (1.16) with such a strong error term.Footnote 3 Note that the special case of (1.16) with \(\mathcal{H}=\{0\}\) is equivalent to the Riemann Hypothesis. Theorem 1.3 makes plausible the notion that (1.16) may hold uniformly for \(\mathcal{H}\subset [0,Y]\) with \(|\mathcal{H}|\leqslant K\), where \(Y,K\) are appropriate functions of \(x\).
2.2 The cutoff \(z(t)\)
In [37], Pólya suggests using a truncation \(x^{1/e^{\gamma}}\) to justify the Hardy-Littlewood conjectures. The observation that the cutoff \(\sqrt{x}\) leads to erroneous prime counts was made by Hardy and Littlewood [19, Sect. 4.3] and is occasionally referred to as “the Mertens Paradox” (see [31]). In discussing the probabilistic heuristic for counting the number of primes below \(x\), Hardy and Littlewood write (here \(\varpi \) denotes a prime) “One might well replace \(\varpi <\sqrt{n}\) by \(\varpi < n\), in which case we should obtain a probability half as large. This remark is in itself enough to show the unsatisfactory character of the argument” and later “Probability is not a notion of pure mathematics, but of philosophy or physics.”
2.3 Connection to Jacobsthal’s function
Any improvement of the lower bound in (1.12) leads to a corresponding improvement of the known upper bound on Jacobsthal’s function \(J(w)\), which we define to be the largest gap which occurs in the set of integers that have no prime factor \(\leqslant w\). Equivalently, \(J(w)\) is the largest gap in \(\mathcal{S} _{w}\). Iwaniec [21] proved that \(J(w)\ll w^{2}\) using his linear sieve bounds. Using Montgomery and Vaughan’s explicit version of the Brun-Titchmarsh inequality [29], the cardinality of the set \(\mathcal{S} _{w}(y):=[0,y] \cap \mathcal{S} _{w}\) for \(w > (y/\log y)^{1/2}\) can be bounded from below by
If the right side is positive, it follows that \(J(w)< y\). Suppose, for example, that \(W_{y} \geqslant \alpha y/\log y\) for large \(y\), where \(0<\alpha \leqslant 1\) is fixed. Mertens’ estimates then imply that
which improves Iwaniec’s upper bound.
We remark that all of the unconditional lower bounds on  , including the current record [11], have utilized the simple inequality
, including the current record [11], have utilized the simple inequality  , where \(y\sim \log x\).
, where \(y\sim \log x\).
2.4 The interval sieve problem and exceptional zeros
The problem of determining \(W_{y}\) asymptotically is connected with the famous problem about exceptional zeros of Dirichlet \(L\)-functions (also known as Siegel zeros or Landau-Siegel zeros); see, e.g., [7, Sects. 14, 20, 21, 22] for background on these and [22] for further discussion.
Definition 2.1
We say that exceptional zeros exist if there is an infinite set \(\mathcal{E} \subset \mathbb{N} \), such that for every \(q\in \mathcal{E} \) there is a real Dirichlet character \(\chi _{q}\) and a zero \(1-\delta _{q}\) with \(L(1-\delta _{q},\chi _{q})=0\) and \(\delta _{q}=o(1/\log q)\) as \(q\to \infty \).
Theorem 2.2
Suppose that exceptional zeros exist. Then
Hence, we almost surely have

and Conjecture 1.2implies that

Our proof of Theorem 2.2, given in Sect. 9, is quantitative, exhibiting an upper bound for \(W_{y}\) in terms of the decay of \(\delta _{q}\). Siegel’s theorem [7, Sect. 21] implies that \(\frac{\log 1/\delta _{q}}{\log q} \to 0\), but we cannot say anything about the rate at which this occurs (i.e., the bound is ineffective). If the rate of decay to zero is extremely slow, then our proof shows that, infinitely often, \(W_{y}=f(y) \frac{y\log _{2} y}{\log y}\), with \(f(y)\to \infty \) extremely slowly. Consequently,  is infinitely often close to the upper bound in (1.15).
is infinitely often close to the upper bound in (1.15).
The related quantity
is known by the theory of upper bound sieves to satisfy \(\widetilde{W}_{y} \leqslant \frac{2y}{\log y}\) (see, e.g., [30]), and it is well known that an improvement of the constant two would imply that exceptional zeros do not exist; see, e.g., Selberg’s paper [39]. Theorem 2.2 (in the contrapositive) similarly asserts that an improvement of the constant zero in the trivial lower bound \(W_{y} \geqslant 0\cdot \frac{y}{\log y}\) implies that exceptional zeroes do not exist. Extending our ideas and those of Selberg, Granville [17] has recently shown that if exceptional zeros exist, then for any real \(r>1\),
where \(f,F\) are the lower and upper linear sieve functions. In particular, \(f(r)=0\) for \(r\leqslant 2\) and \(f(r)>0\) for \(r>2\).
It is widely believed that exceptional zeros do not exist, and this is a famous unsolved problem. Theorem 2.2 indicates that to fully understand \(W_{y}\), it is necessary to solve this problem. Iwaniec’s lectures [22] give a nice overview of the problem of exceptional zeros, attempts to prove that they do not exist, and various consequences of their existence. In the paper [10], the second author shows that if there is a sequence of moduli \(q\) with \(\delta _{q}\ll (\log q)^{-2}\), then one can deduce larger lower bounds for \(J(w)\) and  than are currently known unconditionally.
than are currently known unconditionally.
2.5 Primes in longer intervals
With probability one, the Cramér model  also satisfies
also satisfies

as long as \(x\to \infty \), \(y\leqslant x\), and \(y/\log ^{2} x\to \infty \). However, Maier [25] has shown that the analogous statement for primes is false, namely that for any fixed \(A>1\) one has
The disparity between (2.1) and (2.2) again stems from the uniform distribution of  in residue classes modulo primes. Both models
in residue classes modulo primes. Both models  and
and  satisfy the analogs of (2.2); we omit the proofs. Moreover, the ideas behind Theorem 1.1 can be used to sharpen (2.2), by replacing the right sides of the inequalities by quantities defined in terms of the extremal behavior of \(|[0,y] \cap S_{y^{1/u}}|\) for fixed \(u>1\); we refer the reader to [23, Exercise 30.1] for details. The authors thank Dimitris Koukoulopoulos for this observation.
satisfy the analogs of (2.2); we omit the proofs. Moreover, the ideas behind Theorem 1.1 can be used to sharpen (2.2), by replacing the right sides of the inequalities by quantities defined in terms of the extremal behavior of \(|[0,y] \cap S_{y^{1/u}}|\) for fixed \(u>1\); we refer the reader to [23, Exercise 30.1] for details. The authors thank Dimitris Koukoulopoulos for this observation.
By contrast, on the Riemann Hypothesis, Selberg [38] showed that
holds for almost all \(x\) provided that \(y=y(x) \leqslant x\) satisfies \(y/\log ^{2} x \to \infty \) as \(x \to \infty \).
On a related note, Granville and Lumley [18] have developed heuristics and conjectures concerning the maximum number of primes \(\leqslant x\) lying in intervals of length \(L\), where \(L\) varies between \(\log x\) and \(\log ^{2} x\).
2.6 Remarks on the singular series and prime gaps
If \(y\) is small compared to \(x\), the difference  is a random variable with (essentially) a binomial distribution. Letting \(y\to \infty \) with \(y/\log x\) fixed, the result is a Poisson distribution: for any real \(\lambda >0\) and any integer \(k\geqslant 0\), we have
is a random variable with (essentially) a binomial distribution. Letting \(y\to \infty \) with \(y/\log x\) fixed, the result is a Poisson distribution: for any real \(\lambda >0\) and any integer \(k\geqslant 0\), we have

with probability one. In particular, using  as a model for the primes
as a model for the primes  , this leads to the conjecture that
, this leads to the conjecture that
Gallagher [14] showed that if the Hardy-Littlewood conjectures (1.4) are true uniformly for \(\mathcal{H}\subset [0, \log ^{2} x]\) with fixed cardinality \(|\mathcal{H}|\), then (2.4) follows. His analysis relies on the relation
which asserts that the singular series has an average value of one. Sharper versions of (2.5) exist (see, e.g., Montgomery and Soundararajan [28]); such results, however, are uniform only in a range \(|\mathcal{H}| \ll \log _{2} y\) or so, far too restrictive for our use. Reinterpreting the sum on the left side of (2.5) probabilistically, as we have done above, allows us to adequately deal with a much larger range of sizes \(|\mathcal{H}|\). In particular, it is possible to deduce from a uniform version of (1.16) a uniform version of (2.4), although we have not done so in this paper.
We take this occasion to mention a recent unconditional theorem of Mastrostefano [26, Theorem 1.1], which is related to (2.5), and which states that for any integer \(m\geqslant 0\) there is an \(\varepsilon =\varepsilon (m)>0\) so that whenever \(0<\lambda <\varepsilon \), we have

Establishing the Poisson distribution (2.3) unconditionally, even for some fixed \(\lambda \), seems very difficult.
2.7 The maximal gap in Granville’s model
The claimed bounds in Theorem 1.1 are also satisfied by Granville’s random set  , i.e., one has
, i.e., one has

The proof is very short, and we sketch it here as a prelude to the proof of Theorem 1.1. Consider the elements of  in \((x,2x]\) for \(x\) a power of two. In accordance with (1.14), let \(y\) satisfy \(\log ^{2} x \leqslant y=o(\log ^{2} x \log _{2} x)\) and put \(A:=(y/\log y)^{1/2}\), so that \(A=o(\log x)\). Let \(\theta :=\prod _{p\leqslant A} (1-1/p)^{-1} \sim (e^{\gamma}/2)\log y\) and \(Q:=\prod _{p\leqslant A}p\). For simplicity, we suppose that each \(n\in (x,2x]\) with \((n,Q)=1\) is chosen for inclusion in
in \((x,2x]\) for \(x\) a power of two. In accordance with (1.14), let \(y\) satisfy \(\log ^{2} x \leqslant y=o(\log ^{2} x \log _{2} x)\) and put \(A:=(y/\log y)^{1/2}\), so that \(A=o(\log x)\). Let \(\theta :=\prod _{p\leqslant A} (1-1/p)^{-1} \sim (e^{\gamma}/2)\log y\) and \(Q:=\prod _{p\leqslant A}p\). For simplicity, we suppose that each \(n\in (x,2x]\) with \((n,Q)=1\) is chosen for inclusion in  with probability \(\theta /\log x\); this modification has a negligible effect on the size of the largest gap. Fix \(\varepsilon >0\) arbitrarily small. Let \(X_{m}\) denote the event
with probability \(\theta /\log x\); this modification has a negligible effect on the size of the largest gap. Fix \(\varepsilon >0\) arbitrarily small. Let \(X_{m}\) denote the event  .
.
Let \(D_{m}\) denote the number of integers in \((m,m+y]\), all of whose prime factors are larger than \(A\). If we take \(y:=g((\xi +\varepsilon )\log ^{2} x)\), then
by our assumption that \(W_{y}\log y \sim (\xi +\varepsilon )\log ^{2} x\). Summing on \(x\) and applying Borel-Cantelli, we see that almost surely, only finitely many \(X_{m}\) occur.
For the lower bound, we take \(y:=g((\xi -\varepsilon )\log ^{2} x)\) and restrict to special values of \(m\), namely \(m\equiv b \bmod Q\), where \(b\) is chosen so that
Let \(\mathcal{M} :=\{x< m \leqslant 2x: m\equiv b\bmod Q\}\) and let \(N\) be the number of \(m\in \mathcal{M} \) for which \(X_{m}\) occurs. By the above argument, we see that
By assumption, \(|\mathcal{M} |=x^{1-o(1)}\) and hence the right side is \(> x^{\varepsilon /2}\) for large \(x\). Similarly,
By Chebyshev’s inequality, \(\mathbb{P}(N < \frac{1}{2} \mathbb{E}N) \ll 1/\mathbb{E}N \ll x^{-\varepsilon /2}\). Considering all \(x\) and using Borel-Cantelli, we conclude that almost surely every sufficiently large dyadic \((x,2x]\) contains an \(m\) for which \(X_{m}\) occurs.
We remark that our lower bound argument above works as well for the Cramér model, showing (1.2). We take \(A=Q=\theta =b=1\), and the details are simpler.
3 Preliminaries
3.1 Notation
The indicator function of any set \(\mathcal{T} \) is denoted \(\mathbf{1}_{\mathcal{T} } (n)\). We select residue classes \(a_{p} \bmod p\) uniformly and independently at random for each prime \(p\), and then for any set of primes \(\mathcal{Q} \) we denote by  the ordered tuple \((a_{p}:p\in \mathcal{Q} )\); often we condition our probabilities on
the ordered tuple \((a_{p}:p\in \mathcal{Q} )\); often we condition our probabilities on  for a fixed choice of \(\mathcal{Q} \).
for a fixed choice of \(\mathcal{Q} \).
Probability, expectation, and variance are denoted by ℙ, \(\mathbb{E}\), and \(\mathbb{V} \) respectively. We use \(\mathbb{P}_{\mathcal{Q} }\) and \(\mathbb{E}_{\mathcal{Q} }\) to denote the probability and expectation, respectively, with respect to random  . When \(\mathcal{Q} \) is the set of primes in \((c,d]\), we write
. When \(\mathcal{Q} \) is the set of primes in \((c,d]\), we write  , \(\mathbb{P}_{c,d}\) and \(\mathbb{E}_{c,d}\); if \(\mathcal{Q} \) is the set of primes \(\leqslant c\), we write
, \(\mathbb{P}_{c,d}\) and \(\mathbb{E}_{c,d}\); if \(\mathcal{Q} \) is the set of primes \(\leqslant c\), we write  , \(\mathbb{P}_{c}\) and \(\mathbb{E}_{c}\). In particular, \(\mathbb{P}_{c,d}\) refers to the probability over random
, \(\mathbb{P}_{c}\) and \(\mathbb{E}_{c}\). In particular, \(\mathbb{P}_{c,d}\) refers to the probability over random  , often with conditioning on
, often with conditioning on  .
.
Throughout the paper, any implied constants in symbols \(O\), ≪ and ≫ are absolute (independent of any parameter) unless otherwise indicated. The notations \(F\ll G\), \(G\gg F\) and \(F=O(G)\) are all equivalent to the statement that the inequality \(|F|\leqslant c|G|\) holds with some constant \(c>0\). We write \(F\asymp G\) to indicate that \(F\ll G\) and \(G\ll F\) both hold. The notation \(o(1)\) is used to indicate a function that tends to zero as \(x\to \infty \); in expressions like \(1-o(1)\), the function is assumed to be positive. We write \(F \sim G\) when \(F=(1+o(1)) G\) as \(x\to \infty \).
For a set ℋ of integers, we denote \(\mathcal{H}-\mathcal{H}:=\{h-h': h,h'\in \mathcal{H}\}\), and for any integer \(m\), \(\mathcal{H}+m :=\{ h+m:h\in \mathcal{H}\}\).
3.2 Various inequalities
We collect here some standard inequalities from sieve theory and probability that are used in the rest of the paper.
Lemma 3.1
Upper bound sieve, [30, Theorem 3.8]
For \(1\leqslant w\leqslant p \leqslant y\), \(p\) prime, \(b\in \mathbb{Z} /p\mathbb{Z} \), and an arbitrary interval ℐ of length \(y\), we have uniformly
Lemma 3.2
Azuma’s inequality [1]
Suppose that \(X_{0},\ldots ,X_{n}\) is a martingale with \(|X_{j+1}-X_{j}|\leqslant c_{j}\) for each \(j\). Then
Lemma 3.3
Bennett’s inequality [3]
Suppose that \(X_{1},\ldots ,X_{n}\) are independent random variables such that for each \(j\), \(\mathbb{E}X_{j}=0\), and \(|X_{j}|\leqslant M\) holds with probability one. Then
where \(\sigma ^{2}:=\sum _{j} \mathbb{V} X_{j}\), and
Lemma 3.4
For any \(\mathcal{H}\subset [0,y]\) with \(|\mathcal{H}|=k\), we have
and
Proof
Estimate (3.1) follows from the definition of \(\mathfrak{S} (\mathcal{H})\) and the fact that for \(p>y\), \(|\mathcal{H}\bmod p|=k\). Estimate (3.2) is trivial if ℋ is inadmissible, since then \({\mathfrak{S} (\mathcal{H})}=0\), and otherwise (3.2) is a special case of [15, (6.16)]. □
Lemma 3.5
If \(\mathcal{H}\subseteq [0,y]\) is an admissible \(k\)-tuple and \(t\geqslant 2\) satisfies \(z(t) > y\) and \(k\leqslant t^{1/100}\), then
Proof
Let \(z:=z(t)\). By (1.7), \(z \gg t^{1/e^{\gamma}} \gg t^{0.561}\). Using Lemma 3.4 and (1.7), we have
The lemma now follows since \(k\leqslant t^{1/100}\). □
4 Uniform Hardy-Littlewood from the model
In this section, we prove Theorems 1.3 and 1.4 using the first and second moment bounds provided by the following proposition.
Proposition 4.1
First and second moment bounds
Suppose that \(x\) and \(y\) are integers with \(x\geqslant 3\) and \(\sqrt{x}\leqslant y\leqslant x\), and suppose that \(0\leqslant D\leqslant \sqrt{x}\). Let \(\mathcal{H}\subset [0,D]\) be an admissible tuple with \(k:=|\mathcal{H}|\leqslant \frac{\log x}{(\log _{2} x)^{2}}\), and put

Then
Furthermore,
where
Before turning to the proof of the proposition, we first indicate how it is used to prove the two theorems, starting with Theorem 1.4.
Proof of Theorem 1.4
Fix \(c>3/2\). For any integers \(u\geqslant 2\) and \(v\geqslant 0\), we let

We apply Proposition 4.1 in the case that \(\mathcal{H}=\{0\}\), \(k= 1\) and \(D= 0\). By (4.1), if \(v\geqslant \sqrt{u}\) then
Inequality (4.2) implies that
Let \(x\) be a large integer. For integers \(h,m\) with \(2\sqrt{x} \leqslant 2^{m} \leqslant x\) and \(0\leqslant h\leqslant x/2^{m}-1\), let \(G_{m,h}\) be the event that
For large \(x\), (4.3) implies that
Hence, Chebyshev’s inequality yields the bound
Let \(F_{x}\) denote the event that \(G_{h,m}\) holds for all such \(h,m\). By a union bound, we see that \(\mathbb{P}F_{x}=1-O((\log x)^{2-2c})\). On this event \(F_{x}\), for any integer \(y\) with \(1\leqslant y\leqslant x\), we have
Since \(2c-2>1\), the Borel-Cantelli lemma implies that with probability one, \(F_{2^{s}}\) is true for all large integers \(s\). On this event, \(\Delta (2,x) \ll x^{1/2} (\log x)^{c}\) for all real \(x\geqslant 2\), proving the theorem. □
Proof of Theorem 1.3
Fix \(c\in [1/2,1)\) and \(\varepsilon >0\). For integers \(a\geqslant 2\), \(b\geqslant 0\) and a tuple ℋ, define

Let
Let \(u\) be a large integer in terms of \(c\) and \(\varepsilon \), and let \(F_{u}\) denote the event that
for all integers \(a,b\) satisfying \(u\leqslant a \leqslant a+b \leqslant 2u\) and all admissible tuples ℋ satisfying
The number of such ℋ does not exceed \(u^{100/\log _{2} u}=u^{o(1)}\) as \(u\to \infty \).
We again invoke the moment bounds in Proposition 4.1. Assume ℋ satisfies (4.4) and that \(u\leqslant a\leqslant 2u\) and \(\sqrt{a}\leqslant b\leqslant a\). It follows from (4.1) that
and inequality (4.2) implies
where the implied function \(o(1)\) is uniform over all such ℋ, \(a\) and \(b\). For integers \(h,m\) with \(2\sqrt{u} \leqslant 2^{m} \leqslant u\) and \(0\leqslant h \leqslant u/2^{m}-1\), let \(G_{h,m}\) be the event that for all ℋ satisfying (4.4),
Again, if \(u\) is large enough, the expectation of the left side is at most \(\frac{1}{2} u^{\lambda +\varepsilon /2}\), uniformly over all \(h,m,\mathcal{H}\). By a union bound and Chebyshev’s inequality,
Furthermore, as in the proof of Theorem 1.4, we see that if \(u\) is large enough (in terms of \(c,\varepsilon \)) and if \(G_{h,m}\) holds for all \(h,m\), then \(F_{u}\) holds. Therefore,
By Borel-Cantelli, almost surely \(F_{2^{s}}\) is true for all sufficiently large integers \(s\).
Now assume that we are in the event that \(F_{2^{s}}\) holds for all \(s\geqslant s_{0}\). Let \(x\) be sufficiently large such that \(x \geqslant 2^{3s_{0}+1}\) and \(2^{t-1} < x \leqslant t^{s}\), and let ℋ be an admissible tuple with
Note that whenever \(x^{1/3} \leqslant u=2^{s} \leqslant x\) we have (4.4). Thus, using (3.2),

as required for Theorem 1.3. □
The following lemma is needed in the proof of Proposition 4.1. When an admissible tuple ℋ is fixed, define
Lemma 4.2
Let \(2\leqslant u \leqslant v \leqslant 3u\), and suppose ℋ is an admissible tuple with \(k:=|\mathcal{H}| \geqslant 1\). Then
Proof
We begin with the simple bound
By multiple applications of (1.7),
This completes the proof. □
Proof of Proposition 4.1
Suppose that \(\mathcal{H}\subset [0,D]\) with \(k:=|\mathcal{H}| \leqslant \frac{\log x}{(\log _{2} x)^{2}}\). We may assume that \(D\) is an integer. Write \(\nu _{p}:=|\mathcal{H}\bmod p|\) for every prime \(p\). Since \(z(t)\) is increasing and \(\psi _{u}\) is decreasing in \(u\),
Hence,
By Lemma 4.2 and the bound \(\psi _{u}\ll 1/\log u\), the big-\(O\) term is
since \(y\geqslant \sqrt{x}\) and \(1/e^{\gamma} > 1/2\). This proves that
Lemma 3.5 implies that for each integer \(n\in (x,x+y]\) we have
Estimate (3.2) implies that \(\mathfrak{S} (\mathcal{H}) \leqslant x^{o(1)}\) and this proved the estimate (4.1) of the proposition.
For the second moment bound, let \(v\) be a parameter in \([4k,\log x]\) and set \(Q:=\prod _{p\leqslant v} p\). Given integers \(n_{1}\) and \(n_{2}\) with \(x< n_{1} < n_{2} \leqslant x+y\), define \(m\) and \(b\) by
We consider separately the primes \(\leqslant v\) and those \(>v\), setting
Then
For technical reasons, we use the trivial bound \(\mathbb{E}X_{n_{1}}X_{n_{2}}\leqslant \psi _{n_{1}} \leqslant \psi _{x}\) when \(m\in \mathcal{H}-\mathcal{H}\); the total contribution from such terms is \(\leqslant \psi _{x}k^{2} y\), which is an acceptable error term for (4.2).
Now suppose that \(m\notin \mathcal{H}-\mathcal{H}\). For any prime \(p>v\) and integer \(a\in (-p/2,p/2)\), let
Then, given \(v< p\leqslant z(x+y)\) and \(m\) we have
where \(a\) is the unique integer such that
Clearly, \(\lambda _{a}(p) \leqslant \nu _{p} \leqslant k\), and \(\lambda _{a}(p)=0\) unless \(a\in (\mathcal{H}-\mathcal{H})\cap (-p/2,p/2)\). In addition,
Consequently, for any \(p>v\) we have
with
We remark that \(f_{a}(p)\in (0,1]\) since \(p>v\geqslant 4k\geqslant 4\nu _{p} {\geqslant 4\lambda _{a}(p)}\). For a fixed choice of \(a\in \mathcal{H}- \mathcal{H}\) and fixed \(n_{1}\), extend \(f_{a}\) to a multiplicative function supported on squarefree integers whose prime factors all lie in \(I(n_{1},a):=(\max \{v,2|a| \},z(n_{1})]\). If an integer \(r\) has a prime factor outside the interval \(I(n_{1},a)\) or \(r\) is not squarefree, we set \(f_{a}(r):=0\). Then
(since \(m\notin \mathcal{H}-\mathcal{H}\), we always have \(m-a\ne 0\)). Recalling (4.7) we obtain that
where
We now fix \(n_{1}\) and sum over \(n_{2}\). Let
i.e., \(\mathcal{D} (n_{1})\) is the set of all possible vectors of the numbers \(d_{a}\). We compute
where we have dropped the condition \(n_{2}-n_{1}\notin \mathcal{H}-\mathcal{H}\) on the right side. A crucial observation is that for every \(\mathbf{d}\in \mathcal{D} (n_{1})\), the components \(d_{a}\) are pairwise coprime. Indeed, if \(a,a'\) are two distinct elements of \(\mathcal{H}-\mathcal{H}\) and a prime \(p>\max \{v,2|a|,2|a'|\}\) divides both \(d_{a}\) and \(d_{a'}\), then there is some \(m\in [1,y]\setminus (\mathcal{H}-\mathcal{H})\) so that \(p\,\mid \,d_{a}\,\mid \,(m-a)\) and \(p\,\mid \,d_{a'}\,\mid \,(m-a')\). This implies \(a\equiv a'\pmod{p}\), a contradiction. Hence, the innermost sum is a sum over a single residue class modulo \(d:=Q\prod _{a} d_{a}\). For any \(e\in \mathbb{Z} \) we have by (4.5) that
where we used that \(k\leqslant \log x\) and
Therefore,
Now (4.8) implies that
Hence, combining (4.9) and (4.10), and reinserting terms with \(n_{2}-n_{1}\in \mathcal{H}-\mathcal{H}\), for each \(n_{1}\) we obtain that
Extending the first sum over \(\mathbf{d}\) to all pairwise coprime tuples \(\mathbf{d}\) composed of prime factors in \((v,z(n_{1})]\), and applying (4.8) again, we find that
Finally, summing over \(n_{1}\) we conclude that
where
Since \(X_{n}^{2}=X_{n}\) we arrive at
Comparing this with (4.6), it follows that the variance in question satisfies
To bound \(T\), we consider two cases. First, suppose that \(k\leqslant (\log x)^{1/2} / \log _{2} x\), and let \(v:=4k\). In this case, we argue crudely, using (4.8) and \(\nu _{p}\leqslant k\) for all \(p\), obtaining
The prime number theorem implies that \(\log Q \ll v\) and thus \(QT \ll (\log x)^{k^{2}}\). Therefore, (4.11) implies (4.2).
Next, suppose that
and put
so that \(v\geqslant 4k\) and \(Q=x^{o(1)}\). For a parameter \(U\leqslant x^{5}\), to be chosen later, let
We begin with \(\mathcal{D} _{U}^{-}\). For any parameter \(\alpha > 0\) we have, by (4.8),
Let
so that \(\frac{\log _{3} x}{\log _{2} x} \leqslant \alpha \leqslant 1\) by (4.12). Recalling (4.13), we see that
hence it follows that
Next, we turn to \(\mathcal{D} _{U}^{+}\), and make use of the special structure of \(\mathcal{D} (n_{1})\). For any parameter \(\beta \in [0,1)\) we have
Note that each prime \(p\) can appear at most once in the double product, since \(p\mid (m-a)\) and \(p\mid (m-a')\) implies \(p\mid (a-a')\), which forces \(a=a'\). We split the last product into two pieces according to whether \(p\leqslant w\) or \(p>w\), where \(w\) is a parameter to be chosen later. For any \(m\notin \mathcal{H}-\mathcal{H}\) we have
for large \(x\). We bound the contribution of larger primes trivially using the fact that any integer \(m-a\) is divisible by \(\ll \frac{\log x}{\log _{2} x}\) such primes (here, it is crucial that \(m\ne a\)). Thus, for any \(m\notin \mathcal{H}-\mathcal{H}\) we have
We now put
By (4.12) we have \(\beta \geqslant 0\), and clearly \(\beta <1\). It follows that
Comparing (4.14) with (4.15), we choose \(U\) so that \(U^{2\varrho -1}=yU^{-\frac{1-\varrho}{2\varrho +1}}\), that is,
Since \(1/2+o(1) \leqslant \rho \leqslant 1+o(1)\), the exponent of \(y\) is \(\leqslant 4+o(1) \leqslant 5\) for large \(x\). This gives
Inserting this into (4.11) yields the inequality (4.2), and completes the proof of Proposition 4.1. □
5 Random sieving by small primes
Throughout the sequel, we employ the notation
Throughout this section, we assume that \(x\) and \(y\) are large real numbers that satisfy
where \(W_{y}\) is given by (1.11), and \(\alpha ,\beta \) are fixed with \(0<\alpha <\beta \). Note that (1.12) and (5.2) yield the estimates
We adopt the convention that any constants implied by \(O\) and ≪ may depend on \(\alpha ,\beta \) but are independent of other parameters.
We define
and when the value of \(y\) is clear from context we put
Using a variety of tools, we give sharp probability bounds for \(S_{w}\) at five different “checkpoint” values \(w_{1}< w_{2}< w_{3}< w_{4}< w_{5}\) (defined below), with each \(S_{w_{i+1}}\) controlled in terms of \(S_{w_{i}}\) for \(i=1,2,3,4\). Our arguments are summarized as follows, where the range is a range of primes:
Range | Estimation technique |
|---|---|
\([2,w_{1}]\) | Lower bound by \(W_{y}\) (5.4) |
\((w_{1},w_{2}]\) | Buchstab identity, sieve upper bound (Lemma 5.1) |
\((w_{2},w_{3}]\) | Buchstab identity, large sieve, Bennett inequality (Lemma 5.2) |
\((w_{3},w_{4}]\) | Martingale interpretation, Azuma inequality (Lemma 5.3) |
\((w_{4},w_{5}]\) | Graph interpretation, combinatorial expansion (Lemma 6.1) |
\((w_{5},z]\) |
The most delicate part of the argument is dealing with primes \(p\) near \(\log x\), that is, \(w_{1} \leqslant p\leqslant w_{3}\) (see Lemmas 5.1 and 5.2). To initialize the argument, we observe from definition (1.11) of \(W_{y}\) that we have the lower bound
Now we successively increase the sieving range from \(S_{w_{1}}\) to \(S_{w_{2}}\), and so on, up to \(S_{w_{5}}\).
Lemma 5.1
Sieving for \(w_{1} \,{<}\, p \,{\leqslant}\, w_{2}\)
Let \(w_{1}:=(y/\log y)^{1/2}\) and \(w_{2}:=\log x\,\log _{3}x\). With probability one, we have
Proof
In this section and the next one, we adopt the notation \(R_{p}\) for the residue class \(a_{p}\bmod p\). From the Buchstab identity
we have
The sieve upper bound (Lemma 3.1) and Mertens’ theorem together imply that
where
Using (5.2) and the lower bound \(w_{1}^{2}=S_{w_{1}}C_{y}\geqslant W_{y}C_{y}\) we see that
hence
Inserting this bound into (5.6) we find that
The function \(z(\log _{3} x-\log z)\) is increasing for \(z\leqslant e^{-1}\log _{2} x\), hence by (5.7) we have
and the stated result follows from (5.5). □
Lemma 5.2
Sieving for \(w_{2} < p \leqslant w_{3}\)
Let \(w_{2}:=\log x\,\log _{3}x\) and \(w_{3}:= \log x\,(\log _{2}x)^{2}\). Conditional on  satisfying \(S_{w_{2}} \geqslant \frac{1}{2} W_{y}\), we have
satisfying \(S_{w_{2}} \geqslant \frac{1}{2} W_{y}\), we have
Proof
As in the previous lemma, we start with
Let \(X_{p}:=|\mathcal{S} _{w_{2}}(y)\cap R_{p}|-p^{-1}S_{w_{2}}\) for each prime \(p\in (w_{2},w_{3}]\). The variables \(X_{p}\) are independent and have a mean value of zero, and by the sieve upper bound (Lemma 3.1) it follows that
hence
for some absolute constant \(c>0\). Using Montgomery’s Large Sieve inequality (see [12, Equation (9.18)] or [27]),
which implies that
We apply Bennett’s inequality (Lemma 3.3) with \(t:=S_{w_{2}}/(2\log _{3}x)\). By (5.9), (5.10) and (5.3), we have
and therefore
where the last bound follows from (1.12) and our assumption that \(S_{w_{2}}\geqslant \tfrac{1}{2}W_{y}\). Lemma 3.3 now shows that for some constant \(c'>0\),
Thus, with probability at least \(1-O(x^{-100})\) we have
for sufficiently large \(x\). Recalling (5.8), the proof is complete. □
Lemma 5.3
Sieving for \(w_{3} < p \leqslant w_{4}\)
Let \(w_{3}:=\log x\,(\log _{2}x)^{2}\) and \(w_{4}:=y^{4/3}\). Conditional on  satisfying \(S_{w_{3}}\geqslant \frac{1}{4}W_{y}\), we have
satisfying \(S_{w_{3}}\geqslant \frac{1}{4}W_{y}\), we have
Proof
Let \(p_{0}:=w_{3}\) and let \(p_{1} < \cdots <p_{m}\) be the primes in \((w_{3},w_{4}]\). Using the notation (5.1), we define random variables by
The sequence \(X_{0}, X_{1},\ldots ,X_{m}\) is a martingale since

Note that
where we have used (1.12) in the last step.
We apply Azuma’s inequality (Lemma 3.2). If \(p_{j+1}>y\), then \(|X_{j+1}-X_{j}|\ll 1\) since \(\Theta _{w_{3},p_{j}}^{-1}\ll 1\). In the case that \(p_{j+1} \leqslant y\), Lemma 3.1 shows that for any value of \(R_{p_{j+1}}\) we have
Consequently,
Thus, if \(c>0\) is sufficiently small, then Lemma 3.2 shows that
since by (5.11) we have
Using (5.1) and (5.3) we write
then noting that
for any \(Z>0\) we have
In view of (5.12) this implies that
holds provided that
The result follows by taking \(Z:=\frac{X_{0}}{(\log _{2} x)^{1/2}} = \frac{S_{w_{3}}}{(\log _{2} x)^{1/2}}\) and noting that \(\lambda \geqslant 2\). □
6 Random sieving by large primes
In this section, we adopt the notation
from the previous section; however, we do not assume inequalities (5.2) and (5.3), except in Corollary 6.2 below. We do assume that \(y\) is sufficiently large. Sieving by large primes (\(p>y^{4}\), say) is easier because there is a relatively low probability that \(\mathcal{S} \cap R_{p}\ne \varnothing \) and we are able to deploy combinatorial methods.
Lemma 6.1
Sieving for \(w_{4} < p \leqslant w_{5}\)
Let \(v\) be a real number greater than \(w_{4}:=y^{4/3}\), and let \(\vartheta \in [y^{-1/4},1)\). Conditional on  , we have
, we have
Proof
Put \(\mathcal{S} :=\mathcal{S} _{w_{4}}(y)\), \(\ell :=|\mathcal{S} |=S_{w_{4}}\), and let \(\mathcal {P}\) be the set of primes in \((w_{4},v]\). The random residue classes \(\{R_{p}:p\in \mathcal {P}\}\) give rise to a bipartite graph \(\mathcal {G}\) that has vertex sets \(\mathcal{S} \) and \(\mathcal {P}\), with edges connecting the vertices \(s\in \mathcal{S} \) and \(p\in \mathcal {P}\) if and only if \(s\in R_{p}\) (i.e., \(s\equiv a_{p}\bmod p\)). Since \(0 \leqslant s\leqslant y < w_{4}\), for every \(p\) there is at most one vertex \(s\) joined to it. For any \(s\in \mathcal{S} \), let \(d(s)\) be its degree,
and let \(\mathcal{S} ^{+}\) be the set of vertices in \(\mathcal{S} \) of positive degree:
Finally, we denote by \(\mathbf {d}\) the vector \(\big\langle d(s):s\in \mathcal{S} ^{+}\big\rangle \). In this manner, the random residue classes \(\{R_{p}:p\in \mathcal {P}\}\) determine a subset \(\mathcal{S} ^{+}\subset \mathcal{S} \) and a vector \(\mathbf {d}\).
For any subset \(\mathcal{T} =\{t_{1},\ldots ,t_{m}\}\) in \(\mathcal{S} \) and a vector \(\mathbf {r}=\langle r_{1},\ldots ,r_{m}\rangle \) whose entries are positive integers, let \(E(\mathcal{T} ,\mathbf {r})\) be the event that the random graph \(\mathcal {G}\) described above has \(\mathcal{S} ^{+}=\mathcal{T} \) and \(\mathbf {d}=\mathbf {r}\). Since \(\mathcal{S} \subset [0,y]\) and \(w_{4}>y\), we have \(|\mathcal{S} \cap R_{p}|\leqslant 1\) for all \(p\in \mathcal {P}\), and thus
Fixing the primes \(p_{1},\ldots ,p_{h}\in \mathcal {P}\) with \(R_{p} \cap \mathcal{S} \ne \varnothing \), there are \(\binom{h}{r_{1}\, \ldots \, r_{m}}\) ways to choose the graph’s edges connecting the \(p_{i}\) to \(\mathcal{T} \). Consequently,
Relaxing the conditions on the last sum in (6.1), we find that
For fixed \(m\), there are \(\binom{\ell}{m}\) choices for \(\mathcal{T} \); thus, summing over all \(r_{1},\ldots ,r_{m}\) we conclude that
The complete sum over \(m\) of the right side of (6.2) is equal to \(V e^{U\ell}\), and the peak occurs when \(m=(1-e^{-U})\ell +O(1)\). We also have
Standard large-deviation results for the binomial distribution (such as Lemma 3.2) imply that for any \(\delta >0\),
Recalling that \(\ell :=S_{w_{4}}\), we see that the inequality
implies via (6.3) that
for all large \(x\) since \({w_{4}}:=y^{4/3}\) and \(\ell \leqslant y\). Combining our results above, we conclude that
for all large \(x\), and the proof is complete. □
Combining Lemmas 5.1, 5.2, 5.3 and 6.1 (with \(v:=y^{8}\) and \(\vartheta :=y^{-1/10}\)) we obtain the following result.
Corollary 6.2
Sieving for \(w_{1} < p \leqslant w_{5}\)
Assume (5.2), let \(w_{1}:=(y/\log y)^{1/2}\) and \(w_{5}:=y^{8}\). Conditional on  , we have with probability \(1-O(x^{-100})\) that
, we have with probability \(1-O(x^{-100})\) that
Our next result is a very general tool for handling primes larger than \(y^{4}\).
Lemma 6.3
Sieving for \(w_{5} < p \leqslant z\), I
Let \(w\geqslant y^{4}\) and \(\mathcal {P}\) be a set of primes larger than \(w\) such that \(\sum _{p\in \mathcal {P}} 1/p \geqslant 1/10\). Let \(\mathcal{S} \subseteq \mathcal{S} _{w}\) with \(|\mathcal{S} | \leqslant 10y\), and such that for all \(p\in \mathcal {P}\), \(\mathcal{S} \) is distinct modulo \(p\). Conditional on  , we have for all \(0\leqslant g\leqslant | \mathcal{S} |\):
, we have for all \(0\leqslant g\leqslant | \mathcal{S} |\):
where
Proof
Put \(\ell :=|\mathcal{S} |\), and assume that \(\ell \geqslant 1\) (the case \(\ell :=0\) being trivial). Take \(m:=\ell -g\), and let \(\mathcal{T} \), \(\mathbf {r}\), \(E(\mathcal{T} ,\mathbf {r})\) and \(h\) be defined as in Lemma 6.1 with \(|\mathcal{T} |=m=\ell -g\). As before (see (6.1)) we have
For any prime \(p\in \mathcal {P}\) the elements of \(\mathcal{S} \) lie in distinct residue classes modulo \(p\); this implies that \(\mathbb{P}_{\mathcal {P}}(E(\mathcal{T} ,\mathbf {r}))\) can only be nonzero when \(m=h\) in (6.4) (that is, every \(r_{j}:=1\)). Let \(T_{h}\) be the sum over \(p_{1},\ldots ,p_{h}\) in (6.4). Then
Also, note that
Hence, summing over all vectors \(\mathbf {r}\), we find that
This completes the proof. □
Corollary 6.4
Sieving for \(w_{5} < p \leqslant z\), II
Uniformly for \(z^{1/2} \geqslant w \geqslant y^{4}\), we have
Proof
Let \(\Theta :=\Theta _{w,z}\). By Lemma 6.3 with \(\mathcal{S} :=\mathcal{S} _{w}\cap [0,y]\) and \(\mathcal {P}\) the set of primes in \((w,z]\), we have
□
The next lemma has a weaker conclusion than Lemma 6.3 but is more general and is needed for a second moment argument below in which we derive a lower bound for the largest prime gap in \([0,x]\).
Lemma 6.5
Sieving for \(w_{5} < p \leqslant z\), III
Let \(w\) and \(z\) be real numbers for which \(z^{1/2}\geqslant w\geqslant y^{8}\). Let \(\mathcal{S} \subset \mathcal{S} _{w} \cap [0,e^{y}]\) with \(|\mathcal{S} |\leqslant y\) and such that for every prime \(p>w\), no more than two numbers in \(\mathcal{S} \) lie in any given residue class modulo \(p\). Then
Proof
Put \(\ell :=|\mathcal{S} |\), and let \(\mathcal {P}\) be the set of primes in \((w,z]\), and put
Note that the bound
holds if \(y\) is large enough.
By assumption, for every \(p\in \mathcal{Q} \), \(| \mathcal{S} \cap R_{p}| \leqslant 2\). Let \(E_{m}\) be the event that for \(\mathcal{S} \cap R_{p}\ne \varnothing \) holds for precisely \(m\) primes \(p\in \mathcal{Q} \). Since for any prime \(p\in \mathcal {P}\) the probability that \(\mathcal{S} \cap R_{p}\ne \varnothing \) does not exceed \(\ell /p\), using (6.5) we have
Assume the event \(E_{m}\) occurs, and fix  . If \(\mathcal{S} \) has precisely \(n\) elements covered by \(\bigcup _{p\in \mathcal{Q} }R_{p}\), then \(0\leqslant n\leqslant 2m\), the upper bound being a consequence of our hypothesis on \(\mathcal{S} \). Put
. If \(\mathcal{S} \) has precisely \(n\) elements covered by \(\bigcup _{p\in \mathcal{Q} }R_{p}\), then \(0\leqslant n\leqslant 2m\), the upper bound being a consequence of our hypothesis on \(\mathcal{S} \). Put
so that \(|\mathcal{S} '|=\ell -n\). Lemma 6.3 implies that
since
by (6.5). Now \(\mathbb{P}_{\mathcal{Q} }(E_{0})=1-O(y^{4}/w)\) by (6.6), so we conclude that
This completes the proof. □
7 The behavior of the largest gap
In this section we use the estimates from the previous section to complete the proof of Theorem 1.1. In Theorems 7.1 and 7.2 below, we suppose that
We also note that
and hence
Theorem 7.1
Probabilistic upper bound for gap
For large \(x\),

Theorem 7.2
Probabilistic lower bound for gap
If \(x\) is large then

Proof of Theorem 7.1
Let \(y:=g((1+\varepsilon )\xi (\log \tfrac{x}{2})^{2})\), so that by (7.2) we have
We also have by (1.12) the bounds
Let \(z:=z(x)\). The probability that  has a gap of size \(\geqslant y\) does not exceed the probability that \(\mathcal{S} _{z}\cap [0,x]\) has a gap of size \(\geqslant y\), which in turn is at most
has a gap of size \(\geqslant y\) does not exceed the probability that \(\mathcal{S} _{z}\cap [0,x]\) has a gap of size \(\geqslant y\), which in turn is at most
Let \(w_{1}:=(y/\log y)^{1/2}\) and \(w_{5}:=y^{8}\) as before. Also put \(\eta :=\frac{\log _{4} x}{\log _{3} x}\). Applying Corollary 6.2 together with (7.3), it follows that with probability \(1-O(x^{-100})\) we have
using (7.1) in the final step. Fix  so that \(S_{w_{5}}\) satisfies this inequality. Taking into account that
so that \(S_{w_{5}}\) satisfies this inequality. Taking into account that
Lemma 6.3 now shows that
as required. □
Proof of Theorem 7.2
Set \(y:=g((1-\varepsilon )\xi (\log 2x)^{2})\), so that
Again, (1.12) implies that
Let \(z:=z(x/2)\), \(w_{1}:=(y/\log y)^{1/2}\), \(w_{5}:=y^{8}\) and \(\eta :=\frac{\log _{4} x}{\log _{3} x}\). In particular, \(z\sim (x/2)^{1/e^{\gamma}}\) by (1.7), and
It suffices to show that with high probability, \(\mathcal{S} _{z}\cap (x/2,x]\) has a gap of size \(\geqslant y\), for this implies that  has a gap of size \(\geqslant y\) within \([0,x]\). For the sake of brevity we write
has a gap of size \(\geqslant y\) within \([0,x]\). For the sake of brevity we write
That is, \(F(u,v)\) counts the number of elements in \([u,u+y]\) sieved by the primes \(\leqslant v\). In particular, \(S_{w}=F(0,w)\). There is some vector \((b_{p})_{p\in w_{1}}\) so that there are exactly \(W_{y}\) integers in \([0,y]\) that avoid the residue classes \((b_{p} \bmod p)_{p\leqslant w_{1}}\). Setting
for any  , there is a progression \(b\bmod Q\) such that
, there is a progression \(b\bmod Q\) such that
Specifically, choose \(b\) such that \(b\equiv a_{p}-b_{p}\bmod p\) for all primes \(p\leqslant w_{1}\). Let \(\mathcal{U} \) be the set of integers \(u\equiv b\bmod Q\) such that \([u,u+y]\subset (x/2,x]\). We show that with high probability, \(F(u,z)=0\) for at least one \(u\in \mathcal{U} \).
By Corollary 6.2, with probability at least \(1-O(x^{-100})\), we have for any given \(u\in \mathcal{U} \) the bound
Let \(E\) be the event that this bound holds for every \(u\in \mathcal{U} \). By the union bound, \(\mathbb{P}_{w_{1},w_{5}}(E)\geqslant 1-O(x^{-99})\). Conditioning on \(E\), we denote
The sets \(\mathcal{U} _{r}\) depend only on  , and \(\mathcal{U} _{r}=\varnothing \) unless \(r=(\tfrac{1}{16}+O(\eta ))W_{y}\) by (7.6). Rather than work with all \(r\), we focus on a popular value of \(r\); thus, let \(\ell \) be fixed with the property that \(|\mathcal{U} _{\ell}|\geqslant | \mathcal{U} _{r}|\) for all \(r\). By (7.5), we have
, and \(\mathcal{U} _{r}=\varnothing \) unless \(r=(\tfrac{1}{16}+O(\eta ))W_{y}\) by (7.6). Rather than work with all \(r\), we focus on a popular value of \(r\); thus, let \(\ell \) be fixed with the property that \(|\mathcal{U} _{\ell}|\geqslant | \mathcal{U} _{r}|\) for all \(r\). By (7.5), we have
Combining (7.4) with (7.6) and (7.1), we have
Next, let
which counts those intervals indexed by \(u\in \mathcal{U} _{\ell}\) for which \(\mathcal{F} (u,w_{5})\) is covered by \(\bigcup _{w_{5}< p\leqslant z} R_{p}\). We analyze \(M\) using first and second moments. Firstly, by Lemma 6.3,
where
To bound the second moment of \(M\), apply Lemma 6.5 with \(\mathcal{S} :=\mathcal{F} (u,w_{5}) \cup \mathcal{F} (u',w_{5})\), where \(u\) and \(u'\) are distinct elements of \(\mathcal{U} _{\ell}\). The hypotheses of Lemma 6.5 are satisfied as any prime \(p>w_{5}>y\) can divide at most two elements of \(\mathcal{S} \). We obtain
By (7.7), (7.8) and (7.9) we have
for large \(x\), and hence we bound the variance by
Thus, Chebyshev’s inequality implies
In particular, with probability at least \(1-O(y^{-4})=1-O((\log x)^{-8})\) there is an interval \([u,u+y]\) in \((x/2,x]\) completely sieved out by  . □
. □
Proof of Theorem 1.1
Let \(x_{j}:=2^{j}\) vary over positive integers \(j\), and let \(\varepsilon >0\) be fixed. Theorem 7.1 implies that for large \(j\) we have

The convergence of \(\sum _{j} x_{j}^{-\varepsilon /2}\) implies, via the Borel-Cantelli lemma, that almost surely there is a \(J\) so that

As  and \(g\) are both increasing functions, the above relation implies that for all \(x_{j-1} < x \leqslant x_{j}\) and \(j>J\) we have
and \(g\) are both increasing functions, the above relation implies that for all \(x_{j-1} < x \leqslant x_{j}\) and \(j>J\) we have

In a similar manner, Theorem 7.2 and Borel-Cantelli imply that almost surely there is a \(J\) so that

As before, this implies that

□
8 Large gaps from Hardy-Littlewood
To prove Theorems 1.5 and 1.6, we start with a simple inclusion-exclusion result (a special case of the Bonferroni inequalities or the “Brun pure sieve”).
Lemma 8.1
Brun’s sieve
Suppose that \(y \geqslant 1\), let  be sets of positive integers, and put
be sets of positive integers, and put

and

Then, for any even \(K\) we have \(T\leqslant U_{K}\), and for any odd \(K\) we have \(T\geqslant U_{K}\).
Proof
For any integers \(K,m\geqslant 0\) let
Observe that
hence, taking  we have
we have
where \(\theta \geqslant 0\) if \(K\) is even and \(\theta \leqslant 0\) if \(K\) is odd. Also,
since

and the lemma is proved. □
Proof of Theorem 1.5
Although Theorem 1.5 concerns the behavior of a specific set  , our first task is to express the gap-counting function for
, our first task is to express the gap-counting function for  in terms of the random quantities with which we have been working in the past few sections.
in terms of the random quantities with which we have been working in the past few sections.
First, observe that (1.17) with \(\mathcal{H}=\{0\}\) implies that

and it follows trivially that  . Therefore, by adjusting the implied constant in the conclusion of the theorem, we may assume that
. Therefore, by adjusting the implied constant in the conclusion of the theorem, we may assume that
for a sufficiently large constant \(D\).
Let \(x\) be a large real number, put \(\mathcal{N} :=[x/2,x]\) and let \(y,K\) be integer parameters to be chosen later, with \(K\) odd and with \(K\leqslant \frac{\kappa \log x}{2\log _{2} x}\). Define \(T\) and \(U_{K}\) as in Lemma 8.1. Since \(T\geqslant U_{K}\) by Lemma 8.1, our aim is to show that \(U_{K}\geqslant 1\). Using (1.17) we see that
where
By Lemma 3.5, replacing \(\mathfrak{S} (\mathcal{H})/\log ^{k} t\) with \(V_{\mathcal{H}}(z(t))\) induces an additive error of size \(O(E)\) since \(\kappa \leqslant 1/2\). Also, (1.8) implies that
and we get
Since \(K\) is odd, the sum on \(k\) is a lower bound for \(\mathbb{P}(S_{z(t)}=0)\); adding the term \(k=K+1\) switches the inequality (cf. the proof of Lemma 8.1) and thus
Let
The upper bound sieve (Lemma 3.1) implies the crude bound \(S_{w} \leqslant Cy/\log y\) for some absolute constant \(C\). We now put
With these choices, \(K \leqslant \frac{\kappa \log x}{2\log _{2} x}\) and, using (8.1), we have
It also follows that
for all large \(x\). Corollary 6.4 and the crude bound \(\Theta _{w,z} \leqslant 8\frac{\log y}{\log x}\) imply that
where we used (8.3) in the last step. It remains to show that \(\mathbb{P}_{z(t)}(S_{z(t)}=0)\) is substantially larger. Lemma 6.3 implies immediately that
as required. Combining these estimates with (8.2) gives
the last inequality following from (8.4), the fact that \(D\) is sufficiently large, and that \(y/\log x \ll \kappa /\log _{2} x\). This completes the proof of Theorem 1.5. □
Proof of Theorem 1.6
Let \(x\) be large, let \(\varepsilon >0\), and let \(y:=g((1-\varepsilon )c\,\xi \log ^{2} x)\). By (7.2),
In particular, (5.2) holds, with \(\alpha ,\beta \) depending on \(c\). Also, from (1.12) we have
Let
Again, let \(\mathcal{N} :=(x/2,x]\), and define \(C\) as in the previous proof. We apply Lemma 8.1 with
so that \(K\leqslant \frac{200 C y}{\log x}\). Similarly to (8.2) we get that
where, because the function \(\mathfrak{S} _{z(t)}(\mathcal{H})\) appears already in (1.18), as does the averaging over ℋ, we have
By the same reasoning as in the proof of Theorem 1.5, we get that
where we used (8.6) in the last step.
Let \(w:=y^{8}\) and fix  . By Lemma 6.3 we have
. By Lemma 6.3 we have
Now put \(w_{1}:=(y/\log y)^{1/2}\), and let  be fixed such that \(S_{w_{1}}=W_{y}\). This occurs with probability \(\geqslant x^{-o(1)}\), since \((y/\log y)^{1/2}=o(\log x)\) by (8.6). Conditional on
be fixed such that \(S_{w_{1}}=W_{y}\). This occurs with probability \(\geqslant x^{-o(1)}\), since \((y/\log y)^{1/2}=o(\log x)\) by (8.6). Conditional on  , Corollary 6.2 implies that with probability at least \(1-O(x^{-100})\) we have
, Corollary 6.2 implies that with probability at least \(1-O(x^{-100})\) we have
where \(\eta :=\frac{\log _{4} x}{\log _{3} x}\) as before and the implied constants may depend on \(c\). Now fix \(w\) such that the above holds. Since
(8.5) implies that
where we have used (8.5) in the last step. Inserting this last estimate into (8.10), we conclude that
In particular, the right side of (8.11) has larger order than the right sides in (8.8) and (8.9). Thus, inserting (8.8), (8.9) and (8.11) into (8.7), we conclude that \(U_{K}\geqslant 1\) if \(x\) is sufficiently large depending on \(\varepsilon \). By a simple diagonalization argument, the same claim then holds for some \(\varepsilon =\varepsilon (x)=o(1)\) going to zero sufficiently slowly as \(x \to \infty \). This completes the proof of Theorem 1.6. □
9 The influence of exceptional zeros
In this section, we show that the existence of exceptional zeros implies that \(W_{y}\) is rather smaller than the upper bound in (1.12) infinitely often.
Theorem 9.1
Let \(q\in \mathbb{N} \), and suppose that there is a real Dirichlet character \(\chi _{q}\) mod \(q\) such that \(L(1-\delta _{q},\chi _{q})=0\) and \(0<\delta _{q} \leqslant \frac{c}{\log q}\), where \(c:=1/11^{2}\). For
we have
Proof
Denote by \(\pi (x;q,a)\) the number of primes \(p\leqslant x\) lying in the progression \(a\bmod q\). By hypothesis, \(qy \geqslant q^{1+1/\sqrt{c}}=q^{12}\), therefore we may apply [42, Corollary 1.4], obtaining
where
By Siegel’s Theorem [7, §21], for any \(\varepsilon >0\), \(\delta _{q} \gg _{\varepsilon }q^{-\varepsilon }\). We conclude that
This may also be deduced from Gallagher’s prime number theorem [13, Theorem 7].
Define the residue classes \(a_{p}\) by \(qa_{p}+1\equiv 0\bmod{p}\) when \(p\nmid q\). Let \(\mathcal{T} \) denote the set of \(n\leqslant y\) with \(n\not \equiv a_{p}\bmod{p}\) for all \(p\nmid q\) such that \(p\leqslant \sqrt{y/\log y}\). Then for any \(n\in \mathcal{T} \), \(qn+1\) is either prime or the product of two primes \(>\sqrt{y/\log y}\). Then we make a greedy choice of \(a_{p}\) for \(p\mid q\), choosing successively \(a_{p}\) so that \(a_{p}\bmod p\) covers a proportion at least \(1/p\) of the remaining elements of \(\mathcal{T} \). This shows that
where \(\overline{p}\) is the inverse of \(p\) modulo \(q\). Siegel’s theorem implies that \(\log y \leqslant q^{o(1)}\). Applying the Brun-Titchmarsh theorem to the sum over \(p\), we see that
This completes the proof. □
Proof of Theorem 2.2
Let \(q\in Q\), and apply Theorem 9.1 with \(y=y_{q}\) defined by (9.1). By assumption, \(\frac{\log y_{q}}{\log q} \to \infty \) as \(q\to \infty \), and hence that
This shows that \(W_{y_{q}}=o (y_{q}/\log y_{q})\), and the remaining parts of Theorem 2.2 follow immediately. □
References
Azuma, K.: Weighted sums of certain dependent random variables. Tohoku Math. J. 19, 357–367 (1967)
Baker, R.C., Harman, G., Pintz, J.: The difference between consecutive primes. II. Proc. Lond. Math. Soc. (3) 83(3), 532–562 (2001)
Bennett, G.: Probability inequalities for the sum of independent random variables. J. Am. Stat. Assoc. 57, 33–45 (1962)
Cadwell, J.H.: Large intervals between consecutive primes. Math. Comput. 25, 909–913 (1971)
Cramér, H.: Some theorems concerning prime numbers. Ark. Mat. Astron. Fys. 15(5), 1–32 (1920)
Cramér, H.: On the order of magnitude of the difference between consecutive prime numbers. Acta Arith. 2(1), 23–46 (1936)
Davenport, H.: Multiplicative Number Theory, 3rd edn. Graduate Texts in Mathematics, vol. 74. Springer, New York (2000)
Elsholtz, C.: Upper bounds for prime \(k\)-tuples of size \(\log N\) and oscillations. Arch. Math. (Basel) 82, 33–39 (2004)
Erdős, P., Richards, I.: Density functions for prime and relatively prime numbers. Monatshefte Math. 83, 99–112 (1977)
Ford, K.: Large prime gaps and progressions with few primes. Riv. Mat. Univ. Parma 12(1), 41–47 (2021). Proceedings of Second Symposium on Analytic Number Theory Cetraro, Italy, July 8–12, 2019.
Ford, K., Green, B., Konyagin, S., Maynard, J., Tao, T.: Long gaps between primes. J. Am. Math. Soc. 31(1), 65–105 (2018)
Friedlander, J., Iwaniec, H.: Opera de Cribro. Am. Math. Soc., Providence (2010)
Gallagher, P.X.: A large sieve density estimate near \(\sigma =1\). Invent. Math. 11, 329–339 (1970)
Gallagher, P.X.: On the distribution of primes in short intervals. Mathematika 23(1), 4–9 (1976)
Goldston, D.A., Pintz, J., Yıldırım, C.Y.: Primes in tuples I. Ann. Math. 170, 819–862 (2009)
Granville, A.: Harald Cramér and the distribution of prime numbers, Harald Cramér Symposium, Stockholm, 1993. Scand. Actuar. J. 1, 12–28 (1995)
Granville, A.: Sieving intervals and Siegel zeros. Acta Arith. 205(1), 1–19 (2022)
Granville, A., Lumley, A.: Primes in short intervals: Heuristics and calculations, preprint. arXiv:2009.05000
Hardy, G.H., Littlewood, J.E.: Some problems of Partitio numerorum (III): on the expression of a number as a sum of primes. Acta Math. 44(1), 1–70 (1922)
Hensley, D., Richards, I.: Primes in intervals. Acta Arith. 25, 375–391 (1973/74)
Iwaniec, H.: On the error term in the linear sieve. Acta Arith. 19, 1–30 (1971)
Iwaniec, H.: Conversations on the exceptional character. In: Perelli, A., Viola, C. (eds.) Analytic Number Theory, lectures given at the C.I.M.E. summer school in Cetraro, Italy. Lecture Notes in Mathematics, vol. 1891, pp. 97–132. Springer, Berlin (2002)
Koukoulopoulos, D.: The distribution of prime numbers. To be published
Leikauf, P., Waldvogel, J.: Finding clusters of primes, I, preprint. https://www.sam.math.ethz.ch/~waldvoge/Projects/clprimes03.pdf
Maier, H.: Primes in short intervals. Mich. Math. J. 32(2), 221–225 (1985)
Mastrostefano, D.: Positive proportion of short intervals containing a prescribed number of primes. Bull. Aust. Math. Soc. 100(3), 378–387 (2019)
Montgomery, H.L.: A note on the large sieve. J. Lond. Math. Soc. 43, 93–98 (1968)
Montgomery, H.L., Soundararajan, K.: Primes in short intervals. Commun. Math. Phys. 252(1–3), 589–617 (2004)
Montgomery, H.L., Vaughan, R.C.: The large sieve. Mathematika 20, 119–135 (1973)
Montgomery, H.L., Vaughan, R.C.: Multiplicative Number Theory I. Classical Theory. Cambridge Studies in Advanced Mathematics, vol. 97. Cambridge University Press, Cambridge (2007)
Montgomery, H.L., Wagon, S.: A heuristic for the prime number theorem. Math. Intell. 28(3), 6–9 (2006)
Nicely, T.R.: Enumeration to \(10^{14}\) of the twin primes and Brun’s constant. Va. J. Sci. 46(3), 195–204 (1995)
Nicely, T.R.: New evidence for the infinitude of some prime constellations, preprint. http://www.trnicely.net/ipc/ipc1d.html
Nicely, T.R.: Prime constellations research project, web pages: http://www.trnicely.net/counts.html
Nicely, T.R.: First occurrence prime gaps, web page: http://www.trnicely.net/gaps/gaplist.html
Pintz, J.: Cramér vs. Cramér. On Cramér’s probabilistic model for primes. Funct. Approx. Comment. Math. 37(2), 361–376 (2007)
Pólya, G.: Heuristic reasoning in the theory of numbers. Am. Math. Mon. 66, 375–384 (1959)
Selberg, A.: On the normal density of primes in small intervals, and the difference between consecutive primes. Arch. Math. Naturvidensk. 47(6), 87–105 (1943)
Selberg, A.: Remarks on sieves. In: Proc. 1972 Number Theory Conference, University of Colorado at Boulder, August 14–18, pp. 205–216 (1972)
Shanks, D.: On maximal gaps between successive primes. Math. Comput. 18, 646–651 (1964)
Soundararajan, K.: The distribution of prime numbers. In: Equidistribution in Number Theory, An Introduction. NATO Sci. Ser. II Math. Phys. Chem., vol. 237, pp. 59–83. Springer, Dordrecht (2007)
Thorner, J., Zaman, A.: Refinements to the prime number theorem for arithmetic progressions, preprint. arXiv:2108.10878
Acknowledgements
The authors thank Andrew Granville, Ben Green, D. R. Heath-Brown, Henryk Iwaniec, Dimitris Koukoulopoulos, James Maynard, Carl Pomerance and Joni Teräväinen for useful discussions, especially concerning the interval sieve problem.
Funding
The first author was supported by a grant from the University of Missouri Research Board. The second author was supported by National Science Foundation grants DMS-1501982 and DMS-1802139. The third author was supported by a Simons Investigator grant, the James and Carol Collins Chair, the Mathematical Analysis & Application Research Fund Endowment, and by NSF grant DMS-1764034. Part of the work was accomplished during a visit of the second author to the University of Missouri (August 2017), UCLA (November 2018), the University of Cambridge (March 2019), the University of Oxford (March-June, 2019) and the Institute of Mathematics of the Bulgarian Academy of Sciences (June-July, 2019). He thanks them all for their support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Banks, W., Ford, K. & Tao, T. Large prime gaps and probabilistic models. Invent. math. 233, 1471–1518 (2023). https://doi.org/10.1007/s00222-023-01199-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-023-01199-0





 vs. various approximations
vs. various approximations





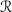 . For example, what is the largest gap between elements of
. For example, what is the largest gap between elements of  below
below