Abstract
Motivated by topology, we develop a general theory of traces and shadows for an endobicategory, which is a pair: bicategory  and endobifunctor
and endobifunctor  . For a graded linear bicategory and a fixed invertible parameter q, we quantize this theory by using the endofunctor \(\Sigma _q\) such that \(\Sigma _q \alpha :=q^{-\deg \alpha }\Sigma \alpha \) for any 2-morphism \(\alpha \) and coincides with \(\Sigma \) otherwise. Applying the quantized trace to the bicategory of Chen–Khovanov bimodules we get a new triply graded link homology theory called quantum annular link homology. If \(q=1\) we reproduce Asaeda–Przytycki–Sikora homology for links in a thickened annulus. We prove that our homology carries an action of
. For a graded linear bicategory and a fixed invertible parameter q, we quantize this theory by using the endofunctor \(\Sigma _q\) such that \(\Sigma _q \alpha :=q^{-\deg \alpha }\Sigma \alpha \) for any 2-morphism \(\alpha \) and coincides with \(\Sigma \) otherwise. Applying the quantized trace to the bicategory of Chen–Khovanov bimodules we get a new triply graded link homology theory called quantum annular link homology. If \(q=1\) we reproduce Asaeda–Przytycki–Sikora homology for links in a thickened annulus. We prove that our homology carries an action of  , which intertwines the action of cobordisms. In particular, the quantum annular homology of an n-cable admits an action of the braid group, which commutes with the quantum group action and factors through the Jones skein relation. This produces a nontrivial invariant for surfaces knotted in four dimensions. Moreover, a direct computation for torus links shows that the rank of quantum annular homology groups depend on the quantum parameter q.
, which intertwines the action of cobordisms. In particular, the quantum annular homology of an n-cable admits an action of the braid group, which commutes with the quantum group action and factors through the Jones skein relation. This produces a nontrivial invariant for surfaces knotted in four dimensions. Moreover, a direct computation for torus links shows that the rank of quantum annular homology groups depend on the quantum parameter q.











Similar content being viewed by others
Notes
Following [31] we say that a bimodule is sweet if it is finitely generated and projective when considered as a left and as a right module separately.
A category is pregraded if its sets of morphisms are graded modules.
Notice the difference between \(\epsilon \) and the evaluation map \( ev {:}\,P^*\otimes P\rightarrow A\), the latter being a homomorphism of (A, A)-bimodules.
A bicategory is small if its 2-morphisms (and so objects as well as 1-morphisms) form a set.
Notice that
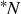 is projective as a left module, but not necessarily as a right one. Hence, in general, it is not a 1-morphism in \(\tilde{\mathbf {R}}\mathbf {ep}\).
is projective as a left module, but not necessarily as a right one. Hence, in general, it is not a 1-morphism in \(\tilde{\mathbf {R}}\mathbf {ep}\).A support of an isotopy is the closure of the set of points that are not stationary under the isotopy.
That is the isomorphism class of a bimodule [M] is identified with \([M']+[M'']\) whenever there is an exact sequence \(0\rightarrow M'\rightarrow M\rightarrow M''\rightarrow 0\).
Formally, objects in
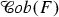 are now symbols \(T\{i\}\) formed by a flat tangle \(T\subset F\) and \(i\in \mathbb {Z}\).
are now symbols \(T\{i\}\) formed by a flat tangle \(T\subset F\) and \(i\in \mathbb {Z}\).Locality means that each picture represents a part of a cobordism inside a ball in \(F\times I\).
Clearly, those diagrams in which each circle carries at most one dot form a free basis for
 .
.Recall that \(M\circ N := N\otimes M\) in \(\mathbf {Birep}\).
References
Asaeda, M., Frohman, C.: A note on the Bar-Natan skein module. Int. J. Math. 18, 1225–1243 (2007). Preprint arXiv:math/0602262
Asaeda, M.M., Przytycki, J.H., Sikora, A.S.: Categorification of the Kauffman bracket skein module of I—bundles over surfaces. Algebra Geom. Topol. 4, 1177–1210 (2004). Preprint arXiv:math/0409414
Auroux, D., Grigsby, J.E., Wehrli, S.M.: Sutured Khovanov homology, Hochschild homology, and the Ozsváth–Szabó spectral sequence. Trans. Am. Math. Soc. 367, 7103–7131 (2015). Preprint arXiv:1303.1986
Bar-Natan, D.: Khovanov homology for tangles and cobordisms. Geom. Topol. 9, 1443–1499 (2005). Preprint arXiv:math/0410495
Bar-Natan, D.: Fast Khovanov homology. J. Knot Theory Ramif. 16, 243–256 (2007). Preprint arXiv:math/0606318
Beliakova, A., Blanchet, C., Gainutdinov, A.M.: Modified Trace is a Symmetric integral. Preprint arXiv:1801.00321
Beliakova, A., Guliyev, Z., Habiro, K., Lauda, A.: Trace as an alternative decategorification functor. Acta Math. Vietam 39, 425–480 (2014). Preprint arXiv:1409.1198
Beliakova, A., Habiro, K., Lauda, A., Zivkovic, M.: Trace decategorification of categorified quantum \(sl_2\), to appear in Adv. Math. Preprint arXiv:1404.1806
Beliakova, A., Hogancamp, M., Putyra, K.K., Wehrli, S.M.: Quantum link homology via trace functor II. Functoriality, in preparation
Beliakova, A., Hogancamp, M., Putyra, K.K., Wehrli, S.M.: Colored annular quantum link homology in preparation
Bénabou, J.: Introduction to Bicategories. Reports of the Midwest Category Seminar. Springer, Berlin (1967)
Ben-Zvi, D., Brochier, A., Jordan, D.: Integrating quantum groups over surfaces: quantum character varieties and topological field theory. Preprint arXiv:1501.04652
Bergman, G.M.: The diamond lemma for ring theory. Adv. Math. 29, 178–218 (1978)
Blanchet, C.: An oriented model for Khovanov homology. J. Knot. Theory Ramif. 19, 291–312 (2010). Preprint arXiv:1405.7246
Boerner, J.: Homology of framed links embedded in thickened surfaces. Preprint arXiv:0810.5566
Braden, T.: Perverse sheaves on Grassmannians. Can. J. Math. 54, 493–532 (2002). Preprint arXiv:math/9907152
Brundan, J., Stroppel, C.: Highest weight categories arising from Khovanov’s diagram algebra I: cellularity. Mosc. Math. J. 11, 685–722 (2011). Preprint arXiv:0806.1532
Brundan, J., Stroppel, C.: Highest weight categories arising from Khovanov’s diagram algebra II: Koszulity. Transform. Groups 15, 1–45 (2010). Preparing arXiv:0806.3472
Caprau, C.: An \({\mathfrak{sl}}(2)\) Tangle Homology and Seamed Cobordisms, Ph.D. Thesis. University of Iowa (2007). E-print: arXiv:0707.3051
Carter, J.S., Saito, M.: Knotted Surfaces and Their Diagrams, Mathematical Surveys and Monographs, vol. 55. American Mathematical Society, Providence (1998)
Chen, Y., Khovanov, M.: An invariant of tangle cobordisms via subquotients of arc rings. Fund. Math. 225, 23–44 (2014). Preprint arXiv:math/0610054
Clark, D., Morrison, S., Walker, K.: Fixing the functoriality of Khovanov homology. Geom. Topol. 13, 1499–1582 (2009). Preprint arXiv:math/0701339
Etingof, P., Gelaki, S., Nikshych, D., Ostrik, V.: Tensor Categories, Lecture notes, MIT (2009). Preprint http://www-math.mit.edu/~etingof/tenscat.pdf
Gelfand, S.I., Manin, Y.I.: Methods of Homological Algebra, Springer Monographs in Mathematics. Springer, Berlin (2003)
Grigsby, J.E., Licata, T.A., Wehrli, S.M.: Annular Khovanov homology and knotted Schur–Weyl representations. Preprint arXiv:1505.04386
Hattori, A.: Rank element of a projective module. Nagoya Math. J. 25, 113–120 (1965)
Henriques, A., Penneys, D., Tener, J.: Categorified trace for module tensor categories over braided tensor categories. Preprint arXiv:1509.02937
Jacobsson, M.: An invariant of link cobordisms from Khovanov homology. Algebra Geom. Top. 4, 1211–1251 (2004). Preprint arXiv:math/0206303
Keller, B.: Invariance and localization for cyclic homology of DG-algebras. J. Pure Appl. Alg. 123, 223–273 (1998)
Khovanov, M.: A categorification of the Jones polynomial. Duke Math. J. 101(3), 359–426 (2000). Preprint arXiv:math/9908171
Khovanov, M.: A functor-valued invariant of tangles. Algebra Geom. Top. 2, 665–741 (2002). Preprint arXiv:math/0103190
Khovanov, M.: Link homologies and Frobenius extensions. Fundam. Math. 190, 179–190 (2006). Preprint arXiv:math/0411447
Lee, E.S.: An endomorphism of the Khovanov invariants. Adv. Math. 197(2), 554–586 (2005). Preprint arXiv:math/0210213
Leinster, T.: Basic bicategories. Preparing arXiv:math/9810017
Loday, J.-L.: Cyclic homology. A Series of Comprehensive Studies in Mathematics, 2nd edn. Springer, Berlin (1998)
MacLane, S.: Categories for the working mathematician, Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, Berlin (1998)
Miličić, D.: Lectures on Derived Categories. Preprint http://www.math.utah.edu/~milicic/Eprints/dercat.pdf
Mitchell, B.: Rings with several objects. Adv. Math. 8, 1–161 (1972)
Morrison, S., Walker, K.: The blob complex. Geom. Topol. 16, 1481–1607 (2005). Preprint arXiv:1009.5025
Ponto, K., Schulman, M.: Shadows and traces in bicategories. J. Homot. Relat. Struct. 8, 151–200 (2013). Preprint arXiv:0910.1306
Queffelec, H., Rose, D.: Sutured annular Khovanov–Rozansky homology. Preprint arXiv:1506.08188
Queffelec, H., Wedrich, P.: Khovanov homology and categorification of skein modules. Preprint
Rasmussen, J.: Khovanov’s invariant for closed surfaces. Preprint arXiv:math/0502527
Roberts, L.: On knot Floer homology in double branched covers. Geom. Topol. 17, 413–467 (2013). Preprint arXiv:0706.0741
Russell, H.M.: The Bar-Natan skein module of the solid torus and the homology of \((n,n)\) Springer varieties. Geom. Dedic. 142, 71–89 (2009). Preprint arXiv:0805.0286
Stallings, J.: Centerless groups—an algebraic formulation of Gottliebs theorem. Topology 4, 129–134 (1965)
Thys, H.: Description topologique des représentations de \(\cal{U}_q(\mathfrak{sl}_{2})\). Ann. Fac. Sci. Toulouse Math. 8(4), 695–725 (1999)
Vogel, P.: Functoriality of Khovanov homology. Preprint arXiv:1505.04545
Weibel, C.A.: An Introduction to Homological Algebra. Cambridge University Press, Cambridge (1995)
Acknowledgements
The authors are grateful to Adrien Brochier, Matthew Hogancamp, Mikhail Khovanov, Slava Krushkal, Aaron Lauda, David Rose, and Paul Wedrich for stimulating discussions. During an early stage of the research Robert Lipshitz suggested to look on higher Hochschild homology of the arc algebras and Ben Webster pointed a connection between Hochschild homology and the global dimension. The first two authors are supported by the NCCR SwissMAP founded by the Swiss National Science Foundation. The third author was supported by the NSF Grant DMS-1111680.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Background survey
Appendix A Background survey
The material presented here is widely known, and the main goal of this section is to fix the notation. Bicategories are treated in the excellent paper [11], whereas [34] is a brief list of basic definitions. The reader is also referred to [23], because many results about monoidal categories immediately translates to bicategories.
1.1 A.1 Representations of 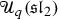
As usual we fix a commutative unital ring  together with an invertible element q. By definition,
together with an invertible element q. By definition,  is the unital associative
is the unital associative  -algebra with generators E, F, K, \(K^{-1}\) and relations
-algebra with generators E, F, K, \(K^{-1}\) and relations
It is a Hopf algebra with the comultiplication  , the counit
, the counit  , and the antipode
, and the antipode  defined by
defined by
Using this Hopf algebra structure, we can regard the category of finite-dimensional representations of  as a monoidal category with duals. The unit in this monoidal category is given by the trivial representation
as a monoidal category with duals. The unit in this monoidal category is given by the trivial representation  , on which
, on which  acts by multiplication by \(\epsilon (X)\) for any
acts by multiplication by \(\epsilon (X)\) for any  .
.
We write  and
and  for the fundamental representation and its dual. We identify both with the rank two module
for the fundamental representation and its dual. We identify both with the rank two module  using the isomorphisms
using the isomorphisms

This equips V with two actions of  that differ by signs:
that differ by signs:

The duality between \(V_1\) and \(V_1^*\) comes with the evaluation and coevaluation maps

that intertwine the action  if \(V\otimes V\) is identified with either \(V_1\otimes V_1^*\) or \(V_1^*\otimes V_1\).
if \(V\otimes V\) is identified with either \(V_1\otimes V_1^*\) or \(V_1^*\otimes V_1\).
The full subcategory of  generated by tensor powers of V admits a graphical representation. Let
generated by tensor powers of V admits a graphical representation. Let  be the Temperley–Lieb category, the linear category with objects finite collections of points on a real line and morphisms generated by flat loopless tangles, i.e. collection of disjoint intervals in \(\mathbb {R}\times I\) with endpoints on the boundary lines. Composition is defined by stacking pictures one onto another and trading each closed component for \(q+q^{-1}\). For example,
be the Temperley–Lieb category, the linear category with objects finite collections of points on a real line and morphisms generated by flat loopless tangles, i.e. collection of disjoint intervals in \(\mathbb {R}\times I\) with endpoints on the boundary lines. Composition is defined by stacking pictures one onto another and trading each closed component for \(q+q^{-1}\). For example,

There is a functor  that assigns \(V^{\otimes n}\) to a collection of n points, whereas caps and cups are sent to the evaluation and evaluation homomorphisms. It is known that
that assigns \(V^{\otimes n}\) to a collection of n points, whereas caps and cups are sent to the evaluation and evaluation homomorphisms. It is known that  is faithful [47].
is faithful [47].
1.2 A.2 Knots and tangles
Let M be an oriented smooth 3-manifold. A proper 1-submanifold \(T\subset M\) is called a tangle. We call it a link if it has no boundary, and a knot if in addition it has one component. All tangles and links in this paper are assumed to be oriented unless stated otherwise. An isotopy of tanglesT and \(T'\) is a smooth map \(\Phi {:}\,M\times I\rightarrow M\) such that each \(\Phi _t := \Phi (-, t)\) is a diffeomorphism fixed at the boundary, \(\Phi _0 = {{\,\mathrm{id}\,}}\), and \(\Phi _1(T) = T'\). If T and \(T'\) are oriented, then we require that the orientation is preserved by \(\Phi _1\).
Denote by \(-T\) the tangle T with reversed orientation of all its components. A tangle cobordism from a tangle \(T_0\) to \(T_1\) is an oriented surface \(S\subset M\times I\) with boundary \(\partial S = -T_0\times \{0\} \cup T_1\times \{1\} \cup (-\partial T_0\times I)\). We shall consider cobordisms only up to an isotopy, in which case they form a category: composition is given by gluing cobordisms, and the identity morphism on a tangle T is represented by the cylinder \(T\times I\subset M\times I\).
When \(M= F\times I\) is a thickened surface, then isotopy classes of oriented tangles in M form a category, with the product induced by stacking, \(M\cup M \cong M\), and tangles with tangle cobordisms form a 2-category.
Notation
We shall write \( Links (M)\) for the set of isotopy classes of oriented links in M, and  for the category of oriented links in M and cobordisms between them. Isotopy classes of oriented tangles in a thickened surface \(F\times I\) form a category
for the category of oriented links in M and cobordisms between them. Isotopy classes of oriented tangles in a thickened surface \(F\times I\) form a category  with the composition induced by stacking, and similarly cobordisms between tangles in \(F\times I\) form a 2-category \(\mathbf {Tan}(F)\). We write simply
with the composition induced by stacking, and similarly cobordisms between tangles in \(F\times I\) form a 2-category \(\mathbf {Tan}(F)\). We write simply  and \(\mathbf {Tan}\) when \(F=\mathbb {R}\times I\).
and \(\mathbf {Tan}\) when \(F=\mathbb {R}\times I\).
Assume M is a line bundle over a surface \(F\) and consider the projection \(M\rightarrow F\) onto the zero section. It maps a generic tangle T to an immersed collection of intervals and circles \(\tilde{T}\subset F\) with only finitely many multiple points, each a transverse intersection of two arcs. A diagram of T is constructed from \(\tilde{T}\) by breaking one of the arcs at each double point as follows. When \(F\) is oriented, then fibers of M admit a canonical orientation and we break the lower arc at each double point of \(\tilde{T}\) (see Fig. 12 for the case \(F=\mathbb {R}\times I\)). In case \(F\) is nonorientable, choose a minimal collection of curves \(\gamma \) that cuts \(F\) into an orientable surface. Then there is a normal field over \(F- \gamma \) and we can construct the diagram as before. Then Reidemeister moves and planar isotopies relate diagrams between isotopic tangles if a crossing is switched when moved through \(\gamma \):

This follows, because the normal field is reversed at points of \(\gamma \).
1.3 A.3 Constructions on categories
Below we review definitions of certain constructions on categories that appear throughout the paper.
1.3.1 Additive closure
We say that a linear category is additive if it has finite direct sums. Each category  admits the additive closure
admits the additive closure , the smallest additive category containing
, the smallest additive category containing  . It is constructed by introducing formal direct sums:
. It is constructed by introducing formal direct sums:
-
an object of
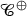 is a finite sequence \((x_1,\ldots ,x_r)\) with
is a finite sequence \((x_1,\ldots ,x_r)\) with 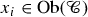 , possibly empty,
, possibly empty, -
a morphism from \((x_1,\ldots ,x_r)\) to \((y_1,\ldots ,y_s)\) is a matrix \((f_{ij})\) of morphisms
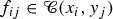 , and
, and -
composition is defined by the matrix multiplication rule.
There is an inclusion  , which takes an object x to the 1-element sequence (x). It is an equivalence of categories if
, which takes an object x to the 1-element sequence (x). It is an equivalence of categories if  is already additive.
is already additive.
1.3.2 Idempotent completion
An endomorphism  satisfying \(p\circ p = p\) is an idempotent. We say that psplits if it decomposes \(p = s\circ r\) such that \(r\circ s\) is an identity morphism. In such a case r is an epimorphism and its codomain is called the image ofp.
satisfying \(p\circ p = p\) is an idempotent. We say that psplits if it decomposes \(p = s\circ r\) such that \(r\circ s\) is an identity morphism. In such a case r is an epimorphism and its codomain is called the image ofp.
A category is idempotent complete if all its idempotents split. Each category  admits its idempotent completion
admits its idempotent completion , also called also the Karoubi envelope of
, also called also the Karoubi envelope of , which is the smallest idempotent complete category containing
, which is the smallest idempotent complete category containing  . It is constructed by taking all idempotents of
. It is constructed by taking all idempotents of  as objects, and defining morphisms from e to \(e'\) as those morphisms f from
as objects, and defining morphisms from e to \(e'\) as those morphisms f from  that \(e'\circ f\circ e\) is well-defined and equal to f. The identity morphism on e is given by the idempotent itself.
that \(e'\circ f\circ e\) is well-defined and equal to f. The identity morphism on e is given by the idempotent itself.
1.3.3 Formal complexes and homotopy category
A formal complexes over a category  is a sequence of objects and morphisms from
is a sequence of objects and morphisms from 
satisfying \(d^{i+1}d^i = 0\) at each place. The morphisms \(d^i\) are called the differential. We say that \((C^\bullet , d)\) is bounded if \(C^i = 0\) except finitely many indices.
A formal chain map from \((C^\bullet , d)\) to \((D^\bullet , d)\) is a collection of morphisms \(f^i{:}\,C^i \rightarrow D^i\) fitting into a commuting ladder

Finally, a formal chain homotopy from \(f^\bullet \) to \(g^\bullet \), both chain maps from \((C^\bullet ,d_C)\) to (\(D^\bullet , d_D)\), is a collection of morphisms \(h^i{:}\,C^i\rightarrow D^{i-1}\) satisfying \(d^{i-1}_D\circ h^i + h^{i+1}\circ d^i_C = g^i - f^i\). In such case we say that \(f^\bullet \) and \(g^\bullet \) are homotopic, which we write \(f\sim g\).
Formal complexes (reps. bounded formal complexes) and chain maps modulo chain homotopies constitute the homotopy category of complexes (resp.
(resp.  ). Isomorphism in these categories are called homotopy equivalences and we usually write \(C^\bullet \simeq D^\bullet \) for complexes that are homotopically equivalent.
). Isomorphism in these categories are called homotopy equivalences and we usually write \(C^\bullet \simeq D^\bullet \) for complexes that are homotopically equivalent.
The categories  and
and  are triangulated [24, 49], which means that they come with a homological degree shift functor and a collection of distinguish triangles satisfying certain axioms. The degree shift functor is usually denoted by [1] and it shifts a complex leftwards, negating the differential at the same time:
are triangulated [24, 49], which means that they come with a homological degree shift functor and a collection of distinguish triangles satisfying certain axioms. The degree shift functor is usually denoted by [1] and it shifts a complex leftwards, negating the differential at the same time:
Distinguished triangles are of the form
where \(\mathrm {cone}^\bullet (f)\) stands for the mapping cone of \(f_{}\), the formal complex
The morphisms \( in ^i{:}\,D^i\rightarrow \mathrm {cone}^i(f^\bullet )\) and \( pr ^i{:}\,\mathrm {cone}^i(f^\bullet )\rightarrow C[1]^i = C^{i+1}\) are the inclusion and projection respectively.
1.4 A.4 Bicategories
A bicategory\(\mathbf {C}\) is a ‘higher level’ analogue of a category. It consists of
-
a class of objects \(\mathrm {Ob}(\mathbf {C})\),
-
a category \(\mathbf {C}(x,y)\) for each pair of objects (x, y), whose objects and morphisms are called 1- and 2-morphisms respectively and represented by single and double arrows,
-
a unit \({{\,\mathrm{id}\,}}_x\in \mathbf {C}(x,x)\) for each object x,
-
a functor \(\circ {:}\,\mathbf {C}(y,z) \times \mathbf {C}(x,y) \rightarrow \mathbf {C}(x,z)\) for each triple of objects (x, y, z), and
-
natural isomorphisms

called associators and unitors, which satisfy the pentagon and triangle axioms [11].
A bicategory is called strict or a 2-category if the natural isomorphisms are identities. We call \(\mathbf {C}\) a locally small bicategory when each category \(\mathbf {C}(x,y)\) is small, and \(\mathbf {C}\) is small when also \(\mathrm {Ob}(\mathbf {C})\) is a set.
Associators and unitors are often omitted for clarity. According to the MacLane’s Coherence Theorem [36, Chapter VII.2] there is only one way how to insert these isomorphisms back when necessary.
Notation
In this paper we denote categories with calligraphic letters  ,
,  , etc., whereas bold letters \(\mathbf {C}\), \(\mathbf {D}\), etc. are reserved for bicategories. Identity morphisms are written as \({{\,\mathrm{id}\,}}_x\), and identity 2-morphisms as \(\mathbf 1_f\). If \(\mathbf {C}\) is a bicategory, then the composition in \(\mathbf {C}(x,y)\) is denoted by \(*\) and called vertical, whereas \(\circ \) is the horizontal composition. These come from the common convention to draw 1-morphisms horizontally and 2-morphisms vertically. For instance, a 2-morphism
, etc., whereas bold letters \(\mathbf {C}\), \(\mathbf {D}\), etc. are reserved for bicategories. Identity morphisms are written as \({{\,\mathrm{id}\,}}_x\), and identity 2-morphisms as \(\mathbf 1_f\). If \(\mathbf {C}\) is a bicategory, then the composition in \(\mathbf {C}(x,y)\) is denoted by \(*\) and called vertical, whereas \(\circ \) is the horizontal composition. These come from the common convention to draw 1-morphisms horizontally and 2-morphisms vertically. For instance, a 2-morphism  is commonly presented as
is commonly presented as

Choose bicategories \(\mathbf {C}\) and \(\mathbf {D}\). A bifunctor\(\mathbf {F}{:}\,\mathbf {C}\rightarrow \mathbf {D}\) consists of a function of objects \(\mathrm {Ob}(\mathbf {C}) \rightarrow \mathrm {Ob}(\mathbf {D})\) and a collection of functors \(\mathbf {C}(x,y) \rightarrow \mathbf {D}(\mathbf {F}x,\mathbf {F}y)\), together with natural 1-morphisms

satisfying certain coherence axioms. They are called morphisms of bicategories in [11], whereas the word homomorphism is reserved for the case when \(\mathfrak m\) and \(\mathfrak i\) are invertible. In such case we say that \(\mathbf {F}\) is a strong bifunctor.
Choose bifunctors \(\mathbf {F},\mathbf {G}{:}\,\mathbf {C}\rightarrow \mathbf {D}\). A natural transformation\(\eta {:}\,\mathbf {F} \rightarrow \mathbf {G}\) is a collection of 1-morphisms \(\eta _x{:}\,\mathbf {F}(x) \rightarrow \mathbf {G}(x)\), one per object \(x\in \mathbf {C}\), and 2-morphisms  , one per 1-morphisms \(f\in \mathbf {C}(x,y)\), such that
, one per 1-morphisms \(f\in \mathbf {C}(x,y)\), such that

for every 2-morphism  . Moreover, \(\eta _f\) must be coherent with all the other canonical 2-isomorphisms (associators, unitors, the structure 2-isomorphisms of \(\mathbf {F}\) and \(\mathbf {G}\)), see [34]. We say that \(\eta \) is strong if each \(\eta _f\) is invertible.
. Moreover, \(\eta _f\) must be coherent with all the other canonical 2-isomorphisms (associators, unitors, the structure 2-isomorphisms of \(\mathbf {F}\) and \(\mathbf {G}\)), see [34]. We say that \(\eta \) is strong if each \(\eta _f\) is invertible.
Finally, let \(\eta ,\nu {:}\,\mathbf {F}\rightarrow \mathbf {G}\) be two natural transformations. A modification\(\Gamma {:}\,\eta \rightarrow \nu \) is a collection of 1-morphisms \(\Gamma _x{:}\,\eta _x\rightarrow \nu _x\), such that \(\nu _f*({{\,\mathrm{\mathbf {1}}\,}}_{\mathbf {G}f}\circ \Gamma _x) = (\Gamma _y\circ {{\,\mathrm{\mathbf {1}}\,}}_{\mathbf {F}f})*\eta _f\) for every 1-morphism \(f{:}\,x\rightarrow y\).
1.4.1 Duals
A bicategory \(\mathbf {C}\) has left duals if each \(f\in \mathbf {C}(x,y)\) admits \({}^*\!f\in \mathbf {C}(y,x)\) together with coevaluation and evaluation 2-morphisms

fitting into commuting triangles

where for clarity associators and unitors are omitted. The morphism \({}^*\!f\) is called the left dual to f. We define the right dual\(f^*\) of f by reversing the order of the horizontal composition in (A.16) and (A.17). If a dual 1-morphism exists, then it is unique up to an isomorphism. In particular, dual pairs are preserved by strong bifunctors.
1.4.2 Examples
Small categories, functors, and natural transformations form a strong bicategory \(\mathbf {Cat}\). A left (resp. right) dual to a functor F is its left (resp. right) adjoint. Hence, not all 1-morphisms in \(\mathbf {Cat}\) are dualizable.
Tangles in a thickened surface \(F\times I\) constitute a bicategory \(\mathbf {Tan}(F)\), which objects are finite collections of points in \(F\), 1-morphisms are tangles with endpoints on \(F\times \partial I\), and 2-morphisms are tangle cobordisms. This bicategory has both left and right duals. Indeed, the mirror image \(T^!\) of a tangle T, obtained by flipping \(F\times I\), is both the left and right dual of T. The evaluation 2-morphism is obtained by revolving T in four dimensions along the input surface \(F\times \{0\}\), i.e. it is the image of the map \((p,t,s)\mapsto (p,t\cos (s\pi ),t\sin (s\pi ))\) with \((p,t)\in T\) and \(s\in I\), suitably normalized (see Fig. 13). The coevaluation is defined dually by a rotation along the output surface \(F\times \{1\}\).
Rings, bimodules, and bimodule maps form a bicategory \(\mathbf {Bimod}\), with horizontal composition given by the tensor product:  for an (A, B)-bimodule M and a (B, C)-bimodule N. This formula comes from interpreting an (A, B)-bimodule M as a functor
for an (A, B)-bimodule M and a (B, C)-bimodule N. This formula comes from interpreting an (A, B)-bimodule M as a functor 
 between the categories of right modules. This bicategory does not have duals. Indeed, an (A, B)-bimodule M has a left (resp. right) dual if and only if it is finitely generated and projective as a right B-module (resp. left A-module). If so, the left and right dual modules are given as the modules of right B-linear and left A-linear morphisms respectively:
between the categories of right modules. This bicategory does not have duals. Indeed, an (A, B)-bimodule M has a left (resp. right) dual if and only if it is finitely generated and projective as a right B-module (resp. left A-module). If so, the left and right dual modules are given as the modules of right B-linear and left A-linear morphisms respectively:

For this reason we usually restrict either to \(\mathbf {Rep}\) (bimodules with left duals) or \(\mathbf {Birep}\) (bimodules with both left and right duals).
Rights and permissions
About this article
Cite this article
Beliakova, A., Putyra, K.K. & Wehrli, S.M. Quantum link homology via trace functor I. Invent. math. 215, 383–492 (2019). https://doi.org/10.1007/s00222-018-0830-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-018-0830-0




 is projective as a left module, but not necessarily as a right one. Hence, in general, it is not a 1-morphism in
is projective as a left module, but not necessarily as a right one. Hence, in general, it is not a 1-morphism in 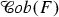 are now symbols
are now symbols  .
.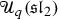

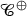 is a finite sequence
is a finite sequence 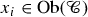 , possibly empty,
, possibly empty,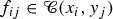 , and
, and

 for a tangle
for a tangle