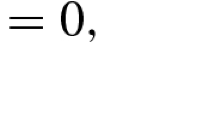Abstract
Singularity formation of the 3D incompressible Euler equations is known to be extremely challenging (Majda and Bertozzi in Vorticity and incompressible flow, Cambridge University Press, Cambridge, vol 27, 2002; Gibbon in Physica D 237(14):1894–1904, 2008; Kiselev, in: Proceedings of the international congress of mathematicians, vol 3, 2018; Drivas and Elgindi in EMS Surv Math Sci 10(1):1–100, 2023; Constantin in Bull Am Math Soc 44(4):603–621, 2007). In Elgindi (Ann Math 194(3):647–727, 2021) (see also Elgindi et al. in Camb J Math 9(4), 2021), Elgindi proved that the 3D axisymmetric Euler equations with no swirl and \(C^{1,\alpha }\) initial velocity develops a finite time singularity. Inspired by Elgindi’s work, we proved that the 3D axisymmetric Euler and 2D Boussinesq equations with \(C^{1,\alpha }\) initial velocity and boundary develop a stable asymptotically self-similar (or approximately self-similar) finite time singularity (Chen and Hou in Commun Math Phys 383(3):1559–1667, 2021) in the same setting as the Hou-Luo blowup scenario (Luo and Hou in Proc Natl Acad Sci 111(36):12968–12973, 2014; Luo and Hou in SIAM Multiscale Model Simul 12(4):1722–1776, 2014). On the other hand, the authors of Vasseur and Vishik (Commun Math Phys 378(1):557–568, 2020) and Lafleche et al. (Journal de Mathématiques Pures et Appliquées 155:140–154, 2021) recently showed that blowup solutions to the 3D Euler equations are hydrodynamically unstable. The instability results obtained in Vasseur and Vishik (2020) and Lafleche et al. (2021) require some strong regularity assumption on the initial data, which is not satisfied by the \(C^{1,\alpha }\) velocity field. In this paper, we generalize the analysis of Elgindi (Ann Math 194(3):647–727, 2021), Chen and Hou (Commun Math Phys 383(3):1559–1667, 2021), Vasseur and Vishik (2020) and Lafleche et al. (2021) to show that the blowup solutions of the 3D Euler and 2D Boussinesq equations with \(C^{1,\alpha }\) velocity are unstable under the notion of stability introduced in Vasseur and Vishik (2020) and Lafleche et al. (2021). These two seemingly contradictory results reflect the difference of the two approaches in studying the stability of 3D Euler blowup solutions.
Similar content being viewed by others
Data Availability
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Beale, J.T., Kato, T., Majda, A.: Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Commun. Math. Phys. 94(1), 61–66 (1984)
Biasi, A.: Self-similar solutions to the compressible Euler equations and their instabilities. Commun. Nonlinear Sci. Numer. Simul. 103, 106014 (2021)
Buckmaster, T., Shkoller, S., Vicol, V.: Formation of shocks for 2D isentropic compressible Euler. Commun. Pure Appl. Math. 75(9), 2069–2120 (2022)
Buckmaster, T., Shkoller, S., Vicol, V.: Formation of point shocks for 3d compressible Euler. Commun. Pure Appl. Math. 76(9), 2073–2191 (2023)
Chen, J.: Singularity formation and global well-posedness for the generalized Constantin–Lax–Majda equation with dissipation. Nonlinearity 33(5), 2502 (2020)
Chen, J.: On the regularity of the De gregorio model for the 3D Euler equations. To appear in J. Eur. Math. Soc., arXiv preprint arXiv:2107.04777, (2021)
Chen, J.: On the slightly perturbed De Gregorio model on \(S^1\). Arch. Ration. Mech. Anal. 241(3), 1843–1869 (2021)
Chen, J.: Remarks on the smoothness of the \( {C}^{1,\alpha }\) asymptotically self-similar singularity in the 3D Euler and 2D Boussinesq equations. arXiv preprint arXiv:2309.00150, (2023)
Chen, J., Hou, T.Y.: Stable nearly self-similar blowup of the 2D Boussinesq and 3D Euler equations with smooth data II: Rigorous numerics. arXiv preprint: arXiv:2305.05660 [math.AP]
Chen, J., Hou, T.Y.: Finite time blowup of 2D Boussinesq and 3D Euler equations with \({C}^{1,\alpha }\) velocity and boundary. arXiv:1910.00173, (2019)
Chen, J., Hou, T.Y.: Finite time blowup of 2D Boussinesq and 3D Euler equations with \({C}^{1,\alpha }\) velocity and boundary. Commun. Math. Phys. 383(3), 1559–1667 (2021)
Chen, J., Hou, T.Y.: On stability and instability of \( {C}^{1,\alpha } \) singular solutions to the 3D Euler and 2D Boussinesq equations. arXiv preprint arXiv:2206.01296, (2022)
Chen, J., Hou, T.Y.: Stable nearly self-similar blowup of the 2D Boussinesq and 3D Euler equations with smooth data I: analysis. arXiv preprint: arXiv:2210.07191v3 [math.AP], (2022)
Chen, J., Hou, T.Y.: Correction to: Finite time blowup of 2D Boussinesq and 3D Euler equations with \(c^{1,\alpha }\) velocity and boundary. Commun. Math. Phys. 399(1), 573–575 (2023)
Chen, J., Hou, T.Y., Huang, D.: On the Finite Time Blowup of the De Gregorio Model for the 3D Euler Equations. Commun. Pure Appl. Math. 74(6), 1282–1350 (2021)
Chen, J., Hou, T.Y., Huang, D.: Asymptotically self-similar blowup of the Hou–Luo model for the 3D Euler equations. Ann. PDE 8(2), 24 (2022)
Choi, K., Hou, T.Y., Kiselev, A., Luo, G., Sverak, V., Yao, Y.: On the finite-time blowup of a 1D model for the 3D axisymmetric Euler equations. CPAM 70(11), 2218–2243 (2017)
Choi, K., Kiselev, A., Yao, Y.: Finite time blow up for a 1D model of 2D Boussinesq system. Commun. Math. Phys. 334(3), 1667–1679 (2015)
Collot, C., Ghoul, T.-E., Masmoudi, N.: Singularity formation for Burgers’ equation with transverse viscosity. In: Annales scientifiques de l’École Normale Supérieure, volume 55, (2022)
Constantin, P.: On the Euler equations of incompressible fluids. Bull. Am. Math. Soc. 44(4), 603–621 (2007)
Córdoba, D., Martínez-Zoroa, L.: Blow-up for the incompressible 3D-Euler equations with uniform \(c^{1,1/2-\epsilon } \cap l^2\) force. arXiv preprint arXiv:2309.08495, (2023)
Cordoba, D., Martinez-Zoroa, L., Zheng, F.: Finite time singularities to the 3D incompressible Euler equations for solutions in \({C}^{1,\alpha } \cap {C}^{\infty }({R}^3 \backslash \{ 0 \} ) \cap {L}^2\). arXiv preprint arXiv:2308.12197, (2023)
De Gregorio, S.: On a one-dimensional model for the three-dimensional vorticity equation. J. Stat. Phys. 59(5–6), 1251–1263 (1990)
De Gregorio, S.: A partial differential equation arising in a 1D model for the 3D vorticity equation. Math. Methods Appl. Sci. 19(15), 1233–1255 (1996)
Drivas, T.D., Elgindi, T.M.: Singularity formation in the incompressible Euler equation in finite and infinite time. EMS Surv. Math. Sci. 10(1), 1–100 (2023)
Elgindi, T.M.: Finite-time singularity formation for \({C}^{1,\alpha }\) solutions to the incompressible Euler equations on \({\mathbb{R} }^3\). Ann. Math. 194(3), 647–727 (2021)
Elgindi, T.M, Ghoul, T.-E., Masmoudi, N.: On the stability of self-similar blow-up for \( {C}^{1,\alpha } \) solutions to the incompressible Euler equations on \({\mathbb{R}}^3\). Camb. J. Math. 9(4), 1035–1075 (2021)
Elgindi, T.M., Ghoul, T., Masmoudi, N.: Stable self-similar blow-up for a family of nonlocal transport equations. Anal. PDE 14(3), 891–908 (2021)
Elgindi, T.M., Jeong, I.-J.: Finite-time singularity formation for strong solutions to the axi-symmetric 3D Euler equations. Ann. PDE 5(2), 1–51 (2019)
Elgindi, T.M., Jeong, I.-J.: On the effects of advection and vortex stretching. Arch. Ration. Mech. Anal. 235(3), 1763–1817 (2019)
Elgindi, T.M., Jeong, I.-J.: Finite-time singularity formation for strong solutions to the Boussinesq system. Ann. PDE 6, 1–50 (2020)
Elgindi, T.M, Pasqualotto, F.: From instability to singularity formation in incompressible fluids. arXiv preprint arXiv:2310.19780, (2023)
Elgindi, T.M, Pasqualotto, F.: Invertibility of a linearized boussinesq flow: a symbolic approach. arXiv preprint arXiv:2310.19781, (2023)
Friedlander, S., Strauss, W., Vishik, M.: Nonlinear instability in an ideal fluid. In: Annales de l’Institut Henri Poincaré C, Analyse non linéaire, vol. 14, pp. 187–209. Elsevier (1997)
Friedlander, S., Vishik, M.M.: Dynamo theory, vorticity generation, and exponential stretching. Chaos Interdiscip. J. Nonlinear Sci. 1(2), 198–205 (1991)
Friedlander, S., Vishik, M.M.: Instability criteria for the flow of an inviscid incompressible fluid. Phys. Rev. Lett. 66(17), 2204 (1991)
Gibbon, J.D.: The three-dimensional Euler equations: Where do we stand? Physica D 237(14), 1894–1904 (2008)
Hou, T.Y.: Potential singularity of the \(3\)D Euler equations in the interior domain. Found. Comput. Math. 23, 2203–2249 (2023)
Hou, T.Y.: The potentially singular behavior of the \(3\)D Navier–Stokes equations. Found. Comput. Math. 23, 2251–2299 (2023)
Hou, T.Y., Huang, D.: A potential two-scale traveling wave singularity for 3D incompressible Euler equations. Phys. D Nonlinear Phenomena. 435, 133257 (2022)
Inoue, A., Miyakawa, T.: On the existence of solutions for linearized Euler’s equation. 282–285 (1979)
Kenig, C.E., Merle, F.: Global well-posedness, scattering and blow-up for the energy-critical, focusing, non-linear Schrödinger equation in the radial case. Invent. Math. 166(3), 645–675 (2006)
Kiselev, A., Ryzhik, L., Yao, Y., Zlatoš, A.: Finite time singularity for the modified SQG patch equation. Ann. Math. 909–948 (2016)
Kiselev, A., Sverak, V.: Small scale creation for solutions of the incompressible two dimensional Euler equation. Ann. Math. 180, 1205–1220 (2014)
Kiselev, A.: Small scales and singularity formation in fluid dynamics. In: Proceedings of the International Congress of Mathematicians, vol. 3 (2018)
Lafleche, L., Vasseur, A.F., Vishik, M.: Instability for axisymmetric blow-up solutions to incompressible Euler equations. Journal de Mathématiques Pures et Appliquées 155, 140–154 (2021)
Landman, M.J., Papanicolaou, G.C., Sulem, C., Sulem, P.-L.: Rate of blowup for solutions of the nonlinear Schrödinger equation at critical dimension. Phys. Rev. A (3) 38(8), 3837–3843 (1988)
Lifschitz, A., Hameiri, E.: Local stability conditions in fluid dynamics. Phys. Fluids A 3(11), 2644–2651 (1991)
Luo, G., Hou, T.Y.: Toward the finite-time blowup of the 3D incompressible Euler equations: a numerical investigation. SIAM Multiscale Model. Simul. 12(4), 1722–1776 (2014)
Luo, G., Hou, T.Y.: Potentially singular solutions of the 3D axisymmetric Euler equations. Proc. Natl. Acad. Sci. 111(36), 12968–12973 (2014)
Majda, A.J., Bertozzi, A.L.: Vorticity and Incompressible Flow, vol. 27. Cambridge University Press, Cambridge (2002)
Martel, Y., Merle, F., Raphaël, P.: Blow up for the critical generalized Korteweg–de Vries equation. I. Dynamics near the soliton. Acta Math. 212(1), 59–140 (2014)
Masmoudi, N., Zaag, H.: Blow-up profile for the complex Ginzburg–Landau equation. J. Funct. Anal. 255(7), 1613–1666 (2008)
McLaughlin, D.W., Papanicolaou, G.C., Sulem, C., Sulem, P.-L.: Focusing singularity of the cubic Schrödinger equation. Phys. Rev. A 34(2), 1200 (1986)
Merle, F., Raphael, P.: The blow-up dynamic and upper bound on the blow-up rate for critical nonlinear Schrödinger equation. Ann. Math. 157–222 (2005)
Merle, F., Raphaël, P., Rodnianski, I., Szeftel, J.: On blow up for the energy super critical defocusing nonlinear Schrödinger equations. Invent. Math. 227(1), 247–413 (2022)
Merle, F., Raphaël, P., Rodnianski, I., Szeftel, J.: On the implosion of a compressible fluid II: singularity formation. Ann. Math. 196(2), 779–889 (2022)
Merle, F., Zaag, H.: Stability of the blow-up profile for equations of the type \(u_t= { \Delta u } + | u|^{ p- 1} u \). Duke Math. J. 86(1), 143–195 (1997)
Merle, F., Zaag, H.: On the stability of the notion of non-characteristic point and blow-up profile for semilinear wave equations. Commun. Math. Phys. 333(3), 1529–1562 (2015)
Oh, S.-J., Pasqualotto, F.: Gradient blow-up for dispersive and dissipative perturbations of the burgers equation. arXiv preprint arXiv:2107.07172, (2021)
Okamoto, H., Sakajo, T., Wunsch, M.: On a generalization of the Constantin–Lax–Majda equation. Nonlinearity 21(10), 2447–2461 (2008)
Plecháč, P., Šverák, V.: On self-similar singular solutions of the complex Ginzburg–Landau equation. Commun. Pure Appl. Math. 54(10), 1215–1242 (2001)
Shao, R., Zhang, P.: On the instability of the possible blow-up solutions to 2D Boussinesq system. J. Differ. Equ. 306, 547–568 (2022)
Vasseur, A.F., Vishik, M.: Blow-up solutions to 3D Euler are hydrodynamically unstable. Commun. Math. Phys. 378(1), 557–568 (2020)
Vishik, M.: Spectrum of small oscillations of an ideal fluid and Lyapunov exponents. J. Math. Pures Appl. (9) 75(6), 531–557 (1996)
Acknowledgements
The research was in part supported by NSF Grants DMS-1907977 and DMS- 1912654, and the Choi Family Gift Fund. We would like to thank Professors Tarek Elgindi, Sasha Kiselev, Vladimir Sverak and Yao Yao for their constructive comments on an earlier version of our paper and for bringing to our attention several relevant references. We are also grateful to the referees for their constructive comments on the original manuscript, which improve the quality of our paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest for this paper.
Additional information
Communicated by Alexandru Ionescu.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Review of the Construction of Unstable Solutions
We provide a brief review of the construction of the unstable solution in [46, 64] via a WKB expansion and explain the connections among the WKB expansion, the bicharacteristics-amplitude ODE system (3.6)–(3.8), and the growth of the unstable solution.
1.1 Construction of the approximate solution
Suppose that \({\textbf{u}}(t, x)\) is a singular solution of (1.1). Denote by \(\gamma _t(x)\) the flow map
The main idea in [64] is to construct an approximate solution to (1.2) using a WKB expansion
for sufficiently small \(\varepsilon \) and the characteristics of the flow, where \(b(t, x) \in {\mathbb {R}}^3\) and S is a scalar. Plugging the above ansatz into (1.2), we obtain
where \( (\nabla {\textbf{u}}) f = f \cdot \nabla {\textbf{u}}= f_j \partial _j u_i e_i \). To eliminate the \(O(\varepsilon ^{-1})\) term, one requires
Then we can rewrite \(R_{\varepsilon }\) as follows
An important observation in [64] is that for high frequency oscillation, i.e. small \(\varepsilon \), the pressure term in (1.2) is almost local. We would like to construct (v, Q) such that
where \(E_{\varepsilon }\) is a small error term. This is possible since Q is one order more regular than a highly oscillatory function \(F(t, x) e^{i S / \varepsilon }\). By integration and exploiting the cancellation, Q can be of order \(O(\epsilon )\). In fact, taking \(\nabla \times \) on both sides, we obtain
To eliminate the \(O(\varepsilon ^{-1})\) term, we require \(\nabla S \times F = 0\), which implies \(F = c(t, x) \nabla S \) for some scalar c(t, x). In this case, one can construct the pressure Q as follows
As a result, the error is given by
Suppose that c is smooth, then the \(L^p\) norm of the error \(E_{\varepsilon }\) is small as \(\varepsilon \rightarrow 0\).
From \(F = c(t, x) \nabla S\) and (A.4), we yield
Using the Lagrangian coordinates and the flow map \(\gamma _t\) (A.1), we get
Denote
The above equation reduces to
Next, we determine the equations for \(b, \xi \). In order for v(t, x) to be incompressible, from the ansatz (A.2) and
we require \( b(t, x) \cdot (\nabla S)(t, x) = 0\) to eliminate the \(O(\varepsilon ^{-1})\) term. In the Lagrangian coordinates, this condition is equivalent to enforcing
Taking the gradient in the transport equation (A.3), we get
Using the Lagrangian coordinates and (A.6), we derive
The incompressible condition (A.8) implies \( \frac{d}{dt} (b_t \cdot \xi _t ) = 0\). Thus, from (A.7) and (A.9), we get
where \(\langle p, q \rangle = p_i q_i \). It follows that
Thus, from (A.1),(A.7),(A.9), \(\gamma _t, \xi _t, b_t\) satisfy the bicharacteristics-amplitude ODE system (3.6)–(3.8) of (1.1) [46, 64]
The above derivation reveals the main idea behind the construction of an approximate solution to (1.2) in [64] and the relationship between the WKB expansion (A.2) and the bicharacteristics-amplitude ODEs (3.6)–(3.8). The last step is to localize the solution v(t, x) to some trajectory and add a correction to v(t, x) (A.2) so that it is incompressible. We refer to [64] for the details.
1.2 Growth of the solution
The solution v(t, x) satisfies (1.2) up to an error similar to (A.5). Since \(E_{\varepsilon }\) contains the highly oscillatory phase \(e^{i S / \varepsilon }\), the error may not be small in \(C^{k, \alpha }\) or \(H^s\) norm. In [64], based on the WKB construction (A.2) and using the smallness of the error in the \(L^p\) norm, the authors constructed an approximate solution to (1.2) with error controlled by \(\varepsilon \). To prove the instability, they further showed the growth of v(t, x). From (A.2), the growth of \(|| v||_p\) is due to \(|| b_t||_p\). The authors showed that if the velocity \({\textbf{u}}(t, x)\) is smooth, the system (3.6)–(3.8) satisfies the following conservations along the characteristic \(\gamma _t(x)\)
where \(\omega = \nabla \times {\textbf{u}}\) is the vorticity of the blowup solution \({\textbf{u}}\), \( \xi _t, b_t, \tilde{b}_t\) are the solution to (3.6)–(3.8) with initial data \(x_0, \xi _0, b_0, \tilde{b}_0\), \( b_0 \cdot \xi _0 = \tilde{b}_0 \cdot \xi _0 = 0\) and \( b_0, \tilde{b}_0, \xi _0\) being linearly independent.
From the first and the third identity, formally, \( b_t \times \tilde{b}_t\) plays a role similar to \(\omega (t, \gamma _t(x))\). Indeed, using the above conservations, the authors further proved
According to the BKM blowup criterion, \(|| \omega (t)||_{\infty }\) must blowup, which leads to the growth of \(b_t\) and \(|| v(t)||_{L^p}\) and implies linear instability.
Appendix B. Embedding Inequalities and Estimates of Nonlinear Terms
We have the following estimates for different norms. The first and last inequality generalize Proposition 7.6 in [11]. The second inequality is exactly Proposition 7.7 in [11]. The third inequality in (B.1) generalizes Lemma 7.11 in [11]. Since the proof essentially uses the estimates in [11], we omit the proof here and refer it to Appendix B in the arXiv version of this paper [12].
Proposition B.1
Let \({{\mathcal {C}}}^k\) and \({{\mathcal {W}}}^{k,\infty }\) be the norms defined in (4.15) and (4.17). For \( k \ge 1\),
We have the following elliptic estimates for the stream function (4.10), (4.6).
Proposition B.2
Assume that \(\alpha \le \frac{1}{4}\) and \(\Omega \in {{\mathcal {H}}}^k, k \ge 3\). Let \(\Psi \) be the solution to (4.6) with boundary condition (4.7). Then we have
The above estimate with \(k =3 \) has been established in [11]. The general case \(k \ge 3\) can be proved similarly. See also [26].
We have the following estimates for the velocity \({{\bar{u}}}\) of the approximate steady state.
Proposition B.3
For \(\alpha \le \frac{1}{4}\) and \(k \ge 5\), we have
The case of \(k = 5\) has been proved in Proposition 7.8 [11]. The general case \(k \ge 5\) follows from a similar argument. See also [26].
Appendix C. Estimate of the Approximate Steady State
Recall from (4.4) that \({{\bar{\Omega }}}, {{\bar{\eta }}}, {{\bar{\xi }}}\) denote the approximate steady state \({{\bar{\omega }}}, {{\bar{\theta }}}_x, \bar{\theta }_y\) under the coordinates \((R, \beta )\), and the formula of \({\bar{\Omega }}, {\bar{\eta }}\) in (4.8).
We generalize Lemma A.6 in [11] from \(k \le 3\) to any k below.
Lemma C.1
The following results apply to any \( k \ge 0, 0 \le i + j \le k, j \ne 0\). (a) For \(f = {\bar{\Omega }}, {\bar{\eta }}, {\bar{\Omega }} - D_R {\bar{\Omega }}, {\bar{\eta }} - D_R {\bar{\eta }}\), we have
Recall the \({{\mathcal {W}}}^{k, \infty }\) norm (4.17). We generalize Lemma A.7 in [11] from \(k = 7\) to any \(k \ge 7\).
Lemma C.2
For any \(k \ge 7\), it holds true that \(\Gamma (\beta ),{\bar{\Omega }}, {\bar{\eta }} \in {{\mathcal {W}}}^{k, \infty }\) with
Recall the \({{\mathcal {K}}}^k\) norm (4.15). We generalize Lemma A.8 in [11] from \(k= 5\) to any \(k \ge 5\) below.
Lemma C.3
Assume that \(0\le \alpha \le \frac{1}{1000}\). For \(R \ge 0, \beta \in [0, \pi /2], k \ge 1\) and \( i + j \le k\), we have
The proofs of Lemmas C.1–C.3 follows from the argument in [11], and thus are omitted.
For the \(L_{12}\) operator (4.10), we generalize Lemma A.4 in [11] from \({{\mathcal {H}}}^3\) to its \({{\mathcal {H}}}^k\) version. The proof follows from a similar argument.
Lemma C.4
Let \(\chi (\cdot ): [0, \infty ) \rightarrow [0, 1]\) be a smooth cutoff function, such that \(\chi (R) = 1\) for \(R \le 1\) and \(\chi (R) = 0\) for \(R \ge 2\). For \( 0 \le k \le n, 0\le l \le n-1, n \ge 3\), we have
Appendix D. Derivation of \(u_r^r( 0,0)\)
We derive the formula (5.28) for \(u_r^r(0, 0)\) using the formula
Recall the coordinates and change of variables (5.27)
where \((r, \vartheta , z)\) is the cylindrical coordinates in \({\mathbb {R}}^3\) (3.1). Note that \(u_r^r(0,0) = -\frac{1}{2} u_z^z(0,0)\) (3.10), we compute \(u_z^z(0, 0)\). Since there is no swirl \(u^{\vartheta } \equiv 0\), we get
Since the above formula is independent of \(z= x_3\) and \(\omega ^{\vartheta }(y)\) is odd in \(y_3\), we yield
Evaluating at \(x = 0\) and using
and \(r = \rho \cos \beta , z = \rho \sin \beta , \beta \in [-\pi /2, \pi /2]\), we obtain
Using \(u_r^r(0,0) = -\frac{1}{2}u_z^z(0,0)\) (3.10) and \(\frac{ d \rho }{\rho } = \frac{1}{\alpha } \frac{dR}{R}\), we prove (5.28).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chen, J., Hou, T.Y. On Stability and Instability of \(C^{1,\alpha }\) Singular Solutions to the 3D Euler and 2D Boussinesq Equations. Commun. Math. Phys. 405, 112 (2024). https://doi.org/10.1007/s00220-024-04978-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00220-024-04978-9