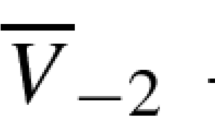Twisted Holography and Celestial Holography from Boundary Chiral Algebra

Abstract

We study the Kaluza–Klein reduction of various 6d holomorphic theories. The KK reduction is analyzed in the BV formalism, resulting in theories that come from the holomorphic topological twist of 3d ${\mathcal {N}} = 2$ supersymmetric field theories. Effective interactions of the KK theories at the classical level can be obtained at all orders using homotopy transfer theorem. We also analyze a deformation of the theories that comes from deforming the spacetime geometry to $SL_2(\mathbb {C})$ due to the brane back-reaction. We study the boundary chiral algebras for the various KK theories. Using Koszul duality, we argue that by properly choosing a boundary condition, the boundary chiral algebra coincides with the universal defect chiral algebra of the original theory. This perspective provides a unified framework for accessing the chiral algebras that arise from both twisted holography and celestial holography programs.

Appendices

A Tangential Cauchy Riemann Complex

Definition A.1

Let M be an real manifold and $T^{\mathbb {C}}M: = TM \otimes _{\mathbb {R}}\mathbb {C}$ its complexified tangent bundle. A CR structure on M is a subbundle $\mathbb {L} \subset T^{\mathbb {C}}M$ such that

• $\mathbb {L}\cap \bar{\mathbb {L}} = \{0\}$.

• $[\mathbb {L},\mathbb {L}] \subset \mathbb {L}$, that is, $\mathbb {L}$ is an integrable distribution.

Suppose M is a real submanifold of $\mathbb {C}^n$ locally defined by real valued functions $\{\rho _i: \mathbb {C}^n \rightarrow \mathbb {R}\}_{i = 1,\dots d}$ that satisfy the independence condition:

$$\begin{aligned} \bar{\partial }\rho _1 \wedge \bar{\partial }\rho _2 \dots \bar{\partial }\rho _d \ne 0. \end{aligned}$$

(A.1)

Then M is a CR manifold called embedded CR submanifold.

We introduce the tangential Cauchy Riemann complex only for embedded CR submanifold.

First we define $\Omega ^{p,q}(\mathbb {C}^n)|_M$ be the restriction of the bundle $\Omega ^{p,q}(\mathbb {C}^n)$ to M. Suppose $\{\rho _i: \mathbb {C}^n \rightarrow \mathbb {R}\}_{i = 1,\dots d}$ is a local defining system of M. We consider

$$\begin{aligned} I^{p,q} {:=} \left\{ \begin{array}{c} \text {the ideal in } \Omega ^{p,q}(\mathbb {C}^n) \text { which is generated by} \\ \rho _i,\bar{\partial }\rho _i, i = 1,\dots d \end{array}\right\} . \end{aligned}$$

(A.2)

Then we define the tangential Cauchy Riemann complex as the following complex of bundle

$$\begin{aligned} \Omega _b^{p,q}(M) = \{\text {The orthogonal complement of } I^{p,q} \text { in } \Omega ^{p,q}(\mathbb {C}^n)|_M\}. \end{aligned}$$

(A.3)

The tangential Cauchy Riemann differential is defined as follows. For an open subset $U \subset M$ and $f \in \Omega _b^{p,q}(U)$, Let ${\tilde{U}}$ be an open subset in $\mathbb {C}^n$ with $U = {\tilde{U}}\cap M$. We choose a ${\tilde{f}} \in \Omega ^{p,q}({\tilde{U}})$ such that $p_M({\tilde{f}}|_M) = f$, where $p_M: \Omega ^{p,q}(\mathbb {C}^n)|_M \rightarrow \Omega _b^{p,q}(M)$ is the orthogonal projection map. We define

$$\begin{aligned} \bar{\partial }_{b}f: = p_M(\bar{\partial }{\tilde{f}}). \end{aligned}$$

(A.4)

One can check that this definition is independent of the choice of ${\tilde{f}}$.

B Harmonic Polynomials on $S^3$

In this appendix, we review some basic facts about harmonic polynomials. Though much of the results hold in other dimensions (see e.g [66]), we focus on $S^3$.

Let $V_N$ be the space of polynomials in $z_1,z_2,{\bar{z}}_1,{\bar{z}}_2$ that are homogeneous of degree N. Let $V_{p,q}$ be the space of homogeneous polynomial of bi-degree (p, q) in $z_1,z_2$ and ${\bar{z}}_1,{\bar{z}}_2$ respectively. We have $V_N = \oplus _{p+q = N}V_{p,q}$. We consider the Laplacian

$$\begin{aligned} \Delta = \frac{\partial ^2}{\partial {\bar{z}}_1 \partial z_1} + \frac{\partial ^2}{\partial {\bar{z}}_1 \partial z_1}, \end{aligned}$$

(B.1)

and define the space of harmonic polynomials

$$\begin{aligned} H_{p,q} = \{f \in V_{p,q}\mid \Delta f = 0 \}. \end{aligned}$$

(B.2)

We emphasize that we used a different notation in the main text, where used half-integer to label the space of harmonic polynomials ${\mathcal {H}}_{j,{\bar{j}}} = H_{2j,2{\bar{j}}}$.

For any homogeneous polynomial $f = \sum _{k}c_kz_1^{k_1}z_2^{k_2}{\bar{z}}_1^{{\bar{k}}_1}{\bar{z}}_2^{{\bar{k}}_2}$, we define a differential operator $\partial _f$ as follows

$$\begin{aligned} \partial _f = \sum _{k}c_k \frac{\partial ^{k_1+k_2+{\bar{k}}_1+{\bar{k}}_2}}{\partial z_1^{k_1} \partial z_2^{k_2} \partial {\bar{z}}_1^{{\bar{k}}_1} \partial {\bar{z}}_2^{{\bar{k}}_2} }. \end{aligned}$$

(B.3)

Denote $||z||^2 = z_1{\bar{z}}_z + z_2{\bar{z}}_2$. We have $\Delta = \partial _{||z||^2}$.

Suppose we have $f\in V_{p,q}$ and $g\in V_{q,p}$, then $\partial _f{\bar{g}}$ is a constant. We define an inner product $\langle \hspace{-2pt}\langle f,g\rangle \hspace{-2pt}\rangle = \partial _f{\bar{g}}$. Under this inner product, we have

$$\begin{aligned} \langle \hspace{-2pt}\langle z_1^{k_1}z_2^{k_2}{\bar{z}}_1^{{\bar{k}}_1}{\bar{z}}_2^{{\bar{k}}_2},{\bar{z}}_1^{k_1}{\bar{z}}_2^{k_2}z_1 ^{{\bar{k}}_1}z_2^{{\bar{k}}_2}\rangle \hspace{-2pt}\rangle = k_1!k_2!{\bar{k}}_1!{\bar{k}}_2!. \end{aligned}$$

(B.4)

It follows that this inner product is Hermitian and SU(2) invariant. A useful property of this inner product is that

$$\begin{aligned} \langle \hspace{-2pt}\langle f, \partial _gh\rangle \hspace{-2pt}\rangle = \partial _f \partial _{{\bar{g}}} {\bar{h}} = \langle \hspace{-2pt}\langle f {\bar{g}}, h\rangle \hspace{-2pt}\rangle . \end{aligned}$$

(B.5)

As a consequence, we have

$$\begin{aligned} \langle \hspace{-2pt}\langle f, \Delta g\rangle \hspace{-2pt}\rangle = \langle \hspace{-2pt}\langle ||z||^2 f, g\rangle \hspace{-2pt}\rangle . \end{aligned}$$

(B.6)

Proposition B.1

• 1. Under the Hermitian form $\langle \hspace{-2pt}\langle -, -\rangle \hspace{-2pt}\rangle$, the orthogonal complement of $||z||^2V_{p - 1,q - 1}$ in $V_{p,q}$ is $H_{p,q}$.

• 2. We have an orthogonal direct sum decomposition

  $$\begin{aligned} V_{p,q} = H_{p,q} \oplus ||z||^2H_{p - 1,q - 1} \oplus ||z||^4H_{p - 1,q - 1} \oplus \dots \end{aligned}$$

  (B.7)

Proof

1. First we prove that $||z||^2V_{p - 1,q - 1}$ is orthogonal to $H_{p,q}$. Let $h \in H_{p,q}$ and $||z||^2 f \in ||z||^2V_{p - 1,q - 1}$. We have

$$\begin{aligned} \langle \hspace{-2pt}\langle ||z||^2 f, h\rangle \hspace{-2pt}\rangle = \langle \hspace{-2pt}\langle f, \Delta h \rangle \hspace{-2pt}\rangle = 0. \end{aligned}$$

(B.8)

For $p,q \ge 1$, $\Delta :V_{p,q} \rightarrow V_{p-1,q-1}$ is surjective. Moreover $H_{p,q} = \ker \Delta |_{V_{p,q}}$. Therefore, $\dim V_{p,q} = \dim H_{p,q} + \dim V_{p-1,q-1}$. As a consequence, we have the following direct sum decomposition

$$\begin{aligned} V_{p,q} = H_{p,q} \oplus ||z||^2V_{p - 1,q - 1}. \end{aligned}$$

(B.9)

2. By induction. $\square$

The above result tells us that for any polynomial $f \in V_{p,q}$, f have the following decomposition into harmonic polynomials

$$\begin{aligned} f = h_0 + ||z||^2h_1 + ||z||^4h_2 \dots \end{aligned}$$

(B.10)

where $h_i \in H_{p - i,q-i}$.

Corollary B.1

The restriction to $S^3$ of every polynomial is a sum of restrictions to $S^3$ of harmonic polynomials.

Since the space of polynomials is dense in $L^2(S^3)$, we have the following

Corollary B.2

$$\begin{aligned} L^2(S^3) = \bigoplus _{p,q\ge 0} H_{p,q}. \end{aligned}$$

(B.11)

Remark B.1

This fact can also be deduced from the Peter-Weyl theorem for SU(2).

We further obtain the harmonic decomposition of tangential Cauchy Riemann complex on $S^3$

$$\begin{aligned} \begin{aligned} \Omega _b^{0,0}(S^3)&= \bigoplus _{p,q \ge 0} H_{p,q},\\ \Omega _b^{0,1}(S^3)&= \bigoplus _{p,q \ge 0} H_{p,q} \epsilon . \end{aligned} \end{aligned}$$

(B.12)

C Homotopy Algebra and Homotopy Transfer

Since this paper heavily uses techniques from homotopy algebra. We briefly review this topic in this appendix. We recommend the survey [67] for a detailed review.

1.1 C.1 Convention and Koszul sign rule

First, we fix the convention for our discussion. We work with $\mathbb {Z}$-graded $\mathbb {C}$-vector space

$$\begin{aligned} V = \bigoplus \limits _{n\in \mathbb {Z}}V_n. \end{aligned}$$

(C.1)

The grading n is related to the ghost number in physics. The degree of an element $v \in V_n$ is denoted by $|v| = n$, and such a v is called a homogeneous element.

For V and W two graded vector spaces, the tensor product $V\otimes W$ and the Hom space ${{\,\textrm{Hom}\,}}(V,W)$ has the following grading

$$\begin{aligned} (V\otimes W)_n = \bigoplus _{i+j = n} V_{i}\otimes W_j, \quad {{\,\textrm{Hom}\,}}(V,W)_{n} = \bigoplus _{i}{{\,\textrm{Hom}\,}}(V_i,W_{i+n}). \end{aligned}$$

We denote the Koszul sign braiding on tensor products to be

$$\begin{aligned} \begin{aligned} \tau _{V,W}:V\otimes W&\rightarrow W\otimes V,\\ v\otimes w&\mapsto (-1)^{|v||w|} w\otimes v. \end{aligned} \end{aligned}$$

The above sign rule induces naturally a sign rule for the action of the symmetric group $S_n$ on the n-th tensor product $V^{\otimes n}$

$$\begin{aligned} \sigma :\;v_1\otimes v_2\otimes \cdots \otimes v_n \rightarrow \epsilon (\sigma ,v)v_{\sigma (1)}\otimes v_{\sigma (2)} \otimes \dots v_{\sigma (n)}, \end{aligned}$$

where $\epsilon (\sigma ,v)$ is called the Koszul sign.

For V a $\mathbb {Z}$ graded vector space, we denote V[n] the degree n-shifted space such that

$$\begin{aligned} V[n]_{m} ~{:=} V_{n+m}. \end{aligned}$$

(C.2)

We also use the notation of suspension sV and desuspension $s^{-1}V$ as follows

$$\begin{aligned} sV ~{:=}\, V[1],\quad s^{-1}V: = V[-1]. \end{aligned}$$

(C.3)

We can also regard s as a degree $-1$ linear map $s: V \rightarrow V[1]$. For a homogeneous $a \in V$, we have $sa \in V[1]$ and $|sa| = |a| - 1$. Similarly, $s^{-1}$ can be regarded as a degree 1 linear map, such that $s^{-1}s = ss^{-1} = 1$.

1.2 C.2 Homotopy algebra

In this appendix, we review the definition of various homotopy algebras including $A_\infty$, $C_\infty$ and $L_\infty$ algebras.

$A_\infty$ algebra

Definition C.1

An $A_\infty$ algebra is a graded vector space $A = \{A_n\}_{n\in \mathbb {Z}}$ with a collection of multi-linear operations

$$\begin{aligned} m_n:A^{\otimes n} \rightarrow A\; \text { of degree } n - 2 \text { for all } n\ge 1, \end{aligned}$$

(C.4)

which satisfy the following relations:

$$\begin{aligned} \sum _{k = 1}^{n}\sum _{j = 0}^{n - k}(-1)^{jk + (n-j-k)}m_{n - k + 1}\circ (\textrm{id}^{\otimes j} \otimes m_k \otimes \textrm{id}^{\otimes n - j - k } ) = 0. \end{aligned}$$

(C.5)

Let’s demonstrate the above relations for small values of n:

• 1. $n = 1$. We have $m_1\circ m_1 = 0$, which means that $m_1$ is a differential on A. We also denote $d = m_1$.

• 2. $n = 2$. We have

  $$\begin{aligned} d m_2(x_1, x_2) = m_2(dx_1, x_2) + (-1)^{|x_1|}m_2(x_1, dx_2). \end{aligned}$$

  (C.6)

  This relation implies $m_1$ is a derivation with respect to the binary product $m_2$.

• 3. $n = 3$. The relation yields

  $$\begin{aligned} m_2 (m_2(x_1,x_2),x_3) - m_2(x_1,m_2(x_2,x_3))&= dm_3(x_1,x_2,x_3) + m_3(dx_1,x_2,x_3) \nonumber \\&\quad + m_3(x_1,dx_2,x_3) + m_3(x_1,x_2,dx_3).\nonumber \\ \end{aligned}$$

  (C.7)

An $A_\infty$ algebra with $m_k = 0$ for $k \ge 3$ is also called a differential graded associative (dga) algebra. For example, the tangential Cauchy–Riemann complex is a dga algebra

There is an equivalent definition of $A_\infty$ algebra in terms of coderivation. We introduce the reduced tensor coalgebra

$$\begin{aligned} {\bar{T}}^c(V) = \bigoplus _{n\ge 1}V^{\otimes n}, \end{aligned}$$

(C.8)

with comultiplication given by

$$\begin{aligned} \bar{\Delta }(v_1\otimes v_2\otimes \dots \otimes v_n) = \sum _{i = 1}^{n-1}(v_1\otimes \dots \otimes v_i)\otimes (v_{i+1}\otimes \dots \otimes v_n). \end{aligned}$$

(C.9)

Recall that a coderivation on a coalgebra $(C,\Delta )$ is a map $L: C \rightarrow C$ such that $\Delta \circ L = (L\otimes 1 + 1\otimes L)\Delta$.

For the (reduced) tensor coalgebra ${\bar{T}}^c(V)$, a coderivation on it is completely determined by its projection $p_V\circ L: {\bar{T}}^c(V) \rightarrow {\bar{T}}^c(V) \rightarrow V$. To see this, we first notice that $p_V\circ L$ is given by a set of maps $L_k \in {{\,\textrm{Hom}\,}}(V^{\otimes k},V),k\ge 1$. Given this set of maps, the coderivation is uniquely given by

$$\begin{aligned} L = \sum _{i\ge 1}^n\sum _{j = 0}^{n-i} \mathbb {1}^{\otimes j}\otimes L_{i}\otimes \mathbb {1}^{n - i - j}. \end{aligned}$$

(C.10)

The structure of an $A_\infty$ algebra on A can be compactly organized into the structure of a square zero coderivation on ${\bar{T}}^c(sA)$.

Proposition C.1

The following data are equivalent

• A collection of linear maps $m_k: A^{\otimes k} \rightarrow A$ of degree $2 - k$ satisfying $A_\infty$ relation.

• A degree 1 coderivation b on ${\bar{T}}^c(A[1])$ satisfying $b^2 = 0$.

Proof

We only sketch the proof here and refer to [68] for more details. Given linear maps $m_k:A^{\otimes k} \rightarrow A$, we define maps $b_k: (sA)^{\otimes k} \rightarrow sA$ by

$$\begin{aligned} b_k = s\circ m_k\circ (s^{-1})^{\otimes k}. \end{aligned}$$

(C.11)

The maps $b_k$ further define a coderivation b on ${\bar{T}}^c(A[1])$ through C.10. One can check that the requirement $b^2 = 0$ is equivalent to the $A_\infty$ relations C.5. $\quad \square$

$C_\infty$ algebra In this paper, the dga algebras that we studied satisfy additional properties of being graded commutative.

$$\begin{aligned} m_2(a,b) = (-1)^{|a||b|} m_2(b,a). \end{aligned}$$

(C.12)

Such algebras are called differential graded commutative (dgc) algebra. The homotopy version of dgc algebra is called $C_\infty$ algebra, which we now define.

A (p, q)-shuffle is a permutation $\sigma \in S_{p+q}$ such that

$$\begin{aligned} \sigma (1)<\sigma (2)< \dots< \sigma (p),\;\;\sigma (p + 1)<\sigma (p + 2)< \dots < \sigma (p+q). \end{aligned}$$

(C.13)

We denote by Sh(p, q) the subset of (p, q)-shuffles in $S_{p+q}$.

We have introduced the reduced tensor coalgebra ${\bar{T}}^c(V) = \bigoplus _{n\ge 1}V^{\otimes n}$. It becomes a Hopf algebra when equipped with the multiplication map called shuffle product

$$\begin{aligned}{} & {} sh((a_1,\dots ,a_p)\otimes (a_{p+1},\dots a_{p+q})) \nonumber \\{} & {} \quad = \sum _{\sigma \in Sh(p,q)}\epsilon (\sigma ,a)(a_{\sigma ^{-1}(1)},a_{\sigma ^{-1}(2)},\dots a_{\sigma ^{-1}(p+q)}). \end{aligned}$$

(C.14)

Definition C.2

A $C_{\infty }$-algebra structure on a graded vector space $A = \{A_n\}_{n\in \mathbb {Z}}$ is an $A_\infty$ structure $(A,\{m_n\}_{n\ge 1})$ such that the set of maps $\{b_k = s\circ m_k \circ (s^{-1})^{\otimes k}, k \ge 1\}$ vanish on the image of the shuffle product $sh:T^c(sA)\otimes T^c(sA) \rightarrow T^c(sA)$.

For example, the element $sa\otimes sb + (-1)^{(|a|+1)(|b| + 1)}sb\otimes sa$ is in the image of the shuffle product. Vanishing of $b_2$ on this element is the same as the graded commutativity of $m_2$.

$L_\infty$ algebra

We also introduce the notion of $L_\infty$ algebra.

Definition C.3

Let ${\mathfrak {g}} = \{{\mathfrak {g}}^n\}_{n \in \mathbb {Z}}$ be a graded vector space. An $L_\infty$ structure on ${\mathfrak {g}}$ is a collection of multi-linear maps

$$\begin{aligned} l_n:{\mathfrak {g}}^{\otimes n} \rightarrow {\mathfrak {g}}\; \text { of degree } n - 2 \text { for all } n\ge 1, \end{aligned}$$

(C.15)

that are graded skew-symmetric:

$$\begin{aligned} l_n(x_{\sigma ^{-1}(1)},\dots ,x_{\sigma ^{-1}(n)}) = (-1)^{\sigma }\epsilon (\sigma ,x) l_n(x_1,\dots ,x_n),\;\;\text { for all } \sigma \in S_n, \end{aligned}$$

(C.16)

and satisfy the following relations:

$$\begin{aligned}{} & {} \sum _{k = 1}^{n}(-1)^{k}\sum _{\sigma \in Sh(k,n - k)}(-1)^{\sigma }\epsilon (\sigma ,x) l_{n - k - 1}(l_{k}(x_{\sigma ^{-1}(1)},\dots ,x_{\sigma ^{-1}(k)}),\nonumber \\{} & {} x_{\sigma ^{-1}(k + 1)},\dots ,x_{\sigma ^{-1}(n)}) = 0. \end{aligned}$$

(C.17)

Let us analyze the defining relations for small values of n:

• 1. $n = 1$. The relation is $l_1\circ l_1 = 0$, which means that $l_1$ is a differential on ${\mathfrak {g}}$.

• 2. $n = 2$. We have

  $$\begin{aligned} l_1(l_2(x_1,x_2)) = l_2(l_1(x_1),x_2) + (-1)^{|x_1|}l_2(x_1,l_1(x_2)) \end{aligned}$$

  (C.18)

  which says that $l_1$ is a derivation with respect to the binary map $l_2$.

• 3. $n = 3$. The relations yields

  $$\begin{aligned}{} & {} l_2(l_2(x_1,x_2),x_3) + (-1)^{(|x_1|+|x_2|)|x_3|}l_2(l_2(x_3,x_1),x_2) \nonumber \\{} & {} \quad + (-1)^{(|x_2|+|x_3|)|x_1|}l_2(l_2(x_2,x_3),x_1) \nonumber \\{} & {} = l_1l_3(x_1,x_2,x_3) + l_3(l_1(x_1),x_2,x_3) + (-1)^{|x_1|}l_3(x_1,l_1(x_2),x_3) \nonumber \\{} & {} \quad + (-1)^{|x_1| + |x_2|}l_3(x_1,x_2,l_1(x_3)). \end{aligned}$$

  (C.19)

  which says that $l_2$ satisfies Jacobi identities up to homotopy given by $l_3$.

There is a similar characterization of $L_\infty$ algebra in terms of a coderivation. Instead of the tensor coalgebra, we consider the reduced symmetric coalgebra ${\bar{S}}^c(V)$ where

$$\begin{aligned} {\bar{S}}^c(V) = \bigoplus _{n \ge 1}\textrm{Sym}^n(V). \end{aligned}$$

The coproduct ${\bar{\Delta }}: {{\bar{S}}}^c(V) \rightarrow {{\bar{S}}}^c(V)\otimes {{\bar{S}}}^c(V)$ is defined by

$$\begin{aligned}{} & {} {\bar{\Delta }}(v_1\cdot v_2\dots v_n)\nonumber \\{} & {} \quad = \sum _{i = 1}^{n-1}\sum _{\sigma \in \text {Sh}(i,n-i)}\epsilon (\sigma ,v)(v_{\sigma ^{-1}(1)}\cdot v_{\sigma ^{-1}(2)}\dots v_{\sigma ^{-1}(i)})\otimes (v_{\sigma ^{-1}(i+1)}\cdot \cdot \cdot v_{\sigma ^{-1}(n)}).\nonumber \\ \end{aligned}$$

(C.20)

Then we have

Proposition C.2

The following data are equivalent

• A collection of linear maps $l_k: {\mathfrak {g}}^{\otimes k} \rightarrow {\mathfrak {g}}$ of degree $2 - k$ satisfying $L_\infty$ relation.

• A degree 1 coderivation Q on ${{\bar{S}}}^c({\mathfrak {g}}[1])$ satisfying $Q^2 = 0$.

1.3 C.3 Homological perturbation lemma

We introduce an important technical tool called the homological perturbation lemma. We refer to [69] for a more detailed discussion.

Let us first consider the following homotopy data of chain complexes.

Definition C.4

A special deformation retract (SDR) from a cochain complex $(A,d_A)$ to $(H,d_H)$ consists of the following data

(C.21)

where i, p are cochain maps and h is a degree $-1$ map on A, such that

$$\begin{aligned} i\circ p-\mathbb {1}_A = d_A\circ h + h\circ d_A,\;\quad p\circ i = \mathbb {1}_{H}, \end{aligned}$$

(C.22)

and

$$\begin{aligned} h\circ i = 0,\; p\circ h = 0,\; h\circ h = 0. \end{aligned}$$

(C.23)

Consider a perturbation $\delta$ to the differential on A:

$$\begin{aligned} d_A' = d_A + \delta ,\;\;d_A'^2 = 0 \end{aligned}$$

(C.24)

The perturbation is called small if $(1 - \delta h)$ is invertible.

Lemma C.1

(Homological perturbation lemma) .Given a SDR data as C.21 and a small perturbation, there is a new SDR:

(C.25)

where the maps above are defined by

$$\begin{aligned} \begin{aligned} d_H'&= d_H+ p(1 - \delta h)^{-1}\delta i,\\ h'&= h + h(1 - \delta h)^{-1}\delta h,\\ p'&= p + p(1 - \delta h)^{-1}\delta h,\\ i'&= i + h(1 - \delta h)^{-1}\delta i. \end{aligned} \end{aligned}$$

(C.26)

The homological perturbation lemma can be regarded as a substitution of the spectral sequence techniques, which provides explicit formulae.

1.4 C.4 Homotopy transfer

Given a dga algebra (or an $A_\infty$ algebra in general) and a chain complex quasi-isomorphic to it, homotopy transfer theorem [34] gives the complex an $A_\infty$ structure. In particular, one gets an $A_\infty$ structure on the cohomology of a dga algebra. We emphasize that there are different approaches to construct this $A_\infty$ structure. In this appendix, we take the approach using homological perturbation lemma [70].

Given a dga algebra $(A,d,\cdot )$. Suppose we can find a SDR to its cohomology

(C.27)

Recall that the dga algebra structure on A is equivalent to a differential b on ${\bar{T}}^c(sA)$. Therefore, we first extend the above SDR to the corresponding tensor coalgebra

Proposition C.3

The following is a SDR

(C.28)

where the differential $Td^s$ is defined by $Td^s = \sum _{n \ge 1} \sum _{i = 0}^{n-1} \mathbb {1}^{i}\otimes (s\circ d\circ s^{-1}) \otimes \mathbb {1}^{n - i - 1}$. The projection and inclusion maps are defined by $Tp^s = \sum _{n\ge 1}(s\circ p\circ s^{-1})^{\otimes n}$ and $Ti^s = \sum _{n\ge 1}(s\circ i\circ s^{-1})^{\otimes n}$. The deformation retract is defined as

$$\begin{aligned} Th^s = \sum _{n\ge 1} \sum _{i = 0}^{n-1} \mathbb {1}^{\otimes i} \otimes (s\circ h\circ s^{-1}) \otimes (s\circ i\circ p\circ s^{-1})^{\otimes n - i - 1}. \end{aligned}$$

The product $\cdot$ on the dga algebra A defined a map $b_2:(sA)^{\otimes 2} \rightarrow sA$ and extend to a map $\delta : {\bar{T}}^c(sA) \rightarrow {\bar{T}}^c(sA)$. Together with the differential $Td^s$, the sum $b = Td^s + \delta : {\bar{T}}^c(sA) \rightarrow {\bar{T}}^c(sA)$ encode the dga algebra structure A in the sense of Proposition C.1. Now we can regard $\delta$ as a perturbation to the differential and apply the homological perturbation lemma. We have the following new SDR

(C.29)

The homological perturbation lemma provides us a formula for all the maps $h',p',i'$. However, only the differential $b_H$ matter to us as it encodes the transferred $A_\infty$ structure on the cohomology H. We have

$$\begin{aligned} b'= Tp^s\circ (1 - \delta \circ Th^s)^{-1}\circ \delta \circ Ti^s = \sum _{n \ge 0}Tp^s\circ ( \delta \circ Th^s)^{n}\circ \delta \circ Ti^s. \end{aligned}$$

(C.30)

If we further expand the above formula into components, we find the usual tree description of the transferred $A_\infty$ structure on H. Let $\mathrm {PBT_n}$ be the set of planar binary rooted trees with n leaves. We consider the following construction that assigns each $T \in \textrm{PBT}_n$ an n array operation $m_T$ on H. The operation $m_T$ is obtained by putting i on the leaves, m on the vertices, h on the internal edges and p on the root. Then we consider

$$\begin{aligned} m_n = \sum _{T \in PBT_n} (\pm ) m_T, \end{aligned}$$

(C.31)

where the $(\pm )$ sign can be tracked by a careful analysis of the Koszul sign rule in C.30.

Theorem C.1

The operations $\{m_n\}_{n \ge 2}$ defined on H by the formulae C.31 form an $A_\infty$-algebra structure on H.

Moreover, the transferred $A_\infty$-algebra $(H,\{m_n\}_{n \ge 2})$ is $A_\infty$ quasi-isomorphic to the dg algebra $(A,d_A,\cdot )$.

In the example of our study, the tangential Cauchy–Riemann complex is graded commutative. We are interested in the transferred structure for dgc algebra. This scenario is analyzed in [37]. For $(A,d,\cdot )$ a dgc algebra, if we regard it as a dga algebra, the $A_\infty$ structure constructed by C.31 actually defines a $C_\infty$ structure.

For homotopy transfer of dg Lie algebra and $L_\infty$ algebra, a similar result can be established. We start with a dg Lie algebra $(L,d,[-,-])$ and consider the transferred structure on its cohomology . Suppose we are given the following SDR

(C.32)

The tensor trick can be extended to the symmetric case

(C.33)

where the differential $Sd^s$ is defined by $Sd^s = \sum _{n \ge 1} \sum _{i = 0}^{n-1} \mathbb {1}^{i}\otimes (s\circ d\circ s^{-1}) \otimes \mathbb {1}^{n - i - 1}$. The projection and inclusion maps are defined by $Sp^s = \sum _{n\ge 1}(s\circ p\circ s^{-1})^{\otimes n}$ and $Si^s = \sum _{n\ge 1}(s\circ i\circ s^{-1})^{\otimes n}$. The deformation retract is defined as

$$\begin{aligned} Sh^s = \sum _{n\ge 1}\frac{1}{n!}\sum _{\sigma \in S_n} \sigma ^{-1}\left( \sum _{i = 0}^{n-1} \mathbb {1}^{\otimes i} \otimes (s\circ h\circ s^{-1}) \otimes (s\circ i\circ p\circ s^{-1})^{\otimes n - i - 1}\right) \sigma . \end{aligned}$$

The Lie bracket $[-,-]$ on L defined a map $Q_2:(sL)^{\otimes 2} \rightarrow sL$ and extend to a map $\delta : {\bar{S}}^c(sL) \rightarrow {\bar{T}}^c(sL)$. We add this differential to the above SDR as a perturbation. Then we have a new SDR, with a new differential on ${\bar{S}}^c(s{\mathfrak {g}})$ given by the following

$$\begin{aligned} Q' = Sp^s\circ (1 - \delta \circ Sh^s)^{-1}\circ \delta \circ Si^s = \sum _{n \ge 0}Sp^s\circ ( \delta \circ Sh^s)^{n}\circ \delta \circ Si^s. \end{aligned}$$

(C.34)

We can expand the above formula into components. This gives us the usual tree description of the transferred $L_\infty$ structure on ${\mathfrak {g}}$. Let $\mathrm {BT_n}$ be the set of binary rooted trees with n leaves. In this case, we need to consider trees not necessarily planar, which means edges can cross each other. We consider the following construction that assigns each $T \in \textrm{BT}_n$ an n array operation $l_T$ on H. The operation $l_T$ is obtained by putting i on the leaves, $[-,-]$ on the vertices, h on the internal edges and p on the root. We consider

$$\begin{aligned} l_n = \sum _{T \in BT_n} (\pm ) l_T. \end{aligned}$$

(C.35)

Then the operations $\{l_n\}_{n \ge 2}$ defined an $L_\infty$-algebra structure on ${\mathfrak {g}}$. Moreover, the $L_\infty$ algebra $({\mathfrak {g}},l_2,l_3,\dots )$ is $L_\infty$ quasi-isomorphic to the dg Lie algebra $(L,d,[-,-])$.

D Computation of (Higher) Products and Brackets

1.1 D.1 Product of $S^3$ harmonics

In this section, we compute the product of two arbitrary $S^3$ harmonics. We first recall the formula 4.28 that decomposes a harmonic polynomial into sum of monomials

$$\begin{aligned} e^{(j,{\bar{j}})}_{m} = \sum _{l}\lambda _{j,{\bar{j}},0}^{-1}C^{j,{\bar{j}};j+{\bar{j}}}_{m -l,l;m} e^{(j)}_{m - l} {\bar{e}}^{{\bar{j}}}_{l}, \end{aligned}$$

(D.1)

where

$$\begin{aligned} \lambda _{j,{\bar{j}},k} = (-1)^k\sqrt{\frac{(2j+1)!(2{\bar{j}} + 1)!}{k!(2j + 2{\bar{j}} - k + 1)!}}. \end{aligned}$$

(D.2)

Then we can write

$$\begin{aligned}{} & {} M(e^{(j_1,{\bar{j}}_1)}_{m_1},e^{(j_2,{\bar{j}}_2)}_{m_2}) \nonumber \\{} & {} \quad = \sum _{l_1,l_2}\lambda _{j_1,{\bar{j}}_1,0}^{-1}\lambda _{j_2,{\bar{j}}_2,0}^{-1}C^{j_1,{\bar{j}}_1;j_1+{\bar{j}}_1}_{m_1 - l_1, l_1;m_1} C^{j_2,{\bar{j}}_2;j_2+{\bar{j}}_2}_{m_2 - l_2, l_2;m_2} M(e^{(j_1)}_{m_1 - l_1}{\bar{e}}^{({\bar{j}}_1)}_{l_1},e^{(j_2)}_{m_2 - l_2}{\bar{e}}^{({\bar{j}}_2)}_{l_2}).\nonumber \\ \end{aligned}$$

(D.3)

To compute $M(e^{(j_1)}_{m_1 - l_1}{\bar{e}}^{({\bar{j}}_1)}_{l_1},e^{(j_2)}_{m_2 - l_2}{\bar{e}}^{({\bar{j}}_2)}_{l_2})$, we consider the product $e^{(j_1)}_{m_1 - l_1}e^{(j_2)}_{m_2 - l_2}$ and ${\bar{e}}^{({\bar{j}}_1)}_{l_1}{\bar{e}}^{({\bar{j}}_2)}_{l_2}$ separately. We find

$$\begin{aligned} \begin{aligned}&M(e^{(j_1)}_{m_1 - l_1}{\bar{e}}^{({\bar{j}}_1)}_{l_1},e^{(j_1)}_{m_1 - l}{\bar{e}}^{({\bar{j}}_1)}_{l_2}) \\ =&\sqrt{\frac{(2j_1+1)(2j_2+1)(2{\bar{j}}_1+1)(2{\bar{j}}_2+1)}{(2j_1 + 2j_2+1)(2{\bar{j}}_1+2{\bar{j}}_2 + 1)}}\\&C^{j_1,j_2;j_1+j_2}_{m_1-l_1,m_2 - l_2,m_1+m_2-l_1-l_2}C^{{\bar{j}}_1,{\bar{j}}_2;{\bar{j}}_1+{\bar{j}}_2}_{l_1,l_2,l_1+l_2} M(e^{(j_1+j_2)}_{m_1+m_2-l_1-l_2},{\bar{e}}^{({\bar{j}}_1+{\bar{j}}_2)}_{l_1+l_2})\\ =&\sum _{k} \lambda _{j_1+j_2,{\bar{j}}_1+{\bar{j}}_2,k}\sqrt{\frac{(2j_1+1)(2j_2+1)(2{\bar{j}}_1+1)(2{\bar{j}}_2+1)}{(2j_1 + 2j_2+1)(2{\bar{j}}_1+2{\bar{j}}_2 + 1)}} \\&\times C^{j_1,j_2;j_1+j_2}_{m_1-l_1,m_2 - l_2;m_1+m_2-l_1-l_2}C^{{\bar{j}}_1,{\bar{j}}_2;{\bar{j}}_1+{\bar{j}}_2}_{l_1,l_2;l_1+l_2} C^{j_1+j_2,{\bar{j}}_1+{\bar{j}}_2;j_1+j_2+{\bar{j}}_1+{\bar{j}}_2 - k}_{m_1+m_2-l_1-l_2,l_1+l_2;m_1+m_2}e^{(j_1+j_2- \frac{k}{2},{\bar{j}}_1+{\bar{j}}_2 - \frac{k}{2})}_{m_1+m_2}. \end{aligned}\nonumber \\ \end{aligned}$$

(D.4)

Therefore

$$\begin{aligned}{} & {} M(e^{(j_1,{\bar{j}}_1)}_{m_1},e^{(j_2,{\bar{j}}_2)}_{m_2})\nonumber \\{} & {} = \sum _{k}\sum _{l_1,l_2}\lambda _{j_1,{\bar{j}}_1,0}^{-1}\lambda _{j_2,{\bar{j}}_2,0}^{-1} \lambda _{j_1+j_2,{\bar{j}}_1+{\bar{j}}_2,k}\sqrt{\frac{(2j_1+1)(2j_2+1)(2{\bar{j}}_1+1)(2{\bar{j}}_2+1)}{(2j_1 + 2j_2+1)(2{\bar{j}}_1+2{\bar{j}}_2 + 1)}} \nonumber \\{} & {} \quad \times C^{j_1,{\bar{j}}_1;j_1+{\bar{j}}_1}_{m_1 - l_1, l_1;m_1} C^{j_2,{\bar{j}}_2;j_2+{\bar{j}}_2}_{m_2 - l_2, l_2;m_2} C^{j_1,j_2;j_1+j_2}_{m_1-l_1,m_2 - l_2;m_1+m_2-l_1-l_2}C^{{\bar{j}}_1,{\bar{j}}_2;{\bar{j}}_1+{\bar{j}}_2}_{l_1,l_2;l_1+l_2} \nonumber \\{} & {} \qquad C^{j_1+j_2,{\bar{j}}_1+{\bar{j}}_2;j_1+j_2+{\bar{j}}_1+{\bar{j}}_2 - k}_{m_1+m_2-l_1-l_2,l_1+l_2;m_1+m_2}e^{(j_1+j_2- \frac{k}{2},{\bar{j}}_1+{\bar{j}}_2 - \frac{k}{2})}_{m_1+m_2}\nonumber \\{} & {} = \sum _{k}\lambda _{j_1,{\bar{j}}_1,0}^{-1}\lambda _{j_2,{\bar{j}}_2,0}^{-1} \lambda _{j_1+j_2,{\bar{j}}_1+{\bar{j}}_2,k}\nonumber \\{} & {} \qquad \sqrt{(2j_1+1)(2j_2+1)(2{\bar{j}}_1+1)(2{\bar{j}}_2+1)(2j_1 + 2{\bar{j}}_1+1)(2j_2+2{\bar{j}}_2 + 1)} \nonumber \\{} & {} \quad \times \begin{Bmatrix} j_1&j_2&j_1+j_2\\{\bar{j}}_1&{\bar{j}}_2&{\bar{j}}_1+{\bar{j}}_2\\j_1+{\bar{j}}_1&j_2+{\bar{j}}_2&j_1+j_2+{\bar{j}}_1+{\bar{j}}_2 - k \end{Bmatrix}C^{j_1+{\bar{j}}_1,j_2+{\bar{j}}_2;j_1+j_2+{\bar{j}}_1+{\bar{j}}_2 - k}_{m_1,m_2;m_1+m_2}e^{(j_1+j_2- \frac{k}{2},{\bar{j}}_1+{\bar{j}}_2 - \frac{k}{2})}_{m_1+m_2}, \nonumber \\ \end{aligned}$$

(D.5)

where $\begin{Bmatrix} j_1&j_2&j_3\\j_4&j_5&j_6\\j_7&j_8&j_9 \end{Bmatrix}$ is the Wigner $9-j$ symbol.

In our study of the higher product on the CR cohomology, a constantly appearing computation is the product of the form $M(e^{(j_1 - \frac{i}{2},{\bar{j}}_1 - \frac{i}{2})}_{m_1},{\bar{e}}^{(\bar{j_2})}_{m_2})$. One can use the above general formula to compute this. Here, we derive an alternative formula that is more succinct. The key is that we use a variation of 4.28 to expand the harmonics polynomial $e^{(j_1 - \frac{i}{2},{\bar{j}}_1 - \frac{i}{2})}_{m_1}$

$$\begin{aligned} e^{(j_1 - \frac{i}{2},{\bar{j}}_1 - \frac{i}{2})}_{m_1} = \sum _{l}\lambda _{j_1,{\bar{j}}_1,i}^{-1} C^{j_1,{\bar{j}}_1;j_1+{\bar{j}}_1 - i}_{m_1 - l,l;m_1}e^{(j_1)}_{m_1 - l}{\bar{e}}^{({\bar{j}}_1)}_{l}. \end{aligned}$$

(D.6)

Therefore, we have

$$\begin{aligned}{} & {} M(e^{(j_1 - \frac{i}{2},{\bar{j}}_1 - \frac{i}{2})}_{m_1},{\bar{e}}^{({\bar{j}}_2)}_{m_2}) \nonumber \\{} & {} = \sum _{l}\lambda _{j_1,{\bar{j}}_1,i}^{-1}\sqrt{\frac{(2{\bar{j}}_1 + 1)(2{\bar{j}}_2 + 1)}{(2{\bar{j}}_1 + 2{\bar{j}}_2 + 1)}} C^{j_1,{\bar{j}}_1;j_1+{\bar{j}}_1 - i}_{m_1 - l,l;m_1} C^{{\bar{j}}_1,{\bar{j}}_2;{\bar{j}}_1+{\bar{j}}_2}_{l,m_2;l+m_2}\nonumber \\{} & {} \qquad M(e^{(j_1)}_{m_1 - l},{\bar{e}}^{({\bar{j}}_1+{\bar{j}}_2)}_{l+m_2} )\nonumber \\{} & {} = \sum _{k\ge 0}\sum _{l}\lambda _{j_1,{\bar{j}}_1,i}^{-1}\lambda _{j_1,{\bar{j}}_1+{\bar{j}}_2;k}\sqrt{\frac{(2{\bar{j}}_1 + 1)(2{\bar{j}}_2 + 1)}{(2{\bar{j}}_1 + 2{\bar{j}}_2 + 1)}} C^{j_1,{\bar{j}}_1;j_1+{\bar{j}}_1 - i}_{m_1 - l,l;m_1} C^{{\bar{j}}_1,{\bar{j}}_2;{\bar{j}}_1+{\bar{j}}_2}_{l,m_2;l+m_2}\nonumber \\{} & {} \qquad C^{j_1,\bar{j_1}+{\bar{j}}_2;j_1+{\bar{j}}_1+{\bar{j}}_2 - k}_{m_1 - l,m_2+l;m_1+m_2}e^{(j_1 - \frac{k}{2},{\bar{j}}_1+{\bar{j}}_2 - \frac{k}{2})}_{m_1 + m_2}\nonumber \\{} & {} = \sum _{k\ge 0} (-1)^{2(j_1+{\bar{j}}_1 + {\bar{j}}_2) - k}\lambda _{j_1,{\bar{j}}_1,i}^{-1}\lambda _{j_1,{\bar{j}}_1+{\bar{j}}_2;k}\sqrt{(2{\bar{j}}_1 + 1)(2{\bar{j}}_2 + 1)(2j_1 + 2{\bar{j}}_1 - 2i + 1)}\nonumber \\{} & {} \quad \times \begin{Bmatrix} {\bar{j}}_1&j_1&j_1+{\bar{j}}_1 - i\\j_1+{\bar{j}}_1 + {\bar{j}}_2 - k&{\bar{j}}_2&{\bar{j}}_1+{\bar{j}}_2 \end{Bmatrix}C^{j_1+{\bar{j}}_1 - i,{\bar{j}}_2;j_1+{\bar{j}}_1+{\bar{j}}_2 - k}_{m_1,m_2;m_1+m_2}e^{(j_1 - \frac{k}{2},{\bar{j}}_1+{\bar{j}}_2 - \frac{k}{2})}_{m_1 + m_2}.\nonumber \\ \end{aligned}$$

(D.7)

Though we write the summation range as $k \ge 0$, the Wigner 6j symbol actually constraint it such that $k \ge i$ and $k \le \min \{2j_1,2{\bar{j}}_1+2{\bar{j}}_2\}$.

1.2 D.2 3-brackets of Poisson BF theory

In this Appendix, we give a general formula for the 3-bracket in the Poisson BF theory. We compute the constant

$$\begin{aligned} (\pi _3)^{p,q;r,s}_{u_1,v_1,u_{2},v_{2}}{} & {} = \frac{(u_1+v_1+1)!(u_2+v_2+1)!}{u_1!v_1!u_2!v_2!}\times {{\,\textrm{Tr}\,}}_{S^3}(w_1^pw_2^q\times p\{ h\{w_1^rw_2^s,{\bar{w}}_1^{u_1}{\bar{w}}_2^{v_1}\epsilon \},\nonumber \\{} & {} \qquad {\bar{w}}_1^{u_2}{\bar{w}}_2^{v_2}\epsilon \} )\nonumber \\{} & {} = \frac{(u_1+v_1+1)!(u_2+v_2+1)!}{u_1!v_1!u_2!v_2!}\times {{\,\textrm{Tr}\,}}_{S^3}({\bar{w}}_1^{u_2}{\bar{w}}_2^{v_2}\epsilon \times p\{w_1^pw_2^q,\nonumber \\{} & {} \qquad h\{w_1^rw_2^s,{\bar{w}}_1^{u_1}{\bar{w}}_2^{v_1}\epsilon \}\} ) \end{aligned}$$

(D.8)

Since $(\pi _3)^{p,q;r,s}_{u_1,v_1,u_{2},v_{2}}$ is only nonzero when $u_1+u_2 = p+r -3,v_1+v_2 = q+s - 3$, we denote $(\pi _3)^{p,q;r,s}_{u,v} {:=} (\pi _3)^{p,q;r,s}_{u,v,p+r - u - 3,q+s-v-3}$ throughout this section.

First, we need to give a SU(2) decomposition of the two bracket $\{-,-\}_{\bar{\pi }}$ on the CR complex. From 6.22, we see that the induced bracket on the CR complex restricted to ${\mathcal {H}}_{j,0}\otimes {\mathcal {H}}_{0,{\bar{j}}}\epsilon$ gives a map

$$\begin{aligned} \begin{aligned} \{-,-\}: {\mathcal {H}}_{j,0}\otimes {\mathcal {H}}_{0,{\bar{j}}}\epsilon&\rightarrow {\mathcal {H}}_{j-\frac{1}{2},0}\otimes {\mathcal {H}}_{0,{\bar{j}}+\frac{1}{2}}\epsilon \\&\cong {\mathcal {H}}_{j - \frac{1}{2},{\bar{j}}+\frac{1}{2}}\epsilon \oplus {\mathcal {H}}_{j - 1,{\bar{j}}}\epsilon \oplus \dots \end{aligned} \end{aligned}$$

(D.9)

We can analyze this map using the same techniques as in Sect. 4.2.

$$\begin{aligned}{} & {} \{-,-\}\circ CG^{-1} (e^{(j + {\bar{j}} - k)}_{j + {\bar{j}} - k}\epsilon ) \nonumber \\{} & {} = \sum _{l = 0}^{k}(-1)^{k} C^{j,{\bar{j}};j + {\bar{j}} - k}_{j,{\bar{j}} - k;j + {\bar{j}} - k} \frac{k!}{(k - l)! l! }\sqrt{\frac{(2j+1)(2{\bar{j}} + 1)!}{k!( 2{\bar{j}}-k)!}} \nonumber \\{} & {} \quad \times (2{\bar{j}} + 2)(lw_1{\bar{w}}_1 - (2j - l)w_2{\bar{w}}_2)w_1^{2j-l - 1}w_2^{l - 1}{\bar{w}}_1^{ k - l}{\bar{w}}_2^{ 2{\bar{j}} - k + l}\epsilon \nonumber \\{} & {} = (-1)^{k+1}\sqrt{\frac{(2j+1)!(2{\bar{j}}+1)!}{k!(2j+2{\bar{j}} - k + 1)!}}\sqrt{(2{\bar{j}} - k + 1)( 2j - k)}(2{\bar{j}} + 2) e^{(j - \frac{1}{2} - \frac{k}{2},{\bar{j}} + \frac{1}{2} - \frac{k}{2} )}_{j + {\bar{j}} - k}.\nonumber \\ \end{aligned}$$

(D.10)

Therefore, the map $\{-,-\}: {\mathcal {H}}_{j,0}\otimes {\mathcal {H}}_{0,{\bar{j}}}\epsilon \rightarrow \bigoplus _{k = 0}^{\min \{2j - 1,2{\bar{j}} + 1\}}{\mathcal {H}}_{j - \frac{1}{2} - \frac{k}{2},{\bar{j}}+\frac{1}{2} - \frac{k}{2}}\epsilon$ is given by

$$\begin{aligned} \{e^{(j)}_m,{\bar{e}}^{({\bar{j}})}_{{\bar{m}}}\epsilon \} = \sum _{k} {\tilde{\lambda }}_{j,{\bar{j}},k}C^{j,{\bar{j}};j + {\bar{j}} - k}_{m,{\bar{m}};m+{\bar{m}}} e^{(j - \frac{1}{2} - \frac{k}{2},{\bar{j}}+\frac{1}{2} - \frac{k}{2})}_{m+{\bar{m}}}\epsilon , \end{aligned}$$

(D.11)

where

$$\begin{aligned} {\tilde{\lambda }}_{j,{\bar{j}},k}{} & {} = (-1)^{k+1}\sqrt{\frac{(2j+1)!(2{\bar{j}}+1)!}{k!(2j+2{\bar{j}} - k + 1)!}}\sqrt{(2{\bar{j}} - k + 1)( 2j - k)}(2{\bar{j}} + 2) \nonumber \\{} & {} = -\sqrt{(2{\bar{j}} - k + 1)( 2j - k)}(2{\bar{j}} + 2) \lambda _{j,{\bar{j}},k}.\nonumber \\ \end{aligned}$$

(D.12)

We emphasis that the bracket restricted to ${\mathcal {H}}_{j,0}\otimes {\mathcal {H}}_{0,{\bar{j}}}$ is different. We have

$$\begin{aligned} \{w_1^pw_2^q,{\bar{w}}_1^r{\bar{w}}_2^s\} = (r+s)(qw_1{\bar{w}}_1 - pw_2{\bar{w}}_2 ) w_1^{p-1}w_2^{q - 1}{\bar{w}}_1^r{\bar{w}}_1^s\epsilon . \end{aligned}$$

(D.13)

As a result, we have

$$\begin{aligned} \{e^{(j)}_m,{\bar{e}}^{({\bar{j}})}_{{\bar{m}}}\} = \sum _{k} -\sqrt{(2{\bar{j}} - k + 1)( 2j - k)}(2{\bar{j}} ) \lambda _{j,{\bar{j}},k}C^{j,{\bar{j}};j + {\bar{j}} - k}_{m,{\bar{m}};m+{\bar{m}}} e^{(j - \frac{1}{2} - \frac{k}{2},{\bar{j}}+\frac{1}{2} - \frac{k}{2})}_{m+{\bar{m}}}.\nonumber \\ \end{aligned}$$

(D.14)

To compute the constant $\pi ^{p,q;r,s}_{u,v}$ we compute the map $p\{w_1^pw_2^q, h\{w_1^rw_2^s,{\bar{w}}_1^{u_1}{\bar{w}}_2^{v_1}\epsilon \}\}$. First, we compute $h\{e^{(j_2)}_{m_2}, {\bar{e}}^{\bar{(j)}}_{{\bar{m}}}\epsilon \}$. Using D.11, we have

$$\begin{aligned} h\{e^{(j_2)}_{m_2}, {\bar{e}}^{\bar{(j)}}_{{\bar{m}}}\epsilon \} = \sum _{i} {\tilde{\lambda }}_{j_2,{\bar{j}},i}h_{j_2 - \frac{1}{2} - \frac{i}{2},{\bar{j}}+\frac{1}{2} - \frac{i}{2}}C^{j_2,{\bar{j}};j_2 + {\bar{j}} - i}_{m,{\bar{m}};m_2+{\bar{m}}} e^{(j_2 - 1 - \frac{i}{2},{\bar{j}}+1 - \frac{i}{2})}_{m_2+{\bar{m}}}. \end{aligned}$$

(D.15)

Then we compute $p\{e^{(j_1)}_{m_1},e^{(j_2 - 1 - \frac{i}{2},{\bar{j}}+1 - \frac{i}{2})}_{m_2 + {\bar{m}}}\}$. Using D.7 we have

$$\begin{aligned} \begin{aligned} p\{e^{(j_1)}_{m_1},e^{(j_2 - 1 - \frac{i}{2},{\bar{j}}+1 - \frac{i}{2})}_{m_2+{\bar{m}}}\}&= \sum _{m'}\lambda _{j_2-1,{\bar{j}}+1,i}^{-1}C^{j_2-1,{\bar{j}}+1;j_2+{\bar{j}} - i}_{m',m_2+{\bar{m}} - m';m_2+{\bar{m}}}p\{e^{(j_1)}_{m_1},e^{(j_2 - 1)}_{m'} {\bar{e}}^{({\bar{j}}+1)}_{m_2+{\bar{m}} - m'}\}\\&= \sum _{m'}\lambda _{j_2-1,{\bar{j}}+1,i}^{-1}C^{j_2-1,{\bar{j}}+1;j_2+{\bar{j}} - i}_{m',m_2+{\bar{m}} - m';m_2+{\bar{m}}}\left( pM( \{e^{(j_1)}_{m_1},e^{(j_2 - 1)}_{m'}\},{\bar{e}}^{({\bar{j}}+1)}_{m_2+{\bar{m}} - m'})\right. \\&\quad \left. +pM( e^{(j_2 - 1)}_{m'},\{e^{(j_1)}_{m_1},{\bar{e}}^{({\bar{j}}+1)}_{m_2+{\bar{m}} - m'} \})\right) . \\ \end{aligned}\nonumber \\ \end{aligned}$$

(D.16)

The first term in the above formula is given by

$$\begin{aligned}{} & {} pM( \{e^{(j_1)}_{m_1},e^{(j_2 - 1)}_{m'}\},{\bar{e}}^{({\bar{j}}+1)}_{m_2+{\bar{m}} - m'})\nonumber \\{} & {} \quad = (-1)^{2{\bar{j}}}\sqrt{\frac{[2j_1 + 1]_2[2j_2 - 1]_2(2j_1 + 2j_2 - 2)(2{\bar{j}}+3)}{2j_1 + j_2 - 3}} C^{j_1,j_2 - 1;j_1 + j_2 - 2}_{m_1,m';m_1+m'}\nonumber \\{} & {} \quad C^{j_1+j_2 - 2,{\bar{j}} + 1,j_1 + j_2 - {\bar{j}} - 3}_{m_1+m',m_2+{\bar{m}} - m';m_1+m_2 + {\bar{m}}} e^{(j_1+j_2 - {\bar{j}} - 3)}_{m_1+m_2+m_3}.\nonumber \\ \end{aligned}$$

(D.17)

The second term can be computed by

$$\begin{aligned}{} & {} pM( e^{(j_2 - 1)}_{m'},\{e^{(j_1)}_{m_1},{\bar{e}}^{({\bar{j}}+1)}_{m_2+{\bar{m}} - m'} \})\nonumber \\{} & {} = \sum _{k} -\sqrt{(2{\bar{j}} - k + 3)( 2j_1 - k)}(2{\bar{j}} + 2)\lambda _{j_1,{\bar{j}} + 1,k} C^{j_1,{\bar{j}}+1,j_1+{\bar{j}}+1 - k}_{m_1,m_2+{\bar{m}} - m';m_1+m_2 + {\bar{m}} - m'}\nonumber \\{} & {} \qquad pM(e^{(j_2 - 1)}_{m'},e^{(j_1 - \frac{1}{2} - \frac{k}{2},{\bar{j}}+ 1 + \frac{1}{2} - \frac{k}{2})}_{m_1+m_2 + {\bar{m}} - m'})\nonumber \\{} & {} = \sum _{k} (-1)^{2(j_1+j_2) - k}\sqrt{(2{\bar{j}} - k + 3)( 2j_1 - k)}(2{\bar{j}} + 2)\lambda _{j_1,{\bar{j}} + 1,k} \lambda _{j_1 - \frac{1}{2},{\bar{j}}+\frac{3}{2},k}^{-1} \nonumber \\{} & {} \quad \sqrt{2j_1(2j_2 + 1)(2{\bar{j}}+4)(2j_1 + 2{\bar{j}} - 2k + 3)}\nonumber \\{} & {} \quad \times \begin{Bmatrix} j_1 - \frac{1}{2}&{\bar{j}} + \frac{3}{2}&j_1 + {\bar{j}} + 1 - k\\j_1+j_2 - {\bar{j}} - 3&j_2 - 1&j_1+j_2 - \frac{3}{2} \end{Bmatrix} C^{j_1,{\bar{j}}+1,j_1+{\bar{j}}+1 - k}_{m_1,m_2+{\bar{m}} - m';m_1+m_2 + {\bar{m}} - m'}\nonumber \\{} & {} \qquad C^{j_1+{\bar{j}}+1 - k,j_2 - 1;j_1+j_2 - {\bar{j}} - 3}_{m_1+m_2+{\bar{m}} - m',m';m_1+m_2+{\bar{m}}} e^{(j_1+j_2 - {\bar{j}} - 3)}_{m_1+m_2+{\bar{m}}}.\nonumber \\ \end{aligned}$$

(D.18)

We find that

$$\begin{aligned} p\{e^{(j_1)}_{m_1},e^{(j_2 - 1 - \frac{i}{2},{\bar{j}}+1 - \frac{i}{2})}_{m_2+{\bar{m}}}\} = \lambda _{j_2-1,{\bar{j}}+1,i}^{-1}\Pi _{j_1,j_2,{\bar{j}};i} C^{j_2+{\bar{j}} - i,j_1;j_1+j_2 - {\bar{j}} - 3}_{m_2+{\bar{m}},m_1,m_1+m_2+{\bar{m}}} e^{(j_1+j_2 - {\bar{j}} - 3)}_{m_1+m_2+{\bar{m}}},\nonumber \\ \end{aligned}$$

(D.19)

where

$$\begin{aligned} \Pi _{j_1,j_2,{\bar{j}};i}{} & {} = (-1)^{2(j_1+j_2) - i}\sqrt{[2j_1 + 1]_2[2j_2 - 1]_2(2j_1 + 2j_2 - 2)(2{\bar{j}}+3)(2j_1 + 2{\bar{j}} - 2i +1)} \nonumber \\{} & {} \quad \times \begin{Bmatrix} j_2 - 1&{\bar{j}} + 1&j_2 + {\bar{j}} - i \\j_1+j_2 - {\bar{j}} - 3&j_1&j_1+j_2 - 2 \end{Bmatrix} \nonumber \\{} & {} \quad + \sum _{k} (-1)^{2(j_1+j_2) - k}\sqrt{[2j_1+1]_2(2j_2 + 1)(2j_2+2{\bar{j}} - 2i +1)(2{\bar{j}} - k + 3)( 2j_1 - k)}(2{\bar{j}} + 2) \nonumber \\{} & {} \quad \times (2j_1 + 2{\bar{j}} - 2k + 3) \begin{Bmatrix} j_1 - \frac{1}{2}&{\bar{j}} + \frac{3}{2}&j_1 + {\bar{j}} + 1 - k\\j_1+j_2 - {\bar{j}} - 3&j_2 - 1&j_1+j_2 - \frac{3}{2} \end{Bmatrix} \nonumber \\{} & {} \qquad \begin{Bmatrix} {\bar{j}} + 1&j_2 - 1&j_1 + {\bar{j}} -i\\j_1+j_2 - {\bar{j}} - 3&j_1&j_1 + {\bar{j}} + 1 - k \end{Bmatrix}. \end{aligned}$$

(D.20)

We have

$$\begin{aligned}{} & {} (\pi _3)^{j_1+m_1,j_1-m_1;j_2+m_2,j_2 - m_2}_{{\bar{j}} - {\bar{m}},{\bar{j}}+{\bar{m}}} \nonumber \\{} & {} {:=} \frac{(-1)^{{\bar{j}} + {\bar{m}}}N(j_1,m_1)N(j_2,m_2)}{N({\bar{j}},{\bar{m}})N(j_1+ j_2 - {\bar{j}} - 3,m_1+m_2+{\bar{m}})}\nonumber \\{} & {} \quad \times \sum _{i} {\tilde{\lambda }}_{j_2,{\bar{j}},i}\lambda _{j_2-1,{\bar{j}}+1,i}^{-1}h_{j_2 - \frac{1}{2} - \frac{i}{2},{\bar{j}}+\frac{1}{2} - \frac{i}{2}}\Pi _{j_1,j_2,{\bar{j}};i}C^{j_2,{\bar{j}};j_2 + {\bar{j}} - i}_{m_2,{\bar{m}};m_2+{\bar{m}}} C^{j_2+{\bar{j}} - i,j_1;j_1+j_2 - {\bar{j}} - 3}_{m_2+{\bar{m}},m_1,m_1+m_2+{\bar{m}}}. \nonumber \\ \end{aligned}$$

(D.21)

This constant gives the quartic interaction of the KK theory of Poisson BF theory.

E Some Identities Involving Pochhammer Symbols

In this appendix, we review some identities involving Pochhammer symbols that are used in the calculation of holography chiral algebra. In the main text, we introduced the descending Pochhammer symbols

$$\begin{aligned}{}[a]_n: = a(a - 1)\dots (a - n + 1) = \frac{(a)!}{(a - n)!}. \end{aligned}$$

(E.1)

We also introduce the ascending Pochhammer symbol

$$\begin{aligned} (a)^{(n)}: = a(a + 1)\dots (a + n - 1) = \frac{(a + n - 1)!}{(a - 1)!}. \end{aligned}$$

(E.2)

The descending and ascending Pochhammer symbols are related to one another by

$$\begin{aligned} (a)^{(n)} = [a+n-1]_n. \end{aligned}$$

(E.3)

The hypergeometric function is defined as a power series using the ascending Pochhammer symbol

(E.4)

The series terminates if either a or b is a nonpositive integer, in which case the function reduces to a polynomial:

(E.5)

The following result is important in obtaining various generalizations of the Chu-Vandermonde’s identity.

Proposition E.1

([71]). For any $k\ge 1$, $x,y \in \mathbb {R}_{+}$, and $a,b > 0$, we have

(E.6)

Taking $x,y = 1$ in the above formula we obtain the Chu-Vandermonde’s identity

$$\begin{aligned} \sum _{i = 0}^k\left( {\begin{array}{c}n\\ i\end{array}}\right) (a)^{(i)}(b)^{(k - i)} = (a+b)^{(k)}. \end{aligned}$$

(E.7)

Corollary E.1

$$\begin{aligned} \sum _{i = l}^n\left( {\begin{array}{c}i\\ l\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) (a)^{(i)}(b)^{(k - i)} =\left( {\begin{array}{c}k\\ l\end{array}}\right) \frac{ (a+b)^{(k)}}{(a+b)^{(l)}}(a)^{(l)}. \end{aligned}$$

(E.8)

Proof

Letting $x \rightarrow 1 + x, y \rightarrow 1$ in the formula E.6, we obtain the following

(E.9)

Expanding both side into a series of x we obtain the formula E.8. $\quad \square$

Corollary E.2

We have the following identity

$$\begin{aligned} \sum _{i = 0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{1}{[a]_i[b]_{k - i}} = \frac{[a+b-k+1]_k}{[a]_k[b]_k}. \end{aligned}$$

(E.10)

Proof

$$\begin{aligned} \sum _{i = 0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{1}{[a]_i[b]_{k - i}}{} & {} = \sum _{i = 0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{(a - k + k - i)!(b-k +i)!}{a!b!} \nonumber \\{} & {} = \sum _{i = 0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{(a - k + 1)^{(k - i)}(a-k)!(b-k +1)^{(i)}(b-k)!}{a!b!}\nonumber \\{} & {} = (a+b-2k + 2)^{(k)}\frac{(a - k)!(b-k)!}{a!b!}\nonumber \\{} & {} = \frac{[a+b-k+1]_k}{[a]_k[b]_k}, \nonumber \\ \end{aligned}$$

(E.11)

where we used the Chu–Vandermonde’s identity E.7 in the third line. $\quad \square$

Corollary E.3

We have the following identity

$$\begin{aligned} \sum _{i = l}^k \left( {\begin{array}{c}i\\ l\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{1}{[a]_i[b]_{k - i}} = \left( {\begin{array}{c}k\\ l\end{array}}\right) \frac{[a+b - k+1]_k}{[a]_{k-l}[b]_k[a+b - 2k+l+1]_l}. \end{aligned}$$

(E.12)

Proof

$$\begin{aligned} \sum _{i = l}^k \left( {\begin{array}{c}i\\ l\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{1}{[a]_i[b]_{k - i}}{} & {} = \sum _{i = l}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ l\end{array}}\right) \frac{(a - k + 1)^{(k - i)}(a-k)!(b-k +1)^{(i)}(b-k)!}{a!b!}\nonumber \\{} & {} = \left( {\begin{array}{c}k\\ l\end{array}}\right) \frac{(a - k)!(b-k)!}{a!b!}\frac{(a+b-2k + 2)^{(k)}}{(a+b - 2k + 2)^{(l)}}(a - k + 1)^{(l)} \nonumber \\{} & {} = \left( {\begin{array}{c}k\\ l\end{array}}\right) \frac{[a+b - k+1]_k}{[a]_{k-l}[b]_k[a+b - 2k+l+1]_l}. \nonumber \\ \end{aligned}$$

(E.13)

$\square$

F Tree-Level Feynman Integrals

In this appendix, we evaluate the tree-level Feynman diagrams that appear in Sect. 9.

$$\begin{aligned} I_k(z) = \int _{z' \in \mathbb {C},s\ge 0}\frac{1}{(|z - z'|^2 + s^2)^{\frac{3}{2}}}\partial _{z'}^k\frac{1}{(|z'|^2 + s^2)^{\frac{3}{2}}} {\bar{z}}s ds dz'd{\bar{z}}'. \end{aligned}$$

(F.1)

First we note that $z^{k+1}I_k(z)$ is a constant independent of z. To see this we shift $z \rightarrow \alpha z,{\bar{z}} \rightarrow \bar{\alpha }{\bar{z}}$. We also shift the integration variable by $z' \rightarrow \alpha z', {\bar{z}}' \rightarrow \bar{\alpha }{\bar{z}}',s\rightarrow |\alpha | s$. $z^{k+1}I_k(z)$ is invariant under this shift. Therefore $z^{k+1}I_k(z)$ is a constant and we have

$$\begin{aligned} I_k(z) = \frac{I_k(1)}{z^{k+1}}. \end{aligned}$$

(F.2)

To efficiently evaluate all $I_k(1)$, we make the following generating function

$$\begin{aligned} I(1,\lambda ): = \sum _{k = 0}^\infty \frac{\lambda ^k}{k!}I_k(1). \end{aligned}$$

(F.3)

By definition we have

$$\begin{aligned} I(1,\lambda ) = \int _{z' \in \mathbb {C},s\ge 0}\frac{1}{(|1 - z'|^2 + s^2)^{\frac{3}{2}}}\frac{1}{((z'+\lambda ){\bar{z}}' + s^2)^{\frac{3}{2}}} s ds dz'd{\bar{z}}'. \end{aligned}$$

(F.4)

We use Schwinger parametrization to rewrite the above integral as follows

$$\begin{aligned} I(1,\lambda ) = \frac{4}{\pi }\int _{u_1,u_2\ge 0}du_1du_2\int _{z' \in \mathbb {C},s\ge 0} ds dz'd{\bar{z}}'(u_1u_2)^{\frac{1}{2}}se^{-u_1(|1 - z'|^2 + s^2) - u_2((z'+\lambda ){\bar{z}}' + s^2)}.\nonumber \\ \end{aligned}$$

(F.5)

We first evaluate the integral over s and find

$$\begin{aligned} I(1,\lambda ) = \frac{4}{\pi }\int _{u_1,u_2\ge 0}du_1du_2\int _{z' \in \mathbb {C}} dz'd{\bar{z}}'\frac{1}{2(u_1 + u_2)}(u_1u_2)^{\frac{1}{2}}e^{-u_1|1 - z'|^2 - u_2(z'+\lambda ){\bar{z}}'}.\nonumber \\ \end{aligned}$$

(F.6)

Evaluate the integral over $z' \in \mathbb {C}$ gives

$$\begin{aligned} I(1,\lambda ) = 2\int _{u_1,u_2\ge 0}du_1du_2 \frac{1}{(u_1 + u_2)^2}(u_1u_2)^{\frac{1}{2}}e^{-\frac{u_1u_2(1 + \lambda )}{(u_1 + u_2)}}. \end{aligned}$$

(F.7)

We make the following change of variable to the Schwinger parameter

$$\begin{aligned} u_1 = u\xi ,\; u_2 = u(1 - \xi ),\; \text { for } u\ge 0,1\le \xi \le 1. \end{aligned}$$

(F.8)

Then we have

$$\begin{aligned} I(1,\lambda ){} & {} = 2\int _0^1d\xi \int _0^\infty du (\xi (1 - \xi ))^{\frac{1}{2}}e^{-(1+ \lambda )u\xi (1 - \xi )}\nonumber \\{} & {} = 2\int _0^1d\xi \frac{1}{(1+ \lambda )\sqrt{\xi (1 - \xi )}}\nonumber \\{} & {} = \frac{2\pi }{1 + \lambda }. \nonumber \\ \end{aligned}$$

(F.9)

We find that

$$\begin{aligned} I_k(z) = (-1)^k\frac{k!}{z^{k+1}}. \end{aligned}$$

(F.10)

More generally, we can consider the following Feynman integral

$$\begin{aligned} I_{l,k}(z) = \int _{z' \in \mathbb {C},s\ge 0}\partial _{z'}^l\frac{1}{(|z - z'|^2 + s^2)^{\frac{3}{2}}}\partial _{z'}^k\frac{1}{(|z'|^2 + s^2)^{\frac{3}{2}}} {\bar{z}}s ds dz'd{\bar{z}}'. \end{aligned}$$

(F.11)

This can be evaluated using integration by part to move the $\partial _{z'}^l$ derivatives to the second position and using the previous result. We find

$$\begin{aligned} I_{l,k}(z) = (-1)^k\frac{(k+l)!}{z^{k+l+1}}. \end{aligned}$$

(F.12)