1 Introduction

The defocusing Ablowitz–Ladik (AL) lattice for the complex functions \(\alpha _j(t)\), \(j\in \mathbb {Z}\) and \(t\in \mathbb {R}\), is the system of nonlinear equations

$$\begin{aligned} i \dot{\alpha }_j =-(\alpha _{j+1}+\alpha _{j-1}-2\alpha _j)+\vert \alpha _j\vert ^2(\alpha _{j-1}+\alpha _{j+1})\,, \end{aligned}$$
(1)

where \(\dot{\alpha }_j =\dfrac{d \alpha _j}{dt}\). We assume N-periodic boundary conditions \(\alpha _{j+N}=\alpha _j\), for all \(j\in \mathbb {Z}\). The AL lattice was introduced by Ablowitz and Ladik [1, 2] as the spatial integrable discretization of the defocusing cubic nonlinear Schrödinger Equation (NLS) for the complex function \(\psi (x,t)\), \(x\in S^1\) and \(t\in \mathbb {R}\):

$$\begin{aligned} i \partial _t \psi (x,t) = -\partial ^2_{x} \psi (x,t) + 2|\psi (x,t) |^2 \psi (x,t). \end{aligned}$$
(2)

The cubic NLS equation was proved to be integrable by Zakharov and Shabat [70].

It is straightforward to verify that the quantity

$$\begin{aligned} K^{(0)}:=\prod _{j=1}^{N}\left( 1-\vert \alpha _j\vert ^2\right) \,, \end{aligned}$$
(3)

is a constant of motion for the AL lattice, namely \(\dfrac{d}{dt}K^{(0)}=0\). This implies that if \(\vert \alpha _j(0)\vert <1\) for all \(j\in \mathbb {Z}\), then \(\vert \alpha _j(t)\vert <1\) for all \(t>0\). We chose the N-dimensional disc \(\mathbb {D}^N\) as the phase space of the AL lattice, here \(\mathbb {D}=\{z\in \mathbb {C}\,\vert \,\vert z\vert <1\}\). On \( \mathbb {D}^N\) we introduce the symplectic form [23, 30]

$$\begin{aligned} \omega = i\sum _{j=1}^{N}\frac{1}{\rho _j^2}\textrm{d}\alpha _j\wedge \textrm{d}\overline{\alpha }_j\,,\quad \rho _j=\sqrt{1-\vert \alpha _j\vert ^2}. \end{aligned}$$
(4)

The corresponding Poisson bracket is defined for functions \(f,g \in \mathcal {C}^\infty (\mathbb {D}^N)\) as

$$\begin{aligned} \begin{aligned} \{f,g\}&= i \sum _{j=1}^{N}\rho _j ^2\left( \frac{\partial f}{\partial \overline{\alpha }_j}\frac{\partial g}{\partial \alpha _j} - \frac{\partial f}{\partial \alpha _j}\frac{\partial g}{\partial \overline{\alpha }_j}\right) \,. \end{aligned} \end{aligned}$$
(5)

The phase shift \(\alpha _j(t)\rightarrow e^{-2 i t}\alpha _j(t)\) transforms the AL lattice into the equation

$$\begin{aligned} i \dot{\alpha }_j =-\rho _j^2(\alpha _{j+1}+\alpha _{j-1}),\quad \rho _j=\sqrt{1-\vert \alpha _j\vert ^2}, \end{aligned}$$
(6)

which we call the reduced AL equation. We remark that the quantity \( - 2\ln (K^{(0)})\) is the generator of the shift \(\alpha _j(t)\rightarrow e^{-2 i t}\alpha _j(t)\), while \(H_1 = K^{(1)} + \overline{K^{(1)}}\) with

$$\begin{aligned} K^{(1)}:=- \sum _{j=1}^{N}\alpha _j\overline{\alpha }_{j+1}, \end{aligned}$$
(7)

generates the flow (6). The AL equations (1) have the Hamiltonian structure

$$\begin{aligned} \dot{\alpha }_j =\{\alpha _j,H_{AL}\},\quad H_{AL}(\alpha _j,\overline{\alpha }_j) = - 2\ln (K^{(0)}) + K^{(1)} + \overline{ K^{(1)}}. \end{aligned}$$
(8)

Integrability. As we have already said, the AL lattice was discovered by Ablowitz and Ladik by discretizing the \(2\times 2\) Zakharov-Shabat Lax pair [1] of the cubic nonlinear Schrödinger equation. For a comprehensive review see [3]. The integrability of the Ablowitz–Ladik system has also been proved by constructing a bi-Hamiltonian structure [9, 23]. A techniques to calculate the \(\tau \)-function correlators has been introduced in [15].

Using the connection between orthogonal polynomials on the unit circle and the AL lattice, Nenciu and Simon [54, 59] constructed a new Lax pair for the AL lattice that sometimes is referred to as the big Lax pair and which put the AL equation on the same foot as the Toda lattice. The link between orthogonal and biorthogonal polynomials on the unit circle and the Ablowitz-Ladik hierarchy (see also [4, 43]) is the analogue of the celebrated link between the Toda hierarchy and orthogonal polynomials on the real line (see e.g. [19]). This link was also generalized to the non-commutative case [14] (see also [16]). Generalization of this construction to other integrable equations has been considered in [55].

To construct the big Lax pair, we follow [54, 59] and we double the size of the chain according to the periodic boundary conditions, thus we consider a chain of 2N particles \(\alpha _1, \ldots , \alpha _{2N}\) such that \(\alpha _j = \alpha _{j+N}\) for \(j=1,\ldots , N\). Define the \(2\times 2\) unitary matrix \(\Xi _j\)

$$\begin{aligned} \Xi _j = \begin{pmatrix} \overline{\alpha }_j &{} \rho _j \\ \rho _j &{} -\alpha _j \end{pmatrix}\, ,\quad j=1,\dots , 2N\, , \end{aligned}$$
(9)

and the \(2N\times 2N\) matrices

$$\begin{aligned} \mathcal {M}= \begin{pmatrix} -\alpha _{2N}&{}&{}&{}&{}&{} \rho _{2N} \\ &{} \Xi _2 \\ &{}&{} \Xi _4 \\ &{}&{}&{} \ddots \\ &{}&{}&{}&{}\Xi _{2N-2}\\ \rho _{2N} &{}&{}&{}&{}&{} \overline{\alpha }_{2N} \end{pmatrix}\, ,\qquad \mathcal {L}= \begin{pmatrix} \Xi _{1} \\ &{} \Xi _3 \\ &{}&{} \ddots \\ &{}&{}&{}\Xi _{2N-1} \end{pmatrix} \,. \end{aligned}$$
(10)

Now let us define the unitary Lax matrix

$$\begin{aligned} \mathcal {E}= \mathcal {L}\mathcal {M}\,, \end{aligned}$$
(11)

that has the structure of a 5-band diagonal matrix

$$\begin{aligned} \begin{pmatrix} *&{}*&{}*&{}&{}&{}&{}&{}&{}&{}*\\ *&{}*&{}*&{}&{}&{}&{}&{}&{}&{}*\\ &{}*&{}*&{}*&{}*&{}&{}&{}&{}&{}\\ &{}*&{}*&{}*&{}*&{}&{}&{}&{}&{}\\ &{}&{}&{}&{}&{}\ddots &{}\ddots &{}&{}&{}\\ &{}&{}&{}&{}&{}&{}*&{}*&{}*&{}*\\ &{}&{}&{}&{}&{}&{}*&{}*&{}*&{}*\\ *&{}&{}&{}&{}&{}&{}&{}*&{}*&{}*\\ *&{}&{}&{}&{}&{}&{}&{}*&{}*&{}*\\ \end{pmatrix}\,. \end{aligned}$$

The matrix \(\mathcal {E}\) is a periodic CMV matrix (after Cantero Morales and Velsquez [17]). The N-periodic reduced AL Eq. (6) is equivalent to the following Lax equation for the matrix \(\mathcal {E}\):

$$\begin{aligned} {\dot{\mathcal {E}}} = i\left[ \mathcal {E}, \mathcal {E}^+ + (\mathcal {E}^+)^\dagger \right] \,, \end{aligned}$$
(12)

where \(^\dagger \) stands for hermitian conjugate and

$$\begin{aligned} \mathcal {E}^+_{j,k} = {\left\{ \begin{array}{ll} \frac{1}{2} \mathcal {E}_{j,j} \quad j = k \\ \mathcal {E}_{j,k} \quad k = j + 1 \, {\,\textrm{mod}\,}\, 2N \, \text{ or } \, k = j + 2 \, {\,\textrm{mod}\,}\, 2N \\ 0 \quad \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(13)

We observe that \((\mathcal {E}^+)^{\dagger }+(\mathcal {E}^{\dagger })^+=\mathcal {E}^{\dagger }\) and \([\mathcal {E},\mathcal {E}^{\dagger }]=0\) because \(\mathcal {E}\) is unitary. Therefore, one can write the Eq. (12) in the equivalent form

$$\begin{aligned} {\dot{\mathcal {E}}} = i\left[ \mathcal {E}, \mathcal {E}^+ -(\mathcal {E}^\dagger )^+\right] \,. \end{aligned}$$
(14)

The formulation (12) implies that the quantities

$$\begin{aligned} K^{(\ell )}=\frac{ \text{ Tr }\left( \mathcal {E}^\ell \right) }{2},\quad \ell =1,\dots , N-1, \end{aligned}$$
(15)

are constants of motion for the defocusing AL system. For example

$$\begin{aligned} K^{(1)}=-\sum _{j=1}^N\alpha _j\overline{\alpha }_{j+1},\quad K^{(2)}=\sum _{j=1}^N[(\alpha _j\overline{\alpha }_{j+1})^2-2\alpha _j\overline{\alpha }_{j+2}\rho _{j+1}^2]\,. \end{aligned}$$

Furthermore, \(K^{(0)}, K^{(1)},\dots , K^{(N-1)}\) are functionally independent and in involution, showing that the N-periodic AL system is integrable [1, 3, 54].

Remark 1

The quantity \(2\Re (K^{(1)})\) generates the reduces AL Eq. (6), while the quantity \(-2\Im (K^{(1)}) \) generates the flow

$$\begin{aligned} \dot{\alpha }_j =(1-\vert \alpha _j\vert ^2)(\alpha _{j+1}-\alpha _j), \end{aligned}$$

which is called Schur flow. The Schur flow emerges in [2] as a spatial discretization of the defocusing modified Korteweg–de Vries equation

$$\begin{aligned} \partial _t f-6f\partial _xf+\partial _x^3 f=0. \end{aligned}$$

For the integration of the Schur flow and its relation to orthogonal polynomial on the unit circle see [32, 60].

Generalized Gibbs ensemble for the Ablowitz–Ladik lattice. The symplectic form \(\omega \) in (4) induces on \(\mathbb {D}^N\) the volume form \(\textrm{d}\text{ vol }=\dfrac{1}{K^{(0)}}\textrm{d}^2 {\varvec{\alpha }}\), with \(\textrm{d}^2 {\varvec{\alpha }}=\prod _{j=1}^{N}(i\textrm{d}\alpha _j\wedge \textrm{d}\overline{\alpha }_j\,) \). We observe that \(\int _{\overline{\mathbb {D}}^N}\textrm{d}\text{ vol }=\infty \), however, we can define the Gibbs measure with respect to the Hamiltonian \(H_{AL}\) in (8) [68]:

$$\begin{aligned} \frac{1}{Z_{\beta }}e^{-\frac{\beta }{2} H_{AL}}\textrm{d}\text{ vol } = \frac{1}{Z_{\beta }}e^{\beta \Re (K^{(1)})}\prod _{j=1}^{N}(1-\vert \alpha _j\vert ^2)^{\beta -1}\textrm{d}^2 {\varvec{\alpha }},\quad \beta >0, \end{aligned}$$
(16)

where \(Z_{\beta }=\int _{\overline{\mathbb {D}}^N}e^{\beta \Re (K^{(1)})}\prod _{j=1}^{N}(1-\vert \alpha _j\vert ^2)^{\beta -1}\textrm{d}^2 {\varvec{\alpha }}<\infty \) is the normalizing constant. The above probability measure is clearly invariant under the Hamiltonian flow \(\alpha _j(0)\rightarrow \alpha _j(t)\) associated to the Ablowitz–Ladik Eq. (1).

Since the Ablowitz–Ladik lattice posses several conserved quantities (15), one can introduce a Generalized Gibbs Ensemble on the phase space \(\mathbb {D}^N\) in the following way. Fix \(\mathbb {N}\ni \kappa \le N-1\) and let us define

$$\begin{aligned} V(z) =\sum _{m=1}^{\kappa }\eta _m \Re (z^m)\, , \end{aligned}$$
(17)

where \(\eta _m \in \mathbb {R}\) are called chemical potentials. Then

$$\begin{aligned} \text{ Tr }\left( V\left( \mathcal {E}\right) \right) =\sum _{m=1}^{\kappa } \eta _m (K^{(m)}+\overline{K^{(m)}} ), \end{aligned}$$

where \(K^{(m)}\) are the AL conserved quantities (15). The finite volume Generalized Gibbs measure can be written as:

$$\begin{aligned} \textrm{d}\mathbb {P}_{AL}(\alpha _1, \ldots , \alpha _{N})= \frac{1}{Z^{AL}_N(V,\beta )}\prod _{j=1}^{N} \left( 1-\vert \alpha _j\vert ^2\right) ^{\beta -1}\exp \left( -\text{ Tr }\left( V\left( \mathcal {E}\right) \right) \right) \textrm{d}^2 {\varvec{\alpha }}\, , \end{aligned}$$
(18)

where \(Z^{AL}_N(V,\beta )\) is the partition function of the system:

$$\begin{aligned} Z^{AL}_N(V,\beta )= \int _{\mathbb {D}^N} \prod _{j=1}^{N} \left( 1-\vert \alpha _j\vert ^2\right) ^{\beta -1}\exp \left( -\text{ Tr }\left( V\left( \mathcal {E}\right) \right) \right) \textrm{d}^2 {\varvec{\alpha }}\, . \end{aligned}$$
(19)

Choosing the initial data of the Ablowitz–Ladik lattice according to the Generalized Gibbs measure (18), the Lax matrix \(\mathcal {E}\) turns into a random matrix. In [51] Mendl and Sphon study the dynamic of the Ablowitz–Ladik lattice at non-zero temperature. They study numerically correlation functions and in particular, introducing the density \(\delta _j=\Re (\alpha _{j+1}\overline{\alpha }_j)\), they study the density-density correlation function

$$\begin{aligned} \mathbb {E}\left[ \delta _j(t)\delta _1(0)\right] -\mathbb {E}\left[ \delta _j(t)\right] \mathbb {E}\left[ \delta _1(0)\right] \,, \end{aligned}$$

where \(\mathbb {E}\left[ \cdot \right] \) is the expectation with respect to Gibbs measure (16). They showed numerically that density-density time correlations in thermal equilibrium have symmetrically located peaks, which travel in opposite directions at constant speed, broaden ballistically and decay as \(1/t^{\gamma }\) when \(t\rightarrow \infty \), where the scaling exponent \(\gamma \) is approximately equal to one. This behaviour is believed to be typical of integrable nonlinear systems.

More quantitative results have been obtained for linear (integrable) systems and for the Toda lattice. It was shown in [34] that the fastest peaks of the correlation functions of harmonic oscillators with short range interactions have a Airy type scaling. Regarding nonlinear integrable systems in [61] Spohn was able to connect the Gibbs ensemble of the Toda lattice to the Dumitriu-Edelman \(\beta \)-ensemble [21]. In this way, the generalized Gibbs free energy of the Toda chain turns out to be related to the \(\beta \)-ensembles of random matrix theory in the mean-field regime [7, 22]. The behaviour of the correlation functions of the Toda chains has been derived by applying the theory of generalized hydrodynamic [20, 62]. We mention also the recent work [36], where the authors derive a large deviation principle for the mean density of states for the Generalized Gibbs measure of the Toda lattice.

2 Statement of the Results

In this manuscript we derive the mean density of states \(\mu ^\beta _{AL}\) of the random Lax matrix \(\mathcal {E}\) sampled according to generalized Gibbs measure (18) and we determine the free energy of the AL generalized Gibbs ensemble

$$\begin{aligned} F_{AL}(V,\beta )=\lim _{N\rightarrow \infty }\frac{1}{N} \log Z^{AL}_N(V,\beta ). \end{aligned}$$

This is achieved by connecting the generalized Gibbs ensemble of the Ablowitz–Ladik lattice to the Killip-Nenciu [42] matrix Circular \(\beta \)-ensemble at high-temperature investigated by Hardy and Lambert [37]. Further connections between discrete integrable systems with Gibbs measure initial data and classes of random matrices has been explored in [33]. For connections between integrable PDEs and random objects see [6].

Let \(\mathcal {M}(\mathbb {T})\) be the space of probability measures on the torus \(\mathbb {T}=[-\pi ,\pi ]\) and for \(\mu \in \mathcal {M}(\mathbb {T})\) let us consider the functional

$$\begin{aligned} \begin{aligned} \mathcal {F}^{(V,\beta )}(\mu )&= 2\int \limits _{\mathbb {T}} V(\theta ) \mu (\theta ) \textrm{d}\theta - \beta \int \int \limits _{\mathbb {T}\times \mathbb {T}} \ln \sin \left( \frac{\vert \theta -\phi \vert }{2}\right) \mu (\theta )\mu (\phi )\textrm{d}\theta \textrm{d}\phi \\ {}&\quad + \int \limits _{\mathbb {T}}\ln \left( \mu (\theta )\right) \mu (\theta )\textrm{d}\theta +\ln (2\pi )\,. \end{aligned} \end{aligned}$$
(20)

Remark 2

Here and below, we make an abuse of notation by denoting the potential \(V(z)=V(e^{i\theta })\) simply by \(V(\theta )\).

For sufficiently regular potential \(V(\theta )\), the functional (20) has a unique minimizer \(\mu _{HT}^{\beta }(\textrm{d}\theta )=\mu _{HT}^{\beta }(\theta )\textrm{d}\theta \), [58], that describes the density of states of the Circular \(\beta \)-ensemble at high-temperature [37]. For finite \(\beta \) and smooth potentials \(V(\theta )\), it has been shown by Hardy and Lambert in [37] that the minimizer \(\mu _{HT}^{\beta }(\textrm{d}\theta )\) has a smooth density and its support is the whole torus \(\mathbb {T}\).

Theorem 1

(First Main theorem). Consider \(\beta >0\) and a smooth potential V as in (17) on the unit circle \(\mathbb {T}\). The mean density of states \(\mu _{AL}^\beta (\textrm{d}\theta ):=\mu _{AL}^\beta (\theta )\textrm{d}\theta \) of the Ablowitz–Ladik Lax matrix \(\mathcal {E}\) in (11) endowed with the probability (18) is absolutely continuous with respect to the Lebesgue measure and takes the form

$$\begin{aligned} \mu _{AL}^\beta (\theta ) = \partial _\beta \left( \beta \mu _{HT}^\beta (\theta )\right) \; a.e., \end{aligned}$$
(21)

where \(\mu _{HT}^\beta \) is the unique minimizer of the functional (20).

To prove the above theorem we derive a relation (see Proposition 8) between the free energy of the \(\beta \)-ensembles at high-temperature, namely the minimum value of the minimizer (20)

$$\begin{aligned} F_{HT}(V,\beta ):= \mathcal {F}^{(V,\beta )}(\mu ^\beta _{HT}), \end{aligned}$$

and the free energy \(F_{AL}(V,\beta )\) of the AL lattice:

$$\begin{aligned} F_{AL}(V,\beta )= \partial _\beta \left( \beta F_{HT}(V,\beta )\right) + \ln (2). \end{aligned}$$

Such relation is obtained via transfer operator techniques.

The particular case \(V(\theta )=2\eta \cos \theta \) corresponds to the free energy associated to the AL Eq. (1), and we show that the minimizer of the functional (20) is obtained via a particular solution of the Double Confluent Heun (DCH) equation.

Theorem 2

(Second main theorem). Fix \(\beta >0\) and let \(V(\theta )=\eta \cos \theta \), where \(\eta \) is a real parameter. There exists \(\varepsilon >0\) such that for all \(\eta \in (-\varepsilon ,\varepsilon )\), the minimizer \(\mu _{HT}^{\beta }(\textrm{d}\theta )=\mu ^{\beta }_{HT}(\theta )\textrm{d}\theta \) of the functional (20) takes the form

$$\begin{aligned} \mu ^{\beta }_{HT}(\theta )= \frac{1}{2\pi } + \frac{1}{\pi \beta }\Re \left( \frac{zv'(z)}{v(z)}\right) _{\big \vert z=e^{i\theta }}\, , \end{aligned}$$
(22)

where v(z) is the unique solution (up to a multiplicative non-zero constant) of the Double Confluent Heun (DCH) equation

$$\begin{aligned} z^2 v''(z) + \left( -\eta + z (\beta +1) + \eta z^2\right) v'(z) +\eta \beta (z +\lambda ) v(z) =0\, \end{aligned}$$
(23)

analytic for \(\vert z\vert \le r\) with \(r\ge 1\). Such solution is differentiable in the parameter \(\eta \) and \(\beta \). The parameter \(\lambda =\lambda (\eta ,\beta )\) in (23) is determined for \( \eta \in (-\varepsilon ,\varepsilon )\) by the solution of the equation

$$\begin{aligned} \lambda (R_1)_{11}+ \frac{\eta }{\beta +1}(R_1)_{21}=0,\quad \end{aligned}$$
(24)

with the condition \(\lambda (\eta =0,\beta )=0\). In the above expression \((R_1)_{jk}\) is the jk entry of the matrix \(R_1\) which is defined by the infinite product

$$\begin{aligned} R_1 =M_1M_2\dots M_k\dots , \quad M_k = \begin{pmatrix} 1 + \frac{\lambda \beta \eta }{k(k+\beta )} &{} \frac{\eta ^2}{k(k+\beta +1)}\\ 1 &{} 0 \end{pmatrix}\,. \end{aligned}$$

We remark that the solution of the double confluent Heun equation has generically an essential singularity at \(z=0\) and \(z=\infty \), and one needs to tune the accessory parameter \(\lambda \) to obtain an analytic solution, for a review see [57]. In our derivation of (23) the parameter \(\lambda \) coincides with the first moment of the measure \(\mu (\theta )\), namely \(\lambda =\int _{\mathbb {T}}\mu (\theta )e^{i\theta }d\theta \). It is a transcendental function of \(\beta \) and \(\eta \) and it is related to the Painlevé III Eq. [24, 47].

Remark 3

Under the change of variable

$$\begin{aligned} v(z)=\exp \left( -\frac{\eta }{2}\left( z+\frac{1}{z}\right) \right) z^{-\frac{\beta +1}{2}}f(z)\,, \end{aligned}$$

the DCH Eq. (23) takes the form of a Schrödinger equation

$$\begin{aligned} f''(z)+q(z)f(z)=0, \end{aligned}$$

with potential q(z) singular at the origin

$$\begin{aligned} q(z)=\frac{1}{z^2}\left( \eta \frac{\beta -1}{2}\left( z+\frac{1}{z}\right) -\frac{\eta ^2}{4}\frac{(z^2-1)^2}{z^2} -\frac{1}{4}(\beta ^2+4\beta +3)+\eta \beta \lambda \right) . \end{aligned}$$

Remark 4

For the case \(V=0\) it was shown in [37] that the minimizer of the functional (42) is the uniform measure on the circle, while for the case \(V(\theta )= \beta V(\theta ) \) and \(\beta \rightarrow \infty \) the minimizer of (20) was considered in [49]. The particular case \( V(\theta )\rightarrow \beta \eta \cos \theta \) and \(\beta \rightarrow \infty \) has first been considered by Gross–Witten [35] and Baik–Deift–Johansson [11]. The measure (22) in Theorem 2 generalizes the result of Gross and Witten [35] and Baik–Deift–Johansson [11] to the high-temperature regime (see Remark 9).

This manuscript is organized as follows. In Sect. 3 we introduce the Circular \(\beta \) ensemble and its high-temperature limit. Then we review results in the literature on Circular \(\beta \) ensemble and we derive some technical results needed to prove our main theorems. In Sect. 4 we prove our first main theorem, namely Theorem 1 and in Sect. 5 we prove Theorem 2. Finally, the most technical parts of our arguments are deferred to the appendices.

3 Circular \(\beta \) Ensemble at High-Temperature

The Circular Ensemble at temperature \(\tilde{\beta }^{-1}\) is a system of N identical particles on the one-dimensional torus \(\mathbb {T}=[-\pi ,\pi ]\) with distribution

$$\begin{aligned} \textrm{d}\mathbb {P}_{\tilde{\beta }} (\theta _1, \ldots , \theta _{N}) = \frac{1}{Z^{C\tilde{\beta } E}_N} \prod _{1\le j<\ell \le N}\vert e^{i\theta _\ell } - e^{i\theta _j}\vert ^{\widetilde{\beta }} \textrm{d}\varvec{\theta },\quad \textrm{d}\varvec{\theta }=\textrm{d}\theta _1\dots \textrm{d}\theta _N \, , \end{aligned}$$
(25)

where \(Z_N^{C\tilde{\beta } E}>0\) is the norming constant, or partition function of the system. For \(\tilde{\beta }=1,2,4\) Dyson observed that the above measure corresponds to the eigenvalue distribution of circular orthogonal ensemble (COE), circular unitary ensemble (CUE) and circular symplectic ensemble (CSE) of random matrix ensembles (see e.g. [25, 50]). For general \(\tilde{\beta }>0\), Killip and Nenciu proved that the Circular \(\beta \) Ensemble can be associated to the eigenvalue distribution of a random sparse matrix, the so-called CMV matrix, after Cantero, Moral, Velázquez [17]. To state their result, we need the following definition.

Definition 1

A complex random variable X with values on the unit disk \(\mathbb {D}\) is \(\Theta _\nu \)-distributed (\(\nu >1\)) if

$$\begin{aligned} \mathbb {E}\left[ f(X)\right] = \frac{\nu -1}{2\pi } \int _{\overline{\mathbb {D}}} f(z)(1-\vert z\vert ^2)^{\frac{\nu -3}{2}}\textrm{d}^2z\, . \end{aligned}$$
(26)

for any measurable function \(f\,:\,\mathbb {D}\rightarrow \mathbb {C}\). When \(\nu = 1\), \(\Theta _1\) is the uniform distribution on the unit circle \(S^1\).

We recall that for \(\mathbb {N}\ni \nu \ge 2\), such measure has the following geometrical interpretation: if \(\textbf{u}=(u_1,u_2,\dots ,u_{\nu +1})\) is chosen at random according to the surface measure on the unit sphere \(S^\nu \) in \(\mathbb {R}^{\nu +1}\), then \(u_1+i u_2\) is \(\Theta _\nu -\)distributed. We can now state the result of Killip-Nenciu.

Theorem 3

(cf. [42] Theorem 1). Consider the block diagonal \(N\times N\) matrices

$$\begin{aligned} M = \text{ diag }\left( \Xi _1,\Xi _3,\Xi _{5} \ldots ,\right) \quad \text{ and } \quad L = \text{ diag }\left( \Xi _{0},\Xi _2,\Xi _4, \ldots \right) \,, \end{aligned}$$
(27)

where the block \(\Xi _j\), \(j=1,\dots , N-1\), takes the form

$$\begin{aligned} \Xi _j = \begin{pmatrix} \overline{\alpha }_j &{} \rho _j \\ \rho _j &{} -\alpha _j \end{pmatrix}\, ,\;\;\rho _j = \sqrt{1-\vert \alpha _j\vert ^2}, \end{aligned}$$
(28)

while \(\Xi _{0} = (1)\) and \(\Xi _{N} = (\overline{\alpha }_{N})\) are \(1\times 1\) matrices. Define the \(N \times N\) sparse matrix

$$\begin{aligned} E = LM, \end{aligned}$$
(29)

and suppose that the entries \(\alpha _j \) are independent complex random variables with \(\alpha _j\sim \Theta _{\widetilde{\beta }(N-j) +1 }\) for \(1\le j\le N-1\) and \(\alpha _{N}\) is uniformly distributed on the unit circle. Then the eigenvalues of E are distributed according to the Circular Ensemble (25) at temperature \(\tilde{\beta }^{-1}\).

We observe that each of the matrices \(\Xi _j\) is unitary, and so are the matrices L and M. As a result, the eigenvalues of E clearly lie on the unit circle. The matrix E is a 5-diagonal unitary matrix that takes the form

$$\begin{aligned} E=\begin{pmatrix} \bar{\alpha }_1&{}\rho _1\bar{\alpha }_2&{}\rho _1\rho _2&{}&{}&{}&{}&{}&{}\\ \rho _1&{}-\alpha _1\bar{\alpha }_2&{}-\alpha _1\rho _2&{}&{}&{}&{}&{}&{}\\ &{}\rho _2\bar{\alpha }_3&{}-\alpha _2\bar{\alpha }_3&{}\rho _3\bar{\alpha }_4&{}\rho _3\rho _4&{}&{}&{}&{}\\ &{}\rho _2\rho _3&{}-\alpha _2\rho _3&{}-\alpha _3\bar{\alpha }_4&{}-\alpha _3\rho _4&{}&{}&{}&{}\\ &{}&{}&{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}&{}&{}\\ &{}&{}&{}&{}&{}\rho _{N-3}\bar{\alpha }_{N-2}&{}-\alpha _{N-3}\bar{\alpha }_{N-2}&{}\rho _{N-2}\bar{\alpha }_{N-1}&{}\rho _{N-2}\rho _{N-1}\\ &{}&{}&{}&{}&{}\rho _{N-3}\rho _{N-2}&{}-\alpha _{N-3}\rho _{N-2}&{}-\alpha _{N-2}\bar{\alpha }_{N-1}&{}-\alpha _{N-2}\rho _{N-1}\\ &{}&{}&{}&{}&{}&{}&{}\bar{\alpha }_{N}\rho _{N-1}&{}-\alpha _{N-1}\bar{\alpha }_N\\ \end{pmatrix}\,. \end{aligned}$$

We are interested in the probability distribution (25) when

  • We add an external field, namely \(d\theta _i\rightarrow e^{-2V(\theta _i)}d\theta _i \) with \(V:\mathbb {T}\rightarrow \mathbb {R}\) a smooth potential;

  • We consider the limit \(\widetilde{\beta }\rightarrow 0\) and \(N \rightarrow \infty \) in such a way that \(\widetilde{\beta }N = 2\beta , \, \beta >0.\) Since \(\widetilde{\beta }\) is interpreted as the inverse of the temperature, such limit is called high-temperature regime.

With the above changes, we arrive to the probability distribution of the Circular ensemble at high-temperature, and with an external potential:

$$\begin{aligned} \textrm{d}\mathbb {P}_{\beta }^V (\theta _1, \ldots , \theta _{N}) = \frac{1}{\mathcal {Z}^{HT}_N(V,\beta )} \prod _{1\le j<\ell \le N}\vert e^{i\theta _\ell } - e^{i\theta _j}\vert ^{\frac{2 \beta }{N}}e^{-2\sum _{j=1}^{N} V(\theta _j)}\textrm{d}\varvec{\theta }\, , \end{aligned}$$
(30)

where \(\mathcal {Z}^{HT}_N(V,\beta )\) is the partition function of the system. Also in this case, we can associate to the above probability distribution a random CMV matrix. The lemma below has probably already appeared in the literature, but for completeness we provide the proof.

Lemma 4

Let E be the CMV matrix (29). Consider the block \(2N\times 2N\) matrix

$$\begin{aligned} \widetilde{E} = \text{ diag }(E,E)\, , \end{aligned}$$
(31)

whose entries are distributed according to

$$\begin{aligned} \textrm{d}\mathbb {P}(\alpha _1, \ldots , \alpha _{N}) = \frac{1}{Z^{HT}_N(V,\beta )} \prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) ^{\beta \left( 1 -\frac{j}{N}\right) -1} e^{-\text{ Tr }(V(\widetilde{E}))} \prod _{j=1}^{N-1}\textrm{d}^2 \alpha _j\frac{\textrm{d}\alpha _N}{i\alpha _N}\,.\nonumber \\ \end{aligned}$$
(32)

Then the eigenvalues of \(\widetilde{E}\) are all double, they lie on the unit circle and are distributed according to (30).

Moreover

$$\begin{aligned} Z^{HT}_N(V,\beta ) = 2^{1-N}\frac{\Gamma \left( \frac{\beta }{N} \right) ^N}{\Gamma (\beta )}\mathcal {Z}^{HT}_N(V,\beta )\,, \end{aligned}$$
(33)

where \(\mathcal {Z}^{HT}_N(V,\beta )\) is the norming constant of the probability distribution (30) and \(Z^{HT}_N(V,\beta ) \) is the norming constant of the probability distribution (32).

Proof

First, we notice that the eigenvalues of \(\widetilde{E}\) are all double, since it is a block diagonal matrix with two identical blocks.

We consider the change of variables \(\alpha _N \rightarrow e^{i \varphi }\), thus (32) becomes:

$$\begin{aligned} \textrm{d}\mathbb {P}(\alpha _1, \ldots ,\alpha _{N-1}, \varphi ) = \frac{ \prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) ^{\beta \left( 1 -\frac{j}{N}\right) -1} e^{-\text{ Tr }(V(\widetilde{E}))} \prod _{j=1}^{N-1}\textrm{d}^2 \alpha _j\textrm{d}\varphi }{Z^{HT}_N(V,\beta )}\,.\nonumber \\ \end{aligned}$$
(34)

Now, let \(e^{i\theta _1}, \ldots ,e^{i\theta _N}\) be the eigenvalues of the CMV matrix E endowed with probability (32), and let \(q_1, \ldots ,q_N\) be the entries of the first row of the unitary matrix Q such that \(Q^\dagger \Theta Q = E\) where \(\Theta =\text{ Diag }(e^{i\theta _1}, \ldots ,e^{i\theta _N})\) and \(\sum _{k=1}^N\vert q_k\vert ^2=1\). We introduce the variable \(\gamma _j = \vert q_j\vert ^2\) for \(j=1,\ldots , N\), then from [42] (Lemma 4.1, and relation (4.14) in Proposition 4.2) we have

$$\begin{aligned}&\vert \Delta (e^{i\varvec{\theta }})\vert ^2 \prod _{j=1}^{N}\gamma _j = \prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) ^{(N-j)}\, , \end{aligned}$$
(35)
$$\begin{aligned}&\left| \frac{\partial \left( \alpha _1, \ldots , \alpha _{N-1}, \varphi \right) }{\partial (\varvec{\theta },{\varvec{\gamma }})}\right| = 2^{1-N} \frac{\prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) }{\prod _{j=1}^{N}\gamma _j}\, , \end{aligned}$$
(36)

here \({\varvec{\gamma }}= (\gamma _1,\ldots ,\gamma _{N-1})\), and \(\Delta (e^{i\varvec{\theta }}) = \prod _{j<\ell }\left( e^{i\theta _j} - e^{i\theta _\ell }\right) \). Applying the previous equalities to (34) we derive

$$\begin{aligned} \begin{aligned}&\textrm{d}\mathbb {P}(\alpha _1,\ldots , \alpha _{N-1}, \varphi )) = \frac{e^{-\text{ Tr }(V(\widetilde{E}))}}{Z^{HT}_N(V,\beta )}\textrm{d}\varphi \prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) ^{\beta \left( 1 -\frac{j}{N} \right) -1} \textrm{d}\alpha _j \textrm{d}\overline{\alpha }_j \\&\qquad {\mathop {=}\limits ^{(36)}} \frac{1}{Z^{HT}_N(V,\beta )}\frac{2^{1-N}}{\prod _{j=1}^{N}\gamma _j} \prod _{j=1}^{N-1}\left( 1 - \vert \alpha _j\vert ^2\right) ^{\beta \left( 1 -\frac{j}{N} \right) } e^{-2\sum _{j=1}^N V(e^{i\theta _j})} \textrm{d}\varvec{\theta }\textrm{d}{\varvec{\gamma }}\\&\qquad {\mathop {= }\limits ^{(35)}}\frac{1}{Z^{HT}_N(V,\beta )} 2^{1-N}\vert \Delta (e^{i\varvec{\theta }})\vert ^{\frac{2\beta }{N}} \prod _{j=1}^N \gamma _j^{\frac{\beta }{N}-1} e^{-2\sum _j V(e^{i\theta _j})} \textrm{d}\varvec{\theta }\textrm{d}{\varvec{\gamma }}\,. \end{aligned} \end{aligned}$$
(37)

Thus, we deduce the relation

$$\begin{aligned} Z^{HT}_N(V,\beta ) = 2^{1-N}\mathcal {Z}^{HT}_N(V,\beta )\, \int _{\Delta } \prod _{j=1}^N \gamma _j^{\frac{\beta }{N} - 1} \textrm{d}\gamma _1\ldots \textrm{d}\gamma _{N-1}\,, \end{aligned}$$
(38)

here \(\Delta \) is the simplex \(\sum _{j=1}^N \gamma _j = 1\). The above integral is a well-known Dirichlet integral that can be computed explicitly (see [42, Lemma 4.4])

$$\begin{aligned} \int _{\Delta } \prod _{j=1}^N \gamma ^{\frac{\beta }{N} - 1} \textrm{d}\gamma _1\ldots \textrm{d}\gamma _{N-1}= \frac{\Gamma \left( \frac{\beta }{N} \right) ^N}{\Gamma (\beta )}\, , \end{aligned}$$
(39)

proving (33). \(\square \)

Let \(e^{i\theta _1},\dots , e^{i\theta _N}\) be the double eigenvalues of the CMV Matrix \(\tilde{E}\) in (31), whose entries are distributed according to (34). The empirical measure is the random probability measure

$$\begin{aligned} \mu _N=\dfrac{1}{N}\sum _{j=1}^N\delta _{e^{i\theta _j}}. \end{aligned}$$
(40)

The mean density of state \(\mu ^\beta _{HT}\) is defined as the non-random probability measure such that

$$\begin{aligned} \int _\mathbb {T}f(\theta ) \mu ^\beta _{HT}(\textrm{d}\theta ) = \lim _{N\rightarrow \infty } \mathbb {E}\left[ \int _\mathbb {T}f(\theta )\mu _N(\textrm{d}\theta )\right] \, , \end{aligned}$$
(41)

for all continuous function f on the torus \(\mathbb {T}\), and the expected value is taken with respect to (32). In order to discuss the large N limit of \(\mu _N\) we have to introduce several quantities. Let \(\mathcal {M}(\mathbb {T})\) be the set of probability measures on the one-dimensional torus \(\mathbb {T}\) and for \(\mu \in \mathcal {M}(\mathbb {T})\) we consider the logarithmic energy [58]

$$\begin{aligned} E (\mu ):= \int \int \limits _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta -\phi }{2}\right) \right| ^{-1}\mu (\textrm{d}\theta )\mu (\textrm{d}\phi )\,. \end{aligned}$$

We define the relative entropy \(K(\mu \vert \mu _0)\) of \(\mu \) with respect to \(\mu _0(\textrm{d}\theta )=\dfrac{\textrm{d}\theta }{2\pi }\) as

$$\begin{aligned} K(\mu \vert \mu _0):=\int _{\mathbb {T}}\log \left( \frac{\mu }{\mu _0}\right) \mu (\textrm{d}\theta ), \end{aligned}$$

when \(\mu \) is absolutely continuous with respect to \(\mu _0\) and otherwise \(K(\mu \vert \mu _0):= +\infty \). The relevant functional is

$$\begin{aligned} \mathcal {F}^{(V,\beta )}(\mu ):=\beta E (\mu )+K(\mu \vert \mu _0)+2\int _{\mathbb {T}}V(\theta )\mu (\textrm{d}\theta ). \end{aligned}$$

When \(\mathcal {F}^{(V,\beta )}(\mu )\) is finite, it follows that \(\mu \) is absolutely continuous with respect to the Lebesgue measure \(\mu _0\) and we can write \(\mu (\textrm{d}\theta )=\mu (\theta )\textrm{d}\theta \). We denote by \(C^{n,1}(\mathbb {T})\) with \(n=0, 1,2,\dots \) the space of n-times differentiable functions whose n-derivative is also Lipschitz continuous.

The following result describes the limiting measure \(\mu ^\beta _{HT}\) in (41) for the circular \(\beta \)-ensembles at high temperature.

Theorem 5

(cf. [37, Proposition 2.1 and 2.5]). Let \(\mathcal {M}(\mathbb {T})\) be the set of probability measures on the one-dimensional torus and \(V \, :\, \mathbb {T}\rightarrow \mathbb {R}\) be a measurable and bounded function. For any \(\beta > 0\) consider the functional \(\mathcal {F}^{(V,\beta )}:\mathcal {M}(\mathbb {T})\rightarrow [0,\infty ]\)

$$\begin{aligned} \mathcal {F}^{(V,\beta )}(\mu ) = 2\int _{\mathbb {T}} V(\theta ) \mu (\theta ) \textrm{d}\theta +\beta E (\mu )+ \int _{\mathbb {T}}\ln \left( \mu (\theta )\right) \mu (\theta )\textrm{d}\theta +\ln (2\pi )\,. \end{aligned}$$
(42)

Then

  1. (a)

    The functional \( \mathcal {F}^{(V,\beta )}(\mu )\) has a unique minimizer \(\mu ^{\beta }_{HT}(\textrm{d}\theta )=\mu ^{\beta }_{HT}(\theta )\textrm{d}\theta \) in \(\mathcal {M}(\mathbb {T})\);

  2. (b)

    \(\mu ^{\beta }_{HT}\) is absolutely continuous with respect to the Lebesgue measure and there is \(0<\delta <1 \) such that

    $$\begin{aligned} \delta \le \frac{\mu ^{\beta }_{HT}(\theta )}{2\pi }\le \delta ^{-1},\quad a.e.\,; \end{aligned}$$
  3. (c)

    If \(V=0\), then \(\mu ^{\beta }_{HT}(\textrm{d}\theta ) = \frac{1}{2\pi }\textrm{d}\theta \);

  4. (d)

    If \(V \in C^{m,1}(\mathbb {T})\), then \(\mu ^{\beta }_{HT} \in C^{m,1}(\mathbb {T})\);

  5. (e)

    The empirical measure \(\mu _N\) in (40) converges weakly and almost surely to the measure \(\mu ^{\beta }_{HT}\) as \(N\rightarrow \infty \).

From the above theorem when the potential V is at least \(C^{2,1}(\mathbb {T})\) the minimizer of the functional \(\mathcal {F}^{(V,\beta )}\) is characterized by the Euler-Lagrange equations

$$\begin{aligned} \dfrac{\delta \mathcal {F}^{(V,\beta )}}{\delta \mu }=2V(\theta ) -2\beta \int _{\mathbb {T}} \ln \sin \left( \frac{\vert \theta -\phi \vert }{2}\right) \mu (\phi )\textrm{d}\phi +\ln \mu (\theta )+1=C(V,\beta )\, \end{aligned}$$
(43)

where \(C(V,\beta )\) is a constant in \(\theta \). Below we derive further properties of the minimizer \(\mu ^{\beta }_{HT}\) following [36].

Lemma 6

For any V(z) as in (17), any \(\beta >0\) the following holds

  1. (a)

    The map \(\beta \rightarrow \inf \left( \mathcal {F}^{(V,\beta )}(\mu )\right) \) is Lipschitz;

  2. (b)

    The maps \(t \rightarrow \inf \left( \mathcal {F}^{(V+t\Re (z^m),\beta )}(\mu )\right) ,\, t \rightarrow \inf \left( \mathcal {F}^{(V+t\Im (z^m),\beta )}(\mu )\right) \) are Lipschitz;

  3. (c)

    Let D be the distance on \(\mathcal {M}(\mathbb {T})\) given by

    $$\begin{aligned} \begin{aligned} D(\mu , \mu ')&= \left( - \int \int \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| (\mu - \mu ')(\textrm{d}\theta )(\mu - \mu ')(\textrm{d}\phi )\right) ^{1/2}\\&= \sqrt{\sum _{k\ge 1} \frac{1}{k}\left| \widehat{\mu }_k - \widehat{\mu }'_k \right| ^2}\,, \end{aligned} \end{aligned}$$
    (44)

    where \(\widehat{\mu }_k = \int _\mathbb {T}e^{ik\theta } \mu (\textrm{d}\theta )\), and we recall that \(\widehat{\log (\vert x\vert )} = \sum _{k\ge 1}k^{-1}\) in distributional sense. Then for any \(\varepsilon >0\) there exists a finite constant \(C_\varepsilon \) such that for all \(\beta ,\beta '>\varepsilon \)

    $$\begin{aligned} D(\mu _{HT}^\beta , \mu _{HT}^{\beta '}) \le C_\varepsilon \left| \beta - \beta ' \right| \,. \end{aligned}$$
    (45)

Remark 5

For a real valued function \(f\in L^2(\mathbb {T})\) with derivative in \(L^2(\mathbb {T})\) we define \(\vert \vert f\vert \vert _{\frac{1}{2}} = \sqrt{\sum _{k\ge 1} k \vert \widehat{f}_k\vert ^2}<\infty \). So, for any measure \(\nu \) with zero mass we deduce that

$$\begin{aligned} \left| \int _{\mathbb {T}} f(\theta ) \nu (\textrm{d}\theta ) \right| ^2&= \left| \sum _{k\ne 0} \widehat{f}_k \overline{\widehat{\nu }_k} \right| ^2= \left| \sum _{k\ne 0} \sqrt{\vert k\vert }\widehat{f}_k \frac{\overline{\widehat{\nu }_k}}{\sqrt{\vert k\vert }}\right| ^2\le \left| \sum _{k\ne 0}\vert k\vert \vert \widehat{f}_k\vert ^2\right| \left| \sum _{k\ne 0} \frac{\vert \widehat{\nu }_k\vert ^2}{\vert k\vert }\right| \nonumber \\ {}&\le 4 \vert \vert f\vert \vert _{\frac{1}{2}}^2 D(\nu , 0)^2 \end{aligned}$$
(46)

where in the first inequality we use Cauchy-Schwartz inequality and in the second one we plug in (44).

Combining (45) and (46) we conclude that for any real valued function f with finite \(\vert \vert f\vert \vert _{\frac{1}{2}}\) norm, the map \(\beta \rightarrow \int _{\mathbb {T}}f\textrm{d}\mu _{HT}^\beta (\textrm{d}\theta )\) is Lipschitz for \(\beta > 0\). As a consequence, the moments of \(\mu _{HT}^\beta \) are almost surely differentiable with respect to \(\beta \).

Proof of Lemma 6

The proof follows the lines of the corresponding one in [36]. To prove points a) and b) we exploit the same ideas, thus we restrict to point a).

For all \(\beta> \beta ' > 0\) we have

$$\begin{aligned} \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta })\le \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta '})= \mathcal {F}^{(V,\beta ')}(\mu _{HT}^{\beta '})+(\beta -\beta ') E (\mu _{HT}^{\beta '}) \end{aligned}$$

and

$$\begin{aligned} \mathcal {F}^{(V,\beta ')}(\mu _{HT}^{\beta '})\le \mathcal {F}^{(V,\beta ')}(\mu _{HT}^{\beta })= \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta })+(\beta ' - \beta ) E (\mu _{HT}^{\beta })\,, \end{aligned}$$
(47)

so that

$$\begin{aligned} (\beta - \beta ') E (\mu _{HT}^{\beta })\le \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta })-\mathcal {F}^{(V,\beta ')}(\mu _{HT}^{\beta '})\le (\beta - \beta ') E (\mu _{HT}^{\beta '})\,. \end{aligned}$$
(48)

Since \( E (\mu _{HT}^{\beta }),\) and \( E (\mu _{HT}^{\beta '})\) are finite we obtain the claim.

We now move to the proof of point c). Setting \(\Delta \mu = \mu _{HT}^{\beta } - \mu _{HT}^{\beta '}\) we deduce that

$$\begin{aligned} \begin{aligned} 0&\ge \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta }) - \mathcal {F}^{(V,\beta )}(\mu _{HT}^{\beta '}) \\&= 2\int _{\mathbb {T}} V(\theta ) \Delta \mu (\textrm{d}\theta ) -2\beta \int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \mu _{HT}^{\beta '}(\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi ) \\ {}&\quad -\beta \int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \Delta \mu (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi )+ \int _{\mathbb {T}} \ln (\mu _{HT}^\beta (\theta )) \mu _{HT}^\beta (\textrm{d}\theta ) \\ {}&\quad - \int _{\mathbb {T}} \ln (\mu _{HT}^{\beta '}(\theta )) \mu _{HT}^{\beta '}(\textrm{d}\theta )\\&= \int _{\mathbb {T}} \ln \left( \frac{\mu _{HT}^\beta (\theta )}{\mu _{HT}^{\beta '}(\theta )}\right) \mu _{HT}^\beta (\textrm{d}\theta ) + 2(\beta '-\beta )\int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \mu _{HT}^{\beta '}(\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi ) \\ {}&\quad -\beta \int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \Delta \mu (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi )\,, \end{aligned} \end{aligned}$$
(49)

where in the second identity we used (43). Since \(\int _{\mathbb {T}}\ln \left( \frac{\mu _{HT}^\beta (\theta )}{\mu _{HT}^{\beta '}(\theta )}\right) \mu _{HT}^\beta (\textrm{d}\theta ) \le 0 \) by Jensen’s inequality, we deduce that

$$\begin{aligned} \beta D\left( \mu _{HT}^{\beta }, \mu _{HT}^{\beta '}\right) ^2 \le 2(\beta - \beta ')\int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \mu _{HT}^{\beta '}(\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi )\,. \end{aligned}$$
(50)

Following [36], we introduce a new probability measure \(\nu \in \mathcal {M}(\mathbb {T})\) in the previous expression, so that

$$\begin{aligned} \begin{aligned} \beta D\left( \mu _{HT}^{\beta '}, \mu _{HT}^{\beta '}\right) ^2&\le 2(\beta - \beta ')\int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \left( \mu _{HT}^{\beta '}-\nu \right) (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi ) \\&\quad + 2(\beta - \beta ')\int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \nu (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi )\,. \end{aligned} \end{aligned}$$
(51)

We chose \(\nu \) in such a way that the function \(g_\nu (\phi ) = \int _{\mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \nu (\textrm{d}\theta )\) is in \(L^2(\mathbb {T})\) with derivative in \(L^2(\mathbb {T})\). With this choice of \(\nu \) and applying (46) we conclude that there exists a constant c such that

$$\begin{aligned} \left| \int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \nu (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi ) \right| \le c D(\mu _{HT}^\beta , \mu _{HT}^{\beta '})\,. \end{aligned}$$
(52)

Next, taking the Fourier transform and apply again the Cauchy-Schwartz inequality as in (46) we obtain

$$\begin{aligned} \begin{aligned} \left| \int _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta - \phi }{2}\right) \right| \left( \mu _{HT}^{\beta '}-\nu \right) (\textrm{d}\theta ) \Delta \mu (\textrm{d}\phi ) \right|&= \left| \sum _{k\ge 1} \frac{1}{k}\widehat{\left( \mu _{HT}^{\beta '}-\nu \right) }_k \overline{\widehat{\Delta \mu _k}}\right| \\ {}&\le D(\mu _{HT}^{\beta '},\nu )D(\mu _{HT}^{\beta '}, \mu _{HT}^{\beta })\,, \end{aligned} \end{aligned}$$
(53)

since \(D(\mu _{HT}^{\beta '},\nu )\) is bounded. Combining (51), (52) and (53) we conclude that there exists a constant \(c_0\) such that

$$\begin{aligned} D(\mu _{HT}^\beta ,\mu _{HT}^{\beta '})\le \frac{c_0}{\beta }(\beta - \beta ')\,, \end{aligned}$$
(54)

from which (45) follows. \(\square \)

For convenience, we define \(F_{HT}(V,\beta )\) as the value of the functional at the minimizer, namely

$$\begin{aligned} F_{HT}(V,\beta ):=\mathcal {F}^{(V,\beta )}(\mu ^\beta _{HT}). \end{aligned}$$
(55)

The quantity \(F_{HT}(V,\beta )\) is referred to as free energy of the Circular \(\beta \) ensemble at high-temperature. It is a standard result that (see e.g. [29])

$$\begin{aligned} F_{HT}(V,\beta )=-\lim _{N\rightarrow \infty }\frac{1}{N}\log \mathcal {Z}^{HT}_N(V,\beta )\,, \end{aligned}$$
(56)

where the partition function \(\mathcal {Z}^{HT}_N(V,\beta )\) of the Circular \(\beta \) ensemble at high-temperature is defined in (30).

Remark 6

We notice that from (33) and (56) we can also obtain the free energy \(F_{HT}(V,\beta )\) from the partition function \(Z^{HT}_N(V,\beta )\) of the CMV matrix ensemble (32), namely:

$$\begin{aligned} F_{HT}(V,\beta ) = - \lim _{N\rightarrow \infty } \frac{\ln (Z^{HT}_N(V,\beta ))}{N} - \ln (2)\, . \end{aligned}$$
(57)

The literature related to the high-temperature regime of the classical \(\beta \)-ensembles is quite broad. For completeness, we mention some of the results in the field. In [7, 8, 22, 27, 37, 65, 66] the authors explicitly computed the mean density of states for the classical Gaussian, Laguerre, Jacobi, and Circular \(\beta \) ensemble at high-temperature. In [7, 8, 27, 37] the densities of states are computed as a solution of some particular ordinary differential equations. On the other hand, in [22, 65, 66] the density of states is constructing from the moment generating functions. Several authors [12, 45, 52, 53, 67] investigated the local fluctuations of the eigenvalues, and they observed that in this regime they are described by a Poisson process. In particular, in [45] Lambert studied the local fluctuations for general Gibbs ensembles on N-dimensional manifolds, moreover he also studied the asymptotic behaviour of the maximum eigenvalue for the classical \(\beta \) ensembles at high-temperature. In [26, 27] the loop equations for the classical \(\beta \)-ensembles at high-temperature are studied, in particular in [26] a duality between high and low temperature is uncovered. There are also results for a Coulomb gas at high temperature in two dimensions [5]. It is worth mentioning also the work [48], where some new tridiagonal random matrix ensembles related to the classical \(\beta \) one at high-temperature are defined.

4 Proof of Theorem 1

The probability distribution (18) of generalized Gibbs ensemble of the Ablowitz–Ladik lattice is very close to the probability distribution (32) of the Circular \(\beta \) ensemble at high-temperature with an external source. Indeed, the only difference between the two ensembles is the exponent of the terms \(\left( 1-\vert \alpha _j\vert \right) \) in the probability distributions (18) and (32) and the fact that the random matrix of the Ablowitz–Ladik lattice is a rank 2 perturbation of the random matrix of the circular \(\beta \)-ensemble. Our first main result contained in Theorem 1 relates the mean density of states of the random Lax matrix \(\mathcal {E}\) of the Ablowitz–Ladik lattice to the mean density of states of the random matrix E from the Circular \(\beta \) ensemble at high-temperature.

To prove the result, we use the moment matching technique and the following lemma.

Lemma 7

([10, Lemma B.1 – B.2]). Let \(\textrm{d}\sigma , \textrm{d}\sigma '\) be two measures defined on \(\mathbb {T}\), with the same moment sequence \(\{u^{(\ell )}\}_{\ell \ge 0}\). If

$$\begin{aligned} \lim _{\ell \rightarrow \infty }\inf \frac{(u^{(2\ell )})^\frac{1}{2\ell }}{\ell } < \infty \, , \end{aligned}$$
(58)

then \(\textrm{d}\sigma = \textrm{d}\sigma '\).

Next we define the free energy of the generalized Gibbs ensemble of the Ablowitz–Ladik lattice at temperature \(\beta ^{-1}\) and in an external field V as:

$$\begin{aligned} F_{AL}(V,\beta ) = -\lim _{N\rightarrow \infty } \frac{1}{N} \ln Z^{AL}_N(V,\beta )\,, \end{aligned}$$
(59)

where the partition function \(Z^{AL}_N(V,\beta )\) is defined in (19). The next proposition shows that the free energy \(F_{AL}(V,\beta )\) of the Generalized Gibbs ensemble of the Ablowitz–Ladik lattice and the free energy \(F_{HT}(V,\beta )\) in (56) of the Circular \(\beta \) ensemble at high-temperature are related. This fact allows us to calculate the moments of the mean density of states of the CMV matrix E in (29) and of the Lax matrix \(\mathcal {E}\) in (11).

Proposition 8

The free energy \(F_{AL}(V,\beta )\) in (59) of the AL lattice and the free energy \(F_{HT}(V,\beta )\) in (56) of the Circular \(\beta \) ensemble at high-temperature are analytic with respect to \(\beta >0\), and are related by

$$\begin{aligned} \partial _\beta \left( \beta F_{HT}(V,\beta )\right) + \ln (2) = F_{AL}(V,\beta ). \end{aligned}$$
(60)

The moments of the density of states \(\mu ^\beta _{AL}\) of the Lax matrix \(\mathcal {E}\) in (11) endowed with the probability measure (18) and the moments of the density of states \(\mu _{HT}\) of the Circular \(\beta \) ensemble in the high-temperature regime (32) are related to the free energies \(F_{AL}(V,\beta )\) and \(F_{HT}(V,\beta )\) by

$$\begin{aligned} \begin{aligned}&\Re \int _\mathbb {T}e^{i\theta m }\mu _{AL}^\beta (\textrm{d}\theta )= \partial _t F_{AL}\left( V + \frac{t}{2}\Re (z^m),\beta \right) _{\vert _{t=0}}\,,\\&\Re \int _\mathbb {T}e^{i\theta m}\mu _{HT}^\beta (\textrm{d}\theta ) = \partial _t F_{HT}\left( V + \frac{t}{2}\Re (z^m),\beta \right) _{\vert _{t=0}}, \end{aligned} \end{aligned}$$
(61)

and analogously for the imaginary part of the moments taking care of using the potential \(V + \frac{t}{2}\Im (z^m)\).

Since the proof of this proposition is rather technical, we postpone it to Appendix A. We are now ready to prove the first main Theorem 1.

Proof of Theorem 1

First, we define \(c_n(\beta ) := \int e^{i\theta n} \mu _{AL}^\beta (\textrm{d}\theta ),\)

\(d_n(\beta ) := \int e^{i\theta n} \mu _{HT}^\beta (\textrm{d}\theta )\). Since the eigenvalues of \(\mathcal {E}\) lie on the unit circle, we deduce the following chain of inequalities:

$$\begin{aligned} \vert c_n(\beta )\vert = \lim _{N\rightarrow \infty }\frac{\left| \mathbb {E}\left[ \text{ Tr }(\mathcal {E}^n)\right] \right| }{2N}\le \lim _{N\rightarrow \infty }\frac{\mathbb {E}\left[ \left| \text{ Tr }(\mathcal {E}^n) \right| \right] }{2N} \le 1\, , \end{aligned}$$
(62)

where the expectation in made according to the Gibbs measure. Thus, from Lemma 7, we obtain that the measure \(\mu _{AL}^\beta (\textrm{d}\theta )\) is uniquely characterized by its moments.

Next, from Proposition 8 and Remark 5 we obtain the relation

$$\begin{aligned} c_n(\beta )= \partial _\beta \left( \beta d_n(\beta )\right) \, \;a.e \end{aligned}$$
(63)

between the moments of the measures \(\mu ^\beta _{AL}(\theta )\) and \(\mu _{HT}^\beta (\theta )\) respectively.

This, together with (63) and Remark 5 implies

$$\begin{aligned} \mu ^\beta _{AL}( \theta ) = \partial _\beta \left( \beta \mu _{HT}^\beta (\theta )\right) \;\;a.e.\,. \end{aligned}$$
(64)

\(\square \)

Our next main result provides an explicit expression of the mean density of states \(\mu _{HT}(\theta )\) for the potential \(V(z)=\eta \Re (z)\). This generalizes the result by Gross and Witten [35] and Baik-Deift-Johansson [11] obtained for finite temperature to the high-temperature regime.

5 Proof of Theorem 2

The proof of Theorem 2 consists of mainly two parts: we first derive from the variational equations with respect to the functional \(\mathcal {F}^{(V,\beta )}\), the double confluent Heun equation (23). Then we show that such equation admits an analytic solution in any compact sets of the complex plane containing the origin. From Theorem 5 we know that the density \(\mu ^\beta _{HT}\) is characterized as the unique minimizer of the functional (42). We follow the ideas developed in [7, 8, 18, 27] to find this minimizer explicitly. We consider the Euler-Lagrange equation of the functional (42), namely

$$\begin{aligned} \dfrac{\delta \mathcal {F}^{(V,\beta )}}{\delta \mu }=2V(\theta ) -2\beta \int _{\mathbb {T}} \ln \sin \left( \frac{\vert \theta -\phi \vert }{2}\right) \mu (\phi )\textrm{d}\phi +\ln \mu (\theta )=C(V,\beta )\, ,\;\;a.e.\nonumber \\ \end{aligned}$$
(65)

where the equation holds almost everywhere, \(C(V,\beta )\) is a constant depending on the potential and \(\beta \), but not on the variable \(\theta \). Differentiating the Euler-Lagrange equation (65) at the minimizer \(\mu _{HT}^\beta (\theta )\) with respect to \(\theta \) we obtain the following integral equation (see [37, Proposition 2.5]):

$$\begin{aligned} \partial _\theta \mu _{HT}^\beta (\theta )+\mu _{HT}^\beta (\theta )[2\partial _\theta (V(\theta ))+\beta \mathcal {H}\mu _{HT}^\beta (\theta )] =0\, , \end{aligned}$$
(66)

where \(\mathcal {H}\) is the Hilbert transform defined on \(L^2(\mathbb {T})\) as

$$\begin{aligned} \mathcal {H}\mu _{HT}^\beta (\theta )= -\text{ p.v. }\int _{\mathbb {T}}\cot \left( \frac{\theta -\phi }{2}\right) \mu _{HT}^\beta (\phi )\textrm{d}\phi \end{aligned}$$
(67)

and \(\text{ p.v. }\) is the Cauchy principal value, that is the limit as \(\varepsilon \rightarrow 0\) of the integral on the torus \(\mathbb {T}\) restricted to the domain \(\vert e^{i\theta }-e^{i\phi }\vert >\varepsilon \). We notice that the Hilbert transform \(\mathcal {H}\) is diagonal on the bases of exponential \(\{e^{in\theta }\}_{n\in \mathbb {Z}}\), meaning that

$$\begin{aligned} \mathcal {H}e^{in\theta } = 2\pi i\text{ sgn }(n)e^{in\theta }\, , \end{aligned}$$
(68)

where \(\text{ sgn }(\cdot )\) is the sign function with the convention that \(\text{ sgn }(0) = 0\).

Setting \(e^{i\theta }=z\) and \(e^{i\phi }=w\), we recognize the Riesz–Herglotz kernel \(\dfrac{z+w}{z-w}\) expressed as

$$\begin{aligned} \dfrac{z+w}{z-w}=-i\cot \left( \frac{\theta -\phi }{2}\right) \,. \end{aligned}$$

Therefore

$$\begin{aligned} \int _{\mathbb {T}}\cot \left( \frac{\theta -\phi }{2}\right) \mu (\phi )\textrm{d}\phi = i + 2\int _{S^1}\dfrac{\mu (\phi )_{\vert e^{i\phi } = w}dw}{z-w}, \end{aligned}$$

where \(S^1\) is the anticlockwise oriented circle, and we used the normalization condition \(\int _{\mathbb {T}}\mu (\phi )\textrm{d}\phi =1\). In the following, in order to simplify the notation, we indicate \(\mu (\phi )_{\vert e^{i\phi } = w}\) just as \(\mu (w)\). We can recast (66) in the form

$$\begin{aligned} z \partial _z \mu (z)+\mu (z)\left[ 2z \partial _zV(z)-\beta + 2i\beta \text{ p.v. }\int _{S^1}\mu (w)\dfrac{\textrm{d}w }{z-w}\right] =0\,. \end{aligned}$$
(69)

For \(z\in \mathbb {C}\backslash S^1\) let us define

$$\begin{aligned} G(z) := \int _{S^1}\mu (w)\dfrac{\textrm{d}w }{w-z} = \frac{i}{2} - \frac{1}{2}\int _{\mathbb {T}}\cot \left( \frac{\theta -\phi }{2}\right) \mu (\phi )\textrm{d}\phi \,, \end{aligned}$$
(70)

and for \(z\in S^1\) let \(G_\pm (z) = \lim _{\widetilde{z} \rightarrow z} G(\widetilde{z}) \) for \(\widetilde{z}\) inside and outside the unit circle respectively. Then by (69)

$$\begin{aligned} \begin{aligned} G_{\pm }(z)&= \pm \pi i\mu (z) + \text{ p.v. }\int _{S^1}\mu (w)\dfrac{\textrm{d}w }{w-z} \\&= \pm \pi i \mu (z) + \frac{i}{2} - \frac{2iz \partial _z V(z) }{2\beta } - \frac{i z \partial _z \mu (z)}{2 \beta \mu (z)}\,. \end{aligned} \end{aligned}$$
(71)

This implies that for \(z\in S^1\) one has

$$\begin{aligned}&G_+(z) + G_-(z) = i - \frac{2iz \partial _z V(z) }{\beta } - \frac{i z \partial _z \mu (z)}{\beta \mu (z)} \, , \end{aligned}$$
(72)
$$\begin{aligned}&G_+(z) - G_-(z) = 2 \pi i\mu (z)\,. \end{aligned}$$
(73)

Multiplying the two previous expressions, one obtains:

$$\begin{aligned} G_+(z)^2 -G_-(z)^2 = 2 \pi i \mu (z)\left( i - \frac{2iz\partial _zV(z) }{\beta } - \frac{ z i \partial _z \mu (z)}{\beta \mu (z)}\right) \,. \end{aligned}$$
(74)

In order to proceed we have to specify the potential V(z), in our case we will consider

$$\begin{aligned} V(z) = \frac{\eta }{2}\left( z + \frac{1}{z}\right) . \end{aligned}$$
(75)

Applying the Sokhtoski-Plemelj formula [28] to the above boundary value problem, one obtains

$$\begin{aligned} G^2(z) = i\int _{S^1} \frac{\mu (w)}{w-z}\textrm{d}w - \frac{i\eta }{\beta }\int _{S^1}\frac{\left( w -\overline{w}\right) \mu (w)}{w-z} \textrm{d}w - \frac{i}{\beta }\int _{S^1}\frac{w \partial _w\mu (w)}{w-z} \textrm{d}w\, . \end{aligned}$$
(76)

The second term in the r.h.s. of the above expression gives

$$\begin{aligned} \begin{aligned} \int _{S^1}\frac{(w-\overline{w}) \mu (w)}{w-z} \textrm{d}w&= \int _{S^1} \frac{w \pm z }{w-z}\mu (w)\textrm{d}w + \frac{1}{z}\int _{S^1}\mu (w)\left( -\frac{1}{w-z} + \frac{1}{w} \right) \textrm{d}w \\&=\left( z G(z) + i\lambda -\frac{G(z)}{z} + \frac{i}{z}\right) \, , \end{aligned} \end{aligned}$$
(77)

where we have defined

$$\begin{aligned} \lambda :=-i \int _{S^1}\mu (w) \textrm{d}w,\quad \lambda \in \mathbb {R}. \end{aligned}$$
(78)

The third term in the r.h.s. of (76) gives

$$\begin{aligned} \begin{aligned} \int _{S^1}\frac{w \partial _w\mu (w)}{w-z} \textrm{d}w&= \int _{S^1}\partial _w\mu (w) \textrm{d}w + z \int _{S^1}\frac{ \partial _w\mu (w)}{w-z} \textrm{d}w \\&=z\int _{S^1}\frac{\mu (w)}{(w-z)^2}\textrm{d}w = z \partial _z G(z), \end{aligned} \end{aligned}$$
(79)

where in these last relations we use the results of Theorem 5 about the regularity of \(\mu \). Now we can rewrite (76) as

$$\begin{aligned} G^2(z) = i G(z) -\frac{i\eta }{\beta }\left( z G(z) +i\lambda - \frac{G(z)}{z} + \frac{i}{z}\right) -\frac{i z \partial _z G(z)}{\beta }\,. \end{aligned}$$
(80)

Remark 7

In the above ODE, the parameter \(\lambda = \lambda (\eta ,\beta )\) depends via (78) implicitly on the function G(z). Our strategy to solve the above equation is to consider \(\lambda \) as a free parameter that is uniquely fixed by the analytic properties of the function G(z).

We can now turn the non-linear first order ODE (80) into a linear second order ODE through the substitution

$$\begin{aligned} G(z) = i + \frac{i z v'(z)}{\beta v(z)}, \end{aligned}$$
(81)

getting:

$$\begin{aligned} z^2 v''(z) + \left( -\eta + z (\beta +1) + \eta z^2\right) v'(z) +\eta \beta (z +\lambda ) v(z) =0\, , \end{aligned}$$
(82)

which is the DCH equation in (23). The solutions to this equation have generically essential singularities at \(z=0\) and \(z=\infty \) and the local description near the singularities depends on the parameter \(\eta \) and \(\beta \). Indeed we have that the two fundamental solutions near \(z=0\) have the following asymptotic behaviour

$$\begin{aligned}&v^{(0)}_1(z)=e^{\eta (z+\frac{1}{z})}z^{1-\beta }\kappa _1(\eta ,\beta ,\lambda ;z),\quad - \frac{3\pi }{2}< \arg (\eta z) < \frac{3 \pi }{2}\, , \end{aligned}$$
(83)
$$\begin{aligned}&v^{(0)}_2(z)=\kappa _2(\eta ,\beta ,\lambda ,z),\quad - \frac{\pi }{2}< \arg (\eta z) < \frac{5 \pi }{2}\, , \end{aligned}$$
(84)

where \(\kappa _{j}(\eta ,\beta ,\lambda ;z)\), \(j=1,2\), are asymptotic series in a neighbourhood of \(z=0\). The quantity \(\lambda \) is usually referred to as accessory parameter. Since G(z) is analytic in the unit disk, continuous up to the boundary, and \(G(0)=i\), we deduce that

$$\begin{aligned} v(z)=v_0\exp \left[ -i\int _{0}^z \beta \frac{G(s)-i}{s}ds\right] ,\quad v_0\ne 0, \end{aligned}$$

has to be analytic in the unit disk. For this reason we seek for a solution v(z) of the DCH equation that is analytic in the unit disk and such that \(v(z) \xrightarrow [z\rightarrow 0]{} v_0 \), where \(v_0\) is a nonzero constant.

Construction of the analytic solution of equation (82). Of the fundamental solutions (83) and (84) of Eq. (82) only the solution (84) has a chance of being analytic near \(z=0\). This occurs if we are able to make the asymptotic series defined by \(\kappa _2(\eta ,\beta ,\lambda ,z)\), into a convergent series. We look for a solution of (82) in the form of a convergent power series

$$\begin{aligned} v(z) = \sum _{k=0}^\infty a_k z^k, \end{aligned}$$
(85)

where \(a_k=a_k(\eta ,\beta ,\lambda )\). This implies the following recurrence relations for the coefficients \(\{a_k\}_{k\in \mathbb {N}}\)

$$\begin{aligned}&\eta (a_0\lambda \beta - a_1) =0\, , \end{aligned}$$
(86)
$$\begin{aligned}&a_k(k^2 + k\beta + \lambda \beta \eta ) + \eta (k-1+\beta ) a_{k-1} - \eta (k+1) a_{k+1} = 0 \,, \quad k > 0\, , \end{aligned}$$
(87)

where we have the freedom to chose \(\lambda \) and \(a_0\). Generically, the above recurrence relation for the coefficients \(\{a_k\}_{k\in \mathbb {N}}\) gives a divergent series in (85). To obtain a convergent series, we follow the ideas in [13, 64].

We start by considering the \(2\times 2 \) matrices \(R^{(s)}_k\) defined as

$$\begin{aligned} R_k^{(s)}= M_kM_{k+1}\dots M_s,\; s\ge k,\;\; M_k = \begin{pmatrix} 1 + \frac{\lambda \beta \eta }{k(k+\beta )} &{} \frac{\eta ^2}{k(k+\beta +1)}\\ 1 &{} 0 \end{pmatrix}\,, \end{aligned}$$
(88)

which satisfy the recurrence relation \(R_k^{(s)}=R_k^{(s-1)}M_s\). The next lemma shows that the limit of \(R_k^{(s)}\) as \(s\rightarrow \infty \) exists.

Lemma 9

Let \(R_k^{(s)}\) be the matrix defined in (88). Then the limit of \(R_k^{(s)}\) as \(s\rightarrow \infty \) exists and

$$\begin{aligned} R_k:=\lim _{s\rightarrow \infty }R_k^{(s)}. \end{aligned}$$
(89)

The matrices \(R_k\), \(k\ge 1\) satisfy the descending recurrence relation:

$$\begin{aligned} R_k = M_k R_{k+1}\quad k \ge 1\, . \end{aligned}$$
(90)

Furthermore each entry of the matrix \(R_k=R_k(\beta ,\eta ,\lambda )\) is differentiable with respect to the parameters \(\beta , \, \eta \), and \(\lambda \).

Since the proof of this lemma is rather technical, we defer it to appendix B. Further, let us define the following function:

$$\begin{aligned} \xi (\eta ,\beta ,\lambda ) := \begin{pmatrix} \lambda&\frac{\eta }{\beta +1} \end{pmatrix} R_1 \begin{pmatrix} 1 \\ 0 \end{pmatrix} . \end{aligned}$$
(91)

We are now ready to prove the following result that will give us a necessary condition to fix the value of \(\lambda \).

Proposition 10

For the values of \(\lambda \) such that

$$\begin{aligned} \xi (\eta ,\beta ,\lambda ) =0, \end{aligned}$$
(92)

where \( \xi (\eta ,\beta ,\lambda ) \) is defined in (91), the Double Confluent Heun equation (82) admits a non-zero solution \(v=v(z,\eta ,\beta )\) defined by the series (85) that is uniformly convergent in \(\vert z\vert \le r\) with \(r\ge 1\). The corresponding coefficients \(\{a_k\}_{k\in \mathbb {N}}\) of the Taylor expansion (85) are given by the relation

$$\begin{aligned}&a_0 = \frac{1}{\beta }\begin{pmatrix} 1&0 \end{pmatrix} R_1 \begin{pmatrix} 1 \\ 0 \end{pmatrix}\, , \end{aligned}$$
(93)
$$\begin{aligned}&a_k = (-1)^k\frac{\eta ^k}{k!(k+\beta )} \begin{pmatrix} 0&1 \end{pmatrix} R_k \begin{pmatrix} 1 \\ 0 \end{pmatrix}\, , \quad k \ge 1 \, \, , \end{aligned}$$
(94)

where the matrices \(R_k\) are defined in (89). For each \(\lambda \) satisfying (92), the solution v(z) of the DCH equation (82), analytic at zero is unique up to a multiplicative factor.

Proof

First, we show that choosing \(a_k\) according to (93)–(94) we obtain a solution of the recurrence (87). We notice that due to the recurrence relation for the matrices \(R_k\) (90), we have that:

$$\begin{aligned} \begin{pmatrix} 0&1 \end{pmatrix} R_k \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1&0 \end{pmatrix} R_{k+1 } \begin{pmatrix} 1 \\ 0 \end{pmatrix}\, . \end{aligned}$$
(95)

Thus, applying the previous equation and (93)–(94), we can recast (87) as:

$$\begin{aligned} \begin{aligned}&\left[ (-1)^{k-1} \frac{\eta ^k}{(k-1)!} \begin{pmatrix} 1&0 \end{pmatrix} R_k + (-\eta )^k\ \frac{k(k+\beta ) + \eta \lambda \beta }{k!(k+\beta )} \begin{pmatrix} 1&0 \end{pmatrix} R_{k+1} \right. \\&\quad \left. + (-1)^{k} \frac{\eta ^{k+2}}{k!(k+1+\beta )} \begin{pmatrix} 0&1 \end{pmatrix} R_{k+1}\right] \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\&= \frac{(-\eta )^{k}}{(k-1)!}\left[ - \begin{pmatrix} 1&0 \end{pmatrix}R_k + \begin{pmatrix} 1 + \frac{\lambda \beta \eta }{k(k+\beta )}&\frac{\eta ^2}{k(k+1+\beta )} \end{pmatrix} R_{k+1}\right] \begin{pmatrix} 1 \\ 0 \end{pmatrix} = 0\, , \end{aligned} \end{aligned}$$
(96)

where in the last equality we have enforced (90). Next we can rewrite (86) in terms of the matrix \(R_1\) exploiting (93)–(94), namely

$$\begin{aligned} 0= \begin{pmatrix} \lambda&\frac{\eta }{\beta +1} \end{pmatrix} R_1 \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \xi (\eta ,\beta ,\lambda )\, , \end{aligned}$$
(97)

which is exactly (91). Since the entries of the matrices \(R_k\) are uniformly bounded, the solution \(v(z)=\sum _{k\ge 0}a_kz^k\) with \(a_k\) as in (94), defines a uniformly convergent Taylor series in \(\vert z\vert <r\) for any \(r\ge 0\) and in particular for any \(r>1\).

To show that the solution analytic at \(z=0\) is unique up to a constant, we consider the Wronkstian \(W(v,\tilde{v})(z)\) of two independent solution v and \(\tilde{v}\) of the Double Confluent Heun equation (82), namely

$$\begin{aligned} W(v,\widetilde{v})(z)=e^{-\eta (z+\frac{1}{z})}z^{-(\beta +1)}(v'(z)\tilde{v}(z)-v(z)\tilde{v}'(z)). \end{aligned}$$

Since \(W'(v,\widetilde{v})(z)=0\), it follows that \(W(v,\widetilde{v})(z)=C\) a constant. If by contradiction we suppose that there are two analytic solutions at \(z=0\), then from the above relation we obtain

$$\begin{aligned} e^{-\eta z}(v'(z)\tilde{v}(z)-v(z)\tilde{v}'(z))=Ce^{\frac{\eta }{z}}z^{\beta +1}\,. \end{aligned}$$

When \(\eta \ne 0\) the left-hand side of the above equation is analytic and the right-hand side is not, that is clearly a contradiction. When \(\eta =0\) then (82) becomes:

$$\begin{aligned} z^2 v''(z) + z(\beta +1)v'(z) =0\, . \end{aligned}$$
(98)

The above equation has two independent solutions, one is the constant solution, which is analytic, the other one is \(v(z) = Cz^{-\beta }\) which is not analytic since \(\beta >0\). \(\square \)

Remark 8

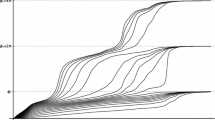
We observe that the Eq. (92) does not uniquely determine \(\lambda \). Indeed, as it is shown in Fig. 1 the function \(\xi (\eta ,\beta ,\lambda )\) may have several zeros for given \(\eta \) and \(\beta \).

Fig. 1
figure 1

Plots of \(\xi (\eta ,\beta ,\lambda )\) for various values of \(\eta ,\beta \)

Full size image

Choice of the parameter \(\lambda \). We will now prove that the parameter \(\lambda \) is uniquely determined in a neighbourhood of \(\eta =0\) by requiring that the solution \(v=v(z,\eta ,\beta )\) depends continuously on the parameter \(\eta \).

Lemma 11

There exists an \(\varepsilon >0\) such that for all \(\eta \in (-\varepsilon ,\varepsilon )\) and \(\beta > 0 \) there is a unique \(\lambda = \lambda (\eta ,\beta )\) such that \(\xi (\eta , \beta , \lambda (\eta ,\beta )) = 0\).

Proof

When \(\eta =0\) the matrix \(R_j=\begin{pmatrix}1&{}0\\ 1&{}0\end{pmatrix}\) so that the only solution of the equation (92) \(\xi (\eta =0,\beta , \lambda ) = 0\) is \(\lambda = 0\). To show the existence of the solution (92) for \(\lambda =\lambda (\eta ,\beta )\) near \(\eta =0\), we use the implicit function theorem. We have to show that \(\partial _\lambda \xi (\eta ,\beta ,\lambda )_{\vert _{(0,\beta ,0)}} \ne 0\). For this purpose, we need to evaluate

$$\begin{aligned} \partial _\lambda \left( M_k\right) _{(\eta = 0,\lambda = 0)} = \begin{pmatrix} 0 &{} 0 \\ 0 &{} 0 \end{pmatrix}\, , \end{aligned}$$

where \(M_k\) is defined in (89). This equation implies that

$$\begin{aligned} \partial _\lambda (\xi (\eta ,\beta ,\lambda ))_{\vert _{(0,\beta ,0)}} = \begin{pmatrix} 1&0\end{pmatrix} \begin{pmatrix} 1 &{} 0 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}=1. \end{aligned}$$

Thus we can apply the implicit function theorem, and we obtain the claim. \(\square \)

We conclude the proof of Theorem 2. When \(\eta =0\) the only analytic solution of DCH equation is \(v(z)=c\), \(c\in \mathbb {C}\backslash \{0\}\). In this case, in principle \(\lambda \) is undetermined. However, from Theorem 5 the minimizer \(\mu ^\beta _{HT}\) of (42) is the uniform measure on the circle and therefore from equation 78 one has \(\lambda =0\). From Lemma 11 when \(\eta \in (-\varepsilon ,\varepsilon )\), there exists a unique \(\lambda (\eta ,\beta )\) that satisfies equation (92) and such that \(\lambda (\eta =0,\beta )=0\) and therefore by Proposition 10 we obtain for \(\eta \in (-\varepsilon ,\varepsilon )\), the unique solution \(v(z,\eta ,\beta )\) of the DCH equation analytic in any compact set \(\vert z\vert \le r\), with \(r>0\) and in particular when \(r=1\). Because of lemma 9 the solution \(v(z,\eta ,\beta )\) is differentiable with respect to the parameters \(\eta \) and \(\beta \).

We remark that \(v(z)\ne 0\) on the unit disc \(\overline{\mathbb {D}}\) because of the relation (81) between the analytic function G(z) and v(z) and the uniqueness of the minimizer \(\mu ^{\beta }_{HT}\) and of the analytic solution v(z) of (82).

To complete our proof of Theorem 2 we recover the explicit expression of \(\mu ^\beta _{HT}(\theta )\) from G(z) and v(z) using the Poisson representation formula (see for example [59, Chapter 1]):

$$\begin{aligned} \mu ^\beta _{HT}(\theta ) = -\frac{1}{2\pi } - \frac{\Re (i G(e^{i\theta }))}{\pi \beta } = \frac{1}{2\pi } + \frac{1}{\pi \beta } \Re \left. \left( \frac{zv'(z)}{v(z)}\right| _{z=e^{i\theta }}\right) \, . \end{aligned}$$
(99)

\(\square \)

Fig. 2
figure 2

The mean density of states \(\mu ^\beta _{HT}\) for different parameters

Full size image

In Fig. 2 we plotted the density of states of the Circular \(\beta \) ensemble in the high-temperature regime with potential \(V(z) = \eta \Re (z)\). To produce this picture and Fig. 1, we used extensively the NumPy [38], and matplotlib [39] libraries.

Remark 9

The Gross–Witten [35] and Baik-Deift-Johannson [11] solution is obtained by making the substitution \(\eta \rightarrow \beta \eta \) and \(\beta \rightarrow \infty \) in Eq. (42) which gives the functional

$$\begin{aligned} \mathcal {F}^{(\eta )}(\mu ):= \int \int \limits _{\mathbb {T}\times \mathbb {T}} \ln \left| \sin \left( \frac{\theta -\phi }{2}\right) \right| ^{-1}\mu (\textrm{d}\theta )\mu (\textrm{d}\phi )+2\eta \int _{\mathbb {T}}\cos (\theta )\mu (\textrm{d}\theta ). \end{aligned}$$

The minimizer is \(\mu (\theta )= \frac{1}{2\pi }\left( 1 - 2\eta \cos \theta \right) \) with \(0\le 2\eta \le 1\). In this case the first moment \(\lambda =-\eta \).

Added note. Independently, H. Spohn [63] discovered the connection between the Ablowitz–Ladik lattice and the circular \(\beta \) ensemble at high-temperature. He also calculated Generalized Gibbs Ensemble averaged field and currents and the associated hydrodynamic equations.