Abstract
We consider the general two-dimensional Zakharov-Shabat systems, which appear in application of the inverse scattering transform (IST) to an important class of nonlinear partial differential equations (PDEs) called integrable systems. We study their integrability in the meaning of differential Galois theory, i.e., their solvability by quadrature. It becomes a key for obtaining analytical expressions for solutions to the PDEs by using the IST. For a wide class of potentials, we prove that they are integrable in that meaning if and only if the potentials are reflectionless. It is well known that for such potentials particular solutions called n-solitons in the original PDEs are yielded by the IST.

Similar content being viewed by others
References
Ablowitz, M.J.: Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons. Cambridge University Press, Cambridge (2011)
Ablowitz, M.J., Fokas, A.S.: Complex Variables: Introduction and Applications, 2nd edn. Cambridge University Press, Cambridge (2003)
Ablowitz, M.J., Kaup, D.J., Newell, A.C., Segur, H.: Nonlinear-evolution equations of physical significance. Phys. Rev. Lett. 31, 125–127 (1973)
Ablowitz, M.J., Kaup, D.J., Newell, A.C., Segur, H.: Inverse scattering transform–fourier analysis for nonlinear problems. Stud. Appl. Math. 53, 249–315 (1974)
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrödinger Systems. Cambridge University Press, Cambridge (2004)
Ablowitz, M.J., Segur, H.: Solitons and Inverse Scattering Transform. SIAM, Philadelphia (1981)
Acosta-Humánez, P.B., Morales-Ruiz, J.J., Weil, J.-A.: Galoisian approach to integrability of Schrödinger equation. Rep. Math. Phys. 67, 305–374 (2011)
Ayoul, M., Zung, N.T.: Galoisian obstructions to non-Hamiltonian integrability. C. R. Math. Acad. Sci. Paris 348, 1323–1326 (2010)
Balser, W.: Formal Power Series and Linear Systems of Meromorphic Ordinary Differential Equations. Springer, New York (2000)
Blázquez-Sanz, D., Yagasaki, K.: Analytic and algebraic conditions for bifurcations of homoclinic orbits I: Saddle equilibria. J. Different. Equ. 253, 2916–2950 (2012)
Blázquez-Sanz, D., Yagasaki, K.: Galoisian approach for a Sturm-Liouville problem on the infinite interval. Methods Appl. Anal. 19, 267–288 (2012)
Coddington, E.A., Levinson, N.: Theory of Ordinary Differential Equations. McGraw-Hill, New York (1955)
Crespo, T., Hajto, Z.: Algebraic Groups and Differential Galois Theory. American Mathematical Society, Providence, RI (2011)
Deift, P., Trubowitz, E.: Inverse scattering on the line. Comm. Pure Appl. Math. 32, 121–251 (1979)
Gu, C., Hu, H., Zhou, Z.: Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry. Springer, Dordrecht, The Netherlands (2005)
Ilyashenko, Y., Yakovenko, S.: Lectures on Analytic Differential Equations. American Mathematical Society, Providence, RI (2008)
Kobayashi K., Yagasaki K.: Singular solitary waves in the KdV equation: rational solitons, positons and negatons, in preparation
Jiménez, S., Morales-Ruiz, J.J., Sánchez-Cauce, R., Zurro, M.-A.: Differential Galois theory and Darboux transformations for integrable systems. J. Geom. Phys. 115, 75–88 (2017)
Lamb, G.L., Jr.: Elements of Soliton Theory. John Wiley and Sons, New York (1980)
Matveev, V.B.: Positons: Slowly decreasing analogues of solitons. Theoret. and Math. Phys. 131, 483–497 (2002)
Morales-Ruiz J.J.: Differential Galois Theory and Non-Integrability of Hamiltonian Systems Birkhäuser, Basel,1999
Morales-Ruiz, J.J., Peris, J.M.: On a Galoisian approach to the splitting of separatrices. Ann. Fac. Sci. Toulouse Math. 8, 125–141 (1999)
Morales-Ruiz, J.J., Ramis, J.P.: Galosian obstructions to integrability of Hamiltonian systems. Methods Appl. Anal. 8, 33–96 (2001)
Newell, A.C.: Solitons in Mathematics and Physics. SIAM, Philadelphia (1985)
Ohmiya, M.: The inverse scattering problem for the Dirac operator and the modified Korteweg-de Vries equation. Osaka J. Math. 16, 249–269 (1979)
Olmedilla, E.: Multiple pole solutions of the nonlinear Schrödinger equation. Phys. D 25, 330–346 (1987)
van der Put, M., Singer, M.F.: Galois Theory of Linear Differential Equations. Springer, New York (2003)
Tsuru, H., Wadati, M.: The multiple pole solutions of the sine-Gordon equation. J. Phys. Soc. Japan 53, 2908–2921 (1984)
Wadati, M., Ohkuma, K.: Multiple-pole solutions of the modified Korteweg-de Vries equation. J. Phys. Soc. Japan 51, 2029–2035 (1982)
Yagasaki, K.: Horseshoes in two-degree-of-freedom Hamiltonian systems with saddle-centers. Arch. Ration. Mech. Anal. 154, 275–296 (2000)
Yagasaki, K.: Galoisian obstructions to integrability and Melnikov criteria for chaos in two-degree-of-freedom Hamiltonian systems with saddle centres. Nonlinearity 16, 2003–2012 (2003)
Yagasaki K.: Analytic and algebraic conditions for bifurcations of homoclinic orbits II: Reversible systems, J. Dynam. Differential Equations, to appear
Yagasaki, K., Yamanaka, S.: Nonintegrability of dynamical systems with homo- and heteroclinic orbits. J. Differen. Equa. 263, 1009–1027 (2017)
Yagasaki, K., Yamanaka, S.: Heteroclinic orbits and nonintegrability in two-degree-of-freedom Hamiltonian systems with saddle-centers. SIGMA Symmetry Integrability Geom. Methods Appl. 15, 049 (2019)
Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62–69 (1972)
Zakharov, V.E., Shabat, A.B.: Interaction between solitons in a stable medium. Sov. Phys. JETP 37, 823–828 (1973)
Acknowledgements
This work was partially supported by the JSPS KAKENHI Grant Number JP17H02859. The author thanks Katsuki Kobayashi for pointing out some errors in the computations of Sect. 4.2. He also appreciates the anonymous referees for their useful comments, which have improved this work.
Data Availability Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author has no conflict of interest to disclose.
Additional information
Communicated by J. Gier
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Relations on Scattering and Reflection Coefficients between (1.1) and (2.6)
Following Sect. 3d of [24] basically, we define the scattering and reflection coefficients for (2.6) (see also Sect. 9.1 of [1]). Equation (2.6) has the Jost solutions
Since
we have the relations
between the Jost solutions to (1.1) and (2.6) by (2.7). Define the scattering coefficients \({\hat{a}}(k)\) and \({\hat{b}}(k)\) for (2.6) as
like (2.5). Since
we have
like (4.2). From (A.2) we obtain
which are compared with (2.5) to yield
Moreover, for the reflection coefficients we have
where \({\hat{\rho }}(k)={\hat{b}}(k)/{\hat{a}}(k)\).
Appendix B. Condition for the Simplicity of Zeros of 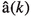
We consider the linear Schrödinger equation (2.6) and follow an approach in the proof of Theorem 1 of [14] to provide a necessary and sufficient condition for a zero of the scattering coefficient \({\hat{a}}(k)\) to be simple.
Let \({\hat{\phi }}(x;k),{\hat{\psi }}(x;k)\) be the Jost solutions satisfying (A.1). Since
by (A.1), we have
by (A.3). Hence,
On the other hand, since \({\hat{\psi }}(x;k)\) is a solution to (2.6), we immediately have
so that
Similarly, we have
Let \(k=k_0\) be a zero of \({\hat{a}}(k)\) with \(\textrm{Im}\,k_0>0\). Then by (A.1) and (A.3) we have
Hence, it follows from (B.2) and (B.3) that
which yield
along with (B.1). Using (A.3), we have the following proposition.
Proposition B .4
The zero \(k=k_0\) of \({\hat{a}}(k)\) with \(\textrm{Im}\,k_0>0\) is simple if and only if
Remark B .5
Assume that q(x) is real on \(\mathbb {R}\) and let \(k=k_0\) be a zero of \({\hat{a}}(k)\). Then \(k_0\) is purely imaginary as stated in Remark 5.4(ii) and we can take a real function on \(\mathbb {R}\) as \({\hat{\psi }}(x;k_0)\), which is a solution to (2.6) with \(k=k_0\) such that \(\lim _{x\rightarrow {\pm } 0}w(x)=0\). Hence, condition (B.4) holds. Thus, any zero of \({\hat{\psi }}(x;k_0)\) is simple, as shown in [14].
Appendix C. Computation of 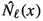 , \(\ell \) = \(1,\ldots ,n\), in a Simple Case
, \(\ell \) = \(1,\ldots ,n\), in a Simple Case
We consider the linear Schrödinger equation (2.6) and compute \({\hat{N}}_\ell (x)\), \(\ell =1,\ldots ,n\), which were defined in Sect. 4.2, when the zeros \(k=k_j\), \(j=1,\ldots ,n\), of \({\hat{a}}(k)\) are all simple.
Substituting (4.11) into (4.10) and setting \(k=k_\ell \), we have
where
Let
and let \(\Delta _\ell (x)\), \(\ell =1,\ldots ,n\), be the determinants of the matrices obtained by replacing the \(\ell \)th column of \(\Delta (x)\) with
Using Cramer’s rule, we represent the solution to the system of linear algebraic equations (C.1) as
In particular, \({\hat{N}}_\ell (x)\), \(\ell =1,\ldots ,n\), are rational functions of \(e^{2ik_jx}\), \(j=1,\ldots ,n\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yagasaki, K. Integrability of the Zakharov-Shabat Systems by Quadrature. Commun. Math. Phys. 400, 315–340 (2023). https://doi.org/10.1007/s00220-022-04610-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04610-8



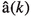
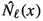 ,
,