Abstract
The rank 1 bosonic ghost vertex algebra, also known as the \(\beta \gamma \) ghosts, symplectic bosons or Weyl vertex algebra, is a simple example of a conformal field theory which is neither rational, nor \(C_2\)-cofinite. We identify a module category, denoted category \(\mathscr {F}\), which satisfies three necessary conditions coming from conformal field theory considerations: closure under restricted duals, closure under fusion and closure under the action of the modular group on characters. We prove the second of these conditions, with the other two already being known. Further, we show that category \(\mathscr {F}\) has sufficiently many projective and injective modules, give a classification of all indecomposable modules, show that fusion is rigid and compute all fusion products. The fusion product formulae turn out to perfectly match a previously proposed Verlinde formula, which was computed using a conjectured generalisation of the usual rational Verlinde formula, called the standard module formalism. The bosonic ghosts therefore exhibit essentially all of the rich structure of rational theories despite satisfying none of the standard rationality assumptions such as \(C_2\)-cofiniteness, the vertex algebra being isomorphic to its restricted dual or having a one-dimensional conformal weight 0 space. In particular, to the best of the authors’ knowledge this is the first example of a proof of rigidity for a logarithmic non-\(C_2\)-cofinite vertex algebra.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A vertex algebra is called logarithmic if it admits reducible yet indecomposable modules on which the Virasoro \(L_0\) operator acts non-semisimply, giving rise to logarithmic singularities in the correlation functions of the associated conformal field theory. There is a general consensus within the research community that many of the structures familiar from rational vertex algebras such as modular tensor categories [1] and, in particular, the Verlinde formula should generalise in some form to the logarithmic case, at least for sufficiently nice logarithmic vertex algebras. To this end, considerable work has been done on developing non-semisimple or non-finite generalisations of modular tensor categories [2,3,4]. However, progress has been hindered by a severe lack of examples, making it hard to come up with the right set of assumptions.
Ghost systems have been used extensively in theoretical physics and quantum algebra. Their applications include gauge fixing in string theory [5], Wakimoto free field realisations [6], quantum Hamiltonian reduction [7] and constructing the chiral de Rham complex on smooth manifolds [8]. Fermionic ghosts at central charge \(c=-2\) in the form of symplectic fermions have received a lot of attention in the past [9,10,11], due to their even subalgebra being one of the first known examples of a logarithmic vertex algebra. In particular, they are one of the few known examples of \(C_2\)-cofinite yet logarithmic vertex algebras [12,13,14]. This family also provides the only known examples of logarithmic \(C_2\)-cofinite vertex algebras with a rigid fusion product [12, 15].
Here we study the rank 1 bosonic ghosts at central charge \(c=2\). One of the motivations for studying this algebra is that it is simple enough to allow many quantities to be computed explicitly, while simultaneously being distinguished from better understood algebras in a number of interesting ways. For example, the bosonic ghosts are not \(C_2\)-cofinite and they were shown to be logarithmic by D. Ridout and the second author in [16], in which the module category to be studied here, denoted category \(\mathscr {F}\), was introduced. The main goals of [16] were determining the modular properties of characters in category \(\mathscr {F}\) and computing the Verlinde formula, using the standard module formalism pioneered by D. Ridout and T. Creutzig [17,18,19], to predict fusion product formulae. Later, D. Adamović and V. Pedić computed the dimensions of spaces of intertwining operators among the simple modules of category \(\mathscr {F}\) in [20], which turned out to match the predictions made by the Verlinde formula in [16]. Here we show that fusion (in the sense of the \(P(w)\)-tensor products of [21]) equips category \(\mathscr {F}\) with the structure of a braided tensor category. This, in particular, implies that category \(\mathscr {F}\) is closed under fusion, that is, the fusion product of any two objects in \(\mathscr {F}\) has no contributions from outside \(\mathscr {F}\) and is hence again an object in \(\mathscr {F}\). We derive explicit formulae for the decomposition of any fusion product into indecomposable direct summands, and we show that fusion is rigid and matches the Verlinde formula of [16].
A further source of interest for the bosonic ghosts is an exciting recent correspondence between four-dimensional super conformal field theory and two-dimensional conformal field theory [22], where the bosonic ghosts appear as one of the smaller examples on the two-dimensional side. Within this context the bosonic ghosts are the first member of a family of vertex algebras called the \({\mathcal {B}}_p\) algebras [23, 24]. The \({\mathcal {B}}_p\)-module categories are conjectured to satisfy interesting tensor categorical equivalences to the module category of the unrolled restricted quantum groups of \(\mathfrak {sl}_2\). It will be an interesting future problem to explore these categorical relations in more detail using the results of this paper.
The paper is organised as follows. In Section 2, we fix notation by giving an introduction to the bosonic ghost algebra and certain important automorphisms called conjugation and spectral flow; construct category \(\mathscr {F}\), the module category to be studied; and give two free field realisations of the bosonic ghost algebra. In Section 3 we begin the analysis of category \(\mathscr {F}\) as an abelian category by using the free field realisations of the bosonic ghost algebra to construct a logarithmic module, denoted \(\mathcal {P}\), on which the operator \(L_0\) has rank 2 Jordan blocks. We further show that \(\mathcal {P}\) is both an injective hull and a projective cover of the vacuum module (the bosonic ghost vertex algebra as a module over itself), and classify all projective modules in category \(\mathscr {F}\), thereby showing that category \(\mathscr {F}\) has sufficiently many projectives and injectives. In Section 4 we complete the analysis of category \(\mathscr {F}\) as an abelian category by classifying all indecomposable modules. In Section 5 we show that fusion equips category \(\mathscr {F}\) with the structure of a vertex tensor category, the main obstruction being showing that certain conditions, sufficient for the existence of associativity isomorphisms, hold. We further show that the simple projective modules of \(\mathscr {F}\) are rigid. In Section 6 we show that category \(\mathscr {F}\) is rigid and determine direct sum decompositions for all fusion products of modules in category \(\mathscr {F}\). In Appendix A we review an argument by Yang [25], which provides sufficient conditions for a technical property, called convergence and extension, required for the existence of associativity isomorphisms. We adjust the argument of Yang slightly to remove certain assumptions on module categories. This adjusted argument proves Theorem 5.7, which should also prove useful for the generalisations of category \(\mathscr {F}\) to other vertex algebras such as those constructed from affine Lie algebras at admissible levels.
2 Bosonic Ghost Vertex Algebra
In this section we introduce the bosonic ghost vertex algebra, along with its gradings and automorphisms. We define the module category which will be the focus of this paper. We also introduce useful tools for the classification of modules and calculation of fusion products, including two free field realisations. Note that we will make specific choices of conformal structure for all vertex algebras considered in this paper and so will not distinguish between vertex algebras, vertex operator algebras and conformal vertex algebras or other similar naming conventions.
2.1 The algebra and its automorphisms
The bosonic ghost vertex algebra (also called \(\beta \gamma \) ghosts) is closely related to the Weyl algebra. Their defining relations resemble each other and the Zhu algebra of the bosonic ghosts is isomorphic to the Weyl algebra. The bosonic ghosts are therefore also often referred to as the Weyl vertex algebra. Due to these connections, we first introduce the Weyl algebra and its modules before going on to consider the bosonic ghosts.
Definition 2.1
The (rank 1) Weyl algebra \(\mathfrak {A}\) is the unique unital associative algebra with two generators \(p,q,\) subject to the relations
and no additional relations beyond those required by the axioms of an associative algebra. The grading operator is the element \(N=qp\).
Definition 2.2
We define the following indecomposable \(\mathfrak {A}\)-modules:
-
(1)
\(\mathbb {C}[x]\), where \(p\) acts as \(\partial /\partial x\) and \(q\) acts as \(x\). Denote this module by \(\overline{\mathcal {V}}\).
-
(2)
\(\mathbb {C}[x]\), where \(p\) acts as \(x\) and \(q\) acts as \(-\partial /\partial x\). Denote this module by \({\mathsf {c}} \overline{\mathcal {V}}\).
-
(3)
\(\mathbb {C}[x,x^{-1}]x^{\lambda }\), \(\lambda \in \mathbb {C}\setminus \mathbb {Z}\), where \(p\) acts as \(\partial /\partial x\) and \(q\) acts as \(x\). Note that shifting \(\lambda \) by an integer yields an isomorphic module. Denote the mutually inequivalent isomorphism classes of these modules by \(\overline{\mathcal {W}_{\mu }}\), where \(\mu \in \mathbb {C}/\mathbb {Z}\), \(\mu \ne \mathbb {Z}\) and \(\lambda \in \mu \).
-
(4)
\(\mathbb {C}[x,x^{-1}]\), where \(p\) acts as \(\partial /\partial x\) and \(q\) acts as \(x\). Denote this module by \(\overline{\mathcal {W}_{0}^+}\). This module is uniquely characterised by the non-split exact sequence
$$\begin{aligned} 0 \longrightarrow \overline{\mathcal {V}} \overset{}{\longrightarrow } \overline{\mathcal {W}_{0}^{+}} \overset{}{\longrightarrow } {\mathsf {c}} \overline{\mathcal {V}} \longrightarrow 0. \end{aligned}$$(2.2) -
(5)
\(\mathbb {C}[x,x^{-1}]\), where \(p\) acts as \(x\) and \(q\) acts as \(-\partial /\partial x\). Denote this module by \(\overline{\mathcal {W}_{0}^-}\). This module is uniquely characterised by the non-split exact sequence
$$\begin{aligned} 0 \longrightarrow {\mathsf {c}} \overline{\mathcal {V}} \overset{}{\longrightarrow } \overline{\mathcal {W}_{0}^{-}} \overset{}{\longrightarrow } \overline{\mathcal {V}} \longrightarrow 0. \end{aligned}$$(2.3)
A module on which \(N=qp\) acts semisimply is called a weight module. Note that \(N\) acts semisimply on all modules above.
Proposition 2.3
(Block [26]). Any simple \(\mathfrak {A}\)-module on which \(N\) acts semisimply is isomorphic to one of those listed in Definition 2.2, Parts (1) – (3).
Definition 2.4
The bosonic ghost vertex algebra \(\mathsf {G}\) is the unique vertex algebra strongly generated by two fields \(\beta ,\gamma \), subject to the defining operator product expansions
and no additional relations beyond those required by vertex algebra axioms.
The bosonic ghost vertex algebra admits a one-parameter family of conformal structures. Here we choose the Virasoro field (or energy momentum tensor) to be
thus determining the central charge to be \(c=2\) and the conformal weights of \(\beta \) and \(\gamma \) to be \(1\) and \(0\), respectively. The bosonic ghost fields can thus be expanded as formal power series with the mode indexing chosen to reflect the conformal weights.
The operator product expansions of \(\beta \) and \(\gamma \) fields imply that their modes generate the bosonic ghost Lie algebra \(\mathfrak {G}\) satisfying the Lie brackets
where \({\mathbf {1}}\) is central and acts as the identity on any \(\mathsf {G}\)-module, since it corresponds to the identity (or vacuum) field.
Within \(\mathsf {G}\) there is a rank 1 Heisenberg vertex algebra generated by the field
A quick calculation reveals that \(J\) is a free boson of Lorentzian signature, not a conformal primary, and that \(J\) defines a grading on \(\beta \) and \(\gamma \) called ghost weight (or ghost number), that is,
Note that for the distinguished elements \(\beta ,\ \gamma ,\ J,\) and \(T\) we suppress the field map symbol \(Y:\mathsf {G}\rightarrow \mathsf {G}[\![z,z^{-1} ]\!]\). For generic elements \(A\in \mathsf {G}\) we will use both \(Y(A,z)\) and \(A(z)\) to denote the field corresponding to \(A\), depending on what is easier to read in the given context.
We make frequent use of two automorphisms of \(\mathfrak {G}\). The first is spectral flow, which acts on the \(\mathfrak {G}\) modes as
The second is conjugation which is given by
These automorphisms satisfy the relation
At the level of fields, these automorphisms act as
The primary utility of the conjugation and spectral flow automorphisms lies in constructing new modules from known ones through twisting.
Definition 2.5
Let \(\mathcal {M}\) be a \(\mathsf {G}\)-module and \(\alpha \) an automorphism. The \(\alpha \)-twisted module \(\alpha \mathcal {M}\) is defined to be \(\mathcal {M}\) as a vector space, but with the action of \(\mathsf {G}\) redefined to be
where the action of \(\mathsf {G}\) on the right-hand side is the original untwisted action of \(\mathsf {G}\) on \(\mathcal {M}\).
Remark
Due to being algebra automorphisms, spectral flow and conjugation twists both define exact covariant functors. Further, the respective ghost and conformal weights \([j,h ]\) of a vector \(m\) in a \(\mathsf {G}\)-Module \(\mathcal {M}\) transform as follows under conjugation and spectral flow.
Since \({\mathsf {c}}^2 \beta _n=-\beta _n\) and \({\mathsf {c}}^2 \gamma _n=-\gamma _n\), we have \({\mathsf {c}}^2 \mathcal {M}\cong \mathcal {M}\), for any \(\mathsf {G}\)-module \(\mathcal {M}\). We shall later see that spectral flow has infinite order and thus the relations (2.12) imply that at the level of the module category spectral flow and conjugation generate the infinite dihedral group.
Theorem 2.6
For any \(\mathsf {G}\)-modules \(\mathcal {M}\) and \(\mathcal {N}\), conjugation and spectral flow are compatible with fusion products in the following sense.
The behaviour of spectral flow under fusion was proven for vertex algebras with finite dimensional conformal weight spaces in [27, Proposition 2.4]. However, the proof does not rely on this fact, and so we can apply the result to \(\mathsf {G}\)-modules, as in [20, Proposition 3.1]. The behaviour of conjugation under fusion was proven in [20, Proposition 2.1], where conjugation was denoted by \(\sigma \) and spectral flow by \(\rho _{\ell }\). There the automorphism g corresponds to \(\sigma ^{-1} {\mathsf {c}}= {\mathsf {c}}\sigma \) here. These formulae mean that the fusion of modules twisted by spectral flow is determined by the fusion of untwisted modules, a simplification we shall make frequent use of.
2.2 Module category
Every \(\mathsf {G}\)-module is a \(\mathfrak {G}\)-module, however, the converse is not true (consider for example the adjoint \(\mathfrak {G}\)-module). The category of smooth \(\mathfrak {G}\)-modules consists of precisely those modules which are also \(\mathsf {G}\)-modules. Such modules are also commonly called weak \(\mathsf {G}\)-modules and we shall use these terms interchangeably. Unfortunately the category of all smooth modules is at present too unwieldy to analyse and so we must invariably consider some subcategory.
In this section we define the module category, which we believe to be the natural one from the perspective of conformal field theory, because it is compatible with the following two necessary conformal field theoretic conditions.
-
(1)
Non-degeneracy of \(n\)-point conformal blocks (chiral correlation functions) on the sphere.
-
(2)
Well-definedness of conformal blocks at higher genera.
Condition (1) can be reduced to the non-degeneracy of two and three-point conformal blocks. The non-degeneracy of two-point conformal blocks requires the module category to be closed under taking restricted duals, while non-degeneracy of three-point conformal blocks requires the module category to be closed under fusion (as, for example, constructed by the \(P(w)\)-tensor product of Huang-Lepowsky-Zhang). Conformal blocks at higher genera can be constructed from those on the sphere provided there is a well-defined action of the modular group on characters. Thus Condition (2) requires characters to be well-defined, that is, for all modules to decompose into direct sums of finite dimensional simultaneous generalised \(J_0\) and \(L_0\) eigenspaces. On any simple such module both \(L_0\) and \(J_0\) will act semisimply. Further, the action of \(J_0\) is semisimple on a fusion product if \(J_0\) acts semisimply on both factors of the product. We can therefore restrict ourselves to a category of \(J_0\)-semisimple modules without endangering closure under fusion. We cannot, however, assume that \(L_0\) will act semisimply in general.
The main tool for identifying and classifying vertex operator algebra modules is Zhu’s algebra. Sadly Zhu’s algebra is only sensitive to modules containing vectors annihilated by all positive modes. Any simple such module is a simple module in the category called \(\mathscr {R}\) below. We will see that \(\mathscr {R}\) is closed under taking restricted duals, however, as can be seen later in Section 6, category \(\mathscr {R}\) is not closed under fusion. Further, it was shown in [16] that the action of the modular group does not close on its characters. Thus a larger category is needed, which will be denoted \(\mathscr {F}\) below. It was shown in [16] that the action of the modular group closes on the characters of \(\mathscr {F}\) and strong evidence was presented that fusion does as well. We will see in Section 6 that category \(\mathscr {F}\) is indeed closed under fusion and that it satisfies numerous other nice properties.
The definition of the module categories mentioned above requires the following choice of parabolic triangular decomposition of \(\mathfrak {G}\).

This decomposition is parabolic, because \(\mathfrak {G}^0\) is not abelian and thus not a choice of Cartan subalgebra. The role of the Cartan subalgebra will instead be played by \({{\,\mathrm{span}\,}}\{{\mathbf {1}}, J_0\}\), which is technically a subalgebra of the completion of \({\mathsf {U}}\left( \mathfrak {G} \right) \) rather than \(\mathfrak {G}\).
Definition 2.7
-
(1)
Let \(\mathsf {G}\)-WMod be the category of smooth weight \(\mathfrak {G}\)-modules, that is the category whose objects are all smooth (or weak) \(\mathsf {G}\)-modules \(\mathcal {M}\) (we follow the conventions of [28] regarding smooth modules) which in addition satisfy that \(J_0\) acts semisimply and whose arrows are all \(\mathfrak {G}\)-module homomorphisms.
-
(2)
Let \(\mathscr {R}\) be the full subcategory of \(\mathsf {G}\)-WMod consisting of those modules \(\mathcal {M}\in \mathsf {G}\)-WMod satisfying
-
\(\mathcal {M}\) is finitely generated,
-
\(\mathfrak {G}^+\) acts locally nilpotently, that is, for all \(m\in \mathcal {M}\), \({\mathsf {U}}\left( \mathfrak {G}^+ \right) m\) is finite dimensional.
-
-
(3)
Let \(\mathscr {F}\) be the full subcategory of \(\mathsf {G}\)-WMod consisting all finite length extensions of arbitrary spectral flows of modules in \(\mathscr {R}\) with real \(J_0\) weights.
The \(\mathfrak {A}\)-modules of Definition 2.2 induce to modules in category \(\mathscr {R}\).
Definition 2.8
Let \(\mathcal {M}\) be a \(\mathfrak {A}\)-module, then we induce \(\mathcal {M}\) to a \(\mathsf {G}\)-module \({{\,\mathrm{Ind}\,}}^{}_{} \mathcal {M}\) in \(\mathscr {R}\) by having \(\mathfrak {G}^+\) act trivially on \(\mathcal {M}\), \(\beta _0\) and \(\gamma _0\) act as \(-p\) and \(q\), respectively, and \(\mathfrak {G}^-\) act freely. We denote
-
(1)
\(\mathcal {V}\cong {{\,\mathrm{Ind}\,}}^{}_{} \overline{\mathcal {V}}\), the vacuum module or bosonic ghost vertex algebra as a module over itself.
-
(2)
\({\mathsf {c}} \mathcal {V}\cong \sigma ^{-1} \mathcal {V}\cong {{\,\mathrm{Ind}\,}}^{}_{} {\mathsf {c}} \overline{\mathcal {V}}\), the conjugation twist of the vacuum module.
-
(3)
\(\mathcal {W}_{\lambda }\cong {{\,\mathrm{Ind}\,}}^{}_{} \overline{\mathcal {W}_{\lambda }}\) with \(\lambda \in \mathbb {C}/\mathbb {Z}\), \(\lambda \ne \mathbb {Z}\).
-
(4)
\(\mathcal {W}_{0}^\pm \cong {{\,\mathrm{Ind}\,}}^{}_{} \overline{\mathcal {W}_{0}^\pm }\).
Note that due to the simple nature of the \(\mathfrak {G}\) commutation relations (2.7) \({{\,\mathrm{Ind}\,}}^{}_{} \mathcal {M}\) is simple whenever \(\mathcal {M}\) is, that is, the modules listed in parts (1) – (3) are simple.
Proposition 2.9
-
(1)
Any simple module in \(\mathscr {R}\) is isomorphic to one of those listed in Parts (1) – (3) of Definition 2.8.
-
(2)
Any simple module in \(\mathscr {F}\) is isomorphic to one of the following mutually inequivalent modules.
$$\begin{aligned} \sigma ^{\ell } \mathcal {V},\qquad \sigma ^{\ell } \mathcal {W}_{\lambda },\qquad \ell \in \mathbb {Z},\ \lambda \in \mathbb {R}/\mathbb {Z},\ \lambda \ne \mathbb {Z}. \end{aligned}$$(2.18) -
(3)
The conjugation twists of simple modules in \(\mathscr {F}\) satisfy
$$\begin{aligned} {\mathsf {c}} \sigma ^{\ell } \mathcal {V}\cong \sigma ^{-1-\ell } \mathcal {V},\qquad {\mathsf {c}} \sigma ^{\ell } \mathcal {W}_{\lambda }\cong \sigma ^{-\ell } \mathcal {W}_{-\lambda },\qquad \ell \in \mathbb {Z},\ \lambda \in \mathbb {R}/\mathbb {Z},\ \lambda \ne \mathbb {Z}. \end{aligned}$$(2.19) -
(4)
The indecomposable modules \(\mathcal {W}_{0}^{\pm }\) satisfy the non-split exact sequences
$$\begin{aligned}&0 \longrightarrow \mathcal {V} \overset{}{\longrightarrow } \mathcal {W}_{0}^{+} \overset{}{\longrightarrow } \sigma ^{-1} \mathcal {V} \longrightarrow 0, \end{aligned}$$(2.20a)$$\begin{aligned}&0 \longrightarrow \sigma ^{-1} \mathcal {V} \overset{}{\longrightarrow } \mathcal {W}_{0}^{-} \overset{}{\longrightarrow } {\mathcal {V}} \longrightarrow 0. \end{aligned}$$(2.20b)
This proposition was originally given in [16, Proposition 1], however, we give it again here for completeness.
Proof
To show Part (1), we use that \(\mathscr {R}\) is precisely the category of weight modules visible to Zhu’s algebra [29]. That is, the simple modules in \(\mathscr {R}\) are in bijection with simple weight modules over the Zhu algebra. Further the Zhu algebra of \(\mathsf {G}\) is isomorphic to the Weyl algebra \(\mathfrak {A}\). Therefore the simple modules of \(\mathscr {R}\) are classified by the simple modules given in Proposition 2.3. Specifically, every simple module in \(\mathscr {R}\) is isomorphic to the simple quotient of an induction of on of the simple modules listed in 2.2, that is, the module listed in Parts (1) – (3) of Definition 2.8.
Part (2) now immediately follows from Part (1), because, by definition, the simple modules of \(\mathscr {F}\) are just spectral flows of those in \(\mathscr {R}\).
To show Part (3), consider first the case when \(\ell =0\), where the identification can be easily verified by direct computation. The identities for general \(\ell \) then follow from the dihedral group relation (2.12).
Finally Part (4) follows from the exact sequences in Definition 2.2 and the fact that induction preserves exactness. Restricting to the conformal weight 0 spaces of these induced sequences recovers the initial exact sequences for modules over the Weyl algebra. So since the Weyl algebra sequences were non-split the induced sequences must be too. \(\square \)
We shall show in Proposition 3.2 that, up to spectral flow twists, the indecomposable modules \(\mathcal {W}_{0}^\pm \) are the only indecomposable length 2 extensions of spectral flows of the vacuum module. In Section 4 we extend the indecomposable modules \(\mathcal {W}_{0}^\pm \) to infinite families of indecomposable modules.
2.3 Restricted duals
As mentioned above, conformal field theories require their representation categories to be closed under taking restricted duals. They are also an essential tool for the computation of fusion products using the Huang-Lepowsky-Zhang (HLZ) double dual construction [21, Part IV], also called the P(w)-tensor product, and so we record the necessary definitions here.
Definition 2.10
Let \(\mathcal {M}\) be a weight \(\mathsf {G}\)-module. The restricted dual (or contragredient) module is defined to be

where the action of \(\mathsf {G}\) is characterised by
and where \(Y(A,z)^{{{\,\mathrm{opp}\,}}}\) is given by the formula
Proposition 2.11
The vertex algebra \(\mathsf {G}\) and its modules have the following properties.
-
(1)
The modes of the generating fields and the Heisenberg field satisfy
$$\begin{aligned} \beta _{n}^{{{\,\mathrm{opp}\,}}} = -\beta _{-n}, \qquad \gamma _{n}^{{{\,\mathrm{opp}\,}}} = \gamma _{-n}, \qquad J_{n}^{{{\,\mathrm{opp}\,}}} = \delta _{n,0} - J_{-n}. \end{aligned}$$(2.24) -
(2)
The restricted duals of spectral flows of the indecomposable modules in Definition 2.8 can be identified as
$$\begin{aligned} \left( \sigma ^{\ell } \mathcal {V} \right) ' \cong \sigma ^{-1-\ell } \mathcal {V},\qquad \left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) ' \cong \sigma ^{-\ell } \mathcal {W}_{-\lambda },\qquad \left( \sigma ^{\ell } \mathcal {W}_{0}^\pm \right) ' \cong \sigma ^{-\ell } \mathcal {W}_{0}^\pm . \end{aligned}$$(2.25) -
(3)
Denote by \({}^*\) the composition of twisting by \({\mathsf {c}}\) and taking the restricted dual, then
$$\begin{aligned} \left( \sigma ^{\ell } \mathcal {V} \right) ^*\cong \sigma ^{\ell } \mathcal {V},\qquad \left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) ^*\cong \sigma ^{\ell } \mathcal {W}_{\lambda },\qquad \left( \sigma ^{\ell } \mathcal {W}_{0}^\pm \right) ^*\cong \sigma ^{\ell } \mathcal {W}_{0}^\mp . \end{aligned}$$(2.26) -
(4)
Let \(\mathcal {A},\mathcal {B}\in \mathscr {F}\) and \(\ell \in \mathbb {Z}\), then the homomorphism and first extension groups satisfy
$$\begin{aligned} {{\,\mathrm{Hom}\,}}\left( \mathcal {A},\mathcal {B} \right)&={{\,\mathrm{Hom}\,}}\left( {\mathsf {c}} \mathcal {A},{\mathsf {c}} \mathcal {B} \right) = {{\,\mathrm{Hom}\,}}\left( \sigma ^{\ell } \mathcal {A},\sigma ^{\ell } \mathcal {B} \right) ={{\,\mathrm{Hom}\,}}\left( \mathcal {B}',\mathcal {A}' \right) ={{\,\mathrm{Hom}\,}}\left( \mathcal {B}^*,\mathcal {A}^* \right) ,\qquad \quad \nonumber \\ {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {A},\mathcal {B} \right)&={{\,\mathrm{Ext}\,}}^{}\left( {\mathsf {c}} \mathcal {A},{\mathsf {c}} \mathcal {B} \right) = {{\,\mathrm{Ext}\,}}^{}\left( \sigma ^{\ell } \mathcal {A},\sigma ^{\ell } \mathcal {B} \right) ={{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}',\mathcal {A}' \right) ={{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^*,\mathcal {A}^* \right) . \end{aligned}$$(2.27)
Proof
Part (1) follows immediately from Definition 2.10.
Part (2): Since \(\sigma ^{\ell } \mathcal {V}\) is simple, \(\left( \sigma ^{\ell } \mathcal {V} \right) '\) is too, due to taking duals being an invertible exact contravariant functor. Further, by the action given in Definition 2.10 it is easy to see that \(\beta _n,\ n\ge \ell +1\) and \(\gamma _m,\ m\ge -\ell \) act locally nilpotently and therefore \(\left( \sigma ^{\ell } \mathcal {V} \right) '\) is an object of both \(\sigma ^{-\ell } \mathscr {R}\) and \(\sigma ^{-1-\ell } \mathscr {R}\). Thus, \(\left( \sigma ^{\ell } \mathcal {V} \right) ' \cong \sigma ^{-1-\ell } \mathcal {V}\).
Similarly, since \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) is simple, \(\left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) '\) is too. The modes \(\beta _n,\ n\ge \ell +1\) and \(\gamma _m,\ m\ge 1-\ell \) act locally nilpotently and therefore \(\left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) '\) is an object of \(\sigma ^{-\ell } \mathscr {R}\). Further, for \(J_0\) homogeneous \(m\in \sigma ^{\ell } \mathcal {W}_{\lambda }\) and \(\psi \in \left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) '\), consider
Thus, \(\left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) ' \cong \sigma ^{-\ell } \mathcal {W}_{-\lambda }.\)
Finally, the duals of \(\sigma ^{\ell } \mathcal {W}_{0}^\pm \) follow from that fact that the duality functor is exact and contravariant, and by applying it to the exact sequences (2.20).
Part (3) follows from composing the formulae of Part (2) with the conjugation twist formulae of Proposition 2.9.
Part (4) follows from \({\mathsf {c}}\), \(\sigma \) and \({}'\) being exact invertible functors, the first two covariant and the last contravariant. \(\square \)
2.4 Free field realisation
We present two embeddings of \(\mathsf {G}\) into a rank 1 lattice algebra constructed from a rank 2 Heisenberg vertex algebra. We refer to [30] for a comprehensive discussion of Heisenberg and lattice vertex algebras.
Let \(\mathsf {H}\) be the rank 2 Heisenberg vertex algebra with choice of generating fields \(\psi ,\theta \) normalised such that they satisfy the defining operator product expansions
By a slight abuse of notation we also use \(\psi \) and \(\theta \) to denote a basis of a rank 2 lattice \(L_\mathbb {Z}={{\,\mathrm{span}\,}}_{\mathbb {Z}}\lbrace \psi ,\theta \rbrace \) with symmetric bilinear lattice form corresponding to the above operator product expansions, that is \(\left( \psi ,\psi \right) =-\left( \theta ,\theta \right) =1\) and \((\psi ,\theta )=0\). Let \(L= {{\,\mathrm{span}\,}}_{\mathbb {R}}\lbrace \psi ,\theta \rbrace \) be the extension of scalars of \(L_{\mathbb {Z}}\) by \(\mathbb {R}\), \(K={{\,\mathrm{span}\,}}_{\mathbb {Z}}\lbrace \psi +\theta \rbrace \) the indefinite rank 1 lattice generated by \(\psi +\theta \) and  . We denote the Fock spaces of \(\mathsf {H}\) by \(\mathcal {F}_{\lambda },\ \lambda \in L\), where the zero mode of a Heisenberg vertex algebra field \(a(z),\ a\in L\) acts as scalar multiplication by \(\left( a,\lambda \right) \). To any vector \(p|\lambda \rangle \) of \(\mathcal {F}_{\lambda }\), where \(p\) is any product of negative index modes of \(\psi ,\theta \), we assign the vertex operators \(\mathrm {V}\left( p|\lambda \rangle ,z \right) :\mathcal {F}_{\mu }\rightarrow \mathcal {F}_{\mu + \lambda }[\![z,z^{-1} ]\!]z^{\left( \lambda ,\mu \right) }\) given by the expansion
. We denote the Fock spaces of \(\mathsf {H}\) by \(\mathcal {F}_{\lambda },\ \lambda \in L\), where the zero mode of a Heisenberg vertex algebra field \(a(z),\ a\in L\) acts as scalar multiplication by \(\left( a,\lambda \right) \). To any vector \(p|\lambda \rangle \) of \(\mathcal {F}_{\lambda }\), where \(p\) is any product of negative index modes of \(\psi ,\theta \), we assign the vertex operators \(\mathrm {V}\left( p|\lambda \rangle ,z \right) :\mathcal {F}_{\mu }\rightarrow \mathcal {F}_{\mu + \lambda }[\![z,z^{-1} ]\!]z^{\left( \lambda ,\mu \right) }\) given by the expansion
where \(Y(p|0 \rangle ,z)\) is the field associated to \(p|0 \rangle \in \mathsf {H}\), and where \({\mathsf {e}}^{\lambda }\in \mathbb {C}[L]\) is the basis element in the group algebra of \(L\) corresponding to \(\lambda \in L\) and satisfies the relations
We abbreviate \(\mathrm {V}\left( |\lambda \rangle ,z \right) \) as \(\mathrm {V}_{\lambda }\left( z \right) \). It is well known that, after specialising the formal variables to complex numbers satisfying \(|z_1|>|z_2|\) and \(|z_2|>|z_1-z_2|\), the product and iterate of vertex operators are equal when evaluated on Fock spaces, that is,
Finally, let \(\mathsf {V}_{K}\) be the lattice vertex algebra extension of \(\mathsf {H}\) along \(K\). The lattice modules
are simple modules for \(\mathsf {V}_{K}\). It will occasionally be convenient to label the lattice modules by a representative \(\lambda \in \Lambda \) rather than the coset itself, that is \({\mathbb {F}}_{\lambda } = {\mathbb {F}}_{\Lambda }\). Note also that our notation differs from conventions common in theoretical physics literature. There, for \(a\in L\), \(\mathrm {V}_{a}\left( z \right) \) would be denoted by \({} {:} {}{{\mathsf {e}}^{a(z)}} {:}\) and \(a(z)\) by \(\partial a(z)\).
Proposition 2.12
-
(1)
The assignment
$$\begin{aligned} \beta (z)\mapsto \mathrm {V}_{\theta +\psi }\left( z \right) ,\qquad \gamma (z)\mapsto {} {:} {}{\psi (z)\mathrm {V}_{-\theta -\psi }\left( z \right) } {:} \end{aligned}$$(2.34)induces an embedding \(\phi _1:\mathsf {G}\rightarrow \mathsf {V}_{K}\). Restricting to the image of this embedding, \(\mathsf {V}_{K}\)-modules can be identified with \(\mathsf {G}\)-modules as
$$\begin{aligned} {\mathbb {F}}_{\ell \psi } \cong \sigma ^{\ell +1} \mathcal {W}_{0}^-, \qquad {\mathbb {F}}_{\Lambda } \cong \sigma ^{\left( \Lambda ,\psi +\theta \right) +1} \mathcal {W}_{\left( \Lambda ,\psi \right) },\quad \Lambda \in L/K, \ \left( \Lambda ,\psi +\theta \right) \in \mathbb {Z}\ \text {and}\ \left( \Lambda ,\psi \right) \ne \mathbb {Z}, \end{aligned}$$(2.35)where \(\left( \Lambda ,\psi \right) \) is the coset in \(\mathbb {R}/\mathbb {Z}\) formed by pairing all representatives of \(\Lambda \) with \(\psi \).
-
(2)
The assignment
$$\begin{aligned} \beta (z)\mapsto {} {:} {}{\psi (z)\mathrm {V}_{\theta +\psi }\left( z \right) } {:} ,\qquad \gamma (z)\mapsto \mathrm {V}_{-\theta -\psi }\left( z \right) \end{aligned}$$(2.36)induces an embedding \(\phi _2:\mathsf {G}\rightarrow \mathsf {V}_{K}\). Restricting to the image of this embedding, \(\mathsf {V}_{K}\)-modules can be identified with \(\mathsf {G}\)-modules as
$$\begin{aligned}&{\mathbb {F}}_{\ell \psi } \cong \sigma ^{\ell } \mathcal {W}_{0}^+, \qquad {\mathbb {F}}_{\Lambda } \cong \sigma ^{\left( \Lambda ,\psi +\theta \right) } \mathcal {W}_{\left( \Lambda ,\psi \right) },\nonumber \\&\Lambda \in L/K, \ \left( \Lambda ,\psi +\theta \right) \in \mathbb {Z}\;\; \text {and}\;\; \left( \Lambda ,\psi \right) \ne \mathbb {Z}, \end{aligned}$$(2.37)where \(\left( \Lambda ,\psi \right) \) is the coset in \(\mathbb {R}/\mathbb {Z}\) formed by pairing all representatives of \(\Lambda \) with \(\psi \).
The embeddings are well known and the identifications of \(\mathsf {V}_{K}\)-modules with \(\mathsf {G}\)-modules follow by comparing characters and was shown in [31, Proposition 4.7] and [20, Proposition 4.1].
Remark
It is well known that there is a natural choice of semisimple module category for the vertex algebra \(\mathsf {V}_{K}\) for which the lattice modules \({\mathbb {F}}_{\Lambda }\), \(\Lambda \in K^*/K\) give an exhaustive list of representatives for simple isomorphism classes of simple objects. Fusion products furnish this module category with the structures of a braided monoidal category which is isomorphic to the category of finite dimensional \(K^{*}/K\) graded vector spaces. The braiding and associativity isomorphisms \(\Omega ,F\) form abelian 3-cocycles whose cohomology classes classify the inequivalent braiding and associativity structures. In the notation of [30, Chapter 12], \(\Omega ,F\) can be expressed in terms of the pairing \(\left( \ ,\ \right) \) on \(L\) and a choice of section \(s:K^{*}/K \rightarrow K^{*}\), that is, a right inverse to the canonical projection map \(\pi : K^{*}\rightarrow K^{*}/K\) such that \(\pi \circ s = {{\,\mathrm{id}\,}}_{K^{*}/K}\) (different choices of \(s\) yield cohomologous results)
Note that in [30] it is assumed that \(K\) is full rank in \(L\) and hence \(K^*/K\) is a finite group, however this assumption is not needed for the cohomological arguments regarding the braiding and associativity structures. For a general lattice, F includes an additional factor dependent on a choice of lattice two-cocycle (unique up to cohomology). Fortunately as K is rank one and even this 2-cocycle can be chosen to be trivial. Here \(K^*\cong \mathbb {Z}\times \mathbb {R}\), where \(\mathbb {Z}\) corresponds to the integer span of \(\psi -\theta \) and \(\mathbb {R}\) to the real span of \(K\). Hence \(K^*/K\cong \mathbb {Z}\times \mathbb {R}/\mathbb {Z}\). If we denote by \({\overline{x}}\in [0,1)\) the unique representative of \(x\in \mathbb {R}/\mathbb {Z}\) in the half open unit interval, then a choice of section \(s\) is given by the formula
Resulting in
Redefining \((\Omega ,F)\) by rescaling by the coboundary \(dk(\alpha ,\beta ,\gamma )=({\mathsf {e}}^{{\mathfrak {i}}\pi \beta _1 \overline{\alpha _2}-{\mathfrak {i}}\pi \alpha _1\overline{\beta _2}},{\mathsf {e}}^{-{\mathfrak {i}}\pi \alpha _1\left( \overline{\beta _2+\gamma _2}-\overline{\beta _2}-\overline{\gamma _2} \right) })\) of the 2-cochain \(k(\alpha ,\beta )={\mathsf {e}}^{-{\mathfrak {i}}\pi \alpha _1\overline{\beta _2}}\) (see [30, Chapter 12] for details regarding coboundary conditions) yields
and we see that the intertwining operators of \(\mathsf {V}_{K}\) lattice modules can be normalised in such a way as to have trivial associators.
Theorem 2.13
-
(1)
Let \({\mathcal {S}}_{1}={{\,\mathrm{Res}\,}}\mathrm {V}_{\psi }\left( z \right) \), then \(\ker \left( {\mathcal {S}}_{1} :\mathsf {V}_{K}\rightarrow {\mathbb {F}}_{\psi } \right) ={{\,\mathrm{im}\,}}\phi _1\), where \(\phi _1: \mathsf {G}\rightarrow \mathsf {V}_{K}\) is the embedding of Proposition 2.12.(1), that is, \({\mathcal {S}}_{1}\) is a screening operator for the free field realisation \(\phi _1\) of \(\mathsf {G}\). Further the sequence
$$\begin{aligned} {\cdots \overset{{\mathcal {S}}_{1}}{\longrightarrow } {\mathbb {F}}_{-\psi } \overset{{\mathcal {S}}_{1}}{\longrightarrow } {\mathbb {F}}_{0} \overset{{\mathcal {S}}_{1}}{\longrightarrow } {\mathbb {F}}_{\psi } \overset{{\mathcal {S}}_{1}}{\longrightarrow } \cdots } \end{aligned}$$(2.42)is exact and is therefore a Felder complex.
-
(2)
Let \({\mathcal {S}}_{2}={{\,\mathrm{Res}\,}}\mathrm {V}_{-\psi }\left( z \right) \), then \(\ker \left( {\mathcal {S}}_{2} :\mathsf {V}_{K}\rightarrow {\mathbb {F}}_{-\psi } \right) ={{\,\mathrm{im}\,}}\phi _2\), where \(\phi _2: \mathsf {G}\rightarrow \mathsf {V}_{K}\) is the embedding of Proposition 2.12.(2), that is, \({\mathcal {S}}_{2}\) is a screening operator for the free field realisation \(\phi _2\) of \(\mathsf {G}\). Further the sequence
$$\begin{aligned} {\cdots \overset{{\mathcal {S}}_{2}}{\longrightarrow } {\mathbb {F}}_{\psi } \overset{{\mathcal {S}}_{2}}{\longrightarrow } {\mathbb {F}}_{0} \overset{{\mathcal {S}}_{2}}{\longrightarrow } {\mathbb {F}}_{-\psi } \overset{{\mathcal {S}}_{2}}{\longrightarrow } \cdots } \end{aligned}$$(2.43)is exact and is therefore a Felder complex.
Proof
We prove part (1) only, as part (2) follows analogously. The operator product expansion of \(\mathrm {V}_{\psi }\left( z \right) \) with the images of \(\beta \) and \(\gamma \) in \(\mathsf {V}_{K}\) are
which are total derivatives in \(z\) implying that \({\mathcal {S}}_{1}={{\,\mathrm{Res}\,}}\mathrm {V}_{\psi }\left( z \right) \) is a screening operator and that \({{\,\mathrm{im}\,}}\phi _1\subset \ker {\mathcal {S}}_{1}\). Therefore, \({\mathcal {S}}_{1}\) commutes with \(\mathsf {G}\) and hence defines a \(\mathsf {G}\)-module map \({\mathbb {F}}_{0}\rightarrow {\mathbb {F}}_{\psi }\). The identification (2.35) implies \({\mathbb {F}}_{0}\cong \sigma ^{} \mathcal {W}_{0}^-\) and \({\mathbb {F}}_{\psi }\cong \sigma ^{2} \mathcal {W}_{0}^-\). By comparing composition factors we see that the kernel must be either \({{\,\mathrm{im}\,}}\phi _1\cong \mathcal {V}\) or all of \({\mathbb {F}}_{0}\), so it is sufficient to show that the map \({\mathcal {S}}_{1}:{\mathbb {F}}_{0}\rightarrow {\mathbb {F}}_{\psi }\) is non-trivial. A quick calculation reveals that
and thus \({\mathcal {S}}_{1}\) is not trivial. By comparing the composition factors of the sequence (2.42) we also see that the sequence is an exact complex if each arrow is non-zero. Finally, the arrows are non-zero because
\(\square \)
Remark
The existence of Felder complexes will not specifically be needed for any of the results that follow, however, it is interesting to note that the bosonic ghosts admit such complexes. These complexes were crucial in [16] for computing the character formulae needed for the standard module formalism via resolutions of simple modules.
3 Projective Modules
In this section we construct reducible yet indecomposable modules \(\mathcal {P}\) on which the \(L_0\) operator has rank 2 Jordan blocks. We further prove that the modules \(\sigma ^{\ell } \mathcal {P}\) and \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) are both projective and injective, and that in particular the \(\sigma ^{\ell } \mathcal {P}\) are projective covers and injective hulls of \(\sigma ^{\ell } \mathcal {V}\) for any \(\ell \in \mathbb {Z}\). We refer readers unfamiliar with homological algebra concepts such as injective and projective modules or extension groups to the book [32] and recall the following result for later use.
Proposition 3.1
For a module \(\mathcal {R}\) which is both projective and injective, the Hom-Ext sequences terminate. That is, if we have the short exact sequence
for modules \(\mathcal {A}\), \(\mathcal {B}\). then this implies that the following two sequences are exact, for any module \(\mathcal {M}\).
Furthermore, \({{\,\mathrm{Hom}\,}}\left( \mathcal {R},- \right) \) and \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {R} \right) \) are exact covariant and exact contravariant functors respectively.
This proposition assists with the calculation of Hom and Ext groups, when all but one of the dimensions in the sequence are known. Using the fact that the Euler characteristic (the alternating sum of the dimensions of the coefficients) of an exact sequence vanishes, there is only one possibility for the remaining group.
Proposition 3.2
The first extension groups of simple modules in \(\mathscr {F}\) satisfy
where \(\lambda \in \mathbb {R}/\mathbb {Z},\ \lambda \ne \mathbb {Z},\ k,\ell \in \mathbb {Z}\) and \(\mathcal {M}\) is any module in \(\mathscr {F}\). In particular the simple modules \(\sigma ^{k} \mathcal {W}_{\lambda }\) are both projective and injective in \(\mathscr {F}\).
Proof
To conclude that \(\sigma ^{k} \mathcal {W}_{\lambda }\) is projective in \(\mathscr {F}\) it is sufficient to show that \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W}_{\lambda },\mathcal {M} \right) =0\) for all simple objects \(\mathcal {M}\in \mathscr {F}\). Injectivity in \(\mathscr {F}\) then follows by applying the \({}^*\) functor and noting that \({\mathcal {W}_{\lambda }}^*\cong \mathcal {W}_{\lambda }\). Let \(\mathcal {M}\in \mathscr {F}\) be simple, then a necessary condition for the short exact sequence
being non-split is that the respective ghost and conformal weights of \(\mathcal {W}_{\lambda }\) and \(\mathcal {M}\) differ only by integers. For simple \(\mathcal {M}\) this rules out \(\mathcal {M}=\sigma ^{\ell } \mathcal {V}\) or \(\mathcal {M}=\sigma ^{\ell } \mathcal {W}_{\mu }\), \(\mu \ne \lambda \). So we consider \(\mathcal {M}=\sigma ^{\ell } \mathcal {W}_{\lambda }\). Assume \(\ell =0\), let \(j\in \lambda \) and let \(v\) be a non-zero vector in the ghost and conformal weight \([j,0]\) space of the submodule \(\mathcal {M}= \mathcal {W}_{\lambda }\subset \mathcal {N}\) and let \(w\in \mathcal {N}\) be a representative of a non-zero coset in the \([j,0]\) weight space of the quotient \(\mathcal {N}/\mathcal {W}_{\lambda }\). Without loss of generality, we can assume that \(w\) is a \(J_0\)-eigenvector and a generalised \(L_0\)-eigenvector. A necessary condition for the indecomposability of \(\mathcal {N}\), is the existence of an element \(U\) in the universal enveloping algebra \({\mathsf {U}}\left( \mathfrak {G} \right) \) such that \(Uv=w\). Since \(v\) has minimal generalised conformal weight all positive modes annihilate \(v\), thus \(Uv\) can be expanded as a sum of products of \(\beta _0\) and \(\gamma _0\) with each summand containing as many \(\beta _0\) as \(\gamma _0\) factors, that is, \(Uv=f(J_0)v\) can be expanded as a polynomial in \(J_0\) acting on \(v\). Since \(\mathcal {N}\in \mathscr {F}\), \(J_0\) acts semisimply, hence \(f(J_0)v\propto v\). Since \(v\) is not a scalar multiple of \(w\), this contradicts the indecomposability of \(\mathcal {N}\). Thus the exact sequence splits or, equivalently, the corresponding extension group vanishes.
Assume \(\mathcal {M}= \sigma ^{\ell } \mathcal {W}_{\lambda }\) with \(\ell \ne 0\), then by applying the \({}^*\) and \(\sigma \) functors, we have \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W}_{\lambda },\sigma ^{\ell } \mathcal {W}_{\lambda } \right) = {{\,\mathrm{Ext}\,}}^{}\left( \sigma ^{\ell } \mathcal {W}_{\lambda },\mathcal {W}_{\lambda } \right) = {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W}_{\lambda },\sigma ^{-\ell } \mathcal {W}_{\lambda } \right) \). Thus the sign of \(\ell \) can be chosen at will and we can assume without loss of generality that \(\ell \ge 1\). Further, from the formulae for the conformal weights of spectral flow twisted modules (2.15), the conformal weights of \(\mathcal {W}_{\lambda }\) and \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) differ by integers if and only if \(\ell \cdot \lambda = \mathbb {Z}\). Let \(j\in \lambda \) be the minimal representative satisfying that the space of ghost weight \(j\) in \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) has positive least conformal weight. The least conformal weight of the ghost weight \(j-1\) space is a negative integer, which we denote by \(-k\). See Figure 1 for an illustration of how the weight spaces are arranged. Let \(v\in \mathcal {N}\) be a non-zero vector of ghost weight \(j\) and generalised \(L_0\) eigenvalue 0, and hence a representative of a non-trivial coset of ghost and conformal weight \([j,0]\) in \(\mathcal {W}_{\lambda }\cong \mathcal {N}/\sigma ^{\ell } \mathcal {W}_{\lambda }\). Further let \(w\in \sigma ^{\ell } \mathcal {W}_{\lambda }\subset \mathcal {N}\) be a non-zero vector of ghost and conformal weight \([j-1,-k]\). Both \(v\) and \(w\) lie in one-dimensional weight spaces and hence span them. If \(\mathcal {N}\) is indecomposable, then there must exist an element \(U\) of ghost and conformal weight \([-1,-k]\) in \({\mathsf {U}}\left( \mathfrak {G} \right) \), such that \(U v=w\). We pick a Poincaré-Birkhoff-Witt ordering such that generators with larger mode index are placed to the right of those with lesser index and \(\gamma _n\) is placed to the right of \(\beta _n\) for any \(n\in \mathbb {Z}\). Thus \(Uv = \sum _{i=1}^k U^{(i)} \gamma _{i} v\), where \(U^{(i)}\) is an element of \({\mathsf {U}}\left( \mathfrak {G} \right) \) of ghost and conformal weight \([0,i-k]\). In \(\mathcal {W}_{\lambda }\), \(\gamma _0\) acts bijectively on the space of conformal weight 0 vectors, hence there exists a \({\tilde{v}} \in \mathcal {N}\) such that \(\gamma _0 {\tilde{v}} = v\). Since at ghost weight \(j\) the conformal weights of \(\mathcal {N}\) are non-negative, we have \(\gamma _n {\tilde{v}}=0\), \(n\ge 1\) and thus \(Uv=\sum _{i=1}^k U^{(i)} \gamma _{i} \gamma _0{\tilde{v}} =\sum _{i=1}^k U^{(i)} \gamma _0\gamma _{i} {\tilde{v}}=0\), contradicting the indecomposability of \(\mathcal {N}\).
Next we consider the extensions of spectral flows of the vacuum module. By judicious application of the \({}^*\) and \(\sigma \) functors, we can identify \({{\,\mathrm{Ext}\,}}^{}\left( \sigma ^{k} \mathcal {V},\sigma ^{\ell } \mathcal {V} \right) = {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V},\sigma ^{k-\ell } \mathcal {V} \right) ={{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V},\sigma ^{\ell -k} \mathcal {V} \right) \). So without loss of generality, it is sufficient to consider the extension groups \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V},\sigma ^{\ell } \mathcal {V} \right) \) or equivalently short exact sequences of the form
Let \(\sigma ^{\ell } \Omega \in \sigma ^{\ell } \mathcal {V}\subset \mathcal {M}\) denote the the spectral flow image of the highest weight vector of \(\mathcal {V}\) and let \(\omega \in \mathcal {M}\) be a \(J_0\)-eigenvector and a choice of representative of the highest weight vector in \(\mathcal {V}\cong \mathcal {M}/\sigma ^{\ell } \mathcal {V}\). We first show that these sequences necessarily split if \(\ell \ne 1\). Assume \(\ell =0\), then the exact sequence can only be non-split if there exists a ghost and conformal weight \([0,0]\) element \(U\) in \({\mathsf {U}}\left( \mathfrak {G} \right) \) such that \(U \omega = a\sigma ^{\ell } \Omega -b\omega \), \(a,b\in \mathbb {C}\), \(a\ne 0\). Without loss of generality we can replace \(U\) by \({\tilde{U}}=U-b{\mathbf {1}}\) to obtain \({\tilde{U}}\omega =a\sigma ^{\ell } \Omega \). Since the conformal weights of \(\mathcal {V}\) are bounded below by 0, they satisfy the same bound in \(\mathcal {M}\) and \(\beta _{n}\omega =\gamma _{n}\omega =0\), \(n\ge 1\), so \({\tilde{U}}\omega \) can be expanded as a sum of products of \(\beta _0\) and \(\gamma _0\) acting on \(\omega \), with each summand containing the same number of \(\beta _0\) and \(\gamma _0\) factors. Equivalently, \({\tilde{U}}\omega \) can be expanded as a polynomial in \(J_0\) acting on \(\omega \). Since \(\omega \) is a \(J_0\)-eigenvector \({\tilde{U}}\omega \propto \omega \). Since \(\omega \) is not a scalar multiple of \(\sigma ^{\ell } \Omega \), \({\tilde{U}}\omega =0\) contradicting indecomposability, and the exact sequence splits.
Assume \(\ell \ge 2\). The ghost and conformal weights of \(\sigma ^{\ell } \Omega \) are \([-\ell ,-\frac{\ell (\ell +1)}{2}]\). Further, from the spectral flow formulae (2.15), one can see that the weight spaces of ghost and conformal weight \([-1,h]\) of \(\sigma ^{\ell } \mathcal {V}\) vanish for \(h<\frac{(\ell +1)(\ell -2)}{2}\) and similarly the \([1,h]\) weight spaces of \(\sigma ^{\ell } \mathcal {V}\) vanish for \(h<\frac{(\ell +1)(\ell +2)}{2}\). Since we are assuming \(\ell \ge 2\), \(\frac{(\ell +1)(\ell \pm 2)}{2}\ge 0\). Thus \(\gamma _n\omega =\beta _n\omega =0\), \(n\ge 1\). If \(\mathcal {M}\) is indecomposable, there must exist a ghost and conformal weight \([-\ell ,-\frac{\ell (\ell +1)}{2}]\) element \(U\) in \({\mathsf {U}}\left( \mathfrak {G} \right) \) such that \(U \omega = \sigma ^{\ell } \Omega \). Since the conformal weight of \(U\) is \(-\ell \), every summand of the expansion of \(U\omega \) into \(\beta \) and \(\gamma \) modes must contain factors of \(\gamma _n\) or \(\beta _n\) with \(n\ge 1\) and we can choose a Poincaré-Birkhoff-Witt ordering where these modes are placed to the right. Thus \(U \omega =0\), contradicting indecomposability and the exact sequence splits.
Assume \(\ell =1\), then \(\sigma ^{} \mathcal {W}_{0}^+\) provides an example for which the exact sequence does not split and the dimension of the corresponding extension group is at least 1. We show that it is also at most 1. Let \(\omega \) and \(\sigma ^{} \Omega \) be defined as for \(\ell \ge 2\). By arguments analogous to those for \(\ell \ge 2\), it follows that the \([1,h]\) weight space vanishes for \(h<0\) and the \([-1,h]\) weight space vanishes for \(h<-1\). Thus \(\beta _{n}\omega =\gamma _{n+1}\omega =0\), \(n\ge 1\). The \([-1,-1]\) weight space of \(\sigma ^{} \mathcal {V}\) is one-dimensional and is hence spanned by \(\sigma ^{} \Omega \). If \(\mathcal {M}\) is indecomposable, there must exist a ghost and conformal weight \([-1,-1]\) element \(U\) in \({\mathsf {U}}\left( \mathfrak {G} \right) \) such that \(U \omega = \sigma ^{} \Omega \). Thus, \(U\omega \) can be expanded as \(f(J_0)\gamma _{1}\omega =f(0)\gamma _1\omega =a\Omega \), where \(f(J_0)\) is a polynomial. Hence the isomorphism class of \(\mathcal {M}\) is determined by the value of \(\gamma _1\omega \) in the one-dimensional \([-1,-1]\) weight space and \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V},\sigma ^{} \mathcal {V} \right) =1\).
\(\square \)
This diagram is a visual aid for the proof of the inextensibility of the simple module \(\mathcal {W}_{\lambda } \in \mathscr {F}\), \(\lambda \in \mathbb {R}/\mathbb {Z}, \lambda \ne \mathbb {Z}\). Here \(\ell \ge 1\), \(\ell \cdot \lambda = \mathbb {Z}\). The nodes represent the (spectral flows of) relaxed highest weight vectors of each module. Weight spaces are filled in grey. Conformal weight increases from top to bottom and ghost weight increases from right to left.
Armed with the above results on extension groups, we can construct indecomposable modules \(\sigma ^{\ell } \mathcal {P}\in \mathscr {F}\), which will turn out to be projective covers and injective hulls of \(\sigma ^{\ell } \mathcal {V}\).
Proposition 3.3
Recall that by the first free field realisation \(\phi _1\) of Proposition 2.12, we can identify \({\mathbb {F}}_{\ell \psi }\cong \sigma ^{\ell +1} \mathcal {W}_{0}^-\). Define the \({\mathcal {S}}_{1}\)-twisted action of \(\mathsf {G}\) on \({\mathbb {F}}_{-\psi }\oplus {\mathbb {F}}_{0}\) by assigning
and determining the action of all other fields in \(\mathsf {G}\) through normal ordering and taking derivatives, where any vertex operator \(\mathrm {V}_{\lambda }\left( z \right) \) whose Heisenberg weight \(\lambda \) is in the coset \([\psi ]=[-\theta ]\) is defined to act as \(0\) on \({\mathbb {F}}_{0}\) and as usual on \({\mathbb {F}}_{-\psi }\).
-
(1)
The assignment is well-defined, that is, it represents the operator product expansions of \(\mathsf {G}\), and hence defines an action of \(\mathsf {G}\) on \({\mathbb {F}}_{-\psi }\oplus {\mathbb {F}}_{0}\), where \(\oplus \) is meant as a direct sum of vector spaces without considering the module structure. Denote the module with this \({\mathcal {S}}_{1}\)-twisted action by \(\mathcal {P}\).
-
(2)
The composite fields \(J(z)={} {:} {}{\beta (z)\gamma (z)}\) : \(T(z)=-{} {:} {}{\beta (z)\partial \gamma (z)}\) : act as
$$\begin{aligned}&J(z)\mapsto \phi _1(J(z))=-\theta (z),\nonumber \\&T(z)\mapsto \phi _1(T(z))+\frac{\mathrm {V}_{\psi }\left( z \right) }{z}= \frac{{} {:} {}{\psi (z)^2 {:}}-{} {:} {}{\theta (z)^2} {:}}{2}-\partial \frac{\psi (z)-\theta (z)}{2}+\frac{\mathrm {V}_{\psi }\left( z \right) }{z}. \end{aligned}$$(3.8)The zero mode \(J_0\) therefore acts semisimply and \(L_0\) has rank 2 Jordan blocks. The vectors \(|-\psi \rangle , |-\psi -\theta \rangle , |\theta \rangle , |0 \rangle \in \mathcal {P}\) satisfy the relations
$$\begin{aligned}&\beta _0|-\psi \rangle =|\theta \rangle ,\quad \gamma _1|-\psi \rangle =-|-\psi -\theta \rangle ,\quad \gamma _0|\theta \rangle =-|0 \rangle ,\nonumber \\&\quad \beta _{-1}|-\psi -\theta \rangle =|0 \rangle ,\quad L_0|-\psi \rangle =|0 \rangle . \end{aligned}$$(3.9) -
(3)
The module \(\mathcal {P}\) is indecomposable and satisfies the non-split exact sequences
$$\begin{aligned}&0 \longrightarrow \sigma ^{} \mathcal {W}_{0}^- \overset{}{\longrightarrow } \mathcal {P} \overset{}{\longrightarrow } \mathcal {W}_{0}^{-} \longrightarrow 0, \end{aligned}$$(3.10a)$$\begin{aligned}&0 \longrightarrow {\mathcal {W}_{0}^+} \overset{}{\longrightarrow } \mathcal {P} \overset{}{\longrightarrow } \sigma ^{} \mathcal {W}_{0}^{+} \longrightarrow 0, \end{aligned}$$(3.10b)which implies that its composition factors are \(\sigma ^{\pm 1} \mathcal {V}\) and \(\mathcal {V}\) with multiplicities 1 and 2, respectively.
-
(4)
\(\mathcal {P}\) is an object in \(\mathscr {F}\).
See Figure 2 for an illustration of how the composition factors of \(\mathcal {P}\) are linked by the action of \(\mathsf {G}\).
The composition factors of \(\mathcal {P}\) with the nodes representing the spectral flows of the highest weight vectors of \(\sigma ^{\ell } \mathcal {V}\) for \(-1 \le \ell \le 1\). The arrows give the action of \(\mathfrak {G}\) modes on the highest-weight vectors of each factor. In this diagram, ghost weight increases to the left and conformal weight increases downwards. Note that there are two copies of \(\mathcal {V}\), illustrated by a small vertical shift in their weights.
Proof
Part (1) follows from [33], where a general procedure was given for twisting actions by screening operators. The field identifications (3.8) of Part (2) follow by evaluating definitions introduced there, while the relations (3.9) follow by applying the field identifications.
To conclude the first exact sequence of Part (3) note that the action of \(\beta \) and \(\gamma \) closes on \({\mathbb {F}}_{0}\cong \sigma ^{} \mathcal {W}_{0}^{-}\), because \(\mathrm {V}_{-\theta }\left( z \right) \) acts trivially and quotienting by \({\mathbb {F}}_{0}\) leaves only \({\mathbb {F}}_{-\psi }\cong \mathcal {W}_{0}^{-}\).
To conclude the second exact sequence, let \(\Omega \) be the highest weight vector of \(\mathcal {V}\) and let \(\sigma ^{\ell } \Omega \) be the spectral flow images of \(\Omega \). Then \(|0 \rangle \in {\mathbb {F}}_{0}\cong \sigma ^{-1} \mathcal {W}_{0}^-\) can be identified with \(\Omega \) in the \(\mathcal {V}\) composition factor of \(\sigma ^{-1} \mathcal {W}_{0}^-\) and \(|-\psi -\theta \rangle \) can be identified with \(\sigma ^{} \Omega \) in the \(\sigma ^{} \mathcal {V}\) composition factor. Further, \(|-\psi \rangle \in {\mathbb {F}}_{-\psi }\cong \mathcal {W}_{0}^-\) can be identified with \(\Omega \) in the \(\mathcal {V}\) composition factor and \(|\theta \rangle \) can be identified with \(\sigma ^{-1} \Omega \) in the \(\sigma ^{-1} \mathcal {V}\) composition factor. See Figure 2 for a diagram of the action of \(\beta \) and \(\gamma \) modes on \(\mathcal {P}\) and how they connect the different composition factors. It therefore follows that \(|0 \rangle \) generates an indecomposable module whose composition factors are \(\sigma ^{-1} \mathcal {V}\) and \(\mathcal {V}\), with \(\mathcal {V}\) as a submodule and \(\sigma ^{-1} \mathcal {V}\) as a quotient. The module therefore satisfies the same non-split exact sequence (2.20) as \(\mathcal {W}_{0}^+\) does and since the extension groups in (3.4) are one-dimensional, this submodule is isomorphic to \(\mathcal {W}_{0}^+\). After quotienting by the submodule generated by \(|\theta \rangle \), the formulae above imply that the quotient is isomorphic to \(\sigma ^{} \mathcal {W}_{0}^+\) and the second exact sequence of Part (3) follows.
Part (4) follows because \(J_0\) acts diagonalisably on \(\mathcal {P}\) and because \(\mathcal {P}\) has only finitely many composition factors all of which lie in \(\mathscr {R}\) or \(\sigma ^{} \mathscr {R}\). \(\square \)
Theorem 3.4
For every \(\ell \in \mathbb {Z}\) the indecomposable module \(\sigma ^{\ell } \mathcal {P}\) is projective and injective in \(\mathscr {F}\), and hence is a projective cover and an injective hull of the simple module \(\sigma ^{\ell } \mathcal {V}\).
Proof
Since spectral flow is an exact invertible functor, it is sufficient to prove projectivity and injectivity of \(\mathcal {P}\), rather than all spectral flow twists of \(\mathcal {P}\). We first show that \(\mathcal {P}\) is injective by showing that \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W},\mathcal {P} \right) =0\) for any simple module \(\mathcal {W}\in \mathscr {F}\). Following that we will show \(\mathcal {P}^*=\mathcal {P}\), which, since \({}^*\) is an exact invertible contravariant functor, implies \(\mathcal {P}\) is also projective.
A necessary condition for the non-triviality of such an extension is ghost weights differing only by integers. We therefore need not consider extensions by \(\sigma ^{\ell } \mathcal {W}_{\lambda }\), \(\lambda \ne \mathbb {Z}\), so we restrict our attention to short exact sequences of the form
If the above extension is non-split, then there must exist a subquotient of \(\mathcal {M}\) which is a non-trivial extension of \(\sigma ^{\ell } \mathcal {V}\) by one of the composition factors of \(\mathcal {P}\). By Proposition 3.2 the above sequence must split if \(|\ell |\ge 3\) and we therefore only consider \(|\ell |\le 2\).
If \(\ell =2\), then the composition factor of \(\mathcal {P}\) non-trivially extending \(\sigma ^{2} \mathcal {V}\) must be \(\sigma ^{} \mathcal {V}\). If the extension is non-trivial, then this subquotient must be isomorphic to \(\sigma ^{2} \mathcal {W}_{0}^-\). Further, if \(\sigma ^{2} \Omega \) is the spectrally flowed highest weight vector of \(\sigma ^{2} \mathcal {V}\) and \(|-\psi -\theta \rangle \in \mathcal {P}\) (see Figure 2) is the spectrally flowed highest weight vector of the \(\sigma ^{} \mathcal {V}\) composition factor of \(\mathcal {P}\), then \(\beta _{-2}\sigma ^{2} \Omega =a |-\psi -\theta \rangle \), \(a\in \mathbb {C}\setminus \{0\}\). The relations (3.9) thus imply
However, \(\beta _{-1}\sigma ^{2} \Omega \) has conformal and ghost weight \([-1,-2]\) and this weight space vanishes for both \(\mathcal {P}\) and \(\sigma ^{2} \mathcal {V}\). Thus \(\beta _{-1}\sigma ^{2} \Omega \) and hence \(a=0\), which is a contradiction.
If \(\ell =1\), then the composition factor of \(\mathcal {P}\) non-trivially extending \(\sigma ^{} \mathcal {V}\) must be \(\mathcal {V}\). There are two such composition factors in \(\mathcal {P}\). Any such non-trivial extension must be isomorphic to \(\sigma ^{} \mathcal {W}_{0}^-\). If the non-trivial extension involves the composition factor whose spectrally flowed highest weight vector is represented by \(|-\psi \rangle \), then \(\beta _{-1}\sigma ^{} \Omega =a |-\psi \rangle \), \(a\in \mathbb {C}\setminus \{0\}\). The relations (3.9) thus imply
However, \(\beta _{0}\sigma ^{} \Omega =0\), so \(a=0\), which is a contradiction. If the non-trivial extension involves the composition factor whose spectrally flowed highest weight vector is represented by \(|0 \rangle \), then there would exist \(a\in \mathbb {C}\setminus \{0\}\) such that \(\beta _{-1}\sigma ^{} \Omega =a|0 \rangle \). But then, by the relations (3.9), \(\beta _{-1}\left( \sigma ^{} \Omega -a \right) |-\psi -\theta \rangle =0\). Hence \(\left( \sigma ^{} \Omega -a \right) |-\psi -\theta \rangle \) generates a direct summand isomorphic to \(\sigma ^{} \mathcal {V}\), making the extension trivial.
If \(\ell =0\), then the composition factor of \(\mathcal {P}\) non-trivially extending \(\mathcal {V}\) must be \(\sigma ^{} \mathcal {V}\) or \(\sigma ^{-1} \mathcal {V}\). If there is a subquotient isomorphic to a non-trivial extension of \(\mathcal {V}\) by \(\sigma ^{-1} \mathcal {V}\), that is, isomorphic to \(\mathcal {W}_{0}^-\), then there exists \(a\in \mathbb {C}\setminus \{0\}\) such that \(\beta _{0}\Omega =a|\theta \rangle \). But then, by the relations (3.9), \(\beta _{0}\left( \Omega -a \right) |\theta \rangle =0\). Hence \(\left( \Omega -a \right) |\theta \rangle \) generates a direct summand isomorphic to \(\mathcal {V}\), making the extension trivial. An analogous argument rules out the existence of subquotient isomorphic a non-trivial extension of \(\mathcal {V}\) by \(\sigma ^{-1} \mathcal {V}\).
The cases \(\ell =-2\) and \(\ell =-1\) follow the same reasoning as \(\ell =2\) and \(\ell =1\), respectively.
Now that we have established that \(\mathcal {P}\) is injective, we can apply the functors \({{\,\mathrm{Hom}\,}}\left( \mathcal {W}_{0}^-,- \right) \) and \({{\,\mathrm{Hom}\,}}\left( \sigma ^{} \mathcal {W}_{0}^+,- \right) \) to the short exact sequences (3.10a) and (3.10b), respectively, to deduce \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W}_{0}^-,\sigma ^{} \mathcal {W}_{0}^- \right) =1=\dim {{\,\mathrm{Ext}\,}}^{}\left( \sigma ^{} \mathcal {W}_{0}^+,\mathcal {W}_{0}^+ \right) \). The indecomposable module \(\mathcal {P}\) is therefore the unique module making the short exact sequences (3.10a) and (3.10b) non-split. By applying the functor \(^*\) to these exact sequences, we see that \(\mathcal {P}^*\) also satisfies these same sequences and hence \(\mathcal {P}\cong \mathcal {P}^*\). This in turn implies \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {P},- \right) =0\) and hence that \(\sigma ^{\ell } \mathcal {P}\) is projective for all \(\ell \in \mathbb {Z}\). \(\square \)
4 Classification of Indecomposables
In this section, we give a classification of all indecomposable modules in category \(\mathscr {F}\). We already know any simple module is isomorphic to either \(\sigma ^{m} \mathcal {W}_{\lambda }\) or \(\sigma ^{m} \mathcal {V}_{}\), and we also know that the \(\sigma ^{m} \mathcal {W}_{\lambda }\) are inextensible due to being injective and projective in \(\mathscr {F}\). We now complete the classification by finding all the reducible indecomposables which can be built as finite length extensions with composition factors isomorphic to spectral flows of \(\mathcal {V}\). To unclutter formulae, we use the notation \(\mathcal {M}_{n} = \sigma ^{n} \mathcal {M}\) for any module \(\mathcal {M}\). The classification of indecomposable modules in \(\mathscr {F}\) closely resembles the classification of indecomposable modules over the Temperley-Lieb algebra with parameter at roots of unity given in [34] and also the classification of indecomposable modules over the \((1,p)\) triplet model given in [35].
The reducible yet indecomposable modules constituting the classification are the spectral flows of the projective module \(\mathcal {P}\), and two infinite families. These two families, denoted \(\mathcal {B}^{m}_{n}\) and \(\mathcal {T}^{m}_{n}\), \(m,n\in \mathbb {Z}\), \(n\ge 1\), are dual to each other with respect to \(^*\), meaning \(\left( \mathcal {B}^{m}_{n} \right) ^*=\mathcal {T}^{m}_{n}\), and further satisfy the identifications \(\mathcal {B}^{1}_{} = \mathcal {T}^{1}_{} = \mathcal {V}_{}\), \(\mathcal {B}^{2}_{} = \sigma ^{} \mathcal {W}_{0}^-\) and \(\mathcal {T}^{2}_{} = \sigma ^{} \mathcal {W}_{0}^+\). The superscript \(m\) is the number of composition factors or length of the module. As a visual aid, we represent these indecomposable modules using Loewy diagrams.

Here the edges indicate the action of \(\mathsf {G}\) and the vertices represent the composition factors. Recall the generating vectors \(u=|-\psi \rangle , \ l=|\theta \rangle , \ r=|-\psi -\theta \rangle , \ d=|0 \rangle \) for the composition factors of \(\mathcal {P}_{}\) in Figure 2 constructed from the first free field realisation Proposition 2.12.(1). We denote their spectral flow images by \(u_n=\sigma ^{n} u,\ l_n=\sigma ^{n} l,\ r_n=\sigma ^{n} r,\ d_n=\sigma ^{n} d\). The letters labelling these vectors have been chosen according to the position of their corresponding composition factor in the Loewy diagram below.

Since \(\mathscr {F}\) has sufficiently many projectives and injectives, every indecomposable module is isomorphic to some quotient of a finite sum of indecomposable projective modules and to a submodule of a finite sum of indecomposable injective modules. We therefore define the two families of reducible yet indecomposable modules, \(\mathcal {B}^{n}_{m}\) and \(\mathcal {T}^{n}_{m}\) as certain images or coimages of homomorphisms from projective to injective modules. We prepare the necessary notation, For \(m\in \mathbb {Z}\) and \(k\in \mathbb {Z}_{>0}\), let
As the \({\mathsf {P}}[ ]\), \({\mathsf {J}}[ ]\) notation suggests, the above modules will be shown to be projective covers and injective hulls of the \(\mathcal {T}^{}_{}\) and \(\mathcal {B}^{}_{}\) modules. Further, for \(n\in \mathbb {Z}\) let \(\psi ^\pm _n:\mathcal {P}_{n}\rightarrow \mathcal {P}_{n\pm 1}\) be the module homomorphisms uniquely characterised by \(\psi ^+_n(u_n)=l_{n+1}\) and \(\psi ^-_n(u_n)=r_{n-1}\). Note that these homomorphisms satisfy the relations
in fact \(\ker \psi ^\pm _{m\pm 1} = {{\,\mathrm{im}\,}}\psi ^\pm _m\). Finally, consider the module homomorphisms \(\psi [\mathcal {M} ]:{\mathsf {P}}[\mathcal {M} ]\rightarrow {\mathsf {J}}[\mathcal {M} ]\), which, for \(\mathcal {M}\) being any of the indecomposables above, are given by the formulae
Definition 4.1
For \(m\in \mathbb {Z}\) and \(k\in \mathbb {Z}_{>0}\), we define the following indecomposable modules
Example
Consider the example of \(\mathcal {T}^{4}_{0}\).

The thick arrows above indicate the edges of the Loewy diagram of the coimage and image. The repeated composition factors \(\mathcal {V}_{1}\) and \(\mathcal {V}_{2}\) in the domain and codomain, respectively, each contribute one factor to the image and coimage and one to the kernel and cokernel as can be seen in the diagrams below.

In the cases of the coimage and the cokernel above, the indicated vectors are to be thought of as representatives of their equivalences classes in their respective quotients.
Theorem 4.2
Any reducible indecomposable module in \(\mathscr {F}\) is isomorphic to one of the following.
The remainder of this section will be dedicated to proving the above theorem. For any module \(\mathcal {M}\), we recall the following two well known substructures. The first is the maximal semisimple submodule of \(\mathcal {M}\), called the socle and which we denote \({{\,\mathrm{soc}\,}}\mathcal {M}\). The second, called the head, is the maximal semisimple quotient of \(\mathcal {M}\), defined to be the quotient of \(\mathcal {M}\) by its radical (the intersection of its maximal proper submodules), which we denote \({{\,\mathrm{hd}\,}}\mathcal {M}\). We also let \({\mathsf {J}}[\mathcal {M} ]\) and \({\mathsf {P}}[\mathcal {M} ]\) denote the injective hull and the projective cover of \(\mathcal {M}\) respectively. We then have the following standard homological algebra result.
Proposition 4.3
For any module \(\mathcal {M}\in \mathscr {F}\), we have
and
Corollary 4.4
The heads and socles of the \(\mathcal {T}^{k}_{m}\) and \(\mathcal {B}^{k}_{m}\) are given by
and the dimensions of Hom groups involving \(\mathcal {V}_{n}\) by the following table.
\(\mathcal {B}^{2k+1}_{m}\) | \(\mathcal {B}^{2k}_{m}\) | \(\mathcal {T}^{2k+1}_{m}\) | \(\mathcal {T}^{2k}_{m}\) | |
|---|---|---|---|---|
\(\dim {{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{n},- \right) \) | \(\sum _{i=0}^{k}\delta _{n,m+2i}\) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i}\) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i+1}\) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i+1}\) |
\(\dim {{\,\mathrm{Hom}\,}}\left( -,\mathcal {V}_{n} \right) \) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i+1}\) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i+1}\) | \(\sum _{i=0}^{k}\delta _{n,m+2i}\) | \(\sum _{i=0}^{k-1}\delta _{n,m+2i}\) |
Thus, for \(\mathcal {M}\) being any of the \(\mathcal {T}^{k}_{m}\) and \(\mathcal {B}^{k}_{m}\) in Definition 4.1, \({\mathsf {P}}[\mathcal {M} ]\) and \({\mathsf {J}}[\mathcal {M} ]\) are the projective cover and injective hull of the indecomposable module \(\mathcal {M}\), respectively.
Proof
The Loewy diagrams for the \(\mathcal {T}^{k}_{m}\) and \(\mathcal {B}^{k}_{m}\) immediately suggest the heads and socles. For example for \(\mathcal {T}^{5}_{0}\) and \(\mathcal {B}^{5}_{0}\) we have the following.

They can, of course, also be easily determined from the calculations similar to those in the example above Theorem 4.2. The dimensions of the Hom groups in the table above, and the projective cover and injective hull formulae then immediately follow by Proposition 4.3. \(\square \)
Lemma 4.5
For \(\mathcal {M}\) being any of the \(\mathcal {T}^{k}_{m}\) and \(\mathcal {B}^{k}_{m}\) in Definition 4.1, the projective and injective presentations of \(\mathcal {M}\) are characterised by the following.
\(\mathcal {M}\) | \(\mathcal {B}^{2k+1}_{m}\) | \(\mathcal {B}^{2k}_{m}\) | \(\mathcal {T}^{2k+1}_{m}\) | \(\mathcal {T}^{2k}_{m}\) |
|---|---|---|---|---|
\(\ker {\left( {\mathsf {P}}[\mathcal {M} ] \rightarrow \mathcal {M} \right) }\) | \(\mathcal {B}^{2k-1}_{m+1}\) | \(\mathcal {B}^{2k}_{m+1}\) | \(\mathcal {T}^{2k+3}_{m-1}\) | \(\mathcal {T}^{2k}_{m-1}\) |
\({{\,\mathrm{coker}\,}}{\left( \mathcal {M}\rightarrow {\mathsf {J}}[\mathcal {M} ] \right) }\) | \(\mathcal {B}^{2k+3}_{m-1}\) | \(\mathcal {B}^{2k}_{m-1}\) | \(\mathcal {T}^{2k-1}_{m+1}\) | \(\mathcal {T}^{2k}_{m+1}\) |
Proof
Observe that we can precompose any of the homomorphisms \(\psi [\mathcal {M} ]\) by any automorphism \(A\) of the domain \({\mathsf {P}}[\mathcal {M} ]\) that consists of a non-zero rescaling chosen independently on each direct summand. Since this is a precomposition by an automorphism, the kernels of \(\psi [\mathcal {M} ]\) and \(\psi [\mathcal {M} ]\circ A\) are isomorphic. Similarly we can postcompose by any automorphism \(B\) of the codomain \({\mathsf {J}}[\mathcal {M} ]\) that consists of a non-zero rescaling, chosen independently on each direct summand. In summary, the homomorphisms \(\psi [\mathcal {M} ]\) and \(B\circ \psi [\mathcal {M} ]\circ A\) have isomorphic images and isomorphic kernels. Appropriately chosen pre- and postcompositions hence allow us to freely rescale each summand in the formulae (4.3). Hence we can define the morphisms
We prove the \(\mathcal {T}^{2k}_{m}\) column of the lemma above, the remaining columns follow by analogous arguments. First the kernel of \(\psi [\mathcal {T}^{2k}_{m} ]\). Note that \({\mathsf {P}}[\mathcal {T}^{2k}_{m} ]={\mathsf {J}}[\mathcal {T}^{2k}_{m-1} ]\) and hence the domain of \(\psi [\mathcal {T}^{2k}_{m} ]\) is equal to the codomain of \({\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]\) and hence these two homomorphisms can be composed. A direct computation using the composition relations (4.2) then shows that \(\psi [\mathcal {T}^{2k}_{m} ]\circ {\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]=0\) and hence \(\ker \psi [\mathcal {T}^{2k}_{m} ]\supset {{\,\mathrm{im}\,}}{\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]\). Finally, \({{\,\mathrm{im}\,}}{\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]\cong {{\,\mathrm{im}\,}}\psi [\mathcal {T}^{2k}_{m-1} ]=\mathcal {T}^{2k}_{m-1}\). By inspection we also see that both \(\ker \psi [\mathcal {T}^{2k}_{m} ]\) and \({{\,\mathrm{im}\,}}{\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]\) have \(2k\) composition factors and hence \(\ker \psi [\mathcal {T}^{2k}_{m} ]= {{\,\mathrm{im}\,}}{\overline{\psi }}[\mathcal {T}^{2k}_{m-1} ]\cong \mathcal {T}^{2k}_{m-1}\). To compute the cokernel of \(\psi [\mathcal {T}^{2k}_{m} ]\), note that \({\mathsf {J}}[\mathcal {T}^{2k}_{m} ]={\mathsf {P}}[\mathcal {T}^{2k}_{m+1} ]\). An analogous argument to the above then proves \({{\,\mathrm{coker}\,}}\psi [\mathcal {T}^{2k}_{m} ]\cong \mathcal {T}^{2k}_{m+1}\). \(\square \)
Combining all of the results above we can now prove Theorem 4.2.
Proof of Theorem 4.2
The idea is to show that any extension of the \(\mathcal {T}^{k}_{m}\) and \(\mathcal {B}^{k}_{m}\) decomposes into a direct sum of the modules listed in (4.5). In particular it is sufficient to only consider extensions by \(\mathcal {V}_{n}\) (as either a submodule or a quotient). We classify the \(\mathcal {T}^{k}_{m}\) modules and the classification of the \(\mathcal {B}^{k}_{m}\) follows from an analogous argument.
We first consider \(\mathcal {T}^{3}_{m}\) as this module constitutes a special case that need to be considered separately form the other \(\mathcal {T}^{k}_{m}\). Recall that we have the respective injective and projective presentations
Applying the \({{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{n},- \right) \) functor to the injective presentation yields (recall Proposition 3.1) the long exact sequence
which implies \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V}_{n},\mathcal {T}^{3}_{m} \right) =\dim {{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{m},\mathcal {V}_{m+1} \right) -\dim {{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{n},\mathcal {P}_{m+1} \right) +\dim {{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{n},\mathcal {T}^{3}_{m} \right) =\delta _{n,m+1}\). Up to isomorphism there therefore exists exactly one indecomposable module with \(\mathcal {V}_{m+1}\) as a quotient and \(\mathcal {T}^{3}_{m}\) as a submodule. The projective module \(\mathcal {P}_{m+1}\) an example of this extension and hence no new indecomposable has been constructed. Similarly, applying the \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {V}_{n} \right) \) functor to the projective presentation above and computing dimensions yields \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {T}^{3}_{m},\mathcal {V}_{n} \right) =\delta _{n,m-1}+\delta _{n,m+1}+\delta _{n,m+3}\). The cases \(n=m-1\) and \(n=m+3\) respectively correspond to \(\mathcal {B}^{4}_{m-1}\) and \(\mathcal {T}^{4}_{m}\), however, \(n=m+1\) requires closer inspection. This final case corresponds to the extension constructed from the non-split exact sequence
where the second arrow is characterised by the generating vector (the \(m+1\)-fold spectral flow of the highest weight vector of \(\mathcal {V}_{}\)) to any linear combination with non-zero coefficients of the two corresponding generating vectors of the two \(\mathcal {V}_{m+1}\) summands of the socles of \(\mathcal {T}^{3}_{m}\) and \(\mathcal {B}^{3}_{m+1}\). A brief calculation reveals that the quotient of \(\mathcal {T}^{2}_{m}\oplus \mathcal {B}^{3}_{m+1}\) by the image of \(\mathcal {V}_{m+1}\) is isomorphic to \(\mathcal {T}^{3}_{m}\) and it is the projection to this quotient that makes up the third arrow in the exact sequence above. Hence no new indecomposables have been constructed.
Next we consider \(\mathcal {T}^{2k+1}_{m}\), \(k\ge 2\). The injective and projective presentations are given by
Again we can compute the dimensions of Ext groups by applying the \({{\,\mathrm{Hom}\,}}\left( \mathcal {V}_{n},- \right) \) and \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {V}_{n} \right) \) and obtain
The non-vanishing Ext groups correspond to the respective non-split exact sequences
where \(\mathcal {T}^{0}_{}\) and \(\mathcal {B}^{0}_{}\) are to be interpreted as the 0 module.
Similar computations for \(\mathcal {T}^{2k}_{m}\), \(k\ge 1\) yield the Ext group dimensions
which correspond to the non-split exact sequences
Extensions of the \(\mathcal {T}^{k}_{m}\) modules therefore only yield indecomposable already accounted for in the list (4.5). The extensions of the \(\mathcal {B}^{}_{}\) modules are computed analogously \(\square \)
We end this section with some characterisations of the classified indecomposable modules which will prove helpful in later sections.
Corollary 4.6
The \(\mathcal {B}^{}_{}\), \(\mathcal {T}^{}_{}\) and \(\mathcal {P}_{}{}\) indecomposable modules are uniquely characterised by the following non-split exact sequences.
Proof
Sequences (4.18a), (4.18b) and (4.18c) follow from the one-dimensionality of the Ext groups in the proof of Theorem 4.2. We illustrate the procedure by which the remainder of the exact sequences can be seen to be non-split, by focussing on the first sequence of (4.18d), starting with the projective presentation of \(\mathcal {B}^{2}_{}\).
We apply the contravariant functor \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {B}^{n-2}_{2} \right) \) to obtain the following long exact sequence.
which evaluates to
Therefore \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2}_{},\mathcal {B}^{n-2}_{2} \right) = 1\), with the nontrivial extension given by (4.18d). The uniqueness of the remaining non-split exact sequences follows analogously, where we determine \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {M},\mathcal {N} \right) \) by applying the functor \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {N} \right) \) to the projective presentation for the module \(\mathcal {M}\) or by applying \({{\,\mathrm{Hom}\,}}\left( \mathcal {M},- \right) \) to the injective presentation of the module \(\mathcal {N}\). \(\square \)
Proposition 4.7
The evaluation of the \(^*\) functor of Proposition 2.11 on reducible indecomposable modules is given by
Proof
The evaluation of the \({}^*\) functor on the \(\mathcal {B}^{}_{}\) and \(\mathcal {T}^{}_{}\) modules follows inductively from the characterising sequences (4.18a), with the base step given by \(\mathcal {V}_{m}^*\cong \mathcal {V}_{m}\). The self duality of \(\mathcal {P}_{}\) is a consequence of Proposition 3.3.(3) and the fact that \(\left( \mathcal {W}_{0}^{\pm } \right) ^*=\mathcal {W}_{0}^{\mp }\), as argued above. \(\square \)
5 Rigid Tensor Category
In this section we prove that fusion furnishes category \(\mathscr {F}\) with the structure of a rigid tensor category and define evaluation and coevaluation maps for the simple projective modules to verify that these modules and maps satisfy the conditions required for rigidity. We refer readers unfamiliar with tensor categories or related notions such as rigidity to [36].
Theorem 5.1
Category \(\mathscr {F}\) with the tensor structures defined by fusion is a braided tensor category.
This theorem follows by verifying certain conditions which were proved to be sufficient in [21], and [37]. To this end, we recall some necessary definitions and results.
Definition 5.2
Let \(\mathsf {V}\) be a vertex algebra and let \(\mathcal {M}\) be a module over \(\mathsf {V}\). Let \(A\le B\) be abelian groups.
-
(1)
The module \(\mathcal {M}\) is called doubly-graded if both \(\mathcal {M}\) and \(\mathsf {V}\) are equipped with second gradations, in addition to conformal weight \(h\in \mathbb {C}\), which take values in B and A, respectively. We will use the notations \(\mathcal {M}^{(j)}\) and \(\mathcal {M}_{[h]}\) to denote the homogeneous spaces with respect to the additional grading or generalised conformal weight, respectively, and denote the simultaneous homogeneous space by \(\mathcal {M}^{(j)}_{[h]}=\mathcal {M}^{(j)}\cap \mathcal {M}_{[h]}\). The action of \(\mathsf {V}\) on \(\mathcal {M}\) is required to be compatible with the \(A\) and \(B\) gradation, that is,
$$\begin{aligned} v_n \mathsf {V}^{(i)} \subset \mathsf {V}^{(i+j)}, \quad v_n \mathcal {M}^{(k)} \subset \mathcal {M}^{(j+k)}, \qquad v \in \mathsf {V}^{(j)}, \ n \in \mathbb {Z}, \ i,j \in A, \ k \in B, \end{aligned}$$(5.1)and
$$\begin{aligned} {\mathbf {1}}\in \mathsf {V}^{(0)}_{[0]}, \qquad \omega \in \mathsf {V}^{(0)}_{[2]}, \end{aligned}$$(5.2)where \({\mathbf {1}}\) is the vacuum vector and \(\omega \) is the conformal vector.
-
(2)
The module \(\mathcal {M}\) is called lower bounded if it is doubly graded and if for each \(j\in B\), \(\mathcal {M}_{[h]}^{(j)}=0\) for \({\text {Re}}h\) sufficiently negative.
-
(3)
The module \(\mathcal {M}\) is called strongly graded with respect to B if it is doubly graded; it is the direct sum of its homogeneous spaces, that is,
$$\begin{aligned} \mathcal {M}=\bigoplus _{\begin{array}{c} h\in \mathbb {C}\\ j\in B \end{array}} \mathcal {M}_{[h]}^{(j)}, \end{aligned}$$(5.3)where the homogeneous spaces \(\mathcal {M}^{(j)}_{[h]}\) are all finite dimensional; and for fixed \(h\) and \(j\), \(\mathcal {M}^{(j)}_{[h+k]}=0\), whenever \(k \in \mathbb {Z}\) is sufficiently negative. The vertex algebra \(\mathsf {V}\) is called strongly graded with respect to A if it is strongly graded as a module over itself.
-
(4)
The module \(\mathcal {M}\) is called discretely strongly graded with respect to B if all conformal weights are real and for any \(j\in B\), \(h\in \mathbb {R}\) the space
$$\begin{aligned} \bigoplus _{\begin{array}{c} {\tilde{h}}\in \mathbb {R}\\ {\tilde{h}}\le h \end{array}}\mathcal {M}^{(j)}_{[{\tilde{h}}]} \end{aligned}$$(5.4)is finite dimensional.
-
(5)
For \(j\in B\), let
 . A strongly graded module \(\mathcal {M}\) is called graded \(C_1\)-cofinite if \((\mathcal {M}/C_1(\mathcal {M}))^{(j)}\) is finite dimensional for all \(j\in B\).
. A strongly graded module \(\mathcal {M}\) is called graded \(C_1\)-cofinite if \((\mathcal {M}/C_1(\mathcal {M}))^{(j)}\) is finite dimensional for all \(j\in B\).
Definition 5.3
Let \(A\le B\) be abelian groups. Let \(\mathsf {V}\) be a vertex algebra graded by \(A\) and let \(\mathcal {M}_1, \mathcal {M}_2\) and \(\mathcal {M}_3\) be modules over \(\mathsf {V}\), graded by \(B\). Denote by \(\mathcal {M}_3\lbrace x \rbrace [\log x ]\) the space of formal power series in \(x\) and \(\log x\) with coefficients in \(\mathcal {M}_3\), where the exponents of \(x\) can be arbitrary complex numbers and with only finitely many \(\log x\) terms. A grading compatible logarithmic intertwining operator of type \(\left( {\begin{array}{c}\mathcal {M}_3\\ \mathcal {M}_1,\ \mathcal {M}_2\end{array}}\right) \) is a linear map
satisfying the following properties.
-
(1)
Truncation: For any \(m_i\in \mathcal {M}_i, i=1,2\), and \(s\ge 0\)
$$\begin{aligned} \left( m_1 \right) _{t+k,s}m_2 = 0 \end{aligned}$$(5.6)for sufficiently large \(k \in \mathbb {Z}\).
-
(2)
\(L_{-1}\)-derivation: For any \(m_1\in \mathcal {M}_1\),
$$\begin{aligned} {\mathcal {Y}}(L_{-1}m_1,x)=\frac{\mathrm {d}}{\mathrm {d}x}{\mathcal {Y}}(m_1,x). \end{aligned}$$(5.7) -
(3)
Jacobi identity:
$$\begin{aligned} x_0^{-1} \delta \left( \frac{x_1-x_2}{x_0} \right) Y(v,x_1) {\mathcal {Y}}\left( m_1,x_2 \right) m_2&= x_0^{-1} \delta \left( \frac{-x_2 +x_1}{x_0} \right) {\mathcal {Y}}\left( m_1,x_2 \right) Y(v,x_1) m_2 \nonumber \\&\quad + x_2^{-1} \delta \left( \frac{x_1 - x_0}{x_2} \right) {\mathcal {Y}}\left( Y(v,x_0) m_1,x_2 \right) m_2 , \end{aligned}$$(5.8)where \(Y\) denotes field map encoding the action of \(\mathsf {V}\) on either \(\mathcal {M}_1,\mathcal {M}_2\) or \(\mathcal {M}_3\) and \(\delta \) denotes the algebraic delta distribution, that is the formal power series
$$\begin{aligned} \delta \left( \frac{y-x}{z} \right) = \sum _{\begin{array}{c} r \in \mathbb {Z}\\ s \ge 0 \end{array}} \left( {\begin{array}{c}r\\ s\end{array}}\right) (-1)^s x^s y^{r-s} z^{-r}. \end{aligned}$$(5.9) -
(4)
Grading compatibility: For any \(m_i\in \mathcal {M}_i^{(j_i)},\ j_i\in B,\ i=1,2\), \(t\in \mathbb {C}\) and \(s\ge 0\)
$$\begin{aligned} \left( m_1 \right) _{t,s}m_2 \in \mathcal {M}_3^{(j_1+j_2)}. \end{aligned}$$(5.10)
Definition 5.4
Let \(A\le B\) be abelian groups. Let \(\mathsf {V}\) be a vertex algebra graded by \(A\) and let \(\mathcal {M}_1\) and \(\mathcal {M}_2\) be modules over \(\mathsf {V}\), graded by \(B\). We define the following properties for functionals \(\psi \in {{\,\mathrm{Hom}\,}}(\mathcal {M}_1\otimes \mathcal {M}_2,{\mathbb {C}})\).
-
(1)
\(P(w)\)-compatibility:
-
(1)
Lower truncation: For any \(v\in \mathsf {V}\), \(v_n\psi =0\), for any sufficiently large \(n\in \mathbb {Z}\).
-
(2)
For any \(v\in \mathsf {V}\) and \(f\in \mathbb {C}[t,t^{-1},(t^{-1}-w)^{-1}]\) the identity
$$\begin{aligned} v f(t)\psi = v \iota _+\left( f(t) \right) \psi \end{aligned}$$(5.11)holds. Here \(\iota _+\) means expanding about \(t=0\) such that the exponents of \(t\) are bounded below and the action of \(\mathsf {V}\otimes \mathbb {C}[t,t^{-1},(t^{-1}-w)^{-1}]\) or \(\mathsf {V}\otimes \mathbb {C}((t))\) on \(\psi \) is characterised by
$$\begin{aligned} \langle vg(t)\psi ,m_1\otimes m_2 \rangle =\langle \psi ,\iota _+\circ T_w\left( v^{{{\,\mathrm{opp}\,}}}g(t^{-1}) \right) m_1\otimes m_2 \rangle + \langle \psi ,m_1\otimes \iota _+\left( v^{{{\,\mathrm{opp}\,}}} g(t^{-1}) \right) m_2 \rangle , \end{aligned}$$(5.12)where \(m_i\in \mathcal {M}_i\), \(v\in \mathsf {V}\), \(g\in \mathbb {C}[t,t^{-1},(t^{-1}-w)^{-1}]\), \(T_w\) replaces \(t\) by \(t+w\), \(v^{{{\,\mathrm{opp}\,}}}={\mathsf {e}}^{t^{-1}L_1}(-t^2)^{L_0}vt^{-2}\), and (assuming \(v\) has conformal weight \(h\)) \(vt^n m_i= v_{n-h+1}m_i\).
Denote by \({{\,\mathrm{COMP}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \) the vector space of all \(P(w)\)-compatible functionals.
-
(1)
-
(2)
\(P(w)\)-local grading restriction:
-
(1)
The functional \(\psi \) is a finite sum of vectors that are both \(B\)-homogeneous and \(L_0\) generalised eigenvectors.
-
(2)
Denote the smallest subspace of \({{\,\mathrm{Hom}\,}}(\mathcal {M}_1\otimes \mathcal {M}_2,{\mathbb {C}})\) containing \(\psi \) and stable under \(V\otimes \mathbb {C}[t,t^{-1}]\) by \(\mathcal {M}_\psi \). Then \(\mathcal {M}_\psi \) must satisfy for any \(r\in \mathbb {C}, b\in B\)
$$\begin{aligned} \dim \left( {\mathcal {M}_\psi }_{[r ]}^{\left( b \right) } \right) < \infty ,\qquad \text {and}\qquad \dim \left( {\mathcal {M}_\psi }_{[r+k ]}^{\left( b \right) } \right) =0, \end{aligned}$$(5.13)for sufficiently large \(k\in \mathbb {Z}\).
Denote by \({{\,\mathrm{LGR}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \) the vector space of all \(P(w)\)-local grading restricted functionals.
-
(1)
Define  .
.
Remark
The variable w in P(w) denotes the insertion point of the tensor product constructed in [21], where it is usually denoted z and hence the tensor product is referred to as the P(z)-tensor product.
Theorem 5.5
(Huang-Lepowsky-Zhang [21, Part IV, Theorem 5.44, 5.45, 5.50]). Let \(A\le B\) be abelian groups. Let \(\mathsf {V}\) be a vertex algebra graded by \(A\) with a choice of module category \(\mathscr {C}\) which is closed under restricted duals and let \(\mathcal {M}_1, \mathcal {M}_2\in \mathscr {C}\) be graded by \(B\). Then \({{\,\mathrm{COMP}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \) and  are modules over \(\mathsf {V}\). Further, if
are modules over \(\mathsf {V}\). Further, if  , then
, then 
In [21]  is originally defined as the image of all intertwining operators with \(\mathcal {M}_1\) and \(\mathcal {M}_2\) as factors, but it is then shown that this is equivalent to the definition given above. The construction of fusion products through Definition 5.4 is sometimes called the HLZ double dual construction. In addition to the primary reference [21], the authors also recommend the survey [38], which relates this construction of fusion to others in the literature.
is originally defined as the image of all intertwining operators with \(\mathcal {M}_1\) and \(\mathcal {M}_2\) as factors, but it is then shown that this is equivalent to the definition given above. The construction of fusion products through Definition 5.4 is sometimes called the HLZ double dual construction. In addition to the primary reference [21], the authors also recommend the survey [38], which relates this construction of fusion to others in the literature.
Theorem 5.6
(Huang-Lepowsky-Zhang [21, Part VIII, Theorem 12.15], Huang [37, Theorem 3.1]). For any vertex algebra and module category \(\mathscr {C}\) satisfying the conditions below, fusion equips category \(\mathscr {C}\) with the structures of an additive braided tensor category.
-
(1)
The vertex algebra and all its modules in \(\mathscr {C}\) are strongly graded and all logarithmic intertwining operators are grading compatible. [21, Part III, Assumption 4.1].
-
(2)
\(\mathscr {C}\) is a full subcategory of the category of strongly graded modules and is closed under the contragredient functor and under taking finite direct sums [21, Part IV, Assumption 5.30].
-
(3)
All objects in \(\mathscr {C}\) have real weights and the non-semisimple part of \(L_0\) acts on them nilpotently [21, Part V, Assumption 7.11].
-
(4)
\(\mathscr {C}\) is closed under images of module homomorphisms [21, Part VI, Assumption 10.1.7].
-
(5)
The convergence and extension properties for either products or iterates holds [21, Part VII, Theorem 11.4].
-
(6)
For any objects \(\mathcal {M}_1, \mathcal {M}_2 \in \mathscr {C}\), let \(\mathcal {M}_{v}\) be the doubly graded \(\mathsf {V}\)-module generated by a \(B\)-homogeneous generalised \(L_0\) eigenvector \(v \in {{\,\mathrm{COMP}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \). If \(\mathcal {M}_{v}\) is lower bounded then \(\mathcal {M}_{v}\) is strongly graded and an object in \(\mathscr {C}\) [37, Theorem 3.1]. Here the action of \(L_0\) is defined by (5.12), given in Definition 5.4.
Conditions (1) – (4) of Theorem 5.6 hold by construction for category \(\mathscr {F}\), so all that remains is verifying Conditions (5) and (6).
Theorem 5.7
Let \(A\le B\) be abelian groups, let \(\mathsf {V}\) be a doubly \(A\)-graded vertex operator algebra and let \(\overline{\mathsf {V}}\) be a vertex subalgebra of \(\mathsf {V}^{(0)}\). Further, let \(\mathcal {W}_i,\ i=0,1,2,3,4\) be doubly \(B\)-graded \(\mathsf {V}\)-modules. Finally let \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\), \({\mathcal {Y}}_3\) and \({\mathcal {Y}}_4\) be logarithmic grading compatible intertwining operators of types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_1,\ \mathcal {W}_4\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_2,\ \mathcal {W}_3\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_4,\ \mathcal {W}_3\end{array}}\right) \) and \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_1,\ \mathcal {W}_2\end{array}}\right) \) respectively. If the modules \(\mathcal {W}_i,\ i=0,1,2,3\) (note \(i=4\) is excluded) are discretely strongly graded, and graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules, then \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\) satisfy the convergence and extension property for products and \({\mathcal {Y}}_3\), \({\mathcal {Y}}_4\) satisfy the convergence and extension property for iterates.
The above theorem follows from the proof of [25, Theorem 7.2], however, in [25] some assumptions are made on the category of strongly graded modules (see [25, Assumption 7.1, Part 3]) which do not hold for \(\mathsf {G}\). Fortunately, the proof of Theorem 5.7 does not depend at all on any categorical considerations or even on the details of the intertwining operators \({\mathcal {Y}}_i\) beyond their types. It merely depends on certain finiteness properties of the modules \(\mathcal {W}_i\). We reproduce the proof of Yang in Appendix A, with some minor tweaks to the arguments, to show that the conclusion of Theorem 5.7 holds, without making any assumptions on the category of all strongly graded modules.
Lemma 5.8
The convergence and extension properties for products and iterates holds for \(\mathscr {F}\).
Proof
If, in the assumptions of Theorem 5.7, we set \(\mathsf {V} = \mathsf {G}\) and grade by ghost weight, so that \(A = \mathbb {Z}\), then the modules of \(\mathscr {F}\) are graded by \(B=\mathbb {R}\). We further choose \(\overline{\mathsf {V}} = \mathsf {G}^{(0)}\), that is, the vertex subalgebra given by the ghost weight 0 subspace of \(\mathsf {G}\). The lemma then follows by verifying that all modules in \(\mathscr {F}\) are discretely strongly graded and graded \(C_1\)-cofinite as modules over \(\overline{\mathsf {V}}\).
All modules in \(\mathscr {F}\) are discretely strongly graded by ghost weight \(j \in \mathbb {R}\). To prove this, we need to check that the simultaneous ghost and conformal weight spaces are finite dimensional and that every ghost weight homogeneous space has lower bounded conformal weights. The simultaneous ghost and conformal weight spaces of objects in \(\mathscr {R}\) and therefore also those of \(\sigma ^{\ell } \mathscr {R}\) are finite dimensional by construction. Thus, since the objects of \(\mathscr {F}\) are finite length extensions of those in \(\sigma ^{\ell } \mathscr {R}\), the objects of \(\mathscr {F}\) also have finite dimensional simultaneous ghost and conformal weight spaces. Similarly we have that the objects in \(\mathscr {F}\) are graded lower bounded and therefore discretely strongly graded.
Next we need to decompose objects of \(\mathscr {F}\) as \(\overline{\mathsf {V}}\)-modules,. It is known that \(\overline{\mathsf {V}}\) is generated by \(\lbrace {} {:} {}{\beta (z) \left( \partial ^n \gamma (z) \right) {:} }, \ n \ge 0 \rbrace \) and is isomorphic to \(W_{1+\infty } \cong W_{3,-2} \otimes {\mathcal {H}}\) where \(W_{3,-2}\) is the singlet algebra at \(c=-2\) and \({\mathcal {H}}\) is a rank 1 Heisenberg algebra [39, 40]. Note that the conformal vector of \(W_{1+\infty }\) is usually chosen so as to have a central charge of \(1\). Since we require \(\overline{\mathsf {V}}\) to embed conformally into \(\mathsf {G}\), that is, to have the same conformal vector as \(\mathsf {G}\) and the central charge of \(\mathsf {G}\) is \(2\), we choose conformal vector of our Heisenberg algebra \({\mathcal {H}}\) so that its central charge is 4 (the conformal structure of \(W_{3,-2}\) is unique). Fortunately, this does not complicate matters, as the simple modules over \({\mathcal {H}}\) are just Fock spaces regardless of the central charge or conformal vector. The tensor factors of \(W_{1+\infty }\) decompose nicely with respect to the free field realisation of Proposition 2.12.(2). The Heisenberg algebra \({\mathcal {H}}\) is generated by \(\theta (z)\) and the singlet algebra \(W_{3,-2}\) is a vertex subalgebra of the Heisenberg algebra generated by \(\psi (z)\).
We denote Fock spaces over the rank 1 Heisenberg algebras generated by \(\psi \) and \(\theta \), respectively, by the same symbol \(\mathcal {F}_{\mu }\), where, the index \(\mu \in \mathbb {C}\) indicates the respective eigenvalues of the zero modes \(\psi _0\) and \(\theta _0\). All simple \(\overline{\mathsf {V}} \cong W_{1 + \infty }\) modules can be constructed via its free field realisation as \(\mathcal {V}_{\left( \lambda ,\psi \right) } \otimes \mathcal {F}_{\left( \lambda ,\theta \right) }\) [41, Corollary 6.1], where \(\mathcal {V}_{\left( \lambda ,\psi \right) }\), as a \(W_{3,-2}\)-module, is the simple quotient of the submodule of \(\mathcal {F}_{\left( \lambda ,\psi \right) }\) generated by the highest weight vector. The homogeneous space \(\left( \sigma ^{\ell } \mathcal {V} \right) ^{(j)}\) is simple, as a \(\overline{\mathsf {V}}\)-module [39, Lemma 4.1], see also [42, 43]. Recall from Proposition 2.12.(2) that with \(K={{\,\mathrm{span}\,}}_{\mathbb {Z}}\lbrace \psi ,\theta \rbrace \) and \(\Lambda \in L/K\), we can construct the simple projective \(\mathsf {G}\)-modules as \({\sigma ^{\left( \Lambda ,\psi +\theta \right) } \mathcal {W}_{\left( \Lambda ,\psi \right) }} \cong {{\mathbb {F}}_{\Lambda }}\). To identify the homogeneous space \(\left( \sigma ^{\left( \Lambda ,\psi +\theta \right) } \mathcal {W}_{\left( \Lambda ,\psi \right) } \right) ^{(j)}\) as a \(\overline{\mathsf {V}}\)-module, we use the fact that \(J(z) = - \theta (z)\), thus the \(\mathbb {R}\)-grading on \({\mathbb {F}}_{\Lambda }\) is given by the eigenvalue of \(-\theta _0\). Therefore, for \(j\in \mathbb {R}\),
For \(\left( \Lambda ,\psi +\theta \right) +j \notin \mathbb {Z}\), \(\mathcal {F}_{\left( \Lambda ,\psi +\theta \right) +j}\) is irreducible as a \({\mathcal {W}}_{3,-2}\) module, by [44, Section 3.2], see also [45, Section 5]. Thus, \(\left( \sigma ^{\left( \Lambda ,\psi +\theta \right) } \mathcal {W}_{\left( \Lambda ,\psi \right) } \right) ^{(j)} \cong \mathcal {F}_{\left( \Lambda ,\psi +\theta \right) +j} \otimes \mathcal {F}_{-j}=\mathcal {V}_{\left( \Lambda ,\psi +\theta \right) +j} \otimes \mathcal {F}_{-j} \). The finite length modules of \(W_{3,-2}\) are all \(C_1\)-cofinite [46, Corollary 14], as are \({\mathcal {H}}\)-modules, since Fock spaces have \(C_1\)-codimension 1. Therefore all \(\overline{\mathsf {V}}\)-modules appearing as the homogeneous spaces of modules in \(\mathscr {F}\) are \(C_1\)-cofinite and the lemma follows. \(\square \)
Lemma 5.9
Let \(\mathcal {M}_1,\mathcal {M}_2\) be modules in \(\mathscr {F}\), let \(\mathcal {W}\) be an indecomposable smooth (or weak) \(\mathsf {G}\) module and let \({\mathcal {Y}}\) be a surjective logarithmic intertwining operator of type \(\left( {\begin{array}{c}\mathcal {W}\\ \mathcal {M}_1,\ \mathcal {M}_2\end{array}}\right) \).
-
(1)
The logarithmic intertwining operator \({\mathcal {Y}}\) is grading compatible and the module \(\mathcal {W}\) is doubly graded.
-
(2)
If \(\mathcal {M}_1\in \sigma ^{k} \mathscr {R} ,\mathcal {M}_2 \in \sigma ^{\ell } \mathscr {R}\), then \(\mathcal {W}\in \mathscr {F}\) and \(\mathcal {W}\) has composition factors only in \(\sigma ^{k+\ell } \mathscr {R}\) and \(\sigma ^{k+\ell -1} \mathscr {R}\).
-
(3)
If \(\mathcal {M}_1\) has composition factors only in \(\sigma ^{k} \mathscr {R}\) and \(\sigma ^{k-1} \mathscr {R}\), and has composition factors only in \(\sigma ^{\ell } \mathscr {R}\) and \(\sigma ^{\ell -1} \mathscr {R}\), \(\mathcal {W}\in \mathscr {F}\) and \(\mathcal {W}\) has composition factors only in \(\sigma ^{k+\ell +i} \mathscr {R}, -3\le i\le 0\).
Proof
Due to the compatibility of fusion with spectral flow, see Theorem 2.6, it is sufficient to only consider \(k=\ell =0\). We prove Part (1) first. Let \(\mathcal {M}_1,\mathcal {M}_2\), be modules in \(\mathscr {F}\). Let \(v\in \mathsf {G}\) be the vector corresponding to the field \(J(z)\) and take the residue with respect to \(x_0\) and \(x_1\) in the Jacobi identity (5.8). This yields
Hence, since the fusion factors \(\mathcal {M}_i\) are graded by ghost weight, the fusion product will be too. This means that the intertwining operator will be grading compatible and \(\mathcal {W}\) must be doubly graded.
Next we prove Part (3). Assume that \(\mathcal {M}_1,\mathcal {M}_2\) have composition factors only in \(\mathscr {R}\) and \(\sigma ^{-1} \mathscr {R}\). Note that \(J_n,\ n\ge 1\) acts locally nilpotently on any object in \(\mathscr {F}\) and that \(\beta _{n-\ell },\ \gamma _{n+\ell },\ n\ge 1\) act locally nilpotently on any object in \(\sigma ^{\ell } \mathscr {R}\) (recall that local nilpotence is one of the defining properties of \(\sigma ^{\ell } \mathscr {R}\)). We first show that \(J_{n},\ \beta _{n+1},\ \gamma _n,\ n\ge 1\) acting locally nilpotently on \(\mathcal {M}_1, \mathcal {M}_2\) implies that \(J_{n},\ \beta _{n+3},\ \gamma _n,\ n\ge 1\) act locally nilpotently on \(\mathcal {W}\). Let \(h\) be the conformal weight of \(v=\beta ,\gamma \) or \(J\), multiply both sides of the Jacobi identity (5.8) by \(x_0^kx_1^{n+h-1},\ n,k\in \mathbb {Z}\) and take residues with respect to \(x_0\) and \(x_1\). This yields
Set \(v=\gamma \) (and thus \(h=0\)) and \(k=0\) in (5.16) to obtain
This implies the local nilpotence of \(\gamma _n,\ n\ge 1\) on \({\mathcal {Y}}\left( m_1,x_2 \right) m_2\) from its local nilpotence on \(m_1\) and \(m_2\). Next consider \(v=J\) (and thus \(h=1\)) and \(k=1\) in (5.16) to obtain
Since \(J_k,\ k\ge 1\) is nilpotent on both \(m_1\) and \(m_2\), we see that \(J_{n}-x_2 J_{n-1}\) is nilpotent for \(n\ge 2\). Recall that the series expansion of the intertwining operator
satisfies a lower truncation condition, that is, for fixed \(s\), if there exists a \(u\in \mathbb {C}\) satisfying \(m_{(u,s)}\ne 0\), then there exists a minimal representative \(t\in u+\mathbb {Z}\) such that \(m_{(t,s)}\ne 0\) and \(m_{(t',s)}=0\) for all \(t'<t\). Since \(J_{n}-x_2 J_{n-1}\) is nilpotent on \({\mathcal {Y}}\left( m_1,x_2 \right) m_2\) it is also nilpotent on the leading term \(m_{(t,s)}\). By comparing coefficients of \(x_2\) and \(\log x_2\) it then follows that \(J_n,\ n\ge 2\) acts nilpotently on \(m_{(t,s)}\) and by induction also on all coefficients of higher powers of \(x_2\). To show that \(J_1\) acts locally nilpotently, assume that \(m_1\) has \(J_0\)-eigenvalue \(j\) and set \(n=1, \ k=0\) in (5.16) to obtain
Thus \(J_1-x_2 j\) is nilpotent, which by the previous leading term argument implies that \(J_1\) is too. Finally, consider \(v=\beta \) (and thus \(h=1\)) and \(k=2\) in (5.16) to obtain
By leading term arguments analogous to those used for \(J_n\), this implies that \(\beta _n\) acts locally nilpotently for \(n\ge 4\).
Consider the subspace \(V\subset \mathcal {W}\) annihilated by \(\beta _{n+3}\), \(\gamma _n\), \(n\ge 1\). Then \(V\) is a module over four commuting copies of the Weyl algebra respectively generated by the pairs \((\beta _0,\gamma _0),\ (\beta _1,\gamma _{-1}),\ (\beta _2,\gamma _{-2}),\ (\beta _3,\gamma _{-3})\). Further, \(V\) is closed under the action of \(J_n,\ n\ge 1\) and restricted to acting on \(V\), the first few \(J_n\) modes expand as
We show that on any composition factor of \(V\) at least three of the four Weyl algebras have a generator acting nilpotently and that thus the induction of such a composition factor is an object in one of the categories \(\sigma ^{i} \mathscr {R},\ -3\le i\le 0\). Let \(C_0\otimes C_1\otimes C_2\otimes C_3\) be isomorphic to a composition factor of \(V\), where \(C_i\) is a simple module over the Heisenberg algebra generated by the pair \((\beta _i,\gamma _{-i})\). Since \(J_1,J_2,J_3\) act locally nilpotently on \(V\) they must also do so on \(C_0\otimes C_1\otimes C_2\otimes C_3\) using the expansions (5.22). If we assume that neither \(\beta _3\) nor \(\gamma _0\) act locally nilpotently on \(C_3\) and \(C_0\), respectively, that is there exist \(c_3\in C_3\) and \(c_0\in C_0\) such that \({\mathsf {U}}\left( \beta _3 \right) c_3\) and \({\mathsf {U}}\left( \gamma _0 \right) c_0\) are both infinite dimensional, and choose \(c_1,c_2,\) to be non-zero vectors in \(C_1\) and \(C_2\), respectively. Then \({\mathsf {U}}\left( J_3 \right) (c_0\otimes c_1\otimes c_2\otimes c_3)\) will be infinite dimensional contradicting the local nilpotence of \(J_3\). So assume \(\beta _3\) acts locally nilpotently but \(\gamma _0\) does not, and let \(c_3\in C_3\) be annihilated by \(\beta _3\) and \(c_0,c_1,c_2\) be non-zero vectors in \(C_0,C_2,C_3\), respectively. On this vector \(J_2\) evaluates to
By the same reasoning as before, unless either \(\beta _2\) or \(\gamma _0\) act nilpotently, we have a contradiction to the nilpotence of \(J_2\), so \(\beta _2\) must act nilpotently on \(c_2\). Repeating this argument for \(J_1\) and assuming \(\beta _2 c_2=0\) we have a contradiction to the nilpotence of \(J_1\) unless \(\beta _1\) acts nilpotently. The composition factor isomorphic to \(C_0\otimes C_1\otimes C_2\otimes C_3\) thus induces to an object in \(\mathscr {R}\). Repeating the previous arguments, assuming that \(\gamma _0\) acts locally nilpotently but \(\beta _3\) does not, implies that \(\gamma _{-1}\) and \(\gamma _{-2}\) must act locally nilpotently to avoid contradictions to the local nilpotence of \(J_1,J_2,J_3\). Such a composition factor would induce to a module in \(\sigma ^{-3} \mathscr {R}\). Finally assume both \(\beta _3\) and \(\gamma _0\) act locally nilpotently, then analogous arguments to those used above applied to the action of \(J_1\) imply that at least one of \(\beta _2\) or \(\gamma _{-1}\) act locally nilpotently. Such a composition factor would induce to an object in \(\sigma ^{-2} \mathscr {R}\) or \(\sigma ^{-1} \mathscr {R}\), respectively.
The final potential obstruction to \(\mathcal {W}\) lying in \(\mathscr {F}\) is that such a submodule might not be finite length. However, if \(\mathcal {W}\) had infinite length, it would have to admit indecomposable subquotients of arbitrary finite length, yet by the classification of indecomposable modules in Theorem 4.2, a finite length indecomposable module with composition factors only in \(\sigma ^{i} \mathscr {R},\ -3\le i\le 0\) has length at most 5. Therefore \(\mathcal {W}\in \mathscr {F}\).
Part (2) follows by a similar but simplified version of the above arguments. \(J_n\) and \(\gamma _n\) continue to satisfy the same nilpotence conditions as above, however for \(\beta \) one needs to reconsider (5.16) with \(k=1\) to conclude that \(\beta _n,\ n\ge 2\) is nilpotent. The remainder of the argument follows analogously. \(\square \)
Proof of Theorem 5.1
We verify that the assumptions of Theorem 5.6 hold, in numerical order. Theorem 5.6 thus implies that category \(\mathscr {F}\) is an additive braided tensor category. Additionally, since category \(\mathscr {F}\) is abelian, it is a braided tensor category.
-
(1)
All modules in category \(\mathscr {F}\) are strongly graded by ghost weight \(j \in \mathbb {R}\). Further, by Lemma 5.9.(1), all logarithmic intertwining operators are grading compatible.
-
(2)
By Proposition 2.11, category \(\mathscr {F}\) is closed under taking restricted duals. Closure under finite direct sums holds by construction, since category \(\mathscr {F}\) is abelian.
-
(3)
The modules in \(\mathscr {F}\) have real conformal weights by definition. The only modules on which the non semi-simple part of \(L_0\) acts non-trivially are \(\sigma ^{m} \mathcal {P}_{n}\), for which it squares to zero.
-
(4)
Closure under images of module homomorphisms holds by construction, since category \(\mathscr {F}\) is abelian.
-
(5)
The convergence and extension properties hold by Lemma 5.8.
-
(6)
Since the \(P(w)\)-tensor product is right exact, by [21, Part IV, Proposition 4.26], and since category \(\mathscr {F}\) has sufficiently many projectives, that is, every module can be realised as a quotient of a direct sum of indecomposable projectives, we can without loss of generality assume \(\mathcal {M}_1\) and \(\mathcal {M}_2\) are indecomposable projective modules, as Condition (6) holding for projective modules implies that it also holds for their quotients. Further, due to the compatibility of fusion with spectral flow, we can pick \(\mathcal {M}_1\) and \(\mathcal {M}_2\) to be isomorphic to \(\mathcal {W}_{\lambda }\) or \(\mathcal {P}\). Let \(\nu \in {{\,\mathrm{COMP}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \) be doubly homogenous and assume that the module \(\mathcal {M}_\nu \) generated by \(\nu \) is lower bounded. By assumption, the functional \(\nu \) therefore satisfies all the properties of \(P(w)\)-local grading restriction except for the finite dimensionality of the doubly homogeneous spaces of \(\mathcal {M}_\nu \). We need to show the finite dimensionality of these doubly homogeneous spaces and that \(\mathcal {M}_\nu \) is an object in \(\mathscr {F}\). Since \(\mathcal {M}_\nu \) is finitely generated (cyclic even) it is at most a finite direct sum. To see this, assume the module admits an infinite direct sum. Then the partial sums define an ascending filtration whose union is the entire module. Hence after some finite number of steps all generators must appear within this filtration, but if this finite sum contains all generators, it must be equal to the entire module and hence all later direct summands must be zero. Denote the direct summands by \(\mathcal {M}_{\nu ,i}, \ i \in I\), where \(I\) is some finite index set. By [21, Part IV, Proposition 5.24] there exists a smooth \(\mathsf {G}\) module \(\mathcal {W}_{\nu ,i}\) such that \(\mathcal {W}_{\nu ,i}^\prime \cong \mathcal {M}_{\nu ,i}\) and a surjective intertwiner of type \(\left( {\begin{array}{c}\mathcal {W}_{\nu ,i}\\ \mathcal {M}_1,\ \mathcal {M}_2\end{array}}\right) \). Hence, by Lemma 5.9, \(\mathcal {W}_{\nu ,i}\in \mathscr {F}\). In particular, since category \(\mathscr {F}\) is closed under taking restricted duals and all its objects have finite dimensional doubly homogeneous spaces, we have \(\mathcal {M}_{\nu ,i}\in \mathscr {F}\) and \(\mathcal {M}_\nu \in \mathscr {F}\).
\(\square \)
Remark
Note that the above proof did not make any use of \(\mathcal {M}_\nu \) being lower bounded to conclude that \(\mathcal {M}_\nu \in \mathscr {F}\) and that membership of category \(\mathscr {F}\) implies lower boundedness.
Lemma 5.10
For \(\lambda \in \mathbb {R}/\mathbb {Z}\), \(\lambda \ne \mathbb {Z},\) the fusion product \(\sigma ^{\ell } \mathcal {W}_{\lambda } \mathbin {\boxtimes }\sigma ^{k} \mathcal {W}_{-\lambda }\) has exactly one direct summand isomorphic to \(\sigma ^{\ell +k-1} \mathcal {P}\).
We will prove the above lemma by showing that  has exactly one submodule isomorphic to \(\mathcal {P}\). This requires finding linear functionals which satisfy \(P(w)\) compatibility. This is very difficult to do in practice, since (5.11) needs to be checked for every vector \(v\in V\). Fortunately there is a result by Zhang which cuts this down to generators. Zhang originally formulated the theorem below for a related type of fusion product called the \(Q(z)\)-tensor product, so we have translated his result to the \(P(w)\)-tensor product, which we use here.
has exactly one submodule isomorphic to \(\mathcal {P}\). This requires finding linear functionals which satisfy \(P(w)\) compatibility. This is very difficult to do in practice, since (5.11) needs to be checked for every vector \(v\in V\). Fortunately there is a result by Zhang which cuts this down to generators. Zhang originally formulated the theorem below for a related type of fusion product called the \(Q(z)\)-tensor product, so we have translated his result to the \(P(w)\)-tensor product, which we use here.
Theorem 5.11
(Zhang [47, Theorem 4.7]). Let \(A\le B\) be abelian groups. Let \(\mathsf {V}\) be a vertex algebra graded by \(A\) with a set of strong generators \(S\) and let \(\mathcal {M}_1\) and \(\mathcal {M}_2\) be modules over \(\mathsf {V}\), graded by \(B\). A functional \(\psi \in {{\,\mathrm{Hom}\,}}(\mathcal {M}_1\otimes \mathcal {M}_2,{\mathbb {C}})\) is said to satisfy the strong lower truncation condition for a vector \(v\in \mathsf {V}\), if there exists an \(N\in \mathbb {N}\) such that for all \(n,m\in \mathbb {Z}\), with \(m\ge N\), we have
Then \(\psi \in {{\,\mathrm{Hom}\,}}(\mathcal {M}_1\otimes \mathcal {M}_2,{\mathbb {C}})\) satisfies the \(P(w)\)-compatibility condition if and only if it satisfies the strong lower truncation condition for all elements of \(S\).
We further prepare some helpful identities.
Lemma 5.12
Let \(\mathcal {M}_1, \mathcal {M}_2\in \mathscr {F}\), \(m_i\in \mathcal {M}_i,\ i=1,2\), and \(\psi \in {{\,\mathrm{COMP}\,}}\left( \mathcal {M}_1,\mathcal {M}_2 \right) \), then we have the identities.
Proof
These identities follow by evaluating (5.12) for the fields \(\beta ,\gamma , J\) and \(T\). \(\square \)
Proof of Lemma 5.10
We shall use the HLZ double dual construction of Definition 5.4. By the compatibility of fusion with spectral flow, Theorem Theorem 2.6, it is sufficient to consider the case \(\ell =k=0\). Note since \(\sigma ^{-1} \mathcal {P}\) is both projective and injective, it must be a direct summand if it appears as either a quotient or a subspace. Further, by Lemma 5.9, all composition factors must lie in categories \(\sigma ^{i} \mathscr {R},\ i=-1,0\). This implies that the composition factors of
 must all lie in \(\sigma ^{i} \mathscr {R},\ i=0,1\). Note further, that \((\sigma ^{-1} \mathcal {P})'\cong \mathcal {P}\) and so we seek to find a copy of \(\mathcal {P}\) within
must all lie in \(\sigma ^{i} \mathscr {R},\ i=0,1\). Note further, that \((\sigma ^{-1} \mathcal {P})'\cong \mathcal {P}\) and so we seek to find a copy of \(\mathcal {P}\) within  . We do so by considering a certain characterising two dimensional subspace of \(\mathcal {P}\). For a \(\mathsf {G}\)-module \(\mathcal {M}\) consider the subspace
. We do so by considering a certain characterising two dimensional subspace of \(\mathcal {P}\). For a \(\mathsf {G}\)-module \(\mathcal {M}\) consider the subspace

From the expansions of \(T(z)\) and \(J(z)\) in terms of the fields \(\beta \) and \(\gamma \), it follows that for any \(m\in K(\mathcal {M})\), \(L_0^2 m=L_{n}m=J_n m=0,\ n\ge 1\). In particular, in the notation of Figure 2, \(K(\mathcal {P})={{\,\mathrm{span}\,}}_{\mathbb {C}}\lbrace |0 \rangle ,|-\psi \rangle \rbrace \) and thus \(K(\mathcal {P})\) is two dimensional and \(L_0\) has a rank 2 Jordan block of generalised eigenvalue 0 on this space. Further, \(\mathcal {P}\) is the only indecomposable module with composition factors in categories \(\sigma ^{i} \mathscr {R},\,i=0, 1\) admitting \(L_0\) Jordan blocks. The remaining indecomposable modules with composition factors in categories \(\sigma ^{i} \mathscr {R},\,i=0, 1\) all have \(K(\mathcal {M})\) subspaces of dimension zero or one.
Let \(\psi \in {{\,\mathrm{Hom}\,}}\left( \mathcal {W}_{\lambda }\otimes \mathcal {W}_{-\lambda },\mathbb {C} \right) \) satisfy \(\beta t^{k+n}(t^{-1}-w)^n\psi =\gamma t^{k+n}(t^{-1}-w)^n\psi =0\) for all \(m\ge 1\). Thus by Theorem 5.11, \(\psi \) satisfies the \(P(w)\)-compatibility property and \(\beta _m\psi =\gamma _{m+1}\psi =0,\ m\ge 1\). If in addition \(\psi \) is doubly homogeneous, then \(\psi \) lies in  . By assumption the left-hand sides of (5.27) and (5.28) vanish for \(k\ge 1\). These relations imply that the value of \(\psi \) on any vector in \(\mathcal {W}_{\lambda }\otimes \mathcal {W}_{-\lambda }\) is determined by its value on tensor products of relaxed highest weight vectors, because negative modes on one factor can be traded for less negative modes on the other factor. For example, for \(k=1, \ n=0\) in (5.27), we have the relation
. By assumption the left-hand sides of (5.27) and (5.28) vanish for \(k\ge 1\). These relations imply that the value of \(\psi \) on any vector in \(\mathcal {W}_{\lambda }\otimes \mathcal {W}_{-\lambda }\) is determined by its value on tensor products of relaxed highest weight vectors, because negative modes on one factor can be traded for less negative modes on the other factor. For example, for \(k=1, \ n=0\) in (5.27), we have the relation
Let \(u_{\pm j}\in \mathcal {W}_{\pm \lambda },\ j\in \pm \lambda \) be a choice of normalisation of relaxed highest weight vectors satisfying \(u_{\pm j-1}=\gamma _0 u_{\pm j}\). This implies \(\beta _0 u_{\pm j}=\pm j u_{1\pm j}\). Since the negative \(\beta \) and \(\gamma \) modes act freely on the simple projective modules \(\mathcal {W}_{\lambda }\) and \(\mathcal {W}_{-\lambda }\), there are no relations in addition to those coming from \(\beta t^{k+n}(t^{-1}-w)^n\psi =\gamma t^{k+n}(t^{-1}-w)^n\psi =0\) for all \(m\ge 1\) . Thus there is a linear isomorphism

Clearly,  is a subspace of
is a subspace of  and so we impose the remaining two relations, the vanishing of \(J_0\) and \(J_1\), via (5.25). The vanishing of \(J_0\psi \) implies
and so we impose the remaining two relations, the vanishing of \(J_0\) and \(J_1\), via (5.25). The vanishing of \(J_0\psi \) implies
Thus \(\psi \) vanishes on \(u_j\otimes u_{-i}\) unless \(i=j-1\). The vanishing of \(J_1\psi \) implies
where we have used \(J_{-1}u_{1-j}=\left( \gamma _{-1}\beta _0+\beta _{-1}\gamma _0 \right) u_{1-j}\). Thus \(\psi \) is completely characterised by its value on a two pairs of relaxed highest weight vectors, say \(u_{j}\otimes u_{1-j}\) and \(u_{j+1}\otimes u_{-j}\). Therefore, the subspace  is two dimensional. Next we show that that \(L_0\) has a rank two Jordan block on it when acting on this space. Let
is two dimensional. Next we show that that \(L_0\) has a rank two Jordan block on it when acting on this space. Let  . If \(\psi \ne 0\), then there exist \(a,b\in \mathbb {C}\), not both zero, such that
. If \(\psi \ne 0\), then there exist \(a,b\in \mathbb {C}\), not both zero, such that
The evaluation of \(L_0\psi \) on \(u_{j}\otimes u_{1-j}\) and \(u_{j+1}\otimes u_{-j}\) is then
Therefore if \(a\ne b\) (a choice which we can make as  is two dimensional), the vectors \(\psi \) and \(L_0\psi \) are linearly independent and span
is two dimensional), the vectors \(\psi \) and \(L_0\psi \) are linearly independent and span  , which also shows that \(L_0\) has a rank two Jordan block. \(\square \)
, which also shows that \(L_0\) has a rank two Jordan block. \(\square \)
Remark
In [16, Section 7] the above fusion product was computed using the NGK algorithm up to certain conjectured additional conditions. In light of the survey [38] explaining the equivalence of the HLZ double dual construction and the NGK algorithm, the authors thought it appropriate to supplement the NGK calculation of [16] with an HLZ double dual calculation here.
Proposition 5.13
For all \(\ell \in \mathbb {Z}\) and \(\lambda \in \mathbb {R}/\mathbb {Z}\), \(\lambda \ne \mathbb {Z}\), the simple module \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) is rigid in category \(\mathscr {F}\), with tensor dual given by \(\left( \sigma ^{\ell } \mathcal {W}_{\lambda } \right) ^\vee =\sigma ^{1-\ell } \mathcal {W}_{-\lambda }\).
Proof
Recall that an object \(\mathcal {M}\) in a tensor category is rigid if there exists an object \(\mathcal {M}^\vee \) (called a tensor dual of \(\mathcal {M}\)) and two morphisms \(e_\mathcal {M}: \mathcal {M}^\vee \mathbin {\boxtimes }\mathcal {M}\rightarrow \mathcal {V}\) and \(i_\mathcal {M}: \mathcal {V}\rightarrow \mathcal {M}\mathbin {\boxtimes }\mathcal {M}^\vee \), respectively, called evaluation and coevaluation, such that the compositions
yield the identity maps \(1_\mathcal {M}\) and \(1_{\mathcal {M}^\vee }\), respectively. Here \(w_1,w_2\) are distinct non-zero complex numbers satisfying \(|w_2|>|w_1|\) and \(|w_2|>|w_2-w_1|\); \(\mathbin {\boxtimes }_w\) indicates the relative positioning of insertion points of fusion factors, that is, the right most factor will be inserted at 0, the middle factor at \(w_1\) and the left most at \(w_2\); Technically there exist distinct notions of left and right duals and the above properties are those for left duals. We prove below that \(\mathcal {M}=\sigma ^{\ell } \mathcal {W}_{\lambda }\) is left rigid. Right rigidity follows from left rigidity due to category \(\mathscr {F}\) being braided.
For \(\mathcal {M}= \sigma ^{\ell } \mathcal {W}_{\lambda }\) we take the tensor dual to be \(\mathcal {M}^\vee = \sigma ^{1-\ell } \mathcal {W}_{-\lambda }\) and we will construct the evaluation and coevaluation morphisms using the first free field realisation (2.34) given in Proposition 2.12.(1). In particular, we have
We denote fusion over the lattice vertex algebra \(\mathsf {V}_{K}\) of the free field realisation by \(\mathbin {\boxtimes }^{\mathsf {ff}}\) to distinguish it from fusion over \(\mathsf {G}\). Recall that the fusion product of Fock spaces over the lattice vertex algebra \(\mathsf {V}_{K}\) of the free field realisation just adds Fock space weights. Thus the fusion product over \(\mathsf {V}_{K}\) of the modules corresponding to \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) and \(\sigma ^{1-\ell } \mathcal {W}_{-\lambda }\) is given by
Therefore we have the \(\mathsf {V}_{K}\)-module map \({\mathcal {Y}}: {\mathbb {F}}_{-\lambda (\theta +\psi ) - \ell \psi } \mathbin {\boxtimes }^{\mathsf {ff}}{\mathbb {F}}_{\lambda (\theta +\psi ) +(\ell - 1) \psi }\rightarrow {\mathbb {F}}_{-\psi }\) given by the intertwining operator that maps the kets in the Fock space \({\mathbb {F}}_{\lambda (\theta +\psi ) +(\ell - 1) \psi }\) to vertex operators, that is, operators of the form (2.30). Since \(\mathsf {V}_{K}\)-module maps are also \(\mathsf {G}\)-module maps by restriction and since the fusion product of two modules over a vertex subalgebra is a quotient of the fusion product over the larger vertex algebra, \({\mathcal {Y}}\) also defines a \(\mathsf {G}\)-module map \( {\mathbb {F}}_{-\lambda (\theta +\psi ) - \ell \psi }\mathbin {\boxtimes }{\mathbb {F}}_{\lambda (\theta +\psi )+ (\ell -1) \psi } \rightarrow {\mathbb {F}}_{-\psi } \cong \mathcal {W}_{0}^-\). Furthermore, the screening operator \({\mathcal {S}}_{1}=\oint \mathrm {V}_{\psi }\left( z \right) \mathrm {d}z\) defines a \(\mathsf {G}\)-module map \({\mathcal {S}}_{1}: {\mathbb {F}}_{-\psi } \rightarrow {\mathbb {F}}_{0} \) with the image being the bosonic ghost vertex algebra \(\mathsf {G}\). Up to a normalisation factor, to be determined later, we define the evaluation map for \(\mathcal {M}=\sigma ^{\ell } \mathcal {W}_{\lambda }\) to be the composition of \({\mathcal {Y}}\) and the screening operator \({\mathcal {S}}_{1}\).
To define the coevaluation we need to identify a submodule of \(\mathcal {M}\mathbin {\boxtimes }\mathcal {M}^\vee \) isomorphic to \(\mathcal {V}\). By Lemma 5.10, we know that \(\mathcal {M}\mathbin {\boxtimes }\mathcal {M}^\vee \) has a direct summand isomorphic to \(\mathcal {P}\), which by Proposition 3.3 we know has a submodule isomorphic to \(\mathcal {V}\). It is this copy of \(\mathcal {V}\) which the coevaluation shall map to. Since \(\mathcal {V}\) is the vector space underlying the vertex algebra \(\mathsf {G}\) and any vertex algebra is generated from its vacuum vector, we characterise the coevaluation map by the image of the vacuum vector.
where the first arrow is the inclusion of \(\mathcal {V}\) into \( {\mathbb {F}}_{0} \cong \mathcal {W}_{0}^- \subset \mathcal {P}\), \({\mathcal {S}}_{1}^{-1}\) denotes picking preimages of \({\mathcal {S}}_{1}\) and \(j\) the unique representative of the coset \(\lambda \) satisfying \(0< j< 1\). Note that the ambiguity of picking preimages of \({\mathcal {S}}_{1}\) in the second arrow is undone by reapplying \({\mathcal {S}}_{1}\) in the fourth arrow and hence the map is well-defined. This map maps to \({\mathbb {F}}_{0}\), which is a submodule of \(\mathcal {P}\) as shown in Proposition 3.3.
Note that since the modules \(\mathcal {M}\) and \(\mathcal {M}^\vee \) considered here are simple, the compositions of coevaluations and evaluations (5.36) are proportional to the identity by Schur’s lemma. Rigidity therefore follows, if we can show that the proportionality factors for (5.36a) and (5.36b) are equal and non-zero.
We determine the proportionality factor for (5.36a) by applying the map to the ket \(|(j-1)\psi +(j-\ell )\theta \rangle \in {\mathbb {F}}_{\lambda (\psi +\theta )+(\ell -1)\theta }\cong \sigma ^{\ell } \mathcal {W}_{\lambda }\). Following the sequence of maps in (5.36a) we get
where \(\oint _{0,w_2}\) denotes a contour about \(0\) and \(w_2\) but not \(w_1\), \(\oint _{w_1,w_2}\) denotes a contour about \(w_1\) and \(w_2\) but not \(0\), and where we have used the fact that the integration contours lie in domains in which the product and iterate of the vertex operators are equal. The proportionality factor is obtained by pairing the above with the dual of the Fock space highest weight vector, which we denote by an empty bra \(\langle |\). Evaluating these matrix elements requires the associativity isomorphisms for replacing products of intertwining operators with their iterates. This is a characterising property of associativity isomorphisms for vertex operator algebra module categories, see [21, Part VII, Theorem 10.6]. The intertwining operators we are considering here are all lattice intertwining operators with lattice modules as codomains. Further, all lattice module endomorphisms are scalar multiples of the identity, therefore the associativity isomorphisms are also scalars. By the remark after Proposition 2.12, these intertwining operators can be normalised such that the associativity scalars are 1. Note that this does not imply that the associativity isomorphisms are trivial on all of category \(\mathscr {F}\), just that they can be scaled away when only considering lattice modules that are isomorphic to simple \(\mathsf {G}\) modules in the free field realisation. The proportionality factor from (5.36a) is therefore given by the matrix element
where
Note that the second equality of (5.42) is where the associativity isomorphisms are used to pass from compositions (or products) of vertex operators to their operator product expansions (also called iterates). For intertwining operators, associativity amounts to the analytic continuation of their series expansions and then reexpanding in a different domain. On the left-hand side of the second equality the intertwining operators (or here specifically vertex operators) are in radial ordering, while on the right-hand side they have been analytically continued and then reexpanded as operator product expansions. By an analogous argument the proportionality factor produced by the sequence of maps (5.36b) is the matrix element
Since both matrix elements are equal, \(I(w_1,w_2)={\tilde{I}}(w_1,w_2)\), rigidity follows by showing that they are non-zero.
We evaluate the four integrals appearing in \(I(w_1,w_2)\). We simplify the first integral using the substitution \(z=w_1x\).
where the second equality follows by deforming the contour about 0 and 1 to a dumbbell or dog bone contour, whose end points vanish because the contributions from the end points are \(O(\varepsilon ^{1+j})\) and \(O(\varepsilon ^{1-j})\) respectively, and \(0<j<1\); and the third equality is the integral representation of the hypergeometric function and \(B\) is the beta function. Similarly,
For the integrals with contours about \(w_1\) and \(w_2\) we use the substitution \(z=w_2-(w_2-w_1)x\) and then again obtain integral representations of the hypergeometric function.
Note that for the three integrals above, the end point contributions of the contour also vanish due to being \(O(\varepsilon ^{j})\) and \(O(\varepsilon ^{1-j})\) for 0 and 1 respectively.
Making use of the hypergeometric and beta function identities
the proportionality factor \(I(w_1,w_2)\) simplifies to
Since \(j \notin \mathbb {Z}\), \(I(w_1,w_2)\) can only vanish, if one of the hypergeometric factors does. We specialise the complex numbers \(w_1,w_2\), such that \(w_2=2w_1\). Then,
and the relationship between contiguous functions implies
Thus \(I(w_1,w_2)\ne 0\) and we can rescale the evaluation map by \(I(w_1,w_2)^{-1}\) so that the sequences of maps (5.36) are equal to the identity maps on \(\mathcal {M}\) and \(\mathcal {M}^\vee \). Thus \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) is rigid. \(\square \)
6 Fusion Product Formulae
In this section we determine the decomposition of all fusion products in category \(\mathscr {F}\). A complete list of fusion products among representatives of each spectral flow orbit is collected in Theorem 6.1, while the proofs of these decomposition formulae have been split into the dedicated Subsections 6.1 and 6.2. To simplify some of the decomposition formulae we introduce dedicated notation for certain sums of spectral flows of the projective module \(\mathcal {P}\). Consider the polynomial of spectral flows
and let
Further, let
Theorem 6.1
-
(1)
Category \(\mathscr {F}\) under fusion is a rigid braided tensor category.
-
(2)
The following is a list of all non-trivial fusion products, those not involving the fusion unit (the vacuum module \(\mathcal {V}\)), in category \(\mathscr {F}\) among representatives for each spectral flow orbit. All other fusion products are determined from these through spectral flow and the compatibility of spectral flow with fusion as given in Theorem 2.6.
Since \(\mathscr {F}\) is rigid, the fusion product of a projective module \(\mathcal {R}\) with any indecomposable module \(\mathcal {M}\) is given by
$$\begin{aligned} \mathcal {R} \mathbin {\boxtimes }\mathcal {M} \cong \bigoplus _{\mathcal {S}} [\mathcal {M}:\mathcal {S}]\; \mathcal {R}\mathbin {\boxtimes }\mathcal {S} , \end{aligned}$$(6.4)where the summation index runs over all isomorphism classes of composition factors of \(\mathcal {M}\) and \([\mathcal {M}:\mathcal {S}]\) is the multiplicity of the composition factor \(\mathcal {S}\) in \(\mathcal {M}\).
For all \(\lambda ,\mu \in \mathbb {R}/\mathbb {Z}\), \(\lambda , \mu , \lambda + \mu \ne \mathbb {Z}\),
$$\begin{aligned} \begin{aligned} {\mathcal {W}_{\lambda }} \mathbin {\boxtimes }{\mathcal {W}_{\mu }}&\cong {\mathcal {W}_{\lambda + \mu }} \oplus \sigma ^{-1} \mathcal {W}_{\lambda + \mu },\\ {\mathcal {W}_{\lambda }} \mathbin {\boxtimes }{\mathcal {W}_{-\lambda }}&\cong \sigma ^{-1} \mathcal {P}. \end{aligned} \end{aligned}$$(6.5)For \(m \ge n \ge 1\), we have the following fusion product formulae.
$$\begin{aligned} \mathcal {B}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {B}^{2n+1}_{}&\cong \mathcal {B}^{2m + 2n +1}_{} \oplus \mathcal {Q}^{m,n}_{1}&\mathcal {T}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {T}^{2n+1}_{}&\cong \mathcal {T}^{2m + 2n +1}_{} \oplus \mathcal {Q}^{m,n}_{1}\nonumber \\ \mathcal {B}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {B}^{2n}_{}&\cong \mathcal {B}^{2n}_{} \oplus \mathcal {Q}^{m,n}_{1}&\mathcal {T}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {T}^{2n}_{}&\cong \mathcal {T}^{2n}_{} \oplus \mathcal {Q}^{m,n}_{1}\nonumber \\ \mathcal {B}^{2m}_{} \mathbin {\boxtimes }\mathcal {B}^{2n}_{}&\cong \mathcal {B}^{2n}_{2m-1} \oplus \mathcal {B}^{2n}_{} \oplus \mathcal {Q}^{m-1,n}_{1}&\mathcal {T}^{2m}_{} \mathbin {\boxtimes }\mathcal {T}^{2n}_{}&\cong \mathcal {T}^{2n}_{2m-1} \oplus \mathcal {T}^{2n}_{} \oplus \mathcal {Q}^{m-1,n}_{1} \end{aligned}$$(6.6a)$$\begin{aligned} \mathcal {T}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {B}^{2n+1}_{}&\cong \mathcal {T}^{2m-2n+1}_{2n} \oplus \mathcal {Q}^{m+1,n}_{}&\mathcal {B}^{2m+1}_{} \mathbin {\boxtimes }\mathcal {T}^{2n+1}_{}&\cong \mathcal {B}^{2m-2n+1}_{2n} \oplus \mathcal {Q}^{m+1,n}_{}\nonumber \\ \mathcal {T}^{2m}_{} \mathbin {\boxtimes }\mathcal {B}^{2n+1}_{}&\cong \mathcal {T}^{2m}_{2n} \oplus \mathcal {Q}^{m,n}_{}&\mathcal {B}^{2m}_{} \mathbin {\boxtimes }\mathcal {T}^{2n+1}_{}&\cong \mathcal {B}^{2m}_{2n} \oplus \mathcal {Q}^{m,n}_{} \nonumber \\ \mathcal {T}^{2m}_{} \mathbin {\boxtimes }\mathcal {B}^{2n}_{}&\cong \mathcal {Q}^{m,n}_{}&\mathcal {B}^{2m}_{} \mathbin {\boxtimes }\mathcal {T}^{2n}_{}&\cong \mathcal {Q}^{m,n}_{} \end{aligned}$$(6.6b)
We split the proof of Theorem 6.1 into multiple parts. Theorem 6.1.(1) is shown in Proposition 6.4. The fusion formulae (6.5), (6.6a), (6.6b) are determined in Propositions 6.2, 6.9 and 6.10 and Lemma 5.10 respectively.
Remark
The fusion product formulae of Theorem 6.1 projected onto the Grothendieck group match the conjectured Verlinde formula of [16, Corollaries 7 and 10], thereby proving that category \(\mathscr {F}\) satisfies the standard module formalism version of the Verlinde formula. It will be an interesting future problem to find a more conceptual and direct proof for the validity of the Verlinde formula, rather than a proof by inspection.
6.1 Fusion products of simple projective modules
In this section we determine the fusion products of the simple projective modules.
Proposition 6.2
For \(\lambda ,\mu \in \mathbb {R}/\mathbb {Z}\), \(\lambda ,\mu ,\lambda + \mu \notin \mathbb {Z}\), we have
Proof
Since \(\mathcal {W}_{\lambda }\) and \(\mathcal {W}_{\mu }\) both lie in category \(\mathscr {R}\), we know, by Lemma 5.9, that the composition factors of the fusion product lie in categories \(\mathscr {R}\) or \(\sigma ^{-1} \mathscr {R}\). Further, since \(J(z)\) is a conformal weight 1 field, its corresponding weight, the ghost weight, adds under fusion. Therefore the only possible composition factors are \(\mathcal {W}_{\lambda +\mu }\) and \(\sigma ^{-1} \mathcal {W}_{\lambda +\mu }\). Since these composition factors are both projective and injective, they can only appear as direct summands and all that remains is to determine their multiplicity. In [20] Adamović and Pedić computed dimensions of spaces of intertwining operators for fusion products of the simple projective modules. In particular, [20, Corollary 6.1] states that
if \(\mathcal {M}\) is isomorphic to \(\sigma ^{\ell } \mathcal {W}_{\lambda +\mu },\,\ell =0,-1\). Thus the proposition follows. \(\square \)
Remark
To prove the above proposition directly without citing the literature, we could have used the two free field realisations in Section 2.4 to construct intertwining operators of the type appearing in equation (6.8), thereby showing that the dimension of the corresponding space of intertwining operators is at least 1. This was also done in [20]. An upper bound of 1 can then easily be determined by calculations involving either the HLZ double dual construction (similar to the calculations done in Lemma 5.10) or the NGK algorithm.
Proposition 6.3
For \(\lambda \in \mathbb {R}/\mathbb {Z}\), \(\lambda \ne \mathbb {Z}\), we have
Proof
By Proposition 5.13, \(\mathcal {W}_{\lambda }\) is rigid and hence its fusion product with a projective module must again be projective. Further, by Lemma 5.9, all composition factors must lie in categories \(\sigma ^{\ell } \mathscr {R},\,\ell =-1, 0\). Finally, since ghost weights add under fusion, the ghost weights of the fusion product must lie in \(\mathbb {Z}\). Thus the fusion product must be isomorphic to a direct sum of some number of copies of \(\sigma ^{-1} \mathcal {P}\). By Lemma 5.10, we know there is exactly one such summand. \(\square \)
Proposition 6.4
Category \(\mathscr {F}\) is rigid.
Proof
Category \(\mathscr {F}\) has sufficiently many injective and projective modules, that is, all simple modules have projective covers and injective hulls, and all projectives are injective and vice-versa. Further, the simple projective modules \(\sigma ^{\ell } \mathcal {W}_{\lambda }\) are rigid and generate the non-simple projective modules under fusion, so all projective modules are rigid. Catefory \(\mathscr {F}\) is therefore a Frobenius category and hence any for short exact sequence with two rigid terms (whose duals are also rigid) the third term is also rigid. This implies that all modules are rigid and hence so is category \(\mathscr {F}\). \(\square \)
Corollary 6.5
Let \(\mathcal {M},\mathcal {N}\in \mathscr {F}\), then
Proof
Due to rigidity, the tensor duality functor \({}^\vee \) defines an equivalence of categories and is therefore exact. Further, the tensor duality functor satisfies
This also implies that \(\mathcal {V}_{k}^\vee = \mathcal {V}_{-k}\). We see that the tensor dual \(\mathcal {M}^\vee \) agrees with \(\sigma ^{} \left( \mathcal {M}' \right) \) on all simple modules in \(\mathscr {F}\). As both \(\left( - \right) ^\vee \) and \(\sigma ^{} \left( - \right) '\) are exact contravariant invertible functors and all reducible indecomposable objects are uniquely characterised by the non-split exact sequences (4.18) with 1-dimensional corresponding extension groups, it follows by induction in module length that \(\mathcal {M}^\vee \cong \sigma ^{} \left( \mathcal {M}' \right) \) for any module in \(\mathscr {F}\). Recalling \(\left( - \right) ^*=c\left( - \right) '\), we further have \(M^*\cong \sigma {}{{\mathsf {c}}{M^\vee }}\). Theorem 2.6 then implies
\(\square \)
6.2 Fusion products of reducible indecomposable modules
In this section we calculate the remaining fusion product formulae involving indecomposable modules in \(\mathscr {F}\). The main tool for determining these fusion products is the fact that category \(\mathscr {F}\) is rigid by Proposition 6.4. Hence fusion is biexact and projective modules form a tensor ideal. We begin by calculating certain basic fusion products from which the remainder can be determined inductively.
Lemma 6.6
Proof
Taking the short exact sequence (2.20a) for \(\mathcal {W}_{0}^+=\mathcal {T}^{2}_{-1}\) and fusing it with \(\mathcal {W}_{0}^-=\mathcal {B}^{2}_{-1}\) yields the short exact sequence
Similarly, fusing the short exact sequence (2.20b) for \(\mathcal {W}_{0}^-\) with \(\mathcal {W}_{0}^+\) yields
If either of the above exact sequences splits there is a contradiction, because if \(\sigma ^{-1} \mathcal {W}_{0}^+\) and \(\mathcal {W}_{0}^+\) are direct summands of \(\mathcal {W}_{0}^{+} \mathbin {\boxtimes }\mathcal {W}_{0}^{-}\), (6.14) is not exact, and if \(\mathcal {W}_{0}^-\) and \(\sigma ^{-1} \mathcal {W}_{0}^-\) are direct summands, (6.15) is not exact. Hence both sequences must be non-split. From (4.18g) in Corollary 4.6, we know that \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \sigma ^{-1} \mathcal {W}_{0}^{-},\mathcal {W}_{0}^{-} \right) =\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {W}_{0}^{+},\sigma ^{-1} \mathcal {W}_{0}^{+} \right) =1\). There is only one candidate for the middle coefficient of these exact sequences, namely \(\sigma ^{-1} \mathcal {P}\). Thus the first fusion rule follows. The other two fusion products by are determined by fusing \(\mathcal {W}_{0}^\pm \) with the short exact sequences for \(\mathcal {W}_{0}^\pm \). The extension groups corresponding to these fused exact sequences are zero-dimensional and hence the sequences split and the lemma follows. \(\square \)
We further prepare the following Ext group dimensions for later use.
Lemma 6.7
The indecomposable modules \(\mathcal {T}^{2n+1}_{}\), \(\mathcal {B}^{m}_{2n+1}\), \(\mathcal {B}^{2n}_{}\) and \(\mathcal {B}^{m}_{2n}\) satisfy
The corresponding extensions are given by \(\mathcal {T}^{2n+m+1}_{}\) and \(\mathcal {B}^{2n+m}_{}\) respectively.
Proof
We start with the following presentation of \(\mathcal {T}^{2n+1}_{}\)
Applying the functor \({{\,\mathrm{Hom}\,}}\left( -,\mathcal {B}^{m}_{2n+1} \right) \) yields
The first coefficient vanishes due to \(\mathcal {T}^{2n+1}_{}\) and \(\mathcal {B}^{m}_{2n+1}\) having no common composition factors. The second coefficient can be shown to vanish using the projective cover formulae in Lemma 4.5 and reading off Hom group dimensions from the Loewy diagrams. For the third coefficient, the only composition factor common to both \(\mathcal {T}^{2n+2}_{}\) and \(\mathcal {B}^{m}_{2n+1}\) is \(\mathcal {V}_{2n+1}\), which occurs as a quotient for \(\mathcal {T}^{2n+2}_{}\) and a submodule for \(\mathcal {B}^{m}_{2n+1}\), so this gives rise to a one dimensional Hom group. The vanishing Euler characteristic then implies that \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {T}^{2n+1}_{},\mathcal {B}^{m}_{2n+1} \right) = 1\) as expected. Furthermore, we can examine \(\mathcal {T}^{2n+m+1}_{}\) to see that it has a \(\mathcal {B}^{m}_{2n}\) submodule which yields \(\mathcal {T}^{2n+1}_{}\) when quotiented out, therefore this is the unique extension characterised by \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {T}^{2n+1}_{},\mathcal {B}^{m}_{2n+1} \right) \).
We can follow the same procedure starting with the projective presentation of \(\mathcal {B}^{2n}_{}\) to obtain the following exact sequence
The dimensions of the Hom groups follow by the same arguments as above, and then \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2n}_{},\mathcal {B}^{m}_{2n} \right) = 1\) follows from the vanishing of the Euler characteristic. Similarly, we see that \(\mathcal {B}^{2n+m}_{}\) provides an extension of \(\mathcal {B}^{2n}_{}\) by \(\mathcal {B}^{m}_{2n}\) and must therefore be the unique one. \(\square \)
We can now determine fusion products when one factor has length 2 and the other has arbitrary length.
Lemma 6.8
The fusion products of length 2 indecomposables with any indecomposable of types \(\mathcal {B}^{}_{}\) or \(\mathcal {T}^{}_{}\) satisfy the following decomposition formulae. For \(n\ge 1\),
Proof
We prove the left column of identities. The right column then follows from Corollary 6.5 and applying the \(^*\) functor. We start with the short exact sequence from (4.18e) satisfied by \(\mathcal {B}^{2n+1}_{}\),
We then take the fusion product with \(\mathcal {B}^{2}_{}\),
Because \(\mathcal {P}_{2n}\) is projective, the sequence splits and we have the recurrence relation
Then, the first fusion product formula of the lemma follows by induction with \(\mathcal {B}^{1}_{} = \mathcal {V}\) as the base case.
We next consider the short exact sequence (4.18c) satisfied by \(\mathcal {B}^{2n+2}_{}\) and fuse it with \(\mathcal {B}^{2}_{}\) to obtain
which evaluates to
Since \(\mathcal {Q}^{n}_{1}\) is injective, it is a direct summand of \(\mathcal {B}^{2n+2}_{} \mathbin {\boxtimes }\mathcal {B}^{2}_{}\). Further, \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2}_{2n+1},\mathcal {B}^{2}_{} \right) = 0\), as the composition factors are seperated by at least two units of spectral flow, and \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V}_{n},\mathcal {V}_{m} \right) \) for \(|n-m| >1\). Hence the sequence splits and we obtain the second fusion product of the lemma.
For the final two fusion products, we perform the same exercises with different exact sequences. For the third and fourth fusion products we use (4.18d), with odd and even length respectively. Fusing with \(\mathcal {T}^{2}_{}\) gives the short exact sequences
In both cases, the sequences split because \(\mathcal {P}_{1}\) is projective. \(\square \)
We now use Lemma 6.8 to prove the fusion product formulae (6.6a) of Theorem 6.1.
Proposition 6.9
The fusion products of indecomposable modules of types \(\mathcal {B}^{}_{}\) and \(\mathcal {T}^{}_{}\) with themselves satisfy the decomposition formulae below, for \(m \ge n \ge 1\).
Proof
We prove the left column of identities. The right column then follows from Corollary 6.5 and applying the \(^*\) functor. First, for both superscripts odd, we take two short exact sequences from (4.18d) and (4.18e) for \(\mathcal {B}^{2n+1}_{}\) and fuse with \(\mathcal {B}^{2m+1}_{}\) to find
Now comparing these exact sequences, and using the fact that \(\mathcal {P}\) is projective, we find that the sequences cannot both split, as they would give different direct sums. For the first short exact sequence, we use Lemma 6.7, to find \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2}_{},\mathcal {B}^{2m+2n-1}_{2} \right) = 1 \), with the extension being given by \(\mathcal {B}^{2m+2n+1}_{}\) so we can determine the fusion product formulae inductively to get
We can deduce the remaining rules from short exact sequences that relate even and odd \(\mathcal {B}^{}_{}\)s. Firstly, we take the two short exact sequences (4.18d) and (4.18f), and fuse them with \(\mathcal {B}^{2m+1}_{}\) to get
Either of these exact sequences splitting would lead to a contradiction, hence both must be non-split. Further, by Lemma 6.7 we find \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2}_{},\mathcal {B}^{2n}_{2} \right) = \dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2n}_{},\mathcal {B}^{2}_{2n} \right) = 1\), with the corresponding non-split extension given by \(\mathcal {B}^{2n+2}_{}\). Therefore
Finally we fuse (4.18c) with \(\mathcal {B}^{2n}_{}\) to find
For \(m \ge n\), \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2n}_{2m+1},\mathcal {B}^{2n}_{} \right) = 0\), which follows because the composition factors are separated by at least two units of spectral flow and \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {V}_{n},\mathcal {V}_{m} \right) = 0\) for \(|n-m| > 1\), the above sequence splits. In the case when \(m=n-1\), we have that \({{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2n}_{2n-1},\mathcal {V}_{k} \right) = 0\) for all the composition factors of \(\mathcal {B}^{2n}_{}\) , that is, \((0 \le k \le 2n-1)\). Hence \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {B}^{2n}_{2n-1},\mathcal {B}^{2n}_{} \right) = 0\) and the above sequence again splits. Thus,
\(\square \)
Proposition 6.10
The fusion products of indecomposable modules of types \(\mathcal {B}^{}_{}\) and \(\mathcal {T}^{}_{}\) with each other satisfy the decomposition formulae below, for \(m \ge n \ge 1\).
Proof
We prove the left column of identities. The right column then follows from Corollary 6.5 and applying the \(^*\) functor to each module. We start with sequences (4.18e) and (4.18d) for odd length \(\mathcal {B}^{}_{}\), and fuse them with \(\mathcal {T}^{2m+1}_{}\) to find
Specialising to n=1 we have
Since \(\mathcal {P}_{}\) is projective, its spectral flows must appear as direct summands in the middle coefficient of the above exact sequences. Thus,
Therefore the module \(\mathcal {A}\) satisfies the exact sequences
Because either of these sequences splitting would lead to a contradiction and the corresponding extension groups are one-dimensional, the sequences uniquely characterise the fusion product. Proceeding by induction, we obtain
Next we take two short exact sequences from (4.18c) and (4.18a), for \(\mathcal {T}^{2m}_{}\) and fuse them with \(\mathcal {B}^{2n+1}_{}\) to get
Again either of these sequences splitting would lead to a contradiction, and by Lemma 6.7, \(\dim {{\,\mathrm{Ext}\,}}^{}\left( \mathcal {T}^{2m-2n-1}_{2n},\mathcal {B}^{2n+1}_{2m-1} \right) = 1\), with the extension being given by \(\mathcal {T}^{2m}_{2n}\), so the second fusion rule follows. Finally, fusing (4.18f) with \(\mathcal {B}^{2n}_{}\), we have
\(\square \)
References
Huang, Y.-Z.: Vertex operator algebras and the Verlinde conjecture. Commun. Contemp. Math. 10, 103–1054 (2008). arXiv:math/0406291
Fuchs, J., Schweigert, C., Stigner, C.: From non-semisimple Hopf algebras to correlation functions for logarithmic CFT. J. Phys. A 46, 494008 (2013). arXiv:1302.4683 [hep-th]
Fuchs, J., Schweigert, C.: Consistent systems of correlators in non-semisimple conformal field theory. Adv. Math. 307, 598–639 (2017). arXiv:1604.01143 [math.QA]
Gannon, T., Creutzig, T.: Logarithmic conformal field theory, log-modular tensor categories and modular forms. J. Phys. A 50, 404004 (2017). arXiv:1605.04630 [math.QA]
Friedan, D., Martinec, E., Shenker, S.: Conformal invariance, supersymmetry and string theory. Nucl. Phys. B 271, 93–165 (1986)
Wakimoto, M.: Fock representation of the algebra \(A_1^{(1)}\). Commun. Math. Phys. 104, 605–609 (1986)
Feigin, B., Frenkel, E.: Quantization of the Drinfeld–Sokolov reduction. Phys. Lett. 246, 75–81 (1990)
Malikov, F., Schechtman, V., Vaintrob, A.: Chiral de Rham complex. Commun. Math. Phys. 204, 439–473 (1999). arXiv:math/9803041
Kausch, H.: Curiosities at \(c = -2\). DAMTP 95–52, 26 (1995). arXiv:hep-th/9510149
Gaberdiel, M., Kausch, H.: A rational logarithmic conformal field theory. Phys. Lett. B 386, 131–137 (1996). arXiv:hep-th/9606050
Gaberdiel, M., Runkel, I.: From boundary to bulk in logarithmic CFT. J. Phys. A 41, 075402 (2008). arXiv:0707.0388 [hep-th]
Runkel, I.: A braided monoidal category for free super-bosons. J. Math. Phys. 55, 59 (2014). arXiv:1209.5554 [math.QA]
Adamović, D., Milas, A.: On the triplet vertex algebra \({\cal{W}}(p)\). Adv. Math. 217, 2664–2699 (2008). arXiv:0707.1857 [math.QA]
Tsuchiya, A., Wood, S.: On the extended \(W\)-algebra of type \(\mathfrak{sl}_2\) at positive rational level. Int. Math. Res. Not. 5357–5435, 2015 (2015). arXiv:1302.6435 [math.QA]
Tsuchiya, A., Wood, S.: The tensor structure on the representation category of the \({\cal{W}}(p)\) triplet algebra. J. Phys. A 46, 445203 (2013). arXiv:1201.0419 [hep-th]
Ridout, D., Wood, S.: Bosonic ghosts at \(c=2\) as a logarithmic CFT. Lett. Math. Phys. 105, 279–307 (2015). arXiv:1408.4185 [hep-th]
Ridout, D.: \(\widehat{\mathfrak{sl}}(2)_{-1/2}\): A case study. Nucl. Phys. B 814, 485–521 (2009). arXiv:0810.3532 [hep-th]
Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models I. Nucl. Phys. B 865, 83–114 (2012). arXiv:1205.6513 [hep-th]
Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models II. Nucl. Phys. B 875, 423–458 (2013). arXiv:1306.4388 [hep-th]
Adamović, D., Pedić, V.: On fusion rules and intertwining operators for the Weyl vertex algebra. J. Math. Phys. 60, 081701 (2019)
Huang, Y.-Z., Lepowsky James, J., Zhang, L.:. Logarithmic tensor product theory I–VIII. arXiv:1012.4193 [math.QA], arXiv:1012.4196 [math.QA], arXiv:1012.4197 [math.QA], arXiv:1012.4198 [math.QA], arXiv:1012.4199 [math.QA], arXiv:1012.4202 [math.QA], arXiv:1110.1929 [math.QA], arXiv:1110.1931 [math.QA]
Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L., van Rees, B.: Infinite chiral symmetry in four dimensions. Commun. Math. Phys. 336, 1369–1433 (2015). arXiv:1312.5344 [hep-th]
Creutzig, T., Ridout, D., Wood, S.: Coset constructions of logarithmic (1, p)-models. Lett. Math. Phys. 104, 553–583 (2014). arXiv:1305.2665 [math.QA]
Auger, J., Creutzig, T., Kanade, S., Rupert, M.: Braided tensor categories related to \({\cal{B}}_p\) vertex algebras. Commun. Math. Phys. 378, 219–260 (2020)
Yang, J.: A sufficient condition for convergence and extension property for strongly graded vertex algebras. Contemp. Math. 711, 119–141 (2018)
Block, R.: The irreducible representations of the Weyl algebra \(A_{1}\). Lect. Notes Math. 740, 69–79 (1979)
Li, H.: The physics superselection principle in vertex operator algebra theory. J. Algebra 196(2), 436–457 (1997)
Frenkel, E., Ben-Zvi, D.: Vertex Algebras and Algebraic Curves, Mathematical Surveys and Monographs, vol. 88. American Mathematical Society, Providence (2001)
Zhu, Y.: Modular invariance of characters of vertex operator algebras. Am. Math. Soc. 9, 237–302 (1996)
Dong, C., Lepowsky, J.: Generalized Vertex Algebras and Relative Vertex Operators. Progress in Mathematics. Birkhäuser, Boston (1993)
Wood, S.: Admissible level \(\mathfrak{osp}(1|2)\) minimal models and their relaxed highest weight modules. Transf. Groups 2020, 57 (2020). arXiv:1804.01200 [math.QA]
Hilton, P., Stammbach, U.: A Course in Homological Algebra. Graduate Texts in Mathematics, 2nd edn. Springer, Berlin (1997)
Fjelstad, J., Fuchs, J., Hwang, S., Semikhatov, A.M., Tipunin, I.Y.: Logarithmic conformal field theories via logarithmic deformations. Nucl. Phys. 633(3), 379–413 (2002). arXiv:hep-th/0201091
Belletête, J., Ridout, D., Saint-Aubin, Y.: Restriction and induction of indecomposable modules over the Temperley–Lieb algebras. J. Phys. 51(4), 045201 (2017). arXiv:1605.05159 [math-ph]
Nagatomo, K., Tsuchiya, A.: The triplet vertex operator algebra \(W(p)\) and the restricted quantum group \({\overline{U}}_q(sl_2)\) at \(q=e^{\frac{\pi i}{p}}\). In: Hasegawa, K., Hayashi, T., Hosono, S., Yamada, Y. (eds.) Exploring New Structures and Natural Constructions in Mathematical Physics, Advanced Studies in Pure Mathematics, Tokyo, vol. 61, pp. 1–49 (2011). Mathematical Society of Japan. arXiv:0902.4607 [math.QA]
Etingof, P., Shlomo, G., Nikshych, D., Ostrik, V.: Tensor Categories. Mathematical Surveys and Monographs, vol. 205. American Mathematical Society, Providence (2015)
Huang, Y.-Z.: On the applicability of logarithmic tensor category theory (2017). arXiv:1702.00133 [math.QA]
Kanade, S., Ridout, D.: NGK and HLZ: fusion for physicists and mathematicians. In: Adamovic, D., Papi, P. (eds.) Affine, Vertex and \(W\)-Algebras. Springer INdAM, vol. 37, pp. 135–181. Springer, Cham (2019) . arXiv:1812.10713 [math-ph]
Wang, W.: \({\cal{W}}_{1+\infty }\) algebra, \({\cal{W}}_3\) algebra, and Friedan–Martinec–Shenker bosonization. Commun. Math. Phys. 195, 95–111 (1998)
Linshaw, A.: Invariant chiral differential operators and the \({\cal{W}}_3\) algebra. J. Pure Appl. Algebra 213, 632–648 (2009)
Adamović, D.: Representations of the vertex algebra \({\cal{W}}_{1+\infty }\) with a negative integer central charge. Commun. Algebra 29(7), 3153–3166 (2001). arXiv:math/9904057
Kac, V., Radul, A.: Representation theory of the vertex algebra \(W_{1 + \infty }\) (1996). arXiv:hep-th/9512150
Matsuo, Y.: Free fields and quasi-finite representation of \(W_{1+\infty }\) algebra. Phys. Lett. 326(1–2), 95–100 (1994). arXiv:hep-th/9312192
Creutzig, T., Milas, A.: False theta functions and the verlinde formula. Adv. Math. 262, 520–545 (2014). arXiv:1309.6037 [math.QA]
Adamović, D., Milas, A.: Logarithmic intertwining operators and \(W(2,2p-1)\) algebras. J. Math. Phys. 48(7), 073503 (2007). arXiv:math/0702081 [math.QA]
Creutzig, T., Milas, A., Rupert, M.: Logarithmic link invariants of \({\overline{U}}_q^h(\mathfrak{sl}_2))\) and asymptotic dimensions of singlet vertex algebras. J. Pure Appl. Algebra 1605, 3224–3247 (2017). arXiv:1605.05634 [math.QA]
Zhang, L.: Vertex tensor category structure on a category of Kazhdan–Lusztig. N. Y. J. Math. 14, 261–284 (2008). arXiv:math/0701260
Huang, Y.-Z.: Differential equations and intertwining operators. Commun. Contemp. Math. 7, 375–400 (2005). arXiv:math/0206206
Knapp, A.: Representation Theory of Semisimple Groups: An Overview Based on Examples. Princeton Landmarks in Mathematics. Princeton University Press, Princeton (1986)
Acknowledgements
SW would like to thank Yi-Zhi Huang, Shashank Kanade, Robert McRae and Jinwei Yang for helpful and stimulating discussions regarding the subtleties of vertex tensor categories, and Ehud Meir for the same regarding finitely generated modules. Both authors are very grateful to Thomas Creutzig for drawing their attention to a mistake relating to convergence and extension properties in a previous version of this manuscript. RA’s research is supported by the EPSRC Doctoral Training Partnership grant EP/R513003/1. SW’s research is supported by the Australian Research Council Discovery Project DP160101520.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C.Schweigert.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Sufficient Conditions for Convergence and Extension—Proof of Theorem 5.7
Appendix A. Sufficient Conditions for Convergence and Extension—Proof of Theorem 5.7
In this section we give a proof of Theorem 5.7 by reviewing reasoning presented by Yang in [25] and showing that certain assumptions on the category of strongly graded modules (see [25, Assumption 7.1, Part 3]) are not required, if one only wishes to conclude that convergence and extension properties hold. Instead all that is required is that the modules considered satisfy suitable finiteness conditions. This appendix closely follows the logic of [25, Sections 5 & 6] and also [48, Section 2].
Throughout this section let \(A \le B\) be abelian groups. Further, let \(\mathsf {V}\) be an \(A\)-graded vertex algebra with a vertex subalgebra \(\overline{\mathsf {V}}\subset \mathsf {V}^{(0)}\). In this section only, all mode expansions of fields from a vertex operator algebra \(\mathsf {V}\) will be of the form \(Y(v,z)=\sum _{n\in \mathbb {Z}} v_{n}z^{-n-1}\) regardless of the conformal weight of \(v\in \mathsf {V}\), that is, \(v_{n}\) refers to the coefficient of \(z^{-n-1}\) rather than the one which shifts conformal weight by \(-n\).
Definition A.1
Let \(\mathcal {W}_0, \mathcal {W}_1, \mathcal {W}_2, \mathcal {W}_3,\mathcal {W}_4\) be \(B\)-graded \(\mathsf {V}\)-modules.
-
(1)
We say that two \(B\)-graded logarithmic intertwining operators \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\) of respective types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_1,\ \mathcal {W}_4\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_2,\ \mathcal {W}_3\end{array}}\right) \) satisfy the convergence and extension property for products if for any \(a_1,a_2,\in B\) and any doubly homogeneous elements \(w_0^\prime \in \mathcal {W}_0^\prime \), \(w_3\in \mathcal {W}_3\), \(w_i\in \mathcal {W}_i^{(a_i)},\ i=1,2\), there exist \(M\in \mathbb {Z}_{\ge 0}\), \(r_1,\dots , r_M,s_1,\dots s_M\in \mathbb {R}\), \(u_1,\dots u_M, v_1,\dots v_M\in \mathbb {Z}_{\ge 0}\) and analytic functions \(f_1(z),\dots , f_M(z)\) on the disc \(|z|<1\) satisfying
$$\begin{aligned} {{\,\mathrm{wt}\,}}w_1+{{\,\mathrm{wt}\,}}w_2 + s_k >N,\quad \text {for each}\ k=1,\dots , M, \end{aligned}$$(A.1)where \(N\in \mathbb {Z}\) depends only on the intertwining operators \({\mathcal {Y}}_1,\ {\mathcal {Y}}_2\) and \(a_1+a_2\), such that as a formal power series the matrix element
$$\begin{aligned} \langle w_0^\prime ,{\mathcal {Y}}_1(w_1,z_1){\mathcal {Y}}_2(w_2,z_2)w_3 \rangle \end{aligned}$$(A.2)converges absolutely in the region \(|z_1|>|z_2|>0\) and may be analytically continued to the multivalued analytic function
$$\begin{aligned} \sum _{k=1}^M z_2^{r_k}(z_1-z_2)^{s_k}(\log z_2)^{u_k}(\log (z_1-z_2))^{v_k}f_k\left( \frac{z_1-z_2}{z_2} \right) \end{aligned}$$(A.3)in the region \(|z_2|>|z_1-z_2|>0\).
-
(2)
We say that two \(B\)-graded logarithmic intertwining operators \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\) of respective types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_4,\ \mathcal {W}_3\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_1,\ \mathcal {W}_2\end{array}}\right) \) satisfy the convergence and extension property for iterates if for any \(a_2,a_3,\in B\) and any doubly homogeneous elements \(w_0^\prime \in \mathcal {W}_0^\prime \), \(w_1\in \mathcal {W}_3\), \(w_i\in \mathcal {W}_i^{(a_i)},\ i=2,3\), there exist \(M\in \mathbb {Z}_{\ge 0}\), \(r_1,\dots , r_M,s_1,\dots s_M\in \mathbb {R}\), \(u_1,\dots u_M, v_1,\dots v_M\in \mathbb {Z}_{\ge 0}\) and analytic functions \(f_1(z),\dots f_M(z)\) on the disc \(|z|<1\) satisfying
$$\begin{aligned} {{\,\mathrm{wt}\,}}w_2+{{\,\mathrm{wt}\,}}w_3 + s_k >N,\quad \text {for each}\ k=1,\dots , M , \end{aligned}$$(A.4)where \(N\in \mathbb {Z}\) depends only on the intertwining operators \({\mathcal {Y}}_1,\ {\mathcal {Y}}_2\) and \(a_2+a_3\), such that as a formal power series the matrix element
$$\begin{aligned} \langle w_0^\prime ,{\mathcal {Y}}_1({\mathcal {Y}}_2(w_1,z_1-z_2)w_2,z_2)w_3 \rangle \end{aligned}$$(A.5)converges absolutely in the region \(|z_2|>|z_1-z_2|>0\) and may be analytically continued to the multivalued analytic function
$$\begin{aligned} \sum _{k=1}^M z_1^{r_k}z_2^{s_k}(\log z_1)^{u_k}(\log z_2)^{v_k}f_k\left( \frac{z_2}{z_1} \right) \end{aligned}$$(A.6)in the region \(|z_1|>|z_2|>0\).
Consider the Noetherian ring \(R=\mathbb {C}[z_1^{\pm 1},z_2^{\pm 1},(z_1-z_2)^{-1}]\). Then for any quadruple of \(B\)-graded \(\mathsf {V}\)-modules \(\mathcal {W}_0, \mathcal {W}_1, \mathcal {W}_2,\mathcal {W}_3,\) and any triple \((a_1,a_2,a_3)\in B^3\), we define the \(R\)-module
where all the tensor product symbols denote complex tensor products. We will generally omit the tensor product symbol separating \(R\) from the \(\mathsf {V}\)-modules. The motivation for considering this module is that for any \(B\)-graded module \(\mathcal {W}_4\) and any pair of grading compatible logarithmic intertwining operators \({\mathcal {Y}}_1, {\mathcal {Y}}_2\) of respective types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_1,\ \mathcal {W}_4\end{array}}\right) \) and \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_2,\ \mathcal {W}_3\end{array}}\right) \) it produces matrix elements via the map \(\phi _{{\mathcal {Y}}_1,{\mathcal {Y}}_2}:T^{(a_1,a_2,a_3)}\rightarrow z_1^h\mathbb {C}\left( \lbrace z_2/z_1 \rbrace \right) [z_1^{\pm 1},z_2^{\pm 1} ]\), where \(h\) is the combined conformal weight of \(w_0^\prime ,\ w_1,\ w_2,\ w_3\) and \(\mathbb {C}\left( \lbrace x \rbrace \right) \) is the space of all power series in \(x\) with bounded below real exponents (the modules \(\mathcal {W}_i\), \(i=0,1,2,3\) will always have real conformal weights below), defined by
where \(\iota : R\rightarrow \mathbb {C}[\![z_2/z_1 ]\!][z_1^{\pm 1},z_2^{\pm 1} ]\) is the map expanding elements of \(R\) such that the powers of \(z_2\) are bounded below. This in turn justifies considering the submodule

where the generators
are preimages of the relations coming from residues of the Jacobi identity for intertwining operators and where \(v_k^*:\mathcal {W}_i^\prime \rightarrow \mathcal {W}_i^\prime \) denotes the adjoint of \(v_k:\mathcal {W}_i\rightarrow \mathcal {W}_i\). Hence \(J^{(a_1,a_2,a_3)}\) lies in the kernel of \(\phi _{{\mathcal {Y}}_1,{\mathcal {Y}}_2}\) for any choice of intertwining operators \({\mathcal {Y}}_1,{\mathcal {Y}}_2\) of the correct types.
Next consider the doubly homogeneous space
to construct the subspaces
These define filtrations on \(T^{(a_1,a_2,a_3)}\) and \(J^{(a_1,a_2,a_3)}\), respectively, since \(F_s(T^{(a_1,a_2,a_3)})\subset F_r(T^{(a_1,a_2,a_3)})\) and \(F_s(J^{(a_1,a_2,a_3)})\subset F_r(J^{(a_1,a_2,a_3)})\), if \(s\le r\), and \(\bigcup _{r\in \mathbb {R}} F_r(T^{(a_1,a_2,a_3)})=T^{(a_1,a_2,a_3)}\) and \(\bigcup _{r\in \mathbb {R}} F_r(J^{(a_1,a_2,a_3)})=J^{(a_1,a_2,a_3)}\). Note that if the \(\mathcal {W}_i, i=0,1,2,3\) are discretely strongly graded, then \(T^{(a_1,a_2,a_3)}_{[r]}\) is a finite sum of finite dimensional doubly homogeneous spaces tensored with \(R\). Hence \(T^{(a_1,a_2,a_3)}_{[r]}\) is a finitely generated free \(R\)-module. Further, \(F_r(T^{(a_1,a_2,a_3)})\) is also a finite sum and hence also a finitely generated free \(R\)-module. Finally, the ring \(R\) is Noetherian and so the submodule \(F_r(J^{(a_1,a_2,a_3)})\) is also finitely generated.
Proposition A.2
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules, then for any \(a_1,a_2,a_3\in B\) there exists \(M\in \mathbb {Z}\) such that for any \(r\in \mathbb {R}\)
Proof
By assumption the modules \(\mathcal {W}_i,\ i=0,1,2,3\) are \(B\)-graded \(C_1\)-cofinite as \({\overline{V}}\)-modules, that is, the spaces

have finite codimension in \(\mathcal {M}^{(a)}\) for \(\mathcal {M}= \mathcal {W}_i,\ i=0,1,2,3\). Thus \(\mathcal {M}^{(a)}_{[h]}\subset C_1(\mathcal {M})^{(a)}\) for sufficiently large conformal weight \(h\in \mathbb {R}\) and hence there exists \(M\in \mathbb {Z}\) such that
We prove the first inclusion of the proposition by induction on \(r\in \mathbb {R}\). If \(r\le M\), then the inclusion is true by \(F_r(T^{(a_1,a_2,a_3)})\) defining a filtration. Next assume that \(F_r(T^{(a_1,a_2,a_3)})\subset F_r(J^{(a_1,a_2,a_3)}) + F_M(T^{(a_1,a_2,a_3)})\) is true for all \(r<s\in \mathbb {R}\) for some \(s>M\). We will show that any element of the homogeneous space \(T^{(a_1,a_2,a_3)}_{[s]}\) can be written as a sum of elements in \(F_s(J^{(a_1,a_2,a_3)})\) and \(F_M(T^{(a_1,a_2,a_3)})\). Since \(s>M\), this homogeneous element is an element of the right-hand side of (A.15). We shall only consider the case of this element lying in the second summand of the right-hand side, as the other cases follow analogously. Without loss of generality we can assume the element has the form \(w_0^\prime \otimes v_{-1}w_1\otimes w_2\otimes w_3\in T^{(a_1,a_2,a_3)}_{[s]}\), where \(w_0^\prime \in \left( \mathcal {W}_0^\prime \right) ^{(a_1+a_2+a_3)}\), \(w_i\in \mathcal {W}_i^{(a_i)}, i=1,2,3\), \(v\in {\overline{V}}_{[h]}, h>0\). By computing the degrees of the summands making up \({\mathcal {A}}(v,w_0^\prime ,w_1,w_2,w_3)\) in (A.10) we see that the three sums over \(k\) all lie in \(F_{s-1}(T^{(a_1,a_2,a_3)})\subset F_{s-1}(J^{(a_1,a_2,a_3)}) + F_M(T^{(a_1,a_2,a_3)})\) and that \({\mathcal {A}}(v,w_0^\prime ,w_1,w_2,w_3)\in F_s(J^{(a_1,a_2,a_3)})\). Further,
Thus \(w_0^\prime \otimes v_{-1}w_1\otimes w_2\otimes w_3\) lies in the sum \(F_{s}(J^{(a_1,a_2,a_3)}) + F_M(T^{(a_1,a_2,a_3)})\) and the first inclusion of the proposition follows. The second inclusion follows from \(F_r(T^{(a_1,a_2,a_3)})\) and \(F_r(J^{(a_1,a_2,a_3)})\) defining filtrations.
\(\square \)
Corollary A.3
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules.
-
(1)
The quotient \(R\)-module \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\) is finitely generated.
-
(2)
For any representative \(w\in T^{(a_1,a_2,a_3)}\), we denote its coset in \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\) by \([w ]\). Let \(w_0^\prime \in \left( \mathcal {W}_0^\prime \right) ^{(a_1+a_2+a_3)}\) and \(w_i\in \mathcal {W}_i^{(a_i)}\) \(i=1,2,3\), and consider the submodules of \(T^{(a_1,a_2,a_3)}/ J^{(a_1,a_2,a_3)}\) given by
 (A.18)
(A.18)Then \(M_1\) and \(M_2\) are finitely generated, in particular, there exist \(m,n\in \mathbb {Z}_{\ge 0}\) and \(a_k(z_1,z_2), b_\ell (z_1,z_2)\in R\), \(1\le k \le m\), \(1\le \ell \le n\) such that
$$\begin{aligned}&[w_0\otimes L_{-1}^m w_1\otimes w_2\otimes w_3 ]+a_1(z_1,z_2)[w_0\otimes L_{-1}^{m-1} w_1\otimes w_2\otimes w_3 ] \nonumber \\&\quad +\cdots +a_m(z_1,z_2)[w_0\otimes w_1\otimes w_2\otimes w_3 ]=0,\nonumber \\&[w_0\otimes w_1\otimes L_{-1}^n w_2\otimes w_3 ]+b_1(z_1,z_2)[w_0\otimes w_1\otimes L_{-1}^{n-1} w_2\otimes w_3 ] \nonumber \\&\quad +\cdots +b_n(z_1,z_2)[w_0\otimes w_1\otimes w_2\otimes w_3 ]=0. \end{aligned}$$(A.19)
Proof
Since \(R\) is a Noetherian ring, Part (1) holds if \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\) is isomorphic to a subquotient of a finitely generated module over \(R\). By Proposition A.2 we have the inclusion and identification
Thus \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\) is isomorphic to a subquotient of the finitely generated module \(F_M(T^{(a_1,a_2,a_3)})\) and Part (1) follows. Part (2) is an immediate consequence of Part (1) and the fact that a submodule of a finitely generated module over a Noetherian ring is again finitely generated. \(\square \)
Theorem A.4
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules, let \(\mathcal {W}_4\) be a \(B\)-graded \(\mathsf {V}\)-module and let \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\) be logarithmic grading compatible intertwining operators of types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_1,\ \mathcal {W}_4\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_2,\ \mathcal {W}_3\end{array}}\right) \), respectively. Then for any homogeneous elements \(w_0^\prime \in \mathcal {W}_0^\prime \), \(w_i\in \mathcal {W}_i\), \(i=1,2,3\), there exist \(m,n\in \mathbb {Z}_{\ge 0}\) and \(a_k(z_1,z_2),b_\ell (z_1,z_2)\in R\), \(1\le k\le m,\ 1\le \ell \le n\) such that the power series expansion of the matrix element
is a solution to the power series expansion of the system of differential equations
in the region \(|z_1|>|z_2|>0\).
Proof
Let \(a_1,a_2,a_3\) be the respective \(B\)-grades of \(w_1,w_2,w_3\), then we can assume that the \(B\)-grade of \(w_0^\prime \) is \(a_1+a_2+a_3\), because otherwise the matrix element vanishes and the theorem follows trivially. Recall the map \(\phi _{{\mathcal {Y}}_1,{\mathcal {Y}}_2}:T^{(a_1,a_2,a_3)}\rightarrow z_1^h \mathbb {C}\left( \lbrace z_2/z_1 \rbrace \right) [z_1^{\pm 1},z_2^{\pm 2} ]\), defined by the formula (A.8). Since \(J^{(a_1,a_2,a_3)}\) lies in the kernel of \(\phi _{{\mathcal {Y}}_1,{\mathcal {Y}}_2}\), we have an induced map
The theorem then follows by applying \({\overline{\phi }}_{{{\mathcal {Y}}_1,{\mathcal {Y}}_2}}\) to the relations (A.19) of Corollary A.3.(2), using the \(L_{-1}\) derivative property of intertwining operators and expanding in the region \(|z_1|>|z_2|>0\). \(\square \)
Systems of differential equations of the form (A.22) have solutions very close to the expansion required if their singular points are regular, see for example [49, Appendix B]. A sufficient condition, whose validity we shall verify shortly, for regularity at a given singular point is that the coefficients \(a_i, b_j\) in the system (A.22) have poles of degree at most \(m-i\) and \(n-j\) respectively. Such singular points are called simple (see [49, Appendix B] for the general definition). The singular points relevant for the convergence and extension property for products are \(z_1=z_2\) and \((z_1-z_2)/z_2=0\).
We need to consider new filtrations in addition to those considered previously. Let \({\overline{R}}=\mathbb {C}[z_1^{\pm 1},z_2^{\pm 2} ]\), then \(R_n=(z_1-z_2)^{-n}{\overline{R}},\ n\in \mathbb {Z}\) equips \(R\) with the structure of a filtered ring in the sense that \(R_n\subset R_m\), if \(n\le m\), \(R=\bigcup _{n\in \mathbb {Z}} R_n\) and \(R_n\cdot R_m\subset R_{m+n}\). The \(R\)-module \(T^{(a_1,a_2,a_3)}\) can then also be equipped with a compatible filtration
in the sense that \(R_r(T^{(a_1,a_2,a_3)})\subset R_s(T^{(a_1,a_2,a_3)})\), if \(r\le s\), \(T^{(a_1,a_2,a_3)}=\bigcup _{r\in \mathbb {R}} R_r(T^{(a_1,a_2,a_3)})\) and \(R_n\cdot R_r(T^{(a_1,a_2,a_3)})\subset R_{n+r}(T^{(a_1,a_2,a_3)})\). Further, let \(R_r (J^{(a_1,a_2,a_3)})=R_r(T^{(a_1,a_2,a_3)})\cap J^{(a_1,a_2,a_3)}\).
Proposition A.5
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules. Then for any \(a_1,a_2,a_3\in B\) there exists \(M\in \mathbb {Z}\) such that for any \(r\in \mathbb {R}\)
Further, \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\) is finitely generated.
Proof
The proof of this proposition mimics the proof of Proposition A.2 once one has verified that the elements \({\mathcal {A}}(u,w_0^\prime ,w_1,w_2,w_3)\), \({\mathcal {B}}(u,w_0^\prime ,w_1,w_2,w_3)\), \({\mathcal {C}}(u,w_0^\prime ,w_1,w_2, w_3)\) and \({\mathcal {D}}(u,w_0^\prime ,w_1,w_2,w_3)\) lie in \(R_{h}(J)\), where \(h\) is the sum of the conformal weights of \(u,w_0^{\prime },w_1,w_2,w_3\). \(\square \)
We also need to consider the \({\overline{R}}\)-module \(U^{(a_1,a_2,a_3)}={\overline{R}}\otimes \left( \mathcal {W}_0^\prime \right) ^{(a_1+a_2+a_3)}\otimes \mathcal {W}_1^{(a_1)}\otimes \mathcal {W}_2^{(a_2)}\otimes \mathcal {W}_3^{(a_3)}\) and denote by \(U^{(a_1,a_2,a_3)}_{[r]}\) the subspace of conformal weight \(r\in \mathbb {R}\). Thus \(U^{(a_1,a_2,a_3)}=\prod _{r\in \mathbb {R}} U_{[r]}^{(a_1,a_2,a_3)}\).
Lemma A.6
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules. For any \(a_1,a_2,a_3\in B\) and any doubly homogeneous vectors \(w_0^\prime \in \left( \mathcal {W}_0^\prime \right) _{[h_0]}^{(a_1+a_2+a_3)}\), \(w_i\in \left( \mathcal {W}_i \right) _{[h_i]}^{(a_i)}\), let \(h=\sum _i h_i\), let \({\overline{h}}\) be the smallest non-negative representative of the coset \(h+\mathbb {Z}\) and let \(m_J\in R_h(J^{(a_1,a_2,a_3)})\), \(m_T\in F_M(T^{(a_1,a_2,a_3)})\) be vectors satisfying
Then there exists \(S\in \mathbb {R}\) such that \({\overline{h}}+S\in \mathbb {Z}_{\ge 0}\) and \((z_1-z_2)^{h+S}m_T\in U^{(a_1,a_2,a_3)}\).
Proof
Note that the existence of the vectors \(m_J,\ m_T\) is guaranteed by Proposition A.5. Choose \(S\in \mathbb {R}\) such that \({\overline{h}}+S\in \mathbb {Z}_{\ge 0}\) and such that for any \(r\le -S\), \(T_{[r]}^{(a_1,a_2,a_3)}=0\). Such an \(S\) must exist, since the conformal weights of \(T^{(a_1,a_2,a_3)}\) are bounded below by assumption. By definition, \(R_r(T^{(a_1,a_2,a_3)})\) is spanned by elements of the form \((z_1-z_2)^{-n}f(z_1,z_2){\widetilde{w}}_0\otimes {\widetilde{w}}_1\otimes {\widetilde{w}}_2\otimes {\widetilde{w}}_3\), where \(f\in {\overline{R}}\) and \(n+\sum _i {{\,\mathrm{wt}\,}}{\widetilde{w}}_i \le r\). The number \(S\) was therefore chosen such that \((z_1-z_2)^{r+S}R_r(T^{(a_1,a_2,a_3)})\subset U^{(a_1,a_2,a_3)}\) whenever \(r+S\in \mathbb {Z}\). Now, by assumption,
The right-hand side of this equality lies in \(R_{h}(T^{(a_1,a_2,a_3)})\) by construction and therefore so does the left-hand side. Hence \((z_1-z_2)^{h+S}m_T\in U^{(a_1,a_2,a_3)}\). \(\square \)
Theorem A.7
Let the \(\mathsf {V}\)-modules \(\mathcal {W}_i,\ i=0,1,2,3\) be discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite as \(\overline{\mathsf {V}}\)-modules, let \(\mathcal {W}_4\) be a \(B\)-graded \(\mathsf {V}\)-module and let \({\mathcal {Y}}_1\), \({\mathcal {Y}}_2\) be logarithmic grading compatible intertwining operators of types \(\left( {\begin{array}{c}\mathcal {W}_0\\ \mathcal {W}_1,\ \mathcal {W}_4\end{array}}\right) \), \(\left( {\begin{array}{c}\mathcal {W}_4\\ \mathcal {W}_2,\ \mathcal {W}_3\end{array}}\right) \), respectively and consider the system of differential equations of Theorem A.4. For the singular points \(z_1=z_2\) and \((z_1-z_2)/z_2=0\) there exist coefficients \(a_k(z_1,z_2),\ b_l(z_1,z_2)\in R\) such that these singular points of the system of differential equations (A.22) satisfied by the matrix elements (A.21) are regular.
Proof
We consider first the singular point \(z_1=z_2\). By Proposition A.5 and Lemma A.6, for any \(k\in \mathbb {Z}_{\ge 0}\) together with a vector \(w_0^\prime \otimes L_{-1}^k w_1\otimes w_2\otimes w_3\in T^{(a_1,a_2,a_3)}\), where the \(w_i\) are doubly homogeneous vectors of total conformal weight \(h\in \mathbb {R}\), there exist \(m_J^{(k)}\in R_{h+k}(J^{(a_1,a_2,a_3)})\) and \(m_T^{(k)}\in F_M(T^{(a_1,a_2,a_3)})\) such that
Let \({\overline{h}}\) be the smallest non-negative representative of the coset \(h+\mathbb {Z}\). Then, by Lemma A.6, there exists \(S\in \mathbb {R}\) such that \({\overline{h}}+S\in \mathbb {Z}_{\ge 0}\) and \((z_1-z_2)^{h+k+S}m_T^{(k)}\in U^{(a_1,a_2,a_3)}\) and thus \((z_1-z_2)^{h+k+S}m_T^{(k)}\in \bigcup _{r\le M}U^{(a_1,a_2,a_3)}_{[r]}\). Since the \(V\)-modules \(\mathcal {W}_i\) are discretely strongly \(B\)-graded and \(B\)-graded \(C_1\)-cofinite, \(\prod _{r\le M}U^{(a_1,a_2,a_3)}_{[r]}\) is a finite sum of finitely generated \({\overline{R}}\)-modules and hence also finitely generated. Thus, since \({\overline{R}}\) is Noetherian, the submodule generated by the \((z_1-z_2)^{h+k+S}m_T^{(k)}\), \(k\in \mathbb {Z}_{\ge 0}\) is also finitely generated. Hence there exists an \(m\in \mathbb {Z}_{\ge 0}\) such that  is a finite generating set for this submodule and subsequently there exist \(c_k(z_1,z_2)\in {\overline{R}}\) such that
is a finite generating set for this submodule and subsequently there exist \(c_k(z_1,z_2)\in {\overline{R}}\) such that
Therefore,
Thus in the quotient module \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\), we obtain (where we again use square brackets to denote cosets)
since \(m_J^{(k)}\in J^{(a_1,a_2,a_3)}\). By a similar line of reasoning there exists an \(n\in \mathbb {Z}_{\ge 0}\) and \(d_\ell (z_1,z_2)\in {\overline{R}}\) such that
Applying the map \(\phi _{{\mathcal {Y}}_1,{\mathcal {Y}}_2}\) defined by (A.8) and using the \(L_{-1}\) property for intertwining operators will then result in a system of differential equations for which \(z_1=z_2\) is a simple, and hence regular, singular point.
To show the regularity of the singular point \((z_1-z_2)/z_2=0\), we introduce new gradings on \(R\) and \(T^{(a_1,a_2,a_3)}\). We assign degree \(-1\) to the variables \(z_1,z_2\), thus giving \(R\) a \(\mathbb {Z}\) grading and then grade \(T^{(a_1,a_2,a_3)}\) by adding \(R\)-degrees and conformal weights. This implies that the elements \({\mathcal {A}}(v,w_0^\prime ,w_1,w_2,w_3), \ {\mathcal {B}}(v,w_0^\prime ,w_1,w_2,w_3), \ {\mathcal {C}}(v,w_0^\prime ,w_1,w_2, w_3)\) and \({\mathcal {D}}(v,w_0^\prime ,w_1,w_2,w_3)\) are homogeneous with respect to this new grading if their arguments are doubly homogeneous. The new grading therefore descends to \(T^{(a_1,a_2,a_3)}/J^{(a_1,a_2,a_3)}\). Further, for doubly homogeneous elements \(w_0^\prime ,w_1,w_2,w_3\), the elements
are also homogeneous. Thus the coefficients \(c_k(z_1,z_2), d_\ell (z_1,z_2)\) of equations (A.31) and (A.32) are elements of degree 0 in \(R\) and can therefore be written as Laurent polynomials in \((z_1-z_2)/z_2\). It then follows that the singular point \((z_1-z_2)/z_2=0\) is regular. \(\square \)
The fact that the matrix element (A.2) satisfies an expansion of the form (A.3) now follows by the reasoning of [48, Theorem 3.5]. A little care is needed when following the reasoning of [48], since there only modules with a diagonalisable action of \(L_0\) are considered. However, as noted in [21, Part VII, Proof of Theorem 11.8 and Remark 11.9] the argument extends easily to modules where \(L_0\) has Jordan blocks. The basic idea is that one can use the \(L_0\) conjugation property of intertwining operators (recall that \(L_0\) is the generator of dilations) to rescale the variables in the matrix element (A.2) by \(z_2\) so that it becomes a function in \(z_3=(z_1-z_2)/z_2\) only and the system of differential equations (A.31) and (A.32) then becomes an ordinary differential equation for \(z_3\) with a regular singularity at \(z_3=0\). Similar reasoning for the matrix element (A.5) leads one to conclude that it satisfies the expansion (A.6). Hence Theorem 5.7 follows.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Allen, R., Wood, S. Bosonic Ghostbusting: The Bosonic Ghost Vertex Algebra Admits a Logarithmic Module Category with Rigid Fusion. Commun. Math. Phys. 390, 959–1015 (2022). https://doi.org/10.1007/s00220-021-04305-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04305-6



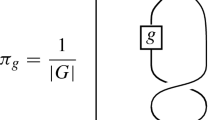


 . A strongly graded module
. A strongly graded module 