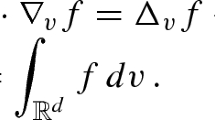Abstract
This paper is devoted to kinetic equations without confinement. We investigate the large time behaviour induced by collision operators with fat tailed local equilibria. Such operators have an anomalous diffusion limit. In the appropriate scaling, the macroscopic equation involves a fractional diffusion operator so that the optimal decay rate is determined by a fractional Nash type inequality. At kinetic level we develop an \(\mathrm {L}^2\)-hypocoercivity approach and establish a rate of decay compatible with the fractional diffusion limit.



Similar content being viewed by others
References
Aceves-Sanchez, P., Cesbron, L.: Fractional diffusion limit for a fractional Vlasov–Fokker–Planck equation. SIAM J. Math. Anal. 51(1), 469–488 (2019)
Ayi, N., Herda, M., Hivert, H., Tristani, I.: A note on hypocoercivity for kinetic equations with heavy-tailed equilibrium. Comptes Rendus Math. 358(3), 333–340 (2020)
Bakry, D., Cattiaux, P., Guillin, A.: Rate of convergence for ergodic continuous Markov processes: Lyapunov versus Poincaré. J. Funct. Anal. 254(3), 727–759 (2008)
Ben Abdallah, N., Mellet, A., Puel, M.: Anomalous diffusion limit for kinetic equations with degenerate collision frequency. Math. Models Methods Appl. Sci. 21(11), 2249–2262 (2011)
Ben-Artzi, J., Einav, A.: Weak Poincaré inequalities in the absence of spectral gaps. Ann. Henri Poincaré 21(2), 359–375 (2020)
Biler, P., Karch, G.: Blowup of solutions to generalized Keller–Segel model. J. Evol. Equ. 10(2), 247–262 (2010)
Biler, P., Karch, G., Laurençot, P.: Blowup of solutions to a diffusive aggregation model. Nonlinearity 22(7), 1559–1568 (2009)
Blanchet, A., Bonforte, M., Dolbeault, J., Grillo, G., Vázquez, J.L.: Asymptotics of the fast diffusion equation via entropy estimates. Arch. Ration. Mech. Anal. 191(2), 347–385 (2009)
Bouin, E., Dolbeault, J., Lafleche, L., Schmeiser, C.: Hypocoercivity and sub-exponential local equilibria. Monatshefte für Mathematik 194(1), 41–65 (2020)
Bouin, E., Dolbeault, J., Mischler, S., Mouhot, C., Schmeiser, C.: Hypocoercivity without confinement. Pure Appl. Anal. 2(2), 203–232 (2020)
Bouin, E., Dolbeault, J., Schmeiser, C.: Diffusion and kinetic transport with very weak confinement. Kinetic Relat. Models 13(2), 345–371 (2020)
Bouin, E., Mouhot, C.: Quantitative fluid approximation in transport theory: a unified approach (2020)
Brezis, H., Ponce, A.C.: Kato’s inequality when \(\Delta u\) is a measure. Comptes Rendus Math. 338(8), 599–604 (2004)
Cao, C.: The kinetic Fokker–Planck equation with weak confinement force. Commun. Math. Sci. 17(8), 2281–2308 (2019)
Cattiaux, P., Nasreddine, E., Puel, M.: Diffusion limit for kinetic Fokker-Planck equation with heavy tails equilibria: the critical case. Kinetic Relat. Models 12(4), 727–748 (2019)
Cesbron, L., Mellet, A., Trivisa, K.: Anomalous transport of particles in plasma physics. Appl. Math. Lett. 25(12), 2344–2348 (2012)
Chen, X., Wang, J.: Weighted Poincaré inequalities for non-local Dirichlet forms. J. Theor. Probab. 30(2), 452–489 (2017)
Crouseilles, N., Hivert, H., Lemou, M.: Numerical schemes for kinetic equations in the anomalous diffusion limit. Part I: the case of heavy-tailed equilibrium. SIAM J. Sci. Comput. 38(2), A737–A764 (2016)
Crouseilles, N., Hivert, H., Lemou, M.: Numerical schemes for kinetic equations in the anomalous diffusion limit. Part II: degenerate collision frequency. SIAM J. Sci. Comput. 38(4), A2464–A2491 (2016)
Degond, P., Goudon, T., Poupaud, F.: Diffusion limit for nonhomogeneous and non-micro-reversible processes. Indiana Univ. Math. J. 49(3), 1175–1198 (2000)
Dolbeault, J., Mouhot, C., Schmeiser, C.: Hypocoercivity for linear kinetic equations conserving mass. Trans. Am. Math. Soc. 367(6), 3807–3828 (2015)
Fournier, N., Tardif, C.: Anomalous diffusion for multi-dimensional critical kinetic Fokker–Planck equations. Ann. Probab. 48(5), 2359–2403 (2020)
Fournier, N., Tardif, C.: One dimensional critical kinetic Fokker–Planck equations, Bessel and stable processes. Commun. Math. Phys. 381(1), 143–173 (2021)
Gualdani, M.P., Mischler, S., Mouhot, C.: Factorization of non-symmetric operators and exponential H-theorem. Mémoires de la Société Mathématique de France. Nouvelle Série 153 153, 1–137 (2017)
Jara, M., Komorowski, T., Olla, S.: Limit theorems for additive functionals of a Markov chain. Ann. Appl. Probab. 19(6), 2270–2300 (2009)
Kato, T.: Schrödinger operators with singular potentials. Isr. J. Math. 13(1972), 135–148 (1973)
Kavian, O., Mischler, S., Ndao, M.: The Fokker–Planck equation with subcritical confinement force. Journal de Mathématiques Pures et Appliquées 151, 171–211 (2021)
Lafleche, L.: Fractional Fokker–Planck equation with general confinement force. SIAM J. Math. Anal. 52(1), 164–196 (2020)
Lafleche, L.: Dynamique de systèmes à grand nombre de particules et systèmes dynamiques. Ph.D. thesis, Paris Sciences et Lettres, Université Paris-Dauphine. https://laurent-lafleche.perso.math.cnrs.fr/docs/These.pdf, 28/06/2019
Landkof, N.S.: Foundations of Modern Potential Theory. Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berucksichtigung der Anwendungsgebiete, Bd. 180. Springer (1972)
Lebeau, G., Puel, M.: Diffusion approximation for Fokker Planck with heavy tail equilibria: a spectral method in dimension 1. Commun. Math. Phys. 366(2), 709–735 (2019)
Mellet, A.: Fractional diffusion limit for collisional kinetic equations: a moments method. Indiana Univ. Math. J. 59(4), 1333–1360 (2010)
Mellet, A., Mischler, S., Mouhot, C.: Fractional diffusion limit for collisional kinetic equations. Arch. Ration. Mech. Anal. 199(2), 493–525 (2011)
Mischler, S., Mouhot, C.: Exponential stability of slowly decaying solutions to the kinetic Fokker–Planck equation. Arch. Ration. Mech. Anal. 221(2), 677–723 (2016)
Nash, J.: Continuity of solutions of parabolic and elliptic equations. Am. J. Math. 80, 931–954 (1958)
Puel, M., Mellet, A., Ben Abdallah, N.: Fractional diffusion limit for collisional kinetic equations: a Hilbert expansion approach. Kinetic Relat. Models 4(4), 873–900 (2011)
Röckner, M., Wang, F.-Y.: Weak Poincaré inequalities and \(L^2\)-convergence rates of Markov semigroups. J. Funct. Anal. 185(2), 564–603 (2001)
Scalas, E., Gorenflo, R., Mainardi, F., Raberto, M.: Revisiting the derivation of the fractional diffusion equation. Fractals 11(supp. 01), 281–289 (2003)
Stein, E.M., Weiss, G.: Interpolation of operators with change of measures. Trans. Am. Math. Soc. 87(1), 159–172 (1958)
Wang, F.-Y., Wang, J.: Functional inequalities for stable-like Dirichlet forms. J. Theor. Probab. 28(2), 423–448 (2015)
Wang, J.: A simple approach to functional inequalities for non-local Dirichlet forms. ESAIM Probab. Stat. 18, 503–513 (2014)
Acknowledgements
This work has been supported by the Project EFI (ANR-17-CE40-0030) of the French National Research Agency (ANR). The authors are deeply indebted to Christian Schmeiser, who was at the origin of the research project and participated to the preliminary discussions while he was visiting as the holder of the Chaire d’excellence of the Fondation Sciences Mathématiques de Paris, also supported by Paris Sciences et Lettres. The project is also part of the Amadeus project Hypocoercivity no. 39453PH. © 2021 by the authors. This paper may be reproduced, in its entirety, for non-commercial purposes.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H.-T. Yau.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Steady States and Force Field for the Fractional Laplacian with Drift
Steady States and Force Field for the Fractional Laplacian with Drift
This appendix is devoted to the Case \({\mathsf {L}}={\mathsf {L}}_3\) of the collision operator \({\mathsf {L}}\), that is, to \({\mathsf {L}}_3 f=\Delta _v^{\sigma /2}f+\nabla _v\cdot \left( E\,f\right) \). Our goal here is to prove that the collision frequency \(\nu (v)\) behaves like \(|v|^{- \beta }\) with \(\beta = \sigma -\gamma \) as \(|v|\rightarrow +\infty \), as claimed in Sect. 1. By Definition (9) of the force field E, we know that
and this implies that, up to an additive constant,
where \(c_\gamma \) and \(C_{d,\sigma }\) are given respectively by (2) and (20).
Proposition 7
Assume that \(\gamma >0\), \(\sigma \in (0,2)\) and let \( \beta =\sigma - \gamma \). There is a positive function \(G\in \mathrm {L}^\infty ({{\mathbb {R}}}^d)\) with \(1/G\in \mathrm {L}^\infty (B_0^c(1))\) such that E is given by
Proof
Let \(u(v)=-\nabla _v\,\big (\frac{1}{|v|^{d+\sigma -2}}*\frac{1}{\left\langle v\right\rangle ^{d+\gamma }}\big )(v)\) so that \(E(v)=C_{d,\sigma } \left\langle v\right\rangle ^{d+\gamma } u(v)\). Since
where \(\left\langle v\right\rangle ^{-(d+\gamma +2)} v\in C^\infty ({{\mathbb {R}}}^d)\cap \mathrm {L}^1(\mathrm dv)\), and \(\sigma <2\), one has \(u\in C^1_{\mathrm {loc}}({{\mathbb {R}}}^d)\) and \(u(0)=0\) which proves the result in \(B_1(0)\). We look for an estimate of \(u(v)\cdot v\) from above and below on \(B_0^c(1)\). Notice that u can also be written as
Depending on the integrability at infinity of \(v/|v|^{d+\sigma }\), that is, whether \(\sigma \in (0,1)\) or not, we have to distinguish two cases.
\(\bullet \) Case \(\sigma \in (0,1)\). Using (29), we have the estimates
and obtain
To get a bound from below on \(u(v)\cdot v\), we cut the integral in two pieces and use the fact that \(|v|>1\) and \(|w-v|<1/2\) implies \(w\cdot v>0\). First
which is positive since \(\left\langle w+v\right\rangle ^2-\left\langle w-v\right\rangle ^2=2\,w\cdot v\ge 0\). The remaining terms are dealt with as follows
since \(|w+v|\ge 2\,|v|-|w-v|\ge \frac{3}{2}\). Finally, if \(|v|>1\) and \(|w-v|<\frac{1}{2}\), we get
so that
This implies \(u(v)\cdot v\ge C\,|v|^{-(d+\sigma -2)}\) for some \(C>0\). Since u is radial, we proved that
where \(G\in \mathrm {L}^\infty ({{\mathbb {R}}}^d)\) and \(G^{-1}\in \mathrm {L}^\infty (B_0^c(1))\) and the conclusion holds with \(\beta =\sigma - \gamma \).
\(\bullet \) Case \(\sigma \in [1,2)\). The gradient of \(v\mapsto |v|^{2-d-\sigma }\) is a distribution of order 1 that can be defined as a principal value. Indeed, in the sense of distributions, for any \(\varphi \in {\mathcal {D}}({{\mathbb {R}}}^d)\), we have
Identity (29) is replaced by
so that, after computations like the ones in the proof of Lemma 10,
Now estimate \(u(v)\cdot v\) by
and
The result follows from the fact that \(d+\gamma>d>d+\sigma -2\). \(\quad \square \)
Rights and permissions
About this article
Cite this article
Bouin, E., Dolbeault, J. & Lafleche, L. Fractional Hypocoercivity. Commun. Math. Phys. 390, 1369–1411 (2022). https://doi.org/10.1007/s00220-021-04296-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04296-4