Abstract
We study the hydrodynamic limit, in the hyperbolic space-time scaling, for a one-dimensional unpinned chain of quantum harmonic oscillators with random masses. To the best of our knowledge, this is among the first examples where one can prove the hydrodynamic limit for a quantum system rigorously. In fact, we prove that after hyperbolic rescaling of time and space, the distribution of the elongation, momentum, and energy averaged under the proper locally Gibbs state converges to the solution of the Euler equation. Moreover, our result indicates that the temperature profile is frozen in any space-time scale; in particular, the thermal diffusion coefficient vanishes. There are two main phenomena in this chain that enable us to deduce this result. First is the Anderson localization, which decouples the mechanical and thermal energy, providing the closure of the equation for energy. The second phenomenon is similar to some sort of decay of correlation phenomena, which let us circumvent the difficulties arising from the fact that our Gibbs state is not a product state due to the quantum nature of the system.
Similar content being viewed by others
Notes
On the physical ground, one could think of these particles as ions/atoms in an insulator crystal interacting with their nearest neighbors. By taking masses to be random, we can imagine that we have a random alloy where we have a combination of different ions/atoms in the lattice. In particular, having this picture in mind, it becomes clear that these particles are distinguishable, and their wave function is not necessarily symmetric/antisymmetric.
By “clean” we refer to the chain where all the masses are equal.
This corresponds to the fact that initially, we are describing our system from viewpoint of an observer in the center of mass.
One can take \(\cap _{k=1}^{n-1} ({\mathcal {D}}({\hat{b}}_k) \cap {\mathcal {D}}({\hat{b}}_k^*)) \) as the proper domain, which is dense in \({\mathcal {H}}_n\).
This modification stems from the fact that in our case \(V_x\) is not positive definite and has a zero eigenvalue.
Notice the difference between the notation
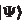 which is used for denoting the member of the Hilbert space, and
which is used for denoting the member of the Hilbert space, and 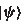 which denotes the finite dimensional vector spaces.
which denotes the finite dimensional vector spaces.We will modify this convention later.
For every linear function \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m \) with corresponding \(m\times n\) matrix A, we define \(||A||_2 =\sup _{|x|_n=1}\frac{|Ax|_m}{|x|_n}\), where |.| denotes the Euclidean norm in \({\mathbb {R}}^n\): \(|x|_n=(\sum _{i=1}^n x_i^2)^{\frac{1}{2}}\).
The gap is as follows: comparing the relations (3.11), (3.12) with (3.14), (3.15) in [6] is not sufficient to close the argument, since the derivative of f and g appears in the RHS instead of f and g.
These solutions are exactly similar to (3.22), where the operators at time zero replaced by the averaged function at time zero.
For every \(\epsilon >0\), take \(\delta =\frac{\epsilon }{{\bar{C}}}\), then for every \(\phi \) in this family, and \(t,t' \in [0,T]\), if \(|t-t'|<\delta \), we have \(|\phi (t)-\phi (t')| \le |t-t'||\phi '(t^*)| \le {\bar{C}}|t-t'| \le \epsilon \), for \(t<t^*<t'\), since all the functions in this family are smooth, and their derivative are uniformly bounded.
Notice that we misuse the bound of the sums in the last expression thanks to the support of \(\zeta _{\epsilon }\).
This constant can be taken equal to \(4\frac{\beta _{max}^2}{m_{min}}\).
Precisely, one can choose \({\mathcal {C}}_0 \) to be equal to \(\frac{m_{max}\beta _{max}}{m_{min}\beta _{min}}\).
One can choose \(c_1={\mathfrak {f}}(c_0)\).
Note that these definition depends on the \(n,x,x'\).
This bound is true for every configuration of masses.
One can simply take \(C_1=||g'||_{\infty }\).
We already discussed the positivity of the terms under the square root in the second line, which can be obtained by the fact that these operators are linear combination of bosonic operators \(\tilde{{\mathfrak {b}}}_k\), and their adjoints, and they are self adjoint, hence, by using Lemma 3.38, we obtain the positivity (more abstract proof is of course possible).
Recall that all the expressions corresponding to the nth component of the r operator is zero, and we bring them in the same sum just to lighten the notation.
Notice that we come back to the notation where we denote the thermal average by
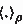 instead of
instead of 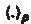 , since there is no confusion here.
, since there is no confusion here.This bound is obvious, since \(|\tilde{{\mathcal {I}}}_k|\) is the solution to the problem of the number of path from (0, 0) to (k, 0) consisting of the vectors \((1,1),(1,-1),(1,0)\), this is equivalent to the number of solution of \(s_1+\dots +s_k=0\), for \(s_i \in \{-1,0,1\}\), which is obviously bounded by \(3^k\). This bound is not sharp and a better asymptotic will be \(\frac{c3^k}{\sqrt{k}}\) for c around \(\frac{1}{2}\), but \(3^{n_*}\) is sufficient for our purposes.
This extension is not necessary, it is done to make our notation coherent; however we do not use this extension.
Here |.| denotes the Euclidean distance in \({\mathbb {R}}^{2[\frac{k}{2}]+2}\).
The case \(y=0\) or \(y=1\), corresponds to the paths which are constructed by vectors of the form \((1,0),(1,-1)\), for \(y=0\), and (1, 0), (1, 1) for \(y=1\). In either case, our argument is similar, where we can modify the set \(\tilde{{\mathcal {I}}}_k\) and function \({\mathcal {F}}\) accordingly.
We do not explain the proof in details since this is a classical result one can find in [9].
References
Aizenman, M., Graf, G.M.: Localization bounds for an electron gas. J. Phys. A: Math. Gen. 31(32), 6783–6806 (1998)
Ajanki, O., Huveneers, F.: Rigorous scaling law for the heat current in disordered harmonic chain. Commun. Math. Phys. 301(3), 841–883 (2011)
Anderson, P.W.: Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958)
Ashcroft, N.W., Mermin, N.D. et al.: Solid State Physics (1976)
Benedikter, N., Porta, M., Schlein, B.: Effective Evolution Equations from Quantum Dynamics. Springer Briefs in Mathematical Physics. Springer, Berlin (2015)
Bernardin, C., Huveneers, F., Olla, S.: Hydrodynamic limit for a disordered harmonic chain. Commun. Math. Phys. 365(1), 215–237 (2019)
Bertini, B., Collura, M., De Nardis, J., Fagotti, M.: Transport in out-of-equilibrium \(xxz\) chains: exact profiles of charges and currents. Phys. Rev. Lett. 117, 207201 (2016)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics 1: C*- and w*-Algebras. Symmetry Groups. Decomposition of States, Operator Algebras and Quantum Statistical Mechanics. Springer, Berlin (1987)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics: Equilibrium States. Models in Quantum Statistical Mechanics, Theoretical and Mathematical Physics. Springer, Berlin (2003)
Braxmeier-Even, N., Olla, S.: Hydrodynamic limit for a Hamiltonian system with boundary conditions and conservative noise. Arch. Ration. Mech. Anal. 213(2), 561–585 (2014)
Casher, A., Lebowitz, J.L.: Heat flow in regular and disordered harmonic chains. J. Math. Phys. 12(8), 1701–1711 (1971)
Castro-Alvaredo, O.A., Doyon, B., Yoshimura, T.: Emergent hydrodynamics in integrable quantum systems out of equilibrium. Phys. Rev. X 6, 041065 (2016)
Cramer, M., Eisert, J.: Correlations, spectral gap and entanglement in harmonic quantum systems on generic lattices. New J. Phys. 8(5), 71 (2006)
de Gosson, M.A.: Symplectic Geometry and Quantum Mechanics. Operator Theory: Advances and Applications. Birkhäuser, Basel (2006)
DeMasi, A., Presutti, E.: Mathematical Methods for Hydrodynamic Limits. Lecture Notes in Mathematics. Springer, Berlin (2006)
Dhar, A.: Heat conduction in the disordered harmonic chain revisited. Phys. Rev. Lett. 86, 5882–5885 (2001)
Doyon, B.: Hydrodynamic projections and the emergence of linearised Euler equations in one-dimensional isolated systems (2020)
Dvoretzky, A.: On the strong stability of a sequence of events. Ann. Math. Stat. 20(2), 296–299 (1949)
Erdős, L., Schlein, B., Yau, H.-T.: Derivation of the cubic non-linear Schrödinger equation from quantum dynamics of many-body systems. Invent. Math. 167(3), 515–614 (2007)
Erdős, L., Schlein, B., Yau, H.-T.: Rigorous derivation of the Gross–Pitaevskii equation with a large interaction potential. J. Am. Math. Soc. 22(4), 1099–1156 (2009) (Full publication date: OCTOBER 2009)
Evans, L.C.: Partial Differential Equations. American Mathematical Society, Providence (2010)
Hall, B.C.: Quantum Theory for Mathematicians. Springer, New York (2013)
Halperin, B.I.: Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982)
Higham, N.J.: Functions of Matrices: Theory and Computation. Society for Industrial and Applied Mathematics, Philadelphia (2008)
Kipnis, C., Landim, C.: Scaling Limits of Interacting Particle Systems. Grundlehren der mathematischen Wissenschaften. Springer, Berlin (2013)
Kittel, C.: Introduction to Solid State Physics, 5th edn (1976)
Komorowski, T., Olla, S.: Ballistic and superdiffusive scales in the macroscopic evolution of a chain of oscillators. Nonlinearity 29(3), 962–999 (2016)
Komorowski, T., Olla, S., Simon, M.: Macroscopic evolution of mechanical and thermal energy in a harmonic chain with random flip of velocities. Kinet. Relat. Models 11(3), 615–645 (2018)
Kunz, H., Souillard, B.: Sur le spectre des opérateurs aux différences finies aléatoires. Commun. Math. Phys. 78(2), 201–246 (1980)
Lieb, E.H., Seiringer, R., Solovej, J.P., Yngvason, J.: The Mathematics of the Bose Gas and Its Condensation. Oberwolfach Seminars. Birkhäuser, Basel (2006)
Lieb, E.H.: Exact analysis of an interacting Bose gas. ii. The excitation spectrum. Phys. Rev. 130, 1616–1624 (1963)
Lieb, E.H., Liniger, W.: Exact analysis of an interacting Bose gas. i. The general solution and the ground state. Phys. Rev. 130, 1605–1616 (1963)
Lieb, E.H., Mattis, D.C.: Mathematical Physics in One Dimension: Exactly Soluble Models of Interacting Particles. Academic Press, Cambridge (2013)
Lyons, R.: Strong laws of large numbers for weakly correlated random variables. Mich. Math. J. 35(3), 353–359 (1988)
Nachtergaele, B., Raz, H., Schlein, B., Sims, R.: Lieb–Robinson bounds for harmonic and anharmonic lattice systems. Commun. Math. Phys. 286(3), 1073–1098 (2009)
Nachtergaele, B., Schlein, B., Sims, R., Starr, S., Zagrebnov, V.: On the existence of the dynamics for anharmonic quantum oscillator systems. Rev. Math. Phys. 22(02), 207–231 (2010)
Nachtergaele, B., Sims, R., Stolz, G.: Quantum harmonic oscillator systems with disorder. J. Stat. Phys. 149(6), 969–1012 (2012)
Nachtergaele, B., Yau, H.-T.: Derivation of the Euler equations from quantum dynamics. Commun. Math. Phys. 243(3), 485–540 (2003)
Olla, S., Varadhan, S.R.S., Yau, H.-T.: Hydrodynamical limit for a Hamiltonian system with weak noise. Commun. Math. Phys. 155(3), 523–560 (1993)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics: Functional Analysis. Methods of Modern Mathematical Physics. Academic Press, Cambridge (1980)
Rubin, R.J., Greer, W.L.: Abnormal lattice thermal conductivity of a one dimensional, harmonic, isotopically disordered crystal. J. Math. Phys. 12(8), 1686–1701 (1971)
Spohn, H.: Large Scale Dynamics of Interacting Particles. Theoretical and Mathematical Physics. Springer, Berlin (2012)
Spohn, H.: Generalized Gibbs ensembles of the classical Toda chain. J. Stat. Phys. 180(1), 4–22 (2020)
Verheggen, T.: Transmission coefficient and heat conduction of a harmonic chain with random masses: asymptotic estimates on products of random matrices. Commun. Math. Phys. 68(1), 69–82 (1979)
Williamson, J.: On the algebraic problem concerning the normal forms of linear dynamical systems. Am. J. Math. 58(1), 141–163 (1936)
Acknowledgements
I would like to thank Stefano Olla for proposing this problem, his support and help during this project. I am also deeply grateful to François Huveneers for numerous enlightening discussions, his help and support. Moreover, I should mention that this work was partially supported by ANR-15-CE40-0020-01 LSD of the French National Research Agency. Furthermore, I would like to thank B. Doyon for pointing out [17]. Finally, I would like to thank the anonymous referees for pointing out various references, and for their illuminating comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. Spohn
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Properties of the Limiting Function
In this section, we study the properties of \(\mathrm {f}^{\mu }_{\beta }\), which is defined in (5.5). We prove a couple of lemmas to facilitate the proof of Theorem 5.4. In particular, we prove the existence of the limit (5.5), this means that \(\mathrm {f}^{\mu }_{\beta }\) is well-defined. Moreover, we show that this function is continuous. Furthermore, we treat the equilibrium case and demonstrate that the function \(\mathrm {f}^{\mu }(\beta _{eq})\) is well defined, i.e. \(\mathrm {f}^{\mu }_{\beta _{eq}}(y)\) does not depend on y. Then we demonstrate the relation (5.36). Finally, we prove a lemma which has been needed in 5.4. All the proofs in this section share the same spirit: We represent  in terms of the Taylor series, then cut the series similar to (5.22), and control the expressions depending on the first part of the Taylor series, using the fact that the number of these terms is finite, \(\beta \) is continuous and bounded, and the distribution of the masses is compactly supported. Finally, we use the fact that the terms depending on the remainder of the series is small.
in terms of the Taylor series, then cut the series similar to (5.22), and control the expressions depending on the first part of the Taylor series, using the fact that the number of these terms is finite, \(\beta \) is continuous and bounded, and the distribution of the masses is compactly supported. Finally, we use the fact that the terms depending on the remainder of the series is small.
Notice that since n is not fixed here, we denote the ensemble average with  , in order to emphasize the dependence on n. Before proceeding, recall the definition of \(A_p^{\beta }\), and \(A_r^{\beta }\) from (3.25), since here n is not fixed and we study matrices with different sizes, we change our notations only in this section and denote these matrices by \(A_n^p\), and \(A_n^r\), respectively i.e.
, in order to emphasize the dependence on n. Before proceeding, recall the definition of \(A_p^{\beta }\), and \(A_r^{\beta }\) from (3.25), since here n is not fixed and we study matrices with different sizes, we change our notations only in this section and denote these matrices by \(A_n^p\), and \(A_n^r\), respectively i.e.
where \(M_{\beta }=M\beta ^{-1}\), with \(M=\mathrm {diag}(m_1,\dots ,m_n)\), \(\beta =\mathrm {diag}(\beta (\frac{1}{n}),\dots ,\beta (\frac{n}{n}))\), and \(\beta ^o=\mathrm {diag}(\beta (\frac{1}{n}),\dots ,\beta (\frac{n-1}{n}))\).
Since all these proofs share the same spirit, we set a handful of notation here:
Recall the average expression  from (5.18):
from (5.18):

Thanks to (5.17), the part corresponding to p can be written as follows:
As we argued in Sect. 5.1, there exists a constant \(c_0>0\), such that for every realization of the masses, and \(\forall n\), \(||A_p^n||_2 \le c_0\). Therefore, using the properties of Taylor series as in (5.25), we observe that \(\forall \epsilon >0\), there exists \(K_*(\epsilon ) \in {\mathbb {N}}\), such that \(\forall n \), \(\forall x \in {\mathbb {I}}_n\), and any realization of the masses we have:
Notice that we can choose \(K_*(\epsilon )\), such that the same bound (A.3) holds when we substitute \(A_n^p\) with \(A_n^r\). Hence, given \(\epsilon >0\) one can define \({\mathfrak {f}}_{\prec }^{\epsilon }(.)\) and \({\mathfrak {f}}_{\succ }^{\epsilon }(.)\) as follows:
In particular, we can rewrite (A.3) in the following way: For any \(\epsilon >0\) there exits \(K_*(\epsilon )\) such that for any n and \(x \in {\mathbb {I}}_n\) we have:
Fix \((k,n) \in {\mathbb {N}}^2\), denote \(A_n^p-\alpha I_{n}\) by \({\tilde{A}}_n^p\), take \(x \in {\mathbb {I}}_n\), and consider the following term: \(\langle x,({\tilde{A}}_n^p)^k x\rangle \). Here we represent this term in a more appropriate manner, introducing following notations. First, recall the random walk representation of \(\langle x,({\tilde{A}}_n^p)^k x\rangle \):
Denote the set of indices with non-zero contribution, in RHS of (A.6) by \({\mathcal {I}}_{n,k}^{x,p}\):
where \({\tilde{A}}_n^p=A_n^p-\alpha I_n\). We denote the elements of \({\mathcal {I}}_{n,k}^{x,p}\) by \({\underline{x}}:=(x_1,\dots ,x_{k-1})\). Notice that there is a bijection between \({\mathcal {I}}_{n,k}^{x,p}\) and the set of paths in \([0,k] \times [0,n] \cap {\mathbb {Z}}^2\) from the point (x, 0) to (x, k), consisting of the following vectors: \((-1,1),(0,1),(1,1) \in {\mathbb {Z}}^2\). In fact, this bijection is given as follows: \(\forall {\underline{x}} \in {\mathcal {I}}_{n,k}^{x,p}\), assign to \({\underline{x}}\) the path which is given by the following points: (0, x), \((1,x_1)\),\(\dots \), \((j,x_j)\), \(\dots \),\((k-1,x_{k-1}),(k,x)\).
Let \(\tilde{{\mathcal {I}}}_{n,k}^{x,p}\) be the set where every element of \({\mathcal {I}}_{n,k}^{x,p}\) shifted by the vector \((x,\dots ,x) \in ({\mathbb {I}}_n)^{k-1}\), precisely define:
We denote each element of \(\tilde{{\mathcal {I}}}_{n,k}^{x,p}\) by \({\underline{\eta }}=(\eta _1,\dots , \eta _{k-1})\). Notice that \({\underline{\eta }} \) corresponds to a path from (0, 0) to (0, k) in \([0,k]\times [-x,n-x] \cap {\mathbb {Z}}^2\) consisting of the aforementioned vectors. Finally, define \(\tilde{{\mathcal {I}}}_k\) as follows:
Observe that each \({\underline{\eta }} \in {\mathcal {I}}_k\), corresponds to a path from (0, 0) to (0, k) in \({\mathbb {Z}}^2\) consisting of \((-1,1),(0,1),(1,1) \in {\mathbb {Z}}^2\).
Having in mind the geometric interpretation of \(\tilde{{\mathcal {I}}}_{n,k}^{x,p}\) and \(\tilde{{\mathcal {I}}}_k\), one can observeFootnote 22:
By using (A.8), we can rewrite the sum in (A.6), as a sum over the set \(\tilde{{\mathcal {I}}}_{n,k}^{x,p}\). Here we introduce a set of notations in order to rewrite each term in (A.6) in a more suitable way.
Fix \(k \in {\mathbb {N}}\), and take \({\underline{\eta }} \in \tilde{{\mathcal {I}}_k}\), then consider the set of indices \({\underline{j}}=(j_{-[\frac{k}{2}]},\dots ,j_0,\dots , j_{[\frac{k}{2}]+1})\) \(\in {\mathbb {Z}}^{2[\frac{k}{2}]+2}\), where \(j_i\ne j_{i'}\) for \(i \ne {i'}\). Correspondingly, let \({\underline{m}}^k\) denotes a vector of \(2[\frac{k}{2}]+2\) masses indexed by \({\underline{j}}\), i.e. \({\underline{m}}^k=(m_{j_{-[\frac{k}{2}]}},\dots ,m_{j_{[\frac{k}{2}]+1}})\), notice that we extended the set of i.i.d random variables \(\{ m_x \}_{x=1}^n\) to the set of i.i.d random variables \(\{m_x\}_{x \in {\mathbb {Z}}}\).Footnote 23 Moreover, let \({\underline{b}}^k \in [\beta _{min},\beta _{max}]^{2[\frac{k}{2}]+2}\) denotes the following vector: \({\underline{b}}^k=(b_{-[\frac{k}{2}]},\dots ,b_{[\frac{k}{2}]+1})\). We define \({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k,{\underline{b}}^k)\) as follows:
where we denoted \(\hat{\eta _i}=\min \{ \eta _i,\eta _{i+1} \}\), and \(\eta _0=\eta _k=0\). The following properties of \({\mathcal {F}}_{k,{\underline{\eta }}}\) are straightforward, since the distribution of the masses is compactly supported and \({\mathcal {F}}_{k,{\underline{\eta }}}\) is continuous on a compact set:
-
\({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k,{\underline{b}}^k)\) is uniformly continuous in the second component, uniformly in the distribution of the masses. More precisely, \(\forall \epsilon >0\), there exists \(\delta >0\) such that if \(|{\underline{b}}^k_1-{\underline{b}}^k_2|< \delta \),Footnote 24 then for any realization of the masses, \(|{\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k,{\underline{b}}^k_1)-{\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k,{\underline{b}}^k_2)| \le \epsilon \).
-
Consider two different set of masses \({\underline{m}}^k_1\) and \({\underline{m}}^k_2\), since masses are i.i.d, we have: \({\mathbb {E}}({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k_1,{\underline{b}}^k))={\mathbb {E}}({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k_2,{\underline{b}}^k))\). Notice that we used the assumption \(j_i \ne j_{i'}\) for \(i \ne i'\).
-
From the above properties, it is clear that taking two set of masses \({\underline{m}}^k_1\) and \({\underline{m}}^k_2\) we have: \(\forall \epsilon >0\), there exists \(\delta >0\) such that if \(|{\underline{b}}^k_1-{\underline{b}}^k_2|< \delta \), then \(|{\mathbb {E}}({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k,_1{\underline{b}}^k_1))-{\mathbb {E}}({\mathcal {F}}_{k,{\underline{\eta }}}({\underline{m}}^k_2,{\underline{b}}^k_2))|< \epsilon \).
Recall that we fixed k and \({\underline{\eta }} \in \tilde{{\mathcal {I}}}_k\). Let us take \(n \in {\mathbb {N}}\) and \(x \in {\mathbb {I}}_n\), then we define the vectors \({\underline{m}}^k(x,n)\), \({\underline{b}}^k(x,n)\) as follows:
Finally, by combining the above notations and definitions, in particular (A.8), (A.11), and (A.12), we end-up with the following identity for \([\frac{k}{2}]+1 \le x \le n- [\frac{k}{2}]+1\):
where we have the second equality thanks to (A.10) and the choice of x. Notice that to check this identity one should compare the definition of \({\mathcal {F}}_{k, {\eta }}\) with the definition of the matrix \({\tilde{A}}_n^p\) in (5.10). Moreover, this identity holds for \(x<[\frac{k}{2}]+1\) and \(x>n-[\frac{k}{2}]+1\) if one slightly modifies the definition of \({\mathcal {F}}_{k,{\underline{\eta }}}\). However, the current form of this identity is sufficient for our purposes. It is worth mentioning that \(\langle x, ({\tilde{A}} ^r_n)^k x \rangle _{n-1}\) can be written in the similar fashion, where one should define \( \tilde{{\mathcal {F}}}_{k,{\underline{\eta }}}\) similar to \({\mathcal {F}}_{k,{\underline{\eta }}}\). One can check that \(\tilde{{\mathcal {F}}}_{k,{\underline{\eta }}}\) has the three aforementioned properties. Since this task is rather straightforward, we only treat the terms corresponding to p and the terms corresponding to r can be treated similarly.
Thanks to (A.4) and (A.13), we can establish the existence of the following limit:  , for every \(y \in [0,1]\). We prove this fact by showing that the sequence
, for every \(y \in [0,1]\). We prove this fact by showing that the sequence  is a Cauchy sequence.
is a Cauchy sequence.
Lemma A.1
Recall the assumption on the distribution of the masses, where \(\mu (x)\) is smooth and supported on \([m_{min},m_{max}]\), \(0< m_{min}< m_{max} < \infty \). We have \(\forall y \in [0,1]\), and \(\forall \epsilon >0\), there exists \(N_0\), such that \(\forall n,l>N_0\), we have  .
.
Proof
Take \(\epsilon >0\), and recall (A.1) then we have:

Since \(\beta \) is continuous, and \(0<\beta _{min} \le \beta (y)\le \beta _{max}\), we have \(\beta _{[ny]}=\beta (\frac{[ny]}{n})\) and \(\beta (\frac{[ly]}{l})\) are sufficiently close. In addition, \({\mathfrak {f}}(A^r_n)\) ,\({\mathfrak {f}}(A^p_n)\) are uniformly bounded in n. Hence, it is sufficient to show
for \(n,l>N_0\) with \(N_0\) large enough. But the terms \(|\epsilon ^{[ny]}_n|\) and \(|\epsilon ^{[ly]}|\) are bounded by \(\frac{{\mathcal {C}}}{n}\) and \(\frac{{\mathcal {C}}}{l}\), respectively. Therefore, for \(N_0\) large enough, they will be small, and it is enough to show:
for proper \(N_0\). Actually, we prove that there exists \(N_0\), such that for \(n,l>N_0\),
The term \(|{\mathbb {E}}( \langle [ny], {\mathfrak {f}}(A_n^r) [ny] \rangle _{n-1} - {\mathbb {E}}( \langle [ly], {\mathfrak {f}}(A^r_l) [ly] \rangle _{l-1}|\) can be treated exactly the same way. In order to demonstrate (A.16), recall the definition of \({\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(A_n^p)\) and \({\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(A_n^r)\) from the expression (A.4), and recall \(K_*(\frac{\epsilon }{4})\), which is given in this definition. Taking advantage of (A.5), we get
By using the fact that \({\mathfrak {f}}(A_n^p)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(A_n^p)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(A_n^p)\), and \({\mathfrak {f}}(A_l^p)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(A_l^p)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(A_l^p)\), it is sufficient to prove that for \(n,l>N_0\):
Since \(K_*(\frac{\epsilon }{4})\) is independent of n and l, it is enough to prove that \(\forall {\tilde{\epsilon }}>0\), there exist \(N_0\) such that \(\forall k \in \{0,\dots ,K_*(\frac{\epsilon }{4})\}\) and \( \forall n,l>N_0\):
Then, taking \({\tilde{\epsilon }}=\frac{\epsilon }{2cK_*(\frac{\epsilon }{4})}\), where c is the bound on \(|a_0|,\dots ,|a_{K_*(\frac{\epsilon }{4})}|\), completes the proof. We can obtain (A.18) by using (A.13) and properties of \({\mathcal {F}}_{k,{\underline{\eta }}}\) as follows: Let us assume \(y \in (0,1)\),Footnote 25 fix \(k \in \{1, \dots K_*(\frac{\epsilon }{4}) \}\), and take \(N'\) such that for \(n,l>N'\) we have: \(K_*(\frac{\epsilon }{4})<[ny]<n-K_*{\frac{\epsilon }{4}}\) and \(K_*(\frac{\epsilon }{4})<[ly]<l-K_*(\frac{\epsilon }{4})\). By this choice we can use (A.13) and observe:
Thanks to the third property of \({\mathcal {F}}_{k,{\underline{\eta }}}\), \(\forall \) \(\epsilon '>0\), there exists \(\delta _{{\underline{\eta }}}(\epsilon ')\) such that for \(|{\underline{b}}^k([ly],l)-{\underline{b}}^k([ny],n)| \le \delta _{{\underline{\eta }}}(\epsilon ')\), we have
On the other hand, since \(\beta (.)\) is continuous, there exist \(N^k_{{\underline{\eta }}}\) such that for \(n,l>N^k_{{\underline{\eta }}}\) and for all \(-[\frac{k}{2}]-1<i<[\frac{k}{2}]+1\), we have
Hence, thanks to the definition of \({\underline{b}}^k\) (A.12), for \(n,l > N_{{\underline{\eta }}}^k\) we get \(|{\underline{b}}^k([ly],l)-{\underline{b}}^k([ny],n)| \le \delta _{{\underline{\eta }}}(\frac{{\tilde{\epsilon }}}{3^{K_*(\frac{\epsilon }{4})}})\). Consequently, if we take \(N_k= \max _{ \{ {\underline{\eta }} \in \tilde{{\mathcal {I}}}_k \} } \{ N_{{\underline{\eta }}}^k , N' \}\), \(\forall n,l > N_k\), we have \(\forall {\underline{\eta }} \in \tilde{{\mathcal {I}}}_k \):
Combining the latter with the estimate \(|\tilde{{\mathcal {I}}}_k| \le 3^k \le 3^{K_*(\frac{\epsilon }{4})}\), we get (A.18). Finally, taking \(N_0 = \max _{\{ k \in {\mathbb {I}}_{K_*(\frac{\epsilon }{4})}\}} \{N_k, N'\}\) finishes the proof.
Notice that in order to deal with the term \(|{\mathbb {E}}( \langle [ny], {\mathfrak {f}}(A_n^r) [ny] \rangle _{n-1} - {\mathbb {E}}( \langle [ly], {\mathfrak {f}}(A^r_l) [ly] \rangle _{l-1}|\) one should properly modify the definition of \({\mathcal {F}}_{{\underline{\eta }},k} \) and \(\tilde{{\mathcal {I}}}^{x,p}_{n,k}\). In particular, in this case \({\mathcal {F}}_{{\underline{\eta }},k}\) is given by:
Since this function satisfies the same properties, the rest of the proof is exactly similar to the previous case.\(\square \)
As an obvious consequence of Lemma A.1 we have:
Corollary A.1.1
\(\forall y \in [0,1]\), the limit  exists, and the function \(\mathrm {f}^{\mu }_{\beta }\) is well-defined.
exists, and the function \(\mathrm {f}^{\mu }_{\beta }\) is well-defined.
Moreover, following the proof of Lemma A.1, we can deduce the following corollary as well:
Corollary A.1.2
In thermal equilibrium i.e. when for \(\beta _{eq} \in (0,\infty )\), \(\beta (y)=\beta _{eq}\) is constant in y, we have:
In particular, the function \(\mathrm {f}^{\mu }(.)\) in (5.35) is well defined.
Proof
In order to proof (A.21) it is enough to show that

We omit the subscript of \(\rho \) since it is clear that we are in thermal equilibrium. Take \(\epsilon >0\), first recall the expression of  (A.1), then rewrite \({\mathfrak {f}}(.)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(.)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(.)\) as it has been defined in (A.4) and observe:
(A.1), then rewrite \({\mathfrak {f}}(.)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(.)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(.)\) as it has been defined in (A.4) and observe:

where we bounded the terms involving \({\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}\) by \(\frac{\epsilon }{2}\), thanks to (A.5). Moreover, \(|\epsilon _{n}^{[ny]}|+|\epsilon _n^{[ny']}|\) is bounded by \(\frac{C}{n}\); therefore, it has been bounded by \(\frac{\epsilon }{2}\), by taking \(n>N_1\), for proper \(N_1\). Lastly, recall \(K_*(\frac{\epsilon }{4})\) from (A.4), and choose \(N_2\) such that for \(n>N_2\),
Thanks to this choice, and by using (A.13), for any \(k \in \{ 1,\dots , K_*(\frac{\epsilon }{4}) \}\) we have:
where, first, we used the fact that in thermal equilibrium we have \({\underline{b}}^k([ny],n)={\underline{b}}^k([ny'],n)\), then we took advantage of the second property of \({\mathcal {F}}_{k,{\underline{\eta }}}\). Therefore, by using the definition of \({\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}\), the term in second line of (A.22) is zero, for \(n>N_2\) (the part corresponding to \(A_n^r\) is completely analogous). Hence taking \(n> \max \{ N_1,N_2 \}\) gives us the desirable result. \(\square \)
Proposition A.1.1
The function \(\mathrm {f}^{\mu }_{\beta }(y): (0,1) \rightarrow {\mathbb {R}}\) is continuous.
Proof
Fix \(\epsilon >0\), and observe
where \(\mathrm {f}^{\mu }_{\beta ,n}(y):={\mathbb {E}}(\langle {\tilde{e}}_{[ny]} \rangle _{\rho ^n})\). Since \(\lim _{n \rightarrow \infty } \mathrm {f}_{\beta ,n}^{\mu }(y)=\mathrm {f}_{\beta }^{\mu }(y)\), if we take \(n>N_1(\epsilon )\), then
Moreover, we claim that there exist \(N_2(\epsilon )\), such that for \(n>N_2(\epsilon )\), there exists \(\delta \) such that for \(|y-y'| < \delta \), \(|\mathrm {f}_{\beta ,n}^{\mu }(y)- \mathrm {f}_{\beta ,n}^{\mu }(y')| < \frac{\epsilon }{2}\). Proving this claim completes the proof, since we can take \(n > \max \{N_1(\epsilon ), N_2(\epsilon ) \}\) and observe that for \(|y-y'|< \delta \), we have \(|\mathrm {f}_{\beta }^{\mu }(y)-\mathrm {f}_{\beta }^{\mu }(y')|<\epsilon \).
However, the proof of this statement follows the same lines of Lemma A.1 and Corollary (A.1.2). Similar to (A.22), we divide \({\mathfrak {f}}(.)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(.)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(.)\), and take \(N_3(\epsilon )\) such that for \(n>N_2(\epsilon )\) we have
Therefore, we have:

where we can find \(N_4\) and \(\delta _0\) such that the last line will be bounded by \(\frac{3 \epsilon }{4}\), for \(n>N_4\) and \(|y-y'|<\delta _0\). Let us take \(N_2(\epsilon )= \max \{N_3(\epsilon ),N_4 \}\). Recall the definition of \({\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(.)\) (A.4) as a Taylor sum up to \(K_*(\frac{\epsilon }{4})\) terms. By using the choice of \(N_2(\epsilon )\) rewrite each term of this sum as a sum over the paths \({\underline{\eta }} \in \tilde{{\mathcal {I}}}_k\) as in (A.13). The rest of the proof boils down to demonstrating the fact that for \(n>N_2(\epsilon )\), for all \(1\le k \le K_*(\frac{\epsilon }{4})\), and for all \({\underline{\eta }} \in \tilde{{\mathcal {I}}}_k\), we have: \(\forall {\hat{\epsilon }}>0\) there exist \(\delta _{k,{\underline{\eta }}}({\hat{\epsilon }})>0\), such that if \(|y-y'| < \delta _{k,{\underline{\eta }}}({\hat{\epsilon }})\) then
However, recalling the definition of \({\underline{b}}^k([ny],n)\) from (A.12), since \(\beta (.)\) is continuous, one can observe that if \(|y-y'|< {\tilde{\delta }}\), \(|{\underline{b}}^k([ny],n)-{\underline{b}}^k([ny'],n)|\) is sufficiently small for a proper choice of \({\tilde{\delta }}\). Therefore, by using the third property of \({\mathcal {F}}_{k,\eta }\), we obtain the desired \(\delta _{k,{\underline{\eta }}}({\hat{\epsilon }})\). Finally, taking
finishes the proof. Notice that here c is the uniform bound on Taylor coefficients \(|a_0|,\dots |a_{K_*({\frac{\epsilon }{4}}})|\). Moreover, the choice of \({\hat{\epsilon }}\) is justified by the bound \(|\tilde{{\mathcal {I}}}_k| \le 3^k\). Furthermore, as usual the part corresponding to r can be treated exactly in the same way. \(\square \)
The next proposition proves (5.36), and illustrates the fact that \(\mathrm {f}_{\beta }^{\mu }(y)\) is in fact a function of inverse temperature at point y i.e. \(\beta (y)\). Since the proof of this proposition is similar to the previous lemma and proposition, we just sketch the proof and only highlight the differences:
Proposition A.1.2
Let \(\beta \in C^0([0,1])\) satisfying the assumptions stated in the definition (2.9). Recall the definition of \(\mathrm {f}^{\mu }_{\beta }:[0,1] \rightarrow {\mathbb {R}}\) from (5.5), and \(\mathrm {f}^{\mu }:(0,\infty ) \rightarrow {\mathbb {R}}\) from (5.35), then we have \(\forall y \in (0,1)\):
Proof
Fix \(y \in (0,1)\) and recall that we denote the average in Gibbs state in thermal equilibrium at inverse temperature \(\beta _{eq}\), with  . Since in thermal equilibrium, we have translation invariance in the limit thanks to (A.21) in Corollary A.1.2, it is enough to prove that \(\forall \epsilon >0\), there exist \(N(\epsilon )\), such that for \(n>N(\epsilon )\):
. Since in thermal equilibrium, we have translation invariance in the limit thanks to (A.21) in Corollary A.1.2, it is enough to prove that \(\forall \epsilon >0\), there exist \(N(\epsilon )\), such that for \(n>N(\epsilon )\):

Let us denote the matrices corresponding to thermal averages at temperature profile \(\beta (.)\) (3.25) by \(A_n^{p,\beta (.)}\) and \(A_n^{r,\beta (.)}\), only for the sake of this proposition. Similarly, denote the same matrices in thermal equilibrium at temperature \(\beta (y)\) by \(A_n^{p,\beta (y)}\), \(A_n^{r,\beta (y)}\). The proof goes as follows: we rewrite (A.28) in terms of \({\mathfrak {f}}(A_n^{p,\beta (.)})\), \({\mathfrak {f}}(A_n^{r,\beta (.)})\), \({\mathfrak {f}}(A_n^{p,\beta (y)})\), and \({\mathfrak {f}}(A_n^{r,\beta (y)})\) thanks to (A.1), up to a vanishing error. Then we decompose \({\mathfrak {f}}(.)={\mathfrak {f}}_{\prec }^{\frac{\epsilon }{4}}(.)+{\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(.)\) and we bound all the terms corresponding to \({\mathfrak {f}}_{\succ }^{\frac{\epsilon }{4}}(.)\) by \(\frac{\epsilon }{2}\), thanks to (A.5). Notice that the definition of \({\mathfrak {f}}\), \({\mathfrak {f}}_{\succ }^{\epsilon }\) and \({\mathfrak {f}}_{\prec }^{\epsilon }\) depends on the matrices through the constants \(\alpha \) and \(K_*(\epsilon )\). Here, we take the definition which is given by matrices \(A_n^{p,\beta (.)}\) and \(A_n^{r,\beta (.)}\). Then it is straightforward to check that \({\mathfrak {f}}(A_n^{r,\beta (y)})\) and \({\mathfrak {f}}(A_n^{p,\beta (y)})\), are well defined and they satisfy the same bounds as in (A.5), since \(\beta _{\min }\le \beta (y) \le \beta _{max}\), and the same uniform bound \(c_0\) in Lemma 5.1 holds for \(||A_n^{p,\beta (y)}||\) and \(||A_n^{r,\beta (y)}||\). The terms involving \({\mathfrak {f}}^{\frac{\epsilon }{4}}_{\prec }\) can be treated similar to Proposition A.1.1, we sketch the terms related to p, the other ones is similar. First, we choose \(N_0(\epsilon )\) such that for \(n> N_0(\epsilon )\), \(K_*(\frac{\epsilon }{4}) \le [ny] \le n-K_*(\frac{\epsilon }{4})\), then we expand each term of the sum appearing in \({\mathfrak {f}}^{\frac{\epsilon }{4}}_{\prec }(.)\) by using the random walk representation in (A.13), similar to (A.26), it is enough to show that for any \({\hat{\epsilon }}>0\), \(1 \le k \le K_*(\frac{\epsilon }{4})\) and \({\underline{\eta }} \in \tilde{{\mathcal {I}}}_k\) there exists N such that for \(n>N\), we have:
where \(\tilde{{\underline{b}}}^k([ny],n)\) is defined analogous to \({\underline{b}}^k([ny],n)\) (A.12) for a constant profile of temperature at inverse temperature \(\beta (y)\) i.e. \(\tilde{{\underline{b}}^k}([ny],n)_i=\beta (y)\) for \(-[\frac{k}{2}] \le i \le [\frac{k}{2}]+1\). However, existence of N such that for \(n>N\) (A.29) holds is evident from the third property of \({\mathcal {F}}_{k,{\underline{\eta }}}\) and the fact that \(\beta (.)\) is continuous. \(\square \)
Recall the definition of  , and the sequence \(n_k\) in the proof of 5.4, where \(n_k \rightarrow \infty \) with \(\frac{n_{k+1}}{n_k} \rightarrow 1\). The following lemma was an essential part of the proof:
, and the sequence \(n_k\) in the proof of 5.4, where \(n_k \rightarrow \infty \) with \(\frac{n_{k+1}}{n_k} \rightarrow 1\). The following lemma was an essential part of the proof:
Lemma A.2
Fix \(\epsilon >0\), then for every realization of the masses, there exists \(N_*\) such that, for every \(n_k>N_*\) and every n with \(n_k \le n < n_{k+1}\), we have: \(\forall x \in {\mathbb {I}}_{n_k}\), with \(n_*<x<n_k-n_*\), \(|Y^n_x -Y^{n_k}_x| \le \epsilon \). Here, \(n_*\) is a constant only depending on \(\epsilon \).
Proof
Fix \(\epsilon >0 \), and recall the definition of \(Y_x^n\), we have

The second term in (A.30) can be treated by using Lemma A.1, and continuity of g (note that we used the choice of n and \(n_k\), where \(\frac{n}{n_k} \rightarrow 1\), as well). Hence, there exits \(N_1\), such that for \(n_k>N_1\), we have:

where \(c_1\) is the bound on |g|, and \(c_2\) is the bound on  .
.
Similarly, for the first term in (A.30)  , it is enough to deal with
, it is enough to deal with  . Thanks to the expression of
. Thanks to the expression of  in (A.1), for proper \(N_2\), we have for \(n>N_2\):
in (A.1), for proper \(N_2\), we have for \(n>N_2\):

where we chose \(N_2\) such that \(|\epsilon ^x_n|+|\epsilon ^x_{n_k}| \le \frac{\epsilon }{6}\). From now on, let us show \(\frac{\epsilon }{c_1C_0}\) by \(\epsilon \). Now it is enough to find \(N_3\), such that for \(n_k>N_3\),
Let us decompose \({\mathfrak {f}}(.)={\mathfrak {f}}^{\frac{\epsilon }{12}}_{\prec }(.)+{\mathfrak {f}}^{\frac{\epsilon }{12}}_{\succ }(.)\) as in (A.4), recall \(K_*(\frac{\epsilon }{12})\) from (A.4) and let \(n_*=K_*(\frac{\epsilon }{12})\), notice that \(n_*\) only depends on \(\epsilon \). Therefore, thanks to (A.5) we have:
Now, it is sufficient to show that
for \(n_k\) sufficiently large. In order to control this term, recall the definition of \({\underline{b}}^k\) from (A.12) and notice that for any \(\delta >0\), there exists \(N_4(\delta )\) such that for \(n_k>N_4(\delta )\), \(|{\underline{b}}^k(x,n)-{\underline{b}}^k(x,n_k)| < \delta \), since \(\beta \) is continuous, \(n_k\le n < n_{k+1}\), and \(\frac{n_{k+1}}{n_k} \rightarrow 1\). By using the first property of \({\mathcal {F}}_{k,{\underline{\eta }}}\), we choose \(\delta >0\) such that
where \(c_1\) is the uniform bound on coefficients \(a_0,\dots ,a_{n_*}\) in (A.4).
Taking \(n>\max \{N_1,N_2,N_3,N_4(\delta ), n_* \}\), and combining this last estimate with the expression of \({\mathfrak {f}}_{\prec }^{\frac{\epsilon }{12}}\) in (A.4) as well as the random walk representation relation (A.13), gives us (A.34) for any \(n_*<x<n-n_*\). The term corresponding to r can be bounded by \(\frac{\epsilon }{6}\) similarly. \(\square \)
B Alternative Coordinates
Describing our system in the r coordinates with \(\sum _{x=1}^n p_x=0\) means that our system is described by an observer at center of mass; hence, macroscopically the center of mass should be fixed as well, i.e., \(\int _0^1 {\bar{p}}(y)dy=0\). Equivalently, this system can be modeled in terms of q coordinates, where one should be careful about the center of mass. Since it is more fashionable to treat quantum harmonic chains in terms of p and q coordinates, in this section, we introduce our model in terms of these coordinates and rewrite the main transformations in terms of q coordinates, in order to illustrate the link between our setup and the conventional one. Define on the Hilbert space \(L^2({\mathbb {R}}^n)\), the following Hamiltonian operator:
where for each \(x \in {\mathbb {I}}_n\), \(q_x\) denotes the position operator of the particle x, i.e. denoting the space variable by \(\pmb {\zeta } \in {\mathbb {R}}^n\), for any  ,
,  , and \(p_x\) denotes the corresponding momentum operator \(p_x=-i \partial \setminus \partial _{\pmb {\zeta }_x}\). Moreover, we assume free boundary conditions: \(q_0=q_1\) and \(q_n=q_{n+1}\). Here \(m_x\) are positive i.i.d random variables.
, and \(p_x\) denotes the corresponding momentum operator \(p_x=-i \partial \setminus \partial _{\pmb {\zeta }_x}\). Moreover, we assume free boundary conditions: \(q_0=q_1\) and \(q_n=q_{n+1}\). Here \(m_x\) are positive i.i.d random variables.
The Hamiltonian (B.1) can be diagonalized with a linear transformation and written as sum of free bosons:
where \(b_k\) and \(b_k^*\) are bosonic annihilation and creation operators with commutation relations \([{\hat{b}}_k^*,{\hat{b}}_{k'}]=\delta _{k,k'}, [{\hat{b}}_k^*,{\hat{b}}_{k'}^*]=[{\hat{b}}_k,{\hat{b}}_{k'}]=0 \). Here \({\hat{p}}_o=\sum _{x=1}^n p_x\) is the total momentum operator. Since \([{\hat{p}}_0,H_n]=0\), after a straightforward analysis, the expression (B.2) indicates that \(H_n\) has a purely continuous spectrum (cf. Remark 3.3 of [36], and Remark 3.6 of [35] for more details). In order to avoid technical difficulties concerning continuous spectrum of \(H_n\), we alternatively define our model in r coordinates. Notice that, one can observe that the Heisenberg dynamics generated by (B.2) on \(L^2({\mathbb {R}}^n)\) is similar to (3.22) up to \({\hat{p}}_0=(\sum _{x=1}^n m_x)^{-1} p_x\) operator which is constant in time.
Another technical problem arising in this description, concerns the density operator \(\rho ^n_{{\bar{p}},{\bar{r}},\beta }=\exp (-{\tilde{H}}_{\beta }^n)\) (2.9). The pseudo-Hamiltonian \({\tilde{H}}_{\beta }^n\) can be written as
where \(\tilde{{\mathfrak {b}}}_k^*\) and \(\tilde{{\mathfrak {b}}}_k\) are another set of bosonic operators (3.35), (B.13), and
Thanks to the definition of \(\tilde{{\mathfrak {p}}}_0\), one can observe that similar to \(H_n\), \({\tilde{H}}_{\beta }^n\) has a continuous spectrum as an operator on \(L^2({\mathbb {R}}^n)\) in this coordinates. Moreover, \(\rho ^n_{{\bar{p}},{\bar{r}},\beta }\) is not trace-class in this description, anymore. Although \(\rho ^n_{{\bar{p}},{\bar{r}},\beta }\) seems to be a natural choice for our locally Gibbs state corresponding to \({\bar{r}}, {\bar{p}}, \beta \), we need to slightly modify it, in order to circumvent the above mentioned technicalities. Recall that the total momentum \({\hat{p}}_o= \sum _{x=1}^n p_x\) is conserved by the dynamics. Ideally, one would be tempted to fix the total momentum apriori to the value prescribed by the macroscopic profile i.e.,
However, this is not convenient for technical reasons, instead we can modify our initial locally Gibbs state as follows: Let us denote \(L^{2}({\mathbb {R}}^n)\) by \({{\mathcal {H}}}_n\), only in this section. Inspiring from diagonalization (3.31), we decompose \({{\mathcal {H}}}_n\) as follows. Let \(\tilde{\pmb {\zeta }}_0:= (\sum _{x=1}^n \frac{m_x}{\beta _x})^{-\frac{1}{2}} \sum _{x=1}^n \frac{m_x}{\beta _x} \pmb {\zeta }_x\), and \(V_{\tilde{\pmb {\zeta }}_0}^{\perp } \subset {{\mathbb {R}}}^n\), be the orthogonal complement of \(\mathrm {Span}(\tilde{\pmb {\zeta }}_0)\). Denote the Lebesgue measure on \(V_{\hat{\pmb {\zeta }}_0}^{\perp } \subset {{\mathbb {R}}}^n\), by \(d\nu _{n-1}\); then, we have: \({{\mathcal {H}}}_n= L^2({{\mathbb {R}}},d\tilde{\pmb {\zeta }}_0) \otimes L^2 (V_{\tilde{\pmb {\zeta }}_0}^{\perp }, d\nu _{n-1}) \equiv {{\mathcal {H}}}_o \otimes {{\mathcal {H}}}_{n-1}^-\). Again appealing to (3.31), observe that \({\tilde{H}}_{\beta }^{n}=\frac{1}{2}\tilde{{\mathfrak {p}}}_0^2+ H_{\beta }^{n,-}\), where
only acts on \({{\mathcal {H}}}_o\) and
only acts on \({{\mathcal {H}}}_{n-1}^-\).
Take  such that
such that  ,
,  ,
,  ; this means the total momentum has the following average and uncertainty:
; this means the total momentum has the following average and uncertainty:  and
and
 , (cf. Remark B.2). Now, we define the locally Gibbs state with “fixed total momentum” as:
, (cf. Remark B.2). Now, we define the locally Gibbs state with “fixed total momentum” as:

where  denotes the projection operator into the subspace spanned by the pure state
denotes the projection operator into the subspace spanned by the pure state  . Notice that \(H_{\beta }^{n,-}\) can be mapped into \(H_{\beta }^n\) (2.10) by a unitary transformation. Consequently, one can check that \(H_{\beta }^{n,-}\) has a discrete spectrum with non-negative eigenvalues (with a process similar to Sect. 3). We can express \(H_{\beta }^{n,-}\) in terms of sum of free bosonic operators, and obtain its spectrum explicitly similar to what we did in Sect. 3. Hence, using spectral theorem, one can observe that \(\rho ^n_{{\bar{p}},{\bar{r}},\beta }\) is well defined and trace-class.
. Notice that \(H_{\beta }^{n,-}\) can be mapped into \(H_{\beta }^n\) (2.10) by a unitary transformation. Consequently, one can check that \(H_{\beta }^{n,-}\) has a discrete spectrum with non-negative eigenvalues (with a process similar to Sect. 3). We can express \(H_{\beta }^{n,-}\) in terms of sum of free bosonic operators, and obtain its spectrum explicitly similar to what we did in Sect. 3. Hence, using spectral theorem, one can observe that \(\rho ^n_{{\bar{p}},{\bar{r}},\beta }\) is well defined and trace-class.
As before, one can observe that  ,
,  , and
, and  are well defined, this suggests that (B.8) is an appropriate modification of (2.9) in this coordinate.
are well defined, this suggests that (B.8) is an appropriate modification of (2.9) in this coordinate.
In order to avoid the aforementioned difficulties, we describe our model in terms of elongation operators. One can argue that elongation operators are “physically” relevant, since in the classical counterpart of our system the elongation is the “real” physical variable, rather than the position of the particles. Let us highlight the relation between these models by a couple of remarks:
Remark B.1
Notice that same result of Theorem 2.1 holds for this system, as well. In fact, initially the previous description can be mapped into this new description via a unitary transformation (cf. Remark 3.3 in [36]). The proof in this new coordinate is basically identical, except for some considerations concerning center of mass, which makes the proof even simpler. For example \({\mathscr {E}}_x^n\) in (3.41) does not appear anymore thanks to the proper choice of  .
.
In the previous description (2.2), by definition we have \(\sum _{x=1}^n p_x=0\). This is because we begin the description of the system by quantizing the classical description corresponding to the observer in center of mass. Consequently, we should take \(\int _0^1 {\bar{p}}(y) dy=0\). In this new coordinates, since we describe the center of mass separately by  , we can take any \({\bar{p}} \in C^1([0,1])\) with non zero average.
, we can take any \({\bar{p}} \in C^1([0,1])\) with non zero average.
Remark B.2
Physically the initial state (B.8), means that initially we prepare our system in the lab such that our system’s center of mass is known and is given by the wave function (pure state)  , where its above mentioned averages (momentum and kinetic energy contribution) is prescribed by the macroscopic profile of momentum and temperature. Furthermore, in this state other degrees of freedom are subjected to thermal and mechanical fluctuations prescribed by the macroscopic profiles (mixed state). Mathematically, this state is more convenient. We should emphasize that the assumption
, where its above mentioned averages (momentum and kinetic energy contribution) is prescribed by the macroscopic profile of momentum and temperature. Furthermore, in this state other degrees of freedom are subjected to thermal and mechanical fluctuations prescribed by the macroscopic profiles (mixed state). Mathematically, this state is more convenient. We should emphasize that the assumption  is not crucial. Our result holds as long as we replace \((\sum _{x=1}^n \frac{m_x}{\beta _x})\) with any constant of order n. One can replace the pure state
is not crucial. Our result holds as long as we replace \((\sum _{x=1}^n \frac{m_x}{\beta _x})\) with any constant of order n. One can replace the pure state  with any mixed state \(\rho _o\) acting on \({\mathcal {H}}_o\), with
with any mixed state \(\rho _o\) acting on \({\mathcal {H}}_o\), with  , such that
, such that

and obtain the similar result.
Notice that the aforementioned constants are random and they have been defined for a realization of the masses. However, in the thermodynamic limit \(\frac{\Pi _0}{n} \rightarrow \int _0^1 {\bar{p}}(y)dy, \) and \(\frac{1}{n} \sum _{x=1}^n \frac{m_x}{\beta _x} \rightarrow \int _{0}^1 \frac{{\bar{m}}}{\beta (y)}dy, \) almost surely, thanks to law of large numbers, which further justifies our choice.
Finally, one can construct such  easily, via an inverse Fourier transform of a Gaussian function.
easily, via an inverse Fourier transform of a Gaussian function.
We show our main transformations in terms of q coordinates: Rewrite the Hamiltonian in q coordinate as:
The proper transformation of q in order to diagonalize the Hamiltonian is
where \({\hat{p}}_k\) is defined as before. We can find the following relation between \({\hat{q}}_k\) and \({\hat{r}}_k\):
Canonical commutation relation (CCR) in terms of q reads:
The inverse is given by
and the Hamiltonian reads
The bosonic operators have the following form in terms of \({\hat{q}}\) coordinates:
In order to expose the aforementioned link further, we introduce the coordinate \(\tilde{{\mathfrak {q}}}_k\) similar to \({\hat{q}}_k\):
Define \({\bar{q}}_x\) as follows: First, construct \({\bar{q}}_x\), for \(x \in {\mathbb {I}}_n\), from \({\bar{r}}_x\), by defining \({\bar{q}}_1={\bar{q}}_0 = c\) (c is an arbitrary constant, corresponding to the macroscopic position of the first particle) and let \({\bar{q}}_x= \sum _{y=1}^{x-1} {\bar{r}}_y + {\bar{q}}_1\). Then, we have \( {\tilde{q}}_x= q_x-{\bar{q}}_x\), which gives us:
Therefore, \(\tilde{{\mathfrak {q}}}_k\) is defined as:
Moreover, it is illuminating to know the relation between \(\tilde{{\mathfrak {r}}}_k\) and \(\tilde{{\mathfrak {q}}}_k\):
The inverse relation for \(\tilde{{\mathfrak {q}}}_k\) is given by:
Finally, the pseudo-Hamiltonian is diagonalized as follows:
Commutation relation is given by
and the bosonic operators are given by:
C Average of Bosonic Operators
Recall the average of bosonic operators (3.38) from Lemma 3.2. One can compute these averages and proof the lemma as follows (Notice that since \(E_0\) is a constant, we can simply omit it from our computation and it does not change the desired averages) :
Proof
First we compute  , using spectral theorem, we expand the trace in the basis of eigenvalues of \(H_{\beta }^n\) i.e.
, using spectral theorem, we expand the trace in the basis of eigenvalues of \(H_{\beta }^n\) i.e.  . Then, the following computation gives us the result: (we abbreviate \(\sum _{k=1}^{n-1} \theta _k \gamma _k\) by \({\bar{\theta }}.{\bar{\gamma }}\), where \({\bar{\gamma }}\) stands for the vector \({\bar{\gamma }}:=(\gamma _1,\dots ,\gamma _{n-1})\))Footnote 26
. Then, the following computation gives us the result: (we abbreviate \(\sum _{k=1}^{n-1} \theta _k \gamma _k\) by \({\bar{\theta }}.{\bar{\gamma }}\), where \({\bar{\gamma }}\) stands for the vector \({\bar{\gamma }}:=(\gamma _1,\dots ,\gamma _{n-1})\))Footnote 26

Now from (3.32), (3.37), observe that

Therefore, since  are orthonormal, we have
are orthonormal, we have

Moreover, if \(k\ne k'\), we have

Since  are orthonormal, if we expand
are orthonormal, if we expand  in the basis of \(H_{\beta }^n\), we deduce the first set of equalities in (3.38). Furthermore, for \(k \ne k'\), we deduce
in the basis of \(H_{\beta }^n\), we deduce the first set of equalities in (3.38). Furthermore, for \(k \ne k'\), we deduce as well.
as well.
On the other hand, if \(k=k'\), the same relations (5.21), (3.32)imply:

thus, we have  . Consequently, we can compute
. Consequently, we can compute  :
:

Since we have the commutator relation \([\tilde{{\mathfrak {b}}}_k ,\tilde{{\mathfrak {b}}}_k^*]=1\), we obtain the last equality:  . \(\square \)
. \(\square \)
Rights and permissions
About this article
Cite this article
Hannani, A. Hydrodynamic Limit for a Disordered Quantum Harmonic Chain. Commun. Math. Phys. 390, 349–423 (2022). https://doi.org/10.1007/s00220-021-04277-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04277-7


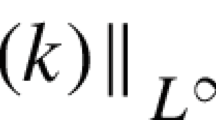

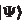 which is used for denoting the member of the Hilbert space, and
which is used for denoting the member of the Hilbert space, and 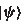 which denotes the finite dimensional vector spaces.
which denotes the finite dimensional vector spaces.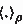 instead of
instead of 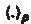 , since there is no confusion here.
, since there is no confusion here.