On the Riemann-Hilbert Problem for a q-Difference Painlevé Equation

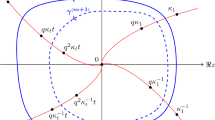
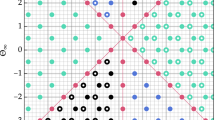
Abstract

A Riemann-Hilbert problem for a q-difference Painlevé equation, known as $q{\text {P}}_{{\text {IV}}}$, is shown to be solvable. This yields a bijective correspondence between the transcendental solutions of $q{\text {P}}_{{\text {IV}}}$ and corresponding data on an associated q-monodromy surface. We also construct the moduli space of $q{\text {P}}_{{\text {IV}}}$ explicitly.

Appendices

Appendix A: A Birational Transformation and Singularities

Define

$$\begin{aligned} g_1&=qf_2^{-1}+a_0a_2f_1^{-1}f_2^{-1}+a_0f_1^{-1}, \end{aligned}$$

(A.1a)

$$\begin{aligned} g_2&=qf_2+a_0a_2f_1f_2+a_0f_1,\end{aligned}$$

(A.1b)

$$\begin{aligned} g_3&=qa_0a_2f_1+qa_0f_1f_2^{-1}+a_0^2a_2f_2^{-1},\end{aligned}$$

(A.1c)

$$\begin{aligned} g_4&=qa_0a_2f_1^{-1}+qa_0f_2f_1^{-1}+a_0^2a_2f_2, \end{aligned}$$

(A.1d)

then $g=(g_1,g_2,g_3,g_4)$ satisfies the algebraic equations (2.9) and the rational inverse of (A.1) is given by

$$\begin{aligned} f_1&=\frac{a_0^2+g_3}{a_0(qa_2+g_1)}=\frac{a_0(qa_2+g_2)}{a_0^2+g_4},\end{aligned}$$

(A.2a)

$$\begin{aligned} f_2&=\frac{q^2+g_4}{a_0a_2(a_0+a_1g_1)}=\frac{a_0a_2(a_0+a_1g_2)}{q^2+g_3}. \end{aligned}$$

(A.2b)

We denote the algebraic surface obtained by cutting $\{g\in {\mathbb {C}}^4\}$ with respect to (2.9) by ${\mathcal {G}}(a)$. The f and g variables are bi-rationally equivalent, and in particular $q{\text {P}}_{{\text {IV}}}(a)$ induces the time-evolution given by Eq. (2.10) on ${\mathcal {G}}(a)$.

While the forward iteration of Eq. (2.10) is singular on ${\mathcal {G}}(a)$, only when $g_3=0$, we show its continuation is possible by means of singularity confinement. It is also possible to regularize these singularities by lifting to the initial value space $(A_2+A_1)^{(1)}$ following Sakai [36].

Namely, if $g_3=0$, then $\overline{g}$ and $\overline{\overline{g}}$ do not exist whereas $\overline{\overline{\overline{g}}}$ does and is given explicitly by

$$\begin{aligned} \overline{\overline{\overline{g}}}_1=&\frac{(1-q^3t^2)g_1+(1-q^2)g_2}{1-q^5t^2},\end{aligned}$$

(A.3a)

$$\begin{aligned} \overline{\overline{\overline{g}}}_2=&\frac{qt^2(1-q^2)g_1+(1-q^3t^2)g_2}{1-q^5t^2},\end{aligned}$$

(A.3b)

$$\begin{aligned} \overline{\overline{\overline{g}}}_3=&g_4+(q^{-2}-1)g_1g_2+q^{-4}(q^2-1)g_1^2+\frac{(1-q^2)(g_1-q^2g_2)((2-q^2)g_1-q^2g_2)}{q^4(1-q^5t^2)}\nonumber \\&+\frac{(1-q^2)^2(g_1-q^2g_2)^2}{q^4(1-q^5t^2)^2},\end{aligned}$$

(A.3c)

$$\begin{aligned} \overline{\overline{\overline{g}}}_4=&0. \end{aligned}$$

(A.3d)

Similarly the inverse time-evolution is singular only when $g_4=0$, in which case the first and second inverse iterates do not exist, whereas the third one does. We say that g(t) is singular at $t_0$ when it does not exist at $t=t_0$. The continuation formulae (A.3) of $q{\text {P}}_{{\text {IV}}}^{\text {mod}}(a)$ can be obtained by means of direct calculation.

Considering the forward iteration, $\overline{g}$ is ill-defined if and only if $g_3=0$. So let us take any $g^*\in {\mathcal {G}}(a)$ with $g_3^*=0$ and perturb around it within ${\mathcal {G}}(a)$, setting

$$\begin{aligned} g_1=g_1^*+{\mathcal {O}}(\epsilon ),\quad g_2=g_2^*+{\mathcal {O}}(\epsilon ),\quad g_3=\epsilon +{\mathcal {O}}(\epsilon ^2),\quad g_4=g_4^*+{\mathcal {O}}(\epsilon ), \end{aligned}$$

in particular $g=g^*+{\mathcal {O}}(\epsilon )$, as $\epsilon \rightarrow 0$. Then direct calculation gives

$$\begin{aligned} \overline{g}_1&=a_0^2a_2(qt^2-1)t^{-2}\epsilon ^{-1}+{\mathcal {O}}(1),\\ \overline{g}_2&=-a_0^2a_2(qt^2-1)\epsilon ^{-1}+{\mathcal {O}}(1),\\ \overline{g}_3&=a_0^4a_2^2q(qt^2-1)^2t^{-2}\epsilon ^{-2}+{\mathcal {O}}(\epsilon ^{-1}),\\ \overline{g}_4&={\mathcal {O}}(\epsilon ), \end{aligned}$$

which diverges, as $\epsilon \rightarrow 0$. Similarly

$$\begin{aligned} \overline{\overline{g}}_1&=-a_0^2a_2(qt^2-1)q^{-2}t^{-2}\epsilon ^{-1}+{\mathcal {O}}(1),\\ \overline{\overline{g}}_2&=a_0^2a_2q^3(qt^2-1)\epsilon ^{-1}+{\mathcal {O}}(1),\\ \overline{\overline{g}}_3&={\mathcal {O}}(\epsilon ),\\ \overline{\overline{g}}_4&=-a_0^4a_2^2q(qt^2-1)^2t^{-2}\epsilon ^{-2}+{\mathcal {O}}(\epsilon ^{-1}), \end{aligned}$$

which diverges, as $\epsilon \rightarrow 0$. However, upon calculating the third iteration, we find

$$\begin{aligned} \overline{\overline{\overline{g}}}_1=&\frac{(1-q^3t^2)g_1^*+(1-q^2)g_2^*}{1-q^5t^2}+{\mathcal {O}}(\epsilon ),\\ \overline{\overline{\overline{g}}}_2=&\frac{qt^2(1-q^2)g_1^*+(1-q^3t^2)g_2^*}{1-q^5t^2}+{\mathcal {O}}(\epsilon ),\\ \overline{\overline{\overline{g}}}_3=&g_4^*+(q^{-2}-1)g_1^*g_2^*+q^{-4}(q^2-1)(g_1^*)^2\\&+\frac{(1-q^2)(g_1^*-q^2g_2^*)((2-q^2)g_1^*-q^2g_2^*)}{q^4(1-q^5t^2)} +\frac{(1-q^2)^2(g_1^*-q^2g_2^*)^2}{q^4(1-q^5t^2)^2}+{\mathcal {O}}(\epsilon ),\\ \overline{\overline{\overline{g}}}_4=&{\mathcal {O}}(\epsilon ). \end{aligned}$$

which converges to (A.3), as $\epsilon \rightarrow 0$. We conclude that the singularity is confined within three iterations. The singularity analysis of the inverse time evolution follows by similar arguments.

Appendix B: Cubic Surface Calculations

Recall the definition of the determinants $\Delta _1$ and $\Delta _2$ in Eqs. (5.9) and (5.1). Each of these determinants defines a cubic equation in the variables $\rho _{1,2,3}^{x,y}$. The aim of this section is to show that these cubics are proportional to each other

$$\begin{aligned} \Delta _2=-\lambda _0^3 \Delta _1, \end{aligned}$$

(B.1)

and that they are proportional to the cubic defined in equation (2.16),

$$\begin{aligned} \Delta _2=\frac{1}{a_1^2a_2^2}\theta _q(a_0,a_1,a_2)\theta _q(-\lambda _0)^2T_{hom}(\rho _1^x,\rho _1^y,\rho _2^x,\rho _2^y,\rho _3^x,\rho _3^y;\lambda _0,a). \end{aligned}$$

(B.2)

Firstly, we derive Eq. (B.1). To this end, let us note that we may alternatively write the functions $v_{1,2,3}$ as

$$\begin{aligned} v_1(z)&=\frac{z}{\lambda _0x_1}\theta _q(z/x_2,z/x_3,-x_1/z\lambda _0),\\ v_2(z)&=\frac{z}{\lambda _0x_2}\theta _q(z/x_1,z/x_3,-x_2/z\lambda _0),\\ v_3(z)&=\frac{z}{\lambda _0x_3}\theta _q(z/x_1,z/x_2,-x_3/z\lambda _0), \end{aligned}$$

due to the symmetries (1.6) of the q-theta function.

Using these alternative expressions for $v_{1,2,3}$ and expanding the difference of both sides of equation (B.1), i.e.

$$\begin{aligned} \Delta =\Delta _2+\lambda _0^3 \Delta _1, \end{aligned}$$

in terms of the variables $\rho _{1,2,3}^{x,y}$, we find that all terms cancel except for

$$\begin{aligned} \Delta = \rho _1^x\rho _2^x\rho _3^x(U_1-U_2)(V_1-V_2), \end{aligned}$$

where

$$\begin{aligned} U_1&=\theta _q\left( -\frac{x_1}{x_2},-\frac{x_2}{x_3},-\frac{x_3}{x_1}\right) ,&V_1&=\theta _q\left( \frac{x_1}{x_2}\lambda ,\frac{x_2}{x_3}\lambda ,\frac{x_3}{x_1}\lambda \right) ,\\ U_2&=\theta _q\left( -\frac{x_2}{x_1},-\frac{x_3}{x_2},-\frac{x_1}{x_3}\right) ,&V_2&=\theta _q\left( \frac{x_2}{x_1}\lambda ,\frac{x_3}{x_2}\lambda ,\frac{x_1}{x_3}\lambda \right) . \end{aligned}$$

However, it follows directly from the symmetries (1.6) of the q-theta function that $U_1=U_2$ and thus $\Delta =0$, which proves equality (B.1).

Next, we derive Eq. (B.2). To this end, we first expand $\Delta _2$ in terms of the variables $\rho _{1,2,3}^{x,y}$, yielding the cubic

$$\begin{aligned} \Delta _2=&\,\delta _{123}\rho _1^x\rho _2^x\rho _3^x +\delta _{23}\rho _1^y\rho _2^x\rho _3^x +\delta _{13}\rho _1^x\rho _2^y\rho _3^x +\delta _{12}\rho _1^x\rho _2^x\rho _3^y\nonumber \\&+\delta _{1}\rho _1^x\rho _2^y\rho _3^y +\delta _{2}\rho _1^y\rho _2^x\rho _3^y +\delta _{3}\rho _1^y\rho _2^y\rho _3^x +\delta _{0}\rho _1^y\rho _2^y\rho _3^y, \end{aligned}$$

(B.3)

with coefficients $\delta _0,\delta _1,\delta _2$ and $\delta _3$ given by

$$\begin{aligned} \delta _0&=\theta _q\left( +\frac{x_1}{x_2},+\frac{x_2}{x_1},+\frac{x_1}{x_3},+\frac{x_3}{x_1},+\frac{x_2}{x_3},+\frac{x_3}{x_2}\right) \theta _q(-\lambda _0)^3,\\ \delta _1&=\theta _q\left( -\frac{x_1}{x_2},+\frac{x_2}{x_1},-\frac{x_1}{x_3},+\frac{x_3}{x_1},+\frac{x_2}{x_3},+\frac{x_3}{x_2}\right) \theta _q(-\lambda _0)^2\theta _q(\lambda _0),\\ \delta _2&=\theta _q\left( +\frac{x_1}{x_2},-\frac{x_2}{x_1},+\frac{x_1}{x_3},+\frac{x_3}{x_1},-\frac{x_2}{x_3},+\frac{x_3}{x_2}\right) \theta _q(-\lambda _0)^2\theta _q(\lambda _0),\\ \delta _3&=\theta _q\left( +\frac{x_1}{x_2},+\frac{x_2}{x_1},+\frac{x_1}{x_3},-\frac{x_3}{x_1},+\frac{x_2}{x_3},-\frac{x_3}{x_2}\right) \theta _q(-\lambda _0)^2\theta _q(\lambda _0), \end{aligned}$$

$\delta _{23},\delta _{13}$ and $\delta _{12}$ given by

$$\begin{aligned} \delta _{23}&=\theta _q\left( +\frac{x_1}{x_2},-\frac{x_2}{x_1},+\frac{x_1}{x_3},-\frac{x_3}{x_1},-\lambda _0\right) h(\lambda _0;x_2,x_3),\\ \delta _{13}&=\theta _q\left( +\frac{x_1}{x_2},-\frac{x_2}{x_1},+\frac{x_2}{x_3},-\frac{x_3}{x_2},-\lambda _0\right) h(\lambda _0;x_1,x_3),\\ \delta _{12}&=\theta _q\left( -\frac{x_1}{x_3},+\frac{x_3}{x_1},+\frac{x_3}{x_2},-\frac{x_2}{x_3},-\lambda _0\right) h(\lambda _0;x_1,x_2), \end{aligned}$$

where

$$\begin{aligned} h(\lambda ;z_1,z_2):=\theta _q(-\frac{z_1}{z_2},-\frac{z_2}{z_1})\theta _q(\lambda )^2-\theta _q(-1)^2\theta _q(-\frac{z_1}{z_2}\lambda ,-\frac{z_2}{z_1}\lambda ), \end{aligned}$$

and the coefficient $\delta _{123}$ given by

$$\begin{aligned} \delta _{123}=&H(\lambda _0), \end{aligned}$$

where

$$\begin{aligned} H(\lambda ):=&+\theta _q\left( -\frac{x_1}{x_2},-\frac{x_2}{x_1},-\frac{x_1}{x_3},-\frac{x_3}{x_1},-\frac{x_2}{x_3},-\frac{x_3}{x_2}\right) \theta _q(\lambda )^3\\&-\theta _q\left( \lambda \frac{x_1}{x_2},\lambda \frac{x_2}{x_1},-\frac{x_1}{x_3},-\frac{x_3}{x_1},-\frac{x_2}{x_3},-\frac{x_3}{x_2}\right) \theta _q(\lambda )\theta _q(-1)^2\\&-\theta _q\left( -\frac{x_1}{x_2},-\frac{x_2}{x_1},\lambda \frac{x_1}{x_3},\lambda \frac{x_3}{x_1},-\frac{x_2}{x_3},-\frac{x_3}{x_2}\right) \theta _q(\lambda )\theta _q(-1)^2\\&-\theta _q\left( -\frac{x_1}{x_2},-\frac{x_2}{x_1},-\frac{x_1}{x_3},-\frac{x_3}{x_1},\lambda \frac{x_2}{x_3},\lambda \frac{x_3}{x_2}\right) \theta _q(\lambda )\theta _q(-1)^2\\&+\theta _q\left( \lambda \frac{x_1}{x_2},-\frac{x_2}{x_1},-\frac{x_1}{x_3},\lambda \frac{x_3}{x_1},\lambda \frac{x_2}{x_3},-\frac{x_3}{x_2}\right) \theta _q(-1)^3\\&+\theta _q\left( -\frac{x_1}{x_2},\lambda \frac{x_2}{x_1},\lambda \frac{x_1}{x_3},-\frac{x_3}{x_1},-\frac{x_2}{x_3},\lambda \frac{x_3}{x_2}\right) \theta _q(-1)^3. \end{aligned}$$

In order to derive Eq. (B.2), we factorise the functions $h(\lambda ;z_1,z_2)$ and $H(\lambda )$ into simple factors of q-theta functions. We start with $h(\lambda ;z_1,z_2)$. Note that this function is an element of the vector space $V_2(1)$, namely, it is analytic in $\lambda$ on ${\mathbb {C}}^*$ and satisfies

$$\begin{aligned} h(q\lambda ;z_1,z_2)=\lambda ^{-2}h(\lambda ;z_1,z_2). \end{aligned}$$

Furthermore, it is easy to see that $h(-1;z_1,z_2)=0$, hence, by Lemma 5.1,

$$\begin{aligned} h(\lambda ;z_1,z_2)=c(z_1,z_2)\theta _q(-\lambda )^2, \end{aligned}$$

(B.4)

for some yet to be determined coefficient $c(z_1,z_2)$ which is independent of $\lambda$. Then, by evaluating equation (B.4) at $\lambda =1$, we obtain

$$\begin{aligned} c(z_1,z_2)=-\theta _q\left( \frac{z_1}{z_2},\frac{z_2}{z_1}\right) \end{aligned}$$

and thus

$$\begin{aligned} h(\lambda ;z_1,z_2)=-\theta _q\left( \frac{z_1}{z_2},\frac{z_2}{z_1}\right) \theta _q(-\lambda )^2. \end{aligned}$$

(B.5)

We follow the same procedure to compute a factorisation of $H(\lambda )$. We note that it is an element of the vector space $V_3(-1)$, i.e. it is analytic on ${\mathbb {C}}^*$ and

$$\begin{aligned} H(q\lambda )=-\lambda ^{-3}H(\lambda ). \end{aligned}$$

Furthermore, it is easy to check by direct calculation that $H(1)=H(-1)=0$, and hence

$$\begin{aligned} H(\lambda )=c_H\theta _q(\lambda )\theta _q(-\lambda )^2, \end{aligned}$$

(B.6)

for some yet to be determined coefficient $c_H$, which is independent of $\lambda$. To determine this constant, we evaluate both sides of Eq. (B.6) at $\lambda =x_1$. By means of analogous calculations as above, we can simplify $H(x_1)$ to obtain

$$\begin{aligned} H(x_1)=\frac{\theta _q(x_1)^3\theta _q(-x_1)^2\theta _q(x_2)^2\theta _q(\frac{x_2}{x_1})^2}{q^2x_1^2x_2^4}, \end{aligned}$$

leading to

$$\begin{aligned} H(\lambda )=\frac{\theta _q(x_1)^2\theta _q(x_2)^2\theta _q(\frac{x_2}{x_1})^2}{q^2x_1^2x_2^4}\theta _q(\lambda )\theta _q(-\lambda )^2. \end{aligned}$$

(B.7)

Now that we have explicit factorisations of the functions $h(\lambda ;z_1,z_2)$ and $H(\lambda )$ (respectively given by Eqs. (B.5) and (B.7)), and thus factorised expressions for the coefficients of the cubic (B.3), Eq. (B.2) follows immediately, upon using the symmetries (1.6) of the q-theta function.