Stability of the Maxwell–Stefan System in the Diffusion Asymptotics of the Boltzmann Multi-species Equation

Abstract

We investigate the diffusion asymptotics of the Boltzmann equation for gaseous mixtures, in the perturbative regime around a local Maxwellian vector whose fluid quantities solve a flux-incompressible Maxwell–Stefan system. Our framework is the torus and we consider hard-potential collision kernels with angular cutoff. As opposed to existing results about hydrodynamic limits in the mono-species case, the local Maxwellian we study here is not a local equilibrium of the mixture due to cross-interactions. By means of a hypocoercive formalism and introducing a suitable modified Sobolev norm, we build a Cauchy theory which is uniform with respect to the Knudsen number $\varepsilon$. In this way, we shall prove that the Maxwell–Stefan system is stable for the Boltzmann multi-species equation, ensuring a rigorous derivation in the vanishing limit $\varepsilon \rightarrow 0$.

Appendix A. Explicit Carleman Representation of the Operator \(\mathbf{K }^{\varepsilon }\)

We here provide the basic tools that are used in Lemma 3.4 to prove the regularizing effect of $\partial ^{\beta }_v\partial ^{\alpha }_x\mathbf{K }^{\varepsilon }$. Looking at the work of Mouhot and Neumann [45] in the mono-species context, the authors recover this property by transferring to the kernel of the compact operator K all the derivatives, which are then computed and estimated explicitly. This analysis is possible mainly because the kernel of K has itself an explicit expression. Ideally, one may want to apply a similar strategy in our multi-species framework, but this would require knowing the structure of the kernel of $\mathbf{K }^{\varepsilon }$.

In this appendix we derive an explicit expression of the kernel of $\mathbf{K }^{\varepsilon }$, following the methods of [17] where a Carleman representation of the Boltzmann multi-species operator was obtained. In particular, we shall rework the pointwise estimates established by the authors, replacing them by a series of pointwise equalities where all the technical computations are made fully explicit.

Let us begin by recalling that $\mathbf{K }^{\varepsilon }=(K^{\varepsilon }_1,\ldots ,K^{\varepsilon }_N)$ can be written componentwise, for any $\mathbf{f }\in L^2\big ({\mathbb {R}}^3,\pmb {\mu }^{-\frac{1}{2}}\big )$, under the kernel form [17, Lemma 5.1]

$$\begin{aligned} \begin{aligned}&K^{\varepsilon }_i(\mathbf{f })(v) \\&\quad =\sum _{j=1}^N C_{ij} \int _{{\mathbb {R}}^3}\left( \frac{1}{|v-v_*|}\int _{\widetilde{E}^{ij}_{v v_*}}\frac{B_{ij}\left( v-V(w,v_*),\frac{v_*-w}{|w-v_*|}\right) }{|w-v_*|}M^{\varepsilon }_i(w)\ \text {d}\widetilde{E}(w)\right) f^*_j\text {d}v_* \\&\qquad + \sum _{j=1}^N C_{ji} \int _{{\mathbb {R}}^3}\left( \frac{1}{|v-v_*|}\int _{E^{ij}_{v v_*}}\frac{B_{ij}\left( v-V(v_*,w),\frac{w-v_*}{|w-v_*|}\right) }{|w-v_*|}M^{\varepsilon }_j(w)\ \text {d}E(w)\right) f_i^*\text {d}v_* \\&\qquad - \sum _{j=1}^N\int _{{\mathbb {R}}^3}\left( \int _{{\mathbb {S}}^2}B_{ij}(\left| v-v_*\right| ,\cos \theta )M^{\varepsilon }_i\text {d}\sigma \right) f^*_j\text {d}v_*, \end{aligned} \end{aligned}$$

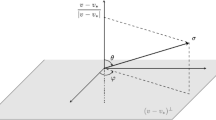
where we have defined $V(w,v_*)=v_*+m_i m_j^{-1}w-m_i m_j^{-1}v$ and called $C_{ij},C_{ji}>0$ some explicit constants which only depend on the masses $m_i, m_j$. Moreover, we have denoted by $\text {d}E$ the Lebesgue measure on the hyperplane $E_{v v_*}^{ij}$, orthogonal to $v-v_*$ and passing through

$$\begin{aligned} V_E(v,v_*)=\frac{m_i+m_j}{2 m_j}v-\frac{m_i-m_j}{2m_j}v_*, \end{aligned}$$

and by $\text {d}\widetilde{E}$ the Lebesgue measure on the space $\widetilde{E}_{v v_*}^{ij}$ which corresponds to the hyperplane $E_{v v_*}^{ij}$ whenever $m_i=m_j$, and to the sphere of radius $R=R(v,v_*)$ and centre $O=O(v,v_*)$

$$\begin{aligned} R = \frac{m_j}{|m_i-m_j|}|v-v_*|, \qquad O = \frac{m_i}{m_i-m_j}v-\frac{m_j}{m_i-m_j}v_*, \end{aligned}$$

whenever $m_i\ne m_j$.

We can thus define, for any $1\leqslant i,j\leqslant N$, the kernels

$$\begin{aligned} \begin{aligned} \kappa _{ij}^{(1)}(v,v_*)&= \frac{C_{ij}}{|v-v_*|}\int _{\widetilde{E}^{ij}_{v v_*}}\frac{B_{ij}\left( v-V(w,v_*),\frac{v_*-w}{|w-v_*|}\right) }{|w-v_*|}M^{\varepsilon }_i(w)\ \text {d}\widetilde{E}(w), \\ \kappa _{ij}^{(2)}(v,v_*)&= \frac{C_{ji}}{|v-v_*|}\int _{E^{ij}_{v v_*}}\frac{B_{ij}\left( v-V(v_*,w),\frac{w-v_*}{|w-v_*|}\right) }{|w-v_*|}M^{\varepsilon }_j(w)\ \text {d}E(w), \\ \kappa _{ij}^{(3)}(v,v_*)&= \int _{{\mathbb {S}}^2}B_{ij}(\left| v-v_*\right| ,\cos \theta )M^{\varepsilon }_i\text {d}\sigma , \end{aligned} \end{aligned}$$

where we have dropped the parameter $\varepsilon$ in order to enlighten our notations. In this way, each $K^{\varepsilon }_i$ can be rewritten as

$$\begin{aligned} K^{\varepsilon }_i(\mathbf{f })(v)=\sum _{j=1}^N\left\{ \int _{{\mathbb {R}}^3}\kappa _{ij}^{(1)}(v,v_*)f^*_j\text {d}v_* + \int _{{\mathbb {R}}^3}\kappa _{ij}^{(2)}(v,v_*)f^*_i\text {d}v_* - \int _{{\mathbb {R}}^3}\kappa _{ij}^{(3)}(v,v_*)f^*_j\text {d}v_*\right\} . \end{aligned}$$

Let us now fix two indices $i,j\in \left\{ 1,\ldots ,N\right\}$ and study each of the three kernels separately.

1.1 A.1. Explicit form of $\kappa _{ij}^{(1)}$

The first kernel is easy to make explicit, since the domain of integration $\widetilde{E}_{v v_*}^{ij}$ is a sphere. We thus perform an initial change of variables consisting on a translation of its centre and a dilation of its radius, in order to end up on ${\mathbb {S}}^2$. In this new coordinate system, $\kappa _{ij}^{(1)}$ writes

$$\begin{aligned} \kappa _{ij}^{(1)}(v,v_*)=\frac{C_{ij}m_j^2}{(m_i -m_j)^2}\left| v-v_*\right| \int _{{\mathbb {S}}^2}\frac{b_{ij}(v,v_*,\omega )}{|R\omega +O-v_*|^{1-\gamma }}M^{\varepsilon }_i(R\omega +O)\ \text {d}\omega , \end{aligned}$$

with $b_{ij}$ being given by

$$\begin{aligned} b_{ij}(v,v_*,\omega ) = b_{ij}\left( \frac{\big (v-V(R\omega +O,v_*)\big )\cdot \big (v_*-\left( R\omega +O\right) \big )}{\left| v-V(R\omega +O,v_*)\right| \left| R\omega +O-v_*\right| }\right) . \end{aligned}$$

Direct computations then show that

$$\begin{aligned} \kappa _{ij}^{(1)}(v,v_*)= & {} C_{ij}c_i |v-v_*|^{\gamma }\int _{{\mathbb {S}}^2}\frac{b_{ij}\left( \omega \cdot \frac{v-v_*}{|v-v_*|}\right) }{\left| \frac{m_i^2+m_j^2}{(m_i-m_j)^2}+\frac{2m_i m_j}{(m_i-m_j)|m_i-m_j|}\frac{(v-v_*)\cdot \omega }{|v-v_*|}\right| ^{1-\gamma }} \nonumber \\&\times e^{-\frac{m_i}{2}\left| R\omega +O\right| ^2+\varepsilon m_i (R\omega +O)\cdot u_i-\varepsilon ^2\frac{m_i}{2}|u_i |^2}\ \text {d}\omega , \end{aligned}$$

(A.1)

where we have renamed for simplicity

$$\begin{aligned} C_{ij}=\frac{C_{ij} m_j^2}{(m_i -m_j)^2}\left( \frac{m_i}{2\pi }\right) ^{3/2}, \end{aligned}$$

the angular part has the form

$$\begin{aligned} b_{ij}\left( \omega \cdot \frac{v-v_*}{|v-v_*|}\right) =b_{ij}\left( \frac{\frac{2m_im_j}{(m_i-m_j)^2}+\frac{m_i^2+m_j^2}{(m_i-m_j)|m_i-m_j|}\frac{(v-v_*)\cdot \omega }{|v-v_*|}}{\frac{m_i^2+m_j^2}{(m_i-m_j)^2}+\frac{2m_im_j}{(m_i-m_j)|m_i-m_j|}\frac{(v-v_*)\cdot \omega }{|v-v_*|}}\right) , \end{aligned}$$

and the exponent explicitly reads

$$\begin{aligned} \begin{aligned} \left| R\omega +O\right| ^2 =&\ \frac{m_j^2}{(m_i-m_j)^2}|v-v_*|^2 +\frac{2 m_j|v-v_*|}{(m_i-m_j)|m_i-m_j|}(m_i v-m_j v_*)\cdot \omega \\&\ + \frac{1}{(m_i-m_j)^2}|m_i v-m_j v_*|^2, \\ (R\omega +O)\cdot u_i =&\ \frac{m_j}{|m_i-m_j|}|v-v_*| \omega \cdot u_i + \frac{(m_i v-m_j v_*)\cdot u_i}{m_i-m_j}. \end{aligned} \end{aligned}$$

This concludes the study for $\kappa _{ij}^{(1)}$.

1.2 A.2. Explicit form of $\kappa _{ij}^{(2)}$

Recovering the explicit expression of $\kappa _{ij}^{(2)}$ is more subtle. We recall that the domain of integration $E_{v v_*}^{ij}$ is the hyperplane orthogonal to $v-v_*$ and passing through

$$\begin{aligned} V_E(v,v_*)=\frac{m_i+m_j}{2 m_j}v-\frac{m_i-m_j}{2m_j}v_*. \end{aligned}$$

Let us consider $\omega \in \big (\text {Span}(v-v_*)\big )^\perp$ and let us make the initial change of variables $w=V_E(v,v_*)+\omega$ which translates $E_{v v_*}^{ij}$ to the parallel hyperplane passing through the origin of ${\mathbb {R}}^3$. Thus $\kappa _{ij}^{(2)}$ transforms into

$$\begin{aligned} \kappa _{ij}^{(2)}(v,v_*) = \frac{C_{ji}}{|v-v_*|}\int _{(v-v_*)^\perp }\frac{b_{ij}(v,v_*,\omega )}{|v-V(v_*,V_E(v,v_*)+\omega )|^{1-\gamma }}M^{\varepsilon }_j(V_E(v,v_*)+\omega )\ \text {d}\omega , \end{aligned}$$

where the angular part writes

$$\begin{aligned} b_{ij}(v,v_*,\omega )= b_{ij}\left( \frac{\big ( v-V(v_*,V_E(v,v_*)+\omega )\cdot \big (V_E(v,v_*)+\omega -v_*\big ) \big )}{\left| v-V(v_*,V_E(v,v_*)+\omega )\right| |V_E(v,v_*)+\omega -v_*|}\right) . \end{aligned}$$

The exponent of the Maxwellian can be computed as follows. We initially develop the square to get

$$\begin{aligned} \left| V_E(v,v_*)+\omega -\varepsilon u_j\right| ^2=\left| V_E(v,v_*)+\omega \right| ^2 -2\varepsilon \big (V_E(v,v_*)+\omega \big )\cdot u_j +\varepsilon ^2| u_j |^2. \end{aligned}$$

The first term can be rewritten as

$$\begin{aligned} \begin{aligned} \left| V_E(v,v_*)+\omega \right| ^2&= \left| \omega +\frac{1}{2}(v+v_*)\right| ^2 +\frac{m_i^2}{4m_j^2}|v-v_*|^2+\frac{m_i}{2m_j}\big (|v|^2-|v_*|^2\big ) \\&= \left| \omega +\frac{1}{2}V^\perp \right| ^2 +\frac{1}{4}\left| V^\parallel \right| ^2+\frac{m_i^2}{4m_j^2}|v-v_*|^2+\frac{m_i}{2m_j}\big (|v|^2-|v_*|^2\big ), \end{aligned} \end{aligned}$$

where we have decomposed $v+v_*=V^\parallel + V^\perp$, with $V^\parallel$ being the projection onto $\text {Span}(v-v_*)$ and $V^\perp$ being the orthogonal part. In the same way, the second term reads

$$\begin{aligned} \big (V_E(v,v_*)+\omega \big )\cdot u_j=\left( \frac{1}{2}V^\parallel +\frac{m_i}{2 m_j}(v-v_*)\right) \cdot u_j + \left( \frac{1}{2}V^\perp +\omega \right) \cdot u_j. \end{aligned}$$

Since by the definition of $V^\parallel$

$$\begin{aligned} \left| V^\parallel \right| ^2 =\frac{\big ((v+v_*)\cdot (v-v_*)\big )^2}{|v-v_*|^2}=\frac{\left| |v|^2-|v_*|^2\right| ^2}{|v-v_*|^2}, \end{aligned}$$

the kernel $\kappa _{ij}^{(2)}$ becomes

$$\begin{aligned} \kappa _{ij}^{(2)}(v,v_*)={\mathcal {P}}_{ij}(v,v_*)\int _{(v-v_*)^\perp }b_{ij}(v,v_*,\omega )W_{ij}(v,v_*,\omega )M^{\varepsilon }_j\left( \omega +\frac{1}{2}V^\perp \right) \text {d}E(\omega ), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {P}}_{ij}(v,v_*)= & {} \frac{C_{ji}}{|v-v_*|} e^{-\frac{m_i^2}{8m_j}|v-v_*|^2-\frac{m_j}{8}\frac{\left| |v|^2-|v_*|^2\right| ^2}{|v-v_*|^2}+\varepsilon \frac{m_i}{2}(v-v_*)\cdot u_j + \varepsilon \frac{m_j}{2}\frac{|v|^2-|v_*|^2}{|v-v_*|}\frac{(v-v_*)\cdot u_j}{|v-v_*|}}\sqrt{\frac{\mu _i}{\mu _i^*}}, \\ b_{ij}(v,v_*,\omega )= & {} b_{ij}\left( \frac{\left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 - |\omega |^2}{\left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 + |\omega |^2}\right) , \qquad \\ W_{ij}(v,v_*,\omega )= & {} \left( \left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 + |\omega |^2\right) ^{\frac{\gamma -1}{2}}. \end{aligned}$$

Finally, it remains to take care of the domain of integration which still depends on $(v,v_*)$. The idea is to transform the hyperplane defined by $(v-v_*)^\perp$ to end up on ${\mathbb {R}}^2$. Proceeding as in [44, Proposition 2.4], we first observe that the integral is even with respect to $v-v_*$, since it only depends on its modulus. Thus, we focus on the set of relative velocities $v-v_*$ such that the first coordinate is nonnegative. Call $e_1$ the first unit vector of the corresponding orthonormal basis and, for any fixed $\frac{v-v_*}{|v-v_*|}$, introduce the linear transformation

$$\begin{aligned} {\mathcal {L}}\left( \frac{v-v_*}{|v-v_*|},{\mathcal {X}}\right) =2\frac{\left( e_1+\frac{v-v_*}{|v-v_*|}\right) \cdot {\mathcal {X}}}{\left| e_1+\frac{v-v_*}{|v-v_*|}\right| ^2}\left( e_1+\frac{v-v_*}{|v-v_*|}\right) -{\mathcal {X}},\quad \forall {\mathcal {X}}\in {\mathbb {R}}^3, \end{aligned}$$

which corresponds to the specular reflection through the axis defined by $e_1+\frac{v-v_*}{|v-v_*|}$. Now, ${\mathcal {L}}$ is a diffeomorphism from $\left\{ {\mathcal {X}}=\left( 0,X\right) , X\in {\mathbb {R}}^2\right\}$ onto $(v-v_*)^\perp$, with unitary Jacobian matrix. Thus, we can use this linear transformation to pass from $(v-v_*)^\perp$ to ${\mathbb {R}}^2$ into the integral of $\kappa _{ij}^{(2)}$, which can be finally explicitly written as

$$\begin{aligned}&\kappa _{ij}^{(2)}(v,v_*) \nonumber \\&\quad ={\mathcal {P}}_{ij}(v,v_*) \int _{{\mathbb {R}}^2}b_{ij}\left( \frac{\left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 - |X|^2}{\left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 + |X|^2}\right) \left( \left( \frac{m_i+m_j}{2m_j}\right) ^2 |v-v_*|^2 + |X|^2\right) ^{\frac{\gamma -1}{2}} \nonumber \\&\qquad \times M^{\varepsilon }_j\left( {\mathcal {L}}\left( \frac{v-v_*}{|v-v_*|},\left( 0,X+\frac{1}{2}\overline{X}\right) \right) \right) \text {d}X, \end{aligned}$$

(A.2)

where we have called $\overline{X}\in {\mathbb {R}}^2$ the preimage of $V^\perp \in (v-v_*)^\perp$ through the transformation ${\mathcal {L}}$, and we have used the straightforward identity

$$\begin{aligned} \left| {\mathcal {L}}\left( \frac{v-v_*}{|v-v_*|},(0,X)\right) \right| =|X|, \quad \forall X\in {\mathbb {R}}^2,\ \forall v,v_*\in {\mathbb {R}}^3. \end{aligned}$$

This concludes the study for $\kappa _{ij}^{(2)}$.

1.3 A.3. Explicit form of $\kappa _{ij}^{(3)}$

The analysis of $\kappa _{ij}^{(3)}$ is the easiest one, since it is already fully explicit. It simply reads

$$\begin{aligned} \kappa _{ij}^{(3)}(v,v_*) = \int _{{\mathbb {S}}^2} b_{ij}\left( \sigma \cdot \frac{v-v_*}{|v-v_*|}\right) |v-v_*|^\gamma M^{\varepsilon }_i(v)\text {d}\sigma . \end{aligned}$$

This concludes its study.