1 Introduction

The ubiquity of non-covalent interactions and their increasingly appreciated role in such fields as material design [1], catalysis [2], medicine [3] and even photochemistry [4,5,6] necessitates the development of computational tools able to describe them. Historically, it has been a challenge, in particular due to the long-range nature and the subtlety of the London dispersion, but recently sophisticated coupled-cluster approaches are becoming more computationally affordable [7, 8] and efficient approaches such as the density functional theory (DFT) [9] have developed ways to treat van der Waals interactions [10]. Molecular interactions can also be computed and analyzed using Symmetry-Adapted Perturbation Theory (SAPT) [11, 12], and other energy decomposition schemes [13, 14] and some progress toward providing the same description for intramolecular interactions has been made [15, 16]. The success of computational methods has not however been extended to systems where the static correlation plays a role. This group includes, apart from somewhat exotic systems like chromium or beryllium dimers, all systems containing significantly stretched or compressed bonds. This is a severe limitation as computational and experimental studies, albeit scarce [17,18,19,20,21], have shown how essential the van der Waals interactions can be in the reaction process.

Capturing molecular interactions in systems where bonds are being twisted or broken is so challenging because one needs to ensure that both the static and the dynamic correlation are accurately described. This usually means one needs to employ a multireference (MR) wavefunction and a good-quality dynamic-correlation correction. What is more, the method should be size-extensive and be able to produce smooth interaction energy surfaces. Favorable scaling with the basis set size is also of value since the description of non-covalent interactions demands high-quality basis sets containing diffuse functions. Popular coupled-cluster methods are of single reference kind and they are prone to fail if applied to interacting strongly correlated systems, unless a high-level CC, with full triples or higher, is employed [22]. The CASPT2 method—often a method of choice for multireference systems—may suffer from lack of size consistency, difficulty with obtaining smooth potential energy curves, and poor accuracy when applied to the description of molecular interactions.

We have recently introduced an Embedding Extended Random Phase Approximation (EERPA) [22] correlation correction and paired it with a simple multireference wavefunction—a strongly orthogonal perfect-pairing generalized valence bond (GVB). GVB wavefunction accounts for electron pair correlation providing correct description of bond breaking process but it lacks long-range correlation. Consequently it is not able to account for weak interactions. Adding dynamic-correlation correction to GVB energy via perturbation theory or linearized multireference coupled-cluster theory allows one to include dispersion interaction component but the accuracy is poor (it must be admitted that the applications are scarce) [23]. EERPA, on the other hand, based on introducing extended random phase approximation correlation correction in an embedding fashion, was shown to be a tailor-made approach for describing intermolecular interactions of multireference systems [22]. It is accurate and numerically stable. What is more, EERPA-GVB is not as computationally demanding as even CCSD(T) method, let alone the higher-level approaches like CCSDT. The cost of computing the EERPA correction is similar to that of the familiar RPA correlation, while the reference GVB wavefunction scales as \(N_{\mathrm{g}}M^4\), where M is the basis set size and \(N_{\mathrm{g}}\)—the number of geminals [24],

The goal of this paper is to explore further capabilities of EERPA and show its usefulness in predicting not only values of interacting energy but also in getting insight into interaction between monomers. We firstly recap the theoretical framework of EERPA-GVB, then we show the method’s robustness using examples of dispersion-dominated and hydrogen-bonded dimers, and finally we analyze the behavior of two van der Waals complexes with twisted or broken bonds.

The perfect-pairing GVB ansatz, being of interest in this paper conforms to the generalized product function form proposed by McWeeny [25] and it reads [26,27,28]

$$\begin{aligned} \varPsi ^{\mathrm{GVB}}=\hat{A}\prod _{I=1}^{N/2}\varPsi ^{I} , \end{aligned}$$
(1)

where N is a number of electrons assumed to be even. Each \(\varPsi ^{I}\) is an antisymmetric two-electron wavefunction, called a geminal. The antisymmetry of the total wavefunction is assured by the antisymmetrizing operator \(\hat{A}\), which includes a proper normalization factor. Geminals are constrained to be strongly orthogonal [25, 29]

$$\begin{aligned} \forall _{I\ne J}\;\;\int \varPsi ^{I}({\mathbf {x}},{\mathbf {x}}^{\prime })\varPsi ^{J}({\mathbf {y}},{\mathbf {x}}^{\prime })\ \hbox {d}{\mathbf {x}}^{\prime }=0 \end{aligned}$$
(2)

(here and elsewhere in the paper \(\mathbf {x,y}\) combines spatial and spin coordinates of a single electron). Additional two constraints imposed on geminals are: singlet symmetry and the constraint that each geminal is expanded in a subspace of only two orbitals. Consequently, each GVB geminal can be written in the following form

$$\begin{aligned} \forall _{I}\;\;\varPsi ^{I}=\varPsi ^{I}({\mathbf {x}}_{1},{\mathbf {x}}_{2})=2^{-1/2} (c_{1_{I}}\varphi _{1_{I}}({\mathbf {r}}_{1})\varphi _{1_{I}}({\mathbf {r}} _{2})+c_{2_{I}}\varphi _{2_{I}}({\mathbf {r}}_{1})\varphi _{2_{I}}({\mathbf {r}} _{2}))(\alpha \beta -\beta \alpha ) . \end{aligned}$$
(3)

The squares of expansion coefficients \(c_{p}\) present in Eq. (3) are the natural occupation numbers \(\{ n_{p}\}\)

$$\begin{aligned} \forall _{p}\ \ \ c_{p}^{2}=n_{p}\in [0,1] , \end{aligned}$$
(4)

\(\{ \varphi _{p}\}\) being a set of the natural orbitals pertaining to the ansatz \(\varPsi ^{\mathrm{GVB}}\).

Strong orthogonality of geminals is a restriction imposed on the wavefunction but in return one is rewarded with a simple expression for the electronic energy reading [28, 30]

$$\begin{aligned} E^{\mathrm{GVB}}& = 2\sum _{p}^N\ n_{p}\ h_{pp}+\sum ^N_{pq}\delta _{I_{p}I_{q}}c_{p} c_{q}\left\langle pp|qq\right\rangle \nonumber \\&\quad +\sum ^N_{pq}(1-\delta _{I_{p}I_{q}} )n_{p}n_{q}\left( 2\left\langle pq|pq\right\rangle -\left\langle pq|qp\right\rangle \right) , \end{aligned}$$
(5)

where \(\left\{ h_{pp}=\left\langle \varphi _{p}|\hat{t}+\hat{\upsilon } _{\rm ext}|\varphi _{p}\right\rangle \right\}\) are one-electron integrals in the representation of the natural orbitals and two-electron integrals are defined using a standard \(r_{1}r_{2}r_{1}r_{2}\) convention. Symbols \(I_{p}\) in Eq. (5) indicate a geminal to which a spinorbital \(\varphi _{p}\) belongs. Thus, a symbol \(\delta _{I_{p}I_{q}}\) equals 1 only if both orbitals p and q are used in expansion of the same geminal (cf. Eq. (3)), whereas \((1-\delta _{I_{p}I_{q}})\) is different from zero for two orbitals p and q belonging to two different geminals. A quick look at the GVB energy expression reveals immediately its main appealing features: electron pair correlation is accounted for due to presence of the middle term (GVB goes beyond a single particle picture), the number of CI coefficients undergoing optimization is only equal to N. In addition, active orbitals in GVB are unique and the number of them is N. Taking into account that in widely used multireference methods like CASSCF or MCSCF the number of CI coefficients is exponentially growing and the choice of active orbitals is often problematic and arbitrary, it becomes clear that the GVB ansatz is more computationally attractive than the latter methods. Deficiencies of GVB have been known, see, e.g., Refs. [31,32,33], and they include a deteriorated performance for molecules described by more than one Lewis structure, failure in dissociating multiple bonds, practical limitation to closed-shell systems and the lack of dispersion energy in weakly interacting systems. Recently we have shown that GVB, when corrected with properly designed correlation energy corrections, yields excellent results for molecules undergoing conformational changes [30, 34], and for molecular interactions [22]. For the convenience of the reader, we will present two correlation energy corrections: ERPA and EERPA. The former is generally applicable and can be seen as extension of the random phase approximation (RPA) [35] correlation energy for multireference wavefunction. EERPA (Embedding ERPA), on the other hand, in its current formulation is applicable to weakly interacting dimers.

Let us begin with the Extended Random Approximation (ERPA). The ERPA equation reads [36,37,38,39]

$$\begin{aligned} \left( \begin{array} {cc} {{\mathcal {A}}} & {{\mathcal {B}}}\\ {{\mathcal {B}}} & {{\mathcal {A}}} \end{array} \right) \left( \begin{array} {c} {\mathbf {X}}^{\nu }\\ {\mathbf {Y}}^{\nu } \end{array} \right) =\omega _{\nu }\left( \begin{array} {cc} -{{\mathcal {N}}} & \mathbf {0}\\ \mathbf {0} & {{\mathcal {N}}} \end{array} \right) \left( \begin{array} {c} {\mathbf {X}}^{\nu }\\ {\mathbf {Y}}^{\nu } \end{array} \right) , \end{aligned}$$
(6)

For a system S the \({{\mathcal {A}}}\), \({{\mathcal {B}}}\), and \({{\mathcal {N}}}\) matrices (assumed to be real-valued) are determined from the one- and two-electron reduced density matrices, \(\gamma ^{S}\) and \(\varGamma ^{S}\), obtained from an assumed reference wavefunction (GVB in this case)

$$\begin{aligned} \forall _{p>q, r>s}\ \ \ {\mathcal {A}}_{pqrs}^{S}&={\mathcal {A}} _{pqrs}(\gamma ^{S},\varGamma ^{S}), \end{aligned}$$
(7)
$$\begin{aligned} \forall _{p>q, r>s}\ \ \ {\mathcal {B}}_{pqrs}^{S}&={\mathcal {A}} _{pqsr}(\gamma ^{S},\varGamma ^{S}), \end{aligned}$$
(8)
$$\begin{aligned} \forall _{p>q,r>s}\ \ \ {\mathcal {N}}_{pqrs}^{S}&=(n_{p} -n_{q})\delta _{pr}\delta _{qs} \end{aligned}$$
(9)

(see Appendix in Ref. [30] for the explicit expressions for the matrix elements of \({{\mathcal {A}}}\) for the GVB wavefunction). The eigenvectors \(\left[ {\mathbf {X}}^{\nu },{\mathbf {Y}}^{\nu }\right]\) provide approximation to reduced transition density matrices that has led to obtaining the following spin-summed ERPA correlation energy expression [30, 34, 40]

$$\begin{aligned} E_{\mathrm{corr}}^{\mathrm{ERPA}}(S)& = \sum _{p>r,q>s}(1-\delta _{I_{p}I_{q} }\delta _{I_{r}I_{s}}\delta _{I_{q}I_{r}})W_{pqrs}^{S}\ \ , \end{aligned}$$
(10)
$$ \begin{aligned}W_{pqrs}^{S}&=\left\{ \sum _{\nu }(n_{r}-n_{p})(n_{s}-n_{q})\left( X_{pr}^{\nu }+Y_{pr}^{\nu }\right) (X_{qs}^{\nu }+Y_{qs}^{\nu })\right. \nonumber \\&\quad \left. - \frac{1}{2}\left[ (1-n_{r})n_{p}+(1-n_{p})n_{r}\right] \delta _{rs}\delta _{pq} \vphantom{\sum_{}} \right\} \left\langle pq|rs\right\rangle. \end{aligned}$$
(11)

Notice that the expression \((1-\delta _{I_{p}I_{q}}\delta _{I_{r}I_{s}} \delta _{I_{q}I_{r}})\) in Eq. (10) vanishes if all orbitals p, q, r, s belong to the same geminal. In this way, intra-geminal correlation energy already included in the GVB ansatz is excluded from \(E_{\mathrm{corr}}^{\mathrm{ERPA}}\) and double counting of correlation is avoided. The ERPA-GVB interaction energy for a dimer consisting of monomers A and B reads

$$\begin{aligned} E_{{\mathrm{ERPA}}{\text{-}}{\mathrm{GVB}}}^\mathrm{Int}& = E_{AB}^{\mathrm{GVB}}+E_{\mathrm{corr}}^{\mathrm{ERPA}}{(AB)} \nonumber \\&\quad -\left( E_{A} ^{\mathrm{GVB}}+E_{\mathrm{corr}}^{\mathrm{ERPA}}(A)+E_{B}^{\mathrm{GVB}}+E_{\mathrm{corr}}^{\mathrm{ERPA}}(B)\right) . \end{aligned}$$
(12)

Thus, the ERPA equations are solved three times: for a dimer, \(S=AB\) and for two monomers, \(S=A\) and \(S=B\).

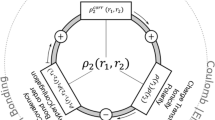
In the EERPA-GVB approach, inspired by one-electron reduced density matrix embedding theory [41], energies of monomers are obtained in the same fashion as in ERPA-GVB but the correlation energy description of a dimer is modified in order to account separately for a correlation of electrons in a monomer embedded in the field of another monomer, and for inter-monomer correlation effects. The EERPA correlation has been defined as follows:

$$\begin{aligned} E_{\mathrm{corr}}^{\mathrm{EERPA}}(AB)=E_{\mathrm{corr}}^{A}+E_{\mathrm{corr}}^{B}+E_{\mathrm{corr}}^{AB} . \end{aligned}$$
(13)

The correlation energy of the monomer A embedded in B, \(E^A_{\mathrm{corr}}\), results from solving truncated ERPA equations with the following matrices

$$\begin{aligned} {{\mathcal {A}}}^{A}& = \left[ {\mathcal {A}}_{pqrs}(\gamma ^{AB},\varGamma ^{AB})\right] _{\begin{array}{c} p>q,r>s\\ pqrs\in \varOmega _{A} \end{array}} , \end{aligned}$$
(14)
$$\begin{aligned} {{\mathcal {B}}}^{A}& = \left[ {\mathcal {B}}_{pqrs}(\gamma ^{AB},\varGamma ^{AB})\right] _{\begin{array}{c} p>q,r>s\\ pqrs\in \varOmega _{A} \end{array}} , \end{aligned}$$
(15)

and

$$\begin{aligned} {{\mathcal {N}}}^{A}=\left[ (n_{p}-n_{q})\delta _{pr}\delta _{qs}\right] _{\begin{array}{c} p>q,r>s\\ pqrs\in \varOmega _{A} \end{array}} , \end{aligned}$$
(16)

where the set \(\varOmega _{A}\) defines excitations originating from an orbital localized on a monomer A (a set \(G_{A}\) includes all occupied orbitals assigned to A) and ending in either another orbital from \(G_{A}\) or an unoccupied orbital (V is a set of all unoccupied orbitals) or one of the weakly occupied orbital localized on a monomer B, i.e.,

$$\begin{aligned} \varOmega _{A}=\left\{ p>r,\,q>s:\;r,s\in G_{A}\;\wedge \;p,q\in G_{A}\cup G_{B}^{\mathrm{weak}}\cup V\right\} , \end{aligned}$$
(17)

where

$$\begin{aligned} G_{B}^{\mathrm{weak}}=\left\{ \varphi _{p}:\;p\in G_{B}\wedge n_{p}<\frac{1}{2}\right\} \ \ . \end{aligned}$$
(18)

The correlation energy \(E_{\mathrm{corr}}^{A}\) entering Eq. (13) results from

$$\begin{aligned} E_{\mathrm{corr}}^{A}=\sum _{\begin{array}{c} p>r,q>s\\ pqrs\in \varOmega _{A} \end{array}}(1-\delta _{I_{p} I_{q}}\delta _{I_{r}I_{s}}\delta _{I_{q}I_{r}})W_{pqrs}^{A} , \end{aligned}$$
(19)

where \(W_{pqrs}^{A}\) is defined in Eq. (11). The energy for a monomer B embedded in A, \(E_{\mathrm{corr}}^{B}\), is obtained analogously. \(E_{\mathrm{corr}}^{AB}\), the remaining term in the EERPA correlation energy expression for a dimer (13), accounts for inter-monomer correlation effects and it is obtained by solving ERPA equations for a dimer with the matrices

$$\begin{aligned} {{\mathcal {A}}}^{AB}& = \left[ {\mathcal {A}}_{pqrs}(\gamma ^{AB},\varGamma ^{AB})\right] _{p>q,r>s} , \end{aligned}$$
(20)
$$\begin{aligned} {{\mathcal {B}}}^{AB}& = \left[ {\mathcal {B}}_{pqrs}(\gamma ^{AB},\varGamma ^{AB})\right] _{p>q,r>s} , \end{aligned}$$
(21)

and

$$\begin{aligned} {{\mathcal {N}}}^{AB}=\left[ (n_{p}-n_{q})\delta _{pr}\delta _{qs}\right] _{p>q,r>s} , \end{aligned}$$
(22)

and computing the correlation energy from the expression

$$\begin{aligned} E_{\mathrm{corr}}^{AB}=\sum _{\begin{array}{c} p>r,q>s\\ pqrs\notin \bar{\varOmega }_{A} \\ pqrs\notin \bar{\varOmega }_{B} \end{array}}(1-\delta _{I_{p}I_{q}}\delta _{I_{r}I_{s}}\delta _{I_{q}I_{r} })W_{pqrs}^{AB}\ \ \ , \end{aligned}$$
(23)

where the set \(\bar{\varOmega }_{A}\) defines intra-monomer contributions

$$\begin{aligned} \bar{\varOmega }_{A}=\left\{ p>r,\,q>s:\;r,s\in G_{A}\;\wedge \;p,q\in G_{A}\cup V\right\} , \end{aligned}$$
(24)

and analogously for \(\bar{\varOmega }_{B}\).

The EERPA-GVB interaction energy results from the supermolecular calculation and it is computed as (cf. Eq. (12))

$$\begin{aligned} E_{\mathrm{EERPA-GVB}}^\mathrm{Int}& = E_{AB}^{\mathrm{GVB}}+E_{\mathrm{corr}}^\mathrm{EERPA}(AB) \nonumber \\&-\left( E_{A} ^{\mathrm{GVB}}+E_{\mathrm{corr}}^{\mathrm{ERPA}}(A)+E_{B}^{\mathrm{GVB}}+E_{\mathrm{corr}}^{\mathrm{ERPA}}(B)\right) \ \ \ , \end{aligned}$$
(25)

where the correlation energy expression for monomers is given by Eqs. (6)–(11). Thus, the difference between EERPA-GVB and the ERPA-GVB interaction energy given in Eq. (12) amounts to a different approach to the correlation energy for a dimer, which for EERPA is given by Eqs. (13)–(24). It should be stressed that in the limit when a distance between monomers tends to infinity the EERPA and the ERPA correlation energy for a dimer become equivalent and the interaction energy tends to inter-monomer correlation energy \(E^{AB}_{\mathrm{corr}}\), which in turn reduces to the second-order dispersion energy [39], i.e.,

$$\begin{aligned} E_{{\mathrm{EERPA}}{\text{-}}{\mathrm{GVB}}}^\mathrm{Int}(R_{AB}\rightarrow \infty )=E_{\mathrm{ERPA-GVB}}^{Int}(R_{AB} \rightarrow \infty )=E^{AB}_{\mathrm{corr}}=E_{\mathrm{disp}}^{(2)}(AB) , \end{aligned}$$
(26)

where \(E^{AB}_{\mathrm{corr}}\) is the inter-monomer correlation term as defined in the EERPA approach, cf. Eq. (13).

2 Weakly bounded complexes in- and out-of-equilibrium geometry in the EERPA-GVB picture

2.1 Computational details

To highlight the properties of the ERPA-GVB and EERPA-GVB approaches, we carried out calculations of interaction energies for a number of weakly interacting dimers bound by hydrogen bonds, such as \(\hbox {NH}_{3}{\cdots }\hbox {H}_{2}\hbox {O}\), hydrogen sulfide and water dimers, and for van der Waals (vdW) complexes where dispersion energy is the driving force, i.e., in \(\hbox {He}{\cdots }\hbox {Ne}\), acetylene and ethene dimers. All systems are described by the aug-cc-pVDZ basis set [42]. To judge the accuracy of those results, we computed CCSD(T) energies as implemented in the DALTON software package [43] in the same basis set. We also performed SAPT2+3(CCD) (hereafter referred to as SAPT) computations [44] using Psi4 software [45].

In addition, we performed an analysis of the basis set dependence (in basis sets aug-cc-\(\hbox {pV}\zeta \hbox {Z}\), where \(\zeta =2,\dots ,6\)) of ERPA-GVB and EERPA-GVB methods using the example of helium dimer.

We have also focused on dimers involving molecules in out-of-equilibrium geometries, i.e., ethene dimer with one of the monomers twisted, ethene–fluorine complex with F–F bond stretched and compressed, and the same complex with ethene molecule twisted. Those computations were also performed in aug-cc-pVDZ basis set.

Interaction energies computed with supermolecular methods were corrected for the basis set superposition error (BSSE) using the Boys’ counterpoise correction [46]. GVB computations were performed in a developer version of DALTON software package [43]. ERPA and EERPA corrections were computed in our in-house code interfaced with DALTON. Core orbitals were correlated. The only orbitals included in the “active” set as described in Ref. [30] were those involved in twisting or stretching of the bonds. The equilibrium geometries of studied complexes were taken from NIB database developed by Truhlar et al. [47].

2.2 Results and discussion

The intuitive understanding of what embedding in the EERPA method does is that it counteracts the counterpoise correction, since the correlation energy for a dimer, Eq. (13), includes embedded-monomer correlation terms, cf. Eq. (19), which are obtained by allowing excitations from one monomer to weakly occupied orbitals on another monomer. One could then wonder whether—if the basis set used is sufficiently large—the counterpoised corrected ERPA and EERPA methods would produce the same results. This is, however, not the case, since the correlation effects included in EERPA are missed in ERPA and this is not related to the basis set size. This conclusion can be illustrated by the example of helium dimer (see Fig. 1) where ERPA-GVB and EERPA-GVB interaction energies nearly parallel each other up to the aug-cc-pV6Z basis set. Notice also that EERPA-GVB curve remains close but above the benchmark MC-ACPF one for all basis sets. Although it is not guaranteed to be the case for all systems, such behavior is a sign of dependable performance of the method.

Fig. 1
figure 1

\(\hbox {He}_{2}\) interaction energy at \(R_{\mathrm {He-He}}=5.6\,{\mathrm {a.u.}}\) computed in aug-cc-\(\hbox {pV}\zeta \hbox {Z}\) basis set. The reference MR-ACPF energies were taken from [48]

Full size image

Already in [22], we have shown that EERPA-GVB describes accurately the dispersion-dominated systems. Here, we reaffirm this statement, adding that for this type of systems EERPA-GVB tends to be on par or even more accurate than SAPT [11, 44] computations (see Table 1). Interestingly, in terms of SAPT energy decomposition scheme, GVB interaction energies are almost exactly the sum of what SAPT identifies as electrostatic, exchange and induction components. While this is a rather intuitive result, it has not been previously demonstrated, since the perfect-pairing strongly orthogonal GVB method is not, as a rule, used for describing non-covalent interactions. The task of the EERPA correction should be therefore to add the dispersion component as well as mixed terms such as exchange–dispersion, exchange–induction and the exchange–induction–dispersion. The latter three play no significant role in the interaction of systems presented in Table 1, but as we shall see later, this is not always the case.

Table 1 Interaction energies of dispersion-dominated systems in kcal/mol computed in aug-cc-pVDZ basis set
Full size table

It is impressive that even in the challenging case of helium–neon interaction, which is purely dispersion-driven, the EERPA-GVB curve stays on top of the CCSD(T) one (see Fig. 2) when even the SAPT energies follows the MP2 curve. The ERPA-GVB minimum is even more shallow than the MP2 one and the GVB method, as expected, does not produce a minimum at all.

Fig. 2
figure 2

\(\hbox {He}{\cdots }\hbox {Ne}\) interaction energy curves computed in aug-cc-pVDZ basis set

Full size image

All three systems presented in Table 1 are single reference and weakly interacting so this is not surprising that both MP2 and SAPT describe them reasonably well. However, EERPA-GVB is clearly the best performer here, not just in the vdW minimum, but also along the entire curves (see Figs. 2 and 3). The ERPA-GVB method underbinds the complexes, while MP2 and SAPT slightly overestimate the interaction energies.

Fig. 3
figure 3

\(\hbox {C}_2\hbox {H}_2\) dimer interaction energy curves computed in aug-cc-pVDZ basis set

Full size image

For hydrogen-bonded systems, EERPA-GVB is less accurate than for van der Waals complexes although it stays superior to the ERPA-GVB, and (obviously) GVB methods. Below we present a set of three hydrogen-bonded systems: water and hydrogen sulfide dimer and water–ammonia complex (see Table 2). For each of them, the electrostatic component is a significant part of the interaction, so already the GVB method reproduces part of the binding. As it has been observed for dispersion-bound complexes, GVB interaction energies stay close to the sums of the electrostatic, exchange and induction components in a SAPT computation. The absolute error of the interaction energies produced by EERPA-GVB is at most \(0.6\,{\mathrm {kcal/mol}}\), but this may amount to as much as \(15\%\) of the binding. What is the reason for this (relative with respect to dispersion-bound systems) inaccuracy? In the first three examples, the exchange–dispersion component of the energy was very small (less than \(8\%\)) compared to the dispersion component. For the considered hydrogen-bonded systems, the exchange–dispersion is between 10 and \(20\%\) of the dispersion energy. The exchange–dispersion component is always positive and can be interpreted as the change in the exchange interaction introduced by the monomer correlation [49]. While the GVB wavefunction itself is antisymmetric, there is no additional antisymmetry-related constraint put on the correlation energy expression. The two-body ERPA correlation component \(E^{AB}_{\mathrm{corr}}\) converges to dispersion energy for well-separated monomers, cf. Eq. (26). From those observations, one can conjecture that the inaccuracies are related to exchange–dispersion component, which is not properly accounted for by EERPA. Indeed, for the \(\hbox {NH}_3{\cdots }\hbox {H}_2\hbox {O}\) complex (see inset in Fig. 5), one can see that in the region of no density overlap the \(E_{AB}^{\mathrm{corr}}\) correlation curve follows the sum of SAPT pure dispersion terms rather than the sum of all terms containing dispersion (dispersion, exchange–dispersion, induction–dispersion and exchange–induction–dispersion).

Table 2 Interaction energies of hydrogen-bonded systems in kcal/mol computed in aug-cc-pVDZ basis set
Full size table

Regardless of this observation, as evident from Figs. 4 and 5, EERPA-GVB is a reliable method for description of hydrogen-bonded systems. In particular in case of \(\hbox {H}_2\hbox {S}\) dimer, it yields a very similar curve as SAPT (see Fig. 4). The shapes of all the curves are correct, and the minima are only slightly too deep.

Fig. 4
figure 4

\(\hbox {H}_2\hbox {S}\) dimer interaction energy curves computed in aug-cc-pVDZ basis set

Full size image
Fig. 5
figure 5

\(\hbox {NH}_3 {\cdots }\hbox {H}_2\hbox {O}\) complex interaction energy curve computed in aug-cc-pVDZ basis set. On the inset, the EERPA correlation is plotted against the sum of SAPT pure dispersion terms and the sum of SAPT pure dispersion and mixed (dispersion–exchange, exchange–dispersion and exchange–dispersion–induction)

Full size image

The true advantage of EERPA-GVB lies however elsewhere, i.e., in its ability to accurately describe the interactions of systems out-of-equilibrium geometry when bonds are stretched or broken and one (or both) of the monomers requires multireference description. This ability gives one a nearly unique opportunity to elucidate the effects of the non-covalent interactions on systems attempting chemical reactions.

Let us look again at the ethylene dimer in \(\hbox {D}_{2d}\) symmetry. We have established that EERPA-GVB describes this system accurately and that the GVB method is responsible for the description of the electrostatic, exchange and induction component of the interaction. Let us now twist the C-C bond in one of the monomers to \(\theta =90^{\circ }\) (see Fig. 6). Clearly, in the attraction region the GVB method produces essentially the same results for both geometries—no binding, which means that the total attraction here is related to the dispersion interaction (including the mixed terms). The binding energy of the twisted complex is more than \(40\%\) smaller than in the flat dimer. While one often intuitively understands dispersion as a “bulk” interaction between electron clouds, not discriminating between different types of bonds, this is not a full picture: according to a frozen-orbital SAPT analysis by Cao and Wong [50], the main contributors to dispersion in the \(\hbox {D}_\mathrm{2d}\) ethylene dimer are \(\sigma {-}\pi\) bond pairs and dihydrogen contacts (where contacts are understood as significant interactions between electron pairs). The reduced attraction can be partly attributed to the geometry change: one of the \(\sigma {-}\sigma\) “contacts” disappears, but most of the reduction has to be attributed to the destruction of C=C \(\pi\) bond. This observation is in agreement with the view of \(\pi\) electrons having larger polarizabilities than \(\sigma\) ones and therefore contributing more to the dispersion interaction [51].

Fig. 6
figure 6

Ethylene dimer interaction energy curves computed in aug-cc-pVDZ basis set

Full size image

A particularly useful feature of EERPA-GVB is its ability to decompose the correlation energy into contributions from pairs of interacting geminals, which are localized on different monomers . This is possible since the inter-monomer correlation energy given in Eq. (23) and used in EERPA is a sum of inter-geminal terms involving orbitals p, q, r, s of which at least one is assigned to one of a geminal \(I_A\) localized on the monomer A and at least one is assigned to a geminal localized on B, \(I_B\)

$$\begin{aligned} pqrs \in I_A \cup I_B \cup V \end{aligned}$$
(27)

where V indicates a set of unoccupied orbitals. Therefore, contribution to inter-monomer correlation energy from a pair of geminals, one localized on A and the other on B can be extracted from \(E^{AB}_{\mathrm{corr}}\) by selecting only terms with indices pertaining to Eq. (27). By excluding terms corresponding to a \(\pi\)-bond-geminal interacting with lone-pair geminals localized on the fluorine atom \(\hbox {F}_1\), closer to the ethylene molecule, one can check how much the \(\pi\)-bond–lone pairs (LP) interaction contributes to the total binding energy of the charge-transfer complex of ethylene and fluorine and how this changes upon the twisting of ethylene molecule. In Fig. 7, we can see that for flat ethylene the \(\pi\)–LP interaction constitutes about \(40\%\) of the total binding. This observation does not hold for twisted ethylene, where the binding energy is small and the role of the corresponding interaction (LP-p orbitals on ethylene) is minor. Hypothesis about the special character of \(\pi\)-bonds in non-covalent interactions is here again reaffirmed.

Fig. 7
figure 7

Ethylene–fluorine complex EERPA-GVB interaction energy curves computed in aug-cc-pVDZ basis set

Full size image

Studying such systems as the complex of fluorine molecule and twisted ethylene brings insight into the interactions of electrons forming different types of bonds, but what is more important, the interactions of molecules out-of-equilibrium geometry have very practical consequences. Namely, they facilitate (or obstruct) chemical reactions. Only recently it has finally been confirmed experimentally that by selective vibration excitation one can accelerate certain chemical reactions [52]  Such an acceleration due to throwing one of the reactants out of equilibrium can be a geometry-related effect (e.g., more favorable relative position of fragments of reactants taking part in the reaction) but it can also be an electronic-structure effect related to a bond twist or stretch.

Take, e.g., the reaction of ethylene fluorination. As the simplest example of organic molecule fluorination, it is interesting both for theorists and experimentalists. Despite its simplicity, there is a large discrepancy between the experimentally and theoretically determined reaction barrier heights [53, 54]. The experimentally observed barrier is lower than those obtained by state-of-the-art theoretical approaches, and it was hypothesized that the thermal vibrations of \(\hbox {F}_2\) molecule may promote reaction [53].

We studied a T-shaped structure of the \(\hbox {C}_2\hbox {H}_4{\cdots }\hbox {F}_2\) complex at different intermolecular distances and \(\hbox {F}_2\) bond lengths (see Fig. 8). One can immediately see that as \(\hbox {F}_2\) bond is stretched, the vdW minimum deepens. A maximal attraction is achieved when the \(\hbox {F}_2\) bond is stretched to c.a. 4.80 a.u. and the distance between the monomers is only 3.20 a.u. While in real systems vibrations do not cause the bonds to be stretched this much, even close to the equilibrium along this stretching mode, the interaction energy grows significantly enough to have impact on the reaction barrier. Additionally, we see that the optimal intermolecular distance diminishes along this stretching mode. While those observations do not allow one to determine the height of the fluorination barrier energy, they do highlight the importance of accurate description of non-covalent interactions, while the molecules are attempting a reaction. Since even highly sophisticated coupled-cluster methods frequently fail at this task [22], it is unsurprising that the computed value of a reaction barrier may be inaccurate.

We have already observed a similar behavior (i.e., attraction growth accompanying a bond stretching) for other vdW complexes in Ref. [22], where we explained it by the increased polarizability of the electrons in the stretched bond region and an electron density buildup in the region between monomers. This causes a rise in both Pauli repulsion and dispersion interaction, which explains the existence of a minimum in the interaction energy along the \(\hbox {F}_2\) bond stretch mode.

Fig. 8
figure 8

Interaction energy map for the \(\hbox {C}_{2}\hbox {H}_{4}{\cdots }\hbox {F}_{2}\) complex. d indicates a distance between a center of mass of the ethylene molecule with the fixed geometry (\(R_\mathrm{CC}=2.53\) a.u., \(R_{\mathrm{CH}}=2.05\) a.u, \(\theta _{\mathrm{HCH}}=117^{\circ }\)) and the position of the F nucleus. \(R_{\mathrm{F-F}}\) denotes the varied bond length. \(R_{\mathrm{eq}}\) and \({d} _{\mathrm{eq}}\) correspond to the geometry of the lowest energy, whereas \(R_{\mathrm{min}}\) and \({d} _{\mathrm{min}}\) to that corresponding to the lowest interaction energy

Full size image

3 Conclusions

We have shown that the Embedding Extended Random Phase Approximation GVB method produces results on par with CCSD(T) for dispersion-dominated van der Waals complexes and is similar in accuracy to SAPT(CCD) when it comes to hydrogen-bonded systems. The method is particularly useful when it comes to non-covalently bonded complexes involving molecules out of their equilibrium geometries, as it is able to simultaneously capture both the energetic effects of bond stretching and twisting and more subtle van der Waals interactions.

To showcase this advantage, we have employed EERPA-GVB to study two unusual vdW systems, for which single-reference methods like MP2 break down. The first, a T-shaped ethylene dimer where one of the C=C bonds was twisted, was compared to its classic, flat counterpart, which highlighted the importance of the \(\pi\)–\(\sigma\) interaction and the particular role that \(\pi\) electrons play in dispersion interactions.

Role of \(\pi\) electrons was shown to be equally prominent in another studied system: a \(\hbox {C}_2\hbox {H}_4{\cdots }\hbox {F}_2\) complex. We have demonstrated the significance of a lone pairs–\(\pi\) interaction, by not only comparing the interaction energy for complexes of twisted and flat ethylene with fluorine, but also by decomposing the inter-monomer correlation energy expression into contributions from interactions between pairs of geminals. Such energy decomposition is also possible for any other system, and since geminals are usually localized on bonds and atoms, it is an excellent and intuitive interpretive tool. It could be employed, e.g., to investigate also \(\pi {-}\pi\), \(\pi {-}\sigma\) and other types of interactions.

Finally, we have shown that stretching the \(\hbox {F}_2\) bond in the same ethylene–fluorine complex causes a significant deepening of the vdW minimum, which is a result of a rise in the dispersion interaction. The enhanced attraction between the molecules may facilitate the ethylene fluorination reaction when the fluorine molecule is thermally excited to a stretching vibrational mode.

We conclude that EERPA-GVB is a useful tool to study molecular interaction qualitatively and quantitatively when bonds stretching, breaking or twisting is involved. This area is largely unexplored due to the lack of theoretical methods of both sufficient accuracy and modest computational cost. EERPA-GVB fills this gap in the computational chemistry toolbox.

Finally, it is worth mentioning that the concept of embedding a group of electrons of one monomer in a field created by electrons in another monomer, exploited in the EERPA correlation correction, can be applied to smaller localized entities, i.e., to geminals. Such an approach would extend the applicability of EERPA to any system and is under development in our group.