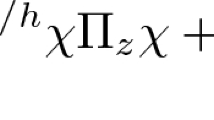Perturbation theory of quantum resonances

Abstract

We propose a contribution to the theory of quantum resonances that combines complex absorbing potentials (CAP) with standard perturbation theory. We start from resolvents that depend on two variables, the complex energy z and a perturbation parameter $\lambda$. The wave functions and the energies of the resonances are expanded in powers of $\lambda$. It is shown that the zero-order terms correspond to the standard CAP method and that higher-order corrections are significant. The introduction of a convergence operator allows to control the convergence of the perturbation series. Due to the discretization of the continuum, the series are generally asymptotic. Finally, we relate the perturbation series to numerically convenient Taylor series. The theory is illustrated on two model examples.

Appendix: Perturbative development of the resolvent

Let H be the Hamiltonian of a quantum system and ${\widehat{R}}$ the resolvent in the complementary space (see (5))

$$\begin{aligned} {\widehat{R}}=\frac{Q}{z-H}. \end{aligned}$$

(25)

It is useful to write ${\widehat{R}}$ in the form

$$\begin{aligned} {\widehat{R}}=\frac{1}{1-{\widehat{C}}}\,{\widehat{R}}^{(0)}. \end{aligned}$$

(26)

In this article, we chose

$$\begin{aligned} {\widehat{R}}^{(0)}=\frac{Q}{z-H(\lambda )};\quad {\widehat{C}}=\frac{Q}{z-H(\lambda )}\,\imath \,\lambda \,{\hat{\epsilon }};\quad H(\lambda )=H-\imath \,\lambda \,{\hat{\epsilon }}. \end{aligned}$$

(27)

$H(\lambda )$ is the complex (non-Hermitian) Hamiltonian of the complex absorbing method. $-\imath \,\lambda \,{\hat{\epsilon }}$ is a complex absorbing potential (CAP) which is introduced for computational reasons. It is a mathematical device that smooths the eigensolutions of H in the continuum when one uses finite basis sets. For investigating the quantum resonances through Green’s functions, one has to face the problem of the incompleteness of the basis sets for describing the continua. This is the main and crucial role devoted to ${\hat{\epsilon }}$. More precisely, ${\hat{\epsilon }}$ has to produce square-integrable functions tailored at convenience.

The expansion

$$\begin{aligned} \frac{1}{1-{\widehat{C}}}=1+{\widehat{C}}+{\widehat{C}}^{2}+\cdots \end{aligned}$$

(28)

introduced in (26) provides the perturbative expansion of ${\widehat{R}}$:

$$\begin{aligned} {\widehat{R}}={\widehat{R}}^{(0)}+{\widehat{R}}^{(1)}+{\widehat{R}}^{(2)}+\cdots ;\quad {\widehat{R}}^{(k)}={\widehat{C}}^k\,{\widehat{R}}^{(0)};\quad k=1,2,\ldots \end{aligned}$$

(29)

The first three terms of the expansion are

$$\begin{aligned} {\widehat{R}}^{(0)}(\lambda )& = \frac{Q}{z-H(\lambda )}\nonumber \\ {\widehat{R}}^{(1)}(\lambda )& = \frac{Q}{z-H(\lambda )}\,\imath \,\lambda \,{\hat{\epsilon }}\,\frac{Q}{z-H(\lambda )}\nonumber \\ {\widehat{R}}^{(2)}(\lambda )& = \frac{Q}{z-H(\lambda )}\,\imath \,\lambda \,{\hat{\epsilon }}\,\frac{Q}{z-H(\lambda )}\,\imath \,\lambda \,{\hat{\epsilon }} \frac{Q}{z-H(\lambda )}\nonumber \\ \cdots \end{aligned}$$

(30)

The above expansion is formally a standard perturbation series, but because $\lambda$ appears also in the denominator of ${\widehat{R}}^{(0)}(\lambda )$, the terms in (30) have the structure of Padé approximants. Nevertheless, in the following, we keep the usual vocabulary of perturbation theory. For practical applications, it is convenient to express the quantities ${\widehat{R}}^{(1)}$, ${\widehat{R}}^{(2)}$, ${\widehat{R}}^{(3)},\ldots$ in terms of the derivatives of ${\widehat{R}}^{(0)}$ with respect to $\lambda$:

$$\begin{aligned} {\widehat{R}}^{(k)}(\lambda )=(-1)^k\,\frac{\lambda ^k}{k!} \, \frac{{\mathrm {d}^{k}{\widehat{R}}^{(0)}(\lambda )}}{{\mathrm {d}\lambda ^k}};\qquad k=1,2,\ldots \end{aligned}$$

(31)

It can be checked that the expression (31) is true for $k=1$ and $k=2$. Its validity for any value of k is proved by recurrence:

The derivative of ${\widehat{R}}^{(k)}$ defined in (29) with respect to $\lambda$ gives

$$\begin{aligned} \lambda \frac{{\mathrm {d}^{}{\widehat{R}}^{(k)}}}{{\mathrm {d}\lambda }}=k \,{\widehat{C}}^{k-1}\, \lambda \frac{{\mathrm {d}^{}{\widehat{C}}}}{{\mathrm {d}\lambda }}\,+\, {\widehat{C}}^{k} \lambda \frac{{\mathrm {d}^{}{\widehat{R}}^{(0)}}}{{\mathrm {d}\lambda }}. \end{aligned}$$

(32)

It can be checked that the two expressions

$$\begin{aligned} \lambda \frac{{\mathrm {d}^{}{\widehat{R}}^{(0)}}}{{\mathrm {d}\lambda }}=-{\widehat{C}}\, {\widehat{R}}^{(0)}\qquad \mathrm{and} \qquad \lambda \frac{{\mathrm {d}^{}{\widehat{C}}}}{{\mathrm {d}\lambda }}={\widehat{C}} \,(1-{\widehat{C}}) \end{aligned}$$

(33)

are true. Introducing (33) in (32) leads to the recurrence relation

$$\begin{aligned} (k+1){\widehat{R}}^{(k+1)}=k\,{\widehat{R}}^{(k)} -\lambda \frac{{\mathrm {d}^{}{\widehat{R}}^{(k)}}}{{\mathrm {d}\lambda }}. \end{aligned}$$

(34)

Finally, introducing (31) in the right-hand side of (34) leads to

$$\begin{aligned} {\widehat{R}}^{(k+1)}=(-1)^{k+1} \frac{\lambda ^{k+1}}{(k+1)!}\,\frac{{\mathrm {d}^{k+1}{\widehat{R}}^{(0)}}}{{\mathrm {d}\lambda ^{k+1}}}. \end{aligned}$$

(35)

The comparison between (31) and (35) demonstrates that if (31) is true for k, it also holds for $k+1$. The recurrence is proven because  (31) is true for $k=1$.

Inside the main text of this article, we consider Green’s functions derived from the reduced resolvent. From (9), (29) provides the expansion of the self-energy

$$\begin{aligned} R(z,\lambda )=R^{(0)}(z,\lambda )\,+\, R^{(1)}(z,\lambda )\,+\,R^{(2)}(z,\lambda )\,+\,\cdots \end{aligned}$$

(36)

The zero-order term reads

$$\begin{aligned} R^{(0)}(z,\lambda )=\langle \phi |H{\widehat{R}}^{(0)} H |\phi \rangle \end{aligned}$$

(37)

and

$$\begin{aligned} R^{(k)}(z,\lambda )=(-1)^k\,\frac{\lambda ^k}{k!}\frac{{\mathrm {d}^{}R^{(0)}}}{{\mathrm {d}\lambda ^k}};\quad k=1,2,\ldots \end{aligned}$$

(38)

Note that if the expansion (36) is finite, R(z) becomes dependent on $\lambda$.