Abstract
We study the performance of some preconditioning techniques for a class of block three-by-three linear systems of equations arising from finite element discretizations of the coupled Stokes–Darcy flow problem. In particular, we investigate preconditioning techniques including block preconditioners, constraint preconditioners, and augmented Lagrangian-based ones. Spectral and field-of-value analyses are established for the exact versions of these preconditioners. The result of numerical experiments are reported to illustrate the performance of inexact variants of the various preconditioners used with flexible GMRES in the solution of a 3D test problem with large jumps in the permeability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The coupled Stokes–Darcy model describes the interaction between free flow and porous media flow. It is a fundamental problem in several fields [14]. In one subregion of the flow domain \(\Omega \) a free-flowing fluid is governed by the (Navier–)Stokes equations; in another subregion, the fluid follows Darcy’s Law. The equations are coupled by conditions across the interface between the two subregions. In this paper we will only consider the case of stationary problems and Stokes flow.
Let \(\Omega \) be a computational domain partitioned into two non-overlapping subdomains \(\Omega _1\) and \(\Omega _2\), separated by an interface \(\Gamma _{12}\). We assume that the flow in \(\Omega _1\) is governed by the stationary Stokes equations:
Here \(\nu >0\) represents the kinematic viscosity, \(\mathbf{u}_1\) and \(p_1\) denote the velocity and pressure in \(\Omega _1\), \(\mathbf{f}_1\) is an external force acting on the fluid, \(\mathbf{I}\) is the identity matrix, and
is the rate of strain tensor. We also assume that the boundary \(\Gamma _2 = \partial \Omega \cap \partial \Omega _2\) of the porous medium is partitioned into disjoint Neumann and Dirichlet parts \(\Gamma _{2N}\) and \(\Gamma _{2D}\), with \(\Gamma _{2D}\) having positive measure. The flow in \(\Omega _2\) is governed by Darcy’s Law:
Here \(p_2\) represents the Darcy pressure in \(\Omega _2\), and the symmetric positive definite (SPD) matrix \(\mathbf{K}\) represents the hydraulic conductivity in the porous medium. The Darcy velocity can be obtained from the pressure using
The coupling between the two flows comes from the following interface conditions on the internal boundary \(\Gamma _{12}\). Let \(\mathbf{n}_{12}\) and \(\mathbf{t}_{12}\) denote the unit normal vector directed from \(\Omega _1\) to \(\Omega _2\) and the unit tangent vector to the interface. Then we impose
The first two conditions enforce mass conservation and the balance of normal forces across the interface; the third condition represents the Beavers–Joseph–Saffman (BJS) law, in which G is an experimentally determined constant. Let
be the Stokes velocity and pressure spaces and let
be the Darcy pressure space. The weak formulation of the coupled Stokes–Darcy problem is:
find \(\mathbf{u}_1 \in \mathbf{X}\), \(p_1 \in Q_1\) and \(p_2\in Q_2\) such that
Here
where
Also,
and
The well-posedness of the weak formulation is a consequence of Brezzi-Fortin theory (see, e.g., [11]). The weak form is discretized using conforming finite elements spaces \(\mathbf{X}^h \subset \mathbf{X}\), \(Q_1^h \subset Q_1\) satisfying the inf-sup condition for the Stokes velocity and pressure, such as the MINI and Taylor–Hood elements. For the Darcy pressure a space of piecewise continuous polynomials \(Q_2^h \subset Q_2\) is used (linear in 2D, quadratic in 3D).
The discrete form of the weak formulation can be cast as a block linear system of the form
where \(A_{\Omega _2 }\), \(A_{\Omega _1}\), \(A_{\Gamma _{12} }\) are the matrices of the discrete bilinear forms and B is the discrete divergence. Under our assumptions \(A_{\Omega _2 }\) and \(A_{\Omega _1}\) are SPD and B has full row rank; we refer the reader to [12, 13] for further details.
We now introduce a slight change of notation and rewrite the previous linear system of equations in the following form:
where \(A_{11}\) and \(A_{22}\) are both SPD, \(A_{21}:=-A_{12}^T\) and B has full row rank. We observe in passing that this system is an example of a double saddle point problem, and that similarly structured systems arise in a number of applications, see [5]. In particular we note that using the following similarity transformation,
where
we can immediately conclude (under our assumptions) the invertibility of \({\mathcal {A}}\) from [5, Proposition 2.1].
The iterative solution of the discrete coupled Stokes–Darcy equations has attracted considerable attention in recent years. Here we limit ourselves to discussing solution algorithms based on preconditioned Krylov subspace methods. In [13], the following two constraint-type preconditioners were proposed for accelerating the convergence of Krylov subspace methods:
Also Cai et al. [12] proposed the following block triangular preconditioner,
where \(M_p\) is the mass matrix associated with the Stokes pressure space, and \(\rho > 0\) is a user-defined parameter. For 2D problems, the preconditioner \({{\mathcal {P}}_{co{n_T}}}\) outperforms the other preconditioners in terms of both iterations and CPU-time when used with GMRES. Exact variants of the preconditioners result in h-independent rates of convergence, as predicted by the theory. For 3D problems, only the inexact variants of these preconditioners are feasible. Of the inexact variants, \({\mathcal {P}}_{T_1,\rho }\) with suitable \(\rho \) requires the least CPU time, according to [13].
The constraint preconditioners and \({\mathcal {P}}_{T_1,\rho }\) are norm equivalent to \({\mathcal {A}}\) in (1) under certain conditions; see [12, 13]. On the other hand, the Field-of-Values (FOV) equivalence of constraint preconditioners with \({\mathcal {A}}\) was proved in [13]. It is well-known that if a preconditioner is norm equivalent to the coefficient matrix of a linear system of equations, the spectra of the preconditioned system remain uniformly bounded and bounded away from zero as the mesh size \(h\rightarrow 0\), see [23] for more details. Here, we directly determine some bounds for the eigenvalues of the preconditioned matrices associated with \({{\mathcal {P}}_{co{n_D}}}\), \({{\mathcal {P}}_{co{n_T}}}\) and \({\mathcal {P}}_{T_1,\rho }\). In particular, we show that the eigenvalues of the preconditioned matrix corresponding to \({{\mathcal {P}}_{co{n_T}}}\) are nicely clustered under certain conditions.
In the present work, we also consider the following block triangular preconditioner:
applied to the augmented linear system of equations \(\bar{{\mathcal {A}}}u={\bar{b}}\), where
and \({\bar{b}}=(b_1; b_2+rB^TQ^{-1}b_3; b_3)\), with Q being an arbitrary SPD matrix and \(r > 0\) a user-defined parameter. Evidently, the linear system of equations \(\bar{{\mathcal {A}}}x={\bar{b}}\) is equivalent to \({{\mathcal {A}}}u={b}\). This approach is motivated by the success of the use of grad-div stabilization and augmented Lagrangian techniques for solving saddle point problems.
The remainder of this paper is organized as follows. In Sect. 2 we derive lower and upper bounds for the eigenvalues of the preconditioned matrices corresponding to all of the above-mentioned preconditioners. In Sect. 3, we establish FOV-type bounds for the preconditioned system associated with the preconditioner of type (5). Some numerical experiments are reported in Sect. 4 to compare the performance of preconditioners, in particular in the presence of inexact solves. Brief conclusive remarks are given in Sect. 5.
Notations. We use “\(\mathrm {i}\)” for the imaginary unit. The notation \(\sigma (A)\) is used for the spectrum of a square matrix A. When all eigenvalues of A are real and positive, we use \(\lambda _{\min }(A)\) and \(\lambda _{\max }(A)\) to respectively represent the minimum and maximum eigenvalues of A. The notation \(\rho (A)\) stands for the spectral radius of A. When A is symmetric positive (semi)definite, we write \(A\succ 0\) (\(A\succcurlyeq 0\)). Furthermore, for two given matrices A and B, by \(A\succ B\) (\(A\succcurlyeq B\)) we mean \(A-B\succ 0\) (\(A-B\succcurlyeq 0\)). For \(H \succ 0\), the corresponding vector norm is given by
whose induced matrix norm is defined by
For given vectors x, y and z of dimensions n, m and p, (x; y; z) will denote a column vector of dimension \(n+m+p\).
2 Spectral analysis
This section is devoted to deriving lower and upper bounds for the eigenvalues of preconditioned matrices \({{\mathcal {P}}^{-1}_{co{n_T}}}{\mathcal {A}}\), \({{\mathcal {P}}^{-1}_{co{n_D}}}{\mathcal {A}}\), \({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}}\) and \({\mathcal {P}}_r^{-1}\bar{{\mathcal {A}}}\). To this end, first, we recall the following basic lemma which is an immediate consequence of Weyl’s Theorem, see [20, Theorem 4.3.1].
Lemma 2.1
Let A and B be two Hermitian matrices. Then,
The following two results provide information on the eigenvalues of the constraint-preconditioned matrices.
Theorem 2.2
Suppose that \({{\mathcal {P}}_{co{n_D}}}\) is defined by (3). The eigenvalues of \({{\mathcal {P}}^{-1}_{co{n_D}}}{\mathcal {A}}\) are either equal to unity, or complex numbers of the form \(1 \pm \mathrm {i} \sqrt{\xi } \), where
Proof
Let \(\lambda \in \sigma ({{\mathcal {P}}^{-1}_{co{n_D}}}{\mathcal {A}})\) with the corresponding eigenvector (x; y; z). Therefore, we have
Notice that \(\lambda =1\) is a possible eigenvalue of \({{\mathcal {P}}^{-1}_{co{n_D}}}{\mathcal {A}}\) with corresponding eigenvector (0; y; z) where \( y\in \text {Ker}(A_{12})\) and z is an arbitrary vector such that y and z are not both zero.
It is also immediate to observe that \(\lambda \ne 1\) implies \(y\ne 0\). Otherwise, in view of (7), we have \(x=0\) when \(y=0\). In this case, Eq. (8) results in \(B^Tz=0\), which is equivalent to \(z=0\) since \(B^T\) has full column rank. Hence, we get \((x;y;z)=(0;0;0)\), which is impossible since (x; y; z) is an eigenvector.
In the rest of proof, we assume that \(\lambda \ne 1\), which implies \(By=0\) by (9). Now, we can compute vector x from (7) as follows:
Multiplying both sides of Eq. (8) by \(y^*\) and recalling that \(A_{21}=-A_{12}^T\), we get
which is equivalent to
from which the assertion follows immediately. \(\square \)
Theorem 2.3
Let \({{\mathcal {P}}_{co{n_T}}}\) be defined by (3). Then
Proof
Let \(\lambda \) be an arbitrary eigenvalue of \({{\mathcal {P}}^{-1}_{co{n_T}}}{\mathcal {A}}\) with the corresponding eigenvector (x; y; z). Therefore, we have,
For \( y\in \text {Ker}(A_{12})\), we observe that \(1\in \sigma ( {{\mathcal {P}}^{-1}_{co{n_T}}}{\mathcal {A}})\) with the corresponding eigenvector (x; y; z) where x and z are arbitrary vectors with at least one of them nonzero when \(y=0\). In the rest of proof, we assume that \(\lambda \ne 1\). From (10), we obtain
Notice that from the fact that \(B^T\) has full column rank, similar to the proof of Theorem 2.2, one can conclude that \(y\ne 0\). In addition, Eq. (12) shows that \(By=0\) when \(\lambda \ne 1\). Now, we first substitute x from the above expression into (11) and then multiply both sides by \((\lambda -1)y^*\), which yields
Using \(A_{21}=-A_{12}^T\), we obtain the following quadratic equation:
where
The roots of (13) are given by \( \lambda _1= 1 \quad \text {and} \quad \lambda _2=1+{\hat{\gamma }}\). This shows that the eigenvalue \(\lambda \in \sigma ({{\mathcal {P}}^{-1}_{co{n_T}}}{\mathcal {A}})\), not being equal to one, can be written in the following form:
which completes the proof. \(\square \)
Remark 2.4
If \(A_{22} \succcurlyeq A_{12}^T A_{11}^{-1} A_{12}\), then from the proof Theorem 2.3 we can conclude that \(\lambda \in [1 , 2]\) for \(\lambda \in \sigma ({{\mathcal {P}}^{-1}_{co{n_T}}}{\mathcal {A}})\). Similarly, from the proof of Theorem 2.2, for \(\lambda \in \sigma ({{\mathcal {P}}^{-1}_{co{n_D}}}{\mathcal {A}})\), we can deduce that \(|\text {Im}(\lambda )| \le 1\) when \(A_{22} \succcurlyeq A_{12}^T A_{11}^{-1} A_{12}\).
We have been able to verify numerically that for linear systems of the form (1) arising from the finite element discretization of coupled Stokes–Darcy flow, the condition \(A_{22} \succ A_{12}^T A_{11}^{-1} A_{12}\) in the above remark is indeed satisfied. In fact, we observed that the condition \(A_{22} \succ A_{12}^T A_{11}^{-1} A_{12}+{\sigma } B^TM^{-1}_pB\) (with \(0 < {\sigma } \le 2\)) holds true for problems of small or moderate size, and numerical tests suggest that it may hold for larger problems as well.
We now turn to the spectral analysis of the block triangular preconditioner \({\mathcal {P}}_{T_1,\rho }\). Based on numerical experiments, Cai et al. [12] pointed out that the performance of \({\mathcal {P}}_{T_1,\rho }\) is not very sensitive to the scaling factor \(\rho \), particularly when it belongs to interval [0.6, 1.05]; see [12, Table 2]. Moreover, it is numerically observed that the spectrum \({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}}\) lies in a semi-annulus which does not include zero and is entirely contained in the right half-plane; see [12, Figure 2]. In what follows, we show that the experimentally observed eigenvalue distribution of \({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}}\) can be theoretically proven for certain values of \(\rho \). To do so, first, we recall a theorem established by Kakeya [21] in 1912.
Theorem 2.5
If \(p(z) = \sum \nolimits _{j = 0}^n {{a_j}{z^j}}\) is a polynomial of degree n with real and positive coefficients, then all the zeros of p lie in the annulus \(R_1\le |z|\le R_2\) where \(R_1=\mathop {\min }\limits _{0\le j \le n-1}a_j/a_{j+1}\) and \(R_2=\mathop {\max }\limits _{0\le j \le n-1}a_j/a_{j+1}\).
Notice that if a monotonicity assumption holds for the coefficients of the polynomial p in the above theorem, i.e., \(0\le a_0 \le a_1 \le \cdots \le a_n\), then all zeros of p are strictly less than unity in modulus. The latter results is the well-known Eneström–Kakeya Theorem [1].
Proposition 2.6
Consider the preconditioned matrix \({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}}\) where \({\mathcal {P}}_{T_1,\rho }\) is defined by (4), with \(\rho >0\). If \(A_{22} \succ A_{12}^T A_{11}^{-1} A_{12}+\rho ^{-1} B^TM^{-1}_pB\) and \(\lambda \in \sigma ({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}})\), then either \(\lambda =1\), or \(\xi \le |\lambda -1 | \le 1 \) and \(|\lambda | > \tau \), for some positive constants \( \xi <1\) and \(\tau \).
Proof
Let \(\lambda \) be an arbitrary eigenvalue of \({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}}\) with the corresponding eigenvector (x; y; z). As a result, we have
Note that \(1 \in \sigma ({\mathcal {P}}^{-1}_{T_1,\rho }{\mathcal {A}})\) with the corresponding eigenvector (0; y; 0) for \(0 \ne y \in \text {Ker} (A_{12}) \). From now on, we assume that \(\lambda \ne 1\). From (15) and (17), we obtain \(x=(\lambda -1)^{-1} A_{11}^{-1}A_{12}y\) and \(z=\rho ^{-1}\lambda ^{-1}(\lambda -1) M_p^{-1} By\), respectively. Notice that y is nonzero, otherwise x and z are both zero which is in contradiction with the fact that (x; y; z) is an eigenvector. In the sequel, without loss of generality, we assume that \(y^*y=1\). Noting that \(A_{21}=-A^T_{12}\), we substitute x and z in (16) which yields
where,
Multiplying both sides of the preceding relation by \(\lambda (1-\lambda )\), we derive
For simplicity, we set \(t=\lambda -1\) and rewrite the previous relation as follows:
It is easy to check that that if \(\lambda \ne 1\), then \(y\in \mathrm{Ker}(B)\cap \mathrm{Ker}(A_{12})\) implies that y is a zero vector, which is impossible. As a result, p and r cannot be both zero. When \(p=0\), we readily obtain
Notice that if \(r=0\) then either \( t= \pm \mathrm {i} \frac{p}{q} \) or \(t+1= 0\). Since \(\lambda \ne 0\), in this case, we only conclude that \(\lambda =1 \pm \mathrm {i} \frac{p}{q}\) and \(\varphi _1< \frac{p}{q} <1\) with
Next, we assume \(r,p\ne 0\) (i.e., \(y \notin \mathrm{Ker}(B)\cup \mathrm{Ker}(A_{12})\)) and rewrite (18) as follows:
By the assumption \( q > r + p\), hence
Therefore, from Theorem 2.5, we conclude that \(\xi \le |t|= |\lambda -1 | \le 1 \) by setting \(\xi =\min \{\varphi _1,\varphi _2\}\) where
keeping in mind that \(\frac{p}{q} \le \frac{p}{q-r}\). Now, from Eq. (18), we observe that
where \( \tau = \mathop {\min }\limits _{} \left\{ {\left. {\xi ^2}{\rho ^{ - 1}}y^*{B^T}M_p^{ - 1}By \right| y \notin \mathrm{Ker}(B)} \right\} >0. \) \(\square \)
Theorem 2.7
Suppose that \({\mathcal {P}}_r\) and \(\bar{{\mathcal {A}}}\) are respectively defined by (5) and (6). The eigenvalues of \({\mathcal {P}}^{-1}_r\bar{{\mathcal {A}}}\) are all real and positive. More precisely, we have
where
with
Proof
For ease of notation, we set \({\bar{A}}_{22}=A_{22}+rB^TQ^{-1}B\). Let \(\lambda \in \sigma ({\mathcal {P}}_r^{-1}\bar{{\mathcal {A}}})\) be an arbitrary eigenvalue with the corresponding eigenvector (x; y; z). Therefore, we have
Notice that for \( y\notin \text {Ker} (B)\), we have that \(\lambda =1\) is an eigenvalue of \({\mathcal {P}}_r^{-1} {\mathcal {A}}\) with the corresponding eigenvector \((0;y;-rQ^{-1}By)\). Also, \(\lambda =1\) is obviously an eigenvalue of \({\mathcal {P}}_r^{-1} {\mathcal {A}}\) associated with eigenvector (0; y; 0) when \(0\ne y\in \text {Ker} (B)\).
In the rest of proof, we assume that \(\lambda \ne 1\). From Eqs. (19) and (21), we respectively derive
The preceding two relations for x and z make it clear that y cannot be the zero vector. Without loss of generality, we may assume that \(\Vert y\Vert _2=1\).
If \( 0 \ne y\in \text {Ker} (B)\), we deduce that \(z=0\). It follows that
recalling that \(A_{21}=-A_{12}^T\). Now, we discuss the case that \( y\notin \text {Ker} (B)\). Substituting vectors x and z into (20) and performing straightforward computations, we obtain
Multiplying both sides of the above relation by \(-\lambda \), we obtain the following quadratic equation:
where
Evidently, \(\gamma =1+{\tilde{\gamma }}+\eta \) with
Observing that \(\gamma ^2-4\eta \ge (1+\eta )^2-4\eta \ge 0\), we have that all of the eigenvalues of \({\mathcal {P}}_r^{-1}\bar{{\mathcal {A}}}\) are real. Moreover, if \(\lambda _1\) and \(\lambda _2\) are the roots of (22) then
Hence, recalling that \({\bar{A}}_{22}=A_{22}+rB^TQ^{-1}B\), we easily obtain
as \(r \rightarrow \infty \), i.e., all eigenvalues satisfying (22) tend to 1 for \(r \rightarrow \infty \). From (22), we have
It is not difficult to verify that
Consequently, in view of the facts that \(\lambda _{\min } (B^TQ^{-1}B)=0\), \(\eta \le 1\) and \(0< \zeta \le \eta \) for \( y\notin \text {Ker} (B)\), we conclude that
Evidently, since \(\eta \le 1\), we have
which completes the proof. \(\square \)
Remark 2.8
Notice that when \(A_{22} \succcurlyeq A_{12}^T A_{11}^{-1} A_{12}\), then from the proof of Theorem 2.7, we obtain that \(\sigma ({\mathcal {P}}_r^{-1}\bar{{\mathcal {A}}})\) lies in the interval [1, 2] in the limit as \(r \rightarrow \infty \). Moreover, “most” of the eigenvalues of the preconditioned matrix are either equal to 1, or tend to 1 as \(r\rightarrow \infty \).
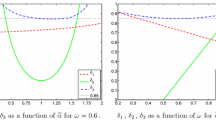
The eigenvalue distribution in Theorem 2.7 and Remark 2.8 is illustrated in Fig. 1. A full description of the test problem and of its finite element discretization can be found in Sect. 4.
3 Field-of-values analysis
In the previous section, we established eigenvalue bounds for the preconditioned matrices. A clustered spectrum (away from 0) often results in rapid convergence, particularly when the preconditioned matrix is close to normal; see [6] for more details. However, the situation is more complicated when the problem is far from normal. Indeed, the eigenvalues may not describe the convergence of nonsymmetric matrix iterations like GMRES; see [19]. The notions of norm equivalence and of field-of-values equivalence often provide the theoretical framework needed to establish optimality of a class of preconditioners for Krylov methods like GMRES [2, 4, 9, 15, 16, 22, 23]; see also [7] for a recent overview.
Here we derive FOV-type bounds for the preconditioned matrix associated with preconditioner \({\mathcal {P}}_r\). For the constraint preconditioners \({{\mathcal {P}}_{co{n_D}}}\) and \({{\mathcal {P}}_{co{n_T}}}\), this equivalence has been established by Chidyagwai et al. [13].
3.1 Basic concepts
In this subsection we briefly overview the required background for establishing FOV-type bounds, see [13, 23] for more details.
We begin by reviewing the notion of spectral equivalence for families of SPD matrices [3]. Recall that two families of SPD matrices \(\{A_n\}\) and \(\{B_n\}\) (parametrized by their dimension n) are said to be spectrally equivalent if there exist n-independent constants \(\alpha \) and \(\beta \) with
Equivalently, \(\{A_n\}\) and \(\{B_n\}\) are spectrally equivalent if the spectral condition number \(\kappa (B_n^{-1}A_n)\) is uniformly bounded with respect to n. Yet another equivalent condition is that the generalized Rayleigh quotients associated with \(A_n\) and \(B_n\) are uniformly bounded:
Note that this is an equivalence relation between families of matrices.
Next, we recall the concepts of H-norm-equivalence and H-field-of-value-equivalence, where H corresponds to a given SPD matrix. For simplicity, in the following we drop the subscript n but it should always be kept in mind that matrices representing discretizations always depend on the dimension n (which in turn depends on the mesh size h). Similarly, with a slight abuse of language we will talk of equivalence of matrices rather than of families of matrices.
Definition 3.1
Two nonsingular matrices \(M,N\in {\mathbb {R}}^{n\times n}\) are H-norm-equivalent, \(M{ \sim _H}N\), if there exist positive constants \(\alpha _0\) and \(\beta _0\) independent of n such that the following holds for all nonzero \(x\in {\mathbb {R}}^n\):
Equivalently, \(M{ \sim _H}N\) is equivalent to
Definition 3.2
Let H be an \(n\times n\) symmetric positive definite matrix and let \(A\in {\mathbb {R}}^{n\times n}\). The H-field of values of A is the set
Definition 3.3
Two nonsingular matrices \(M,N\in {\mathbb {R}}^{n\times n}\) are H-field-of-values-equivalent, \(M{ \approx _H}N\), if there exist positive constants \(\alpha _0\) and \(\beta _0\) independent of n such that the following holds for all nonzero \(x\in {\mathbb {R}}^n\):
This definition implies that if \(M{ \approx _H}N\), the H-field of values of \(MN^{-1}\) lies in the right half-plane and is both bounded and bounded away from 0 uniformly in n.
Remark 3.4
If M and N are symmetric positive definite and \(H=I_n\), then \(M{ \approx _H}N\) reduces to spectral equivalence.
Proposition 3.5
Let M and N be two symmetric nonsingular matrices such that \(M{ \approx _H}N\) where H is a given symmetric positive definite matrix. Then \(M^{-1}{ \approx _{H^{-1}}}N^{-1}\).
Proof
The result follows from some algebraic computations. Note that M and N are both symmetric and relations (24) hold for some constant \(\alpha _0\) and \(\beta _0\).
Let v be an arbitrary nonzero vector. Setting \(y=H^{-1}v\), we have
Now setting \(y=MN^{-1}z\) in the above relation, we find that
To complete the proof, we need to show that there exists \({\hat{\beta }}_0\) such that
For an arbitrary nonzero vector v, we have that
Consequently, setting \(v=N^{-1}My\), we derive
Now, we set \(y=Hx\) which together with the above relation implies that
Defining \({{\hat{\beta }}}_0=\alpha _0^{-1}\), we obtain
which completes the proof. \(\square \)
Remark 3.6
With a similar argument used in the proof of the above proposition, one can verify that \(M{ \approx _H}N\) implies \(N{ \approx _H}M\) for any symmetric nonsingular matrices M, N and symmetric positive definite matrix H with appropriate dimensions.
We also recall the following useful definitions and properties.
Definition 3.7
Let \(M\in {\mathbb {R}}^{m\times n}\) and let \(H_1\in {\mathbb {R}}^{n\times n}\), \(H_2\in {\mathbb {R}}^{m\times m}\) be two symmetric positive definite matrices, then
Note that when \(H_1=H_2=H\) and \(m=n\), the above definition reduces to the following standard matrix norm,
Also, it can be seen that
It can be shown that when \(H_1=H_2=H\), from the above relation, we have
We further observe that
where \(H_3\) is a given arbitrary SPD matrix of the appropriate size.
Henceforth we assume that the matrix \({\mathcal {A}}\in {\mathbb {R}}^{n\times n}\) satisfies the following stability conditions [12, 13]:
where \(c_1\) and \(c_2\) are positive constants independent of n, and the matrix H is SPD. For the coupled Stokes–Darcy problem H is a block diagonal matrix with diagonal blocks \(H_1\in {\mathbb {R}}^{n_1\times n_1}\) and \(H_2\in {\mathbb {R}}^{n_2\times n_2} \) (with \(n_1 + n_2 = n\)) given by
where \(M_p\) denotes the mass matrix for the Stokes pressure space; see [13] for more details.
Similar to [13], we also need the following results from [23] which can be obtained making use of the stability conditions (25).
Lemma 3.8
Let (25) hold, then \(H\sim _{H^{-1}} {\mathcal {A}}\) and \(H^{-1}\sim _{H} {\mathcal {A}}^{-1}\), and in particular
Lemma 3.9
Let (25) hold and assume that \({\mathcal {P}}\sim _{H^{-1}} H\), then
Lemma 3.10
Let (25) hold, then \(\Vert {A}\Vert _{H_1,H_1^{-1}} \le c_1\), \(\Vert C\Vert _{H_1,H_2^{-1}} \le c_1\), where \(C=\left[ 0~B\right] \) and
Lemma 3.11
Let (25) hold. If there exists \(c_3\) independent of \(n_1\) such that
then \(S=CA^{-1}C^T\) satisfies \(S\sim _{H_2^{-1}} H_2\) and \(H_2^{-1} \sim _{H_2} S^{-1}\), where C and A are defined as in Lemma 3.10. Hence, there exists \(c_4\) independent of \(n_1\) such that \(\Vert S^{-1}\Vert _{H_2^{-1},H_2}\le c_4\) .
Lemma 3.12
[13, Lemma 3.8] \(\Vert M\Vert _{H_1,H_2^{-1}}=\Vert M^T\Vert _{H_2,H_1^{-1}}\)
3.2 FOV-type bounds
The following proposition is established in [17] for symmetric matrices. In [18, Poposition 2.1], it is pointed out that the result remains true for nonsymmetric matrices as well.
Proposition 3.13
Suppose that A is a general \(n\times n\) matrix, C is full row rank \(p\times n\) matrix \((p\le n)\), and W is a \(p\times p\) matrix. Define,
If \({\mathcal {K}}:={\mathcal {K}}(0)\) is nonsingular, then \({\mathcal {K}}(W)\) is a nonsingular matrix for any nonzero W and
Let us consider the following partitioning for \(\bar{{\mathcal {A}}}\) and write the matrix in the form of (28),
As a result, from Proposition 3.13, we have
The above discussion allows one to find sufficient conditions which ensure that stability conditions similar to (25) hold for \(\bar{{\mathcal {A}}}\). In particular, it turns out that stability conditions for \(\bar{{\mathcal {A}}}\) can be deduced from (25) by suitable choices of Q including the case that \(Q=M_p\). To this end, we recall the following observation, which is a consequence of [23, Lemma 2.1] and Lemma 3.12.
Remark 3.14
Let the matrices H and \({\mathcal {A}}\) be defined as before. Then
In view of the above remark, we need to establish that \({\Vert \bar{{\mathcal {A}}}\Vert _{{H},H^{ - 1}}} \) and \({\Vert \bar{{\mathcal {A}}}^{-1}\Vert _{H^{ - 1},H}}\) are bounded from above in order to show that \(\bar{{\mathcal {A}}}\) satisfies stability conditions similar to (25). Notice that (25) together with (29) imply that
On the other hand, we have that
It is known that \(\Vert C^T\Vert _{H_2,H_1^{-1}} = \Vert C\Vert _{H_1,H_2^{-1}}\). Therefore, by Lemma 3.10, the following inequality holds when the first condition in (25) is satisfied:
From the above discussions, it can be observed that if we set \(Q=M_p\) then Eqs. (32) and (33) reduce to the following inequalities, respectively:
and
In order to deal with the augmented system, the following lemma provides a useful expression for the Schur complement. The lemma is an immediate consequence of Proposition 3.13, see [10, Lemma 4.1] for more details.
Lemma 3.15
Let \(A\in {\mathbb {R}}^{n\times n}\) and \(B\in {\mathbb {R}}^{m\times n}\) \((m \le n)\). Let \(\gamma \in {\mathbb {R}}\), and suppose that A, \(A+\gamma B^TW^{-1}B\), \(BA^{-1}B^T\), and \(B(A+\gamma B^TW^{-1}B)^{-1}B^T\) are all nonsingular matrices. Then
We denote the negative Schur complement associated with \(\bar{{\mathcal {A}}}\) by \({\bar{S}}\). By the above lemma, it is immediate to see that
Hence, we have
Assuming that the assumption of Lemma 3.11 holds, we readily obtain
For simplicity we set \({\bar{A}}=A+rC^TQ^{-1}C\), \(S_A=A_{22}-A_{21}A_{11}^{-1}A_{12}\), and \(S_{{{\bar{A}}}}=S_A+rB^TQ^{-1}B\). It is well known (see, e.g., [8, page 18]) that
in which \(A_{21}=-A_{12}^T\). Straightforward computations show that
Hence, considering the singularity of \(S_A^{ - 1/2}{B^T}{Q^{ - 1}}BS_A^{ - 1/2}\), one can conclude that
Let \(H_1\) be defined by (26). Under the assumptions of Lemma 3.11, we now show that
for some \({\bar{c}}_3\). The assumption (27) is equivalent to \({\left\| {A^{ - 1}} \right\| _{H_{1}^{ - 1},{H_{1}}}}\le c_3^{-1}\); see [23, Lemma 2.1]. In order to show that \({\left\| {{{\bar{A}}}^{ - 1}} \right\| _{H_{1}^{ - 1},{H_{1}}}}\) is bounded from above by a constant, we need to show that the norm of each four blocks of \(H_{1}^{1/2} {{{\bar{A}}}^{ - 1}} H_{1}^{1/2}\) is bounded from above. To this end, we first note that
hence \({\left\| {S_{{{\bar{A}}}}^{ - 1}} \right\| _{A_{22}^{ - 1},{A_{22}}}}<1\) from (36). By Lemma 3.10 we have \(\Vert {A}\Vert _{H_1,H_1^{-1}} \le c_1\). On the other hand, we have that \(\Vert {A}\Vert ^2_{H_1,H_1^{-1}}=1+\Vert {A}_{21}\Vert ^2_{A_{11},A_{22}^{-1}}\) as \(A_{21}=-A_{12}^T\) and \(H_1\) is a block diagonal matrix with blocks \(A_{11}\) and \(A_{22}\). This ensures that \(\Vert {A}_{21}\Vert _{A_{11},A_{22}^{-1}}=\Vert {A}_{12}\Vert _{A_{22},A_{11}^{-1}} \le c_1\). For the (1, 1) block of \({\bar{A}}^{-1}\), we get
Now, Eq. (36) implies that
It is not difficult to verify that
Therefore, the above relation together with the fact that \({\left\| {S_{{\bar{A}}}^{ - 1}} \right\| _{A_{22}^{ - 1},{A_{22}}}} <1\) and inequality (37) show that \({\left\| {{{\bar{A}}}^{ - 1}} \right\| _{H_{1}^{ - 1},{H_{1}}}}\le {\bar{c}}_3^{-1}\) for some constant \({{\bar{c}}}_3\), i.e., \({{\bar{c}}}_3^{-1}=1+(1+c_1)^2\). Let us assume that there exists a constant \({\bar{\eta }}\) such that
Then, by virtue of the above observation, Eqs. (32), (33) and (35), we can find constants \({\bar{c}}_1\), \({\bar{c}}_2\) and \({\bar{c}}_4\) such that
and \( {\left\| {\bar{S}}^{-1} \right\| _{{H}_2^{-1},H_2}} \le {\bar{c}}_4 \) provided the stability conditions (25) hold for \({\mathcal {A}}\). As pointed earlier, if \(Q=M_p\) then \(\lambda _{\max } (M_pQ^{-1})=1\) and we get \({{\bar{\eta }}}=r\). In practice, the matrix \(M_p\) can be efficiently approximated by its main diagonal. Therefore, we suggest choosing Q as the main diagonal of \(M_p\) in numerical experiments. In the sequel, we assume that Q is chosen such that there exits an \({{\bar{\eta }}}\) for which (38) holds. Consequently, similar to Lemma 3.11, the following lemma can be stated.
Lemma 3.16
Let the assumptions of Lemma 3.11 hold and suppose there exists \({{\bar{\eta }}} > 0 \) such that (38) is satisfied independent of n. Then \({{\bar{S}}}\sim _{H_2^{-1}} H_2\) and \(H_2^{-1} \sim _{H_2} {{\bar{S}}}^{-1}.\) Hence, there exists \({{\bar{c}}}_4\) independent of n such that \(\Vert {{\bar{S}}}^{-1}\Vert _{H_2^{-1},H_2}\le {{\bar{c}}}_4\), where \({{\bar{S}}}=C{{\bar{A}}}^{-1}C^T.\)
Consider again the matrix \(\bar{ {\mathcal {A}}}\) in the following form:
We note that for \(r=0\), \({{\bar{A}}}= A\) and \(\bar{ {\mathcal {A}}}\) reduces to
The constraint preconditioners can be written in the following form
and it is shown that \({{\mathcal {P}}_{con}} \) is H-norm equivalent (and consequently H-f.o.v equivalent) to the operator \({\mathcal {A}}\) where
with \(H_1\) and \(H_2\) being symmetric positive definite given by (26) under suitable conditions, see [13].
Now consider the following preconditioner:
where Q is symmetric positive definite and \(r>0\) is given. Here, we comment that Q can be taken to be any SPD matrix such that (38) holds for a constant \({{\bar{\eta }}} > 0 \).
For simplicity, we rewrite \({\mathcal {P}}_{r}\) as follows:
with the obvious definition of \({{\bar{P}}}\). Now we establish a proposition which will be useful in proving norm-equivalence of the preconditioner \({\mathcal {P}}_{r}\) to \(\bar{{\mathcal {A}}}\). To this end, we first need to recall the following well known fact.
Theorem 3.17
[20, Theorem 7.7.3] Let A and B be two \(n\times n\) real symmetric matrices such that A is positive definite and B is positive semidefinite. Then \(A \succcurlyeq B\) if and only if \(\rho (A^{-1}B) \le 1,\) and \(A\succ B\) if and only if \(\rho (A^{-1}B) < 1\).
Proposition 3.18
Under the assumptions of Lemma 3.16, if
then there there exists \({\bar{c}}_4\) independent of n such that \(\Vert r Q^{-1}\Vert _{H_2^{-1},H_2}\le {{\bar{c}}}_4\) where \({{\bar{S}}}=C{{\bar{A}}}^{-1}C^T.\)
Proof
First note that Theorem 3.17 implies
Since \(H_2\) is a symmetric positive definite matrix, we have \(H_2^{-1/2}({{\bar{S}}}-\frac{1}{r} Q) H_2^{-1/2} \preccurlyeq 0\). As a result, for any nonzero unit vector x, we have
which is equivalent to
Lemma 3.16 ensures that there exists \({{\bar{c}}}_4\) such that \({\left\| {{\bar{S}}}^{ - 1} \right\| _{H_2^{-1},H_2}} \le {{\bar{c}}}_4\). Hence, from the preceding relation, we deduce that
for any nonzero vector x with \(\Vert x\Vert _2=1\). \(\square \)
Proposition 3.19
Let the stability conditions (25) and the assumptions of Proposition 3.18 hold. Suppose that \(H_1\) and \({\bar{P}}\) are defined as in (26) and (41), respectively. If \( P\sim _{H_1^{-1}} H_1\) then \({{\bar{P}}}\sim _{H_1^{-1}} H_1\), where P is obtained from \({{\bar{P}}}\) by setting \(r=0\).
Proof
By the assumptions, there exist \(\alpha _0\) and \(\beta _0\) such that
It is obvious that
Consequently, we have
Now from Lemma 3.10 and Proposition 3.18, we find that for \({{\bar{\beta }}}_0=\beta _0+c_1^2{{\bar{c}}}_4\), we have
Note that
and
where \({{\bar{A}}} _{22}= A _{22}+rB^TQ^{-1}B\). Since \(\left\| A_{22}^{1/2}{{\bar{A}}} _{22}^{ - 1}A_{22}^{1/2} \right\| _2 = 1\), we have that
Recalling that \(\Vert {A}_{21}\Vert _{A_{11},A_{22}^{-1}}=\Vert {A}_{12}\Vert _{A_{22},A_{11}^{-1}} \le c_1\), from the preceding inequality we deduce that \({\left\| {H_1^{}{{{{\bar{P}}} }^{ - 1}}} \right\| _{H_1^{ - 1}}}\le {{\bar{\alpha }}}_0^{-1}\) for \({{\bar{\alpha }}}_0^{-1}=2+c_1^2\), which completes the proof. \(\square \)
The proof of the next theorem follows from a similar argument used in [13, Theorem 3.9], where \( P_{con}\sim _{H_1^{-1}} H_1\) was an assumption. In view of the previous proposition, the assumption \({{\bar{P}}}\sim _{H_1^{-1}} H_1\) in the theorem is a consequence of the fact that \( P\sim _{H_1^{-1}} H_1\), where P is the block upper triangular part of A. On the other hand, the matrix \(P_{con}\) in the constraint preconditioners \({{\mathcal {P}}}_{co{n_D}}\) and \({{\mathcal {P}}}_{co{n_T}}\) is, respectively, the block diagonal and block lower triangular part of A. However, considering Eq. (26), one can see that if \( P_{con}\) and P are the block lower or the block upper triangular part of A, then \( P_{con}\sim _{H_1^{-1}} H_1\) and \( P\sim _{H_1^{-1}} H_1\) can be deduced from \(\Vert {A}_{21}\Vert _{A_{11},A_{22}^{-1}}=\Vert {A}_{12}\Vert _{A_{22},A_{11}^{-1}} \le c_1\). More precisely, it turns out that
and
We comment that if \(P_{con}\) is the block diagonal part of A, then
Therefore, in the analysis of [13, Section 3], there is no need to require that \(P_{con}\sim _{H_1^{-1}} H_1\) for establishing FOV bounds (independent of the mesh-width) when the preconditioner is applied “exactly”, i.e., when direct methods are used for the block solves.
Theorem 3.20
Let H and \({\mathcal {P}}_r\) be defined as in (40) and (41), respectively. In addition to the hypotheses of Proposition 3.18, assume that \(r>0\) is such that
If \({{{\bar{P}}}} \sim _{H_1^{-1}} H_1\), then \({\mathcal {P}}_r \sim _{H^{-1}} \bar{{\mathcal {A}}}\) and \({{\mathcal {P}}}_r^{-1} \sim _H \bar{ {\mathcal {A}}}^{-1}\).
Proof
When the stability conditions (39) hold, considering Lemma 3.9, we only need to show that \({\mathcal {P}}_r \sim _{H^{-1}} H\). To this end we need to derive upper bounds (independent of n) for \(\Vert {\mathcal {P}}_r H^{-1}\Vert _{H^{-1}} = \Vert H^{-1/2} {\mathcal {P}}_r H^{-1/2} \Vert _2\) and \(\Vert H {\mathcal {P}}_r^{-1}\Vert _{H^{-1}} = \Vert H^{1/2} {\mathcal {P}}_r^{-1} H^{1/2}\Vert _2\). The assumption \({{\bar{P}}}\sim _{H_1^{-1}} H_1\) implies that there exist positive constants \( \alpha _1\) and \(\beta _1\) such that \(\Vert {{\bar{P}}}H_1^{-1}\Vert _{H_1^{-1}} \le \beta _1\) and \(\Vert H_1{{\bar{P}}}^{-1}\Vert _{H_1^{-1}} \le \alpha _1^{-1}\). Evidently, we have
Notice that from (44), we get
By Lemmas 3.10 and 3.12 , we have
Furthermore, we have
Consequently, we have
From the assumption, \(\Vert H_1{{\bar{P}}}^{-1}\Vert _{H_1^{-1}} = \Vert H_1^{1/2}{{{\bar{P}}}^{ - 1}}H_1^{1/2}\Vert _2\le \alpha _1^{-1}\). In addition, Proposition 3.18 ensures that \(\left\| {r {Q^{ - 1}}} \right\| _{H_2^{ - 1},H_2^{}}=\Vert r H_2^{1/2}{Q^{ - 1}}H_2^{1/2}\Vert _2 \le {{\bar{c}}}_4\). Observing that
we obtain
Therefore, it is immediate to see that
which completes the proof. \(\square \)
Remark 3.21
By Theorem 3.17, assumption (44) is equivalent to setting the following lower bound for r:
Noting that
we deduce that the condition (44) holds for \(r \ge {\lambda _{\max } (Q)}/{\lambda _{\min } (H_2)}\).
We are now in a position to establish the main result of this section.
Theorem 3.22
Let \(\bar{{\mathcal {A}}}\), \({\mathcal {P}}_r\) be defined as before. In addition to the hypotheses of Proposition 3.18, suppose that the condition (44) is satisfied and there exists a constant \(\nu >0\) such that for any nonzero \(y\in {\mathbb {R}}^{n_2}\) the following inequality holds:
where \({\tilde{S}}_r=C{\bar{P}}^{-1}C^T=C(P+rC^TQ^{-1}C)^{-1}C^T\). If \(r>1 \) and \({{\bar{A}}}\approx _{H^{-1}_1}{\bar{P}}\), then there exists \(\rho _0 > 0\) such that \(\bar{{\mathcal {A}}}\approx _{H^{-1}} {\mathcal {P}}_r\) for all \(r \ge \rho _0\) provided
Proof
The assumption \({{\bar{A}}}\approx _{H^{-1}_1}{{\bar{P}}}\) implies \({{\bar{A}}}\sim _{H_1^{-1}}{{\bar{P}}}\). On the other hand, we have \({{\bar{A}}}\sim _{H_1^{-1}} H_1\) in view of stability conditions (39). As a result, we can deduce that \({{\bar{P}}}\sim _{H_1^{-1}} H_1\). Therefore, by the previous theorem, \(\Vert \bar{{\mathcal {A}}}{\mathcal {P}}^{-1}_r\Vert _{H^{-1}}\) is bounded from above.
Let \(x=(x_1;x_2)\) be given. To complete the proof, in the sequel, we show that there exists a positive constant \(\tau \) such that
Next, observe that
From \({{\bar{A}}}\approx _{H_1^{-1}} {{\bar{P}}}\) we know that there exists a positive constat \(\alpha _0\) such that
By some simple computations, we have
By making use of \(\left\| {{{\bar{A}}}{{{\bar{P}}}^{ - 1}} - I} \right\| _{H_1^{ - 1}} \le r^{-1}\), it can be observed that
The fact that \({{\bar{P}}}\sim _{H_1^{-1}} H_1\) ensures the existence of a positive constant \(\alpha _1\) such that
Hence, we obtain
Evidently, by the assumption (45), we have
From Eqs. (46)–(50), we derive the following bound
Since \(r > 1\), we have
where \(\gamma = {c_1}({{{\bar{c}}}_4} + \alpha _1^{ - 1})\). If we set
then it holds that
for \(r \ge \rho _0\). Hence,
therefore we can take \(\tau = \frac{\alpha _0}{2}\) and the proof is complete. \(\square \)
Remark 3.23
The assumption that \(r>1\) in the inequality \(\Vert {{\bar{A}}}{{\bar{P}}}^{-1} -I\Vert _{H^{-1}_1} \le r^{-1} \) can be relaxed if we assume that there exists a constant \(c_5\) such that \(\Vert Q^{-1}\Vert _{H_2^{-1},H_2}\le c_5\). Then, there is no need to set the assumption \(r\ge 1\) in the statement of Theorem 3.22. Indeed, in view of Eq. (47), Eq. (48) can be replaced by
since \(r\left\| {{{\bar{A}}}{{{\bar{P}}}^{ - 1}} - I} \right\| _{H_1^{ - 1}} \le 1\). Thus, in the proof of previous theorem \(\rho _0\) can be taken to be
with \(\gamma = {c_1}({c_5} + \alpha _1^{ - 1})\), while the rest of the proof remains unchanged after removing the restriction \(r \ge 1\).
For the sake of generality, we add the following remark showing that the above result can be stated under weaker conditions.
Remark 3.24
In Proposition 3.18, the assumption (42) was used to deduce that \(\Vert rQ^{-1}\Vert _{H_2^{-1},H_2}\) is bounded above by a constant. On the other hand, the condition (44) ensures that
Following the preceding discussion, the assumption (44) can be relaxed by setting the condition that
is bounded above by a constant. Now, in view of the following equality
one can relax the assumptions (42) and (44). To this end, we need to choose r and Q such that \( \frac{1}{r}Q\sim _{H_2^{-1}} H_2. \)
We have checked numerically that for linear systems of the form (1) arising from the finite element discretization of coupled Stokes–Darcy flow, the condition \(\lambda _{\max } (A_{22}^{-1}A_{12}^T A_{11}^{-1} A_{12}) \le 0.5\) holds true for problems of small or moderate size. As seen in Theorem 3.22, it is assumed that \({{\bar{A}}}\approx _{H^{-1}}{{\bar{P}}}\). Note that for \(r=0\) this condition reduces to \(A\approx _{H^{-1}_1} P\) which is similar to the assumption in [13, Theorem 3.10]. The following proposition establishes sufficient conditions under which \({{\bar{A}}}\approx _{H^{-1}_1} {{\bar{P}}}\).
Proposition 3.25
Let \({\bar{A}}\) and \({\bar{P}}\) be defined by
where \(A_{21}=-A_{12}^T\) and \(H_1\) is given by (26). If the stability conditions (39) hold, then there exists \(\beta _0 >0\) such that
Furthermore, assume that \(A_{22} \succcurlyeq A_{12}^T A_{11}^{-1} A_{12}\) and \(\lambda _M:=\lambda _{\max }(A_{22}^{ - 1}A_{12}^TA_{11}^{ - 1}{A_{12}}) \le 3/4\). If the following relation holds:
then \({{\bar{A}}} { \approx _{H_1^{-1}}}{{\bar{P}}}\).
Proof
It is straightforward to check that
having in mind that \(A_{12}^T=-A_{21}\). Moreover, we have that
where we made use of
\(\left\| A_{22}^{1/2}{{\bar{A}}} _{22}^{ - 1}A_{22}^{1/2} \right\| _2 = 1\) and \(\Vert {A}_{12}^T\Vert _{A_{11},A_{22}^{-1}}=\Vert {A}_{12}\Vert _{A_{22},A_{11}^{-1}} \le c_1\).
To prove the assertion, we need to show that there exists \(\alpha _0\) such that
To this end, we first show that the assumption (51) guarantees that the matrix \({\mathcal {F}}=\frac{1}{2}I+A_{22}^{-1/2}\hat{S}{\bar{A}}_{22}^{-1}A_{22}^{1/2}\) (where we set \( \hat{S}:=A_{12}^TA_{11}^{-1}A_{12}\) for notational simplicity) is positive semi-definite, in the sense that the quadratic form \(\langle {\mathcal {F}}z, z\rangle \) is nonnegative for any real vector z. We comment that \({\mathcal {F}}\) is symmetric positive definite for \(r=0\) since in this case \({\bar{A}}_{22}=A_{22}\).
By the Sherman-Morrison-Woodbury matrix identity we have
hence we can write
where E is a symmetric positive semi-definite matrix given by
Next, we observe that the nonzero eigenvalues of E are the same as those of the matrix
and that the spectrum of \(\tilde{E}\) is given by
Notice that the function \(g_r(x)=\frac{rx}{1+rx}\) is monotonically increasing for \(x,r>0\). Hence, we have
Let z be an arbitrary real vector, then, using the above relation, we have
as claimed. Considering (52), we can rewrite \({H_1^{-1/2}}{{{\bar{A}}}{{{\bar{P}}}^{ - 1}}} {H_1^{1/2}}\) as follows:
By assumption, we have
Now let \(x=(x_1;x_2)\) be an arbitrary nonzero vector and \(w=H_1^{-1/2} x\) (with block partitioning \(w=(w_1;w_2)\)). Using the Cauchy–Schwarz inequality and some straightforward computations, we obtain
Setting \(\alpha _0=\frac{1}{4}\), the proof is complete.
\(\square \)
We end this section with the following comments on assumption (45) in Theorem 3.22.
Remark 3.26
Assume that \(\tilde{S}_0\approx _{H^{-1}_2} Q\), where \({\tilde{S}}_0=C{P}^{-1}C^T=BA_{22}^{-1}B^T\). As a result of Remark 3.6, there exists a constant \({{\tilde{\gamma }}} \) (independent of n) such that \(\nonumber \left\| {Q{\tilde{S}}_0^{ - 1}} \right\| _{H_2^{ - 1}}^{} \le {{\tilde{\gamma }}}\). The assumption \(\tilde{S}_0\approx _{H^{-1}_2} Q\) implies that there exists \(\nu _0>0\) such that
for any nonzero vector y. Next, we show that we can find \(\nu >0\) such that (45) holds for \(r< \nu _0^{-1}\). Note that using Lemma 3.15, we obtain
Let y be an arbitrary nonzero vector and set \(y=Q{\tilde{S}}_r^{-1}w\). Now, using a similar argument to the one in [9, Page 781], we get
where \(t={\frac{{{{\left\langle {w,w} \right\rangle }_{H_2^{ - 1}}}}}{{\left\| {Q{\tilde{S}}_0^{ - 1}w} \right\| _{H_2^{ - 1}}^2}}}\) and \(k={\frac{{{{\left\langle {w,Q{\tilde{S}}_0^{ - 1}w} \right\rangle }_{H_2^{ - 1}}}}}{{\left\| {Q{\tilde{S}}_0^{ - 1}w} \right\| _{H_2^{ - 1}}^2}}}\). Notice that setting \(z=Q{\tilde{S}}_0^{-1}w\), using the assumption (53), we have
Let \(f(x)=\frac{{\nu _0 + rx}}{{2(1 + {r^2}x)}}\). The function f(x) is monotonically increasing for \(0< r < \nu _0^{-1}\). Using the fact that \(t\ge {\tilde{\gamma }}^{-2}\), it follows that
where \(\nu = \frac{{\nu _0 + r{\tilde{\gamma }}^{-2}}}{{2(1 + {r^2}{\tilde{\gamma }}^{-2})}}\). Finally, we observe that in [23, Theorem 3.8], for the case \(r=0\), it is assumed that \(Q^{-1}\approx _{H^{}_2} \tilde{S}_0^{-1}\). Here we point out that Proposition 3.5 shows that \(\tilde{S}_0\approx _{H^{-1}_2} Q\) is a consequence of \(\tilde{S}_0^{-1}\approx _{H^{}_2} Q^{-1}\) (which is equivalent to \(Q^{-1}\approx _{H^{}_2} \tilde{S}_0^{-1}\) by Remark 3.6).
4 Numerical experiments
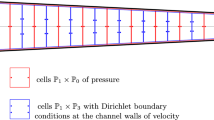
In practice, all the preconditioners considered so far must be applied inexactly, especially when solving 3D problems. Whether the mesh-independent behavior is retained or not by the inexact variants is not clear a priori; as we will see, the choice of inexact solver may impact some preconditioners more than others. In this section we illustrate the performance of inexact variants of the block preconditioners using a test problem, taken from [13, Subsection 5.3], which corresponds to a 3D coupled flow problem in a cube \(\Omega =\Omega _1 \cup \Omega _2\) with \(\Omega _1=[0,2]\times [0,2] \times [1,2] \) and \(\Omega _2=[0,2]\times [0,2] \times [0,1]\). The porous medium \(\Omega _2\) contains an embedded impermeable cube \([0.75,1.25]\times [0.75,1.25]\times [0, 0.50]\). The hydraulic conductivities of the porous medium and embedded impermeable enclosure are \(\kappa _1 \mathbf{I}\) an \({\kappa }_2 \mathbf{I}\), respectively, with \(\kappa _1 = 1\) and \(\kappa _2 = 10^{-10}\). The kinematic viscosity is set to \(\nu = 1.0\). On the horizontal part of \(\Gamma _1=\partial \Omega _1 \cap \partial \Omega \) we prescribe \(\mathbf{u}_1 = (0,0,-1)^T\) at \(z=2\) and the no-slip condition on the lateral sides of \(\Gamma _1\). We prescribe homogeneous Dirichlet boundary conditions on \(\Gamma _2=\partial \Omega \cap \partial \Omega _2\) (\(z=0\)) and homogeneous Neumann conditions on the rest of the boundary of the porous medium. The large jump in the hydraulic conductivity in the porous medium region makes this problem challenging.
We report the performances of several preconditioner variants in conjunction with FGMRES [24]. The initial guess is taken to be the zero vector and the iterations are stopped once \(\Vert {\mathcal {A}}u_k-b\Vert _2{\le 10^{-7}} \Vert b\Vert _2\) (or \(\Vert \bar{{\mathcal {A}}}u_k-{\bar{b}}\Vert _2{\le 10^{-7}} \Vert {\bar{b}}\Vert _2\) for the augmented Lagrangian variants) where \(u_k\) is the obtained k-th approximate solution. In addition, we have used right-hand sides corresponding to random solution vectors and averaged results over 10 test runs. At each iteration of FGMRES, we need to solve at least two SPD linear systems as subtasks. To this end we applied two different approaches, discussed in the following two subsections.
All computations were carried out on a computer with an Intel Core i7-10750H CPU @ 2.60GHz processor and 16.0GB RAM using MATLAB.R2020b.
4.1 Implementation based on IC-CG
First we present the results of experiments in which, inside FGMRES, the SPD subsystems were solved inexactly by the preconditioned conjugate gradient (PCG) method using loose tolerances. More precisely, the inner PCG solver for linear systems with coefficient matrix \(A_{11}\) (\(A_{22}\) and \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\)) was terminated when the relative residual norm was below \(10^{-1}\) (respectively, \(10^{-2}\)) or when the maximum number of 5 (respectively, 25) iterations was reached. In the implementation of the preconditiner \({\mathcal {P}}_{T_1,\rho }\), the inverse of \(M_p\) was applied inexactly using PCG with a relative residual tolerance of \(10^{-2}\) and a maximum number of 20 iterations. The preconditioner for PCG are incomplete Cholesky factorizations constructed using the MATLAB function “ichol(., opts)” where opts.type =’ict’ with drop tolerances between \(10^{-4}\) and \(10^{-2}\). The FGMRES iteration count is reported in the tables under “Iter”. Under “Iter\(_{{pcg}_i}\)” (“Iter\(_{{cg}_i}\)”) we further report the total number of inner PCG (or CG) iterations performed for solving the linear systems corresponding to block (i, i) of the preconditioner, where \(i=1,2\). For more details, in the “Appendix” we summarize the implementation of preconditioners \({{\mathcal {P}}^{}_{co{n_D}}}\), \({{\mathcal {P}}^{}_{co{n_T}}}\) and \({\mathcal {P}}^{}_{T_1,\rho }\) in Algorithms 1-3.
For the linear system corresponding to \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\), we distinguish between two approaches:
-
Approach I. The matrix \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\) is not formed explicitly and the CG method is used without preconditioning with a relative residual tolerance of \(10^{-3}\) and a maximum allowed number of 25 iterations.
-
Approach II. The matrix \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\) is formed explicitly, and PCG with incomplete Cholesky preconditionign was used. We note that while we could successfully compute the “ichol” factor without diagonal shifts for the two smallest problem sizes, adding the shift 0.01 was found to be necessary for larger sizes. We further note that with this approach we can use larger values of r, leading to faster FGMRES convergence.
In Tables 1 and 2 , we report the performance \({\mathcal {P}}_{r}\) for Approaches I and II. From the results presented, we can see that even when implemented inexactly, the augmented Lagrangian-based preconditioner \({{\mathcal {P}}}_r\) results in convergence rates of FGMRES that are essentially mesh-independent, as predicted by our theoretical analysis. As for the number of inner PCG iterations, we observe some differences in the results obtained with Approaches I and II. In the case of Approach I we see an increase in the total number of inner PCG iterations as the mesh is refined, reflecting the known fact that the CG method, with or without incomplete Cholesky preconditioning, is not mesh-independent in general. With Approach II this increase is not observed, however, the total timings are much higher and still scale superlinearly with the number of degrees of freedom. This is due to the fact that explicitly forming the augmented matrix \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\) and computing its incomplete Cholesky factorization leads to a considerably less sparse matrix and superlinear growth in the fill-in in the incomplete factors, and thus to more expensive PCG iterations. We conclude that with \({\mathcal {P}}_{r}\), Approach I is to be preferred to Approach II.
In Table 3, we report the results corresponding to the constraint preconditioners. Our numerical tests illustrate that in the inexact implementation of these preconditioners using IC-CG for the inner SPD linear solves, the outer iteration counts grow each time the mesh size is halved. Hence, the mesh-independence of the outer FGMRES iteration is lost when the preconditioner is applied inexactly using incomplete Cholesky as the preconditioner for the inner PCG iterations. We add that in our implementation of these preconditioners, we approximated \(BA_{22}^{-1}B^T\) by \(M_p\) and solved the corresponding linear system using PCG with a maximum number of 25 iterations and relative residual tolerance tolerance \(10^{-2}\) and with incomplete Cholesky preconditioning where “opts.droptol” was set to \(10^{-2}\). We also tried approximating \(BA_{22}^{-1}B^T\) by the diagonal of \(M_p\) but the results were generally worse and we do not report them here.
Next, we consider inexact variants of the following block triangular preconditioners,
and
In Tables 4 and 5 , we present results for \(\rho = 0.6\). In [12], it was experimentally observed that the performance of \({\mathcal {P}}_{T_1,\rho }\) is not sensitive to \(\rho \) when \(\rho \in [0.6,1.05]\). However, based on our experimental results, we found the optimum value \(\rho =0.6\). For more details, we report the results for two different cases (referred as Cases I and II) in Tables 4 and 5 by setting “opts.droptol” to be \(10^{-4}\) and \(10^{-2}\), respectively. Similar to \({\mathcal {P}}_{r}\), in Table 4, it is seen that for \({\mathcal {P}}_{T_1,0.6}\), the outer iteration count for FGMRES remains essentially constant as the grid is refined, in agreement with our analysis for the exact case. Although the results in Table 5 indicate a better performance of the preconditioner for the first three problem sizes, the number of outer iterations increases drastically for the largest problem size.
From these results we see that replacing the inexact solves involving the mass matrix \(M_p\) with a simple diagonal scaling involving the diagonal of \(M_p\) leads to a degradation of the rate of convergence. We found that in terms of CPU time, this degradation more than offsets the savings obtained by using simple diagonal scalings in place of solves of linear systems involving \(M_p\).
Overall, when the subsystems associated with the block preconditioners are solved using (P)CG with incomplete Cholesky factorization, the fastest solution times are achieved with the inexact variant of the augmented Lagrangian preconditionr \({\mathcal {P}}_r\) using what we called “Approach I”. For the largest size problems, this approach is about 3.3 times faster, in terms of CPU time, than the block triangular preconditioner from [12], which is in turn far more efficient than the inexact variants of the constraint preconditioners. Furthermore, the construction cost of the incomplete Cholesky factorizations used with these preconditioners is negligible. The CPU time scaling of all these methods with respect to the mesh size is, however, superlinear in the number of unknowns due to the use of IC preconditioning in conjunction with the CG method to perform the inner iterations.
4.2 Implementation based on ARMS preconditioner
In an attempt to have better scalability of the number of inner iterations with respect to mesh refinements, as an alternative to using IC-CG, we performed some experiments with an algebraic multilevel solver for approximately solving the subsystems associated with the block preconditioners. We chose the MATLAB implementation of the ARMS preconditioner [25], which can be downloaded from https://www-users.cs.umn.edu/~saad/software/.
Since the ARMS preconditioner is not SPD, for inexact solves involving sub-blocks we use it with GMRES (with relative residual tolerance 0.1 and a maximum number of iterations equal to 20) in conjunction with ARMS. With this approach, all tested preconditioners (including constraint preconditioners) appear robust, displaying mesh-independent convergence of the outer FGMRES iteration, and faster convergence of the inner iterations. The obtained numerical results are shown in Tables 6 for the block triangular, constraint preconditioners, and the augmented Lagrangian-based preconditioner. To implement the preconditioner \({\mathcal {P}}_r\), the subsystem corresponding to sub-block (1, 1) is solved by GMRES in conjunction with the ARMS preconditioner. For the subsystem associated with \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\), forming the ARMS preconditioner is not practically feasible for the larger problem sizes. Therefore, the matrix \({{A_{22}} + r{B^T}{Q^{ - 1}}B}\) is not formed explicitly and the corresponding system is solved by the preconditioned GMRES where the ARMS preconditioner for \(A_{22}\) is used. As before, we report under “Iter” the number of (outer) FGMRES iterations. Under “Iter\(_i\)” we report the total number of inner iterations performed for solving the linear systems corresponding to block (i, i) of the preconditioner where \(i=1,2\). To obtain results in Table 6, PCG with tolerance \(10^{-2}\) and a maximum of 20 iterations was used for solving linear systems associated with \(M_p\). The corresponding total number of iterations are given under “Iter\(_{{M_p}}\)”.
Iteration times were also found to exhibit better (though not perfect) scalability than in the experiments described in the previous subsection. The construction costs for ARMS, however, appear to be prohibitive, at least in the MATLAB implementation, completely off-setting any gains in performance. In particular, for the largest problem sizes it takes hours to compute the ARMS preconditioners.
We can see from these experiments that for all preconditioners tested, both the number of outer FGMRES iterations and (for large enough problem sizes) the total number of inner preconditioned GMRES and CG iterations remain almost constant, with outer iteration counts even improving for smaller mesh sizes. As mentioned, however, this improved scaling behavior comes at the price of much higher preconditioner construction costs. The reported solution times show that in conjunction with ARMS, the augmented Lagrangian-based preconditioner \({\mathcal {P}}_r\) is both efficient and fairly robust with respect to the parameter r, and outperforms all other preconditioners for large enough problem sizes. However, it does not outperform the implementation of \({\mathcal {P}}_r\) based on IC-CG for the inner solves. Given the enormous set-up costs associated with ARMS, we conclude that its use does not bring about any actual advantage in terms of times to solution, at least when working in MATLAB.
In conclusion, the results of our experiments indicate that among all preconditioner variants we tested, the inexact variant of \({\mathcal {P}}_r\) with IC-CG inner solves (Approach I) is, by a large margin, the fastest solver in terms of total solution times.
5 Conclusions
In this paper we have provided a theoretical analysis of several types of block preconditioners for the discrete Stokes–Darcy problem. Both eigenvalue bounds and FOV-equivalence have been considered, completing the analyses given in [12] and in [13]. Our analysis extends previous results and explains the experimentally observed mesh-independence of the exact variants of the block preconditioner based on the augmented Lagrangian approach.
Numerical experiments show that inexact variants of these block preconditioners may or may not retain mesh-independence, depending on the solver used for the inexact solves. All preconditioners show near mesh-independence when a multilevel algebraic solver (ARMS) is used for the inexact solves, but this preconditionr is found to have exceedingly high construction costs. When cheaper inner solvers based on incomplete Cholesky-preconditioned CG are used, the fastest total solution times are achieved by the augmented Lagrangian-type preconditioner. It is possible, of course, that better results may be achieved with different multilevel solvers.
Future work should consider the development of similar preconditioners for the coupled Navier–Stokes–Darcy model.
References
Anderson, N., Saff, S.H., Varga, R.S.: On the Eneström-Kakeya theorem and its sharpness. Linear Algebra Appl. 28, 5–16 (1979)
Aulisa, E., Bornia, G., Howle, V., Ke, G.: Field-of-values analysis of preconditioned linearized Rayleigh-Bénard convection problems. J. Comput. Appl. Math. 369, art. 112582 (2020)
Axelsson, O., Barker, V.A.: Finite Element Solution of Boundary Value Problems: Theory and Computation, SIAM Classics in Applied Mathematics 35. Society for Industrial and Applied Mathematics, Philadelphia (2001)
Beckermann, B., Goreinov, S.A., Tyrtyshnikov, E.E.: Some remarks on the Elman estimate for GMRES. SIAM J. Matrix Anal. Appl. 27, 72–778 (2005)
Beik, F.P.A., Benzi, M.: Iterative methods for double saddle point systems. SIAM J. Matrix Anal. Appl. 39, 902–921 (2018)
Benzi, M.: Preconditioning techniques for large linear systems: a survey. J. Comput. Phys. 182, 418–477 (2002)
Benzi, M.: Some uses of the field of values in numerical analysis. Boll. Unione Matematica Italiana 14, 159–177 (2021)
Benzi, M., Golub, G.H., Liesen, J.: Numerical solution of saddle point problems. Acta Numer. 14, 1–137 (2005)
Benzi, M., Olshanskii, M.A.: Field-of-values convergence analysis of augmented Lagrangian preconditioners for the linearized Navier–Stokes problem. SIAM J. Numer. Anal. 49, 770–788 (2011)
Benzi, M., Olshanskii, M.A.: An augmented Lagrangian-based approach to the Oseen problem. SIAM J. Sci. Comput. 28, 2095–2113 (2006)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, Springer Series in Computational Mathematics vol. 44. Springer, Berlin (2013)
Cai, M., Mu, M., Xu, J.: Preconditioning techniques for a mixed Stokes/Darcy model in porous media applications. J. Comput. Appl. Math. 233, 346–355 (2009)
Chidyagwai, P., Ladenheim, S., Szyld, D.B.: Constraint preconditioning for the coupled Stokes–Darcy system. SIAM J. Sci. Comput. 38, A668–A690 (2016)
Discacciati, M., Quarteroni, A.: Navier–Stokes/Darcy coupling: modeling, analysis and numerical approximation. Rev. Mat. Complut. 22, 315–426 (2009)
Eisenstat, S.C., Elman, H.C., Schultz, M.H.: Variational iterative methods for nonsymmetric systems of linear equations. SIAM J. Numer. Anal. 20, 345–357 (1983)
Elman, H.C.: Iterative Methods for Sparse Nonsymmetric Systems of Linear Equations. Ph.D. Thesis, Yale University, Department of Computer Science (1982)
Fletcher, R.: An ideal penalty function for constrained optimization. In: Nonlinear Programming, 2, pp. 121–163. Academic Press, New York (1974)
Golub, G.H., Greif, C.: On solving block-structured indefinite linear systems. SIAM J. Sci. Comput. 24, 2076–2092 (2003)
Greenbaum, A., Pták, V., Strakoš, Z.: Any nonincreasing convergence curve is possible for GMRES. SIAM J. Matrix Anal. Appl. 17, 465–469 (1996)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1985)
Kakeya, S.: On the limits of roots of an algebraic equation with positive coefficient. Tôhoku Math. J. First Series 2, 140–142 (1912)
Klawonn, A., Starke, K.: Block preconditioners for nonsymmetric saddle point problems. Numer. Math. 81, 577–594 (1999)
Loghin, D., Wathen, A.J.: Analysis of preconditioners for saddle-point problems. SIAM J. Sci. Comput. 25, 2029–2049 (2004)
Saad, Y.: A flexible inner-outer preconditioned GMRES algorithm. SIAM J. Sci. Comput. 14, 461–469 (1993)
Saad, Y., Suchomel, B.: ARMS: an algebraic recursive multilevel solver for general sparse linear systems. Numer. Linear Algebra Appl. 9, 359–378 (2002)
Acknowledgements
The authors would like to thank Scott Ladenheim for providing the test problem. Thanks also to three anonymous referees for their careful reading of the manuscript and helpful suggestions.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
For the sake of clarity, we summarize the required steps for implementation of the constraint preconditioners and \({\mathcal {P}}^{}_{T_1,\rho }\) inside FGMRES in the following algorithms. We recall that in the numerical experiments the matrix \(BA_{22}^{-1}B^T\) was replaced by \(M_p\).



Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beik, F.P.A., Benzi, M. Preconditioning techniques for the coupled Stokes–Darcy problem: spectral and field-of-values analysis. Numer. Math. 150, 257–298 (2022). https://doi.org/10.1007/s00211-021-01267-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01267-8