Skip to main content
SpringerLink
Log in

New analysis and recovery technique of mixed FEMs for compressible miscible displacement in porous media

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

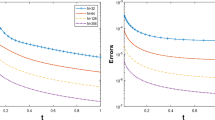
Numerical methods and analysis for compressible miscible flow in porous media have been investigated extensively in the last several decades. Amongst those methods, the lowest-order mixed method is the most popular one in practical applications. The method is based on the linear Lagrange approximation for the concentration and the lowest order (zero-order) Raviart–Thomas mixed approximation for the Darcy velocity/pressure. However, the existing error analysis only provides the first-order accuracy in \(L^2\)-norm for all three physical components in spatial direction, which was proved under certain extra restrictions on both time step and spatial meshes. The analysis is not optimal for the concentration mainly due to the strong coupling of the system and the drawback of the traditional approach which leads to serious pollution to the numerical concentration in analysis. The main task of this paper is to present a new analysis and establish the optimal error estimate of the commonly-used linearized lowest-order mixed FEM. In particular, the second-order accuracy for the concentration in spatial direction is proved unconditionally. Moreover, we propose a simple recovery technique to obtain a new numerical Darcy velocity/pressure of second-order accuracy by re-solving an elliptic pressure equation. Also we extend our analysis to a second-order time discrete scheme to obtain optimal error estimates in both spatial and temporal directions. Numerical results are provided to confirm our theoretical analysis and show the efficiency of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Arbogast, T., Juntumen, N., Pool, J., Wheeler, M.: A discontinuous Galerkin methods for two phase flow in a porous medium enforcing \(H(div)\) velocity and continuous capillary pressure. Comput. Geosci. 17, 1055–1078 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Amirat, Y., Moussaoui, M.: Analysis of a one-dimensional model for compressible miscible displacement in porous media. SIAM J. Math. Anal. 26, 659–674 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  3. Amirat, Y., Shelukhin, V.: Global weak solutions to equations of compressible miscible flows in porous media. SIAM J. Math. Anal. 38, 1825–1846 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bear, J., Bachmat, Y.: Introduction to Modeling of Transport Phenomena in Porous Media. Springer, New York (1990)

    Book  MATH  Google Scholar 

  5. Bahriawati, C., Carstensen, C.: Three Matlab implementations of the lowest-order Raviart–Thomas MFEM with a posteriori error control. Comput. Methods Appl. Math. 5, 333–361 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications. Springer, Heidelberg (2013)

    Book  MATH  Google Scholar 

  7. Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Springer, New York (2002)

    Book  MATH  Google Scholar 

  8. Cai, W., Wang, J., Wang, K.: Convergence analysis of Crank–Nicolson Galerkin–Galerkin FEMs for miscible displacement in porous media. J. Sci. Comput. 83, 1–26 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  9. Cai, W., Li, B., Lin, Y., Sun, W.: Analysis of fully discrete FEM for miscible displacement in porous media with Bear–Scheidegger diffusion tensor. Numer. Math. 141, 1009–1042 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cannon, J.R., Lin, Y.: Non-classical \(H^1\) projection and Galerkin methods for non-linear parabolic integro-differential equations. Calcolo 25, 187–201 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cannon, J.R., Lin, Y.: A priori \(L^2\) error estimates for finite-element methods for nonlinear diffusion equations with memory. SIAM J. Numer. Anal. 27, 595–607 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cheng, A.J.: The optimal error estimate of the finite element method in the \(L^\infty (J;H^1(\Omega ))\) norm for a problem of miscible compressible displacement in porous media. Numer. Math. J. Chin. Univ. 16, 134–144 (1994)

    MATH  Google Scholar 

  13. Cheng, H., Droniou, J., Le, K.N.: Convergence analysis of a family of ELLAM schemes for a fully coupled model of miscible displacement in porous media. Numer. Math. 141, 353–397 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chou, S.H., Li, Q.: Mixed finite element methods for compressible miscible displacement in porous media. Math. Comput. 57, 507–527 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  15. Douglas, J.J., Roberts, J.E.: Numerical methods for a model for compressible miscible displacement in porous media. Math. Comput. 41, 441–459 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  16. Douglas, J.J., Roberts, J.E.: Global estimates for mixed methods for second order elliptic equations. Math. Comput. 44, 39–52 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  17. Douglas, J.J., Ewing, R., Wheeler, M.F.: A time-discretization procedure for a mixed finite element approximation of miscible displacement in porous media. RAIRO Anal. Numer. 17, 249–265 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ewing, R.E., Yuan, Y.R., Li, G.: Time stepping along characteristics for a mixed finite-element approximation for compressible flow of contamination from nuclear waste in porous media. SIAM. J. Numer. Anal. 26, 1513–1524 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ewing, R.E. (ed.): The Mathematics of Reservoir Simulation. Frontiers in Applied Mathematics. SIAM, Philadelphia (1983)

  20. Ewing, R.E., Wang, H.: A summary of numerical methods for time-dependent advection-dominated partial differential equations. J. Comput. Appl. Math. 128, 423–445 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ewing, R.E., Russell, T.F., Wheeler, M.F.: Convergence analysis of an approximation of miscible displacement in porous media by mixed finite elements and a modified method of characteristics. Comput. Methods Appl. Mech. Eng. 47, 73–92 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  22. Feng, X.: Strong solutions to a nonlinear parabolic system modeling compressible miscible displacement in porous media. Nonlinear Anal. 23, 1515–1531 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  23. Guo, H., Yang, Y.: Bound-preserving discontinuous Galerkin method for compressible miscible displacement in porous media. SIAM J. Sci. Comput. 39, A1969–A1990 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Gao, H., Sun, W.: Optimal error analysis of Crank-Nicolson lowest-order Galerkin-mixed FEM for incompressible miscible flow in porous media. Numer. Methods PDEs 36, 1773–1789 (2020)

    Article  Google Scholar 

  25. Hu, H., Chen, Y., Huang, Y.: A characteristic finite element two-grid algorithm for a compressible miscible displacement problem. Adv. Comput. Math. 46, 15 (2020)

  26. Lee, S., Wheeler, M.F.: Adaptive enriched Galerkin methods for miscible displacement problems with entropy residual stabilization. J. Comput. Phys. 331, 19–37 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  27. Li, B., Sun, W.: Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J. Numer. Anal. 51, 1959–1977 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Li, B., Sun, W.: Regularity of the diffusion-dispersion tensor and error analysis of Galerkin FEMs for a porous medium flow. SIAM J. Numer. Anal. 53, 1418–1437 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Li, B., Wang, J., Sun, W.: The stability and convergence of fully discrete Galerkin–Galerkin FEMs for porous medium flows. Commun. Comput. Phys. 15, 1141–1158 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Li, D., Wang, J.: Unconditionally optimal error analysis of Crank-Nicolson Galerkin FEMs for a strongly nonlinear parabolic system. J. Sci. Comput. 72, 892–915 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  31. Memon, S., Nataraj, N., Pani, A.K.: An a posteriori error analysis of mixed finite element Galerkin approximations to second order linear parabolic problems. SIAM J. Numer. Anal. 50, 1367–1393 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  32. Mohamed, A.N.A., Pani, A.K.: Mixed finite element methods for compressible miscible displacement problems in reservoir studies, Functional analysis with current applications in science, technology and industry (Aligarh, 1996), 332–352, Pitman Res. Notes Math. Ser., 377, Longman, Harlow (1998)

  33. Nirenberg, L.: An extended interpolation inequality. Ann. Scuola Norm. Sup. Pisa 3(20), 733–737 (1966)

    MathSciNet  MATH  Google Scholar 

  34. Park, E.-J.: Mixed finite element methods for generalized Forchheimer flow in porous media. Numer. Methods Partial Differ. Equ. 21, 213–228 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  35. Raviart, P.A., Thomas, J.M.: A Mixed Finite Element Method for 2-nd Order Elliptic Problems, Mathematical Aspects of Finite Element Methods, Lecture Notes in Mathematics, vol. 606, pp. 292–315. Springer, New York (1977)

    Google Scholar 

  36. Scheidegger, A.E.: The Physics of Flow Through Porous Media. The MacMillan Company, New York (1957)

    Book  MATH  Google Scholar 

  37. Scovazzi, G., Wheeler, M.F., Mikelić, A., Lee, S.: Analytical and variational numerical methods for unstable miscible displacement flows in porous media. J. Comput. Phys. 335, 444–496 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  38. Sun, W., Wu, C.: New analysis of Galerkin-mixed FEMs for incompressible miscible flow in porous media. Math. Comput. 90, 81–102 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  39. Sun, W., Wu, C.: Efficient fully discrete Galerkin-mixed FEMs for incompressible miscible flow in porous media. Int. J. Numer. Anal. Model. 17, 350–367 (2020)

    MathSciNet  MATH  Google Scholar 

  40. Thomée, V.: Galerkin Finite Element Methods For Parabolic Problems. Springer, New York (1997)

    Book  MATH  Google Scholar 

  41. Wang, H.: An optimal-order error estimate for a family of ELLAM-MFEM approximations to porous medium flow. SIAM J. Numer. Anal. 46, 2133–2152 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  42. Wang, H., Liang, D., Ewing, R.E., Lyons, S.L., Qin, G.: An ELLAM-MFEM solution technique for compressible fluid flows in porous media with point sources and sinks. J. Comput. Phys. 159, 344–376 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  43. Wang, H., Liang, D., Ewing, R.E., Lyons, S.L., Qin, G.: An ELLAM approximation for highly compressible multicomponent flows in porous media. Comput. Geosci. 6, 227–251 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  44. Wang, H., Zhao, W., Ewing, R.E.: A numerical modeling of multicomponent compressible flows in porous media with multiple wells by an Eulerian–Lagrangian method. Comput. Vis. Sci. 8, 69–81 (2005)

    Article  MathSciNet  Google Scholar 

  45. Wang, H., Zhao, W., Ewing, R.E., Al-Lawatia, M., Espedal, M.S., Telyakovskiy, A.S.: A Eulerian–Lagrangian solution technique for single-phase compositional flow in three-dimensional porous media. Comput. Math. Appl. 52, 607–624 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  46. Wang, H., Zheng, X.: An optimal-order error estimate of the lowest-order ELLAM-MFEM approximation to miscible displacement in three space dimensions. J. Comput. Appl. Math. 375, 112819 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  47. Wang, J., Si, Z., Sun, W.: A new error analysis of characteristics-mixed FEMs for miscible displacement in porous media. SIAM J. Numer. Anal. 52, 3300–3020 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  48. Wheeler, M.F.: A priori \(L^2\) error estimates for Galerkin approximations to parabolic partial differential equations. SIAM J. Numer. Anal. 10, 723–759 (1973)

    Article  MathSciNet  Google Scholar 

  49. Xu, Z., Yang, Y.: High-order bound-preserving discontinuous Galerkin methods for compressible miscible displacements in porous media on triangular meshes. J. Comput. Phys. 378, 110–128 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  50. Yan, Y.: Postprocessing the finite element method for semilinear parabolic problems. SIAM J. Numer. Anal. 44, 1681–1702 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  51. Zlámal, M.: Curved elements in the finite element method I. SIAM J. Numer. Anal. 10, 229–240 (1973)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to thank the anonymous referees for their valuable suggestions and comments and also, Professor R. An (Wenzhou University) and Dr. J. Wang (BCSRC, Beijing) for providing a FreeFEM code and Fig. 2.

Author information

Authors and Affiliations

  1. Advanced Institute of Natural Science, Beijing Normal University at Zhuhai, Zhuhai, People’s Republic of China

    Weiwei Sun

  2. Division of Science and Technology, United International College (BNU-HKBU), Zhuhai, 519087, People’s Republic of China

    Weiwei Sun

Authors
  1. Weiwei Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiwei Sun.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The research is partially supported by a Grant from National Natural Science Foundation of China under Grant Number 12071040 and internal funds (R5202009, R72021111) from United International College (BNU-HKBU)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, W. New analysis and recovery technique of mixed FEMs for compressible miscible displacement in porous media. Numer. Math. 150, 179–215 (2022). https://doi.org/10.1007/s00211-021-01249-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-021-01249-w

Mathematics Subject Classification

Search

Navigation