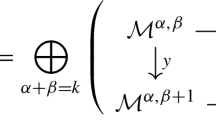Hodge cohomology with a ramification filtration, I

Abstract

We consider a filtration on the cohomology of the structure sheaf indexed by (not necessarily reduced) divisors “at infinity”. We show that the filtered pieces are functorial with respect to transfers, have fpqc descent, and are so called cube invariant. In the presence of resolution of singularities and weak factorisation they are invariant under blowup “at infinity”. As such, they lead to a realisation functor from Kahn, Miyazaki, Saito and Yamazaki’s category of motives with modulus over a characteristic zero base field.

1 Introduction

In his celebrated work [31], Voevodsky constructed the triangulated category of mixed motives ${\textbf{DM}}^{{{\text {eff}}}}_k$ over a field k. This is a categorification of Bloch’s higher Chow groups in the sense that for X, Y quasi-projective and X smooth and equidimensional of dimension d there are isomorphisms¹

$$\begin{aligned} \hom _{{\textbf{DM}}^{{{\text {eff}}}}_k}(M(X), M^c(Y)(q)[p]) \cong CH_{d-q}(X \times Y, 2q-p) \end{aligned}$$

In the series of papers [15,16,17], Kahn, Miyazaki, Saito and Yamazaki define and study a triangulated category ${\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k$ which contains Voevodsky’s category ${\textbf{DM}}^{{{\text {eff}}}}_k$ as a full subcategory. One of their motivations is to obtain a motivic framework where one can study various non-$\mathbb {A}^1$-invariant cohomology. An example of such a cohomology is the coherent cohomology $H^i_{{{\text {Zar}}}}(-, \mathcal {O})$ of the structure sheaf $\mathcal {O}$. Indeed, $\mathcal {O}$ is represented by $\mathbb {A}^1$ which is contractible in ${\textbf{DM}}^{{{\text {eff}}}}_k$ by definition.

Another example of a non-$\mathbb {A}^1$-invariant theory is higher Chow groups with modulus studied by Kerz–Saito [18] and Binda–Saito [5], generalising the additive higher Chow groups of Bloch–Esnault [3], Rülling [24], Park [22], and Krishna–Levine [13]. These higher Chow groups with modulus are directly related to the relative de Rham complex by a regulator map studied in [5]. The category ${\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k$ is hoped to be a categorifaction of higher Chow groups with modulus, and the realisation functor defined in this work and its sequel [14] should be some kind of categorical version of this regulator map.²

Somewhat surprisingly, it has be unknown for a long time whether the most obvious non-$\mathbb {A}^1$-invariant cohomology theory $H^i_{{{\text {Zar}}}}(-, \mathcal {O})$ is representable in ${\mathbf {{\underline{M}}DM}}_k^{{\text {eff}}}$ or not. In this paper we show that it is, at least over any field of characteristic 0 (see Cor. 1.2 below). As a consequence, we observe another fact, also surprisingly unknown for a long time, that ${\mathbf {{\underline{M}}DM}}_k^{{\text {eff}}}$ is strictly larger than ${\textbf{DM}}_k^{{\text {eff}}}$.

In fact, we will represent a suitable filtration of $H^i_{{{\text {Zar}}}}(-, \mathcal {O})$ graded by formal conductors: for any choice of open immersion $X \subseteq \overline{X}$ and invertible sheaf of ideals $\mathcal {I}\subseteq \mathcal {O}_{\overline{X}}$ whose vanishing locus $X^\infty = {{\underline{\textrm{Spec}}}}(\mathcal {O}_{\overline{X}}/\mathcal {I})$ satisfies $X = \overline{X}{\setminus } X^\infty$, we can consider the image of the morphism³

$$\begin{aligned} H^q ((\overline{X},X^\infty ),\underline{M}\mathcal {O}):=H^q_{{{\text {Zar}}}}(\overline{X}, \sqrt{\mathcal {I}} \otimes \mathcal {I}^{\otimes -1}) \rightarrow H^q_{{{\text {Zar}}}}(X, \mathcal {O}_X). \end{aligned}$$

In this way, we obtain a filtration on the cohomology of X indexed by the multiplicity of effective Cartier divisors. Moreover, one can prove that this filtration is exhaustive.

$$\begin{aligned} \mathop {\varinjlim }\limits _{n \ge 1} H^q ((\overline{X},n\cdot X^\infty ),\underline{M}\mathcal {O}) \xrightarrow {\sim } H^q_{{{\text {Zar}}}}(X, \mathcal {O}_X). \end{aligned}$$

As such, instead of the smooth varieties which generate ${\textbf{DM}}^{{{\text {eff}}}}_k$, the category ${\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k$ is generated by modulus pairs. A modulus pair can be defined as a pair $\mathcal {X}= (\overline{X}, X^\infty )$ such that $\overline{X}$ is a variety, $X^\infty \subseteq \overline{X}$ is a closed subscheme, and $X^\circ := \overline{X}\setminus X^\infty$ is smooth.⁴ In the same way that $M(X) \in {\textbf{DM}}^{{{\text {eff}}}}_k$ represents the cohomology of X, the object $M(\mathcal {X}) \in {\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k$ represents a filtered piece of the cohomology of $X^\circ$, namely the cohomology with ramification bounded by $X^\infty$.

Our main theorem is the following.

Theorem 1.1

[Theorem 7.3] Let k be a field satisfying resolution of singularities and weak factorisation in the sense of Def.A.4, e.g., a field of characteristic zero, Cor.A.6, Thm.A.7. Then there exists an object $\underline{M}\mathcal {O}\in {\mathbf {{\underline{M}}DM}}^{{\text {eff}}}_k$ such that for any smooth variety $\overline{X}$, any effective Cartier divisor $X^\infty$ with normal crossings support, and any $n \in \mathbb {Z}$ we have

$$\begin{aligned} \hom _{{\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_{k}} (M(\mathcal {X}), \underline{M}\mathcal {O}[n]) \cong H_{{{\text {Zar}}}}^{n}\left( \overline{X}, \mathcal {O}(X^\infty {-} |X^\infty |)\right) . \end{aligned}$$

where $\mathcal {O}(X^\infty {-} |X^\infty |)$ is the line bundle associated to the divisor $X^\infty {-} |X^\infty |$.

As an immediate corollary of Theorem 1.1, we obtain:

Corollary 1.2

For any $X \in {\textbf{Sm}}_k$, by taking $\mathcal {X}= (X,\varnothing )$ in Theorem 1.1, we have a representation of the cohomology of the structure sheaf.

$$\begin{aligned} \hom _{{\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_{k}} (M(X,\varnothing ), \underline{M}\mathcal {O}[n]) \cong H_{{{\text {Zar}}}}^{n} (X, \mathcal {O}). \end{aligned}$$

And of course:

Corollary 1.3

The canonical fully faithful inclusion

$$\begin{aligned} {\textbf{DM}}^{{{\text {eff}}}}_k \subseteq {\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k \end{aligned}$$

is not essentially surjective.

The strategy can be summarised as follows. We define $\underline{M}\mathcal {O}$ on ${\mathbf {{\underline{P}}Sm}}_k$ (recalled in Sect. 2) and show that it is a quasi-coherent étale sheaf, Sect. 3, then show that its Nisnevich fibrant replacement is blowup invariant, Sect. 4, cube invariant, Sect. 5, and has transfers, Sect. 6.

We begin in Sect. 2 with a recollection of the general theory, and in particular the construction of ${\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}}$. We have tried to make these recollections as simple and streamlined as possible in an attempt to make the theory of motives with modulus more accessible to outsiders. Indeed, one of the motivations to constructing a realisation functor was to connect the specialised theory with the wider mathematical world. In Appendix A, we collect some definitions and facts about resolution of singularities and weak factorisations. In Appendix B, we give a self-contained proof that ${\mathrm {{\underline{M}}Zar}}$ (resp. ${\underline{\textrm{M}}}\acute{\textrm{e}}{\textrm{t}}$) cohomology can be calculated as the colimit of Zariski cohomology (resp. étale cohomology) over abstract admissible blowups.

In future work, this paper’s results and techniques will be used to develop the analogue of Corollary 1.2 for $H^p_{{{\text {Zar}}}}(X, \Omega ^q_X)$, as well as Hochschild homology with modulus satisfying an HKR isomorphism.

Related work. The object $\underline{M}\mathcal {O}$ is motiviated by, and is essentially the ${\mathrm {{\underline{M}}Nis}}$-sheafification of, the analogous presheaf described in [23]. This was already known to be cube invariant but not abstract admissible blowup invariant. Cf. also Binda–Saito [5] and Ivorra–Yamazaki, [10].

In [4] a Hodge-type realization with log poles is constructed which should compare to the realisation constructed in this paper in case of reduced divisor or in case there is no divisor at infinity (that is, the case of tame ramification or the case of arbitrary ramification with no pole restriction).

There is also work in progress by Marco D’Addezio, [6], who studies the ${\mathrm {{\underline{M}}Zar}}$-sheafification of $(\overline{X}, X^\infty ) \mapsto \Gamma (\overline{X}, \mathcal {O}_{\overline{X}})$ (although he writes “simply marked schemes” for modulus pairs and “v-Zariski” for ${\mathrm {{\underline{M}}Zar}}$).

2 Review of the general theory

In this section, we recall basic definitions concerning the category of modulus pairs, Rec. 2.1, modulus topologies, Rec. 2.3, finite correspondences in the modulus setting, Rec. 2.5, and the construction of ${\mathbf {{\underline{M}}DM}}^{{{\text {eff}}}}_k$, Rec. 2.6. One can find more details in many places: [15,16,17, 21, Sect. 1], [12, Chap.5, Chap.6].

We fix a perfect base field k with the case of interest being ${\text {char}}(k) = 0$. We restrict our attention to modulus pairs over k with smooth interior so as not to frighten the reader, but a large part of what we write holds over general bases, cf. [12].

Recollection 2.1

[Modulus pairs]

• (1) A modulus pair.⁵ over k is a pair

  $$\begin{aligned} \mathcal {X}= (\overline{X}, X^\infty ) \end{aligned}$$

  such that

  • (a) $\overline{X}$ (called the total space) is a separated k-scheme of finite type,

  • (b) $X^\infty \subseteq \overline{X}$ (called the modulus) is an effective Cartier divisor, and

  • (c) $X^\circ := \overline{X}\setminus X^\infty$ (called the interior) is smooth over k.

• (2) An ambient k-morphism $(\overline{X}, X^\infty ) \rightarrow (\overline{Y}, Y^\infty )$ of modulus pairs is a k-morphism $f: \overline{X}\rightarrow \overline{Y}$ of the underlying schemes, such that $X^\infty \ge f^*Y^\infty$.⁶

• (3) ${\mathbf {{\underline{P}}Sm}}_k$ is the category formed by modulus pairs over k, together with ambient k-morphisms.

• (4) ${\mathbf {{\underline{M}}Sm}}_k$ is the category of modulus pairs over k. It is constructed by formally inverting the class $\Sigma$ of abstract admissible blowups⁷: i.e., those ambient morphisms $f: (\overline{X}, X^\infty ) \rightarrow (\overline{Y}, Y^\infty )$ such that

  • (a) $\overline{X}\rightarrow \overline{Y}$ is proper,

  • (b) $X^\infty = f^*Y^\infty$, and

  • (c) $X^\circ \rightarrow Y^\circ$ is an isomorphism.

  In symbols,

  $$\begin{aligned} {\mathbf {{\underline{M}}Sm}}_k:= {\mathbf {{\underline{P}}Sm}}_k[\Sigma ^{-1}]. \end{aligned}$$

  It is shown in [16, Prop. 1.7.2] (cf. also [12, Prop. 1.21]) that $\Sigma$ admits a right calculus of fractions, so

  $$\begin{aligned} \hom _{{\mathbf {{\underline{M}}Sm}}_k}(\mathcal {Y}, \mathcal {X}) = \varinjlim _{\mathcal {Y}' \rightarrow \mathcal {Y}\in \Sigma } \hom _{{\mathbf {{\underline{P}}Sm}}_k}(\mathcal {Y}', \mathcal {X}) \end{aligned}$$

  and the colimit is filtered; in fact its indexing category is a filtered poset. In particular every morphism in ${\mathbf {{\underline{M}}Sm}}_k$ can be written in the form $f \circ s^{-1}$ where $s \in \Sigma$ and f is ambient.

• (5) The category ${\mathbf {{\underline{P}}Sm}}_k$⁸ has categorical fibre products $\mathcal {Y}= \mathcal {T}\times _{\mathcal {S}} \mathcal {X}$ in the case $T^\circ \rightarrow S^\circ$ is smooth and $f: \mathcal {T}\rightarrow \mathcal {S}$ is minimal, i.e., in the case $T^\infty = j^*S^\infty$, [12, Lem.1.32, Prop.1.33].

  • (a) If $\overline{T}\rightarrow \overline{S}$ is flat, then $\overline{Y}= \overline{T}\times _{\overline{S}} \overline{X}$ and $Y^\infty = X^\infty |_{\overline{Y}}$.

  • (b) If f is an admissible blowup, then $\overline{Y}$ is the strict transform of $\overline{X}$.

  • (c) For a general minimal f, the total space $\overline{Y}$ is the scheme theoretic closure of $T^\circ \times _{S^\circ } X^\circ$ in $\overline{T}\times _{\overline{S}} \overline{X}$.

• (6) The category ${\mathbf {{\underline{M}}Sm}}_k$ admits fibre products $\mathcal {T}\times _{\mathcal {S}} \mathcal {X}$ along any morphism with $T^\circ \rightarrow S^\circ$ smooth, [12, Thm. 1.40].⁹ The canonical functor ${\mathbf {{\underline{P}}Sm}}_k \rightarrow {\mathbf {{\underline{M}}Sm}}_k$ preserves the fibre products in item (5).

Remark 2.2

By the universal property of localisation, the category ${{\textbf{PSh}}}({\mathbf {{\underline{M}}Sm}}_k)$ is canonically identified with the full subcategory of ${{\textbf{PSh}}}({\mathbf {{\underline{P}}Sm}}_k)$ consisting of those presheaves which send abstract admissible blowups to isomorphisms. Since abstract admissible blowups are categorical monomorphisms in ${\mathbf {{\underline{P}}Sm}}_k$, this is precisely the category of sheaves for the topology on ${\mathbf {{\underline{P}}Sm}}_k$ generated by abstract admissible blowups. In symbols, ${{\textbf{PSh}}}({\mathbf {{\underline{M}}Sm}}_k) = {{\textbf{Shv}}}_\Sigma ({\mathbf {{\underline{P}}Sm}}_k)$, cf. [12, Sect. A.1].

Recollection 2.3

[Modulus topologies]

• (1) The Zariski topology on ${\mathbf {{\underline{P}}Sm}}_k$ is generated by families

  $$\begin{aligned} \{f_i: (\overline{U}_i, U^\infty _i) \rightarrow (\overline{X}, X^\infty )\}_{i \in I} \end{aligned}$$

  (2.1)

  of minimal morphisms such that $\{\overline{U}_i \rightarrow \overline{X}_i\}_{i \in I}$ is a Zariski covering in the classical sense. Zariski coverings on ${\mathbf {{\underline{P}}Sm}}_k$ form a pretopology in the sense of [25, Exposé II].

• (2) The MZariski topology or ${\mathrm {{\underline{M}}Zar}}$-topology on ${\mathbf {{\underline{M}}Sm}}_k$ is generated by images of Zariski coverings under the localisation functor ${\mathbf {{\underline{P}}Sm}}_k \rightarrow {\mathbf {{\underline{M}}Sm}}_k$. Zariski coverings do not form a pretopology on ${\mathbf {{\underline{M}}Sm}}_k$. In general the coverings of the pretopology they generate consists of various iterated compositions of abstract admissible blowups, inverses of abstract admissible blowups, and Zariski coverings. However, such families can always be refined by one of the form

  $$\begin{aligned} \{\mathcal {U}_i \rightarrow \mathcal {Y}\rightarrow \mathcal {X}\}_{i \in I} \end{aligned}$$

  (2.2)

  where $\{\mathcal {U}_i \rightarrow \mathcal {Y}\}$ is a Zariski covering and $\mathcal {Y}\rightarrow \mathcal {X}$ is an abstract admissible blowup, [12, Cor. 4.21].

• (3) The ${\mathrm {{\underline{M}}Nis}}$, ${\underline{\textrm{M}}}\acute{\textrm{e}}{\textrm{t}}$, and ${\mathrm {{\underline{M}}fppf}}$ topologies are defined in the analogous way to ${\mathrm {{\underline{M}}Zar}}$. There are also more exotic topologies considered in [12] but we do not use them here.

Remark 2.4

By Eq. (2.2) and Remark 2.2 the category ${{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Zar}}}({\mathbf {{\underline{M}}Sm}}_k)$ is canonically identified with the full subcategory of ${{\textbf{Shv}}}_{{{\text {Zar}}}}({\mathbf {{\underline{P}}Sm}}_k)$ consisting of those sheaves which send abstract admissible blowups to isomorphisms. In symbols, one could write ${{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Zar}}}({\mathbf {{\underline{M}}Sm}}_k) = {{\textbf{Shv}}}_{\Sigma ,{{\text {Zar}}}}({\mathbf {{\underline{P}}Sm}}_k)$.

Recollection 2.5

[Finite correspondences]

• 1. Write ${\textbf{Cor}}_k$ for Voevodsky’s category of finite correspondences, [31]. Objects are smooth k-schemes and $\hom _{{\textbf{Cor}}_k}(X, Y)$ is the free abelian group

  $$\begin{aligned} \mathbb {Z}\left\{ Z\ \big |\ \begin{array}{c} Z \subseteq X \times Y \text { is an integral closed subscheme, and } \\ Z \rightarrow X \text { is finite and dominates an irreducible component of} X \end{array} \right\} . \end{aligned}$$

  There is a canonical functor ${\textbf{Sm}}_k \rightarrow {\textbf{Cor}}_k$ which sends a morphism $f: X \rightarrow Y$ to the graph $[f]:= \sum \delta (X_i)$ where $X_i \subseteq X$ are the irreducible components of X and $\delta : X \rightarrow X \times Y$ is the graph morphism $x \mapsto (x, f(x))$. If $f: X' \rightarrow X$ is étale and $\sum n_i Z_i \in \hom _{{\textbf{Cor}}_k}(X, Y)$ any correspondence, then $\alpha \circ [f] = \sum n_i \sum Z'_{ij}$ where $Z'_{ij}$ are the irreducible components of $X' \times _X Z_i$.

• 2. The structure presheaf $\mathcal {O}$ on ${\textbf{Sm}}_k$ which send X to $\Gamma (X,\mathcal {O}_X)$ has a structure of transfers in the sense that there exists $\mathcal {O}_{{{\text {tr}}}}: {\textbf{Cor}}_k^{op} \rightarrow {\textbf{Ab}}$ such that $\mathcal {O}_{{{\text {tr}}}}|_{{\textbf{Sm}}_k} = \mathcal {O}$, [27].

• 3. We write ${\mathbf {{\underline{M}}Cor}}_k$ for the category of modulus correspondences.¹⁰ Objects are the same as ${\mathbf {{\underline{M}}Sm}}_k$ and for $\overline{X}$ integral, morphism groups can be defined as the intersections

  

  where the colimit is over ambient minimal morphisms $\mathcal {W}\rightarrow \mathcal {X}$ such that $\overline{W}\rightarrow \overline{X}$ is proper surjective, $W^\circ \rightarrow X^\circ$ is finite, and $\overline{W}$ is integral, cf. [12, Cor. 4.21, Prop. 4.37, Cor. 5.31],¹¹ More explicitly, for $X^\circ$ integral, a correspondence $\alpha : X^\circ \rightarrow Y^\circ$ belongs to ${\mathbf {{\underline{M}}Cor}}_k (\mathcal {X},\mathcal {Y})$ if and only if there exists a proper surjective morphism $\overline{W}\rightarrow \overline{X}$ with $W^\circ \rightarrow X^\circ$ finite and $\overline{W}$ integral, and a finite sum $\sum n_i f_i$ of morphisms¹²$f_i: \mathcal {W}\rightarrow \mathcal {Y}$ such that $\alpha |_{{\text {Spec}}(k(W^\circ ))} = \sum n_i f_i^\circ |_{{\text {Spec}}(k(W^\circ ))}: {\text {Spec}}(k(W^\circ )) \rightarrow Y^\circ$, where $\mathcal {W}= (\overline{W}, \overline{W}\times _{\overline{X}} X^\infty )$.

  

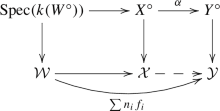
  Taking graphs induces a covariant functor ${\mathbf {{\underline{M}}Sm}}_k \rightarrow {\mathbf {{\underline{M}}Cor}}_k$.

Recollection 2.6

• (1) An additive presheaf on ${\mathbf {{\underline{M}}Cor}}_k$ is called a modulus presheaf with transfers. Let $\tau \in \{{{\text {Zar}}}, {{\text {Nis}}}, {\acute{\textrm{e}}{\textrm{t}}}\}$. A modulus presheaf with transfers is called a $\tau$-sheaf with transfers if for any modulus pair $\mathcal {X}$, the presheaf $(F|_{{\mathbf {{\underline{M}}Sm}}_k})_{\mathcal {X}}$ on the small site $\overline{X}_{\tau }$ is a $\tau$-sheaf, where $F|_{{\mathbf {{\underline{M}}Sm}}_k}$ denotes the restriction via the graph functor ${\mathbf {{\underline{M}}Sm}}_k \rightarrow {\mathbf {{\underline{M}}Cor}}_k$. One can prove that ${{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k)$ is a Grothendieck abelian category using the usual methods, [12, Cor. 6.8], i.e., by showing that the forgetful functor admits a left adjoint

  $$\begin{aligned} a_{{{\text {tr}}}}: {{\textbf{PSh}}}({\mathbf {{\underline{M}}Cor}}_k) \rightarrow {{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k) \end{aligned}$$

  which becomes sheafification when restricted to ${\mathbf {{\underline{M}}Sm}}_k$. Moreover, by classical arguments with input from [12],¹³ for any $F \in {{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k)$ we have

  $$\begin{aligned} Ext^\bullet (\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}), F) \cong H_{{\mathrm {{\underline{M}}Nis}}}^\bullet (\mathcal {X}, F) \end{aligned}$$

  (2.3)

  where $\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}) = \hom _{{\mathbf {{\underline{M}}Cor}}_k}(-, \mathcal {X})$.

• (2) In analogy with ${\textbf{DM}}_k^{{{\text {eff}}}}$ from [31] the category ${\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}}$ is defined to be the Verdier quotient

  $$\begin{aligned} {\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}} = \frac{D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))}{\biggl \langle \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}\otimes {\overline{\square }}) \rightarrow \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}) \biggm | \mathcal {X}\in {\mathbf {{\underline{M}}Cor}}_k \biggr \rangle } \end{aligned}$$

  by the two term complexes $[\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}\otimes {\overline{\square }}) \rightarrow \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X})]$ where $\mathcal {X}\otimes {\overline{\square }}= (\overline{X}\times \mathbb {P}^1, X^\infty \times \mathbb {P}^1 + \overline{X}\times \{\infty \})$. Since the generators $\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X})$ are compact, [12, Thm. 4.47], the localisation functor admits a right adjoint, and ${\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}}$ can be identified with the full subcategory

  $$\begin{aligned}&{\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}} \cong \\ \biggl \{ K \in&D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))\ |\ \mathbb {H}_{{\mathrm {{\underline{M}}Nis}}}^\bullet (\mathcal {X}, K) \cong \mathbb {H}_{{\mathrm {{\underline{M}}Nis}}}^\bullet (\mathcal {X}\otimes {\overline{\square }}, K) \biggr \} \nonumber \end{aligned}$$

  (2.4)

  of objects with cube invariant hypercohomology, cf Eq. (2.3).

3 The presheaf $\underline{M}\mathcal {O}$

Definition 3.1

If A is any ring and $f \in A$ a nonzero divisor we write

$$\begin{aligned} \underline{M}\mathcal {O}(A, f):= \{ a/f \in A[f^{-1}]: a \in \sqrt{(f)} \subseteq A \}. \end{aligned}$$

Of course, $A \subseteq \underline{M}\mathcal {O}(A, f)$ with equality if f is invertible, and on the other side, $\bigcup _{n \ge 0} \underline{M}\mathcal {O}(A, f^n) = A[f^{-1}]$.

Example 3.2

If $A = \mathbb {Q}[x_1, \dots , x_n]$ and $f = x_1^{r_1}\dots x_i^{r_i}$ with $r_1, \dots , r_i > 0$ then

$$\begin{aligned} \underline{M}\mathcal {O}(A, f) = \tfrac{1}{x_1^{r_1{-}1}\dots x_i^{r_i{-}1}} \mathbb {Q}[x_1, \dots , x_n]. \end{aligned}$$

More generally, if A is a UFD, $f_1, \dots , f_i \in A$ are pair-wise distinct irreducible elements, and $f = f_1^{r_1} \dots f_i^{r_i}$ with $r_1, \dots , r_i > 0$ then

$$\begin{aligned} \underline{M}\mathcal {O}(A, f) = \tfrac{1}{f_1^{r_1{-}1}\dots f_i^{r_i{-}1}}A. \end{aligned}$$

In particular, $\underline{M}\mathcal {O}(A, f)$ is free of rank one in this case.

Lemma 3.3

Suppose $\phi : A \rightarrow B$ is a homomorphism of rings equipped with nonzero divisors f, g respectively, such that $\phi (f)$ divides g. Then $A[f^{-1}] \rightarrow B[g^{-1}]$ induces a morphism of submodules

$$\begin{aligned} \underline{M}\mathcal {O}(A, f) \rightarrow \underline{M}\mathcal {O}(B, g). \end{aligned}$$

Proof

If $g = \phi (f)$, the question is whether $\frac{1}{\phi (f)}\phi (\sqrt{fA}) \subseteq \frac{1}{\phi (f)}\sqrt{\phi (f)B}$ or equivalently, whether $\phi (\sqrt{fA}) \subseteq \sqrt{\phi (f)B}$, which is clear since $a^n = fh$ for some h implies $\phi (a)^n =\phi (f)h'$ for some $h'$. If $A = B$, so $g = fh$ for some h, the question is whether $\frac{1}{f}\sqrt{fA} \subseteq \frac{1}{fh}\sqrt{fhA}$ or equivalently, whether $h\sqrt{fA} \subseteq \sqrt{fhA}$ which is also clear since if $a^n = fj$ for some j and $n \ge 1$ then $(ha)^n = fhj'$ for some $j'$. We get the general case by factoring the given morphism as $(A, f) \rightarrow (B, \phi (f)) \rightarrow (B, g)$. $\square$

Proposition 3.4

Suppose that A is a ring, $f \in A$ is a nonzero divisor and $A \rightarrow B$ a faithfully flat morphism (in particular, the images of f in B and $B \otimes _A B$ are again nonzero divisors). Then

$$\begin{aligned} 0 \rightarrow \underline{M}\mathcal {O}(A, f) \rightarrow \underline{M}\mathcal {O}(B, f) \rightarrow \underline{M}\mathcal {O}(B \otimes _A B, f) \end{aligned}$$

is exact, where we write f also for the images in B and $B\otimes _A B$ to lighten the notation.

Proof

By definition, the sub-A-module $\underline{M}\mathcal {O}(A, f) \subseteq A[\tfrac{1}{f}]$ is the image of $\sqrt{fA} \subseteq A$ under the composition $A \hookrightarrow A[\tfrac{1}{f}] {\mathop {\rightarrow }\limits ^{1/f}} A[\tfrac{1}{f}]$ where the second morphism is multiplication by 1/f. The analogue holds for $\underline{M}\mathcal {O}(B, f)$ and $\underline{M}\mathcal {O}(B \otimes _A B, f)$ so it suffices to show that the exact sequence $0 \rightarrow A \rightarrow B \rightarrow B \otimes _A B$ induces an exact sequence $0 \dashrightarrow \sqrt{fA} \dashrightarrow \sqrt{fB} \dashrightarrow \sqrt{fB \otimes _A B}$ of sub-A-modules. This is a straightforward diagram chase. Exactness at $\sqrt{fA}$ follows from $A \subseteq B$ and $A \rightarrow B$ being a ring homomorphism. For exactness at $\sqrt{fB}$, suppose we are given $a \in A$ such that $a^n = fb$ for some $n \ge 1$ and $b \in B$. Then $b \in A[\tfrac{1}{f}] \subseteq B[\tfrac{1}{f}]$, so $b\mapsto 0 \in B \otimes _A B[\tfrac{1}{f}]$, so in fact, $b \in A \subseteq B$, and $a \in \sqrt{fA}$. $\square$

Lemma 3.5

Let $\phi : A \rightarrow B$ be an étale homomorphism and $f \in A$ a nonzero divisor. Then the canonical isomorphism $A[f^{-1}] \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} B[\phi (f)^{-1}]$ induces an isomorphism of submodules

$$\begin{aligned} \underline{M}\mathcal {O}(A, f) \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} \underline{M}\mathcal {O}(B, \phi (f)). \end{aligned}$$

Example 3.6

Even though $\underline{M}\mathcal {O}$ is an fpqc sheaf, Rem. 3.8, the statement of Lemma 3.5 does not generalise to flat morphisms. For $(\mathbb {C}[[t^2]], t^4) \rightarrow (\mathbb {C}[[t]], t^4)$ the morphism $B \otimes _A \underline{M}\mathcal {O}(A, f) \rightarrow \underline{M}\mathcal {O}(B, f)$ is $t^{-2}\mathbb {C}[[t]] \rightarrow t^{-3}\mathbb {C}[[t]]$. Of course, this does not preclude the possibility that the comparisons $H_{{{\text {Zar}}}}^n(\overline{X}, \underline{M}\mathcal {O}) \rightarrow H_{{{\text {fppf}}}}^n(\overline{X}, \underline{M}\mathcal {O})$ be isomorphisms.

Proof

First note that we have $\phi (\sqrt{fA})B = \sqrt{\phi (f)}B$ because $\phi$ is étale: Indeed, to prove this claim it suffices to show that $\psi : (A/fA)_{{{\text {red}}}} \otimes _A B \rightarrow (B /\phi (f)B)_{{{\text {red}}}}$ is an isomorphism. By [26, 033B] the ring $(A/fA)_{{{\text {red}}}} \otimes _A B$ is already reduced because it is étale over the reduced ring $(A/fA)_{{{\text {red}}}}$, so it suffices that ${\text {Spec}}(\psi )$ be a surjective closed immersion. This happens because $(A/fA) \otimes _A B \rightarrow B /\phi (f)B$ is an isomorphism, and ${\text {Spec}}((A/fA)_{{{\text {red}}}}) \rightarrow {\text {Spec}}(A/fA)$ and ${\text {Spec}}(B /\phi (f)B)_{{{\text {red}}}} \rightarrow {\text {Spec}}(B/\phi (f)B$ are surjective closed immersions.

Now since $A \rightarrow B$ is flat, $\sqrt{fA} \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} \phi (\sqrt{fA})B$ so we have $\sqrt{fA} \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} \sqrt{\phi (f)}B$, and therefore $\frac{1}{f} \sqrt{fA} \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} \frac{1}{\phi (f)}\sqrt{\phi (f)}B$, considered as submodules of $A[f^{-1}] \otimes _A B {\mathop {\rightarrow }\limits ^{\sim }} B[\phi (f)^{-1}]$. $\square$

Theorem 3.7

There is a unique étale sheaf $\underline{M}\mathcal {O}$ on ${\mathbf {{\underline{P}}Sm}}_k$ such that for affine modulus pairs with principal modulus $({\text {Spec}}(A), (f))$ we have $\underline{M}\mathcal {O}({\text {Spec}}(A), (f)) = \underline{M}\mathcal {O}(A, f)$. Furthermore, this is quasi-coherent as an étale sheaf. In particular, its Zariski, Nisnevich, and étale cohomologies agree, and vanish for affines.

Remark 3.8

The proofs we have written actually show that the assignment $(A,f) \mapsto \underline{M}\mathcal {O}(A, f)$ extends to a fpqc sheaf on the big category ${\mathbf {{\underline{P}}SCH}}$, which is quasi-coherent as an étale sheaf but not quasi-coherent as an fpqc sheaf. However, we are not using this category, nor flat topologies in this article in an attempt to make the material more accessible to a wider audience. See also Example 3.6.

Proof

Define $\underline{M}\mathcal {O}$ to be the Zariski-sheafification of the right Kan extension from affines to all of ${\mathbf {{\underline{P}}Sm}}_k$. On affines, the Zariski sheafification is the same as the right Kan extension because of Proposition 3.4. This Zariski sheaf is automatically an étale-sheaf by Proposition 3.4 and [26, 03O1] (or [20, Prop. II.1.5]).

Lemma 3.5 says that this étale sheaf is quasi-coherent in the sense of [20, Exa.II.1.2(d), Cor.II.1.6], so the cohomologies agree, [20, Rem.III.3.8], and vanish for affines by [26, 01XB]. $\square$

4 Blow-up invariance of $R\Gamma (-,\underline{M}\mathcal {O})$

In the previous section, we have constructed a Zariski (in fact fpqc) sheaf $\underline{M}\mathcal {O}$ of abelian groups on ${\mathbf {{\underline{P}}Sm}}_k$ which is quasi-coherent as an étale sheaf. Our next goal is to prove that $\underline{M}\mathcal {O}$ and its cohomology presheaves are invariant under suitable blow-ups. For global sections $\underline{M}\mathcal {O}$ we need a normality assumption, Prop. 4.4. For the cohomology we assume normal crossings, Prop. 4.7.

To begin with we characterise of elements of $\underline{M}\mathcal {O}(A,f)$ in Lemma 4.1, and show that if A is normal, $\underline{M}\mathcal {O}(A,f)$ is normal in the sense of Barth,.¹⁴ Lem. 4.2.

Lemma 4.1

Let A be a ring, $f \in A$ a nonzero divisor, and $a \in A[f^{-1}]$. Then $a \in \underline{M}\mathcal {O}(A,f)$ if and only if for some $n \ge 0$ both $fa, (fa)^na \in A$.

Proof

Certainly, if $a \in \underline{M}\mathcal {O}(A,f)$, then $af \in \sqrt{(f)} \subseteq A$ so $(af)^{n+1} = bf$ for some $n \ge 0, b \in A$ so $(af)^na \in A$ for some $n \ge 0$. On the other hand, if $af, (af)^na \in A$ for some $n \ge 0$, then $af \in \sqrt{(f)}$ so $a \in \underline{M}\mathcal {O}(A, f)$. $\square$

Lemma 4.2

Let A be a Noetherian normal domain and $f \in A$ a nonzero divisor. Then there is an equality

$$\begin{aligned} \underline{M}\mathcal {O}(A, f) = \bigcap _{\text {height } \mathfrak {p}= 1} \underline{M}\mathcal {O}(A_\mathfrak {p}, f) \end{aligned}$$

of sub-A-modules of ${\text {Frac}}(A)$.

Remark 4.3

Lemma 4.2 is a kind of valuative criterion for global sections. There is a much more general version of this lemma. The more general version is valid for any ring A equipped with a nonzero divisor f, and the local rings $A_\mathfrak {p}$ are replaced with local rings of the relative Riemann–Zariski space, denoted $Val_{{\text {Spec}}A[f^{-1}]}({\text {Spec}}(A))$ in Temkin’s article, [29]. As such Proposition 4.4 also holds for general modulus pairs, but with the restriction that $\mathcal {O}_{\overline{X}}$ be integrally closed in $j_*\mathcal {O}_{X^\circ }$, where $j:X^\circ \subseteq \overline{X}$ is the inclusion.

Proof

The inclusion $\underline{M}\mathcal {O}(A, f) \subseteq \bigcap _{\text {height } \mathfrak {p}= 1} \underline{M}\mathcal {O}(A_\mathfrak {p}, f)$ comes from Lemma 4.1. Suppose we have an element a on the right. Then for all height one primes $\mathfrak {p}$, we have $a \in A_\mathfrak {p}[f^{-1}] = A[f^{-1}]_\mathfrak {p}$ and there exists $n_{\mathfrak {p}}$ such that $fa, (fa)^{n_{\mathfrak {p}}} a \in A_\mathfrak {p}$ by Lemma 4.1. Since $\in A$ is an open condition, for each $\mathfrak {p}$, there exists an open neighborhood $U_{\mathfrak {p}}$ of $\mathfrak {p}$ on which fa and $(fa)^{n_{\mathfrak {p}}}a$ are still regular functions. Since ${\text {Spec}}A$ is quasi-compact, there exists a finite family $\mathfrak {p}_1,\dots ,\mathfrak {p}_m$ such that ${\text {Spec}}A = \cup _{i=1}^m U_{\mathfrak {p}_i}$. Set $n:=\max (n_{\mathfrak {p}_1},\dots ,n_{\mathfrak {p}_m})$. Then we have $fa \in A$ and $(fa)^n \in A$, and hence belongs to the left hand side, as desired. $\square$

Proposition 4.4

Suppose that $\overline{Y}\rightarrow \overline{X}$ is a proper surjective morphism of schemes with Noetherian normal target, and $X^\infty$ is an effective Cartier divisor on $\overline{X}$ such that $Y^\infty = \overline{Y}\times _{\overline{X}} X^\infty$ is also an effective Cartier divisor. Then the square

is Cartesian. In particular, there is a unique presheaf on ${\mathbf {{\underline{M}}Sm}}_k$ whose restriction to ${\mathbf {{\underline{P}}Sm}}_k$ agrees with $\underline{M}\mathcal {O}$ on integrally closed modulus pairs.

Proof

By definition $\underline{M}\mathcal {O}$ is a Zariski sheaf, Thm. 3.7, Rem. 3.8, so we can assume $\overline{X}$ is affine and integral and $X^\infty$ has a global generator, say $X^\infty = (f)$. Suppose $a \in \mathcal {O}(X^\circ )$ is a section whose image in $\mathcal {O}(Y^\circ )$ lies in $\underline{M}\mathcal {O}(\mathcal {Y})$. For all points $y \in \overline{Y}$, by Lemma 4.1 there is some $n_y \ge 0$ for which fa and $(fa)^{n_y}a$ are in $\mathcal {O}_{\overline{Y}, y}$. Since $\overline{Y}$ is quasi-compact, there is some n which works for all y. So in fact, fa and $(fa)^{n}a$ are in $\mathcal {O}(\overline{Y})$. Applying Lemma 4.1 again, it suffices to show that fa and $(fa)^{n}a$ are in $\mathcal {O}(\overline{X})$. Since $\overline{X}$ is Noetherian and normal, it suffices to show that they are in the dvrs $\mathcal {O}_{\overline{X},x}$ for points $x \in \overline{X}$ of codimension one, Lem. 4.2. Choose any point y in the fibre of ${\text {Spec}}(k(\overline{X}))$ such that $k(y) / k(\overline{X})$ is a finite extension of fields. Choose also an extension of the valuation of $\mathcal {O}_{\overline{X},x}$ to $L = k(y)$ and let $\mathcal {O}_L$ be the corresponding valuation ring. Since $\overline{Y}\rightarrow \overline{X}$ is proper, the morphism ${\text {Spec}}(\mathcal {O}_L) \rightarrow {\text {Spec}}(\mathcal {O}_{\overline{X},x}) \rightarrow \overline{X}$ factors as ${\text {Spec}}(\mathcal {O}_L) \rightarrow \overline{Y}$, so we find that the images of fa and $(fa)^{n}a$ in L are in fact in $\mathcal {O}_L$. That is, they have value $\ge 0$. Hence, they are in $\mathcal {O}_{\overline{X},x}$. $\square$

Remark 4.5

Since $\mathcal {O}= \hom (-, \mathbb {A}^1)$ is an h-sheaf on the category of normal schemes, [30, Prop. 3.2.10], it follows from Prop. 3.4 and Prop. 4.4 that $\underline{M}\mathcal {O}$ is an h-sheaf on normal modulus pairs, but we will not need this.

Notation 4.6

In the following proposition and proof we use $\underline{M}\mathcal {O}_{\overline{X}} = \underline{M}\mathcal {O}|_{\overline{X}_{{{\text {Zar}}}}}$ or $\underline{M}\mathcal {O}_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}} = \underline{M}\mathcal {O}|_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}}$ for the restrictions to the small Zariski, resp. étale sites.

Proposition 4.7

[Blow-up invariance of $\underline{M}\mathcal {O}$ and its cohomologies] Take $\mathcal {X}\in {\mathbf {{\underline{P}}Sm}}_k$ normal crossings and suppose that $Z \subseteq \overline{X}$ is a closed subscheme that has normal crossings with $X^\infty$ (see Def. A.1 for the terminology). Let $f: \overline{Y}\rightarrow \overline{X}$ be the blowup with centre Z, and $Y^\infty = f^* X^\infty$. Then the canonical morphism in the derived category of quasi-coherent $\mathcal {O}_{\overline{X}}$-modules

$$\begin{aligned} \underline{M}\mathcal {O}_{\overline{X}} \rightarrow Rf_*\underline{M}\mathcal {O}_{\overline{Y}} \end{aligned}$$

is an isomorphism.

Proof

Since the étale and Zariski cohomologies of $\underline{M}\mathcal {O}$ agree, Thm. 3.7, it suffices to show that the morphism $\alpha : \underline{M}\mathcal {O}_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}} \rightarrow Rf_*\underline{M}\mathcal {O}_{\overline{Y}_{{\acute{\textrm{e}}{\textrm{t}}}}}$ is an isomorphism, where now $Rf_*$ is the direct image between the small étale sites. Since this question is étale local, it suffices to find for each point $x \in \overline{X}$ an étale morphism $\overline{U}\rightarrow \overline{X}$ whose image contains x, and such that $\underline{M}\mathcal {O}_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}}|_{\overline{U}} \rightarrow Rf_*\underline{M}\mathcal {O}_{\overline{Y}_{{\acute{\textrm{e}}{\textrm{t}}}}}|_{\overline{U}}$ is an isomorphism.

Fix a point $x \in \overline{X}$. By the definition of normal crossings with $X^\infty$ (Def. A.1), there exists a diagram

$$\begin{aligned} \overline{X}\xleftarrow {p} \overline{U}\xrightarrow {q} \mathbb {A}^n = {\text {Spec}}k[t_1,\dots ,t_n] \end{aligned}$$

of étale morphisms such that $x \in p(\overline{U})$, $p^*X^\infty = q^*H$ and $Z \times _{\overline{X}} \overline{U}= Z_0 \times _{\mathbb {A}^n} \overline{U}$, where $H=\{\prod _{a \in A} t_a^{r_a}=0\}$ and $Z_0=\{t_b=0, \forall b \in B\}$ for some $r_a > 0$ and $A,B\subset \{1,\dots ,n\}$. Therefore, replacing f by $f|_{\overline{U}}$, we may assume that there exists an étale morphism $q: \overline{X}\rightarrow \mathbb {A}^n$ such that $X^\infty = q^* H$ and $Z=Z_0 \times _{\mathbb {A}^n} \overline{X}$ with $H = \{t_1^{m_1}\cdots t_r^{m_r}=0\}$ and $Z_0=\{t_b=0, \forall b \in B\}$ as above.

Since $\overline{X}\rightarrow \mathbb {A}^n$ is étale (hence flat), we obtain a cartesian diagram

where $f_0$ is the blow-up of $\mathbb {A}^n$ at $Z_0$ and $q'$ is the morphism induced by the universal property of blow-up. Suppose that we know that the assertion of Prop. 4.7 holds for $f_0$. That is, suppose that, setting $\mathcal {A}:=(\mathbb {A}^n,H)$ and $\mathcal {Y}_0:=(\overline{Y}_0,f_0^*H)$, we have an isomorphism $\underline{M}\mathcal {O}_{\mathbb {A}^n} \cong Rf_{0*} \underline{M}\mathcal {O}_{\overline{Y}_0}$. By applying $q^* = Rq^*$ to this isomorphism and by using the flat base change $q^* Rf_{0*} \cong Rf_* q^{\prime *}$ [26, 02KH], we obtain

$$\begin{aligned} q^* \underline{M}\mathcal {O}_{\mathbb {A}^n} \cong q^* Rf_{0*} \underline{M}\mathcal {O}_{\overline{Y}_0} \cong Rf_* q^{\prime *} \underline{M}\mathcal {O}_{\overline{Y}_0}. \end{aligned}$$

On the other hand, we have $q^* \underline{M}\mathcal {O}_{\mathbb {A}^n} = \underline{M}\mathcal {O}_{\overline{X}}$ and $q^{\prime *} \underline{M}\mathcal {O}_{\overline{Y}_0} = \underline{M}\mathcal {O}_{\overline{Y}}$ by quasi-coherence since q and $q'$ are étale by construction. Assembling all these isomorphisms leads to the isomorphism $\underline{M}\mathcal {O}_{\overline{X}} \cong Rf_*\underline{M}\mathcal {O}_{\overline{Y}}$, and applying Thm. 3.7 again gets us to the desired isomorphism $\underline{M}\mathcal {O}_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}} \cong Rf_*\underline{M}\mathcal {O}_{\overline{Y}_{{\acute{\textrm{e}}{\textrm{t}}}}}$.

So it now suffices to prove Proposition 4.7 in the special case $f_0: {\textbf{Bl}}_{\mathbb {A}^n} Z_0 \rightarrow \mathbb {A}^n$. This is done by direct calculation in Proposition 4.11 below, using Lemma 4.10 to reduce to the case $Z_0 = \{0\}$. $\square$

Here is a counter-example suggesting that in Proposition 4.7 we need to at least assume that $\overline{X}$ has rational singularities inside the divisor.

Example 4.8

[Gabber] Suppose $f: \overline{Y}\rightarrow \overline{X}$ is a resolution of singularities of some $\overline{X}$ with non-rational singularities. That is, such that $R^if_*\mathcal {O}_{\overline{Y}} \ne 0$ for some $i > 0$. Suppose that $\overline{X}$ admits a reduced effective Cartier divisor $X^\infty$ containing the singularities such that $Y^\infty = f^*X^\infty$ is also reduced. Then $\underline{M}\mathcal {O}_{(\overline{Y}, Y^\infty )} = \mathcal {O}_{\overline{Y}}$ and $\underline{M}\mathcal {O}_{(\overline{X}, X^\infty )} = \mathcal {O}_{\overline{X}}$ so by assumption $\underline{M}\mathcal {O}_{\mathcal {X}} \rightarrow Rf_*\underline{M}\mathcal {O}_{\mathcal {Y}}$ is not an isomorphism.

An explicit example can be produced by considering the affine cone over an elliptic curve (for example): Suppose that $E \subseteq \mathbb {P}^2_k$ is a smooth curve with $H^1(E, \mathcal {O}_E) \ne 0$, e.g., an elliptic curve, and choose a $\mathbb {P}^1_k \subseteq \mathbb {P}^2_k$ such that $\mathbb {P}^1_k \cap E$ is reduced. Let $CE \subseteq \mathbb {A}^3_k$ be the affine cone over E (we recall a construction below). Let $BE = Bl_{CE} \{0\} \rightarrow CE$ be the blowup of the singular point of CE. Equip CE and BE with the pullbacks $C^\infty$, $B^\infty$ of the effective Cartier divisor $\mathbb {A}^2_k \subseteq \mathbb {A}^3_k$ corresponding to the $\mathbb {P}^1_k \subseteq \mathbb {P}^2_k$ chosen above, and set $\mathcal {B}= (BE, B^\infty )$, $\mathcal {C}= (CE, C^\infty )$. We claim that

$$\begin{aligned} H^1_{{{\text {Zar}}}}(BE, \underline{M}\mathcal {O}_{\mathcal {B}}) \supseteq H_{{{\text {Zar}}}}^1(E, \mathcal {O}_E) \ne 0 \end{aligned}$$

(4.1)

and therefore

$$\begin{aligned} \underline{M}\mathcal {O}_{\mathcal {C}} \rightarrow Rf_*\underline{M}\mathcal {O}_{\mathcal {B}} \end{aligned}$$

is not an isomorphism where $f: BE \rightarrow CE$ is the canonical morphism. Note CE is affine, so $H^1_{{{\text {Zar}}}}(BE, \underline{M}\mathcal {O}_{\mathcal {B}})$ is precisely the space of global sections of the quasi-coherent sheaf $R^1f_*\underline{M}\mathcal {O}_{\mathcal {B}}$.

We recall a construction of BE, CE. To begin with, recall that the blowup $Bl_{\mathbb {A}^3}\{0\}$ of $\mathbb {A}^3$ in the origin is canonically identified with the total space of the line bundle $\mathcal {O}_{\mathbb {P}^2}(1)$ on $\mathbb {P}^2$ via a retraction $\pi : Bl_{\mathbb {A}^3}\{0\} \rightarrow \mathbb {P}^2$ to the exceptional divisor $\mathbb {P}^2 \subseteq Bl_{\mathbb {A}^3}\{0\}$.¹⁵ Then one can define $BE \subseteq Bl_{\mathbb {A}^3} \{0\}$ and $CE \subseteq \mathbb {A}^3$ by forming the Cartesian square on the left and the surjection f. We also have the further Cartesian square on the right coming from the inclusion of the exceptional divisor $\mathbb {P}^2 \subseteq Bl_{\mathbb {A}^3}\{0\}$.

Note $\mathbb {P}^2 \cup \pi ^{-1}\mathbb {P}^1 = g^{-1}\mathbb {A}^2 \subseteq Bl_{\mathbb {A}^3} \{0\}$, so $E \cup \theta ^{-1}(\mathbb {P}^1 \cap E) = B^\infty = f^{-1}C^\infty$.

For the inclusion of Eq. 4.1, first note that since $\mathbb {P}^1_k \cap E$ is reduced, the effective Cartier divisor $B^\infty$ is reduced. Indeed, $\pi$ and therefore $\theta$ is an $\mathbb {A}^1$-bundle. So

$$\begin{aligned} \underline{M}\mathcal {O}_{\mathcal {B}} \cong \mathcal {O}_{BE}. \end{aligned}$$

(4.2)

Since affine schemes have no higher coherent cohomology, we have $R^j\theta _*\mathcal {O}_{BE} = 0$ for $j > 0$ and so the spectral sequence $H^i_{{{\text {Zar}}}}(E, R^j\theta _*\mathcal {O}_{BE}) \implies H^{i+j}_{{{\text {Zar}}}}(BE, \mathcal {O}_{BE})$ gives an isomorphism

$$\begin{aligned} H^1_{{{\text {Zar}}}}(BE, \mathcal {O}_{BE}) \cong H^1_{{{\text {Zar}}}}(E, \theta _*\mathcal {O}_{BE}). \end{aligned}$$

(4.3)

Then by definition¹⁶$BE = {{\underline{\textrm{Spec}}}}\oplus _{i \ge 0} \mathcal {O}_E(i)$ which contains the direct summand $\mathcal {O}_E$:

$$\begin{aligned} \theta _*\mathcal {O}_{BE} \cong \mathcal {O}_E \oplus \mathcal {F}\end{aligned}$$

(4.4)

Combining Eqs. (4.2), (4.3), and (4.4) gives Eq.(4.1).

Remark 4.9

Note that CE in Example 4.8 is normal, since it is regular in codimension one, and complete intersection. The singularity is contained inside the divisor $C^\infty$. Of course, BE is also normal, since it’s an affine bundle over a smooth curve, and therefore also smooth.

Lemma 4.10

For any ring A and for any non-zero divisor $f \in A$, we have

$$\begin{aligned} \underline{M}\mathcal {O}(A[t],f) \cong \underline{M}\mathcal {O}(A,f)[t]. \end{aligned}$$

Proof

Let $I=(f)$. By unpacking the definition of $\underline{M}\mathcal {O}$, we are immediately reduced to showing the equality $\sqrt{I[t]} = \sqrt{I}[t]$ of ideals of A[t]. We first prove $\sqrt{I[t]} \subset \sqrt{I}[t]$. Since $\sqrt{I[t]}$ is the smallest radical ideal containing I[t], it suffices to show that $\sqrt{I}[t]$ is a radical ideal. This means by definition that the quotient ring $A[t]/\sqrt{I}[t]$ is reduced. But this follows from $A[t]/\sqrt{I}[t] \cong A/\sqrt{I} [t]$. To see the opposite inclusion $\sqrt{I[t]} \supset \sqrt{I}[t]$, take any polynomial $\sum _i a_i t^i$ of degree d with $a_i \in \sqrt{I}$. Then for each i, there exists $n_i >0$ such that $a_i^{n_i} \in I$. Take an integer $N > (d+1)\max \{n_i\}$. Then one checks that $(\sum _i a_i t^i)^N \in I[t]$, and hence $\sum _i a_i t^i \in \sqrt{I[t]}$. $\square$

Proposition 4.11

Consider the blowup $f: \overline{B}= {\textbf{Bl}}_{\mathbb {A}^n}\mathbb {A}^d \rightarrow \overline{A}$ of affine space $\overline{A}= {\text {Spec}}(k[t_1, \dots , t_n])$ along a sub-affine space $\mathbb {A}^d \subset \mathbb {A}^n$, equip $\overline{A}$ with the divisor $A^\infty = t_1^{r_1} \dots t_i^{r_i}$ with $r_j, i \ge 1$ and equip $\overline{B}$ with the pullback $B^\infty$ to obtain an abstract admissible blowup $\mathcal {B}= (\overline{B}, B^\infty ) \rightarrow (\overline{A}, A^\infty ) = \mathcal {A}$. Then we have

$$\begin{aligned} \underline{M}\mathcal {O}_{\overline{A}} \cong Rf_*\underline{M}\mathcal {O}_{\overline{B}} \end{aligned}$$

where $\underline{M}\mathcal {O}_{\overline{A}} = \underline{M}\mathcal {O}|_{\overline{A}_{{{\text {Zar}}}}}$ means restriction to the small Zariski site (and similar for $\underline{M}\mathcal {O}_{\overline{B}}$).

Proof

First we reduce the assertion to the case that $d=0$. Note that $\mathbb {A}^n \cong \mathbb {A}^{n-d} \times \mathbb {A}^d$ and $\mathbb {A}^d \cong \{0\} \times \mathbb {A}^d$. These identifications induce an isomorphism

$$\begin{aligned} {\textbf{Bl}}_{\mathbb {A}^n} \mathbb {A}^d \cong ({\textbf{Bl}}_{\mathbb {A}^{n-d}} \{0\}) \times \mathbb {A}^d \end{aligned}$$

since strict transform along a flat morphism is a pullback [26, 0805]. Combining this with Lemma 4.10, we are reduced to the case $\mathbb {A}^d=\{0\}$.

Now assume $\mathbb {A}^d=\{0\}$. Observe that the pullback $f^*|A^\infty |$ of the support $|A^\infty |$ is $f^*|A^\infty | = |B^\infty | + (i{-}1)E$, where E is the exceptional divisor of the blowup. So

$$\begin{aligned} f^*\mathcal {O}(A^\infty {-} |A^\infty |) = \mathcal {O}(f^*A^\infty {-} f^*|A^\infty |)&= \mathcal {O}(B^\infty {-} |B^\infty |) \otimes \mathcal {O}((1{-}i)E)\\&= \mathcal {O}(B^\infty {-} |B^\infty |)(i{-}1). \end{aligned}$$

Since we are dealing with vector bundles, we can apply the projection formula [26, 01E8] to find

$$\begin{aligned} Rf_*(\underline{M}\mathcal {O}_{\overline{B}}) = Rf_*(f^*(\underline{M}\mathcal {O}_{\overline{A}})(1-i)) = \underline{M}\mathcal {O}_{\overline{A}} \otimes _{\mathcal {O}_{\overline{A}}} Rf_*\mathcal {O}_{\overline{B}}(1-i). \end{aligned}$$

So the result follows from the calculation Proposition 4.12 of $Rf_*\mathcal {O}_{\overline{B}}(1-i)$ since we have $1 \le i \le n$ and therefore $-1-n < 1-n \le 1-i \le 0$. $\square$

Proposition 4.12

[Note that the case $i \ge 0$ is treated in [SGA6, VII, Lem. 3.5]] Let k be a ring and write $\mathbb {A}^n:= \mathbb {A}^n_k$ for all $n \ge 0$. Let $f: B_{n+1} = Bl_{\mathbb {A}^{n+1}}\{0\} \rightarrow \mathbb {A}^{n+1}$ be the blowup of affine $(n+1)$-space at the origin, and let $\mathcal {O}(1)$ be the line bundle associated to the exceptional divisor. Set $\mathcal {O}(i):= \mathcal {O}(1)^{\otimes i}$ for all $i \in \mathbb {Z}$. Then $f_*\mathcal {O}(i)$ is the coherent sheaf associated to $I^i$ where I is the ideal of the origin, and we set $I^i:= \Gamma (\mathbb {A}^{n+1}, \mathcal {O}_{\mathbb {A}^{n+1}})$ for $i < 0$. Moreover, we have

$$\begin{aligned} R^qf_*(\mathcal {O}(i)) = 0 \end{aligned}$$

for all $q > 0$ and $i > {-n-1}$.

Proof

The statement about global sections follows from a direct calculation. Indeed, if $\mathbb {A}^n = {\text {Spec}}(k[t_0, \dots , t_n])$, then on the kth standard open

$$\begin{aligned} U_k:= {\text {Spec}}(k[\tfrac{t_0}{t_k}, \dots , t_k, \dots , \tfrac{t_n}{t_k}]) \subset B_{n+1}, \end{aligned}$$

the line bundle $\mathcal {O}(i)$ is the free sub-k-module of $k[t_0, \dots , t_n, t_0^{-1}, \dots , t_n^{-1}]$ generated by monomials $t_0^{r_0} \dots t_n^{r_n}$ such that $r_j \ge 0$ for $j \ne k$, and $r_k \ge i - \sum _{j \ne k} r_j$. The intersection $\bigcap _{k = 0}^n \mathcal {O}(i)(U_k)$ of these groups is the free abelian group generated by monomials $t_0^{r_0} \dots t_n^{r_n}$ subject to the condition $r_0, \dots , r_n \ge 0$ if $i \le 0$, and subject to the further condition $\sum _j r_j \ge i$ if $i \ge 0$. Hence, the claim in the statement.

Next we prove the vanishing assertion. Since $R^qf_*(\mathcal {O}(i))$ is a coherent sheaf on $\mathbb {A}^{n+1}$, it suffices to show that its global section vanishes. Consider the short exact sequences

$$\begin{aligned} 0 \rightarrow \mathcal {O}_{B_{n+1}}(i+1) \rightarrow \mathcal {O}_{B_{n+1}}(i) \rightarrow \phi _*(\mathcal {O}_{\mathbb {P}^{n}}(i)) \rightarrow 0 \end{aligned}$$

where $\phi : \mathbb {P}^{n} \hookrightarrow B_{n+1}$ is the canonical inclusion of the exceptional divisor.

$$\begin{aligned} \cdots \rightarrow R^{q} f_*\mathcal {O}_{B_{n+1}}(i+1) \rightarrow R^{q} f_*\mathcal {O}_{B_{n+1}}(i) \rightarrow R^{q} f_*\phi _*(\mathcal {O}_{\mathbb {P}^{n}}(i)) \rightarrow \cdots . \end{aligned}$$

Moreover, noting that $\phi$ is an affine morphism, we have

$$\begin{aligned} R^{q} f_*\phi _*(\mathcal {O}_{\mathbb {P}^{n}}(i)) = H^q (\mathbb {P}^n,\mathcal {O}_{\mathbb {P}^{n}}(i)), \end{aligned}$$

which is well known to vanish when $i > -(n+1)$, [8, Prop.2.1.12], [26, 01XT]. By Serre vanishing for proper morphisms (which is valid for any noetherian base, see [8, Prop. 2.6.1], [26, Lem. 0B5U]), since $\mathcal {O}(1)$ is ample, there is some N such that $R^qf_*(\mathcal {O}_{B_{n+1}}(i)) = 0$ for all $i \ge N$ and $q > 0$. Therefore, descending induction starting with $i = N$ shows that $R^qf_*\mathcal {O}_{B_{n+1}}(i) = 0$ for $q > 0$ and $i > {-(n+1)}$. $\square$

5 Cube invariance of $R\Gamma (-, \underline{M}\mathcal {O})$

The goal of this section is to prove that the cohomology presheaves of modulus global sections satisfy cube invariance. First we prepare a general criterion for cohomological cube invariance. We will use it in Proposition 5.4 to show cube invariance on nice modulus pairs for $\underline{M}\mathcal {O}$.

Lemma 5.1

Let F be an additive presheaf on ${\mathbf {{\underline{P}}Sm}}_k$, and let $\tau \in \{{{\text {Zar}}},{{\text {Nis}}},{\acute{\textrm{e}}{\textrm{t}}}\}$. Let $\mathcal {X}= (\overline{X},X^\infty )$ be a modulus pair such that $\overline{X}$ is quasi-compact and $F_{\mathcal {X}}$ is a quasi-coherent sheaf of $\mathcal {O}$-modules on the small site $\overline{X}_{\tau }$. Suppose moreover that for any affine open subscheme $\overline{U}= {\text {Spec}}A \subset \overline{X}$ with $U^\infty := X^\infty \cap \overline{U}= {\text {Spec}}A/(f)$ a principal Cartier divisor, the sequence of A-modules

$$\begin{aligned} 0 \rightarrow F(A,f) \rightarrow F(A[t],f) \oplus F(A[\tfrac{1}{t}],f/t) \rightarrow F(A[t,\tfrac{1}{t}],f) \rightarrow 0 \end{aligned}$$

(5.1)

is exact. Then, for any $i \in \mathbb {Z}$, the first projection $\mathcal {X}\boxtimes {\overline{\square }}\rightarrow \mathcal {X}$ induces an isomorphism of abelian groups

$$\begin{aligned} H_\tau ^i (\overline{X}, F_{\mathcal {X}}) \xrightarrow {\sim } H_\tau ^i (\overline{X}\times \mathbb {P}^1, F_{\mathcal {X}\boxtimes {\overline{\square }}}). \end{aligned}$$

Notation 5.2

The operation $\boxtimes$ is the restriction of $\otimes : {\mathbf {{\underline{M}}Cor}}_k \times {\mathbf {{\underline{M}}Cor}}_k \rightarrow {\mathbf {{\underline{M}}Cor}}_k$ to ${\mathbf {{\underline{M}}Sm}}_k$. That is, for modulus pairs $\mathcal {X}, \mathcal {Y}$, the total space of $\mathcal {X}\boxtimes \mathcal {Y}$ is $\overline{X}\times \overline{Y}$ and the divisor is $X^\infty \times \overline{Y}+ \overline{X}\times Y^\infty$. Note that this almost never represents the Cartesian product in ${\mathbf {{\underline{M}}Sm}}_k$.

Proof

It suffices to treat the case $\tau ={{\text {Zar}}}$ since the étale and Zariski cohomology agree if F is a quasi-coherent étale sheaf, [20, Rem.III.3.8]. By Mayer-Vietoris and induction on the minimal size of a finite affine covering of $\overline{X}$, we are reduced to the case when $\overline{X}$ is affine. Let $\mathbb {P}^1 = U_0 \cup U_1$ be the standard open covering. Then, for any $i=0,1$ and $j>1$, we have $H_{{{\text {Zar}}}}^j (\overline{X}\times U_{i},F_{\mathcal {X}\boxtimes {\overline{\square }}}) = 0$ since $\overline{X}\times U_i$ is affine and $F_{\mathcal {X}}$ is quasi-coherent by assumption. Therefore, the Mayer-Vietoris long exact sequence is simplified as

$$\begin{aligned} 0 \rightarrow H_{{{\text {Zar}}}}^0 (\mathbb {P}^1_{\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) \rightarrow H_{{{\text {Zar}}}}^0 (U_{0,\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) \oplus H_{{{\text {Zar}}}}^0 (U_{1,\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) {\mathop {\rightarrow }\limits ^{(*)}} H_{{{\text {Zar}}}}^0 (U_{01,\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}})\nonumber \\ \end{aligned}$$

(5.2)

$$\begin{aligned} \rightarrow H_{{{\text {Zar}}}}^1 (\mathbb {P}^1_{\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) \rightarrow 0, \end{aligned}$$

where $U_{01} = U_0 \cap U_1$, and $(-)_{\overline{X}} = (-) \times \overline{X}$. Note that when $\overline{X}= {\text {Spec}}(A)$, the morphism (*) in Eq. (5.2) is none-other-than the second morphism in the sequence Eq. (5.1) in the statement. Therefore, the right exactness of Eq. (5.1) shows

$$\begin{aligned} H_{{{\text {Zar}}}}^1 (\mathbb {P}^1_{\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) = 0 = H_{{{\text {Zar}}}}^1 (\overline{X},F_{\mathcal {X}}) \end{aligned}$$

and the left exactness of Eq. (5.1) shows $H_{{{\text {Zar}}}}^0 (\mathbb {P}^1_{\overline{X}},F_{\mathcal {X}\boxtimes {\overline{\square }}}) = H_{{{\text {Zar}}}}^0 (\overline{X},F_{\mathcal {X}})$. $\square$

Now, we move on to the proof of the cube invariance of the cohomology of $\underline{M}\mathcal {O}$. We start with the following lemma.

Lemma 5.3

Suppose that A is reduced and f is a nonzero divisor. Then we have

$$\begin{aligned} \underline{M}\mathcal {O}(A[t], f) = \underline{M}\mathcal {O}(A[t], ft). \end{aligned}$$

Proof

The A[t]-module $\underline{M}\mathcal {O}(A[t], f)$ is the image of $\sqrt{fA[t]}$ in $A[t, t^{-1}, f^{-1}]$, under multiplication by $f^{-1}$, and analogously, $\underline{M}\mathcal {O}(A[t], ft)$ is the image of $\sqrt{ftA[t]}$ under multiplciation by $t^{-1}f^{-1}$. So the claimed equality is true as long as $t^{-1}f^{-1}\sqrt{tfA[t]} =f^{-1}\sqrt{fA[t]}$, or equivalently, $\sqrt{tfA[t]} = t\sqrt{fA[t]}$. In the polynomial ring A[t], we always have $\sqrt{(tf)} = \sqrt{(t)} \cap \sqrt{(f)}$ (cf. $Z_{{\text {red}}}\cup Z'_{{{\text {red}}}} = (Z \cup Z')_{{{\text {red}}}}$ for closed subschemes $Z, Z'$), and since our A is reduced, the latter is $(t) \cap \sqrt{(f)}$. So to finish it suffices to see that $(t) \cap \sqrt{(f)} = t \sqrt{(f)}$. Conceptually, this is true because ${{\text {Tor}}}_1^{A[t]}(A[t]/(t), A[t]/\sqrt{(f)}) = 0$. Concretely, for ideals I, J in a general ring R we always have $I \cap J \supseteq IJ$. For $\subseteq$, suppose we choose an element on the left, i.e., $a = tb$ and $a^n = fc$ for some $a, b, c \in A[t]$ and $n \ge 1$. Then $t^nb^n = fc$, so all coefficients of the polynomial $b^n$ are divisible by f. That is, $b \in \sqrt{(f)}$ so $a = tb \in t\sqrt{(f)}$. $\square$

Proposition 5.4

Suppose that (A, f) is a modulus pair with A reduced. Then

$$\begin{aligned} 0 \rightarrow \underline{M}\mathcal {O}(A,f) \rightarrow \underline{M}\mathcal {O}(A[t],f) \oplus \underline{M}\mathcal {O}(A[\tfrac{1}{t}],f/t) \rightarrow \underline{M}\mathcal {O}(A[t, \tfrac{1}{t}],f) \rightarrow 0 \end{aligned}$$

(5.3)

is a short exact sequence. Consequently, for any $\mathcal {X}\in {\mathbf {{\underline{P}}Sm}}_k$ with $\overline{X}$ reduced and for $\tau \in \{{{\text {Zar}}},{{\text {Nis}}},{\acute{\textrm{e}}{\textrm{t}}}\}$, we have

$$\begin{aligned} H^n_{\tau }(\mathcal {X}, \underline{M}\mathcal {O}) = H^n_{\tau }(\mathcal {X}{\boxtimes } {\overline{\square }}, \underline{M}\mathcal {O}). \end{aligned}$$

Proof

Since A is reduced, by Lem. 5.3, we may replace $\underline{M}\mathcal {O}(A[\tfrac{1}{t}],f/t)$ with $\underline{M}\mathcal {O}(A[\tfrac{1}{t}],f)$. Then the sequence Eq.(5.3) is a subsequence of the exact sequence

$$\begin{aligned} 0 \rightarrow A[\tfrac{1}{f}] \rightarrow A[\tfrac{1}{f}][t] \oplus A[\tfrac{1}{f}][\tfrac{1}{t}] \rightarrow A[\tfrac{1}{f}][t, \tfrac{1}{t}] \rightarrow 0. \end{aligned}$$

(5.4)

Exactness of Eq. (5.3) at $\underline{M}\mathcal {O}(A,f)$ follows from left exactness of Eq. (5.4).

Let’s show exactness of Eq. (5.3) in the middle. Suppose that we have a cycle (a, b) in the middle of Eq. (5.3). By exactness of Eq. (5.4), $a = b$ is in $A[\tfrac{1}{f}]$. Moreover, by Lem. 4.1 it satisfies $af, (af)^na \in A[t] \cap A[\tfrac{1}{t}] = A$ for some $n \ge 0$. Hence, it comes from an element of $\underline{M}\mathcal {O}(A, f)$.

Now let’s show right exactness of Eq. (5.3). Suppose that it is not surjective. Choose an element $a = \sum _{i = m}^\ell a_it^i \in \underline{M}\mathcal {O}(A[t, \tfrac{1}{t}], f)$ not in the image. If $\ell \le 0$ or $m \ge 0$, then this element is in the image (because it satisfies $af, (af)^na \in A[t, \tfrac{1}{t}]$ for some n) so we must have $m < 0$ and $\ell > 0$. We prove that the condition $\ell > 0$ leads to a contradiction as follows. Suppose that we have chosen an element such that $\ell$ is minimal. The highest degree term of $(af)^na$ is $(a_\ell t^\ell f)^{n} a_\ell t^\ell$. But then from $af, (af)^na \in A[t, \tfrac{1}{t}]$ we deduce that $a_\ell t^\ell f$ and $(a_\ell t^\ell f)^{n} a_\ell t^\ell$ are in A[t], so $a_\ell t^\ell$ is in the image of $\underline{M}\mathcal {O}(A[t], f)$. Since a is not in the image, $a - a_\ell t^\ell$ is also not in the image, so a did not have minimal $\ell$; a contradiction.

Finally, the second assertion in the statement follows from Lem. 5.1 since $\underline{M}\mathcal {O}|_{\overline{X}_{{\acute{\textrm{e}}{\textrm{t}}}}}$ is quasi-coherent étale sheaf by Prop. 3.4. $\square$

Remark 5.5

The above exactness is false if A is not reduced, as one sees immediately from the example $(A, f) = (k[\epsilon ]/\epsilon ^2, 1)$. Indeed, in this case we have

$$\begin{aligned} \underline{M}\mathcal {O}(A[t], f)&= A[t] \\ \underline{M}\mathcal {O}(A[\tfrac{1}{t}], f/t)&= A[\tfrac{1}{t}] + \langle \epsilon \rangle t \\ \underline{M}\mathcal {O}(A[t, \tfrac{1}{t}], f)&= A[t, \tfrac{1}{t}] \\ \end{aligned}$$

giving global sections of $A + \langle \epsilon \rangle t$, instead of A.

6 Transfers on $\underline{M}\mathcal {O}$

We observe that the structure of presheaf with transfers on $\mathcal {O}$ recalled in Recollections 2.5(2) induces a structure of presheaf with transfers on $\underline{M}\mathcal {O}$.

Lemma 6.1

Let $\mathcal {X}, \mathcal {Y}\in {\mathbf {{\underline{M}}Sm}}_k$ with $\overline{X}$ normal, and $\alpha \in \hom _{{\mathbf {{\underline{M}}Cor}}_k}(\mathcal {X}, \mathcal {Y}) \subseteq \hom _{{\textbf{Cor}}_k}(X^\circ , Y^\circ )$. Then there exists a unique map $\underline{M}\mathcal {O}(\mathcal {Y}) \rightarrow \underline{M}\mathcal {O}(\mathcal {X})$ making the following diagram commute:

Proof

By definition, Rec.2.5(3), there is a morphism of modulus pairs $\mathcal {W}\rightarrow \mathcal {X}$ such that $\overline{W}$ is integral, $\overline{W}\rightarrow \overline{X}$ is proper surjective, $W^\circ \rightarrow X^\circ$ is finite, and the composition $\mathcal {W}\rightarrow \mathcal {X}\rightarrow \mathcal {Y}$ is a finite sum of morphisms of modulus pairs. Normalising, we can assume $\overline{W}$ is integrally closed in $W^\circ$. As such, the morphism $(*)$ in the diagram

certainly exists, and is unique by injectivity of $\underline{M}\mathcal {O}(\mathcal {W}) \subseteq \mathcal {O}(W^\circ )$. By Proposition 4.4 the square on the right is Cartesian, so the morphism $(**)$ also exists and is unique. $\square$

7 Hodge realisation for $\underline{M}\mathcal {O}$

We now combine the above to prove our main theorem for $\underline{M}\mathcal {O}$, Theorem 7.3. The idea is that $R\Gamma _{{{\text {Nis}}}}(-, \underline{M}\mathcal {O})$ can be equipped with transfers, and should be blow up invariant and cube invariant. Sadly, Example 4.8 below shows that $R\Gamma _{{{\text {Nis}}}}(-, \underline{M}\mathcal {O})$ is not blowup invariant without some stricter hypotheses. We use normal crossings.

Notation 7.1

Write ${\mathbf {{\underline{M}}Sm}}_k^{{{\text {nc}}}} \subseteq {\mathbf {{\underline{M}}Sm}}_k$ (resp. ${\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}} \subseteq {\mathbf {{\underline{M}}Cor}}_k$) for the full subcategory of quasi-projective normal crossings modulus pairs.

Remark 7.2

In general, we have the following.

• 1. If $\mathcal {Y}\rightarrow \mathcal {X}$ is an abstract admissible blowup, then $\mathcal {Y}\otimes {\overline{\square }}\rightarrow \mathcal {X}\otimes {\overline{\square }}$ is again an abstract admissible blowup.¹⁷ So any functor on ${\mathbf {{\underline{M}}Cor}}_k$ which sends $\mathcal {X}\otimes {\overline{\square }}\rightarrow \mathcal {X}$ to an isomorphism, also sends $\mathcal {Y}\otimes {\overline{\square }}\rightarrow \mathcal {Y}$ to an isomorphism.

• 2. If $\mathcal {X}\in {\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}}$ then $\mathcal {X}\otimes {\overline{\square }}\in {\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}}$.

If k satisfies (RoS), then we also have:

• (1) The inclusions ${\mathbf {{\underline{M}}Sm}}_k^{{{\text {nc}}}} \subseteq {\mathbf {{\underline{M}}Sm}}_k$ and ${\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}} \subseteq {\mathbf {{\underline{M}}Cor}}_k$ are equivalences of categories.

• (2) Consequently, the canonical comparison functor

  $$\begin{aligned} \frac{D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}}))}{\biggl \langle \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}\otimes {\overline{\square }}) \rightarrow \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}): \mathcal {X}\in {\mathbf {{\underline{M}}Cor}}_k^{{{\text {nc}}}} \biggr \rangle } \rightarrow \frac{D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))}{\biggl \langle \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}\otimes {\overline{\square }}) \rightarrow \mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}): \mathcal {X}\in {\mathbf {{\underline{M}}Cor}}_k \biggr \rangle } \end{aligned}$$

  is an equivalence of categories.

Theorem 7.3

Suppose that k satisfies (RoS) and (WF), Def. A.4, e.g., $char(k) {=} 0$. Then there is a unique object $\underline{M}\mathcal {O}\in {\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}}$ such that for $\mathcal {X}$ with normal crossings we have

$$\begin{aligned} \hom _{{\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}}}(M(\mathcal {X}), \underline{M}\mathcal {O}[n]) \cong H^n_{{{\text {Zar}}}}(\overline{X}, \sqrt{\mathcal {I}} \otimes \mathcal {I}^{-1}) \end{aligned}$$

where $\mathcal {I}$ is the sheaf of ideals associated to $X^\infty$.

Proof

Consider $\underline{M}\mathcal {O}\in {{\textbf{PSh}}}({\mathbf {{\underline{M}}Sm}}_k)$ from Proposition 4.4. By Lemma 6.1 this factors through ${\mathbf {{\underline{M}}Cor}}_k$. Consider its image $\underline{M}\mathcal {O}$ in $D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))$. For any $\mathcal {X}\in {\mathbf {{\underline{M}}Cor}}_k$ we have

$$\begin{aligned} \hom _{D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))}(\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}), \underline{M}\mathcal {O}[n])&=Ext^n(\mathbb {Z}_{{{\text {tr}}}}(\mathcal {X}), \underline{M}\mathcal {O}) \nonumber \\&{\mathop {=}\limits ^{Eq.(2.3)}} H_{{\mathrm {{\underline{M}}Nis}}}^n(\mathcal {X}, \underline{M}\mathcal {O}) \nonumber \\&{\mathop {=}\limits ^{Prop.B.7}} \mathop {\varinjlim }\limits _{\mathcal {Y}\rightarrow \mathcal {X}} H_{{{\text {Nis}}}}^n(\mathcal {Y}, \underline{M}\mathcal {O}) \end{aligned}$$

(7.1)

where the colimit is over abstract admissible blowups. Consider the case that $\mathcal {X}\in {\mathbf {{\underline{M}}Sm}}_k^{{{\text {nc}}}}$. By Proposition A.8 we can assume all $\overline{Y}$ are actual blowups of $\overline{X}$, and by (RoS) we can assume that all $\mathcal {Y}$ are normal crossings. By (WF), such $\mathcal {Y}\rightarrow \mathcal {X}$ are zig zags of abstract admissible blowups $\mathcal {V}\rightarrow \mathcal {W}$ such that $\overline{V}\rightarrow \overline{W}$ is a blowup in a regular centre that has normal crossings with $W^\infty$. Since $\mathcal {X}\in {\mathbf {{\underline{M}}Sm}}_k^{{{\text {nc}}}}$ by Proposition 4.7 (and Theorem 3.7) the functor $H_{{{\text {Nis}}}}^n(-, \underline{M}\mathcal {O})$ sends such $\mathcal {V}\rightarrow \mathcal {W}$ to isomorphisms. So

$$\begin{aligned} \text {Eq.}(7.1) \cong H_{{{\text {Nis}}}}^n(\mathcal {X}, \underline{M}\mathcal {O}); \qquad \text { for normal crossings } \mathcal {X}. \end{aligned}$$

Finally, by Proposition 5.4 we deduce that Eq. (7.1) is cube invariant, at least for normal crossings $\mathcal {X}$. But this is sufficient to deduce that it is cube invariant for all $\mathcal {X}\in {\mathbf {{\underline{M}}Sm}}_k$, Rem.7.2. So $\underline{M}\mathcal {O}$ lies in the full subcategory ${\mathbf {{\underline{M}}DM}}_k^{{{\text {eff}}}} \subseteq D({{\textbf{Shv}}}_{{\mathrm {{\underline{M}}Nis}}}({\mathbf {{\underline{M}}Cor}}_k))$. $\square$

Appendices

Appendix A: Resolution of singularities and weak factorisations

Definition A.1

Let $\mathcal {X}$ be a modulus pair and $Z \subseteq \overline{X}$ a closed subscheme. We will say that Z has strict normal crossings with $X^\infty$ if for every point $x \in \overline{X}$ the local ring $\mathcal {O}_{\overline{X}, x}$ is regular, and there exists a regular system of parameters.¹⁸$t_1,..., t_n \in \mathcal {O}_{\overline{X}, x}$ such that

$$\begin{aligned} X^\infty |_{{\text {Spec}}(\mathcal {O}_{\overline{X}, x})} = \prod _{a \in A} t_a^{r_a}, \qquad \text { and } \qquad Z|_{{\text {Spec}}(\mathcal {O}_{\overline{X}, x})} = {\text {Spec}}(\mathcal {O}_{\overline{X},x} / \langle t_b: b \in B \rangle ) \end{aligned}$$

for some $r_a > 0$ and $A, B \subseteq \{1,..., n\}$.

We will say that Z has normal crossings with $X^\infty$ if there exists an étale covering $\overline{V}\rightarrow \overline{X}$ such that $Z \times _{\overline{X}} \overline{V}$ has strict normal crossings with $V^\infty$. We say that $\mathcal {X}$ is a normal crossings modulus pair if $\varnothing$ has normal crossings with $X^\infty$.

Remark A.2

Note, $A \cap B \ne \varnothing$ is allowed; in particular, $Z \subseteq X^\infty$ is allowed.

Definition A.3

[cf. [1, Sect. 1.2]] Suppose that $f: \mathcal {Y}\rightarrow \mathcal {X}$ is a abstract admissible blowup between normal crossings modulus pairs, such that $\overline{Y}\rightarrow \overline{X}$ is an actual blowup of noetherian qe regular schemes. A weak factorisation of $\mathcal {Y}\rightarrow \mathcal {X}$ is a factorisation of f in ${\mathbf {{\underline{M}}SCH}}$.¹⁹

$$\begin{aligned} \mathcal {Y}= \mathcal {V}_0 {\mathop {\cong }\limits ^{s_1}} \mathcal {V}_1 {\mathop {\cong }\limits ^{s_2}} \mathcal {V}_2 \cong \dots {\mathop {\cong }\limits ^{s_l}} \mathcal {V}_l = \mathcal {X}\end{aligned}$$

such that for each $i = 1, \dots , l$, either $s_i$ or $s_i^{-1}$ is an abstract admissible blowup in ${\mathbf {{\underline{P}}SCH}}$ whose total space $\mathcal {V}_{i-1} \rightarrow \mathcal {V}_i$ (resp. $\mathcal {V}_{i-1} \leftarrow \mathcal {V}_i$) is the blowup of a regular closed subscheme which has normal crossings with $V^\infty _i$ (resp. $V^\infty _{i-1}$).

Definition A.4

Consider the following properties that a field k might satisfy.

• (RoS) For every $\mathcal {X}\in {\mathbf {{\underline{P}}Sm}}_k$, there exists an abstract admissible blowup $\mathcal {Y}\rightarrow \mathcal {X}$ such that $\mathcal {Y}$ is normal crossings and $\overline{Y}\rightarrow \overline{X}$ is an actual blowup.

• (WF) Every abstract admissible blowup $f: \mathcal {Y}\rightarrow \mathcal {X}$ in ${\mathbf {{\underline{P}}Sm}}_k$ such that $\overline{Y}, \overline{X}$ are smooth and $\overline{Y}\rightarrow \overline{X}$ is an actual blowup, admits a weak factorisation.

Theorem A.5

[Resolution of Singularities, [28, Thm.1.1], [9]] Let X be a Noetherian quasi-excellent integral scheme of characteristic zero. Then X admits a semi-strict embedded resolution of singularities. In particular, for every closed subscheme $Z \subseteq X$ there is a blowup $f: X' \rightarrow X$ with centre disjoint from the regular locus of X, such that $X'$ is regular, $Z \times _X X'$ is a normal crossings divisor.

Corollary A.6

If k is characteristic zero then k satisfies (RoS).

Theorem A.7

[Weak Factorisation, cf. [1, Thm.1.2.1]] If k is characteristic zero then k satisfies (WF).

Notice that (RoS) and (WF) deal with actual blowups. To can turn abstract admissible blowups into actual blowups we using the following.

Proposition A.8

[Temkin] Suppose that $\mathcal {Y}\rightarrow \mathcal {X}$ is an abstract admissible blowup in ${\mathbf {{\underline{P}}Sm}}_k$ with $\overline{X}$ quasi-projective (e.g., affine) and integral. Then there exists a second abstract admissible blowup $\mathcal {Y}' \rightarrow \mathcal {Y}$ such that $\overline{Y}' \rightarrow \overline{X}$ is an actual blowup.

Proof

This is essential [29, Cor.3.4.8] which says that any $X^\circ$-modification $\overline{Y}\rightarrow \overline{X}$ is dominated by an $X^\circ$-blow up $\overline{Y}' \rightarrow \overline{X}$. Here $X^\circ$-modification is a factorisation $X^\circ \rightarrow \overline{Y}\rightarrow \overline{X}$ into a schematically dominant morphism $X^\circ \rightarrow \overline{Y}$ and a proper morphism $\overline{Y}{\mathop {\rightarrow }\limits ^{f}} \overline{X}$, and an $X^\circ$-blow up is an $X^\circ$-modification $\overline{Y}' \rightarrow \overline{X}$ such that there exists an f-ample $\mathcal {O}_{\overline{Y}'}$-module $\mathcal {L}$ equipped with a global section which is invertible on $X^\circ$. The existence of the ample sheaf $\mathcal {L}$ implies that f is projective, [26, 0B45], and therefore it is an actual blow up, [19, 8.1.24]. $\square$

Appendix B: Comparison of $\tau$ and ${\mathrm {{\underline{M}}}}\tau$-cohomologies.

Our goal in this subsection is Prop. B.7 which says that the ${\mathrm {{\underline{M}}}}\tau$-cohomology is the colimit over abstract admissible blowups of that $\tau$-cohomology for $\tau = {{\text {Zar}}}, {\acute{\textrm{e}}{\textrm{t}}}$.

The same proof works for ${{\text {fppf}}}$, but we have been diligently avoiding ${\mathbf {{\underline{M}}Sch}}_k$ in this article.

Recollection B.1

[Small sites]

• 1. The small Zariski site $\mathcal {X}_{{{\text {Zar}}}}$ on a modulus pair is the full subcategory of $({\mathbf {{\underline{P}}Sm}}_k)_{/\mathcal {X}}$ whose objects are minimal morphisms $(\overline{U}, U^\infty ) \rightarrow (\overline{X}, X^\infty )$ such that $\overline{U}\rightarrow \overline{X}$ is an open immersion i.e., minimal open immersions. It is canonically equivalent to the small Zariski site $\overline{X}_{{{\text {Zar}}}}$ of the total space $\overline{X}$.

• 2. The small ${\mathrm {{\underline{M}}Zar}}$ site $\mathcal {X}_{{\mathrm {{\underline{M}}Zar}}}$ on a modulus pair is the essential image of $\mathcal {X}_{{{\text {Zar}}}}$. It follows from [12, Lem. 1.32, Thm. 2.13] that all objects of $\mathcal {X}_{{\mathrm {{\underline{M}}Zar}}}$ are of the form

  $$\begin{aligned} \mathcal {V}{\mathop {\rightarrow }\limits ^{t^{-1}}} \mathcal {V}' {\mathop {\rightarrow }\limits ^{f}} \mathcal {X}' {\mathop {\rightarrow }\limits ^{s}} \mathcal {X}\end{aligned}$$

  where s, t are (the images of) abstract admissible blowups in ${\mathbf {{\underline{P}}Sm}}$ and f is the image of a minimal open immersion. Similarly, every morphism in $\mathcal {X}_{{\mathrm {{\underline{M}}Zar}}}$ is also of this form.

• 3. The small sites $\mathcal {X}_{{{\text {Nis}}}}$, $\mathcal {X}_{{\acute{\textrm{e}}{\textrm{t}}}}$, $\mathcal {X}_{{\mathrm {{\underline{M}}Nis}}}$, $\mathcal {X}_{{\underline{\textrm{M}}}\acute{\textrm{e}}{\textrm{t}}}$ are defined analogously.

Lemma B.2

Let $\tau \in \{{{\text {Zar}}},{{\text {Nis}}},{\acute{\textrm{e}}{\textrm{t}}}\}$. Then, for any modulus pair $\mathcal {X}$ over k, the functor

$$\begin{aligned} \alpha : \overline{X}_{\tau } \rightarrow \mathcal {X}_{{\mathrm {{\underline{M}}}}\tau }; \quad \overline{U}\mapsto (\overline{U}, X^\infty \times _{\overline{X}} \overline{U}) \end{aligned}$$

preserves finite limits.

Note that finite limits do exist in $\mathcal {X}_{{\mathrm {{\underline{M}}}}\tau }$, cf.Rec.2.1(6).

Proof

Since $\alpha$ send the terminal object to the terminal object, it suffices to show that it preserves fiber products. This follows from the fact that for any diagram of ambient minimal morphisms $\mathcal {B}\rightarrow \mathcal {A}\leftarrow \mathcal {C}$, the modulus pair

$$\begin{aligned} (\overline{B}\times _{\overline{A}} \overline{C}, \hbox { the pullback of}\ A^\infty ) \end{aligned}$$

represents the fiber product $\mathcal {B}\times _{\mathcal {A}} \mathcal {C}$ in ${\mathbf {{\underline{M}}Sm}}_k$, [12, Prop.1.33]. (Note that this does not hold for non-minimal morphisms). $\square$

Corollary B.3

The functor $\alpha$ in Lemma B.2 commutes with the skeleton functors and the coskeleton functors,²⁰ More precisely, for any simplicial object K in $\overline{X}_\tau$ and for any $n \ge 0$, we have an isomorphism ${{\text {sk}}}_n(\alpha (K)) \cong \alpha ({{\text {sk}}}_n K)$ and ${{\text {cosk}}}_n(\alpha (K)) \cong \alpha ({{\text {cosk}}}_n K)$.

Proof

Since the skeleton functor is induced by the restriction by the inclusion $\Delta _{\le n} \subset \Delta$, we obviously have ${{\text {sk}}}_n( \alpha (K)) = \alpha ({{\text {sk}}}_n K)$. To show the other assertion, by Lemma B.2 it suffices to note that ${{\text {cosk}}}_n$ is constructed by finite limits (see [26, 0183]). $\square$

Lemma B.4

Let $\tau \in \{{{\text {Zar}}},{\acute{\textrm{e}}{\textrm{t}}}\}$. Let $\mathcal {X}$ be a modulus pair over k, and let $\overline{U}_\bullet$ be an n-truncated simplicial object in $\overline{X}_{\tau }$ for some $n \ge 0$. Define an n-truncated simplicial object $\mathcal {U}_\bullet$ in $\mathcal {X}_{{\mathrm {{\underline{M}}}}\tau }$ by $\mathcal {U}_i:= (\overline{U}_i,X^\infty \times _{\overline{X}} \overline{U}_i)$. Then $\overline{U}_\bullet$ is an n-truncated $\tau$-hypercovering if and only if $\mathcal {U}_\bullet$ is an n-truncated ${\mathrm {{\underline{M}}}}\tau$-hypercovering.

Proof

First we treat the case $n=0$. If $\overline{U}_0 \rightarrow \overline{X}$ is a $\tau$-covering, then $\mathcal {U}_0 \rightarrow \mathcal {X}$ is an ${\mathrm {{\underline{M}}}}\tau$-covering by definition of ${\mathrm {{\underline{M}}}}\tau$. Conversely, suppose that $\mathcal {U}_0 \rightarrow \mathcal {X}$ is an ${\mathrm {{\underline{M}}}}\tau$-covering. Since $\overline{U}_0 \rightarrow \overline{X}$ is étale (resp. locally an open immersion) as an object of $\overline{X}_{\acute{\textrm{e}}{\textrm{t}}}$ (resp. $\overline{X}_{{\text {Zar}}}$), it suffices to show that it is surjective. By [12, Cor. 4.21], the associated morphism $\mathcal {U}_0 \rightarrow \mathcal {X}$ in ${\mathbf {{\underline{M}}Sm}}_k$ is refined by a composition of minimal ambient morphisms

$$\begin{aligned} \mathcal {V}\xrightarrow {f} \mathcal {X}' \xrightarrow {s} \mathcal {X}, \end{aligned}$$

where s is an abstract admissible blow-up, and f is a $\tau$-covering. So we have the solid commutative square

in ${\mathbf {{\underline{M}}Sm}}_k$. As we observed in Recollection 2.1 the morphism $\phi$ can be written as a composition $\phi = g \circ t^{-1}$ for some abstract admissible blowup t and some minimal morphism t, giving the dashed morphisms making a commutative triangle. Since t, f and s are surjective on the total spaces, so is $\mathcal {U}_0 \rightarrow \mathcal {X}$.

Next we treat the case $n > 0$. For any $m < n$, consider the canonical morphisms

$$\begin{aligned} c: \overline{U}_{m+1} \rightarrow ({{\text {cosk}}}_m {{\text {sk}}}_m \overline{U}_\bullet )_{m+1} \end{aligned}$$

(7.2)

and

$$\begin{aligned} d: \mathcal {U}_{m+1} \rightarrow ({{\text {cosk}}}_m {{\text {sk}}}_m \mathcal {U}_\bullet )_{m+1}, \end{aligned}$$

where c is a morphism of schemes and d is a morphism in ${\mathbf {{\underline{M}}Sm}}_k$. Since we know that $\overline{U}_0 \rightarrow \overline{X}$ is a $\tau$-covering if and only if $\mathcal {U}_0 \rightarrow \mathcal {X}$ is an ${\mathrm {{\underline{M}}}}\tau$-covering by the base case $n=0$, it remains to show that c is a $\tau$-covering if and only if d is an ${\mathrm {{\underline{M}}}}\tau$-covering. But by Cor. B.3, we may assume that the underlying scheme of ${{\text {cosk}}}_m {{\text {sk}}}_m \mathcal {U}_\bullet$ is given by ${{\text {cosk}}}_m {{\text {sk}}}_m \overline{U}_\bullet$, and hence that d is represented by c. Then the desired assertion follows from the base case $n=0$. $\square$

Lemma B.5

Let $\tau \in \{{{\text {Zar}}},{\acute{\textrm{e}}{\textrm{t}}}\}$, and $\mathcal {X}$ a modulus pair over k. Then, for any finite diagram $\mathcal {U}_\bullet :I \rightarrow \mathcal {X}_{{\mathrm {{\underline{M}}}}\tau }$, there exist an abstract admissible blow-up $\mathcal {X}' \rightarrow \mathcal {X}$ and a finite diagram $\overline{V}_\bullet :I \rightarrow \overline{X}'_{\tau }$ such that $\mathcal {V}_\bullet \rightarrow \mathcal {X}' \rightarrow \mathcal {X}$ is isomorphic to $\mathcal {U}_\bullet \rightarrow \mathcal {X}$, where $\mathcal {V}_i:= (\overline{V}_i,X^\infty \times _{\overline{X}} \overline{V}_i)$ for each $i \in I$.

Proof

We discuss the étale case, but the same argument works for the Zariski case. As we observed in Recollection B.1, every object of $\mathcal {X}_{{\underline{\textrm{M}}}\acute{\textrm{e}}{\textrm{t}}}$ is of the form $\mathcal {V}{\mathop {\rightarrow }\limits ^{t^{-1}}} \mathcal {V}' {\mathop {\rightarrow }\limits ^{f}} \mathcal {X}' {\mathop {\rightarrow }\limits ^{s}} \mathcal {X}$ where s, t are the images in ${\mathbf {{\underline{M}}Sm}}_k$ of abstract admissible blowups, and $\mathcal {V}' \in \mathcal {X}'_{{\acute{\textrm{e}}{\textrm{t}}}}$. So up to replacing $\mathcal {U}_\bullet$ with an isomorphic diagram, and replacing $\mathcal {X}$ with a sufficiently large abstact admissible blowup, we can assume that all $\mathcal {U}_i$ are in the strict image of $\mathcal {X}_{{\acute{\textrm{e}}{\textrm{t}}}} \rightarrow \mathcal {X}_{{\underline{\textrm{M}}}\acute{\textrm{e}}{\textrm{t}}}$ (not just in the essential image).

Again applying Recollection B.1, for every $\phi : i \rightarrow j$ in I, we can write $\mathcal {U}_\phi : \mathcal {U}_i \rightarrow \mathcal {U}_j$ as

$$\begin{aligned} \mathcal {U}_i {\mathop {\rightarrow }\limits ^{t_\phi ^{-1}}} \mathcal {W}_\phi {\mathop {\rightarrow }\limits ^{s_\phi f_\phi }} \mathcal {U}_j \end{aligned}$$

with $f_\phi$, $s_\phi$, $t_\phi$ as above. This gives a new diagram indexed by the barycentric subdivision sd(I) of the directed graph I. Here, sd(I) is the directed graph which has a span $i {\mathop {\leftarrow }\limits ^{\sigma _\phi }} \phi {\mathop {\rightarrow }\limits ^{\psi _\phi }} j$ for every edge $i {\mathop {\rightarrow }\limits ^{\phi }} j$ of I.²¹ By construction, this new diagram factors as $sd(I) {\mathop {\rightarrow }\limits ^{\mathcal {V}}} {\mathbf {{\underline{P}}Sm}}\rightarrow {\mathbf {{\underline{M}}Sm}}$. Now consider the disjoint unions $\mathcal {W}= \sqcup _{Ar(I)} \mathcal {W}_\phi$ and $\mathcal {U}= \sqcup _{Ar(I)} \mathcal {U}_{target(\phi )}$ with the canonical morphisms $\mathcal {W}{\mathop {\rightarrow }\limits ^{t}} \mathcal {U}\rightarrow \mathcal {X}$ in ${\mathbf {{\underline{P}}Sm}}$. By (the proof of) [12, Thm.2.13] there exists an abstract admissible blowup $\mathcal {X}' \rightarrow \mathcal {X}$ in ${\mathbf {{\underline{P}}Sm}}$ such that when we form the pullbacks

in ${\mathbf {{\underline{P}}Sm}}$, the morphism $(*)$ becomes an isomorphism in ${\mathbf {{\underline{P}}Sm}}$. It follows that $\mathcal {X}' \times _\mathcal {X}\mathcal {V}_\bullet : sd(I) \rightarrow {\mathbf {{\underline{P}}Sm}}$ is actually indexed by I, since all “backwards” edges $\sigma _\phi$ of sd(I) are sent to isomorphisms. The horizontal morphisms $(**)$ are abstract admissible blowups, so they assemble to give a natural isomorphism from $\mathcal {X}' \times _\mathcal {X}\mathcal {V}_\bullet$ to $\mathcal {U}_\bullet$ in ${\mathbf {{\underline{M}}Sm}}$. So now we have a diagram in ${\mathbf {{\underline{P}}Sm}}_{/\mathcal {X}}$ whose objects are all in $\mathcal {X}_{{\acute{\textrm{e}}{\textrm{t}}}}$. Since the inclusion $\mathcal {X}_{{\acute{\textrm{e}}{\textrm{t}}}} \rightarrow {\mathbf {{\underline{P}}Sm}}_{/\mathcal {X}}$ is fully faithful, our new diagram factors through $\mathcal {X}_{{\acute{\textrm{e}}{\textrm{t}}}}$. $\square$

Corollary B.4

Let $\tau \in \{{{\text {Zar}}},{\acute{\textrm{e}}{\textrm{t}}}\}$. Let $\mathcal {X}$ be a modulus pair over k, and let $\mathcal {U}_\bullet$ be an n-truncated ${\mathrm {{\underline{M}}}}\tau$-hypercovering of $\mathcal {X}$ in ${\mathbf {{\underline{M}}Sm}}_k$ for some $n \ge 0$. Then there exists an abstract admissible blow-up $\mathcal {X}' \rightarrow \mathcal {X}$ and an n-truncated $\tau$-hypercovering $\overline{U}'_\bullet \rightarrow \overline{X}'$ such that the induced morphism of simplicial objects $\mathcal {U}'_\bullet \rightarrow \mathcal {X}' \rightarrow \mathcal {X}$ is isomorphic to $\mathcal {U}_\bullet \rightarrow \mathcal {X}$, where $\mathcal {U}'_m:= (\overline{U}'_m,X^\infty \times _{\overline{X}} \overline{U}'_m)$ for each $m \le n$.

Proof

By Lem. B.5, there exist an abstract admissible blow-up $\mathcal {X}' \rightarrow \mathcal {X}$ and a simplicial object $\overline{V}_\bullet$ in $\overline{X}'_\tau$ such that $\mathcal {V}_\bullet \rightarrow \mathcal {X}' \rightarrow \mathcal {X}$ is isomorphic to $\mathcal {U}_\bullet \rightarrow \mathcal {X}$, where $\mathcal {V}_\bullet$ is given by $\mathcal {V}_m:= (\overline{V}_m,X^\infty \times _{\overline{X}} \overline{V}_m)$. Since $\mathcal {U}_\bullet \rightarrow \mathcal {X}$ is an n-truncated ${\mathrm {{\underline{M}}}}\tau$-hypercovering and since $(\mathcal {U}_\bullet \rightarrow \mathcal {X}) \cong (\mathcal {V}_\bullet \rightarrow \mathcal {X}')$, Lem. B.4 shows that $\overline{V}_\bullet \rightarrow \overline{X}'$ is an n-truncated $\tau$-hypercovering. $\square$

Proposition B.7

For any modulus pair $\mathcal {X}$ over k and any presheaf of abelian groups $F \in {{\textbf{PSh}}}(\mathcal {X}_{{\mathrm {{\underline{M}}}}\tau })$, we have

$$\begin{aligned} R^n \Gamma _{{\mathrm {{\underline{M}}}}\tau }(\mathcal {X}, F) = \mathop {\varinjlim }\limits _{\mathcal {X}' \rightarrow \mathcal {X}} R^n \Gamma _{\tau }(\overline{X}', F|_{\overline{X}'_{\tau }}) \end{aligned}$$

for all $n\in \mathbb {Z}$ and $\tau \in \{{{\text {Zar}}}, {\acute{\textrm{e}}{\textrm{t}}}\}$, where the colimit is over abstract admissible blowups.

Proof

By Verdier’s hypercovering theorem, [SGA4, Expose V, Sec.7, Thm.7.4.1], for any category with finite limits C equipped with a finitary²² topology $\tau$, and additive presheaf of abelian groups F we have

$$\begin{aligned} H^n_\tau (C, F) \cong \varinjlim _{U_\bullet \rightarrow X} H^n(F(U_\bullet )) \end{aligned}$$

where the colimit is the filtered colimit over the category of m-truncated hypercoverings of the terminal object X and $m > n$. In particular, we have

$$\begin{aligned} R^n \Gamma _{{\mathrm {{\underline{M}}}}\tau }(\mathcal {X}, F) = \mathop {\varinjlim }\limits _{\mathcal {U}_\bullet \rightarrow \mathcal {X}} H^n (F(\mathcal {U}_\bullet )), \end{aligned}$$

and

$$\begin{aligned} \mathop {\varinjlim }\limits _{\mathcal {X}' \rightarrow \mathcal {X}}R^n \Gamma _{\tau }(\overline{X}', F|_{\overline{X}'_{\tau }}) = \mathop {\varinjlim }\limits _{\mathcal {X}' \rightarrow \mathcal {X}}\mathop {\varinjlim }\limits _{\overline{U}'_\bullet \rightarrow \overline{X}'} H^n (F(\mathcal {U}'_\bullet )), \end{aligned}$$

where $\mathcal {U}_\bullet \rightarrow \mathcal {X}$ runs over $(n+1)$-truncated ${\mathrm {{\underline{M}}}}\tau$-hypercoverings of $\mathcal {X}$, $\overline{U}'_\bullet \rightarrow \overline{X}'$ runs over $(n+1)$-truncated $\tau$-hypercoverings of $\overline{X}'$, and $\mathcal {U}'_\bullet := (\overline{U}'_i, X^{\prime \infty } \times _{\overline{X}'} \overline{U}'_i)_i$. Note that there exists a natural morphism

$$\begin{aligned} \mathop {\varinjlim }\limits _{\mathcal {X}' \rightarrow \mathcal {X}}\mathop {\varinjlim }\limits _{\overline{U}'_\bullet \rightarrow \overline{X}'} H^n (F(\mathcal {U}'_\bullet )) \rightarrow \mathop {\varinjlim }\limits _{\mathcal {U}_\bullet \rightarrow \mathcal {X}} H^n (F(\mathcal {U}_\bullet )) \end{aligned}$$

since the index category on the left is contained in the one on the right. It suffices to show the inclusion of the opposite direction, but this is a direct consequence of Corollary B.4. $\square$