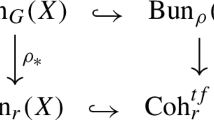Anticanonical geometry of the blow-up of $\mathbb {P}^4$ in 8 points and its Fano model

Abstract

Building on the work of Casagrande–Codogni–Fanelli, we develop our study on the birational geometry of the Fano fourfold $Y=M_{S,-K_S}$ which is the moduli space of semi-stable rank-two torsion-free sheaves with $c_1=-K_S$ and $c_2=2$ on a polarised degree-one del Pezzo surface $(S,-K_S)$. Based on the relation between Y and the blow-up of $\mathbb {P}^4$ in 8 points, we describe completely the base scheme of the anticanonical system $|{-}K_Y|$. We also prove that the Bertini involution $\iota _Y$ of Y, induced by the Bertini involution $\iota _S$ of S, preserves every member in $|{-}K_Y|$. In particular, we establish the relation between $\iota _Y$ and the anticanonical map of Y, and we describe the action of $\iota _Y$ by analogy with the action of $\iota _S$ on S.

1 Introduction

Fano manifolds are classified up to dimension three. There are 10 deformation families of 2-dimensional Fano manifolds, and 105 deformation families of 3-dimensional Fano manifolds (classified by Mori-Mukai and Iskovskih, see [21, 22, 26, 30]).

In dimension 4, toric Fano manifolds have been classified by Batyrev [1] and Sato [28]. The full classification of smooth Fano fourfolds is still to be achieved: only those of index at least two have been completely classified (see [12, 13, 15, 16, 31, 33]). The index one case is not yet complete: Küchle constructed a number of examples with Picard number one, and explained some known results with lists of related problems (see [24]). To find and classify Fano fourfolds of index one, Coates, Corti and others have embarked on a program using mirror symmetry ([6], and see a list of examples in [7]), where heavy computer calculations are involved. A complete classification might not be desirable, but it is interesting to exhibit some Fano fourfolds with special geometric properties, for example, those with Picard number $\rho$ close to the conjectural boundary $\rho \le 18$, or those whose anticanonical system has non-empty base locus. In order to study Fano manifolds with large Picard number (see [3]), Casagrande introduced the invariant called Lefschetz defect, and developed fruitful results in this direction [4, 9].

Let $Y{:}{=}M_{S,-K_S}$ be the moduli spaces of semi-stable rank-two torsion-free sheaves with $c_1=-K_S$, $c_2=2$ on a polarised degree-one del Pezzo surface $(S,-K_S)$. The moduli spaces $Y=M_{S,-K_S}$ form a remarkable family of smooth Fano fourfolds with Picard number 9. As moduli spaces, the birational geometry of Y can be entirely described by the variation of stabitity conditions: the wall-and-chamber structure of the effective cone $\text {Eff}(M_{S,L})$, given by the Mori chamber decomposition, matches up with the wall-and-chamber structure of a convex rational polyhedral cone in $H^2(S,\mathbb {R})$, determined by the stability conditions (see [27, Sect. 2] and [5, Sect. 5]).

The study of this family is motivated by two issues. Firstly, for Fano fourfolds with large Picard number (e.g. at least 7), only few examples which are not products of del Pezzo surfaces are known. As pointed out in [5, Sect. 1,B], the family of Fano fourfolds Y is the only known example of Fano fourfolds with Picard number at least 9, which is not a product of surfaces. Secondly, it is delicate to find examples of Fano fourfolds whose anticanonical system has non-empty base locus, since most Fano fourfolds classified so far are toric, which implies that any ample line bundle on them is globally generated. Some examples are constructed in [20, Chapter 6.3] as complete intersections of two hypersurfaces in weighted projective spaces; two families are identified in [29] as Fano fourfolds with Picard number 3 and having some contraction onto a smooth Fano threefold. In [5, Thm. 1.10], it is shown that the base locus of the anticanonical system $|{-}K_Y|$ has positive dimension. Therefore, the geometry of Y is worth detailed understanding.

A. The anticanonical system of the Fano model Y. The birational geometry of $Y= M_{S,-K_S}$ is related to the birational geometry of the blow-up X of $\mathbb {P}^4$ at 8 points. In [5, Lem. 5.18], an explicit relation between X and Y is given: the Fano fourfold Y is obtained from X by flipping the strict transforms of the lines through all pairs of blown up points and of the quartic curves through 7 blown up points in $\mathbb {P}^4$. Thanks to this relation between X and Y, it is shown in [5, Lem. 7.5, Cor. 7.6] that the base locus of $|{-}K_Y|$ contains the strict transform $R_Y$ of a smooth rational quintic curve passing through the 8 blown up points in $\mathbb {P}^4$, and that $|{-}2K_Y|$ is base-point-free. We complete the study of the anticanonical system and show more precisely that:

Theorem 1.1

For the Fano fourfold $Y{:}{=}M_{S,-K_S}$, the base scheme of $|{-}K_Y|$ is the reduced smooth curve $R_Y$.

As a direct application, we obtain the smoothness of a general member in the anticanonical system.

Corollary 1.2

Let $D\in |{-}K_Y|$ be a general divisor. Then D is smooth.

B. The Bertini involution of the Fano model Y. Now we turn our attention to the automorphism group of Y. In [5, Sect. 4], a group morphism $\rho$ between the Picard groups of the degree-one del Pezzo surface S and of the moduli spaces $Y=M_{S,-K_S}$ is defined. This morphism $\rho$ induces an isomorphism between the automorphism groups of S and of Y (see [5, 6.15]). In particular, there is an involution $\iota _Y$ of Y which is induced by the Bertini involution $\iota _S$ of S.

We mention here that another motivation behind the study of the Bertini involution $\iota _Y$ is the understanding of the corresponding birational involutions $\iota _X$ of X and $\iota _{\mathbb {P}^4}$ of $\mathbb {P}^4$. These birational maps $\iota _X$ and $\iota _{\mathbb {P}^4}$ are classically known, as they can be defined via the Cremona action of the Weyl group $W(E_8)$ on sets of 8 points in $\mathbb {P}^4$ (see [10, 32]). Nevertheless, the classical definitions of $\iota _X$ and $\iota _{\mathbb {P}^4}$ do not give a geometric description of these maps. In [5, Prop. 8.9, Cor. 8.10], a factorisation of these maps is given as smooth blow-ups and blow-downs using the interpretation of X as a moduli space of vector bundles on S. In view of the relation among Y, X and $\mathbb {P}^4$, understanding one of the involutions helps describe the behaviour of the others.

By the analogy of Y and S, one expects that the action of $\iota _Y$ on Y has similar properties as the action of $\iota _S$ on S, where the latter is well understood (see for example [11, 8.8.2]). To emphasize their analogy, we recall that the Bertini involution $\iota _S$ on S can be described as follows. The bianticanonical system $|{-}2K_S|$ is base-point-free and defines a 2:1-cover with image a quadric cone in $\mathbb {P}^3$. The Bertini involution $\iota _S$ is then defined to be the associated covering involution. By construction, the Bertini involution $\iota _S$ on S preserves every element of $|{-}2K_S|$. Since a divisor $D\in |{-}K_S|$ defines an element $2D\in |{-}2K_S|$, we see that $\iota _S$ preserves every divisor in $|{-}K_S|$. In view of the abstract construction of $\iota _Y$ on the Fano fourfold Y, the same method cannot be applied to decide whether $\iota _Y$ preserves every divisor in $|{-}K_Y|$. However, by analysing the anticanonical map of Y, we show that the same property holds for Y.

Theorem 1.3

The Bertini involution $\iota _Y$ of the Fano fourfold $Y{:}{=}M_{S,-K_S}$ preserves every divisor in $|{-}K_Y|$, so we have a factorisation of the anticanonical map $\varphi _{|{-}K_Y|}$:

We will see in Theorem 1.5 that the anticanonical map $\varphi _{|{-}K_Y|}$ has generically degree 4 onto its image, and thus by the above theorem this map factors rationally into two double covers.

To understand the Bertini involution $\iota _Y$ on the Fano fourfold, our approach is analysing its behaviour on a special surface $W_Y$ which is invariant by $\iota _Y$. This surface $W_Y$ is the strict transform of the cubic scroll swept out by the pencil of elliptic normal quintics in $\mathbb {P}^4$ through the 8 blown up points; in particular, it contains the curve $R_Y$. Inspired by the similarity with degree-one del Pezzo surfaces, we study the morphism defined by the restricted bianticanonical system of Y on $W_Y$, and we give the following description of $\iota _Y$ restricted to $W_Y$.

Proposition 1.4

The Bertini involution $\iota _Y$ of the Fano fourfold $Y{:}{=}M_{S,-K_S}$ preserves the surface $W_Y$, and its restriction $\iota _Y|_{W_Y}$ on $W_Y$ is the biregular involution defined by the double covering

$$\begin{aligned}\phi _{|{-}2K_Y|_{W_Y}}:W_Y \rightarrow V_{2,4}\subset \mathbb {P}^7,\end{aligned}$$

where $V_{2,4}\simeq \mathbb {F}_2$ is a rational normal scroll of bidegree (2, 4). In particular, the Bertini involution $\iota _Y$ acts as the identity on the curve $R_Y$ and $\iota _Y$ induces an involution on each elliptic fibre $F_Y$ of $W_Y\rightarrow \mathbb {P}^1$.

Furthermore, there exists a smooth curve $R'\sim 3(R_Y+F_Y)$ of genus 4 on the surface $W_Y$, such that $R'$ is disjoint from $R_Y$ and contained in the fixed locus of $\iota _Y$.

Since $R_Y$ is contained in the fixed locus of the Bertini involution $\iota _Y$, the involution can be lifted to the blow-up $\tilde{Y}$ of Y along the curve $R_Y$. We establish the relation between the resolved anticanonical map and the lifted involution on $\tilde{Y}$ as follows.

Theorem 1.5

Let $\mu :\tilde{Y}\rightarrow Y$ be the blow-up of $Y{:}{=}M_{S,-K_S}$ along the base curve $R_Y$ of $|{-}K_Y|$, and E be the exceptional divisor. Let $f:\tilde{Y}\rightarrow \mathbb {P}(H^0(Y,\mathcal {O}_Y(-K_Y))^{\vee })\simeq \mathbb {P}^5$ be the morphism defined by the base-point-free linear system $|\mu ^*(-K_Y)-E|$. Then f has generically degree 4 with image Q a smooth quadric hypersurface in $\mathbb {P}^5$, and f contracts the strict transform of the surface $W_Y$ to a conic in $\mathbb {P}^5$. Moreover, $f|_E:E\rightarrow f(E)$ is a finite birational morphism such that the image f(E) has degree 4 in $\mathbb {P}^5$.

Furthermore, the Bertini involution $\iota _Y$ of Y can be lifted to $\tilde{Y}$, and the lifted involution $\iota _{\tilde{Y}}$ acts as the identity on E. Moreover, f factors through the quotient $\tilde{Y}/\iota _{\tilde{Y}}$:

As open questions, one may like to understand the quotient $\tilde{Y}/\iota _{\tilde{Y}}$, the geometric interpretation of $\tilde{Y}/\iota _{\tilde{Y}}\rightarrow Q$, and to describe completely the fixed locus of $\iota _{\tilde{Y}}$ (see Lemma 4.16).

Plan. We briefly explain the organisation of the paper. In Sect. 2, we summarise some results in [5], including the geometry of the Fano model $Y{:}{=}M_{S,-K_S}$, the connection between the blow-up X of $\mathbb {P}^4$ at 8 points and the degree-one del Pezzo surface S, and the relation between X and Y. We finish by recalling some basic properties of the Bertini involution of a degree-one del Pezzo surface.

In Sect. 3, we investigate the anticanonical system $|{-}K_Y|$ and the bianticanonical system $|{-}2K_Y|$. We prove Proposition 1.1 by an additional analysis on the simplicial facets of the cone of effective divisors on Y. We also give some auxiliary results on $|{-}K_Y|$ and $|{-}2K_Y|$, which serve as key ingredients in the study of the Bertini involution of Y.

In Sect. 4, we study the action of the Bertini involution of Y. Section 4.1 is devoted to the proof of Proposition 1.4. We study the morphism defined by the bianticanonical system $|{-}2K_Y|$ restricted to the surface $W_Y$. Computations by Macaulay2 show that the image of $W_Y$ is a surface of degree 6 in $\mathbb {P}^7$, which helps us to describe completely the morphism; in particular, the morphism is finite of degree 2 and gives an involution on the surface $W_Y$. By examining the action of this covering involution, we show that it coincides with the Bertini involution $\iota _Y$ restricted to the surface $W_Y$.

In Sect. 4.2, we study the geometry of the anticanonical map of Y. Computations by Macaulay2 show that the image of Y by the antincanonical map is a smooth quadric hypersurface Q in $\mathbb {P}^5$. We are then ready to prove Theorem 1.3. The strategy is to prove by contradiction: we suppose that $\iota _Y$ does not preserve every divisor in $|{-}K_Y|$. We show that in this case, $\iota _Y$ induces a non-trivial involution $\iota _Q$ on Q. We then obtain a contradiction by analysing the fixed locus of the induced involution $\iota _Q$ and by studying the geometry of a special sub-linear systems of $|{-}K_Y|$ consisting of divisors containing the surface $W_Y$. Theorem 1.5 is obtained as a consequence of the study to prove Theorem 1.3.

In Appendix A, we include the code for several computations in Sects. 3 and 4 using the software system Macaulay2.

2 Preliminaries

In this paper we work over the field $\mathbb {C}$.

We fix S a general del Pezzo surface of degree one. We will see in 2.2.1 that we can associate to a degree-one del Pezzo surface S a blow-up X of $\mathbb {P}^4$ at 8 points in general linear position; for general S, the associated X is a blow-up of $\mathbb {P}^4$ at 8 general points. Note that we will need this general condition on the 8 blow-up points in $\mathbb {P}^4$ to apply Lemma 3.1.

Let $M_{S,L}$ be the moduli space of semi-stable (with respect to $L\in \text {Pic}(S)$ ample) rank-two torsion free sheaves $\mathcal {F}$ on S with $c_1(\mathcal {F})=-K_S$ and $c_2(\mathcal {F})=2$. Then it follows from the classical properties of the determinant line bundle that for the polarisation $L=-K_S$, the moduli space $Y{:}{=}M_{S,-K_S}$ is Fano.

For the degree-one del Pezzo surface S, we introduce the following notions (see [5, Sect. 2.1]). A conic on S is a smooth rational curve such that $-K_S\cdot C=2$ and $C^2=0$. Every such conic yields a conic bundle $S\rightarrow \mathbb {P}^1$ having C as fibre. There are 2160 conics (as classes of a curve) in $H^2(S,\mathbb {Z})$. A big divisor h on S which realises S as the blow-up $\sigma :S\rightarrow \mathbb {P}^2$ at 8 distinct points is called a cubic. We have $h=\sigma ^*\mathcal {O}_{\mathbb {P}^2}(1)$. There are 17280 cubics (as classes of a curve) in $H^2(S,\mathbb {Z})$.

Notation 2.1

Given a cubic h, we use the following notation:

• $\sigma _h:S\rightarrow \mathbb {P}^2$ is the birational map defined by h

• $q_1,\dotsc ,q_8\in \mathbb {P}^2$ are the points blown up by $\sigma _h$

• $e_i\subset S$ is the exceptional curve over $q_i$, for $i=1\dotsc ,8$

• $C_i\subset S$ is the transform of a general line through $q_i$, so that $C_i\sim h-e_i$, for $i=1,\dotsc ,8$

• $\ell _{ij}\subset S$ is the transform of the line $\overline{q_iq_j}\subset \mathbb {P}^2$, so that $\ell _{ij}\sim h-e_i-e_j$ and $\ell _{ij}$ is a $(-1)$-curve, for $1\le i<j\le 8$.

2.1 The Fano model Y

By [5, Prop. 1.6], the moduli space $Y{:}{=}M_{S,-K_S}$ is a smooth, rational Fano fourfold with index one and Picard number 9. For such a moduli space Y, the determinant map $\rho :H^2(S,\mathbb {R})\rightarrow H^2(Y,\mathbb {R})$ is an isomorphism (see [5, Thm. 1.3]) and yields a completely explicit description of the relevant cones of divisors $\text {Eff}(Y)$, $\text {Mov}(Y)$ and $\text {Nef}(Y)$, as well as the cone of effective curves $\text {NE}(Y)$. We cite the following statements for the cone of effective divisors $\text {Eff}(Y)$ and the cone of effective curves $\text {NE}(Y)$, and refer the readers to [5, Sect. 6] for the description of the other relevant cones.

Proposition 2.2

[5, Sect. 2.3, Cor. 6.2] The determinant map $\rho :H^2(S,\mathbb {R})\rightarrow H^2(Y,\mathbb {R})$ yields an isomorphism between $\mathcal {E}$ and $\text {Eff}(Y)$, where $\mathcal {E}$ is the subcone of $\text {Nef}(S)$ generated by the conics:

$$\begin{aligned} \mathcal {E}{:}{=}\langle C\,|\,C\text { a conic}\rangle \subset H^2(S,\mathbb {R}). \end{aligned}$$

Hence, the cone $\text {Eff}(Y)$ has 2160 extremal rays, each generated by a fixed divisor $E_C$, where $C\subset S$ is a conic.

Moreover, given a cubic h, $(2h+K_S)^{\perp }\cap \mathcal {E}$ is a simplicial facet (i.e. a face of codimension one) of $\mathcal {E}$, generated by the conics $C_i$ for $i=1,\dots ,8$ (notations as in Notation 2.1). Hence, the fixed divisors $E_{C_i}$ for $i=1,\dots ,8$ generate a simplicial facet of $\text {Eff}(Y)$.

Proposition 2.3

[5, Prop. 1.7] The cone of effective curves $\text {NE}(Y)$ has 240 extremal rays, and is isomorphic to $\text {NE}(S)$. If $\ell$ is a $(-1)$-curve on S, the corresponding extremal ray of $\text {NE}(Y)$ is generated by the class of a line $\Gamma _{\ell }$ in $P_{\ell }\cong \mathbb {P}^2\subset Y$. The corresponding elementary contraction is a small contraction, sending $P_{\ell }$ to a point.

The determinant map $\rho$ also relates the two automorphism groups $\text {Aut}(Y)$ and $\text {Aut}(S)$. By [5, Thm. 1.9], the map $\psi :\text {Aut}(S)\rightarrow \text {Aut}(Y)$ given by $\psi (\phi )[\mathcal {F}]=[(\phi ^{-1})^*\mathcal {F}]$, for $\phi \in \text {Aut}(S)$ and $[\mathcal {F}]\in Y$, is a group isomorphism. In particular, $\text {Aut}(Y)$ is finite; if S is general, then

$$\begin{aligned}\text {Aut}(Y)=\{\text {Id}_Y,\iota _Y\},\end{aligned}$$

where $\iota _Y:Y\rightarrow Y$ is induced by the Bertini involution of S. We still call the involution $\iota _Y{:}{=}\psi (\iota _S)$ of Y the Bertini involution. Explicitly, $\iota _Y:Y\rightarrow Y$ is given (see [5, Def.6.19]) by $\iota _Y([\mathcal {F}])=[\iota _S^*\mathcal {F}]$. We have a commutative diagram:

(1)

Finally, motivated by the analogy with del Pezzo surface of degree one, the study of the base loci of the anticanonical and the bianticanonical linear systems of Y gives the following:

Theorem 2.4

[5, Thm. 1.10] The linear system $|{-}K_Y|$ has a base locus of positive dimension, while the linear system $|{-}2K_Y|$ is base point free.

2.2 The blow-up X of $\mathbb {P}^4$ at 8 general points

2.2.1 Degree one del Pezzo surfaces and blow-ups of $\mathbb {P}^4$ in 8 points

For $S=\text {Bl}_{q_1,\dots ,q_8}\mathbb {P}^2$ and $X=\text {Bl}_{p_1,\dots ,p_8}\mathbb {P}^4$ the blow-ups respectively of $\mathbb {P}^2$ and $\mathbb {P}^4$ at 8 general points, there is a classical association between these two varieties due to Gale duality. Here we give a brief outline on the definition and main properties of the association for readers’ convenience; we refer to [10] for more details. The classical Gale transform is an involution that takes an ordered non-degenerate set $\Gamma \subset \mathbb {P}^2$ of 8 points to an ordered non-degenerate set $\Gamma '\subset \mathbb {P}^4$ of 8 points, defined up to a linear transformation of $\mathbb {P}^4$. More precisely, if we choose homogeneous coordinates so that the points of $\Gamma \subset \mathbb {P}^2$ have as coordinates the rows of the matrix

$M = \begin{pmatrix} I_{3} \\ A \end{pmatrix},$

where $I_{3}$ is an $3\times 3$ identity matrix and A is an $5\times 3$ matrix, then the Gale transform of $\Gamma$ is the set of points $\Gamma '$ whose homogeneous coordinates in $\mathbb {P}^4$ are the rows of the matrix

$M'= \begin{pmatrix} A^T \\ I_{5} \end{pmatrix},$

where $A^T$ is the transpose of A.

Recall that the 8 points of $\Gamma$ (resp. of $\Gamma '$) are in general linear position if every maximal minor of M (resp. of $M'$) is non-zero, or equivalently, every subset of 3 points in $\Gamma$ (resp. of 5 points in $\Gamma '$) spans $\mathbb {P}^2$ (resp. $\mathbb {P}^4$).

Consider the diagonal action of $\text {Aut}(\mathbb {P}^2)$ on $(\mathbb {P}^2)^8$ and similarly the action of $\text {Aut}(\mathbb {P}^4)$ on $(\mathbb {P}^4)^8$. In both cases, every semistable point set is also stable (see [10, page 25, Corollary]). We may thus consider the GIT quotients $P_2^8{:}{=}\big ( (\mathbb {P}^2)^8 \big )^s/\text {Aut}(\mathbb {P}^2)$ and $P_4^8{:}{=}\big ( (\mathbb {P}^4)^8 \big )^s/\text {Aut}(\mathbb {P}^4)$. The Gale transform is an algebraic construction which induces an isomorphism $a:P_2^8\simeq P_4^8$. In particular, to every stable ordered set of 8 points in $\mathbb {P}^2$, we associate a stable ordered set of 8 points in $\mathbb {P}^4$, unique up to projective equivalence, and vice versa.

The two paragraphs below are summarised from [5, 2.21]; for further details of the association, we refer to [5, 2.18]. Let h be a cubic on S. We associate to (S, h) a blow-up X of $\mathbb {P}^4$ in 8 points in general linear position as follows.

Let $q_1,\dotsc ,q_8\in \mathbb {P}^2$ be the points blown up under the birational morphism $S\rightarrow \mathbb {P}^2$ defined by h (the points $q_1,\dots ,q_8$ are in general linear position by [5, Rem. 2.20]), and let $p_1,\dotsc ,p_8\in \mathbb {P}^4$ be the associated points to $q_1,\dotsc ,q_8\in \mathbb {P}^2$ (the points $p_1,\dots ,p_8$ are in general linear position by [5, Lem. 2.19]). Then we set

$$\begin{aligned} X=X_h=X_{(S,h)}\,{:}{=}\, \text {Bl}_{p_1,\dotsc ,p_8}\mathbb {P}^4. \end{aligned}$$

We always assume that $q_1,\dotsc ,q_8\in \mathbb {P}^2$ and $p_1,\dotsc ,p_8\in \mathbb {P}^4$ are associated as ordered sets of point. Note that since the points $q_1,\dots ,q_8$ are in general linear position, they are stable by [10, Chapter II, Thm. 1]. This yields an open subset $U_{dP}\subset P_2^8$. If $(p_1,\dots ,p_8)\in a(U_{dP})$, then $p_1,\dots ,p_8\in \mathbb {P}^4$ are in general linear position. For general S, the associated X is a blow-up of $\mathbb {P}^4$ in 8 general points.

Conversely, let X be a blow-up of $\mathbb {P}^4$ in 8 general points. Differently from the case of surfaces, the blow-up map $X\rightarrow \mathbb {P}^4$ is unique and thus X determines $p_1,\dotsc ,p_8\in \mathbb {P}^4$ up to projective equivalence. The 8 points $p_1,\dots ,p_8\in \mathbb {P}^4$ in turn determine $q_1,\dotsc ,q_8\in \mathbb {P}^2$ up to projective equivalence, and thus a pair (S, h) such that $X\cong X_{(S,h)}$. The pair (S, h) is unique up to isomorphism, therefore S is determined up to isomorphism, and h is determined up to the action of the automorphism group $\text {Aut}(S)$ on cubics.

2.2.2 Notation for the blow-up X of $\mathbb {P}^4$ at 8 points

Let $p_1,\dotsc ,p_8\in \mathbb {P}^4$ be 8 points in general linear position, and set $X{:}{=}\text {Bl}_{p_1,\dotsc ,p_8}\mathbb {P}^4$. We use the following notation:

• $E_i\subset X$ is the exceptional divisor over $p_i\in \mathbb {P}^4$, for $i=1,\dotsc ,8$

• $H\in \text {Pic}(X)$ is the pull-back of $\mathcal {O}_{\mathbb {P}^4}(1)$

• $L_{ij}\subset X$ is the transform of the line $\overline{p_ip_j}\subset \mathbb {P}^4$, for $1\le i<j\le 8$

• $e_i\subset E_i$ is a line, for $i=1,\dotsc ,8$

• $\gamma _i\subset \mathbb {P}^4$ is the rational normal quartic through $p_1,\dotsc ,\check{p}_i,\dotsc ,p_8$, for $i=1,\dotsc ,8$

• $\Gamma _i\subset X$ is the transform of $\gamma _i\subset \mathbb {P}^4$, for $i=1,\dotsc ,8$.

2.3 From the blow-up X to the Fano model Y

We recall the explicit relation between X and Y:

Lemma 2.5

[5, Lem. 5.18] The birational map $\xi :X\dasharrow Y$ is the composition of 36 (K-positive) flips: first the flips of $L_{ij}$ for $1\le i<j\le 8$, and then the flips of $\Gamma _k$ for $k=1,\dotsc ,8$. There is a commutative diagram:

where $\widehat{X}\rightarrow X$ is the blow-up of the curves $L_{ij}$ and $\Gamma _k$, with every exceptional divisor isomorphic to $\mathbb {P}^1\times \mathbb {P}^2$ with normal bundle $\mathcal {O}(-1,-1)$, and $\widehat{X}\rightarrow Y$ is the blow-up of 36 pairwise disjoint smooth rational surfaces.

Notation 2.6

We use the following notation:

• $P_{\ell _{ij}}\subset Y$ is the flipped surface replacing $L_{ij}\subset X$, for $1\le i<j\le 8$

• $P_{e_k}\subset Y$ is the flipped surface replacing $\Gamma _k\subset X$, for $k=1,\dots ,8$.

We will sometimes write $\xi _h:X_h\dasharrow Y$ to stress that $X_h$ and $\xi _h$ depend on the chosen cubic h (while Y does not). Denote by $\eta _h$ the composition map:

2.4 The Bertini involution of S

We recall some basic properties of the Bertini involution of a del Pezzo surface of degree one.

Proposition 2.7

[11, Thm. 8.3.2] Suppose that S is a del Pezzo surface of degree 1. Then

• (i) $|{-}K_S|$ is a pencil of genus 1 curves with smooth general member and one base point;

• (ii) $|{-}2K_S|$ is base-point-free and defines a morphism $\phi _{|{-}2K_S|}:S\rightarrow \mathbb {P}^3$ which is finite of degree 2 with image Q a quadric cone.

The Bertini involution $\iota _S:S\rightarrow S$ is the biregular involution defined by the double covering

$$\begin{aligned}\phi _{|{-}2K_S|}:S\rightarrow Q.\end{aligned}$$

For S general, $\iota _S$ is the unique non-trivial automorphism of S. The pull-back $\iota _S^*$ acts on $\text {Pic}(S)$ (and on $H^2(S,\mathbb {R})$) by fixing $K_S$ and acting as $-1$ on $K_S^{\perp }$ (see [11, §8.8.2]). This yields:

$$\begin{aligned} \iota _S^*\gamma =2(\gamma \cdot K_S)K_S-\gamma \quad \text { for every }\,{\gamma \in H^2(S,\mathbb {R}).} \end{aligned}$$

(2)

The fixed locus of $\iota _S$ is a smooth irreducible curve of genus 4 isomorphic to the branch curve of the double cover and the base point of $|{-}K_S|$. The fixed curve belongs to the linear system $|{-}3K_S|$.

3 Anticanonical and bianticanonical linear systems of the Fano model Y

Let S be a general degree-one del Pezzo surface, and $Y{:}{=}M_{S,-K_S}$ be the associated Fano fourfold. To analyse the anticanonical linear system $|{-}K_Y|$, we introduce a special surface as follows.

Lemma 3.1

[5, Lem. 7.2] Let $p_1,\dotsc ,p_8\in \mathbb {P}^4$ be general points. Then there is a pencil of elliptic normal quintics in $\mathbb {P}^4$ through $p_1,\dotsc ,p_8$, which sweeps out a cubic scroll $W\subset \mathbb {P}^4$.

Let moreover $q_1,\dotsc ,q_8\in \mathbb {P}^2$ be the associated points to $p_1,\dotsc ,p_8\in \mathbb {P}^4$. Then there is a birational map $\alpha :W\rightarrow \mathbb {P}^2$ such that $\alpha (p_i)=q_i$ for $i=1,\dotsc ,8$, $\alpha$ sends the pencil of elliptic normal quintics to the pencil of plane cubics through $q_1,\dotsc ,q_8$, and $\alpha$ is the blow-up of the ninth base point $q_0\in \mathbb {P}^2$ of the pencil of plane cubics.

Remark 3.2

In order to make computations with Macaulay2, we first choose 8 points in $\mathbb {P}^4$ and we verify that the 8 chosen points are in general linear position, i.e. every maximal minor of the matrix whose rows are the homogeneous coordinates of the 8 points is non-zero. Then we verify that there is a pencil of elliptic normal quintic curves through the 8 chosen points and they sweep out a cubic scroll in $\mathbb {P}^4$ (see Listing 4)). In the rest of the paper, all computations with Macaulay2 concerning the linear system $\mathcal {M}$ of quintic hypersurfaces with multiplicity at least 3 at 8 general points use these 8 chosen points.

Let $W'\subset X$ be the transform of the cubic scroll $W\subset \mathbb {P}^4$. By [5, (7.3)], we have the following diagram:

(3)

where $\eta :W'\rightarrow W$ is the blow-up of $p_1,\dotsc ,p_8$, so the composition $\alpha '{:}{=}\alpha \circ \eta :W'\rightarrow \mathbb {P}^2$ is the blow-up of $q_0,\dotsc ,q_8$. Thus $W'$ is isomorphic to the blow-up of S in the base point of $|{-}K_S|$. Hence, there is an elliptic fibration $\pi :W'\rightarrow \mathbb {P}^1$, where the smooth fibres are the transforms of the elliptic normal quintics through $p_1,\dotsc ,p_8$ in $\mathbb {P}^4$, and every fibre is integral.

Lemma 3.3

[5, Lem. 7.4] The surface $W'\subset X$ is disjoint from $L_{ij}$ for $1\le i<j\le 8$ and from $\Gamma _k$ for $k=1,\dotsc ,8$, and $W'$ is contained in the open subset where $\xi :X\dasharrow Y$ is an isomorphism.

We denote by $W_Y$ the strict transform of $W'$ in Y. Then $W_Y\simeq W'$.

Lemma 3.4

[5, Lem. 7.5, Lem. 7.7, Rem. 7.10] We have $(-K_X)_{|W'}=\mathcal {O}_{W'}(R+2F)$ and $R=\text {Bs}|(-K_X)_{|W'}|$, where $F\subset W'$ is a fibre of the elliptic fibration, and $R\subset W'$ is a $(-1)$-curve and a section of the elliptic fibration. The curves R and F satisfy $-K_X\cdot R=-K_X\cdot F=1$ and $E_i\cdot R=E_i\cdot F=1$ for every $i=1,\dots ,8$, so $R\equiv F$ in X and $\xi (R)\equiv \xi (F)$ in Y.

Moreover, let $R_4\subset \mathbb {P}^4$ be the images of R under $\eta :W'\subset X\rightarrow W\subset \mathbb {P}^4$ (see diagram (3)). Then $R_4$ is a smooth rational quintic curve through $p_1,\dotsc ,p_8$

Corollary 3.5

[5, Cor. 7.6] The base locus of $|{-}K_X|$ contains the smooth rational curve R, and the base locus of $|{-}K_Y|$ contains the smooth rational curve $\xi (R)$.

We denote by $R_Y$ the smooth rational curve $\xi (R)$ contained in the base locus of $|{-}K_Y|$, and $F_Y$ a fibre of the elliptic fibration $W_Y\rightarrow \mathbb {P}^1$.

Lemma 3.6

The normal bundle $\mathcal {N}_{R_Y/Y}\cong \mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}^{\oplus 2}.$

Proof

Since $R_4$ is a rational quintic curve in $\mathbb {P}^4$, one has

$$\begin{aligned}\mathcal {N}_{R_4/\mathbb {P}^4}\cong \mathcal {O}_{\mathbb {P}^1}(a)\oplus \mathcal {O}_{\mathbb {P}^1}(b)\oplus \mathcal {O}_{\mathbb {P}^1}(c)\end{aligned}$$

with $a\le b\le c$ and $a+b+c=5\times (4+1)-2=23$ (by [8, first paragraph, p.806]). Since $\mathcal {T}_{\mathbb {P}^4}|_{R_4}\twoheadrightarrow \mathcal {N}_{R_4/\mathbb {P}^4}\rightarrow 0$, one has that $\mathcal {N}_{R_4/\mathbb {P}^4}$ is ample. Hence, we deduce that $a,b,c>0$.

In order to compute the normal bundle of $R_4$ using Macaulay2, we first remark the following: since $R_4$ is a smooth rational curve of degree 5 in $\mathbb {P}^4$, we expect that the normal bundle $\mathcal {N}_{R_4/\mathbb {P}^4}$ splits as equally as possible (see [8, Thm. 2.7]). Since we can measure the positivity of the normal bundle $\mathcal {N}_{R_4/\mathbb {P}^4}$ more precisely by the twist of its dual bundle, and since $\mathcal {O}_{\mathbb {P}^4}(1)\otimes \omega ^*_{R_4}\simeq \mathcal {O}_{\mathbb {P}^1}(7)$, we compute $h^0(R_4,\mathcal {N}^*_{R_4/\mathbb {P}^4}\otimes \mathcal {O}_{\mathbb {P}^4}(1)\otimes \omega ^*_{R_4})$ using Macaulay2 (see Listing 2) and we obtain:

$$\begin{aligned} h^0(R_4,\mathcal {N}^*_{R_4/\mathbb {P}^4}\otimes \mathcal {O}_{\mathbb {P}^4}(1)\otimes \omega ^*_{R_4})=1,\end{aligned}$$

i.e. $h^0(\mathbb {P}^1,\mathcal {O}_{\mathbb {P}^1}(-a+7)\oplus \mathcal {O}_{\mathbb {P}^1}(-b+7)\oplus \mathcal {O}_{\mathbb {P}^1}(-c+7))=1$. Together with $0<a\le b\le c$, we deduce $a=7$ and $b,c>7$. Hence, $b=c=8$. Therefore, by [17, B.6.10], one has

$$\begin{aligned} \mathcal {N}_{R/X}\cong \mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}^{\oplus 2}. \end{aligned}$$

As R is disjoint from the indeterminacy locus of the map $\xi _h$, we deduce

$$\begin{aligned} \mathcal {N}_{R_Y/Y}\cong \mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}^{\oplus 2}. \end{aligned}$$

$\square$

Lemma 3.7

The base locus $\text {Bs}|{-}K_Y|$ is given by $R_Y$, possibly union some other components contained in $\xi (E_k),P_{e_k}$ and $P_{\ell _{ij}}$, for $k=1,\dots ,8$ and $1\le i<j\le 8$. Moreover, the scheme structure of $\text {Bs}|{-}K_Y|$ is generically reduced along $R_Y$.

Proof

In $\mathbb {P}^4$, let $\mathcal {M}$ be the linear system of quintic hypersurfaces with multiplicity at least 3 at 8 general points. Then by Macaulay2 (see Listing 1, also [5, Remark 7.8]), the base ideal $\mathfrak {b}(\mathcal {M})$ is the intersection of the ideals of 28 line $\overline{p_ip_j}$ for $1\le i<j\le 8$, the ideals of 8 rational normal quartic curves $\gamma _k$ for $k=1,\dots ,8$ and the ideal of the rational quintic curve $R_4$ through the 8 points $p_1,\dots ,p_8$. Therefore, in the open subset of Y where $\eta _h:Y\dashrightarrow \mathbb {P}^4$ is an isomorphism, the base scheme of $|{-}K_Y|$ is the reduced curve $R_Y$. Recall that the restriction of $\eta _Y^{-1}:\mathbb {P}^4\dashrightarrow Y$ on the curve $R_4$ is not an isomorphism exactly at the 8 blow-up points of $\mathbb {P}^4$. Hence the base scheme of $|{-}K_Y|$ has reduced scheme structure on the curve $R_Y$ cut out by the 8 points of intersection with the 8 exceptional divisors $\xi (E_1),\dots ,\xi (E_8)$. $\square$

Note that we will see in the proof of Theorem 1.1 that the scheme structure of $\text {Bs}|{-}K_Y|$ is reduced along the curve $R_Y$. This is achieved by choosing another cubic $h'$ on the degree-one del Pezzo surface S and by considering another map $\eta _{h'}:Y\dashrightarrow \mathbb {P}^4$ with different exceptional divisors, so that we get 8 different points of intersection on the curve $R_Y$.

Lemma 3.8

The base locus of the anticanonical system $|{-}K_Y|$ is disjoint from the surfaces $P_{\ell _{ij}}$ and $P_{e_k}$, for $1\le i<j\le 8$ and $k=1,\dots ,8$.

Proof

Consider the commutative diagram in Lemma 2.5:

where $p:\hat{X}\rightarrow X$ is the blow-up of X along the curves $L_{ij}$ and $\Gamma _k$ with every exceptional divisor isomorphic to $\mathbb {P}^1\times \mathbb {P}^2$, and $q:\hat{X}\rightarrow Y$ is the blow-up of 36 pairwise disjoint smooth rational surfaces $P_{\ell _{ij}}$ and $P_{e_k}$, for $1\le i<j\le 8$ and $k=1,\dots ,8$.

Suppose by contradiction that there exists a base point y of $|{-}K_Y|$ contained in some flipped surface that we denote by P (which is one of the surfaces $P_{\ell _{ij}}$ or $P_{e_k}$). Denote by $C\subset X$ the corresponding flipping curve (which is one of the curves $L_{ij}$ or $\Gamma _k$).

Let E be the sum of exceptional divisors over $L_{ij}$ for $1\le i<j\le 8$ and over $\Gamma _k$ for $k=1,\ldots ,8$. Since

$$\begin{aligned} p^*(-K_X)-2E = -K_{\hat{X}}= q^*(-K_Y)-E, \end{aligned}$$

one has

$$\begin{aligned} q^*(-K_Y)=p^*(-K_X)-E. \end{aligned}$$

Let $E_y\simeq \mathbb {P}^1$ be the exceptional fibre in $\hat{X}$ above y. Then $E_y$ is contained in $\text {Bs}|q^*(-K_Y)|=\text {Bs}|p^*(-K_X)-E|$. Moreover, since $E_y$ is the fibre of $q|_{E_P}:E_P\rightarrow P$, where $E_P\simeq \mathbb {P}^1\times \mathbb {P}^2\subset \hat{X}$ is the exceptional divisor over P with $p:E_P\rightarrow C$, we obtain that $E_y\subset E_P$ is mapped surjectively onto C by the map p.

Since the blow-up of the 8 points $X=\text {Bl}_{p_1,\dots ,p_8}\rightarrow \mathbb {P}^4$ is an isomorphism near a general point of C, the base scheme of $|{-}K_X|$ is generically reduced along C by Lemma 3.7. Hence, the linear system $|p^*(-K_X)-E|$ is base-point-free above the generic point of C. This contradicts the fact that $\text {Bs}|p^*(-K_X)-E|$ contains a curve which is mapped surjectively onto C. $\square$

Remark 3.9

More generally, the proof of Lemma 3.8 shows the following. Let X, Y be smooth projective fourfolds. Let $\xi :X\dashrightarrow Y$ be an anti-flip. In [23, Thm. 1.1], Kawamata showed that for smooth projective fourfolds, there exists only one type of flip and it is obtained by blowing up a $\mathbb {P}^2$ with normal bundle $\mathcal {O}_{\mathbb {P}^2}(-1)^{\oplus 2}$ (the exceptional locus of the blowing up is $\mathbb {P}^2\times \mathbb {P}^1$) and blowing down this $\mathbb {P}^2\times \mathbb {P}^1$ to $\mathbb {P}^1$. Thus $\xi$ (anti-)flips a smooth curve $C\subset X$ to a smooth surface $P\subset Y$. If $\text {Bs}|{-}K_X|$ is reduced in the generic point of C, then $|{-}K_Y|$ is base-point-free on P.

Corollary 3.10

The curve $R_Y$ is the unique base curve in $\text {Bs}|{-}K_Y|$ of anticanonical degree 1. Therefore, $R_Y$ is independent of the choice of cubic h.

Proof

By Lemmas 3.7 and 3.8, it suffices to consider the curves contained in some exceptional divisor $\xi (E_i)$, for $i=1,\dots ,8$, which are the possible base curve in $\text {Bs}|{-}K_Y|$ other than $R_Y$.

Let $C\subset \text {Bs}|{-}K_Y|$ be a base curve contained in some exceptional divisor $\xi (E_i)$, for $i=1,\dots ,8.$ Let $\tilde{C}$ be its strict transform in X. By Lemma 3.8, the curve C is disjoint from the indeterminacy locus of $\xi ^{-1}$. Hence, one has $-K_Y\cdot C=-K_X\cdot \tilde{C}$ and $\tilde{C}\subset E_i.$

Since $-K_X=5H-3\sum _{j=1}^8 E_j$, $H\cdot \tilde{C}=0,$ $E_j\cdot \tilde{C}=0$ for $j\ne i$, and $E_i\cdot \tilde{C}\le -1$, one has

$$\begin{aligned}-K_Y\cdot C=-K_X\cdot \tilde{C}\ge 3.\end{aligned}$$

Therefore, the curve $R_Y$ is the unique base curve satisfying $-K_Y\cdot R_Y=-K_X\cdot R=1$. $\square$

Corollary 3.11

Let $B\subset Y$ be an irreducible component of $\text {Bs}|{-}K_Y|$ with reduced scheme structure, which is distinct from $R_Y$. Then for every simplicial facet $\langle E_{C_1},\dots , E_{C_8} \rangle$ of $\text {Eff}(Y)$ (notation as in Notation 2.1 and Proposition 2.2), there exists a unique $E_{C_i}$ for $i=1,\dots ,8$ such that $B\subset E_i$.

Proof

Given a cubic h, consider the simplicial facet $\langle E_{C_1},\dots , E_{C_8} \rangle$ of $\text {Eff}(Y)$, where $C_i\sim h-e_i$ for $i=1,\dots ,8$ (notation as in Notation 2.1). Then $E_{C_i}$ are the strict transforms of the exceptional divisors $E_i\simeq \mathbb {P}^3\subset X_h= X$ under $\xi _h = \xi :X\dashrightarrow Y$.

Since B is distinct from $R_Y$, we deduce that B is contained in some fixed divisor $E_{C_i}$ by Lemmas 3.7 and 3.8. By the construction of the composition of flips $\xi$ (see Lemma 2.5), the intersection of two fixed divisors $E_{C_j}$ and $E_{C_k}$ (for $k\ne j$) is the union of the flipped surfaces $P_{\ell _{jk}}$ and $P_{e_l}$ for $l\ne j,k$. Hence, by Lemma 3.8, the fixed divisor $E_i$ containing B is unique.

$\square$

Proof of Theorem 1.1

We first show that $R_Y$ is the unique irreducible component of the (set-theoretic) base locus of $|{-}K_Y|$.

Let h be a cubic. Let $C_i$ be a conic such that $C_i\sim h-e_i$ for $i=1,\dots ,8$ (notation as in Notation 2.1). Let $E_i{:}{=}E_{C_i}$, where we use the notation of Proposition 2.2. By the same proposition, $E_1,\dots ,E_8$ generate a simplicial facet of $\text {Eff}(Y)$. Suppose by contradiction that there exists another component B distinct from $R_Y$ of the base locus of $|{-}K_Y|$. Then by Corollary 3.11, we may suppose that $B\subset E_1$ and $B\not \subset E_2, E_3,\dots ,E_8.$

Let i, j, k, l be distinct indices in $\{ 1,\dots , 8\}$. Consider the conics $C'_l$ such that $C'_l\sim 2h-e_i-e_j-e_k-e_l$ and the corresponding fixed divisors $F_{ijkl}{:}{=}E_{2h-e_i-e_j-e_k-e_l}$.

Claim. The fixed divisors $E_i,E_j,E_k$ and $F_{ijkl}$ for $l\in \{1,\dots ,8\}$ distinct from i, j, k generate a simplicial facet of $\text {Eff}(Y)$.

Indeed, by Proposition 2.2, it is enough to find a cubic $h'$ such that $2h'+K_S$ is orthogonal to the 8 conics $C_i,C_j,C_k$ and $C'_l$ for $l\in \{1,\dots ,8\}$ distinct from i, j, k.

We take $h'\sim 2h-e_i-e_j-e_k$. Then we can check that

$$\begin{aligned} C_i&\sim h'-\ell _{jk},\\ C_j&\sim h'-\ell _{ik},\\ C_k&\sim h'-\ell _{ij},\\ C'_l&\sim h'-e_l, \end{aligned}$$

and $2h'+K_S$ is orthogonal to the above 8 conics. Moreover, $h'$ is nef and big, and the corresponding birational map $\sigma _{h'}:S\rightarrow \mathbb {P}^2$ contracts the 8 pairwise disjoint $(-1)$-curves $\ell _{jk},\ell _{ik},\ell _{ij},e_l$ for $l\ne i,j,k$. Hence, $h'$ is a cubic. This proves the claim.

We will repeatedly use Corollary 3.11 in the following.

• Consider the simplicial facet generated by $E_1,E_2,E_3,F_{1234},F_{1235},F_{1236},F_{1237},F_{1238}$. Then $B\not \subset F_{1234},F_{1235},F_{1236},F_{1237},F_{1238}.$

• Consider the simplicial facet generated by $E_2,E_3,E_4,F_{1234},F_{2345},F_{2346},F_{2347},F_{2348}$. Then B is contained in one of the fixed divisors $F_{2345},F_{2346},F_{2347},F_{2348}$. We may suppose that $B\subset F_{2345}.$ Then $B\not \subset F_{2346},F_{2347},F_{2348}.$

• Consider the simplicial facet generated by $E_2,E_3,E_5,F_{1235},F_{2345},F_{2356},F_{2357},F_{2358}$. Then $B\not \subset F_{2356},F_{2357},F_{2358}$.

• Consider the simplicial facet generated by $E_2,E_3,E_6,F_{1236},F_{2346},F_{2356},F_{2367},F_{2368}$. Then by what precedes, we know that B is contained in one of the fixed divisors $F_{2367},F_{2368}$. We may suppose that $B\subset F_{2367}$. Then $B\not \subset F_{2368}$.

• Consider the simplicial facet generated by $E_2,E_3,E_7,F_{1237},F_{2347},F_{2357},F_{2367},F_{2378}$. Then $B\not \subset F_{2378}$.

• Finally, consider the simplicial facet generated by $E_2,E_3,E_8,F_{1238},F_{2348},F_{2358},F_{2368},F_{2378}$. Then by what precedes, we know that B is contained in none of these 8 fixed divisors, which contradicts Corollary 3.11.

Therefore, the curve $R_Y$ is the unique irreducible component of the base locus of $|{-}K_Y|$.

Now we show that the base scheme of $|{-}K_Y|$ is the reduced curve $R_Y$, i.e. there are no embedded points. Indeed, given a cubic h, consider the birational map $\eta _h:Y\dashrightarrow \mathbb {P}^4$. By Lemmas 3.7 and 3.8, the base scheme of $|{-}K_Y|$ is the reduced curve $R_Y$ with possible embedded points which have support in the 8 points of intersection with the 8 exceptional divisors of $\eta _h$. By varying h, we may consider another map $\eta _{h'}:Y\dashrightarrow \mathbb {P}^4$ with other 8 exceptional divisors, so that we get 8 different points of intersection on $R_Y$. Such a cubic $h'$ exists because otherwise, there is a base point y on $R_Y$ such that for every simplicial facet $\langle E_{C_1},\dots , E_{C_8} \rangle$ of $\text {Eff}(Y)$ the point y is contained in a unique $E_{C_i}$, and thus we obtain a contradiction by replacing B with y in the above paragraph. Hence, there is no embedded base point on $R_Y$. $\square$

Proof of Corollary 1.2

Since the base scheme $\text {Bs}|{-}K_Y|$ is the smooth curve $R_Y$ by Proposition 1.1, we can apply [25, Prop. 6.8] which implies that a general member in $|{-}K_Y|$ is smooth. $\square$

In the rest of this section, we collect some auxiliary results which will be used in Sect. 4.

Lemma 3.12

For a general point $x\in R_4$ (notation as in Lemma 3.4), there exists a unique divisor in $\mathcal {M}$ which has multiplicity 3 at x: it is the secant variety of the elliptic normal quintic through the nine points $p_1,\dots ,p_8$ and x.

By varying x on $R_4$, one obtains a one-dimensional family Sec of divisors in $\mathcal {M}$ with scheme-theoretic intersection $\text {Bs}Sec$ defined by the ideal $\mathfrak {b}(Sec)$. Then

$$\begin{aligned} (\mathfrak {b}(Sec):\mathfrak {b}(\mathcal {M})):\mathfrak {I}_W=\mathfrak {I}_W, \end{aligned}$$

where the scheme defined by the ideal $\mathfrak {I}_W$ is the reduced surface W.

Proof

We choose a random point x on $R_4$ which is not one of the 8 blown up points. The choice of such a random point is achieved by using the random function in Macaulay2 to generate a random hyperplane in $\mathbb {P}^4$ and intersect the hyperplane with the curve $R_4$ to obtain a point. Let $\mathcal {M}_{x,3}$ be the linear subspace of divisors in $\mathcal {M}$ having multiplicity at least 3 at the point x. Then $\dim \mathcal {M}_{x,3}=0$ by $\mathtt{Macaulay2}$ (see Listing 3) and thus the unique element in $\mathcal {M}_{x,3}$ is the secant variety $Sec(E_x)$, where $E_x$ is the elliptic normal quintic in W passing through the point x and the 8 blown up points.

Let Sec be the family of secant varieties $Sec(E_x)$ for x varying on $R_4$ and $\mathfrak {b}(Sec)$ be the ideal associated to the scheme-theoretic intersection $\text {Bs}Sec$ of the family Sec. Let $\mathfrak {b}_3(Sec)$ be the ideal associated to the scheme-theoretic intersection of three general secant varieties in Sec (obtained by choosing three distinct random points on $R_4$ and intersecting the corresponding secant varieties).

By $\mathtt{Macaulay2}$ (see Listing 4), the quotient $\mathfrak {I}_S{:}{=}(\mathfrak {b}_3(Sec):\mathfrak {b}(\mathcal {M}))$ has degree 6 and dimension 2. Let $\mathfrak {I}_W$ be the ideal of singular locus of the variety defined by $\mathfrak {I}_S$. Then by $\mathtt{Macaulay2}$ (see Listing 4), $\mathfrak {I}_W$ has dimension 2 and degree 3; moreover, the variety defined by $\mathfrak {I}_W$ is smooth and one has $(\mathfrak {I}_S:\mathfrak {I}_W) = \mathfrak {I}_W.$ Since each of these secant varieties in Sec contains the cubic scroll W, we deduce that the variety defined by $\mathfrak {I}_W$ is indeed the surface W.

Let $\mathcal {M}_W$ be the sub-linear system of effective divisors in $\mathcal {M}$ containing the surface W. By Macaulay2 (see Listing 5), the base ideal $\mathfrak {b}(\mathcal {M}_W)$ is equal to $\mathfrak {b}_3(Sec)$. Since Sec is a family of divisors in $\mathcal {M}_W$, we deduce that $\mathfrak {b}_3(Sec)=\mathfrak {b}(Sec)=\mathfrak {b}(\mathcal {M}_W)$. $\square$

Lemma 3.13

The surface $W_Y$ is unique, i.e. $W_Y$ is independent of the choice of cubic h. Therefore, $W_Y$ is disjoint from every one of the loci $P_\ell$ of the small extremal rays of Y.

Proof

Let $Sec_Y$ be the family of the strict transforms in Y of the secant varieties in Sec. Let $\mathcal {M}_{Y,3}$ be the family of divisors in $|{-}K_Y|$ having multiplicity 3 at some point on $R_Y$. Then the two families $\mathcal {M}_{Y,3}$ and $Sec_Y$ are equal, as $\dim \mathcal {M}_{x,3}=0$ for a general point $x\in R_4$ by Lemma 3.12 and $\eta _h$ is an isomorphism at the generic point of $R_4$.

Suppose by contradiction that $W_Y$ depends on h. Then there exist two distinct surfaces $W_{Y,h}$ and $W_{Y,h'}$. Let $\text {Bs}\mathcal {M}_{Y,3}$ be the scheme-theoretic intersection of the family $\mathcal {M}_{Y,3}$. Then by Lemma 3.12, one has the following set-theoretic inclusion:

$$\begin{aligned} \text {Bs}M_{Y,3} \supset W_{Y,h}\cup W_{Y,h'}. \end{aligned}$$

Since $W_{Y,h'}$ contains the curve $R_Y$ which is generically in the locus where $\xi ^{-1}_h:Y\dashrightarrow X_h$ is an isomorphism, we deduce that $W_{Y,h'}$ is not contracted by $\xi ^{-1}_h$.

Since the surface $\xi ^{-1}_h(W_{Y,h'})$ contains the curve R, this surface cannot be contained in any exceptional locus $E_i$, $i=1,\ldots ,8$ of $X_h\rightarrow \mathbb {P}^4$, and thus it cannot be contracted; we denote by $W_{h'}$ its image in $\mathbb {P}^4$. Therefore, $\text {Bs}Sec$ contains two distinct surfaces W and $W_{h'}$, which contradicts Lemma 3.12.

Since by Lemma 3.3 the surface $W_Y$ is disjoint from the indeterminacy locus of the map $\xi ^{-1}_h:Y\dasharrow X_h$, which is a union of some of the loci $P_\ell$ (depending on h), and $W_Y$ is the same for all h, we deduce that $W_Y$ is disjoint from every one of the loci $P_\ell$. $\square$

Lemma 3.14

• (i) We have $h^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))=3$. The restriction

  $$\begin{aligned}r_1:H^0(Y,\mathcal {O}_Y(-K_Y))\rightarrow H^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))\end{aligned}$$

  is surjective.

• (ii) We have $h^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))=8$. The restriction

  $$\begin{aligned}r_2:H^0(Y,\mathcal {O}_Y(-2K_Y))\rightarrow H^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))\end{aligned}$$

  is surjective.

Proof

Since $-K_{W_Y}\sim F_Y$ and $-K_Y|_{W_Y}\sim R_Y+2F_Y$ by Lemma 3.4, by the Riemann-Roch formula one has $\chi (W_Y,-K_Y|_{W_Y})=3$. Since $-K_Y|_{W_Y}$ is ample on $W_Y$ and $-K_{W_Y}$ is nef, by Kodaira vanishing theorem one has

$$\begin{aligned}h^j(W_Y,\mathcal {O}_{W_Y}(-K_Y))=h^j(W_Y,\mathcal {O}_{W_Y}(K_{W_Y}-K_{W_Y}+(-K_Y)))=0\end{aligned}$$

for $j=1,2$. Therefore, $h^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))=3$. The same argument can be applied to obtain $h^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))=8$.

(i) By Macaulay2 (see Listing 5),

$$\begin{aligned} h^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(5)\otimes \mathcal {I}_{p_1,\dots ,p_8}^3\otimes \mathcal {I}_{W})=3. \end{aligned}$$

Since $H^0(Y,\mathcal {O}_{Y}(-K_Y))\simeq H^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(5)\otimes \mathcal {I}_{p_1,\dots ,p_8}^3)$, and the surface $W_Y$ is disjoint from the indeterminacy locus of $\eta _h$ by Lemma 3.3 and $W_Y$ is not contained in the exceptional locus of $\eta _h$, we deduce

$$\begin{aligned} H^0(Y,\mathcal {O}_{Y}(-K_Y)\otimes \mathcal {I}_{W_Y})\simeq H^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(5)\otimes \mathcal {I}_{p_1,\dots ,p_8}^3\otimes \mathcal {I}_{W}). \end{aligned}$$

Hence,

$$\begin{aligned} h^0(Y, \mathcal {O}_{Y}(-K_Y)\otimes \mathcal {I}_{W_Y})=3. \end{aligned}$$

As $h^0(Y,\mathcal {O}_Y(-K_Y))=6$ and $h^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))=3$, we deduce that the restriction morphism

$$\begin{aligned} H^0(Y,\mathcal {O}_Y(-K_Y))\rightarrow H^0(W_Y,\mathcal {O}_{W_Y}(-K_Y)) \end{aligned}$$

is surjective.

(ii) By Macaulay2 (see Listing 7),

$$\begin{aligned} h^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(10)\otimes \mathcal {I}_{p_1,\dots ,p_8}^6\otimes \mathcal {I}_{W})=21. \end{aligned}$$

Since $H^0(Y,\mathcal {O}_{Y}(-2K_Y))\simeq H^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(10)\otimes \mathcal {I}_{p_1,\dots ,p_8}^6)$ and by the same argument as above, we deduce

$$\begin{aligned} H^0(Y,\mathcal {O}_{Y}(-2K_Y)\otimes \mathcal {I}_{W_Y})\simeq H^0(\mathbb {P}^4,\mathcal {O}_{\mathbb {P}^4}(10)\otimes \mathcal {I}_{p_1,\dots ,p_8}^6\otimes \mathcal {I}_{W}). \end{aligned}$$

Hence,

$$\begin{aligned} h^0(Y, \mathcal {O}_{Y}(-2K_Y)\otimes \mathcal {I}_{W_Y})=21. \end{aligned}$$

As $h^0(Y,\mathcal {O}_Y(-2K_Y))=29$ and $h^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))=8$, we deduce that the restriction morphism

$$\begin{aligned} H^0(Y,\mathcal {O}_Y(-2K_Y))\rightarrow H^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y)) \end{aligned}$$

is surjective. $\square$

4 The Bertini involution of the Fano model Y

Let S be a degree-one del Pezzo surface, and $Y{:}{=}M_{S,-K_S}$ be the associated Fano fourfold. In this section, we study the action of the Bertini involution $\iota _Y$ on the Fano fourfold Y, which is analogous to the action of the Bertini involution $\iota _S$ on the surface S. We first notice that by the diagram (1) and the behaviour of $\iota _S$ described in (2), the invariant part of $H^2(Y,\mathbb {R})$ by the action of $\iota _Y$ is $\mathbb {R}K_Y$.

4.1 Action of the Bertini involution on the surface $W_Y$

In this subsection, we further our study of the involution $\iota _Y$ by looking at its action on the surface $W_Y$ (which is the strict transform of the cubic scroll swept out by the pencil of elliptic normal quintics in $\mathbb {P}^4$). The aim of this subsection is to prove Proposition 1.4.

We start by showing that the surface $W_Y$ is invariant by the Bertini involution $\iota _Y$.

Lemma 4.1

The Bertini involution $\iota _Y$ preserves the curve $R_Y$ and the surface $W_Y$. Moreover, $(\iota _Y|_{W_Y})^*(e_i)\sim -2K_Y|_{W_Y}-e_i$ and $(\iota _Y|_{W_Y})^*(F_Y)\sim F_Y$, where $e_i$ is the exceptional curve of $\eta _h|_{W_Y}:W_Y\rightarrow W$ for $i=1,\dots ,8$.

Proof

Since $\iota _Y$ preserves the family of divisors in the anticanonical system $|{-}K_Y|$, the involution $\iota _Y$ preserves the base locus of $|{-}K_Y|$. Thus $\iota _Y(R_Y)=R_Y$ by Proposition 1.1.

Let x be a general point in $R_Y$. Then by Lemma 3.12, there exists a unique divisor in $|{-}K_Y|$ having multiplicity 3 at x: it is the strict transform in Y of the secant variety of the elliptic normal quintic through $p_1,\dots ,p_8$ and $\eta _h(x)$ in $\mathbb {P}^4$. In particular, this divisor has multiplicity 3 along the elliptic fibre of $W_Y$ through x. By varying x in $R_Y$, this gives a one-dimensional family $\mathcal {M}_{Y,3}$ of divisors in $|{-}K_Y|$, which is preserved by $\iota _Y$. On the other hand, the intersection of these divisors is the surface $W_Y$, so $W_Y$ is preserved by $\iota _Y$. Let $D_1\in M_{Y,3}$ and $D_2=\iota _Y(D_1)\in M_{Y,3}$. Let $F_1$ (resp. $F_2$) be the elliptic fibre of $W_Y$ along which $D_1$ (resp. $D_2$) has multiplicity 3. Then $\iota _Y(F_1)=F_2$, and thus $\iota _Y$ preserves the family of elliptic fibres of $W_Y$, i.e. $(\iota _Y|_{W_Y})^*(F_Y)\sim F_Y$.

By [5, 7.12], one has $\iota _Y^*(\xi (E_i))\sim -2K_Y-\xi (E_i)$. Hence, $(\iota _Y|_{W_Y})^*(e_i)\sim -2K_Y|_{W_Y}-e_i.$ $\square$

Now we investigate the morphism defined by the linear system $|{-}2K_Y|_{W_Y}|$.

Proposition 4.2

The linear system $|{-}2K_Y|_{W_Y}|$ defines a finite morphism $\phi :W_Y\rightarrow V\subset \mathbb {P}^7$ of degree 2, where $V=V_{2,4}\simeq \mathbb {F}_2$ is a rational normal scroll of bidegree (2, 4). There is a non-trivial involution i of $W_Y$ such that $\phi =\phi \circ i$. Moreover, i is the identity on $R_Y$ and i induces an involution on each elliptic fibre of $W_Y$.

Proof

Since $h^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))=8$ (see Lemma 3.14), and $|{-}2K_Y|$ is base-point-free by Theorem 2.4, the linear system $|{-}2K_Y|_{W_Y}|$ defines a morphism $\phi :W_Y\rightarrow V\subset \mathbb {P}^7$, where V is the image of $W_Y$.

Claim. V is a surface of degree 6 in $\mathbb {P}^7$, the image of an elliptic fibre $F_Y$ by $\phi$ is a line and the image of $R_Y$ by $\phi$ is a conic.

Since the restriction morphism $H^0(Y,\mathcal {O}_Y(-2K_Y))\rightarrow H^0(W_Y,\mathcal {O}_{W_Y}(-2K_Y))$ is surjective by Lemma 3.14 (ii), the restriction of the morphism $\phi _{|{-}2K_Y|}$ defined by $|{-}2K_Y|$ to the surface $W_Y$ coincides with the morphism $\phi$, i.e. $\phi =\phi _{|{-}2K_Y|}|_{W_Y}$.

In $\mathbb {P}^4$, let $2\mathcal {M}$ be the linear system of hypersurfaces of degree 10 with multiplicity at least 6 at the 8 general points $p_1,\ldots ,p_8$. Consider the map $\phi _{2\mathcal {M}}$ defined by the linear system $2\mathcal {M}$. Then by Macaulay2 (see Listing 8), the image of the surface W by $\phi _{2\mathcal {M}}$ is a surface of degree 6, the image of an elliptic normal quintic through the 8 points by $\phi _{2\mathcal {M}}$ is a line and the image of the rational quintic $R_4$ through the 8 points by $\phi _{2\mathcal {M}}$ is a conic. This proves the claim.

Since $(-2K_Y|_{W_Y})^2=4(R_Y+2F_Y)^2=12$, and the image of $W_Y$ by $\phi$ is of degree 6, we deduce that $\phi$ is of degree 2. As $-K_Y$ is ample, the morphism $\phi$ does not contract any curve and thus it is a finite morphism of degree 2.

Since the linear system $|{-}2K_Y|_{W_Y}|$ has no fixed divisor, the image V is not contained in any hyperplane of $\mathbb {P}^7$ (see for example [2, II.6]), i.e. V is non-degenerate. Hence, V is a non-degenerate irreducible surface of degree 6 (variety of minimal degree) in $\mathbb {P}^7$, and by [18, p. 525] we deduce that V is a rational normal scroll $V_{k,l}$ of bidegree (k, l), with $0\le k\le l$ and $k+l=6$. In particular, V is isomorphic to one of the following: a cone over a rational normal curve of degree 6, $\mathbb {P}^1\times \mathbb {P}^1$, or a Hirzebruch surface $\mathbb {F}_{l-k}$, where the minimal section is mapped to the rational normal curve of degree k, and the fibres are mapped to lines. Therefore, $\phi$ is a finite morphism between two normal surfaces and by [14, (2.3)], there is a non-trivial involution i of $W_Y$ such that $\phi =\phi \circ i$ and $V\simeq W_Y/i$.

Since the restriction of $\phi$ to a general fibre $F_Y$ induces a finite morphism from an elliptic curve to a line $l\subset V$, which cannot be an isomorphism, we deduce that $\phi ^{-1}(l)=F_Y$ as $\phi$ is of degree 2. Hence, i induces an involution on $F_Y$.

Since $-2K_Y|_{W_Y}$ is i-invariant, one has $2(i^*(-K_Y|_{W_Y})-(-K_Y|_{W_Y}))\sim 0$. As $\text {Pic}(W_Y)$ is torsion-free (this is because $W_Y$ is isomorphic to $\mathbb {P}^2$ blown up at 9 points), we deduce that $i^*(-K_Y|_{W_Y})\sim -K_Y|_{W_Y}$. Since $R_Y$ is the base locus of $|{-}K_Y|_{W_Y}|$, the curve $R_Y$ is preserved by i. We claim that $R_Y$ is contained in the ramification locus of $\phi$. Indeed, suppose that $R_Y$ is not contained in the ramification locus of $\phi$. Then there exists a curve $C\subset V$ such that $R_Y=\phi ^*(C)$. As $R_Y$ is a $(-1)$-curve on $W_Y$, one has

$$\begin{aligned} -1=R_Y^2=(\phi ^*(C))^2=\text {deg}\phi \cdot C^2, \end{aligned}$$

i.e. $C^2=-\frac{1}{2}$. Hence, C is not Cartier on V, i.e. V is singular. In view of the classification of minimal degree varieties, we see that V is a cone. But there is no curve with negative self-intersection number on a cone, which leads to a contradiction. Therefore, $R_Y$ is in the ramification locus. As $\phi$ is a double cover, we deduce that i is the identity on $R_Y$.

Let $C=\phi (R_Y)$. Since $R_Y$ is contained in the ramification locus of $\phi$, and every point in $R_Y$ has ramification index 2, one has

$$\begin{aligned} R_Y^2=\bigg (\frac{1}{2}\phi ^*(C)\bigg )^2=\frac{1}{2}C^2. \end{aligned}$$

Since $R_Y$ is a $(-1)$-curve on $W_Y$, one has $C^2=-2$. Therefore, $V=V_{2,4}\simeq \mathbb {F}_2$, and $\phi (R_Y)$ is minimal section of $\mathbb {F}_2$ which is a conic. $\square$

Remark 4.3

Since $\phi$ is a finite morphism of degree 2 between smooth surfaces, the ramification locus is a smooth divisor on $W_Y$ (see [14, (2.5)]). Let e be the minimal section of $V\simeq \mathbb {F}_2$ and f be a fibre of V. Let D be the ramification divisor. Then

$$\begin{aligned} K_{W_Y}\sim \phi ^*(K_S)+D. \end{aligned}$$

As $K_{W_Y}\sim -F_Y=-\phi ^*(f)$, and $K_S\sim -2e-4f$, one has

$$\begin{aligned} D\sim \phi ^*(2e+3f). \end{aligned}$$

Let $B\subset V$ be the branch locus. Then $D=\frac{1}{2}\phi ^*B$ and thus $B\sim 4e+6f$. As e is contained in the branch locus, we can write $B=e+B_1$, where $B_1$ is a smooth curve disjoint from e. Then $B_1\sim 3e+6f$. Notice that $B_1$ is irreducible. Indeed, suppose that $B_1$ has at least two disjoint irreducible components. Then we can decompose $B_1$ as

$$\begin{aligned} B_1 \sim (e + bf) + (2e + (6-b)f) \end{aligned}$$

with $0\le b \le 6$ and $(e + bf)\cdot (2e + (6-b)f)=0$. Hence $b=-2$, which leads to a contradiction.

Hence $D=R_Y + R'$, where $R'\sim \frac{1}{2}\phi ^*(3e+6f)=3(R_Y+F_Y)$ is a smooth curve of genus 4 which is disjoint from $R_Y$.

Remark 4.4

By Macaulay2 (see Listing 13), the bianticanonical morphism $\phi _{|-2K_Y|}$ has generically degree 1, even though its restriction $\phi {:}{=}\phi _{|-2K_Y|}|_{W_Y}:W_Y\rightarrow V\subset \mathbb {P}^7$ to the surface $W_Y$ has degree 2.

Finally, we compare the action of the two automorphisms i and $\iota _Y|_{W_Y}$ on $W_Y$.

Lemma 4.5

Let $e_i$ be the exceptional curves of $\eta _h|_{W_Y}:W_Y\rightarrow W$ for $i=1,\dots ,8$. Then

$$\begin{aligned} i^*(e_i)\sim -2K_Y|_{W_Y}-e_i. \end{aligned}$$

Proof

For $i=1,\dots ,8$, by Macaulay2 (see Listing 9), there exists a unique hypersurface of degree 10 with multiplicity at least 7 at the point $p_i$ and multiplicity at least 6 at $p_j$ for $j\ne i$. Moreover, this hypersurface does not contain the surface W. Therefore, the linear system $|{-}2K_Y|_{W_Y}-e_i|$ is non-empty.

Let $R_i\in |{-}2K_Y|_{W_Y}-e_i|$. Since $-K_Y|_{W_Y}\sim R_Y+2F_Y$, and $R_Y\cdot e_i=F_Y\cdot e_i=1$, one has $R_i^2=-1$, and $R_i\cdot F_Y=R_i\cdot R_Y=1$. Hence, $R_i$ is a $(-1)$-curve on $W_Y$.

Since $e_i+R_i\in |{-}2K_Y|_{W_Y}|=\phi ^*|\mathcal {O}_V(1)|$, one has $R_i\sim i^*(e_i)$. $\square$

Proposition 4.6

The involution i coincides with the restriction of the Bertini involution $\iota _Y$ on the surface $W_Y$, i.e. $\iota _Y|_{W_Y}=i.$

Proof

We first show that $(\iota _Y|_{W_Y})^*=i^*$. By Lemma 4.2, Lemma 4.5 and Lemma 4.1, it is enough to show that $R_Y, F_Y$ and $e_i$ for $i=1,\dots , 8$ form a basis of $H^2(W_Y,\mathbb {R})$.

Since $W'$ is disjoint from the indeterminacy locus of $\xi _h$, it is equivalent to show that R, F and $e_i$ for $i=1,\dots , 8$ form a basis of $H^2(W',\mathbb {R})$. We have the following diagram (see (3)):

where $\alpha$ is the blow-up of $\mathbb {P}^2$ at one point and $\eta$ is the blow-up of W at $p_1,\dots ,p_8$. Moreover, let $e_0\subset W$ be the $(-1)$-curve and $f_0\subset W$ be a fibre of the $\mathbb {P}^1$-bundle on W, then by Lemma 3.1 and Lemma 3.4, one has $F\sim \eta ^*(2e_0+3f_0)-\sum _{i=1}^8 e_i$ and $R\sim \eta ^*(e_0+4f_0)-\sum _{i=1}^8 e_i$. Therefore, R, F and $e_i$ for $i=1,\dots ,8$ form a basis of $H^2(W',\mathbb {R})$.

We have a group homomorphism $\rho _1:\text {Aut}(W_Y)\rightarrow \text {Aut}(H^2(W_Y,\mathbb {R}))$ given by $g\mapsto (g^{-1})^*$. Let $\text {Aut}(R_Y,W_Y)$ be the subgroup of automorphisms in $\text {Aut}(W_Y)$ fixing the curve $R_Y$. We show that the restriction $\rho _1:\text {Aut}(R_Y,W_Y)\rightarrow \text {Aut}(H^2(W_Y,\mathbb {R}))$ is injective, which implies $\iota _Y|_{W_Y}=i$ since $(\iota _Y|_{W_Y})^*=i^*$.

Since $R_Y$ is a $(-1)$-curve on $W_Y$, by blowing down $R_Y$, we obtain a rational surface $S'$ with $(-K_{S'})^2=1$, and the curve $R_Y$ is contracted to a point $x_0\in S'$. We denote by $\beta :W_Y\rightarrow S'$ the blow-up of $S'$ at $x_0$. Since $-K_{W_Y}$ is nef, we obtain that $-K_{S'}$ is nef by the projection formula (see for example [19, Appendix A, A4]). Moreover, since every fibre of $W_Y\rightarrow \mathbb {P}^1$ is integral, there is no $K_{S'}$-trivial curve. Hence, $S'$ is a del Pezzo surface of degree one. By [11, Prop. 8.2.39], the homomorphism $\rho _2:\text {Aut}(S')\rightarrow \text {Aut}H^2(S',\mathbb {R})$ is injective.

Let $\text {Aut}(x_0,S')$ be the subgroup of automorphisms in $\text {Aut}(S')$ fixing the point $x_0$. Then $\text {Aut}(x_0,S')\simeq \text {Aut}(R_Y,W_Y)$. Since $\text {Pic}(W_Y)\simeq \beta ^*\text {Pic}(S')\oplus \mathbb {Z}[R_Y]$, the image $\rho _1(\text {Aut}(R_Y,W_Y))$ is contained in a subgroup $G_1$ of $\text {Aut}(H^2(W_Y,\mathbb {R}))$ such that $G_1\simeq \text {Aut}(H^2(S',\mathbb {R}))$. Hence, we have the following diagram:

Since $\rho _2$ is injective, the restriction $\rho _1:\text {Aut}(R_Y,W_Y)\rightarrow G_1\subset \text {Aut}(H^2(W_Y,\mathbb {R}))$ is injective. $\square$

Proof of Proposition 1.4

The first paragraph follows from Lemma 4.1, Proposition 4.2 and Proposition 4.6. The second paragraph follows from Remark 4.3. $\square$

4.2 Action of the Bertini involution on the anticanonical system

In this subsection, we study the action of the involution $\iota _Y$ on the anticanonical system $|{-}K_Y|$. This is closely related to the anticanonical map of $Y= M_{S,-K_S}$.

Lemma 4.7

Let $\mu :\tilde{Y}\rightarrow Y$ be the blow-up of Y along the curve $R_Y$ which is the base scheme of $|{-}K_Y|$. Let E be the exceptional divisor and $\tilde{D}$ be the strict transform of a general member $D\in |{-}K_Y|$. Then $|\tilde{D}|=|\mu ^*(-K_Y)-E|$ is base-point-free and induces a morphism $f:\tilde{Y}\rightarrow \mathbb {P}(H^0(Y,\mathcal {O}_Y(-K_Y))^{\vee })\simeq \mathbb {P}^5$ with image Q a smooth quadric hypersurface, and f has generically degree 4. We have the following commutative diagram:

(4)

The following statements hold:

• (i) The Bertini involution $\iota _Y$ can be lifted to an involution $\iota _{\tilde{Y}}$ of $\tilde{Y}$, which preserves the exceptional divisor E and induces an involution on each $\mathbb {P}^2$ above a point of $R_Y$.

• (ii) The Bertini involution $\iota _Y$ induces a regular involution $\iota _{\mathbb {P}^5}$ of $\mathbb {P}^5$, which preserves the quadric hypersurface Q. Denote by $\iota _Q$ its restriction on Q. Then $\iota _Q\circ f=f\circ \iota _{\tilde{Y}}$.

Proof

In $\mathbb {P}^4$, let $\mathcal {M}$ be the linear system of quintic hypersurfaces with multiplicity at least 3 at 8 general points. Then by Macaulay2 (see Listing 10), the image of $\mathbb {P}^4$ by the map defined by $\mathcal {M}$ is a smooth quadric hypersurface Q in $\mathbb {P}^5$.

Let E be the exceptional divisor of f. Since

$$\begin{aligned}\mu ^*(-K_Y)^4=(-K_Y)^4=13,\end{aligned}$$

$$\begin{aligned}\mu ^*(-K_Y)\cdot E^3=-K_Y\cdot R_Y=1,\end{aligned}$$

$$\begin{aligned}\mu ^*(-K_Y)^3\cdot E=\mu ^*(-K_Y)^2\cdot E^2=0,\end{aligned}$$

$$\begin{aligned}E^4=-K_Y\cdot R_Y+2g(R_Y)-2 =-1,\end{aligned}$$

one has $\widetilde{D}^4=8$. Hence $\phi _{|{-}K_Y|}$ (and also f) has generically degree 4.

• (i) Follows from the fact that $R_Y$ is contained in the fixed locus of $\iota _Y$ (see Proposition 1.4).

• (ii) The pull-back $\iota _Y^*$ induces an involution on $H^0(-K_Y,\mathcal {O}_Y(-K_Y))$, and thus an involution of $\mathbb {P}(H^0(Y,\mathcal {O}_Y(-K_Y))^{\vee })\simeq \mathbb {P}^5$ preserving $\phi _{|{-}K_Y|}(Y)=Q$.

Let $s\in H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\tilde{D}))$ be a global section which is zero at the point $\iota _{\tilde{Y}}(x)$, where x is a point in $\tilde{Y}$. Then for $s'{:}{=}\iota _{\tilde{Y}}^*(s)\in H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\iota _{\tilde{Y}}^*\tilde{D}))\simeq H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\tilde{D}))$, one has

$$\begin{aligned} s'(x)=(\iota _{\tilde{Y}}^*(s))(x)=s(\iota _{\tilde{Y}}(x))=0. \end{aligned}$$

Hence,

$$\begin{aligned}\phi _{|\tilde{D}|}(\iota _{\tilde{Y}}(x))=\{ s\in H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\tilde{D})) \mid s(\iota _{\tilde{Y}}(x))=0\},\\\phi _{|\iota _{\tilde{Y}}^*\tilde{D}|}(x)=\{ s'\in H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\iota _{\tilde{Y}}^*\tilde{D})) \mid s'(x)=0\}.\end{aligned}$$

Therefore, we obtain the following commutative diagram:

Thus, $\iota _Q\circ f=f\circ \iota _{\tilde{Y}}$. $\square$

Remark 4.8

The following statements are equivalent:

• (a) The Bertini involution $\iota _Y$ preserves every divisor in $|{-}K_Y|$.

• (b) The action $\iota _Y^*:H^0(Y,\mathcal {O}_Y(-K_Y))\rightarrow H^0(Y,\mathcal {O}_Y(-K_Y))$ is $\text {Id}$ or $-\text {Id}$.

• (c) The involution $\iota _{\mathbb {P}^5}$ of $\mathbb {P}^5$ (resp. $\iota _Q$ of Q) is the identity.

Recall that we have a special surface $W_Y\subset Y$ containing $R_Y$, which is an elliptic fibration $W_Y\rightarrow \mathbb {P}^1$ with fibre $F_Y$. With the same notation as in Lemma 4.7, we describe the image of $W_Y$ in $Q\subset \mathbb {P}^5$.

Lemma 4.9

Every elliptic fibre $F_Y$ (resp. its strict transform $\tilde{F}_Y\subset \tilde{Y}$) is contracted by $\phi _{|{-}K_Y|}$ (resp. by f). Moreover, the image of the surface $W_Y$ (resp. its strict transform $\tilde{W}_Y\subset \tilde{Y}$) is a conic C in $Q\subset \mathbb {P}^5$.

Furthermore, the curve $\tilde{R}_Y{:}{=}\tilde{W}_Y\cap E$ is contained in the fixed locus of $\iota _{\tilde{Y}}$, and the conic C is contained in the fixed locus of $\iota _Q$.

Proof

Since $-K_Y\cdot F_Y=1$, one has $\tilde{D}\cdot \tilde{F}_Y=0$, where $\tilde{D}$ is the strict transform of a general member $D\in |{-}K_Y|$. Hence f contracts the elliptic fibres of $\tilde{W}_Y$ and $f(\tilde{W}_Y)$ is a curve.

As $-K_Y|_{W_Y}=R_Y+2F_Y$, one has $\tilde{D}|_{\tilde{W}_Y}=(\mu ^*(-K_Y)-E)|_{\tilde{W}_Y}=2\tilde{F}_Y$. Moreover, since $\tilde{D}$ is the pullback by f of a hyperplane in $\mathbb {P}^5$ and $\tilde{W}_Y$ is contracted by f to a curve in $\mathbb {P}^5$, we deduce that the curve $f(\tilde{W}_Y)$ has degree 2, i.e. the morphism f sends $\tilde{W}_Y$ to a conic in $\mathbb {P}^5$.

By Lemma 4.7 (i), $\iota _{\tilde{Y}}$ induces an involution on each fibre $\mathbb {P}^2$ of $\mu |_E:E\rightarrow R_Y$. Since $W_Y$ is preserved by $\iota _Y$ by Proposition 1.4, its transform $\tilde{W}_Y\subset \tilde{Y}$ is also preserved by $\iota _{\tilde{Y}}$. Therefore, the curve $\tilde{R}_Y{:}{=}\tilde{W}_Y\cap E$ (which is a section of $\mu |_E$) is invariant. Since $R_Y$ is in the fixed locus of $\iota _Y$ by Proposition 1.4, it follows that $\tilde{R}_Y$ is contained in the fixed locus of $\iota _{\tilde{Y}}$. By Lemma 4.7 (ii), $f(\tilde{R}_Y)=f(\tilde{W}_Y)=C$ is contained in the fixed locus of $\iota _{Q}$. $\square$

The rest of this subsection is devoted to the proofs of Theorems 1.3 and 1.5. To show that $\iota _Y$ preserves every divisor in $|{-}K_Y|$, our strategy is to exclude the other remaining case by analysing the anticanonical map.

Lemma 4.10

If the action $\iota _Y^*$ on $H^0(Y,\mathcal {O}_Y(-K_Y))$ is not $\pm \text {Id}$, then

$$\begin{aligned}H^0(Y,\mathcal {O}_Y(-K_Y))=V_1\oplus V_2,\end{aligned}$$

where $V_1$ is the sub-vector space of global sections vanishing on the surface $W_Y$, and $V_2$ is uniquely determined as eigenspace corresponding to the eigenvalue 1 or $-1$ of $\iota _Y^*$, with $\dim V_1=\dim V_2=3$. More precisely, $\iota _Y^*$ acts as $\text {Id}$ or $-\text {Id}$ on $V_i$ for $i=1,2$.

Proof

In $\mathbb {P}^4$, let $\mathcal {M}$ be the linear system of quintic hypersurfaces with multiplicity at least 3 at 8 general points. Let $\mathcal {M}_W$ be the sub-linear system of effective divisors in $\mathcal {M}$ containing the surface W. By $\mathtt{Macaulay2}$ (see Listing 5), one has $\mathfrak {b}(\mathcal {M}_W) = \mathfrak {b}(Sec)$ (see Lemma 3.12 for notation) for the base ideals. Moreover, if $v_1,v_2$ and $v_3$ form a basis of $H^0(\mathbb {P}^4,\mathcal {I}_W\otimes \mathcal {O}_{\mathbb {P}^4}(5)\otimes \mathcal {I}_{p_1,\dots ,p_8}^3)\simeq \mathbb {C}^3$, and if we pick three scalars $\lambda _1$, $\lambda _2$ and $\lambda _3$ generated by the random function in $\mathtt{Macaulay2}$, then the effective divisor in $\mathcal {M}_W$ defined by the global section $\lambda _1v_1+\lambda _2v_2+\lambda _3v_3$ is singular along two elliptic normal quintic curves $E_p, E_q$ through the 8 blown up points (by $\mathtt{Macaulay2}$, see Listing 6); note that the two elliptic curves may coincide, in which case the divisor has multiplicity at least 3 along this elliptic curve, and in fact the divisor is the secant variety of the elliptic curve. Moreover, there exists a unique divisor in $\mathcal {M}_W$ which is singular along $E_p$ and $E_q$, as $H^0(\mathbb {P}^4,\mathcal {I}_W\otimes \mathcal {O}_{\mathbb {P}^4}(5)\otimes \mathcal {I}_{p_1,\dots ,p_8}^3)\simeq H^0(\mathbb {P}^1,\mathcal {O}_{\mathbb {P}^1}(2))\simeq \mathbb {C}^3$.

Let $V_1\subset H^0(Y,\mathcal {O}_Y(-K_Y))$ be the sub-vector space of global sections vanishing on the surface $W_Y$. Let $|V_1|$ be the corresponding sub-linear system (i.e. the linear system of effective divisors in $|{-}K_Y|$ containing the surface $W_Y$). Then $\iota _Y$ preserves the family of divisors in $|V_1|$, as $\iota _Y$ preserves the surface $W_Y$ by Proposition 1.4. Since $W_Y$ is disjoint from the indeterminacy locus of the map $\eta _h:Y\dashrightarrow \mathbb {P}^4$, and the intersection of $W_Y$ with the exceptional locus of $\eta _h$ is the union of 8 points, we deduce that a general member in $|V_1|$ is singular along two elliptic fibres $F_{Y,1}, F_{Y,2}$ of $W_Y$, and there exists a unique divisor in $|V_1|$ which is singular along $F_{Y,1}$ and $F_{Y,2}$. Since $\iota _Y$ preserves every elliptic fibre $F_Y$ of $W_Y$ (see Proposition 1.4), we deduce that $\iota _Y$ preserves every divisor in $|V_1|$, i.e. the action of $\iota _Y^*$ on $V_1$ is $\text {Id}$ or $-\text {Id}$.

By Lemma 3.14(i), we have the following short exact sequence:

$$\begin{aligned} 0\rightarrow H^0(Y,\mathcal {O}_{Y}(-K_Y)\otimes \mathcal {I}_{W_Y}) \rightarrow H^0(Y,\mathcal {O}_Y(-K_Y))\overset{r_1}{\rightarrow } H^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))\rightarrow 0. \end{aligned}$$

Hence, $H^0(Y,\mathcal {O}_Y(-K_Y))=V_1\oplus V_2$ with $V_1\simeq \text {Ker}r_1$ and $V_2\simeq \text {Im}r_1$.

By Proposition 1.4, every elliptic fibre $F_Y$ is preserved by $\iota _Y$ and $R_Y$ is fixed by $\iota _Y$. Since $-K_Y|_{W_Y}=2F_Y+R_Y$, we deduce that $\iota _Y$ preserves every divisor in $|{-}K_Y|_{W_Y}$. Thus the action of $(\iota _Y|_{W_Y})^*$ on $H^0(W_Y,\mathcal {O}_{W_Y}(-K_Y))$ is $\text {Id}$ or $-\text {Id}$. As $\iota _Y^*$ is not $\pm \text {Id}$ on $H^0(Y,\mathcal {O}_Y(-K_Y))$, we deduce that $V_2$ can be uniquely determined as the eigenspace corresponding to the eigenvalue 1 or $-1$ of $\iota _Y^*$. $\square$

Let $\{s_{11},s_{12},s_{13}\}$ (resp. $\{s_{21},s_{22},s_{23}\}$) be a basis of $V_1$ (resp. of $V_2$). Suppose that $\iota _Q$ is not the identity. Then for $y\in Y\backslash R_Y$, one has

$$\begin{aligned} \iota _Q(\phi _{|{-}K_Y|}(y))=[s_{11}(y):s_{12}(y):s_{13}(y):-s_{21}(y):-s_{22}(y):-s_{23}(y)] \end{aligned}$$

(5)

by Lemma 4.10. Moreover, if y is a fixed point of $\iota _Y$, then by Lemma 4.7 (ii), $\phi _{|{-}K_Y|}(y)$ is fixed by $\iota _Q$. Thus by (5), one has $s_{11}(y)=s_{12}(y)=s_{13}(y)=0$ or $s_{21}(y)=s_{22}(y)=s_{23}(y)=0$, i.e. $y\in \text {Bs}|V_1|$ or $y\in \text {Bs}|V_2|$.

Now for $i=1,2$, let $\widetilde{V}_i\subset H^0(\tilde{Y},\mathcal {O}_{\tilde{Y}}(\mu ^*(-K_Y)-E))$ be the sub-vector space of global sections which are the linear spans of $\tilde{s}_{ij}$ with $j=1,2,3$, where $\tilde{s}_{ij}$ is the strict transform of the global section $s_{ij}\in V_i$. Hence, if a point $y\in \tilde{Y}$ is fixed by $\iota _{\tilde{Y}}$, then by repeating the argument in above paragraph, we obtain $y\in \text {Bs}|\widetilde{V}_1|$ or $y\in \text {Bs}|\widetilde{V}_2|$. To summarise, we have the following corollary.

Corollary 4.11

Suppose that $\iota _Q$ is not the identity. If a point $y\in \tilde{Y}$ is fixed by $\iota _{\tilde{Y}}$, then $y\in \text {Bs}|\widetilde{V}_1|$ or $y\in \text {Bs}|\widetilde{V}_2|$.

Recall that we have the normal bundle $\mathcal {N}_{R_Y/Y}\cong \mathcal {O}_{\mathbb {P}^1}(-1)\oplus \mathcal {O}_{\mathbb {P}^1}^{\oplus 2}$ by Lemma 3.6. Hence $E=\mathbb {P}(\mathcal {N}_{R_Y/Y}^*)\simeq \mathbb {P}(\mathcal {O}_{\mathbb {P}^1}(1)\oplus \mathcal {O}_{\mathbb {P}^1}^{\oplus 2})$. Denote by $\xi$ a tautological divisor associated to $\mathcal {O}_{\mathbb {P}(\mathcal {N}_{R_Y/Y}^*)}(1)$, and $F_E$ a fibre of the projection $E=\mathbb {P}(\mathcal {N}_{R_Y/Y}^*)\rightarrow R_Y\simeq \mathbb {P}^1$. Let l be an exceptional curve of $\mu$ and $\gamma$ be the curve which generates the other extremal ray $\Gamma$ of $\text {NE}(E)$ such that $-K_E\cdot \gamma$ is the length of $\Gamma$. Then

$$\begin{aligned} F_E\cdot l=0, \quad F_E\cdot \gamma =1, \\ \xi \cdot l=1, \quad \xi \cdot \gamma =0. \end{aligned}$$

Moreover, $\tilde{R}_Y\sim l+\gamma$.

With the same notation as in Lemma 4.7, we may describe the image f(E) as follows.

Remark 4.12

The exceptional divisor E is isomorphic to the blow-up B of $\mathbb {P}^3$ at a line (and B is embedded in $\mathbb {P}^1\times \mathbb {P}^3$ with bidegree (1, 1)).

Let $\tilde{D}\subset \tilde{Y}$ be the strict transform of a general member $D\in |{-}K_Y|$. Then $(\tilde{D}|_E)^3=4$, hence $\tilde{D}|_E\sim \xi +F_E$ is very ample, with $h^0(E,\mathcal {O}_E(\tilde{D}))=7$. Thus the corresponding linear system embeds B in $\mathbb {P}^6$ as a hyperplane section of the Segre embedding of $\mathbb {P}^1\times \mathbb {P}^3$ in $\mathbb {P}^7$, and B has degree 4. Hence, $f|_E$ is given by the projection of B from a point x outside B in $\mathbb {P}^6$ (in fact, it is given by a sub-linear system of $|\tilde{D}|$ of dimension 5, which is still base-point-free).

If the point x is general, then the projection is birational and the image has degree 4 in $\mathbb {P}^5$. There could be special point x such that the projection has degree 2, and the image is a 3-dimensional quadric in $\mathbb {P}^5$. In any case, the image of a fibre $F_E$ is a plane in $\mathbb {P}^5$.

Lemma 4.13

Suppose that $\iota _Q$ is not the identity. Then $\iota _{\tilde{Y}}|_E$ is not the identity, and the following statements hold:

• (i) The fixed locus of $\iota _{\tilde{Y}}|_E$ is the disjoint union $S_E\cup C_2$, where $S_E=\text {Bs}|\widetilde{V}_1|\cap E$ is the unique member in $|\xi -F_E|$ isomorphic to $\mathbb {P}^1\times \mathbb {P}^1$, and $C_2=\text {Bs}|\widetilde{V}_2|\cap E$ is a curve satisfying $C_2\sim l+\gamma$ which is mapped surjectively to $R_Y$.

• (ii) The fixed locus of $\iota _{\mathbb {P}^5}$ is two disjoint planes $\mathbb {P}^2_1\cup \mathbb {P}^2_2$ such that $f(S_E)=\mathbb {P}^2_1$ and that $f(C_2)$ is a conic contained in $\mathbb {P}^2_2$. Furthermore, f(E) is a 3-dimensional quadric in $\mathbb {P}^5$.

Proof

Suppose by contradiction that $\iota _{\tilde{Y}}|_E$ is the identity. Then by Corollary 4.11, one has $E\subset \text {Bs}|\widetilde{V}_1|$ or $E\subset \text {Bs}|\widetilde{V}_2|$. Since $|\widetilde{V}_i|\subset |\mu ^*(-K_Y)-E|$ for $i=1,2$, this contradicts the fact that there is no divisor in $|{-}K_Y|$ having multiplicity at least 2 along $R_Y$ by Macaulay2 (see Listing 11).

(i) Since $\iota _{\tilde{Y}}|_{E}$ is not the identity and $\iota _Y|_{R_Y}$ is the identity, we have that $\iota _{\tilde{Y}}|_{F_E}$ is not the identity. Thus $\iota _{\tilde{Y}}|_{F_E}$ is a non-trivial involution on $F_E\simeq \mathbb {P}^2$, and we obtain that the fixed locus of $\iota _{\tilde{Y}}|_{F_E}$ is the disjoint union of a point and a line (which correspond respectively to the two non-empty eigenspaces of the involution $\iota _{\tilde{Y}}|_{F_E}\in \text {PGL}_2(\mathbb {C})$).

We first describe the base locus of $|\widetilde{V}_1|$. Since by Macaulay2 (see Listing 5), one has $\mathfrak {b}(\mathcal {M}_W) = \mathfrak {b}(Sec)$ (see Lemma 3.12 for notation) for the base ideals. Thus the base locus of $|V_1|$ contains the surface $W_Y$ with multiplicity 2 by Lemma 3.12. Therefore, the base locus of $|\widetilde{V}_1|$ contains the strict transform $\tilde{W}_Y\subset \tilde{Y}$. Moreover, since a general member in $|V_1|$ is singular along two elliptic fibres of $W_Y$, a local computation shows that every member in $|\widetilde{V}_1|$ contains two fibres $F_E$ above the two points on $R_Y$ where it is singular. As $\tilde{D}|_E\sim \xi +F_E$, we deduce that the unique member $S_E\in |\xi -F_E|$ is contained in the base locus of $|\widetilde{V}_1|$. Therefore, $\text {Bs}|\widetilde{V}_1|\cap E=S_E\simeq \mathbb {P}^1\times \mathbb {P}^1$, and $S_E\cap \tilde{W}_Y=E\cap \tilde{W}_Y=\tilde{R}_Y$.

Now we describe the base locus of $|\widetilde{V}_2|$. Since $|\mu ^*(-K_Y)-E|$ is base-point-free, $\text {Bs}|\widetilde{V}_2|$ is disjoint from the surface $S_E$. Let $D_2$ be a general member in $|V_2|$. Since $D_2$ does not contain the surface $W_Y$, and $D_2|_{W_Y}=R_Y+2F_Y$, we deduce that the intersection of the singular locus $\text {Sing}D_2$ with the curve $R_Y$ contains at most one point (which is a singularity of multiplicity two). Hence a general member in $|\widetilde{V}_2|$ contains at most one fibre $F_E$ of $E\rightarrow R_Y$.

Claim. $\text {Bs}|\widetilde{V}_2|\cap E$ has dimension at most one.

Suppose that there is a surface $S_2\subset \text {Bs}|\widetilde{V}_2|\cap E$. Since $\tilde{D}|_E\sim \xi +F_E$, one has $S_2\in |\xi |$ or $S_2\in |\xi +F_E|$. As $\xi \cdot \tilde{R}_Y=F_E\cdot \tilde{R}_Y=1$, one has $S_2\cdot \tilde{R}_Y>0$, which contradicts the fact that $S_2$ is disjoint from $S_E$. This proves the claim.

Note that $\text {Bs}|\widetilde{V}_2|\cap E$ has dimension one. This is because the fixed locus of $\iota _{\tilde{Y}}|_{F_E}$ is the disjoint union of a point and a line, and $\text {Bs}|\widetilde{V}_1|\cap F_E$ is a line. Thus by Corollary 4.11, the fixed point disjoint from the fixed line is contained in $\text {Bs}|\widetilde{V}_2|\cap F_E$. Therefore, $\text {Bs}|\widetilde{V}_2|\cap E$ is a curve which is mapped surjectively to $R_Y$.

Denote by $C_2$ the curve $\text {Bs}|\widetilde{V}_2|\cap E$. Since $C_2$ is disjoint from $S_E\in |\xi -F_E|$, one has $(\xi -F_E)\cdot C_2=0$ and thus $C_2\sim m(\gamma +l)$ with $m\ge 1$. As $(\tilde{D}|_E)^2\sim (\xi +F)^2\sim \gamma +3l$, we deduce that $C_2\sim \gamma + l$. Hence $C_2$ is an irreducible curve which is mapped surjectively to $R_Y$.

(ii) Since $\iota _Q$ is not the identity (i.e. $\iota _{\mathbb {P}^5}$ is not the identity), the fixed locus of $\iota _{\mathbb {P}^5}$ is the union of two disjoint sub-linear spaces $\mathbb {P}^i\cup \mathbb {P}^j$ with $i+j=4$, which correspond respectively to the two eigenspaces of the involution $\iota _{\mathbb {P}^5}\in \text {PGL}_5(\mathbb {C})$. Therefore, the fixed locus of $\iota _{\mathbb {P}^5}$ is two disjoint planes $\mathbb {P}^2_1$ and $\mathbb {P}^2_2$ by the equation (5).

By Remark 4.12, $f(S_E)$ has dimension 2. Hence, $f(S_E)\subset Q$ is one of the two planes $\mathbb {P}^2_1$ and $\mathbb {P}^2_2$ contained in the fixed locus of $\iota _{\mathbb {P}^5}$. We may denote $f(S_E)=\mathbb {P}^2_1$. Following the discussion in Remark 4.12, we now describe the map $f|_{S_E}$: the restricted linear system $|\tilde{D}|_E|_{S_E}$ embeds the surface $S_E$ in $\mathbb {P}^3$ as the Segre embedding of $\mathbb {P}^1\times \mathbb {P}^1$ in $\mathbb {P}^3$, and the image $S_E'$ has degree 2. Hence, $f|_{S_E}$ is given by the projection of $S_E'$ from a point outside $S_E'$ in $\mathbb {P}^3$. The projection has degree 2 and the image is the plane $\mathbb {P}^2_1$. Note that in Remark 4.12, the projection of B from a point x outside B in $\mathbb {P}^6$ cannot be birational, as the projection of $S_E'\subset B$ from the point x in $\mathbb {P}^3\subset \mathbb {P}^6$ has degree 2. Therefore, f(E) is a 3-dimensional quadric in $\mathbb {P}^5$.

Since $\tilde{D}\cdot C_2=(\xi +F_E)\cdot (\gamma +l)=2$, the image $f(C_2)$ is a conic. As $f(C_2)$ is disjoint from $f(S_E)$, we deduce that $f(C_2)$ is contained in $\mathbb {P}^2_2$. $\square$

Corollary 4.14

The involution $\iota _Q$ is the identity, and thus the Bertini involution $\iota _Y$ preserves every divisor in $|{-}K_Y|$ and f factors through the quotient $\tilde{Y}/\iota _{\tilde{Y}}$ via the lifted involution $\iota _{\tilde{Y}}$.

Proof

Suppose by contradiction that $\iota _Q$ is not the identity. We use the notation as in Lemma 4.13.

Since the restricted linear system $|\tilde{D}|_E|_{S_E}$ embeds the surface $S_E$ in $\mathbb {P}^3$ as the Segre embedding of $\mathbb {P}^1\times \mathbb {P}^1$ in $\mathbb {P}^3$ with image $S_E'$ a quadric surface, the map $f|_{S_E}$ is given by the projection of $S_E'$ from a point outside $S_E'$ in $\mathbb {P}^3$. The projection has degree 2, and $f(S_E)=\mathbb {P}^2_1$ by Lemma 4.13. Therefore, $f|_{S_E}:S_E\simeq \mathbb {P}^1\times \mathbb {P}^1\rightarrow \mathbb {P}^2_1$ is a double cover branched over a non-singular conic $\Delta$ in $\mathbb {P}^2_1$; moreover, the image of any line on $S_E$ is a tangent line to $\Delta$, and conversely the preimage of each tangent line on $\Delta$ is two lines on $S_E$, one from each ruling.

Let $D\in |V_1|$ be a general member and $\tilde{D}\in |\widetilde{V}_1|$ be its strict transform. Then by Lemma 4.13, $\tilde{D}\cap E$ contains the surface $S_E$ and two distinct $\mathbb {P}^2$ (denoted by $F_{E_1}$ and $F_{E_2}$) above the two points on $R_Y$ where D is singular. Thus $f(\tilde{D})$ contains $f(F_{E_1}){=}{:}\Pi _1$ and $f(F_{E_2}){=}{:}\Pi _2$ which are two planes in $\mathbb {P}^5$ by Remark 4.12. Moreover, $\Pi _1$ and $\Pi _2$ are distinct. This is because $F_{E_1}\cap S_E$ and $F_{E_2}\cap S_E$ are two distinct lines of a same ruling of $S_E\simeq \mathbb {P}^1\times \mathbb {P}^1$, and thus their images in $\mathbb {P}^2_1=f(S_E)$ are two distinct tangent lines to $\Delta$ by the above discussion. Therefore, $f(\tilde{D})\cap f(E)$ contains three distinct planes $\mathbb {P}^2_1,\Pi _1,\Pi _2$. This contradicts the fact that $f(\tilde{D})$ is a hyperplane in $\mathbb {P}^5$ and f(E) is a 3-dimensional quadric in $\mathbb {P}^5$ (so that their intersection is a surface of degree 2 in $\mathbb {P}^5$).

Therefore, $\iota _Q$ is the identity. By Lemma 4.7 (ii), one has $f=f\circ \iota _{\tilde{Y}}$. Thus f factors through the quotient $\tilde{Y}/\iota _{\tilde{Y}}$. $\square$

Corollary 4.15

The morphism $f|_E:E\rightarrow f(E)$ is birational, and f(E) has degree 4 in $\mathbb {P}^5$. Moreover, the restricted involution $\iota _{\tilde{Y}}|_E$ is the identity.

Proof

By Remark 4.12, either $f|_E$ has degree 2 and the image is a 3-dimensional quadric in $\mathbb {P}^5$, or $f|_E$ is finite birational and the image has degree 4 in $\mathbb {P}^5$. We will show that the first case cannot happen.

Suppose that $f|_E$ has degree 2 and f(E) is a 3-dimensional quadric in $\mathbb {P}^5$. We will follow the same argument as in the proof of Corollary 4.14. By Lemma 4.13 (with the same notation), for a general member $D\in |V_1|$, its strict transform $\tilde{D}\in |\widetilde{V}_1|$ contains the surface $S_E\subset E$. Moreover, $\tilde{D}$ contains the two distinct fibres (denoted by $F_{E_1}$ and $F_{E_2}$) of $\mu |_E:E\rightarrow R_Y$ above the two points on $R_Y$ where D is singular. Hence, $f(\tilde{D})\cap f(E)$ contains the surface $f(S_E)$ and the two planes $f(F_{E_1}),f(F_{E_2})$ (which may coincide).

• (a) If $f|_{S_E}$ has degree 2, then the same argument as in the proof of Corollary 4.14 shows that $f(S_E),f(F_{E_1}),f(F_{E_2})$ are 3 distinct planes.

• (b) If $f|_{S_E}$ has degree 1, then $f(S_E)$ is either a non-normal surface or isomorphic to $S_E\simeq \mathbb {P}^1\times \mathbb {P}^1$. Thus $f(S_E)$ has degree at least 2 in $\mathbb {P}^5$.

This contradicts the fact that $f(\tilde{D})\cap f(E)$ is a surface of degree 2 in $\mathbb {P}^5$. Therefore, $f|_E$ is finite birational and f(E) has degree 4 in $\mathbb {P}^5$.

Now suppose that $\iota _{\tilde{Y}}|_E$ is not the identity. Since $f|_E=f|_E\circ \iota _{\tilde{Y}}|_E$ by Corollary 4.14, we deduce that $f|_E$ has degree 2, which leads to a contradiction. $\square$

Proof of Theorem 1.3

Follows from Corollary 4.14. $\square$

Proof of Theorem 1.5

Follows from Lemmas 4.7, 4.9, and Corollaries 4.14, 4.15. $\square$

Lemma 4.16

With notation from Theorem 1.5, the fixed locus of $\iota _{\tilde{Y}}$ is $E\cup Res$, where Res has dimension at most 2 and its intersection with every $\tilde{P}_{\ell }$ is non-empty and zero-dimensional, where $\tilde{P}_{\ell }\subset \tilde{Y}$ is the strict transform of $P_\ell$ (see notation in Proposition 2.3).

Proof

Let $P_\ell \simeq \mathbb {P}^2$ be the exceptional locus of a small extremal contraction of Y. Then $\iota _Y(P_\ell )=P_{\iota _S^*(\ell )}$ is also the exceptional locus of some small extremal contraction of Y and $P_\ell$ intersects $\iota _Y(P_\ell )$ transversally at 3 points by [5, Rem. 2.15 (c), Lem. 6.4]. Therefore, the intersection of $P_\ell$ with the fixed locus of $\iota _Y$ is non-empty and zero-dimensional.

As $R_Y\subset W_Y$ is disjoint from any $P_\ell$ by Lemma 3.13, we deduce that E is disjoint from any $\tilde{P}_{\ell }$. Therefore, $Res\cap \tilde{P}_\ell$ is non-empty and zero-dimensional; hence so is $\mu (Res)\cap P_\ell$ for any $P_\ell$. Suppose that $\mu (Res)$ contains a divisorial component $D_{Res}$. By the cone theorem, $D_{Res}$ has positive intersection with some extremal ray of $\text {NE}(Y)$; such an extremal ray is generated by a class of line $\Gamma _{\ell _0}$ in $P_{\ell _0}\simeq \mathbb {P}^2\subset Y$ by Proposition 2.3. Therefore, $D_{Res}\cap P_{\ell _0}$ has dimension 1, which contradicts the fact that $D_{Res}\cap P_{\ell _0}$ is zero-dimensional. Hence, $\mu (Res)$ has dimension at most 2 and so does Res. $\square$

Remark 4.17

With notation from Theorem 1.5, the computations by Macaulay2 (see Listing 12) show the following.

• It is expected that $f^{-1}(f(E))=E$ (since the points in $f(E)\subset Q\subset \mathbb {P}^5$ are expected to correspond to those whose preimage by the map phi1, defined by the linear system of quintic hypersurfaces through the 8 blow-up points with multiplicity at least 3, is undefined in $\mathbb {P}^4$). It follows that the ramification divisor of f is $E+E'$, where $E'\in |3(\mu ^*(-K_Y)-E)|$ has generically degree 2 to its image by f.

• The fixed locus Res (see notation in Lemma 4.16) by $\iota _{\tilde{Y}}$ is expected to have dimension 2 (as the points in f(Res) are expected to correspond to those whose preimage by phi1 has exactly one point).

A Computations by Macaulay2

We set up the projective space $\mathbb {P}^4$:

We choose 8 points in $\mathbb {P}^4$:

We compute the ideal II defined by the 6 quintic hypersurfaces through the 8 points with multiplicity at least 3:

We check that II is the intersection of the ideal LL of the 28 lines, the ideal RN of the 8 quartics and the ideal I5 of a smooth rational quintic curve:

We compute the normal bundle of the smooth rational quintic curve:

We choose three points on the smooth rational quintic curve:

We compute the three quintic hypersurfaces with multiplicity 3 at the 8 points and the point P1 (resp. P2 and resp. P3):

We compute the elliptic normal quintic curve along which the quintic hypersurface Q1 is singular:

We compute the intersection of the three quintic hypersurfaces and obtain the cubic scroll W:

We compute the quintic hypersurfaces through the 8 points with multiplicity at least 3, and containing the surface W:

We look at the singular locus of a quintic hypersurface through the 8 points with multiplicity at least 3 and containing the surface W:

We see that the singular locus of the quintic hypersurface QW is the set defined by the ideal EE. We deduce by the computations that this set consists of two elliptic normal quintic curves lying on the surface W, and intersecting at the 8 points.

Now we compute the hypersurfaces of degree 10 through the 8 points with multiplicity at least 6. To reduce the running time, we add the 8 points step by step and eliminate hypersurfaces of degree higher than 10 at the end of each step:

We compute the hypersurfaces of degree 10 through the 8 points with multiplicity at least 6 containing the surface W:

We compute the image of the elliptic normal quintic E1 via the map defined by the linear system of hypersurfaces of degree 10 through the 8 points with multiplicity at least 6:

We compute the image of the rational quintic curve I5 via the map defined by the linear system of hypersurfaces of degree 10 through the 8 points with multiplicity at least 6:

We compute the image of the surface W via the map defined by the linear system of hypersurfaces of degree 10 through the 8 points with multiplicity at least 6:

We compute the hypersurfaces of degree 10 with multiplicity at least 7 at the point I_0 and multiplicity at least 6 at the other 7 points:

And we obtain a unique such hypersurface of degree 10; now we check if this hypersurface contains the surface W:

We compute the image of $\mathbb {P}^4$ via the map defined by the linear system of quintic hypersurfaces through the 8 points with multiplicity at least 3.

This is achieved by an indirect method: we generate an ideal JJ which has the same behaviour as the ideal II defined by the 6 quintic hypersurfaces through the 8 points with multiplicity at least 3. Then we compute the image of $\mathbb {P}^4$ via the map defined by this ideal JJ.

We check that there is no quintic hypersurfaces through the 8 points with multipilicity at least 3 and having multiplicity at least 2 along the smooth rational quintic curve I5:

To understand the ramification locus of the map phi1 defined by the linear system of quintic hypersurfaces through the 8 points with multiplicity at least 3 in $\mathbb {P}^4$, we take many points randomly in the image Q and look at the degree of the fibre of each of them.

To compute the generic degree of the map phi2 defined by the linear system of hypersurfaces of degree 10 through the 8 points with multiplicity at least 6, we take many points randomly in $\mathbb {P}^4$ and look at the degree of the fiber of each point’s image in Q.