Abstract
We classify and explicitly construct the irreducible graded representations of anti-spherical Hecke categories which are concentrated one degree. Each of these homogeneous representations is one-dimensional and can be cohomologically constructed via a BGG resolution involving every (infinite dimensional) standard representation of the category. We hence determine the complete first row of the inverse parabolic p-Kazhdan–Lusztig matrix for an arbitrary Coxeter group and an arbitrary parabolic subgroup. This generalises the Weyl–Kac character formula to all Coxeter systems (and their parabolics) and proves that this generalised formula is rigid with respect to base change to fields of arbitrary characteristic.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The discovery of counterexamples to the expected bounds of Lusztig’s conjecture was an earthquake in representation theory. It marked the beginning of a new era of Lie theory, in which diagrammatic Hecke categories play centre stage in our attempts to understand the structure of algebraic groups in terms of parabolic “p-Kazhdan–Lusztig polynomials". There are precious few general results concerning either the simple representations of these diagrammatic Hecke categories, or the underlying combinatorics of parabolic p-Kazhdan–Lusztig polynomials.
We let \(\Bbbk \) denote an algebraically closed field of characteristic \(p>2\). Given W an arbitrary Coxeter group and P an arbitrary parabolic subgroup, we classify and construct the homogeneous (simple) representations of the anti-spherical Hecke category \({\mathcal {H}}_{P\backslash W}^\Bbbk \) (note that \({\mathcal {H}}_{P\backslash W}^\Bbbk \) is a \(\Bbbk \)-linear graded category and so this notion makes sense) constructed from the “geometric realisation" of W. We prove that a \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module is homogeneous if and only if it is one-dimensional if and only if it is the simple \(L(1_{P\backslash W})\) labelled by the identity coset \(1_{P\backslash W}\in {^PW}\) (and we provide a basis of \(L(1_{P\backslash W})\) by way of Libedinsky’s light leaves construction).
Theorem A
The anti-spherical Hecke category \( {\mathcal {H}}_{P\backslash W}^\Bbbk \) admits a unique homogeneous simple module, \(L( 1_{P\backslash W})\), labelled by the identity coset \(1_{P\backslash W}\). This simple module is a one-dimensional quotient of the infinite-dimensional standard \( {\mathcal {H}}_{P\backslash W}^\Bbbk \)-module \(\Delta ( 1_{P\backslash W})\).
Concurrently, we provide a cohomological construction of the unique homogeneous \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module by way of a BGG resolution. Within this BGG resolution, every one of the (infinite-dimensional) standard \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-representations \(\Delta ( w)\) for \(w\in {^PW}\) appears in degree as dictated by the length function on the underlying Hecke algebra. Our BGG resolutions allow us to calculate the complete first row of the inverse parabolic p-Kazhdan–Lusztig matrix for W an arbitrary Coxeter group and P an arbitrary parabolic subgroup. This provides the first family of explicit (inverse) p-Kazhdan–Lusztig polynomials to admit a uniform description across arbitrary Coxeter groups and their parabolic subgroups. In the case that W is an affine Weyl group and P is the maximal finite parabolic subgroup this gives new character formulas for representations of the corresponding algebraic groups through [1, 2].
Theorem B
Associated to the unique homogeneous simple \( {\mathcal {H}}_{P\backslash W}^\Bbbk \)-module, \(L( 1_{P\backslash W})\), we have a complex \({ C_\bullet (1_{P\backslash W})= \bigoplus _{ w \in {^PW}}\Delta (w)\langle \ell (w)\rangle } \) with differential given by an alternating sum over all “simple reflection homomorphisms". This complex is exact except in degree zero, where \(H_0(C_\bullet ( 1_{P\backslash W}))=L( 1_{P\backslash W}).\) We hence conclusively generalise the Weyl–Kac character formula to all (parabolic) Coxeter systems via the formula
and thus conclude that the first row of the inverse parabolic p-Kazhdan–Lusztig matrix has entries \((- v)^{\ell (w)}\) regardless of the characteristic \(p\ne 2\).
Specialising to the case of (affine) Weyl groups, our character formulas and resolutions have a long history. For finite Weyl groups, Bernstein–Gelfand–Gelfand constructed their eponymous resolutions in the context of finite dimensional Lie algebras [8]. For Kac–Moody Lie algebras these were the subject of Kac–Kazhdan’s conjecture [34] (over \({\mathbb {C}}\)) which was verified by Wakimoto (for \(W=\widehat{{\mathfrak {S}}}_2\) [46]), Hayashi (for classical type [25]) and Feigin, Frenkel, and Ku (in full generality [22, 36]) and was extended to arbitrary fields by Mathieu [40] and subsequently reproven by Arakawa using W-algebras [3, 4]. For parabolic subgroups of finite Weyl groups, our resolutions were first constructed in [37] and went on to have spectacular applications in the study of the Laplacian on Euclidean space [15]. For the infinite dihedral Weyl group with two generators, these resolutions were generalised to the Virasoro and blob algebras of algebraic statistical mechanics [21, 23, 41]. For W the finite symmetric group and P a maximal parabolic, these resolutions were one of the highlights of Brundan–Stroppel’s founding work on categorical representation theory [10, 11]. For W the affine symmetric group and P the maximal finite parabolic and \(\Bbbk ={{\mathbb {C}}}\), Theorem B proves a recent conjecture of Berkesch–Griffeth–Sam [5] concerning BGG resolutions of unitary modules for Cherednik algebras.
Kazhdan–Lusztig conjectured that much of combinatorial Lie theory should generalise beyond the realm of Weyl groups (where our resolutions admit the geometric realisations discussed above) to arbitrary Coxeter groups. Hecke categories provide the structural perspective in which the Kazhdan–Lusztig conjecture was finally proven [19] and serve as the archetypal setting for studying all Lie theoretic objects. In this light, Theorem B provides the prototype for all the aforementioned BGG resolutions and vastly generalises their construction to all parabolic Coxeter systems (which are poorly understood in general, but include for example the finite, affine, compact, paracompact, hypercompact, and Lorentzian Coxeter groups) and to fields of positive characteristic — the instances for Lie groups, Kac–Moody Lie algebras, and their parabolic analogues are merely the examples for which a classical geometric structure exists.
Our proof is surprisingly elementary, the key idea is to exploit the the inductive nature of the light leaves construction. This plays off both the monoidal structure and the highest-weight structure of the Hecke category, which are compatible with certain truncated restriction functors. Our proof is more compact than many of the proofs for (affine) Weyl groups cited above and should be accessible to those who are new to the research area.
1.1 p-Kazhdan–Lusztig polynomials
The anti-spherical Kazhdan–Lusztig polynomials for crystallographic Coxeter systems were first studied in the language of Hecke categories by Libedinsky–Williamson over the complex numbers [38]. The authors remark that their localisation methods do not carry over to fields of positive characteristic and so they do not define p-Kazhdan–Lusztig polynomials (or light leaves bases) in their paper. In this paper we make the (rather trivial) observation that one does not need such localisation methods in order to define p-Kazhdan–Lusztig polynomials (or light leaves bases). In Sect. 1.6 we discuss under what circumstances one can restrict to \({\mathbb {Z}} \subset {{\mathbb {C}}}\) and hence obtain light leaves bases by “reduction modulo p". In this manner, we define the p-Kazhdan–Lusztig polynomials for arbitrary (parabolic) Coxeter systems.
With this machinery in place, we note that Theorem B provides the first instance of a complete row/column of the (inverse) (p-)Kazhdan–Lusztig matrix to be calculated for all Coxeter groups (and their parabolics). This is especially noteworthy considering just how difficult it is to calculate p-Kazhdan–Lusztig polynomials — for example, the current state-of-the-art “billiards conjecture” of Jensen–Lusztig–Williamson describes an infinitesimally small region of the p-Kazhdan–Lusztig matrix in type \({A}_2 \backslash {\widehat{A}}_2\) [31, 39]. The only other examples of p-Kazhdan–Lusztig polynomials which are explicitly known are the famous “torsion explosion" counter examples to the Lusztig conjecture [47]. Therefore we expect our examples of (characteristic-free) p-Kazhdan–Lusztig polynomials to be of wide interest in their community, as they provide the most general family of these polynomials calculated to date.
2 The diagrammatic Hecke categories
We begin by recalling the basics of diagrammatic Hecke categories. Almost everything from this section is lifted from Elias–Williamson’s original paper [20] or is an extension of their results to the parabolic setting [38].
Remark 1.1
The cyclotomic quotients of (anti-spherical) Hecke categories are small categories with finite-dimensional morphism spaces given by the light leaves basis of [20, 38]. Working with such a category is equivalent working to with a locally unital algebra, as defined in [12, Section 2.2], see [12, Remark 2.3]. Throughout this paper we will work in the latter setting. The reader who prefers to think of categories can equivalently phrase everything in the this paper in terms of categories and representations of categories.
2.1 Coxeter systems
Let (W, S) be a Coxeter system: W is the group generated by the finite set S subject to the relations  for
for  satisfying
satisfying  and that
and that  if and only if
if and only if  . Let \(\ell : W \rightarrow {\mathbb {N}}\) be the corresponding length function. Let \({\mathcal {L}} = {\mathbb {Z}}[v,v^{-1}]\) be the ring of Laurent polynomials with integer coefficients in one variable \(v\).
. Let \(\ell : W \rightarrow {\mathbb {N}}\) be the corresponding length function. Let \({\mathcal {L}} = {\mathbb {Z}}[v,v^{-1}]\) be the ring of Laurent polynomials with integer coefficients in one variable \(v\).
Consider \(S_P \subseteq S\) an arbitrary subset and \((P, S_P)\) its corresponding Coxeter group. We say that \((P, S_P)\) is the parabolic subgroup corresponding to the set \(S_P\subseteq S\). We denote by \(^ PW \subseteq W\) the set of minimal coset representatives in \(P\backslash W\).
Given an expression \({{\underline{w}}}=\sigma _1\sigma _2\cdots \sigma _\ell \) for \(\sigma _i\in W\) for \(1\leqslant i \leqslant \ell \), we let w be the corresponding element of W. We define a subword of \({{\underline{w}}}\) to be a sequence \({\textsf {t}}=(t_1,t_2,\dots ,t_\ell )\in \{0,1\}^\ell \) and we set \({{\underline{w}}}^{\mathsf {t}}:=\sigma _1^{t_1}\sigma _2^{t_2}\cdots \sigma _\ell ^{t_\ell }\) and we emphasise that \(s_i^0=1_W \in W\). We write \(y\leqslant w\) if for some (or equivalently, every) reduced expression \({{\underline{w}}}\) there exists a subword \({\mathsf {t}}\) and a reduced expression \({{\underline{y}}}\) such that \({{\underline{w}}}^{\mathsf {t}}={{\underline{y}}}\). We let \(\mathrm{exp}_P^\ell (w)\) denote the set of all expressions \({{\underline{w}}}=\sigma _1\sigma _2\cdots \sigma _\ell \) of w of length \(\ell \) such that \(\sigma _1\dots \sigma _k \in {^PW}\) for each \(1\leqslant k \leqslant \ell \), we let \(\mathrm{exp}_P (w)=\cup _{\ell \geqslant 0}\mathrm{exp}_P^\ell (w)\), and \( \mathrm{exp}_P^{\ell }=\cup _{w \in W}\mathrm{exp}_P^\ell (w)\). We set \(\mathrm{rexp}_P (w):= \mathrm{exp}_P^{\ell (w)} (w)\).
2.2 Bi-coloured quantum numbers and Cartan matrices
We define the x- and y- bicoloured quantum numbers as follows. First set
and then inductively define
When k is odd, \([k]_x=[k]_y\). The following definition allows one to speak of Cartan matrices of Coxeter groups.
Definition 1.2
Let \(\Bbbk \) be a complete local ring in which 2 is invertible. A balanced Cartan matrix of (W, S) over \(\Bbbk \) is an \(|S| \times |S|\)-matrix  such that
such that
-
(1)
for all
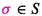 we have
we have 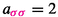 ;
; -
(2)
for all distinct
 such that
such that 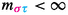 , set
, set 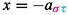 and
and 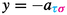 . We require that
. We require that 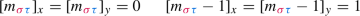 (1.3)
(1.3)
2.3 Soergel graphs
Let (W, S) denote an arbitrary Coxeter system with S finite. Given  we define the monochrome Soergel generators to be the framed graphs
we define the monochrome Soergel generators to be the framed graphs

and given any  with \(m_{\sigma \tau }=m<\infty \) we have the bi-chrome generator
with \(m_{\sigma \tau }=m<\infty \) we have the bi-chrome generator

for m odd, or even respectively. Here the northern edges are coloured with the sequence

for m odd or even respectively and the southern edges are coloured

for m odd or even respectively. We define the northern/southern reading word of a Soergel generator (or its dual) to be word in the alphabet S obtained by reading the colours of the northern/southern edge of the frame respectively (ignoring any \(\emptyset \) symbols). Pictorially, we define the duals of these generators to be the graphs obtained by reflection through their horizontal axes. Non-pictorially, we simply swap the sub- and superscripts. We denote this duality by \(*\). For example, the dual of the fork generator is pictured as follows

Given any two (dual) Soergel generators D and \(D'\) we define \(D\otimes D'\) to be the diagram obtained by horizontal concatenation (and we extend this linearly). The northern/southern colour sequence of \(D\otimes D'\) is the concatenation of those of D and \(D'\) ordered from left to right. Given any two (dual) Soergel generators, we define their product \(D\circ D'\) to be the vertical concatenation of D on top of \(D'\) if the southern reading word of D is equal to the northern reading word of \(D'\) and to be zero otherwise. Finally, we define a Soergel graph to be any graph obtained by repeated horizontal and vertical concatenation of the Soergel generators and their duals.
2.4 Some specific graphs
For \({{\underline{w}}}=\sigma _1\dots \sigma _\ell \) an expression, we define

and given \(k>1\) and  we set
we set

to be the alternately coloured idempotent on k strands (so that the final strand is  - or
- or  -coloured if k is odd or even respectively). Given
-coloured if k is odd or even respectively). Given  with
with  even, let
even, let

be two reduced expressions for \(w\in W\). We say that \({{\underline{w}}}\) and \({\underline{{{\underline{w}}}}}\) are adjacent and we set

(similarly for m odd). Now, given a sequence of adjacent reduced expressions,
and the value q is minimal such that this sequence exists, then we set
While this element is not uniquely defined, only the minimality will matter for our purposes (Fig. 1).
Example 1.3
The left and righthand diagrams depicted in Fig. 2 are both of the form \({\textsf { braid}}^{{\underline{w}}}_{{\underline{{{\underline{w}}}}}}\) for

The corresponding sequences of adjacent reduced expressions are recorded in the Zamolodchikov relation pictured in Fig. 2.
2.5 The diagrammatic Hecke categories
Let (W, S) be a Coxeter system with a balanced Cartan matrix  . Suppose
. Suppose  with
with  . In order to save space, we set
. In order to save space, we set

We are now ready to inductively define the Jones–Wenzl projector  to be the element
to be the element

and the Jones–Wenzl projector  to be the element
to be the element

We remark that in each case the leftmost strand is coloured with  and the second term has coefficient equal to a ratio of x-bicoloured quantum integers. The pictorial version of the first recursion (for \(2k+1\) odd) is as follows
and the second term has coefficient equal to a ratio of x-bicoloured quantum integers. The pictorial version of the first recursion (for \(2k+1\) odd) is as follows

The elements  and
and  are the same as the above except with the inverted colour pattern and coefficients equal to y-bicoloured quantum integers. Specifically, we set
are the same as the above except with the inverted colour pattern and coefficients equal to y-bicoloured quantum integers. Specifically, we set  to be the element
to be the element

and we set  to be the element
to be the element

Finally, we define  and
and  to be the evaluation of the diagrams
to be the evaluation of the diagrams  and
and  respectively at
respectively at  and
and  .Footnote 1 The Jones-Wenzl relation for m = 3 is pictured in Fig. 2.
.Footnote 1 The Jones-Wenzl relation for m = 3 is pictured in Fig. 2.
Definition 1.4
Let \(\Bbbk \) be an arbitrary commutative ring. Let (W, S) be a Coxeter system with a balanced Cartan matrix  over a commutative ring \(\Bbbk \). We define \({\mathcal {H}}^\Bbbk _W\) to be the locally-unital associative \({\mathbb {Z}}\)-graded \(\Bbbk \)-algebra spanned by all Soergel-graphs, with duality \(*\), and multiplication given by vertical concatenation of diagrams modulo the following local relations and their duals.
over a commutative ring \(\Bbbk \). We define \({\mathcal {H}}^\Bbbk _W\) to be the locally-unital associative \({\mathbb {Z}}\)-graded \(\Bbbk \)-algebra spanned by all Soergel-graphs, with duality \(*\), and multiplication given by vertical concatenation of diagrams modulo the following local relations and their duals.

For each  we have monochrome relations
we have monochrome relations

For every ordered pair  with
with  , the bi-chrome relations: The two-colour barbell,
, the bi-chrome relations: The two-colour barbell,

If  we also have the fork-braid relations
we also have the fork-braid relations

for m odd and even, respectively. We require the cyclicity relation,

for m odd or even, respectively. We have the Jones–Wenzl relations

for m odd or even, respectively. For  with
with  and
and  , we have
, we have

We have the three Zamolodchikov relations: for a type \(A_3\) triple with  and
and  we have that
we have that

For a type \(B_3\) triple  such that
such that  ,
,  ,
,  , we have that
, we have that

and for a type \(H_3\) triple  such that
such that  ,
,  ,
,  , we have a final \(H_3\) relationFootnote 2, for which we refer to [20, Definition 5.2]. Further, we require the bifunctoriality relation
, we have a final \(H_3\) relationFootnote 2, for which we refer to [20, Definition 5.2]. Further, we require the bifunctoriality relation
and the monoidal unit relation
for all diagrams \({\textsf {D}}_1,{\textsf {D}}_2,{\textsf {D}}_3,{\textsf {D}}_4\) and all words \({{\underline{w}}},{{\underline{x}}}\). Finally, we require the (non-local) cyclotomic relation

The \({\mathbb {Z}}\)-grading on the algebra \({\mathcal {H}}^\Bbbk _{ W}\) is defined on the generators (and their duals) as follows:

for  arbitrary and \(m\geqslant 2\).
arbitrary and \(m\geqslant 2\).
Remark 1.5
The cyclotomic relation amounts to considering diagrammatic Soergel modules instead of diagrammatic Soergel bimodules, or equivalently, to considering finite dimensional \(\Bbbk \)-modules rather than modules of finite rank over the polynomial ring, R, generated by the “barbells”,  , for
, for  . If we omit the cyclotomic relation in the above definition of \({\mathcal {H}}_W\) we obtain a diagrammatic Bott–Samelson category \({\mathcal {H}}_\mathrm{BS}\) for W (viewed as a locally unital associative \(\Bbbk \)-algebra).
. If we omit the cyclotomic relation in the above definition of \({\mathcal {H}}_W\) we obtain a diagrammatic Bott–Samelson category \({\mathcal {H}}_\mathrm{BS}\) for W (viewed as a locally unital associative \(\Bbbk \)-algebra).
Diagrammatic Bott–Samelson categories are normally defined using a reflection representation  of the Coxeter group W called a realisation. Our construction of \({\mathcal {H}}_\mathrm{BS}\) implicitly uses the universal realisation of W with respect to the balanced Cartan matrix
of the Coxeter group W called a realisation. Our construction of \({\mathcal {H}}_\mathrm{BS}\) implicitly uses the universal realisation of W with respect to the balanced Cartan matrix  , defined as follows. Abusing notation slightly, let \(V^*\) be a free \(\Bbbk \)-module with basis
, defined as follows. Abusing notation slightly, let \(V^*\) be a free \(\Bbbk \)-module with basis  , and let \(V=(V^*)^*\). For each
, and let \(V=(V^*)^*\). For each  define
define  by setting
by setting  for all
for all  . The Coxeter group W acts on \(V^*\) via
. The Coxeter group W acts on \(V^*\) via  for all
for all  and \(\beta \in V^*\). If \({\mathcal {H}}_\mathrm{BS}'\) is the Bott–Samelson category for another realisation of W with the same Cartan matrix, then there is a unique monoidal functor \({\mathcal {H}}_\mathrm{BS} \rightarrow {\mathcal {H}}_\mathrm{BS}'\), which descends to an isomorphism after taking cyclotomic quotients (cf. [45, Lemma 11.2]).
and \(\beta \in V^*\). If \({\mathcal {H}}_\mathrm{BS}'\) is the Bott–Samelson category for another realisation of W with the same Cartan matrix, then there is a unique monoidal functor \({\mathcal {H}}_\mathrm{BS} \rightarrow {\mathcal {H}}_\mathrm{BS}'\), which descends to an isomorphism after taking cyclotomic quotients (cf. [45, Lemma 11.2]).
Definition 1.6
Given \(S_P\subseteq S\) we define the anti-spherical Hecke category \({\mathcal {H}}^\Bbbk _{P \backslash W} \) to be the quotient of \({\mathcal {H}}^\Bbbk _W\) by the homogeneous (non-local) relation

for all  and \({{\underline{w}}}\in \text {exp}(w)\) for \(w\in W\).
and \({{\underline{w}}}\in \text {exp}(w)\) for \(w\in W\).
2.6 Parabolic light leaves tableaux and cellular bases
We now recall the combinatorics of cellular bases for diagrammatic Hecke categories. This is well known in the non-parabolic setting (see e.g. [20, §6.1] or [17, Chapter 10.4]); a good reference for this material in the parabolic setting is [38, §5]. Our notation is closely analogous to that in previous work of the first and second authors ( [7] and [6]) and Ryom–Hansen [44]. In particular, we will use the language of tableaux (rather than words in the Coxeter generators) to describe the indexing sets for our cellular bases. We provide extended examples after the definitions see Examples 1.16 and 1.19 (in particular, we highlight the role played by the parabolic in these examples).
We will consider certain truncations of \({\mathcal {H}}^\Bbbk _{P\backslash W}\), and to that end we define, for any \(w \in {^P}W\), a poset
partially ordered by the Bruhat order. Fix \({{\underline{w}}}=\sigma _1\dots \sigma _\ell \in \text {exp}_P^\ell (w)\) (not necessarily reduced). Given \({\mathsf {t}}\) a subword of \({{\underline{w}}}\in \text {exp}_P^\ell (w)\), we define \({\text {Shape}}_{k}({\mathsf {t}})=\sigma _1 ^{t_1} \sigma _2^{t_2} \dots \sigma _k^{t_k} \in W \) for \(1\leqslant k\leqslant \ell \). In the non-parabolic case, the set of tableaux of shape x and weight \({{\underline{w}}}\) will then be given by
and we define the set of parabolic tableaux of shape x and weight \({{\underline{w}}}\) to be
Finally, we take the union over all possible weights to obtain the set of all parabolic tableaux
Given  and \({\mathsf {t}}\in \mathrm{Std}^P_{\leqslant {{\underline{w}}}}( x )\), we define
and \({\mathsf {t}}\in \mathrm{Std}^P_{\leqslant {{\underline{w}}}}( x )\), we define

and this will be the backbone of how we grow the cellular bases. We can decompose the diagrammatic anti-spherical Hecke category in the following manner,
and hence regard this algebra as a locally unital associative algebra in the sense of [12, Section 2.2]. Each one of these finite-dimensional pieces \({\textsf {1}}_{{\underline{v}} }{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{{\underline{w}}}\) is the space of morphisms between the Bott–Samelson objects labelled by \({{\underline{v}} }\) and \({{\underline{w}}}\).
Recall that given \({{\underline{w}}}=\sigma _1\sigma _2\cdots \sigma _\ell \) and \({\textsf {t}}=(t_1,t_2,\dots ,t_\ell )\in \{0,1\}^\ell \), we set \({{\underline{w}}}^{\mathsf {t}}:=\sigma _1^{t_1}\sigma _2^{t_2}\cdots \sigma _\ell ^{t_\ell }\). We define
In particular, we will wish to consider the subalgebras
in order to understand \({\mathcal {H}}_{P\backslash W}^\Bbbk \). We will construct a spanning set of \( {\textsf {1}}_{ \leqslant {{\underline{w}}}}{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{ \leqslant {{\underline{w}}}} \) in an iterative fashion. For any fixed expression \({{\underline{w}}}\in \text {exp}_P (w)\), we have an embedding

given by  . Note that the image of this embedding lies inside an idempotent truncation of
. Note that the image of this embedding lies inside an idempotent truncation of  . We consider each of these embeddings in turn (for all
. We consider each of these embeddings in turn (for all  ) in order to provide the iterative construction of the “anti-spherical light leaves" elements of \({\mathcal {H}}_{P\backslash W}^\Bbbk \).
) in order to provide the iterative construction of the “anti-spherical light leaves" elements of \({\mathcal {H}}_{P\backslash W}^\Bbbk \).
We now inductively construct the light leaves basis. For \({\mathsf {t}}\in \mathrm{Std}_{\leqslant 1_W}(1_W)\), we formally set \(c_{\mathsf {t}}=1_\emptyset \) and we recall that \({\mathsf {t}}^+\) and \({\mathsf {t}}^-\) are defined in equation(1.36). If  , then for any \( {{\underline{y}}}\in \mathrm{rexp}_P (y)\),
, then for any \( {{\underline{y}}}\in \mathrm{rexp}_P (y)\),  , \({{\underline{y}}}^-\in \mathrm{rexp}_P (y)\) and \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(y)\) we define
, \({{\underline{y}}}^-\in \mathrm{rexp}_P (y)\) and \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(y)\) we define

If  , then we let
, then we let  be a reduced expression for y. For any \({{\underline{y}}}^+\in \mathrm{rexp}_P (y )\),
be a reduced expression for y. For any \({{\underline{y}}}^+\in \mathrm{rexp}_P (y )\),  and
and  we define
we define

Fix a choice of reduced expression \({{\underline{x}}}\) for \(x\in {\mathcal {P}}_{\leqslant w}\) and construct elements \(c_{\mathsf {s}}, c_{\mathsf {t}}\) for \({\mathsf {s}},{\mathsf {t}}\in \mathrm{Std}^P_{\leqslant w}( x)\). We set \( c_{{\mathsf {s}}{\mathsf {t}}}:= (c_{\mathsf {s}}^*) c_{\mathsf {t}}\).
The definition of the anti-spherical Hecke category \({\mathcal {H}}^\Bbbk _{P \backslash W}\) is extremely general, making sense over arbitrary rings and Coxeter systems. In order for it to be well behaved we will make the following (very mild) assumption.
Assumption 1.7
The anti-spherical light leaves elements
are \(\Bbbk \)-linearly independent in \({\textsf {1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}^\Bbbk _{P \backslash W} {\textsf {1}}_{\leqslant {{\underline{w}}}}\).
Theorem 1.8
([20, Section 6.4] and [38, Theorem 5.3]) If Assumption 1.7 holds, then the algebra \({\textsf {1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}^\Bbbk _{P \backslash W} {\textsf {1}}_{\leqslant {{\underline{w}}}}\) is finite-dimensional with graded cellular basis (1.18) with respect to the Bruhat ordering on \( {\mathcal {P}}_{\leqslant w}\) and anti-involution \(*\). For \(\Bbbk \) a field, we have that \({\textsf { 1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}^\Bbbk _{P \backslash W} {\textsf {1}}_{\leqslant {{\underline{w}}}}\) is quasi-hereditary.
Proof
In the proof of [38, Theorem 5.3] it is proven that (1.18) always spans, so Assumption 1.7 implies that it is in fact a basis. Cellularity is not mentioned explicitly, but follows in a completely analogous fashion to [20, Section 6.4]. The only point of the theorem which is not explicitly stated in [20, Section 6.4] and [38, Theorem 5.3] is that the algebra is quasi-hereditary. However, this is immediate from the fact that each layer of the cellular basis contains (at least one) idempotent \(c_{{\mathsf {s}}{\mathsf {s}}}={\textsf { 1}}_{{\underline{x}}}\) for \({\mathsf {s}}\) the unique tableau in \( \mathrm{Std}_{\leqslant {{\underline{x}}}}(x)\subseteq \mathrm{Std}_{\leqslant {{\underline{w}}}}(x)\). \(\square \)
Remark 1.9
We note that when Assumption 1.7 does not hold, the analogue of Soergel’s categorification theorem for \({\mathcal {H}}^\Bbbk _{P \backslash W}\) is false [38, Theorem 6.2]. In this instance it is debatable whether \({\mathcal {H}}^\Bbbk _{P \backslash W}\) should even be called the “anti-spherical Hecke category”! The following result is our attempt to give a reasonably general condition for when Assumption 1.7 holds.
Theorem 1.10
([38, Theorem 5.3]) Let \({\mathcal {O}}\) be a complete local ring in which 2 is invertible, and let  be a balanced Cartan matrix for W over \({\mathcal {O}}\). If the universal realisation for W with respect to
be a balanced Cartan matrix for W over \({\mathcal {O}}\). If the universal realisation for W with respect to  is faithful, then Assumption 1.7 holds for \({\mathcal {H}}_{P \backslash W}^{{\mathcal {O}}}\), the anti-spherical Hecke category defined over \({\mathcal {O}}\) with respect to
is faithful, then Assumption 1.7 holds for \({\mathcal {H}}_{P \backslash W}^{{\mathcal {O}}}\), the anti-spherical Hecke category defined over \({\mathcal {O}}\) with respect to  . Moreover, if there is a ring homomorphism \({\mathcal {O}} \rightarrow \Bbbk \) such that
. Moreover, if there is a ring homomorphism \({\mathcal {O}} \rightarrow \Bbbk \) such that  is the image in \(\Bbbk \) of
is the image in \(\Bbbk \) of  , then Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\).
, then Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\).
Proof
Assumption 1.7 is preserved by base change, so the second statement follows immediately from the first. The special case where \({\mathcal {O}}={\mathbb {R}}\) and  is the “geometric” Cartan matrix for W over \({\mathbb {R}}\) is proved in [38, Proposition 5.5]. In fact this proof is valid for any universal realisation over a complete local ring in which the “parabolic property” [38, 2.3] holds, including faithful realisations. \(\square \)
is the “geometric” Cartan matrix for W over \({\mathbb {R}}\) is proved in [38, Proposition 5.5]. In fact this proof is valid for any universal realisation over a complete local ring in which the “parabolic property” [38, 2.3] holds, including faithful realisations. \(\square \)
There are two incredibly important realisations upon which we now focus our attention.
Example 1.11
Let p be an odd prime.
-
(1)
Let \(\Bbbk \) be any field of characteristic p and let W be a crystallographic Coxeter group. Let A be a generalised Cartan matrix for W, and let
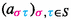 be the image of A over \(\Bbbk \). Set \({\mathcal {O}}={\mathbb {Z}}_p\) take
be the image of A over \(\Bbbk \). Set \({\mathcal {O}}={\mathbb {Z}}_p\) take 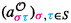 to be the image of A over \({\mathcal {O}}\). The universal realisation for W with respect to A is faithful (see e.g. [33, Chapter 3]), so the same holds true over \({\mathcal {O}}\). Thus Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\) by Theorem 1.10.
to be the image of A over \({\mathcal {O}}\). The universal realisation for W with respect to A is faithful (see e.g. [33, Chapter 3]), so the same holds true over \({\mathcal {O}}\). Thus Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\) by Theorem 1.10. -
(2)
Let \(\Bbbk \) be a field of characteristic p which contains the algebraic integers
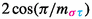 for all
for all  , and define the “geometric” Cartan matrix by setting
, and define the “geometric” Cartan matrix by setting 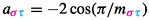 . As mentioned above, it is known that the universal realisation with respect to this Cartan matrix over \({\mathbb {R}}\) is faithful, so the same holds true over
. As mentioned above, it is known that the universal realisation with respect to this Cartan matrix over \({\mathbb {R}}\) is faithful, so the same holds true over 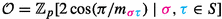 . Thus Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\) by Theorem 1.10.
. Thus Assumption 1.7 holds for \({\mathcal {H}}^\Bbbk _{P \backslash W}\) by Theorem 1.10.
Remark 1.12
Typically the realisations in Example 1.11 do not satisfy the parabolic property over \(\Bbbk \). For example, suppose W is an affine Weyl group,  is the (image in \(\Bbbk \) of the) associated affine Cartan matrix, and P is the finite Weyl subgroup. Then the corresponding realisation from Example 1.11(1) does not satisfy the parabolic property [26, Lemma 1.11]. This is also discussed in [38, Sections 2.3 and 3.1].
is the (image in \(\Bbbk \) of the) associated affine Cartan matrix, and P is the finite Weyl subgroup. Then the corresponding realisation from Example 1.11(1) does not satisfy the parabolic property [26, Lemma 1.11]. This is also discussed in [38, Sections 2.3 and 3.1].
Remark 1.13
In particular, we note that if \(\Bbbk \) is algebraically closed and of odd (or infinite) characteristic then Assumption 1.7 holds for the geometric Cartan matrix (by Example 1.11(2)). Thus the reader unfamiliar with realisations can focus on just this case.
Remark 1.14
We have assumed that \(p\ne 2\) as we do not wish to discuss the technicalities of Demazure surjectivity. Demazure surjectivity sometimes fails for the natural and geometric realisations in characteristic 2 (even for crystallographic types). One can fix this technicality, but the details are tedious and are often glossed over entirely in the literature (see for example the \(B_2\) and \(C_2\) examples for \(p=2\) [32]).
Fix \(x \in {^P}W\) and \({{\underline{x}}}\) a reduced word. We define right “cell" ideals
We define the standard \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module, \(\Delta _{{\mathcal {H}}_{P\backslash W}}(x)\), as follows:
We will almost always drop the subscript and simply write \( \Delta (x) := \Delta _{{\mathcal {H}}_{P\backslash W}} (x)\). We recall that the cellular structure allows us to define, for each \( x \in {^PW}\), a bilinear form \(\langle \ ,\ \rangle ^{ x} \) on \(\Delta (x) \) which is determined by
for any \({\mathsf {s}},{\mathsf {t}},{\mathsf {u}},{\mathsf {v}}\in \mathrm{Std}^P (x )\). When \(\Bbbk \) is a field, we obtain a complete set of non-isomorphic simple \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-modules L(x) for \(x \in {^PW} \) via exact sequences as follows:
We will not discuss projective indecomposable \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-modulesFootnote 3. The right \(1_{\leqslant {{\underline{w}}}} {\mathcal {H}}_{P\backslash W}^\Bbbk 1_{\leqslant {{\underline{w}}}} \)-modules
for \(x \in {\mathcal {P}}_{\leqslant {{\underline{w}}}}\) provide complete sets of non-isomorphic standard and simple modules respectively. The projective indecomposable \(1_{\leqslant {{\underline{w}}}} {\mathcal {H}}_{P\backslash W}^\Bbbk 1_{\leqslant {{\underline{w}}}} \)-modules \(P_{\leqslant w} ( x)\) are the direct summands
Assumption 1.15
For the remainder of the paper, we will assume that \(\Bbbk \) is a field of characteristic \(p\ne 2\).
Example 1.16
Let W be the affine symmetric group \(\widehat{{\mathfrak {S}}}_3\) with generators  ,
,  ,
,  and let P be the maximal finite parabolic generated by
and let P be the maximal finite parabolic generated by  and
and  . The Coxeter graph and Bruhat graphs are depicted in Fig. 3. For
. The Coxeter graph and Bruhat graphs are depicted in Fig. 3. For  , the algebra \({\textsf {1}}_{ \leqslant {{\underline{w}}}}{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{ \leqslant {{\underline{w}}}} \) has graded dimension
, the algebra \({\textsf {1}}_{ \leqslant {{\underline{w}}}}{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{ \leqslant {{\underline{w}}}} \) has graded dimension
where the sum is over the squares of the graded dimensions of the standard modules, which have labels

respectively. For example, the basis of the 9-dimensional standard module has basis

We have that \({\mathcal {H}}_{P\backslash W}\) is the quotient of \({\mathcal {H}}_W\) by the 2-sided ideal

We have a functor
We have that
This is simply because every basis element of the standard module is killed by taking this quotient (this is mentioned explicitly in the proof of [38, Theorem 5.3]).
Example 1.17
We continue with Example 1.16, we note that  and that
and that  . For those unfamiliar with anti-spherical light leaves, we now illustrate the manner in which a basis element of \( {\mathcal {H}}_{ W}^\Bbbk \) will die when we take the quotient \( {\mathcal {H}}_{P\backslash W}^\Bbbk \). We have that the
. For those unfamiliar with anti-spherical light leaves, we now illustrate the manner in which a basis element of \( {\mathcal {H}}_{ W}^\Bbbk \) will die when we take the quotient \( {\mathcal {H}}_{P\backslash W}^\Bbbk \). We have that the  -module
-module  is \((v^2+2v+1)\)-dimensional and spanned by the diagrams
is \((v^2+2v+1)\)-dimensional and spanned by the diagrams

however the  -module
-module  is \((v+1)\)-dimensional module with basis
is \((v+1)\)-dimensional module with basis

We illustrate how this works with the second diagram in (1.29). We rewrite the second diagram using the Jones–Wenzl relation (depicted explicitly in Fig. 1) as follows

We recall that  ; therefore the first diagram is now zero by the
; therefore the first diagram is now zero by the  relation and the second diagram belongs to the 2-sided cell-ideal generated by
relation and the second diagram belongs to the 2-sided cell-ideal generated by  .
.
In fact, no diagram in (1.30) has a rightmost  -strand. In more detail, we have
-strand. In more detail, we have  , so for any tableau \({\mathsf {t}}\) of shape
, so for any tableau \({\mathsf {t}}\) of shape  and weight ending in
and weight ending in  , the light leaf \(c_{{\mathsf {t}}}\) factors through
, the light leaf \(c_{{\mathsf {t}}}\) factors through  . By the above reasoning \(c_{{\mathsf {t}}}\) must therefore vanish in \({\mathcal {H}}_{P \backslash W}\). More generally, if
. By the above reasoning \(c_{{\mathsf {t}}}\) must therefore vanish in \({\mathcal {H}}_{P \backslash W}\). More generally, if  then there are no parabolic tableaux of shape y and weight ending in
then there are no parabolic tableaux of shape y and weight ending in  . This illustrates an important aspect of the restriction functors we will define in the next section, and we will refer back to this example in the proof of Corollary 1.18.
. This illustrates an important aspect of the restriction functors we will define in the next section, and we will refer back to this example in the proof of Corollary 1.18.
2.7 Branching rules for standard modules
We define the  -restriction functor
-restriction functor

where

denotes the ordinary restriction functor defined by the embedding of equation (1.15). While we use the term restriction for  , we emphasise that this functor does not preserve the underlying vector space. This is because the inclusion 1.15 is the non-unital inclusion of an idempotent subalgebra, so restriction kills the complementary idempotent.
, we emphasise that this functor does not preserve the underlying vector space. This is because the inclusion 1.15 is the non-unital inclusion of an idempotent subalgebra, so restriction kills the complementary idempotent.
Theorem 1.8 has the following immediate corollary.
Corollary 1.18
Let  , with \(x, y \in {^P}W\). We have that
, with \(x, y \in {^P}W\). We have that

and

where the submodule is isomorphic to \(\Delta _{\leqslant {{\underline{w}}}}(y)\) (respectively \(\Delta _{\leqslant {{\underline{w}}}}(y)\langle 1 \rangle \)) and the quotient module is isomorphic to \(\Delta _{\leqslant {{\underline{w}}}}(x)\langle -1 \rangle \) (respectively \(\Delta _{\leqslant {{\underline{w}}}}(x)\)). Finally, if  , then
, then

Proof
We have that the maps


for \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(y)\) are injective  -homomorphisms by construction. Similarly, the maps
-homomorphisms by construction. Similarly, the maps


for \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(x)\) are  -isomorphisms by construction (as we have simply multiplied on the right by an element of the algebra). On the other hand, if
-isomorphisms by construction (as we have simply multiplied on the right by an element of the algebra). On the other hand, if  , then
, then  by the light leaves construction, so
by the light leaves construction, so  . We refer back to Example 1.17 for an illustrative example. \(\square \)
. We refer back to Example 1.17 for an illustrative example. \(\square \)
Example 1.19
We continue with the notation of Example 1.16. We consider the restriction functor  for
for  and
and  (note that
(note that  for \({{\underline{w}}}\) as in Example 1.16). The southern reading words of the first three diagrams in Eq. 1.25 are not of the form
for \({{\underline{w}}}\) as in Example 1.16). The southern reading words of the first three diagrams in Eq. 1.25 are not of the form  for some \(y\leqslant x\) and therefore these diagrams are sent to zero by the restriction functor. The remaining diagrams in the first row of Eq. 1.25 form a submodule, isomorphic to
for some \(y\leqslant x\) and therefore these diagrams are sent to zero by the restriction functor. The remaining diagrams in the first row of Eq. 1.25 form a submodule, isomorphic to  , the isomorphism is depicted on basis elements in Fig. 4. The diagrams from the second row of Eq. 1.25 form a quotient module, isomorphic to
, the isomorphism is depicted on basis elements in Fig. 4. The diagrams from the second row of Eq. 1.25 form a quotient module, isomorphic to  , the isomorphism is depicted on basis elements in Fig. 5.
, the isomorphism is depicted on basis elements in Fig. 5.
The reader will notice that this sequence is non-split. To see this, note that the monochrome diagrams from the first row of Eq. 1.25 are both obtained from the monochrome diagram in the second row as follows:

Whereas, there does not exist any  such that either
such that either

2.8 p-Kazhdan–Lusztig polynomials
The categorical (rather than geometric) definition of the p-Kazhdan–Lusztig polynomials is given via the diagrammatic character of [20, Definition 6.23]. In the language of this paper, the definition of the anti-spherical p -Kazhdan–Lusztig polynomial, \({^p}{n}_{x,y}(v)\) for \(x,y\in {^PW}\), is as follows,
for any \(x,y\leqslant w\) and \({\underline{x}}\in {\textsf { rex}}_P(x),{\underline{y}}\in {\textsf {rex}}_P(y)\), \({{\underline{w}}}\in {\textsf { rex}}_P(w)\) are arbitrary (note that the definition of these polynomials is independent of \({{\underline{w}}}\)). The anti-spherical p-Kazhdan–Lusztig polynomials are recorded in the \(|{^PW}|\times |{^PW}|\)-matrix
and we set
to be the inverse of this matrix (which exists, as \(\mathbf{D}_{P\backslash W}\) is lower uni-triangular). The non-parabolic (p-)Kazhdan–Lusztig polynomials are obtained by setting \(P=\{1_W\}\leqslant W\).
3 The classification and construction of homogeneous \({\mathcal {H}}^\Bbbk _{P \backslash W}\)-modules
It is, in general, a hopeless task to attempt to understand all p-Kazhdan–Lusztig polynomials or to understand all simple \({\mathcal {H}}^\Bbbk _{P \backslash W}\)-modules. In particular, it was shown in [47] that one can embed certain number-theoretic questions (for which no combinatorial solution could possibly be hoped to exist) into the p-Kazhdan–Lusztig matrices of affine symmetric groups.
Thus we restrict our attention to classes of modules which we can hope to understand. Over the complex numbers, the first port of call would be to attempt to understand the unitary modules; for Lie groups this ongoing project is Vogan’s famous Atlas of Lie groups. Over arbitrary fields, the notion of unitary no longer makes sense; however, for graded algebras the homogeneous representations seem to provide a suitable replacement. For quiver Hecke algebras, the homogeneous representations were classified and constructed by Kleshchev–Ram [35]. For (quiver) Hecke algebras of symmetric groups, the notions of unitary and homogeneous representations coincide over the complex field [9, Theorem 8.1] and the beautiful cohomological and structural properties of these (homogeneous) representations are entirely independent of the field [9, 35].
In this section, we fix W an arbitrary Coxeter group and fix P an arbitrary parabolic subgroup and we classify and construct the homogeneous representations of the diagrammatic Hecke category \({\mathcal {H}}_{P \backslash W}\). We first provide a cohomological construction of the module \(L(1_{P \backslash W})\) via a BGG resolution. This cohomological construction allows us to immediately deduce a basis-theoretic construction of \(L(1_{P \backslash W})\), from which we easily read-off the fact that \(L(1_{P \backslash W})\) is homogeneous. We then prove that L(w) is inhomogeneous for any \(1\ne w \in {^PW}\).
Definition 2.1
Given \(w, y\in {^PW}\), we say that (w, y) is a Carter–Payne pair if \(y\leqslant w\) and \(\ell (y)=\ell (w)-1\). We let \({\textsf {CP}}_\ell \) denote the set of Carter–Payne pairs (w, y) with \(\ell (w)=\ell \in {{\mathbb {N}}}\).
For \(P\subseteq W\) an affine Weyl group an its maximal finite parabolic subgroup, the following family of homomorphisms were first considered (in the context of algebraic groups) by Carter–Payne in [13].
Theorem 2.2
For \((w,y) \in {\textsf {CP}}_\ell \), pick an arbitrary reduced expression \({{\underline{w}}}=\sigma _1\dots \sigma _\ell \) and suppose that \({{\underline{y}}}=\sigma _1\dots \sigma _{p-1}{\widehat{\sigma }}_p \sigma _{p+1}\dots \sigma _\ell \) is the subexpression of y obtained by deleting precisely one element \(\sigma _p \in S\). We have that
is \(v^1\)-dimensional. Given choices of \({{\underline{w}}}\) and \({{\underline{y}}}\) as above this homomorphism space is spanned by the map
for \({\mathsf {t}}\in \mathrm{Std}(w)\).
Proof
Since \( {\mathcal {P}}_{\leqslant w} \) is a co-saturated subset of \({^P}W\), we can truncate to the algebra \({\textsf {1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}^\Bbbk _{P \backslash W}{\textsf {1}}_{\leqslant {{\underline{w}}}}\) by [14, Appendix A3.13]. We have that
by Theorem 1.8, as there is a unique tableau \({\mathsf {t}}\) with shape y [28, Theorem 5.8]. Moreover this space is of strictly positive degree, namely \(v^1\). Whereas, the character of the simple head, L(y) of \(\Delta (y) \), is invariant under swapping \(v\) and \(v^{-1}\) by [27, Proposition 2.18]. Therefore
By our assumption that (w, y) is a Carter–Payne pair, there does not exist an \(x\in W\) such that \(y< x < w\). We now apply this assumption twice. Firstly, we note that \( [ \Delta _{\leqslant {{\underline{w}}}} (y): L_{\leqslant {{\underline{w}}}}(x)]\ne 0\) implies that \(y\leqslant x \leqslant w\). Putting this together with Eq. 2.1 we have that \( \mathrm {rad}( \Delta _{\leqslant {{\underline{w}}}} (y))= L_{\leqslant {{\underline{w}}}}( w)\langle 1 \rangle \) and the graded decomposition number is equal to
Now applying our assumption again, we conclude that this homomorphism factors through the projection \(P_{\leqslant w}(w)\rightarrow \Delta _{\leqslant {{\underline{w}}}}(w)\) by highest weight theory and so we have
and thus the result follows. \(\square \)
We set \({\mathcal {P}}_{ \ell } = \{ w \in {^PW} \mid \ell (w)=\ell \}\) for each \(\ell \in {{\mathbb {N}}}\). Following a construction going back to work of Bernstein–Gelfand–Gelfand and Lepowsky [8, 24], we are going to define a complex of graded \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-modules
where
We will refer to this as the BGG complex. We momentarily assume that \(P=1\leqslant W\) is the trivial parabolic (so that \({^PW}=W\)). Suppose \(w, z\in W\) such that \(\ell (w)=\ell (z)+2\) and \( w> z\) in the Bruhat ordering. By [8, Lemma 10.3] there exists a unique pair of distinct elements \(x,y \in W\) such that \(w>x,y>z\). We refer to the quadruple \(w,x,y,z \in W\) as a diamond and we have homomorphisms of \({\mathcal {H}}^\Bbbk _W\)-modules

given by our Carter–Payne homomorphisms. By a generalization of [8, Lemma 10.4] to arbitrary Coxeter groups (see [28, §6.17]), it is possible to pick a sign \( \varepsilon (\alpha ,\beta )\) for each Carter–Payne pair \((\alpha ,\beta )\) such that for every diamond the product of the signs associated to its four arrows is equal to \(-1\). We can now define the \({\mathcal {H}}^\Bbbk _{ W}\)-differential \(\delta _\ell :\Delta _{\ell } \rightarrow \Delta _{\ell -1}\) for \(\ell \geqslant 1\) to be the sum of the maps
over all Carter–Payne pairs \((\alpha ,\beta )\in {\textsf {CP}}_\ell \). We let \( C_\bullet (1_{ W}) = \bigoplus _{\ell \geqslant 0 }{ \Delta }_\ell \langle \ell \rangle \) together with the differential \((\delta _\ell )_{\ell \geqslant 0}\).
Lemma 2.3
We have that \(\varphi ^{ w}_{x} \varphi ^{x}_ {z}= \varphi ^{w}_{y} \varphi _{z}^{y} \).
Proof
We truncate to consider a subalgebra \({\textsf {1}}_{\leqslant {{\underline{w}}}} {\mathcal {H}}_{ W}^\Bbbk {\textsf {1}}_{\leqslant {{\underline{w}}}}\) for \({{\underline{w}}}=\sigma _1 \sigma _2\cdots \sigma _\ell \) a fixed reduced expression of \(w\in W\). Since \(\ell (x)=\ell (y)=\ell -1\) there are unique subexpressions \({{\underline{x}}},{{\underline{y}}}\) for x, y respectively inside \({{\underline{w}}}\). Similarly there are unique subexpressions for z inside \({{\underline{x}}},{{\underline{y}}}\), which induce subexpressions \({{\underline{z}} }_x,{{\underline{z}} }_y\) for z inside \({{\underline{w}}}\). On the other hand, there is a unique diagram in \( \Delta _{\leqslant {{\underline{w}}}}(z)1_{{{\underline{w}}}}\) of maximal degree equal to \(\ell (w)-\ell (z)=2\), this diagram is equal to
for some \(1\leqslant t<u\leqslant \ell \). The corresponding reduced expression
is equal to (at least) one of the expressions \({{\underline{z}} }_x \) or \( {{\underline{z}} }_y\). Without loss of generality, we suppose it is \({{\underline{z}} }_y\); this implies that
We now consider the other composition \(\varphi ^{w}_{x} \varphi ^{x}_ {z}\). Let \(1\leqslant p<q \leqslant \ell \) denote the indices of the terms \(\sigma _p\) and \(\sigma _q\) which are deleted from \({{\underline{w}}}\) to obtain \({{\underline{z}} }_x\). If \({{\underline{z}} }_x \ne {{\underline{z}} }_y\) then \({{\underline{x}}}= \sigma _1\dots \sigma _{q-1}{\widehat{\sigma }}_q \sigma _{q+1}\dots \sigma _\ell \), whereas \(\sigma _1\dots \sigma _{p-1}{\widehat{\sigma }}_p \sigma _{p+1}\dots \sigma _\ell \) is a non-reduced expression. It follows from Humphrey’s Deletion condition [28, Section 5.8] that there exists some \(q'<p<q\) and that the subexpression \({{\underline{z}} }'= \sigma _1\dots \sigma _{q'-1}{\widehat{\sigma }}_{q'} \sigma _{q'+1}\dots \sigma _{p-1}{\widehat{\sigma }}_p \sigma _{p+1}\dots \sigma _\ell \) is also a reduced expression for z. By applying a sequence of braids we may assume that \(q'=p-1\) and \(q=p+1\) (so that the cancellation in the non-reduced expression involves two adjacent reflections); thus we can apply the (local) relation

to see that
(Any diagram with less than \(\ell (z)\) propagating strands is zero; thus the second term in Eq. 2.6 is immediately zero and the third term is zero by the barbell and cyclotomic relations.) Now we consider the expression obtained from \({{\underline{w}}}\) by deleting \(\sigma _{q'}\). If it is reduced, then by uniqueness of maximal degree basis elements, the expression obtained by deleting \(\sigma _{q'}\) and \(\sigma _p\) must be \({{\underline{z}} }_y\), and we are done. Otherwise, we can repeat the above process. This must eventually terminate, as the indices of the deleted generators get smaller with each step at which point, we deduce that
and the result follows, as we are working in the standard module \(\Delta (z)={{\mathcal {H}}_{W}^{\leqslant z}}/ {{\mathcal {H}}_{W}^{<z}}\). \(\square \)
Corollary 2.4
We have that \( \mathrm{Im}({\delta }_{\ell +1}) \subseteq \mathrm{ker}({\delta }_{\ell }) \), in other words \( C_\bullet (1_{ W})\) is a complex.
Proof
We have defined the differential (via the scalars \(\varepsilon (w,z)\)) so that the composition \(\delta _\ell \delta _{\ell -1}\) restricted to a given diamond is equal to \( \varphi ^{ w}_{ x} \varphi ^{ x}_ {z} - \varphi ^{ w}_{y} \varphi _{z}^{y} \) and so the result follows from Lemma 2.3. \(\square \)
Now, we apply the quotient functor \(:{\mathcal {H}}_{ W}\mathrm{-mod }\rightarrow {\mathcal {H}}_{P\backslash W}\mathrm{-mod}\) to \(C_\bullet (1_{ W})\) and hence obtain \( C_\bullet (1_{P \backslash W}) = \bigoplus _{\ell \geqslant 0 }{ \Delta }_\ell \langle \ell \rangle \) together with the differential \((\delta _\ell )_{\ell \geqslant 0}\). (We have abused notation slightly by identifying the differentials for \( {\mathcal {H}}_{P\backslash W}\)- and \({\mathcal {H}}_{ W} \)-modules.)
Proposition 2.5
We have that \( C_\bullet (1_{ P\backslash W})\) is a complex.
Proof
For arbitrary \(P\leqslant W\), we note that \({\mathcal {H}}_{P\backslash W}\) is the quotient of \({\mathcal {H}}_{W}\) by the parabolic annihilation relation (1.14). Taking quotients preserves complexes and so the result follows from Corollary 2.4. \(\square \)
Remark 2.6
In the quotient, diamonds can “collapse”. For example, if \(y\not \in {^P}W\) then we obtain

in which case, we have that \(\varphi ^{w}_{x} \varphi ^{x}_ {{{\underline{z}} }}= 0\). (To see this, simply note that the equality \(\varphi ^{w}_{x} \varphi ^{x}_ {z}= \varphi ^{w}_{y} \varphi _{z}^{y} \) continues to hold, but that the righthand-side of the equality factors through the zero module). For example, this happens in Example 1.16 with  ,
,  ,
,  , and \(z= 1_W\).
, and \(z= 1_W\).
We have already encountered one drawback of the  -restriction functors from the previous section: they kill any standard module \(\Delta _{\leqslant {{\underline{w}}}}(x)\) such that
-restriction functors from the previous section: they kill any standard module \(\Delta _{\leqslant {{\underline{w}}}}(x)\) such that  (and therefore the simple head is also killed). To remedy this, we define slightly larger algebras
(and therefore the simple head is also killed). To remedy this, we define slightly larger algebras
and we define \(\mathrm{Res}^{\ell +1}_{\ell } : {\textsf {1}}_{\leqslant \ell +1}{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{\leqslant \ell +1} \rightarrow {\textsf {1}}_{\leqslant \ell }{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{\leqslant \ell }\) to be the functor

Lemma 2.7
Let \( 1_{P\backslash W} \ne x,w \in {^PW}\) and suppose that \(x\leqslant w\). We have that

for some  and \({{\underline{w}}}\in \mathrm{exp}_P(w)\). Therefore \(\mathrm{Res}_{ \ell }^ { \ell +1}( L (x){\textsf {1}}_{ \leqslant \ell +1})= 0\) implies \( x=1_{P\backslash W}\).
and \({{\underline{w}}}\in \mathrm{exp}_P(w)\). Therefore \(\mathrm{Res}_{ \ell }^ { \ell +1}( L (x){\textsf {1}}_{ \leqslant \ell +1})= 0\) implies \( x=1_{P\backslash W}\).
Proof
For \( 1_{P\backslash W}\ne x \in {^PW}\), there exists some  , \(x' \in {^PW}\) such that
, \(x' \in {^PW}\) such that  . In which case,
. In which case,  is a reduced expression for x and
is a reduced expression for x and  . Our assumption that
. Our assumption that  implies that the preimage of
implies that the preimage of  under the map of (1.15) is equal to \( {\textsf {1}}_{{{\underline{x}}}' } \in {{\textsf {1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}_{P \backslash W}{\textsf {1}}_{\leqslant {{\underline{w}}}}}\) and so the result follows. \(\square \)
under the map of (1.15) is equal to \( {\textsf {1}}_{{{\underline{x}}}' } \in {{\textsf {1}}_{\leqslant {{\underline{w}}}}{\mathcal {H}}_{P \backslash W}{\textsf {1}}_{\leqslant {{\underline{w}}}}}\) and so the result follows. \(\square \)
We are now ready to prove that \( C_\bullet (1_{P \backslash W}) \) is a BGG resolution of the \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module \(L(1_{P\backslash W})\). For W the affine symmetric group, P the maximal finite parabolic and \(\Bbbk ={{\mathbb {C}}}\), the existence of these BGG resolutions was conjectured by Berkesch–Griffeth–Sam in [5]. This conjecture was proven by way of the KZ-functor in the context of the quiver Hecke algebras of type A (by the first and third authors with José Simental, [9]). In type A, the diagrammatic Hecke categories and (truncations of) quiver Hecke algebras were recently shown to be isomorphic in [6]. Thus the following theorem generalises the BGG resolutions [5, 9] to all Coxeter groups, W, and all parabolic subgroups, P, and arbitrary fields, \(\Bbbk \).
Theorem 2.8
Fix W an arbitrary Coxeter group and fix P an arbitrary parabolic subgroup. The \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-complex \(C_\bullet (1_{P\backslash W})\) is exact except in degree zero, where \(H_0(C_\bullet (1_{P\backslash W}))=L(1_{P\backslash W}).\) Moreover, we have that
Proof
By applying the restriction functor to Proposition 2.5, we have that
forms a complex of \({\textsf {1}}_{\leqslant \ell }{\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{\leqslant \ell } \)-modules. Moreover, we can idempotent-truncate

and hence obtain a complex of \({\textsf {1}}_{\leqslant {{\underline{w}}}}{ {\mathcal {H}}_{P\backslash W}^\Bbbk {\textsf {1}}_{\leqslant {{\underline{w}}}} }\)-modules (through the identification of  ). Let \(x,y\in {^PW}\) with
). Let \(x,y\in {^PW}\) with  . For \(y \in {^PW}\), we have that already seen that
. For \(y \in {^PW}\), we have that already seen that

and

where in both cases the submodule is isomorphic to \(\Delta _{\leqslant {{\underline{w}}}}(y)\) and the quotient module is isomorphic to \(\Delta _{\leqslant {{\underline{w}}}}(x)\). Since  , we have that
, we have that

for any \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(x)\) or \({\mathsf {t}}\in \mathrm{Std}_{\leqslant {{\underline{w}}}}(y)\) by definition. Therefore, we have that

for \(x,y\in {^PW}\) where
is simply the graded shift of the identity map for \({{\underline{z}} }={{\underline{x}}},{{\underline{y}}}\) for \(x,y \in W\). This implies that

with differential

Thus we have that

for all \(j\geqslant 0\). Now, summing over all  , \(w\in W\), and \({{\underline{w}}}\in \text {exp}_P^\ell (w)\) we deduce that
, \(w\in W\), and \({{\underline{w}}}\in \text {exp}_P^\ell (w)\) we deduce that
forms a complex with zero homology in every degree. By Lemma 2.7, we have that restriction kills no simple \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module L(w) for \(1\ne w\in {^P}W\). Moreover,
and \([{\textsf {1}}_{\ell +1}\Delta (w):{\textsf {1}}_{\ell +1} L (1_{P\backslash W})]=0\) for \( 1_{P\backslash W}\ne w \in {^P}W\) simply because the highest weight structure on \({\mathcal {H}} _{P \backslash W}\) is given by the Bruhat order. Therefore
Finally, we have proven that \(L(1_{P\backslash W})\) is killed by multiplication by the idempotent  at the \(\ell \)th point for any \(\ell \geqslant 1\) and for any
at the \(\ell \)th point for any \(\ell \geqslant 1\) and for any  Thus \(L(1_{P\backslash W})\) is spanned by \(c_{\mathsf {s}}\) for \({\mathsf {s}}\) the empty tableau, as required. \(\square \)
Thus \(L(1_{P\backslash W})\) is spanned by \(c_{\mathsf {s}}\) for \({\mathsf {s}}\) the empty tableau, as required. \(\square \)
We immediately deduce the following corollary, which is new even for the classical (inverse) parabolic and non-parabolic Kazhdan–Lusztig polynomials (in other words, for \(\Bbbk \) the complex field). Indeed, this seems to be the first non-trivial family of parabolic (p-)Kazhdan–Lusztig polynomials which admits a uniform construction across all Coxeter groups and all parabolic subgroups.
Corollary 2.9
(The Weyl–Kac character formula for Coxeter groups) In the graded Grothendieck group of \({\mathcal {H}}_{{P \backslash W}}\), we have that
Thus the complete first row of the inverse p-Kazhdan–Lusztig matrix is given by
for all \(w\in {^PW}\).
Theorem 2.10
The module \(L(1_{P\backslash W})\) is both the unique homogeneous \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module and the unique 1-dimensional \({\mathcal {H}}_{P\backslash W}^\Bbbk \)-module.
Proof
That the module \(L(1_{P\backslash W})\) is homogeneous is clear (as it is 1-dimensional). We now prove the converse, namely for any \(1\ne w\in {^PW} \) we show that L(w) is inhomogeneous and of dimension strictly greater than 1. Let \(1\ne w\in {^PW}\) and choose \(\tau \) such that  . By Theorem 1.8, the elements
. By Theorem 1.8, the elements

span  . The former is homogeneous of degree \(+1\) and the latter is homogeneous of degree \(-1\). We have that
. The former is homogeneous of degree \(+1\) and the latter is homogeneous of degree \(-1\). We have that

and

since the degree of this element is \(+2\) (whereas the degree of the idempotent spanning the weight space of the cell module is, of course, of degree 0) and

Therefore the Gram matrix for this weight space of the cellular form is the \(2\times 2\)-matrix with 0s on the diagonal and 1s off the diagonal. This matrix has rank 2 and so neither element in (2.23) belongs to the radical of the cellular form. Therefore both elements in (2.23) belong to  and the result follows. \(\square \)
and the result follows. \(\square \)
Remark 2.11
We recall from the introduction that the conjecture of Berkesch–Griffeth–Sam (or rather, its equivalent formulation for homogeneous representations of quiver Hecke algebras) follows immediately from Theorem B. This might be surprising to the reader familiar with the homogeneous representations of quiver Hecke algebras. In [35] it is shown that there are up to \(e-1\) distinct homogeneous representations of any block of the quiver Hecke algebras (and for sufficiently large rank, there are precisely \(e-1\) such representations for a “regular block"). Whereas, in this paper we have seen that there is precisely one homogeneous representation of \({\mathcal {H}}_{P\backslash W}^\Bbbk \) for \({\mathfrak {S}}_{h}=P\subset W=\widehat{{\mathfrak {S}}}_{h} \) for \(h \in {{\mathbb {N}}}\). Therefore, one might think that there are “more" homogeneous representations of the quiver Hecke algebra. However, for each \(1\leqslant h <e\) there is an isomorphism between a finite truncation of \({\mathcal {H}}_{P\backslash W}^\Bbbk \) and the Serre quotient of the quiver Hecke algebra corresponding to the set of partitions with at most h columns [6]. Through these isomorphisms, one can obtain the \(e-1\) distinct BGG resolutions of the \(e-1\) distinct homogeneous simple modules of the quiver Hecke algebra predicted by Berkesch–Griffeth–Sam [5].
We now provide an elementary infinite family of simple modules which do not admit BGG resolutions, in order to justify our claim in the introduction that such resolutions are “rare". In [8] an example of such a simple for \(W={\mathfrak {S}}_4\) is given. We focus on the simplest case, namely that of the anti-spherical category controlling the algebraic group \( \mathrm{SL}_2(\Bbbk )\).
Proposition 2.12
Let \(\Bbbk \) be a field of finite characteristic \(p> 0\). There exist infinitely many simple \({\mathcal {H}}_{ {\mathfrak {S}}_2\backslash \widehat{{\mathfrak {S}}}_2}^\Bbbk \)-modules which do not admit BGG resolutions.
Proof
This is a standard Temperley–Lieb type result, we provide references in Remark 2.14 below but we include a proof for the sake of completeness. The Coxeter presentation of \(\widehat{{\mathfrak {S}}}_2\) is  and we let P denote the finite parabolic generated by the reflection
and we let P denote the finite parabolic generated by the reflection  . We will provide an infinite family of examples of \(x\in W\) such that \(\mathrm {rad}(\Delta (x))\) is not generated by the homomorphic images of standard modules, thus showing that each such L(x) does not admit a BGG resolution. For \(n\in {{\mathbb {N}}}\), we set
. We will provide an infinite family of examples of \(x\in W\) such that \(\mathrm {rad}(\Delta (x))\) is not generated by the homomorphic images of standard modules, thus showing that each such L(x) does not admit a BGG resolution. For \(n\in {{\mathbb {N}}}\), we set

so that, in the notation of Eq. 1.5, we have

Suppose that L(y) is a subquotient of \(\Delta (x)\) and that L(y) belongs to the submodule generated by the homomorphic images of standard modules. Then L(y) must be in the image of a homomorphism from \(\Delta (y)\) or \(\Delta (z)\) by highest weight theory. (In more detail, we simply note that \([\Delta (w):L(y)]\ne 0\) implies that \(w\leqslant y\) and that \( {{\,\mathrm{Hom}\,}}_{{\mathcal {H}}_{P\backslash W}^\Bbbk }(\Delta (w), \Delta (x))\ne 0\) implies that \(x\leqslant w\) and therefore \(x\leqslant w \leqslant y\); thus \(w\in \{x,y,z\}\).) The module \(\Delta ( x){\textsf {1}}_{{\underline{y}}}\) is \(({np}-1)\)-dimensional and spanned by the light leaves basis elements

for \(1\leqslant k < {np}\). We now calculate the full submodule structures of standard modules and hence verify that L(y) is not in the image of any homomorphism \( {{\,\mathrm{Hom}\,}}_{{\mathcal {H}}_{P\backslash W}^\Bbbk }(\Delta (w), \Delta (x))\) for \(w \in \{x,y,z\}\).
Decomposition numbers. We will prove that the Gram matrix of \(\Delta (x){\textsf {1}}_{{\underline{y}}}\) has rank \(\dim (\Delta _{\leqslant {{\underline{y}}}}(x))-\dim (L_{\leqslant {{\underline{y}}}}(y))=np-1-1=np-2\). Thus proving that \([\Delta (x):L(y)]=1 \) using Eq. 1.22 (this is a standard cellular argument). The Gram-matrix of the cell-form of \(\Delta ( x){\textsf {1}}_{{\underline{y}}}\) has \(-2\) for each of the diagonal entries and 1 for each of the super and subdiagonals (in other words, it is equal to \(-1\) times the Cartan matrix of type \(A_{np-1}\)). The determinant of this matrix is np which is zero in \(\Bbbk \). Over \(\Bbbk \), the rank of this matrix is \(np-2\) and so \([\Delta (x): L(y) ] = 1\) as required.
Submodule structures and homomorphisms. By considering the light leaves basis, one deduces that \(\Delta _{\leqslant {{\underline{y}}}}(y))=L_{\leqslant {{\underline{y}}}}(y)\) is 1-dimensional and that \(\Delta _{\leqslant {{\underline{y}}}}(z))\) is 2-dimensional with simple head \(L_{\leqslant {{\underline{y}}}}(z)\) and simple socle \(L_{\leqslant {{\underline{y}}}}(y)\). Suppose that the socle of \(\Delta _{\leqslant {{\underline{y}}}}(x))\) contains a submodule isomorphic to \(L_{\leqslant {{\underline{y}}}}(y)\). This submodule must be the span of some element \(g=\sum \alpha _k f_k\) for \(\alpha _k \in \Bbbk \) with \(gf_k^*\) vanishing in \(\Delta _{\leqslant {{\underline{y}}}}(x)\) for all \(1\leqslant k<np\), i.e.
for all \(1\leqslant k <np\). We have that \(f_{k\pm 1} f_k^*={\textsf { 1}}_{{\underline{x}}}\) and \(f_{k }f_k^*=-2\cdot {\textsf {1}}_{{\underline{x}}}\) modulo \({\mathcal {H}}_{ {\mathfrak {S}}_2\backslash \widehat{{\mathfrak {S}}}_2}^{<x}\). Thus
for some \(\alpha \in \Bbbk \setminus \{0\}\). However, we notice that for g as above,

and so the submodule generated by g contains \(L_{\leqslant {{\underline{y}}}}(z)\) as a submodule. Thus \(\Delta _{\leqslant {{\underline{y}}}}(x)\) is uniserial with simple head \(L_{\leqslant {{\underline{y}}}}(x)\), simple socle \(L_{\leqslant {{\underline{y}}}}(z)\), and the middle composition factor \(L_{\leqslant y}(y)\). Thus \(L_{\leqslant {{\underline{y}}}}(x)\) not the image of a homomorphism from \(\Delta _{\leqslant {{\underline{y}}}}(z)\) or \(\Delta _{\leqslant {{\underline{y}}}}(y)\), as required. \(\square \)
Remark 2.13
There is a theory of \({``\mathrm SL}_2(\Bbbk )\)-strings" for algebraic groups. This theory allows to inflate decomposition numbers and extension groups between standard modules for \(\mathrm{SL}_2(\Bbbk )\) to calculate certain decomposition numbers and homomorphisms between standard modules for arbitrary algebraic groups (see [30, Part II, 5.21 (2)] and [18, Introduction] for decomposition numbers and extension groups respectively). One can use the equivalence between algebraic groups and anti-spherical Hecke categories from [42] in order to translate these statements to the setting of \({\mathcal {H}}_{P\backslash W}\)-modules (in the case that P is the maximal parabolic of an affine Weyl group W). Thus one can use Proposition 2.12 to provide many examples of simple \({\mathcal {H}}_{P\backslash W}\)-modules which do not admit BGG resolutions. We do not go into further details here.
Remark 2.14
Through the isomorphism of [6], we can rephrase the above as a question concerning decomposition numbers and homomorphisms for the symmetric group \({\mathfrak {S}}_{np^2+p}\) in characteristic \(p>2\). We let \(S(\lambda )\) denote the Specht module and \(D(\mu )\) is the simple head for \(\lambda ,\mu \) partitions (the latter p-regular). We have that \( [S( np^2,p): D(np^2+p) ] = 1, \) however \( D({np^2+p} )\) is not in the image of any homomorphism \( {{\,\mathrm{Hom}\,}}_{\Bbbk {\mathfrak {S}}_{np^2+p}}(S(\lambda ) ,S(np^2,p) ))\). This example was already known to Gordon James in [29, 24.5 Examples] for \(p=2\) and the general case is similar, see [29, 24.4 Theorem] and [29, 24.15 Theorem]. For p arbitrary, the full submodule structures of Specht modules labelled by 2-part partitions were determined in [43].
Notes
Here we are using the fact that Jones–Wenzl projectors can be can be computed “generically” [16, Theorem 6.13].
To the authors’ knowledge, this relation has not been explicitly determined (but can be given more computing power). We invite the reader to either believe that this can be written down (as is now standard in this area) or to read all results in this paper “modulo" any Coxeter group W with a parabolic subgroup of type \(H_3\).
“That whereof we cannot speak, thereof we must remain silent", Wittgenstein.
References
Andersen, H. H., Jantzen, J. C., Soergel, W.: Representations of quantum groups at a \(p\)th root of unity and of semisimple groups in characteristic \(p\): independence of \(p\), Astérisque, no. 220, 321 (1994)
Achar, P., Makisumi, S., Riche, S., Williamson, G.: Koszul duality for Kac-Moody groups and characters of tilting modules. J. Am. Math. Soc. 32(1), 261–310 (2019)
Arakawa, T.: A new proof of the Kac-Kazhdan conjecture. Int. Math. Res. Not. Art. ID 27091, 5 (2006)
Arakawa, T.: Representation theory of\(\mathscr {W}\)-algebras, Invent. Math. 169(2), 219–320 (2007)
Berkesch Zamaere, C., Griffeth, S., Sam, S. V.: Jack polynomials as fractional quantum Hall states and the Betti numbers of the\((k+1)\)-equals ideal, Comm. Math. Phys. 330 (2014), no. 1, 415–434. MR 3215587
Bowman, C., Cox, A., Hazi, A.: Path isomorphisms between quiver Hecke and diagrammatic Bott–Samelson endomorphism algebras. arXiv:2005.02825
Bowman, C., Cox, A., Hazi, A., Michailidis, D.: Path combinatorics and light leaves for quiver Hecke algebras. Math. Z. 300(3), 2167–2203 (2022)
Bernstein, I. N., Gelfand, I. M., Gelfand, S. I.: Differential operators on the base affine space and a study of \({\mathfrak{g}}\)-modules. 21–64
Bowman, C., Norton, E., Simental, J.: On BGG resolutions of unitary modules for quiver Hecke and Cherednik algebras. Selecta Math. (N.S.) 28(2), Paper No. 29, 71 (2022)
Brundan, J., Stroppel, C.: Highest weight categories arising from Khovanov’s diagram algebra. II. Koszulity. Transform. Groups 15(1), 1–45 (2010)
Brundan, J., Stroppel, C.: Highest weight categories arising from Khovanov’s diagram algebra III: category \({\cal{O}}\). Represent. Theory 15, 170–243 (2011)
Brundan, J., Stroppel, C.: Semi-infinite highest weight categories. arXiv:1808.08022 (2017)
Carter, R.W., Payne, M.T.J.: On homomorphisms between Weyl modules and Specht modules. Math. Proc. Camb. Philos. Soc. 87(3), 419–425 (1980)
Donkin, S.: The \(q\)-Schur Algebra, London Mathematical Society Lecture Note Series, vol. 253. Cambridge University Press, Cambridge (1998)
Eastwood, M.: Higher symmetries of the Laplacian. Ann. Math. (2) 161(3), 1645–1665 (2005)
Elias, B., Williamson, G.: Localized calculus for the Hecke category. arXiv:2011.05432
Elias, B., Makisumi, S., Thiel, U., Williamson, G.: Introduction to Soergel bimodules, RSME Springer Series, vol. 5, Springer, Cham (2020)
Erdmann, K.: \({\rm Ext}^1\)for Weyl modules of\({\rm SL}_2(K)\). Math. Z. 218(3), 447–459 (1995)
Elias, B., Williamson, G.: The Hodge theory of Soergel bimodules. Ann. Math. (2) 180(3), 1089–1136 (2014)
Elias, G., Williamson, G.: Soergel calculus, Represent. Theory 20, 295–374 (2016)
Felder, G.: BRST approach to minimal models, Nuclear Phys. B 317 (1989), no. 1, 215–236. MR 995219
Feigin, B., Frenkel, E.: Affine Kac-Moody algebras at the critical level and Gelfand-Dikiui algebras. Infinite analysis, Part A, B (Kyoto, 1991), Adv. Ser. Math. Phys., vol. 16, World Sci. Publ., River Edge, NJ, pp. 197–215 (1992)
Gainutdinov, A., Jacobsen, J., Saleur, H., Vasseur, R.: A physical approach to the classification of indecomposable Virasoro representations from the blob algebra. Nuclear Phys. B 873(3), 614–681 (2013)
Garland, H., Lepowsky, J.: Lie algebra homology and the Macdonald-Kac formulas, Invent. Math. 34 (1976), no. 1, 37–76. MR 0414645
Hayashi, T.: Sugawara operators and Kac-Kazhdan conjecture, Invent. Math. 94 (1988), no. 1, 13–52. MR 958588
Hazi, A.: Matrix recursion for positive characteristic diagrammatic Soergel bimodules for affine Weyl groups, arXiv:1708.07072
Hu, J., Mathas, A.: Graded cellular bases for the cyclotomic Khovanov-Lauda-Rouquier algebras of type \(A\). Adv. Math. 225(2), 598–642 (2010)
Humphreys, J.: Reflection groups and Coxeter groups, Cambridge Studies in Advanced Mathematics, vol. 29. Cambridge University Press, Cambridge (1990)
James, G.D.: The Representation Theory of the Symmetric Groups. Lecture Notes in Mathematics, vol. 682. Springer, Berlin (1978)
Jantzen, J. C.: Representations of algebraic groups, second ed., Mathematical Surveys and Monographs, vol. 107, American Mathematical Society, Providence, RI, (2003)
Jensen, L.: Correction of the Lusztig-Williamson billiards conjecture, arXiv:2105.04665 (2017)
Jensen, T., Williamson, G.: The\(p\)-canonical basis for Hecke algebras, Categorification and higher representation theory, Contemp. Math., vol. 683, Amer. Math. Soc., Providence, RI, (2017), pp. 333–361. MR 3611719
Kac, V.: Infinite dimensional Lie algebras, 3rd edn. Cambridge University Press, Cambridge (1990)
Kac, V. G., Kazhdan, D. A.: Structure of representations with highest weight of infinite-dimensional Lie algebras, Adv. in Math. 34 (1979), no. 1, 97–108. MR 547842
Kleshchev, A., Ram, A.: Homogeneous representations of Khovanov–Lauda algebras, J. Eur. Math. Soc. 12 (2012), 1293–1306. MR 2999126
Ku, J.: Structure of the Verma module\(M(-\rho )\)over Euclidean Lie algebras, J. Algebra 124 (1989), no. 2, 367–387. MR 1011602
Lepowsky, J.: A generalization of the Bernstein-Gelfand-Gelfand resolution, J. Algebra 49 (1977), no. 2, 496–511. MR 476813
Libedinsky, N., Williamson, G.: The anti-spherical category, in preparation, previous version at arXiv:1702.00459v1
Lusztig, G., Williamson, G.: Billiards and tilting characters for\(\rm SL_3\), SIGMA Symmetry Integrability Geom. Methods Appl. 14 (2018), 015, 22 pages. MR 3766576
Mathieu, O.: On some modular representations of affine Kac-Moody algebras at the critical level, Compositio Math. 102 (1996), no. 3, 305–312. MR 1401425
Martin, P., Saleur, H.: The blob algebra and the periodic Temperley-Lieb algebra. Lett. Math. Phys. 30(3), 189–206 (1994)
Riche, S., Bezrukavnikov, R.: Hecke action on the principal block, arXiv:2009.10587
Reuter, A.: The submodule structure of Specht modules, J. Algebra 271 (2004), no. 2, 768–797. MR 2025550
Ryom-Hansen, S.: Jucys-Murphy elements for Soergel bimodules, J. Algebra 551 (2020), 154–190. MR 4057514
Riche, S., Williamson, G.: Tilting modules and the\(p\)-canonical basis, Astérisque (2018), no. 397, ix+184
Wakimoto, Minoru: Fock representations of the affine Lie algebra\(A^{(1)}_1\), Comm. Math. Phys. 104 (1986), no. 4, 605–609. MR 841673
Williamson, G.: Schubert calculus and torsion explosion, J. Amer. Math. Soc. 30 (2017), no. 4, 1023–1046, With a joint appendix with A. Kontorovich and P. J. McNamara. MR 3671935
Acknowledgements
We would like to thank George Lusztig and Stephen Donkin for their helpful comments. We would also like to thank the anonymous referees for their detailed reading of the paper and their helpful suggestions. The authors are grateful for funding from EPSRC grant EP/V00090X/1, the Royal Commission for the Exhibition of 1851, and European Research Council grant No. 677147, respectively.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bowman, C., Hazi, A. & Norton, E. The modular Weyl–Kac character formula. Math. Z. 302, 2207–2232 (2022). https://doi.org/10.1007/s00209-022-03084-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-022-03084-7



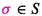 we have
we have 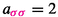 ;
; such that
such that 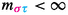 , set
, set 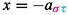 and
and 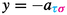 . We require that
. We require that 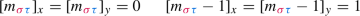



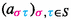 be the image of A over
be the image of A over 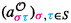 to be the image of A over
to be the image of A over 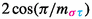 for all
for all  , and define the “geometric” Cartan matrix by setting
, and define the “geometric” Cartan matrix by setting 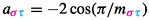 . As mentioned above, it is known that the universal realisation with respect to this Cartan matrix over
. As mentioned above, it is known that the universal realisation with respect to this Cartan matrix over 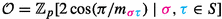 . Thus Assumption
. Thus Assumption 

 as in Example
as in Example  in the short exact sequence of
in the short exact sequence of 
 as in Example
as in Example  in the short exact sequence of
in the short exact sequence of