The Abel map for surface singularities III: Elliptic germs

Abstract

The present note is part of a series of articles targeting the theory of Abel maps associated with complex normal surface singularities with rational homology sphere links (Nagy and Némethi in Math Annal 375(3):1427–1487, 2019; Nagy and Némethi in Adv Math 371:20, 2020; Nagy and Némethi in Pure Appl Math Q 16(4):1123–1146, 2020). Besides the general theory, by the study of specific families we wish to show the power of this new method. Indeed, using the general theory of Abel maps applied for elliptic singularities in this note we are able to prove several key properties for elliptic singularities (e.g. the statements of the next paragraph), which by ‘old’ techniques were not reachable. If $({\widetilde{X}},E)\rightarrow (X,o)$ is the resolution of a complex normal surface singularity and $c_1:{\mathrm{Pic}}({\widetilde{X}})\rightarrow H^2({\widetilde{X}},{\mathbb {Z}})$ is the Chern class map, then ${\mathrm{Pic}}^{l'}({\widetilde{X}}):= c_1^{-1}(l')$ has a (Brill–Noether type) stratification $W_{l', k}:= \{{\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}})\,:\, h^1({\mathcal {L}})=k\}$. In this note we determine it for elliptic singularities together with the stratification according to the cycle of fixed components. E.g., we show that the closure of any $W(l',k)$ is an affine subspace. For elliptic singularities we also characterize the End Curve Condition and Weak End Curve Condition in terms of the Abel map, we provide several characterization of them, and finally we show that they are equivalent.

1 Introduction

1.1 .

Recall that the classical Brill–Noether problem for curves is the following. Let C be a smooth complex projective curve and let $c_1:{\mathrm{Pic}}(C)\rightarrow H^2(C,{\mathbb {Z}})={\mathbb {Z}}$ be the first Chern class map. Set ${\mathrm{Pic}}^l(C):=c_1^{-1}(l)$. Then one considers the stratification of ${\mathrm{Pic}}^l(C)$ according to the $h^1$-values, namely, $W_{l,k}:=\{{\mathcal {L}}\in {\mathrm{Pic}}^l(C)\,:\, h^1({\mathcal {L}})=k\}$. The problem is to determine the values (l, k) for which $W_{l,k}$ is non-empty and in such cases to describe the different non-empty strata $W_{l,k}$. (This depends heavily on the analytic structure of C.) For details see e.g. [1, 7].

1.1.1 .

For complex normal surface singularities the analogue question can be formulated as follows. Let (X, o) be such a singularity and let us fix a resolution $\phi :({\widetilde{X}},E)\rightarrow (X,o)$. We will assume that the link is a rational homology sphere (RHS), equivalently, that the dual resolution graph $\Gamma$ is a tree of ${{\mathbb {P}}}^1$’s. (In some parts of the presentation we will drop this assumption, however in the final key statements it is necessary, see 2.2.13 and the paragraph after Theorem 3.3.5 for further comments.) We consider the lattice $L:=H_2({\widetilde{X}},{\mathbb {Z}})$, it is freely generated by the irreducible exceptional divisors and it is endowed with the negative definite intersection form.

Then one has the exponential exact sequence

$$\begin{aligned} 0\rightarrow H^1({{\mathcal {O}}}_{{\widetilde{X}}})\simeq {\mathrm{Pic}}^0({\widetilde{X}}) \rightarrow {\mathrm{Pic}}({\widetilde{X}}) {\mathop {\longrightarrow }\limits ^{c_1}} L':=H^2({\widetilde{X}},{\mathbb {Z}})\rightarrow 0. \end{aligned}$$

Here $L'$ might serve also as the dual lattice of L. Then for any possible Chern class $l'\in L'$ set ${\mathrm{Pic}}^{l'}({\widetilde{X}}):= c_1^{-1}(l')$. (Note that while ${\mathrm{Pic}}^l(C)$ for a smooth curve is a compact complex torus, in the surface singularity case ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ is an affine space ${\mathbb {C}}^{p_g}$, where $p_g$ is the geometric genus of (X, o).) Following [14, 15] we consider the stratification $W_{l', k}:=\{ {\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}})\, :\, h^1({\mathcal {L}})=k\}$. Again, the goal is to describe the spaces $W_{l',k}$. In general, they depend in a rather arithmetical way on the combinatorics of the resolution graph $\Gamma$ and also on the analytic structure of (X, o) supported on the topological type determined by $\Gamma$. Usually the spaces $W_{l',k}$ are neither open, nor closed, not even quasi-projective. Their closure might be nonlinear, or even singular. Though in the theory of singularities several results are known for the possible $h^1({\mathcal {L}})$-values (vanishing theorems, coarse topological bounds), a systematic study of the spaces $W_{l',k}$ was missing. In the series of articles (starting with [14, 15] and the present one) the authors aim to fill in this necessity.

In order to understand (and detect) general and peculiar properties of the $W_{l',k}$-stratification it is highly desirable to describe it completely for certain key non-trivial families of singularities. In this note this task is fulfilled for elliptic germs.

1.1.2 .

The main tool in the study of the W-stratification (similarly as in the curve case) is the Abel map $c^{l'}(Z):{\mathrm{ECa}}^{l'}(Z)\rightarrow {\mathrm{Pic}}^{l'}(Z)$, where $Z\in L$ is a nonzero effective cycle, and ${\mathrm{ECa}}^{l'}(Z)$ is the space of effective Cartier divisors on Z, cf. [8,9,10]. (We emphasize again some major differences compared with the curve case: ${\mathrm{ECa}}^{l'}(Z)$ is not compact, and $c^{l'}$ is not proper, a fact which creates extra difficulties in the study of the fibers.) If $Z\gg 0$ then ${\mathrm{Pic}}^{l'}(Z)={\mathrm{Pic}}^{l'}({\widetilde{X}})$, and the W-stratification can be analysed via the fiber structure of the Abel map $c^{l'}$. Besides the general theory, some concrete families of singularities were already analysed, e.g. superisolated and weighted homogeneous ones (partially) in [14], the generic analytic structure (as an extreme bound case of the theory) in [15]; see also [16]. In this manuscript we provide a complete description for elliptic singularities (with RHS link). Surprisingly, the new results and the needed developed machinery regarding the Abel map reshapes the ‘classical’ theory of elliptic singularities as well.

For the theory of elliptic singularities the reader might consult [13, 18, 28, 33, 35,36,37,38,39]. The main technical machinery, which guides most of the properties of an elliptic singularity is the elliptic sequence defined by Laufer and Yau. In the numerical Gorenstein case, we will use this sequence; however, for the non-numerically Gorenstein case we introduce a new sequence, which mimics the numerical Gorenstein case better and it is more relevant for our purposes. (For the comparison of the old and new sequences see [17]).

The members of the elliptic sequences, and the Artin fundamental cycles and the canonical cycles on different supports satisfy several key compatibility properties; these relations are formulated (elegantly) in the minimal resolution. In any other resolution, they became uneasy and unpleasant. On the other hand, in [14] we developed several properties of the space of effective Cartier divisors and of the Abel map in the context of a good resolution: in several local verifications the normal crossing property of the exceptional curves was used. Therefore, strictly speaking, in this note we analyse only those elliptic singularities (with rational homology sphere links) whose minimal resolution is good. The interested reader is invited to extend the results for the remaining few cases (when the minimal resolution is not good, see e.g. [13] for their list in the minimally elliptic case, and also a model how one extends statements valid for the other general cases to these special germs). Hence, in the sequel, ‘elliptic’ means elliptic with these restrictions.

1.1.3 .

In the body of the paper we prove that for elliptic singularities the Abel map has several very pleasant properties (see Theorem 6.1.1 below), which are not valid for arbitrary singularities.

Theorem

• (a) The closure $\overline{ {\mathrm{im}}(c^{l'}(Z))}$ of the image of the Abel map $c^{l'}(Z)$ is an affine subspace of ${\mathrm{Pic}}^{l'}(Z)$.

• (b) $h^1({\mathcal {L}})$ is uniform on $\overline{ {\mathrm{im}}(c^{l'}(Z))}$ (whose value is computable).

This solves the Brill–Noether problem on the image $\overline{ {\mathrm{im}}(c^{l'}(Z))} \subset {\mathrm{Pic}}^{l'}(Z)$. However, usually $\overline{ {\mathrm{im}}(c^{l'}(Z))}\not ={\mathrm{Pic}}^{l'}(Z)$. Recall that the image of $c^{l'}$ consists of line bundles without fixed components. Hence, to complete the picture, we need to analyse the possible cycles of fixed components, and twisting a certain bundle with the cycle of its fixed components (hence creating bundles without fixed components) we reduce the Brill–Noether problem to the study of several Abel map images.

The facts that the elliptic sequence imposes some ‘total-ordered structure’ of invariants, and that the closure of the Abel maps are affine subspaces, are inherited by the W-stratification as well:

Theorem

(Cf. Sect. 7) For elliptic Gorenstein singularities the W-stratification is organized in a flag of linear subspaces reflecting completely the concatenated structure of the elliptic sequence. Moreover, the corresponding dimensions can also be determined. (In the non-Gorenstein case some additional ‘isolated wandering points’ might also appear; for details see Theorem 7.4.1 and Remark 7.4.2.)

The W-stratification of the Picard groups according to the $h^1$-values (for different levels of generality) is completely described in Sect. 7. In Sect. 8 we provide even a finer stratification according to the cycles of fixed components.

1.1.4 .

The second main goal of the article is to analyse elliptic surface singularities satisfying the ‘End Curve Condition’ (ECC) and ‘Weak End Curve Condition’ (WECC). Singularities with ECC were introduced by Neumann and Wahl [25]. They coincide with the very important family of splice quotient singularities [26]. Their construction requires that the corresponding singularity link is a rational homology sphere. Here we focus on the WECC case as well: the WECC imposes a weaker condition. It appeared naturally in certain questions targeting generalizations of the construction of the splice quotient equations, in the generalization of certain surgery formulae and in $p_g$-formulae from the splice quotient singularities to more general cases (e.g. in Okuma’s work), and also in the study of Abel maps by the authors [14, 15]. (In the WECC case the strict transform of an end-curve function can intersect the end-exceptional curve even non-transversally and by any intersection multiplicity contrary to the ECC case when the intersection is transversal. However, the RHS link-requirement is preserved.) It turns out that for a normal surface singularity both ECC and WECC can be elegantly characterized by the mutual position of the ‘natural’ line bundles and the images of the Abel maps, cf. 9.1. (By a natural line bundle we associate in a universal way to a given Chern class a line bundle having that Chern class [21, 27], cf. 2.1.5 here. They are generalizations of bundles of type ${{\mathcal {O}}}_{{\widetilde{X}}}(l)$, $l\in L$ to the rational cycles $l'\in L'$.)

Recall that a graph $\Gamma$ is the dual graph of a resolution of a certain singularity (analytic type) with ECC if and only if it satisfies the ‘semigroup and congruence conditions’ of Neumann and Wahl [25], or equivalently, if it satisfies the ‘monomial condition’ of Okuma [29]. In Theorem 9.3.1, valid for elliptic germs, we provide a similar combinatorial condition (we call it ‘extension criterion of the elliptic sequence’), which guarantees the existence of an analytic structure satisfying the WECC. In fact, using this, we prove in Theorem 9.4.2 that for elliptic singularities the ECC and WECC are equivalent:

Theorem

• (a) If an elliptic graph $\Gamma$ admits a WECC analytic structure then it admits an ECC as well. In particular, the three topological conditions—the ‘semigroup and congruence conditions’, the ‘monomial condition’ and the ‘extension criterion’—are equivalent.

• (b) If an elliptic (X, o) satisfies WECC then it satisfies ECC too (hence it is a splice quotient).

1.1.5 .

The structure of the article is the following. Section 2 recalls the preliminary notions regarding surface singularities, Abel map, modified Abel map, and their relationships with differential forms. Section 3 reviews facts regarding elliptic singularities and defines the ‘new’ elliptic sequence. In Sect. 4, we prove several identities and inequalities regarding $h^1({\mathcal {L}})$, ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$, we analyse the possible cycles of fixed components, and we study certain compatibilities with the elliptic sequences. In Sect. 5 we analyse with details an example with pathological cycle of fixed components. Section 6 treats the Abel map of elliptic singularities. Several examples are listed. In Sect. 7 we describe the stratification of ${\mathrm{Pic}}({\widetilde{X}})$ according to $h^1$, while in Sect. 8 the stratification according to $h^1$ and the fixed components. The last section contains the study of ECC and WECC elliptic singularities. We present two topological and two analytical characterizations of germs satisfying WECC.

2 Preliminaries and notations

2.1 Notations regarding a resolution [11, 14, 19, 21, 23]

Let (X, o) be the germ of a complex analytic normal surface singularity.

Let $\phi :{\widetilde{X}}\rightarrow X$ be a resolution of (X, o) with exceptional curve $E:=\phi ^{-1}(0)$, and let $\cup _{v\in {{\mathcal {V}}}}E_v$ be the irreducible decomposition of E. Define $E_I:=\sum _{v\in I}E_v$ for any subset $I\subset {{\mathcal {V}}}$.

The lattice $L:=H_2({\widetilde{X}},{\mathbb {Z}})$ is endowed with the natural negative definite intersection form $(\,,\,)$. It is freely generated by the classes of $\{E_v\}_{v\in {\mathcal {V}}}$. The dual lattice is $L'={\mathrm{Hom}}_{\mathbb {Z}}(L,{\mathbb {Z}}) \simeq \{ l'\in L\otimes {\mathbb {Q}}\,:\, (l',L)\in {\mathbb {Z}}\}$. It is generated by the (anti)dual classes $\{E^*_v\}_{v\in {\mathcal {V}}}$ defined by $(E^{*}_{v},E_{w})=-\delta _{vw}$ (where $\delta _{vw}$ stays for the Kronecker symbol). $L'$ is also identified with $H^2({\widetilde{X}},{\mathbb {Z}})$.

All the $E_v$-coordinates of any $E^*_u$ are strict positive. We define the Lipman cone as ${{\mathcal {S}}}':=\{l'\in L'\,:\, (l', E_v)\le 0 \ \text{ for } \text{ all } v\}$. As a monoid it is generated over ${{\mathbb {Z}}}_{\ge 0}$ by $\{E^*_v\}_v$. Write also ${{\mathcal {S}}}:={{\mathcal {S}}}'\cap L$.

The intersection form embeds L into $L'$ with $L'/L\simeq \mathrm{Tors}( H_1(M,{\mathbb {Z}}))$, which is abridged by H. The class of $l'$ in H is denoted by $[l']$.

There is a natural partial ordering of $L'$ and L: we write $l_1'\ge l_2'$ if $l_1'-l_2'=\sum _v r_vE_v$ with every $r_v\ge 0$. We set $L_{\ge 0}=\{l\in L\,:\, l\ge 0\}$ and $L_{>0}=L_{\ge 0}{\setminus } \{0\}$.

The support of a cycle $l=\sum n_vE_v$ is defined as $|l|=\cup _{n_v\not =0}E_v$.

If $H_1(M,{\mathbb {Q}})=0$ then each $E_v$ is rational, and the dual graph of any good resolution is a tree.

The geometric genus $h^1({\widetilde{X}}, {{\mathcal {O}}}_{{\widetilde{X}}})$ of (X, o) is denoted by $p_g$. It is independent of the choice of ${\widetilde{X}}$.

2.1.1 Minimal cycles in $L'_{\ge 0}$ and in ${{\mathcal {S}}}'$

Consider the semi-open cube $Q:=\{\sum _v l'_v E_v\in L' \ | \ 0\le l'_v<1\}$. For any $h\in H$, Q contains a unique representative $r_h$ so that $[r_h]=h$. Similarly, for any $h\in H$ there is a unique minimal element of $\{l'\in L' \ | \ [l']=h\}\cap {\mathcal {S}}'$, which will be denoted by $s_h$. One has $s_h\ge r_h$; in general, $s_h \ne r_h$ (see e.g. Example 3.2.6).

2.1.2 A ‘Laufer-type’ computation sequence targeting ${\mathcal {S}}'$

Recall the following fact:

Lemma 2.1.3

[20, Lemma 7.4] Fix any $l'\in L'$.

• (1) There exists a unique minimal element $s(l')$ of $(l'+L_{\ge 0})\cap {\mathcal {S}}'$.

• (2) $s(l')$ can be found via the following computation sequence $\{z_i\}_i$ connecting $l'$ and $s(l')$: set $z_0:=l'$, and assume that $z_i$ ($i\ge 0$) is already constructed. If $(z_i,E_{v(i)})>0$ for some $v(i)\in {\mathcal {V}}$ then set $z_{i+1}=z_i+E_{v(i)}$. Otherwise $z_i\in {\mathcal {S}}'$ and necessarily $z_i=s(l')$.

In general the choice of the individual vertex v(i) might not be unique, nevertheless the final output $s(l')$ is unique. From definitions, if $l'=r_h$ then $s(l')=s_h$.

The (anti)canonical cycle $Z_K\in L'$ is defined by the adjunction formulae $(Z_K, E_v)=(E_v,E_v)+2-2g_v-2\delta _v$ for all $v\in {\mathcal {V}}$, where $g_v$ and $\delta _v$ denote the genus of $E_v$ and the sum of the delta invariants of the singularities of $E_v$. (It is the first Chern class of the dual of the line bundle $\Omega ^2_{{\widetilde{X}}}$.) We write $\chi :L'\rightarrow {\mathbb {Q}}$ for the (Riemann–Roch) expression $\chi (l'):= -(l', l'-Z_K)/2$.

The singularity (or, its topological type) is called numerically Gorenstein if $Z_K\in L$. (Since $Z_K\in L$ if and only if the line bundle $\Omega ^2_{X{\setminus } \{o\}}$ of holomorphic 2-forms on $X{\setminus } \{o\}$ is topologically trivial, see e.g. [6], the $Z_K\in L$ property is independent of the resolution). (X, o) is called Gorenstein if $Z_K\in L$ and $\Omega ^2_{{\widetilde{X}}}$ (the sheaf of holomorphic 2-forms) is isomorphic to ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_K)$ (or, equivalently, if the line bundle $\Omega ^2_{X{\setminus } \{o\}}$ is holomorphically trivial). If ${\widetilde{X}}$ is a minimal resolution then (by the adjunction formulae) $Z_K\in {{\mathcal {S}}}'$. In particular, $Z_K-s_{[Z_K]}\in L_{\ge 0}$.

Lemma 2.1.4

Assume that $Z_K\in {{\mathcal {S}}}'$, hence $Z_K\ge s_{[Z_K]}$. Then $p_g=0$ whenever $Z_K=s_{[Z_K]}$. If $Z_K>s_{[Z_K]}$ then $p_g=h^1({{\mathcal {O}}}_{Z_K-s_{[Z_K]}})$. More generally, $h^1({\widetilde{X}}, {\mathcal {L}})=h^1(Z_K-s_{[Z_K]}, {\mathcal {L}})$ for any ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$ with $c_1({\mathcal {L}})\in -{{\mathcal {S}}}'$.

Proof

By generalized Kodaira or Grauert–Riemenschneider type vanishing $h^1({\widetilde{X}}, {\mathcal {O}}_{{\widetilde{X}}}(-\lfloor Z_K\rfloor ))=0$. Hence, if $\lfloor Z_K\rfloor =0$ then $p_g=0$. Otherwise, using the exact sequence $0\rightarrow {\mathcal {O}}_{{\widetilde{X}}}(-\lfloor Z_K\rfloor ))\rightarrow {\mathcal {O}}_{{\widetilde{X}}} \rightarrow {\mathcal {O}}_{\lfloor Z_K\rfloor }\rightarrow 0$ we get $h^1({{\mathcal {O}}}_{\lfloor Z_K\rfloor })=p_g$. Next, consider the computation sequence from Lemma 2.1.3 applied for $l'=r_{[Z_K]}$. By induction we prove that $h^1({{\mathcal {O}}}_{Z_K-z_i})=p_g$. Hence, since $s(r_{[Z_K]})=s_{[Z_K]}$, the output of the induction is $h^1({{\mathcal {O}}}_{Z_K-s_{[Z_K]}})=p_g$. For $i=0$ we have just verified the statement, since $Z_K-r_{[Z_K]}=\lfloor Z_K\rfloor$. Then use the cohomological exact sequence associated with $0\rightarrow {{\mathcal {O}}}_{E_{v(i)}}(-Z_K+z_{i+1})\rightarrow {{\mathcal {O}}}_{Z_K-z_i}\rightarrow {{\mathcal {O}}}_{Z_K-z_{i+1}}\rightarrow 0$ and the vanishing $h^1({{\mathcal {O}}}_{E_{v(i)}}(-Z_K+z_{i+1}))=0$.

More generally, $h^1({\widetilde{X}},{\mathcal {L}})=h^1(Z_K-z_i,{\mathcal {L}})$ for any i by similar argument. $\square$

2.1.3 Natural line bundles

Let $\phi :({\widetilde{X}},E)\rightarrow (X,o)$ be as above. In the sequel we assume that the link is a rational homology sphere (required in the next construction and in 2.2). Consider the ‘exponential’ cohomology exact sequence (with $H^1({\widetilde{X}}, {{\mathcal {O}}}_{{\widetilde{X}}}^*)={\mathrm{Pic}}({\widetilde{X}})$ and $H^1({\widetilde{X}}, {{\mathcal {O}}}_{{\widetilde{X}}})={\mathrm{Pic}}^0({\widetilde{X}})$)

$$\begin{aligned} 0\rightarrow {\mathrm{Pic}}^0({\widetilde{X}})\longrightarrow \mathrm{Pic}({\widetilde{X}}){\mathop {\longrightarrow }\limits ^{c_1}}H^2({\widetilde{X}},{\mathbb {Z}})\rightarrow 0. \end{aligned}$$

(2.1.6)

Here $c_1({\mathcal {L}})\in H^2({\widetilde{X}},{\mathbb {Z}})=L'$ is the first Chern class of ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$. Then (based on the fact that the link is a rational homology sphere, hence ${\mathrm{Pic}}^0({\widetilde{X}})$ is torsion free), see e.g. [21, 27], there exists a unique homomorphism (split) $s_1:L'\rightarrow {\mathrm{Pic}}({\widetilde{X}})$ of $c_1$ such that $c_1\circ s_1=id$ and $s_1$ restricted to L is $l\mapsto {{\mathcal {O}}}_{{\widetilde{X}}}(l)$. The line bundles $s_1(l')$ are called natural line bundles of ${\widetilde{X}}$. For several equivalent definitions of them see [21]. E.g., ${\mathcal {L}}$ is natural if and only if one of its powers has the form ${{\mathcal {O}}}_{{\widetilde{X}}}(l)$ for some integral cycle $l\in L$ supported on E. In order to have a uniform notation we write ${{\mathcal {O}}}_{{\widetilde{X}}}(l')$ for $s_1(l')$ for any $l'\in L'$.

2.2 The Abel map [14]

As above, let ${\mathrm{Pic}}({\widetilde{X}})=H^1({\widetilde{X}},{{\mathcal {O}}}_{{\widetilde{X}}}^*)$ be the group of isomorphism classes of holomorphic line bundles on ${\widetilde{X}}$. The first Chern class map $c_1:{\mathrm{Pic}}({\widetilde{X}})\rightarrow L'$ is surjective; write ${\mathrm{Pic}}^{l'}({\widetilde{X}})=c_1^{-1}(l')$. Since $H^1(M,{\mathbb {Q}})=0$, ${\mathrm{Pic}}^0({\widetilde{X}})\simeq H^1({\widetilde{X}},{{\mathcal {O}}}_{{\widetilde{X}}})\simeq {\mathbb {C}}^{p_g}$.

Similarly, if $Z\in L_{>0}$ is an effective non-zero integral cycle supported by E, then ${\mathrm{Pic}}(Z)=H^1(Z,{{\mathcal {O}}}_Z^*)$ denotes the group of isomorphism classes of invertible sheaves on Z. Again, it appears in the exact sequence $0\rightarrow {\mathrm{Pic}}^0(Z)\rightarrow {\mathrm{Pic}}(Z){\mathop {\longrightarrow }\limits ^{c_1}} L'(|Z|)\rightarrow 0$, where ${\mathrm{Pic}}^0(Z)=H^1(Z,{{\mathcal {O}}}_Z)$. Here L(|Z|) denotes the sublattice of L generated by the base element $E_v\subset |Z|$, and $L'(|Z|)$ is its dual.

Though for any effective cycle Z the Abel map might have its own peculiar properties, in this manuscript we always assume that all the $E_v$-coefficients of Z are sufficiently large, denoted by $Z\gg 0$. Under this assumption one has several stability properties, e.g. $L'(|Z|)=L'$, ${\mathrm{Pic}}(Z)={\mathrm{Pic}}({\widetilde{X}})$, or $h^1(Z,{\mathcal {L}})=h^1({\widetilde{X}},{\mathcal {L}})$ for any ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$.

For any $Z\gg 0$ let ${\mathrm{ECa}}(Z)$ be the space of (analytic) effective Cartier divisors on Z. Their supports are zero-dimensional in E. Taking the line bundle of a Cartier divisor provides the Abel map $c=c(Z):{\mathrm{ECa}}(Z)\rightarrow {\mathrm{Pic}}(Z)$. Let ${\mathrm{ECa}}^{l'}(Z)$ be the set of effective Cartier divisors with Chern class $l' \in L'$, i.e. ${\mathrm{ECa}}^{l' }(Z):=c^{-1}({\mathrm{Pic}}^{l'}(Z))$. The restriction of c is denoted by $c^{l'}:{\mathrm{ECa}}^{l'}(Z)\rightarrow {\mathrm{Pic}}^{l'}(Z)$.

A line bundle ${\mathcal {L}}\in {\mathrm{Pic}}^{l'}(Z)$ is in the image ${\mathrm{im}}(c^{l'})$ if and only if it has a section without fixed components, that is, if $H^0(Z,{\mathcal {L}})_{reg}\not =\emptyset$, where $H^0(Z,{\mathcal {L}})_{reg}:=H^0(Z,{\mathcal {L}}){\setminus } \cup _v H^0(Z-E_v, {\mathcal {L}}(-E_v))$. By this definition (see (3.1.5) of [14]) ${\mathrm{ECa}}^{l'}(Z)\not =\emptyset$ if and only if $-l'\in {{\mathcal {S}}}'{\setminus } \{0\}$. It is advantageous to have a similar statement for $l'=0$ too, hence we redefine ${\mathrm{ECa}}^0(Z)$ as $\{\emptyset \}$, a set/space with one element (the empty divisor), and $c^0:{\mathrm{ECa}}^0(Z)\rightarrow {\mathrm{Pic}}^0(Z)$ by $c^0(\emptyset )={{\mathcal {O}}}_Z$. In particular,

$$\begin{aligned} H^0(Z,{\mathcal {L}})_{reg}\not =\emptyset \ \Leftrightarrow \ {\mathcal {L}}={{\mathcal {O}}}_Z\ \Leftrightarrow \ {\mathcal {L}}\in {\mathrm{im}}(c^0) \ \ \text{ whenever } c_1({\mathcal {L}})=0. \end{aligned}$$

(2.2.1)

Hence, the previous equivalence extends to this $l'=0$ case too and one has the uniform statement

$$\begin{aligned} {\mathrm{ECa}}^{l'}(Z)\not =\emptyset \ \Leftrightarrow \ -l'\in {{\mathcal {S}}}'. \end{aligned}$$

(2.2.2)

Sometimes (e.g. in Sect. 9) even for ${\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}})$ we write ${\mathcal {L}}\in {\mathrm{im}}(c^{l'})$ whenever ${\mathcal {L}}|_Z\in {\mathrm{im}}(c^{l'}(Z))$ for some $Z\gg 0$. This is equivalent with the fact that ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$ has no fixed components.

It turns out that ${\mathrm{ECa}}^{l'}(Z)$ is a smooth complex algebraic variety of dimension $(l',Z)$ and the Abel map is an algebraic regular map. For more properties and applications see [14, 15].

2.2.1 The modified Abel map

For any $Z\gg 0$ let ${{\mathcal {O}}}_Z(l')$ be the restriction of the natural line bundle ${{\mathcal {O}}}_{{\widetilde{X}}}(l')$ to Z. (In fact, ${{\mathcal {O}}}_Z(l')$ can be defined in an identical way as ${{\mathcal {O}}}_{{\widetilde{X}}}(l')$ starting from the exponential cohomological sequence $0\rightarrow {\mathrm{Pic}}^0(Z)\rightarrow {\mathrm{Pic}}(Z)\rightarrow H^2({\widetilde{X}},{\mathbb {Z}})\rightarrow 0$ as well.) Multiplication by ${{\mathcal {O}}}_{Z}(-l')$ gives an isomorphism of the affine spaces ${\mathrm{Pic}}^{l'}(Z)\rightarrow {\mathrm{Pic}}^0(Z)$. Furthermore, we identify (via the exponential exact sequence) ${\mathrm{Pic}}^0(Z)$ with the vector space $H^1(Z, {{\mathcal {O}}}_Z)=H^1({\widetilde{X}},{{\mathcal {O}}}_{{\widetilde{X}}})$.

It is convenient to replace the Abel map $c^{l'}$ with the composition

$$\begin{aligned} {\widetilde{c}}^{l'}:{\mathrm{ECa}}^{l'}(Z){\mathop {\longrightarrow }\limits ^{c^{l'}}} {\mathrm{Pic}}^{l'}(Z){\mathop {\longrightarrow }\limits ^{{{\mathcal {O}}}_Z(-l')}} {\mathrm{Pic}}^0(Z){\mathop {\longrightarrow }\limits ^{\simeq }} H^1({{\mathcal {O}}}_Z). \end{aligned}$$

The advantage of this new set of maps is that all the images sit in the same vector space $H^1({{\mathcal {O}}}_Z)$.

2.2.2 The monoid (or multiplicative) structure of divisors and of the modified Abel map

Consider the natural additive structure $s^{l'_1,l'_2}(Z):{\mathrm{ECa}}^{l'_1}(Z)\times {\mathrm{ECa}}^{l'_2}(Z)\rightarrow {\mathrm{ECa}}^{l'_1+l'_2}(Z)$ ($l'_1,l'_2\in -{{\mathcal {S}}}'$) provided by the sum of the divisors. One verifies (see e.g. [14, Lemma 6.1.1]) that $s^{l'_1,l'_2}(Z)$ is dominant and quasi-finite. There is a parallel multiplication ${\mathrm{Pic}}^{l'_1}(Z)\times {\mathrm{Pic}}^{l'_2}(Z)\rightarrow {\mathrm{Pic}}^{l'_1+l'_2}(Z)$, $({\mathcal {L}}_1,{\mathcal {L}}_2)\mapsto {\mathcal {L}}_1\otimes {\mathcal {L}}_2$, which satisfies $c^{l_1'+l'_2}\circ s^{l'_1,l'_2}= c^{l'_1} \otimes c^{l'_2}$ in ${\mathrm{Pic}}^{l'_1+l'_2}$. This, in the modified case, using ${{\mathcal {O}}}_Z(l'_1+l'_2)={{\mathcal {O}}}_Z(l'_1)\otimes {{\mathcal {O}}}_Z(l'_2)$, it reads as ${\widetilde{c}}^{l_1'+l'_2}\circ s^{l'_1,l'_2}= {\widetilde{c}}^{l'_1} + {\widetilde{c}}^{l'_2}$ in $H^1({{\mathcal {O}}}_Z)$. The above properties imply

$$\begin{aligned} {\mathrm{im}}({\widetilde{c}}^{l_1'})+ {\mathrm{im}}({\widetilde{c}}^{l_2'})\subset {\mathrm{im}}({\widetilde{c}}^{l_1'+l_2'})\subset \overline{ {\mathrm{im}}({\widetilde{c}}^{l_1'})+ {\mathrm{im}}({\widetilde{c}}^{l_2'})}. \end{aligned}$$

(2.2.5)

Definition 2.2.6

For any $l'\in -{{\mathcal {S}}}'$ let $A_Z(l')$—or just $A(l')$—be the smallest dimensional affine subspace of $H^1({{\mathcal {O}}}_Z)$ which contains ${\mathrm{im}}({\widetilde{c}}^{l'})$. Let $V_Z(l')$, or $V(l')$, be the parallel vector subspace of $H^1({{\mathcal {O}}}_Z)$, the translation of $A_Z(l')$ to the origin.

For any $I\subset {{\mathcal {V}}}$, $I\not =\emptyset$, let $(X_I,o_I)$ be the multigerm ${\widetilde{X}}/_{\cup _{v \in I}E_v}$ at its singular points, obtained by contracting the connected components of $\cup _{v \in I}E_v$ in ${\widetilde{X}}$. If $I=\emptyset$ then by convention $(X_I,o_I)$ is a smooth germ.

Theorem 2.2.7

[14, Prop. 5.6.1, Lemma 6.1.6 and Th. 6.1.9] Assume that $Z\gg 0$.

• (a) For any $-l'=\sum _va_vE^*_v\in {{\mathcal {S}}}'$ let the $E^*$-support of $l'$ be $I(l'):=\{v\,:\, a_v\not =0\}$. Then $V(l')$ depends only on $I(l')$. (This motivates us to write $V(l')$ as V(I) where $I=I(l')$.)

• (b) $V(I_1\cup I_2)=V(I_1)+V(I_2)$ and $A(l_1'+l_2')= A(l_1')+A(l_2')$.

• (c) $\dim V(I)=h^1({{\mathcal {O}}}_Z)-h^1({{\mathcal {O}}}_{Z|_{{{\mathcal {V}}}{\setminus } I}})= p_g(X,o)-p_g(X_{{{\mathcal {V}}}{\setminus } I},o_{{{\mathcal {V}}}{\setminus } I})$.

• (d) If ${\mathcal {L}}^{im}_{gen}$ is a generic bundle of  ${\mathrm{im}}(c^{l'})$ then $h^1(Z,{\mathcal {L}}^{im}_{gen})=p_g(X,o)-\dim ({\mathrm{im}}(c^{l'}))$.

• (e) For $n\gg 1$ one has ${\mathrm{im}}({\widetilde{c}}^{nl'})=A(nl')$, and $h^1(Z,{\mathcal {L}})= p_g(X_{{{\mathcal {V}}}{\setminus } I(l')},o_{{{\mathcal {V}}}{\setminus } I(l')})$ for any ${\mathcal {L}}\in {\mathrm{im}}(c^{nl'})$.

For different other geometric reinterpretations of $\dim V_Z(I)$ see also [14, Sect. 9].

2.2.3 The linear subspace arrangement $\{V_Z(I)\}_I\subset {\mathbb {C}}^{p_g}$ and differential forms

The arrangement $\{V(I)\}_I$ transforms into a linear subspace arrangement of $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})$ via the (Laufer) non-degenerate pairing $H^1({{\mathcal {O}}}_Z)\otimes H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})\rightarrow {\mathbb {C}}$ (cf. [14, 7.3]) as follows. Let $\Omega (I)$ be the subspace $H^0(\Omega ^2_{{\widetilde{X}}}(Z|_{{{\mathcal {V}}}{\setminus } I}))/H^0(\Omega ^2_{{\widetilde{X}}})$ in $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})$ (that is, the subspace generated by those forms which have no poles along generic points of any $E_v$, $v\in I$).

Proposition 2.2.9

[14, 8.3] Via Laufer duality $V(I)= \Omega (I)^*.$

2.2.4 The $\dim {\mathrm{im}}(c^{l'})$ and differential forms

Next we recall a statement from [14, Sect. 10]. For simplicity we will assume that $l'=-E^*_v$ for some $v\in {{\mathcal {V}}}$. This means that any divisor $D\in {\mathrm{ECa}}^{l'}({\widetilde{X}})$ with Chern class $l'$ is a transversal cut (disc) of $E_v$ at a certain point $p\in E_v{\setminus } \cup _{u\not =v}E_u$. Let us fix some local coordinates (u, v) in some neighbourhood U of p such that $\{u=0\}=E_v\cap U$, while D has local equation v. Any local section of $\Omega ^2_{{\widetilde{X}}}(Z)$ ($Z\gg 0$ as above) near p has local form $\omega =\sum _{i\in {\mathbb {Z}}, j\in {\mathbb {Z}}_{\ge 0}} a_{i,j} u^i v^jdu\wedge dv$. We define the residue ${\mathrm{Res}}_D(\omega )=(w/dv)|_{v=0}:= \sum _{i}a_{i,0}u^i du$.

Proposition 2.2.11

[14, Corollary 10.1.2] Assume that $\{\omega _1,\ldots , \omega _{p_g}\}$ are fixed representatives of a basis of $H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}}(Z))/H^0({\widetilde{X}},\Omega ^2 _{{\widetilde{X}}})$ (where $Z\gg 0$). Set

$$\begin{aligned} {{\mathcal {H}}}:=\{(a_1,\ldots ,a_{p_g})\in {{\mathbb {C}}}^{p_g}: {\mathrm{Res}}_{D}(\textstyle {\sum }_\alpha a_{\alpha }\omega _{\alpha }) \ \text{ has } \text{ no } \text{ pole } \text{ along } D\}. \end{aligned}$$

Then $h^1(Z,{{\mathcal {O}}}_{Z}(D))=\dim ({{\mathcal {H}}})$, and the number of independent relations between $(a_1,\ldots , a_{p_g})$, $p_g-h^1(Z,{{\mathcal {O}}}_{Z}(D))$, is the dimension of the image of the tangent map ${\mathrm{im}}T_Dc^{l'}(T_D{\mathrm{ECa}}^{l'}(Z))$.

In particular, $\dim ({\mathrm{im}}(c^{l'}(Z)))$ is the number of independent relations for D generic.

The following Corollary will be relevant in the case of elliptic germs.

Corollary 2.2.12

In the situation of Proposition 2.2.11 assume that the forms $\{\omega _j\}_{j=d+1}^{p_g}$ have no poles along $E_v$, while the non-trivial poles of $\{\omega _j\}_{j=1}^{d}$ along $E_v$ are all distinct. Then $\dim {\mathrm{im}}(c^{l'})=d$.

Proof

For generic D (or, generic local equation v as in 2.2.10), $\{{\mathrm{Res}}_D(\omega _j)\}_{j=1}^d$ have different non-trivial poles at $u=0$. $\square$

Remark 2.2.13

In the definition of the natural line bundles and of the modified Abel map the rational homology sphere link assumption is necessary. Furthermore, the theory of Abel maps was also developed in [14] under this condition. Since our goal is to present an application of this theory, here we also impose the RHS restriction for our elliptic germs. Usually, in surface singularity theory, having this assumption one hopes that several invariants will be guided by the topology of the link. In the present situation this also happens: the final picture of the W-stratification follows the combinatorics of the link rather closely.

3 Elliptic singularities. The elliptic sequence.

Let (X, o) be a complex surface singularity as in 2.1 and let $\phi :{\widetilde{X}}\rightarrow X$ be a resolution. In the first part of our discussions (up to the second part of Theorem 3.3.5) we will not impose any restriction regarding the link.

3.1 Elliptic singularities

Let $Z_{min}\in L$ be the minimal (or fundamental) cycle of the resolution $\phi$, that is, $\min \{{{\mathcal {S}}}{\setminus } 0\}$ [2, 3]. Recall that (X, o) is called elliptic if $\chi (Z_{min})=0$, or equivalently, $\min _{l\in L_{>0}}\chi (l)=0$ [13, 36]. It is known that if we decrease the decorations (Euler numbers), or we take a full subgraph of an elliptic graph, then we get either an elliptic or a rational graph.

Let C be the minimally elliptic cycle [13, 18], that is, $\chi (C)=0$ and $\chi (l)>0$ for any $0<l<C$. There is a unique cycle with this property, and if $\chi (D)=0$ ($D\in L$) then necessarily $C\le D$. In particular, $C\le Z_{min}$. In the sequel we assume that the resolution is minimal. Then $Z_K\in {{\mathcal {S}}}'{\setminus } 0$, hence in the numerically Gorenstein case $Z_{min}\le Z_K$ by the minimality of $Z_{min}$ in ${{\mathcal {S}}}{\setminus } 0$.

The minimally elliptic singularities were introduced by Laufer in [13]. In a minimal resolution they are characterized (topologically) by $Z_{min}=Z_K=C$. Moreover, (X, o) is minimally elliptic if and only if $p_g(X,o)=1$ and (X, o) is Gorenstein. For details see [13, 18, 19].

For more on elliptic singularities consult [13, 18, 28, 33, 35,36,37,38,39].

3.2 Elliptic sequences

One of the most important tools in the study of elliptic singularities are the elliptic sequences. The elliptic sequence is a set of integral cycles associated with the topological type (graph). They were introduced by Laufer and Yau, for the definition in the general (non numerically Gorenstein) case see [37, 39]. In the numerically Gorenstein case the construction is simpler, see also [18, 19, 28]. This second case will be recalled below. In fact, we will use an elliptic sequence even in the non numerically Gorenstein case, but not the ‘classical’ one defined by Laufer and Yau: we define a new one, whose structure is much closer to the structure of sequences associated with numerically Gorenstein graphs (and to the non-integral cycle $Z_K$). In fact, after the first step of the construction (which produces a rational cycle) we hit a numerically Gorenstein support, and the continuation of the sequence is the one imposed by the numerically Gorenstein case.

In the next discussions below $\phi$ is a minimal resolution.

3.2.1 The construction of the elliptic sequence; the numerically Gorenstein case [18, 19, 28, 37, 39]

The elliptic sequence consists of a sequence of integral cycles $\{Z_{B_j}\}_{j=0}^m$, where $Z_{B_j}$ is the minimal cycle supported on the connected reduced cycle $B_j$. $\{B_j\}_{j=0}^m$ are defined inductively as follows. For $j=0$ one takes $B_0=E$, hence $Z_{B_0}=Z_{min}$. Then $C\le Z_{min}=Z_{B_0}\le Z_K$. If $Z_{B_0}=Z_K$ then we stop, $m=0$, this situation corresponds to the minimally elliptic case.

Otherwise one takes $B_1:=|Z_K-Z_{B_0}|$. One verifies that $|C|\subseteq B_1\varsubsetneq B_0$, $B_1$ is connected, and it supports a numerically Gorenstein elliptic topological type with canonical cycle $Z_K-Z_{B_0}$. (Furthermore, $(E_v,Z_{B_0})=0$ for any $E_v\subset B_1$. The proof of all these facts are similar to the proof of Lemma 3.2.3 below.) In particular, $C\le Z_{B_1}\le Z_K-Z_{B_0}$. Then we repeat the inductive argument. If $Z_{B_1}= Z_K-Z_{B_0}$, then we stop, $m=1$. Otherwise, we define $B_2:=|Z_K-Z_{B_0}-Z_{B_1}|$. $B_2$ again is connected, $|C|\subseteq B_2 \varsubsetneq B_1$, and supports a numerically Gorenstein elliptic topological type with canonical cycle $Z_K-Z_{B_0}-Z_{B_1}$. After finitely many steps we get $Z_{B_m}=Z_K-Z_{B_0}-\cdots -Z_{B_{m-1}}$, hence the minimal cycle and the canonical cycle on $B_m$ coincide. This means that $B_m$ supports a minimally elliptic singularity with $Z_{B_m}=C$.

We say that the length of the elliptic sequence $\{Z_{B_j}\}_{j=0}^m$ is $m+1$.

3.2.2 The construction of the (new) elliptic sequence; the non-numerically Gorenstein case

Assume that $Z_K\not \in L$, that is, $r_{[Z_K]}\not =0$. Since the resolution is minimal, $Z_K\in {{\mathcal {S}}}'$, hence $Z_K\ge s_{[Z_K]}$. By Lemma 2.1.4$Z_K> s_{[Z_K]}$. We will use the following notations: $B_{-1}:=E$, $Z_{B_{-1}}:=s_{[Z_K]}$ and $B_0:=|Z_K-s_{[Z_K]}|$. (Note that $Z_{B_{-1}}\in L'{\setminus } L$.)

Lemma 3.2.3

• (a) $\chi (s_{[Z_K]})=0$.

• (b) $B_0$ is connected, $C\subseteq B_0\varsubsetneq E$, and $(E_v,Z_{B_{-1}})=0$ for any $E_v\subset B_0$.

• (c) $B_0$ supports a numerically Gorenstein elliptic topological type with canonical cycle $Z_K-s_{[Z_K]}$.

Proof

(a)–(b) Write $l:=Z_K-s_{[Z_K]}$. Then $\chi (s_{[Z_K]})=\chi ( Z_K-l)=\chi (l)$. Since (X, o) is elliptic $\chi (s_{[Z_K]})=\chi (l)\ge 0$. Also, $(s_{[Z_K]},l)\le 0$ since $s_{[Z_K]}\in {{\mathcal {S}}}'$. On the other hand, $0=\chi (Z_K)=\chi (l+s_{[Z_K]})=\chi (l)+\chi (s_{[Z_K]})-(l,s_{[Z_K]})$. Then by the previous inequalities the expressions from the right hand side are $\ge 0$, hence necessarily $\chi (s_{[Z_K]})=\chi (l)=(l,s_{[Z_K]})=0$. If l has more connected components, say $\cup _il_i$, then $\chi (l_i)=0$ for all i, hence each $l_i$ contains/dominates a minimally elliptic cycle (cf. [13]), a fact which contradicts the uniqueness of the minimally elliptic cycle. Hence $|l|=B_0$ is connected and $|C|\subset B_0$. Furthermore, $(l, s_{[Z_K]})=0$ shows that $|l|\not =E$.

(c) $C\subseteq B_0\varsubsetneq E$ shows that $\min _{|l|\subset B_0, \, l>0} \chi (l)=0$, hence $B_0$ supports an elliptic topological type. Moreover, from $(l, s_{[Z_K]})=0$ we read that for any $E_v$ from the support of l one has $(E_v,s_{[Z_K]})=0$, or $(E_v,Z_K-s_{[Z_K]})=(E_v,Z_K)$, hence $Z_K-s_{[Z_K]}\in L$ is the canonical cycle on $B_0$. $\square$

Then, as a continuation of the sequence, starting from $B_0$ and its integral canonical class $Z_K-s_{[Z_K]}$, we construct the sequence $\{Z_{B_j}\}_{j=0}^m$ as in the numerically Gorenstein case.

We say that the elliptic sequence $\{Z_{B_j}\}_{j=-1}^m$ has length $m+1$ and ‘pre-term’ $Z_{B_{-1}}=s_{[Z_k]}\in L'$.

In order to have a uniform notation, in the numerically Gorenstein case we set $Z_{B_{-1}}:=0$ (which, in fact, is $s_{[Z_k]}$). In both cases, in a unified notation (see also [18, 2.11]),

$$\begin{aligned} (E_v,Z_{B_j})=0 \ \ \text{ for } \text{ any } E_v\subset B_{j+1} \ \ \ (-1\le j< m). \end{aligned}$$

(3.2.4)

Remark 3.2.5

The construction of $\{B_j\}_j$ can be handled uniformly as follows. For any connected support B let $Z_K(B)$ be the canonical cycle associated with the graph supported by B and let $s^*(B)$ be the smallest nonzero element of ${{\mathcal {S}}}'(B)$ with $[s^*(B)]=[Z_K(B)]$ in $L'(B)/L(B)$. Then we proceed inductively: the first support is E, and once $B_j$ is known then one sets $B_{j+1}:=|Z_K(B_j)-s^*(B_j)|$. We prefer to index them in such a way that $B_0$ is the first numerically Gorenstein support.

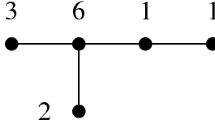
Example 3.2.6

Consider the next elliptic graph

where the $(-2)$-vertices are unmarked. $Z_K$ and $s_{[Z_K]}$ are the following cycles:

$B_0$ is obtained by deleting $E_1$ from E, while $B_1$ by deleting $E_1$ and $E_2$. The length is $m+1=2$.

The elliptic sequence imposes some kind of ‘linearity’ of the structure of the graph. E.g., the following statement holds (probably some parts of it are already known in the literature).

Lemma 3.2.7

Consider an elliptic graph $\Gamma$ with elliptic sequence supports $B_{-1},B_0, \ldots , B_m$ and vertices ${{\mathcal {V}}}$. Assume that we can glue to the graph a new vertex $v_{new}$ by an edge $(v,v_{new})$, $v\in {{\mathcal {V}}}$, such that the new graph is still elliptic. Then the $E_v$-multiplicity of the fundamental cycle $Z_{min}$ (in $\Gamma$) is 1 and $v \not \in B_1$. Next, assume that $\Gamma$ is numerically Gorenstein. If the genus $g_v$ of $E_v$ is zero then v is necessarily an end-vertex, and the $E_v$-multiplicity of $Z_K$ is 1 too (and the multiplicity of the adjacent vertex is 2). If $g_v=1$ then $\Gamma =\{v\}$ and $Z_K=E_v$.

Proof

Suppose that $v \in B_1$. Then the multiplicity of $E_v$ in $Z_{B_0} + Z_{B_1}$ is at least 2. But $\chi (Z_{B_0} + Z_{B_1}) = 0$, cf. (3.2.4), hence $\chi (Z_{B_0} + Z_{B_1}+E_{new}) < 0$, which contradicts the ellipticity of the large graph. By Laufer’s algorithm [12] there exists a computation sequence of the fundamental cycle of the large graph such that one of its terms is $Z_{min}=Z_{min}(\Gamma )$ while the next one is $Z_{min}+E_{new}$. Since $\chi (Z_{min})=\chi (Z_{min}+E_{new})=0$, we get that the coefficient $m_{E_v}(Z_{min})$ of $E_v$ in $Z_{min}$ is 1. In the numerically Gorenstein case, since $v\not \in B_1$ we get that $m_{E_v}(Z_{K})=1$ too. If $g_v=0$ then by the adjunction formula v is either an end-vertex (as in the statement) or it has two neighbours both with multiplicity 1. But this last case would generate (by repeating the argument for the two neighbours) an infinite string, all with multiplicity one, which cannot happen. If $g_v=1$ then use again the adjunction formula.

$\square$

Example 3.2.8

The next graphs are both numerically Gorenstein, with $m=3$. The dash-boxes show the supports $B_3\subset B_2\subset B_1\subset B_0$. In both cases $B_1{\setminus } B_2$ has more connected components. However, in the first case the two components are adjacent with different vertices of $B_2$, while in the second case pairs of components are adjacent with the same vertex of $B_2$. These adjacency properties will be crucial in Theorem 9.3.1. Furthermore, in both examples we create nodes in the zones $B_i{\setminus } B_{i+1}$. Both graphs can be continued as (infinite) series of numerically Gorenstein graphs by adding pairs of vertices to each string (similarly as their last extension).

3.3 The cycles $C_t$ and $C_t'$

Set $C_t:=\sum _{i=-1}^t Z_{B_i}$ and $C_t':=\sum _{i=t}^m Z_{B_i}$, $-1\le t\le m$. E.g. $C_m=Z_K$ and, in general, $C'_j$ is the canonical cycle of $B_j$. Furthermore, $\chi (Z_{B_j})=\chi (C_j)=\chi (C_j')=0$.

The next Lemma generalizes [18, Lemma 2.13] valid in the numerically Gorenstein case.

Lemma 3.3.1

Assume that $l' \in {{\mathcal {S}}}'$, $[l'] = [Z_K]$ and $l' \le Z_K$. Then $l'\in \{C_{-1}, C_0, \ldots , C_m \}$.

Proof

Since $0\le l'-Z_{B_{-1}}\le Z_K-Z_{B_{-1}}=Z_K(B_0)$ and by (3.2.4) $l'-Z_{B_{-1}}\in {{\mathcal {S}}}(B_0)$, the statement reduces to the numerically Gorenstein case. (Alternatively, using the analogue of the previous line as an inductive step one can proceed also by induction on m. The first step is as follows. If $l'-Z_{B_{-1}}\not =0$ then $l'-Z_{B_{-1}}\in {{\mathcal {S}}}(B_0) {\setminus } \{0\}$, hence $l'-Z_{B_{-1}}\ge Z_{B_{0}}$. Then $0\le l'-Z_{B_{-1}}-Z_{B_{0}}\le Z_K-Z_{B_{-1}}-Z_{B_{0}}=C'_1$, that is, $l'-Z_{B_{-1}}-Z_{B_{0}}$ is supported on $B_1$ and it belongs to ${{\mathcal {S}}}(B_1)$. Then the induction runs.) $\square$

Remark 3.3.2

The cycles $\{C_i\}_{i=0}^m$, or their supports $\{B_i\}_{i=0}^m$, satisfy several other universal properties as well. E.g., assume that the graph is numerically Gorenstein, and let $I\subset {{\mathcal {V}}}$, $I\not =\emptyset$, such that I supports a numerically Gorenstein (connected) subgraph. Then I is one of the supports $\{B_i\}_{i=0}^m$.

Indeed, suppose, that $I \ne B_0$. Then, by induction, it is enough to prove $I \subset B_1$. Let the canonical cycle on I be $Z \in L$. Then $(Z_K- Z , E_v) = 0$ for all $E_v \subset |Z|$. Otherwise, if $E_v \not \subset |Z|$, we have $(Z_K, E_v) \le 0$ and $(Z, E_v) \ge 0$, so $(Z_K - Z, E_v) \le 0$. This means, that $Z_K - Z \in {{\mathcal {S}}}'$, $Z_K - Z > 0$, $Z_K - Z \in L$. These imply that $Z_K - Z \ge Z_{min}$, hence $Z \le C'_1$ and $I=|Z|\subset B_1$.

Next, assume that the graph is not numerically Gorenstein. Then we claim that the support of any numerically Gorenstein (connected) subgraph belongs again to $\{B_i\}_{i=0}^m$. First we show that the largest numerically Gorenstein subgraph is supported by $B_0$. (Then the rest follows from the previous paragraph.) Indeed, if I is its support and Z is the canonical cycle on this support, then similarly as above, $Z_K-Z\in {{\mathcal {S}}}'$, hence $Z_K-Z\ge s_{[Z_K]}$. This reads as $Z\le Z_K-s_{[Z_K]}$, or $|Z|\subset B_0$.

Remark 3.3.3

Even if the graph is numerically Gorenstein, the list of antinef cycles $l\in {{\mathcal {S}}}$ with $l\not \ge Z_K$ is much larger than the list given in Lemma 3.3.1. Indeed, take e.g $l=2Z_{min}$, which usually is $\not \le Z_K$ and $\not \ge Z_K$.

3.3.1 .

Let ${\widetilde{X}}_j$ be a small neighbourhood of $\cup _{E_v\subset B_j}E_v$ in ${\widetilde{X}}$, and consider the singularities $(X_j,o_j):=({\widetilde{X}}_j/B_j,o_j)$ obtained by contraction of $B_j$, $-1\le j\le m$. In particular, $(X_{-1},o_{-1})$ is defined in the non-numerically Gorenstein case, it is (X, o), and $(X_0,o_0)$ is the first numerically Gorenstein germ in the sequence. The last one, $(X_m,o_m)$, is minimally elliptic (hence automatically Gorenstein).

Before we recall the next characterization of Gorenstein elliptic singularities we mention that any numerically Gorenstein topological type admits Gorenstein structure [32]. (But the generic analytic structure is Gorenstein only in the Klein and the minimally elliptic case [13, Th. 4.3], see also [15, Prop. 5.9.1].)

We recall the following facts from [18, Statements 2.10, 3.5 and 4.11].

Theorem 3.3.5

Assume that (X, o) is a numerically Gorenstein elliptic singularity. Then the following facts are equivalent:

• (a) $p_g=m+1$;

• (b) $h^1({{\mathcal {O}}}_{C'_j})=m-j+1$, $h^1({{\mathcal {O}}}_{C_j})= j+1$ and $h^1({\widetilde{X}},{{\mathcal {O}}}(-C_j))=m-j$ for all $0\le j\le m$;

• (c) For any $0\le j\le m-1$, there exists $f_j\in H^0({\tilde{X}},{{\mathcal {O}}}(-C_j))$, such that for any $E_v\subset B_{j+1}$ the vanishing order of $f_j$ on $E_v$ is exactly the multiplicity of $C_j$ at $E_v$;

• (d) The line bundles ${{\mathcal {O}}}_{C'_{j+1}}(-C_j)$ are trivial for $0\le j\le m-1$;

• (d’) The line bundles ${{\mathcal {O}}}_{C'_{j+1}}(-Z_{B_j})$ are trivial for $0\le j\le m-1$.

Additionally, if the link is a rational homology sphere then (a) is equivalent with any of the following conditions:

• (e) The singularities $(X_j,o_j)$ are Gorenstein for all $0\le j\le m-1$;

• (f) The singularity (X, o) is Gorenstein.

Since in the next discussions the equivalence (a) $\Leftrightarrow$ (f) has an accentuated role (and in the application of the results regarding the Abel map from 2.2 and [14] we need a link restriction) in the sequel we assume that the link is a rational homology sphere. (For certain extensions see also [28].)

The implication (f)$\Rightarrow$ (e) from above says that if the top singularity of the tower $\{(X_j,o_j)\}_j$ is Gorenstein then all the others (automatically with smaller support) are necessarily Gorenstein. This fact applied for a fixed $(X_j,o_j)$ says that if one of the singularities $(X_j,o_j)$ is Gorenstein, then all the others $\{(X_i,o_i)\}_{i>j}$ with smaller support are Gorenstein too. In fact, one has the following statement of Okuma. Set

$$\begin{aligned} {{\mathcal {A}}}_{gor}:=\{\, j\,|\, 0\le j\le m, \ (X_j,o_j)\ \text{ is } \text{ Gorenstein }\,\} \ \ \text{ and } \ \ \alpha :=\min \{{{\mathcal {A}}}_{gor}\}. \end{aligned}$$

(3.3.6)

Then by the above discussion ${{\mathcal {A}}}_{gor}=\{j\,|\, \alpha \le j\le m\}$ and the following facts hold as well.

Theorem 3.3.7

[28, Corollary 2.15] $p_g(X,o)=p_g(X_\alpha ,o_\alpha )=\#{{\mathcal {A}}}_{gor}=m+1-\alpha$. Furthermore, the line bundles ${{\mathcal {O}}}_{C'_{j+1}}(-C_j)$ are trivial for $\alpha \le j\le m-1$.

3.3.2 Discussion

Assume that (X, o) is Gorenstein, and let us consider the function $f_j$ from Theorem 3.3.5(c). Let ${\mathrm{div}}_E(f_j)$ be the part of its divisor supported on E. Write ${\mathrm{div}}_E(f_j)$ as $C_j+x_j$. Then the support of $x_j$ contains no $E_v$ from $B_{j+1}$. Therefore, for such an $E_v$ one has $(E_v,C_j+x_j)\le 0$ (since ${\mathrm{div}}_E(f_j)\in {{\mathcal {S}}}$), $(E_v,C_j)=0$ (by (3.2.4)) and $(E_v,x_j)\ge 0$ (by the above support condition), hence necessarily $(E_v,x_j)=0$. Therefore, in the support of $x_j$ there is no $E_v$, which intersects $B_{j+1}$ nontrivially.

Remark 3.3.9

The support condition of functions $f_j$ can be improved slightly more, but not too much. Indeed, in the Gorenstein case $Z_{max}=Z_{min}$ [18, Sect. 5], that is, ${{\mathcal {O}}}_{{\widetilde{X}}}(-C_0)$ has no fixed components (so, $f_0$ can be chosen such that $x_0=0$). However, in general, a similar choice for $f_j$ (with $x_j=0$) is not possible. See e.g. the elliptic singularity $\{x^2+y^3+z^{6m+7}=0\}$. Nevertheless, using Theorem 4.2.1, if $C^2\not =-1$ then there exists a function F with ${\mathrm{div}}_E(F)=Z_K$, hence a general combination of $f_j$ and F has the property that ${\mathrm{div}}_E(f_j+\alpha F)=C_j$. (In general, the maximum what one can get via inductive steps using Gorenstein property is that the vanishing order of $f_j$ on $E_v$ is exactly the multiplicity of $C_j$ at $E_v$ for any $E_v\subset B_{j}$. See again $\{x^2+y^3+z^{6m+7}=0\}$.)

3.4 The space $H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}}(Z))/H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}})$ for elliptic singularities

Assume that (X, o) is Gorenstein and that the link is RHS. Then each $(X_j,o_j)$ is Gorenstein, and, in fact, their Gorenstein forms are related. Indeed, let $\omega _0\in H^0( \Omega ^2_{{\widetilde{X}}}(Z_K))$ be the Gorenstein form of (X, o) (that is, the section which trivializes $\Omega ^2_{{\widetilde{X}}{\setminus } E}$) and consider the function $f_j\in H^0({\widetilde{X}}, {{\mathcal {O}}}(-C_j))$ given by Theorem 3.3.5(c), $0\le j\le m-1$. Then $\omega _{j+1}:=f_j\omega _0$ has pole $C'_{j+1}$, and (by the discussion from 3.3.8) its restriction to a small neighbourhood of $\cup _{E_v\subset B_{j+1}}E_v$ is a Gorenstein form of $(X_{j+1},o_{j+1})$. Furthermore, the classes of $\{\omega _j\}_{j=0}^m$ generate $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})$.

Next, assume an arbitrary numerically Gorenstein singularity with $\alpha =\min \{{{\mathcal {A}}}_{gor}\}$ as in Theorem 3.3.7. Then the statement of the previous paragraph can be applied for $(X_\alpha ,o_\alpha )$. In this way we get forms $\{\omega _j'\}_{j=\alpha }^m$ in $H^0({\widetilde{X}}_{\alpha }, \Omega ^2_{{\widetilde{X}}_{\alpha }}(C'_\alpha ))$, whose classes in $H^0({\widetilde{X}}_{\alpha }, \Omega ^2_{{\widetilde{X}}_{\alpha }}(C'_\alpha ))/H^0({\widetilde{X}}_{\alpha }, \Omega ^2_{{\widetilde{X}}_{\alpha }})$ generate this vector space of dimension $p_g({\widetilde{X}}_\alpha )=m+1-\alpha$.

We claim that these forms (more precisely, some representatives of their classes modulo $H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}})$) can be extended to forms $\{\omega _j\}_{j=\alpha }^m$ in $H^0({\widetilde{X}}, \Omega ^2_{{\widetilde{X}}}(C'_\alpha ))$, such that their classes generate the vector space $H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}}(C'_0))/H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}})$ of dimension $p_g(X,o)=p_g({\widetilde{X}}_\alpha )$. The pole of $\omega _j$ is $C_j'$ for each j.

Indeed, set $I:={{\mathcal {V}}}{\setminus } B_\alpha$. Then, by Theorem 3.3.7, $p_g(X,o)=p_g(X_\alpha ,o_\alpha )$, hence part (c) of Theorem 2.2.7 reads as $V(I)=0$. But this via Proposition 2.2.9 implies that $\Omega (I)$ is the total space $H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}}(C'_0))/H^0({\widetilde{X}},\Omega ^2_{{\widetilde{X}}})$. On the other hand, from $\Omega (I)$ there is a well-defined restriction to $H^0({\widetilde{X}}_{\alpha }, \Omega ^2_{{\widetilde{X}}_{\alpha }}(C'_\alpha ))/H^0({\widetilde{X}}_{\alpha }, \Omega ^2_{{\widetilde{X}}_{\alpha }})$, which is a priori injective; but since the two dimensions agree, it is necessarily bijective.

Corollary 3.4.1

The linear subspace arrangement $\{\Omega (I)\}_{I\subset {{\mathcal {V}}}}$ in $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})\simeq {\mathbb {C}}^{p_g }$ reduces to the flag consisting of subspaces (where by $\omega$’s we denote their classes as well):

$$\begin{aligned} 0\subset {\mathbb {C}}\langle \omega _m\rangle \subset \cdots \subset {\mathbb {C}}\langle \omega _{\alpha +1}, \ldots , \omega _m\rangle \subset {\mathbb {C}}\langle \omega _\alpha , \ldots , \omega _m\rangle = {\mathbb {C}}^{m+1-\alpha }. \end{aligned}$$

In fact, for any I the subspace $\Omega (I)$ is determined uniquely by $j_I:=\min \{j\,|\, I\cap B_j=\emptyset \}= \max \{j\,|\, I\cap B_{j-1}\not =\emptyset \}$ as $\Omega (I)={\mathbb {C}}\langle \omega _{\max \{\alpha , j_I\}}, \ldots , \omega _m\rangle$.

4 Line bundles on ${\widetilde{X}}$. Preliminary cohomological statements

Fix an elliptic singularity with RHS link and its minimal resolution ${\widetilde{X}}$.

4.1 Cohomology of the line bundles

Assume first that (X, o) is numerically Gorenstein and fix some $j\in \{0,\ldots , m+1\}$.

Lemma 4.1.1

Let l be the cycle of fixed components of some ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$.

• (a) If $l\ge C_{j-1}$ then $h^1({\mathcal {L}})\le p_g({\widetilde{X}}_{j})$. (This for $j=0$ reads as follows: if $l\ge 0$ then $h^1({\mathcal {L}}) \le p_g({\widetilde{X}})$, while for $j=m+1$ says that if $l\ge Z_K$ then $h^1({\mathcal {L}})=0$.)

• (b) Assume that $\min \{l,Z_K\}=C_{j-1}$ (cf. Lemma 3.3.1). Then ${\mathcal {L}}(-C_{j-1})|_{C_j'}\in {\mathrm{Pic}}(C_j')$ is trivial and $h^1({\widetilde{X}},{\mathcal {L}})=h^1({\widetilde{X}},{\mathcal {L}}(-C_{j-1}))=h^1(C_j',{\mathcal {L}}(-C_{j-1})|_{C_j'})=p_g({\widetilde{X}}_j)$. Furthermore, if (X, o) is Gorenstein, then ${\mathcal {L}}|_{C_j'}\in {\mathrm{Pic}}(C_j')$ is trivial too.

Proof

(a) If $l=0$ then a section trivializes ${\mathcal {L}}$ and ${\mathcal {L}}={{\mathcal {O}}}_{{\widetilde{X}}}$. Hence $h^1({\mathcal {L}})=p_g({\widetilde{X}})$. Otherwise, since $l\in {{\mathcal {S}}}$, $l\ge Z_{min}$. If $l\ge Z_K$ then in the cohomological exact sequence of $0\rightarrow {\mathcal {L}}(-Z_K)\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_{Z_K}\rightarrow 0$ we have $H^0({\mathcal {L}}(-Z_K))=H^0({\mathcal {L}})$ (from the definition of l) and $h^1({\mathcal {L}}(-Z_K))=0$ (from the vanishing theorem), hence $h^1({\mathcal {L}})=\chi ({\mathcal {L}}|_{Z_K})=0$. Hence, the statement holds for $m=0$. Then we proceed by induction.

Since $l\ge Z_{min}$ we can assume $j\ge 1$. In the cohomology exact sequence of $0\rightarrow {\mathcal {L}}(-C_{j-1})\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_{C_{j-1}}\rightarrow 0$ we have $H^0({\mathcal {L}}(-C_{j-1}))=H^0({\mathcal {L}}(-l))=H^0({\mathcal {L}})$, hence $\chi ({\mathcal {L}}|_{C_{j-1}})-h^1({\mathcal {L}}(-C_{j-1}))+h^1({\mathcal {L}})=0$. Since $\chi ({\mathcal {L}}|_{C_{j-1}})=0$ we get $h^1({\mathcal {L}})=h^1({\mathcal {L}}(-C_{j-1}))$. Next, from $0\rightarrow {\mathcal {L}}(-Z_K)\rightarrow {\mathcal {L}}(-C_{j-1})\rightarrow {\mathcal {L}}(-C_{j-1})|_{C' _{j}}\rightarrow 0$ and vanishing $h^1({\mathcal {L}}(-Z_K))=0$, we also have $h^1({\mathcal {L}}(-C_{j-1}))=h^1({\mathcal {L}}(-C_{j-1})|_{C'_{j}})$. Since ${\mathcal {L}}(-C_{j-1})|_{C'_{j}}\in {\mathrm{Pic}}^0(C'_{j})$, by induction, $h^1({\mathcal {L}}(-C_{j-1})|_{C'_{j}})\le p_g({\widetilde{X}}_{j})$.

(b) By the proof of (a) we have that $h^1({\mathcal {L}})=h^1({\mathcal {L}}(-C_{j-1}))=h^1({\mathcal {L}}(-C_{j-1})|_{C_j'})$.

Write l as $C_{j-1}+x$. Then |x| contains no $E_v$ from $B_j$. Furthermore, for such $E_v\subset B_j$, $(E_v,l)\le 0$, $(E_v,C_{j-1})=0$, $(E_v,x)\ge 0$ (as in 3.3.8), hence necessarily $(E_v,x)=0$, that is $B_j\cap |x|=\emptyset$. This shows that ${\mathcal {L}}(-C_{j-1})|_{C_j'}$ is trivialized by the restriction of the generic section of ${\mathcal {L}}(-C_{j-1})$.

In the Gorenstein case use the fact that ${{\mathcal {O}}}(-C_{j-1})|_{C_j'}$ is trivial (cf. Theorem 3.3.5). $\square$

Fix ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$ such that $c_1({\mathcal {L}})\in -{{\mathcal {S}}}'$. Recall that by Lemma 2.1.4 the computation of $h^1({\widetilde{X}},{\mathcal {L}})$ reduces to the numerically Gorenstein case: $h^1({\mathcal {L}})=h^1({\mathcal {L}}|_{Z_K-s_{[Z_K]}})$.

Theorem 4.1.2

Let I be the $E^*$-support of $c_1({\mathcal {L}})$ and assume that $I\cap B_{j-1}\not =\emptyset$ for some $j>0$. Then

• (a) $h^1({\widetilde{X}},{\mathcal {L}})=h^1(C'_j,{\mathcal {L}}|_{C'_j})=h^1({\widetilde{X}}_j,{\mathcal {L}}|_{{\widetilde{X}}_j})$. (For $j-1=m$ this reads as follows: if $I\cap B_m\not =\emptyset$ then $h^1({\widetilde{X}},{\mathcal {L}})=0$.)

• (b) $h^1({\widetilde{X}},{\mathcal {L}})\le p_g({\widetilde{X}}_j)$.

Proof

Lemma 2.1.4 reduces the statements to the numerically Gorenstein case.

(a) Similar reductions were used in [13, 18, 19]. For the convenience of the reader we provide the details. By Lemma  2.1.4 the second equality follows, and also $h^1({\widetilde{X}}, {\mathcal {L}})=h^1(C'_0,{\mathcal {L}})$ (since $C'_0=Z_K-s_{[Z_K]}$). Hence we need to show $h^1(C'_0,{\mathcal {L}})=h^1(C'_j,{\mathcal {L}})$.

Chose $u\in I\cap B_{j-1}$. We construct a computation sequence which connects 0 with $\sum _{k=0}^{j-1} Z_{B_k}$. This is a sequence of cycles $\{z_i\}_{i=0}^t$ with $z_0=0$ and $z_t=\sum _{k=0}^{j-1} Z_{B_k}$, such that $z_{i+1}=z_i+E_{v(i)}$, where $v(i)\in {{\mathcal {V}}}$ is conveniently chosen. We construct the sequence as concatenated of several ones, each one being the (Laufer) computation sequence of a minimal cycle (cf. [19, 5.8]). Indeed, for each $0\le k\le j-1$ let $\{z_{k,i}\}_i$ be a computation sequence starting with $z_{k,0}=E_u$ and ending with $z_{k,t_k}=Z_{B_k}$, such that at every step $z_{k,i+1}=z_{k,i}+E_{v(i)}$ one has $(E_{v(i)},z_{k,i})>0$, cf. [12]. Then we glue these sequences as follows. The first element is 0. Then we list all the elements of the sequence $\{z_{0,i}\}_i$. This ends with $Z_{B_0}$. The next element is $Z_{B_0}+E_u=Z_{B_0}+z_{1,0}$. Then we continue with $Z_{B_0}+z_{1,i}$ adding all elements of $\{z_{1,i}\}_i$. This ends with $Z_{B_0}+Z_{B_1}$. Then we repeat the procedure and continue with $Z_{B_0}+Z_{B_1}+E_u$ and all $Z_{B_0}+Z_{B_1}+z_{2,i}$. We call the steps $0\rightsquigarrow E_u$, $Z_{B_0}\rightsquigarrow Z_{B_0}+E_u$, $Z_{B_0}+Z_{B_1}\rightsquigarrow Z_{B_0}+Z_{B_1}+E_u$, etc., ‘gluing steps’, all the other $z_i\rightsquigarrow z_{i+1}$ are ‘normal steps’. Using (3.2.4) one verifies that along a normal step $(E_{v(i)},z_{i})>0$, while along a gluing step $(E_{v(i)},z_{i})=0$. Note that $\{C'_0-z_i\}_i$ is a decreasing sequence connecting $C'_0$ with $C'_j$. We claim that along the sequence the integer $h^1(C'_0-z_i,{\mathcal {L}})$ stays constant. Indeed, in

$$\begin{aligned} H^1(E_{v(i)}, {\mathcal {L}}(-C'_0+z_{i+1}))\rightarrow H^1(C'_0-z_i,{\mathcal {L}})\rightarrow H^1(C'_0-z_{i+1},{\mathcal {L}})\rightarrow 0 \end{aligned}$$

one has $h^1(E_{v(i)}, {\mathcal {L}}(-C'_0+z_{i+1}))=h^0(E_{v(i)}, {\mathcal {L}}^*(-z_i))$. But analysing both cases (normal and gluing steps) we realize that $(E_{v(i)}, -c_1({\mathcal {L}})-z_i)<0$, hence this last cohomology group vanishes indeed.

(b) By part (a) we have to show that $h^1(C'_j,{\mathcal {L}})\le p_g({\widetilde{X}}_j)$. Set $j_I:=\max \{j\,|\, I\cap B_{j-1}\not =\emptyset \}$. Since $j_I\ge j$, hence $p_g({\widetilde{X}}_{j_I})\le p_g({\widetilde{X}}_j)$, and $h^1({\widetilde{X}},{\mathcal {L}})=h^1({\widetilde{X}}_{j_I},{\mathcal {L}}|_{{\widetilde{X}}_{j_I}})$ by (a), it is enough to verify that $h^1({\widetilde{X}}_{j_I},{\mathcal {L}}|_{{\widetilde{X}}_{j_I}})\le p_g({\widetilde{X}}_{j_I})$. Note also that ${\mathcal {L}}|_{{\widetilde{X}}_{j_I}}\in {\mathrm{Pic}}^0({\widetilde{X}}_{j_I})$. Hence we need to show that for a numerically Gorenstein elliptic singularity if ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$ then $h^1({\mathcal {L}})\le p_g({\widetilde{X}})$. This follows from Lemma 4.1.1(a). $\square$

Remark 4.1.3

In general, for arbitrary (non-elliptic) singularity, it is not true that $h^1({\widetilde{X}},{\mathcal {L}})\le p_g(X,o)$ for any line bundle ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}})$, cf. [16, Remark 5.3.3 and Example 5.3.4], see also [14, Prop. 5.7.1].

Remark 4.1.4

In any situation $h^1({\widetilde{X}},{\mathcal {L}})$ equals some $h^1(Z, {\mathcal {L}})$, e.g. for $Z=\lfloor Z_K\rfloor$ or even $Z_K-s_{[Z_K]}$, cf. Lemma 2.1.4. Furthermore, if one wishes a reduction to a smaller supported cycle, say to $Z|_B$ (as in theorem 4.1.2(a)), then the existence of an isomorphism of type $H^1(Z,{\mathcal {L}})\rightarrow H^1(Z|_B,{\mathcal {L}}|_{Z|_B})$ usually is obtained using the vanishing of $H^1( Z|_{{{\mathcal {V}}}{\setminus } B}, {\mathcal {L}}(-Z|_B))$, which is guaranteed whenever ${\mathcal {L}}$ is sufficiently positive along ${{\mathcal {V}}}{\setminus } B$. Note that in the above theorem, in the elliptic case, this reduction can be done with a ‘minimal positivity requirement’ of ${\mathcal {L}}$ along ${{\mathcal {V}}}{\setminus } B$. See the statement and the proof of Theorem 4.2.1 as well.

The fact that only such ‘minimal positivity’ is needed is a key additional property of elliptic singularities, which makes them special. (For another key special property, the ‘distinct pole property’ see Remarks 6.1.2–6.1.3.)

4.2 The cycle of fixed components of the line bundles

Assume that (X, o) is numerically Gorenstein and we fix ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$. We denote the cycle of fixed components of ${\mathcal {L}}$ by l.

Theorem 4.2.1

If (X, o) is either minimally elliptic or $C^2\not =-1$ then the following facts hold.

• (a) ${\mathcal {L}}(-Z_K)$ has no fixed components.

• (b) l belongs to $\{0,C_0,C_1, \ldots , C_m\}$.

Proof

Assume first that (X, o) is minimally elliptic (and the resolution is minimal, hence $Z_K=Z_{min}$). We recall the following facts, valid in this situation, cf. [13, Lemma 3.3].

Fix any pair $E_v$ and $E_u$ ($E_v\not =E_u$) of irreducible exceptional divisors. Then there exists a computation sequence for $Z_{min}$ which starts with $E_v$ (i.e. $z_1=E_v$) and ends with $E_u$ (i.e. $E_{v(t-1)}=E_u$. Recall that necessarily $(z_{v(t-1)},E_u)=2$), cf. [13]. Moreover, let $E_v$ be an irreducible component whose coefficient in $Z_{min}$ is strictly greater than one, then there exists a computation sequence for $Z_{min}$ which starts and ends with $E_v$.

Next we prove that for any $E_v$ one has $h^1({\mathcal {L}}(-Z_K-E_v))<h^0(E_v, {\mathcal {L}}(-Z_K))$. Note that this implies that $H^0({\mathcal {L}}(-Z_K-E_v))\hookrightarrow H^0({\mathcal {L}}(-Z_K))$ is not onto. We use similar arguments as in [13, Lemma 3.12].

Assume that there exists a computation sequence $\{z_i\}_{i=1}^t$ with $z_1=E_v$ and ends at some $E_u$ such that $(E_u,Z_{min})<0$. Then consider the infinite sequence $\{x_i\}_{i}$: $Z_{min}+z_1,\ldots , Z_{min}+z_i,\ldots , Z_{min}+Z_{min},2 Z_{min}+z_1,\ldots , 3Z_{min}, 3Z_{min}+z_1,\ldots .$ Then $H^1({\mathcal {L}}(-x_{i+1}))\rightarrow H^1({\mathcal {L}}(-x_i))$ is onto, hence $\alpha :H^1({\mathcal {L}}(-(n+1)Z_{min}-E_v))\rightarrow H^1({\mathcal {L}}(-Z_{min}-E_v))$ is onto for any $n\ge 0$. Compose this with $\beta :H^1({\mathcal {L}}(-Z_{min}-E_v))\rightarrow H^1(nZ_{min},{\mathcal {L}}(-Z_{min}-E_v))$ to get an exact sequence. But, by formal neighbourhood theorem, $\beta$ is an isomorphism for $n\gg 0$, hence $\alpha =0$, or $h^1({\mathcal {L}}(-Z_{min}-E_v))=0$.

If such a computation sequence does not exist, then $E_v$ is the only component with $(Z_{min},E_v)<0$, and the coefficient of $E_v$ in $Z_{min}$ is 1. In this case we consider a computation sequence $\{z_i\}_i$ which starts with $E_v$ and ends at some other $E_u$, and a sequence $\{y_i\}_i$ which starts with $E_u$ and ends at $E_v$. Take the infinite sequence $\{x_i\}_{i}$: $Z_{min}+z_1,\ldots , Z_{min}+z_i,\ldots , 2Z_{min},2Z_{min}+y_1,\ldots , 2Z_{min}+y_i,\ldots , 3Z_{min}, 3Z_{min}+y_1,\ldots .$ Then $H^1({\mathcal {L}}(-x_{i+1}))\rightarrow H^1({\mathcal {L}}(-x_i))$ is onto, except when we pass from $2Z_{min}-E_u$ to $2Z_{min}$, in which case the corank is 1. Hence, $\alpha$ has corank at most one, $h^1({\mathcal {L}}(-Z_{min}-E_v))\le 1$. But $h^0(E_v, {\mathcal {L}}(-Z_{min}))\ge 2$.

Next, consider the case when (X, o) is numerically Gorenstein with $m>0$. We will generalize the first argument presented above. Fix any $v\in {{\mathcal {V}}}$. Let ${{\mathcal {V}}}_m$ be the set of vertices $\{v\,:\, E_v\subset B_m,\ (E_v, Z_{B_m})<0\}$. Clearly, it is nonempty. Moreover, if $v\in {{\mathcal {V}}}_m$ then by (3.2.4) $(E_v,Z_K)<0$ too. Recall that along any computation sequence of $Z_{min}$ one has $(E_{v(i)},z_i)=1$ except one step when it ‘jumps’, that is, $(E_{v(i)},z_i)=2$. We claim that for any $v\in {{\mathcal {V}}}$ there exists $u\in {{\mathcal {V}}}_m$ and a computation sequence $\{z_i\}_i$ which starts with $E_v$ and jumps at $E_u$. Indeed, we construct the computation sequence as follows: it starts with $E_v$ and then we add consecutively the shortest string of $E_w$’s connecting $E_v$ with $B_m$. Let the last element of the string (the first one which is supported in $B_m$) be $E_{v'}$. (If $E_v\subset B_m$ then $E_{v'}$ is just $E_v$; and also, it can happen that $v'$ either belongs to ${{\mathcal {V}}}_m$, or not.) Then we continue starting from $E_{v'}$ to construct the computation sequence of $Z_{B_m}$ which jumps at $E_u$. If ${{\mathcal {V}}}_m\not =\{v'\}$ this is possible. If ${{\mathcal {V}}}_m=\{v'\}$ and the multiplicity of $Z_{B_m}$ at $E_u$ is $\ge 2$ then again it is possible (for both cases see above). Otherwise $Z_{B_m}^2=-1$ which case is excluded. Then, finally, after we completed $Z_{B_m}$, we continue (in an arbitrary way) Laufer’s algorithm to complete $Z_{min}$. If we concatenate this computation sequence as in the first part of minimally elliptic situation (that is, $Z_K+z_1, \ldots , Z_K+Z_{min}, Z_K+Z_{min}+z_1, \ldots$), we obtain (by the very same argument) that $h^1({\mathcal {L}}(-Z_{K}-E_v))=0$.

(b) $l\in {{\mathcal {S}}}$ and by (a) $l\le Z_K$ too. Hence the statement follows from Lemma 3.3.1. $\square$

It is instructive to compare this last theorem with the example from Sect. 5, which shows that without the required assumptions of the theorem $l>Z_K$ might happen.

4.2.1 Question

Does the statement of Theorem 4.2.1(b) hold under Gorenstein assumption (even if $C^2=-1$)? (Compare with Sect. 5.)

5 An example

5.1 .

Let us fix the following minimal resolution graph $\Gamma$ (where the $(-2)$-vertices are unmarked).

It is a numerically Gorenstein graph with $L'=L$ and $m=1$, hence $Z_K=Z_{min}+C$ ($C=Z_{B_1}$). $B_1$ is obtained by deleting $E_1$; $Z_{min}=E_1^*$, $Z_K=E_2^*$. Note that $C^2=-1$.

We show that any non-Gorenstein analytic type supported by this topological type admits a special unique line bundle ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$ such that the cycle of fixed components l of ${\mathcal {L}}$ is $2Z_{min}$, which is $>Z_K$. (In any other situation $l\le Z_K$, hence $l\in \{0,Z_{min}, Z_K\}$, cf. Lemma 3.3.1.)

We will break the discussion into several steps.

5.1.1 The starting point

The cycle l of fixed components is zero if and only if ${\mathcal {L}}\simeq {{\mathcal {O}}}_{{\widetilde{X}}}$. Otherwise, since $l\in {{\mathcal {S}}}$, necessarily $l\ge Z_{min}$. In the sequel we assume $l\ge Z_{min}$.

5.1.2 Inequalities for l

We claim that (a) if $l>Z_{min}$ then $l\ge Z_K$, and (b) if $l>Z_K$ then $l\ge 2 Z_{min}$. (Here the only needed property of l is $l\in {{\mathcal {S}}}$.)

For (a) use Lemma 2.1.3. According to this algorithm, if $E_1\subset |l-Z_{min}|$ then $l\ge 2Z_{min}$, and if $E_v\subset |l-Z_{min}|$ $(E_v\not =E_1)$ then $l\ge Z_K$. For (b) let us denote by $\Gamma _8$ the $E_8$-subgraph of $\Gamma$ (obtained from $\Gamma$ by deleting $E_1$ and $E_2$). Assume that $l>Z_K$ but $l\not \ge 2Z_{min}$. Then $l=Z_K+x$ with $x>0$ and x supported on the $\Gamma _8$ subgraph. Then for any $v\in {{\mathcal {V}}}(\Gamma _8)$ one has $(x,E_v)=(l,E_v)\le 0$, hence $x\in {{\mathcal {S}}}(\Gamma _8){\setminus } \{0\}$, hence $x\ge Z_{min}(\Gamma _8)$. In particular, the coefficient of x at $E_3$ is $\ge 2$. But then $(l, E_2)\le 0$ fails, which is a contradiction.

5.1.3 .

Using the exact sequence $0\rightarrow {\mathcal {L}}(-Z_{min})\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_{Z_{min}}\rightarrow 0$ and $H^0({\mathcal {L}}(-Z_{min}))=H^0({\mathcal {L}})$ and $\chi (Z_{min})=0$ we get that $h^1({\mathcal {L}}(-Z_{min}))=h^1({\mathcal {L}})$.

5.1.4 Characterization of $l\not =Z_{min}$

We claim that $l>Z_{min}$ if and only if $h^1({\mathcal {L}}(-Z_{min}))=0$.

Consider the exact sequence $0\rightarrow {\mathcal {L}}(-Z_K)\rightarrow {\mathcal {L}}(-Z_{min})\rightarrow {\mathcal {L}}(-Z_{min})|_{C}\rightarrow 0$. Here $h^1({\mathcal {L}}(-Z_K))=0$ and $\chi ({\mathcal {L}}(-Z_{min})|_{C})=0$. Therefore, (use also 5.1.2) $l>Z_{min} \, \Leftrightarrow \, l\ge Z_K \, \Leftrightarrow \, H^0({\mathcal {L}}(-Z_K))=H^0({\mathcal {L}}(-Z_{min}))\, \Leftrightarrow \, h^1({\mathcal {L}}(-Z_{min}))=0$.

5.1.5 Characterization of fixed components of ${\mathcal {L}}(-Z_K)$

Note first that $Z_K+E_1=2Z_{min}$. Using 5.1.2(b) one obtains that ${\mathcal {L}}(-Z_K)$ has a nontrivial fixed component if and only if $E_1$ is a fixed component. Then from the exact sequence $0\rightarrow {\mathcal {L}}(-2Z_{min})\rightarrow {\mathcal {L}}(-Z_K)\rightarrow {\mathcal {L}}(-Z_K)|_{E_1}\rightarrow 0$ one gets that $E_1$ is a fixed component of ${\mathcal {L}}(-Z_K)$ if and only if $h^1({\mathcal {L}}(-2Z_{min}))\not =0$ if and only if $h^1({\mathcal {L}}(-2Z_{min}))=1$.

5.1.6 .

By 5.1.2l is either $Z_{min}$, or $Z_K$, or it is $>Z_K$. We claim that in the Gorenstein case $l>Z_K$ cannot happen. Indeed, if $l>Z_K$ then $h^1({\mathcal {L}}(-Z_{min}))=0$ (by 5.1.4) and $h^1({\mathcal {L}}(-2Z_{min}))\not =0$ (by 5.1.5). On the other hand, (X, o) is Gorenstein if and only if $Z_{min}=Z_{max}$ (cf. Theorems 3.3.5 and 3.3.8–3.3.9). Hence ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{min})$ has no fixed components, let s be a generic section of it (that is, s is the generic linear section). Then consider the exact sequence $0\rightarrow {\mathcal {L}}(-Z_{min}){\mathop {\longrightarrow }\limits ^{\cdot s}}{\mathcal {L}}(-2Z_{min})\rightarrow {{\mathcal {C}}}\rightarrow 0$ where $\cdot s$ is the multiplication by s and ${{\mathcal {C}}}$ is a Stein cut of $E_1$ with $h^1({{\mathcal {C}}})=0$. Hence $h^1({\mathcal {L}}(-Z_{min}))\ge h^1({\mathcal {L}}(-2Z_{min}))$, which is a contradiction.

5.1.7 .

Next assume that $l>Z_K$. By the above discussion this means that $l\ge 2Z_{min}$, (X, o) is not Gorenstein and it has $p_g=1$, $h^1({\mathcal {L}}(-Z_{min}))=h^1({\mathcal {L}})=0$ (cf. 5.1.3–5.1.4), $h^1({\mathcal {L}}(-2Z_{min}))=1$ (cf. 5.1.5). From the exact sequence $0\rightarrow {\mathcal {L}}(-l)\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_l\rightarrow 0$, $H^0 ({\mathcal {L}}(-l))=H^0({\mathcal {L}})$, and $h^1({\mathcal {L}})=0$ we get that necessarily

$$\begin{aligned} \chi (l)=h^1({\mathcal {L}}(-l)). \end{aligned}$$

(5.1.8)

On the other hand, from the definition of l we have that ${\mathcal {L}}(-l)\in {\mathrm{im}}(c^{-l})$, hence by Theorem 6.1.1(8) and Theorem 2.2.7(c) $h^1({\mathcal {L}}(-l))= p_g(X_{{{\mathcal {V}}}{\setminus } I},o_{{{\mathcal {V}}}{\setminus } I})$, where I is the $E^*$-support of l.

Clearly $I\not =\emptyset$. We consider two cases. If $I\not =\{E_1\}$, then $(X_{{{\mathcal {V}}}{\setminus } I},o_{{{\mathcal {V}}}{\setminus } I})$ is necessarily rational with $p_g(X_{{{\mathcal {V}}}{\setminus } I},o_{{{\mathcal {V}}}{\setminus } I})=0$, hence $\chi (l)=0$ too. We claim that this cannot happen, since $l>Z_K$ implies $\chi (l)>0$. Indeed, consider $x:=Z_K-l\in L_{<0}$, and the Laufer sequence from Lemma 2.1.3 connecting x with $s(x)=0$. Along the sequence $\chi$ is non-increasing and in the very last step before $z_t=0$ we have $z_{t-1}=-E_v$ for a certain v. But $\chi (-E_v)>0$ hence $\chi (l)>0$ too.

(The fact that $l\in {{\mathcal {S}}}$ and $\chi (l)=0$ imply $l\in \{C_i\}_i$ can be deduced also from [35, Th. 6.3], or also from the structure of the graded root associated with elliptic singularities, cf. [20].)

In particular, the only remaining possibility is the second case $I=\{E_1\}$. This means that $l=nE_1^*=nZ_{min}$ for some $n\ge 2$. In this case $(X_{{{\mathcal {V}}}{\setminus } I},o_{{{\mathcal {V}}}{\setminus } I})$ is the minimally elliptic singularity $(X_1,o_1)$ with $p_g(X_1,o_1)=1$, hence form (5.1.8) we have $\chi (l)=1$. Since $\chi (nZ_{min})=n(n-1)/2$, we get that $n=2$ is the unique possibility.

So to sum up, if $l>Z_K$ then necessarily $l=2Z_{min}$ (and (X, o) must satisfy all the cohomological restrictions listed at the beginning of this subsection).

5.1.8 .

We show that $l=2Z_{min}$ can be realized for some special ${\mathcal {L}}$ indeed.

Fix any non-Gorenstein analytic type (X, o) and its resolution ${\widetilde{X}}$ with dual graph $\Gamma$.

First we consider the Abel map $c^{-Z_{min}}$. Since the $E^*$-support I of $Z_{min}=E_1^*$ is $E_1$, $p_g=1$ (cf. 3.3.5) and this $p_g$ is already supported on C, from Theorem 2.2.7 it follows that $\dim (V(I))=0$. Hence ${\mathrm{im}}(c^{-Z_{min}})$ is a point, say ${{\mathcal {B}}}_1\in {\mathrm{Pic}}^{-Z_{min}}$. Since $Z_{min}\not =Z_{max}$ (the non-Gorenstein property, see again Theorem 3.3.5), ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{min})$ has nontrivial fixed components, that is, ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{min})\not \in {\mathrm{im}}(c^{-Z_{min}})$. In other words, ${\mathcal {L}}_1:= {{\mathcal {B}}}_1(Z_{min})= {\mathrm{im}}({\widetilde{c}}^{-Z_{min}})\not =0$ in ${\mathrm{Pic}}^0$.

By additivity, cf. 2.2.4, ${\mathrm{im}}(c^{-2Z_{min}})$ is a point too, say ${{\mathcal {B}}}_2\in {\mathrm{Pic}}^{-2Z_{min}}$, and set ${\mathcal {L}}_2:= {{\mathcal {B}}}_2(2Z_{min}) = {\mathrm{im}}({\widetilde{c}}^{-2Z_{min}})\in {\mathrm{Pic}}^0$. By additivity again, ${\mathcal {L}}_2={\mathcal {L}}_1+{\mathcal {L}}_1$ (using additive notation of the group structure of ${\mathrm{Pic}}^0=H^1({{\mathcal {O}}}_{{\widetilde{X}}})={\mathbb {C}}$), hence ${\mathcal {L}}_2\not =0$ as well.

We set ${\mathcal {L}}:={\mathcal {L}}_2\in {\mathrm{Pic}}^0$. Then ${\mathcal {L}}(-2Z_{min})={{\mathcal {B}}}_2= {\mathrm{im}}(c^{-2Z_{min}})$, hence Theorem 6.1.1(8) applies and we get $h^1({\mathcal {L}}(-2Z_{min}))=1$.

Consider next the bundle ${\mathcal {L}}(-Z_{min})={{\mathcal {B}}}_2(Z_{min})$. Its restriction to $C'_1=C$ is ${{\mathcal {O}}}_{C'_1}(Z_{min})$ (Indeed, the restriction of ${\mathrm{ECa}}^{-Z_{min}}$ to $C'_1$ is the empty divisor, hence the restriction of ${{\mathcal {B}}}_2$ to $C'_1$ is the trivial bundle). Furthermore, by Theorem 3.3.5(d) ${{\mathcal {O}}}_{C'_1}(Z_{min})$ is not the trivial bundle in ${\mathrm{Pic}}^0(C'_1)$. By Theorem 4.1.2(a) we get that $h^1({\mathcal {L}}(-Z_{min}))=h^1(C'_1, {{\mathcal {O}}}_{C'_1}(Z_{min}))$. However, since ${{\mathcal {O}}}_{C'_1}(Z_{min})$ is nontrivial, $h^1(C'_1, {{\mathcal {O}}}_{C'_1}(Z_{min}))=0$ by [18, Sect. 3]. Therefore, $h^1({\mathcal {L}}(-Z_{min}))=0$. This combined with 5.1.3 shows that $h^1({\mathcal {L}})=0$ too.

Finally, use again $0\rightarrow {\mathcal {L}}(-2Z_{min})\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_{2Z_{min}}\rightarrow 0$. Since $h^1({\mathcal {L}})=0$ we get that $h^1({\mathcal {L}}|_{2Z_{min}})=0$ too. Therefore, from $\chi (2Z_{min})=1$ one gets that $h^0({\mathcal {L}}|_{2Z_{min}})=1$. Since $h^1({\mathcal {L}}(-2Z_{min}))=1$ too, one obtains that $H^0({\mathcal {L}}(-2Z_{min}))\hookrightarrow H^0({\mathcal {L}})$ is an isomorphism. This shows that the cycle of fixed components l of ${\mathcal {L}}(-2Z_{min})$ is $\ge 2Z_{min}$. But by the previous discussions $l\le 2Z_{min}$ always. Hence $l=2Z_{min}$.

5.1.9 .

${\mathcal {L}}$ constructed in 5.1.9 satisfies another uniqueness property as well. Recall that $Z_K=E_2^*$. The image of $c^{-Z_K}=c^{-E^*_2}$ is 1-dimensional, and in fact (using the Laufer integration formula [14, Sect. 7] applied to the unique differential form of pole one along $E_2$) it is the bijective image of ${\mathrm{ECa}}^{-E^*_2}(Z_{min})={\mathbb {C}}^*$ (the moving divisor/point along $E_2{\setminus } (E_1\cup E_3)$). Since $Z_{min}$ is the cohomological cycle (or, for any $Z\ge Z_{min}$ one has ${\mathrm{Pic}}^0(Z)={\mathrm{Pic}}^0(Z_{min})$), ${\mathrm{im}}(c^{-E^*_2}(Z))={\mathrm{im}}(c^{-E^*_2}(Z_{min}))$, see also diagram (3.1.1) from [14]. Hence ${\mathrm{im}}(c^{-Z_K})={\mathbb {C}}^*$ in ${\mathrm{Pic}}^{-Z_K} ={\mathbb {C}}$. In other words, ${\mathrm{Pic}}^{-Z_K}{\setminus } {\mathrm{im}}(c^{-Z_K})$ consists of one point. This is exactly ${\mathcal {L}}(-Z_K)$ (since this bundle has a nontrivial cycle of fixed components). In other words, ${{\mathcal {B}}}_2(E_1)$ is the gap point ${\mathrm{Pic}}^{-Z_K}{\setminus } {\mathrm{im}}(c^{-Z_K})$ of ${\mathrm{Pic}}^{-Z_K}$.

This example suggests fully the subtlety of the cycle of fixed components l of a bundle ${\mathcal {L}}$ compared with $h^1({\mathcal {L}})$. In ${\mathrm{Pic}}^{-Z_K}$ any line bundle has $h^1=0$ by the generalized Grauert–Riemenschneider vanishing. However, ${\mathrm{Pic}}^{-Z_K}$ might have a nontrivial interesting stratification according to l (and even the possible values of l are not evident at all).

5.1.10 .

Consider the situation from 5.1.9. It is instructive to determine the possible values l for all line bundles ${\mathcal {L}}_n:={{\mathcal {B}}}_n(nZ_{min})\in {\mathrm{Pic}}^0$, where ${{\mathcal {B}}}_n={\mathrm{im}}(c^{-nZ_{min}})$, $n\ge 0$. Clearly, for $n=0$ we have $l=0$. If $n=1$ then ${\mathcal {L}}_1(-Z_{min})={{\mathcal {B}}}_1$ is in the image of the Abel map, hence by Theorem 6.1.1$h^1({\mathcal {L}}_1(-Z_{min}))=1$. Hence by 5.1.3$l=Z_{min}$. If $n=2$ we already know that $l=2Z_{min}$.

Next assume that $n\ge 3$. Then the restrictions to $C'_1$ of both ${\mathcal {L}}_n(-Z_{min})={{\mathcal {B}}}((n-1)Z_{min})$ and ${\mathcal {L}}_n(-2Z_{min})={{\mathcal {B}}}((n-2)Z_{min})$ are nontrivial (the restriction of ${{\mathcal {B}}}_n$ is trivial, while of ${{\mathcal {O}}}(Z_{min})$ is not), hence $h^1$ of both bundles is zero by [18, Sect. 3]. Hence by 5.1.3 and 5.1.5 one obtains $l=Z_K$.

(The reader is invited to repeat the discussion for all ${{\mathcal {B}}}_n(mZ_{min})$ as well.)

Finally let us provide $h^1({\mathcal {L}}_n)$ for all $n\ge 0$. If $n=0$ then ${\mathcal {L}}_0={{\mathcal {O}}}$, hence $h^1({\mathcal {L}}_0)=1$. For $n=1$ one has $h^1({\mathcal {L}}_1)=h^1({\mathcal {L}}_1(-Z_{min}))=h^1({{\mathcal {B}}}_1)=1$ too, cf. 6.1.1(8). For $n=2$ by 5.1.9$h^1({\mathcal {L}}_2)=0$. If $n\ge 3$, in the exact sequence $0\rightarrow {\mathcal {L}}_n(-Z_K)\rightarrow {\mathcal {L}}_n\rightarrow {\mathcal {L}}_n|_{Z_K}\rightarrow 0$ one has $H^0({\mathcal {L}}_n(-Z_K))=H^0({\mathcal {L}}_n)$ and $\chi ({\mathcal {L}}_n|_{Z_K})=0$, hence $h^1({\mathcal {L}}_n)=h^1({\mathcal {L}}_n(-Z_K))=0$.

This shows that although for several different Chern classes $l'$ it can happen that they have the same $I(l')$ and $V(I(l'))$, the corresponding affine spaces $\overline{ {\mathrm{im}}( {\widetilde{c}}^{l'})}$ might be different, so each individual affine subspace preserves some information about $l'$, more than just $I(l')$. The above computation shows that even the $h^1$-behaviour along these subspaces might vary.

6 The Abel map of elliptic singularities

6.1 The subspace arrangement $\{V(I\}_I$

Let us consider the minimal resolution of an elliptic singularity whose link is a rational homology sphere. For $Z\gg 0$ and $l'\in -{{\mathcal {S}}}'$ we consider the Abel map $c^{l'}:{\mathrm{ECa}}^{l'}(Z)\rightarrow {\mathrm{Pic}}^{l'}(Z)$ and its modified version ${\widetilde{c}}^{l'}:{\mathrm{ECa}}^{l'}(Z)\rightarrow H^1({{\mathcal {O}}}_Z)={\mathbb {C}}^{p_g}$. Recall from 2.2.6 that $A(l')$ is the smallest dimensional affine subspace of $H^1({{\mathcal {O}}}_Z)$, which contains ${\mathrm{im}}({\widetilde{c}}^{l'})$, and $V(l')$ is its translation to the origin, the parallel vector subspace. By Theorem 2.2.7$V(l')$ depends only on the $E^*$-support $I=I(l')$ of $l'$, hence it can be denoted by V(I) as well.

If $I=\{u\}$ for a certain $u\in {{\mathcal {V}}}$ then we write V(u) instead of V(I).

Usually, for an arbitrary singularity, the linear subspace arrangement $\{V(I)\}_I$ of $H^1({{\mathcal {O}}}_Z)$ can be very complicated. However, the duality $V(I)=\Omega (I)^*$ (cf. Proposition 2.2.9) and the special ‘flag’-structure of $\{\Omega (I)\}_I$ (cf. Corollary 3.4.1) impose the following structure.

For the definition of $\alpha$ see (3.3.6).

Theorem 6.1.1

With the above notations the following facts hold.

• (1) $V(u) =0$ if $u\in B_{-1}{\setminus } B_0$ (in the $Z_K\not \in L$ case). In any case, $V(u) =0$ if $u\in B_{0}{\setminus } B_\alpha$.

• (2) $V(u) = V(v)$, if $u, v \in B_j {\setminus } B_{j+1}$ for some $0 \ge j \ge m$ (with the notation $B_{m+1} = \emptyset$).

• (3) $V(u) \subset V(v)$, if $u \in B_i {\setminus } B_{i+1}$ and $v \in B_j {\setminus } B_{j+1}$ for some $m \ge j \ge i \ge 0$.

• (4) $\dim V(u) = k+1$ whenever $u\in B_{\alpha +k}{\setminus } B_{\alpha +k+1}$, where $0\le k\le m-\alpha$.

• (5) For any $I \subset {{\mathcal {V}}}$ let i be the maximal number, such that there exists a vertex $u \in I$ with $u \in B_i {\setminus } B_{i+1}$. Then $V(I)=V(u)$. Hence, the linear subspace arrangement $\{V(I)\}_{I\subset {{\mathcal {V}}}}$ is the flag $\{V(B_{\alpha +k}{\setminus } B_{\alpha +k+1})\}_{0\le k\le m-\alpha }$ in ${\mathbb {C}}^{p_g}={\mathbb {C}}^{m-\alpha +1}$, where $\dim (V(B_{\alpha +k}{\setminus } B_{\alpha +k+1}))=k+1$.

• (6) $\dim {\mathrm{im}}(c^{-E_{u}^*}(Z)) = \dim V(u)$ for every vertex $u\in {{\mathcal {V}}}$.

• (7) $\dim {\mathrm{im}}(c^{l'}(Z)) = \dim V(I(l'))$, where $l'\in -{{\mathcal {S}}}'$ (hence $\dim {\mathrm{im}}(c^{l'}(Z)) =\dim {\mathrm{im}}(c^{nl'}(Z))$ for $n\ge 1$). In particular, $\overline{{\mathrm{im}}({\widetilde{c}}^{l'}(Z))} = A(l')$.

• (8) $h^1$ is uniform on $\overline{ {\mathrm{im}}(c^{l'}(Z))} \subset {\mathrm{Pic}}^{l'}(Z)$: $h^1({\mathcal {L}}) = p_g - \dim V(I(l') )=p_g(X_{{{\mathcal {V}}}{\setminus } I(l')},o_{{{\mathcal {V}}}{\setminus } I(l')})$ for every ${\mathcal {L}}\in \overline{{\mathrm{im}}(c^{l'}(Z))}$.

• (9) If ${\mathcal {L}}\in \overline{ {\mathrm{im}}(c^{l'}(Z))}$ (e.g., if ${\mathcal {L}}$ has no fixed components) then $h^1 ({\mathcal {L}}^{\otimes n})=h^1({\mathcal {L}})$ for $n\ge 1$.

• (10) All the fibers of $c^{l'}(Z):{\mathrm{ECa}}^{l'}(Z)\rightarrow {\mathrm{Pic}}^{l'}(Z)$ have the same dimension $(l',Z)-\dim V(I(l'))$.

Property (9) for bundles of type ${\mathcal {L}}={{\mathcal {O}}}_{{\widetilde{X}}}(-Z)$ $(Z\in L_{\ge 0})$ was proved by Okuma in [31] too.

Proof

Parts (1)–(5) follow from the duality statement of Proposition 2.2.9 and the structure of the $\{\Omega (I)\}_I$ linear subspace arrangement from Corollary 3.4.1. The interested reader might verify the duality directly through the Laufer integration detailed in [14, Sect. 7].

(6) In general, cf. 2.2.6, $\dim {\mathrm{im}}(c^{l'}(Z)) \le \dim V(l')$. Assume that $u\in B_i{\setminus } B_{i+1}$. If $i<\alpha$ then by (1) and by the previous inequality we are done. Otherwise, by the general statement of Corollary 2.2.12 and from the structure of the poles of differential forms constructed in 3.4 it follows that $\dim {\mathrm{im}}(c^{-E_{u}^*}(Z))=i+1-\alpha$. On the other hand, by (4), $\dim V(u)=i+1-\alpha$ as well.

(7) We reduce the statement to (6) via the multiplicative structure from Sect. 2.2.4 and Theorem 2.2.7. Firstly, $s^{l'_1,l'_2}(Z)$ is dominant and quasi-finite. Therefore, for $l'=\sum a_vE^*_v$, one has $\dim V(l')=\dim (\sum _{a_v\not =0} V(v))= \dim (\sum _{a_v\not =0} {\mathrm{im}}({\widetilde{c}}^{a_vE^*_v}))= \dim {\mathrm{im}}({\widetilde{c}}^{l'})$.

(8) If ${\mathcal {L}}^{im}_{gen}$ is a generic element of ${\mathrm{im}}(c^{l'})$ then $h^1({\mathcal {L}}^{im}_{gen})= p_g-\dim {\mathrm{im}}(c^{l'})$ (cf. Theorem 2.2.7(d)), which equals $p_g-\dim V(l')$ by (7). Hence, by semicontinuity (see e.g. [14, Lemma 5.2.1]), $h^1({\mathcal {L}})\ge p_g-\dim V(l')$ for any ${\mathcal {L}}\in \overline{{\mathrm{im}}(c^{l'}(Z))}$. On the other hand, by Proposition 4.1.2$h^1({\mathcal {L}})\le p_g-\dim V(I(l'))$. (See also Theorem 2.2.7(c).)

For (9) use (8) and (10) follows from [14, Lemma 3.1.7]. $\square$

Remark 6.1.2

(a) Parts (6)–(7) can be compared with Theorem 2.2.7(e). Theorem 6.1.1 says that in the case of elliptic singularities there is no need to take any multiple $nl'$ in order to obtain the maximal stabilized dimension of ${\mathrm{im}}(c^{nl'})$, that is, $\dim \,{\mathrm{im}}(c^{l'})=\dim \,{\mathrm{im}}(c^{nl'})$ for any $l'\in -{{\mathcal {S}}}'$ and $n\ge 1$. As a consequence, the closure of any ${\mathrm{im}}(c^{l'})$ is an affine space.

Similarly, parts (8)–(9) can also be compared with Theorem 2.2.7(e): in order to have a uniform $h^1$-behaviour along the (closure of the image), no stabilization is needed either.

By (6)–(7)–(9) the stabilization takes place from the very first term. The main property of elliptic singularities, which is responsible for this fact, is the existence of forms $\{\omega _j\}_{j=1}^{p_g}$, which form a basis of $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})$ ($Z\gg 0$), and which satisfies the assumption of Corollary 2.2.12. In the context of any singularity, we will call this property the ‘distinct pole property’. It means the following: For any $v\in {{\mathcal {V}}}$ let ${{\mathcal {J}}}_v$ be the index set of those forms $\omega _j$ (from this list), which have nontrivial pole along $E_v$. Then the poles along $E_v$ of all forms $\{\omega _j\}_{j\in {{\mathcal {J}}}_v}$ are pairwise distinct.

For elliptic germs this property is guaranteed by Corollary 3.4.1, since the pole of each $\omega _j$ is $C'_j$.

The point is that if a normal surface singularity (with rational homology sphere link) admits a set of $p_g$ independent forms with the ‘distinct pole property’ then the above stabilization properties (6)–(7)–(9) hold. This follows from Propositions 2.2.9 and 2.2.11 proved in [14].

It is natural to ask whether the ‘distinct pole property’ is an idiosyncrasy merely of elliptic singularities. The answer is no, there are many germs with this property, see e.g. the next example.

Example 6.1.3

A singularity with ‘distinct pole property’. Consider the following resolution graph (the associated minimal one can be obtained by blowing down the two ‘cusps’.) The graph is not elliptic, $\min \chi =-1$ (and it has two distinct candidates for the elliptic cyle).

It is realized e.g. by the hypersurface singularity with non-degenerate Newton boundary $\{z^3+x^{13}+y^{13}+x^2y^2=0\}$. This analytic structure has $p_g=5$ and it is clearly Gorenstein. Let $\omega$ be the Gorenstein form (with pole $Z_K$). Then the classes of the five forms $\omega , \, \omega x, \, \omega x^2, \, \omega y, \, \omega y^2$ constitute a basis of $H^0(\Omega ^2_{{\widetilde{X}}}(Z))/H^0(\Omega ^2_{{\widetilde{X}}})$ ($Z\gg 0$), and they satisfy the ‘distinct pole property’ (the verification is left to the reader; the divisor of x is $E_1^*$, while the divisor of y is $E^*_2$).

In fact, even if we take the generic analytic structure on this graph (cf. [15]), the property survives. Indeed, in this case $p_g=2$ [15] and the two cycles of poles of the corresponding two differential forms have even distinct support. They are supported on the two minimally elliptic subgraphs obtained by deleting the two central $(-3)$ vertices. Hence, again they satisfy the ‘distinct pole property’.

(In fact we expect that the ‘distinct pole property’ is true for any analytic type supported on this graph. It is really amazing that for such graphs, when for any analytic type supported on them the ‘distinct pole property’ holds, the ‘stability’ analytic property ‘$h^1 ({\mathcal {L}}^{\otimes n})=h^1({\mathcal {L}})$ for $n\ge 1$ and ${\mathcal {L}}$ without fixed components’ is imposed by the combinatorics of the graph.)

6.2 The WECC and ECC properties and the set $\{{\mathrm{im}}({\widetilde{c}}^{l'})\}_{l'}$ [14, Sect. 9]

The mutual position of the natural line bundle ${{\mathcal {O}}}_Z(l')$ and ${\mathrm{im}}(c^{l'})$ (or, equivalently, of 0 and ${\mathrm{im}}({\widetilde{c}}^{l'})$) is codified in the following submonoid of ${{\mathcal {S}}}'$. We set ${{\mathcal {S}}}_{im}':= \{-l'\,:\, {{\mathcal {O}}}_Z(l')\in {\mathrm{im}}(c^{l'})\}= \{-l'\,:\, 0\in {\mathrm{im}}({\widetilde{c}}^{l'})\}$. In other words, $l'\in {{\mathcal {S}}}'_{im}$ if and only if ${{\mathcal {O}}}_Z(-l')$ has no fixed components.

As usual, we define the saturation of a submonoid ${{\mathcal {M}}}\subset {{\mathcal {S}}}'$ as $\overline{{{\mathcal {M}}}}:=\{l'\in {{\mathcal {S}}}'\,: nl'\in {{\mathcal {M}}} \ \text{ for } \text{ some } n\ge 1\}$. Accordingly, $\overline{{{\mathcal {S}}}'_{im}}=\{-l'\in {{\mathcal {S}}}'\,: \, 0\in {\mathrm{im}}({\widetilde{c}}^{nl'}) \ \text{ for } \text{ some } n\ge 1\}$.

Recall also that we say that a resolution ${\widetilde{X}}$ satisfies the ‘End Curve Condition’ (ECC) if $E^*_v\in {{\mathcal {S}}}'_{im}$ for any end vertex v. The terminology was introduced by Neumann and Wahl in the context of splice quotient singularities [25]. By the ‘End Curve Theorem’ [26] ${\widetilde{X}}$ satisfies ECC if and only the analytic type is splice quotient associated with the dual graph of ${\widetilde{X}}$. Furthermore, given a resolution graph $\Gamma$, a singularity resolution ${\widetilde{X}}$ with dual graph $\Gamma$ and ECC exists if and only if the graph satisfies the ‘semigroup and congruence conditions’ of Neumann–Wahl [25], or, equivalently, the ‘monomial condition’ of Okuma [29].

We say that ${\widetilde{X}}$ satisfies the ‘Weak End Curve Condition’ (WECC) if $E^*_v\in \overline{{{\mathcal {S}}}'_{im}}$ for any end vertex v. In fact, by [14, Proposition 9.2.2], ${\widetilde{X}}$ satisfies the WECC if and only if $\overline{{{\mathcal {S}}}'_{im}}={{\mathcal {S}}}'$. In general, $\overline{{{\mathcal {S}}}'_{im}}\not ={{\mathcal {S}}}'$, for concrete examples see [14] (or below in Example 6.3.3).

6.3 The set $\{\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}\}_{l'}\subset H^1({{\mathcal {O}}}_Z)$

By Theorem 6.1.1(7) $\overline{ {\mathrm{im}}(c^{l'})}=A(l')$ is an affine space of dimension $\dim V(l')$. Furthermore, by the general result Theorem 2.2.7(e), if $n\gg 1$ then ${\mathrm{im}}(c^{nl'})$ is automatically closed, hence it equals $\overline{ {\mathrm{im}}(c^{nl'})}=A(nl')$, a parallel affine space with $A(l')$ of the same dimension. (Indeed, use (7) for $nl'$ and $V(nl')=V(l')$ from Theorem 2.2.7(a).)

Remark 6.3.1

• (a) Even for elliptic singularities it can happen that ${\mathrm{im}}(c^{l'})\not =\overline{{\mathrm{im}}(c^{l'})}$. For a non-Gorenstein example see e.g. 5.1.10. For a Gorenstein example we can take even the very same graph as in Sect. 5, and its hypersurface realization $\{x^2+y^3+z^{17}=0\}$ with $p_g=2$ and $Z_K=E^*_2$. Then by Theorem 6.1.1(7)–(8) $c^{-Z_K}=c^{-E^*_2}$ is dominant. We claim that ${{\mathcal {O}}}(-E^*_2)\not \in {\mathrm{im}}(c^{-E^*_2})$ (though ${\widetilde{X}}$ satisfies the ECC, i.e. ${{\mathcal {O}}}(-E^*_v)\in {\mathrm{im}}(c^{-E^*_v})$ for any end-vertex v, and also ${{\mathcal {O}}}(-nE^*_2)\in {\mathrm{im}}(c^{-nE^*_2})$ for $n\gg 1$).

  This can be proved as follows. Note that $E_1^*$ and $E^*_2$ cannot be realized as divisors of functions (restricted to E) simultaneously, since the linking number of their arrows is one, or equivalently, if $f_1,f_2$ are some realizations then the degree of $(f_1,f_2):(X,o)\rightarrow ({\mathbb {C}}^2,0)$ would be one. Since in this hypersurface case (or any Gorenstein case) $E^*_1$ is realized, $E^*_2$ cannot be realized.

• (b) Note that WECC says that $0\in {\mathrm{im}}({\widetilde{c}}^{-nE^*_v})$ for all end vertices v (and $n\gg 1$). This in the elliptic case implies that ${\mathrm{im}}({\widetilde{c}}^{-nE^*_v})=V(-nE^*_v)=V(-E^*_v)$, hence $\overline{ {\mathrm{im}}({\widetilde{c}}^{-E^*_v})}=V(-E^*_v)$, or $0\in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_v})}$. Nevertheless, from $0\in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_v})}$ the inclusion $0\in {\mathrm{im}}({\widetilde{c}}^{-E^*_v})$ (that is, the ECC property) in general cannot be guaranteed yet (by a general argument valid for any normal surface singularity). However, in the present situation it will hold and it will be proved later in Theorem 9.4.2.

6.3.1 The structure of the affine subspaces $\{\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}\}_{l'}$

of ${\mathrm{Pic}}^0$ is the following. First, recall that the structure of the linear subspace arrangement $\{V(I)\}_I$ is very simple, it is a flag. Associated with a fixed V(I) there are several (in general, infinitely many) associated parallel affine subspaces of type $\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}$. Indeed, as in Theorem 6.1.1(5), for any $I \subset {{\mathcal {V}}}$ let i be the maximal number, such that there exists a vertex $u \in I$ with $u \in B_i {\setminus } B_{i+1}$. For all $l'$, such that $I(l')$ has the same i, all the affine spaces $\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}$ have the same dimension, and are parallel to the same $V(I(l'))$. (Their shifts have even an additional ‘semigroup structure’ in the sense that if $A(l')=a(l')+V(l')$ then $A(nl')=n\cdot a(l')+V(l')$.)

In particular, if two subspaces of type $\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}$ intersect each other nontrivially, then one of them should contain the other one.

Example 6.3.3

It can really happen that these parallel affine subspaces do not collapse into one vector space (namely into V(I)), see e.g. any elliptic singularity which does not satisfy ECC. For example, the points $\{{\mathcal {L}}_n\}_{n\ge 1}$ in 5.1.11 are all parallel affine subspaces associated with $V(Z_{min})=0$.

Next we present a Gorenstein case as well.

Take $\{z^2=(u^2-w)(u^{11}-w^3)\}$ with the next graph (where the $(-2)$-vertices are unmarked):

One verifies that $m=1$, hence $p_g=2$. Let the flag of $\{V(I)\}_I$’s be denoted by $0\subset V\subset {\mathbb {C}}^2$, where $\dim (V)=1$, cf. 6.1.1(5).

This topological type does not support any analytic structure with ECC (it does not satisfy the semigroup or the monomial condition at the $(-4)$-node). In fact, later we will show that this graph does not admit any analytic type with WECC either. This will follow either from Theorem 9.2.7 directly, or from Theorem 9.4.2 using the nonexistence of the ECC structure. Hence, for the present Gorenstein structure WECC fails at least at one of the end-vertices.

On the other hand, one verifies that ${\mathrm{div}}_E(w)=E_1^*$, ${\mathrm{div}}_E(z)=E_0^*+E^*_2$, ${\mathrm{div}}_E(u^2-w)=2E_0^*$, ${\mathrm{div}}_E(u^{11}-w^3)=2E_2^*$. (In fact if we denote ${\mathrm{div}}(z)$ by $E_0^*+E^*_2+D_0+D_2$, where $D_0$ and $D_2$ are two transversal cuts of $E_0$ and $E_2$ respectively, then ${\mathrm{div}}(u^2-w)=2E_0^*+2D_0$ and ${\mathrm{div}}(u^{11}-w^3)=2E_2^*+2D_2$.) Hence $E_0^*,\, E_1^*,\, E^*_2\in \overline{ {{\mathcal {S}}}'_{im}}$. Therefore, the only obstruction for WECC can be caused by $E_3$ or $E_4$. But, ${\mathrm{div}}_E(u)=E_3^*+E^*_4$. (The strict tranform is $\{u=z^2-w^4=0\}$, whose two components are permuted by the ${\mathbb {Z}}_2$-Galois action of the double covering $u\mapsto u,\ w\mapsto w,\, z\mapsto -z$.) Hence there exists $D_j\in {\mathrm{ECa}}^{-E^*_j}$ ($j=3,4$), so that ${{\mathcal {O}}}_{{\widetilde{X}}}(D_3+D_4+E_3^*+E^*_4)=0$. This means that the two points ${\mathcal {L}}_j:={{\mathcal {O}}}_{{\widetilde{X}}}(D_j+E^*_j)\in {\mathrm{im}}( {\widetilde{c}}^{-E^*_j})$ ($j=3,4$) satisfy ${\mathcal {L}}_3+{\mathcal {L}}_4=0$ in ${\mathrm{Pic}}^0$. Note also that $V(E^*_3)=V(E^*_4)=V$ (use 6.1.1); hence ${\mathcal {L}}_3+{\mathcal {L}}_4=0$ implies that WECC $\Leftrightarrow \, 0\in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_3})} \, \Leftrightarrow \, 0\in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_4})}$. Since WECC does not hold, we get that $0 \not \in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_3})}$ and $0\not \in \overline{{\mathrm{im}}({\widetilde{c}}^{-E^*_4})}$. Furthermore, $\overline{{\mathrm{im}}({\widetilde{c}}^{-nE^*_3})}=n{\mathcal {L}}_3+V$ and $\overline{{\mathrm{im}}({\widetilde{c}}^{-nE^*_4})}=-n{\mathcal {L}}_3+V$ $(n\ge 1)$. All these 1-dimensional affine subspaces are distinct parallel ones in ${\mathrm{Pic}}^0={\mathbb {C}}^2$, all associated with V. (The Galois action is $n\mapsto -n$.)

V can also be realized as some $\overline{{\mathrm{im}}({\widetilde{c}}^{l'})}$. Indeed, since $Z_{min}=E_3^*+E_4^*={\mathrm{div}}_E(u)$, $0\in \overline{{\mathrm{im}}({\widetilde{c}}^{-Z_{min}})}$, hence $V=\overline{{\mathrm{im}}({\widetilde{c}}^{-Z_{min}})}$.

7 The stratification of ${\mathrm{Pic}}^{l'}$ according to $h^1$

7.1 Definition of the strata $W_{l',k}$

Definition 7.1.1

[14, 5.8] We fix any singularity, one of its resolutions ${\widetilde{X}}$, and $l'\in -{{\mathcal {S}}}'$. We define $W_{l', k} = \{{\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}}) : h^1({\widetilde{X}}, {\mathcal {L}}) = k\}$. Its closure in ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ will be denoted by $\overline{W_{l', k}}$.

If it is necessary, when we handle several resolution spaces, we might also write $W_{l', k}({\widetilde{X}})$.

E.g., by Theorem 2.2.7(d) and semicontinuity, if $c: = p_g - \dim {\mathrm{im}}(c^{l'}(Z))$, then $\overline{{\mathrm{im}}(c^{l'}(Z))}\subset \overline{W_{l', c}}$.

Hence, for each $l'\in -{{\mathcal {S}}}'$, ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ has a stratification into constructible subsets according to ${\mathcal {L}}\mapsto h^1({\mathcal {L}})$. Consider again the setup of elliptic singularities as in the previous sections. We will describe the above stratification in several steps.

7.2 The general reduction to $l'=0$

For any fixed $l'\in -{{\mathcal {S}}}'$ let $I=I(l')$ be the $E^*$-support of $l'$, and let $0\le i\le m+1$ be the maximal index with $I\cap B_{i-1}\not =\emptyset$. ($i=0$ happens when $I=\emptyset$.)

Let K be the kernel of $\pi _i:H^1({{\mathcal {O}}}_{{\widetilde{X}}})\rightarrow H^1({{\mathcal {O}}}_{{\widetilde{X}}_i})$, reinterpreted as the kernel of ${\mathrm{Pic}}^0({{\mathcal {O}}}_{{\widetilde{X}}})\rightarrow {\mathrm{Pic}}^0({{\mathcal {O}}}_{{\widetilde{X}}_i})$. Note that if ${\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}})$ then ${\mathcal {L}}|_{{\widetilde{X}}_i}$ has trivial Chern class, hence the restriction induces a well-defined affine map $\pi _i^{l'}:{\mathrm{Pic}}^{l'}({\widetilde{X}})\rightarrow {\mathrm{Pic}}^0({\widetilde{X}}_i)$. The group K acts on ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ via $({\mathcal {L}}^0,{\mathcal {L}})\in K\times {\mathrm{Pic}}^{l'}({\widetilde{X}})$, $({\mathcal {L}}^0,{\mathcal {L}})\mapsto {\mathcal {L}}^0\otimes {\mathcal {L}}$. Thus, the orbits are exactly the affine fibers of $\pi _i^{l'}$.

Proposition 7.2.1

• (a) ${\mathcal {L}}\mapsto h^1({\mathcal {L}})$ is constant along the fibers of $\pi _i^{l'}$.

• (b) $W_{l',k}({\widetilde{X}})=(\pi _i^{l'})^{-1} (W_{0,k}({\widetilde{X}}_i))$.

Proof

If $({\mathcal {L}}^0,{\mathcal {L}})\in K\times {\mathrm{Pic}}^{l'}({\widetilde{X}})$, then $c_1({\mathcal {L}}^0\otimes {\mathcal {L}})=c_1({\mathcal {L}})=l'$, hence by Theorem 4.1.2 one gets $h^1({\mathcal {L}}^0\otimes {\mathcal {L}})=h^1({\mathcal {L}}^0\otimes {\mathcal {L}}|_{{\widetilde{X}}_i})= h^1({\mathcal {L}}|_{{\widetilde{X}}_i})$. $\square$

In particular, the $h^1$-stratification of ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ is completely determined (as a pull-back via an affine map) by the $h^1$-stratification of ${\mathrm{Pic}}^0({\widetilde{X}}_i)$. This reduces its study to the $l'=0$ case.

In the next Sects. 7.3 and 7.4 we clarify the $l'=0$ case. Though the statements for the Gorenstein and non-Gorenstein cases can be formulated uniformly, we still decided to separate the two cases; in this way we can emphasize better the peculiarities of both situations.

7.3 The case (X, o) Gorenstein and $l'=0$

For any $j\in \{0,\ldots , m+1\}$ we denote the natural linear projection $H^1({{\mathcal {O}}}_{{\widetilde{X}}})\rightarrow H^1({{\mathcal {O}}}_{{\widetilde{X}}_j})$ by $\pi _j$, and we also interpret it as the restriction ${\mathrm{Pic}}^0({\widetilde{X}})\rightarrow {\mathrm{Pic}}^0({\widetilde{X}}_j)={\mathrm{Pic}}^0(C'_j)$. (Here and below, by convention, $C_{-1}= C'_{m+1}=0$ and $H^1({{\mathcal {O}}}_{{\widetilde{X}}_{m+1}})=0$.)

We write $W_{0,k}$ for $W_{0,k}({\widetilde{X}})$. Recall that $m+1=p_g$.

Theorem 7.3.1

Assume that (X, o) is Gorenstein, and we fix some ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$. Let l be the cycle of fixed components of ${\mathcal {L}}$ and write ${\widetilde{l}}:=\min \{l,Z_K\}$. (${\widetilde{l}}\in \{C_{-1}, C_0,\ldots , C_m\}$ by Lemma 3.3.1.)

(Coarse version:) The following facts are equivalent:

• (a) ${\widetilde{l}}\in \{C_{-1}, C_0,\ldots , C_{j-1}\}$;

• (b) ${\mathcal {L}}\in \ker (\pi _j)$;

• (b’) ${\mathcal {L}}(-C_{j-1})|_{C'_j}\in {\mathrm{Pic}}^0(C'_j)$ is trivial;

• (c) ${\mathcal {L}}\in \overline{ W_{0, p_g-j}}$;

• (d) ${\mathcal {L}}\in \overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}(Z)) }$ (via identification ${\mathrm{Pic}}^0(Z)={\mathrm{Pic}}^0({\widetilde{X}})$, where $Z\gg 0$).

In particular, each $\overline{ W_{0, p_g-j}}$ is irreducible, it is a j-dimensional linear subspace of ${\mathrm{Pic}}^0({\widetilde{X}})$, and, in fact, it equals both $\overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}} (Z)})$ and $\ker (\pi _j)$. E.g., $W_{0,p_g}=\{{{\mathcal {O}}}_{{\widetilde{X}}}\}$ and $\overline{ W_{0,0}}={\mathrm{Pic}}^0({\widetilde{X}})$. Furthermore, $W_{0,p_g-j+1}\subset \overline{ W_{0, p_g-j}}$ whenever $j>0$ and $W_{0, p_g-j}= \overline{ W_{0, p_g-j}}{\setminus } \overline{ W_{0, p_g-j+1}}$.

(Fine version:) The following facts are equivalent:

• (f-a) ${\widetilde{l}}= C_{j-1}$;

• (f-b) ${\mathcal {L}}\in \ker (\pi _j){\setminus } \ker (\pi _{j-1})$;

• (f-c) ${\mathcal {L}}\in W_{0, p_g-j}$.

Proof

First we prove the ‘Coarse version’. Notice that (b) reads as ${\mathcal {L}}|_{C'_j}$ is trivial, hence (b)$\Leftrightarrow$(b’) follows from the triviality of ${{\mathcal {O}}}_{C'_j}(-C_{j-1})$, cf. Theorem 3.3.5.

(a)$\Rightarrow$(b) follows from Lemma 4.1.1(b): if ${\widetilde{l}}=C_{i-1}$ $(i\le j)$ then ${\mathcal {L}}|_{C_i'}$ is trivial, hence ${\mathcal {L}}|_{C_j'}$ is trivial too.

(b)$\Leftrightarrow$(d) By restriction, ${\mathrm{im}}(c^{-C_{j-1}})\subset \{{\widetilde{{\mathcal {L}}}} \in {\mathrm{Pic}}^{-C_{j-1}}({\widetilde{X}})\,:\, {\widetilde{{\mathcal {L}}}}|_{C_j'}={{\mathcal {O}}}_{C_j'}\}$. That is, via (b)$\Leftrightarrow$(b’), ${\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})\subset \ker (\pi _j)$. This implies $\overline{{\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})} \subset \ker (\pi _j)$ too. Note that $\overline{{\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})}$ is an affine subspace of dimension j (cf. Theorem 6.1.1) and $\dim \ker (\pi _j)=j$ too (cf. Theorem 3.3.5). Therefore, $\overline{{\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})} = \ker (\pi _j)$.

(c)$\Rightarrow$(a) Fix some ${\mathcal {L}}\in W_{0, p_g-j}\subset {\mathrm{Pic}}^0({\widetilde{X}})$. This means that $h^1({\mathcal {L}})=p_g-j$. Now, we know that ${\widetilde{l}}$ associated with ${\mathcal {L}}$ is $C_{i-1}$ for some i, cf. Lemma 3.3.1. By Lemma 4.1.1(b) $h^1({\mathcal {L}})=p_g-i$, hence using $h^1({\mathcal {L}})=p_g-j$ one gets $i=j$. If ${\mathcal {L}}\in \overline{ W_{0, p_g-j}}{\setminus } W_{0, p_g-j}$, then by semicontinuity of $h^1$ one has $h^1({\mathcal {L}})=p_g-j'$ for some $j'< j$, hence by the very same argument ${\widetilde{l}}=C_{j'-1}$.

(b)$\Rightarrow$(c) Assume that ${\mathcal {L}}|_{C_j'}$ is trivial. Then $h^1({\mathcal {L}})\ge h^1({\mathcal {L}}|_{C'_j})= h^1({{\mathcal {O}}}_{C'_j})=p_g-j$ (cf. Theorem 3.3.5). If $h^1 ({\mathcal {L}})=p_g-j$, then we are done. Next assume that $h^1 ({\mathcal {L}})=p_g-j'>p_g-j$ for some $j'<j$. Then by the implication (c)$\Rightarrow$(b) already proved, from $h^1({\mathcal {L}})=p_g-j'$ we get ${\mathcal {L}}\in \ker (\pi _{j'})$. Consider a convergent sequence of line bundles $\{{\mathcal {L}}_n\}_n$ in $\ker (\pi _j){\setminus } \ker (\pi _{j-1})$ with $\lim _{n\rightarrow \infty }{\mathcal {L}}_n={\mathcal {L}}$. As above, but now for ${\mathcal {L}}_n$, $h^1({\mathcal {L}}_n)\ge h^1({\mathcal {L}}_n|_{C'_j})=p_g-j$. However, here necessarily we should have equality (otherwise, if $h^1({\mathcal {L}}_n)> p_g-j$ then by the implication (c) $\Rightarrow$(b) ${\mathcal {L}}_n\in \ker (\pi _{j-1})$, which leads to a contradiction.) Hence ${\mathcal {L}}_n\in W_{0,p_g-j}$ and ${\mathcal {L}}=\lim _{n\rightarrow \infty }{\mathcal {L}}_n\in \overline{W_{0,p_g-j}}$.

The fine version follows directly from the coarse one. $\square$

Remark 7.3.2

The ‘fine version’ cannot be completed with (f-d)${\mathcal {L}}\in {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}(Z))$, as a forth condition equivalent with (f-a) $\Leftrightarrow$ (f-b)$\Leftrightarrow$(f-c).

Indeed, (f-d) $\Rightarrow$ (f-a,f-b,f-c) does not hold. Take for example a Gorenstein singularity with $m=1$, and ${\mathcal {L}}:={{\mathcal {O}}}$. Then ${{\mathcal {O}}}(-Z_{min})$ has no fixed components [18, Sect. 5], that is, ${{\mathcal {O}}}\in {\mathrm{im}}({\widetilde{c}}^{-Z_{min}})$, hence (f-d) holds for $j=1$. On the other hand, ${{\mathcal {O}}}\not \in W_{0,1}$.

However, the opposite implication (f-a,f-b,f-c) $\Rightarrow$ (f-d) holds whenever $l\le Z_K$ (e.g. when either $C^2\not =-1$, or when (X, o) is minimally elliptic, for details see Theorem 4.2.1). In such case ${\widetilde{l}}=l$. Hence, if ${\widetilde{l}}=C_{j-1}$ then in fact $l=C_{j-1}$, or ${\mathcal {L}}(-C_{j-1})$ has no fixed components, ${\mathcal {L}}(-C_{j-1})\in {\mathrm{im}}(c^{-C_{j-1}})$ and ${\mathcal {L}}\in {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$.

7.3.1 Question

Does $W_{0,p_g-j}\subset {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$ hold for any Gorenstein singularity?

7.4 The case (X, o) non-Gorenstein and $l'=0$

Fix an elliptic numerically Gorenstein singularity with length $m+1$ and minimal resolution ${\widetilde{X}}$. Let $\alpha$ be defined as in (3.3.6). Recall that $p_g({\widetilde{X}})=p_g({\widetilde{X}}_j)$ and ${\mathrm{Pic}}^0({\widetilde{X}})={\mathrm{Pic}}^0({\widetilde{X}}_j)={\mathrm{Pic}}^0(C'_j)$ for any $0\le j\le \alpha$.

Theorem 7.4.1

We fix some ${\mathcal {L}}\in {\mathrm{Pic}}^0({\widetilde{X}})$ and we denote by l the cycle of fixed components of ${\mathcal {L}}$. We also set ${\widetilde{l}}:=\min \{l,Z_K\}$.

Fix any $j\in \{0, \ldots , \alpha \}$. Then for any such j, ${\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$ consists of a single point and

$$\begin{aligned} \Big \{{\mathcal {L}}\,:\, {\mathcal {L}}(-C_{j-1})|_{C'_j} \ \text{ is } \text{ trivial } \text{ in } \ {\mathrm{Pic}}^0(C' _j)\Big \}= {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}). \end{aligned}$$

Moreover, one has the next inclusions as well:

$$\begin{aligned} \{{\mathcal {L}}\,:\, {\widetilde{l}}=C_{j-1}\}\subset {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}) \ \ \text{ and } \ \ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})\subset \cup _{j'\le j} \{{\mathcal {L}}\,:\, {\widetilde{l}}=C_{j'-1}\}. \end{aligned}$$

Furthermore, $W_{0,p_g({\widetilde{X}})}=\cup _{j=0}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$. Corresponding to $j=0$ (when $C_{-1}={\widetilde{l}}=l=0$), ${\mathrm{im}}({\widetilde{c}}^{-C_{-1}})=\{{\mathcal {L}}:\, {\widetilde{l}}=C_{-1}\}={{\mathcal {O}}}$, the origin $0\in {\mathrm{Pic}}^0({\widetilde{X}})$.

About the position of the other points corresponding to $1\le j\le \alpha$ we claim nothing (see also Remark 7.4.2 and Questions 7.4.3). (In the next discussions we refer to them as ‘wandering points’.)

Corresponding to the indices $j\in \{0, \alpha +1,\alpha +2,\ldots , m+1\}$ we have similar statements as in Theorem 7.3.1. Namely:

(Coarse version:) For any $j\in \{0, \alpha +1, \alpha +2,\ldots , m+1\}$ the following facts are equivalent:

• (a) ${\widetilde{l}}\in \{C_{-1}, C_\alpha , C_{\alpha +1}, \ldots , C_{m+1}\}$;

• (b) ${\mathcal {L}}\in \ker (\pi _j)$;

• (b’) ${\mathcal {L}}(-C_{j-1})|_{C'_j}\in {\mathrm{Pic}}^0(C'_j)$ is trivial;

• (c) ${\mathcal {L}}\in \overline{ W_{0, p_g({\widetilde{X}}_j)}}$;

• (d) ${\mathcal {L}}\in \overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}(Z)) }$ (via identification ${\mathrm{Pic}}^0(Z)={\mathrm{Pic}}^0({\widetilde{X}})$, where $Z\gg 0$).

In particular, for any $j>\alpha$, each $\overline{ W_{0, p_g({\widetilde{X}}_j)}}$ is irreducible, it is a $(p_g({\widetilde{X}})-p_g({\widetilde{X}}_j))$-dimensional linear subspace of ${\mathrm{Pic}}^0({\widetilde{X}})$, and, in fact, it equals both $\overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}} (Z)})$ and $\ker (\pi _j)$. E.g., $\overline{ W_{0,0}}={\mathrm{Pic}}^0({\widetilde{X}})$. Furthermore, $W_{0,p_g({\widetilde{X}}_{j-1})}\subset \overline{ W_{0, p_g({\widetilde{X}}_j)}}$ whenever $j\ge \alpha +2$ and the same is true for $j=\alpha +1$ too if we disregard the points $\cup _{j=1}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})\subset W_{0,p_g({\widetilde{X}})}$.

(Fine version:) If we disregard the points $\cup _{j=1}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})\subset W_{0,p_g({\widetilde{X}})}$, then for any $j\in \{0, \alpha +1, \alpha +2,\ldots , m+1\}$ the following facts are equivalent:

• (f-a) ${\widetilde{l}}= C_{j-1}$;

• (f-b) ${\mathcal {L}}\in \ker (\pi _j){\setminus } \ker (\pi _{j-1})$;

• (f-c) ${\mathcal {L}}\in W_{0, p_g({\widetilde{X}}_j)}$.

Proof

The proof of Theorem 7.3.1 can be adapted. Let us prove the statements valid for $l\le \alpha$.

Since the restriction ${\mathrm{Pic}}^{-C_{j-1}}({\widetilde{X}})\rightarrow {\mathrm{Pic}}^0(C'_j)$ is an affine isomorphism, $\{{\mathcal {L}}: {\mathcal {L}}(-C_{j-1})|_{C'_j}={{\mathcal {O}}}_{C'_j}\}$ is a point. Since ${\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})\subset \{{\mathcal {L}}: {\mathcal {L}}(-C_{j-1})|_{C'_j}={{\mathcal {O}}}_{C'_j}\}$, the two sets (both of cardinality one) must agree. Furthermore, $\{{\mathcal {L}}; {\widetilde{l}}=C_{j-1}\}\subset \{{\mathcal {L}}: {\mathcal {L}}(-C_{j-1})|_{C'_j}={{\mathcal {O}}}_{C'_j}\}$ by Lemma 4.1.1(b). However, if ${\mathcal {L}}\in {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$ then ${\mathcal {L}}(-C_{j-1})\in {\mathrm{im}}(c^{-C_{j-1}})$, hence ${\widetilde{l}}\le C_{j-1}$.

Next, $\cup _{j=0}^\alpha \{{\mathcal {L}}; {\widetilde{l}}=C_{j-1}\} \subset W_{0,p_g({\widetilde{X}})}$ by Lemma 4.1.1(b) and Theorem 3.3.7. Finally, assume that ${\mathcal {L}}\in W_{0,p_g}$. Then, by definition, $h^1({\mathcal {L}})=p_g$. On the other hand, assume that its ${\widetilde{l}}$ is some $C_{i-1}$. Then by Lemma 4.1.1(b) $h^1({\mathcal {L}})=p_g({\widetilde{X}}_i)$, hence $i\le \alpha$ and ${\mathcal {L}}\in \{{\mathcal {L}}: {\widetilde{l}}\le C_{\alpha -1}\}$.

The second case $j\in \{0, \alpha +1,\ldots , m+1\}$ follows analogously as the proof of the Gorenstein case, once we replace the statement (d) of Theorem 3.3.5 with Theorem 3.3.7. $\square$

Remark 7.4.2

• (a) If $l'=0$ then the $\{\overline{W_{0,k}}\}_k$ stratification is determined by a flag $\{0\}\cup \{ \overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}(Z)) }\}_{j\ge \alpha +1}$ of linear vector spaces whose dimensions are increasing one-by-one from 0 to $p_g$, and also by the ‘wandering points’ $\cup _{j=1}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$, all of them being in $W_{0,p_g({\widetilde{X}})}$. All the irreducible components of $\overline{W_{0,k}}$ are affine subspaces of type $\overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}}(Z)) }$ ($0\le j\le m+1$), if $k<p_g$ then they are even linear subspaces. The non-linear ones are all points.

• (b) See Sect. 5 for a non-Gorenstein singularity with $m=1$, $\alpha =1$, where there is a ‘wandering point’ ${\mathcal {L}}_1\not =0$ (cf. 5.1.9–5.1.11). Since the position of the points $\cup _{j=1}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$ is ‘unpredictable’, we called them ‘wandering’.

7.4.1 Questions

• (1) Are the wandering points all distinct? Are they all different than 0 ? (That is, is the cardinality of $\cup _{j=0}^\alpha {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}})$ exactly $\alpha +1$?)

• (2) Are the wandering points in $\overline{ W_{0, p_g-1}}$? Or, do they wander ‘even more’ ?

• (3) How does the position of the wandering points reflect the variation of the analytic structure of (X, o) ?

Remark 7.4.4

For an index subset $I\subset {{\mathcal {V}}}$ consider the set of all Chern classes $l'$ with $I(l')=I$, and also the corresponding affine subspaces $\overline{ {\mathrm{im}}({\widetilde{c}}^{l' })}$ (indexed by $l'$ with $I(l')=I$). Among them only a few might serve as irreducible component of some $\overline{W_{0,k}}$. See for example in 5.1.11 the set of points $\{{\mathcal {L}}_n\}_{n\ge 0}$, among which only $\{0,{\mathcal {L}}_1\}$ are components of $W_{0,1}$. (Note that in this case $h^1({\mathcal {L}}_n)=0$ for all $n\ge 2$.) For further role of closures of Abel images $\overline{ {\mathrm{im}}({\widetilde{c}}^{l' })}$ in even finer stratifications see Sect. 8.

7.4.2 Question

Can those members of $\overline{ {\mathrm{im}}({\widetilde{c}}^{l' })}$, which serve as components of some $\overline{W_{0,k}}$, be characterized by some universal property? Are they characterized by the maximality of $h^1$?

7.5 The case (X, o) arbitrary elliptic and $l'\in -{{\mathcal {S}}}'$ arbitrary

For any ${\widetilde{X}}$ and ${\mathcal {L}}$ with $c_1({\mathcal {L}})\in -{{\mathcal {S}}}'$, by Lemma 2.1.4, $h^1({\widetilde{X}}, {\mathcal {L}})=h^1(Z_K-s_{[Z_K]}, {\mathcal {L}})$. In this way the $h^1$-stratification of an arbitrary elliptic singularity is reduced to the case of numerically Gorenstein ones.

Furthermore, if (X, o) is numerically Gorenstein, then by Proposition 7.2.1 the $h^1$-stratification is reduced to the $l'=0$ case. If ${\widetilde{X}}_i$ is Gorestein then one has to combine Proposition 7.2.1 with Theorem 7.3.1, otherwise Theorem 7.3.1 should be replaced by the more general Theorem 7.4.1.

We invite the reader to complete the details writing down the corresponding set-identities.

Remark 7.5.1

Recall that in the numerically Gorenstein case the identity $W_{l',k}({\widetilde{X}})=(\pi _i^{l'})^{-1}(W_{0,k}({\widetilde{X}}_i))$ holds (for the notation and the statement see 7.2 and Proposition 7.2.1). On the other hand, by Theorem 7.4.1, $\overline{ W_{0,k}({\widetilde{X}}_i)}$ equals $\overline{ {\mathrm{im}}({\widetilde{c}}^{-C_{j-1}({\widetilde{X}}_i)})}$ for some cycle $C_{j-1}({\widetilde{X}}_i)\in L({\widetilde{X}}_i)$ associated with the singularity $(X_i,o_i)$. We show that a similar structure statement is valid for $\overline{ W_{l',k}({\widetilde{X}})}$ too, that is, $\overline{ W_{l',k}({\widetilde{X}})}$ is the closure of the image of a certain Abel map (at the level of ${\widetilde{X}}$).

First, let us shift $W_{l,k}({\widetilde{X}})$ into ${\mathrm{Pic}}^0({\widetilde{X}})$ (where the images of modified Abel maps ${\widetilde{c}}$ live). That is, for each $l'$, via identification ${\mathrm{Pic}}^{l'}{\mathop {\longrightarrow }\limits ^{{{\mathcal {O}}}(-l')}} {\mathrm{Pic}}^0$, we transport $W_{l',k}$ into $W^0_{l',k}:={{\mathcal {O}}}(-l')\cdot W_{l',k}\subset {\mathrm{Pic}}^0({\widetilde{X}})$. In other words,

$$\begin{aligned} W^0_{l',k}:=\{{\mathcal {L}}^0\in {\mathrm{Pic}}^0({\widetilde{X}})\,:\, h^1({\mathcal {L}}^0(l'))=k\}\subset {\mathrm{Pic}}^0({\widetilde{X}}). \end{aligned}$$

(7.5.2)

Its closure in ${\mathrm{Pic}}^0({\widetilde{X}})$ will be denoted by $\overline{W_{l', k}^0}$. Note also that $W^0_{0,k}=W_{0,k}$.

Consider first the notations and situation from Proposition 7.2.1. First we analyze the Abel map ${\mathrm{im}}( c^{-l'}):{\mathrm{ECa}}^{l'}({\widetilde{X}})\rightarrow {\mathrm{Pic}}^{l'}({\widetilde{X}})$. By Theorem 6.1.1 one gets $\dim {\mathrm{im}}(c^{l'})=\dim V(I(l'))$. On the other hand, the dimension of $(\pi _i^{l'})^{-1}(0)$ in ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ is $p_g({\widetilde{X}})-p_g({\widetilde{X}}_i)=\dim V(I(l'))$ too, cf. the same Theorem 6.1.1. In particular, $\overline{{\mathrm{im}}(c^{l'})}=(\pi _i^{l'})^{-1}(0)$ in ${\mathrm{Pic}}^{l'}({\widetilde{X}})$.

Next, write $C_{j-1}({\widetilde{X}}_i)\in L({\widetilde{X}}_i)\subset L'({\widetilde{X}}_i)$ as $\sum _{v} a_vE^*_v({\widetilde{X}}_i)$ in ${{\mathcal {S}}}({\widetilde{X}}_i)\subset L'({\widetilde{X}}_i)$, and define its lift $C_{j-1}^{lift}:=\sum _{v} a_vE^*_v({\widetilde{X}})$ into ${{\mathcal {S}}}'({\widetilde{X}})\subset L'({\widetilde{X}})$. One sees that the restriction of $C_{j-1}^{lift}$ is exactly $C_{j-1}({\widetilde{X}}_i)$, hence $\overline{ {\mathrm{im}}( c^{-C_{j-1}^{lift}})}$ restricted projects exactly onto $\overline{ {\mathrm{im}}( c^{-C_{j-1}({\widetilde{X}}_i)})}$. This shows that $\overline{ {\mathrm{im}}( c^{l'-C_{j-1}^{lift}})}$, as a subspace of ${\mathrm{Pic}}^{l'-C_{j-1}^{lift}}({\widetilde{X}})$, shifted by ${{\mathcal {O}}}_{{\widetilde{X}}}(C_{j-1}^{lift})$ into ${\mathrm{Pic}}^{l'}({\widetilde{X}})$, is exactly $\overline{W_{l',k}({\widetilde{X}})}$ (cf. (2.2.5)). Therefore,

$$\begin{aligned} \overline{ {\mathrm{im}}( {\widetilde{c}}^{l'-C_{j-1}^{lift}})}=\overline{ W^0_{l',k}({\widetilde{X}})}. \end{aligned}$$

(7.5.3)

For another, more ‘theoretical’ presentation of $\overline{ W^0_{l',k}({\widetilde{X}})}$ as $\overline{ {\mathrm{im}}( {\widetilde{c}}^{l'-l})}$ (with certain additional properties) see Theorem 8.1.2.

8 The stratification of ${\mathrm{Pic}}^{l'}$ according to the base components

8.1 Notations

Fix a resolution and $l'\in -{{\mathcal {S}}}'$ as above. In the previous section we considered the stratification of ${\mathrm{Pic}}^{l'}({\widetilde{X}})$ provided by the value ${\mathcal {L}}\mapsto h^1({\mathcal {L}})$, namely by $W_{l',k}=\{{\mathcal {L}}\in {\mathrm{Pic}}^{l'}({\widetilde{X}})\,:\, h^1({\mathcal {L}})=k\}$. It is convenient to shift $W_{l,k}$ into ${\mathrm{Pic}}^0({\widetilde{X}})$ as follows (cf. (7.5.2)). For each $l'$ the identification ${\mathrm{Pic}}^{l'}{\mathop {\longrightarrow }\limits ^{{{\mathcal {O}}}(-l')}} {\mathrm{Pic}}^0$ transports $W_{l',k}$ into $W^0_{l',k}:={{\mathcal {O}}}(-l')\cdot W_{l',k}\subset {\mathrm{Pic}}^0({\widetilde{X}})$. That is,

$$\begin{aligned} W^0_{l',k}:=\{{\mathcal {L}}^0\in {\mathrm{Pic}}^0({\widetilde{X}})\,:\, h^1({\mathcal {L}}^0(l'))=k\}\subset {\mathrm{Pic}}^0({\widetilde{X}}). \end{aligned}$$

Now we will consider a much ‘finer’ stratification. Again, it is convenient to shift the structure into ${\mathrm{Pic}}^0({\widetilde{X}})$, this has the advantage that the strata can be compared more naturally with subspaces of type $\overline{ {\mathrm{im}}({\widetilde{c}}^{l''})}\subset {\mathrm{Pic}}^0(Z)= {\mathrm{Pic}}^0({\widetilde{X}})$ $(Z\gg 0)$. The strata in $W_{l',k}$ are defined as follows

$$\begin{aligned} F_{l',k}(l):=\{ {\mathcal {L}}\in W_{l',k}\,:\, \text{ the } \text{ cycle } \text{ of } \text{ fixed } \text{ components } \text{ of } \ {\mathcal {L}}\ \text{ is } l\in L_{\ge 0}\}. \end{aligned}$$

This stratification shifted (via identity ${\mathcal {L}}={\mathcal {L}}^0(l')$) provides a stratification of $W^0_{l',k}$ as well:

$$\begin{aligned} F^0_{l',k}(l):=\{ {\mathcal {L}}^0 \in W^0_{l',k}\,:\, \text{ the } \text{ cycle } \text{ of } \text{ fixed } \text{ components } \text{ of } \ {\mathcal {L}}^0(l') \ \text{ is } l\in L_{\ge 0}\}\subset {\mathrm{Pic}}^0({\widetilde{X}}). \end{aligned}$$

We denote by ${\mathfrak {I}}$ the set $\{\overline{ {\mathrm{im}}({\widetilde{c}}^{l''})}\}_{l''}$ indexed by all possible $l''\in - {{\mathcal {S}}}'$. Our goal is to describe for the fixed $l'\in -{{\mathcal {S}}}'$ the sets $\{F^0_{l',k}(l)\}_{k\in {\mathbb {Z}}_{\ge 0}, l\in L_{\ge 0}}$ in terms of certain elements of ${\mathfrak {I}}$. This automatically will provide a new characterization of the sets $\{W^0_{l',k}\}_{k\in {\mathbb {Z}}_{\ge 0}}$ as well, besides the one provided in the previous section. Though the next theorem has some overlaps with statements from the previous section regarding the W-stratification, we prefer this presentation since it provides a uniform presentation of the two types of stratification showing their interactions. (Even more, we deliberately use a formulation and proof independent of Sect. 7 with the hope that this version can serve as a prototype for arbitrary cycle Z, not necessarily $Z\gg 0$, or for more general singularities.)

For the fixed $l'\in -{{\mathcal {S}}}'$ and $k\in {\mathbb {Z}}_{\ge 0}$ we define ${\mathfrak {I}}_{l',k}$ by decreasing induction as follows. For $k>p_g$ we set ${\mathfrak {I}}_{l',k}=\emptyset$ (note that by Theorem 4.1.2 we know that $W_{l',k}=\emptyset$ for $k>p_g$; check also that the identity (8.1.1) from below has no solution in these cases). Assume next that ${\mathfrak {I}}_{l',k' }$ is already defined for any $k'>k$. Then, by definition, ${\mathfrak {I}}_{l',k}$ consists of the set of subspaces of type $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ of ${\mathfrak {I}}$ indexed by

$$\begin{aligned} \left\{ \begin{array}{ll} (i) &{}\quad l\in L_{\ge 0} \ \ \text{ such } \text{ that } \ \ l'-l\in -{{\mathcal {S}}}',\\ (ii) &{}\quad k+\chi (l)+(l,l')=p_g-\dim V(I(l'-l)), \\ (iii) &{}\quad \overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})} \text{ is } \text{ not } \text{ included } \text{ in } \text{ any } \text{ subspace } \text{ indexed } \text{ from } \cup _{k'>k}{\mathfrak {I}}_{l',k'}. \end{array}\right. \end{aligned}$$

(8.1.1)

Though the set ${\mathfrak {I}}$ can be infinite (see e.g. Example 6.3.3), each set ${\mathfrak {I}}_{l',k}$ is finite. Indeed, by (8.1.1) (ii) $\chi (l)+(l,l')$ is bounded, hence by the negative definiteness of the intersection from, all the possible l cycles are sitting in a finite ellipsoid and constitute a finite set.

Theorem 8.1.2

(Structure Theorem of the $h^1$- and ‘base-component’-stratification) Fix $Z\gg 0$ and $l'$, k as above.

• (a) Each irreducible component of $\overline{W^0_{l',k}}$ and $\overline{F^0_{l',k}(l)}$ is an affine subspace of ${\mathrm{Pic}}^0$, in fact, it is an element of ${\mathfrak {I}}$.

• (b) The irreducible component of $\overline{W^0_{l',k}}$ are the maximal elements of ${\mathfrak {I}}_{l',k}$ (with respect to the inclusion). Moreover,

  $$\begin{aligned} W^0_{l',k}=\overline{W^0_{l',k}}\ {\setminus } \ \cup _{k'>k} \overline{W^0_{l',k'}}. \end{aligned}$$

• (c) An irreducible component of $\overline{W^0_{l',k}}$ might contain several subspaces of type $\overline{F^0_{l',k}(l)}$, there is a maximal one which equals it. Any subspace of type $\overline{F^0_{l',k}(l)}$ is nonempty if and only if $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ belongs to ${\mathfrak {I}}_{l',k}$, and in such a case $\overline{F^0_{l',k}(l)}$ is irreducible and equals $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ of dimension $\dim V(I(l'-l))$. (Note that for each l there exists exactly one such subspace.)

In particular, the collection of subspaces $\overline{F^0_{l',k}(l)}$ in $\overline{W^0_{l',k}}$ coincide with the set of affine subspaces $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ indexed by ${\mathfrak {I}}_{l',k}$. The maximal ones fill in the irreducible components of $\overline{W^0_{l',k}}$, the other ones are proper affine subspaces of these irreducible components.

If $\overline{F^0_{l',k}(l)}=\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ for such an l then

$$\begin{aligned} F^0_{l',k}(l)= W^0_{l',k}\cap {\mathrm{im}}({\widetilde{c}}^{l'-l}). \end{aligned}$$

(8.1.3)

Proof

Parts (b) and (c) imply (a). We start to prove (b). Note also that during the proof all the appeared cycles l sit in the bounded ellipsoid $\{l:\ \chi (l)+(l,l')\le p_g\}$, hence we can assume that not only $Z\gg 0$ but all the possible cycles of type $Z-l$ are also ‘large’ (so, both Z and $Z-l$ can be replaced by ${\widetilde{X}}$ in $h^1$-computations, if we wish). Hence, sometimes we will omit Z or $Z-l$.

(I) Let S be an irreducible component of $\overline{W^0_{l',k}}$, and choose ${\mathcal {L}}^0\in S\cap W^0_{l',k}$. Then ${\mathcal {L}}:={\mathcal {L}}^0(l')\in W_{l',k}$ and it satisfies $h^1({\mathcal {L}})=k$. Assume that $l\in L_{\ge 0}$ is the cycle of fixed components of ${\mathcal {L}}$, hence $H^0(Z,{\mathcal {L}})=H^0(Z-l,{\mathcal {L}}(-l))$ and $H^0(Z-l,{\mathcal {L}}(-l))_{reg}\not =\emptyset$. Then, by (2.2.2) necessarily $l'-l\in -{{\mathcal {S}}}'$ and ${\mathcal {L}}(-l)\in {\mathrm{im}}(c^{l'-l})$ (or, ${\mathcal {L}}^0\in {\mathrm{im}}({\widetilde{c}}^{l'-l})$). From the exact sequence (whenever $l>0$) $0\rightarrow {\mathcal {L}}(-l)|_{Z-l}\rightarrow {\mathcal {L}}|_Z\rightarrow {\mathcal {L}}|_l\rightarrow 0$ we get that $\chi ({\mathcal {L}}|_l)-h^1({\mathcal {L}}(-l)) +h^1({\mathcal {L}})=0$, or $h^1({\mathcal {L}}(-l))=k+\chi (l)+(l',l)$. On the other hand, by Theorem 6.1.1(8) we have $h^1({\mathcal {L}}(-l))= p_g-\dim V(I(l'-l))$, hence l satisfies (8.1.1)(ii) as well.

Since (8.1.1)(ii) has no solution for $k>p_g$, we get that in such cases $\overline{W^0_{l',k}}=\emptyset$, and the choice of ${\mathfrak {I}}_{l',k}=\emptyset$ is also supported. Then we prove (b) by decreasing induction on k. Fix again $k\le p_g$ and assume that the statement is already proved for all $k'$ with $k'>k$. Consider again the situation from the previous paragraph: let S be an irreducible component of $\overline{W^0_{l',k}}$, ${\mathcal {L}}^0\in S\cap W^0_{l',k}$ and ${\mathcal {L}}={\mathcal {L}}^0(l')$, $h^1({\mathcal {L}})=k$. Then we verified that there exists $l\in L_{\ge 0}$ so that ${\mathcal {L}}^0\in {\mathrm{im}}({\widetilde{c}}^{l'-l})$, $l'-l\in - {{\mathcal {S}}}'$ and it satisfies (8.1.1)(ii). Note that the subspace $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ cannot be included in any subspace index by any ${\mathfrak {I}}_{l',k'}$ with $k'>k$ since by inductive step all the subspaces indexed by ${\mathfrak {I}}_{l',k'}$ belong to $\cup _{k'>k}\overline{W^0_{l',k'}}$, hence all their elements ${{\mathcal {K}}}^{0}$ satisfy $h^1({{\mathcal {K}}}^{0}(l'))>k$; however ${\mathcal {L}}^0 \in \overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ with $h^1({\mathcal {L}}^0(l'))=k$. Therefore, l belongs to ${\mathfrak {I}}_{l',k}$.

(II) Now, by taking ${\mathcal {L}}^0$ generic in S, the inclusion ${\mathcal {L}}^0\in {\mathrm{im}}({\widetilde{c}}^{l'-l})$ implies $S\subset \overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$, where the subspace $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ is indexed from ${\mathfrak {I}}_{l',k}$.

(III) Conversely, consider some ${\bar{l}}\in L_{\ge 0}$ such that the subspace $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ is indexed from ${\mathfrak {I}}_{l',k}$ and $S\subset \overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$. Let ${{\mathcal {K}}}^0$ be a generic bundle of $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$, and write ${{\mathcal {K}}}:={{\mathcal {K}}}^0(l')$. From Theorem 6.1.1(8)

$$\begin{aligned} h^1({{\mathcal {K}}}(-{\bar{l}}))=p_g-\dim V(I(l'-{\bar{l}})). \end{aligned}$$

(8.1.4)

By a computation $\chi ({\bar{l}})+(l',{\bar{l}})=\chi (Z,{{\mathcal {K}}})-\chi (Z-{\bar{l}},{{\mathcal {K}}}(-{\bar{l}}))$, and the right hand side also equals

$$\begin{aligned} h^0(Z, {{\mathcal {K}}})-h^1(Z,{{\mathcal {K}}})- h^0(Z-{\bar{l}}, {{\mathcal {K}}}(-{\bar{l}}))+h^1(Z-{\bar{l}},{{\mathcal {K}}}(-{\bar{l}})). \end{aligned}$$

This combined with (8.1.1) and (8.1.4) give

$$\begin{aligned} h^1({{\mathcal {K}}}^0(l'))=h^1({{\mathcal {K}}})=h^0(Z, {{\mathcal {K}}})- h^0(Z-{\bar{l}}, {{\mathcal {K}}}(-{\bar{l}}))+k\ge k. \end{aligned}$$

(8.1.5)

We claim that necessarily $h^1({{\mathcal {K}}}^0(l'))= k$. Indeed, since $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ contains the bundle ${\mathcal {L}}^0$ with $h^1({\mathcal {L}}^0(l'))=k$ (cf. (I)-(II)), its generic bundle ${{\mathcal {K}}}^0$ cannot satisfy $h^1({{\mathcal {K}}}^0(l'))>k$ by the semicontinuity of $h^1$. Hence, the generic element of $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ belongs to $W^0_{l',k}$, which implies that $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}= S$. This in particular also shows, cf. (8.1.5), that the cycle of fixed components of ${{\mathcal {K}}}$ is ${\bar{l}}$. Finally note that l is maximal in ${\mathfrak {I}}_{l',k}$. Indeed, assume that there exists an overset of type $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$, then by the above discussion $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ equals S too, hence it must equal $\overline{ {\mathrm{im}}({\widetilde{c}}^{l'-l})}$ as well.

For the irreducibility see part (V) as well.

This ends the proof of part (b). Next we prove (c). We will repeat several steps of the proof of (b), but now applied for the irreducible components of $\overline{F^0_{l',k}(l)}$.

(IV) Let S be an irreducible component of $\overline{F^0_{l',k}(l)}$, and choose ${\mathcal {L}}^0\in S\cap F^0_{l',k}(l)$. Set ${\mathcal {L}}:={\mathcal {L}}^0(l')\in W_{l',k}$, hence $h^1({\mathcal {L}})=k$. Next, assume that $l\in L_{\ge 0}$ is the cycle of fixed components of ${\mathcal {L}}$. Then, similarly as in (I), ${\mathcal {L}}^0\in {\mathrm{im}}({\widetilde{c}}^{l'-l})$, $l'-l\in -{{\mathcal {S}}}'$, l satisfies (8.1.1), and $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$ belongs to ${\mathfrak {I}}_{l',k}$.

By taking ${\mathcal {L}}^0$ generic in $S\cap F^0_{l',k}(l)$ we get $S\subset \overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$.

Conversely, as in (III) for ${\bar{l}}=l$, one shows that $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})} \subset S$ too, hence necessarily $S= \overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$. Since for fixed $l',k$ and l there is a unique affine subspace of type $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$ with these data, $\overline{F^0_{l',k}(l)}$ should only have one irreducible component, which equals $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$.

Note that from ${\mathcal {L}}^0\in {\mathrm{im}}({\widetilde{c}}^{l'-l})$ we also have $F^0_{l',k}(l)\subset W^0_{l',k}\cap {\mathrm{im}}({\widetilde{c}}^{l'-l})$. The opposite inequality also follows as above (or as in (III)) since in the presence of $W^0_{l',k}$ we automatically have $h^1({{\mathcal {K}}}^0(l'))=k$. This shows (8.1.3) as well.

(V) In (IV) we proved that each $\overline{F^0_{l',k}(l)}$ is irreducible and equals some $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$ from ${\mathfrak {I}}_{l',k}$. Next we plan to show that any subspace from ${\mathfrak {I}}_{l',k}$ is realized in this way by some $\overline{F^0_{l',k}(l)}$. (In fact, in this step we really exploit the ‘support condition’ (iii) from (8.1.1).) We proceed as in (III).

Fix $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$ from ${\mathfrak {I}}_{l',k}$. Let ${{\mathcal {K}}}^0$ be a generic bundle from ${\mathrm{im}}({\widetilde{c}}^{l'-l})$, set ${{\mathcal {K}}}:={{\mathcal {K}}}^0(l')\in {\mathrm{Pic}}^{l'}$. Then (8.1.4) is still valid, and as in (III) one also has

$$\begin{aligned} h^1({{\mathcal {K}}})=h^0(Z, {{\mathcal {K}}})- h^0(Z-l, {{\mathcal {K}}}(-l))+k\ge k. \end{aligned}$$

We claim that $h^1({{\mathcal {K}}})= k$. Assume that this is not the case, that is, $k':=h^1({{\mathcal {K}}})>k$. Let ${\bar{l}}$ be the cycle of fixed components of ${{\mathcal {K}}}$. Then, as above, ${{\mathcal {K}}}\in \overline{{\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ with $h^1({{\mathcal {K}}})=k'$. By the inductive step, we can assume that $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ is indexed from ${\mathfrak {I}}_{l',k'}$. Since ${{\mathcal {K}}}^0$ was chosen generically from $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$, we get that $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-l})}$ is included in a space of type $\overline{{\mathrm{im}}({\widetilde{c}}^{l'-{\bar{l}}})}$ from ${\mathfrak {I}}_{l',k'}$, a contradiction.

Hence $h^1({{\mathcal {K}}})=k$, $h^0(Z, {{\mathcal {K}}})=h^0(Z-l, {{\mathcal {K}}}(-l))$ and ${{\mathcal {K}}}^0(l'-l)\in {\mathrm{im}}(c^{l'-l})$. That is, ${{\mathcal {K}}}^0\in F^0_{l',k}(l)$ for a generic bundle ${{\mathcal {K}}}^0$ of ${\mathrm{im}}({\widetilde{c}}^{l'-l})$. $\square$

Remark 8.1.6

The explicit determination of the index set ${\mathfrak {I}}_{l',k}$—even in concrete examples—is not trivial at all. The system (8.1.1) is not totally combinatorial, it depends on the analytic structure (on the choice of $p_g$). But, even if we fix $p_g=m-\alpha +1$ (between the possible topological values 1 and $m+1$), a fact which makes $\dim V(I(l'-l))$ topological as well (cf. Theorem 6.1.1(5)), the list of solutions of the combinatorial equation $\chi (l)+(l,l')+ \dim V(I(l'-l))=c$ is still hard. We consider it as a real challenge (see also Sect. 8.1.8 and the two examples after it).

Furthermore, the description/characterization of the non-closed sets ${\mathrm{im}}({\widetilde{c}}^{l'-l})$ (indexed by ${\mathfrak {I}}_{l',k}$), respectively of $F^0_{l',k}(l)$, is even harder.

8.1.1 Problem

Is it true that $F^0_{l',k}(l)= {\mathrm{im}}({\widetilde{c}}^{l'-l})$ (with the notations of Theorem 8.1.2) ?

8.1.2 .

In Example 8.1.9 we show that the F-stratification of a certain W can be non-trivial, while Example 8.1.12 presents a different case when the F-stratification is trivial (based on an additional geometric argument).

Example 8.1.9

Consider the elliptic graph from Sect. 5. It has $m=1$, hence $p_g\le 2$. The maximal value $p_g=2$ can be realized e.g. by the hypersurface singularity $\{x^2+y^3+z^{17}=0\}$; see also Remark 6.3.1.

Assume in the sequel that $p_g=2$. Furthermore, assume also that $l'=-Z_K$. In this case by Kodaira type or Grauert–Riemenschneider vanishing $h^1({\mathcal {L}})=0$ for any ${\mathcal {L}}\in {\mathrm{Pic}}^{-Z_K}({\widetilde{X}})$, hence $W_{-Z_K,0}={\mathrm{Pic}}^{-Z_K}({\widetilde{X}})={\mathbb {C}}^2$. In fact, from the point of view of Proposition 7.2.1 the situation is also trivial: $p_g({\widetilde{X}}_i)=0$, hence ${\mathrm{Pic}}^{-Z_K}({\widetilde{X}})$ consists of a unique stratum , namely $W_{-Z_K,0}$.

On the other hand, we will see that the ‘fixed component’ stratification is not trivial.

First note that $\overline{ {\mathrm{im}}(c^{l'})}$ is 2-dimensional, hence it is ${\mathrm{Pic}}^{l'}$, and along it $h^1=0$, hence $\overline{ {\mathrm{im}}(c^{l'})}=W_{l',0}$. To find the F-stratification we have to find the solutions for $l\in L_{\ge 0}$ of the system $Z_K+l\in {{\mathcal {S}}}$ and

$$\begin{aligned} \chi (l)-(l,Z_K)=2-\dim V(I(-Z_K-l)). \end{aligned}$$

(8.1.10)

One solution is $l=0$ which provides ${\mathrm{im}}(c^{l'})$. The other solution is $l=E_1$ (see Sect. 5 for notation). In this case $Z_K+E_1=2Z_{min}\in {{\mathcal {S}}}$, and $\chi (l)-(l,Z_K)=\dim V(I(2Z_{min}))=1$, hence (8.1.10) is satisfied. We will show that these are the only solutions. Indeed, assume that $l>0$ is such a solution. Then $\chi (l)-(l,Z_K)=\chi (-l)>0$ (see the third paragraph in 5.1.7), hence $\dim V(I(-Z_K-l))\le 1$. But, since $Z_K+l>0$ and the singularity is Gorenstein, $\dim V(I(-Z_K-l))\ge 1$ too. On the other hand, if $\dim V(I(-Z_K-l))= 1$ then $Z_K+l=nZ_{min}$ for some $n\ge 2$. Hence, $\chi (l)-(l,Z_K)=\chi (-l)=\chi (Z_K-nZ_{min})=\chi (nZ_{min})=n(n-1)/2$. This shows that necessarily $n=2$.

In conclusion, ${\mathbb {C}}={\mathrm{im}}({\widetilde{c}}^{-2Z_{min}})=F^0_{-Z_K,0}(E_1)$ and ${\mathbb {C}}^2{\setminus } {\mathbb {C}}={\mathrm{im}}({\widetilde{c}}^{-Z_K})=F^0_{-Z_K,0}(0)$.

Remark 8.1.11

Though the set of subspaces of type $\{\overline{ F^0_{l',k}(l)} \}_l$ is in bijection with ${\mathcal {I}}_{l', k}$ (completely defined/described above), sometimes, in order to reduce the possible candidate solutions of (8.1.1) we can use some additional geometric restrictions as well (which, by Theorem 8.1.2, are automatically satisfied, but this fact might not be so transparent from (8.1.1)). E.g., if l is a solution, hence $\{\overline{ F^0_{l',k}(l)} \}_l$ is a non-empty stratum, then necessarily $\dim V(I(l'-l))=\dim \, {\mathrm{im}}(c^{l'-l})\le \dim \overline{ W_{l',k}}$, and equality $\dim V(I(l'-l))<\dim \overline{ W_{l',k}}$ whenever $\overline{{\mathrm{im}}(c^{l'-l})}$ is a proper subspace of $\overline{ W_{l',k}}$. See the next Example for such an argument.

Example 8.1.12

Consider the minimal resolution graph of a Gorenstein elliptic singularity, and fix $v\in B_0{\setminus } B_1$. Then ${\mathrm{im}}(c^{-E^*_v})$ has dimension 1 (cf. Theorem 6.1.1). Recall that ${\mathcal {L}}\in {\mathrm{Pic}}^{-E^*_v}$ belongs to ${\mathrm{im}}(c^{-E^*_v})$ if and only if it has no fixed components. We show that $\overline{{\mathrm{im}}(c^{-E^*_v})}={\mathrm{im}}(c^{-E^*_v})$, that is, if ${\mathcal {L}}\in \overline{{\mathrm{im}}(c^{-E^*_v})}$, then ${\mathcal {L}}$ has no fixed components. Since $h^1$ along $\overline{{\mathrm{im}}(c^{-E^*_v})}$ is $p_g-1$ (cf. Theorem 6.1.1(8)), this fact reads also as $W_{-E^*_v,p_g-1}=\overline{ W_{-E^*_v,p_g-1}}=F_{-E^*_v,p_g-1}(0)$. (This fact will be used in the sequel, e.g. in the proof of Lemma 9.2.5.)

Indeed, assume that ${\mathcal {L}}\in \overline{{\mathrm{im}}(c^{-E^*_v})}{\setminus } {\mathrm{im}}(c^{-E^*_v})$, and let $l\in L_{\ge 0}$ be the cycle of fixed components of ${\mathcal {L}}$. Then from the exact sequence $0\rightarrow {\mathcal {L}}(-l)\rightarrow {\mathcal {L}}\rightarrow {\mathcal {L}}|_l\rightarrow 0$ (or from (8.1.1)) we get that $l+E^*_v\in {{\mathcal {S}}}'$ and $p_g-1+\chi (l)+(l,-E^*_v)=p_g-\dim V(I(-E^*_v-l))$. Since $\chi (l)\ge 0$, $(l,-E^*_v)\ge 0$ and $\dim V(I(-E^*_v-l))$ is necessarily at least 1 ($E^*+l>0$ and (X, o) is Gorenstein), we get that

$$\begin{aligned} l\in L_{\ge 0},\ \chi (l)=0, \ (l,-E^*_v)=0, \ l+E^*_v\in {{\mathcal {S}}}', \ \text{ and } E^*\text{-support } \text{ of } E^*_v+l \subset B_0{\setminus } B_1\nonumber \\ \end{aligned}$$

(8.1.13)

We claim that the only solution of (8.1.13) is $l=0$. To verify from the combinatorics of the graph that no $l>0$ can be a solution of (8.1.13) might be tedious. But geometrically we see it as follows: this F-stratum is zero dimensional, hence the corresponding $\dim V(I(l'-l))=\dim \, {\mathrm{im}}(c^{l'-l})$ must be zero, but we already know that $\dim V(I(l'-l))$ is 1.

Example 8.1.14

(Continuation of Example 6.3.3) Here we exemplify how the condition (8.1.1)(iii) might enter in the picture. Consider the situation from Example 6.3.3, and set $l'=-E^*_4$.

From Theorem 4.1.2 we get that for any ${\mathcal {L}}\in {\mathrm{Pic}}^{-E^*_4}$ one has $h^1({\mathcal {L}})=h^1({\mathcal {L}}|_{{\widetilde{X}}_1})\le 1$. In particular ${{\mathcal {I}}}_{-E^*_4,k}=\emptyset$ for $k\ge 2$. Next, $W_{-E^*_4,1}=\overline{ {\mathrm{im}}(c^{-E^*_4})}$ is irreducible of dimension 1. Moreover, by Example 8.1.12, $\overline{ {\mathrm{im}}(c^{-E^*_4})}= {\mathrm{im}}(c^{-E^*_4})$, hence $l=0$ along $\overline{W_{-E^*_4,1}}=W_{-E^*_4,1}$.

Next, for $k=0$ we consider the system (8.1.1). Hence $E^*_4+l\in {{\mathcal {S}}}'$, $\chi (l)+(l, -E^*_4)=2-\dim V(I(-E^*_4-l))$. Here, for any solution, $\dim V\ge 1$ since the support of $E^*_4+l$ is non-trivial and the germ is Gorenstein.

First assume that $\dim V=2$. Then $\chi (l)=(l,E^*_4)=0$ and $E^*_4+l\in {{\mathcal {S}}}'$. This shows that

$$\begin{aligned} |l|\subset {{\mathcal {V}}}{\setminus } v_4 \text{ and } l\in {{\mathcal {S}}}({{\mathcal {V}}}{\setminus } v_4) \text{ with } \chi (l)=0. \end{aligned}$$

(8.1.15)

We claim that the only solution is $Z_0=Z_{min}({{\mathcal {V}}}{\setminus } v_4)$. [Indeed, by (8.1.15), $l=Z_0+l_1$, $l_1\ge 0$, $\chi (l_1)=(l_1, Z_0)=0$, hence $l_1$ is supported on the $E_8$ rational subgraph with $\chi =0$, hence $l_1=0$.] Hence $\overline{ F^0_{-E^*_4,0}(Z_0)} = \overline{ {\mathrm{im}}( {\widetilde{c}}^{-E^*_4-Z_0})}$, it has dimension 2, hence it is $\overline{ W^0_{-E^*_4,0}}={\mathrm{Pic}}^0$.

Next assume that $\dim V=1$ and $\chi (l)+(l, -E^*_4)=1$. $\dim V=1$ happens exactly when $0\not =E^*_4+l=nE^*_4+mE^*_3$ for some $n,m\in {\mathbb {Z}}_{\ge 0}$. We invite the reader to verify that the only solution is $l=Z_{min}$. However, $\overline{ {\mathrm{im}}({\widetilde{c}}^{-E^*_4-Z_{min}})} = \overline{ {\mathrm{im}}({\widetilde{c}}^{-E^*_4})}$, and this last one is a member of ${{\mathcal {I}}}_{-E^*_4,1}$. Hence $\overline{ {\mathrm{im}}({\widetilde{c}}^{-E^*_4-Z_{min}})} \not \in {{\mathcal {I}}}_{-E^*_4,0}$, and along $W_{-E^*_4,0}$ one has $l=Z_0=Z_{min}-E_4$.

Recall that ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_4) \not \in \overline{ {\mathrm{im}}(c^{-E^*_4})}=W_{-E^*_4,1}$. Hence $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_4))=0$. In particular, the cycle of fixed components of ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_4)$ is $Z_{min}-E_4$.

9 Elliptic singularities with WECC

9.1 WECC for arbitrary singularities

Recall, that by definition, a minimal resolution ${\widetilde{X}}$ of a normal surface singularity satisfies WECC if and only if $E^*_v\in \overline{ {{\mathcal {S}}}'_{im} }$ for any end-vertex, that is, if for some $n>0$ one has ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE^*_v)\in {\mathrm{im}}(c^{-nE^*_v})$, see also 6.3. By [14, Prop. 9.2.2] this happens exactly when $\overline{ {{\mathcal {S}}}'_{im} }={{\mathcal {S}}}'$, that is, for any $l'\in {{\mathcal {S}}}'$ there is a certain $n>0$ so that ${{\mathcal {O}}}_{{\widetilde{X}}}(-nl')\in {\mathrm{im}}(c^{-nl'})$. (Recall, cf. 2.2, that ${{\mathcal {O}}}_{{\widetilde{X}}}(l')\in {\mathrm{im}}(c^{l'})$ means that ${{\mathcal {O}}}_{Z}(l')\in {\mathrm{im}}(c^{l'})$ for $Z\gg 0$, or, equivalently, ${{\mathcal {O}}}_{{\widetilde{X}}}(l')$ has no fixed components.)

As a comparison, ECC for ${\widetilde{X}}$, by definition, is given by the condition ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)\in {\mathrm{im}}(c^{-E^*_v})$ for any end-vertex v. (This can also be compared with the criterion (9.2.2) valid for elliptic singularities.) It is known (see e.g. [29, (2.15)] or [23, 5.27]) that ECC is closed by taking ‘sub-singularities’. This means the following. For any connected union $E_{I}:=\cup _{w\in I}E_w$, where $I\subset {{\mathcal {V}}}$, take ${\widetilde{X}}_I$ a convenient small neighbourhood of $E_I$ in ${\widetilde{X}}$, then ${\widetilde{X}}_I$—as the resolution of $(X_I, o_I):= ({\widetilde{X}}_I/E_I,E_I/E_I)$—satisfies ECC as well. The very same proof gives the following.

Lemma 9.1.1

Fix any (not necessarily elliptic) singularity and one of its resolutions ${\widetilde{X}}$. Then WECC of ${\widetilde{X}}$ is closed by taking ‘sub-singularities’.

We will use the same notations even if $E_I$ is not connected, in such cases $(X_I,o_I)$ is a multigerm. We set $\{I_j\}_j$ for the connected components of I.

9.1.1 .

Before we state the next result, we warn the reader that, in general, the restriction to a certain ${\widetilde{X}}_I$ of a natural line bundle of ${\widetilde{X}}$ is not natural (that is, ${{\mathcal {O}}}_{{\widetilde{X}}}(l')|_{{\widetilde{X}}_I}\not = {{\mathcal {O}}}_{{\widetilde{X}}_I}(R(l'))$, where R is the Chern class restriction). By the next statements we prove that an analytic structure is free from this pathology if and only if it satisfies WECC.

In order to test the fact that the restriction of any natural line bundle is natural it is enough to verify that ${{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{I_j}}$ is natural for any vertex v and j, where $I:={{\mathcal {V}}}{\setminus } v$ and $I_j$ is a component of I. Indeed, first note that it is enough to test only integral cycles. Next, ${{\mathcal {O}}}_{{\widetilde{X}}}(E_u)|_{{\widetilde{X}}_{I_j}}={{\mathcal {O}}}_{{\widetilde{X}}_{I_j}}(E_u)$ for any $u\not =v$, hence by additivity applied for ${{\mathcal {O}}}_{{\widetilde{X}}}(l)$ ($l\in L$) the claim follows. Amazingly, this property fits perfectly with the WECC.

Lemma 9.1.3

As above, consider any singularity and one of its resolutions ${\widetilde{X}}$. Fix any vertex $v\in {{\mathcal {V}}}$ and set $I:={{\mathcal {V}}}{\setminus } v$, $I=\cup _jI_j$. Then

$$\begin{aligned} E^*_v \in \overline{ {{\mathcal {S}}}'_{im}} \ \ \ \text{ if } \text{ and } \text{ only } \text{ if } \ \ \ {{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{I_j}} \ \ \ \text{ is } \text{ natural } \text{ for } \text{ every } j. \end{aligned}$$

Proof

‘$\Rightarrow$’ Take $n\gg 0$ so that $nE^*_v\in L$ and write $nE^*_v=\sum _j l_j+m_vE_v$, where $l_j\in L({\widetilde{X}}_{I_j})_{>0}$. The assumption guarantees that ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE^*_v)\in {\mathrm{im}}(c^{-nE^*_v})$, hence the existence of a divisor $D\in {\mathrm{ECa}}^{-nE^*_v}({\widetilde{X}})$ with ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE^*_v)={{\mathcal {O}}}_{{\widetilde{X}}}(D)$. Therefore, ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE^*_v)|_{{\widetilde{X}}_{I_j}}={{\mathcal {O}}}_{{\widetilde{X}}}(D)|_{{\widetilde{X}}_{I_j}}={{\mathcal {O}}}_{{\widetilde{X}}_{I_j}}$. This reads as ${{\mathcal {O}}}_{{\widetilde{X}}}(m_vE_v)|_{{\widetilde{X}}_{I_j}}={{\mathcal {O}}}_{{\widetilde{X}}_{I_j}}(-l_j)$, hence ${{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{I_j}}$ is natural.

‘$\Leftarrow$’ If ${{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{I_j}}$ is natural then ${{\mathcal {O}}}_{{\widetilde{X}}}(m_vE_v)|_{{\widetilde{X}}_{I_j}}$ has the form ${{\mathcal {O}}}_{{\widetilde{X}}_{I_j}}(-l_j)$ for a certain $m_v\gg 0$. This means that for a convenient large n, such that $nE^*_v$ has the form $\sum _j l_j+m_vE_v$, we get that ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE_v^*)|_{{\widetilde{X}}_{I}}$ is trivial. Consider next the restriction $\pi _I : {\mathrm{Pic}}^{-nE^*_v}({\widetilde{X}})\rightarrow {\mathrm{Pic}}^0({\widetilde{X}}_I)$. Then $(\pi _I)^{-1}(0)$ is an affine subspace of dimension $h^1({{\mathcal {O}}}_{{\widetilde{X}}})-h^1({{\mathcal {O}}}_{{\widetilde{X}}_I})$. The same is true for the affine subspace ${\mathrm{im}}(c^{-nE^*_v})$ for $n\gg 0$. Since ${\mathrm{im}}(c^{-nE^*_v})\subset (\pi _I)^{-1}(0)$, the two subspaces should agree. Thus, ${{\mathcal {O}}}_{{\widetilde{X}}}(-nE^*_v)\in {\mathrm{im}}(c^{-nE^*_v})$ for $n\gg 0$. $\square$

Corollary 9.1.4

(Characterization of WECC for arbitrary singularity) Under the condition of Lemma 9.1.3 the following facts are equivalent:

• (a) WECC for ${\widetilde{X}}$;

• (b) ${{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{{{\mathcal {V}}}{\setminus } v}}$ is natural for any end vertex v;

• (c) ${{\mathcal {O}}}_{{\widetilde{X}}}(E_v)|_{{\widetilde{X}}_{I_j}}$ is natural for any $v\in {{\mathcal {V}}}$ and j;

• (d) ${{\mathcal {O}}}_{{\widetilde{X}}}(-l)|_{{\widetilde{X}}_{{{\mathcal {V}}}{\setminus } I}}\in {\mathrm{Pic}}^0({\widetilde{X}}_{{{\mathcal {V}}}{\setminus } I})$ is trivial for any $l\in {{\mathcal {S}}}$ with $E^*$-support I;

• (e) The restriction to any ${\widetilde{X}}_I$ of any natural line bundle of ${\widetilde{X}}$ is natural.

Proof

Use Lemma 9.1.3 and its proof and the comment from 9.1.2. $\square$

9.2 WECC for elliptic singularities. First consequences.

In the elliptic case, cf. Theorem 6.1.1, since ${\mathrm{im}}(c^{nl'})=\overline{ {\mathrm{im}}(c^{nl'})}$ and ${{\mathcal {O}}}_{{\widetilde{X}}}(nl')\in \overline{ {\mathrm{im}}( c^{nl'})}\ \Leftrightarrow \ 0 \in \overline{ {\mathrm{im}}( {\widetilde{c}}^{nl'})}\ \Leftrightarrow \ 0 \in \overline{ {\mathrm{im}}( {\widetilde{c}}^{l'})}\ \Leftrightarrow \ {{\mathcal {O}}}_{{\widetilde{X}}}(l')\in \overline{ {\mathrm{im}}( c^{l'})}$ for $n\gg 0$, we get the following.

Corollary 9.2.1

(First analytic characterization of WECC for elliptic ${\widetilde{X}}$)

$$\begin{aligned} {\mathrm{WECC}}\ \Leftrightarrow \ {{\mathcal {O}}}_{{\widetilde{X}}}(l')\in \overline{ {\mathrm{im}}(c^{l'})} \ \text{ for } \text{ any } l'\in -{{\mathcal {S}}}'. \end{aligned}$$

(9.2.2)

We invite the reader to review the definition of the analytic multivariable Poincaré series $P({{\mathbf {t}}})$, associated with a fixed resolution of a normal surface singularity e.g. from [22, 23], or [4, 5], see also [14, 2.3.6]. Usually $P({{\mathbf {t}}})$ is not topological. However, for singularities, which satisfy ECC $P({{\mathbf {t}}})$ equals the topological series $Z({{\mathbf {t}}})$, cf. [23].

Corollary 9.2.3

• (a) If ${\widetilde{X}}$ is elliptic, numerically Gorenstein and it satisfies WECC then it is Gorenstein too. More generally, if ${\widetilde{X}}$ is elliptic, non-numerically Gorenstein and it satisfies WECC then $(X_0,o_0)$ is Gorenstein.

• (b) If ${\widetilde{X}}$ is elliptic and it satisfies WECC then the analytic Poincaré series $P({{\mathbf {t}}})$ is determined by the resolution graph. (The identity $P({{\mathbf {t}}})=Z({{\mathbf {t}}})$ will be proved later.)

Proof

(a) By part (d) of Corollary  9.1.4${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{B_0})|_{B_1}$ is trivial. Using induction and Lemma 9.1.1 we get that in fact ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{B_j})|_{B_{j+1}}$ are trivial for all $0\le j\le m-1$. Then apply part (d’)$\Leftrightarrow$(f) of Theorem 3.3.5. For the second part use the first part and Lemma 9.1.1 again.

(b) First note that $(X_0,o_0)$ satisfies WECC (cf. Lemma 9.1.1), hence it is Gorenstein (by part (a)). In particular, $p_g$ is topological. Furthermore, it is known, see e.g. [22, 4.2], that $P({{\mathbf {t}}})$ can be recovered from the dual resolution graph of ${\widetilde{X}}$ combined with the knowledge of the cohomology groups $\{h^1({{\mathcal {O}}}_{{\widetilde{X}}}(l'))\}_{l'\in -{{\mathcal {S}}}'}$ of natural line bundles indexed by $-{{\mathcal {S}}}'$. However, for each such $l'$ one has ${{\mathcal {O}}}_{{\widetilde{X}}}(l')\in \overline{{\mathrm{im}}(c^{l'})}$ and $h^1$ along $\overline{{\mathrm{im}}(c^{l'})}$ is topological (apply Theorem 6.1.1 for a Gorenstein singularity). $\square$

Remark 9.2.4

Corollary 9.2.3(a) can be compared with the following statement. Assume that the link of a singularity (X, o) is a rational homology sphere. Then, if (X, o) is numerically Gorenstein and ${\mathbb {Q}}$-Gorenstein, then it is Gorenstein. (Recall that weighted homogeneous singularities, or those which satisfy ECC, are ${\mathbb {Q}}$-Gorenstein.)

Lemma 9.2.5

• (a) Assume that (X, o) is elliptic, numerically Gorenstein and ${\widetilde{X}}$ satisfies WECC (hence it is automatically Gorenstein, cf. Corollary  9.2.3). If $v\in B_0{\setminus } B_1$ then $E^*_v\in {{\mathcal {S}}}'_{im}$ (that is, ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)\in {\mathrm{im}}(c^{-E^*_v})$).

• (b) Assume that (X, o) is elliptic, non numerically Gorenstein and ${\widetilde{X}}$ satisfies WECC. If $v\in B_{-1}{\setminus } B_0$ then $E^*_v\in {{\mathcal {S}}}'_{im}$. Moreover, ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)$ has no base point.

Proof

In both cases, from (9.2.2) ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)\in \overline{ {\mathrm{im}}(c^{-E^*_v})}$. In case (a), by Corollary 9.2.3 the singularity is Gorenstein, hence by Example 8.1.12$\overline{ {\mathrm{im}}(c^{-E^*_v})}= {\mathrm{im}}(c^{-E^*_v})$. In case (b), by Theorem 6.1.1, ${\mathrm{im}}(c^{-E^*_v})$ is a point, hence $\overline{ {\mathrm{im}}(c^{-E^*_v})}= {\mathrm{im}}(c^{-E^*_v})$. Therefore, in both cases ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)\in {\mathrm{im}}(c^{-E^*_v})$. In case (b) use again that ${\mathrm{im}}(c^{-E^*_v})$ is a point, hence any ‘moved’ effective Cartier divisor from ${\mathrm{ECa}}^{-E^*_v}$ is the zero-set of a section. $\square$

Example 9.2.6

Example 6.3.3 shows that the WECC in the above Lemma 9.2.5 is necessary.

The previous lemma guarantees that in the elliptic WECC Gorenstein case ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)$ $(v\in B_0{\setminus } B_1)$ has no fixed components. The next result focuses on the possible base points.

Theorem 9.2.7

(Elliptic Gorenstein/WECC extension obstruction) Assume that (X, o) is elliptic and Gorenstein with minimal resolution ${\widetilde{X}}$. Let us denote the dual graph by $\Gamma$ and we fix a vertex $v\in B_0{\setminus } B_1$.

• (a) Assume that $\Gamma$ can be extended to a larger elliptic graph $\Gamma '$ by adding a new vertex w connected to $\Gamma$ by an edge (v, w). Then ${{\mathcal {O}}}_{{\widetilde{X}}}(-E_v^*)$ does not admit $E_v$ as its fixed component (though any other $E_u$, $u\not =v$, might be fixed, cf. Example 8.1.14), and along $E_v$ it has a unique base point.

• (b) Assume that the elliptic $\Gamma '$ (obtained from $\Gamma$ as in (a)) is the dual graph of a resolution ${\widetilde{X}}'$, and ${\widetilde{X}}$ can be identified with a small neighbourhood of  $\cup _{v\in {{\mathcal {V}}}(\Gamma )}E_v$ in ${\widetilde{X}}'$. If ${\widetilde{X}}'$ satisfies WECC then ${{\mathcal {O}}}_{{\widetilde{X}}}(-E_v^*)$ has a unique base point (along E), which is exactly $p:=E_v\cap E_w$.

In particular, ${\widetilde{X}}$ cannot be embedded as a subsingularity in an elliptic WECC ${\widetilde{X}}''$ which has two additional irreducible exceptional curves intersecting $E_v$ transversally in two different points $p_1,p_2\in E_v{\setminus } \cup _{u\in {{\mathcal {V}}}(\Gamma ){\setminus } v}E_u$.

Proof

(a) We consider the cohomological exact sequence associated with $0\rightarrow {{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-E_v)\rightarrow {{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)\rightarrow {{\mathcal {O}}}_{E_v}(-E^*_v)\rightarrow 0$. Then ${{\mathcal {O}}}_{E_v}(-E^*_v)\simeq {{\mathcal {O}}}_{{{\mathbb {P}}}^1}(1)$, hence $H^0({{\mathcal {O}}}_{E_v}(-E^*_v)) ={\mathbb {C}}^2$ and $H^1({{\mathcal {O}}}_{E_v}(-E^*_v)) =0$. We will show that $h^1( {{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-E_v))=h^1( {{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)) +1$. Using the cohomological exact sequence, this is equivalent with the fact that the dimension of the image of $\rho : H^0({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v))\rightarrow H^0({{\mathcal {O}}}_{E_v}(-E^*_v))={\mathbb {C}}^2$ is 1. This shows that $E_v$ is not fixed (since $H^0({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-E_v))\hookrightarrow H^0({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v))$ is not onto), $E_v$ supports a base point (since $\dim ({\mathrm{im}}\rho )=1$) and the base point is unique (since $(E_v,-E^*_v)=1$).

First we handle $h^1( {{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-E_v))$. Note that v is an end-vertex by Lemma 3.2.7, and $m_{E_v}(Z_{min})=m_{E_v}(Z_K)=1$. On the other hand, it is known, cf. [21, Proposition 4.3.3], that for any $l'\in L'$ there exists a unique $s(l')\in {{\mathcal {S}}}'$ with $s(l')-l'\in L_{\ge 0}$, and minimal with these two properties. Then $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-l'))$ and $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-s(l')))$ can be compared topologically. Indeed, there exists a Laufer type computation sequence $\{z_i\}_{i=0}^t$ so that $z_0=l'$, $z_t=s(l')$, and $z_{i+1}=z_i+E_{v(i)}$ such that $(z_i,E_{v(i)})>0$ for $i<t$. Then, from a long exact sequence we get $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-z_{i+1}))=h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-z_{i}))- h^1({{\mathcal {O}}}_{{\mathbb {P}}^1}(-(z_i,E_{v(i)})))$.

Now, in our case, one sees that $s(E^*_v+E_v)=E^*_v+Z_{min}$, and the above computation sequence is in fact $E^*_v+z_i'$, where $\{z_i'\}_i$ is the computation sequence connecting $E_v$ with $Z_{min}$ (compare the Laufer algorithms for the two cases and use the fact that $m_{E_v}(Z_{min})=1$). Hence, from ellipticity, there exists exactly one step when $(z_i,E_{v(i)})=2$ and in all other steps it is 1. Hence $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*-E_v))=h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-Z_{min}))+1$.

Next, in the case of both line bundles ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)$ and ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-Z_{min})$ the $E^*$-support is included in $B_0{\setminus } B_1$ (use the assumption and (3.2.4)). Hence, by Theorem 4.1.2$h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v))=h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)|_{{\widetilde{X}}_1})$ and $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-Z_{min}))=h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-Z_{min})|_{{\widetilde{X}}_1})$. But ${{\mathcal {O}}}_{{\widetilde{X}}}(-Z_{min})|_{{\widetilde{X}}_1}$ is trivial by the Gorenstein property, cf. Theorem 3.3.5 (note that ${\mathrm{Pic}}({\widetilde{X}}_1)={\mathrm{Pic}}(C'_1)$). Hence $h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v-Z_{min})=h^1({{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v))$.

(b) Next, assume that ${\widetilde{X}}'$ (hence, by Lemma 9.1.1${\widetilde{X}}$ too) satisfies WECC. Then ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)$ has no fixed components at all (cf. 9.2.5). Since $(E_u,-E^*_v)=\delta _{uv}$, it can have a base point only along $E_v$, where it really has one by (a). Let the disc $E_w\cap {\widetilde{X}}$ be $D_w$. Having the WECC for ${\widetilde{X}}'$, we can choose a divisor $D\in {\mathrm{ECa}}({\widetilde{X}}')$, which intersects $E({\widetilde{X}}')$ only along $E_w{\setminus } E_v$, and an integer m such that ${{\mathcal {O}}}_{{\widetilde{X}}'}(m(\iota (E^*_v)+E_w)+D)$ is trivial. (Here $\iota$ is the embedding $L({\widetilde{X}})\otimes {\mathbb {Q}}\rightarrow L({\widetilde{X}}')\otimes {\mathbb {Q}}$.) Then ${{\mathcal {O}}}_{{\widetilde{X}}'}(m(\iota (E^*_v)+E_w))|_{{\widetilde{X}}}={{\mathcal {O}}}_{{\widetilde{X}}}(E^*_v+D_w)^{\otimes m}$ is trivial too. Since ${\mathrm{Pic}}({\widetilde{X}})$ has no torsion, ${{\mathcal {O}}}_{{\widetilde{X}}}(E^*_v+D_w)$ is also trivial. Hence there is a section of ${{\mathcal {O}}}_{{\widetilde{X}}}(-E^*_v)$ which vanishes along $D_w$, hence at p too. $\square$

Remark 9.2.8

An elliptic Gorenstein analytic structure does not satisfy necessarily WECC. Indeed, take e.g. the germ from Example 6.3.3, or the graph from the right hand side from Example 3.2.8: they do not satisfy the above WECC extension property. On the other hand, the graph from the left hand side in Example 3.2.8 carries a WECC analytic structure by the next Theorem 9.3.1.

Note also that the identity $P({{\mathbf {t}}})=Z({{\mathbf {t}}})$ characterizes ECC, cf. [24, Theorem 7.2.1]. Therefore, for these Gorenstein but not WECC singularities $P({{\mathbf {t}}})=Z({{\mathbf {t}}})$ also fails.

9.3 First topological characterization of the existence of WECC structure

In the following we will give a topological characterization in terms of the combinatorics of the minimal resolution graph $\Gamma$ for the existence of a WECC analytic type supported on $\Gamma$.

Theorem 9.3.1

(Extension criterion of the elliptic sequence) Fix an elliptic minimal graph $\Gamma$ with elliptic sequence $B_{-1}, \ldots , B_m$. Then there exists a singularity with minimal resolution ${\widetilde{X}}$ with dual graph $\Gamma$, which satisfies WECC, if and only if for every $0\le i \le m$ and for any vertex $v \in B_i {\setminus } B_{i+1}$, v has at most one neighbour in $B_{i-1}$.

Proof

The extension obstruction from Theorem 9.2.7 (applied via Corollary 9.2.3) shows that the combinatorial restriction is necessary. Now, we fix a graph $\Gamma$, which satisfies the gluing obstruction of the statement, and we wish to construct a WECC analytic type supported on it. The construction builds a resolution space ${\widetilde{X}}$ by analytic plumbing based on induction on m. If $m=0$ then the graph is minimally elliptic, hence any analytic realization satisfies ECC [25], hence WECC too.

Next, we assume that ${\widetilde{X}}_i$ was already constructed, and it satisfies WECC. Fix $v\in B_i$, which has a neighbour w in $B_{i-1}$. By assumption, v admits only one such w. By Lemma 3.2.7$v\not \in B_{i+1}$, and by Lemma 9.2.5${{\mathcal {O}}}_{{\widetilde{X}}_i}(-E^*_v)\in {\mathrm{im}}(c^{-E^*_v})$ (here all invariants are associated with ${\widetilde{X}}_i$). Hence, there exists a divisor $D_w$ of ${\widetilde{X}}_i$ such that ${{\mathcal {O}}}_{{\widetilde{X}}_i}(-E^*_v)={{\mathcal {O}}}_{{\widetilde{X}}_i}(D_w)$. The Chern class shows that $D_w$ is smooth and it intersects $E_v$ transversally and it intersects no other exceptional curve. [The ‘Extension Theorem’ 9.2.7 and its proof show that $D_w\cap E_v$ is uniquely determined by the analytic type of ${\widetilde{X}}_i$, it is the base point of ${{\mathcal {O}}}_{{\widetilde{X}}_i}(-E^*_v)$.] Then let $T_w$ be an analytic disc bundle over $E_w$ with Chern number $E_w^2$, and we analytically glue $T_w$ to ${\widetilde{X}}_i$ in such a way that ${\widetilde{X}}_i\cap E_w=D_w$. We proceed similarly for all other such $w\in B_{i-1}{\setminus } B_i$ vertices, which have a neighbour in $B_{i}$. (We call such w a contact vertex.) The other disc bundles (corresponding to vertices $w\in B_{i-1}{\setminus } B_i$, which have no neighbours in $B_i$) are glued arbitrarily. The obtained resolution space will be denoted by ${\widetilde{X}}_{i-1}$.

We claim that ${\widetilde{X}}_{i-1}$ supports a singularity with WECC. In the proof we use Corollary 9.1.4(c)$\Rightarrow$(a). According to this, we need to verify that

$$\begin{aligned} {{\mathcal {O}}}_{{\widetilde{X}}_{i-1}}(E_u)|_{{\widetilde{X}}_{B_{i-1}{\setminus } u}} \text{ is } \text{ natural } \text{ for } \text{ any } \text{ vertex } u\in B_{i-1}. \end{aligned}$$

(9.3.2)

First we prove a lemma. In order to formulate it, let us fix a connected subgraph supported on ${\overline{B}}$ with $B_i\subset {\overline{B}}\varsubsetneq B_{i-1}$. Note that the maximal numerical Gorenstein support in ${\overline{B}}$ is $B_i$. [Indeed, ${\overline{B}}$ has a unique maximal numerically Gorenstein subgraph with length $m+1-i$ by Remark 3.3.2, but $B_i$ satisfies this requirement.]

Lemma 9.3.3

Fix ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}}_{{\overline{B}}})$. Then ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}}_{{\overline{B}}})$ is natural $\Leftrightarrow$${\mathcal {L}}|_{{\widetilde{X}}_i}\in {\mathrm{Pic}}({\widetilde{X}}_i)$ is natural.

Proof

‘$\Rightarrow$’ Fix $n\gg 0$ so that ${\mathcal {L}}^{\otimes n}={{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}} (\sum n_uE_u)$ with $n_u\in {\mathbb {Z}}$. If $E_u\cap E_{B_i}=\emptyset$ then ${{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}} (E_u)|_{{\widetilde{X}}_i}$ is trivial, if $u\subset B_i$ then ${{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}} (E_u)|_{{\widetilde{X}}_i}$ is obviously natural, and if $u=w$ is a contact vertex then ${{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}} (E_w)|_{{\widetilde{X}}_i}={{\mathcal {O}}}_{{\widetilde{X}}_i}(D_w)$ is natural by construction.

‘$\Leftarrow$’ Note that the restriction ${\mathrm{Pic}}^{l'}({\widetilde{X}}_{{\overline{B}}}) \rightarrow {\mathrm{Pic}}^{R(l')}({\widetilde{X}}_i)$ is an isomorphism (here $l'\in L'({\widetilde{X}}_{{\overline{B}}})$, and $R(l')$ is its restriction). Now, if the restriction of ${\mathcal {L}}\in {\mathrm{Pic}}({\widetilde{X}}_{{\overline{B}}})$ is natural, then ${\mathcal {L}}^n|_{{\widetilde{X}}_i}={{\mathcal {O}}}_{{\widetilde{X}}_i}(l)$ for some $n\in {\mathbb {Z}}$ and $l\in L({\widetilde{X}}_i)$. Consider ${{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}}(\iota (l))$, where $i:L(B_i)\rightarrow L({\overline{B}})$ is the lattice embedding. Then ${{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}}(\iota (l))|_{{\widetilde{X}}_i}={{\mathcal {O}}}_{{\widetilde{X}}_i}(l)={\mathcal {L}}^n|_{{\widetilde{X}}_i}$, hence by the injectivity of the restriction ${\mathcal {L}}^n={{\mathcal {O}}}_{{\widetilde{X}}_{{\overline{B}}}}(\iota (l))$. $\square$

Now we verify (9.3.2). If $u\in B_{i-1}{\setminus } B_i$ then $B_{i-1}{\setminus } u$ has a connected component ${\overline{B}}$ with $B_i\subset {\overline{B}}\varsubsetneq B_{i-1}$, and maybe some other components, all of them supporting rational graphs. Along the rational components any bundle is automatically natural. Then ${{\mathcal {O}}}_{{\widetilde{X}}_{i-1}}(E_u)|_{{\widetilde{X}}_{B_{i-1}{\setminus } u}}$ is natural by Lemma 9.3.3, since its restriction to ${\widetilde{X}}_i$ is natural (this last statement can be proved as the part ‘$\Rightarrow$’ of Lemma 9.3.3).

Next, assume that $u\in B_i$. Let j (where $m+1\ge j>i$) be maximal so that $u\in B_{j-1}$. Then, similarly as in the previous case, ${{\mathcal {O}}}_{{\widetilde{X}}_{i-1}}(E_u)|_{{\widetilde{X}}_{B_{i-1}{\setminus } u}}$ is natural whenever its restriction to ${\widetilde{X}}_j$ is natural. (For $j=m+1$ this reads as follows: all the components are rational, hence the restricted bundle is natural.) This follows from the WECC of ${\widetilde{X}}_i$. $\square$

9.4 Further topological/analytical characterizations of the WECC structure

In this subsection we will prove the following two statements: if a minimal elliptic graph supports an analytic structure with WECC then it necessarily supports also one with ECC. Even more, any analytic structure with WECC satisfies in fact ECC too.

We wish to separate sharply these two statements for the following reason. Recall that the existence of an analytic structure with ECC is topological: it exists if and only if the graph either satisfies the semigroup and congruence conditions of Neumann–Wahl [25], or the monomial condition of Okuma [29]. In this article we will use the monomial condition (for definition see below). Hence, the first statement basically is equivalent with the fact that a WECC elliptic singularity necessarily must satisfy the combinatorial monomial condition. (The other direction is already in the literature: the monomial condition assures the existence of a splice quotient analytic type [29], while splice quotients by their construction satisfy ECC, hence WECC too.)

An immediate consequence of this is that the ‘old’ combinatorial criteria, namely the semigroup-congruence condition, or the monomial condition, for elliptic graph are equivalent with the existence of the extension criterion from Theorem 9.3.1 (which is much easier to test!).

The second part is analytical in nature, it says that in the elliptic case for any analytic structure already the WECC itself guarantees ECC. Recall that by the ‘End Curve Theorem’ [26, 30] the ECC is equivalent with splice quotient analytic type. Hence, a consequence of our next theorem is that in the elliptic case the three notions—splice quotient, WECC, ECC—are equivalent.

Definition 9.4.1

[29] $\Gamma$ satisfies the monomial condition (MC) if for any node (rupture vertex) v and any connected full subgraph $\Gamma _i$ of $\Gamma {\setminus } v$ there exists an effective cycle $C_i$ supported on $\Gamma _i$ such that $(E^*_v+C_i,E_u)=0$ for any $u\in {{\mathcal {V}}}(\Gamma _i)\cup \{v\}$, which is not an end-vertex of $\Gamma$ sitting in ${{\mathcal {V}}}(\Gamma _i)$.

[In fact, below, we will use only the ‘melody’ of this definition: MC is satisfied iff any node v and any $\Gamma _i$ satisfy some combinatorial property, which not necessarily should be specified.]

Theorem 9.4.2

Fix an elliptic minimal resolution graph $\Gamma$.

• (1) (Second topological characterization of the existence of an analytic structure with WECC) $\Gamma$ supports an analytic structure with WECC if and only if it satisfies MC.

• (2) (Second analytic characterization of an analytic structure with WECC) Assume that $\Gamma$ supports an analytic structure with WECC. Then any such structure satisfies ECC too.

Proof

We will prove the two statements by simultaneous induction on the number of vertices $|{{\mathcal {V}}}|$. For minimally elliptic or rational graphs the statements are true, because any minimally elliptic or rational singularity is splice quotient. Thus, assume that the statements are valid for graphs with less than k vertices, and assume, that $|{{\mathcal {V}}}| = k$.

We claim that it is enough to prove (1), because (1) implies (2). Indeed, if $P({{\mathbf {t}}}) = \sum _{l' \in S'} p(l') {{\mathbf {t}}}^{l'}$ is the analytic multivariable Poincaré series then an analytic structure satisfies ECC if and only if $p(E_v^*) = 1$ for every end vertex v (this follows basically from the definition of P). On the other hand, if a WECC analytic structure exists, then all of them have the same $P({{\mathbf {t}}})$ determined topologically, cf. Corollary 9.2.3(b). By part (1) a structure with ECC also exists, for which $p(E_v^*) = 1$. Since ECC is WECC too, for all WECC structures $p(E_v^*) = 1$. Hence any WECC is ECC.

In the sequel we focus on part (1), where $\Gamma$ is an elliptic minimal resolution graph with $|{{\mathcal {V}}}| = k$. We assume the existence of an analytic structure ${\widetilde{X}}$ with WECC (on $\Gamma$) and we wish to prove MC.

Assume that MC fails at a certain node v and branch $\Gamma _1$ of $\Gamma {\setminus } v$. Denote by $v_1,\ldots , v_\delta$ the adjacent vertices of v in $\Gamma$ with $v_1\in {{\mathcal {V}}}(\Gamma _1)$, $\delta \ge 3$. [In fact, by the inductive step, we can even assume that ${{\mathcal {V}}}(\Gamma )={{\mathcal {V}}}(\Gamma _1)\cup \{v, v_2,v_3\}$, otherwise we take the subgraph with these vertices, it is WECC by restriction, cf. 9.1.1, it is ECC by induction, hence it satisfies MC at $\Gamma _1$, which is a contradiction. But this reduction does not really help in the next proof.] Besides $\Gamma _1$ we will consider several graphs. $\Gamma _1^v$ denotes the full subgraph $\Gamma _1\cup \{v\}$ of $\Gamma$. $\Gamma _1^m$ is obtained from $\Gamma _1^v$ by modifying the decoration of v by a very negative integer $N\ll 0$. Furthermore, the ‘extended–modified’ $\Gamma _1^{me}$ is obtained from the full subgraph $\Gamma _1\cup \{v, v_2,\ldots , v_\delta \}$ of $\Gamma$ by replacing all decorations of $\{v, v_2,\ldots , v_\delta \}$ by N.

We claim that $\Gamma _1^{me}$ is elliptic. Indeed, if we take subgraphs or we decrease decorations of an elliptic graph we get an elliptic or rational graph. However, $\Gamma _1^{me}$ has a node and branch for which MC fails, so it cannot be rational (since rational singularities are splice quotient [25]).

Lemma 9.4.3

• (a) Let $B_0=B_0(\Gamma ^{me}_1)$ be the support of the maximal numerically Gorenstein subgraph in $\Gamma ^{me}_1$ (cf. Remark 3.3.2). Then $\{v_2,\ldots , v_\delta \}\cap B_0= \emptyset .$

• (b) Both $\Gamma _1^m$ and $\Gamma _1^v$ are elliptic graphs.

Proof

(a) Assume $v_2\in B_0$. Then by the uniqueness of the maximal numerically Gorenstein subgraph and by symmetry we get $\{v_2,\ldots , v_\delta \}\subset B_0$, and by the connectedness of $B_0$ we get $v\in B_0$ too. By decreasing $N\ll 0$ the fundamental cycle of any subgraph is non-increasing, hence $Z_K(B_0)=\sum _{i\ge 0} Z_{min}(B_i)\in L$ is non-increasing too. In particular, it must stabilize to an integral cycle independent of N. Let the coefficients of $E_v$ and $E_{v_j}$ be $m_v$ and $m_{v_j}$. Then by the adjunction formula applied for $v_j$ we get that necessarily $m_{v_j}=1$ and $m_v=2$ ($j\ge 2$). But then the adjunction formula for v gives an N-dependent relation, which is a contradiction.

(b) Since $\Gamma _1^{me}$ is elliptic, part (a) shows that $\Gamma _1^m=\Gamma _1^{me}{\setminus } \{v_2,\ldots , v_\delta \}$ contains the elliptic cycle, hence $\Gamma _1^m$ is elliptic. $\Gamma _1^v$ being a subgraph of $\Gamma$ is either elliptic or rational; but it cannot be rational since then $\Gamma _1^m$ would also be rational. $\square$

Starting from the analytic type ${\widetilde{X}}$ we construct an analytic type supported on $\Gamma _1^{me}$ with ECC. This will contradict the fact that for $\Gamma _1^{me}$ MC fails. The construction has several steps.

Step 1. Consider a tubular neighbourhood ${\widetilde{X}}^v_1$ of exceptional divisors indexed by $\Gamma ^v_1$ in ${\widetilde{X}}$. It can be considered as a resolution space. By Lemma 9.1.1 it satisfies WECC. Since $|{{\mathcal {V}}}(\Gamma ^v_1)|<k$, by the inductive step it satisfies ECC too. In particular, since v is an end-vertex of $\Gamma _1^v$, ${{\mathcal {O}}}_{{\widetilde{X}}^v_1}(-E^*_v)$ has no fixed components. Moreover, by WECC extension Theorem  9.2.7, $v\not \in B_0(\Gamma ^v_1)$. [Indeed, $B_0(\Gamma _1^v)=\Gamma _1^v$ implies that $\Gamma _1^v$ is numerically Gorenstein, being numerically Gorenstein and WECC it is Gorenstein by 9.2.3, this contradicts  9.2.7 since the graph can be extended as WECC by more than two vertices $v_{j}$]. Therefore, by Lemma 9.2.5${{\mathcal {O}}}_{{\widetilde{X}}^v_1}(-E^*_v)$ has no base points either.

Step 2. We claim that $v_0\not \in B_0(\Gamma _1^m)$. Indeed, otherwise $\Gamma _1^m$ is numerically Gorenstein. Similarly as in the proof of Lemma 9.4.3, by decreasing $N\ll 0$ the integral cycle $Z_K(\Gamma _1^m)$ stabilizes, and by adjunction formula its $E_v$-multiplicity is 1, independently of N. But then the very same integral cycle might serve as the canonical cycle of $\Gamma _1^v$ too, which contradicts the fact that $\Gamma _1^v$ is not numerically Gorenstein (see Step 1).

Step 3. Fix a (generic) section $s\in H^0({{\mathcal {O}}}_{{\widetilde{X}}^v_1}(-E^*_v))$, set ${\mathrm{div}}(s)=C$, which is a transversal smooth cut of $E_v$ in ${\widetilde{X}}^v_1$. Blow up the infinitesimal near point $C\cap E_v$ several times (that is, blow up $C\cap E_v$ by creating the new exceptional curve $E_{new}$, then blow up the intersection of $E_{new}$ with the strict transform of $E_v$, etc.). We blow it up so many times that in the created total space $Bl({\widetilde{X}}^v_1)$ the strict transform of $E_v$ (still denoted by $E_v$) will have Euler number N. Identify the subgraph determined by the strict transforms of exceptional curves by $\Gamma _1^m$, and let ${\widetilde{X}}^m_1$ be a tubular neighbourhood of them in $Bl({\widetilde{X}}^v_1)$. Since we have blown up $C\cap E_v$, where C is the zero of an end curve function, $Bl({\widetilde{X}}^v_1)$ remains ECC.

Then, by restriction, ${\widetilde{X}}^m_1$ is also ECC, cf. 9.1, in particular ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_v)$ has no fixed components. We claim that along $E_v$ it has no base point either. Indeed, since ${{\mathcal {O}}}_{{\widetilde{X}}^v_1}(-E^*_v)$ has no base points (cf. Step 1), all the sections of this bundle lifted to $Bl({\widetilde{X}}^v_1)$ and restricted to ${\widetilde{X}}^m_1$ provide sections of ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_v)$. [The fact that ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_v)$ has no base points also shows that $\Gamma _1^m$ is not numerically Gorenstein. Indeed, otherwise, being WECC too, it would be Gorenstein with elliptic extension, hence with a base point of ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_v)$ by 9.2.7(a).]

Step 4. We fix (generic) sections $s_i\in H^0({{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_v))$, $2\le i\le \delta$. Write ${\mathrm{div}}(s_i)=C_i$, they are transversal cuts of $E_v$ in ${\widetilde{X}}^m_1$ with ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(C_i+E^*_v)={{\mathcal {O}}}_{{\widetilde{X}}^m_1}$ in ${\mathrm{Pic}}({\widetilde{X}}^m_1)$. Then we make along each $C_i$ an analytic plumbing by gluing a disc bundle over $E_{v_i}$ with Euler number N to ${\widetilde{X}}^m_1$ such that $E_{v_i}\cap {\widetilde{X}}^m_1=C_i$. In this way we get a resolution space ${\widetilde{X}}^{me}_1$ associated with $\Gamma _1^{me}$.

In fact, for these analytic gluings, any transversal cut $C'$ works (instead of $C_i$’s considered above). Indeed, by Step 2 we have $v\not \in B_0({\widetilde{X}}^m_1)$. In particular, the image of the Abel map $c^{-E^*_v}$ (associated with a large cycle $Z\subset L({\widetilde{X}}^m_1)$) is a point, hence any $C'\in {\mathrm{ECa}}^{-E^*_v}({\widetilde{X}}^m_1)$ satisfies ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(C'+E^*_v)\simeq {{\mathcal {O}}}_{{\widetilde{X}}^m_1}$. This together with the construction from the proof of Theorem 9.3.1 also shows that ${\widetilde{X}}^{me}_1$ satisfies WECC. Therefore Corollary 9.1.4 applies and

$$\begin{aligned} {{\mathcal {O}}}_{{\widetilde{X}}^{me}_1}(l'))|_{{\widetilde{X}}^m_1}={{\mathcal {O}}}_{{\widetilde{X}}^m_1}(R(l'))) \quad (R \text{ is } \text{ the } \text{ restriction}). \end{aligned}$$

(9.4.4)

We claim that ${\widetilde{X}}^{me}_1$ satisfies ECC as well. Let us focus first on an end vertex u of $\Gamma ^{me}_1$ different than $v_{i}$ ($i\ge 2$). By Lemma 9.4.3 we know that the restriction $H^1({{\mathcal {O}}}_{{\widetilde{X}}^{me}_1})\rightarrow H^1({{\mathcal {O}}}_{{\widetilde{X}}^{m}_1})$ is an isomorphism, hence we have a bijection ${\mathrm{Pic}}^{-E^*_u}({\widetilde{X}}^{me}_1)\rightarrow {\mathrm{Pic}}^{E^*_u}({\widetilde{X}}^{m}_1)$ too. This bijection together with ${{\mathcal {O}}}_{{\widetilde{X}}^m_1}(-E^*_u)\in {\mathrm{im}}(c^{-E^*_u}({\widetilde{X}}^m_1))$ (ECC for ${\widetilde{X}}^m_1$) and (9.4.4) gives that ${{\mathcal {O}}}_{{\widetilde{X}}^{me}_1}(-E^*_u)\in {\mathrm{im}}(c^{-E^*_u}({\widetilde{X}}^{me}_1))$, hence it gives ECC for ${\widetilde{X}}^{me}_1$ and for the vertex u.

Finally, take the end vertex $u=v_i$ ($i\ge 2$) of $\Gamma ^{me}_1$. Since ${\widetilde{X}}^{me}_1$ satisfied WECC and $u\not \in B_0(\Gamma ^{me}_1)$, by Lemma 9.2.5 we get ${{\mathcal {O}}}_{{\widetilde{X}}^{me}_1}(-E^*_u)\in {\mathrm{im}}(c^{-E^*_u}({\widetilde{X}}^{me}_1))$ again. $\square$

Example 9.4.5

Consider the weighted homogeneous hypersurface elliptic singularity $\{x^{11}=z^2-y^{4}\}$. It has $m=1$ hence $p_g=2$. Its graph is (where the $(-2)$-vertices are unmarked):

This analytic structure satisfies ECC (e.g., since it is weighted homogeneous). The point is that it has a (positive weight, topological constant and $p_g$-constant) hypersurface deformation $(X_t,o)=\{x^{11}=z^2-y^4+tyx^9\}$, such that for $t\not =0$ the germ $(X_t,o)$ is not a splice quotient. In other words, the topological type admits a splice quotient analytic structure, however, the hypersurface/Gorenstein analytic type $(X_{t\not =0},o)$ does not satisfy ECC. This can be verified similarly as in the case treated in [34, 3.2.12] and [26, Ex. 10.4] by checking that the deformation monomial cannot be realized by splice quotient equations. By our results, this analytic type does not satisfy WECC either. However, we do not know any ‘elementary’ method to verify this statement, not even for this particular example. (This shows that usually the ‘direct’ verification of WECC can be very hard.)