Dominant and global dimension of blocks of quantised Schur algebras

Abstract

Group algebras of symmetric groups and their Hecke algebras are in Schur-Weyl duality with classical and quantised Schur algebras, respectively. Two homological dimensions, the dominant dimension and the global dimension, of the indecomposable summands (blocks) of these Schur algebras S(n, r) and $S_q(n,r)$ with $n \geqslant r$ are determined explicitly, using a result on derived invariance in Fang, Hu and Koenig (J Reine Angew Math 770:59–85, 2021).

1 Introduction

Schur algebras have been fundamental objects in representation theory since its early days. In 1901, Schur proved in his thesis what in modern terms is called an equivalence of categories, between the polynomial representations of the general linear group $GL_n(k)$ over an infinite field k of characteristic zero, and representations of symmetric groups $\Sigma _r$ where r varies and the relevant partitions do not have more than n parts. The polynomial representations of a fixed degree r are exactly the representations of the (classical) Schur algebra S(n, r). In 1927, Schur proved, in any characteristic, a double centraliser property—now called Schur-Weyl duality—between the Schur algebra S(n, r) for $n \geqslant r$ and the group algebra $k \Sigma _r$. (See Green’s book [18] for a perfect account.) Later on, Friedlander and Suslin showed that strict polynomial functors also coincide with the representations of S(n, r) [17].

While classical Schur algebras are crucial in the representation theory of general linear groups (over infinite fields) in describing characteristic, their quantised versions, the quantised (or q-) Schur algebras introduced by Dipper and James [5], are important tools for representation theory of finite general linear groups in non-describing characteristic. These algebras are in Schur-Weyl duality with the Hecke algebras of symmetric groups and also interesting in their generic form. Beilinson, Lusztig and MacPherson used a projective limit of quantised Schur algebras, which they showed to contain a quantised enveloping algebra of type A as a subalgebra.

Representations of quantised Schur algebras form highest weight categories. In particular, these algebras have finite global dimension, that is, cohomology vanishes from a certain degree on. The global dimensions of $S_q(n,r)$ with $n \geqslant r$ have been determined by Totaro [30] (classical case) and Donkin [6] (quantised case). Schur-Weyl duality gives a fundamental connection between classical or quantised general linear groups and symmetric groups or Hecke algebras. The strength of this connection is measured by the dominant dimension of the Schur algebra; this has been determined in [13, 16] where the relevance of the dominant dimension in this context is made precise.

These results are, however, not the end of the story. Like group algebras of finite groups, Schur algebras are hardly ever indecomposable as algebras. Usually they decompose into a direct sum of indecomposable summands called blocks. For these blocks much less is known than for the Schur algebras themselves, and the traditional methods could not be extended to the blocks. For instance, the formulae for dominant dimension and global dimension of Schur algebras $S_q(n,r)$ with $n \geqslant r$ just give lower and upper bounds, respectively, for these two dimensions for blocks. The aim of this article is to give precise formulae. To prove these formulae new methods are needed. These come from the derived equivalences constructed by Chuang and Rouquier [3] and from our previous work [11] showing that in particular situations derived equivalences—very much unlike in general situations—do preserve the two homological dimensions we want to compute. As a consequence we can reduce the problem to very special blocks (with trivial core) and solve it there combinatorially, using the results for the full Schur algebras.

To state the main result, some notation is needed: Let k be a field of characteristic $p \geqslant 0$, and q a non-zero element in k. The quantised Schur algebra $S_{q}(n,r)$ ($n\geqslant r$) is isomorphic to the endomorphism algebra of the direct sum of all the permutation modules $M^{\lambda }$ over the associated Hecke algebra ${{{\mathcal {H}}}}_{q}(r)$ of the symmetric group $\Sigma _{r}$, where $\lambda$ ranges over all compositions of r into at most n parts.

If q is not a root of unity, or $q=1$ when $p=0$, then $S_{q}(n,r)$ is semisimple, and all blocks have dominant dimension infinity and global dimension zero. Assume now that $S_{q}(n,r)$ is not semisimple. Then q is a root of unity and there is a smallest positive integer $\ell$ such that $1+q+\cdots +q^{\ell -1}=0$. The classical Schur algebra is the case $q=1$. Then the quantum characteristic $\ell$ coincides with the characteristic p.

The blocks of $S_{q}(n,r)$ are parameterised by $(\tau , w)$, where $w \leqslant r/\ell$ is a non-negative integer, called the $\ell$-weight, and $\tau$ is an $\ell$-core partition of size $r-w\ell$. The corresponding block of $S_{q}(n, r)$ is denoted by ${\mathbf {B}}_{\tau ,w}$. When a block ${\mathbf {B}}_{\tau ,w}$ of $S_{q}(n,r)$ is not simple (that is, $w \ne 0$), then $S_{q}(n,r)$ is not semisimple and $\ell$ is a positive number at least two.

The following main result gives explicit formulae for the dominant and the global dimension of each block ${\mathbf {B}}_{\tau ,w}$.

Theorem 1.1

Let ${\mathbf {B}}$ be a block of $S_{q}(n,r)$ for $n\geqslant r$.

• (a) When ${\mathbf {B}}$ is simple, that is, it has weight $w=0$, then ${\mathbf {B}}$ has infinite dominant dimension and global dimension zero.

• (b) When ${\mathbf {B}}$ is not simple, then ${\mathbf {B}}={\mathbf {B}}_{\tau ,w}$ with $\ell$-weight $w > 0$ and $\ell$-core $\tau$. Then:

  • 1. The dominant dimension of ${\mathbf {B}}_{\tau , w}$ satisfies

    $$\begin{aligned} {{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\tau , w} = 2(\ell -1). \end{aligned}$$

  • 2. The global dimension of ${\mathbf {B}}_{\tau ,w}$ is

    $$\begin{aligned} {{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\tau ,w}=2(\ell w-\alpha _p(w)) \end{aligned}$$

    where $\alpha _p(w)$ is the sum of the digits in the p-adic expansion of w for $p > 0$ and $\alpha _p(w) = w$ for $p=0$.

In the classical case, when $q=1$ and $p > 0$, a non-simple block ${\mathbf {B}}_{\tau , w}$ has global dimension $2(pw - \alpha _p(w))$ and dominant dimension $2(p-1)$.

Apart from the case of simple blocks, the dominant dimension of a block does not depend on its weight or core. Its global dimension does not depend on the core either. It does, however, very much depend on w, and using the derived equivalence classification of blocks [3], global dimension unexpectedly turns out to be a complete derived invariant of blocks:

Corollary 1.2

Let ${\mathbf {B}}$ and $\mathbf {B'}$ be blocks of Schur algebras $S_{q}(n,r)$ for $n\geqslant r$ and $S_{q}(n',r')$ for $n'\geqslant r'$ respectively. Then ${\mathbf {B}}$ and $\mathbf {B'}$ are derived equivalent if and only if they have the same global dimension.

For the Schur algebras themselves, this is not true; for instance when $p=2$, S(4, 4) and S(5, 5) have the same global dimension. They are, however, not derived equivalent, since they have different numbers of simple modules.

This article is about classical and quantised Schur algebras S(n, r) with $n \geqslant r$ and the term Schur algebra always refers to these Schur algebras unless stated otherwise.

Determining the global or dominant dimension of Schur algebras S(n, r) with $n < r$ still is an open problem, and even less is known about these dimensions of the blocks. This article does not contribute to these problems. Results determining the global or dominant dimension of some classes of Schur algebras S(n, r) with $n < r$ can be found in the articles [24, 27, 28] for global dimension and extension groups and [10] for dominant dimension.

2 Algebras, homological dimensions and dualities

This Section is devoted to collecting all necessary ingredients involved in Theorem 1.1 and its proof. Throughout this paper, all algebras are finite dimensional algebras over a fixed field k.

2.1 Dominant dimension and global dimension

Dominant dimension was introduced by Nakayama in his study of complete homology theory [26] and received a systematical study later on by Tachikawa, Morita, Yamagata and many others, see [25, 32] and the references therein. Recent progress is partly motivated by [22], with the main focus on exploring the roles of dominant dimension in various contexts [10, 13, 16, 22], different characterisations [12, 14, 15] and the invariance under certain types of equivalences of categories [2, 11].

Definition 2.1

Let A be an algebra, and let

$$\begin{aligned} 0\rightarrow A\rightarrow I^0 \rightarrow I^1\rightarrow I^2\rightarrow \cdots \end{aligned}$$

be a minimal injective resolution of the left regular A-module. The dominant dimension of A, denoted by ${{\,\mathrm{{\mathrm{domdim}}}\,}}A$, is the largest number $d\geqslant 0$ (or $d=\infty$) such that $I^t$ is projective for all $t<d$ (or for all t).

The opposite algebra $A^\mathrm{op}$ has the same dominant dimension as A [32], and semisimple algebras have dominant dimension infinity. If ${{\,\mathrm{{\mathrm{domdim}}}\,}}A\geqslant 1$, then the injective hull of A is a faithful projective-injective left A-module; if ${{\,\mathrm{{\mathrm{domdim}}}\,}}A\geqslant 2$, then each faithful projective-injective left A-module satisfies the double centraliser property: $A\cong \mathrm{End}_B(P)$ where $B = \mathrm{End}_A(P)^\mathrm{op}$ [32].

The following characterisation of dominant dimension due to Müller is fundamental.

Proposition 2.2

(Müller [25]) Let A be an algebra and $n\geqslant 2$ be a natural number. Then ${{{\,\mathrm{{\mathrm{domdim}}}\,}}A\geqslant n}$ if and only if there exists an idempotent e in A such that eA is a faithful projective and injective right A-module, $\mathrm{Hom }_{eAe}(eA,eA)\cong A$ and $\mathrm{Ext}^i_{eAe}(eA,eA)=0$ for $1\leqslant i\leqslant n-2$.

Global dimension is one of the most important homological dimensions, intended to measure the homological complexity of algebras.

Definition 2.3

The global dimension of an algebra A, denoted by ${{\,\mathrm{gldim}\,}}A$, is the supremum of the projective dimensions of finitely generated left A-modules.

Semisimple algebras have global dimension zero. If $0< {{\,\mathrm{gldim}\,}}A<\infty$, then ${{\,\mathrm{gldim}\,}}A$ equals the maximal number t such that $I^t\ne 0$ in a minimal injective resolution of A; this implies ${{\,\mathrm{{\mathrm{domdim}}}\,}}A \leqslant {{\,\mathrm{gldim}\,}}A$ and in particular finiteness of ${{\,\mathrm{{\mathrm{domdim}}}\,}}A$.

2.2 Hecke algebras and Schur algebras

Let k be a field of characteristic $p\geqslant 0$, and q a non-zero element in k. For a natural number r, let $\Sigma _r$ be the symmetric group on r letters and let ${\mathcal {H}}_q(r)$ be the associated Hecke algebra over k which is given by the generators $\{T_1,\ldots , T_{r-1}\}$ and relations, see [6, 23]

$$\begin{aligned} \begin{array}{llll} (T_i+1)(T_i-q)=0, \quad &{}&{}(1\leqslant i\leqslant r-1);\\ T_iT_j=T_jT_i, \qquad &{}&{}(|i-j|>1);\\ T_iT_{i+1}T_i= T_{i+1}T_iT_{i+1},\quad &{}&{}(1\leqslant i\leqslant r-2). \end{array} \end{aligned}$$

For a natural number n, let $\Lambda (n,r)$ be the set of sequences $\lambda =(\lambda _1,\ldots , \lambda _n)$ of non-negative integers with $\lambda _1+\cdots +\lambda _n=r$, and let $\Lambda ^+(n,r)$ be the subset of $\Lambda (n,r)$ consisting of weakly decreasing sequences.

For $\lambda \in \Lambda (n,r)$, the parabolic Hecke algebra associated with $\lambda$ is the k-subalgebra ${\mathcal {H}}_q(\Sigma _\lambda )$ of ${\mathcal {H}}_q(r)$, generated by $T_1, \dots , T_{\lambda _1 -1}, T_{\lambda _1 + 1}, \dots , T_{\lambda _1 + \lambda _2 + 1}, \dots , T_{\lambda _1 + \lambda _2 + \lambda _3 +1 }, \dots , T_{r-1}$. It is isomorphic to the algebra ${\mathcal {H}}_q(\lambda _1)\otimes _k\cdots \otimes _k {\mathcal {H}}_q(\lambda _n)$.

Let k be the trivial ${\mathcal {H}}_q(\Sigma _\lambda )$-module where all $T_i$’s in ${\mathcal {H}}_q(\Sigma _\lambda )$ act as the scalar q. Let

$$\begin{aligned} M^\lambda = {\mathcal {H}}_q(r)\otimes _{{\mathcal {H}}_q(\Sigma _\lambda )} k,\quad S_q(n,r) = \mathrm{End}_{{\mathcal {H}}_q(r)}\Bigg (\bigoplus _{\lambda \in \Lambda (n,r)}M^\lambda \Bigg ). \end{aligned}$$

The left ${\mathcal {H}}_q(r)$-module $M^\lambda$ is called a permutation module, and $S_q(n,r)$ is called the quantised Schur algebra. There is an isomorphism $M^{\mu }\cong M^{\nu }$ for $\mu ,\nu \in \Lambda (n,r)$, if $\nu$ is obtained from $\mu$ by permuting its entries (see [6, 4.4 (1) (i)]).

Recall now some basic facts about representations of $S_q(n,r)$ from [5, 6], which we only formulate in the case $n\geqslant r$, although some results extend to the case $n<r$.

Young modules. For each $\lambda \in \Lambda ^+(n,r)$, the permutation module $M^\lambda$ admits a decomposition into indecomposable direct summands, as

$$\begin{aligned} M^\lambda \cong \bigoplus _{\mu \in \Lambda ^+(n,r)} (Y^\mu )^{\oplus K_{\lambda ,\mu }} \end{aligned}$$

The indecomposable summands $Y^\mu$ are called Young modules. The multiplicities $K_{\lambda ,\mu }$’s satisfy: $K_{\lambda ,\lambda }=1$ and $K_{\lambda ,\mu }\ne 0$ unless $\mu \unrhd \lambda$, i.e., $\mu _1+\cdots +\mu _s \geqslant \lambda _1+\cdots +\lambda _s$ for all $s\geqslant 1$.

Blocks. An algebra decomposes uniquely into a direct sum of algebra direct summands, called blocks. The blocks of the quantised Schur algebra $S_q(n,r)$ with $n\geqslant r$ are labelled by pairs $(\tau , w)$, which are defined as follows: Let $\ell$ be the least natural number, if existing, such that $1+q+\cdots +q^{\ell -1}=0$ in k, and set $\ell =\infty$ otherwise; $\ell$ is always at least two as $q \ne 0$. When $p=0$ and $q=1$, then $\ell = \infty$; when $p \ne 0$ and $q=1$, then $\ell =p$. For each $\lambda \in \Lambda ^+(n,r)$, there is a uniquely determined pair $(\tau , w)$ where $w\geqslant 0$ is called the $\ell$-weight and $\tau \in \Lambda ^+(n, r-\ell w)$ is called the $\ell$-core of $\lambda$, see Chapter 2 of [31] for the precise definitions.

Theorem 2.4

(James and Mathas [20]) The blocks of the quantised Schur algebra $S_q(n,r)$ with $n\geqslant r$ are in one-to-one correspondence with the pairs $(\tau ,w)$ where $w\geqslant 0$ and $\tau$ is an $\ell$-core partition (that is, it has $\ell$-weight 0) of size $n-w\ell$.

Dominant dimension and global dimension. If $\ell >r$, the quantised Schur algebra $S_q(n,r)$ with $n\geqslant r$ is semisimple and hence has dominant dimension infinity and global dimension zero. A lower bound for the dominant dimension of $S_q(n,r)$ for $n\geqslant r$ and $q=1$ was obtained in [21], and was shown in [13] to be the exact formula; for general q, a lower bound obtained implicitly in [7, Proposition 10.5] was also shown to be the exact formula [16]. The global dimension of $S_q(n,r)$ for $n\geqslant r$ was obtained first in [30] for $q=1$, and in [6, p.126] for general q. To state these formulae, recall some terminology on the $(\ell , p)$-expansions [6].

Fix $a, b\in {\mathbb {N}}\cup \{\infty \}$, the (a, b)-adic expansion of a positive integer n is the expression

$$\begin{aligned} n = n_0 + a(n_1+n_2b+n_3b^2+\cdots ) \end{aligned}$$

with $n_i\in {\mathbb {Z}}$ for all i and $0\leqslant n_0<a, 0\leqslant n_1,n_2,\ldots <b$. The sum of all digits in this expansion, namely $n_0+n_1+n_2+\cdots$ is denoted by $d_{a, b}(n)$ ( [6, Section 4.8]). Then $d_{\infty ,b}(n)= n$, and $d_{1,b}$ is the sum of all digits in the b-adic expansion of n, which is denoted by $\alpha _b(n)$ in [30]. We also set, for simplicity,

$$\begin{aligned} d_{a, 0} = d_{a, \infty } = n_0+n_1. \end{aligned}$$

Theorem 2.5

([6, 13, 16, 30]) The dominant dimension of $S_q(n,r)$ for $n\geqslant r$ is given by

$$\begin{aligned} {{\,\mathrm{{\mathrm{domdim}}}\,}}S_q(n,r) = \left\{ \begin{array}{ll} \infty , &{} {\ell >r;} \\ 2(\ell -1), &{} {\ell \leqslant r.} \end{array} \right. \end{aligned}$$

The global dimension of $S_q(n,r)$ for $n\geqslant r$ is given by

$$\begin{aligned} {{\,\mathrm{gldim}\,}}S_q(n,r)= 2(r-d_{\ell ,p}(r)). \end{aligned}$$

Remark 2.6

Theorem 2.5 directly implies the (known) equivalence of the following statements, for $n\geqslant r$: (1) ${{\,\mathrm{gldim}\,}}S_q(n,r)=0$; (2) $\ell >r$; and (3) ${{\,\mathrm{{\mathrm{domdim}}}\,}}S_q(n,r)=\infty$.

2.3 Dualities

An anti-automorphism $\theta$ of a finite dimensional algebra A is said to preserve simples if $\mathrm{Hom }_k({}^{\theta }S, k)\cong S$ for every simple left module S. Here ${}^{\theta }S$ is the right A-module with A-action defined by $m\cdot a=\theta (a)m$.

The following lemma shows that the class of algebras admitting anti-automorphisms preserving simples is closed under taking block algebras. This applies in particular to all cellular algebras.

Lemma 2.7

Let A be a finite dimensional algebra. If A admits an anti-automorphism preserving simples, then so do the block algebras of A.

Proof

The anti-automorphism $\theta$ restricts to an anti-automorphism of the centre Z(A) of A: $za=az$ for all a implies $\theta (az)=\theta (za)$ and hence $\theta (z) b = b \theta (z)$ for all $b=\theta (a)$. Thus, $\theta$ sends primitive central idempotents to primitive central idempotents. Multiplication by a primitive central idempotent e fixes all simple modules S in the block eAe, since e is the identity of this block. If $\theta (e) \ne e$ then $\theta (e)$ is a summand of $1-e$, that is $\theta (e)e = 0$, and thus $\theta (e)$ annihilates the block eAe and in particular its module S, which is a contradiction to $\mathrm{Hom }_k({}^{\theta }S, k)\cong S.$ $\square$

Corollary 2.8

Let A be a block of a quantised Schur algebra $S_q(n,r)$ (for any n, r). Then A admits an anti-automorphism preserving simples.

Proof

Quantised Schur algebras do admit an anti-automorphism preserving simples, see Section 4.1 in [6]. $\square$

3 Proof of Theorem 1.1

The dominant and the global dimensions of the quantised Schur algebras $S_q(n, r)$ with $n\geqslant r$ are known (see Theorem 2.5). To get precise formulae for the blocks, we are going to use that these blocks have been classified by Chuang and Rouquier, up to derived equivalence.

Theorem 3.1

(Chuang and Rouquier [3], Subsection 7.6) Let $n \geqslant r$ and $m \geqslant s$. Two blocks ${\mathbf {B}}_{\tau , w}$ and ${\mathbf {B}}_{\tau ', w'}$ of quantised Schur algebras $S_q (n,r)$ and $S_q(m,s)$ are derived equivalent if they have the same $\ell$-weight, that is, $w = w'$.

This theorem can in fact be formulated as an equivalence. The ‘only if’ direction is implicit in [3]: A derived equivalence preserves the number of simple modules and this implies $w = w'$ (see Chapter 2 in [31] and Subsections 7.5 and 7.6 in [3].) The ’only if’ direction also is a consequence of the proof of Theorem 1.1.

In general, derived equivalences are far from preserving dominant dimension or global dimension. Unexpectedly, however, there exists a particular situation where these homological invariants are preserved.

Recall that an algebra A over k is k-split if $\mathrm{End}_A(S)\cong k$ for all simple A-modules S. Quantised Schur algebras (and in general all cellular algebras) are k-split, and thus so are their blocks.

Theorem 3.2

(Fang et al. [11]) Let A and B be derived equivalent finite dimensional k-split algebras. Assume that both A and B have anti-automorphisms that preserve simples. Then

(1) ${{\,\mathrm{gldim}\,}}A = {{\,\mathrm{gldim}\,}}B$;

(2) if A and B have non-zero dominant dimension, then ${{\,\mathrm{{\mathrm{domdim}}}\,}}A= {{\,\mathrm{{\mathrm{domdim}}}\,}}B$.

This theorem, applied to quantised Schur algebras, constitutes a main ingredient in the proof of Theorem 1.1.

Corollary 3.3

For $n\geqslant r$ and $m \geqslant s$, the two blocks ${\mathbf {B}}_{\tau , w}$ of $S_q(n,r)$ and ${\mathbf {B}}_{\tau ',w'}$ of $S_q(m,s)$ have the same dominant and the same global dimension if $w=w'$.

Proof

For $n\geqslant r$ and $m \geqslant s$, the two blocks ${\mathbf {B}}_{\tau , w}$ of $S_q(n,r)$ and ${\mathbf {B}}_{\tau ',w'}$ of $S_q(m,s)$ are derived equivalent if $w=w'$, by Theorem 3.1. Blocks of quantised Schur algebras with $n \geqslant r$ have dominant dimension at least 2 by Schur-Weyl duality, and satisfy the condition in Theorem 3.2, by Corollary 2.8. The corollary now is an immediate consequence of Theorem 3.2. $\square$

The following lemma will be used for an induction argument in the proof of Theorem 1.1.

Lemma 3.4

Assume $2\leqslant \ell <\infty$. Then the function $g(s) = \ell s - d_{1,p}(s)$ is strictly increasing, i.e., $g(s)<g(s+1)$ for $s\in {\mathbb {N}}$.

Proof

Since $g(s+1) - g(s) = \ell - d_{1,p}(s+1) + d_{1,p}(s)$ and $\ell \geqslant 2$, it is enough to show the inequality ${d_{1,p}(s+1) - d_{1,p}(s)\leqslant 1}$.

If $p=0$ or $p=\infty$, then $d_{1, p}(s)= s$ for all $s\in {\mathbb {N}}$ and thus $d_{1,p}(s+1) - d_{1,p}(s)= 1$.

If $p\not \in \{ 0, \infty \}$, let $s = s_0+s_1p+\cdots$ be the p-adic expansion of s. Let a be maximal such that $s_0=\cdots =s_{a-1}= p-1$. Then

$$\begin{aligned} d_{1,p}(s+1) - d_{1,p}(s)= 1+ \sum _{i\geqslant a} s_i - \sum _{i\geqslant 0} s_i = \left\{ \begin{array}{ll} 1, &{} {a=0;} \\ 1-a(p-1), &{} {a>0.} \end{array} \right. \end{aligned}$$

Altogether, $d_{1,p}(s+1)-d_{1,p}(s)\leqslant 1$, as desired. $\square$

Proof of Theorem 1.1

(Dominant dimension formula) By Theorem 2.4, for $n\geqslant \ell w$, the algebra $S_q(n, \ell w)$ has a block ${\mathbf {B}}_{\emptyset ,w}$. Corollary 3.3 implies that ${{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\tau ,w}={{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\emptyset ,w}$. Thus it suffices to show

$$\begin{aligned} {{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\emptyset ,w} = \left\{ \begin{array}{ll} 2(\ell -1), &{} {w>0;} \\ \infty , &{} {w=0.} \end{array} \right. \end{aligned}$$

If $w=0$, then ${\mathbf {B}}_{\emptyset , w}$ is simple and so has infinite dominant dimension. If $w>0$, then the quantised Schur algebra $S_q(n,\ell w)$ is not semisimple and has dominant dimension $2(\ell -1)$ by Theorem 2.5. Thus ${\mathbf {B}}_{\emptyset , w}$, as a block algebra of $S_q(n,\ell w)$, has dominant dimension at least $2(\ell -1)$. To prove the dominant dimension formula, it remains to prove that

$$\begin{aligned} {{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\emptyset , w} \leqslant 2(\ell -1). \end{aligned}$$

Let e be an idempotent in ${\mathbf {B}}_{\emptyset ,w}$ such that $e {\mathbf {B}}_{\emptyset ,w}$ is a minimal faithful right ${\mathbf {B}}_{\emptyset ,w}$-module. Then ${\mathbf {b}}_{w}=e{\mathbf {B}}_{\emptyset ,w}e$ is a block of ${\mathcal {H}}_q(\ell w)$, since the blocks of $S_q(\ell w, \ell w)$ and of ${\mathcal {H}}_q(\ell w)$ are in one-to-one correspondence under the Schur functor (see [6, p. 39]); this also can be seen as a consequence of Schur-Weyl duality. Moreover,

$$\begin{aligned} e{\mathbf {B}}_{\emptyset , w} = \bigoplus (Y^\mu )^{\oplus a_\mu } \end{aligned}$$

as ${\mathbf {b}}_w$-modules. This sum runs over all $\mu \in \Lambda ^+(n,\ell w)$ with $\ell$-core $\emptyset$ and each $a_\mu$ is positive [6]. Choose $\nu = (\ell , 1,\ldots , 1)$ and $\mu =(\ell w)$ in $\Lambda ^+(n,\ell w)$. Then $\nu$ and $\mu$ both have $\ell$-core $\emptyset$. Now by the Eckmann-Shapiro Lemma

$$\begin{aligned} \mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\ell w)}(M^\nu , Y^\mu )\cong \mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\ell w)}({\mathcal {H}}_q(\ell w)\otimes _{{\mathcal {H}}_q(\Sigma _\nu )} k, k)\cong \mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\Sigma _\nu )}(k,k)\ne 0, \end{aligned}$$

since $Y^\mu = M^\mu = k$. The non-vanishing of $\mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\Sigma _\nu )}(k,k)$ follows by identifying $\Sigma _\nu$ with $\Sigma _{\ell }$ and using that ${{\,\mathrm{{\mathrm{domdim}}}\,}}S_q(\ell ,\ell )=2(\ell -1)$, which has been shown in [9, Corollary 4.3] and [16] for the quantised case and in [13, Theorem 2.2] for the classical case. In [13] it is explained how this relates to the cohomology of ${\mathcal {H}}_q(\Sigma _{\ell })$. Alternatively, $\mathrm{Ext}^{2(\ell -1)-1}(k, k)\ne 0$ can be computed directly as follows: As explained in [8, Sect. 3.2], the weight one blocks of Hecke algebras have been determined by Uno and shown by Jost to be Morita equivalent to the principal block of ${\mathcal {H}}_q(\ell )$. The latter algebra is a Brauer tree algebra and its basic algebra has been described by quiver and relations in [8, Sect. 3.2]. The trivial module k satisfies $\Omega ^{2(\ell -1)} (k)=k$ and hence $\Omega ^{2(\ell -1)-1} (k)=\Omega ^{-1}k$. As the algebra is indecomposable, symmetric and not simple, ${\underline{\mathrm{Hom }}}(\Omega ^{-1}k, k) \ne 0$. Therefore, $\mathrm{Ext}^{2(\ell -1)-1}(k, k)\ne 0$.

Hence, there exists an indecomposable direct summand $Y^\lambda$ of $M^\nu$ such that

$$\begin{aligned} \mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\ell w)}(Y^\lambda , Y^\mu )\ne 0. \end{aligned}$$

In particular, $Y^\lambda$ and $Y^\mu$ belong to the same block of ${\mathcal {H}}_q(\ell w)$, i.e. $\lambda$ also has $\ell$-core $\emptyset$. Now both $Y^\lambda$ and $Y^\mu$ are direct summands of $e{\mathbf {B}}_{\emptyset , w}$, so

$$\begin{aligned} \mathrm{Ext}^{2(\ell -1)-1}_{{\mathbf {b}}_w}(e{\mathbf {B}}_{\emptyset , w},e{\mathbf {B}}_{\emptyset , w})\supseteq \mathrm{Ext}^{2(\ell -1)-1}_{{\mathcal {H}}_q(\ell w)}(Y^\lambda , Y^\mu )\ne 0 \end{aligned}$$

By Proposition 2.2, it follows that ${{\,\mathrm{{\mathrm{domdim}}}\,}}{\mathbf {B}}_{\emptyset , w} \leqslant 2(\ell -1)$.

(Global dimension formula) The formula in Theorem 1.1 means precisely that

$$\begin{aligned} {{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\tau , w}=2g(w) \end{aligned}$$

where g(w) is defined in Lemma 3.4.

By Corollary 3.3, ${{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\tau , w} = {{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\emptyset , w}$. Hence it suffices to show that ${{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\emptyset , w} = 2 g(w)$. We proceed by induction on w. If $w=0$, the formula holds trivially since $g(0)=0$ and ${\mathbf {B}}_{\emptyset , w}$ is simple, hence of global dimension zero. Assume the formula to hold for all $w'<w$. The global dimension of $S_q(n, \ell w)$, which is 2g(w) (see Theorem 2.5), is the maximum of the global dimensions of its blocks. By Theorem 2.4, $S_q(n, \ell w)$ has a block ${\mathbf {B}}_{\emptyset , w}$ and all other blocks have $\ell$-weights $w'<w$, and therefore have global dimension $2g(w')$ which is less than 2g(w) by Lemma 3.4. Hence ${{\,\mathrm{gldim}\,}}{\mathbf {B}}_{\emptyset , w}=2g(w)$ as desired.

Proof of Corollary 1.2

Global dimension is a derived invariant of blocks of quantised Schur algebras by Corollary 3.3. Theorem 1.1 and Lemma 3.4 imply that blocks have different global dimensions when they are not derived equivalent.

Remarks

• (1) In terms of Rouquier’s cover theory [29], the quantised Schur algebra $S_q(n,r)$ is a quasi-hereditary cover of the Hecke algebra ${\mathcal {H}}_q(r)$ of covering degree $(\ell -1)$ by Theorem 2.5 and [13], that is, $S_q(n,r)$ is an $(\ell -1)$-cover, but not an $\ell$-cover of ${\mathcal {H}}_q(r)$. Our result implies a particular property of the cover; each block of $S_q(n,r)$ is a quasi-hereditary cover of the corresponding block of ${\mathcal {H}}_q(r)$, of the same dominant dimension. This property may be formulated as saying that the covering is uniform of covering degree $\ell -1$.

• (2) When k has characteristic zero or bigger than the weight w, the dominant dimensions of the blocks ${\mathbf {B}}_{\tau , w}$ have been determined in [16] by using Chuang and Tan’s complete description of the corresponding Rouquier blocks [4].

• (3) All weight two blocks ${\mathbf {B}}_{\tau ,2}$ of quantised Schur algebras $S_q(n,r)$ are not only derived equivalent, but also stably equivalent of Morita type, and hence have the same dominant and global dimensions, as well as the same representation dimension. Indeed, by carefully examining the tilting complexes constructed by Chuang and Rouquier [3, Sect. 6], the induced derived equivalences are seen to be almost $\nu$-stable [19, Sect. 1], and hence induce stable equivalences of Morita type. However, the derived equivalences between blocks of arbitrary weight, constructed by Chuang and Rouquier [3] are not in general almost $\nu$-stable.

  For instance, when $\mathrm{char}\, k=2$, the blocks ${\mathbf {B}}_{\emptyset , 3}$ and ${\mathbf {B}}_{(1), 3}$ of Schur algebras are derived equivalent. These two blocks correspond to each other under the reflection $s_0$ of the Weyl group of the affine Kac-Moody algebra $\widehat{{{\mathfrak {s}}}{{\mathfrak {l}}}_2}$. We shall show that the derived equivalence constructed in [3] is not almost $\nu$-stable.

  In the following diagram

  

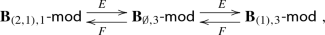
  the functors E and F are induced by the functors $\mathrm{Tr}^0$ and $\mathrm{Tr}_0$, respectively, investigated in [1].

  The indecomposable projective modules over ${\mathbf {B}}_{\tau , w}$ are written as $P(\lambda )$, where $\lambda$ runs over partitions of $|\tau |+2w$ with 2-core $\tau$.

  The tilting complex $T^{\bullet }$ over ${\mathbf {B}}_{(1), 3}$ constructed in [3, Sect. 6] has the following form

  $$\begin{aligned} 0\longrightarrow \bigoplus _{\lambda } E^{(2)}F P(\lambda )\longrightarrow \bigoplus _{\lambda } E P(\lambda )\longrightarrow 0, \end{aligned}$$

  where $E^{(2)}X\oplus E^{(2)}X\cong E^2X$ for all ${\mathbf {B}}_{(2,1), 1}$-modules X. The terms of the tilting complex can be calculated as follows. For each partition $\lambda$ of 6 with empty 2-core, the projective module $P(\lambda )$ has a filtration by standard modules $\Delta (\mu )$ with multiplicities given by the corresponding column of the decomposition matrix of ${\mathbf {B}}_{\emptyset , 3}$. Applying the exact functor E (respectively, F) to $\Delta (\mu )$ results in a module with a filtration by standard modules corresponding to partitions obtained by adding one 0-addable (respectively, removing one 0-removable) node, each with multiplicity 1, see Theorem A in [1]. In this way, one gets the multiplicities of the standard modules in $E^{(2)}F P(\lambda )$ and $E P(\lambda )$. The decomposition matrix is lower uni-triangular and invertible. Writing the multiplicities as a column vector and multiplying by the inverse of the decomposition matrix of ${\mathbf {B}}_{(1), 3}$ from the left hand side gives the multiplicities of $P(\mu )$ as a direct summand of $E^{(2)}F P(\lambda )$ and $E P(\lambda )$, where $\mu$ runs over partitions of 7 with 2-weight 3. The decomposition matrices can be found, for example, in the Appendix of [23]. Removing the common direct summands of $T^0$ and $T^{-1}$ reduces $T^{\bullet }$ to a complex without contractible direct summands. The direct summands of the complex are as follows.

  $$\begin{aligned}&\quad 0\longrightarrow P(2^2,1^3)^2\longrightarrow P(1^7)\longrightarrow 0\\&\quad 0\longrightarrow P(2^2,1^3)\longrightarrow 0\longrightarrow 0\\&\quad 0\longrightarrow P(2^2,1^3)\longrightarrow P(3,2,1^2)\longrightarrow 0\\&\quad 0\longrightarrow P(2^2,1^3)\oplus P(4,2,1)^2\longrightarrow P(3,1^4)\longrightarrow 0\\&\quad 0\longrightarrow P(4,2,1)\longrightarrow P(3,2^2)\longrightarrow 0\\&\quad 0\longrightarrow P(4,2,1)\longrightarrow 0\longrightarrow 0\\&\quad 0\longrightarrow P(4,2,1)^2\longrightarrow P(3^2,1)\longrightarrow 0\\&\quad 0\longrightarrow P(4,2,1)\longrightarrow P(5,2)\longrightarrow 0\\&\quad 0\longrightarrow P(4,2,1)\longrightarrow P(5,1^2)\longrightarrow 0\\&\quad 0 \longrightarrow 0\longrightarrow P(7)\longrightarrow 0 \end{aligned}$$

  By the definition of almost $\nu$-stable derived equivalences, indecomposable non-injective projective modules can occur only in degree zero. However, both P(4, 2, 1) and P(5, 2) are non-injective, and occur in the degrees $-1$ and 0, respectively. (Non-injectivity follows from Section 4.3, (1), (4)(ii) and (9), in [6].) This shows that the derived equivalence is not almost $\nu$-stable.