Abstract
We construct new examples of rational Gushel-Mukai fourfolds, giving more evidence for the analog of the Kuznetsov Conjecture for cubic fourfolds: a Gushel–Mukai fourfold is rational if and only if it admits an associated K3 surface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A Gushel-Mukai fourfold is a smooth prime Fano fourfold \(X\subset {\mathbb {P}}^8\) of degree 10 and index 2 (see [21]). These fourfolds are parametrized by a coarse moduli space \({\mathcal {M}}_4^{GM}\) of dimension 24 (see [5, Theorem 5.15]), and the general fourfold \([X]\in {\mathcal {M}}_4^{GM}\) is a smooth quadratic section of a smooth hyperplane section of the Grassmannian \({\mathbb {G}}(1,4)\subset {\mathbb {P}}^9\) of lines in \({\mathbb {P}}^4\).
In [3] (see also [4,5,6]), following Hassett’s analysis of cubic fourfolds (see [12, 13]), the authors studied Gushel-Mukai fourfolds via Hodge theory and the period map. In particular, they showed that inside \({\mathcal {M}}_4^{GM}\) there is a countable union \(\bigcup _d {\mathcal {GM}}_d \) of (not necessarily irreducible) hypersurfaces parametrizing Hodge-special Gushel-Mukai fourfolds, that is, fourfolds that contain a surface whose cohomology class does not come from the Grassmannian \({\mathbb {G}}(1,4)\). The index d is called the discriminant of the fourfold and it runs over all positive integers congruent to 0, 2, or 4 modulo 8 (see [3]). However, as far as the authors know, explicit geometric descriptions of Hodge-special Gushel-Mukai fourfolds in \({\mathcal {GM}}_d\) are unknown for \(d>12\). In Theorem 3.3, we shall provide such a description when \(d=20\).
As in the case of cubic fourfolds, all Gushel-Mukai fourfolds are unirational. Some rational examples are classical and easy to construct, but no examples have yet been proved to be irrational. Furthermore, there are values of the discriminant d such that a fourfold in \({\mathcal {GM}}_d\) admits an associated K3 surface of degree d. For instance, this occurs for \(d=10\) and \(d=20\). The hypersurface \({\mathcal {GM}}_{10}\) has two irreducible components, and the general fourfold in each of these two components is rational (see [3, Propositions 7.4 and 7.7] and Examples 2.1 and 2.2). Some of these fourfolds were already studied by Roth in [22]. As far as the authors know, there were no other known examples of rational Gushel-Mukai fourfolds. In Theorem 3.4, we shall provide new examples of rational Gushel-Mukai fourfolds that belong to \({\mathcal {GM}}_{20}\).
A classical and still open question in algebraic geometry is the rationality of smooth cubic hypersurfaces in \({\mathbb {P}}^5\) (cubic fourfolds for short). An important conjecture, known as Kuznetsov’s Conjecture (see [1, 14, 18, 19]) asserts that a cubic fourfold is rational if and only if it admits an associated K3 surface in the sense of Hassett/Kuznetsov. This condition can be expressed by saying that the rational cubic fourfolds are parametrized by a countable union \(\bigcup _d {\mathcal {C}}_d\) of irreducible hypersurfaces inside the 20-dimensional coarse moduli space of cubic fourfolds, where d runs over the so-called admissible values (the first ones are \(d=14,26,38,42,62\)). The rationality of cubic fourfolds in \({\mathcal {C}}_{14}\) was proved by Fano in [8] (see also [2]), while rationality in the case of \({\mathcal {C}}_{26}\) and \({\mathcal {C}}_{38}\) was proved in [23]. Very recently, in [24], rationality was also proved in the case of \({\mathcal {C}}_{42}\). The proof of this last result shows a close relationship between cubic fourfolds in \({\mathcal {C}}_{42}\) and the Gushel-Mukai fourfolds in \({\mathcal {GM}}_{20}\) constructed in this paper. This beautiful geometry was discovered with the help of Macaulay2 [10].
2 Generality on Gushel-Mukai fourfolds
In this section, we recall some general facts about Gushel-Mukai fourfolds which were proved in [3] (see also [4,5,6]).
A Gushel-Mukai fourfold \(X\subset {\mathbb {P}}^8\), GM fourfold for short, is a degree-10 Fano fourfold with \(\mathrm {Pic}(X) = \mathbb {Z}[ {\mathcal {O}}_X(1)]\) and \(K_X\in |{\mathcal {O}}_X(-2)|\). Equivalently, X is a quadratic section of a 5-dimensional linear section of the cone in \({\mathbb {P}}^{10}\) over the Grassmannian \({\mathbb {G}}(1,4)\subset {\mathbb {P}}^9\) of lines in \({\mathbb {P}}^4\). There are two types of GM fourfolds:
-
quadratic sections of hyperplane sections of \(\mathbb G(1,4)\subset {\mathbb {P}}^9\) (Mukai or ordinary fourfolds, [21]);
-
double covers of \(\mathbb G(1,4)\cap {\mathbb {P}}^7\) branched along its intersection with a quadric (Gushel fourfolds, [11]).
There exists a 24-dimensional coarse moduli space \({\mathcal {M}}_4^{GM}\) of GM fourfolds, where the locus of Gushel fourfolds is of codimension 2. Moreover, we have a period map \(\mathfrak {p}:{\mathcal {M}}_4^{GM}\rightarrow {\mathcal {D}}\) to a 20-dimensional quasi-projective variety \(\mathcal D\), which is dominant with irreducible 4-dimensional fibers (see [5, Corollary 6.3]).
For a very general GM fourfold \([X]\in {\mathcal {M}}_4^{GM}\), the natural inclusion
of middle Hodge groups is an equality. A GM fourfold X is said to be Hodge-special if the inclusion (2.1) is strict. This means that the fourfold X contains a surface whose cohomology class “does not come” from the Grassmannian \({\mathbb {G}}(1,4)\). Hodge-special GM fourfolds are parametrized by a countable union of hypersurfaces \(\bigcup _d {\mathcal {GM}}_d\subset {\mathcal {M}}_4^{GM}\), labelled by the positive integers \(d\equiv 0,2\), or 4 (mod 8) (see [3, Lemma 6.1]). The image \({\mathcal {D}}_d=\mathfrak {p}({\mathcal {GM}}_d)\) is a hypersurface in \({\mathcal {D}}\), which is irreducible if \(d\equiv 0\) (mod 4), and has two irreducible components \({\mathcal {D}}_d'\) and \({\mathcal {D}}_d''\) if \(d\equiv 2\) (mod 8) (see [3, Corollary 6.3]). The same holds true for \({\mathcal {GM}}_d\).
In some cases, the value of d can be explicitly computed from the geometry of Hodge-special GM fourfolds (see [3, Section 7]). Indeed, let \(X\subset {\mathbb {P}}^8\) be an ordinary GM fourfold containing a smooth surface S such that \([S]\in A(X){\setminus } A(\mathbb G(1,4))\). We may write \([S]=a\sigma _{3,1}+b\sigma _{2,2}\) in terms of Schubert cycles in \(\mathbb G(1,4)\) for some integers a and b. We then have \([X]\in {\mathcal {GM}}_d\), where d is the absolute value of the determinant (or discriminant) of the intersection matrix in the basis \((\sigma _{1,1|X}, \sigma _{2|X}-\sigma _{1,1|X}, [S])\). That is
where
For some values of d, the non-special cohomology of the GM fourfold \([X]\in {\mathcal {GM}}_d\) looks like the primitive cohomology of a K3 surface. In this case, as in the case of cubic fourfolds, one says that X has an associated K3 surface. The first values of d that satisfy the condition for the existence of an associated K3 surface are: 2, 4, 10, 20, 26, 34. We refer to [3, Section 6.2] for precise definitions and results.
In Examples 2.1 and 2.2 below, we recall the known examples of rational GM fourfolds, which all have discriminant 10. In Sect. 3, we shall construct rational GM fourfolds of discriminant 20.
Example 2.1
A \(\tau \)-quadric surface in \({\mathbb {G}}(1,4)\) is a linear section of \({\mathbb {G}}(1,3)\subset {\mathbb {G}}(1,4)\); its class is \(\sigma _{1}^2\cdot \sigma _{1,1} = \sigma _{3,1}+ \sigma _{2,2}\). In [3, Proposition 7.4], it was proved that the closure \(D_{10}'\subset {\mathcal {M}}_4^{GM}\) of the family of fourfolds containing a \(\tau \)-quadric surface is the irreducible hypersurface \(\mathfrak {p}^{-1}({\mathcal {D}}_{10}')\), and that the general member of \(D_{10}'\) is rational. Furthermore, they are all rational by [17] or [4, Theorem 4.15].
In [24, Theorem 5.3], a different description of \(D_{10}'\) and another proof of the rationality of its general member were given.
The rationality for a general fourfold \( [X] \in D_{10}' \) also follows from the fact that a \( \tau \)-quadric surface S, inside the unique del Pezzo fivefold \( Y \subset {\mathbb {P}}^8 \) containing X, admits a congruence of 1-secant lines, that is, through the general point of Y, there passes just one line contained in Y which intersects S.
Example 2.2
A quintic del Pezzo surface is a two-dimensional linear section of \({\mathbb {G}}(1,4)\); its class is \(\sigma _{1}^4 = 3\sigma _{3,1} + 2 \sigma _{2,2}\). In [3, Proposition 7.7], it was proved that the closure \(D_{10}''\subset {\mathcal {M}}_4^{GM}\) of the family of fourfolds containing a quintic del Pezzo surface is the irreducible hypersurface \(\mathfrak {p}^{-1}({\mathcal {D}}_{10}'')\).
The proof of the rationality of a general fourfold \([X]\in D_{10}''\) is very classical. Indeed in [22], Roth remarked that the projection from the linear span of a quintic del Pezzo surface contained in X induces a dominant map
whose generic fibre is a quintic del Pezzo surface. By a result of Enriques (see [7, 25]), a quintic del Pezzo surface defined over an infinite field K is K-rational. Thus, the fibration \( \pi \) admits a rational section and X is rational.
3 A Hodge-special family of Gushel-Mukai fourfolds
Let \(S\subset {\mathbb {P}}^8\) be the image of \({\mathbb {P}}^2\) via the linear system of quartic curves through three simple points and one double point in general position. Then S is a smooth surface of degree 9 and sectional genus 2 cut out in \({\mathbb {P}}^8\) by 19 quadrics.
Lemma 3.1
Let \(S\subset {\mathbb {P}}^8\) be a rational surface of degree 9 and sectional genus 2 as above. Then S can be embedded in a smooth del Pezzo fivefold \(Y={\mathbb {G}}(1,4)\cap {\mathbb {P}}^8\) such that in the Chow ring of \({\mathbb {G}}(1,4)\), we have
Moreover, there exists an irreducible component of the Hilbert scheme parameterizing such surfaces in Y which is generically smooth of dimension 25.
Proof
Using Macaulay2 [10] (see Sect. 4), we constructed a specific example of a surface \(S\subset {\mathbb {P}}^8\) as above which is embedded in a del Pezzo fivefold \(Y\subset {\mathbb {P}}^8\) and satisfies (3.1). Moreover we verified in our example that \(h^0(N_{S,Y})=25\) and \(h^1(N_{S,Y})=0\). Thus, [S] is a smooth point in the corresponding Hilbert scheme \({\mathrm {Hilb}}_Y^{\chi ({\mathcal {O}}_S(t))}\) of subschemes of Y, and the unique irreducible component of \({\mathrm {Hilb}}_Y^{\chi ({\mathcal {O}}_S(t))}\) containing [S] has dimension 25. \(\square \)
Remark 3.2
After our construction, in a preliminary version of this paper, of an explicit example of a surface as in Lemma 3.1, [24, Section 4] provided an explicit geometric description of an irreducible 25-dimensional family of these surfaces inside a del Pezzo fivefold, confirming the claim of Lemma 3.1.
Theorem 3.3
Inside \({\mathcal {M}}_4^{GM}\), the closure \(D_{20}\) of the family of GM fourfolds containing a surface \(S\subset {\mathbb {P}}^8\) as in Lemma 3.1 is the irreducible hypersurface \({\mathfrak p}^{-1}({\mathcal {D}}_{20})\).
Proof
Let \(Y={\mathbb {G}}(1,4)\cap {\mathbb {P}}^8\) be a fixed smooth del Pezzo fivefold and let \({\mathcal {S}}\) be the 25-dimensional irreducible family of rational surfaces \(S\subset Y\) of degree 9 and sectional genus 2 described in Lemma 3.1. Let \({\mathcal {GM}}_{Y} = \mathbb {P}(H^0({\mathcal {O}}_{Y}(2)))\) denote the family of GM fourfolds contained in Y, that is, the family of quadratic sections of Y. The dimension of \({\mathcal {GM}}_{Y}\) is \( h^0({\mathcal {O}}_{{\mathbb {P}}^8}(2)) - h^0({\mathcal {I}}_{Y,{\mathbb {P}}^8}(2)) - 1 = 39\).
Consider the incidence correspondence
and let

be the two natural projections. Then \(p_1\) is a surjective morphism and, for \([S]\in {\mathcal {S}}\) general, the fibre \(p_1^{-1}(S) \simeq {\mathbb {P}}(H^{0}({\mathcal {I}}_{S,Y}(2)))\) is irreducible of dimension \(h^0({\mathcal {I}}_{S,{\mathbb {P}}^8}(2)) - h^0({\mathcal {I}}_{Y,{\mathbb {P}}^8}(2)) - 1 = 13\). It follows that I has a unique irreducible component \(I^0\) that dominates \({\mathcal {S}}\) and that component has dimension \(25 + 13 = 38\).
Using Macaulay2 (see [15]), we verified in a specific example of a GM fourfold X containing a surface \([S]\in {\mathcal {S}}\) that \(H^0(N_{S,X}) = 0\). By semicontinuity, we deduce that \(p_2\) is a generically finite morphism onto its image and that \(p_2(I^0)\) has dimension 38. It is therefore a hypersurface in \({\mathcal {GM}}_Y\). Since all smooth hyperplane sections of the Grassmannian \({\mathbb {G}}(1,4)\subset {\mathbb {P}}^9\) are projectively equivalent, \({\mathcal {GM}}_Y\) dominates \({\mathcal {M}}_4^{GM}\) and the fourfolds X that we have constructed form an irreducible hypersurface in \({\mathcal {M}}_4^{GM}\).
Finally, by applying (2.2) and (2.3), we get that a general such [X] lies in \(\mathfrak {p}^{-1}({\mathcal {D}}_{20})\).
This proves the theorem. \(\square \)
Theorem 3.4
Every GM fourfold belonging to the family \(D_{20}\) described in Theorem 3.3 is rational.
Proof
Let \(Y\subset {\mathbb {P}}^8\) be a del Pezzo fivefold and let \(S\subset Y\) be a general rational surface of degree 9 and sectional genus 2 belonging to the 25-dimensional family described in Lemma 3.1 and Remark 3.2.
The restriction to Y of the linear system of cubic hypersurfaces with double points along S gives a dominant rational map
whose general fibre is an irreducible conic curve which intersects S at three points. Thus S admits inside Y a congruence of 3-secant conic curves. This implies that the restriction of \(\psi \) to a general GM fourfold X containing S and contained in Y is a birational map to \({\mathbb {P}}^4\).
The existence of the congruence of 3-secant conics can be also verified as follows. The linear system of quadrics through S induces a birational map
onto a fivefold Z of degree 33 and cut out by 21 quadrics. Let \(p\in Y\) be a general point. Then one sees that through \(\phi (p)\) there pass 7 lines contained in Z. Of these, 6 are the images of the lines passing through p and which intersect S, while the remaining line come from a single 3-secant conic to S passing through p.
The claim about the rationality of every \([X]\in D_{20}\) follows from the rationality of a general \([X]\in D_{20}\) and from the main result in [17] or from [4, Theorem 4.15]. \(\square \)
Remark 3.5
The inverse map of the birational map \(\psi :X\dashrightarrow {\mathbb {P}}^4\) described in the proof of Theorem 3.4 is defined by the linear system of hypersurfaces of degree 9 having double points along an internal projection to \({\mathbb {P}}^4\) of a smooth surface \(T\subset {\mathbb {P}}^5\) of degree 11 and sectional genus 6 cut out by 9 cubics. This surface T is an internal triple projection of a smooth minimal K3 surface of degree 20 and genus 11 in \({\mathbb {P}}^{11}\).
Actually, this was the starting point for this work. In fact, from the results of [24], we suspected that a triple internal projection of a minimal K3 surface of degree 20 and genus 11 could be related to a GM fourfold of discriminant 20.
4 Explicit computations
In the proof of Lemma 3.1, we claimed that there exists an example of a rational surface \(S\subset {\mathbb {P}}^8\) of degree 9 and sectional genus 2 which is also embedded in \({\mathbb {G}}(1,4)\) and satisfies \([S]=6\,\sigma _{3,1} + 3\, \sigma _{2,2}\). In an ancillary file (see [15]), we provide the explicit homogeneous ideal of such a surface which contains the ideal generated by the Plücker relations of \({\mathbb {G}}(1,4)\). The class [S] in terms of the Schubert cycles \(\sigma _{3,1}\) and \(\sigma _{2,2}\) can be easily calculated using, for instance, the Macaulay2 package SpecialFanoFourfolds.
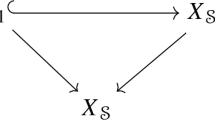
In the following, we explain the main steps of the procedure we followed to construct the surface in \({\mathbb {G}}(1,4)\). We start by taking a general nodal hyperplane section of a smooth Fano threefold of degree 22 and sectional genus 12 in \(\mathbb {P}^{13}\) (see [20, 26]). The projection of this surface from its node yields a smooth K3 surface \(T\subset {\mathbb {P}}^{11}\) of degree 20 and sectional genus 11 which contains a conic (see [16]). Then we take a general triple projection of T in \({\mathbb {P}}^5\), which is a smooth surface of degree 11 and sectional genus 8 (this follows from [27, Proposition 4.1] and [9, Theorem 10] in the case when the K3 surface T is general). Let \(T'\subset {\mathbb {P}}^4\) be a general internal projection of this surface in \({\mathbb {P}}^5\). Then \(T'\) is a singular surface of degree 10 and sectional genus 8, cut out by 13 quintics. The linear system of hypersurfaces of degree 9 having double points along \(T'\) gives a birational map \( \eta : {\mathbb {P}}^4\dashrightarrow X\subset {\mathbb {P}}^8 \) onto a GM fourfold X, whose inverse map is defined by the restriction to X of the linear system of cubic hypersurfaces having double points along a smooth surface \(S\subset X\) of degree 9 and sectional genus 2. Finally, to determine explicitly the surface S, one can exploit the fact that the general quintic hypersurface corresponds via \(\eta \) to the general quadric hypersurface (inside X) containing S. Indeed, behind the scenes, we have an occurrence of a flop, similar to the Trisecant Flop considered in [24]. In particular, we have a commutative diagram

where \(m_1\) and \(m_2\) are the birational maps defined, respectively, by the linear system of quintics through \(T'\) and by the linear system of quadrics through S. Moreover, M is a fourfold of degree 33 in \({\mathbb {P}}^{12}\) cut out by 21 quadrics.
Change history
21 June 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00209-021-02777-9
References
Addington, N., Thomas, R.: Hodge theory and derived categories of cubic fourfolds. Duke Math. J. 163(10), 1886–1927 (2014)
Bolognesi, M., Russo, F., Staglianò, G.: Some loci of rational cubic fourfolds. Math. Ann. 373(1), 165–190 (2019)
Debarre, O., Iliev, A., Manivel, L.: Special prime Fano fourfolds of degree \(10\) and index \(2\), recent advances in algebraic geometry: a volume in honor of Rob Lazarsfeld’s 60th birthday. In: Hacon, C., Mustaţă, M., Popa, M. (eds.) Math. Soc. Lecture Note Ser., pp. 123–155. Cambridge Univ. Press, London (2015)
Debarre, O., Kuznetsov, A.: Gushel-Mukai varieties: classification and birationalities. Algebr. Geom. 5, 15–76 (2018)
Debarre, O., Kuznetsov, A.: Gushel–Mukai varieties: moduli, to appear in Internet. J. Math. (2018)
Debarre, O., Kuznetsov, A.: Gushel-Mukai varieties: linear spaces and periods. Kyoto J. Math. 59(4), 897–953 (2019)
Enriques, F.: Sulla irrazionalità da cui può farsi dipendere la resoluzione di un’equazione algebrica \(f(x, y, z)=0\) con funzioni razionali di due parametri. Math. Ann. 49, 1–23 (1897)
Fano, G.: Sulle forme cubiche dello spazio a cinque dimensioni contenenti rigate razionali del \(4^\circ \) ordine. Comment. Math. Helv. 15(1), 71–80 (1943)
Fontanari, C., Sernesi, E.: Non-surjective Gaussian maps for singular curves on K3 surfaces. Collect. Math. 70(1), 107–115 (2019)
Grayson, D.R., Stillman, M.E.: Macaulay2—a software system for research in algebraic geometry (version 1.14). (2019). http://www.math.uiuc.edu/Macaulay2/
Gushel, N.P.: Fano varieties of genus \(6\). Izv. Akad. Nauk USSR Ser. Mat. 46(6), 1159–1174 (1982). (in Russian) (English transl.: (1983) Math. USSR-Izv. 21(3):445–459)
Hassett, B.: Some rational cubic fourfolds. J. Algebr. Geom. 8(1), 103–114 (1999)
Hassett, B.: Special cubic fourfolds. Comp. Math. 120(1), 1–23 (2000)
Hassett, B.: Cubic fourfolds, K3 surfaces, and rationality questions. In: Pardini, R., Pirola, G.P. (eds.) Rationality Problems in Algebraic Geometry, pp. 29–66. Springer International Publishing, Cham, Levico Terme (2016)
Hoff, M., Staglianò, G.: Ancillary macaulay2 files. (2019). https://www.math.uni-sb.de/ag/schreyer/index.php/people/researchers/74-michael-hahn
Kapustka, M.: Projections of Mukai varieties. Math. Scand. 123(2), 191–219 (2018)
Kontsevich, M., Tschinkel, Y.: Specialization of birational types. Invent. Math. 217(2), 415–432 (2019)
Kuznetsov, A.: Derived categories of cubic fourfolds, cohomological and geometric approaches to rationality problems. Prog. Math. 282, 219–243 (2010)
Kuznetsov, A.: Derived categories view on rationality problems. In: Pardini, R., Pirola, G.P. (eds.) Rationality Problems in Algebraic Geometry, pp. 67–104. Springer International Publishing, Cham, Levico Terme (2016)
Mukai, S., Umemura, H.: Minimal rational threefolds. In: Raynaud, M., Shioda, T. (eds.) Algebraic geometry. Lecture notes in mathematics, vol. 1016, pp. 490–518. Springer, Berlin, Heidelberg (1983)
Mukai, S.: Biregular classification of Fano 3-folds and Fano manifolds of coindex 3. Proc. Natl. Acad. Sci. USA 86(9), 3000–3002 (1989)
Roth, L.: Algebraic varieties with canonical curve sections. Ann. Mat. Pura Appl. 29(1), 91–97 (1949)
Russo, F., Staglianò, G.: Congruences of \(5\)-secant conics and the rationality of some admissible cubic fourfolds. Duke Math. J. 168(5), 849–865 (2019)
Russo, F., Staglianò, G.: Trisecant Flops, their associated K3 surfaces and the rationality of some Fano fourfolds. (2019)
Shepherd-Barron, N.I.: The rationality of quintic del Pezzo surfaces—a short proof. Bull. Lond. Math. Soc. 24(3), 249–250 (1992)
Schreyer, F.-O.: Geometry and algebra of prime Fano 3-folds of genus 12. Compos. Math. 127(3), 297–319 (2001)
Voisin, C.: Segre classes of tautological bundles on Hilbert schemes of surfaces. Algebr. Geom. 6(2), 186–195 (2019)
Acknowledgements
This work started during the Macaulay2 workshop held at the Saarland University in September 2019. We would like to thank the organizers for bringing us together as well as Hoang Le Truong. We also wish to thank Francesco Russo and Olivier Debarre for very relevant suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hoff, M., Staglianò, G. New examples of rational Gushel-Mukai fourfolds. Math. Z. 296, 1585–1591 (2020). https://doi.org/10.1007/s00209-020-02498-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-020-02498-5