Almost simple geodesics on the triply-punctured sphere

Abstract

In this paper we study closed hyperbolic geodesics $\gamma$ on the triply-punctured sphere $M = {\widehat{{\mathbb C}}}- \{0,1,\infty \}$ that are almost simple, in the sense that the difference $\delta = I(\gamma )-L(\gamma )$ between the self-intersection number of $\gamma$ and its combinatorial (word) length is fixed. We show that for each fixed $\delta$, the number of almost simple geodesics with $L(\gamma )=L$ is given by a quadratic polynomial $p_\delta (L)$, provided $L \ge \delta + 4$.

Appendix A: Counting self-intersections

Fig. 7

Generators a, b, c for $\pi _1(M)$, and the corresponding Cayley graph H

In this section we give a combinatorial formula for the self-intersection number I(w). This formula was used to produce the data in Table 1. We also obtain the following useful quadratic lower bound on the intersection number:

Theorem A.1

Let $w \in G$ be a cyclically reduced word in the generators a, b, c and their inverses. Suppose that $L(w) \ge 2$ and no two consecutive letters of w are the same. Then we have $I(w) \ge L(w)^2/6$.

Group theory Let $G = \pi _1(M,p)$, where $M = {\widehat{{\mathbb C}}}- \{0,1,\infty \}$ and p is a point in the upper halfplane. In this section we will use the presentation

$$\begin{aligned} G = \langle a,b,c : \,abc={\text {id}} \rangle \end{aligned}$$

(A.1)

for $\pi _1(M,p)$. It is related to the description of G in Sect. 2 by the change of variables

$$\begin{aligned} a = xy,\quad b = yz \;\;\;\text {and}\;\;\;c = zx. \end{aligned}$$

(A.2)

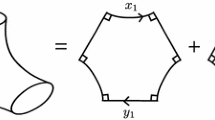
The presentation (A.1) corresponds to the generating loops for $\pi _1(M,p)$ shown at the left in Fig. 7. A portion of the Cayley graph H of G is show at the right. There is a natural realization of H as a graph in the plane, consistent with the ribbon graph structure on H / G inherited from M. The graph H is a proxy for the universal cover ${\mathbb H}$ of M. It carries a canonical metric where each edge has length one.

Intersection numbers Any two points in H lie on a unique complete geodesic $\delta \subset H$. The intersection number $i(\alpha ,\beta )$ of a pair of geodesics in H is defined to be 1 if $\alpha$ and $\beta$cross in the plane; equivalently, if their endpoints are linked at infinity. Otherwise $i(\alpha ,\beta ) = 0$. Note that geodesics cannot meet without crossing; in particular, we have $i(\alpha ,\alpha )=0$.

Reduced words Every $w \in G$ has a unique expression as a reduced word in the generators a, b, c and their inverses ${\overline{a}}, {\overline{b}}, {\overline{c}}$. A reduced word has minimal length among all products representing the same element of G. Concretely, this means that pairs of consecutive letters like ab, bc and ca must be avoided, since they can be replaced by ${\overline{c}}, {\overline{a}}$ and ${\overline{b}}$ respectively.

We let L(w) denote the length of w as a reduced word in a, b, c. This notion of length is consistent with the definition $L(w) = \ell (w)/2$ given in Sect. 2, as can be seen using Eq. (A.2).

Stabilizers of geodesics We say $w \in G$ is cyclically reduced if it minimizes L(w) among all elements in its conjugacy class. Concretely, this means that patterns like ab are also avoided when we regard the first and last letters of w as consecutive.

Aside from the identity, every element $w \in G$ stabilizes a unique geodesic $\delta _w \subset H$. This geodesic passes through the identity element $e \in H$ if and only if w is cyclically reduced. If w is primitive, then it generates the stabilizer of $\delta _w$. Similarly, w stabilizes a unique geodesic $\widetilde{\gamma }_w$ in the universal cover ${\mathbb H}$ of M provided $L(w) \ge 2$.

Self-intersection numbers Now let us fix a primitive, cyclically reduced word

$$\begin{aligned} w = g_1 g_2 \cdots g_n \in G \end{aligned}$$

with $n = L(w) \ge 2$. Its cyclically reduced conjugates are given by

$$\begin{aligned} w_i = g_i g_{i+1} \cdots g_n g_1 \cdots g_{i-1}, \end{aligned}$$

$i=1,2,\ldots ,n$. Let $\delta _i$ denote the geodesic through the origin $e \in H$ stabilized by $w_i$, and let

$$\begin{aligned} \deg _e(\delta _i \cup \delta _j) = |\{g_i,{\overline{g}}_{i-1},g_j,{\overline{g}}_{j-1}\}| \end{aligned}$$

(A.3)

denote the number of edges of $\delta _i \cup \delta _j$ incident to the vertex $e \in H$.

Algorithms to compute $I(w) = I(\gamma _w)$ in various situations are well-known; see e.g. [5, 7]. For the case at hand, we will show:

Theorem A.2

For any primitive,  cyclically reduced word $w \in G,$ we have

$$\begin{aligned} I(w) = \frac{1}{4} \sum _{1 \le i,j \le n} i(\delta _i,\delta _j) (\deg _e(\delta _i,\delta _j) - 2). \end{aligned}$$

(A.4)

Proof

We take as our point of departure the following expression for the self-intersection number as a sum over double cosets:

$$\begin{aligned} I(w) = \frac{1}{2} \sum _{[g] \in \langle w \rangle \backslash G / \langle w \rangle } i(g \cdot \delta _w,\delta _w). \end{aligned}$$

(A.5)

This formula is easily justified using hyperbolic geometry, by observing that $g \cdot \widetilde{\gamma }_w$ intersects $\widetilde{\gamma }_w$ in ${\mathbb H}$ iff $i(g \cdot \delta _w,\delta _w) = 1$. Each nonzero term in the sum corresponds to a multiple point $p \in \gamma$ together with an ordered pair of branches of $\gamma$ through p, and contributes 1 / 2 to the total intersection number $I(\gamma _w) = I(w)$.

To connect formulas (A.5) and (A.4), suppose that $i(g \cdot \delta _w,\delta _w) = 1$. Then

$$\begin{aligned} (g\cdot \delta _w) \cap \delta _w \end{aligned}$$

is a compact geodesic interval in H with endpoints $h_1, h_2 \in G$. Translating by $h_1^{-1}$, we obtain a pair of geodesics passing through e, each stabilized by a conjugate of w; hence

$$\begin{aligned} (h_1^{-1} g \cdot \delta _w, h_1^{-1} \cdot \delta _w) = (\delta _i,\delta _j) \end{aligned}$$

for some $1\le i,j \le n$. The intersection number is preserved by translation, so $i(\delta _i,\delta _j) = 1$.

If $h_1 = h_2$ then $\delta _i$ and $\delta _j$ cross transversally at e; hence $\deg _e(\delta _i \cap \delta _j) = 4$ and we obtain a contribution of 1 / 2 to the sum in formula (A.4). If $h_1 \ne h_2$ then the degree is 3, and we obtain two terms, one from $h_1$ and one from $h_2$, each contributing 1 / 4 to the same sum. All the nonzero terms in Eq. (A.4) arise in this way, and hence the two sums are equal. $\square$

Algorithmic considerations The term $i(\delta _i,\delta _j)$ appearing in formula (A.4) can be readily computed by comparing the cyclic orderings of the edges of $\delta _i$ and $\delta _j$ at the endpoints of the segment $\delta _i \cap \delta _j$. The degree is computed by Eq. (A.3).

Fig. 8

Chords represent geodesics passing through the origin $e \in H$

Proof of Theorem A.1

Let $\mathcal{A}= \{a,b,c,{\overline{a}},{\overline{b}},{\overline{c}}\} \subset G$ be the alphabet consisting of the generators of G and their inverses. We can also regard $\mathcal{A}$ as the cyclically ordered set of vertices of H adjacent to e. Let P be a hexagon whose sides are labeled by the elements of $\mathcal{A}$ in the same cyclic order; see Fig. 8. A chord [u, v] is an unordered pair of distinct elements $u,v \in \mathcal{A}$ labeling non-adjacent sides of P. For example, the chords incident to side a are given by [a, b], $[a,{\overline{b}}]$ and [a, c].

The set of all chords K consists of 9 elements. We will also regard the set K as a basis for the vector space ${\mathbb R}^K$. Define a symmetric bilinear form on ${\mathbb R}^K$ by $Q(k,k') = 1$ if the chords k and $k'$ cross in P, and $Q(k,k') = 0$ otherwise. (By definition, two chords incident to the same side of P do not cross.) It is easily checked that Q is an indefinite form of signature (6, 3), by diagonalizing the given matrix.

Let $S = \{a,b,c\}$, and let

$$\begin{aligned} \partial : {\mathbb R}^K \rightarrow {\mathbb R}^S \end{aligned}$$

be the linear boundary map that counts $+1$ when a generator occurs as an endpoint of a chord, and $-1$ when its inverse occurs. (For example, $\partial ([a,b]) = a+b$, while $\partial ([a,{\overline{b}}]) = a-b$.) Let

$$\begin{aligned} \lambda : {\mathbb R}^K \rightarrow {\mathbb R}\end{aligned}$$

be the length function defined by summing the coordinates; that is, by setting $\lambda (k)=1$ for each chord k. One can now readily verify that $Q|{\text {Ker}}(\partial )$ is positive-definite, and that for any vector $v \in {\text {Ker}}(\partial )$, we have

$$\begin{aligned} Q(v,v) \ge \lambda (v)^2/3. \end{aligned}$$

(A.6)

(The minimum is achieved on vectors that give weight zero to all chords that join opposite sides, and equal weights to the rest.)

Now let $w = g_1 \cdots g_n \in G$ be a primitive, cyclically reduced word such that no pair of adjacent letters $(g_{i-1},g_i)$ are equal. (Here $g_n$ is adjacent to $g_1$.) This condition, plus the fact that w is reduced, insures that the sides of P labeled by ${\overline{g}}_{i-1}$ and $g_i$ are not adjacent. Thus we may associate to w the sequence of chords

$$\begin{aligned} k_i = [{\overline{g}}_{i-1},g_i], \end{aligned}$$

$i=1,\ldots ,n$.

Let $v = \sum _1^n k_i \in {\mathbb R}^K$. Then clearly ${\overline{\partial }}(v) = 0$ and $\lambda (v) = L(w) = n$. Using formula (A.4), it is also easy to see that

$$\begin{aligned} I(w) \ge \frac{1}{2} \sum _{1 \le i,j \le n} Q(k_i,k_j) = \frac{1}{2} Q(v,v). \end{aligned}$$

Indeed, when $Q(k_i,k_j) = 1$ the geodesics $\delta _i$ and $\delta _j$ cross transversally, with degree 4, at the identity element $e \in H$, and hence we obtain a contribution of 1 / 2 to the sum in formula (A.4). Referring to inequality (A.6), we obtain the desired inequality

$$\begin{aligned} I(w) \ge \lambda (v)^2/6 = L(w)^2 / 6. \end{aligned}$$

$\square$