The Cauchy problem for $\fancyscript{D}$-modules on Ran spaces

Abstract

We will adopt an elementary approach to $\fancyscript{D}$-modules on Ran spaces in terms of two-limits; the aim here is to define the category of coherent $\fancyscript{D}$-modules, characteristic varieties and non-characteristic maps. An application will be the proof of the Cauchy–Kowaleski–Kashiwara theorem in this setting.

Appendix

There are two other natural categories, $\mathrm{{\mathfrak {S}} }^+(\mathcal{{I}})$ and $\mathrm{{\mathfrak {S}} }^-(\mathcal{{I}})$.

Definition 6.13

• (a) An object $F$ of $\mathrm{{\mathfrak {S}} }^+(\mathcal{{I}})$ (resp. $\mathrm{{\mathfrak {S}} }^-(\mathcal{{I}})$) is a family $\{(F_i, \phi _s)\}_{i,s}$ ($i\in \mathcal{{I}}$, $s\in \mathrm{Mor }(\mathcal{{I}})$) where

  • (i) for any $i\in \mathcal{{I}}$, $F_i$ is an object of $\mathrm{{\mathfrak {S}} }(i)$,

  • (i) for any morphism $s:i_1\xrightarrow []{}i_2$ in $\mathcal{{I}}$, $\phi _s :F_{i_1} \xrightarrow []{}\rho _s (F_{i_2})$ (resp. $\phi _s :\rho _s (F_{i_2}) \xrightarrow []{}F_{i_1}$) is a morphism such that

    • for all $i \in \mathcal{{I}}$, $\phi _{{{\mathrm{id}}}_i} = {{\mathrm{id}}}_{F_i}$,

    • for any sequence $i_1\xrightarrow []{s}i_2\xrightarrow []{t}i_3$ of morphisms in $\mathcal{{I}}$, the following diagram commutes

      

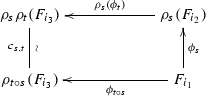      (6.3)

      (resp. the following diagram commutes

      

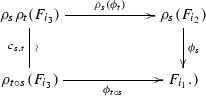      (6.4)

• (b) A morphism $f:\{(F_i,\phi _s)\}_{i,s}\xrightarrow []{}\{(F'_i,\phi '_s)\}_{i,s}$ in $\mathrm{{\mathfrak {S}} }^+(\mathcal{{I}})$ (resp. $\mathrm{{\mathfrak {S}} }^-(\mathcal{{I}})$) is a family of morphisms $f_i:F_i\xrightarrow []{}F'_i$ such that for any $s:i_1\xrightarrow []{}i_2$, the diagram below commutes:

  

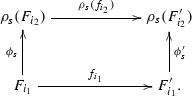  (6.5)

  (resp. the diagram below commutes:

  

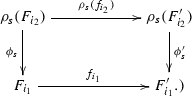  (6.6)

We consider $\mathrm{{\mathfrak {S}} }(\mathcal{{I}})$ as the full subcategory of $\mathrm{{\mathfrak {S}} }^+(\mathcal{{I}})$ or $\mathrm{{\mathfrak {S}} }^-(\mathcal{{I}})$ consisting of objects $\{(F_i, \phi _s)\}_{i\in \mathcal{{I}},s\in \mathrm{Mor }(\mathcal{{I}})}$ such that for all $s\in \mathrm{Mor }(\mathcal{{I}})$, the morphisms $\phi _s$ are isomorphisms and we denote by $\iota ^+_\mathcal{{I}}:\mathrm{{\mathfrak {S}} }(\mathcal{{I}}) \xrightarrow []{}\mathrm{{\mathfrak {S}} }^+(\mathcal{{I}})$ and $\iota ^-_\mathcal{{I}}:\mathrm{{\mathfrak {S}} }(\mathcal{{I}}) \xrightarrow []{}\mathrm{{\mathfrak {S}} }^-(\mathcal{{I}})$ the natural faithful functors.