A complete family of Alexandrov–Fenchel inequalities for convex capillary hypersurfaces in the half-space

Abstract

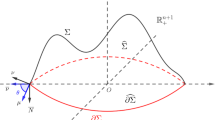
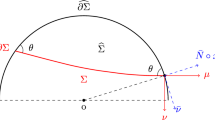
In this paper, we study the locally constrained inverse curvature flow for hypersurfaces in the half-space with $\theta$-capillary boundary, which was recently introduced by Wang et al. (Math Ann 388:2121–2154, 2024). Assume that the initial hypersurface is strictly convex with the contact angle $\theta \in (0,\pi /2].$ We prove that the solution of the flow remains to be strictly convex for $t>0,$ exists for all positive time and converges smoothly to a spherical cap. As an application, we prove a complete family of Alexandrov–Fenchel inequalities for convex capillary hypersurfaces in the half-space with the contact angle $\theta \in (0,\pi /2].$ Along the proof, we develop a new tensor maximum principle for parabolic equations on compact manifold with proper Neumann boundary condition.

Appendix A: Approximation result

In this appendix, we prove that a convex hypersurface $\Sigma$ with $\theta$-capillary boundary in the half-space can be approximated by a sequence of strictly convex hypersurfaces with $\theta$-capillary boundary in the half-space in the $C^{2,\alpha }$ sense. Note that the free boundary case (i.e. $\theta =\frac{\pi }{2}$) in the unit ball was treated by Lambert and Scheuer in [21]. We adapt their idea and include a proof for the case of capillary hypersurfaces in the half-space.

Let $\Sigma \subset \overline{{{\mathbb {R}}}}_{+}^{n+1}$ be a convex hypersurface with capillary boundary supported on $\partial \overline{{\mathbb {R}}}_{+}^{n+1}$ at a contact angle $\theta \in (0,\frac{\pi }{2}],$ which is given by the embedding $x_0:M \rightarrow \overline{{{\mathbb {R}}}}_{+}^{n+1}$ of a compact manifold M with non-empty boundary. We consider the mean curvature flow

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t x=-H\nu +V, &{}\quad \text {in}\ M \times [0,T),\\ \langle \bar{N}\circ x,\nu \rangle =\cos (\pi -\theta ), &{}\quad \text {on}\ \partial M \times [0,T),\\ x(\cdot ,0)=x_0(\cdot ) &{}\quad \text {on} \ M, \end{array}\right. \end{aligned}$$

(A.1)

and denote $\Sigma _t=x(M,t),$ where V is tangential component of $\partial _t x$ and satisfies $V\vert _{\partial \Sigma _t}=-H\cot \theta \mu .$

The short time existence of flow (A.1) can be obtained by a similar argument as in [30] by Stahl.

Theorem A.1

For any $\alpha \in (0,1),$ the flow (A.1) admits a unique solution : 

$$\begin{aligned} x(\cdot ,t)\in C^{\infty }(M\times (0,\delta ])\cap C^{2+\alpha ,1+\frac{\alpha }{2}}(M\times [0,\delta ]), \end{aligned}$$

where $\delta >0$ is a small constant.

Then we can prove the following approximation result:

Theorem A.2

Suppose that $\Sigma _t,$ $t\in [0,\delta )$ is a solution to the flow (A.1) starting from the convex hypersurface $\Sigma .$ Then $\Sigma _t$ is strictly convex for all time $t>0$ as long as the flow exists.

Proof

Note that the height function $\langle x,e_{n+1}\rangle$ attains its global maximum in the interior point of $\Sigma ,$ we can find a strictly convex point in the interior by attaching a large sphere to $\Sigma$ from above.

Let

$$\begin{aligned} \chi (x,t)=\min _{|\xi |=1}{h_{ij}\xi ^i\xi ^j}. \end{aligned}$$

Since $h_{ij}$ is smooth, the function $\chi (x,t)$ is Lipschitz continuous in space and by a cut-off function argument, we find a smooth function $\phi _0:M\rightarrow {\mathbb {R}}$ such that $0\le \phi _0\le \chi (x,0)$ and there exists an interior point y such that $\phi _0(y)>0.$ We extend the function $\phi _0$ to $\phi :M\times [0,\delta ')\rightarrow {\mathbb {R}}$ by solving a linear parabolic PDE:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial }{\partial t}\phi =\Delta \phi +\nabla _V\phi , &{}\quad \text {in}\ M \times [0,\delta '),\\ \nabla _{\mu }\phi =0 &{}\quad \text {on}\ \partial M \times [0,\delta '),\\ \phi (\cdot ,0)={\phi }_0(\cdot ) &{}\quad \text {on} \ M, \end{array}\right. \end{aligned}$$

(A.2)

where $\Delta$ and $\nabla$ are Laplacian operator and Levi-Civita connection with respect to the induced metric on $\Sigma _t=x(M,t)$ of the flow (A.1). The solution $\phi$ of (A.2) exists at least for a short time interval $[0,\delta ').$ By the strong maximum principle for scalar functions (see [30, Corollary 3.2]), we have $\phi >0$ for all $x\in M$ and $t\in (0,\delta ').$

We take $\tau =\frac{1}{2}\min \{\delta ,\delta '\}$ and consider the tensor:

$$\begin{aligned} M_{ij}=h_{ij}-\phi g_{ij} \end{aligned}$$

(A.3)

for the time interval $t\in [0,\tau ).$ By the construction of $\phi _0,$ we see that $M_{ij}\ge 0$ at time $t=0.$ We now apply the tensor maximum principle (i.e. Theorem 1.2) to deduce that $M_{ij}\ge 0$ is preserved along the flow (A.1).

By a direct computation using Proposition 3.1 for ${\mathcal {F}}=-H,$ we have:

$$\begin{aligned} \frac{\partial }{\partial t} M_{ij}=\Delta M_{ij}+\nabla _{V} M_{ij}+N_{ij}, \end{aligned}$$

(A.4)

where

$$\begin{aligned} N_{ij}&=|A|^2 M_{ij}+|A|^2\phi g_{ij}-2HM_i^k M_{kj}\nonumber \\&\quad -2H\phi M_{ij}+M_j^k\nabla _{i}{V_k}+M_i^k\nabla _{j}{V_k}. \end{aligned}$$

We easily see that whenever $M_{ij}\ge 0$ and $M_{ij}\xi ^i=0$ at a point, we have

$$\begin{aligned} N_{ij}\xi ^i\xi ^j=|A|^2\phi \ge 0, \end{aligned}$$

(A.5)

and thus the condition (1.11) is satisfied. The boundary condition (1.12) can be checked similarly as in Theorem 5.2, using Proposition 2.1 and the fact that

$$\begin{aligned} \nabla _{\mu }H=\cot \theta h_{\mu \mu }H \end{aligned}$$

on the boundary $\partial \Sigma _t$ (see (3.11)). Hence Theorem 1.2 implies that $M_{ij}\ge 0$ is preserved along the flow (A.1) for time $t\in [0,\tau ),$ and it follows that $\Sigma _t$ is strictly convex for time interval $(0,\tau ).$

To show the strict convexity for the whole time interval $(0,\delta ),$ we fix a time $t_0\in (0,\tau ).$ Since $\Sigma _t$ is strictly convex at time $t_0,$ then there exists a constant $\varepsilon >0,$ such that $h_{ij}\ge \varepsilon g_{ij}$ holds everywhere on $\Sigma _{t_0}.$ A similar procedure as above can be used to show that $\tilde{M}_{ij}=h_{ij}-\varepsilon g_{ij}\ge 0$ is preserved along the flow (A.1) for all time $t>t_0$ as long as the flow (A.1) exists, which finishes the proof. $\square$