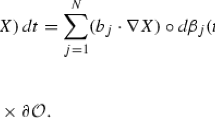Abstract
Consider stochastic partial differential equations (SPDEs) with fully local monotone coefficients in a Gelfand triple \(V\subseteq H \subseteq V^*\):
where
are measurable maps, \(L_2(U,H)\) is the space of Hilbert–Schmidt operators from U to H and W is a U-cylindrical Wiener process. Such SPDEs include many interesting models in applied fields like fluid dynamics etc. In this paper, we establish the well-posedness of the above SPDEs under fully local monotonicity condition solving a longstanding open problem. The conditions on the diffusion coefficient \(B(t,\cdot )\) are allowed to depend on both the H-norm and V-norm. In the case of classical SPDEs, this means that \(B(\cdot ,\cdot )\) could also depend on the gradient of the solution. The well-posedness is obtained through a combination of pseudo-monotonicity techniques and compactness arguments.
Similar content being viewed by others
Data availability
Not applicable.
References
Aldous, D.: Stopping times and tightness. Ann. Prob. 6(2), 335–340 (1978)
Antonopoulou, D.C., Karali, G., Millet, A.: Existence and regularity of solution for a stochastic Cahn–Hilliard/Allen–Cahn equation with unbounded noise diffusion. J. Differ. Equ. 260(3), 2383–2417 (2016)
Barbu, V., Da Prato, G., Röckner, M.: Stochastic Porous Media Equations. Lecture Notes in Mathematics., vol. 2163. Springer, Berlin (2016)
Billingsley, P.: Convergence of Probability Measures. Wiley, New York (1999)
Brézis, H.: Équations et inéquations non linéaires dans les espaces vectoriels en dualité. Ann. Inst. Fourier 18(1), 115–175 (1968)
Brzeźniak, Z., Liu, W., Zhu, J.: Strong solutions for SPDE with locally monotone coefficients driven by Lévy noise. Nonlinear Anal. Real World Appl. 17, 283–310 (2014)
Brzeźniak, Z., Hausenblas, E., Razafimandimby, P.A.: Stochastic reaction–diffusion equations driven by jump processes. Potential Anal. 49(1), 131–201 (2018)
Brzeźniak, Z., Hausenblas, E., Razafimandimby, P.A.: Some results on the penalised nematic liquid crystals driven by multiplicative noise: weak solution and maximum principle. Stoch. Partial Differ. Equ. Anal. Comput. 7(3), 417–475 (2019)
Cahn, J.W., Hilliard, J.E.: Free energy for a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28(2), 258–267 (1958)
Cairoli, R., Dalang, R.C.: Sequential Stochastic Optimization. Wiley, New York (1996)
Cardon-Weber, C.: Cahn–Hilliard stochastic equation: existence of the solution and of its density. Bernoulli 7(5), 777–816 (2001)
Es-Sarhir, A., von Renesse, M.-K.: Ergodicity of stochastic curve shortening flow in the plane. SIAM J. Math. Anal. 44(1), 224–244 (2012)
Gnann, M.V., Hoogendijk, J., Veraar, M.C.: Higher order moments for SPDE with monotone nonlinearities (2022). ArXiv:2203.15307v1
Goldys, B., Röckner, M., Zhang, X.: Martingale solutions and Markov selections for stochastic partial differential equations. Stoch. Process. Appl. 119(5), 1725–1764 (2009)
Gyöngy, I.: On stochastic equations with respect to semimartingales III. Stochastics 7(4), 231–254 (1982)
Hirano, N.: Nonlinear evolution equations with nonmonotonic perturbations. Nonlinear Anal. 13(6), 599–609 (1989)
Hofmanová, M., Seidler, J.: On weak solutions of stochastic differential equations II. Stoch. Anal. Appl. 31(4), 663–670 (2013)
Hofmanová, M., Zhang, T.: Quasilinear parabolic stochastic partial differential equations: existence, uniqueness. Stoch. Process. Appl. 127(10), 3354–3371 (2017)
Ikeda, N., Watanabe, S.: Stochastic Differential Equations and Diffusion Processes. North-Holland Publishing Co., Kodansha Ltd, Amsterdam, Tokyo (1989)
Jakubowski, A.: On the Skorokhod topology. Ann. Inst. H. Poincaré Probab. Statist. 22(3), 263–285 (1986)
Kosmala, T., Riedle, M.: Variational solutions of stochastic partial differential equations with cylindrical Lévy noise. Discrete Contin. Dyn. Syst. Ser. B 26(6), 2879–2898 (2021)
Krylov, N.V., Rozovskiĭ, B.L.: Stochastic evolution equations. In: Current problems in mathematics, volume 14 (Russian), pp. 71–147, 256 (1979)
Lin, F., Liu, C.: Nonparabolic dissipative systems modeling the flow of liquid crystals. Comm. Pure Appl. Math. 48(5), 501–537 (1995)
Lions, J.-L.: Quelques méthodes de résolution des problèmes aux limites non linéaires. Dunod, Paris (1969)
Liu, W.: Existence and uniqueness of solutions to nonlinear evolution equations with locally monotone operators. Nonlinear Anal. 75(18), 7543–7561 (2011)
Liu, W.: Well-posedness of stochastic partial differential equations with Lyapunov condition. J. Differ. Equ. 255(3), 572–592 (2013)
Liu, W., Röckner, M.: SPDE in Hilbert space with locally monotone coefficients. J. Funct. Anal. 259(11), 2902–2922 (2010)
Liu, W., Röckner, M.: Local and global well-posedness of SPDE with generalized coercivity conditions. J. Differ. Equ. 254(2), 725–755 (2013)
Liu, W., Röckner, M.: Stochastic Partial Differential Equations: An Introduction. Universitext, Springer, Berlin (2015)
Liu, C., Shen, J.: A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Phys. D 179(3–4), 211–228 (2003)
Medjo, T.T.: On the existence and uniqueness of solution to a stochastic 2D Allen–Cahn–Navier–Stokes model. Stoch. Dyn. 19(1), 1950007 (2019)
Minty, G.J.: Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 29, 341–346 (1962)
Neelima, ŠD.: Coercivity condition for higher moment a priori estimates for nonlinear SPDEs and existence of a solution under local monotonicity. Stochastics 92(5), 684–715 (2020)
Nguyen, P., Tawri, K., Temam, R.: Nonlinear stochastic parabolic partial differential equations with a monotone operator of the Ladyzenskaya–Smagorinsky type, driven by a Lévy noise. J. Funct. Anal. 281(8), 109157 (2021)
Pardoux, E.: Sur des équations aux dérivées partielles stochastiques monotones. C. R. Acad. Sci. 275, A101–A103 (1972)
Pardoux, E.: Équations aux dérivées partielles stochastiques non linéaires monotones. Ph.D. thesis, Université Paris XI (1975)
Prévôt, C., Röckner, M.: A concise course on stochastic partial differential equations. Lecture Notes in Mathematics, volume 1905, Springer (2007)
Ren, J., Röckner, M., Wang, F.Y.: Stochastic generalized porous media and fast diffusion equations. J. Differ. Equ. 238(1), 118–152 (2007)
Renardy, M., Rogers R.C.: An Introduction to Partial Differential Equations. Texts in Applied Mathematics, volume 13, Springer (2004)
Röckner, M., Wang, F.-Y.: Non-monotone stochastic generalized porous media equations. J. Differ. Equ. 245(12), 3898–3935 (2008)
Röckner, M., Zhang, X.: Stochastic tamed 3D Navier–Stokes equations: existence, uniqueness and ergodicity. Probab. Theory Related Fields 145(1–2), 211–267 (2009)
Shioji, N.: Existence of periodic solutions for nonlinear evolution equations with pseudo monotone operators. Proc. Am. Math. Soc. 125(10), 2921–2929 (1997)
Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Math. Pura Appl. 146(1), 65–96 (1987)
Temam, R.: Navier–Stokes equations: theory and numerical analysis. American Mathematical Society (2001)
Vallet, G., Zimmermann, A.: Well-posedness for a pseudomonotone evolution problem with multiplicative noise. J. Evol. Equ. 19(1), 153–202 (2019)
Vallet, G., Zimmermann, A.: Well-posedness for nonlinear SPDEs with strongly continuous perturbation. Proc. Roy. Soc. Edinburgh Sect. A 151(1), 265–295 (2021)
Xu, X., Zhao, L., Liu, C.: Axisymmetric solutions to coupled Navier–Stokes/Allen–Cahn equations. SIAM J. Math. Anal. 41(6), 2246–2282 (2010)
Yue, P., Feng, J., Liu, C., Shen, J.: A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 515, 293–317 (2004)
Zeidler, E.: Nonlinear functional analysis and its applications: II/B: Nonlinear monotone operators. Springer (1990)
Zhang, X.: On stochastic evolution equations with non-Lipschitz coefficients. Stoch. Dyn. 9(4), 549–595 (2009)
Acknowledgements
This work is partly supported by National Key R &D Program of China (No.2022YFA1006001) and by National Natural Science Foundation of China (Nos. 12131019, 12001516, 11721101), the Fundamental Research Funds for the Central Universities (Nos. WK3470000031, WK3470000024).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Röckner, M., Shang, S. & Zhang, T. Well-posedness of stochastic partial differential equations with fully local monotone coefficients. Math. Ann. (2024). https://doi.org/10.1007/s00208-024-02836-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00208-024-02836-6