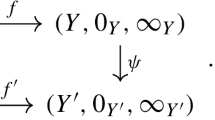Quantum Lefschetz property for genus two stable quasimap invariants

Abstract

By the reduced component in a moduli space of stable quasimaps to n-dimensional projective space $\mathbb {P}^n$ we mean the closure of the locus in which the domain curves are smooth. As in the moduli space of stable maps, we prove the reduced component is smooth in genus 2, degree $\ge 3$. Then we prove the virtual fundamental cycle of the moduli space of stable quasimaps to a complete intersection X in $\mathbb {P}^n$ of genus 2, degree $\ge 3$ is explicitly expressed in terms of the fundamental cycle of the reduced component of $\mathbb {P}^n$ and virtual cycles of lower genus $<2$ moduli spaces of X.

1 Introduction

Computing Gromov–Witten invariants of the quintic 3-fold X has attracted interests of both mathematicians and physicists due to its importance in mirror symmetry, which mainly studies Calabi–Yau 3-folds. One effective way to conquer this computation is to relate them with GW invariants of $\mathbb {P}^4$ in which X is embedded. Then we apply virtual localisation [23] for the natural torus action on $\mathbb {P}^4$ to compute them. We will call this principle relating GW invariants of X and $\mathbb {P}^4$ the quantum Lefschetz property.

The name, quantum Lefschetz, is originally from the formula between genus 0 virtual cycles: Let $\iota : M(X)\hookrightarrow M(\mathbb {P}^4)$ be the moduli spaces of stable maps to $X\hookrightarrow \mathbb {P}^4$, respectively. On $M(\mathbb {P}^4)$ there is a coherent sheaf $V:=\pi _*\textsf{f}^*\mathcal {O}_{\mathbb {P}^4}(5)$ defined via the universal curve $\pi :C\rightarrow M(\mathbb {P}^4)$ and the universal map $\textsf{f}:C\rightarrow \mathbb {P}^4$. In genus 0, $M(\mathbb {P}^4)$ is smooth and V is a vector bundle. Then the quantum Lefschetz formula [29] asserts that

$$\begin{aligned} \iota _*[M(X)]^{\textrm{vir}} \ = \ e(V) \ \cap \ [M(\mathbb {P}^4)]. \end{aligned}$$

(0.1)

Unfortunately, it turns out that (0.1) does not hold for higher genus invariants [22]. So we need more sophisticated version of the quantum Lefschetz property for higher genus invariants.

Meanwhile, the explicit relationship between GW and stable quasimap invariants of X is known to be wall-crossing formula [14, 16, 40]. Since we may expect a relatively simpler version of quantum Lefschetz property for higher genus quasimap invariants, wall-crossing formula allows us to study simpler quantum Lefschetz property to compute GW invariants. For instance the original quantum Lefschetz formula (0.1) holds true for genus 1 quasimap invariants, so it dramatically helps the computation of genus 1 GW invariants [30].

We notice that there have been several interesting quantum Lefschetz formulae for higher genus GW or quasimap invariants, or relationships between invariants of X and other invariants, developed in a recent few years [1, 3, 5, 7, 9,10,11, 17, 18, 20, 30, 33, 34, 41, 43]. These lead us some actual computations of higher genus invariants [4, 20, 24, 25, 30, 38, 42]. In our paper we would like to introduce one more quantum Lefschetz formula for genus 2 quasimap invariants. Our formulae (0.2), (0.4) contain Zinger-type reduced virtual cycles, which have not been studied in any of references above for genus $\ge 2$ yet. Since it is expected to have some interesting properties—such as integrability—we hope our new formulae would suggest some idea in studying higher genus invariants.

To construct Zinger-type reduced virtual cycles, we need to study the reduced components on which the cycles are supported (conjecturally), in the moduli spaces of stable maps or stable quasimaps to $\mathbb {P}^n$. It is firstly addressed in [26, 39] where they studied genus 1 stable maps. Later [2, 27] studied genus 2 stable maps in different ways—[27] is closer to the original idea of [26, 39], whereas [2] uses curves with Gorenstein singularities. Although [2] studied more general target spaces, we follow the idea of [27] to construct our reduced virtual cycles due to its advantage on computations.

We consider a slight more general situation. Let $X = \{f_1 = \cdots = f_m = 0\}$ be a complete intersection in projective space $\mathbb {P}^n$, where $f_i \in \Gamma (\mathbb {P}^n, \mathcal {O}_{\mathbb {P}^n}(\ell _i))$. When $n=4$, $m=1$ and $\ell _1=5$ it recovers a quintic threefold X. We denote by $Q_{g,k,d}(X)\hookrightarrow Q_{g,k,d}(\mathbb {P}^n)$ the moduli spaces of stable quasimaps to $X\hookrightarrow \mathbb {P}^n$ of genus g, degree d with k marked points. Using the universal curve and map

we define $V_{g,k,d}:=\oplus _{i=1}^m\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$, where $\mathcal {O}(d):=[\mathbb {C}^{n+1}\times \mathbb {C}/\mathbb {C}^*]$ is a bundle defined by weight d representation. Let $Q^{\textrm{red}}_{g,k,d}(\mathbb {P}^n)$ be the closure of the open substack in $Q_{g,k,d}(\mathbb {P}^n)$ on which $R^1\pi _*\textsf{f}^*\mathcal {O}(1)$ vanishes

$$\begin{aligned} Q^{\textrm{red}}_{g,k,d}(\mathbb {P}^n)\,=\ \textrm{closure}\left( Q_{g,k,d}(\mathbb {P}^n)\smallsetminus \textrm{supp}R^1\pi _*\textsf{f}^*\mathcal {O}(1)\right) \ \subset \ Q_{g,k,d}(\mathbb {P}^n). \end{aligned}$$

Then on the proper birational base change $\widetilde{Q}_{g,k,d}(\mathbb {P}^n)\rightarrow Q_{g,k,d}(\mathbb {P}^n)$ in Sect. 2.4, the proper transform of $Q^{\textrm{red}}_{g,k,d}(\mathbb {P}^n)$ is smooth and $V_{g,k,d}$ over there is a bundle. We denote by $\mathbb {L}_j$ the tautological line bundle $a_j^*\omega _\pi$ associated to the j-th marked point, which forms a section $a_j:Q_{g,k,d}(\mathbb {P}^n)\rightarrow C$ of $\pi$, where $\omega _\pi$ denotes the relative dualising sheaf of $\pi$. We often omit the subscript j in $\mathbb {L}_j$ throughout the paper when it is clear.

Then we prove the following quantum Lefschetz formula for a Calabi–Yau 3-fold.

Theorem 1

When X is a Calabi-Yau 3-fold, $d\ge 3$, we have an equivalence in homology group of $Q_{2,0,d}(X)$,

$$\begin{aligned}{}[Q_{2,0,d}(X)]^{\textrm{vir}} = \ {}&e^{\textrm{ref}}(V_{2,0,d})\cap [Q_{2,0,d}^{\textrm{red}}(\mathbb {P}^n)] \\ \nonumber&- \frac{c_1(\mathbb {L})}{24}\cap [Q_{1,1,d}(X)]^{\textrm{vir}} \\ \nonumber&+ \frac{1}{24^2}\left( \frac{c_1(\mathbb {L}_1)c_1(\mathbb {L}_2)}{2}-\frac{3(\textrm{ev}^*_1 c_2(T_X) + \textrm{ev}^*_2 c_2(T_X))}{2} \right) \cap [Q_{0,2,d}(X)]^{\textrm{vir}} . \end{aligned}$$

(0.2)

Using the defining section $f=(f_i)_i\in \Gamma (\mathbb {P}^n,\oplus _i\mathcal {O}(\ell _i))$ of $X\subset \mathbb {P}^n$, the first term in the RHS of (0.2) is localised to $Q(X):=Q_{2,0,d}(X)$ via refined Euler class $e^{\textrm{ref}}(V_{2,0,d})$ [21, Section 14.1]¹ defined by the section $\pi _*\textsf{f}^*f\in \Gamma (V_{2,0,d})$ cutting out $Q(X)=(\pi _*\textsf{f}^*f)^{-1}(0)$. The last two terms in the RHS are cycles on Q(X) via the pushforwards of embeddings,

• (1) $\iota _1: \overline{M}_{1,1} \times Q_{1,1,d}(X) \hookrightarrow Q(X)$,

• (2) $\iota _2: \overline{M}_{1,1} \times Q_{0,2,d}(X) \times \overline{M}_{1,1} \xrightarrow {2:1} Q(X)$.

In fact, we have these extra terms in (0.2) as the sheaf $\oplus _iR^1\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$ on Q(X) does not vanish on the image of $\iota _1$. Note that the image of $\iota _2$ is contained in the image of $\iota _1$, but the rank of $\oplus _iR^1\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$ jumps on the image of $\iota _2$. This is why we have the two extra terms in (0.2).

This sheaf $\oplus _iR^1\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$ does not vanish on the image of

• (3) $\iota _3: \overline{M}_{1,2} \times Q'_{0,2,d}(X) \hookrightarrow Q(X)$,

where $Q'_{0,2,d}(X)\hookrightarrow Q_{0,2,d}(X)$ is the closed substack on which the two evaluation maps are the same $\textrm{ev}_1=\textrm{ev}_2$,

as well. So it could have contributed nontrivially to the formula. Also there might be another nontrivial contribution from its intersection with the image of $\iota _1$. (Note that it does not intersect with the image of $\iota _2$.) And these are all the places where $\oplus _iR^1\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$ does not vanish exactly. So we may not expect there are more extra contributions to the formula. Actually we have the formula in Theorem 2 below for a general complete intersection $X\subset \mathbb {P}^n$ including the four contributions. The third and fourth contributions vanishe when X is a Calabi–Yau 3-fold, and Theorem 1 is obtained by Theorem 2 as a special case.

Before stating Theorem we introduce some (Chow) cohomology classes to simplify the statement. Denoting by $\mathcal {H}$ the Hodge bundle $\pi _*\omega _\pi$ we define the classes on the product $\overline{M}_{g_1,k_1+\{a\}}\times Q_{g_2,k_2+\{a\},d}(X)$,

$$\begin{aligned}&K_a\ :=\ \frac{c\,(\mathcal {H}^\vee \boxtimes \textrm{ev}^*_a T_X)}{c\,(\mathbb {L}^\vee _a \boxtimes \mathbb {L}^\vee _a)},\ A^t_a\ :=\ \frac{c\,(\mathcal {H}^\vee \boxtimes \textrm{ev}^*_a T_X)}{c\,(\mathbb {L}^\vee _a \boxtimes 1)^t},\ B_a\ :=\ \frac{1}{c\,(1 \boxtimes \mathbb {L}^\vee _a)}\quad \text {and} \\&[C_a]_{\dim X-2-t}\ :=\ \frac{t(t+1)}{2}c_1(\mathcal {H}^\vee )c_{\dim X-3-t}(\textrm{ev}_a^*T_X)-(t+1)c_{\dim X-2-t}(\textrm{ev}_a^*T_X). \end{aligned}$$

We omit the subscript a when the node a is clear. We denote by $[K]_i$, $[A^t]_i$, $[B]_i$ the degree i parts. We also define a (Chow) homology class

$$\begin{aligned}{}[Q'_{0,2,d}(X)]^{\textrm{vir}} \ :=\ (\textrm{ev}_1 \times \textrm{ev}_2)^*\Delta _X \cap [Q_{0,2,d}(X)]^{\textrm{vir}} \end{aligned}$$

(0.3)

using the diagonal class $\Delta _X\in A^{\dim X}(X\times X)$. The bundle $V_{2,0,d}$ on $Q^{\textrm{red}}_{2,0,d}(\mathbb {P}^n)$ is defined by $\oplus _i \pi _*\textsf{f}^*\mathcal {O}(\ell _i)$.

Theorem 2

For $d \ge 3$, we have an equivalence in the Chow group of $Q_{2,0,d}(X)$,

$$\begin{aligned}&[Q_{2,0,d} (X)]^{\textrm{vir}} = \; e^{\textrm{ref}}(V_{2,0,d}) \cap [Q^{\textrm{red}}_{2,0,d}(\mathbb {P}^n)] \nonumber \\&\quad + [K_1]_{\dim X-1} \cap \left( [\overline{M}_{1,\{1\}}] \times [Q_{1,\{1\},d}(X)]^{\textrm{vir}} \right) \nonumber \\&\quad + \left( \frac{[K_1 K_2]_{2\dim X-2}}{2}-[K_1]_{\dim X-1}[K_2]_{\dim X-1} \right) \nonumber \\&\quad \cap \left( \, [\overline{M}_{1,\{1\}}] \times [Q_{0,\{1,2\},d}(X)]^{\textrm{vir}} \times [\overline{M}_{1,\{2\}}] \, \right) \\ \nonumber&\quad + \frac{1}{2} \sum _{i=0}^{\dim X-1} [A^{i+1}_1]_{\dim X-1-i}[B_1B_2]_{i-1} \cap \left( [\overline{M}_{1,\{1,2\}}] \times [Q'_{0,\{1,2\},d}(X)]^{\textrm{vir}} \right) \\&\quad + \sum _{i= 1}^{\dim X-2} \left( [C_3]_{\dim X-2+i}-[A^{i+2}_3]_{\dim X-2-i}\right) [B_1B_2]_{i-1}\nonumber \\&\quad \cap \left( [\overline{M}_{1,\{3\}}] \times [\overline{M}_{0,\{1,2,3\}}] \times [Q'_{0,\{1,2\},d}(X)]^{\textrm{vir}} \right) . \nonumber \end{aligned}$$

(0.4)

In Remark 5.2 we explain $A^{i+1}_1=A^{i+1}_2$ on $\overline{M}_{1,1}\times Q'_{0,2,d}(X)$

, so the fourth term is not so strange. We emphasise Theorem 2 is a result in the Chow group whereas Theorem 1 is in homology.

1.1 Notation

For a morphism $f: X \rightarrow Y$ of spaces and a perfect complex $\mathbb {E}$ on Y, we often denote by $\mathbb {E}|_X$ the derived pullback $f^*\mathbb {E}$. We sometimes regard a locally free sheaf E as its total space.

We denote by $\mathfrak {M}_{g,k,d}$, or simply by $\mathfrak {M}$, the Artin stack of prestable curves with non-negative integer on each component (playing a role of degree) whose sum is d. Similarly $\mathfrak {M}^{line}_{g,k,d}$, or simply $\mathfrak {M}^{line}$, denotes the Artin stack of curves with degree d line bundles. The Artin stack of curves with degree d divisors is denoted by $\mathfrak {M}^{div}_{g,k,d}$, or simply $\mathfrak {M}^{div}$.

We denote by $Q^{(i)}$ the image of $\iota _i$ in the picture above (i) for either the moduli spaces of stable quasimaps or the p-fields spaces. For instance on $Q^{(3)}$, the evaluation maps (of the $g=0$ quasimap) are the same $\textrm{ev}_1=\textrm{ev}_2$. Furthermore, we use the script (i) for relevant objects of the embedding $\iota _i$ unless it needs an explanation. For instance a bundle on $Q^{(i)}$ will be denoted with the script (i).

For variables with two subindices $y_{ij}$, we say $y_i=0$ if $y_{ij}=0$ for all j. Also we say $y=0$ if $y_{ij}=0$ for all i and j.

2 Stable quasimaps, p-fields and the plan

2.1 Stable quasimaps

A genus g,degree d quasimap to the complete intersection $X\subset \mathbb {P}^n$ cut out by homogeneous polynomials $f_i\in \Gamma (\mathbb {P}^n,\mathcal {O}(\ell _i))$ with k marked points is a triple (C, L, u) where C is a genus g, projective, nodal, prestable curve with k marked points, L is a degree d line bundle on C, and $u = (u_0,\dots ,u_n)$ is a section of $L^{\oplus n+1}$ such that

$$\begin{aligned} f_i(u)=0 \in \Gamma (C, L^{\otimes \ell _i}) \quad \text {for all}\quad i. \end{aligned}$$

(1.1)

Note that a pair $(L,u:\mathcal {O}_C\rightarrow L^{\oplus n+1})$ defines a map $\textsf{f}:C\rightarrow [\mathbb {C}^{n+1}/\mathbb {C}^*]$. Conversely, when a map $\textsf{f}:C\rightarrow [\mathbb {C}^{n+1}/\mathbb {C}^*]$ is given, we obtain a pair $(\textsf{f}^*\mathcal {O}(1),u:\mathcal {O}_C\rightarrow \textsf{f}^*\mathcal {O}(1)^{\oplus n+1})$. Hence a triple (C, L, u) can be considered to be a pair $(C,\textsf{f})$ satisfying $L=\textsf{f}^*\mathcal {O}(1)$. A quasimap is stable if it satisfies the stability conditions²

$$\begin{aligned}&-\ \omega _{C}^{\log } \otimes L^{\varepsilon } \text { is ample on} C \text {for any} \varepsilon >0, \text {and}\\&-\ \text {the zero of }u~\text {is a divisor which does not meet nodes nor marked points.}\qquad \nonumber \end{aligned}$$

(1.2)

We denote by $Q_{g,k,d}(X)$, or simply by Q(X), the moduli space of stable quasimaps. By [13, 15, 35], it is proper and equipped with a natural perfect obstruction theory so that the virtual fundamental class

$$\begin{aligned} \left[ Q(X) \right] ^{\textrm{vir}} \ \in \ A_{\textrm{vdim}}(Q(X) ) \end{aligned}$$

(1.3)

is defined, where $\textrm{vdim}$ denotes the virtual dimension

$$\begin{aligned} \textrm{vdim} \ =\ (\dim X - 3)(1-g) + k - c_1(K_X)\cap d\!\cdot \![line]. \end{aligned}$$

The stable quasimap invariant of X is defined to be an integration over this virtual class.

The reason why the quantum Lefschetz property for the quasimap invariants is simpler is because a quasimap does not have a rational component with less than two special points (called a rational tail) on its domain curve.

2.2 Stable quasimaps with p-fields

We have seen in Introduction that the coherent sheaf $R^1V:=\oplus _iR^1\pi _*\textsf{f}^*\mathcal {O}(\ell _i)$ on $Q(\mathbb {P}^n)$ may not vanish. We denote by $Q_{p,g,k,d}(\mathbb {P}^n)$, or simply by $Q_p$, its dual space

$$\begin{aligned} Q_p \,=\ \textrm{Spec}_{\mathcal {O}_{Q(\mathbb {P}^n) } } \left( \textrm{Sym} R^1V \right) . \end{aligned}$$

Its fibre at $(C,L,u)=(C,\textsf{f})\in Q(\mathbb {P}^n)$ is then $\oplus _iH^1(C,\textsf{f}^*\mathcal {O}(\ell _i))^\vee =\oplus _iH^0(C,\omega _C\otimes \textsf{f}^*\mathcal {O}(-\ell _i))$ by Serre duality. Since $L=\textsf{f}^*\mathcal {O}(1)$, $Q_p$ parametrises $(C,L,u,p=(p_1,\ldots , p_m))$ where (C, L, u) is a stable quasimap to $\mathbb {P}^n$ and

$$\begin{aligned} p_i \in \Gamma (C, \omega _C \otimes L^{-\ell _i}). \end{aligned}$$

Recall that imposing the condition (1.1) defines the space Q(X) from $Q(\mathbb {P}^n)$, whereas the above extra data determines $Q_p$ from $Q(\mathbb {P}^n)$. We will call the section $p=(p_1,\dots ,p_m)$ p-fields.

The space $Q_p$ may not be proper, but still comes with a natural perfect obstruction theory, so that the virtual fundamental class

$$\begin{aligned}{}[Q_p]^{\textrm{vir}} \ \in \ A_{\textrm{vdim}}(Q_p) \end{aligned}$$

is defined. Denoting by $\mathcal {L}:=\textsf{f}^*\mathcal {O}(1)$ the universal line bundle on the universal curve, the dual perfect obstruction theory relative to $\mathfrak {M}^{line}$ is defined to be

$$\begin{aligned} \mathbb {E}^{\vee }_{Q_p/\mathfrak {M}^{line}}&:= (R\pi _*\mathcal {L}^{\oplus n+1} \oplus \bigoplus _i R\pi _*(\omega _{\pi }\otimes \mathcal {L}^{\otimes -\ell _i}))|_{Q_p}\nonumber \\&\cong (R\pi _*\mathcal {L}^{\oplus n+1} \oplus \bigoplus _i (R\pi _*\mathcal {L}^{\otimes \ell _i})^{\vee } [-1])|_{Q_p}. \end{aligned}$$

(1.4)

Using the map $f=(f_1,\ldots ,f_m):\mathbb {C}^{n+1}\rightarrow \mathbb {C}^m$ inducing $R\pi _*\mathcal {L}^{\oplus n+1}\rightarrow \oplus _iR\pi _*\mathcal {L}^{\otimes \ell _i}$, the pairing defines the cosection $\mathbb {E}^{\vee }_{Q_p/\mathfrak {M}^{line}} \rightarrow \mathcal {O}_{Q_p}[-1]$. The p-field spaces and cosections are firstly introduced by Chang–Li in [6] to find a localised class $[Q_p]^{\textrm{vir}} _{\textrm{loc}}$ of $[Q_p]^{\textrm{vir}}$ to a smaller space $j: Q(X) \hookrightarrow Q_p$,

$$\begin{aligned}{}[Q_p]^{\textrm{vir}} _{\textrm{loc}}\ \in \ A_{\textrm{vdim}}(Q(X)), \ \ \ j_*[Q_p]^{\textrm{vir}} _{\textrm{loc}} \ =\ [Q_p]^{\textrm{vir}} , \end{aligned}$$

(1.5)

using cosection localisation [28]. Then they proved GW invariants of X are equal to those defined over p-field spaces up to sign. This result is improved in [8, 12, 31, 37]: the localised class $[Q_p]^{\textrm{vir}} _{\textrm{loc}}$ is equal to the class $[Q(X)]^{\textrm{vir}}$ defined in (1.3) up to sign

$$\begin{aligned}{}[Q(X)]^{\textrm{vir}} \ =\ (-1)^{d(\sum _i \ell _i) + m(1-g) }[Q_p]^{\textrm{vir}} _{\textrm{loc}}. \end{aligned}$$

(1.6)

2.3 Plan of the proof of Theorem 2

Using (1.6) we replace $[Q(X)]^{\textrm{vir}}$ with $\pm [Q_p]^{\textrm{vir}} _{\textrm{loc}}$ in the statement of Theorem 2. An advantage in using $Q_p$ rather than Q(X) is that it is locally a nice cut-out of a smooth space. In Sect. 2, we describe this explicit cut-out model of $Q_p$ after the suitable base-change of $Q_p$ in Sect. 2.4. Using this, we compute the intrinsic normal cone of $Q_p$ in Sect. 3.2 to obtain a decomposition of the virtual class

$$\begin{aligned}{}[Q_{p,2,0,d}]^{\textrm{vir}} _{\textrm{loc}} \ =\ [Q_p^{\textrm{red}}]^{\textrm{vir}} \ +\ [Q_p^{(1)}]^{\textrm{vir}} \ +\ [Q_p^{(2)}]^{\textrm{vir}} \ +\ [Q_p^{(3)}]^{\textrm{vir}} . \end{aligned}$$

(1.7)

Note that the indices ‘red’, ‘(1)’, ‘(2)’ and ‘(3)’ reflect their geometric origins labelled above. So $Q_p^{(1)},Q_p^{(2)},Q_p^{(3)}$ are supported on the images of the node-identifying morphisms $\iota _i$, ignoring p-fields. In fact we will investigate that they are bundles over the images in Sect. 3.2.

Then in Sect. 4, we prove that $[Q_p^{\textrm{red}}]^{\textrm{vir}}$ follows the original quantum Lefschetz formula (0.1)

$$\begin{aligned}{}[Q_{p}^{\textrm{red}}]^{\textrm{vir}} \ =\ (-1)^{d(\sum _i \ell _i) - m} \; e^{\textrm{ref}}(V_{2,0,d})\ \cap \ [Q_{2,0,d}^{\textrm{red}}(\mathbb {P}^n)]. \end{aligned}$$

And we show the i-th cycle $[Q_p^{(i)}]^{\textrm{vir}}$ is a part of the RHS of (0.4). For $i=1$ for instance, we obtain

$$\begin{aligned}{}[Q_p^{(1)}]^{\textrm{vir}} \ =\ (-1)^m\left[ \frac{c(\mathcal {H}^\vee \boxtimes \textrm{ev}^*T_X)}{c(\mathbb {L}^\vee \boxtimes \mathbb {L}^\vee )} \right] _{n-m-1} \cap \left( [\overline{M}_{1,1}] \times [Q^{\textrm{red}}_{p,1,1,d}]^{\textrm{vir}} \right) \end{aligned}$$

(1.8)

via the pushforward by $\iota _1$. A very brief interpretation of this equality is that the difference of the obstruction bundles defining $[Q_p^{(1)}]^{\textrm{vir}}$ and $[Q^{\textrm{red}}_{p,1,1,d}]^{\textrm{vir}}$ (in the K-group of $Q_p^{(1)}$, via the pullback) can be written in terms of the bundle structure of $Q_p^{(1)}$ over the image of $\iota _1$ as well as the pullback bundles of $\mathcal {H}^\vee \boxtimes \textrm{ev}^*T_X$, $\mathbb {L}^\vee \boxtimes \mathbb {L}^\vee$. To realise this interpretation to give an actual proof, we do massage spaces and bundles—deformations, blowups and twistings by divisors, etc.—in Sect. 5 so that we can get a tidy form (1.8). Once we do these for all i, then by using [32, Theorem 1.1]

$$\begin{aligned} e^{\textrm{ref}}(V_{1,1,d}) \cap [Q_{1,1,d}^\textrm{red}(\mathbb {P}^n)] \ =\ [Q_{1,1,d}(X)]^{\textrm{vir}} -[K]_{\dim X-1}\cap ([\overline{M}_{1,1}]\times [Q_{0,2,d}(X)]^{\textrm{vir}} ) \end{aligned}$$

together with (1.6), the decomposition (1.7) proves Theorem 2.

3 Local defining equations of the p-field space

For a morphism of vector bundles $d: A \rightarrow B$ over a smooth Artin stack M, we consider the kernel of d as a space

$$\begin{aligned} \ker d\,=\ \textrm{Spec}_{\mathcal {O}_M}\left( \textrm{Sym}(\textrm{coker} d^*)\right) \ \subset \ A\ =\ \textrm{Spec}_{\mathcal {O}_M}\left( \textrm{Sym}A^*\right) . \end{aligned}$$

Denoting by $\tau _A$ the tautological section, $\ker d$ has a cut-out model

(2.1)

Hence the pullback complex $\{d: A \rightarrow B\}|_{\ker d}$ defines a dual perfect obstruction theory of $\ker d$ relative to M.

The purpose of this section is to write $Q_p$ as (an open substack of) $\ker d$ over $\mathfrak {M}^{div}$.

3.1 Cut-out model of the p-field space

Unlike considering $\mathfrak {M}^{line},$ there is no canonical forgetful morphism of the p-field space $Q_p \rightarrow \mathfrak {M}^{div}$. But it is defined locally as follows. For a point $(C,L,u,p) \in Q_p$, $u=(u_0,\ldots , u_n)$ is not identically zero on any component of C. So we can pick a combination ${\textbf{u}}=\sum a_iu_i\in H^0(C,L)$ whose zero ${\textbf{u}}^{-1}(0)\subset C$ defines a divisor on C and does not intersect with the special points. Since it is an open condition we have a morphism

$$\begin{aligned} Q_p \ \longrightarrow \ \mathfrak {M}^{div}, \ \ \ (C,L,u,p) \ \longmapsto \ (C, {\textbf{u}}^{-1}(0)) \end{aligned}$$

on a local neighborhood.

Let $\mathcal {D}$ be the universal divisor on the universal curve $\pi : \mathcal {C}\rightarrow \mathfrak {M}^{div}$ and consider the complex

$$\begin{aligned} R\pi _*\mathcal {O}_{\mathcal {C}}(\mathcal {D})^{\oplus n} \oplus \bigoplus _i \left( R\pi _*\mathcal {O}_{\mathcal {C}}(\ell _i\mathcal {D})[1] \right) ^{\vee }. \end{aligned}$$

(2.2)

It is explained in [31, Section 3] that we can choose its representative $A{\mathop {\longrightarrow }\limits ^{d}} B$ such that the stability condition (1.2) defined on $\ker d$ is lifted to the total space of A. So this lifted stability condition defines the open substack of A. Then the cut-out model (2.1) restricted to this open substack gives a local cut-out model of $Q_p$ relative to $\mathfrak {M}^{div}$.

Since we work locally, we may assume A and B are trivial bundles. Then d can be considered as a multi-valued function

$$\begin{aligned} d\ :\ \mathfrak {M}^{div}\times \mathbb {C}^{{{\,\textrm{rank}\,}}A}\ \longrightarrow \ \mathbb {C}^{{{\,\textrm{rank}\,}}B} \end{aligned}$$

(2.3)

defining $Q_p$ as (an open substack of) its zero. In the rest of the section, we find a simple expression of d by coordinate changes and blowups.

3.2 Key lemma

Now we focus on $(g,k)=(2,0)$ throughout the section. We work étale locally on $\mathfrak {M}^{div}$, sometimes without mentioning it. For instance by an element of $\Gamma (\mathcal {O}_{\mathfrak {M}^{div}})$, we mean an étale local function of $\mathfrak {M}^{div}$.

As we have explained in Introduction, considering stable quasimaps has a big advantage in making the quantum Lefschetz formula less complicated than considering stable maps. But there is (essentially only) one technical thing to check, which is obvious in stable maps—near a domain curve of a stable map $\textsf{f}: C \rightarrow \mathbb {P}^n$, $\textsf{f}^*\mathcal {O}(1)$ is linearly equivalent to $\mathcal {O}(\sum _{i=1}^d \mathcal {D}_i)$ with disjoint, fiberwise degree 1 divisors $\mathcal {D}_i$. Unfortunately it is not immediately seen near a domain curve of a stable quasimap. Since this was the important starting point to find local cut-out models for stable map moduli spaces in [26, 27] we need the following Lemma.

In fact, the Lemma is quite general—it holds near any prestable curve, including a domain curve of a stable quasimap, in genus 2. Let $\mathcal {D}$ be an effective divisor of $\deg =d \ge 3$ on the universal curve $\mathcal {C}$ of $\mathfrak {M}$ supported off the special points.

Lemma 2.1

Locally $\mathcal {D}$ is linearly equivalent to a sum $\sum _{i=1}^d \mathcal {D}_i$ of disjoint divisors of degree 1 at each fiber.

The key idea of the proof is to construct a covering map $\mathcal {C}\rightarrow \mathbb {P}^1$ by picking two linearly independent sections $H^0(\mathcal {C},\mathcal {O}(\mathcal {D}))$, whose dim $= d+1-g+\dim H^1(\mathcal {C},\mathcal {O}(\mathcal {D}))\ge 2$, not having common zeros. Then the inverse image of a generic point of $\mathbb {P}^1$ is d-many distinct points.

Proof

Pick any local divisor $\mathcal {B}$ on $\mathcal {C}$ lying on the minimal genus 2 subcurve, having degree 1 at each fiber and not meeting $\mathcal {D}$. Because $\mathcal {B}\cap \mathcal {D}= \emptyset$, the evaluation morphism $\pi _*(\mathcal {O}_{\mathcal {C}}(\mathcal {D})) \rightarrow \mathcal {O}_{\mathcal {C}}(\mathcal {D})|_{\mathcal {B}} \cong \mathcal {O}_{\mathfrak {M}}$ is surjective, where $\pi : \mathcal {C}\rightarrow \mathfrak {M}$ denotes the projection morphism. This induces an exact sequence

$$\begin{aligned} 0\ \rightarrow \ \pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}-\mathcal {B})\ \rightarrow \ \pi _*(\mathcal {O}_{\mathcal {C}}(\mathcal {D}))\ \rightarrow \ \mathcal {O}_{\mathfrak {M}}\ \rightarrow \ 0. \end{aligned}$$

(2.4)

Meanwhile, as in [27, Section 2.3], we can choose other divisors $\mathcal {A}_1$ and $\mathcal {A}_2$ lying on the minimal genus 2 subcurve such that

• $\mathcal {A}_1$, $\mathcal {A}_2$, $\mathcal {B}$ are disjoint to each other, and

• $\mathcal {A}_1$, $\mathcal {A}_2$ lie on different components if the genus 2 component consists of two genus 1 components.

Picking the divisors in this way ensures $R^1\pi _*(\mathcal {D}+\mathcal {A}_1+\mathcal {A}_2-\mathcal {B})=0$. So $\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}+ \mathcal {A}_1 + \mathcal {A}_2-\mathcal {B})$ is a rank d vector bundle and hence locally is $\mathcal {O}_{\mathfrak {M}}^{\oplus d}$. By [27, Equation (2.5)], we obtain a sequence

(2.5)

Since $d \ge 3$, we can pick a nonzero local section $s\in \Gamma \left( \pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}+ \mathcal {A}_1 + \mathcal {A}_2-\mathcal {B})\right)$ mapping to 0 by $\textrm{ev}_{\mathcal {A}_1} \oplus \textrm{ev}_{\mathcal {A}_2}$. Then it factors through $\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}-\mathcal {B})$, and hence, by (2.4), it can be considered as a section

$$\begin{aligned} s\,\ \mathcal {O}_{\mathcal {C}} \ \longrightarrow \ \mathcal {O}_{\mathcal {C}}(\mathcal {D}), \end{aligned}$$

which is zero on $\mathcal {B}$. Since the canonical section $s_{\mathcal {D}}$ of $\mathcal {D}$ does not vanish on $\mathcal {B}$, $s_{\mathcal {D}}$ and s are linearly independent on every fiber.

The common zero $\mathcal {D}'$ of s and $s_{\mathcal {D}}$ has then fiberwise degree $d' \le d-1$ (which may not be constant at each fiber) because s is zero on $\mathcal {B}$ but $s_{\mathcal {D}}$ is not. Then at a fiber the sections $s \otimes s^{-1}_{\mathcal {D}'}$, $s_{\mathcal {D}} \otimes s^{-1}_{\mathcal {D}'}$ of $\mathcal {O}(\mathcal {D}-\mathcal {D}')$ defines a degree $d-d'$ morphism $\phi : \mathcal {C}\rightarrow \mathbb {P}^1$. Since it cannot be degree 1 (which means $\phi$ is an isomorphism), we actually have $d' \le d-2$. A generic fiber $\phi ^{-1}([a;b])$ consists of distinct divisors $\mathcal {D}_1$,..., $\mathcal {D}_{d-d'}$ away from $\mathcal {D}'$, and hence we have

$$\begin{aligned} \mathcal {O}_{\mathcal {C}}(\mathcal {D}-\mathcal {D}') \ \cong \ \mathcal {O}_{\mathcal {C}}\left( \sum _{i=1}^{d-d'} \mathcal {D}_i\right) . \end{aligned}$$

Note that since $\mathcal {D}' + \sum \mathcal {D}_i$ is defined by $bs-as_{\mathcal {D}}$ this isomorphism is not only at the fiber, but an isomorphism locally on $\mathfrak {M}$.

If $d' \ge 3$, we do the same procedure by replacing $\mathcal {D}'$ by $\mathcal {D}$ until we get $d' \le 2$. Then we proved the lemma unless $d'=2$. Now let us assume that $d'=\deg \mathcal {D}' =2$. Doing the same procedure for $\mathcal {D}:=\mathcal {D}'+\mathcal {D}_1$ which has degree 3, the procedure terminates since $d'\le \deg \mathcal {D}-2=3-2=1$. Hence the proof is completed. $\square$

Considering the universal divisor $\mathcal {D}$ on the universal curve $\mathcal {C}$ on $\mathfrak {M}^{div}$, we obtain the following immediate corollary from the exact sequences (2.4), (2.5) in the proof of Lemma 2.1.

Corollary 2.2

In the derived category of a local neighborhood of $\mathfrak {M}^{div}$, we obtain an isomorphism induced by (2.4)

$$\begin{aligned} R\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}) \ {}&\cong \ R\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}- \mathcal {B}) \oplus [\mathcal {O}_{\mathfrak {M}^{div}} {\mathop {\longrightarrow }\limits ^{0}} 0]. \end{aligned}$$

And the sequence (2.5) induces an isomorphism

In addition, a similar idea of [27, Lemma 2.4.1] allows us to have one more isomorphism.

Lemma 2.3

The canonical monomorphisms induce an isomorphism

$$\begin{aligned}&\oplus ^d_{i=1} \pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}_i + \mathcal {A}_1 + \mathcal {A}_2 - \mathcal {B}) \ \cong \ \pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}_1 + \cdots + \mathcal {D}_d + \mathcal {A}_1 + \mathcal {A}_2 - \mathcal {B}). \end{aligned}$$

Combining all these Lemma 2.1, Corollary 2.2 and Lemma 2.3, we observe that $R\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D})$ is quasi-isomorphic to

(2.6)

3.3 Diagonalisation of the local representative

Picking any local identification $\pi _* \mathcal {O}_{\mathcal {C}}(\mathcal {D}_i + \mathcal {A}_1 + \mathcal {A}_2 - \mathcal {B}) \cong \mathcal {O}_{\mathfrak {M}^{div}}$, $\tiny {\textrm{ev}_{\!\mathcal {A}_1}\oplus \textrm{ev}_{\!\mathcal {A}_2}}$ in (2.6) can be written as a $2 \times d$ matrix $(c_{ji})$, $c_{ji} \in \Gamma (\mathcal {O}_{\mathfrak {M}^{div}})$.

The goal of this section is to transform the matrix $(c_{ji})$ to a nice diagonal form

$$\begin{aligned} (c_{ji}) \sim \left( \begin{array}{ccccc} c_1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} c_2 &{} 0 &{} \cdots &{} 0 \end{array} \right) =: c \end{aligned}$$

by using row and column operations near a domain curve of a stable quasimap. In fact it is already studied by Hu–Li–Niu [27, Section 5] over the domain curves of stable maps: on a neighbourhood of a fixed domain curve they found a diagonal form. It depends on a type of a boundary component in which the domain curve is. Since the domain curves of stable quasimaps are simpler than the ones of stable maps, Hu–Li–Niu already gave an answer to our goal. Below we list the cases which will appear as the domain curves of stable quasimaps.

(1) Near a domain curve in the generic image of $\overline{M}_{1,1}\times \mathfrak {M}^{div}_{1,1,d} \hookrightarrow \mathfrak {M}^{div}_{2,0,d}$ one can find a diagonal matrix c with

$$\begin{aligned} c_1\ =\ 1, \ \ \ c_2\ =\ \zeta , \end{aligned}$$

where $\zeta$ is the node smoothing function in $\Gamma (\mathcal {O}_{\mathfrak {M}^{div}})$. Combining with the fact that there are no rational tails on the domain curves in $Q_{2,0,d}(\mathbb {P}^n)$, the proof comes from [27, Section 5.3, Case 1]. The $(c_{ji})$ matrix of [27] in this case contains node smoothing functions of rations tails and an information of necessary blowups due to their existence. It is simplified to our matrix.

(2) Near a domain curve in the image of $\iota _2: \overline{M}_{1,1}\times \mathfrak {M}^{div}_{0,2,d}\times \overline{M}_{1,1} \xrightarrow {2:1} \mathfrak {M}^{div}_{2,0,d}$ one can find it to be

$$\begin{aligned} c_1\ =\ \zeta _1, \ \ \ c_2\ =\ \zeta _2, \end{aligned}$$

where $\zeta _1$ and $\zeta _2$ are the node smoothing functions in $\Gamma (\mathcal {O}_{\mathfrak {M}^{div}})$. The proof is in [27, Section 5.5, Case 1]. Note that the diagonal form in (1) is recovered by $\zeta _2\ne 0$.

(3) Near a domain curve in the image of $\overline{M}_{1,2}\times \mathfrak {M}^{div}_{0,2,d} \hookrightarrow \mathfrak {M}^{div}_{2,0,d}$ we need a blowup to obtain a diagonal transform of $(c_{ji})$. Before we discuss it in the following Section, we introduce some useful facts which we will use.

When the curve is not in the intersection with the image of (1), the entries $c_{ji}$ in the matrix $(c_{ji})$ are non-vanishing functions by [27, Proposition 2.5.1]. Therefore the matrix $(c_{ji})$ can be transformed to

$$\begin{aligned} \left( \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \det _{12} &{} \det _{13} &{} \det _{14} &{} \cdots &{} \det _{1d} \end{array} \right) \end{aligned}$$

where $\det _{k\ell }:= \det \left( \begin{array}{cc} c_{1k} &{} c_{1\ell } \\ c_{2k} &{} c_{2\ell } \end{array} \right)$

. Computing the ranks of co/kernels of $\tiny {\textrm{ev}_{\!\mathcal {A}_1}\oplus \textrm{ev}_{\!\mathcal {A}_2}}$, we observe that $\det _{1i}$ is a linear combination of the node smoothing functions $\zeta _1$ and $\zeta _2$. Moreover by [27, Section 5.4, Case 1] and [27, Lemma 2.7.3 (3)], we may assume that the first two determinants can be written as

$$\begin{aligned} \det \nolimits _{12} = \zeta _1 + a \cdot \zeta _2,\ \ \ \det \nolimits _{13} = \zeta _2 + b \cdot \zeta _1, \end{aligned}$$

with $ab\ne 1$. Hence the matrix is transformed to

$$\begin{aligned} \left( \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \zeta _1 &{} \zeta _2 &{} 0 &{} \cdots &{} 0 \end{array} \right) . \end{aligned}$$

(2.7)

(1$\;\cap \;$3). When the curve is in the intersection with the image of (1), [27, Section 5.4, Case 2] and [27, Lemma 2.7.3 (3)] show the matrix is transformed to

$$\begin{aligned} \left( \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \zeta \zeta _1 &{} \zeta \zeta _2 &{} 0 &{} \cdots &{} 0 \end{array} \right) , \end{aligned}$$

(2.8)

where $\zeta$ is the node smoothing function for the component (1).

(4) Near a generic domain curve from the reduced space, one can find it to be

$$\begin{aligned} c_1\ =\ 1, \ \ \ c_2\ =\ 1. \end{aligned}$$

The proof is in [27, Section 5.2, Case 2]. This diagonal form is recovered from (1) by letting $\zeta \ne 0$.

3.4 Base change

Consider the blowup spaces

$$\begin{aligned} \widetilde{\mathfrak {M}}:= \textrm{Bl}_{\mathfrak {M}_{1,2,0} \times \mathfrak {M}_{0,2,d}} \mathfrak {M}_{2,0,d} \ \text { and } \ \widetilde{\mathfrak {M}}^{div} \,=\ \mathfrak {M}^{div}\times _{\mathfrak {M}} \widetilde{\mathfrak {M}}. \end{aligned}$$

On $\widetilde{\mathfrak {M}}^{div}$, the matrices (2.7) and (2.8) can be transformed to be diagonal forms.

Outside of the intersection with the component in (1), the boundary component $\mathfrak {M}_{1,2,0} \times \mathfrak {M}_{0,2,d}$ is $\{\zeta _1=\zeta _2=0\}$ locally. Thus on a neighborhood of the exceptional divisor, we know either $\zeta _1|\zeta _2$ or $\zeta _2|\zeta _1$. Without loss of generality, we may assume that $\zeta _1|\zeta _2$. Then the matrix (2.7) can be transformed to

$$\begin{aligned} \left( \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \zeta _1 &{} 0 &{} \cdots &{} 0 \end{array} \right) . \end{aligned}$$

Hence on the blowup, the matrix c for the case (3) in Sect. 2.3 has a form with $c_1=1$, $c_2=\zeta _1$. Furthermore, the diagonal form in (4) is recovered by this by $\zeta _1\ne 1$.

Similarly on the intersection with the component in (1), (2.8) is transformed to

$$\begin{aligned} \left( \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \zeta \zeta _1 &{} 0 &{} \cdots &{} 0 \end{array} \right) . \end{aligned}$$

Note that the diagonal form in (1) is recovered by this by $\zeta _1\ne 1$.

The global forgetful morphism $Q_p \rightarrow \mathfrak {M}$ defines the base change $b:\widetilde{Q}_p:= Q_p \times _{\mathfrak {M}} \widetilde{\mathfrak {M}}\rightarrow Q_p$. Then the pullbacks of the perfect obstruction theory and the cosection defines the cosection localised virtual cycle

$$\begin{aligned}{}[\widetilde{Q}_p]^{\textrm{vir}} _{\textrm{loc}} \ \in \ A_{\textrm{vdim}}(\widetilde{Q}_X). \end{aligned}$$

By [19, Theorem 5.0.1], we obtain the base-change morphism of b between the (intrinsic) normal cones, which is of degree 1. In [31, Theorem 1.1], it is explained that cosection localised Gysin maps are bivariant operators, so they commute with proper push-forwards. These two prove

$$\begin{aligned} b_*[\widetilde{Q}_p]^{\textrm{vir}} _{\textrm{loc}} \ =\ [Q_p]^{\textrm{vir}} _{\textrm{loc}}. \end{aligned}$$

3.5 Local cut-out model of $\widetilde{Q}_p$

Recall that we obtained an explicit representative (2.6) of $R\pi _*\mathcal {O}(\mathcal {D})$ with the diagonal matrices c in Sects. 2.3 and 2.4 as its differential morphism. We emphasise once again that $\mathcal {D}$ need not be the universal divisor, cf. Lemma 2.1. So we apply these diagonalisations to get a local cut-out model not only of $\widetilde{Q}(\mathbb {P}^n):=Q(\mathbb {P}^n)\times _{\mathfrak {M}}\widetilde{\mathfrak {M}}$, but also of the p-field space $\widetilde{Q}_p$, relative to $\widetilde{\mathfrak {M}}^{div}$ as discussed in Sect. 2.1. The induced local defining Eq. (2.3) is

(2.9)

Here, the morphisms $\prod _{j=1}^n\left( \mathbb {C}^{2} \times \mathbb {C}^{d-1}\right) \rightarrow \mathbb {C}^{2n}$ and $\mathbb {C}^{2\,m}\rightarrow \prod ^m_{i=1} \left( \mathbb {C}^2 \oplus \mathbb {C}^{d\ell _i-1} \right)$ above represent the complexes $R\pi _*\mathcal {O}(\mathcal {D})^{\oplus n}$ and $\left( \oplus _{i}R\pi _*\mathcal {O}(\ell _i\!\cdot \!\mathcal {D})[1]\right) ^\vee$, respectively, whose direct sum is the local perfect obstruction theory (2.2). So at a point $z=(C,D)\in \mathfrak {M}^{div}$, the kernel of the first morphism (which is linear)

$$\begin{aligned} \prod _{j=1}^n\left( \mathbb {C}^{2} \times \mathbb {C}^{d-1}\right) \longrightarrow \mathbb {C}^{2n},\ \prod _j((x_{1j},x_{2j}),v_j)\longmapsto (c_1(z)x_{1j}, c_2(z)x_{2j})_{1\le j\le n} \end{aligned}$$

parametrises sections, $\Gamma (C,\mathcal {O}(D)^{\oplus n})$. Hence together with z, it parametrises objects in $\widetilde{Q}(\mathbb {P}^n)$. The kernel of the second morphism

$$\begin{aligned} \mathbb {C}^{2m}\longrightarrow \prod _{i=1}^m\left( \mathbb {C}^{2} \times \mathbb {C}^{d\ell _i-1}\right) ,\ ((p_{1i},p_{2i}))_{1 \le i \le m}\longmapsto \prod _i\left( (c_1(z) p_{1i}, c_2(z)p_{2i}), 0 \right) \end{aligned}$$

parametrises p-fields, $\Gamma (C,\oplus _i \omega _C\otimes \mathcal {O}(-\ell _iD))$.

4 Perfect obstruction theories, cones and virtual cycles

4.1 Perfect obstruction theories

Although the cut-out model (2.9) is useful in computational aspects, there are also two crucial drawbacks. One is it is not global and the other is this does not give a cut-out model over $\widetilde{\mathfrak {M}}^{line}$ since $\widetilde{\mathfrak {M}}^{div}\rightarrow \widetilde{\mathfrak {M}}^{line}$ is not smooth. For later use it is important how we can apply computations with the cut-out model (2.9) to the perfect obstruction theory over $\widetilde{\mathfrak {M}}$ or $\widetilde{\mathfrak {M}}^{line}$. In this section, we explain this.

First we recall the perfect obstruction theories. We keep denoting by $\pi : \mathcal {C}\rightarrow \widetilde{Q}_p$ the pullback of the universal curve. The local perfect obstruction theory relative to $\widetilde{\mathfrak {M}}^{div}$ is

$$\begin{aligned} \mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}^{div}} = \left( R\pi _*\mathcal {O}_{\mathcal {C}}(\mathcal {D})^{\oplus n} \right) ^\vee \oplus \bigoplus _i R\pi _*\mathcal {O}_{\mathcal {C}}(\ell _i\mathcal {D}) [1], \end{aligned}$$

which is just the pullback of the dual of (2.2). Globally $\widetilde{Q}_p$ comes equipped with the perfect obstruction theory relative to $\mathfrak {M}^{line}$

$$\begin{aligned} \mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}^{line}} = \left( R\pi _*\mathcal {L}^{\oplus n+1} \right) ^\vee \oplus \bigoplus _i R\pi _*\mathcal {L}^{\ell _i} [1], \end{aligned}$$

where $\mathcal {L}$ is the universal line bundle over the universal curve. And the cone of the composition

$$\begin{aligned} \mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}^{line}}[-1]\ \longrightarrow \ \mathbb {L}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}^{line}}[-1]\ \longrightarrow \ \mathbb {L}_{\widetilde{\mathfrak {M}}^{line}/\widetilde{\mathfrak {M}}}|_{\widetilde{Q}_p} \end{aligned}$$

defines the global perfect obstruction theory $\mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}}$ relative to $\mathfrak {M}$. Here $\mathbb {L}$ denotes the cotangent complex. Then we have the following diagram of triangles

In particular the middle horizontal triangle tells us that the local cut-out model (2.9) defines $\mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}}$ as well as $\mathbb {E}_{\widetilde{Q}_p/ \widetilde{\mathfrak {M}}^{div}}$ since $\widetilde{\mathfrak {M}}^{div}\rightarrow \widetilde{\mathfrak {M}}$ is smooth.³

So one way from local to global is to consider this forgetful morphism $\widetilde{\mathfrak {M}}^{div} \rightarrow \widetilde{\mathfrak {M}}$. Via the morphism of perfect obstruction theories

$$\begin{aligned} \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}\ \longrightarrow \ \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}^{div}}, \end{aligned}$$

computations can move from one to the other, where the former is global whereas the latter is local. For instance the smoothness shows that the two intrinsic normal cones

$$\begin{aligned} \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}^{div}} \ \text { and }\ \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}} \end{aligned}$$

are related, the former maps to the latter via the morphism of bundle stacks

$$\begin{aligned} h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}^{div}}^{\vee }\right) \ \longrightarrow \ h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}^{\vee }\right) , \end{aligned}$$

which is actually an affine $T_{\widetilde{\mathfrak {M}}^{div}/\widetilde{\mathfrak {M}}}$-bundle, that is, the morphism is fit in the exact sequence $T_{\widetilde{\mathfrak {M}}^{div}/\widetilde{\mathfrak {M}}}\rightarrow h^1/h^0(\mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}^{div}}^{\vee })\rightarrow h^1/h^0(\mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}^{\vee })$ of bundle stacks. The precise proof is in [29, Proposition 3], but it is more or less obvious thanks to the smoothness. Then the local computation of the cone on the LHS using the cut-out model (2.9) will give the computation of the cone on the RHS.

A solution to $\widetilde{\mathfrak {M}}^{line}$ is to consider the forgetful morphism $\widetilde{\mathfrak {M}}^{line} \rightarrow \widetilde{\mathfrak {M}}$. Since it is smooth as well the morphism of perfect obstruction theories

$$\begin{aligned} \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}\ \longrightarrow \ \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}^{line}}, \end{aligned}$$

induces the relationship of the two intrinsic normal cones

$$\begin{aligned} \mathfrak {C}_{ \widetilde{Q}_p / \widetilde{\mathfrak {M}}^{line}}\ \text { and }\ \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}, \end{aligned}$$

namely, the former maps to the latter via the morphism of bundle stacks

$$\begin{aligned} h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}^{line}}^{\vee }\right) \ \longrightarrow \ h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}^{\vee }\right) \end{aligned}$$

as before. It is also an affine $T_{\widetilde{\mathfrak {M}}^{line}/\widetilde{\mathfrak {M}}}$-bundle, and so is $\mathfrak {C}_{ \widetilde{Q}_p / \widetilde{\mathfrak {M}}^{line}}$ over $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}$.

4.2 Virtual cycles

As it is briefly explained in Sect. 1, the space $\widetilde{Q}_p$ is decomposed into four irreducible components

$$\begin{aligned} \widetilde{Q}_p \ =\ \widetilde{Q}_p^{\textrm{red}} \ \cup \ \widetilde{Q}_p^{(1)} \ \cup \ \widetilde{Q}_p^{(2)} \ \cup \ \widetilde{Q}_p^{(3)}, \end{aligned}$$

(3.1)

cf. the pictures in Introduction. From the local cut-out model (2.9) relative over $\widetilde{\mathfrak {M}}^{div}$, an étale local neighborhood of $\widetilde{Q}_p$ is the spectrum of a ring

$$\begin{aligned} R\,=\ B[x,p,v]\; /(c_1x_{1j}, c_2x_{2j},c_1p_{1i}, c_2p_{2i}), \end{aligned}$$

where $\textrm{Spec}(B)$ is a smooth neighborhood of $\widetilde{\mathfrak {M}}^{div}$. From this we can read the decomposition (3.1) as follows:

(1) Near a point in $\widetilde{Q}_p^{(1)}\setminus (\widetilde{Q}_p^{(2)}\cup \widetilde{Q}_p^{(3)})$, we have seen $c_2=1$ in Sect. 2.3. Hence there exists a neighbourhood of the image in $\mathfrak {M}$ whose inverse has irreducible components⁴

$$\begin{aligned} \widetilde{Q}_p^{(1)}= \{c_1=x_2=p_2=0\}, \ \ \widetilde{Q}_p^{\textrm{red}} = \{x=p=0\}. \end{aligned}$$

(2) Consider a point in $\widetilde{Q}_p^{(2)}$. As the point is a 2 : 1 image, we consider an étale neighbourhood. In this case, there exists an étale neighbourhood whose inverse image has

$$\begin{aligned} \widetilde{Q}_p^{(2)} =&\ \{c_1=c_2=0\} \;,\ \widetilde{Q}_p^{\textrm{red}}=\{x=p=0\}\;, \\ \widetilde{Q}_p^{(1)} =&\ \{c_1=x_2=p_2=0\}\cup \{c_2=x_1=p_1=0\}. \end{aligned}$$

Beware that this does not mean $\widetilde{Q}_p^{(1)}$ is reducible. The above description is on the étale neighbourhood. Note that $\widetilde{Q}_p^{(2)}$ does not meet $\widetilde{Q}_p^{(3)}$. So the neighbourhood can be chosen not to meet $\widetilde{Q}_p^{(3)}$.

(3) Near a point in $\widetilde{Q}_p^{(3)}\setminus \widetilde{Q}_p^{(1)}$, we have $c_2=1$. So there exists a neighbourhood whose inverse image has

$$\begin{aligned} \widetilde{Q}_p^{(3)}= \{c_1=x_2=p_2=0\}, \ \ \widetilde{Q}_p^{\textrm{red}} = \{x=p=0\}. \end{aligned}$$

(1$\;\cap \;$3) Near a point in $\widetilde{Q}_p^{(1)}\cap \widetilde{Q}_p^{(3)}$, $c_1$ is divisible by the two node smoothing functions, say $\zeta _1$ and $\zeta _3$ here. There exists a neighbourhood whose inverse image has

$$\begin{aligned} \widetilde{Q}_p^{(1)}= \{\zeta _1=x_2=p_2=0\}, \ \ \widetilde{Q}_p^{(3)}= \{\zeta _3=x_2=p_2=0\}, \ \ \widetilde{Q}_p^{\textrm{red}} = \{x=p=0\}. \end{aligned}$$

(4) Near a point outside $\widetilde{Q}_p^{(1)}\cap \widetilde{Q}_p^{(2)}\cap \widetilde{Q}_p^{(3)}$, we have $c_1=c_2=1$. Thus there exists a neighbourhood in $\widetilde{Q}_p$ on which $\textrm{Spec}(R)$ defines $\widetilde{Q}_p^{\textrm{red}}$.

Then the intrinsic normal cone $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}$ can be decomposed into

$$\begin{aligned} \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}} \ =\ \mathfrak {C}^{\textrm{red}}\ \cup \ \mathfrak {C}^{(1)}\ \cup \ \mathfrak {C}^{(2)}\ \cup \ \mathfrak {C}^{(3)} \ \cup \ \text {others}, \end{aligned}$$

(3.2)

each of the first four terms is defined to be the closure of the complement open part in $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}$. For instance,

$$\begin{aligned} \mathfrak {C}^{\textrm{red}}\ \text { is the closure of }\ \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}} |_{\widetilde{Q}_p \setminus \widetilde{Q}_p^{(1)} \cup \widetilde{Q}_p^{(2)} \cup \widetilde{Q}_p^{(3)}}\ \subset \ \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}. \end{aligned}$$

They are actually the closures in $h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}^{\vee }\right)$ since $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}\subset h^1/h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}^{\vee }\right)$ is a closed substack. In fact, one can check from the cut-out model (2.9) that ‘others’ in (3.2) is empty so that we obtain a decomposition

$$\begin{aligned} \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}} \ =\ \mathfrak {C}^{\textrm{red}}\ \cup \ \mathfrak {C}^{(1)}\ \cup \ \mathfrak {C}^{(2)}\ \cup \ \mathfrak {C}^{(3)}. \end{aligned}$$

(3.3)

Here is a brief explanation. Letting $A:=B[x,v,p]$, one can read the decomposition of $C_{R/A}:=C_{\textrm{Spec}R/\textrm{Spec}A}$, a pullback of $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}^{div}}$, from its spectrum of

$$\begin{aligned} \frac{R\; [X_{1j},X_{2j},P_{1i},P_{2i}]}{\left( \begin{array}{c} x_{1k}X_{1l}-x_{1l}X_{1k},\ x_{1k}P_{1l}-p_{1l}X_{1k},\ p_{1k}P_{1l}-p_{1l}P_{1k}, \\ x_{2k}X_{2l}-x_{2l}X_{2k},\ x_{2k}P_{2l}-p_{2l}X_{2k},\ p_{2k}P_{2l}-p_{2l}P_{2k} \end{array} \right) .} \end{aligned}$$

(3.4)

We know there are not higher order relations in $X_1,X_2,P_1,P_2$ in (3.4). Away from the intersections, the cone is a bundle on each irreducible component. So all relations are linear here. As Spec of (3.4) is the union of their closures which is contained in the cone, there should not be higher order relations on the intersections neither.

(1) Near a point over $\widetilde{Q}_p^{(1)}\setminus (\widetilde{Q}_p^{(2)}\cup \widetilde{Q}_p^{(3)})$ ($c_2=1$, $x_2=p_2=0$), $C_{R/A}$ is decomposed into irreducible components

$$\begin{aligned} C^{\;\!(1)}:= \{c_1=x_2=p_2=0\}, \ \ C^{\;\!\textrm{red}}:= \{x=p=0\}. \end{aligned}$$

We can check irreducibility as follows. We observe that $C^{\;\!\textrm{red}}$ is the bundle over the smooth variety $\textrm{Spec}(B[v])$ since $x=p=0$ kills the relations. In precise, it is the spectrum of

$$\begin{aligned} (B[v]/(c_1) )[X_{1j}, X_{2j}, P_{1i}, P_{2i}]. \end{aligned}$$

(3.5)

Therefore it is irreducible. On the other hand, we observe that $C^{\;\!(1)}$ is the spectrum of

$$\begin{aligned} \frac{(B[x_1,p_{1i},v]/(c_1) )[X_{1j}, X_{2j}, P_{1i}, P_{2i} ] }{ (x_{1k}X_{1l}-x_{1l}X_{1k},\ x_{1k}P_{1l}-p_{1l}X_{1k},\ p_{1k}P_{1l}-p_{1l}P_{1k}) }. \end{aligned}$$

This is a fibration over a smooth variety $\textrm{Spec}( B[v,X_{2j},P_{2i}]/(c_1) )$, whose fiber is an affine cone of the one-point blow-up $\textrm{Bl}_0 \mathbb {C}^{n+m}$ in the space $\mathbb {C}^{n+m} \times \mathbb {C}^{n+m}$. Thus it is also irreducible. We can show irreducibility of the components in other cases in a similar manner.

The irreducibility ensures these are the base changes of $\mathfrak {C}^{(1)}$ and $\mathfrak {C}^{\textrm{red}}$, respectively. Note that over $(x_1,p_1)\ne 0$, $C^{\;\!(1)}$ is a bundle because $X_2,P_2$ are free variables and $(X_1,P_1)$ should be proportional to $(x_1,p_1)$.

(2) Near a point over $\widetilde{Q}^{(2)}_p$, $C_{R/A}$ is decomposed into

$$\begin{aligned}&C^{\;\!(2)} := \{c_1=c_2=0\}, \ \ C^{\;\!(1)} := \{c_1=x_2=p_2=0\}\cup \{c_2=x_1=p_1=0\}, \\&\quad C^{\;\!\textrm{red}} := \{x=p=0\}. \end{aligned}$$

These are the base changes of $\mathfrak {C}^{(2)}$, $\mathfrak {C}^{(1)}$ and $\mathfrak {C}^{\textrm{red}}$, respectively. Over $(x_1,p_1)\ne 0$, $(x_2,p_2)\ne 0$, $C^{\;\!(2)}$ is a rank 2 bundle.

(3) Near a point over $\widetilde{Q}_p^{(3)}\setminus \widetilde{Q}_p^{(1)}$ ($c_2=1$, $x_2=p_2=0$), $C_{R/A}$ is decomposed into

$$\begin{aligned} C^{\;\!(3)}:= \{c_1=x_2=p_2=0\}, \ \ C^{\;\!\textrm{red}}:= \{x=p=0\}. \end{aligned}$$

These are the base changes of $\mathfrak {C}^{(3)}$ and $\mathfrak {C}^{\textrm{red}}$, respectively. Over $(x_1,p_1)\ne 0$, $C^{\;\!(3)}$ is a bundle.

(1$\;\cap \;$3) Near a point over $\widetilde{Q}^{(1)}_p\cap \widetilde{Q}^{(3)}_p$, $c_1$ is divisible by $\zeta _1\zeta _3$. In this case, $C_{R/A}$ is decomposed into

$$\begin{aligned} C^{\;\!(1)}:= \{\zeta _1=x_2=p_2=0\}, \ \ C^{\;\!(3)}:= \{\zeta _3=x_2=p_2=0\}, \ \ C^{\;\!\textrm{red}}:= \{x=p=0\}. \end{aligned}$$

Both $C^{\;\!(1)}$ and $C^{\;\!(3)}$ are bundles over $(x_1,p_1)\ne 0$.

(4) Near a point over $\widetilde{Q}^{\textrm{red}}_p\setminus (\widetilde{Q}_p^{(1)}\cap \widetilde{Q}_p^{(2)}\cap \widetilde{Q}_p^{(3)})$ ($c_1=c_2=1$, $x=p=0$), $C_{R/A}$ is $C^{\;\!\textrm{red}} = \{x=p=0\}$ which is a bundle.

So we could check there is no ‘others’ in $\mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}^{div}}$. Combining this with the (local) equivalence of

$$\begin{aligned} \mathfrak {C}_{ \widetilde{Q}_p / \widetilde{\mathfrak {M}} }\ \text { and }\ \mathfrak {C}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}^{div}} \ = \ [C_{R/A} /T_{A/B}|_R ] \end{aligned}$$

discussed in Sect. 3.1 gives the decomposition (3.3).

Note that the cut-out model (2.9) tells us the morphism $d(c \circ \tau ):T_A|_R \rightarrow C_{R/A}$ (defining the quotient via the composition $T_{A/B}\rightarrow T_A$) takes

$$\begin{aligned} \partial _{x_1}, \partial _{x_2}, \partial _{p_1}, \partial _{p_2} \ {}&\longmapsto \ c_1\partial _{X_1}, c_2\partial _{X_2}, c_1\partial _{P_1}, c_2\partial _{P_2}, \nonumber \\ \partial _{c_1}, \partial _{c_2} \ {}&\longmapsto \ \sum _jx_{1j}\partial _{X_{1j}} + \sum _ip_{1i}\partial _{P_{1i}}, \sum _jx_{2j}\partial _{X_{2j}} + \sum _ip_{2i}\partial _{P_{2i}}, \end{aligned}$$

(3.6)

because $X_1\circ c\circ \tau =c_1x_1$, $X_2\circ c\circ \tau =c_2x_2$, $P_1\circ c\circ \tau =c_1p_1$ and $P_2\circ c\circ \tau =c_2p_2$. So for instance, we have $dX_1(d(c\circ \tau )\partial _{x_1})=c_1$ which implies $d(c\circ \tau )\partial _{x_1}=c_1\partial _{X_1}$.

The cosection introduced in [6] defining the localised virtual cycle $[Q_p]^{\textrm{vir}} _{{\textrm{loc}} }$ mentioned in (1.5) is indeed defined on the obstruction sheaf $h^1\left( \mathbb {E}^\vee _{Q_p/\mathfrak {M}^{line}}\right)$ over $\mathfrak {M}^{line}$. So this gives a morphism $\mathbb {E}^\vee _{Q_p/\mathfrak {M}^{line}}\rightarrow \mathcal {O}_{Q_p}[-1]$ in the derived category. It is proven in [6] that this actually factors through the absolute dual perfect obstruction theory $\mathbb {E}^\vee _{Q_p}\rightarrow \mathcal {O}_{Q_p}[-1]$. So the composition $\mathbb {E}^\vee _{Q_p/\mathfrak {M}}\rightarrow \mathbb {E}^\vee _{Q_p}\rightarrow \mathcal {O}_{Q_p}[-1]$ defines the cosection localised Gysin map on the bundle stack $h^1/h^0(\mathbb {E}^\vee _{Q_p/\mathfrak {M}})$ [28].

For Definition below, we use the perfect obstruction theory over $\widetilde{\mathfrak {M}}$

. The pullback $\mathbb {E}^\vee _{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}\rightarrow \mathcal {O}_{\widetilde{Q}_p}[-1]$ of the above then defines the cosection localised Gysin map on the bundle stack $h^1/h^0(\mathbb {E}^\vee _{\widetilde{Q}_p/\widetilde{\mathfrak {M}}})$. We apply this to the decomposition 3.3.

Definition 3.1

The virtual cycle of the reduced part

$$\begin{aligned}{}[\widetilde{Q}^{\textrm{red}}_p]^{\textrm{vir}} \ \in \ A_{\textrm{vdim}} (\widetilde{Q}_X \cap \widetilde{Q}^{\textrm{red}}_p) \end{aligned}$$

is defined by the image of $[\mathfrak {C}^{\textrm{red}}]$ by the cosection localised Gysin map. The cycles $[\widetilde{Q}^{(1)}_p]^{\textrm{vir}}$, $[\widetilde{Q}^{(2)}_p]^{\textrm{vir}}$ and $[\widetilde{Q}^{(3)}_p]^{\textrm{vir}}$ are similarly defined by using $[\mathfrak {C}^{(1)}]$, $[\mathfrak {C}^{(2)}]$ and $[\mathfrak {C}^{(3)}]$ respectively.

Hence we obtain a decomposition of the virtual class

$$\begin{aligned}{}[\widetilde{Q}_{p}]^{\textrm{vir}} _{\textrm{loc}} \ =\ [\widetilde{Q}_p^{\textrm{red}}]^{\textrm{vir}} \ +\ [\widetilde{Q}_p^{(1)}]^{\textrm{vir}} \ +\ [\widetilde{Q}_p^{(2)}]^{\textrm{vir}} \ +\ [\widetilde{Q}_p^{(3)}]^{\textrm{vir}} \end{aligned}$$

providing (1.7) by the pushdown.

5 Quantum Lefschetz property for the reduced virtual cycle

Consider the bundle $V:=V_{2,0,d}$ in Theorems 1 and 2, which is precisely defined to be

$$\begin{aligned} V\,=\ \oplus _i \pi _*\mathcal {L}^{\otimes \ell _i}\ =\ h^0\left( \mathbb {E}_{\widetilde{Q}_p/\widetilde{Q}(\mathbb {P}^n)}[-1]|_{\widetilde{Q}_p^{\textrm{red}}}\right) , \end{aligned}$$

where $\mathcal {L}$ is the universal line bundle on the universal curve $\pi :\mathcal {C}\rightarrow \widetilde{Q}^{\textrm{red}}_p$. As in Sect. 2.5, by replacing $\mathcal {L}$ with $\mathcal {O}(\mathcal {D})$ locally, we can use the local cut-out model (2.9) to check V is locally free, cf. [27, Proposition 2.1.3]. Beware that this does not mean $h^1(\mathbb {E}_{\widetilde{Q}_p/\widetilde{Q}(\mathbb {P}^n)}[-1]|_{\widetilde{Q}_p^{\textrm{red}}})$

is locally free. Each point in $\widetilde{Q}_p^{\textrm{red}}$ has a section data $u \in \Gamma (C, L^{\oplus n+1})$ via the morphism $\widetilde{Q}_p^{\textrm{red}} \hookrightarrow \widetilde{Q}_p$. Then, the defining equations of X, $f_1,\ldots , f_m$ takes the universal section u to a section $f(u) = (f_i(u))_{1\le i \le m} \in \Gamma \left( V\right)$ in $h^0$. It defines the refined Euler class $e^{\textrm{ref}}(V)$ for Theorems 1 and 2.

Before proving the following proposition, note that we can prove it almost in a same manner as [33, Proposition 4.1], [34, Section 4.3]. But here, we will give another proof.

Note that $(-1)^{\textrm{rank}V}=(-1)^{d(\sum _i \ell _i) - m}$ and $\widetilde{Q}^{\textrm{red}}_p = \widetilde{Q}^{\textrm{red}}(\mathbb {P}^n)$, which is smooth.

Proposition 4.1

The reduced virtual cycle satisfies the original quantum Lefschetz formula (0.1)

$$\begin{aligned}{}[\widetilde{Q}^{\textrm{red}}_p]^{\textrm{vir}} \ =\ (-1)^{d(\sum _i \ell _i) - m}e^{\textrm{ref}}(V) \ \cap \ [\widetilde{Q}^{\textrm{red}}(\mathbb {P}^n)]. \end{aligned}$$

Proof

Consider the induced perfect obstruction theory, that comes from the cut-out model (2.9), and its restriction over $\widetilde{Q}^{\textrm{red}}_{p}$ ($\widetilde{Q}_p^{red}$ is an open dense subset of $\widetilde{\mathfrak {M}}^{div} \times \prod _{j=1}^n(\mathbb {C}^{d-1})$). It induces a local representative of $\mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}}$, which is

$$\begin{aligned} \widetilde{Q}^{\textrm{red}}_{p} \times \mathbb {C}^{2n} \times \mathbb {C}^{2m} \times \prod _{j=1}^n \mathbb {C}^{d-1} \ {}&\longrightarrow \ \widetilde{Q}^{\textrm{red}}_{p} \times F:= \mathbb {C}^{2n} \times \mathbb {C}^{2m} \times \prod ^m_{i=1} \mathbb {C}^{d\ell _i-1} , \\ u\times (x_{1j}, x_{2j}, p_{1i}, p_{2i}, v_j )\ {}&\longmapsto \ u \times (c_1 x_{1j}, c_2 x_{2j}, c_1p_{1i}, c_2p_{2i}, 0 ). \nonumber \end{aligned}$$

(4.1)

The cone decomposition in Sect. 3.2, (3.5) says that

$$\begin{aligned} C^{\textrm{red}} = \widetilde{Q}^{\textrm{red}}_{p} \times \mathbb {C}^{2n} \times \mathbb {C}^{2m} \subset F. \end{aligned}$$

(4.2)

On the other hand, we have the following morphism:

$$\begin{aligned} h^1/h^0 \left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}} \right) \rightarrow h^1 \left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}} \right) \rightarrow h^1\left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{Q}(\mathbb {P}^n) }|_{\widetilde{Q}_p^\textrm{red}} \right) \rightarrow V^{\vee }. \end{aligned}$$

Here, the first arrow is the morphism from the bundle stack to its coarse moduli space, which is also a stack. The second arrow comes from the decomposition

$$\begin{aligned} h^1\left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} } \right) = p^* h^1\left( \mathbb {E}^{\vee }_{\widetilde{Q}(\mathbb {P}^n) / \widetilde{\mathfrak {M}} } \right) \oplus h^1\left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{Q}(\mathbb {P}^n) } \right) \end{aligned}$$

for the projection $p: \widetilde{Q}_p \rightarrow \widetilde{Q}(\mathbb {P}^n)$, which comes from [32, (3.15)]. The third arrow is the canonical morphism.

The local representative of $\mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}}$, (4.1), says that the composition $h^1/h^0 \left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}} \right) \rightarrow V^{\vee }$ is an epimorphism. Moreover, (4.2) says that its kernel is locally represented by $C^\textrm{red}$ in F, therefore it is equal to $\mathfrak {C}^{red} \subset h^1/h^0 \left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}} \right)$.

Hence, by using the functorial property of the cosection localised Gysin map [36, Theorem 1.4], we have

$$\begin{aligned}{}[\widetilde{Q}_p^\textrm{red}]^{\textrm{vir}} = 0^!_{ h^1/h^0 \left( \mathbb {E}^{\vee }_{\widetilde{Q}_p / \widetilde{\mathfrak {M}} }|_{\widetilde{Q}_p^\textrm{red}} \right) , {\textrm{loc}} } [\mathfrak {C}^\textrm{red}] = 0^!_{V^\vee , f(u)^\vee }[\widetilde{Q}_p^\textrm{red}]. \end{aligned}$$

Note that the composition of $\mathbb {E}^\vee _{\widetilde{Q}_p}|_{\widetilde{Q}_p^{\textrm{red}}}\rightarrow V^\vee [-1]$

with $f(u)^\vee [-1]$ is the given cosection. Hence $[\widetilde{Q}_p^\textrm{red}]^{\textrm{vir}}$ is equal to

$$\begin{aligned} 0^!_{V^\vee , f(u)^\vee }[\widetilde{Q}_p^\textrm{red}]\ =\ (-1)^{{{\,\textrm{rank}\,}}V}e^{\textrm{ref}}(V,f(u)) \ =\ (-1)^{{{\,\textrm{rank}\,}}V} e^{\textrm{ref}}(V). \end{aligned}$$

$\square$

6 Lower genus contributions from the rest cycles

6.1 Cones in the obstruction bundle

In this section we consider our space $\widetilde{Q}_p$ over $\widetilde{\mathfrak {M}}$, so use the perfect obstruction theory $\mathbb {E}_{\widetilde{Q}_p /\widetilde{\mathfrak {M}}}$, the decomposition (3.3) and Definition 3.1 for virtual cycles. Letting

$$\begin{aligned} A\,=\ \widetilde{\mathfrak {M}}^{div} \times \prod _{j=1}^{n} \left( \mathbb {C}^{2} \times \mathbb {C}^{d-1}\right) \times \mathbb {C}^{2m} \end{aligned}$$

be the local smooth space of the cut-out model (2.9) having forgetful map $A\rightarrow \widetilde{\mathfrak {M}}$, the dual perfect obstruction theory $\mathbb {E}^{\vee }_{\widetilde{Q}_p /\widetilde{\mathfrak {M}}}$ is locally isomorphic to

$$\begin{aligned} \left. \left[ \, T_{A/\widetilde{\mathfrak {M}}} \ \xrightarrow {d(c \circ \tau )} \ \mathcal {O}_A^{\oplus 2n} \oplus \bigoplus _i \mathcal {O}_A^{\oplus d\ell _i +1} \, \right] \right| _{\widetilde{Q}_p}. \end{aligned}$$

Using this local expression we check that $h^{-1} \left( \mathbb {E}_{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}|_{\widetilde{Q}_p^{(i)}} \right)$

is locally free. We denote its dual by $E^{(i)}$. Note that $E^{(i)}$ is not $h^{1}\left( \mathbb {E}^\vee _{\widetilde{Q}_p / \widetilde{\mathfrak {M}}}|_{\widetilde{Q}_p^{(i)}}\right)$

which is not locally free on the intersection. Outside of the intersection, they are isomorphic. So $E^{(i)}$ is the obstruction bundle there. There is an induced morphism from the bundle $E^{(i)}$ to the obstruction sheaf which is an isomorphism outside of the intersection, but it is not even an injection on the intersection.

Picking any global locally free representative $[F_0 {\mathop {\longrightarrow }\limits ^{d}} F_1]$ of $\mathbb {E}^\vee _{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}$, we obtain a diagram

Using this we define $C^{(i)}\hookrightarrow E^{(i)}$ to be the image of the pullback of $\mathfrak {C}^{(i)}\hookrightarrow [F_1/F_0]$. Then by the functorial property [36, Theorem 1.4] the cycle $0^!_{E^{(i)},\text {loc}}[C^{(i)}]$

is $[\widetilde{Q}_p^{(i)}]^{\textrm{vir}}$ by Definition 3.1. We denote this Kiem-Li’s cosection localised Gysin map $0^!_{E^{(i)},\text {loc}}$ by $e^{\textrm{KL}}(E^{(i)})$⁵ so that we can write

$$\begin{aligned}{}[\widetilde{Q}_p^{(i)}]^{\textrm{vir}} \ =\ e^{\textrm{KL}}(E^{(i)})\cap [C^{(i)}]. \end{aligned}$$

(5.1)

Now we consider other intrinsic normal cones $\mathfrak {C}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}}$ of $\widetilde{Q}_p^{(i)}$

over $\widetilde{\mathfrak {M}}$. Since $\widetilde{Q}_p^{(i)}$ is smooth over its image in $\widetilde{\mathfrak {M}}$, we obtain the perfect tangent complex $\mathbb {T}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}} }\cong \left[ T_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}^{(i)}}\ \xrightarrow {0} N_{\widetilde{\mathfrak {M}}^{(i)}/\widetilde{\mathfrak {M}}}(Z_i)|_{\widetilde{Q}_p^{(i)}} \right]$

, where $\widetilde{\mathfrak {M}}^{(i)}\subset \widetilde{\mathfrak {M}}$ is the image of

• (1) $\widetilde{\mathfrak {M}}_{1,1,0} \times \widetilde{\mathfrak {M}}_{1,1,d}$,

• (2) $\widetilde{\mathfrak {M}}_{1,1,0} \times \widetilde{\mathfrak {M}}_{0,2,d} \times \widetilde{\mathfrak {M}}_{1,1,0}$,

• (3) $\widetilde{\mathfrak {M}}_{1,2,0} \times \widetilde{\mathfrak {M}}_{0,2,d}$,

under the node-identifying morphism. Here, $Z_i\subset \widetilde{\mathfrak {M}}^{(i)}$

denotes the divisor defined to be the intersection $\widetilde{\mathfrak {M}}^{(1)}\cap \widetilde{\mathfrak {M}}^{(3)}$ when $i=1,3$ and $Z_2=\emptyset$. We need this twisting by $Z_i$ because locally the normal bundle of $Z(\zeta _1\zeta _3)$ restricted to $Z(\zeta _1)$ is different from that of $Z(\zeta _1)$ by the divisor of the intersection. Then the cone $\mathfrak {C}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}}$

is isomorphic to the bundle stack $h^1/h^0(\mathbb {T}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}})$

. We define its pullback

$$\begin{aligned} C_{(i)}\,=\ N_{\widetilde{\mathfrak {M}}^{(i)}/\widetilde{\mathfrak {M}}}(Z_i)|_{\widetilde{Q}_p^{(i)}}. \end{aligned}$$

Then the composition $\mathbb {T}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}} \rightarrow \mathbb {T}_{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}|_{\widetilde{Q}_p^{(i)}}\rightarrow \mathbb {E}^\vee _{\widetilde{Q}_p/\widetilde{\mathfrak {M}}}|_{\widetilde{Q}_p^{(i)}}$ defines the morphism

$$\begin{aligned} C_{(i)} \ \longrightarrow \ \mathfrak {C}_{\widetilde{Q}_p^{(i)}/\widetilde{\mathfrak {M}}^{(i)}}\times _{[F_1/F_0]} F_1\ \longrightarrow \ F_1|_{\widetilde{Q}_p^{(i)}}\ \longrightarrow \ E^{(i)}. \end{aligned}$$

(5.2)

Using (3.6), we see that the first arrow is locally

• (1) $\partial _{c_1} \in C_{(1)} \longmapsto d(c \circ \tau )(\partial _{c_1})$,

• (2) $\partial _{c_1}, \partial _{c_2} \in C_{(2)} \longmapsto d(c \circ \tau )(\partial _{c_1}), d(c \circ \tau )(\partial _{c_2})$,

• (3) $\partial _{c_1} \in C_{(3)} \longmapsto d(c \circ \tau )(\partial _{c_1})$.

Since $d(c \circ \tau )(\partial _{c_1})$ annihilates the defining equations of $C^{(i)}$, for instance

$$\begin{aligned} d(c \circ \tau )(\partial _{c_1}) (d(x_{1l}X_{1k}-x_{1k}X_{1l}))\ =\ 0, \end{aligned}$$

the morphism $C_{(i)} \rightarrow E^{(i)}$ factors through

$$\begin{aligned} C_{(i)}\ \longrightarrow \ C^{(i)}\ \hookrightarrow \ E^{(i)}. \end{aligned}$$

Outside of the intersections with other components, $C_{(i)}$ maps isomorphic to $C^{(i)}\subset E^{(i)}$. On the intersections it maps to zero as $d(c \circ \tau )(\partial _{c_j})$ vanishes on either $x_1=p_1=0$ or $x_2=p_2=0$. Since $C_{(i)}$ is a bundle we may expect an advantage of using $C_{(i)}$ instead of $C^{(i)}$ for computing (5.1). This is not an absurd fantasy since they are isomorphic outside of the intersections.

Example 5.1

The local structure ring (3.4) tells us that $C^{(1)}$ is (locally) the spectrum of

$$\begin{aligned} \frac{R/(x_2,p_2,c_1) \; [X_{1j},P_{1i}]}{\left( \begin{array}{c} x_{1k}X_{1l}-x_{1l}X_{1k},\ x_{1k}P_{1l}-p_{1l}X_{1k},\ p_{1k}P_{1l}-p_{1l}P_{1k} \end{array} \right) .} \end{aligned}$$

So $C^{(1)}$ is a line bundle over $(x_1,p_1)\ne 0$, but has the full rank at $(x_1,p_1)=0$. Meanwhile by its definition $C_{(1)}$

is (locally) the spectrum of $R/(x_2,p_2,c_1)[Y]$, where the variable Y is a coordinate of $\partial _{c_1}$. Hence $C_{(1)}$ is a line bundle. The morphism $C_{(1)} \rightarrow C^{(1)}$ is

$$\begin{aligned} X_{1j} \ \longmapsto \ x_{1j}Y, \ \ \ P_{1i} \ \longmapsto \ p_{1i}Y. \end{aligned}$$

It maps isomorphically over $(x_1,p_1)\ne 0$, but zero over $(x_1,p_1)=0$.

Over the blowup B of $R/(x_2,p_2,c_1)$ along $(x_1,p_1)=0$ with the homogeneous coordinate functions ${\textbf{x}}_1,{\textbf{p}}_1$, we consider the cone

$$\begin{aligned} \frac{B \; [X_{1j},P_{1i}]}{\left( \begin{array}{c} \textbf{x}_{1k}X_{1l}-\textbf{x}_{1l}X_{1k},\ \textbf{x}_{1k}P_{1l}-\textbf{p}_{1l}X_{1k},\ \textbf{p}_{1k}P_{1l}-\textbf{p}_{1l}P_{1k} \end{array} \right) } \end{aligned}$$

pushed down to $C^{(1)}$ along the blowdown morphism. The pullback cone $C_{(1)}|_B$ maps to this cone, which is isomorphic outside of the exceptional locus. Since it is a morphism between line bundles, the cone is isomorphic to $C_{(1)}|_B$ twisted by the exceptional divisor. Hence we can use its pushdown instead of $[C^{(1)}]$ in (5.1).

6.2 Outline of the proof of Theorem 2

Letting $p_1=p_2=0$, (2.9) gives a local cut-out model of $\widetilde{Q}:=\widetilde{Q}(\mathbb {P}^n)$. The decomposition (3.1) of $\widetilde{Q}_p$ then gives rise to the corresponding one of $\widetilde{Q}$,

$$\begin{aligned} \widetilde{Q}\ =\ \widetilde{Q}^{red}\ \cup \ \widetilde{Q}^{(1)}\ \cup \ \widetilde{Q}^{(2)}\ \cup \ \widetilde{Q}^{(3)}. \end{aligned}$$

Then the components $\widetilde{Q}^{(i)}$ are the images of the following node-identifying morphisms

• (1) $\tilde{\iota }_{1}: \overline{M}_{1,1} \times \widetilde{Q}^{\textrm{red}}_{1,1,d} \hookrightarrow \widetilde{Q}$,

• (2) $\tilde{\iota }_{2}: \overline{M}_{1,1} \times Q_{0,2,d} \times \overline{M}_{1,1} {\mathop {\longrightarrow }\limits ^{2:1}} \widetilde{Q}$,

• (3) $\tilde{\iota }_{3}: \overline{M}_{1,2} \times \mathbb {P}Q'_{0,2,d} \hookrightarrow \widetilde{Q}$.

In (1), $\widetilde{Q}^{\textrm{red}}_{1,1,d}$ is the blowup of $Q^{\textrm{red}}_{1,1,d}$ along $\overline{M}_{0,3}\times Q'_{0,2,d}$, where $Q'_{0,2,d}\subset Q_{0,2,d}$ is defined by $\textrm{ev}_1=\textrm{ev}_2$. The blowup locus is a part of the intersection $\overline{M}_{1,1}\times \overline{M}_{0,3}\times Q'_{0,2,d}$ of (1) and (3) before the blowup. In (3), $\mathbb {P}Q'_{0,2,d}$

denotes the projectivisation of $\mathbb {L}_1^{\vee }\oplus \mathbb {L}_2^{\vee }$, sum of dual tautological line bundles over $Q'_{0,2,d}$. The following Remark explains why $\widetilde{Q}^{(3)}$ is the image of $\tilde{\iota }_{3}$.

Remark 5.2

In fact, $\widetilde{Q}^{(3)}$ should be (the image of) projectivisation of the pullback of

$$\begin{aligned} N_{\mathfrak {M}_{1,2,0}\times \mathfrak {M}_{0,2,d}/\mathfrak {M}_{2,0,d}}\ \cong \ (\mathbb {L}^{\vee }_{1} \boxtimes \mathbb {L}^{\vee }_{1}) \oplus (\mathbb {L}^{\vee }_{2} \boxtimes \mathbb {L}^{\vee }_{2}) \end{aligned}$$

on $\overline{M}_{1,2} \times Q'_{0,2,d}$ since $\widetilde{Q}$ is the base change of the blowup. It is equal to $\overline{M}_{1,2} \times \mathbb {P}Q'_{0,2,d}$

if $\mathbb {L}_1\cong \mathbb {L}_2$ on $\overline{M}_{1,2}$. Note that the evaluation map $H^0(\omega _C)\otimes T_{C,a_j} \rightarrow \mathbb {C}$ induces a morphism $\mathcal {H}\rightarrow \mathbb {L}_j$ from Hodge to tautological line bundle on $\overline{M}_{1,2}$. In [43, pp.1221–1222], Zinger proved that it maps isomorphically to

$$\begin{aligned} \mathcal {H}\ \xrightarrow {\ \sim \ }\ \mathbb {L}_j(-D)\ \hookrightarrow \ \mathbb {L}_j, \end{aligned}$$

where $D= \overline{M}_{1,1}\times \overline{M}_{0,3} \hookrightarrow \overline{M}_{1,2}$ is a boundary divisor of a collision of the two marked points. Thus we have $\mathbb {L}_1 \cong \mathcal {H}(D) \cong \mathbb {L}_2.$

As we have mentioned in Sect. 1, local computation with (2.9) tells us that the i-th p-field space $\widetilde{Q}_p^{(i)}$ is a vector bundle over $\widetilde{Q}^{(i)}$,

$$\begin{aligned} \widetilde{Q}_p^{(i)}\ \cong \ h^0 \left( \left. \left( \oplus _{j=1}^m R\pi _* \left( \mathcal {L}^{-\ell _j}\otimes \omega _{\mathcal {C}_{\widetilde{Q}}} \right) \right) \right| _{\widetilde{Q}^{(i)}} \right) . \end{aligned}$$

To avoid a confusion, we denote it by $P^{(i)}$ when we consider it as a bundle or as a locally free sheaf of local sections of $\widetilde{Q}_p^{(i)}\rightarrow \widetilde{Q}^{(i)}$, but use $\widetilde{Q}_p^{(i)}$ for the space. So the pullback of $P^{(i)}$ on $\widetilde{Q}_p^{(i)}$ is the tautological bundle. On $\widetilde{Q}_p^{(i)}$, the obstruction bundle $E^{(i)}$ was defined in Sect. 5.1. It is proven in [32, Equation (3.15)] that $E^{(i)}$ is decomposed into $E^{(i)}=E_1^{(i)}\oplus E_2^{(i)}$,

$$\begin{aligned} E_1^{(i)} = h^{-1} \left. \left( \mathbb {E}_{\widetilde{Q} / \widetilde{\mathfrak {M}}}|_{\widetilde{Q}^{(i)}} \right) \right| ^\vee _{\widetilde{Q}_p^{(i)}}, \ \ E_2^{(i)}= R^1\pi _* \left( \oplus _{i=1}^m \mathcal {L}^{\otimes -\ell _i} \otimes \omega _{\mathcal {C}} \right) \cong \pi _* \left( \oplus _{i=1}^m \mathcal {L}^{\otimes \ell _i}\right) ^\vee . \end{aligned}$$

From now on for simplicity, we denote by $\textbf{Q}^{(i)}$ the domain of the morphism $\tilde{\iota }_i$, by $\textbf{Q}_p^{(i)}$ the fiber product $\textbf{Q}^{(i)}\times _{Q^{(i)}}Q^{(i)}_p$ and by $\textbf{P}^{(i)}$ the pullback of $P^{(i)}$. Explicitly,

• (1) $\textbf{Q}^{(1)} = \overline{M}_{1,1} \times \widetilde{Q}_{1,1,d}^\textrm{red}$,

• (2) $\textbf{Q}^{(2)} = \overline{M}_{1,1} \times Q_{0,2,d} \times \overline{M}_{1,1}$,

• (3) $\textbf{Q}^{(3)} = \overline{M}_{1,2} \times \mathbb {P}Q'_{0,2,d}$,

and the bundle $\textbf{P}^{(i)}$ is

• (1) $\textbf{P}^{(1)} = \mathcal {H}\, \boxtimes \, \oplus _{i=1}^m \textrm{ev}^* \mathcal {O}_{\mathbb {P}^n}(-\ell _i)$,

• (2) $\textbf{P}^{(2)} = \left( \mathcal {H}\boxtimes \oplus _{i=1}^m \textrm{ev}_1^* \mathcal {O}_{\mathbb {P}^n}(-\ell _i) \boxtimes \mathcal {O}_{\overline{M}_{1,1}} \right) \bigoplus \left( \mathcal {O}_{\overline{M}_{1,1}} \boxtimes \oplus _{i=1}^m \textrm{ev}_2^* \mathcal {O}_{\mathbb {P}^n}(-\ell _i) \boxtimes \mathcal {H}\right)$,

• (3) $\textbf{P}^{(1)} = \mathcal {H}\, \boxtimes \, \oplus _{i=1}^m \textrm{ev}_1^* \mathcal {O}_{\mathbb {P}^n}(-\ell _i)$.

Recall that in (3), the two evaluation maps are the same $\textrm{ev}_1=\textrm{ev}_2$. We denote by

$$\begin{aligned} \tilde{\iota }_{p,i}\,\ \textbf{Q}_p^{(i)}\ \longrightarrow \ \widetilde{Q}_p^{(i)}. \end{aligned}$$

the base change of the node-identifying morphism $\widetilde{\iota }_i$. and let $\textbf{E}^{(i)}:= \tilde{\iota }_{p,i}^* E^{(i)}$. Then the decomposition $\textbf{E}^{(i)}=\textbf{E}_1^{(i)}\oplus \textbf{E}_2^{(i)}$ is

• (1) $\textbf{E}_1^{(1)} = \mathcal {H}^\vee \boxtimes \textrm{ev}^*T_{\mathbb {P}^n}$, $\textbf{E}_2^{(1)} = \mathcal {O}_{\overline{M}_{1,1}}\boxtimes (\oplus _i \pi _*\mathcal {L}^{\otimes \ell _i})^{\vee }$,

• (2) $\textbf{E}_1^{(2)} = \left( \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_{\mathbb {P}^n}\boxtimes \mathcal {O}_{\overline{M}_{1,1}}\right) \oplus \left( \mathcal {O}_{\overline{M}_{1,1}} \boxtimes \textrm{ev}_2^*T_{\mathbb {P}^n}\boxtimes \mathcal {H}^\vee \right)$, $\textbf{E}_2^{(2)} = \mathcal {O}_{\overline{M}_{1,1}} \boxtimes \left( \oplus _i \pi _*\mathcal {L}^{\otimes \ell _i} \right) ^{\vee }\boxtimes \mathcal {O}_{\overline{M}_{1,1}}$,

• (3) $\textbf{E}_1^{(3)} = \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_{\mathbb {P}^n}$, $\textbf{E}_2^{(3)} = \mathcal {O}_{\overline{M}_{1,2}}\boxtimes (\oplus _i \pi _*\mathcal {L}^{\otimes \ell _i})^{\vee }$.

Then the pullback cosection $\sigma ^{(i)}: \textbf{E}^{(i)} \rightarrow \mathcal {O}_{\textbf{Q}^{(i)}_p}$ is decomposed into

$$\begin{aligned} \sigma _1^{(i)}: \textbf{E}_1^{(i)} \rightarrow \mathcal {O}_{\textbf{Q}^{(i)}_p}\ \text { and }\ \sigma _2^{(i)}: \textbf{E}_2^{(i)} \rightarrow \mathcal {O}_{\textbf{Q}^{(i)}_p}. \end{aligned}$$

The cosection on the dual perfect obstruction theory (1.4) is decomposed into p.(df/dx)

and f. These correspond to $\sigma _1^{(i)}$ and $\sigma _2^{(i)}$, respectively.

Using these cosections, we can define Kiem-Li’s cosection localised Gysin maps $e^{\textrm{KL}}(\textbf{E}^{(i)})$

and $e^{\textrm{KL}}(\textbf{E}^{(i)}_j)$. Letting ${\textbf{C}}^{(i)}:= \tilde{\iota }_{p,i}^* C^{(i)}$, the multiplicative property of $e^{\textrm{KL}}$ [36, Theorem 1.4] tells us that (5.1) becomes

$$\begin{aligned}{}[\widetilde{Q}_p^{(i)}]^{\textrm{vir}}&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_*\left( e^{\textrm{KL}}(\textbf{E}^{(i)})\cap [\textbf{C}^{(i)}]\right) \\&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_*\left( e^{\textrm{KL}}(\textbf{E}_1^{(i)}) \cap e^{\textrm{KL}}(\textbf{E}_2^{(i)}) \cap [\textbf{C}^{(i)}] \right) . \nonumber \end{aligned}$$

(5.3)

Since the second cosection $\sigma ^{(i)}_2$ on $\textbf{E}^{(i)}_2\cong (\oplus _i \pi _*\mathcal {L}^{\otimes \ell _i})^\vee$

is defined by the (dual of) defining equation f as on V in Sect. 4, the cycle $e^{\textrm{KL}}(\textbf{E}_2^{(i)})\cap [\textbf{C}^{(i)}]$ is supported on

$\textbf{E}_1^{(i)} \times _{\textbf{Q}^{(i)}_p} Z((\sigma ^{(i)}_2)^\vee )\cong \textbf{E}_1^{(i)} \times _{\textbf{Q}^{(i)}_p} Z(f(u))$, where f(u) is the pullback equation on $Q(\mathbb {P}^n)$ defined in (1.1). This support is isomorphic to $\textbf{E}_1^{(i)} \times _{\textbf{Q}^{(i)}_p} \textbf{Q}^{(i)}_p(X)$

, where $\textbf{Q}^{(i)}_p(X):=\textbf{Q}^{(i)}_p\times _{Q(\mathbb {P}^n)} Q(X)$. Then the restriction of the first cosection $\sigma ^{(i)}_1$

to this support $\textbf{E}_1^{(i)} \times _{\textbf{Q}^{(i)}_p} \textbf{Q}^{(i)}_p(X)$ is induced by the surjection

$$\begin{aligned} df\,\ T_{\mathbb {P}^n}|_X\ \twoheadrightarrow \ \oplus _i \mathcal {O}_{\mathbb {P}^n}(\ell _i)|_X \end{aligned}$$

whose kernel is $\ker (df) = T_X$, as follows. On $\textbf{Q}^{(i)}_p(X)$, df defines a short exact sequence of bundles

$$\begin{aligned} 0\ \longrightarrow \ \textbf{K}^{(i)}\ \longrightarrow \ \textbf{E}^{(i)}_1\ \longrightarrow \ (\textbf{P}^{(i)})^\vee \ \longrightarrow \ 0, \end{aligned}$$

(5.4)

where

• (1) $\textbf{K}^{(1)}:= \mathcal {H}^\vee \boxtimes \textrm{ev}^*T_X$,

• (2) $\textbf{K}^{(2)}:= \left( \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_X\boxtimes \mathcal {O}_{\overline{M}_{1,1}}\right) \oplus \left( \mathcal {O}_{\overline{M}_{1,1}} \boxtimes \textrm{ev}_2^*T_X\boxtimes \mathcal {H}^\vee \right)$,

• (3) $\textbf{K}^{(3)}:= \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_X$.

Then the tautological section of $\textbf{P}^{(i)}$ defines a cosection of $(\textbf{P}^{(i)})^\vee$, and the composition defines a cosection of $\textbf{E}^{(i)}_1$ on $\textbf{Q}^{(i)}_p(X)$, which is the restriction of $\sigma ^{(i)}_1$. Applying the multiplicative property [36, Theorem 1.4] to the sequence (5.4), we have

$$\begin{aligned} e^{\textrm{KL}}\left( \textbf{E}_1^{(i)}\right) \cap \left( e^{\textrm{KL}}(\textbf{E}_2^{(i)}) \cap [\textbf{C}^{(i)}] \right) = e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap \left( e^{\textrm{KL}}(\textbf{E}_2^{(i)}) \cap [\textbf{C}^{(i)}] \right) , \end{aligned}$$

(5.5)

where $e^{\textrm{FM}}$ denotes the Fulton-MacPherson intersection homomorphism, or Gysin map.

In Sects. 5.3 and 5.4, we will explain the second and third equalities below, respectively. The rest equalities and notations are explained after the equations:

$$\begin{aligned}{}[\widetilde{Q}_p^{(i)}]^{\textrm{vir}}&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap \left( e^{\textrm{KL}}\left( \textbf{E}_2^{(i)}\right) \cap [\textbf{C}^{(i)}] \right) \right) \nonumber \\&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap \left( e^{\textrm{KL}}\left( \textbf{E}_2^{(i)}\right) \cap [\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p] \right) \right) \\ \nonumber&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap \left( e^{\textrm{KL}}\left( \textbf{E}_2^{(i)}\right) \cap [\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p] \right) \right) \\ \nonumber&= \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap [\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p(X)]^{\textrm{vir}} \right) \\ \nonumber&= \frac{(-1)^{m\cdot i}}{\deg (\tilde{\iota }_{i})}(\tilde{\iota }_{i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap \left[ \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)} \right] ^{\textrm{vir}} \right) \\ \nonumber&= \frac{(-1)^{m\cdot i}}{\deg (\tilde{\iota }_{i})}(\tilde{\iota }_{i})_* \left( e\left( \frac{\textbf{K}^{(i)}|_{\textbf{Q}^{(i)}(X)} }{\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)} } \right) \cap [\textbf{Q}^{(i)}(X)]^{\textrm{vir}} \right) . \end{aligned}$$

(5.6)

The first equality is from (5.3) and (5.5). We denote by $\textbf{C}_{(i)}$ the pullback of $C_{(i)}$ (5.2) to $\textbf{Q}^{(i)}_p$. Since $C_{(i)}$ is a bundle, so is $\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}$ over $\textbf{Q}^{(i)}$ which is smooth. Mimicking Proposition 4.1, we can prove $e^{\textrm{KL}}(\textbf{E}_2^{(i)}) \cap [\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p]$ is the pullback cycle of

• (1) $(-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{1,1,d}) \cap \left( [\overline{M}_{1,1}] \times [\widetilde{Q}_{1,1,d}^\textrm{red}(\mathbb {P}^n)]\right)$,

• (2) $(-1)^{d(\sum _i \ell _i)+m}e^{\textrm{ref}}(V_{0,2,d}) \cap \left( [\overline{M}_{1,1}] \times [Q_{0,2,d}(\mathbb {P}^n)] \times [\overline{M}_{1,1}]\right)$,

• (3) $(-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{0,2,d}) \cap \left( [\overline{M}_{1,2}] \times [\mathbb {P}Q'_{0,2,d}]\right)$,⁶

via $\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p(X)\rightarrow \textbf{Q}^{(i)}(X):=\textbf{Q}^{(i)}\times _{Q(\mathbb {P}^n)}Q(X)$.

We denote this pullback cycle by $[\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p(X)]^{\textrm{vir}}$. Hence this explains the fourth equality. Similarly, we denote the pullback cycle in $A_*(\textbf{Q}^{(i)}(X))$ by $[\textbf{Q}^{(i)}(X)]^{\textrm{vir}}$ and that in $A_*(\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)})$ by $[ \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)} ]^{\textrm{vir}}$.

The cosection on $(\textbf{P}^{(i)})^\vee$ is given by the tautological section of $\textbf{Q}^{(i)}_p(X)\cong \textbf{P}^{(i)}|_{\textbf{Q}^{(i)}(X)}$.

So we obtain the fifth equality. In Sect. 5.4, we will see the bundle $\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)}$(after twisting by a divisor) is contained in $\textbf{E}^{(i)}_1|_{\textbf{Q}^{(i)}(X)}$

. Since there is no p-fields, the composition of the tautological section of $\textbf{E}^{(i)}_1|_{\textbf{Q}^{(i)}(X)}$

and the homomorphism $\textbf{E}^{(i)}_1|_{\textbf{Q}^{(i)}(X)}\rightarrow (\textbf{P}^{(i)})^\vee |_{\textbf{Q}^{(i)}(X)}$

in (5.4) is zero on the cone. Hence the cone is contained in the kernel $\textbf{K}^{(i)}|_{\textbf{Q}^{(i)}(X)}$

, which proves the last equality.

In the RHS of the second equality we denote by $\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}$

the closure of the restriction of $\textbf{C}^{(i)}$ to $\textbf{Q}^{(i)}{\setminus } \text {intersections}$. Then the second equality holds if the cone $\textbf{C}^{(i)}$ is isomorphic to the product $\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p$.

Unfortunately $\textbf{C}^{(i)}$ is not the product, but we deform it to the product and then use this deformation to prove the second equality. We work this in Sect. 5.3.

We know $\textbf{C}_{(i)}\rightarrow \textbf{C}^{(i)}$ (5.2) is isomorphic outside of the intersection. Then taking twistings by divisors after blowups, it induces an isomorphism which implies the third equality. This work is addressed in Sect. 5.4.

After we get (5.6), we prove Theorem 2 in Sect. 5.5. When X is a Calabi-Yau 3-fold we prove Theorem 1 in Sect. 5.6.

6.3 Deformation of the cone

We start this section with our cone $\textbf{C}^{(i)}\hookrightarrow \textbf{E}^{(i)}=\textbf{E}^{(i)}_1\oplus \textbf{E}^{(i)}_2$. The intersection $\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)}\hookrightarrow \textbf{E}^{(i)}_2$ is defined to be a cut-out of $\textbf{C}^{(i)}$ by the tautological section of $\textbf{E}^{(i)}_1$. Hence we have

$$\begin{aligned} C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} / \textbf{C}^{(i)}}\ \hookrightarrow \ \textbf{E}^{(i)}_1\oplus \textbf{E}^{(i)}_2=\textbf{E}^{(i)} \end{aligned}$$

This cone is a deformation of $\textbf{C}^{(i)}$ via deformation to the normal cone [21, Chapter 5]. If we write $\textbf{C}^{(i)}=\{(x,p,X,P)\;|\;(x,p)\in \textbf{Q}^{(i)}_p,\, X\in \textbf{E}^{(i)}_1|_{(x,p)},\, P\in \textbf{E}^{(i)}_2|_{(x,p)}\}$, it is

$$\begin{aligned} C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} / \textbf{C}^{(i)}}=\lim _{t\rightarrow \infty }\{(x,p,tX,P)\;|\;(x,p,X,P)\in \textbf{C}^{(i)}_{}\}\ \hookrightarrow \ \textbf{E}^{(i)}_1\oplus \textbf{E}^{(i)}_2=\textbf{E}^{(i)}. \end{aligned}$$

Since $\sigma ^{(i)}_1$ and $\sigma ^{(i)}_2$ are independent of P and X, respectively, and they vanish on $\textbf{C}^{(i)}$, they are zero on $C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} / \textbf{C}^{(i)}}$ either.

Lemma 5.3

The restriction of the cone $C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} / \textbf{C}^{(i)}}$ to $\textbf{Q}_p^{(i)}\subset \textbf{C}^{(i)} \cap \textbf{E}_2^{(i)}$ is its component. Moreover it is isomorphic to a product

$$\begin{aligned} \left. C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} / \textbf{C}^{(i)}} \right| _{\textbf{Q}_p^{(i)}}\ \cong \ \textbf{C}^{(i)}_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}} \textbf{Q}^{(i)}_p. \end{aligned}$$

(5.7)

Other components vanish after taken by $e^{\textrm{KL}}(\textbf{E}^{(i)})$.

Proof

We prove this by using the local coordinate rings in Sect. 3.2 obtained by the cut-out model (2.9). Recall from (3.4) that locally $C^{(i)}$ is Spec of

$$\begin{aligned} \frac{R [X_{1j},X_{2j},P_{1i},P_{2i}]}{\left( \begin{array}{c} x_{1k}X_{1l}-x_{1l}X_{1k},\ x_{1k}P_{1l}-p_{1l}X_{1k},\ p_{1k}P_{1l}-p_{1l}P_{1k}, \\ x_{2k}X_{2l}-x_{2l}X_{2k},\ x_{2k}P_{2l}-p_{2l}X_{2k},\ p_{2k}P_{2l}-p_{2l}P_{2k} \end{array} \right) ,} \end{aligned}$$

(5.8)

where $R= B[x,p]\; /(c_1x_{1}, c_2x_{2},c_1p_{1}, c_2p_{2})$ is a local coordinate ring of $\widetilde{Q}_p$.

In a neighborhood of a point in $\widetilde{Q}_p^{(1)}$ or $\widetilde{Q}_p^{(3)}$, we have seen $c_1=1$ in Sects. 2.3 and 2.4, hence $x_1=p_1=0$. Pulling back via the node-identifying morphism, $\textbf{C}^{(i)}$ is a component defined by $\{c_2=0\}$ as described in Sect. 3.2 and $\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} \subset \textbf{C}^{(i)}$ is defined by $\{ X_2 = 0 \}=\{ X_{21} = \dots = X_{2n} = 0 \}$

. Recall that it is a cut-out by the tautological section of $\textbf{E}^{(i)}_1$

. Introducing a partner variable $X'_2$ of $X_2$ which forms a basis of $(\textbf{E}^{(i)}_1)^\vee$ (hence they are linear functions on $\textbf{E}^{(i)}_1$), the cone $C_{\textbf{C}^{(i)} \cap \textbf{E}_2^{(i)} \textbf{C}^{(i)}}$ is Spec of

$$\begin{aligned} \frac{R/(c_2,x_1,p_1) [X_{1j},X'_{2j},P_{1i},P_{2i}]}{\left( \begin{array}{c} x_{2k}X'_{2l}-x_{2l}X'_{2k},\ x_{2k}P_{2l},\ p_{2k}P_{2l}-p_{2l}P_{2k} \end{array} \right) .} \end{aligned}$$

Then it is the union of $\{x_2=0\}$ and $\{P_2=0\}$. We show the component $\{x_2=0\}$ vanishes by $e^{\textrm{KL}}(\textbf{E}^{(i)})$. To do so it is enough to show that it vanishes by $e^{\textrm{KL}}(\textbf{E}_1^{(i)})$ by [36, Theorem 1.4]. We show this by degree reason. The cycle $e^{\textrm{KL}}(\textbf{E}_1^{(i)})\cap \{x_2=0\}$ is of degree

$$\begin{aligned}&\dim \left( B[x,p]/(c_2,x_1,x_2,p_1)\right) [X_1,X'_2,P_1,P_2]/(p_{2k}P_{2l}-p_{2l}P_{2k})-{{\,\textrm{rank}\,}}\textbf{E}_1^{(i)} \\&=\, \dim B[X_1,X'_2,P_1,p_2]-{{\,\textrm{rank}\,}}\textbf{E}_1^{(i)}\, =\, \dim B[x,p] - {{\,\textrm{rank}\,}}\textbf{E}_1^{(i)}\, =\, \dim B[x,p]-n-1. \end{aligned}$$

On the other hand, $e^{\textrm{KL}}(\textbf{E}_1^{(i)})\cap \{x_2=0\}$ is contained in the degeneracy locus of the cosection $\{p_2=0\}$. It is contained in $R/(c_2,x,p)\; [X_{1},P_{1},P_{2}]$ which has dimension less than or equal to $\dim B[x,p]-n-2.$ Thus $e^{\textrm{KL}}(\textbf{E}_1^{(i)})\cap \{x_2=0\}=0$. The component $\{P_2=0\}$ is Spec of

$$\begin{aligned} \frac{(B[x]/(c_2,x_1))\; [X_{1},X'_{2},P_{1}]}{\left( \begin{array}{c} x_{2k}X'_{2l}-x_{2l}X'_{2k} \end{array} \right) } \,[p_2]\ \cong \ (5.8)|_{c_2=x_1=p_1=0,\; p_2=P_2=0,\; X_2=X'_2}[p_2] \end{aligned}$$

which defines the cone (5.7).

The cone $\textbf{C}^{(2)}$ is defined by $\{c_1=c_2=0\}$, and $\textbf{C}^{(2)}\cap \textbf{E}^{(2)}$ is $\{X_1=X_2=0\}$ in addition. Then it has 4 components

$$\begin{aligned} \{x_1=x_2=0\}\ \cup \ \{x_1=P_2=0\}\ \cup \ \{P_1=x_2=0\}\ \cup \ \{P_1=P_2=0\}. \end{aligned}$$

Similarly we can show the first three will be killed by $e^{\textrm{KL}}(\textbf{E}^{(2)})$ by degree reason. Precisely the first one is killed by $e^{\textrm{KL}}(\textbf{E}_1^{(2)})$. The bundle $\textbf{E}^{(2)}_1$ is decomposed into two parts because its dual is generated by $X_1,X_2$. We use each to kill the second and third ones. The fourth one is the cone (5.7). $\square$

Lemma 5.3 shows

$$\begin{aligned} e^{\textrm{KL}}(\textbf{E}^{(i)})\cap [\textbf{C}^{(i)}]\ =\ e^{\textrm{KL}}(\textbf{E}^{(i)})\cap [\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p], \end{aligned}$$

which proves the second equality of (5.6)

6.4 Local freeness of cones

In this section we relate the vector bundle $\textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}$

and the cone $\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}$. We suppress the notations $|_{\textbf{Q}^{(i)}}$ and ${}_{\textbf{Q}^{(i)}}$ throughout the section, which means $p=0$ and $p=P=0$ with local coordinates, respectively.

For $i=1,3$, we consider the blowup $b^{(i)}: \widehat{\textbf{Q}}^{(i)} \rightarrow \textbf{Q}^{(i)}$ along the preimage of the intersection $\widetilde{Q}^{(i)} \cap \widetilde{Q}^{\textrm{red}}$. Let $\textbf{D}^{(i)}$ denote the exceptional divisor.

Lemma 5.4

For $i=1,3$, the bundle $(b^{(i)*}\textbf{C}_{(i)})(\textbf{D}^{(i)})$ maps injectively to $b^{(i)*}\textbf{E}^{(i)}_1$. Moreover, the cycle $[(b^{(i)*}\textbf{C}_{(i)})(\textbf{D}^{(i)})]\in A_*(b^{(i)*}\textbf{E}^{(i)}_1)$ pushes down to $[\textbf{C}^{(i)}]\in A_*(\textbf{E}^{(i)}_1)$.

Proof

Consider the pullback morphism $\textbf{C}_{(i)} \rightarrow \textbf{E}^{(i)}$ of (5.2) and its composition with the projection to the first summand $\textbf{E}^{(i)}\rightarrow \textbf{E}^{(i)}_1$,

$$\begin{aligned} \textbf{C}_{(i)}\ \longrightarrow \ \textbf{E}^{(i)}_1. \end{aligned}$$

(5.9)

It is an injection outside of the intersection because $\textbf{C}_{(i)}$

maps isomorphically to $\textbf{C}^{(i)}$ there, which is contained in $\textbf{E}^{(i)}_1$ as $P=0$ on $\textbf{C}^{(i)}$ locally. It vanishes on the preimage of the intersection by (3.6) and the computation below (5.2). Hence the twisting of the pullback $(b^{(i)*}\textbf{C}_{(i)})(\textbf{D}^{(i)})$ maps injectively to $b^{(i)*}\textbf{E}^{(i)}_1$.

The cycle $[(b^{(i)*}\textbf{C}_{(i)})(\textbf{D}^{(i)})]$ pushes down to the closure of the image of (5.9) which is $[\textbf{C}^{(i)}]$. $\square$

For $i=2$, we consider the composition of two blowups $b^{(2)}: \widehat{\textbf{Q}}^{(2)} \rightarrow \textbf{Q}^{(2)}$: the blowup along the preimage of the intersection $\widetilde{Q}^{(2)} \cap \widetilde{Q}^{\textrm{red}}$ first and then the blowup along the proper transform of the preimage of the intersection $\widetilde{Q}^{(2)} \cap \widetilde{Q}^{(1)}$. Let $\textbf{D}^{(2,1)}$, $\textbf{D}^{(2,2)}$

denote the exceptional divisors of the first and the second blowups, respectively. Then $\textbf{D}^{(2,2)}$ is decomposed into $\textbf{D}^{(2,2)}=\textbf{D}^{(2,2)}_1+\textbf{D}^{(2,2)}_2$

because the proper transform of the preimage of $\widetilde{Q}^{(2)} \cap \widetilde{Q}^{(1)}$ is a disjoint union of two different components corresponding to the nodes. Locally we can check that the first blowup is taken along $\{x_1=0\}\cap \{x_2=0\}$. Then the proper transforms of $\{x_1=0\}$ and $\{x_2=0\}$ are disjoint. Let $\textbf{D}^{(2)}_1:=\textbf{D}^{(2,1)}+\textbf{D}^{(2,2)}_1$ and $\textbf{D}^{(2)}_2:=\textbf{D}^{(2,1)}+\textbf{D}^{(2,2)}_2$.

Recall that the bundle $\textbf{C}_{(2)}$ is the pullback of the normal bundle $N_{\mathfrak {M}_{1,1} \times \mathfrak {M}_{0,2} \times \mathfrak {M}_{1,1} / \mathfrak {M}_{2,0} }$,

$$\begin{aligned} \textbf{C}_{(2)}\ \cong \ (\mathbb {L}_1^{\vee }\otimes \mathbb {L}^{\vee }_{1} ) \oplus ( \mathbb {L}_2^{\vee }\otimes \mathbb {L}_{2}^{\vee }). \end{aligned}$$

Lemma 5.5

The bundle $(b^{(2)*}\textbf{C}_{(2)})(\textbf{D}^{(2)}):=b^{(2)*}\left( \mathbb {L}_1^{\vee }\otimes \mathbb {L}_{1}^{\vee }\right) (\textbf{D}^{(2)}_1) \oplus \; b^{(2)*}\big ( \mathbb {L}_2^{\vee } \otimes \mathbb {L}_{2}^{\vee }\big ) (\textbf{D}^{(2)}_2)$ maps injectively to $b^{(2)*}\textbf{E}^{(2)}_1$ and its fundamental cycle in $A_*(b^{(2)*}\textbf{E}^{(2)}_1)$ pushes down to $[\textbf{C}^{(2)}]\in A_*(\textbf{E}^{(2)}_1)$.

Proof

The morphism (5.9) for $i=2$ is an injection outside of both $\widetilde{Q}^{\textrm{red}}$ and $\widetilde{Q}^{(1)}$. It is of rank 1 on the preimage of $\widetilde{Q}^{(1)}{\setminus }\widetilde{Q}^{\textrm{red}}$ and vanishes on the preimage of $\widetilde{Q}^{\textrm{red}}$. So the twisting by $\textbf{D}^{(2,1)}$ of the pullback of $\textbf{C}^{(2)}$ by the first blowup is of rank 1 on the proper transform. Hence $(b^{(2)*}\textbf{C}_{(2)})(\textbf{D}^{(2)})$ injects into $b^{(2)*}\textbf{E}^{(2)}_1$.

As the closure of the image of (5.9) for $i=2$ is $[\textbf{C}^{(i)}]$, the cycle $[(b^{(2)*}\textbf{C}_{(2)})(\textbf{D}^{(2)})]$ pushes down to $[\textbf{C}^{(2)}]$. $\square$

We now use Lemmas 5.4 and 5.5 to explain the third equality of (5.6). In fact, these Lemmas show

$$\begin{aligned} e^{\textrm{KL}}(\textbf{E}^{(i)})\cap [\textbf{C}^{(i)}_{\textbf{Q}^{(i)}}\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p]\ =\ e^{\textrm{KL}}(\textbf{E}^{(i)})\cap b^{(i)}_*[(b^{(i)*} \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}}(\textbf{D}^{(i)})\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p]. \end{aligned}$$

Hence from the third equality, (5.6) must be

$$\begin{aligned}&\frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap \left( e^{\textrm{KL}}\left( \textbf{E}_2^{(i)}\right) \cap b^{(i)}_*\left[ (b^{(i)*} \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}})(\textbf{D}^{(i)})\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p\right] \right) \right) \\ \nonumber&\quad = \frac{1}{\deg (\tilde{\iota }_{p,i})}(\tilde{\iota }_{p,i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap e^{\textrm{KL}}\left( (\textbf{P}^{(i)} )^{\vee }\right) \cap b^{(i)}_*\left[ (b^{(i)*} \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}})(\textbf{D}^{(i)})\times _{\textbf{Q}^{(i)}}\textbf{Q}^{(i)}_p(X)\right] ^{\textrm{vir}} \right) \\ \nonumber&\quad = \frac{(-1)^{m\cdot i}}{\deg (\tilde{\iota }_{i})}(\tilde{\iota }_{i})_* \left( e^{\textrm{FM}}\left( \textbf{K}^{(i)}\right) \cap b^{(i)}_*\left[ (b^{(i)*} \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)})(\textbf{D}^{(i)}) \right] ^{\textrm{vir}} \right) \\ \nonumber&\quad = \frac{(-1)^{m\cdot i}}{\deg (\tilde{\iota }_{i})}(\tilde{\iota }_{i})_*b^{(i)}_* \left( e\left( \frac{\textbf{K}^{(i)}|_{\widehat{\textbf{Q}}^{(i)}(X)} }{(b^{(i)*} \textbf{C}_{(i)}|_{\textbf{Q}^{(i)}(X)})(\textbf{D}^{(i)}) } \right) \cap [\widehat{\textbf{Q}}^{(i)}(X)]^{\textrm{vir}} \right) . \end{aligned}$$

Meanwhile [34, Lemma 4.1] shows $\textbf{D}^{(i)}$ in the denominator in the last equation does not contribute to the result after pushdown. This means we get (5.6)

$$\begin{aligned}{}[\widetilde{Q}_p^{(i)}]^{\textrm{vir}} \ =\ \frac{(-1)^{m\cdot i}}{\deg (\widetilde{\iota }_{i})}(\widetilde{\iota }_{i})_* \left( \left[ \frac{ c( \textbf{K}^{(i)}) }{c(\textbf{C}_{(i)})} \right] _{\star } \cap [\textbf{Q}^{(i)}(X)]^{\textrm{vir}} \right) , \end{aligned}$$

(5.10)

where $\star =\dim X-1$ for $i=1,3$ and $\star =2\dim X-2$ for $i=2$.

6.5 Proof of Theorem 2

Recall that $b:\widetilde{Q}_p\rightarrow Q_p$ is the base change of the blowup morphism. In this Section, we compute $[Q_p^{(i)}]^{\textrm{vir}} :=b_*([\widetilde{Q}_p^{(i)}]^{\textrm{vir}} )$ explicitly using (5.10) to get Theorem 2.

6.5.1 $i=1$ case

Lemma 5.6

We have

$$\begin{aligned}{}[Q_p^{(1)}]^{\textrm{vir}}&= (-1)^{d(\sum _i \ell _i) + m}\, [K]_{\dim X-1} \cap \left( [\overline{M}_{1,1}] \times [Q_{1,1,d}(X)]^{\textrm{vir}} \right) \\ \nonumber&\quad - (-1)^{d(\sum _i \ell _i) + m} \,[K_1]_{\dim X-1}[K_2]_{\dim X-1}\\&\quad \cap \left( \, [\overline{M}_{1,1}] \times [Q_{0,2,d}(X)]^{\textrm{vir}} \times [\overline{M}_{1,1}] \, \right) \\&\quad - (-1)^{d(\sum _i \ell _i) + m} \sum _{a\ge 1}[A^{a+2}]_{\dim X-2-a}[B_1B_2]_{a-1}\\&\quad \cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [Q'_{0,2,d}(X)]^{\textrm{vir}} \right) , \end{aligned}$$

where the cohomology classes $K= \frac{c\,(\mathcal {H}^\vee \boxtimes \;\textrm{ev}^* T_X)}{c\,(\mathbb {L}^\vee \boxtimes \; \mathbb {L}^\vee )}$, $A^t=\frac{c\,(\mathcal {H}^\vee \boxtimes \; \textrm{ev}_1^*T_X)}{c\,(\mathbb {L}^\vee \boxtimes \; 1)^{t}}$ and $B=\frac{1}{c\,(\mathbb {L}^\vee )}$ are defined in Introduction. In the last term, $A^{a+2}$ is defined using the marked point of $\overline{M}_{1,1}$ and B is defined using the ones of $Q'_{0,2,d}(X)$ as described in Theorem 2.

Proof

Recall from Sect. 5.2 that

• $\textbf{K}^{(1)} = \mathcal {H}^\vee \boxtimes \textrm{ev}^*T_X$,

• $\textbf{C}_{(1)} \cong \mathbb {L}^\vee \boxtimes \mathbb {L}^\vee (Z)$,

• $[\textbf{Q}^{(1)}(X)]^{\textrm{vir}} = (-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{1,1,d}) \cap \left( [\overline{M}_{1,1}] \times [\widetilde{Q}_{1,1,d}^\textrm{red}(\mathbb {P}^n)]\right)$.

Here $Z=\mathbb {P}Q'_{0,2,d}\subset \widetilde{Q}^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)$ is the exceptional divisor which is a projectivisation over $\overline{M}_{0,3}\times Q'_{0,2,d}\subset Q^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)$ as defined in the beginning of Sect. 5.2. We use these to compute (5.10) for $i=1$.

First of all, as $c_1(\mathbb {L}^\vee \boxtimes \mathbb {L}^\vee )|_{\overline{M}_{1,1}\times Z}=c_1(\mathbb {L}^\vee \boxtimes \mathcal {O})$ we can compute

$$\begin{aligned} \frac{ c( \textbf{K}^{(1)}) }{c(\textbf{C}_{(1)})} \ =\ K+c(\mathcal {H}^\vee \boxtimes \textrm{ev}^*T_X)\sum _{a\ge 1}(-1)^a \frac{c_1(\mathcal {O}_{\widetilde{Q}^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)}(Z))^a}{(1+c_1(\mathbb {L}^\vee ))^{a+1}}. \end{aligned}$$

Then by the projection formula for the morphism $b:\widetilde{Q}^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)\rightarrow Q^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)$

applied to (5.10), the contribution of the first term K in the RHS to $[Q_p^{(1)}]^{\textrm{vir}}$ is

$$\begin{aligned} (-1)^{d(\sum _i \ell _i) + m}\, [K]_{\dim X-1}e^{\textrm{ref}}(V_{1,1,d}) \cap \left( [\overline{M}_{1,1}] \times [Q^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)] \right) . \end{aligned}$$

By [32, Theorem 1.1], we obtain

$$\begin{aligned}&e^{\textrm{ref}}(V_{1,1,d}) \cap [Q_{1,1,d}^\textrm{red}(\mathbb {P}^n)] \\&\quad = [Q_{1,1,d}(X)]^{\textrm{vir}} - [K]_{\dim X-1}\cap \left( \, [\overline{M}_{1,1}] \times [Q_{0,2,d}(X)]^{\textrm{vir}} \, \right) . \end{aligned}$$

So the contribution becomes

$$\begin{aligned}&(-1)^{d(\sum _i \ell _i) + m}\, [K]_{\dim X-1} \cap \left( [\overline{M}_{1,1}] \times [Q_{1,1,d}(X)]^{\textrm{vir}} \right) \\ \nonumber&\quad - (-1)^{d(\sum _i \ell _i) + m} \,[K_1]_{\dim X-1}[K_2]_{\dim X-1} \cap \left( \, [\overline{M}_{1,1}] \times [Q_{0,2,d}(X)]^{\textrm{vir}} \times [\overline{M}_{1,1}] \, \right) . \end{aligned}$$

We next compute the contribution of the second term. This term is the pushforward of the cycle on $\overline{M}_{1,1}\times \overline{M}_{0,3}\times \mathbb {P}Q'_{0,2,d}$,

$$\begin{aligned} c(\mathcal {H}^\vee \boxtimes \mathcal {O}\boxtimes \text {ev}^*T_X)\sum _{a\ge 0} (-1)^{a+1}\frac{c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1))^a}{(1+c_1(\mathbb {L}^\vee ))^{a+2}} =-\sum _{a\ge 0}A^{a+2}c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a \end{aligned}$$

(5.11)

because the normal bundle $\mathcal {O}_Z(Z)$ is $\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1)$.

To compute its contribution to $[Q_p^{(1)}]^{\textrm{vir}}$ using the projection formula for the embedding $\overline{M}_{1,1}\times \overline{M}_{0,3}\times \mathbb {P}Q'_{0,2,d} \hookrightarrow \overline{M}_{1,1}\times \widetilde{Q}^{\textrm{red}}_{1,1,d}(\mathbb {P}^n)$, we need to cap (5.11) with $(-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{0,2,d}) \cap ([\overline{M}_{1,1}]\times [\overline{M}_{0,3}]\times [\mathbb {P}Q'_{0,2,d}])$

instead of $[\textbf{Q}^{(1)}(X)]^{\textrm{vir}} = (-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{1,1,d}) \cap ([\overline{M}_{1,1}] \times [\widetilde{Q}_{1,1,d}^\textrm{red}(\mathbb {P}^n)])$ in degree of $[Q_p^{(1)}]^{\textrm{vir}}$ which is $d(n+1-\sum \ell _i)-\dim X+3$. For this projection formula, we use $V_{1,1,d}|_{\overline{M}_{0,3}\times Q'_{0,2,d}}\cong V_{0,2,d}$.

And then we need to push it down to $\overline{M}_{1,1} \times \overline{M}_{0,3} \times Q'_{0,2,d}(X)$ via the blowdown morphism b.

Note that the blowdown morphism b over $\mathbb {P}Q'_{0,2,d}$ is the projection morphism $b: \mathbb {P}Q'_{0,2,d}\rightarrow Q'_{0,2,d}(\mathbb {P}^n)$. Then by definition of Segre classes [21, Chapter 3.1], we have

$$\begin{aligned} b_* \left( c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a \cap [\mathbb {P}Q'_{0,2,d}]\right)= & {} s_{a-1}\left( \mathbb {L}^{\vee }_{1}\oplus \mathbb {L}^{\vee }_{2} \right) \cap [Q'_{0,2,d}(\mathbb {P}^n)]\\= & {} [B_1B_2]_{a-1}\cap [Q'_{0,2,d}(\mathbb {P}^n)]. \end{aligned}$$

So capping (5.11) with $[\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [\mathbb {P}Q'_{0,2,d}]$ and pushing it down to $\overline{M}_{1,1} \times \overline{M}_{0,3} \times Q'_{0,2,d}(\mathbb {P}^n)$, the projection formula gives

$$\begin{aligned} -\sum _{a\ge 1}[A^{a+2}]_{\dim X-2-a}[B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [Q'_{0,2,d}(\mathbb {P}^n)]\right) \end{aligned}$$

(5.12)

in degree $d(n+1)-\dim X +3$. Then the contribution to $[Q_p^{(1)}]^{\textrm{vir}}$ is $(-1)^{d(\sum _i \ell _i)+m}e^{\textrm{ref}}(V_{0,2,d}) \cap$ (5.12). To compute it we would like to calculate first

$$\begin{aligned}&e^{\textrm{ref}}(V_{0,2,d}) \cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [Q'_{0,2,d}(\mathbb {P}^n)]\right) \in A_{d(n+1-\sum \ell _i)}(\overline{M}_{1,1}\nonumber \\&\quad \times \overline{M}_{0,3}\times Q_{0,2,d}(X)). \end{aligned}$$

(5.13)

Denoting by $j: Q'_{0,2,d}(\mathbb {P}^n) \hookrightarrow Q_{0,2,d}(\mathbb {P}^n)$ the embedding and by $\overline{V}_{0,2,d}$ the bundle $\oplus _{i=1}^{m} \pi _* \mathcal {L}^{\ell _i}$ on $Q_{0,2,d}(\mathbb {P}^n)$, the evaluation morphism gives rise to a sequence

$$\begin{aligned} 0\ \longrightarrow \ V_{0,2,d} \ \longrightarrow \ j^*\overline{V}_{0,2,d} \ \xrightarrow {\ \textrm{ev}_1-\,\textrm{ev}_2\ }\ \textrm{ev}_1^*\oplus _{i=1}^{m} \mathcal {O}(\ell _i) \ \longrightarrow \ 0. \end{aligned}$$

Denoting by $\Delta _{\mathbb {P}^n}\in A^{n}(\mathbb {P}^n \times \mathbb {P}^n)$ the diagonal class, (5.13) becomes

$$\begin{aligned} \frac{e^{\textrm{ref}}(\overline{V}_{0,2,d})}{e(\oplus _{i=1}^{m} \mathcal {O}(\ell _i))}&\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times \left( (\textrm{ev}_1\times \textrm{ev}_2)^*\Delta _{\mathbb {P}^n}\cap [Q_{0,2,d}(\mathbb {P}^n)]\right) \right) \nonumber \\&=\ [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times \left( \frac{(\textrm{ev}_1\times \textrm{ev}_2)^*\Delta _{\mathbb {P}^n}}{e(\oplus _{i=1}^{m} \mathcal {O}(\ell _i))} \cap [Q_{0,2,d}(X)]^{\textrm{vir}} \right) \\&=\ [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [Q'_{0,2,d}(X)]^{\textrm{vir}} \nonumber \end{aligned}$$

where $[Q'_{0,2,d}(X)]^{\textrm{vir}}$ is the cycle defined in (0.3). Note that $\Delta _{\mathbb {P}^n}|_X=e(T_{\mathbb {P}^n}|_X)$ and $\Delta _X|_X=e(T_X)$. Hence the contribution is

$$\begin{aligned} - (-1)^{d(\sum _i \ell _i) + m} \sum _{a\ge 1}[A^{a+2}]_{\dim X-2-a}[B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [Q'_{0,2,d}(X)]^{\textrm{vir}} \right) . \end{aligned}$$

$\square$

6.5.2 $i=2$ case

Recall from Sect. 5.2 that

• $\textbf{K}^{(2)} = \left( \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_X\boxtimes \mathcal {O}_{\overline{M}_{1,1}}\right) \oplus \left( \mathcal {O}_{\overline{M}_{1,1}} \boxtimes \textrm{ev}_2^*T_X\boxtimes \mathcal {H}^\vee \right)$,

• $\textbf{C}_{(2)} \cong (\mathbb {L}_1^{\vee }\otimes \mathbb {L}^{\vee }_{1} ) \oplus ( \mathbb {L}_2^{\vee }\otimes \mathbb {L}_{2}^{\vee })$,

• $[\textbf{Q}^{(2)}(X)]^{\textrm{vir}} = (-1)^{d(\sum _i \ell _i)+m}e^{\textrm{ref}}(V_{0,2,d}) \cap \left( [\overline{M}_{1,1}] \times [Q_{0,2,d}(\mathbb {P}^n)] \times [\overline{M}_{1,1}]\right)$.

Putting these to (5.10) for $i=2$ we have the following Lemma.

Lemma 5.7

We have

$$\begin{aligned}{}[Q^{(2)}_p]^{\textrm{vir}} = \frac{(-1)^{d(\sum _i \ell _i) + m}}{2} \,[K_1K_2]_{2\dim X-2} \cap \left( \, [\overline{M}_{1,1}] \times [Q_{0,2,d}(X)]^{\textrm{vir}} \times [\overline{M}_{1,1}] \, \right) . \end{aligned}$$

6.5.3 $i=3$ case

Lemma 5.8

We have

$$\begin{aligned}{}[Q_p^{(3)}]^{\textrm{vir}} \ {}&=\ (-1)^{d(\sum _i \ell _i) + m} \sum _{a\ge 0}^{\dim X-1} [A^{a+1}]_{\dim X-1-a} [B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,2}] \times [Q'_{0,2,d}(X)]^{\textrm{vir}} \right) \\&\quad +(-1)^{d(\sum _i \ell _i) + m}\sum _{a\ge 0} [C]_{\dim X-2-a}[B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [ Q'_{0,2,d}(X)]^{\textrm{vir}} \right) , \end{aligned}$$

where the cohomology class $[C]_{\dim X-2-a}= \frac{a(a+1)}{2}c_1(\mathcal {H}^\vee )c_{\dim X-3-a}(\textrm{ev}_1^*T_X)-(a+1)c_{\dim X-2-a}(\textrm{ev}_1^*T_X)$ is defined in Introduction. In the last term, $[C]_{\dim X-2-a}$ is defined using the marked point of $\overline{M}_{1,1}$ and B is defined using the ones of $Q'_{0,2,d}(X)$ as described in Theorem 2.

Proof

Recall from Sect. 5.2 that

• $\textbf{K}^{(3)} = \mathcal {H}^\vee \boxtimes \textrm{ev}_1^*T_X$,

• $\textbf{C}_{(3)} \cong \mathbb {L}^\vee (Z) \boxtimes \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1)$,

• $[\textbf{Q}^{(3)}(X)]^{\textrm{vir}} = (-1)^{d(\sum _i \ell _i)}e^{\textrm{ref}}(V_{0,2,d}) \cap \left( [\overline{M}_{1,2}] \times [\mathbb {P}Q'_{0,2,d}]\right)$

where $\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1)$ is the tautological line bundle of $\mathbb {P}Q'_{0,2,d} = \mathbb {P}(\mathbb {L}^{\vee }_{1}\oplus \mathbb {L}^{\vee }_{2})$

and $Z=\overline{M}_{1,1}\times \overline{M}_{0,3}\subset \overline{M}_{1,2}$ is a divisor. We use these to compute (5.10) for $i=3$. The class $c\,(\textbf{K}^{(3)})/c\,(\textbf{C}_{(3)})$ expands to

$$\begin{aligned} \frac{c\,(\textbf{K}^{(3)})}{1\!+\! c_1(\mathbb {L}^\vee )+c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1))}+\sum _{a\ge 1}(-1)^a \frac{c\,(\textbf{K}^{(3)})c_1(\mathcal {O}_{\overline{M}_{1,2}}(Z))^a}{(1\!+\! c_1(\mathbb {L}^\vee )\!+\!c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1)))^{a+1}}. \end{aligned}$$

We compute the contribution of the first term to $[Q_p^{(3)}]^{\textrm{vir}}$. It expands to

$$\begin{aligned} \frac{c\,(\textbf{K}^{(3)})}{1+ c_1(\mathbb {L}^\vee )+c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1))}\ {}&=\ c\,(\textbf{K}^{(3)})\cdot \sum _{a\ge 0} \frac{(-1)^a\cdot c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(-1))^a}{(1+ c_1(\mathbb {L}^\vee ))^{a+1}}\\&=\ \sum _{a\ge 0} A^{a+1}\cdot c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a. \end{aligned}$$

So its degree $(\dim X-1)$-part is

$$\begin{aligned} \sum _{a\ge 0}^{\dim X-1} [A^{a+1}]_{\dim X-1-a}\cdot c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a. \end{aligned}$$

Capping this with $[\overline{M}_{1,2}] \times [\mathbb {P}Q'_{0,2,d}]$ and pushing it down to $\overline{M}_{1,2} \times Q'_{0,2,d}(\mathbb {P}^n)$, it becomes

$$\begin{aligned} \sum _{a\ge 0}^{\dim X-1} [A^{a+1}]_{\dim X-1-a} [B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,2}] \times [Q'_{0,2,d}(\mathbb {P}^n)]\right) . \end{aligned}$$

(5.14)

So the contribution to $[Q_p^{(3)}]^{\textrm{vir}}$ is $(-1)^{d(\sum _i \ell _i)+m}e^{\textrm{ref}}(V_{0,2,d}) \cap$ (5.14) which is

$$\begin{aligned} (-1)^{d(\sum _i \ell _i) + m} \sum _{a\ge 0}^{\dim X-1} [A^{a+1}]_{\dim X-1-a} [B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,2}] \times [Q'_{0,2,d}(X)]^{\textrm{vir}} \right) . \end{aligned}$$

Now we compute the contribution of the second term. It is the pushforward of the cycle in $\overline{M}_{1,1}\times \overline{M}_{0,3}\times \mathbb {P}Q'_{0,2,d}$,

$$\begin{aligned} c(\mathcal {H}^\vee \boxtimes \mathcal {O}\boxtimes \textrm{ev}_1^*T_X)\sum _{a\ge 0} (-1)^{a+1}\frac{c_1(\mathcal {H}^\vee )^a}{(1\!-\! c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1)))^{a+2}}. \end{aligned}$$

Here we used the fact that the normal bundle $\mathcal {O}_Z(Z)$ is isomorphic to the dual Hodge bundle $\mathcal {H}^\vee$ and the bundle $\mathbb {L}$ lies on the point $\overline{M}_{0.3}$ (so its first Chern class is zero). As $c_1(\mathcal {H}^\vee )^2=0$, this becomes

$$\begin{aligned} c(\mathcal {H}^\vee \boxtimes \mathcal {O}\boxtimes \textrm{ev}_1^*T_X)\left( \frac{-1}{(1\!-\! c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1)))^{2}}+\frac{c_1(\mathcal {H}^\vee )}{(1\!-\! c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1)))^{3}}\right) \end{aligned}$$

which extends to

$$\begin{aligned} -c(\mathcal {H}^\vee \boxtimes \mathcal {O}\boxtimes \textrm{ev}_1^*T_X)\sum _{a\ge 0} \left( (a+1)\cdot c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a - \frac{(a+1)(a+2)}{2}c_1(\mathcal {H}^\vee )c_1(\mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a\right) . \end{aligned}$$

Its degree $\dim X-2$ part is

$$\begin{aligned} \sum _{a\ge 0}\left( \frac{a(a+1)}{2}c_1(\mathcal {H}^\vee )c_{\dim X-3-a}(\textrm{ev}_1^*T_X)-(a+1)c_{\dim X-2-a}(\textrm{ev}_1^*T_X)\right) c_1( \mathcal {O}_{\mathbb {P}Q'_{0,2,d}}(1))^a. \end{aligned}$$

Capping it with $[\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [\mathbb {P}Q'_{0,2,d}]$ and pushing it down to $\overline{M}_{1,1} \times \overline{M}_{0,3} \times Q'_{0,2,d}(\mathbb {P}^n)$, it becomes

$$\begin{aligned} \sum _{a\ge 0} [C]_{\dim X-2-a}[B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [ Q'_{0,2,d}(\mathbb {P}^n)]\right) \end{aligned}$$

(5.15)

in degree $d(n+1)-\dim X+3$. So the contribution to $[Q_p^{(3)}]^{\textrm{vir}}$ is $(-1)^{d(\sum _i \ell _i)+m}e^{\textrm{ref}}(V_{0,2,d}) \cap$ (5.15) which is

$$\begin{aligned} (-1)^{d(\sum _i \ell _i) + m}\sum _{a\ge 0} [C]_{\dim X-2-a}[B_1B_2]_{a-1}\cap \left( [\overline{M}_{1,1}] \times [\overline{M}_{0,3}] \times [ Q'_{0,2,d}(X)]^{\textrm{vir}} \right) . \end{aligned}$$

$\square$

Then Lemmas 5.6–5.8 and (1.6) prove Theorem 2.

6.6 Calabi–Yau 3-folds

Suppose that X is a Calabi-Yau 3-fold. Set

$$\begin{aligned} \alpha := c_1(\mathcal {H}^\vee \boxtimes 1), \ \ \beta := c_2(1\boxtimes \textrm{ev}^*T_X),\ \ \psi := c_1(1\boxtimes \mathbb {L}). \end{aligned}$$

6.6.1 $i=1$ case

Then since $\alpha = c_1(\mathbb {L}^\vee \boxtimes 1)$ we have

$$\begin{aligned}{}[K]_2\ =\ \left[ \frac{c\,(\mathcal {H}^\vee \boxtimes \textrm{ev}^*T_{X})}{c\,(\mathbb {L}^\vee \boxtimes \mathbb {L}^{\vee })}\right] _{2} \ = \ \left[ \frac{(1 + 3\alpha + \beta ) }{ (1 + \alpha - \psi ) } \right] _2. \end{aligned}$$

Its nontrivial contribution to the integration over $[\overline{M}_{1,1}] \times (e^{\textrm{ref}}(V_{1,1,d}) \cap [Q_{1,1,d}^\textrm{red}(\mathbb {P}^n)])$ is only $-\alpha \psi$. On the other hand, since $(\textrm{ev}_1 \times \textrm{ev}_2)^*(\Delta _X) \in H^{6}(Q_{0,2,d}(X))$ and the (complex) degree of $[Q_{0,2,d}(X)]^{\textrm{vir}}$ is 2, we have $[Q'_{0,2,d}(X)]^{\textrm{vir}} =0$. Hence

$$\begin{aligned}{}[Q^{(1)}_p]^{\textrm{vir}} \ =\ -\frac{(-1)^{d(\sum _i \ell _i) + m}}{24}\; c_1(\mathbb {L})\cap (e^{\textrm{ref}}(V_{1,1,d}) \cap [Q_{1,1,d}^\textrm{red}(\mathbb {P}^n)]) \end{aligned}$$

Using [32, Corollary 1.3]

$$\begin{aligned} e^{\textrm{ref}}(V_{1,1,d}) \cap [Q_{1,1,d}^\textrm{red}(\mathbb {P}^n)] = [Q_{1,1,d}(X)]^{\textrm{vir}} - \frac{c\,(\mathbb {L})}{12}[Q_{0,2,d}(X)]^{\textrm{vir}} , \end{aligned}$$

we obtain

$$\begin{aligned}{}[Q^{(1)}_p]^{\textrm{vir}}&= -\frac{(-1)^{d(\sum _i \ell _i) + m}}{24}\; c_1(\mathbb {L})\cap [Q_{1,1,d}(X)]^{\textrm{vir}} \nonumber \\&\quad + 2\frac{(-1)^{d(\sum _i \ell _i) + m}}{24^2}c_1(\mathbb {L}_1)c_1(\mathbb {L}_2)\cap [Q_{0,2,d}(X)]^{\textrm{vir}} . \end{aligned}$$

(5.16)

6.6.2 $i=2$ case

Similarly we have

$$\begin{aligned} \left[ K_1K_2\right] _{4} = \left[ \frac{(1 + 3\alpha _1 + \beta _1)}{(1 + \alpha _1 - \psi _1)} \cdot \frac{(1 + 3\alpha _2 + \beta _2)}{(1 + \alpha _2 - \psi _2)} \right] _4. \end{aligned}$$

The nontrivial contribution is $\alpha _1\alpha _2 (-3 \psi _1\psi _2 - 3\beta _1 - 3\beta _2)$. Hence we obtain

$$\begin{aligned}{}[Q^{(2)}_p]^{\textrm{vir}} \ {}&=\ \frac{(-1)^{d(\sum _i \ell _i) + m} }{2} \alpha _1\alpha _2 (-3 \psi _1\psi _2 - 3\beta _1 - 3\beta _2) \nonumber \\&\quad \cap \left( [\overline{M}_{1,1}] \times [Q_{0,2,d}(X)]^{\textrm{vir}} \times [\overline{M}_{1,1}] \right) \nonumber \\&= -(-1)^{d(\sum _i \ell _i) + m} \frac{3}{2\cdot 24^2} (c_1(\mathbb {L}_1)c_1(\mathbb {L}_2)\nonumber \\&\quad +c_2(\textrm{ev}_1^*T_X)+c_2(\textrm{ev}_2^*T_X)) \cap [Q_{0,2,d}(X)]^{\textrm{vir}} \end{aligned}$$

(5.17)

6.6.3 $i=3$ case

Since $[Q'_{0,2,d}(X)]^{\textrm{vir}} =0$, we have $[Q_p^{(3)}]^{\textrm{vir}} = 0$.

By (5.16), (5.17) and (1.6), we prove Theorem 1.