On the regularity of weak solutions to the fluid–rigid body interaction problem

Abstract

We study a 3D fluid–rigid body interaction problem. The fluid flow is governed by 3D incompressible Navier–Stokes equations, while the motion of the rigid body is described by a system of ordinary differential equations describing conservation of linear and angular momentum. Our aim is to prove that any weak solution satisfying certain regularity conditions is smooth. This is a generalization of the classical result for the 3D incompressible Navier–Stokes equations, which says that a weak solution that additionally satisfy Prodi–Serrin $L^r-L^s$ condition is smooth. We show that in the case of fluid–rigid body the Prodi–Serrin conditions imply $W^{2,p}$ and $W^{1,p}$ regularity for the fluid velocity and fluid pressure, respectively. Moreover, we show that solutions are $C^{\infty }$ if additionally we assume that the rigid body acceleration is bounded almost anywhere in time variable.

Appendices

Appendix

1.1 Time derivatives-general case

In Sect. 4, we have presented the proof of Proposition 2.2 for case $l=1$. Here we are going to present the induction step for general $l\in {{\mathbb {N}}}$. The proof in general case is conceptually the same, but with more complicated expressions in the equations.

Let $l\ge 1$ and let us assume that

$$\begin{aligned} \begin{aligned}&\partial _t^{l-1}\widetilde{\textbf{U}},\partial _t^{l-1}{\textbf{U}}\in W^{1,p}(\varepsilon ,T;L^p(\Omega _F))\cap L^{p}(\varepsilon ,T;W^{2,p}(\Omega _F)), \\&\partial _t^{l-1}\widetilde{P},\partial _t^{l-1}P\in L^{p}(\varepsilon ,T;{W^{1,p}(\Omega _F)\,/\,{{\mathbb {R}}}}), \\&\frac{\textrm{d} ^{l-1}}{\textrm{d} t ^{l-1}}\widetilde{\textbf{A}},\frac{\textrm{d} ^{l-1}}{\textrm{d} t ^{l-1}}{\textbf{A}}, \frac{\textrm{d} ^{l-1}}{\textrm{d} t ^{l-1}}\widetilde{\varvec{\Omega }},\frac{\textrm{d} ^{l-1}}{\textrm{d} t ^{l-1}}{\varvec{\Omega }}\in W^{1,p}(\varepsilon ,T), \end{aligned} \end{aligned}$$

for all $\varepsilon >0$ and $1\le p <\infty$. We consider the problem (3.1) with right hand side

$$\begin{aligned} \begin{aligned}&F^{*} = F_l^{*} = F(\textbf{U}^{*},P^{*}) + tF_l(\textbf{U},P) + \partial _t^l\textbf{U}, \\&G^{*} = G_l^{*} = G(\textbf{A}^{*}) + tG_l(\textbf{A}) + \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}, \\&H^{*} = H_l^{*} = H(\varvec{\Omega }^{*}) + tH_l(\varvec{\Omega }) + \mathcal {J}\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }, \end{aligned} \end{aligned}$$

(6.1)

where

$$\begin{aligned} F_l(\textbf{U},P)= & {} \sum _{p=0}^{l-1}\left( {\begin{array}{c}l\\ p\end{array}}\right) \left( \mathcal {F}_{l-p}\left( \partial _t^{p}\textbf{U}\right) - \mathcal {G}_{l-p}\left( \partial _t^{p}P \right) \right) \nonumber \\= & {} \sum _{p=0}^{l-1}\left( {\begin{array}{c}l\\ p\end{array}}\right) \Big ( \mathcal {L}_{l-p}\left( \partial _t^{p}\textbf{U}\right) - \mathcal {M}_{l-p}\left( \partial _t^{p}\textbf{U}\right) \nonumber \\{} & {} - \mathcal {N}_{l-p}\left( \partial _t^{p}\textbf{U}\right) - \mathcal {G}_{l-p}\left( \partial _t^{p}P \right) \Big ) \end{aligned}$$

(6.2)

$$\begin{aligned} G_l(\textbf{A})= & {} -\sum _{p=0}^{l-1}\left( {\begin{array}{c}l\\ p\end{array}}\right) \frac{\textrm{d} ^{l-p}}{\textrm{d} t ^{l-p}}\widetilde{\varvec{\Omega }}\times \frac{\textrm{d} ^{p}}{\textrm{d} t ^{p}}\textbf{A},\nonumber \\ H_l(\varvec{\Omega })= & {} -\sum _{p=0}^{l-1}\left( {\begin{array}{c}l\\ p\end{array}}\right) \frac{\textrm{d} ^{l-p}}{\textrm{d} t ^{l-p}}\widetilde{\varvec{\Omega }}\times \mathcal {J}\left( \frac{\textrm{d} ^{p}}{\textrm{d} t ^{p}}\varvec{\Omega }\right) . \end{aligned}$$

(6.3)

Subscript $l-p$ in operators $\mathcal {L}_{l-p}$, $\mathcal {M}_{l-p}$, $\mathcal {N}_{l-p}$ and $\mathcal {G}_{l-p}$ denotes $(l-p)$^th order time derivative of the coefficients in operators $\mathcal {L}$, $\mathcal {M}$, $\mathcal {N}$ and $\mathcal {G}$. As for $l=1$, to show that described problem has a unique solution $(\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})$ such that

$$\begin{aligned} \begin{aligned}&\textbf{U}_l^{*}\in H^1(0,T;L^2(\Omega _F))\cap L^2(0,T;H^{2}(\Omega _F)), \\&P_l^{*}\in L^2(0,T;{H^{1}(\Omega _F)\,/\,{{\mathbb {R}}}}), \\&\textbf{A}_l^{*},\varvec{\Omega }_l^{*}\in H^1(0,T) \end{aligned} \end{aligned}$$

(6.4)

it is sufficient to show that

$$\begin{aligned} \begin{aligned}&\mathcal {R} = tF_l(\textbf{U},P)+\partial _t^l\textbf{U}, \quad \mathcal {R}_{\textbf{a}} = tG_l(\textbf{A})+\frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}\textbf{A}, \quad \mathcal {R}_{\varvec{\omega }} = tH_l(\varvec{\Omega })+\frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}\varvec{\Omega }. \end{aligned} \end{aligned}$$

satisfy

$$\begin{aligned} \begin{aligned}&\mathcal {R}\in L^2(0,T;L^2(\Omega _{F})) \quad \mathcal {R}_{\textbf{a}}\in L^2(0,T), \quad \mathcal {R}_{\varvec{\omega }} \in L^2(0,T). \end{aligned} \end{aligned}$$

All the terms can be estimated as in Sect. 4, so by Proposition 3.1 there exists a unique strong solution $(\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})$ of (3.1) with the right hand side (6.1) satisfying (6.4). Again, we have to prove that the obtained solution equals $\left( t\partial _t^l\textbf{U},t\partial _t^l P,t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A},t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\right)$.

Lemma 6.1

Let $(\textbf{U},P,\textbf{A},\varvec{\Omega })$ be a unique strong solution for (2.4), and $(\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})$ be a unique strong solution for (3.1) with the right hand side (6.1) satisfying (6.4). Suppose that

$$\begin{aligned} \begin{aligned}&\textbf{U}, \widetilde{\textbf{U}}\in W^{l-1,p}(\varepsilon ,T;W^{2,p}(\Omega _F))\cap W^{l,p}(\varepsilon ,T;L^{p}(\Omega _F)), \\&P, \widetilde{P}\in W^{l-1,p}(\varepsilon ,T;{W^{1,p}(\Omega _F)\,/\,{{\mathbb {R}}}}), \\&\textbf{A},\varvec{\Omega }, \widetilde{\textbf{A}}, \widetilde{\varvec{\Omega }}\in W^{l,p}(\varepsilon ,T)\cap W^{1,\infty }(\varepsilon ,T) \end{aligned} \end{aligned}$$

(6.5)

hold for some $l\in {{\mathbb {N}}}$ and for all $\varepsilon >0$ and all $1\le p<\infty$. Then

$$\begin{aligned} (\textbf{U}_{l}^{*},P_{l}^{*},\textbf{A}_{l}^{*},\varvec{\Omega }_{l}^{*}) = \left( t\partial _t^l\textbf{U},t\partial _t^l P,t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A},t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\right) . \end{aligned}$$

(6.6)

1.2 Proof of Lemma 6.1

Let $(\textbf{U},P,\textbf{A},\varvec{\Omega })$ be a unique strong solution for (2.4) satisfying (6.5) and let $(\textbf{U}_{l}^{*},P_{l}^{*},\textbf{A}_{l}^{*},\varvec{\Omega }_{l}^{*})$ be a unique strong solution for (3.1) with the right hand side (6.1). We want to show (6.6). Since we have already shown that the statement is valid for $l=1$ in Sect. 4.1, we can suppose that $l\ge 2$.

We use Galerkin approximations $(\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)$, as in Sect. 4.1, and assume that

$$\begin{aligned} \Vert \textbf{U}^m\Vert _{W^{l-1,\infty }(\varepsilon ,T;L^2(\Omega ))} + \Vert \textbf{U}^m\Vert _{H^{l-1}(\varepsilon ,T;H^1(\Omega ))} <M, \end{aligned}$$

for some constant $M>0$. This assumption comes from the previous step of the induction.

We want to show that

$$\begin{aligned} \Vert \partial _t^l\textbf{U}^m\Vert _{L^{\infty }(\varepsilon ,T;L^2(\Omega ))} + \Vert \partial _t^l\textbf{U}^m\Vert _{L^{2}(\varepsilon ,T;H^1(\Omega ))} <M. \end{aligned}$$

for some constant $M>0$, which implies that

$$\begin{aligned} \partial _t^l\widetilde{\textbf{U}},\partial _t^l{\textbf{U}}\in L^{\infty }(\varepsilon ,T;L^2(\Omega ))\cap L^{2}(\varepsilon ,T;H^1(\Omega )). \end{aligned}$$

By (4.16) approximation $(\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)$ satisfies

$$\begin{aligned} \begin{aligned}&\int _{\Omega }\mathbb {G}\partial _{t}{\textbf{U}^m} \cdot {\varvec{\Psi }}_i \, \textrm{d} \textbf{y}+ \left\langle \mathbb {G}\mathcal {F}\textbf{U}^m,\varvec{\Psi }_i\right\rangle - G(\textbf{A}^m)\cdot \varvec{\Psi }_i^{\textbf{a}} - H(\varvec{\Omega }^m)\cdot \varvec{\Psi }_i^{\varvec{\omega }} = 0 \end{aligned} \end{aligned}$$

for $i=1,\ldots m$. We differentiate the equation in time l times

$$\begin{aligned}{} & {} \int _{\Omega }\partial _t^l(\mathbb {G}\partial _{t}{\textbf{U}^m}) \cdot \varvec{\Psi }_i \, \textrm{d} \textbf{y}- \left\langle \mathbb {\mathbb {G}}\mathcal {F}(\partial _t^l\textbf{U}^m),\varvec{\Psi }_i\right\rangle - \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left\langle \partial _t^k(\mathbb {G}\mathcal {F})(\partial _t^{l-k}\textbf{U}^m),\varvec{\Psi }_i\right\rangle \\{} & {} \qquad - G\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m\right) \cdot \varvec{\Psi }_i^{\textbf{a}} - H\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m\right) \cdot \varvec{\Psi }_i^{\varvec{\omega }} - \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\textbf{A}^m\right) \cdot \varvec{\Psi }_i^{\textbf{a}}\right. \\{} & {} \qquad \left. + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\varvec{\Omega }^m\right) \cdot \varvec{\Psi }_i^{\varvec{\omega }} \right) \\{} & {} \quad =0, \end{aligned}$$

multiply by $\frac{\textrm{d} ^l}{\textrm{d} t ^l}c_{im}$ and sum over i form 1 to m to obtain

$$\begin{aligned}{} & {} \int _{\Omega }\partial _t^l(\mathbb {G}\partial _{t}{\textbf{U}^m}) \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}- \left\langle \mathbb {\mathbb {G}}\mathcal {F}(\partial _t^l\textbf{U}^m),\partial _t^l\textbf{U}^m\right\rangle \\{} & {} \quad - \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left\langle \partial _t^k(\mathbb {G}\mathcal {F})(\partial _t^{l-k}\textbf{U}^m),\partial _t^l\textbf{U}^m\right\rangle \\{} & {} \quad - G\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m\right) \cdot \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m - H\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m\right) \cdot \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m \\{} & {} \quad - \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\textbf{A}^m\right) \cdot \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\varvec{\Omega }^m\right) \cdot \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m \right) =0. \end{aligned}$$

Then we integrate the equation on $[t_1,t_2]\subset (0,T]$ and, in the same way as in Sect. 4.1.1, estimate

$$\begin{aligned}&\int _{\Omega }\partial _t^l(\mathbb {G}\partial _{t}{\textbf{U}^m}) \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\\&\quad = \int _{\Omega }\mathbb {G}\partial _{t}^{l+1}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}+ \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega }\partial _t^k\mathbb {G}\,\partial _{t}^{l-k+1}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\\&\quad = \frac{1}{2}\frac{\textrm{d} }{\textrm{d} t }\int _{\Omega }\mathbb {G}\partial _{t}^{l}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}-\int _{\Omega }\partial _{t}\mathbb {G}\,\partial _{t}^{l}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\\&\qquad + \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega }\partial _t^k\mathbb {G}\,\partial _{t}^{l-k+1}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\\&\qquad \left| -\int _{t_1}^{t_2}\int _{\Omega }\partial _{t}\mathbb {G}\,\partial _{t}^{l}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\textrm{d} \tau + \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{t_1}^{t_2}\int _{\Omega }\partial _t^k\mathbb {G}\,\partial _{t}^{l-k+1}{\textbf{U}^m} \cdot \partial _{t}^l{\textbf{U}^m} \, \textrm{d} \textbf{y}\textrm{d} \tau \right| \\&\quad \le C\Vert \textbf{U}^m\Vert _{H^l(t_1,t_2;L^2(\Omega ))}^2 \\&\qquad \left| \int _{t_1}^{t_2}\left\langle \mathbb {G}\mathcal {F}\left( \partial _t^l\textbf{U}^m\right) ,\partial _{t}^l{\textbf{U}^m}\right\rangle \textrm{d} \tau - \int _{t_1}^{t_2}\int _{\Omega _{F}}2|{{\mathbb {D}}}\partial _t^l\textbf{U}^m|^2\,\textrm{d} \textbf{y}\textrm{d} \tau \right| \\&\quad \le \left( \Vert g_{ik}g^{il}-\delta _{ik}\delta _{il}\Vert _{L^{\infty }(0,T;L^{\infty }(\Omega ))} +\mu \right) \int _{t_1}^{t_2}\int _{\Omega _{F}}|\nabla \partial _t^l\textbf{U}^m|^2\,\textrm{d} \textbf{y}\textrm{d} \tau \\&\qquad + C\int _{t_1}^{t_2}\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}^2\,\textrm{d} \tau \end{aligned}$$

The only difference from Sect. 4.1.1 is in the following estimate

$$\begin{aligned}&\left| \int _{t_1}^{t_2}\sum _{k=1}^l\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega _F} \partial _t^k(\mathbb {G}\mathcal {M})(\textbf{U}^m),\partial _t^l\textbf{U}^m\,\textrm{d} \textbf{y}\textrm{d} \tau \right| \\&\quad \le {\int _{t_1}^{t_2}}\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}^2\,\textrm{d} \tau + C\left( \Vert \widetilde{\textbf{A}}\Vert _{W^{l,4}(t_1,t_2)} \right. \\&\qquad \left. + \Vert \widetilde{\varvec{\Omega }}\Vert _{W^{l,4}(t_1,t_2)} \right) ^2 \Vert \textbf{U}^m\Vert _{W^{l-2,4}(t_1,t_2;H^{1}(\Omega _F))}^2 \\&\qquad + C\left( \Vert \widetilde{\textbf{A}}\Vert _{W^{l-1,\infty }(t_1,t_2)} + \Vert \widetilde{\varvec{\Omega }}\Vert _{W^{l-1,\infty }(t_1,t_2)} \right) ^2 \Vert \textbf{U}^m\Vert _{H^{l-1}(t_1,t_2;H^{1}(\Omega _F))}^2 \\&\quad \le {\int _{t_1}^{t_2}}\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}^2\,\textrm{d} \tau + C \Vert \textbf{U}^m\Vert _{H^{l-1}(t_1,t_2;H^{1}(\Omega _F))}^2. \end{aligned}$$

The last inequality follows from the fact that $\widetilde{\textbf{A}}, \widetilde{\varvec{\Omega }}\in W^{l,4}(\varepsilon ,T)\cap W^{1,\infty }(\varepsilon ,T)$ and embedding $W^{l-2,4}(t_1,t_2;H^{1}(\Omega _F))\hookrightarrow H^{l-1}(t_1,t_2;H^{1}(\Omega _F))$ for $l\ge 2$. Therefore, we get

$$\begin{aligned}&\left| \int _{t_1}^{t_2}\left\langle \partial _t^k(\mathbb {G}\mathcal {F})(\partial _t^{l-k}\textbf{U}^m),\partial _t^l\textbf{U}^m\right\rangle \,\textrm{d} \textbf{y}\textrm{d} \tau \right| \\&\quad \le \mu \int _{t_1}^{t_2}\int _{\Omega _{F}}|\nabla \partial _t^l\textbf{U}^m|^2\,\textrm{d} \textbf{y}\textrm{d} \tau + C\int _{t_1}^{t_2}\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}^2\,\textrm{d} \tau \\&\qquad + C \Vert \textbf{U}^m\Vert _{H^{l-1}(t_1,t_2;H^{1}(\Omega _F))}^2 \end{aligned}$$

All together, we get

$$\begin{aligned}&\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}(t_2) + \Vert {{\mathbb {D}}}\partial _t\textbf{U}^m\Vert _{L^2(t_1,t_2;L^2(\Omega _F))}^2 \\&\quad \le C\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}(t_1) + C\int _{t_1}^{t_2}\Vert \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega )}^2\textrm{d} t \\&\qquad + C\left( \Vert g_{ik}g^{il}-\delta _{ik}\delta _{il}\Vert _{L^{\infty }(0,T;L^{\infty }(\Omega ))} +\mu \right) \int _{t_1}^{t_2}\Vert \nabla \partial _t^l\textbf{U}^m\Vert _{L^2(\Omega _F)}^2\,\textrm{d} \tau \\&\qquad + C \Vert \textbf{U}^m\Vert _{H^{l-1}(t_1,t_2; H^1(\Omega _F))}^2, \end{aligned}$$

for arbitrary $\mu >0$, where $\Vert g_{ik}g^{il}-\delta _{ik}\delta _{il}\Vert _{L^{\infty }(0,T;L^{\infty }(\Omega ))}$ is small for small T. Now, we take sufficiently small T, integrate the inequality on $t_1\in (\varepsilon ,t_2)$ and by Gronwall’s Lemma we find

$$\begin{aligned}&\Vert \partial _t^l\textbf{U}^m(t)\Vert _{L^2(\Omega )}^2 + \int _{\varepsilon }^{t}\Vert {{\mathbb {D}}}\partial _t^l\textbf{U}^m\Vert _{L^2(\Omega _F)}^2\,\textrm{d} \tau \le M, \end{aligned}$$

where constant $M>0$ depends on the norms $\Vert \widetilde{\textbf{U}}\Vert _{H^{l-1}(\varepsilon ,T;H^1(\Omega ))}$, $\Vert \textbf{U}^m\Vert _{H^{l-1}(0,T;H^1(\Omega ))}$, $\Vert \widetilde{\textbf{A}}\Vert _{W^{1,\infty }(\varepsilon ,T)}$, $\Vert \widetilde{\textbf{A}}\Vert _{W^{l,4}(\varepsilon ,T)}$, $\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{1,\infty }(\varepsilon ,T)}$, $\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{l,4}(\varepsilon ,T)}$ and T. Finally, in the limit we get that $\partial _t^l\textbf{U}\in L^2(\varepsilon ,T;H^1(\Omega ))\cap L^{\infty }(\varepsilon ,T;L^2(\Omega ))$, for all $\varepsilon >0$.

1.2.1 Uniqueness

In previous section, we showed that $\partial _t^l\textbf{U}\in L^2(\varepsilon ,T;H^1(\Omega ))\cap L^{\infty }(\varepsilon ,T;L^2(\Omega ))$, for all $\varepsilon >0$. Now we are able to show that $\textbf{U}_{l}^{*}=t\partial _t^l\textbf{U}$. We know that $(\textbf{U}, P)$ satisfies

$$\begin{aligned}{} & {} \int _{\Omega _F}\partial _{t}^k\mathbb {G}\, \partial _{t}^{l-k+1}\textbf{U}\cdot \varvec{\psi }\, \textrm{d} \textbf{y}-\int _{\Omega _F} \partial _{t}^k\mathbb {G}\, \partial _{t}^{l-k}\left( \mathcal {F}(\textbf{U})\right) \cdot \varvec{\psi }\, \textrm{d} \textbf{y}\nonumber \\{} & {} \quad + \int _{\Omega _F}\partial _{t}^k\mathbb {G}\,\partial _{t}^{l-k}(\mathcal {G}(P)) \cdot \varvec{\psi }\, \textrm{d} \textbf{y}= 0, \quad 1\le k \le l, \end{aligned}$$

(6.7)

for all $\varvec{\psi }\in V(0)$, and $(\textbf{U}_{l}^{*}, P_{l}^{*},\textbf{A}_{l}^{*},\varvec{\Omega }_{l}^{*})$ satisfies

$$\begin{aligned}{} & {} \int _{\Omega _F}\mathbb {G}\partial _{t}{\textbf{U}_{l}^{*}} \cdot \varvec{\psi }\, \textrm{d} \textbf{y}+ \frac{\textrm{d} }{\textrm{d} t }\textbf{A}_{l}^{*}\cdot \varvec{\psi }_{\textbf{a}} + \frac{\textrm{d} }{\textrm{d} t }(\mathcal {J}{\varvec{\Omega }_{l}^{*}})\cdot \varvec{\psi }_{\varvec{\omega }} \nonumber \\{} & {} \quad + \left\langle \mathbb {G}\mathcal {F}(\textbf{U}_{l}^{*}),\varvec{\psi }\right\rangle + t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( \left\langle \mathbb {G}\mathcal {F}_k (\partial _t^{l-k}\textbf{U}),\varvec{\psi }\right\rangle +\int _{\Omega _F}\mathbb {G}\mathcal {G}_l( \partial _t^{l-k}P) \cdot \varvec{\psi }\, \textrm{d} \textbf{y}\right) \nonumber \\{} & {} \quad - G(\textbf{A}_{l}^{*})\cdot \varvec{\psi }_{\textbf{a}} - H(\varvec{\Omega }_{l}^{*})\cdot \varvec{\psi }_{\varvec{\omega }} - t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\textbf{A}\right) \cdot \varvec{\psi }_{\textbf{a}} + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\varvec{\Omega }\right) \cdot \varvec{\psi }_{\varvec{\omega }} \right) \nonumber \\{} & {} \quad -\int _{\Omega _F}\mathbb {G}\partial _{t}^l{\textbf{U}} \cdot \varvec{\psi }- \left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}\textbf{A}\right) \cdot \varvec{\psi }_{\textbf{a}} - \left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}\varvec{\Omega }\right) \cdot \varvec{\psi }_{\varvec{\omega }} =0, \end{aligned}$$

(6.8)

where

$$\begin{aligned} \left\langle \mathbb {G}\,\mathcal {F}_k(\partial _{t}^{l-k}\textbf{U}),\varvec{\psi }\right\rangle =- \int _{\Omega _F}\mathbb {G}\,\mathcal {F}_k(\partial _{t}^{l-k}\textbf{U}) \cdot \varvec{\psi }\, \textrm{d} \textbf{y},\quad 1\le k\le l. \end{aligned}$$

For $(\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})=h(t)({\varvec{\Psi }}_j,{\varvec{\Psi }}_j^{\textbf{a}},{\varvec{\Psi }}_j^{\varvec{\omega }})$ we have

$$\begin{aligned}{} & {} \int _{\Omega _F}\mathbb {G}\partial _{t}{\partial _t^l\textbf{U}^m} \cdot \varvec{\psi }\, \textrm{d} \textbf{y}+ \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega _F}\partial _t^k\mathbb {G}\,{\partial _t^{l-k+1}\textbf{U}^m} \cdot \varvec{\psi }\, \textrm{d} \textbf{y}\nonumber \\{} & {} \quad + \frac{\textrm{d} ^l}{\textrm{d} t ^l}\mathcal {J}\left( \frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }^m\right) \cdot \varvec{\psi }_{\varvec{\omega }} + \frac{\textrm{d} ^{l+1}}{\textrm{d} t ^{l+1}}\textbf{A}^m\cdot \varvec{\psi }_{\textbf{a}} + \left\langle \mathbb {\mathbb {G}}\mathcal {F}(\partial _t^l\textbf{U}^m),\varvec{\psi }\right\rangle \nonumber \\{} & {} \quad + \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left\langle \mathbb {G}\mathcal {F}_k(\partial _t^{l-k}\textbf{U}^m),\varvec{\psi }\right\rangle + \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left\langle \partial _t^k \mathbb {G}\,\partial _t^{l-k}\left( \mathcal {F}(\textbf{U}^m)\right) ,\varvec{\psi }\right\rangle \nonumber \\{} & {} \quad - G\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m\right) \cdot \varvec{\psi }_{\textbf{a}} - H\left( \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m\right) \cdot \varvec{\psi }_{\varvec{\omega }} - \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\textbf{A}^m\right) \cdot \varvec{\psi }_{\textbf{a}} + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}\varvec{\Omega }^m\right) \cdot \varvec{\psi }_{\varvec{\omega }} \right) \nonumber \\{} & {} \quad =0, \end{aligned}$$

(6.9)

where

$$\begin{aligned} \left\langle \partial _t^k\mathbb {G}\,\partial _t^{l-k}\left( \mathcal {F}(\textbf{U})\right) ,\varvec{\psi }\right\rangle =- \int _{\Omega _F}\partial _t^k\mathbb {G}\,\partial _t^{l-k}\left( \mathcal {F}(\textbf{U})\right) \cdot \varvec{\psi }\, \textrm{d} \textbf{y},\quad 1\le k\le l. \end{aligned}$$

We multiply the above equation by t and subtract from the previous one with

$$\begin{aligned} (\widehat{\textbf{U}}^m,\widehat{\textbf{A}}^m,\widehat{\varvec{\Omega }}^m) = \left( \textbf{U}_{l}^{*}-t\partial _t^l\textbf{U}^m,\, \textbf{A}_{l}^{*}-t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}^m,\, \varvec{\Omega }_{l}^{*}-t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }^m \right) \end{aligned}$$

Then, by using (6.7), we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Omega _F}\mathbb {G}\partial _{t}\widehat{\textbf{U}}^m \cdot \varvec{\psi }\, \textrm{d} \textbf{y}+ t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega _F}\partial _t^k\mathbb {G}\,{\partial _t^{l-k+1}({\textbf{U}}-{\textbf{U}^m})} \cdot \varvec{\psi }\, \textrm{d} \textbf{y}\\&\quad + \frac{\textrm{d} }{\textrm{d} t }\widehat{\textbf{A}}^m\cdot \varvec{\psi }_{\textbf{a}} + \frac{\textrm{d} }{\textrm{d} t }(\mathcal {J}{\widehat{\varvec{\Omega }}^m})\cdot \varvec{\psi }_{\varvec{\omega }} \\&\quad - \left\langle \mathbb {G}\mathcal {F}(\widehat{\textbf{U}}^m),\varvec{\psi }\right\rangle - t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( \left\langle \mathbb {G}\mathcal {F}_k (\partial _t^{l-k}({\textbf{U}}-{\textbf{U}^m})),\varvec{\psi }\right\rangle \right. \\&\quad \left. + \left\langle \partial _t^k \mathbb {G}\,\partial _t^{l-k}\left( \mathcal {F}({\textbf{U}}-{\textbf{U}^m})\right) ,\varvec{\psi }\right\rangle \right) \\&\quad { - t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{\Omega _F}\mathbb {G}\mathcal {G}_l (\partial _t^{l-k}P) \cdot \varvec{\psi }\, \textrm{d} \textbf{y}} -t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) { \int _{\Omega _F}\partial _{t}^k\mathbb {G}\,\partial _{t}^{l-k}(\mathcal {G}(P)) \cdot \varvec{\psi }\, \textrm{d} \textbf{y}} \\&\quad - G(\widehat{\textbf{A}}^m)\cdot \varvec{\psi }_{\textbf{a}} - H(\widehat{\varvec{\Omega }}^m)\cdot \varvec{\psi }_{\varvec{\omega }} \\&\quad - {t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}(\textbf{A}-\textbf{A}^m)\right) \cdot \varvec{\psi }_{\textbf{a}} + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}(\varvec{\Omega }-\varvec{\Omega }^m)\right) \cdot \varvec{\psi }_{\varvec{\omega }} \right) } \\&\quad -\int _{\Omega _F}\mathbb {G}\partial _{t}^l({\textbf{U}}-{\textbf{U}^m}) \cdot \varvec{\psi }\,\textrm{d} \textbf{y}\\&\quad - \left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}(\textbf{A}-\textbf{A}^m)\right) \cdot \varvec{\psi }_{\textbf{a}} - \left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}(\varvec{\Omega }-\varvec{\Omega }^m)\right) \cdot \varvec{\psi }_{\varvec{\omega }} =0 \end{aligned} \end{aligned}$$

It can be shown that the terms with the pressure cancels, i.e. it holds

$$\begin{aligned} \sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \mathbb {G}\mathcal {G}_l (\partial _t^{l-k}P) +\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \partial _{t}^k\mathbb {G}\,\partial _{t}^{l-k}(\mathcal {G}(P)) = 0, \end{aligned}$$

(6.10)

and after integrating above equation on (0, t), we get

$$\begin{aligned}&\int _{\Omega _F}\mathbb {G}(t)\widehat{\textbf{U}}^m(t) \cdot \varvec{\psi }(t) \, \textrm{d} \textbf{y}-\int _{0}^{t}\int _{\Omega _F}\mathbb {G}\widehat{\textbf{U}}^m \cdot \partial _{t}\varvec{\psi }\, \textrm{d} \textbf{y}\textrm{d} \tau -\int _{0}^{t}\int _{\Omega _F}\partial _t\mathbb {G}\widehat{\textbf{U}}^m \cdot \partial _{t}\varvec{\psi }\, \textrm{d} \textbf{y}\textrm{d} \tau \\&\qquad + t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{0}^{t}\int _{\Omega _F}\partial _t^k\mathbb {G}\,{\partial _t^{l-k+1}(\textbf{U}-\textbf{U}^m)} \cdot \varvec{\psi }\, \textrm{d} \textbf{y}\,\textrm{d} \tau \\&\qquad +\widehat{\textbf{A}}^m(t)\cdot \varvec{\psi }_{\textbf{a}}(t) + \mathcal {J}{\widehat{\varvec{\Omega }}^m}(t)\cdot \varvec{\psi }_{\varvec{\omega }}(t) - \int _{0}^{t} \left( \widehat{\textbf{A}}^m\cdot \frac{\textrm{d} }{\textrm{d} t }\varvec{\psi }_{\textbf{a}} + \mathcal {J}{\widehat{\varvec{\Omega }}^m}\cdot \frac{\textrm{d} }{\textrm{d} t }\varvec{\psi }_{\varvec{\omega }} \right) \,\textrm{d} \tau \\&\qquad - \int _{0}^{t} \left\langle \mathbb {G}\mathcal {F}(\widehat{\textbf{U}}^m),\varvec{\psi }\right\rangle \,\textrm{d} \tau - t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{0}^{t}\left( \left\langle \mathbb {G}\mathcal {F}_k (\partial _t^{l-k}(\textbf{U}-\textbf{U}^m)),\varvec{\psi }\right\rangle + \left\langle \partial _t^l \mathbb {G}\,\partial _t^{l-k}\mathcal {F}(\textbf{U}-\textbf{U}^m),\varvec{\psi }\right\rangle \right) \,\textrm{d} \tau \\&\qquad - \int _{0}^{t}\left( G(\widehat{\textbf{A}}^m)\cdot \varvec{\psi }_{\textbf{a}} + H(\widehat{\varvec{\Omega }}^m)\cdot \varvec{\psi }_{\varvec{\omega }} \right) \,\textrm{d} \tau \\&\qquad - {t\sum _{k=1}^{l}\left( {\begin{array}{c}l\\ k\end{array}}\right) \int _{0}^{t}\left( G_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}(\textbf{A}-\textbf{A}^m)\right) \cdot \varvec{\psi }_{\textbf{a}} + H_k\left( \frac{\textrm{d} ^{l-k}}{\textrm{d} t ^{l-k}}(\varvec{\Omega }-\varvec{\Omega }^m)\right) \cdot \varvec{\psi }_{\varvec{\omega }} \right) \,\textrm{d} \tau } \\&\qquad -\int _{0}^{t}\int _{\Omega _F}\mathbb {G}\partial _{t}^l({\textbf{U}}-{\textbf{U}^m}) \cdot \varvec{\psi }\,\textrm{d} \textbf{y}\,\textrm{d} \tau - \int _{0}^{t}\left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}(\textbf{A}-\textbf{A}^m)\right) \cdot \varvec{\psi }_{\textbf{a}}\,\textrm{d} \tau \\&\qquad - \int _{0}^{t}\left( \frac{\textrm{d} ^{l}}{\textrm{d} t ^{l}}(\varvec{\Omega }-\varvec{\Omega }^m)\right) \cdot \varvec{\psi }_{\varvec{\omega }}\,\textrm{d} \tau =0. \end{aligned}$$

We let $m\rightarrow \infty$ and obtain the equation

$$\begin{aligned} \begin{aligned}&\int _{\Omega _F}\mathbb {G}(t)\widehat{\textbf{U}}(t) \cdot \varvec{\psi }(t) \, \textrm{d} \textbf{y}-\int _{0}^{t}\int _{\Omega _F}\widehat{\textbf{U}} \cdot \partial _{t}(\mathbb {G}\varvec{\psi }) \, \textrm{d} \textbf{y}\textrm{d} \tau \\&\qquad +\widehat{\textbf{A}}(t)\cdot \varvec{\psi }_{\textbf{a}}(t) + \mathcal {J}{\widehat{\varvec{\Omega }}}(t)\cdot \varvec{\psi }_{\varvec{\omega }}(t) - \int _{0}^{t} \left( \widehat{\textbf{A}}\cdot \frac{\textrm{d} }{\textrm{d} t }\varvec{\psi }_{\textbf{a}} + \mathcal {J}{\widehat{\varvec{\Omega }}}\cdot \frac{\textrm{d} }{\textrm{d} t }\varvec{\psi }_{\varvec{\omega }} \right) \,\textrm{d} \tau \\&\qquad - \int _{0}^{t} \left\langle \mathbb {G}\mathcal {F}(\widehat{\textbf{U}}),\varvec{\psi }\right\rangle \,\textrm{d} \tau - \int _{0}^{t}\left( G(\widehat{\textbf{A}})\cdot \varvec{\psi }_{\textbf{a}} + H(\widehat{\varvec{\Omega }})\cdot \varvec{\psi }_{\varvec{\omega }} \right) \,\textrm{d} \tau =0 \end{aligned} \end{aligned}$$

where

$$\begin{aligned} (\widehat{\textbf{U}},\widehat{\textbf{A}},\widehat{\varvec{\Omega }}) = \left( \textbf{U}_{l}^{*}-t\partial ^l\textbf{U},\textbf{A}_{l}^{*}-\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A},\varvec{\Omega }_{l}^{*}-t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\right) . \end{aligned}$$

By the linearity and the density, the above equality holds for all $(\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})\in \mathbb {V}$. Then we can substitute

$$\begin{aligned} (\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }}) = (\widehat{\textbf{U}},\widehat{\textbf{A}},\widehat{\varvec{\Omega }}) \end{aligned}$$

and get the equality

$$\begin{aligned}{} & {} \frac{1}{2} \left\| (\nabla \textbf{X}\widehat{\textbf{U}})(t) \right\| _{L^2(\Omega )}^2 -\int _{0}^t\int _{\Omega }\nabla \textbf{X}^T\partial _t\nabla \textbf{X}\widehat{\textbf{U}}\cdot \widehat{\textbf{U}}\,\textrm{d} \textbf{y}\textrm{d} \tau \\{} & {} \quad - \int _{0}^{t} \left\langle \mathbb {G}\mathcal {F}(\widehat{\textbf{U}}),\widehat{\textbf{U}}\right\rangle \,\textrm{d} \tau - \int _{0}^{t}\left( G(\widehat{\textbf{A}})\cdot \widehat{\textbf{A}} + H(\widehat{\varvec{\Omega }})\cdot \widehat{\varvec{\Omega }} \right) \,\textrm{d} \tau =0. \end{aligned}$$

Now, as in Sect. 4, we can get the estimate

$$\begin{aligned}{} & {} \left\| \widehat{\textbf{U}}(t) \right\| _{L^2(\Omega )}^2 + C_1\int _{0}^{t}\int _{\Omega _F} |{{\mathbb {D}}}\widehat{\textbf{U}}|^2 \, \textrm{d} \textbf{y}\textrm{d} \tau \le \int _{0}^{t}C\left\| \widehat{\textbf{U}}(\tau ) \right\| _{L^2(\Omega )}^2 \textrm{d} \tau \\{} & {} \quad +\mu \int _{0}^{t}\int _{\Omega _F} |{{\mathbb {D}}}\widehat{\textbf{U}}|^2 \, \textrm{d} \textbf{y}\textrm{d} \tau \end{aligned}$$

for all $\mu >0$ and for sufficiently small $\mu$ we get

$$\begin{aligned} \begin{aligned}&\left\| \widehat{\textbf{U}}(t) \right\| _{L^2(\Omega )}^2 \le \int _{0}^{t}C\left\| \widehat{\textbf{U}}(\tau ) \right\| _{L^2(\Omega )}^2 \textrm{d} \tau . \end{aligned} \end{aligned}$$

Finally, Gronwall’s Lemma implies $\widehat{\textbf{U}}=0$ which means that $\textbf{U}_{l}^{*}=t\partial _t^l\textbf{U}$. Then the equations for $\textbf{U}$ and $\textbf{U}_l^{*}$ give $\nabla P_l^{*}=t\nabla \partial _t P$, and since $\textbf{U}_l^{*}=\textbf{A}_l^{*}+ \varvec{\Omega }_l^{*}\times \textbf{y}$ and $\partial _t\textbf{U}=\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}+ \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\times \textbf{y}$ on $\overline{S_0}$, it follows that $\textbf{A}_l^{*}=t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}$ and $\varvec{\Omega }_l^{*}=t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }$.

Notation

Label	Description	Definition/1st appearance
$(\widetilde{\textbf{u}}, \widetilde{p},\widetilde{\varvec{\omega }},\widetilde{\textbf{a}})$	Solution for the original nonlinear problem (1.6) on physical domain	Section 2.1
$(\textbf{u}, p,\varvec{\omega },\textbf{a})$	Solution for the linear problem (2.1) on the physical domain	Section 2.1
$(\widetilde{\textbf{U}}, \widetilde{P},\widetilde{\varvec{\Omega }},\widetilde{\textbf{A}})$	Solution for the nonlinear problem on the cylindrical domain	Section 2.2, Eq. (2.3)
$(\textbf{U}, P,\varvec{\Omega },\textbf{A})$	Solution for the linear problem (2.4) on the cylindrical domain	Section 2.2, Eq. (2.3)
$(\varvec{\varphi }, \varvec{\varphi }_{\varvec{\omega }}, \varvec{\varphi }_{\textbf{a}})$	Test function on the physical domain	Definition 1.1
$(\varvec{\psi }, \varvec{\psi }_{\varvec{\omega }}, \varvec{\psi }_{\textbf{a}})$	Test function on the cylindrical domain	Section 4.1
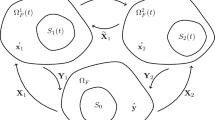
$\textbf{X}(t,\textbf{y})$	Changes of variables	Section 2.2
$\textbf{Y}(t,\textbf{x})$	Changes of variables	Section 2.2
$F(\textbf{U},P)$, $G(\textbf{A}), H(\varvec{\Omega })$	Right-hand side of the linear problem (2.4) on the cylindrical domain,	Equations (2.5) and (2.6)
	$F(\textbf{U},P) = (\mathcal {L}-\Delta )\textbf{U}-\mathcal {M}\textbf{U}-\mathcal {N}\textbf{U}-(\mathcal {G}-\nabla )P$
$\mathcal {L}\textbf{U}$	The transformed Laplace operator	Equation (2.7)
$\mathcal {M}\textbf{U}$	The transformation of time derivative and gradient	Equation (2.9)
$\mathcal {N}\textbf{U}$	The transformation of the convection term	Equation (2.8)
$\mathcal {G}P$	$\mathcal {G}P=\nabla \textbf{Y}\nabla \textbf{Y}^T\nabla P$, the transformation of the gradient of the pressure	Equation (2.10)
$\mathcal {F}\textbf{U}$	$\mathcal {F}\textbf{U}= \mathcal {L}\textbf{U}-\mathcal {M}\textbf{U}-\mathcal {N}\textbf{U}-\mathcal {G}P$	Equation (4.12)
$({\textbf{U}}^{*}, {P}^{*},{\varvec{\Omega }}^{*},{\textbf{A}}^{*})$	The fixed point, the solution for the transformed problem	Section 3
$(\widehat{\textbf{U}}, \widehat{P},\widehat{\varvec{\Omega }},\widehat{\textbf{A}})$	The fixed point, functions on the right-hand side	Section 3
$F^{*}$, $G^{*}$, $H^{*}$	The right-hand side for the Stokes problem	Section 3
$X_{p,q}^T$, $Y_{p,q}^T$	$X_{p,q}^T :=W^{1,p}(0,T;L^q(\Omega _{F}))\cap L^p(0,T;W^{2,q}(\Omega _F))$ $Y_{p,q}^T := L^p(0,T; {W}^{1,q}(\Omega _{F}))$	Section 3, Theorem 3.1
$F_l(\textbf{U},P)$	“$F_l(\textbf{U},P)=\partial _{t}^l(F({\textbf{U}},{P}))-F(\partial _{t}^l{\textbf{U}},\partial _{t}^l{P})$”	(4.6)–(4.9)
$G_l(\textbf{A})$	“$G_l(\textbf{A})=\frac{d^l}{{dt}^l}(G(\textbf{A}))-G\left( \frac{d^l}{{dt}^l}\textbf{A}\right)$”	(4.5) ($l=1$) and (6.3) (general case)
$H_l(\varvec{\Omega })$	“$H_l(\varvec{\Omega })=\frac{d^l}{{dt}^l}(H(\varvec{\Omega }))-H\left( \frac{d^l}{{dt}^l}\varvec{\Omega }\right)$”	(4.5) ($l=1$) (6.3) (general case)
$\mathcal {G}_l(P)$	The operator obtained by taking lth order time derivative of the coefficients in operator $\mathcal {G}$, i.e. $\mathcal {G}_l(P)=\partial _t^l(\nabla \textbf{Y}\nabla \textbf{Y}^T)\nabla P$	Section 4.1 (l = 1), Appendix 6.1 (general case)
$\mathcal {F}_l(\textbf{U})$	$\mathcal {F}_l(\textbf{U}) = \mathcal {L}_l(\textbf{U})-\mathcal {M}_l(\textbf{U})-\mathcal {N}_l(\textbf{U})-\mathcal {G}_l(P)$, $\mathcal {L}_l, \mathcal {M}_l, \mathcal {N}_l$ are operators obtained by taking lth order time derivative of the coefficients in operators $\mathcal {L}, \mathcal {M}, \mathcal {N}$	Section 4.1 (l = 1), Appendix 6.1 (general case)
$\mathbb {G}$	$\mathbb {G}=\nabla \textbf{X}^T\nabla \textbf{X}$	Section 4.1