Abstract
We are interested in finding for which positive integers D we have rational solutions for the equation \(x^3+y^3=D.\) The aim of this paper is to compute the value of the L-function \(L(E_D, 1)\) for the elliptic curves \(E_D: x^3+y^3=D\). For the case of p prime \(p\equiv 1\mod 9\), two formulas have been computed by Rodriguez-Villegas and Zagier. We have computed formulas that relate \(L(E_D, 1)\) to the square of a trace of a modular function at a CM point. This offers a criterion for when the integer D is the sum of two rational cubes. Furthermore, when \(L(E_D, 1)\) is nonzero we get a formula for the number of elements in the Tate–Shafarevich group and we show that this number is a square when D is a norm in \({\mathbb {Q}}[\sqrt{-3}]\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the current paper we are interested in finding which positive integers D can be written as the sum of two rational cubes:
Despite the simplicity of the problem, an elementary approach to solving the Diophantine equation fails. However, we can restate the problem in the language of elliptic curves. After making the equation homogeneous, we get the equation \(x^3+y^3=Dz^3\) that has a rational point at \(\infty =[1:-1:0]\). Moreover, after a change of coordinates \( X=12D\frac{z}{x+y}\), \( Y=36D\frac{x-y}{x+y}\) the equation becomes:
which defines an elliptic curve over \({\mathbb {Q}}\) written in its Weierstrass affine form.
Thus the problem reduces to finding if the group of rational points \(E_D({\mathbb {Q}})\) of the elliptic curve \(E_D\) is non-trivial. We assume D cube free and \(D\ne 1,2\) throughout the paper. In this case \(E_D({\mathbb {Q}})\) has trivial torsion (see [27]), thus (1) has a solution iff \(E_D({\mathbb {Q}})\) has positive rank. From the Birch and Swinnerton-Dyer (BSD) conjecture, this is conjecturally equivalent to the vanishing of \(L(E_D, 1)\).
Without assuming BSD, from the work of Coates–Wiles [3] (or more generally Gross–Zagier [9] and Kolyvagin [17]), when \(L(E_D, 1)\ne 0\) the rank of \(E_D({\mathbb {Q}})\) is 0, thus we have no rational solutions in (1).
In the case of prime numbers, Sylvester conjectured that we have solutions in (1) in the case of \(D \equiv 4, 7, 8 \mod 9\). In the cases of D prime with \(D \equiv 2, 5\mod 9\), D is not the sum of two cubes. This follows from a 3-descent argument (given in the 19th century by Sylvester, Lucas and Pepin).
We define the invariant
where \( \varOmega _{D}= \frac{\sqrt{3}}{6\pi \root 3 \of {D}}\varGamma \left( \frac{1}{3}\right) ^3\) is the real period and \(c_{3D}=\prod \nolimits _{p|3D} c_p\) is the product of the Tamagawa numbers \(c_p\) corresponding to the elliptic curve \(E_D\) at the unramified places p|3D. The definition is made such that in the case of \(L(E_D, 1)\ne 0\) we expect to get from the full BSD conjecture:

where  is the order of the Tate–Shafarevich group.
is the order of the Tate–Shafarevich group.
From the work of Rubin [25], \(L(E_D, 1)\ne 0\) implies the order of  is finite. Furthermore, using the Cassels–Tate pairing, Cassels proved in [2] that when
is finite. Furthermore, using the Cassels–Tate pairing, Cassels proved in [2] that when  is finite the order
is finite the order  is a square. We actually show that, when D is a norm in \({\mathbb {Q}}[\sqrt{-3}]\), \(S_D\) is an integer square up to an even power of 3. Current work in Iwasawa theory shows that for semistable elliptic curves at the good primes p we have
is a square. We actually show that, when D is a norm in \({\mathbb {Q}}[\sqrt{-3}]\), \(S_D\) is an integer square up to an even power of 3. Current work in Iwasawa theory shows that for semistable elliptic curves at the good primes p we have  , where
, where  is the \(p^{\infty }\)-torsion part of
is the \(p^{\infty }\)-torsion part of  (see [14]). However, this cannot be applied at the place 3 in our case, as this is a prime of bad reduction for \(E_D\).
(see [14]). However, this cannot be applied at the place 3 in our case, as this is a prime of bad reduction for \(E_D\).
By computing the value of \(S_D\), one can determine when we have solutions in (1) and, assuming the full BSD conjecture, one can find in certain cases the order of  :
:
-
(i)
\(S_D\ne 0\) \(\Longrightarrow \) no solutions in (1)
-
(ii)
\(S_D\ne 0\)

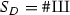 integer square
integer square -
(iii)
\(S_D=0\)
 have solutions in (1).
have solutions in (1).
The goal of the current paper is to compute several formulas for \(S_D\). In [24], Rodriguez-Villegas and Zagier computed formulas for \(L(E_p, 1)\) in the case of primes \(p\equiv 1\mod 9\). In the current paper we are extending on their results and compute similar formulas for all integers D.
Our main theorem is the following:
Theorem 1
For \(D=\prod \nolimits _{p_i\equiv 1(3)} p_i^{e_i}\), \(S_D\) is an integer square up to an even power of 3.
Theorem 1 above follows from the formula for \(S_D\) presented below. Let \(K={\mathbb {Q}}[\sqrt{-3}]\). For D a norm in K, we write \(D=D_1D_2^2\) such that \(D_0=D_1D_2\) is the radical of D. Let \(\pi _1, \pi _2 \equiv 1 \mod 3\) be elements of norm \(D_1\) and \(D_2\) respectively. Let \(\sigma (D)\) the number of distinct primes dividing D and \(\varphi \) Euler’s totient function.
Theorem 2
Using the above notation, let \(D=\prod \nolimits _{p_i\equiv 1(3)} p_i^{e_i}\) be a positive integer that is a product of split primes in K and \(D_0=\prod _{p|D} p\) be its radical. Then \(S_D\) is an integer square up to an even power of 3 and we have:
where the term \(T_D/3\) is an integer if \(\sigma (D)\) is even and \(T_D/\sqrt{-3}\) is an integer if \(\sigma (D)\) is odd. Moreover, we have the formula:
where:
-
\(\theta _r(z)=\sum \nolimits _{n\in {\mathbb {Z}}}(-1)^n e^{\pi i \left( n+\frac{r}{D} -\frac{1}{6}\right) ^2 z}\), for \(r=0, 1\) are theta functions of weight 1/2,
-
\(\tau =\frac{-b+\sqrt{-3}}{2}\) is a CM point such that \(b^2\equiv -3\mod 12D^2\) and \((\pi _1\pi _2)^2\) divides \((\tau )\),
-
\(H_{{\mathscr {O}}}\) is the ray class field of modulus \(3D_0\),
-
\(\omega ^{k_0}\) is the unique cube root of unity that makes \(T_D/3\) or \(T_D/\sqrt{-3}\) an integer.
This theorem follows from a more general result for all integers D prime to 6 that is proved using automorphic methods:
Theorem 3
For all integers D prime to 6, \(3c_{3D} S_D\) is an integer and we have the formula:
where \( \varTheta _K(z)=\sum \nolimits _{a, b\in {\mathbb {Z}}}e^{2\pi i z (a^2+b^2-ab)}\) is the theta function of weight one associated to the number field K, \(\omega =\frac{-1+\sqrt{-3}}{2}\) is a third root of unity, and \(H_{3D}\) is the ring class field associated to the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_{K}\).
Note that each of the elliptic curves \(E_D\) is a cubic twist of \(E_1\). In the case of quadratic twists of elliptic curves, an important tool in computing the values of the L-functions is the work of Waldspurger [32]. For example, this is used to obtain Tunnell’s theorem for congruent numbers in [31]. However, the cubic twist case proves to be significantly more difficult. We instead take advantage of the fact that \(E_D\) is an elliptic curve with complex multiplication by \({\mathscr {O}}_K={\mathbb {Z}}[\omega ]\) the ring of integers of the number field K. Then from CM theory there is a Hecke character \(\chi _{E_D}:{\mathbb {A}}_K^{\times }/K^{\times }\rightarrow {\mathbb {C}}^{\times }\) such that \(L(E_D, s)=L(s, \chi _{E_D})\) and we compute the value of \(L(s, \chi _{E_D})\) using automorphic methods.
We present now an outline of the proof of Theorem 3. To compute the value of \(L(s, \chi _{E_D})\) we look at the Hecke character adelically and using Tate’s thesis we compute Tate’s zeta function \(Z(s, \chi _{E_D}, \varPhi _K)\) for \(\varPhi _K\) a Schwartz–Bruhat function in \({\mathscr {S}}({\mathbb {A}}_K)\). After integrating we get a linear combination of Eisenstein series. By evaluation at \(s=1\), we write \(L(E_D, 1)\) as a linear combination of theta functions at CM-points. We further show using Shimura’s reciprocity law that the terms are all Galois conjugates over K.
The idea of the proof of Theorem 2 is based on factoring each weight one theta function \(\varTheta _K(z)\) into a product of theta functions of weight 1/2. The method we are using is a factorization lemma of Rodriguez-Villegas and Zagier from [23] applied to the formula in Theorem 3. This gives us the square of a linear combination of theta functions evaluated at CM points. Finally, using Shimura reciprocity law, we show that all the factors are Galois conjugates to each other and recover an integer square.
Note that using the formula (4) we can show that an integer D cannot be written as the sum of two cubes by computationally checking whether \(L(E_D, 1)\ne 0\). Furthermore, assuming BSD,  and thus we can compute the expected order of
and thus we can compute the expected order of  explicitly. We provide below some examples when \(S_D\ne 0\) that we computed using PARI:
explicitly. We provide below some examples when \(S_D\ne 0\) that we computed using PARI:
D |
| D |
| D |
|
|---|---|---|---|---|---|
\(19\cdot 37\) | 1 | \(37\cdot 73\) | 1 | \(13 \cdot 19 \cdot 79\) | 1 |
\(31\cdot 43\) | 1 | \(43\cdot 67\) | 1 | \(13 \cdot 19 \cdot 61\) | 1 |
\(31 \cdot 79\) | 1 | \(43 \cdot 193\) | 4 | \(13\cdot 37 \cdot 61\) | 1 |
\(31\cdot 97 \) | 1 | \(61\cdot 67\) | 1 | \(13\cdot 43\cdot 73\) | 1 |
\(61\cdot 103\) | 1 | \(61 \cdot 139\) | 1 | \(31\cdot 37\cdot 43\) | 1 |
2 Background
Let \(K={\mathbb {Q}}[\sqrt{-3}]\) and denote \({\mathscr {O}}_K={\mathbb {Z}}[\omega ]\) its ring of integers, where \(\omega =\frac{-1+\sqrt{-3}}{2}\) is a fixed cube root of unity. We will denote by \(K_v\) the completion of K at the place v, \({\mathscr {O}}_{K_v}\) the ring of integers of \(K_v\), and for a prime p in \({\mathbb {Z}}\) we define \(K_p=K\otimes _{{\mathbb {Q}}}{\mathbb {Q}}_p\) and \({\mathscr {O}}_{K_p}={\mathscr {O}}_K\otimes _{{\mathbb {Z}}} {\mathbb {Z}}_p\) the semilocal ring of integers. Note that \(K_p=\prod \nolimits _{v|p} K_v \cong {\mathbb {Q}}_p[x]/(x^2-3)\) and \({\mathscr {O}}_{K_p} \cong \prod \nolimits _{v|p} {\mathscr {O}}_{K_v}\).
2.1 The L-function
Our goal is to compute several formulas for the central value of the L-function \(L(E_D, 1)\) of the elliptic curve \(E_D: x^3+y^3=Dz^3\). The elliptic curve \(E_D\) has complex multiplication (CM) by \({\mathscr {O}}_K\). Then from CM theory (see [27, Chapter II]) we can find a Hecke character \(\chi :{\mathbb {A}}_{K}^{\times }/K^{\times } \rightarrow {\mathbb {C}}\) corresponding to the elliptic curve \(E_D\) such that \(L(E_D, s)=L(s, \chi )\). We can compute explicitly \(\chi =\chi _D\varphi \) (see Ireland and Rosen [13, Chapter 18], for more details), where \(\varphi \) is the Hecke character of infinity type (1, 0) corresponding to \(E_1\) and \(\chi _D\) is the Hecke character corresponding to the cubic twist. More precisely, writing the characters classically, we have:
-
\(\varphi : I(3) \rightarrow K^{\times }\) is defined on the set of ideals prime to 3 by \(\varphi ({\mathscr {A}})=\alpha \), where \(\alpha \) is the unique generator of the ideal \({\mathscr {A}}\) such that \(\alpha \equiv 1 \mod 3\).
-
\(\chi _D: {{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D}) \rightarrow \{1, \omega , \omega ^2\}\) is the cubic character defined below in Sect. 2.2; it is defined over \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\) the ring class group corresponding to the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_K\).
Note that, for \(\text {Re}(s)>1\), the L-function can be expanded as
2.2 The cubic character
We define the cubic character \(\chi _D\) and recall some of its properties following Ireland and Rosen [13]. For \(\alpha \in {\mathscr {O}}_K\) prime to 3, we define the cubic residue character \(\left( \frac{\alpha }{\cdot }\right) _3:I(3\alpha )\rightarrow \{1, \omega , \omega ^2\}\), where \(I(3\alpha )\) is the set of fractional ideals of K prime to \(3\alpha \). For a prime ideal \({\mathfrak {p}}\) of K, we define \(\left( \frac{\alpha }{{\mathfrak {p}}}\right) _3=\omega ^j\), for \(0\le j\le 2\) such that
It is extended multiplicatively on the fractional ideals of \(I(3\alpha )\).
The character \(\chi _D\) is defined following [13] to be:
We also define \(\chi _{\pi }({\mathscr {A}})=\overline{\left( \frac{\pi }{{\mathscr {A}}}\right) _3}\) where \(\pi \) is a generator of an ideal of norm D. Note that \(\overline{\chi _{\pi }({\mathscr {A}})}=\chi _{{\overline{\pi }}}({\overline{{\mathscr {A}}}})\).
An important result is the cubic reciprocity law (see [13] for more details):
Theorem 4
(Cubic reciprocity law) For \(\pi _1, \pi _2 \equiv 2 \mod 3\) generators of the prime ideals \({\mathfrak {p}}_1, {\mathfrak {p}}_2\) prime to 3, we have \( \left( \frac{\pi _1}{\pi _2}\right) _3=\left( \frac{\pi _2}{\pi _1}\right) _3.\)
It follows immediately from the cubic reciprocity law that for \(\alpha \equiv \pm 1\mod 3\), we have \(\chi _D(\alpha )=\chi _{\alpha }(D)\). Also from the cubic reciprocity it follows that \(\chi _D((\alpha ))=1\) for \(\alpha \equiv a \mod 3D\), where a is an integer prime to 3D. Thus \(\chi _D\) is trivial on the ideals of \(P_{{\mathbb {Z}}, 3D}=\{ (\alpha )\): \(\alpha \in K\) such that \(\alpha \equiv a \mod 3D\) for some integer a such that \((a, 3D)=1\)}. The ring class group of the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_K\) is \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})=I(3D)/P_{{\mathbb {Z}}, 3D}\), where I(3D) is the set of fractional ideals prime to 3D, and thus \(\chi _D\) is invariant on \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\).
2.3 Hecke characters
A classical Hecke character \({\widetilde{\chi }}: I(f)\rightarrow {\mathbb {C}}^{\times }\) of conductor f can be expressed on the set of principal ideals P(f) prime to f in the form \( {\widetilde{\chi }}((\alpha ))={\widetilde{\epsilon }}(\alpha ){\widetilde{\chi }}^{-1}_{0}(\alpha ),\) where \({\widetilde{\varepsilon }}: ({\mathscr {O}}_K/f{\mathscr {O}}_K)^{\times } \rightarrow {\mathbb {T}}\) is a character taking values in a finite group \({\mathbb {T}}\) and \({\widetilde{\chi }}_{0}\) is an infinity type continuous character, meaning that \({\widetilde{\chi }}_{0}:{\mathbb {C}}^{\times }\rightarrow {\mathbb {C}}^{\times }\) is a continuous character.
The idelic Hecke character is a continuous character \(\chi : {\mathbb {A}}^{\times }/K^{\times } \rightarrow {\mathbb {C}}^{\times }\). There is a unique correspondence between the idelic and the classical Hecke characters defined as follows: at \(\infty \) for \(z\in {\mathbb {C}}\) we define \(\chi _{\infty }(z)={{\widetilde{\chi }}_0}^{-1}(z)\) for \(z\in {\mathbb {C}}^{\times }\) and at the places \(v\not \mid f\) we define \(\chi ({\mathscr {O}}_v^{\times }\varpi _v)={\widetilde{\chi }}({\mathfrak {p}}_v)\), for \(\varpi _v\) a uniformizer of \({\mathscr {O}}_{K_v}\) and \({\mathfrak {p}}_v\) the prime corresponding to the place v. At the places v|f, the value of \(\chi _v\) can be determined using the Weak Approximation Theorem.
We are interested in the character \(\chi =\chi _{D}\varphi \) defined before. By abuse of notation, we will use \(\varphi , \chi _{D}\) both for the classical and the adelic Hecke characters.
Recall \(\varphi :I(3)\rightarrow {\mathbb {C}}^{\times }\) is the Hecke character defined by \(\chi ((\alpha ))=\alpha \) for \(\alpha \equiv 1 \mod 3\). For the place \(v\not \mid 3\), denote by \(\varpi _v\) a uniformizer of \({\mathscr {O}}_{K_v}\) such that \(\varpi _v\equiv 1\mod 3\). Then for \(\varphi : {\mathbb {A}}_{K}^{\times } \rightarrow {\mathbb {C}}^{\times }\), we have:
-
\(\varphi _v(p)=-p\), \(\varphi _v({\mathscr {O}}_{K_v}^{\times })=1\), for \(v=p, p\equiv 2 \mod 3\),
-
\(\varphi _v(\varpi _v)=\varpi _v\), \(\varphi _v({\mathscr {O}}_{K_v}^{\times })=1\), for \(v|p, p \equiv 1 \mod 3\),
-
\(\varphi _{\infty }(x_{\infty })=x_{\infty }^{-1}\), at \(v=\infty \).
Recall \(\chi _{D}:I(3D)\rightarrow \{1, \omega , \omega ^2\}\) is the cubic character and we showed that it is well-defined on \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\), the ring class group for the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_K\). We define the character \(\chi _D\) adelically over \(K^{\times }\setminus {\mathbb {A}}_{K, f}^{\times }/U(3D)\simeq {{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\), where \(U(3D)=(1+3{\mathbb {Z}}_3[\omega ])\prod \nolimits _{p|D}{({\mathbb {Z}}+D{\mathscr {O}}_{K_p})^{\times }}\prod \nolimits _{p\not \mid 3D}{({\mathscr {O}}_{K_p})}^{\times }\).
Note that we can rewrite \(l_f\in {\mathbb {A}}_{K, f}^{\times }\) in the form \(l_f=kl_1\) with \(k\in K^{\times }\) and \(l_1\in \prod \nolimits _{v\not \mid \infty } {\mathscr {O}}_{K_v}^{\times }\). We can find \(k_1\in {\mathscr {O}}_K\) such that \(k_1 \equiv l_1 \mod 3D{\mathscr {O}}_{K_v}\) and we define \(\chi _{D, f}(l)=\chi _{D, f}(l_1)=\chi _{D}((k_1)).\) More precisely, we get:
-
\(\chi _{D, v}(\varpi _v)=\chi _{D}({\mathfrak {p}}_v)\) and \(\chi _{D, v}({\mathscr {O}}_{K_v}^{\times })=1\), if \(v\not \mid 3D\),
-
\(\chi _{D,\infty }(x_{\infty })=1\), at \(v=\infty \).
The values of \(\chi _D\) and \(\varphi \) at the ramified places can be computed using the Weak approximation theorem.
3 \(L(E_D, 1)\) and Tate’s zeta function
In this section we will compute the value of \(L(E_D, 1)=L(1, \chi _D\varphi )\), working with \(\chi _D, \varphi \) as automorphic Hecke characters. Let \(K={\mathbb {Q}}[\sqrt{-3}]\) and \(\omega =\frac{-1+\sqrt{-3}}{2}\) a fixed cube root of unity as before. We will show the following result:
Theorem 5
For \( S_D=\frac{2\sqrt{3}\pi D^{-1/3}}{c_{3D} \varGamma \left( \frac{1}{3}\right) ^3}L(E_D, 1) \), we have \(3c_{3D} S_D \in {\mathbb {Z}}\) and
where \(\varTheta _K(z)=\sum \nolimits _{m, n\in {\mathbb {Z}}} e^{2\pi i (m^2+n^2-mn)z}\), \(H_{3D}\) is the ring class field for the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_{K}\) and \(c_{3D}=\prod \nolimits _{p|3D} c_p\) is the product of the Tamagawa numbers \(c_p\) of \(E_D\).
We will compute the formula (5) using Tate’s zeta function. We start by recalling some background and notation.
3.1 Haar measure
We take \(V=K\) as a quadratic vector space over \({\mathbb {Q}}\) with the norm as its quadratic form. We take \(dx_v\) to be the self-dual additive Haar measure and \(d^{\times } \alpha _v\) the multiplicative Haar measure \(d^{\times }_vx_v=\frac{dx_v}{|x_v|_v}\) normalized such that \({{\,\mathrm{vol}\,}}({\mathscr {O}}_{K_v}^{\times })=1\), if \(v\not \mid \infty \), and \(d^{\times }z =\frac{dz}{|z|_{\infty }}\) where dz is the usual Lebesgue measure, and \(|z|_{\infty }=|z|_{{\mathbb {C}}}^2\) is the square of the usual absolute value over \({\mathbb {C}}\). We use the same normalization for the Haar measure as in Tate’s thesis (see [1, Section 3.1]).
3.2 Schwartz–Bruhat functions
We choose the Schwartz–Bruhat function \(\varPhi _f\in S({\mathbb {A}}_{K, f})\) such that Tate’s zeta function \(Z(s, \varPhi , \chi _D\varphi )\) defined below to be nonzero. More precisely, \(\varPhi _f=\prod \nolimits _{v\not \mid \infty } \varPhi _v\), where:
-
\(\varPhi _v={{\,\mathrm{char}\,}}_{{\mathscr {O}}_{K_v}}\) for \(v\not \mid 3D\),
-
\(\varPhi _p=\sum \nolimits _{(a, D)=1}{{\,\mathrm{char}\,}}_{(a+D{\mathscr {O}}_{K_p})}\) for p|D,
-
\(\varPhi _v={{\,\mathrm{char}\,}}_{(1+3{\mathscr {O}}_{K_v})}\) for \(v=\sqrt{-3}\).
3.3 Tate’s zeta function
We recall Tate’s zeta function. For a Hecke character \(\chi :{\mathbb {A}}_{K}^{\times }/K^{\times } \rightarrow {\mathbb {C}}^{\times }\) and a Schwartz–Bruhat function \(\varPhi \in {\mathscr {S}}({\mathbb {A}}_{K})\), Tate’s zeta function is defined locally as \( Z_v(s, \chi _v, \varPhi _v)=\int \nolimits _{K_v^{\times }} \chi _{v}(\alpha _v) |\alpha _v|^s_v \varPhi _v(\alpha _v) d^{\times } \alpha _v\), and globally as \(Z(s, \chi , \varPhi )=\prod \nolimits _v Z_v(s, \chi _v, \varPhi _v)\). As a global integral this is
It has meromorphic continuation to all \(s\in {\mathbb {C}}\) and in our case it is entire. We will compute \(Z_f(s, \chi _f, \varPhi _f)\) for \(\chi =\chi _D\varphi \) and the Schwartz–Bruhat function \(\varPhi _f\) chosen above.
From Tate’s thesis (see [1, Proposition 3.1.4]), we have the equality of local factors \(L_v(s, \chi _D\varphi )=Z_v(s, \chi _D\varphi )\) at all the unramified places, and thus \( L(s, \chi _D\varphi )=Z_f(s, \chi _D\varphi )\prod \nolimits _{p|3D}\frac{L_p(s, \chi _{D, p}\varphi _p)}{Z_p(s, \chi _{D, p}\varphi _p, \varPhi _p)}\). As \(\varphi , \chi _D\) and \(|\cdot |\) are trivial when \(\varPhi _{p}\) is nonzero for p|3D, we can compute easily
and this equals \(\frac{1}{6}\prod _{p|D}(p-\left( \frac{p}{3}\right) )^{-1}\). The terms \(L_p(s, \chi _D\varphi )=1\) for p|3D by definition. Thus for all s and for \(\varPhi \) the Schwartz–Bruhat function chosen above, we have:
where \( V_{3D}=\frac{1}{6}\prod _{p|D}(p-\left( \frac{p}{3}\right) )^{-1}\).
Next we compute the value of \(Z_f(s, \chi _{D, f}\varphi _f, \varPhi _f)\) as a linear combination of Hecke characters and use (6) to get the value of \(L(s, \chi _{D, f}\varphi _f)\):
Lemma 6
For all \(s\in {\mathbb {C}}\) and the Schwartz–Bruhat function \(\varPhi _f \in {\mathscr {S}}({\mathbb {A}}_{K, f})\) chosen above, we have:
where \( I(s, \alpha _f, \varPhi _f)=\sum \nolimits _{k\in K^{\times }} \frac{k}{|k|_{{\mathbb {C}}}^{2s}} \varPhi _f(k\alpha _f)\) and \(U(3D)=(1+3{\mathbb {Z}}_3[\omega ])\prod \nolimits _{v|D}{({\mathbb {Z}}+D{\mathscr {O}}_{K_p})^{\times }}\) \(\prod \nolimits _{v\not \mid 3D}{{\mathscr {O}}_{K_v}^{\times }}\).
Proof
We first take the quotient by \(K^{\times }\) in the integral defining \(Z_f(s, \chi _D\varphi , \varPhi _f)\) and get:
We have \(\chi _{D, f}(k\alpha '_f)=\chi _{D, \infty }^{-1}(k)\chi _{D, f}(\alpha '_f)=\chi _{D, f}(\alpha '_f),\) \(\varphi _f(k\alpha '_f)=\varphi _{\infty }^{-1}(k)\varphi _f(\alpha '_f)=k\varphi _f(\alpha '_f)\) and \(|k\alpha '_f|^s_f=|k|^{-s}_{\infty }|\alpha _f|^s_f=|k|_{{\mathbb {C}}}^{-2s}|\alpha _f'|_f^s\), where \(| \cdot |_{{\mathbb {C}}}\) is the usual absolute value over \({\mathbb {C}}\). Then the integral reduces to:
Furthermore, our Schwartz–Bruhat functions \(\varPhi _f(k\alpha _f')\) are invariant on U(3D). Similarly, \(|\cdot |_f\) is trivial on units, thus on U(3D), while \(\chi _D\) is invariant on U(3D) by definition. Moreover, \(\varphi \) is trivial on all the units at all the unramified places, while, at 3, \(\varphi \) is invariant under \(1+3{\mathbb {Z}}_3[\omega ]\), thus it is trivial on all of U(3D). Thus we can take the quotient by U(3D) as well. Note that the integral is now a finite sum:
We compute \({{\,\mathrm{vol}\,}}(U(3D))={{\,\mathrm{vol}\,}}(1+3{\mathbb {Z}}_3[\omega ]) \prod \nolimits _{p|D}{{\,\mathrm{vol}\,}}({\mathbb {Z}}+D{\mathscr {O}}_{K_p})=V_{3D}\) and, changing notation, we get:
Finally together with (6) we get the result of the lemma. \(\square \)
3.4 Representative classes of \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\)
We will use the following lemma (see [22]) that is easy to show:
Lemma 7
Any primitive ideal of \({\mathscr {O}}_K\) can be written in the form \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) as a \({\mathbb {Z}}\)-module, where b is an integer (determined only modulo 2a) such that \(b^2\equiv -3 \mod 4a\) and \({{\,\mathrm{Nm}\,}}{\mathscr {A}}=a\).
Conversely, given an integer satisfying the above congruence and \({\mathscr {A}}\) defined as above, we get that \({\mathscr {A}}\) is an ideal in \({\mathscr {O}}_K\) of norm a.
We will use the notation \(k_{{\mathscr {A}}}\) for the generator \(k_{{\mathscr {A}}}\equiv 1\mod 3\) of a primitive ideal \({\mathscr {A}}\) in \({\mathscr {O}}_K\). If we choose a lattice such that \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\), we denote the corresponding CM point \(\tau _{{\mathscr {A}}}=\frac{-b+\sqrt{-3}}{2a}.\)
We can write adelically \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D}) \simeq U(3D)\setminus {\mathbb {A}}_{K, f}^{\times }/K^{\times }\). This follows from the Strong approximation theorem, as K is a PID and thus we have \( U(3D)\setminus {\mathbb {A}}_{K, f}^{\times }/K^{\times }\cong (\prod \nolimits _{p|3D}({\mathscr {O}}_{K_p})^{\times }/({\mathbb {Z}}+3D{\mathscr {O}}_{K_p})^{\times }) /\left<-\omega \right>.\) Then we can define the map
given by
where we choose the representative \(\pm \alpha \omega ^{k}\), such that \(\alpha _3\equiv 1\mod 3\), and \(k_{\alpha }\) is an element of \({\mathscr {O}}_K\) such that \(k_{\alpha }\equiv \alpha _v \mod 3D\). Note that this is well defined as \((k_{\alpha })\) gives us a unique class in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\), and two elements \(\alpha _1, \alpha _2\) get sent to the same class in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\) only if \(\alpha _1\equiv \alpha _2 \mod 3D\).
Thus for \(\alpha _f \in {\widehat{{\mathscr {O}}}}_K\) we can choose a class \([{\mathscr {A}}_{\alpha }]\) in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\) by taking a representative \({\mathscr {A}}_{\alpha _f}=(k_{\alpha })\), for \(k_{\alpha }\in {\mathscr {O}}_{K}\) such that \(k_{\alpha } \equiv \alpha _p \mod 3D{\mathscr {O}}_{K_p}\) for p|3D. Note that this choice is not unique. However, we can pick the representatives \({\mathscr {A}}_{\alpha }\) to be primitive ideals.
Thus we can further write \({\mathscr {A}}_{\alpha }\) as a \({\mathbb {Z}}\)-lattice \({\mathscr {A}}_{\alpha }=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\), where \(a={{\,\mathrm{Nm}\,}}{\mathscr {A}}_{\alpha }\) and b is chosen (not uniquely) such that \(b^2\equiv -3 \mod 4a\). We define the corresponding CM point \(\tau _{{\mathscr {A}}_{\alpha }}=\frac{-b+\sqrt{-3}}{2a}\).
3.5 Eisenstein series of weight 1
We will now connect \(I(s, \alpha _f, \varPhi _f)=\sum \nolimits _{k\in K^{\times }} \frac{k}{|k|_{{\mathbb {C}}}^{2s}} \varPhi _f(k\alpha _f)\) to an Eisenstein series. We define the following classical Eisenstein series of weight 1:
Here the sum is taken over all \(m, n \in {\mathbb {Z}}\) except for the pair (0, 0), and \(\varepsilon =\left( \frac{\cdot }{3}\right) \) is the quadratic character associated to the field extension \(K/{\mathbb {Q}}\). Note also that from quadratic reciprocity we have \(\left( \frac{-3}{\cdot }\right) =\left( \frac{\cdot }{3}\right) \).
The Eisenstein series \(E_{\varepsilon }(s, z)\) does not converge absolutely for \(s=0\), but we can still compute its value using the Hecke trick (see [11]). We compute its Fourier expansion at \(s=0\) in the following section.
Using this notation, we have the following equality:
Lemma 8
For \(\alpha _f \in \prod \nolimits _{v\not \mid \infty } {\mathscr {O}}_{K_v}^{\times }\), let \({\mathscr {A}}_{\alpha _f}=(k_{\alpha })\) be a choice of an ideal in the corresponding class of \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\). We write \({\mathscr {A}}_{\alpha }=[a_{\alpha }, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) and take \(\tau _{{\mathscr {A}}_{\alpha }}=\frac{-b+\sqrt{-3}}{2a_{\alpha }}\) the corresponding CM point. Then we have:
Remark 9
Note that the variable \(\tau _{\overline{{\mathscr {A}}_{\alpha }}}\) on the left hand side is not uniquely defined. However, the right-hand side depends only on the class \([{\mathscr {A}}_{\alpha }]\) in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\).
Proof
Recall that \( I(s, \alpha _f, \varPhi _f)=\sum _{k\in K^{\times }} \frac{k}{|k|_{{\mathbb {C}}}^{2s}} \varPhi _f(k\alpha _f)\). We need to compute \(\varPhi _f(k\alpha _f)\). Note that \(\varPhi _v(k\alpha _v)\ne 0\) only for \(k\alpha _v \in {\mathscr {O}}_{K_v}\) at all places v, and since \(\alpha _v \in {\mathscr {O}}_{K_v}^{\times }\), we must have \(k\in {\mathscr {O}}_{K_v}\) as well for all v. This implies \(k\in {\mathscr {O}}_{K}\) and for all places \(v\not \mid 3D\) we get \(\varPhi _v(k\alpha _v)=1\) for \(k\in {\mathscr {O}}_K\). Thus we can rewrite:
where \(\varPhi _{3D}=\prod _{v|3D} \varPhi _v\) and \(\alpha _{3D}=(\alpha _v)_{v|3D}\).
We can further compute \(\varPhi _v(k\alpha _v)\) for v|3D. Recall that we defined the Schwartz–Bruhat functions \(\varPhi _p={{\,\mathrm{char}\,}}_{({\mathbb {Z}}+3D{\mathscr {O}}_{K_p})^{\times }}\) for p|D and \(\varPhi _3={{\,\mathrm{char}\,}}_{(1+3{\mathbb {Z}}_3[\omega ])}\). Then we have \(\varPhi _{3D}(k\alpha _{3D})\ne 0\) iff \(k\alpha _p \in a+3D{\mathscr {O}}_{K_p}\) for some integer a, \((a, p)=1\) and, for \(p=3\), \(k\alpha _{3}\in 1+3{\mathscr {O}}_{K_3}\).
Recall that we defined \(k_{\alpha }\) such that \(k_\alpha \equiv \alpha _p \mod 3D{\mathscr {O}}_{K_p}\) for all p|3D. Then \(kk_{\alpha } \in a+3D{\mathscr {O}}_{K_p}\) for \((a, p)=1\) and \(kk_{\alpha }\in 1+3{\mathbb {Z}}_3[\omega ]\). Furthermore, for \(k\in {\mathscr {O}}_K\) we actually have \(\varPhi _{3D}(k\alpha _{3D})=\varPhi _{3D}(kk_{\alpha })\). Then we can rewrite \(I(s, \alpha _f, \varPhi _f)\) using \(k_{\alpha }\) as \( I(s, \alpha _f, \varPhi _f)=\sum \nolimits _{k\in {\mathscr {O}}_K} \frac{k}{|k|_{{\mathbb {C}}}^{2s}} \varPhi _{3D}(kk_{\alpha }).\) We can rewrite this further:
Finally, we will make this explicit. Note that we must have \(kk_{\alpha } \in {\mathscr {A}}_{\alpha }\), where \({\mathscr {A}}_{\alpha }=(k_{\alpha })\), as well as \(kk_{\alpha }\in a_p+D{\mathscr {O}}_{K_p}\) for some integer \(a_p\), \((a_p, p)=1\), and \(kk_{\alpha }\in 1+3{\mathbb {Z}}_3[\omega ]\). By the Chinese remainder theorem, we can find an integer a such that \(a\equiv a_p \mod D\) and \(a\equiv 1 \mod 3\). Then \(kk_{\alpha }\in (a+D\prod \nolimits _{p|3D}{\mathscr {O}}_{K_p}) \cap {\mathscr {O}}_K\), thus \(kk_{\alpha } \in P_{{\mathbb {Z}}, 3D} \cap P_{1, 3}\). Here \(P_{{\mathbb {Z}}, 3D}=\{k \in K: k\equiv a\mod 3D{\mathscr {O}}_{K} ~\text {for some integer}~ a, (a, 3D)=1\}\) and \( P_{1, 3}=\{k\in K: k\equiv 1 \mod 3\}\). We rewrite:
Finally, we want to write the elements of \( {\mathscr {A}}_{\alpha } \cap P_{{\mathbb {Z}}, D}\cap P_{1, 3}\) explicitly. Recall that we can write \({\mathscr {A}}_{\alpha }\) as a \({\mathbb {Z}}\)-lattice \({\mathscr {A}}_{\alpha }=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\). Then all of the elements of \({\mathscr {A}}\) are of the form \(ma+n\frac{-b+\sqrt{-3}}{2}\) for some integers \(m, n\in {\mathbb {Z}}\). Moreover, note that the intersection of \({\mathscr {A}}\) and \(P_{{\mathbb {Z}}, 3D}=\{k \in {\mathscr {O}}_K: k \equiv n \mod 3D, \text {for some integer}~ n, (n, 3D)=1\}\) is \(\{ma+3Dn\frac{-b+\sqrt{-3}}{2}: m, n \in {\mathbb {Z}}\}\). Further taking the intersection with \(P_{1, 3}\), we must have \(ma\equiv 1\), thus, as a is norm in \({\mathscr {O}}_K\), \(m \equiv 1 \mod 3\), and we can rewrite \(I(s, \alpha _f, \varPhi _f)\) in the form:
By changing \(n\rightarrow -n\) and taking out a factor of \(a^{1-2s}\), we have:
Note that for \(Re(s)>1\) the integral converges absolutely, and we can rewrite the sum as:
where \(\varepsilon (m)=\left( \frac{m}{3}\right) \) is the usual quadratic character. On the right hand side we recognize the Eisenstein series \(E_{\varepsilon }(2s-2, \tau _{\overline{{\mathscr {A}}_{\alpha }}})\) and we get \(I(s, \alpha _f, \varPhi _f) = \frac{1}{2}\frac{a^{1-s}}{k_{\alpha }}E_{\varepsilon }(2s-2, D\tau _{\overline{{\mathscr {A}}_{\alpha }}}).\) By analytic continuation, we can extend the equality to all \(s\in {\mathbb {C}}\). \(\square \)
Now we can rewrite the linear combination in Lemma 6 by taking representatives \({\mathscr {A}}\) for the classes of \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\). Note that for \(\alpha \in {\widehat{{\mathscr {O}}}}_K^{\times }\) with \(\alpha \equiv 1\mod 3\) we have \(\varphi _f(\alpha _f)=1\) and
Using the lemma above and after inverting each class \({\mathscr {A}}\rightarrow {\overline{{\mathscr {A}}}}\) in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\), we get:
Corollary 10
For all s, taking representative ideals \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) for the classes in the ring class group \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\), we have:
where \({\mathscr {A}}=(k_{{\mathscr {A}}})\) with \(k_{{\mathscr {A}}}\equiv 1\mod 3\) and \(\tau _{{\mathscr {A}}}=\frac{-b+\sqrt{-3}}{2a}\) the associated CM points.
3.6 Fourier expansion of \(E_{\varepsilon }(s, z)\) at \(s=0\)
We want to connect the Eisenstein series \( E_{\varepsilon }(s, z)=\sum _{c, d} {'}\frac{\varepsilon (d)}{(3cz+d)|3cz+d|^{2s}}\), where \( \sum \nolimits _{c, d} {'}\) denotes the sum over all \(c, d\in {\mathbb {Z}}\) with \((c, d)\ne (0, 0)\), to the theta function
associated to the number field K. It is a modular form of weight 1 for the congruence group \(\varGamma _1(3)\). Note that this differs from the theta function \(\varTheta _K\) chosen by Rodriguez-Villegas and Zagier in [24] by a factor of 1/2.
More precisely, we are going to show the following version of the Siegel–Weil theorem:
Theorem 11
\( E_{\varepsilon }(0, z)=2L(1, \varepsilon )\varTheta _K(z)\).
Proof
We will show this by computing the Fourier expansion of \(E_{\varepsilon }(s, z)\) at \(s=0\) using the Hecke trick and comparing it to the Fourier expansion of \(\varTheta _K(z)\). We will follow closely the exposition of Pacetti [20]. This is also done by Hecke in [11]. We first rewrite \(E_{\varepsilon }(s, z)\) in the form:
where \( \sum _{d}{'}\) denotes the sum over all \(d\in {\mathbb {Z}}\), \(d\ne 0\). We define for z in the upper-half plane \(H(z, s)=\sum \nolimits _{m\in {\mathbb {Z}}}\frac{1}{(z+m)|z+m|^{2s}}\) and then we can rewrite the form above as:
Pacetti [20], following Shimura [29, Lemma 1, p. 84], computed the Fourier expansion of H(z, s) when \(s\rightarrow 0\) to be \(\lim \nolimits _{s\rightarrow 0} H(s, z)=-\pi i -2\pi i \sum \nolimits _{n=1}^{\infty } q^n\). It gives us in the relation above:
We compute separately the inner sum and get:
where \(G(\varepsilon )=\sum \nolimits _{r=0}^2 \varepsilon (r)\omega ^r=\sqrt{-3}\) is the quadratic Gauss sum corresponding to \(\varepsilon \). Then we can rewrite:
Since \(\varepsilon \) is a quadratic character, we compute \(L(1, \varepsilon )=\frac{\pi \sqrt{3}}{9}\) (see Kowalski [18]) and this gives us the Fourier expansion:
It is easy to show that \(\sum _{m|n}\varepsilon (m)\) represents the number of ideals of norm n in \({\mathscr {O}}_K\), thus we got \(\frac{2\pi \sqrt{3}}{9} (1+6\sum \nolimits _{{\mathscr {A}}}e^{2 \pi i ({{\,\mathrm{Nm}\,}}{\mathscr {A}}) z})\). Moreover \(|{\mathscr {O}}_K^{\times }|=6\) and \({{\,\mathrm{Nm}\,}}_{K/{\mathbb {Q}}}(m+n\omega )=m^2+n^2-mn\) and thus we can recognize the sum in the bracket on the RHS of (7) to equal the theta function \(\varTheta _K(z)\), which finishes the proof. \(\square \)
3.7 Formula for \(L(1, \chi _D\varphi )\)
Applying Corollary 10 for \(s=1\) we get
Furthermore, from Theorem 11, this is the same as:
We need one more step before rewriting the formula as a trace. We will use the following lemma:
Lemma 12
For \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) a primitive ideal of norm \({{\,\mathrm{Nm}\,}}{\mathscr {A}}=a\), with generator \({\mathscr {A}}=(k_{{\mathscr {A}}})\), where \(k_{{\mathscr {A}}}\equiv 1 \mod 3\) and \(\tau _{{\mathscr {A}}}=\frac{-b+\sqrt{-3}}{2}\), we have:
Proof
Since \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) as a \({\mathbb {Z}}\)-lattice, we can write its generator \(k_{{\mathscr {A}}} \) in the form \(k_{{\mathscr {A}}}=ma+3n\frac{-b+\sqrt{-3}}{2}\) for some integers m, n such that \(m\equiv 1(3)\) and \(\gcd (m, 3n)=1\). Then we can find integers A, B such that \(mA+3nB=1\), and thus \(\left( {\begin{matrix}A &{}\quad B \\ 3n &{}\quad m \end{matrix}}\right) \) is a matrix in \(\varGamma _1(3)\). Since \(\varTheta (z)\) is a modular form of weight 1 for \(\varGamma _1(3)\), we have \( \varTheta _K\left( \left( {\begin{matrix}A &{}\quad B \\ 3n &{}\quad m \end{matrix}}\right) \tau _{{\mathscr {A}}}\right) =\left( m+3n\tau _{{\mathscr {A}}}\right) \varTheta _K\left( \tau _{{\mathscr {A}}}\right) \).
Noting that \(3n\tau _{{\mathscr {A}}}+m=k_{{\mathscr {A}}}/a=1/\overline{k_{{\mathscr {A}}}}\), we can compute the term on the LHS to be \(\varTheta _K((A\tau _{{\mathscr {A}}}+B)\overline{k_{{\mathscr {A}}}})\) and, after expanding, we are evaluating \(\varTheta _K\) at \(-3nA\frac{b^2+3}{4a}+abB+\frac{b(-mA+3nB)}{2}+\frac{\sqrt{-3}}{2}\). Note that \(mA-3nB=1\) implies that mA and 3nB have different parities. Also, b is odd and \(b^2+3\equiv 0 \mod 4a\). Then \(-3nA\frac{b^2+3}{4a}+abB+\frac{b(-mA+3nB)+1}{2}\in {\mathbb {Z}}\) and thus using the period 1 of \(\varTheta _K\) we get \(\varTheta _K\left( \left( {\begin{matrix}A &{}\quad B \\ 3n &{}\quad m \end{matrix}}\right) \tau _{{\mathscr {A}}}\right) =\varTheta _K\left( \omega \right) \). This finishes the proof. \(\square \)
Using the Lemma above we can rewrite (8) as:
Now we will rewrite the formula (9) as a trace. We can define \(f(z)=\frac{\varTheta _K(Dz)}{\varTheta _K(z)}\) and this is a modular function for \(\varGamma _0(3D)\). We will prove in Sect. 5 in Proposition 39 that \(f(\omega )\in H_{3D}\), the ring class field of corresponding to the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_{K}\). Moreover, we show in the same proposition that, for \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) a primitive ideal in \({\mathscr {O}}_K\), we have the Galois conjugate:
where \(\sigma _{{\mathscr {A}}}\) is the Galois action corresponding to the ideal \({\mathscr {A}}\) via the Artin map.
Furthermore, from we have \((D^{1/3})^{\sigma _{{\mathscr {A}}}^{-1}}=D^{1/3}\chi _D({\mathscr {A}})\) and then formula (9) becomes:
Moreover, \(D^{1/3} \in H_{3D}\) (see for example Cohn [4]). Thus we can rewrite the sum on the left hand side as \({{\,\mathrm{Tr}\,}}_{H_{3D}/K} \left( D^{1/3}\frac{\varTheta _K(D\omega )}{\varTheta _K(\omega )}\right) \). We can compute the extra terms as well. Rodriguez-Villegas and Zagier in [24] cite \(\varTheta _K\left( \frac{-9+\sqrt{-3}}{18}\right) =-6\varGamma \left( \frac{1}{3}\right) ^3 /(2\pi )^2\). Using several of the properties of \(\varTheta _K\) proved in the Appendix ((27) and Lemma 41), we can compute \(\varTheta \left( \omega \right) =\varGamma \left( \frac{1}{3}\right) ^3/(2\pi ^2)\).
As the real period \(\varOmega _D\) of the elliptic curve \(E_D\) is \(\varOmega _D=D^{-1/3}\frac{\sqrt{3}\varGamma \left( \frac{1}{3}\right) ^3}{6\pi }\), we get the formula of Theorem 5:
Note that this implies \(S_D \in K\). Moreover, as \(D^{1/3}\varTheta (D\omega )/\varTheta (\omega )\) is invariant under complex conjugation, we get \(S_D\in {\mathbb {R}}\). Since \(K\cap {\mathbb {R}}={\mathbb {Q}}\), this furthermore implies \(S_D\in {\mathbb {Q}}\). We will show in Sect. 4.5 that actually \(3c_{3D}S_D \in {\mathbb {Z}}\).
Remark 13
If we take \(D=D_1D_2^2\) such that \(D_0=D_1D_2\) is square-free, note that the character \(\chi _D=\chi _{D_1}\overline{\chi _{D_2}}\) is well defined on the class group \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D_0})\). Then the above computations work for \(D_0\) and the character \(\chi _{D}=\chi _{D_1}\overline{\chi _{D_2}}\) instead of \(\chi _{D_0}=\chi _{D_1}\chi _{D_2}\) and we get:
Note that, for \(D=D_1D_2^2\), \(L(E_D, s)=L(s, \chi _{D_1}\overline{\chi _{D_2}}\varphi )\) and thus we have:
As before we have \((D_1^{1/3}D_2^{2/3})^{\sigma _{{\mathscr {A}}}^{-1}}=D_1^{1/3}\chi _{D_1}({\mathscr {A}})D_2^{2/3} \overline{\chi _{D_2}({\mathscr {A}})}\) and finally we can write the expression above as:
4 Second formula for \(S_D\)
For \(r\in {\mathbb {Z}}\), \(\mu \in \{1/2, 1/6\}\), we define the theta functions of weight 1/2:
Throughout the paper we will use the notation \(r\in {\mathbb {Z}}/D{\mathbb {Z}}\) to mean any family of representatives for the residues \(r \mod D\). We denote \(\theta _0=\theta _{0, 1/6}\). Note that \(\theta _0(z)=\eta (z/3)\), where \(\eta \) is the Dedekind eta function, while \(\sum \nolimits _{\begin{array}{c} r\in {\mathbb {Z}}/D{\mathbb {Z}}\\ r\equiv 1 (6) \end{array}} \theta _{r, 1/6}(z)=\eta \left( \frac{z}{3D^2}\right) \).
In this section we will use a Factorization formula of Rodriguez-Villegas and Zagier from [23] to show the following theorem, that is a restatement of Theorem 2 from the Introduction:
Theorem 14
In the case of \(D=\prod \nolimits _{p_i\equiv 1 (3)} p_i^{e_i}\), let \(D_0=\prod \nolimits _{p_i|D} p_i\) be the radical of D and \(\sigma (D)\) the number of distinct prime divisors of D. Then \(S_D\) is an integer square up to an even power of 3 and we have:
where \(T_D/3 \in {\mathbb {Z}}\) if \(\sigma (D)\) is even and \(T_D/\sqrt{-3}\in {\mathbb {Z}}\) if \(\sigma (D)\) is odd. We have the exact formula:
Here \(\tau =\frac{-b+\sqrt{-3}}{2}\) is a CM-point, with \(b^2\equiv -3 \mod 12D^2\), \(\pi _1, \pi _2\) are elements in \({\mathscr {O}}_K\) such that \(\pi _1, \pi _2\equiv 1\mod 3\), \(\pi _1\pi _2\) has norm \(D_0\) and \(\pi _1\pi _2^2\) has norm D, and such that \((\pi _1\pi _2)^2\) divides the ideal \(\left( \frac{-b+\sqrt{-3}}{2}\right) \), \(H_{{\mathscr {O}}}\) is the ray class field of modulus \(3D_0\) and \(\omega ^{k_0}\) is the unique cube root of unity that makes \(T_D\) real or purely imaginary.
Below we discuss the details of D square-free. All definitions and proofs can be easily extended to all \(D=D_1D_2^2\) by using the formula (13) with \(D_0=D_1D_2\) square-free. We do this in Sect. 4.6.
Take \(\tau =\frac{-b+\sqrt{-3}}{2}\) a CM point such that \(b^2\equiv -3 \mod 12 D^2\) and an element \(\pi \equiv 1\mod 3\) of norm D in \({\mathscr {O}}_K\) such that \(\pi ^2\) divides the ideal \((\frac{-b+\sqrt{-3}}{2})\).
We will use the notation:
-
\(\varTheta _{\mu }(\tau )= {\left\{ \begin{array}{ll} \frac{3}{2}\varTheta _K\left( \tau \right) -\frac{1}{2}\varTheta _K \left( \tau /3\right) , &{}\quad \text { for } \mu =1/6 \\ \varTheta _K\left( \tau /3\right) ,&{}\quad \text { for } \mu =1/2. \end{array}\right. }\)
-
\(S_{\mu }=\frac{2}{3}\sum _{[{\mathscr {A}}]\in {{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})}\frac{\varTheta _{\mu }(D\tau _{{\mathscr {A}}})}{\varTheta _K(\tau _{{\mathscr {A}}})} \chi _{D}({\mathscr {A}})D^{1/3}\).
In Theorem 3 we have proved that \(3c_{3D}S_D=S_{1/6}+1/2S_{1/2}.\) We are actually going to show in Corollary 23 that \(S_{1/2}=0\), thus it is enough to compute the formula (14) for \(S_{1/6}\).
Using a Factorization formula of Rodriguez-Villegas and Zagier from [23] we will write the theta functions \(\varTheta _{\mu }\) of weight 1 as linear combinations of products of theta functions of weight 1/2 in Proposition 17. We define:
We show in Lemma 26 that \(S_{1/6}=|R_{D, 1/6}(\tau )D^{-1/3}|^2\). Moreover, if we denote
for a cubic root of unity \(\omega ^{k_0}\), then \(S_{1/6}=|T_{D, 1/6}(\tau )|^2\).
We show in Lemma 30 that \(T_D=\frac{1}{\varphi (D)}{{\,\mathrm{Tr}\,}}_{H_{{\mathscr {O}}}/K} \frac{\theta _{1, 1/6}(\tau )}{\theta _0(\tau )} {\overline{\pi }}^{-2/3}\omega ^{k_0}\) and that \(T_{D} \in K\). Furthermore, we show in proposition 25 that \(T_D=(-1)^{\sigma (D)}\overline{T_D}\) and thus \(T_D\in {\mathbb {Q}}\) or \(T_D/\sqrt{-3} \in {\mathbb {Q}}\) and thus
Moreover, in Sect. 4.5 we show that \(3c_{3D} S_D\) is an integer, hence \(T_D/3\in {\mathbb {Z}}\) for \(\sigma (D)\) even and \(T_D/\sqrt{-3}\in {\mathbb {Z}}\) for \(\sigma (D)\) odd.
Finally, for D a product of split primes, we have \(S_D\ne 0\) only for \(D\equiv 1\mod 9\). In this case we can compute the Tamagawa numbers to be \(c_{3D}=3^{1+\sigma (D)}\) using Tate’s algorithm (see [28, Chapter IV.9]). Thus we have:
Hence \(S_D\) is an integer square up to an even power of 3 and this finishes the proof of Theorem 14.
For the reader’s convenience, we summarize the notations used in the whole chapter in the table below:
Sums | Theta functions and ratios |
|---|---|
\(S_D=\frac{1}{3}\sum _{[{\mathscr {A}}] \in {{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D_0})} \frac{\varTheta _K(D_0\tau _{{\mathscr {A}}})}{\varTheta _K(\tau _{{\mathscr {A}}})}\chi _{D}({\mathscr {A}})D^{1/3}\) | \(\varTheta _K(z)=\sum \nolimits _{a, b\in {\mathbb {Z}}}e^{2\pi i z (a^2+b^2-ab)}\) |
\(S_{\mu }=\frac{2}{3}\sum _{[{\mathscr {A}}]\in {{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})}\frac{\varTheta _{\mu }(D\tau _{{\mathscr {A}}})}{\varTheta _K(\tau _{{\mathscr {A}}})} \chi _{D}({\mathscr {A}})D^{1/3}t\) | \({\left\{ \begin{array}{ll}\varTheta _{1/2}(\tau )=\varTheta _K\left( \tau /3\right) , \\ \varTheta _{1/6}(\tau )=\frac{3}{2}\varTheta _K\left( \tau \right) -\frac{1}{2}\varTheta _K\left( \tau /3\right) , \end{array}\right. } \) |
\(R_{D, \mu }(z)\) \(=\sum \nolimits _{\begin{array}{c} r \in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times } \\ r\equiv 1 (6) \end{array}} \frac{\theta _{r, \mu }(3z)}{\theta _0(3z)}\chi _{\pi }(r)\) | \(\theta _{r, \mu }(z)=\sum \nolimits _{n\in {\mathbb {Z}}}(-1)^n e^{\pi i \left( n+\frac{r}{D}-\frac{1}{2}\right) ^2 z}\) |
\(\theta _{0}(z)=\theta _{0, 1/6}(z)=\eta (z/3)\) | |
\(\ \ \ \ \ \ \ \ \ \ \ \ \ =\sum _{\begin{array}{c} r \in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times } \\ r\equiv 1 (6) \end{array}} F_{r, \mu }(z)\chi _{\pi }(r)\) | \( f_{r, \mu }(z)=\frac{\theta _{r, \mu }(z)}{\theta _0(z)}\) , \(F_{r, \mu }(z)=f_{r, \mu }(3z)\) |
\( R^{(D), \mu }(z)=\sum _{\begin{array}{c} r \in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times } \\ r\equiv 1 (6) \end{array}} F^{(r), \mu }(z)\chi _{{\overline{\pi }}}(r)\) | \( \theta ^{(r), \mu }(z)=\sum \nolimits _{n\in {\mathbb {Z}}} e^{\pi i (n-\mu )^2 z} (-1)^n e^{2\pi i nr/D}\) |
\( F^{(r), \mu }(z)=\frac{\theta ^{(r), \mu }(3z)}{\theta _0(3z)}\) | |
\( T_D=R_{D, 1/6}(\tau /3) {\overline{\pi }}^{-2/3} \omega ^{k_0}\) | |
\(M_D=R_{D, 1/6}(\tau /3) {\overline{\pi }}^{-2/3}\) |
4.1 Factorization lemma
As in the previous section, we write a primitive ideal \({\mathscr {A}}\) as a lattice \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) for \(a={{\,\mathrm{Nm}\,}}({\mathscr {A}})\) and \(b^2\equiv -3\mod 4a\). We also define the CM point \(\tau _{{\mathscr {A}}}=\frac{-b+\sqrt{-3}}{2a}\) corresponding to the \({\mathbb {Z}}\)-lattice. We also denote by \(k_{{\mathscr {A}}}\) the generator of \({\mathscr {A}}\) such that \(k_{{\mathscr {A}}}\equiv 1 (3)\) and we write the generator in the form \(k_{{\mathscr {A}}}=n_a a+ m_a \tau _{{\mathscr {A}}}\).
We start by recalling the Factorization Formula of Rodriguez-Villegas and Zagier from [23]. It is used to decompose theta functions of weight 1 evaluated at CM points as sums of products of theta functions of weight 1/2 also evaluated at CM points.
Below we recall from [23, Theorem, page 7] for the simplified case of \(\alpha =p=0\):
Theorem 15
(Factorization formula) For \(a\in {\mathbb {Z}}_{>0}\), \(\mu , \nu \in {\mathbb {Q}}\), \(z=x+yi\in {\mathbb {C}}\), we have:
where \( \theta \left[ \begin{matrix}\mu \\ \nu \end{matrix}\right] (z)=\sum \nolimits _{n\in {\mathbb {Z}}+\mu }e^{\pi in^2z+2\pi i \nu n}\) is a theta function of weight 1/2.
A direct application of this is the following:
Lemma 16
With notation as above, we have:
Proof
Plugging in \(\mu +\frac{r}{D}\) for \(\mu \) and Dz for z in (15), and summing up for r in \({\mathbb {Z}}/D{\mathbb {Z}}\), we get:
Exchanging the two sums on the RHS we get
The inner sum \(\sum \nolimits _{r\in {\mathbb {Z}}/D{\mathbb {Z}}} e^{2\pi i nr/D}\) equals D when D|n, and 0 otherwise, thus we are only summing over the integers n that are multiples of D. Rewriting \(n=Dn'\), after simplifying we get the result of the lemma.\(\square \)
Using the lemma above and the notation \(\theta _{r, \mu }(z)=\sum \nolimits _{n\in {\mathbb {Z}}}(-1)^n e^{\pi i \left( n+\frac{r}{D}-\mu \right) ^2 z}\), we show:
Proposition 17
For ideals \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}, {\mathscr {A}}_1=[a_1, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) and b such that \(b^2\equiv -3 \mod 4D^2a^2a_1\), we have:
Proof
We apply Lemma 16 for \(\mu =-1/6\) and \(\nu =1/2\), D odd, \(z=\frac{-b+\sqrt{-3}}{2Daa_1}\). It is easy to see on the LHS of the equation that we have \(\theta \left[ {\begin{matrix}-1/6+\frac{r}{D}\\ -a/2 \end{matrix}}\right] \left( z\right) = e^{-a\pi ir/D} e^{a\pi i/6}\theta _{r, \mu }(z), \) and, as \(a\equiv 1 (\text {mod}~ 6)\), also \(\theta \left[ {\begin{matrix} -a/6+\frac{ar}{D} \\ 1/2 \end{matrix}}\right] \left( z\right) =e^{\pi i ar/D} e^{-\pi i/6} \theta _{ar, \mu }(z)\). Moreover, since \(D\equiv 1 (\text {mod}~ 6)\) we simplify the term \(e^{-2\pi i nD/6}=e^{-2\pi i n/6}\) and we can also compute \( \frac{\sqrt{2ay}}{\sqrt{D}}=\frac{\root 4 \of {3}}{D\sqrt{a_1}}\). We get:
Now we only have to show that the RHS equals \(\varTheta _{\mu }(D\tau _{{\mathscr {A}}})\). We claim:
Since the absolute values of the two sides already agree, we only need to show that the arguments agree as well, meaning \( 2\pi i \left( \frac{m}{2}+\frac{n}{2} +\frac{Dmn}{2a}\right) \equiv -2\pi i \frac{|naa_1D-m\frac{-b+\sqrt{-3}}{2}|^2}{aa_1D}D\frac{b}{6a} \mod 2\pi i {\mathbb {Z}}.\) This is equivalent to showing that
and this follows easily from the conditions on \(a, a_1, b\) and D.
Finally, we claim that \( \varTheta _{\mu }(z)=\sum _{m,n \in {\mathbb {Z}}} e^{2\pi in(\mu +1/2)}e^{2\pi i\frac{|m\cdot \frac{b+\sqrt{-3}}{2}+naa_1|^2}{aa_1}z}\), which would finish the proof. This is immediate for \(\mu =1/2\). For \(\mu =1/6\) denote
Then we can write
Note that \(E_{*, 0}(z)=\varTheta _K(3z)\) and \(E_{*, 1}=E_{*, 2}\), as we can change \(n\rightarrow -n, m \rightarrow -m\) in the Fourier expansion. Thus we get on the RHS the term \(\varTheta (3z)+(\omega +\omega ^2)E_{*, 1}(z)=\varTheta (3z)-E_{*, 1}(z)\). Furthermore \(\varTheta (z)=E_{*, 1}(z)+E_{*, 2}(z)+E_{*, 0}(z)\), thus we get \(E_{*, 1}(z)=\frac{1}{2}(\varTheta (z)-\varTheta (3z)).\) Plugging in \(E_{*, 1}(z)\) above we get the result of the proposition. \(\square \)
A particular case of Lemma 17 is for \(D=1\). As \(\varTheta \left( \tau _{A}/3\right) =0\) from Lemma 43 from the Appendix, we get:
Corollary 18
For \(b^2\equiv -3\mod 12a^2a_1\) and \({\mathscr {A}}, {\mathscr {A}}_1\) as above, we have
Let:
Taking the ratios of the theta functions in Proposition 17 and Corollary 18 we get:
Corollary 19
Under the same conditions as above, we have:
We are interested in the Galois conjugates of \(f_{r, \mu }(\tau )\) for \(\tau =\frac{-b+\sqrt{-3}}{2}\) such that \(b^2\equiv -3 \mod 12D^2\). For \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) a primitive ideal and \(k_{{\mathscr {A}}}\equiv 1\mod 3\) its generator, we write \(k_{{\mathscr {A}}}\) in the form \(k_{{\mathscr {A}}}=n_{a}a+m_{a}\frac{-b+\sqrt{-3}}{2}\) with \(3|m_a\) and \(n_a\equiv 1(3)\).
In Sect. 5.2, we compute the Galois conjugates of \(f_{r, \mu }(\tau )\) using Shimura reciprocity’s law in two ways. We first show in Lemma 38 that
where \(\sigma _{{\mathscr {A}}}\) is the Galois action corresponding to the ideal \({\mathscr {A}}\) via the Artin map. With the same notation, we show in Proposition 40 that
where \(n'_a\equiv n_a (3D)\) with \(n'_a\) odd. Thus we get the following lemma:
Lemma 20
For an ideal \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]\) generated by \(n_a a+m_a\frac{-b+\sqrt{-3}}{2}\) such that \(m_a \equiv 0\mod 3\), \(n_a\equiv 1 \mod 3\) and \(b^2\equiv -3 \mod 12aD^2\), we have:
for \(n'_a\equiv n_a (3D)\) with \(n'_a\) odd.
Using the lemma above, we can rewrite Corollary 19:
Corollary 21
Under the same conditions as above, for \({\mathscr {A}}=(n_aa+m_a\frac{-b+\sqrt{-3}}{2})\), \({\mathscr {A}}_1=(n_{a_1}a_1+m_{a_1}\frac{-b+\sqrt{-3}}{2})\) with \(b^2\equiv -3 \mod 12a^2a_1D^2\), we have:
where \(n'_a\equiv n_a (3D)\), \(n'_{a_1}\equiv n_{a_1} (3D)\) and \(n'_a, n'_{a_1}\) odd.
4.2 \(S_D\) as an absolute value
In the following we will use Corollary 21 for a choice of representative ideals for the classes of the ring class group \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\). We show first:
Proposition 22
For \(\tau =\frac{-b+\sqrt{-3}}{2}\) such that \(b^2\equiv -3\mod 12D^2\) and \(\pi \equiv 1 \mod 3\) an element of norm of D such that \((\pi )^2\) divides \((\frac{-b+\sqrt{-3}}{2})\), we have:
Proof
The structure of the ring class group of conductor 3D for \(D=\prod \nolimits _{p_i\equiv 1\mod 3} p_i\) is given by \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\cong ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }\) (see for example Cox [5]). We will choose as representatives for the classes of \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\) ideals \({\mathscr {A}}_s\) such that \({{\,\mathrm{Nm}\,}}{\mathscr {A}}_s \equiv s\mod D\). For b fixed, \(b^2\equiv -3\mod 12D\), we take:
where \(a_s={{\,\mathrm{Nm}\,}}({\mathscr {A}}_s)\equiv s\mod D\), \(n_s\equiv 1\mod 3D\), \(m_s\equiv 0 \mod 3\). Note that this gives us \(m\equiv b^{-1}(s-1) \mod 3D\). Moreover, it is easy to check that the ideals \({\mathscr {A}}_s\) for \(s\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }\) are in different classes in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\).
We take as before \(\pi \) the element of norm D such that \((\pi )^2\) divides the ideal \((\tau )=(\frac{-b+\sqrt{-3}}{2})\). Then note that \(\chi _{D}(\alpha )=\chi _{\pi }(\frac{\alpha }{{\overline{\alpha }}})=\chi _{\pi }(\frac{\alpha ^2}{|\alpha |^2})\). As \(b\equiv \sqrt{-3} \mod \pi \), we get \(\alpha _s=n_s a_s + m_s\frac{-b+\sqrt{-3}}{2} \equiv s \mod \pi \) and thus \(\chi _{\pi }((\alpha _s))=\chi _{\pi }(s^2/s)=\chi _{\pi }(s)\).
Taking representatives \(s\in {\mathbb {Z}}/D{\mathbb {Z}}, s\equiv 1\mod 6\), we get \(m_s\equiv 0\mod 6\) and \(n_s\equiv 1\mod 6\). Summing up over \(r\in {\mathbb {Z}}/D{\mathbb {Z}}\) with \(r\equiv 1\mod 6\) and taking \({\mathscr {A}}_1=(1)\) in Corollary 21, we get:
Summing up for all \(\{s\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }, s\equiv 1 (6)\}\) and rearranging the terms, we get:
Finally, we will further modify the sums on the RHS in order to sum up over \(r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }\) as well. In order to emphasize the dependence of \(\theta _{r, \mu }\) on D we will use only for the current proof the notation
Moreover, for \(p_{i_1}\dots p_{i_k}|D\), denote:
We claim that for \(k\ge 1\) we have \(S_{p_{i_1}\dots p_{i_k}}=0\). Note that we can rewrite
thus showing \(S_{p_{i_1}\dots p_{i_k}}=0\) for \(k\ge 1\) proves our result.
To see that \(S_{p_{i_1}\dots p_{i_k}}=0\), let \(D'=D/(p_{i_1}\dots p_{i_k})\). We recognize each of the inner sums \( \sum \nolimits _{\begin{array}{c} r'\in {\mathbb {Z}}/D'{\mathbb {Z}}\\ r\equiv 1 (\text {mod}~ 6) \end{array}} f_{sr'/D'} (\tau ) \overline{f_{r'/D'}(\tau )}\) of \(S_{p_{i_1}\dots p_{i_k}}\) to be equal to \( \frac{D'}{3/2}\frac{\varTheta _{\mu }\left( D'\tau _{{\mathscr {A}}_s}\right) }{\varTheta \left( \tau _{{\mathscr {A}}_s}\right) }\) from (18) for \(D=D'\).
Denote \(m=D/D'\). From the properties of the cubic character, we have \(\chi _D=\chi _m \chi _{D'}\). Moreover, from our choice of ideals, we have \(\frac{\varTheta _{\mu }\left( D'\tau _{{\mathscr {A}}_s}\right) }{\varTheta \left( \tau _{{\mathscr {A}}_s}\right) } =\frac{\varTheta _{\mu }\left( D'\tau _{{\mathscr {A}}_{s'}}\right) }{\varTheta \left( \tau _{{\mathscr {A}}_{s'}}\right) }\) for \(s\equiv s' \mod 3D'\), as \({\mathscr {A}}_s\) and \({\mathscr {A}}_{s'}\) are in the same class in \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D'})\). Then we can rewrite the sum as:
In the inner sum we are summing over s modulo m for all s in \( ({\mathbb {Z}}/m{\mathbb {Z}})^{\times }\). Moreover, \(\chi _m({\mathscr {A}}_s)\) is a nontrivial character as a function of s, as \(m^{1/3}\chi _m({\mathscr {A}}_s)=(m^{1/3})^{\sigma _{{\mathscr {A}}_s}}=m^{1/3}\) for all \({\mathscr {A}}_s\) iff \(m^{1/3}\in K\). As we are summing a non-trivial character over a group, the sum is 0. This finishes the proof. \(\square \)
Using the above proposition now it is easy to see:
Corollary 23
\(S_D=\frac{1}{3c_{3D}}S_{1/6}\) and \(S_{1/2}=0\).
Proof
As \(3c_{3D}S_D=S_{1/6}+1/2S_{1/2}\), if \(S_{1/2}=0\) we have \(3S_Dc_{3D}=S_{1/6}\). Thus it is enough to show \(S_{1/2}=0\). More precisely we will show that
equals 0 for any z, in particular for \(z=\tau \). Since we showed that \(S_{1/2}=D^{-2/3}|R(\tau ) |^2\) in Proposition 22, we get \(S_{1/2}=0\).
To show \(U(z)=0\), note that \(\theta _{r, 1/2}(z)=-\theta _{2D-r, 1/2}(z)\), while \(\chi _{\pi }(2D-r)=\chi _{\pi }(r)\). As both \(r, 2D-r\equiv 1\mod 6\) and D odd, the terms cancel each other out in the sum and we get \(U(z)=0\). \(\square \)
Finally, from Proposition 22 and Corollary 23 we get:
Proposition 24
For \(\tau =\frac{-b+\sqrt{-3}}{2}\) such that \(b^2\equiv -3\mod 12D^2\), we have \(S_{D}=\frac{1}{3c_{3D} }S_{1/6}\) and
4.3 \(S_D\) as a square
In the following we will rewrite Proposition 24 so that we get a square. Define \(F_{r, \mu }(z)=f_{r, \mu }(3z)\) and take:
With this notation, we have showed in Proposition 22 that \( S_{1/6}=|R_{D,1/6}(\tau /3)D^{-1/3}|^2.\) One can show that \(R_{D, 1/6}^3(\tau /3)\in K\) and actually \(R_{D, 1/6}(\tau /3)\) is really close to being an integer. We will show in this section the following:
Proposition 25
For \(\sigma (D)\) the number of prime divisors of D, we have:
where \(T_D=R_{D, 1/6}(\tau /3) {\overline{\pi }}^{-2/3} \omega ^{k_0}\) and \(T_D=(-1)^{\sigma (D)}\overline{T_D}\) and thus \(T_D\) is real or purely imaginary. Here \(\omega ^{k_0}\) is the unique cube root that makes \(T_D\) real or purely imaginary.
We are going to show first in Lemma 26 that \(R_{D, 1/6}(\tau )\) and \(R_{D, 1/6}(\tau /3)\) differ only by a cubic root of unity \(\omega ^{k}\), and thus \(S_{1/6}=|R_{D, 1/6}(\tau )D^{-1/3}|^2\). In Proposition 27 we show that \( R_{D, 1/6}(\tau )=(-1)^{\sigma (D)}\frac{{\overline{\pi }}^{2/3}}{\pi ^{2/3}}\overline{R_{D, 1/6}(\tau )} \omega ^{k'}\).
Defining \(T_D = R_{D, 1/6}(\tau /3) {\overline{\pi }}^{-2/3} \omega ^{k_0}\) for \(k_0=k+k'\), this is equivalent to \(T_D=(-1)^{\sigma (D)}\overline{T_D}\) and thus
which is the result of Proposition 25 above.
4.3.1 Relating \(S_D\) to \(R_{D, 1/6}(\tau )\)
We will first show that \(S_{1/6}=|R_{D, 1/6}(\tau )D^{-1/3}|^2\) in Lemma 26. Define the theta function \( \theta ^{(r), \mu }(z)=\sum \nolimits _{n\in {\mathbb {Z}}} e^{\pi i (n-\mu )^2 z} (-1)^n e^{2\pi i nr/D}\) and the ratio \( F^{(r), \mu }(z)=\frac{\theta ^{(r), \mu }(3z)}{\theta _0(3z)}.\) We introduce this notation, as we will use the transformation mentioned in Lemma 48 in the Appendix:
Using also \(\theta _{0}(3z)=\frac{1}{\sqrt{-iz}} \theta _0(-3/z)\) and taking the ratio with (19) we get:
Then, using (20), we are ready to show:
Lemma 26
For \(\tau =\frac{-b+\sqrt{-3}}{2}\) such that \(b^2\equiv -3\mod 12D^2\), we have:
where \(\omega ^k\) is a cubic root of unity. Furthermore, this implies \( S_{1/6}=|R_{D, 1/6}(\tau )D^{-1/3}|^2. \)
Proof
Let \(b'\equiv b\mod 4D^2\), and \(b'\not \equiv 0\mod 3\). Without loss of generality we can actually pick \(b, b'\) such that \((b^2+3)/12D^2\) and \((b'^2+3)/4D^2\) are prime to 3D. Let \(\pi \equiv 1(3)\) be an element of norm D such that \((\pi )^2\) divides \((\tau )\). Then we can find ideals \({\mathscr {A}}, {\mathscr {A}}'\) prime to 3D such that:
We can write the generators \(k_{{\mathscr {A}}}, k_{{\mathscr {A}}'} \equiv 1 \mod 3\) of \({\mathscr {A}}\) and \({\mathscr {A}}'\), respectively, in the form \(k_a=an_a+m_a\frac{-b+\sqrt{-3}}{2}\), \(k_{a'}=a'n_{a'}+m_{a'}\frac{-b+\sqrt{-3}}{2}\), where \(m_a, m_a'\equiv 0 \mod 3\), and \(n_a, n_a'\equiv 1\mod 3\). Let \(\tau _{{\mathscr {A}}}=\frac{-b+\sqrt{-3}}{2a}, \tau _{{\mathscr {A}}'}=\frac{-b'+\sqrt{-3}}{2a'}\).
We are going to show that:
-
(i)
\(R_{D, 1/6}(\tau _{{\mathscr {A}}'})=R_{D, 1/6}(\tau _{{\mathscr {A}}}/3)\)
-
(ii)
\(R_{D, 1/6}(\tau _{{\mathscr {A}}}/3)=\chi _{{\overline{\pi }}}(n_a)R_{D, 1/6}(\tau /3)\)
These two relations will imply:
-
(iii)
\(R_{D, 1/6}(\tau )=\chi _{{\overline{\pi }}}(n_a)\chi _{\pi }(n_{a'})R_{D, 1/6}(\tau /3)\).
In order to show (i), note that it is enough to show that \(F_{r, 1/6}(\tau _{{\mathscr {A}}'})=F_{r, 1/6}(\tau _{{\mathscr {A}}}/3)\). We have \(-1/(\tau _A/3)=-{\overline{\tau }}/D^2\) and \(-1/\tau _{{\mathscr {A}}'}=-{\overline{\tau }}/D^2\) as well and we will use (20) for both \(\tau _{{\mathscr {A}}}/3\) and \(\tau _{{\mathscr {A}}'}/3\). First for \(z=\tau _{{\mathscr {A}}}/3\) we get:
Applying (20) also for \(\tau _{{\mathscr {A}}'}\) we get similarly
where \(\tau '=\frac{-b'+\sqrt{-3}}{2}\).
Finally, note that \( F^{(s), 1/6}(z+8D^2)=F^{(s), 1/6}(z)\), thus since \(b\equiv b'\mod 8D^2\) we also have \(F^{(s), 1/6}(-\overline{\tau '}/D^2)=F^{(s), 1/6}(-{\overline{\tau }}/D^2)\) for \(s=\pm 3r\). Similarly we have
\( F^{(-3r), 1/2}(-\overline{\tau '}/D^2)=F^{(-3r), 1/2}(-{\overline{\tau }}/D^2)\), thus \(F_{r, 1/6}(\tau _{{\mathscr {A}}}/3)=F_{r, 1/6}(\tau _{{\mathscr {A}}'})\) as claimed.
To show (ii), as \(f_{r, 1/6}(z)=F_{r, 1/6}(z/3)\), note that from Lemma 20 we have
\(F_{r, 1/6}(\tau /3)^{\sigma _{{\mathscr {A}}}^{-1}}=F_{r, 1/6}(\tau _{{\mathscr {A}}}/3)=F_{n'_ar, 1/6}(\tau /3)\) where \(n_a\equiv n'_a \mod 3D\) and \(n'_a\) odd. This further implies that \(R_{D, 1/6}(\tau _{{\mathscr {A}}}/3)=\chi _{{\overline{\pi }}}(n_a)R_{D, 1/6}(\tau /3)\).
To show (iii), note that we are in the conditions of Lemma 38 from Sect. 5, as \(F_{r, 1/6}\) is a modular function of level \(18D^2\). Then \(F_{r, 1/6}(\tau )^{\sigma _{{\mathscr {A}}'}^{-1}}=F_{r, 1/6}(\tau _{{\mathscr {A}}'})\) and thus we get \(R_{D, 1/6}(\tau _{{\mathscr {A}}'})=(R_{D, 1/6}(\tau ))^{\sigma _{{\mathscr {A}}'}^{-1}}.\)
We can rewrite this as \((R_{D, 1/6}(\tau _{{\mathscr {A}}'}))^{\sigma _{{\mathscr {A}}'}}=R_{D, 1/6}(\tau )\) and using (i), we get
\(R_{D, 1/6}(\tau )=R_{D, 1/6}(\tau _{{\mathscr {A}}}/3)^{\sigma _{{\mathscr {A}}'}}\). From (ii), this is \(R_{D, 1/6}(\tau )=\chi _{{\overline{\pi }}}(n_a)R_{D, 1/6}(\tau /3)^{\sigma _{{\mathscr {A}}'}}\). Using Lemma 20, we have \(F_{r, 1/6}(\tau /3)^{\sigma _{{\mathscr {A}}'}^{-1}}=F_{n_{a'}r, 1/6}(\tau /3)\), thus \(R_{D, 1/6}(\tau /3)^{\sigma _{{\mathscr {A}}'}}=\chi _{\pi }(n_{a'})R_{D, 1/6}(\tau /3)\). Finally this implies
\(R_{D, 1/6}(\tau )=\chi _{{\overline{\pi }}}(n_a)\chi _{\pi }(n_{a'})R_{D, 1/6}(\tau /3)\) and we take \(\omega ^k=\chi _{{\overline{\pi }}}(n_a)\chi _{\pi }(n_{a'})\) to get the result. \(\square \)
4.3.2 Relating \(R_{D, 1/6}(\tau )\) to its complex conjugate
Now we want to show that \(R_{D, 1/6}(\tau )\) equals \(\overline{R_{D, 1/6}(\tau )}\) up to a nice factor. As before we let \(\tau =\frac{-b+\sqrt{-3}}{2}\) and \(\pi \) such that \((\pi )^2\) divides \((\tau )\). We will show:
Proposition 27
For some cubic root of unity \(\omega ^{k'}\), we have:
Using the notation \(T_D=R_{D, 1/6}(\tau ) {\overline{\pi }}^{-2/3}\omega ^{k'}\) this is equivalent to \(T_D=(-1)^{\sigma (D)}\overline{T_D}\).
Note that we can think of \(\omega ^{k'}\) as the unique root of unity which makes
\(R_{D, 1/6}(\tau )\omega ^{k'}{\overline{\pi }}^{-2/3}\) either real or purely imaginary. We actually give a formula for \(\omega ^{k'}\) in the proof of Proposition 27.
We first define the linear combination:
Note that we use \(\chi _{\pi }\), unlike in \(R_{D, \mu }\).
We choose \(b\equiv b' \mod 4D^2\) such that \(3\not \mid b'\) and we can find \({\mathscr {A}}'\) as in the proof of Lemma 26 such that \({\mathscr {A}}'(\pi )^2=\left( \frac{-b'+\sqrt{-3}}{2}\right) \). Then from the transformation (20) we have \(F_{r, 1/6}(\tau _{{\mathscr {A}}'})=(-1)^r\frac{(-1)^{\frac{D-1}{6}}\omega }{\sqrt{-3}}(F^{(3r), 1/6}(-{\overline{\tau }}/D^2)-\omega F^{(-3r), 1/6}(-{\overline{\tau }}/D^2)-\omega ^2F^{(-3r), 1/2}(-{\overline{\tau }}/D^2))\). Writing the full linear combination for \(r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }\), \(r\equiv 1(6)\) and multiplying by \(\chi _{\pi }(3)\), we get:
Note that above we related \(R_{D, 1/6}(\tau )\) to \(\overline{R^{(D), \mu }}\) for \(\mu \in \{1/2, 1/6\}\). In order to show Proposition 27 we also want to relate \(R^{(D), \mu }\) back to \(R_{D, \mu }\), and we do that in the lemma below:
Lemma 28
We have the equality
where \( G(\chi _{{\overline{\pi }}})=\sum _{r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }} \chi _{{\overline{\pi }}}(r)e^{2\pi i nr/D}\) is the Gauss sum corresponding to the character \(\chi _{{\overline{\pi }}}\).
Proof
Recall \( R^{(D), \mu }(z/D^2)=\sum \nolimits _{r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }}F^{(r), \mu }(z/D^2)\chi _{{\overline{\pi }}}(r)\), where
\( F^{(r), \mu }(z/D^2)=\frac{\theta ^{(r), \mu }(3z/D^2)}{\theta _0(3z/D^2)}\). We show first that, for r odd, we can rewrite the terms \(\theta ^{(r), \mu }(3z/D^2)\) as:
From the definition, we have \( \theta ^{(r), \mu }(3z)=\sum _{n\in {\mathbb {Z}}} e^{\pi i (n-D\mu )^2 3z} (-1)^n e^{2\pi i nr/D }\). Choosing as before \(s \in {\mathbb {Z}}/D{\mathbb {Z}}\) such that \(s\equiv 1 \mod 6\), we sum over all n modulo D:
We can rewrite this as \( \theta ^{(r), \mu }(3z)=-\sum \nolimits _{\begin{array}{c} s\in {\mathbb {Z}}/D{\mathbb {Z}}\\ s\equiv 1(6) \end{array}} \theta _{s, \mu }(D^23z) e^{2\pi i sr/D }\) and changing \(z\rightarrow z/3D^2\) we get (22).
Plugging in \(z=\tau /D^2\) in (22) and dividing by \(\theta _0(3\tau )\) we have further
Moreover from Lemma 44 in the Appendix:
thus we get:
Going back to the linear combination, we get
We switch the two sums and get:
Note that if \(\gcd (s, D)=D_1>1\), then the inner sum equals 0. This is easily seen by writing \(s=D_1s_1\), \(D_2=D/D_1\), and rewriting
where \(\pi = \pi _1\pi _2\) and \({{\,\mathrm{Nm}\,}}(\pi _i)=D_i\), for \(i=1,2\). Thus we are left in our sum only with s prime to D, and we can rewrite:
This is exactly \(R^{(D), \mu }(\tau /D^2)= \frac{(-1)^{(D+1)/2}}{{\overline{\pi }}}\sum _{\begin{array}{c} (s\in {\mathbb {Z}}/D{\mathbb {Z}})^{\times }\\ s\equiv 1(6) \end{array}}F_{s, \mu }\left( \tau \right) \chi _{\pi }(s) G(\chi _{{\overline{\pi }}})\), which equals \((-1)^{(D+1)/2}\frac{G(\chi _{{\overline{\pi }}})}{{\overline{\pi }}} R_{D, \mu }(\tau ),\) and thus we get the result of our lemma. \(\square \)
Proof of Proposition 27
Recall from Eq. (21), we have
Rewriting the RHS using Lemma 28, then
Finally, since we noted that \( R_{D, 1/2}(z)=0\) in the proof of Lemma 23, for any z, then we get \( R_{D, 1/6}(\tau _{{\mathscr {A}}'})=\chi _{{\overline{\pi }}}(3)\frac{G(\chi _{\pi })}{\pi }\overline{R_{D, 1/6}(\tau )}.\)
Now using the details of the proof of Lemma 26, recall that
thus
To actually compute the term on the RHS, we recall a few facts about cubic Gauss sums (see [13, Chapter 9]). We can write \(\pi =\prod \nolimits _{p_i |D} \pi _i\), where \(\pi _i\) is a generator of norm \(p_i\) with \(\pi _i \equiv 1 (3)\). Then:
\(\square \)
Moreover, we can actually compute each \(G(\chi _{\pi _i})\) up to a cubic root of unity. From [13, Chapter 9.4], we have \(G(\chi _{\pi _i})^3=-p{\overline{\pi }}_i\) for \(\pi _i\equiv 1\mod 3\). Thus we get \(G(\chi _{\pi _i})=-\overline{\pi _i}^{2/3}\pi _i^{1/3} \omega ^{k_i}\) for some \(k_i\in \{0, 1, 2\}\),
Then \( \frac{G(\chi _{\pi })}{\pi }=(-1)^{\sigma (D)} \omega ^{k_D} \frac{{\overline{\pi }}^{2/3}}{\pi ^{2/3}}\), where \(k_D=\sum k_i\), which together with (24) gives us Proposition 27 for \(\omega ^{k'}=\chi _{\pi }(n_{a'})\chi _{{\overline{\pi }}}(3)\omega ^{k_D}\).
From Lemma 26 and Proposition 27, we get \(T_D=R_{D, 1/6}(\tau /3){\overline{\pi }}^{-2/3}\omega ^{k_0}\) for \(k_0=k+k'\), and thus:
Corollary 29
\(S_D=(-1)^{\sigma (D)} T_D^2\).
4.4 Invariance under the Galois action
Define
We will write below \(M_D\) as a trace.
Lemma 30
\(M_{D}\in K\) and we can write it as a trace:
where \(H_{{\mathscr {O}}}\) is the ray class field of modulus 3D, \(\varphi \) is Euler’s totient function and \(f_{1, 1/6}(\tau )=\theta _{1, 1/6}(\tau )/\theta _0(\tau )\)
Recall we defined \(T_D=R_{D, 1/6}(\tau ) {\overline{\pi }}^{-2/3}\omega ^{k'}\) and from Lemma 26 we have \(T_D=R_{D, 1/6}(\tau /3) {\overline{\pi }}^{-2/3}\omega ^{k_0}\) for \(k_0=k+k'\). As \(T_D=(-1)^{\sigma }\overline{T_D}\) from Proposition 27, we get immediately from Lemma 30:
Corollary 31
\(T_D\in {\mathbb {Q}}\) when \(\sigma (D)\) even and \(T_D/\sqrt{-3}\in {\mathbb {Q}}\) when \(\sigma (D)\) odd and we have the formula:
Proof of Lemma 30:
We can write explicitly \(M_D=\sum \nolimits _{\begin{array}{c} r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times } \\ r\equiv 1 (6) \end{array}} f_{r, 1/6}(\tau ) \chi _{\pi }(r) {\overline{\pi }}^{-2/3}\). For an ideal \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) with generator \(k_a=\left( n_a a+m_a\frac{-b+\sqrt{-3}}{2}\right) \) with \(6|m_a\), \(n_a\equiv 1 (6)\), we are going to have the Galois transformation:
To show this, note that from Lemma 20 we have \(f_{r, 1/6}(\tau )^{\sigma _{{\mathscr {A}}}^{-1}}=f_{rn_{a}, 1/6}(\tau )\). We compute \(({\overline{\pi }}^{1/3})^{\sigma _{{\mathscr {A}}}^{-1}}=\chi _{{\overline{\pi }}}({\mathscr {A}}) {\overline{\pi }}^{1/3}\). Furthermore, \(\chi _{{\overline{\pi }}}({\mathscr {A}})=\overline{\left( \frac{{\overline{\pi }}}{{\mathscr {A}}}\right) _3}=\left( \frac{\pi }{{\overline{{\mathscr {A}}}}}\right) _3=\left( \frac{\pi }{n_aa+m_ab}\right) _3\) and \(n_a(n_aa+m_ab)^2 \equiv a \mod \pi \), so we have \(\left( \frac{\pi }{n_aa+m_ab}\right) _3=\left( \frac{\pi }{n_a^{-1}}\right) _3=\overline{\left( \frac{\pi }{n_a}\right) _3}=\chi _{\pi }(n_a)\).
Moreover, taking the ideals \({\mathscr {A}}_{r}^{\circ }=\left( 1+b^{*}(1-r^*)\frac{-b+\sqrt{-3}}{2}\right) \), where \(b^*\equiv b^{-1} \mod D\) and \(r^{*}\equiv r^{-1}\mod D\), we have \({{\,\mathrm{Nm}\,}}{\mathscr {A}}_r^{\circ }=a_{{\mathscr {A}}_r^{\circ }}\equiv r^{-1} \mod 3D \) and \(n_{{\mathscr {A}}_r^{\circ }}\equiv r \mod 3D\), and then:
We will show in the next section in Proposition 40 that \(f_{1, 1/6}(\tau )\in H_{{\mathscr {O}}}\). Define the group \(G_0=\{[{\mathscr {A}}_{r}^{\circ }], r\in ({\mathbb {Z}}/D{\mathbb {Z}})^{\times }, r\equiv 1\mod 6\}\). It is a subgroup of \({{\,\mathrm{Gal}\,}}(H_{{\mathscr {O}}}/K)\) and \(G_0\) is isomorphic to \(({\mathbb {Z}}/D{\mathbb {Z}})^{\times }\). We define the fixed field of \(G_0\) in \({{\,\mathrm{Gal}\,}}(H_{{\mathscr {O}}}/K)\) to be \(H_0=\{h\in H_{{\mathscr {O}}}: \sigma (h)=h, \forall \sigma \in G_0\}\) and Galois theory implies \({{\,\mathrm{Gal}\,}}(H_{{\mathscr {O}}}/H_0)\cong G_0\). Then we can rewrite the relation above as
As we will show in the next section in Proposition 40, \(f_{r, 1/6}(\tau )\) with \(r\equiv 1\mod 6\) are all the Galois conjugates of \(f_{1, 1/6}(\tau )\), thus \(M_{D}\in K\). Then we can take the trace further to K to get
and this equals \(\prod \nolimits _{p|D}(p-1) {{\,\mathrm{Tr}\,}}_{H_{{\mathscr {O}}}/H_0} (f_{1, 1/6}(\tau ){\overline{\pi }}^{-2/3}).\) \(\square \)
Remark 32
Using the notation from the proof of Lemma 30, one can actually show similarly that \(\kappa =R_{D, 1/6}D^{-1/3}\) equals:
and \(\kappa ^3\in K\). However, \(\kappa \notin K\).
4.5 Integrality
In Sect. 3 we have showed that \(S_D\in {\mathbb {Q}}\). We will show below that \(S_{1/6}\in {\mathbb {Z}}\), thus \(3c_{3D} S_D \in {\mathbb {Z}}\).
Recall that \(S_{1/6}= 3c_{3D}S_D={{\,\mathrm{Tr}\,}}_{H_{3D}/K}\frac{\varTheta (D\omega )}{\varTheta (\omega )} D^{1/3}\). Note that it is enough to show that \(D^{1/3}\varTheta (D\omega )/\varTheta (\omega )\) is an algebraic integer, as its trace would be a rational number as well as an algebraic integer, thus an integer. Moreover, it is enough to show that \(\varTheta (D\omega )/\varTheta (\omega )\) is an algebraic integer.
We cite the following standard result (see for example [19]):
Lemma 33
Let f(z) be a modular function for \(\varGamma (N)\) such that for all \(\gamma \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\) we have \(f\circ \gamma \) holomorphic on the upper half plane \({\mathscr {H}}\) and f has Fourier coefficients at \(\infty \) that are algebraic integers. Then, for \(\tau \) a CM point, \(f(\tau )\) is an algebraic integer.
First we will show that \(2\frac{\varTheta (D\omega )}{\varTheta (\omega )}\) is an algebraic integer. We have showed that \( \frac{3}{2}\varTheta (\omega ) = \root 4 \of {3}|\theta _0(\tau )|^2\). Then \( 2\frac{\varTheta (D\omega )}{\varTheta (\omega )}=3^{3/4}\frac{\varTheta (D\omega )}{|\theta _0(\tau )|^2.}=3^{3/4}e^{-2\pi i/24}\frac{\varTheta (-D{\overline{\tau }})}{\theta _0(-{\overline{\tau }})^2.}\)
Since \(e^{-2\pi i/24}3^{3/4}\) is an algebraic integer, it is enough to show that \(\frac{\varTheta (-D{\overline{\tau }})}{\theta _0(-{\overline{\tau }})^2}\) is one as well. Recall that \(\theta _0(z)=\eta (z/3)\) and take \( f_0(z)=\frac{\varTheta (Dz)}{\eta (z/3)^2}\).
Note that:
-
\(f_0\) is a modular function for \(\varGamma (36D)\);
-
\(f_0(\gamma z)\) is holomorphic on \({\mathscr {H}}\) for all \(\gamma \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\);
-
\(f_0(\gamma z)\) has Fourier coefficients that are algebraic integers in its Fourier expansion at \(\infty \) for all \(\gamma \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\).
These properties can be checked using the properties of \(\varTheta _K\) from the Appendix ((27) and Lemma 41), as well as the properties of \(\eta (z)\). Note that we are in the conditions of Lemma 33, thus \(f(\tau )\) is an algebraic integer. This implies that \(2\frac{\varTheta (D\omega )}{\varTheta (\omega )}\) is an algebraic integer, hence \(2S_{1/6}\) is an integer.
Now we will show that \(DS_{1/6}\) is an integer as well by showing that \(D\frac{2}{3}\frac{\varTheta _{1/6}(D\omega )}{\varTheta (\omega )}\) is an algebraic integer. Using Lemma 16 for \(\mu \in \{-1/2, -1/6\}\), \(\nu =1/2\), \(a=1\), \(z=D\frac{-3+\sqrt{-3}}{2}\), we can rewrite:
Taking the quotient by \(\frac{3}{2}\varTheta (\tau ) = \root 4 \of {3}|\theta _0(\tau )|^2\), we get:
Recall \( f_{r, \mu }(z)=\frac{\theta _{r, \mu }(z)}{\theta _0(z)}\) for \(\mu \in \{1/2, 1/6\}\) and note that:
-
\(f_{r, \mu }\) is a modular function for \(\varGamma (18D^2)\);
-
\(f_{r, \mu }(\gamma z)\) is holomorphic on \({\mathscr {H}}\) for all \(\gamma \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\);
-
\(f_{r, \mu }(\gamma z)\) has Fourier coefficients that are algebraic integers in its Fourier expansion at \(\infty \) for all \(\gamma \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\).
To see the last property, we can either compute explicitly the transformations of \(\theta _{r, \mu }(\gamma z)\) and \(\theta _0(\gamma z)\) and get a Fourier expansion with coefficients in \({\mathscr {O}}_K[\zeta _{24}, \zeta _{D^2}]\), or interpret the theta functions as generating series attached to counting points on certain lattices and get the Fourier coefficients of their ratio to be in \({\overline{{\mathbb {Z}}}}\).
Thus we are in the conditions of Lemma 33, hence \(f_{r, \mu }(\tau )\) is an algebraic integer. This implies that \(D\frac{\varTheta _{1/6}(D\omega )}{\varTheta (\omega )}\) is an algebraic integer, and thus the trace \(DS_{1/6}=D{{\,\mathrm{Tr}\,}}_{H_{3D}/K}\frac{\varTheta _{1/6}(D\omega )}{\varTheta (\omega )}D^{1/3}\), which is a rational number, is indeed an integer. Since we already showed that \(2S_{1/6}\) is an integer, we get \(S_{1/6}\in {\mathbb {Z}}\) when D is odd.
If we note that \(|\theta _0(\tau )|^2=|\eta (\tau /3)|^2=\sqrt{3}|\eta (\tau )|^2\), then we can also show similarly that \(\frac{\theta _{r, \mu }(\tau )}{\eta (\tau )}\) is an algebraic integer, and thus \(DS_{1/6}/\sqrt{3}\) is an algebraic integer. Since \(S_{1/6}\in {\mathbb {Z}}\), this implies 3 divides \(S_{1/6}\).
Finally, since \(S_{1/6}=(-1)^{\sigma _D}T_D^2\) and \(S_{1/6}\) is an integer, from Corollary 31 we get:
Corollary 34
\(T_D/3\in {\mathbb {Z}}\) when \(\sigma (D)\) even and \(T_D/\sqrt{-3}\in {\mathbb {Z}}\) when \(\sigma (D)\) odd.
Note that this implies that \(\omega ^{k_0}\) is the unique choice for a cube root of unity such that \(T_D\) or \(T_D/\sqrt{-3}\) is an integer.
4.6 Case of D not square free
We present below the case of D not square free. We write \(D=D_1D_2^2\) such that \(D_1D_2\) square free. Note that if we try to apply the steps before directly to (9) for D not square-free some of the details of Proposition 22 no longer hold. Instead we use the formula (13):
for \(D_0=D_1D_2\). All the details of the proof for the square-free case will follow through and we only briefly mention the steps.
We apply the factorization formula and obtain the factorization from Corollary 19:
We use this to show similarly to the proof of Proposition 24 that:
where \({\mathscr {A}}_s=[a_s, \frac{-b+\sqrt{-3}}{2}]\) with \({{\,\mathrm{Nm}\,}}(a_s)\equiv s \mod D_1D_2\). Take \(\pi _1\) a generator of \(D_1\) and \(\pi _2\) is the generator of \(D_2\) such that \(\left( \frac{-b+\sqrt{-3}}{2}\right) \) is divisible by \((\pi _1\pi _2)^2\). Then \(\chi _D({\mathscr {A}}_s)=\chi _{\pi _1}(s)\overline{\chi _{\pi _2}(s)}\).
The main difference is when we compute the complex conjugate of
as we get \(R_{D, 1/6}(\tau )=\frac{G(\chi _{\pi _1}\chi _{\overline{\pi _2}})}{\pi _1\pi _2}\overline{R_{D, 1/6}(\tau )}\) and this equals
for a cubic root of unity \(\omega ^{k'}\). Then we can rewrite:
where \(T_D=\sum \nolimits _{\begin{array}{c} s\in ({\mathbb {Z}}/D_1D_2{\mathbb {Z}})^{\times } \\ s\equiv 1 (6) \end{array}}f_{s, 1/6} \left( \tau \right) \chi _{\pi _1}(s)\overline{\chi _{\pi _2}(s)} \overline{\pi _1}^{-2/3} \pi _2^{1/3} \omega ^{k_0}\), and we can show that this is the trace:
where \(H_{{\mathscr {O}}}\) is the ray class field for the modulus \(D_0\) and \(\omega ^{k_0}\) is a cubic root of unity. Moreover, we can further show as in Sect. 4.5 that \(T_D/3 \in {\mathbb {Z}}\) when \(\sigma (D)\) even and \(T_D/\sqrt{-3} \in {\mathbb {Z}}\) when \(\sigma (D)\) odd.
Finally, we have \(S_D\ne 0\) for D split only for \(D\equiv 1 \mod 9\) and in this case we can compute the Tamagawa number \(c_{3D}\) to be equal to \(3^{1+\sigma (D)}\) using Tate’s algorithm (see [28, Chapter IV.9]). Thus \(S_D\) is an integer square up to an even power of 3 and it equals:
5 Shimura reciprocity law
We present below some background on Shimura’s reciprocity law following the exposition of Stevenhagen [30]. For more details also see Gee [7].
Let \({\mathscr {F}}\) be the field of modular functions over \({\mathbb {Q}}\). From CM theory (see for example [30]), it is known that if \(\tau \in K\cap {\mathscr {H}}\) and \(f\in {\mathscr {F}}\), then we have \(f(\tau )\in K^{ab}\), where \(K^{ab}\) is the maximal abelian extension of K. Shimura’s reciprocity law gives us a way to compute the Galois conjugates \(f(\tau )^{\sigma }\) of \(f(\tau )\) when acting with \(\sigma \in {{\,\mathrm{Gal}\,}}(K^{ab}/K)\). We recall that \({\mathscr {F}}=\bigcup _{N\ge 1} {\mathscr {F}}_N\), where \({\mathscr {F}}_N\) is the space of modular functions of level N.
As the restriction maps between the fields \({\mathscr {F}}_N\) are in correspondence with the natural maps between the groups \({{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/N{\mathbb {Z}})/\{\pm 1\}\), we can take the projective limit to get the isomorphism \( {{\,\mathrm{Gal}\,}}({\mathscr {F}}/{\mathscr {F}}_1)\cong {{\,\mathrm{GL}\,}}_2({\widehat{{\mathbb {Z}}}})/\{\pm 1\} .\)
When working over \({\mathbb {Q}}\), one has an isomorphism \({{\,\mathrm{Gal}\,}}({\mathscr {F}}_{N}/{\mathscr {F}}_{1})\cong {{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/N{\mathbb {Z}})/\{\pm 1\}\) and the maps on \({\mathscr {F}}_N\) are given by projecting \({{\,\mathrm{GL}\,}}_2({\widehat{{\mathbb {Z}}}})/\{\pm 1\} \rightarrow {{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/N{\mathbb {Z}})/\{\pm 1\}.\) We define the actions of \({{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/N{\mathbb {Z}})/\{\pm 1\}\) explicitly:
-
Action of \(\alpha \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}}/N{\mathbb {Z}})\) on \({\mathscr {F}}_N\). We have \((f(\tau ))^{\sigma _{\alpha }}=f^{\alpha }(\tau )=f(\alpha \tau ),\) where \(\alpha \) is acting on the upper half plane via fractional linear transformations.
-
Action of \(\left( {\begin{matrix} 1&{}\quad 0 \\ 0 &{}\quad d\end{matrix}}\right) \in ({\mathbb {Z}}/N{\mathbb {Z}})^{\times }\) on \({\mathscr {F}}_N\). Note that for \(f\in {\mathscr {F}}_N\) we have a Fourier expansion \(f(z)=\sum \nolimits _{n\ge 0} a_n q^{n/N}\) with coefficients \(a_n\in {\mathbb {Q}}(\zeta _N)\), \(q=e^{2\pi i z}\). If we denote \(u_d=\left( {\begin{matrix} 1&{}\quad 0 \\ 0 &{}\quad d\end{matrix}}\right) \), then the action of \(\sigma _{u_d}\) is given by \((f(\tau ))^{\sigma _{u_d}}=f^{u_d}(\tau )=\sum \nolimits _{n \ge 0} a_n^{\sigma _d} q^{n/N},\)
where \(\sigma _d\) is the Galois action in \({{\,\mathrm{Gal}\,}}({\mathbb {Q}}(\zeta _N)/{\mathbb {Q}})\) that sends \(\zeta _N \rightarrow \zeta _N^d\).
To further get all the automorphisms of \({\mathscr {F}}\) we need to consider the action of \({{\,\mathrm{GL}\,}}_2( {\mathbb {A}}_{{\mathbb {Q}}, f})\) and for that it is enough to define the action of \({{\,\mathrm{GL}\,}}_2({\mathbb {Q}})^{+}\) on \({\mathscr {F}}\):
-
Action of \(\alpha \in {{\,\mathrm{GL}\,}}_2({\mathbb {Q}})^{+}\) on \({\mathscr {F}}\). We define \(f^{\alpha }(\tau )=f(\alpha \tau ),\) where \(\alpha \) acts by fractional linear transformations.
Let \({\mathscr {O}}\) be the order of K generated by \(\tau \) i.e. \({\mathscr {O}}={\mathbb {Z}}[\tau ]\). We define the matrix \(g_\tau (x)\) to be the unique matrix in \({{\,\mathrm{GL}\,}}_2({\mathbb {A}}_{{\mathbb {Q}}})\) such that \(x\left( \begin{matrix} \tau \\ 1\end{matrix}\right) =g_{\tau }(x)\left( \begin{matrix} \tau \\ 1 \end{matrix}\right) \). We can compute it explicitly. To do that, consider the minimal polynomial of \(\tau \) to be \(p(X)=X^2+BX+C\). Then if we write \(x_p \in {\mathbb {Q}}_p^{\times }\) in the form \(x_p=s_p\tau +t_p \in {\mathbb {Q}}_p^{\times }\) with \(s_p, t_p \in {\mathbb {Q}}_p\), we can compute \( g_{\tau }(x_p)=\left( \begin{matrix}t_p-s_pB &{}\quad -s_pC \\ s_p &{}\quad t_p \end{matrix}\right) \).
Using the map \(g_{\tau }\) above, we have:
Theorem 35
(Shimura’s reciprocity law) For \(f\in {\mathscr {F}}\) and \(x\in {\mathbb {A}}_{K, f}^{\times }\), we have:
where \(\sigma _x\) is the Galois action corresponding to the idele x via the Artin map, \(g_{\tau }\) is defined above and the action of \(g_{\tau }(x)\) is the action in \({{\,\mathrm{GL}\,}}_2( {\mathbb {A}}_{{\mathbb {Q}}, f})\).
Note that the elements of \(K^{\times }\) have trivial action. This can be easily seen by embedding \(K^{\times } \hookrightarrow {{\,\mathrm{GL}\,}}_2({\mathbb {Q}})^{+}\) via \(k\hookrightarrow g_{\tau }(k)\). Noting that \(\tau \) is fixed by the action of the torus \(K^{\times }\), we have \(f^{g_{\tau }(k^{-1})}(\tau )=f(g_{\tau }(k^{-1})\tau )=f(\tau ).\)
We can also rewrite the theorem for ideals in K. Let \(f \in {\mathscr {F}}_N\) and \({\mathscr {O}}={\mathbb {Z}}[\tau ]\) of conductor M. Going through the Artin map, we can restate Shimura’s reciprocity in this case in the form:
where \({\mathscr {A}}\) is an ideal prime to MN, \(\sigma _{{\mathscr {A}}}\) is the Galois action corresponding to the ideal \({\mathscr {A}}\) through the Artin map, and \(g_{\tau }({\mathscr {A}})=g_{\tau }((\alpha )_{p|{{\,\mathrm{Nm}\,}}({\mathscr {A}})}).\) Note that \(g_{\tau }({\mathscr {A}})\) is unique up to multiplication by roots of unity in K. However, these have trivial action on f at the unramified places \(p|{{\,\mathrm{Nm}\,}}({\mathscr {A}})\).
5.1 Galois conjugates of \(f(\omega )\)
We denote \( f(z)=\frac{\varTheta _K(Dz)}{\varTheta _K(z)}\). We are interested in finding the Galois conjugates of \(f(\omega )\). By checking directly computationally and using the fact that both \(\varTheta _K(Dz)\) and \(\varTheta _K(z)\) have Fourier expansions in \(({\mathbb {Z}}\llbracket q \rrbracket )^{\times }\), where \(q=e^{2\pi i z}\), we get the standard result:
Lemma 36
The function f(z) is a modular function of level 3D with integer Fourier coefficients at the cusp \(\infty \).
From CM-theory, if \(f\in {\mathscr {F}}_{3D}\) and \(\tau \) a generator of \({\mathscr {O}}_K\), we have \(f(\tau )\in H_{{\mathscr {O}}}\) the ray class field of modulus 3D. Recall \(H_{3D}\) is the ring class field for the order \({\mathscr {O}}_{3D}={\mathbb {Z}}+3D{\mathscr {O}}_K\), and we actually have:
Lemma 37
\(f(\omega )\in H_{3D}\).
We give below a computational proof. However this can also be seen via Katz’s modular interpretation of algebraic modular forms by thinking of \(\omega \in {\mathscr {H}}\) corresponding to a point \([(E, C)]\in Y_0(3D)[H_{3D}]\) (where E is an elliptic curve and C is a torsion subgroup of \(E({\mathbb {C}})\) of degree 3D), via the projection map \({\mathscr {H}}\rightarrow Y_0(3D)={\mathscr {H}}/\varGamma _0(3D)\) (see Katz [15] for more details).
Proof
We need to show that \(f(\omega )\) is invariant under \({{\,\mathrm{Gal}\,}}(K^{ab}/H_{3D})\). Via the Artin map, we can pick as representatives the ideal classes \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\), where \(a={{\,\mathrm{Nm}\,}}{\mathscr {A}}\) and \(b^2\equiv -3 \mod 4a\), corresponding to the Galois classes of \({{\,\mathrm{Gal}\,}}(K^{ab}/H_{3D})\). Then we can pick a generator of the ideal \({\mathscr {A}}\) written in the form \(ta+s\frac{-b+\sqrt{-3}}{2}\) where \(t, s\in {\mathbb {Z}}\) and 3D|s. As \(f(\omega )=f(\tau )\), where \(\tau =\frac{-b+\sqrt{-3}}{2}\), from Shimura’s reciprocity law, we have:
Here \(g_{\tau }({\mathscr {A}})=\left( {\begin{matrix} ta-sb &{}\quad -sca \\ s &{}\quad ta \end{matrix}} \right) _{p|3D}\), where \(ca=\frac{b^2+3}{4}\). Then we can rewrite the action of \(g_{\tau }({\mathscr {A}})\) explicitly as:
Since 3D|s, the matrix \(\left( {\begin{matrix} ta-sb &{}\quad -sc \\ s &{}\quad t \end{matrix}} \right) \in \varGamma _0(3D)\) and f(z) is invariant under its action, while, since \((a, 3D)=1\) and f has rational Fourier coefficients at \(\infty \), the action of \(\left( {\begin{matrix} 1 &{}\quad 0 \\ 0 &{}\quad a \end{matrix}} \right) _{p|3D}\) is trivial. Thus \(f(\omega )\) is invariant under the Galois action coming from U(3D) and this finishes the proof. \(\square \)
Now we would like to compute the Galois conjugates of \(f(\omega )\) under the action of \({{\,\mathrm{Gal}\,}}(H_{3D}/K)\). We will first show the following general result:
Lemma 38
Let \(F\in {\mathscr {F}}_N\) be a modular function of level N with rational Fourier coefficients in its Fourier expansion at \(\infty \). Let \(\tau =\frac{-b+\sqrt{-3}}{2}\) be a CM point and let \({\mathscr {A}}=\left[ a, \frac{-b+\sqrt{-3}}{2}\right] _{{\mathbb {Z}}}\) be a primitive ideal prime to N. Then we have the Galois action:
Proof
From Shimura’s reciprocity law, we have \(F(\tau )^{\sigma _{{\mathscr {A}}}^{-1}}=F^{g_{\tau }({\mathscr {A}})} (\tau ).\) Note that the minimal polynomial of \(\tau \) is \(p_{\tau }(X)=X^2+bX+\frac{b^2+3}{4}\). Let \(\alpha \) be a generator of \({\mathscr {A}}\). Then we can write \(\alpha \) in the form \(\alpha =ta+s\tau \) and we have \(g_{\tau }({\mathscr {A}})=\left( {\begin{matrix} ta-sb &{}\quad -s\frac{b^2+3}{4} \\ -s &{}\quad ta\end{matrix}}\right) _{p|a}\). We can rewrite the matrix in the form \(g_{\tau }({\mathscr {A}}) = \left( {\begin{matrix} ta-sb &{}\quad \frac{b^2+3}{4a} \\ -s &{}\quad t\end{matrix}}\right) _{p|a} \left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{p|a}.\) As the matrix \(\left( {\begin{matrix} ta-sb &{}\quad -\frac{b^2+3}{4a} \\ -s &{}\quad t\end{matrix}}\right) _{p|a}\) is an element of \({{\,\mathrm{SL}\,}}_2({\mathbb {Z}}_p)\) for \(p\not \mid N\), it has trivial action. Then we have \(F^{g_{\tau }({\mathscr {A}})}(\tau ) = F^{\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{p|a}}(\tau ).\)
We rewrite the matrix \(\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{p|a}=\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad 1/a \end{matrix}}\right) _{p\not \mid a}\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{{\mathbb {Q}}}\), where \(\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad 1/a \end{matrix}}\right) _{p\not \mid a}\in {{\,\mathrm{GL}\,}}_2({\widehat{{\mathbb {Z}}}})\) and \(\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{{\mathbb {Q}}}\in {{\,\mathrm{GL}\,}}_2({\mathbb {Q}})^{+}\). Note that the action of \(\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad 1/a \end{matrix}}\right) _{p\not \mid a}\) is the same as the action of \(\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad 1/a \end{matrix}}\right) _{p|N}\). However, since F has rational Fourier coefficients in its Fourier expansion, this action is trivial. Thus we are left with \(F^{g_{\tau }({\mathscr {A}})}(\tau ) = F^{\left( {\begin{matrix} 1 &{}\quad 0\\ 0 &{}\quad a \end{matrix}}\right) _{{\mathbb {Q}}}}(\tau ) = F(\tau /a)\), which finishes the proof. \(\square \)
We apply the lemma above to our case:
Proposition 39
Take the primitive ideals \({\mathscr {A}}=\left[ a, \frac{-b+\sqrt{-3}}{2}\right] _{{\mathbb {Z}}}\) to be the representatives of the classes of the ring class group \({{\,\mathrm{Cl}\,}}({\mathscr {O}}_{3D})\) such that all norms \(a={{\,\mathrm{Nm}\,}}{\mathscr {A}}\) are relatively prime to each other and \(b^2\equiv -3 \mod 4a\) for all the norms a.
Then the Galois conjugates of \(f(\omega )=\frac{\varTheta _K(D\omega )}{\varTheta _K(\omega )}\) are the terms \(\left( \frac{\varTheta _K(D\omega )}{\varTheta _K(\omega )}\right) ^{\sigma _{{\mathscr {A}}}^{-1}} = \frac{\varTheta _K\left( D\tau _{{\mathscr {A}}}\right) }{\varTheta _K\left( \tau _{{\mathscr {A}}}\right) }.\)
Proof
We note that \(\frac{\varTheta _K(D\omega )}{\varTheta _K(\omega )}=\frac{\varTheta _K\left( D\tau \right) }{\varTheta _K\left( \tau \right) }\) and apply Lemma 38 to \(\tau =\frac{-b+\sqrt{-3}}{2}\) and \(f(z)=\frac{\varTheta _K(Dz)}{\varTheta _K(z)}\). These are the only Galois conjugates, as we showed that \(f(\tau )\in H_{3D}\). \(\square \)
5.2 Galois conjugates of \(f_{r, \mu }(\tau )\)
Recall that we defined \( f_{r, \mu }(z)=\frac{\theta _{r, \mu }(z)}{\theta _{0}(z)}\). This is a modular function for \(\varGamma (18D^2)\) when \(\mu =1/2\) and for \(\varGamma (9D^2)\) when \(\mu =1/6\) (see Lemma 46 in the Appendix). From CM-theory then \(f_{r, \mu }(\tau )\in H_{{\mathscr {O}}'}\), where \(H_{{\mathscr {O}}'}\) is the ray class field of modulus \(18D^2\) for \(\mu =1/2\) and of modulus \(9D^2\) for \(\mu =1/6\). Note that this also follows from the moduli interpretation of algebraic modular forms (see [15]). However, we want to descend to the ray class field \(H_{{\mathscr {O}}}\) of modulus 3D.
In order to do that we compute the Galois conjugates of \(f_{r, \mu }(\tau )\) over K using Shimura’s reciprocity law for \(\tau =\frac{-b+\sqrt{-3}}{2}\), with \(b^2\equiv -3\mod 12D^2\). Note that \(\tau \) has the minimum polynomial \(X^2+bX+\frac{b^2+3}{4}\). Thus we have to compute the action of all \( g_{\tau }((x_p)_p)=\prod \nolimits _p\left( {\begin{matrix} t_p-s_pb &{}\quad -s_p\frac{b^2+3}{4} \\ s_p &{}\quad t_p \end{matrix}} \right) _p\) on \(f_{r, \mu }(\tau )\). We will prove that the Galois action from Shimura’s reciprocity law is given by the following:
In our case we want to compute the Galois conjugates of \(f_{r, \mu }(\tau )\)
Proposition 40
For \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) an ideal prime to 6D such that \(b^2\equiv -3 \mod 12Da^2\). Let \(k_{{\mathscr {A}}}=n_aa+m_a\frac{-b+\sqrt{-3}}{2}\) be the generator of \({\mathscr {A}}\) such that \(3|m_a\) and \(n_a\equiv 1 \mod 3\), then for \(\tau =\frac{-b+\sqrt{-3}}{2}\) we have:
where \(n_a\equiv n'_a \mod 3D\) and \(n_{a'}\) odd. Moreover, these are all the Galois conjugates of \(f_{r, \mu }(\tau )\) and \(f_{r, \mu }(\tau )\) is in \(H_{{\mathscr {O}}}\) the ray class field of modulus 3D.
Proof
We will compute the Galois conjugates of \(f_{r, \mu }(\tau )\) using Shimura’s reciprocity law adelically first. As the action of \(K^{\times }\prod _{v\not \mid 6D} {\mathscr {O}}_{K_v}^{\times }\) is trivial, we need to compute the action of \(\prod _{v|6D} {\mathscr {O}}_{K_v}^{\times }\). We project the action of \((g_{\tau }(x_v))_{v|6D}\) to \(g_{\tau }(x')\in {{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/18D^2{\mathbb {Z}})\). From the Chinese remainder theorem, we can find \(k_0\in K\) such that
\(k_0 \equiv x_p\mod 72D^2{\mathbb {Z}}_p\) for all p|6D. Note that \(k_0\) is independent of the choice of \(\tau \) and \(g_{\tau }(x) \equiv g_{\tau }(k_0)\) in \({{\,\mathrm{GL}\,}}_2({\mathbb {Z}}/18D^2{\mathbb {Z}})\).
Moreover, \((\pm \omega ^i)_p \hookrightarrow {\mathbb {A}}_{K_f}^{\times }\) acts trivially, thus we can consider the action of \(k_0(\pm \omega ^j)\) instead, for \(j \in \{0, 1, 2\}\). We pick \(k_0=A+B\omega \) such that \(v_3(B)\ge 1\), \(A\equiv 1(3)\). By possibly changing b to \(b:=b+18D^2\) above (this does not affect the value of \(f_{r, \mu }(\tau ))\) as noted in Remark 47 in the Appendix), we can find \(b'\equiv b \mod 18D^2{{\,\mathrm{Nm}\,}}k_0\) such that \(k_0=ta+s\frac{-b'+\sqrt{-3}}{2}\) with \(ta-sb' \equiv 1\mod 6\). Let \(\tau '=\frac{-b'+\sqrt{-3}}{2}\) and we have:
where \(g_{\tau '}((k_0)_{6D})=\left( {\begin{matrix} ta-sb' &{}\quad -sc'a \\ s &{}\quad ta \end{matrix}}\right) ,\) with \(c'a=\frac{b'^2+3}{4}\).
We will now compute \(f_{r, \mu }^{g_{\tau }(x)_{p|6D}}(\tau )\). We write the matrix \(g_{\tau '}((k_0)_{6D})\) as a product \(g_{\tau '}((k_0)_{6D})=\left( {\begin{matrix} ta-sb' &{}\quad -sc' \\ s &{}\quad t \end{matrix}}\right) _{p|6D}\left( {\begin{matrix} 1 &{}\quad 0 \\ 0 &{}\quad a \end{matrix}}\right) _{p|6D}\). Note that \(\left( {\begin{matrix} 1 &{}\quad 0 \\ 0 &{}\quad a \end{matrix}}\right) _{p|6D}\) acts trivially on \(f_{r, \mu }\) as the functions \(\theta _{r, \mu }(z)\) and \(\theta _0(z)\) have rational Fourier coefficients in its Fourier expansion at \(\infty \), and thus so does \(f_{r, \mu }(z)\). Thus we need to compute the action
Using the transformation of Lemma 45 from the Appendix for both \(\theta _{r, \mu }\) and \(\theta _0\), as we have \(3D^2|s\) and \(ta-sb\equiv 1\mod 6\), and further noting that \(9|sc'\), we get precisely:
Since \((ta-sb')t \equiv 1\mod D^2\), we can rewrite this as \(f_{t'^{-1}r, \mu }(\tau ')\) for \(t\equiv t \mod D\) and \(t'\equiv 1 \mod 6\). Note that t is prime to D. Thus we have showed so far that the Galois conjugates of \(f_{r, \mu }(\tau )\) are the terms \(f_{s, \mu }(\tau )\), where \(\gcd (s, D)=\gcd (r, D)\). Moreover, we have nontrivial Galois action only for \(k_0=ta+s\frac{-b+\sqrt{-3}}{2}\) with \(t\not \equiv 1\mod D\). Furthermore, it implies that \(f(\tau )\in H_{{\mathscr {O}}}\), the ray class field of modulus 3D.
Finally, we would like to express the Galois action using ideals. For a primitive ideal \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) prime to 6D with a generator \((k_{{\mathscr {A}}})=(n_aa+m_a\frac{-b+\sqrt{-3}}{2})\) with \(n_a\equiv 1 \mod 6\) and \(3|m_a\), we have the correspondence map between ideles and ideals given by \( x=(k_{{\mathscr {A}}})_{p\not \mid 6D} \leftrightarrow {\mathscr {A}}=(k_{{\mathscr {A}}})\). Picking the representatives \(k_{{\mathscr {A}}}\) as above, we have:
where \(n_a\equiv n'_a \mod 3D\) and \(n'_a\) odd. After changing \(r \rightarrow n_{a}'^{-1} r\), we get the result of the Galois action from the proposition. \(\square \)
References
Bump, D.: Automorphic Forms and Representations, vol. 55. Cambridge University Press, Cambridge (1998)
Cassels, J.W.S.: Arithmetic on curves of genus 1, IV. Proof of the Hauptvermutung. J. Reine Angew. Math. 211, 95–112 (1962)
Coates, J., Wiles, A.: On the conjecture of Birch and Swinnerton-Dyer. Invent. Math. 39, 233–251 (1977)
Cohn, H.: Introduction to the Construction of Class Fields. Dover Publications, New York (1985)
Cox, D.A.: Primes of the form \(x^2+ny^2\): Fermat, class field theory, and complex multiplication. Wiley, New York (2011)
Dasgupta, S., Voight, J.: Heegner Points and Sylvester’s Conjecture, Arithmetic Geometry (2009)
Gee, A.: Class fields by Shimura reciprocity. Universiteit van Amsterdam, PhD diss. (2001)
Gelbart, S.: Weil’s Representation and the Spectrum of the Metaplectic Group, vol. 530. Springer, Berlin (2006)
Gross, B., Zagier, D.: Heegner points and derivatives of \(L\)-series. Invent. Math. 84(2), 225–320 (1986)
Hanke, J.: Quadratic Forms and Automorphic Forms. Quadratic and Higher Degree Forms, pp. 109–168. Springer, New York (2013)
Hecke, E.: Mathematische Werke, Auftrage der Akademie der Wissenschaften zu Gottingen Vandenhoeck & Ruprecht (1959)
Hida, H.: Elliptic Curves and Arithmetic Invariants. Springer, New York (2013)
Ireland, K., Rosen, M.: A Classical Introduction to Modern Number Theory, vol. 84. Springer Science and Business Media, New York (2013)
Jetchev, D., Skinner, C., Wan, X.: The Birch and Swinnerton–Dyer formula for elliptic curves of analytic rank one (preprint) (2015). arXiv:1512.06894
Katz, N.M.: \(p\)-adic interpolation of real analytic Eisenstein series. Ann. Math. (2) 104(3), 459–571 (1976)
Köhler, G.: Eta Products and Theta Series Identities. Springer Science and Business Media, New York (2011)
Kolyvagin, V.A.: Finiteness of \(E(\mathbb{Q})\) and Ш\((E;\mathbb{Q})\) for a subclass of Weil curves. Math. USSR Izvestiya 32(3) (1989)
Kowalski, E.: Automorphic forms, L-functions and number theory (March 12–16), Three introductory lectures
Lang, S.: Elliptic Functions. Springer, New York (1987)
Pacetti, A.: A formula for the central value of certain Hecke \(L\)-functions. J. Number Theory 113(2), 339–379 (2005)
Prasad, D.: A Brief Survey on the Theta Correspondence, Number Theory, January 3–6, 1996. Ramanujan Mathematical Society, Tiruchirapalli (1998)
Rodriguez-Villegas, F.: On the square root of special values of certain \(L\)-series. Invent. Math. 106(1), 549–573 (1991)
Rodriguez-Villegas, F., Zagier, D.: Square root of central values of Hecke \(L\)-functions. In: Gouvea, F.Q., Yui, N. (eds.) Advances in Number Theory, pp. 81–99. Clarendon Press, Oxford (1993)
Rodriguez-Villegas, F., Zagier, D.: Which primes are sums of two cubes?, Number theory (Halifax, NS, 1994), CMS Conf. Proc., vol. 15. American Mathematical Society, Providence, pp. 295–306 (1995)
Rubin, K.: The “main conjectures” of Iwasawa theory for imaginary quadratic fields. Invent. Math. 103, 25–68 (1991)
Selmer, E.S.: The diophantine equation \(ax^3 +by^3 +cz^3 = 0\). Acta Math. 85, 203–362 (1951)
Silverman, J.: The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, vol. 106. Springer, New York (1986)
Silverman, J.: Advanced Topics in the Arithmetic of Elliptic Curves, vol. 151. Springer Science and Business Media, New York (2013)
Shimura, G.: On the holomorphy of certain Dirichlet series. Proc. Lond. Math. Soc. 31(3), 79–98 (1975)
Stevenhagen, P.: Hilbert’s 12th Problem, Complex Multiplication and Shimura Reciprocity. Department of Mathematics, Computer Science, Physics and Astronomy, University of Amsterdam, Amsterdam (1998)
Tunnell, J.B.: A classical diophantine problem and modular forms of weight \(3/2\). Invent. Math. 72, 323–334 (1983)
Waldspurger, J.L.: Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. 60, 375–484 (1981)
Yuan, X., Zhang, S.-W., Zhang, W.: The Gross–Zagier Formula on Shimura Curves, vol. 184. Princeton University Press, Princeton (2013)
Acknowledgements
Open access funding provided by Projekt DEAL. The author thanks Xinyi Yuan for suggesting the problem and for valuable insights. We also thank Don Zagier for encouragement to finish the result in the current form, very helpful discussions and for help with using PARI for computational purposes. We thank the anonymous referee for the careful feedback that helped improve the paper. We also thank the Max Planck Institute for Mathematics in Bonn and Tsinghua University in Beijing for their hospitality.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Wei Zhang.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Properties of theta functions
Appendix: Properties of theta functions
1.1 Properties of \(\varTheta _K\) and \(\eta \)
We have a functional equation for the theta function (see [16, Section 11.1]):
Furthermore, we can compute the transformation of \(\varTheta _K(z\pm 1/3)\) in the lemma below:
Lemma 41
\( \varTheta \left( z+k/3\right) =(1-\omega ^{2k})\varTheta (3z)+\omega ^{2k}\varTheta (z)\) for \(k\in {\mathbb {Z}}\).
Proof
For \(k=1\), we can split the sum \(\varTheta \left( z+\frac{1}{3}\right) =\sum \nolimits _{m, n \in {\mathbb {Z}}}e^{2\pi i (m^2+n^2-mn)\left( z+\frac{1}{3}\right) } \) in two parts, depending on whether or not the ideal \((m+n\omega )\) is prime to \((\sqrt{-3})\). The part of the sum for which \((\sqrt{-3})|(m+n\omega )\) gives us \(\sum \nolimits _{m, n \in {\mathbb {Z}}}e^{2\pi i (m^2+n^2-mn)\left( 3z+1\right) } = \varTheta (3z+1) = \varTheta (3z).\)
The part of the sum for which \((\sqrt{-3})\not \mid (m+n\omega )\) can be rewritten as
\(\omega \sum \nolimits _{\begin{array}{c} m, n \in {\mathbb {Z}}, \\ (\sqrt{-3})\not \mid (m+n\omega ) \end{array}}e^{2\pi i (m^2+n^2-mn)z}\) since \(m^2+n^2-mn \equiv 1(3)\). We rewrite this sum as the sum of two terms \(\omega \sum \nolimits _{m, n \in {\mathbb {Z}}}e^{2\pi i (m^2+n^2-mn)z}-\omega \sum \nolimits _{\begin{array}{c} m, n \in {\mathbb {Z}}, \\ (\sqrt{-3})|(m+n\omega ) \end{array}}e^{2\pi i (m^2+n^2-mn)z}\). Finally we recognize the two terms as \(\omega \varTheta (z)-\omega \varTheta (3z).\)
Going back to our initial computation, we get \(\varTheta \left( z+1/3\right) =\varTheta (3z)+\omega \varTheta (z)-\omega \varTheta (3z)=(1-\omega )\varTheta (3z)+\omega \varTheta (z),\) and this finishes the proof of the first formula. We can show the case \(k=2\) by applying the equality for \(k=1\) and plugging in \(z-1/3\) for z. \(\square \)
By applying the functional equation (27) for \(z=\frac{-3+\sqrt{-3}}{6}\) we get the following easy lemma:
Lemma 42
\(\varTheta _K\left( \frac{-3+\sqrt{-3}}{6}\right) =0\).
Using the lemma above, we get the following result that we use in the proof of Corollary 18:
Lemma 43
For a primitive ideal \({\mathscr {A}}=[a, \frac{-b+\sqrt{-3}}{2}]_{{\mathbb {Z}}}\) prime to 3 such that \(b^2\equiv -3 \mod 12a\), we have \(\varTheta _K\left( \frac{-b+\sqrt{-3}}{6a}\right) =0.\)
Proof
The proof is similar to that of Lemma 12. We can write the generator of primitive ideal \({\mathscr {A}}=\left[ a, \frac{-b+\sqrt{-3}}{2}\right] \) in the form \( k_{{\mathscr {A}}}=ma+n\frac{-b+\sqrt{-3}}{2}\) for some integers m, n and following similar steps as in Lemma 12, we get \(\varTheta _K\left( \frac{-b+\sqrt{-3}}{6}\right) =(m-n\frac{-b+\sqrt{-3}}{2a})\varTheta _K\left( \frac{-b+\sqrt{-3}}{6a}\right) .\) From the previous lemma, we know the LHS equals 0, thus \(\varTheta _K\left( \frac{-b+\sqrt{-3}}{6a}\right) =0\) as well. \(\square \)
We also use the following lemma in the proof of Lemma 28:
Lemma 44
For \(b^2\equiv -3 \mod 12D^2\) and \(\pi \) of norm D such that the ideal \((\pi )^2\) divides \(\left( \frac{-b+\sqrt{-3}}{2}\right) \), we have for \(\tau =\frac{-b+\sqrt{-3}}{2}\):
Proof
We apply Corollary 18 twice to get: \( (-1)^{\frac{D-1}{6}}\frac{\theta _0(\tau /D^2)}{\theta _0(\tau )} \frac{\theta _0\left( {\overline{\tau }}\right) }{\theta _0\left( {\overline{\tau }}\right) } = \frac{\varTheta _K\left( \tau /D\right) }{\varTheta _K\left( \tau \right) }.\)
Then from Lemma 12, we have the RHS equal to \({\overline{\pi }}\). Furthermore, we can pick \(b\equiv b'\mod 8D^2\), \(b\equiv 0\mod 3\) and \(b'\equiv 1\mod 3\). Denote \(\tau '=\frac{-b'+\sqrt{-3}}{2}\). We can pick without loss of generality \(b, b'\) such that \((b^2+3)/D^2\) and \((b'^2+3)/D^2\) are prime to D. Then we can find ideals \({\mathscr {A}}, {\mathscr {A}}'\) prime to D such that \({\mathscr {A}}(\pi )^2(\sqrt{-3})=(\tau )\) and \({\mathscr {A}}'(\pi )^2=(\tau ')\). Let \(a={{\,\mathrm{Nm}\,}}{\mathscr {A}}, a'={{\,\mathrm{Nm}\,}}{\mathscr {A}}'\) and then we have:
Similarly we compute \( \frac{\eta ({\overline{\tau }})}{\eta \left( {\overline{\tau }}/D^2\right) } = \frac{\eta (\overline{\tau '})}{\eta \left( \overline{\tau '}/D^2\right) } = \frac{\eta \left( \frac{\tau '}{a'D^2}\right) }{\eta \left( \frac{\tau '}{a'}\right) } = \left( \frac{\eta \left( \tau '/D^2\right) }{\eta \left( \tau '\right) }\right) ^{\sigma _{{\mathscr {A}}'}^{-1}}.\) Note that we also have \( \frac{\eta \left( \frac{\tau '}{D^2}\right) }{\eta \left( \tau '\right) } =\frac{\eta \left( \frac{\tau }{D^2}\right) }{\eta \left( \tau \right) }\), and thus we have \( \frac{\eta \left( \frac{\tau }{D^2}\right) }{\eta \left( \tau \right) } = (-1)^{\frac{D-1}{6}}{\overline{\pi }}.\) \(\square \)
1.2 Properties of \(\theta _{r, \mu }\)
Recall that for \(r\in {\mathbb {Z}}\), \(\mu \in \{1/2, 1/6\}\), we have defined the theta function
We will write \(\theta _{r, \mu }\) as an automorphic theta function (see for example [10]). Using the standard notation (see [33]):
for \(\phi \in {\mathscr {S}}({\mathbb {A}}_{{\mathbb {Q}}})\) a Schwartz–Bruhat function, the Weil representation r for \({{\,\mathrm{SL}\,}}_2({\mathbb {A}}_{{\mathbb {Q}}})\) is defined by:
-
\(r\left( m(a)\right) \phi (x)=\chi _{0}(a)|a|^{1/2} \phi (ax)\)
-
\(r\left( n(b)\right) \phi (x) = \psi (bx^2) \phi (x)\)
-
\(r\left( w\right) \phi (x)=\gamma {\widehat{\phi }}(x),\)
where \(\psi _p(x)=e^{-2\pi i {{\,\mathrm{Frac}\,}}_p(x)}\) and \(\psi _{\infty }(x)=e^{2\pi i x}\), \(\gamma \) is an 8th root of unity, and \(\chi _0\) is a quadratic character. Here we choose the self-dual Haar measure such that \(\widehat{{\widehat{\phi }}}(-x)=\phi (x)\). Note that this is the same Haar measure as chosen in Tate’s thesis for the global field \({\mathbb {Q}}\) (see [1, Section 3.1]).
We define the Schwartz–Bruhat functions \(\phi ^{r, \mu }=\prod \nolimits _v \phi _v^{r, \mu }\) for \(\theta _{r, \mu }\) by taking \(\phi ^{r, \mu }_{\infty }(x)=e^{-2\pi x^2 }\), \(\phi ^{r, \mu }_p = {{\,\mathrm{char}\,}}_{{\mathbb {Z}}_p+\frac{r}{D}-\mu }\) for \(p\ne 2\) and \(\phi ^{r, \mu }_2(x) = e^{\pi i {{\,\mathrm{Frac}\,}}_2(x) }{{\,\mathrm{char}\,}}_{{\mathbb {Z}}_2-1/2}(x)\). Then for the theta function
for \(g_z=\left( {\begin{matrix} y^{1/2} &{}\quad y^{-1/2}x \\ 0 &{}\quad y^{-1/2} \end{matrix}}\right) \), we can compute \( \theta (g_z, \phi ^{r, \mu }) = e^{-\pi i {{\,\mathrm{Frac}\,}}_2 \mu }(-1)^ry^{1/4}\theta _{r, \mu }(2z).\) For this type of standard computation see for example [10].
Using the properties of the Weil representation and the definition above for \(\theta _{r, \mu }\), after a straightforward computation we get the following lemma that we use in the proof of Proposition 40, as well as below for Lemma 46 that is used in Sect. 5.2:
Lemma 45
For \(\left( {\begin{matrix} a&{}\quad b \\ c &{}\quad d \end{matrix}}\right) \in {{\,\mathrm{SL}\,}}_2({\mathbb {Z}})\) such that \(3D^2|b\) and \(a\equiv 1 \mod 6\), we have the transformation:
where \(t_{1/2}=0\) and \(t_{1/6}=1\).
Proof
Let \(\phi =\phi ^{\mu , r}\). Recall that \( \theta (g_{z/2}, \phi ) = e^{-\pi i {{\,\mathrm{Frac}\,}}_2 \mu }(-1)^r(y/2)^{1/2}\theta _{r, \mu }(z).\) We have
and we will compute separately the LHS and the RHS using the definition of the Weil representation. To compute the RHS, we rewrite the matrix \(\left( {\begin{matrix}d &{}\quad -b/2 \\ -2c &{}\quad a \end{matrix}}\right) \) as
\(m(a^{-1})n(-ba/2) m(-1)w\cdot n(2c/a)\cdot w\).
At \(p\not \mid 6D\), the action of \(\left( {\begin{matrix}d &{}\quad -b/2 \\ -2c &{}\quad a \end{matrix}}\right) \) is trivial. For p|D, we can easily compute the Fourier transform \(\widehat{\phi _p}(x)= e^{-2\pi i {{\,\mathrm{Frac}\,}}_p(2rx/D)}{{\,\mathrm{char}\,}}_{{\mathbb {Z}}_p}(x)\). Using \(v_p(c/a)\ge 0\) and \(v_p(ba/2)\ge 2\), we get the action of \(\left( {\begin{matrix}d &{}\quad -b/2 \\ -2c &{}\quad a \end{matrix}}\right) \) on \(\phi _p\) to equal \({{\,\mathrm{char}\,}}_{{\mathbb {Z}}_p+\frac{ar}{D}}(x).\)
For \(p=3\), the computation is similar. For \(\mu =1/2\) we get \(\chi _{0, 3}(a)\phi _3(x)\), while for \(\mu =1/6\) we get \(\chi _{0, 3}(a)e^{-2\pi i {{\,\mathrm{Frac}\,}}_3(\frac{ba/2}{9})}\phi _3(x)\).
For \(p=2\), we have the Fourier transform \(\widehat{\phi _2}(x)= e^{\pi i/2}e^{-2\pi i{{\,\mathrm{Frac}\,}}_2(x)}{{\,\mathrm{char}\,}}_{\frac{1}{2}({\mathbb {Z}}_2+1/2)}(x)\). Using \(v_2(2c/a)\ge 1\) and \(v_2(ba)\ge 0\) we get \(\chi _{0, 2}(a)e^{\pi i (a-1)/2} e^{2\pi i {{\,\mathrm{Frac}\,}}_2(\frac{ba-c/a}{8})}\phi _2(x)\).
This finishes the computation, as we got \(\theta (m(\sqrt{2})^{-1}g_{z}, \left( {\begin{matrix}a &{}\quad b/2 \\ 2c &{}\quad d \end{matrix}}\right) ^{-1}_f, \phi )\) to equal:
where \(c_0=\chi _{0, 6}(a) e^{\pi i (a-1)/2} e^{2\pi i {{\,\mathrm{Frac}\,}}_2(\frac{ba-c/a}{8})}e^{2\pi i t_{\mu } {{\,\mathrm{Frac}\,}}_3(\frac{ba/2}{9})}\).
For the LHS of (28) we have \(r(g_z)\phi _{\infty }(m)=y^{1/4} e^{2\pi i zm^2}\). Using the Weil representation action we get
and thus combining with (29) we get the result of the lemma. \(\square \)
It follows immediately by applying the lemma above for \(\theta _{r, \mu }\) and \(\theta _0\) that:
Lemma 46
\(f_{r, 1/2}\) is a modular function for \(\varGamma (18D^2)\) and \(f_{r, 1/6}\) is a modular function for \(\varGamma (6D^2)\).
Remark 47
Also from Lemma 45 it is easy to see that \(f_{r, \mu }(z+9D^2)=f_{r, \mu }(z)\).
We can also straightforwardly compute the transformation under \(w=\left( {\begin{matrix} 0 &{}\quad 1 \\ -1 &{}\quad 0 \end{matrix}}\right) \) of \(\theta _{r, \mu }\) and get the Lemma 48 below. This lemma is essential for the proof of Lemma 26.
Lemma 48
We have the transformation:
where \( \theta ^{(r), \mu }(z)=\sum \nolimits _{n\in {\mathbb {Z}}} e^{\pi i (n-\mu )^2 z} (-1)^n e^{2\pi i nr/D}\).
Proof
Denote \(\phi =\phi ^{r, 1/6}\). Then for \(g_{Z/2}=\left( {\begin{matrix} (Y/2)^{1/2} &{}\quad (Y/2)^{-1/2}(X/2)\\ 0 &{}\quad (Y/2)^{-1/2} \end{matrix}}\right) \) and \(w=\left( {\begin{matrix} 0 &{}\quad 1 \\ -1 &{}\quad 0 \end{matrix}}\right) \) we have \(\theta (g_{Z/2}, \phi )=\theta (wg_{Z/2}, w\phi )\). We compute \(\theta (wg_{Z/2}, w\phi )\) below:
-
At \(\infty \): \( r(w g_{Z/2})\phi _{\infty }(x)=\frac{\gamma _{\infty }(Y/2)^{1/2} e^{4\pi i x^2 (-1/Z)}}{\sqrt{-iZ}}.\)
-
At p|D: \( r(w\phi _p) = \gamma _p e^{-2\pi i {{\,\mathrm{Frac}\,}}_p(2xr/D) }{{\,\mathrm{char}\,}}_{{\mathbb {Z}}_p}(x)\).
-
At \(p=3\): \( r(w\phi _3)=\gamma _3e^{-2\pi i {{\,\mathrm{Frac}\,}}_3(2x/3)}{{\,\mathrm{char}\,}}_{{\mathbb {Z}}_3}(x)\).
-
At \(p=2\): \( r(w\phi _2)=\gamma _2e^{-\pi i/2} e^{2\pi i {{\,\mathrm{Frac}\,}}_2(x)}{{\,\mathrm{char}\,}}_{\frac{1}{2}({\mathbb {Z}}_2+1/2)}(x). \)
Writing all these together, we get:
Changing \(n \rightarrow -n-\frac{D-1}{2}\) we get on the RHS:
Taking the separate sums depending on \(n \mod 3\) we get a sum:
Thus we got \( e^{2\pi i \frac{D-1}{3}}(-1)^{\frac{D-1}{2}}\omega \frac{(Y/2)^{1/4}}{\sqrt{-iZ}}(\theta ^{(-3r), 1/6}(9(-\frac{1}{Z}))-\omega \theta ^{(3r), 1/6}(9(-\frac{1}{Z}))-\omega ^2\theta ^{(-3r), 1/2}(9(-\frac{1}{Z}))).\) Taking \(Z=3z\) and using
we get the result of the lemma.
\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosu, E. Central values of L-functions of cubic twists. Math. Ann. 378, 1327–1370 (2020). https://doi.org/10.1007/s00208-020-02018-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-020-02018-0




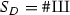 integer square
integer square have solutions in (
have solutions in (

