Abstract
In the supercritical range of the polytropic indices \(\gamma \in (1,\frac{4}{3})\) we show the existence of smooth radially symmetric self-similar solutions to the gravitational Euler–Poisson system. These solutions exhibit gravitational collapse in the sense that the density blows up in finite time. Some of these solutions were numerically found by Yahil in 1983 and they can be thought of as polytropic analogues of the Larson–Penston collapsing solutions in the isothermal case \(\gamma =1\). They each contain a sonic point, which leads to numerous mathematical difficulties in the existence proof.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and the Main Result
The rigorous description of stellar collapse in the context of Newtonian gravity is a fundamental mathematical problem. It is believed, at least for some classes of initial data, that on approach to singularity a self-gravitating gaseous star will enter an approximately self-similar regime [15, 20, 26, 28, 30], which will intertwine the spatial and the time scales in a universal manner dictated by the scaling symmetries of the problem. The purpose of this paper is to construct radially symmetric examples of exactly self-similar imploding solutions for the full range of the supercritical polytropic pressure laws.
A self-gravitating Newtonian star is described using the gravitational Euler–Poisson equations, coupling the isentropic compressible Euler equations to a gravitational potential. In three spatial dimensions, under the assumption of radial symmetry, these equations take the form
where the principal unknowns \(\rho (t,r)\) and u(t, r) are the density and radial velocity of the star, respectively, and depend only on time t and the radial coordinate \(r=|x|\). Equation (1.1) gives the conservation of mass and (1.2) is the conservation of momentum with the given pressure law and gravitational force. We will assume throughout that the pressure \(p=P(\rho )\) satisfies the polytropic equation of state
and the mass function m(t, r) is defined by
Notice that the term \(\frac{m}{r^2}\) appearing in the momentum equation (1.2) corresponds to the radial component of the gravitational force field \(\nabla \phi \) generated by the gravitational potential \(\phi \), which by definition solves the Poisson equation
This is easily checked under the assumptions of radial symmetry.
A natural criticality scale is introduced in the problem by varying the polytropic index \(\gamma \) in the pressure law (1.3). It is easily checked that the nonlinear flow associated with (1.1)–(1.3) is invariant under the scaling transformation
This scaling is in fact the only invariant scaling for the compressible Euler–Poisson system, by contrast to the compressible Euler equations which allow for a 2-parameter family of invariant scalings, see for example [23].
When \(\gamma >\frac{4}{3}\) the problem is mass-subcritical with respect to the scaling (1.5), see [14]. In this case, under the assumption of finite total mass and energy, it is known that no collapsing solutions can exist, see [6]. In the mass-critical case, there is a well-known finite-dimensional family of collapsing stars discovered by Goldreich and Weber [9], see also [7, 8, 22]. The goal of this paper is to prove the existence of self-similar solutions describing gravitational collapse in the mass-supercritical regime \(\gamma \in (1,\frac{4}{3})\).
Motivated by (1.5), we define the self-similar variable
and formally look for solutions to (1.1)–(1.3) of the form
Substituting this ansatz into the continuity equation (1.1) and dropping the tilde notation, we derive
Multiplying through by \(y^2\), we simplify to find
which we integrate to get a representation for the self-similar local mass as
Thus we derive from the momentum equation (1.2) the second self-similar equation
It will be convenient in what follows to work with the re-scaled relative velocity, rather than working directly with the velocity u. The new relative velocity is defined as
We therefore arrive at the self-similar ODE system
Equivalently we may rewrite the system in the form
We refer to (1.13) as the self-similar Euler–Poisson system. Clearly, this system has a singularity at \(y=0\). However, there is a further singularity which occurs whenever \(\gamma \rho ^{\gamma -1}-y^2\omega ^2=0\). This is of fundamental importance and the presence of such singularities, as we shall explain below, is unavoidable in the study of smooth self-similar solutions to (1.13) satisfying physically reasonable boundary conditions. This motivates the following definition.
Definition 1.1
(Sonic point) Let \((\rho (\cdot ),\omega (\cdot ))\) be a \(C^1\)-solution to the self-similar Euler–Poisson system (1.13) on the interval \((0,\infty )\). A point \(y_*\in (0,\infty )\) such that
is called a sonic point.
If \(y_*\) is a sonic point, then the hypersurface defined by the relation \(r(t)=\sqrt{\kappa }y_*(-t)^{2-\gamma }\) corresponds to the backward acoustic cone emanating from the origin (0, 0) ([2, 23]). It satisfies the relation \(\dot{r}(t) = u(t,r(t))-c_s(t,r(t))\), where \(c_s\) is the sound speed \(c_s=\frac{\textrm{d}P}{\textrm{d}\rho }= \sqrt{\kappa \gamma \rho ^{\gamma -1}}\).
We are looking for smooth solutions which are both regular at the (scaling) origin \(y=0\) and satisfy suitable decay conditions as \(y\rightarrow \infty \). Taking Taylor expansions at the origin and in the far-field (as \(y\rightarrow \infty \)), we see that we require the initial and asymptotic boundary conditions
From these conditions, it is clear that any continuous solution of (1.13) and (1.14)–(1.15) must have at least one sonic point \(y_*>0\).
In the isothermal case \(\gamma =1\), the existence of global solutions satisfying (1.13) and (1.14)–(1.15) has a long history in the astrophysics literature, primarily relying on numerical methods. In their seminal works, Larson [20] and Penston [26] independently showed (numerically) the existence of a globally defined solution satisfying (1.14)–(1.15) and with only a single sonic point present. Subsequently, Hunter [16] numerically constructed a full sequence of further solutions, commonly referred to as Hunter-type solutions, each of which also has a single sonic point (see also the work of Shu [28] and the later work of Whitworth and Summers [29]). Despite the physically simplifying assumption \(\gamma =1\), these families of solutions attracted a lot of attention in the physics literature as possible prototype models for the behaviour of the core in late stages of gravitational collapse. In fact, the Larson–Penston (henceforth, LP) solutions were judged to be the more stable solutions under subsequent numerical analysis [2, 21, 25]. They also play an important role in the Newtonian criticality theory and the resolution of the so-called self-similarity hypothesis, see [15].
However, the assumption that the flow is isothermal received criticism on physical grounds, for example by Yahil [30], who pointed out that the physical condition of finite energy is violated unless \(\gamma >\frac{6}{5}\). The value \(\gamma =\frac{6}{5}\) plays the role of the energy-critical exponent with respect to the scaling (1.5), see [14]. More importantly, different values of \(\gamma >1\) allow us to encode stars with different thermodynamic properties and it is therefore important to understand the space of self-similar flows in the range \(\gamma \in (1,\frac{4}{3})\). In the range \(\gamma \in [\frac{6}{5},\frac{4}{3})\), Yahil [30] constructed a family of numerical self-similar solutions to (1.13) with finite energy. These solutions share certain characteristics with the isothermal LP solution. For example, the physical radial velocity remains strictly negative (except at the scaling origin, where it vanishes) up to the collapse time in both the Yahil solutions and the LP solutions. This property does not hold for Hunter solutions and has been tied to the possible dynamic instabilities of such solutions by Maeda–Harada [21]. This leads us to the following definition.
Definition 1.2
(Yahil-type solution) Let \(\gamma \in (1,\frac{4}{3})\). A pair of \(C^1\) functions \((\rho ,\omega )\) defined on a connected interval \(I\subset [0,\infty )\) satisfying the self-similar Euler–Poisson system (1.13) is said to be of Yahil-type if
-
(i)
There exists a unique sonic point \(y_*\in I\);
-
(ii)
For all \(y\in I\), \(\rho (y)>0\) and for all \(y\in I\setminus \{0\}\), \(u(y)<0\).
Recently, the first three authors were able to construct LP solutions in the case \(\gamma =1\) in [12]. The main result of this paper is to show that Yahil solutions exist for the full physical range \(\gamma \in (1,\frac{4}{3})\), including the finite energy range (\(\gamma >\frac{6}{5}\)).
Theorem 1.3
For each \(\gamma \in (1,\frac{4}{3})\), there exists a global, real-analytic, Yahil-type solution \((\rho ,\omega )\) of (1.13), (1.14)–(1.15) with a single sonic point \(y_*\) and satisfying the natural, physical conditions
In addition, both \(\rho \) and \(\omega \) are strictly monotone on their domain of definition:
The proof of this theorem is a consequence of a delicate analysis of the nonautonomous dynamical system (1.13) in the regions separated by the sonic point \(y_*\), presented in Sections 3 and 4 . The combination of results derived in these two sections gives Theorem 1.3 and the short argument is given in Section 5.
The most famous class of special solutions to the radially symmetric Euler–Poisson system are the Lane-Emden steady stars [4], known to be of finite mass and energy if \(\gamma \in [\frac{6}{5},2)\). Their dynamic stability is a classical subject, and in the case \(\gamma >\frac{4}{3}\) they are known to be linearly stable and conditionally nonlinearly stable [27]. By contrast, when \(\gamma \in [\frac{6}{5},\frac{4}{3})\) the Lane-Emden stars are unstable [17, 18]. In the critical case \(\gamma =\frac{4}{3}\), the Lane-Emden stars are spectrally stable, but nonlinearly unstable. The latter statement follows by observing that the above mentioned Goldreich-Weber (henceforth GW) collapsing stars can be chosen initially to be arbitrarily close to the corresponding steady Lane-Emden stars. In fact, due to the mass-critical nature of the problem, the GW collapse is a consequence of an effective separation of variables in the problem, where the solution corresponds to a time-modulated spatial profile, which satisfies a Lane-Emden-like equation. By time-reversal, there also exist global-in-time expanding GW-solutions, whose nonlinear stability was shown in [14].
The solutions constructed in Theorem 1.3 (\(1<\gamma <\frac{4}{3}\)) are very different from the GW solutions (\(\gamma =\frac{4}{3}\)), and owe their existence to a subtle balancing of the three dominant forces in the problem: inertia, pressure, and gravity. A completely different portion of the phase-space is populated by the so-called dust-like collapsing stars, which have been shown to exist in [13]. The solutions constructed in [13] do not honour the scaling invariance implied by (1.5), but are instead to a leading order approximated by the so-called dust solutions, which solve (1.1)–(1.2) without the pressure term p.
As explained above, the most exciting physical feature of the self-similar solutions that we construct is their behaviour in the inner core region, as a possible model of typical stellar collapse scenario. Nevertheless, for completeness we also discuss some global properties of the solution, in particular the size of the total mass and total energy. The solutions constructed in Theorem 1.3 have infinite total mass
as can easily be seen from the asymptotic behaviour (1.15). A short calculation shows that for any fixed \(t<0\), asymptotically as \(r\rightarrow \infty \)
where \(m(t,r) := 4\pi \int _0^r \rho (t,s) s^2{\text {d}}\!s\) is the mass contained in a ball of radius r. On the other hand, the total energy
of the solutions constructed in Theorem 1.3 is finite when \(\gamma \in (\frac{6}{5},\frac{4}{3})\) and infinite for \(\gamma \in (1,\frac{6}{5}]\). This can be easily seen from (1.18) and the asymptotic behaviour \(u(t,r)_{r\rightarrow \infty }\sim r^{\frac{1-\gamma }{2-\gamma }}\) for any fixed \(t<0\), which is established later in Lemma 3.9.
A further surprising outcome of our work is the provision of a new context within which to consider the above mentioned distinction between the LP- and Hunter-type solution. In the context of the isothermal problem (\(\gamma =1\)), the demand that the solution be regular produces two possible algebraic “branches" for the Taylor expansion coefficients at the sonic point. The LP-solution constructed in [12] belongs to one of them, all the Hunter solutions to the other, and the branches intersect at exactly one point. When \(\gamma >1\), we will show that there are two analogous branches. Remarkably, in the formal \(\gamma \rightarrow 1\) limit one of them converges to two portions of the two isothermal branches that together form a continuous curve containing both the LP- and Hunter solutions in the isothermal case. We thus term the solutions coming off this \(\gamma >1\)-branch the Larson–Penston–Hunter- (LPH-) type solutions. We comment on this further in Section 1.1, while the detailed analysis can be found in Section 2.
1.1 Methodology
Due to the importance that the sonic condition will play throughout all of the subsequent analysis, we define here a function
Definition 1.4
(Sonic, supersonic, and subsonic) We say that the flow is subsonic whenever \(G(y;\rho ,\omega )>0\), supersonic when \(G(y;\rho ,\omega )<0\), and sonic when \(G(y;\rho ,\omega )=0\).
For convenience, we denote by \(h(\rho ,\omega )\) the function
The system (1.13) may then be written concisely as
There are two known, explicit solutions to the system (1.21), the Friedmann solution
which satisfies the initial condition (1.14) at the origin, but fails the asymptotic boundary condition (1.15), and the far-field solution,
which satisfies the asymptotic boundary condition (1.15) but fails the initial condition (1.14) . Note that the constant \(k>0\) is well-defined due to \(\gamma <4/3\).
The Friedmann and far-field solutions have sonic points at \(y_F(\gamma )\), \(y_f(\gamma )\), respectively, with
For all \(\gamma \in (1,\frac{4}{3})\), we see that \(0<y_f(\gamma )<y_F(\gamma )<\infty \). Henceforth, we will drop the explicit dependence on \(\gamma \) for \(y_f\) and \(y_F\), emphasising that for each \(\gamma \in (1,\frac{4}{3})\), \([y_f,y_F]\) is a compact interval.
The system of ODE (1.13) is challenging since, as explained above, the flow must pass through a sonic point. The requirement of smoothness at such a point then leads to a number of mathematical difficulties. Generically, if we stipulate that some \(y_*\in (0,\infty )\) be a sonic point, then the flow around that point will not be global. It is only for special values of \(y_*\) where the corresponding solution is in fact globally defined on \([0,\infty )\). In a recent pioneering study of self-similar solutions for the compressible Euler system with the equation of state \(P(\rho )={\frac{\gamma -1}{\gamma }}\rho ^\gamma \) (\(\gamma >1\)), Merle, Raphaël, Rodnianski, and Szeftel [23] systematically developed the existence theory for \(C^\infty \)-self-similar solutions of the Euler flow; the underlying \(2\times 2\) system of ODE is in this case autonomous (in contrast to (1.13)). The smoothness of the self-similar solutions across the sonic point is in fact a crucial ingredient in the proof of their (finite codimension) nonlinear stability [24]. For some related numerical results see the subsequent work [1].
We will seek a solution with sonic point at some \(y_*\in (y_f,y_F)\). Making the formal Taylor expansion around the sonic point \(y_*\), we set
In order to have a smooth solution through \(y_*\), we require that the values \(\rho _0=\rho (y_*)\) and \(\omega _0=\omega (y_*)\) are constrained by the two identities
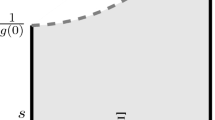
For all \(y_*\in [y_f,y_F]\), we will show below that there is a unique pair \((\rho _0,\omega _0)\) satisfying these two conditions. When we come to solve for the first order coefficients \((\rho _1,\omega _1)\), however, we see that the picture becomes more complicated. In fact, there are again two possible branches from which the coefficients may be chosen. However, as we next explain, it is natural to view the \(\gamma =1\)-case as a degenerate case. Namely, the possible pairs lie on graphs as shown in Fig. 1, parametrised by \(\omega _0\) (equivalently, by \(y_*\)). In this case, the LP solution constructed in [12] lies in the region of the LP branch for which \(\omega _0<\frac{1}{2}\) (equivalently \(y_*>2\)) while the numerically constructed Hunter solutions all lie in the region \(\omega _0>\frac{1}{2}\) (equivalently \(y_*<2\)), compare also [16, Fig. 2].
However, as soon as we increase \(\gamma >1\), a bifurcation occurs. The picture then looks like one of the cases in Fig. 2. The Hunter and LP solutions in the case \(\gamma =1\) actually live on the same branch of the solutions, a feature that is concealed in the isothermal case by the degeneracy that makes the branches coalesce at this value. For \(\gamma >1\), the analogue of the isothermal LP solution is the global solution with a unique sonic point \(y_*\) such that the first order coefficient \(\rho _1\) lies on the joint LP-Hunter (henceforth LPH) branch, and with maximal \(y_*\) (equivalently minimal \(\omega _0\)) - this is the lower (blue) branch in Fig. 2. Such a solution will be shown to correspond to the Yahil-type solution that we are looking to construct, see Definition 1.2.
Once we have correctly identified the branch of solutions on which the LPH-type solution should lie, we seek the globally defined Yahil-type solution whose Taylor expansion at the sonic point is of LPH-type (see Definition 2.12 for the precise meaning). We then proceed in four key steps, as in the earlier work of the first three authors, [12].
Step 1: The first step is to complete the Taylor expansion at each potential sonic point \(y_*\in [y_f,y_F]\) to obtain a local, analytic solution around \(y_*\), denoted by
When clear from the context, we shall occasionally drop the dependence on \(y_*\) in the notation above. In comparison to [12], the convergence of the Taylor series is significantly complicated by the presence of the term \(\rho ^{\gamma -1}\) with its non-integer power. Various technical tricks are employed, using the Faà di Bruno formula, to control the size of the coefficients arising in the expansion, while interval arithmetic is employed to control rigorously the sign of three key quantities (see (2.64)–(2.66) and Appendix C.2 below).
Step 2: Second, we show that the local solution arising from each \(y_*\in [y_f,y_F]\) may be extended globally to the right, remains supersonic, and satisfies the correct asymptotic boundary condition (1.15). This is based on the identification of several invariant regions to the right. Compared with the isothermal case, the key property to show is that the flow remains supersonic, a fact that is no longer trivially true. The asymptotics follow easily from the global existence and bounds obtained.
Step 3: The third, and key, step is to show that there exists a critical value \({\bar{y}}_*\) for which the local analytic solution extends smoothly up to the singular point at the origin with limit \(\omega (y)\rightarrow \frac{4-3\gamma }{3}\) as \(y\rightarrow 0\). Similarly to [12], this \({\bar{y}}_*\) is found as the infimum of a fundamental set
It is here that many of the additional complications arising from the choice \(P(\rho )=\rho ^\gamma \), \(\gamma >1\) make themselves felt. Many of the invariances that were easily available in the case \(\gamma =1\) are either significantly harder to prove or fail altogether. For example, we no longer have that the region \(\{\omega >\frac{1}{2}\}\) is invariant as y decreases. These losses are due to the non-linear structure of the quantities \(h(\rho ,\omega )\) and \(G(y;\rho ,\omega )\). Whereas, for \(\gamma =1\), the sets in phase space in which h or G have a constant sign are simply half-spaces (parametrised by y due to the non-autonomous nature of the system), for \(\gamma >1\), they have a much more complicated structure, with a change in the geometry of the set \(\{h(\rho ,\omega )=0\}\) especially at \(\gamma =\frac{10}{9}\), see Lemma 2.1. This makes itself felt at a number of levels. For example, the sets \(\{\omega '(y)=0\}\) and \(\{\omega ''(y)=0\}\) in the \((\rho ,\omega )\)-plane have an intersection in the region \(\{h<0,G>0\}\), something which cannot happen for \(\gamma =1\), while there are no obvious invariant regions for G either.
To resolve the difficulties caused by these features, we prove a new and stronger property for the relative velocity \(\omega (y;y_*)\) for all \(y_*\in Y\): monotonicity with respect to y. By a careful analysis of the phase plane and a continuity argument, we are able to show that for all \(y_*\in Y\), the function \(\omega (y;y_*)\) is strictly monotone as long as it remains above the Friedmann solution. This property, which is proved in the key Proposition 4.14 below, allows us to propagate a lower bound for the quantity G to the left, preventing the formation of additional sonic points and allowing us to extend the solution as far as the origin, \(y=0\).
Step 4: The final step in the scheme is to show that the solution \((\rho (y;{\bar{y}}_*),\omega (y;{\bar{y}}_*))\) connects smoothly to the origin. More precisely, we show that the solution is analytic on \([0,\infty )\). This is achieved by exploiting again the monotonicity proved for \(\omega \) to demonstrate that \(\omega (\cdot ;{\bar{y}}_*)\) attains the boundary condition \(\omega (0;{\bar{y}}_*)=\frac{4-3\gamma }{3}\) and that the density remains both bounded and monotone. This greatly simplifies the proof of the equivalent step in [12] and removes the need for a topological upper- and lower solution argument of the kind used in [12].
At three points throughout the proof (twice in the Taylor expansion at the sonic point in Propositions 2.9 and 2.10 and then once more in extending the solution to the right in the technical Lemma 3.4), we require an understanding of the sign of key quantities depending polynomially on \(\omega \) and \(\gamma \). As the quantities are significantly too complicated to control by hand, we employ rigorous interval arithmetic, a means of computer-assisted proof that has been used several times recently to resolve open questions in the theory of PDE, see for example [3, 5, 10]. A useful overview of the method and its applications, along with a wealth of references to recent applications, can be found in [11]. Unlike in these works, our use of interval arithmetic is elementary, as we perform most of the analysis directly, only employing interval arithmetic to find bounds for the maxima and minima of certain explicit polynomial quantities.
The paper is organised as follows. Details of the sonic point expansion, the definition of the LPH-type solutions, and the local existence of real-analytic solutions in the vicinity of the sonic point are presented in Section 2. In Section 3 we show that for any \(y_*\in [y_f,y_F]\) there exists an LPH-type solution on \([y_*,\infty )\) and provide a detailed asymptotic description of the solution as \(y\rightarrow \infty \). Section 4 is devoted to the existence problem to the left of the sonic point, and contains some of the key conceptual insights of the paper. In particular, Proposition 4.17 shows that there exists a \(\bar{y}_*\in [y_f,y_F]\) such that the associated local LPH-type solution extends to the whole interval \((0,{\bar{y}}_*]\). The main theorem is then easily obtained by gluing together the constructed left- and right solutions, and the proof is presented in Section 5.
Several technical lemmas are stated and proved in Appendices A and B . Appendix A contains the standard existence and uniqueness argument away from the sonic points, while Appendix B contains the details of an involved combinatorial argument used to prove the existence of real-analytic solution in a neighbourhood of a sonic point. Several of our arguments in Sections 3 and 4 involve complicated multinomial expressions depending on \(\gamma \), \(\omega _0\), and \(y_*\). Their signs play a crucial role in the proofs and we resort to rigorous, computer-assisted proofs by way of interval arithmetic to check the relevant signs. Appendix C contains all the details of such arguments including the associated interval arithmetic code. Finally, Appendix D contains a detailed proof of some of the key continuity properties of the LPH-type solutions, used heavily in Section 4. Such a proof is not standard in the literature, but is quite similar to a related proof in [12], and the details are therefore moved to an appendix.
Data availability All data generated or analysed during this study are included in this published article.
2 The Sonic Point
As discussed in the introduction, our strategy for constructing a solution to the system (1.13) is to begin from a sonic point \(y_*\), obtain a solution locally around this point, and then to extend to both the left and to the right. The purpose of this section is to provide the solution locally around the sonic point. This is a difficult endeavour, as it requires us to first clarify how the condition of smoothness (in fact analyticity) at the sonic point affects our definition of the solution we seek after. This will lead us to the notion of the Larson–Penston–Hunter (LPH) branch. The next step involves a combinatorial argument that shows that locally around the sonic point there indeed exist analytic solutions of the LPH-type.
2.1 The Formal Taylor Expansion
Any smooth solution to the flow (1.13) must satisfy that, at any sonic point, \(y_*\), the values \(\rho _0=\rho (y_*)\), \(\omega _0=\omega (y_*)\) satisfy the constraint
For notational reasons, we define
so that \(h(\rho ,\omega )=0\) corresponds to \(\rho =f_1(\omega )\). The structure of the level set \(h(\rho ,\omega )=0\), equivalently \(\rho =f_1(\omega )\), will play an important role, both in solving for the Taylor coefficients at the sonic point (see Lemma 2.2 below), but also in demonstrating certain crucial invariances along the flow in Section 4.2.
Lemma 2.1
Let \(\gamma \in (1,\frac{4}{3})\) and consider the function \(f_1(\omega )\) on the domain \(\omega \in (0,2-\gamma )\). On this domain, \(f_1\) is uniformly convex with a global minimum at
For \(\gamma \in (1,\frac{10}{9})\), the inequality \(\omega _*<\frac{4-3\gamma }{3}\) holds while the inequality is reversed if \(\gamma \in (\frac{10}{9},\frac{4}{3})\) and equality holds at \(\gamma =\frac{10}{9}\).
In particular, \(f_1'(\omega _*)=0\) and, if \(\gamma \in (1,\frac{10}{9}]\), we have \(f_1'(\omega )\ge 0\) for all \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\) (with strict inequality if at least one of \(\gamma <\frac{10}{9}\) or \(\omega >\frac{4-3\gamma }{3}\) holds). If \(\gamma \in (\frac{10}{9},\frac{4}{3})\), then for \(\omega \in [\frac{4-3\gamma }{3},\omega _*)\), \(f_1'(\omega )<0\) and for \(\omega \in (\omega _*,2-\gamma ]\), \(f_1'(\omega )>0\).
The proof is by a simple, direct calculation, and so we omit it.
Figure 3 plots the level set \(h(\rho ,\omega )=0\) in the \((\rho ,\omega )\) plane for the cases \(\gamma =1.08,\frac{10}{9},1.2\) and \(\omega \in \big [\frac{4-3\gamma }{3},2-\gamma \big ]\). The minimum for \(\gamma \ge \frac{10}{9}\) occurs at \(\omega =\sqrt{\frac{(\gamma -1)(2-\gamma )}{2}}\ge \frac{4-3\gamma }{3}\) as stated in Lemma 2.1.
Lemma 2.2
For any \(y_*\in [y_f,y_F]\), where \(y_f\), \(y_F\) are defined as in (1.24), there exists a unique pair \((\rho _0(y_*),\omega _0(y_*))\) with \(\rho _0(y_*)\ge {\underline{\rho }}>0\), where \({{\underline{\rho }}}\) depends only on \(\gamma \), satisfying
Moreover, the mapping \(y_*\mapsto \omega _0(y_*)\) is a strictly decreasing function for \(y_*\in [y_f,y_F]\) with
Proof
We begin by recalling the definition of the function \(f_1(\omega )\) from (2.2) and define also a function \(f_2(\omega ;y_*)\) so that
As discussed above, the constraint \(h(\rho _0,\omega _0)=0\) is equivalent to \(\rho _0=f_1(\omega _0)\), while we see easily that \(G(y_*,\rho _0,\omega _0)=0\) if and only if \(\rho _0=f_2(\omega _0;y_*)\). So we seek \(\omega _0(y_*)\) such that \(f_1(\omega _0(y_*))=f_2(\omega _0(y_*);y_*)\). This value is then defined to be \(\rho _0(y_*)\). We easily check that
Moreover, as \(y_f\), \(y_F\) are the sonic points corresponding to the far-field and Friedmann solutions, respectively, we also know that
Noting then that
we see that for any \(y_*\in (y_f,y_F)\), we have
and so
Thus, by the intermediate value theorem, we see that \(\omega _0(y_*)\) exists as required, and hence so does \(\rho _0(y_*)\). The uniqueness follows from the following observations:
Thus at any point \(\omega >0\) such that \(f_2(\omega ;y_*)\ge f_1(\omega )\), we have
and so the uniqueness follows easily. The monotonicity properties of \(y_*\mapsto \omega _0(y_*)\) then follow directly from (2.6) and \(f_{2,\omega }(\omega _0(y_*),y_*)-f_{1,\omega }(\omega _0(y_*))>0\) as
To find the uniform lower bound \(\rho _0\ge {\underline{\rho }}>0\), we note that \(\rho _0=f_1(\omega _0)\). As \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\), we easily obtain \(f_1(\omega _0)\ge \frac{(4-3\gamma )(\gamma -1)}{4\pi }>0\) as required. \(\quad \square \)
We seek a local solution around a sonic point \(y_*\in [y_f,y_F]\) via a Taylor expansion. To that end, we now derive the necessary relations for the coefficients of the expansion. Suppose we have an analytic solution of system (1.13). Then, after rearranging, we have
We write the formal power series
By Lemma 2.2, we see that a choice of \(y_*\in [y_f,y_F]\) defines a unique pair of values \((\rho _0,\omega _0)\) for the Taylor series. We define the obvious notation
We recall the Faà di Bruno formula for the N-th derivative of a composition,
where
Taking \(f(x)=x^{\gamma -1}\), \(g(y)=\rho (y)\) in this formula, we therefore obtain
and thus we have the power series
Throughout this section, for \(N<0\), we set coefficients \(\rho _{N},\omega _N\) etc to be zero.
Lemma 2.3
For each \(N\ge 1\), the power series coefficients satisfy the relations
Proof
We begin the proof by noting the identities, for a general power series,
where we define \(b_{N}=0\) for any \(N<0\).
Step 1: Derive (2.15).
We begin by substituting the power series into (2.7). The left hand side of this equation then becomes
The right hand side of (2.7) becomes
Equating the N-th order terms of (2.17) and (2.18), we have the claimed relation (2.15), that is, for all \(N\in {\mathbb {N}}\cup \{0\}\),
Step 2: Derive (2.16).
To prove from (2.8), we begin by expanding the term \(\frac{4-3\gamma -3\omega }{y}\big (\gamma \rho ^{\gamma -1}-y^2\omega ^2\big )\) by noting first that
Then we find
Thus, expanding (2.8) and equating terms of the same order, we find
This is (2.16). \(\square \)
Before studying the solvability of this system for the higher order coefficients, we first collect a pair of identities satisfied by the first order coefficients, \((\rho _1,\omega _1\)).
Lemma 2.4
(First order Taylor coefficients) Let \(\gamma \in (1,\frac{4}{3})\) and consider the formal Taylor expansion (2.9). Let
Then the pair (R, W) satisfies the following system of algebraic equations:
with the additional constraint
Proof
In the case \(N=1\), we note that \(P_1=(\gamma -1)\rho _0^{\gamma -2}\rho _1\), \((\omega ^2)_1=2\omega _1\omega _0\) etc to find from (2.15)
where we have used (2.1) twice.
From (2.16) we get
where we have used (2.1) again. Rearranging (2.25), we can use (2.1) further to write
Thus, using also the sonic condition to replace \(\gamma \rho _0^{\gamma -2}=\frac{y_*^2\omega _0^2}{\rho _0}\) and dividing through by \(\rho _0\), we recall the definitions of R, W and arrive at
that is, we have (2.22).
Working now from (2.26), we rearrange to find
which is exactly (2.23).
To show (2.24), we work from (1.21). Multiplying the first equation by \(\rho \), the second by \(\omega \) and summing, we obtain
Substituting in the formal Taylor expansion and grouping the terms at order zero, we find
Multiplying through by \(\frac{y_*}{\rho _0}\) and recalling (2.21) we arrive at (2.24). \(\square \)
Remark 2.5
The coefficients of the quadratics in (2.22)–(2.23) depend only on \(\gamma \) and on \(\omega _0\) (hence also on \(y_*\)).
Our next lemma establishes the key recursive relation that will allow us to compute the N-th order Taylor coefficients in terms of \((\rho _k,\omega _k)\), \(0\le k\le N-1\).
Lemma 2.6
Let \(N\ge 2\) and define the matrix \({\mathcal {A}}_N\) by
where the matrix coefficients \({\mathcal {A}}^N_{ij}\), \(i,j\in \{1,2\}\) depend on N, \(\gamma \), \(\omega _0\), \(\rho _1\) and \(\omega _1\) and are given explicitly by (2.42)–(2.45) below. Then the coefficients \((\rho _N,\omega _N)\) in the formal series expansion (2.9) satisfy the algebraic equation
where the polynomials \({\mathcal {F}}_N\) and \({\mathcal {G}}_N\) are given by (2.33) and (2.40) below.
Proof
We begin from (2.15) and group the terms on the left hand side as follows.
where
and we have applied the definition of \(P_j\) to isolate the term with a \(\rho _N\) contribution as
and also recalled
Studying the right hand side of (2.15), we expand to isolate terms at order N and then apply (2.1) to eliminate terms with factors of \(\frac{4\pi }{4-3\gamma }\) as follows:
where
where we have applied (2.1). Thus, as (2.30) is equal to (2.31), we rearrange to arrive at
Thus we have found
Considering now (2.16), we expand the left hand side as above as
where
where we have applied the definition of \(P_j\) to isolate the term with a \(\rho _N\) contribution.
Working with the right hand side of (2.16), we have
where
Grouping the terms on the first two lines here, we again expand \(P_N\) to find the contribution
where we have again applied (2.1). Setting
we substitute (2.39) back into (2.37) and equate with (2.35) to arrive at
Thus we have
So we have found the claimed identity with
\(\square \)
Lemma 2.7
Consider the formal series expansion (2.9) and recall the definitions
Then the map \(N\mapsto \det ({\mathcal {A}}_N)\) is a quadratic polynomial of the form
where \(A_0\), \(A_1\), and \(A_2\) are \((\gamma ,\omega _0,R,W)\)-dependent functions given by the formulas:
Proof
We begin with the following identity. Multiplying (2.22) by \((\gamma -1)\omega _0^2\) and (2.23) by \(2\omega _0\) and summing, we get
Now we expand the determinant as
We first re-group the quadratic terms in (R, W) and substitute (2.51) to get
Substituting this into (2.52), we group the terms by order in N as
where
and \(A_0\) is the remainder. Simplifying these expressions and that for \(A_0\) results in (2.48)–(2.50) to conclude the proof. \(\square \)
2.2 Branch Selection
To find solutions that are smooth through the sonic point, we must first calculate the first order Taylor coefficients \((\rho _1,\omega _1)\) as functions of the parameters \(\gamma \) and \(y_*\).
Lemma 2.8
(The two solution branches) Let \(\gamma \in (1,\frac{4}{3})\) be given and let \(y_*\in [y_f(\gamma ),y_F(\gamma )]\). There exist exactly two pairs \((R_i,W_i)\), \(i=1,2\) solving the system of algebraic equations (2.22), (2.23), (2.24). The functions \(R_i\) are given by
where
is strictly positive for all \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\), \(\gamma \in (1,\frac{4}{3})\).
For any \(i=1,2\), \(W_i\) is determined by \(R_i\) through the formula
Proof
By rearranging (2.22), we see
Rearranging (2.24) to solve for W as
we obtain the claimed relation (2.57). We then substitute this into (2.58) to obtain the following quadratic for R:
with roots \(R_1\), \(R_2\) as claimed in (2.54)–(2.55) from the quadratic formula. We postpone the verification that \(s(\omega _0)>0\) to Appendix C.1.
One can check that equation (2.23) is also satisfied by these roots by similarly substituting (2.57) into (2.23) then simplifying. This again yields a quadratic in R which, on inspection, turns out to be exactly (2.60) up to a factor of \(\omega _0\), and hence has the same roots. \(\square \)
We will see in the following Subsection 2.3 that the physically relevant solution branch is that given by \((R_1,W_1)\). We therefore collect some useful estimates on the coefficients derived from this branch.
Proposition 2.9
Let \(\gamma \in (1,\frac{4}{3})\) be given and let \(y_*\in [y_f(\gamma ), y_F(\gamma )]\) and consider the branch \((R_1,W_1)\) defined in Lemma 2.8. Then
Moreover, if \(\gamma \in [\frac{10}{9},\frac{4}{3})\), then the upper bound on \(R_1\) may be taken to satisfy
where the inequality is strict provided either \(\gamma >\frac{10}{9}\) or \(y_*<y_F\).
Finally,
Proof
The proof relies in part on interval arithmetic and it is presented in detail in Appendix C.1. \(\square \)
Proposition 2.10
(Positivity of \(\det {\mathcal {A}}_N\)) Let \(\gamma \in (1,\frac{4}{3})\) be given and let \(y_*\in [y_f(\gamma ), y_F(\gamma )]\). Let \(A_0,A_1,A_2\) be functions of \(\rho _0,\omega _0, R,W\) given by (2.48)–(2.50) and assume that \(R=R_1\) and \(W=W_1\), where the branch \((R_1,W_1)\) is defined in Lemma 2.8.
-
(i)
The following inequalities hold:
$$\begin{aligned} A_2&>0, \end{aligned}$$(2.64)$$\begin{aligned} 4A_2+A_1&>0, \end{aligned}$$(2.65)$$\begin{aligned} 4A_2+2A_1+A_0&>0 \end{aligned}$$(2.66) -
(ii)
There exist constants \(c_1,c_2>0\), depending only on \(\gamma \), so that
$$\begin{aligned} c_1N^2\le \det {\mathcal {A}}_N\le c_2N^2, \ \ N\ge 2. \end{aligned}$$(2.67)In particular, the matrix \({\mathcal {A}}_N\) is invertible for all \(N\ge 2\) and the formal Taylor coefficients \((\rho _N,\omega _N)\) are well-defined through the formula
$$\begin{aligned} \begin{pmatrix} \rho _N\\ \omega _N \end{pmatrix}={\mathcal {A}}_N^{-1}\begin{pmatrix} {\mathcal {F}}_N\\ {\mathcal {G}}_N \end{pmatrix}, \ \ N\ge 2, \end{aligned}$$(2.68)where the source terms \({\mathcal {F}}_N\), \({\mathcal {G}}_N\) are defined in Lemma 2.6.
-
(iii)
There exists a constant \(\beta _0=\beta _0(y_*, \gamma )>0\) such that
$$\begin{aligned} | \rho _N|\le \frac{\beta _0}{N} \left( |{\mathcal {F}}_N| + \frac{1}{N} |{\mathcal {G}}_N| \right) \end{aligned}$$(2.69)$$\begin{aligned} |\omega _N| \le \frac{\beta _0}{N} \left( |{\mathcal {G}}_N| + \frac{1}{N} |{\mathcal {F}}_N| \right) . \end{aligned}$$(2.70)
Proof
Proof of part (i). The proof of (2.64)–(2.66) relies on interval arithmetic and it is presented in detail in Appendix C.2.
Proof of part (ii). Since \(\det {\mathcal {A}}_2=y_*^2\big (4A_2+2A_1+A_0\big )>0\) by (2.66) and, for \(N\ge 2\), \(\frac{{\text {d}}\!}{{\text {d}}\!N}\det {\mathcal {A}}_N=y_*^2\big (2NA_2+A_1\big )\ge y_*^2\big (4A_2+A_1\big )\), it follows from (2.65)–(2.66) that
These estimates then easily imply (2.67). Claim (2.68) is an obvious consequence of the invertibility of \({\mathcal {A}}_N\) and Lemma 2.6.
Proof of part (iii). From (2.68) it follows that
and thus (2.69)–(2.70) follow directly from (2.67) and (2.42)–(2.45). \(\square \)
2.3 Larson–Penston–Hunter- (LPH-) Type Solutions
In order to distinguish the relevant solution branch for the first order Taylor coefficients, we compare directly to the situation in the case \(\gamma =1\).
Lemma 2.11
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f(\gamma ),y_F(\gamma )]\), and consider the functions \(R_i\), \(i=1,2\) as in Lemma 2.8 as functions of both \(\omega _0(y_*)\) and \(\gamma \). As \(\gamma \rightarrow 1\), these coefficients satisfy the limits
Proof
The identities for the limit as \(\gamma \rightarrow 1^+\) for \(R_i\) follow directly from the identities (2.54)–(2.55). \(\square \)
Thus, to maintain compatibility with the LP solution in the case \(\gamma =1\), we note that, in that case, the sonic point lies in the interval (2, 3) with \(\frac{\rho '(y_*)y_*}{\rho (y_*)}=-1\) (compare [12]), and hence the LP-type branch, for \(\gamma >1\), should be chosen to be the 1-branch. In this case, we find that the limit of \(W_1(\omega _0)\) as \(\gamma \rightarrow 1\) is \(1-2\omega _0\), again in compatibility with the \(\gamma =1\) case resolved in [12].
This motivates the following definition.
Definition 2.12
(Larson–Penston–Hunter (LPH) type solutions) Let \(\gamma \in (1,\frac{4}{3})\) be given and let \(y_*\in [y_f(\gamma ),y_F(\gamma )]\). We say that a sequence \((\rho _N,\omega _N)\), \(N\in {\mathbb {N}}\) associated with a formal power series expansion
is of Larson–Penston–Hunter (LPH) type if the following properties are satisfied
-
(i)
$$\begin{aligned} G(y_*,\rho _0,\omega _0)=0,\quad h(\rho _0,\omega _0)=0. \end{aligned}$$(2.77)
-
(ii)
$$\begin{aligned} \rho _1:=\frac{\rho _0R_1}{y_*}, \ \ \ \ \omega _1:=\frac{W_1}{y_*}, \end{aligned}$$(2.78)
where the pair \((R_1,W_1)\) corresponds to the branch defined by (2.54) and (2.57) from Lemma 2.8.
-
(iii)
For any \(N\ge 2\), the coefficients \((\rho _N,\omega _N)\) satisfy the recursive relation (2.68).
If the series (2.76) converge, we say that the functions \(\rho \) and \(\omega \) are of LPH-type.
Remark 2.13
As shown in Proposition 2.10, the matrix \({\mathcal {A}}_N\) defined in Lemma 2.6 is indeed invertible for all \(N\ge 2\) and therefore for any LPH-type sequence the coefficients \((\rho _N,\omega _N)\), \(N\ge 2\) are therefore uniquely determined as functions of \(\rho _0,\omega _0,\rho _1,\omega _1\).
2.4 The Induction Argument and the Series Convergence
In order to prove the convergence of the formal power series (2.9) we prove the crucial lemma, which establishes favourable growth bounds for the coefficients \((\rho _N,\omega _N)\). The proof is based on involved combinatorial arguments that are presented in Appendix B, culminating in Lemma B.6.
Lemma 2.14
Let \(\gamma \in (1,\frac{4}{3})\) and \(\alpha \in (1,2)\) be given. Let \((\rho _N,\omega _N)\), \(N\in {\mathbb {N}}\) be the coefficients in the formal Taylor expansion of \(\rho ,\omega \) about \(y=y_*\) given by Proposition 2.10. Then there exists a constant \(C>1\) such that for any \(y_*\in [y_f(\gamma ),y_F(\gamma )]\) the bounds
hold for all \(N\ge 2\).
Proof
We use mathematical induction to prove the lemma. When \(N=2\) clearly there exists a constant \({\bar{C}}={\bar{C}}(y_*,\alpha )>0\) such that the claimed bounds hold true as the recursive relation (2.68) defining \((\rho _2,\omega _2)\) involves only products of continuous functions composed with \((y_*,\rho _0,\omega _0,\rho _1,\omega _1)\), all of which are bounded.
Suppose now that for some \(N\ge 3\), (2.79)–(2.80) hold for all \(2\le m\le N-1\). This implies that the assumptions (B.30)–(B.31) hold true and thus by Lemma B.6 we conclude that (B.32)–(B.33) hold. Therefore, from Proposition 2.10 and (B.32)–(B.33) we obtain
for some universal constant \(c>0\). Similarly,
It is now clear that we can choose \(C=C(\gamma ,y_*)\) sufficiently large so that the claimed estimates (2.79)–(2.80) hold at N. Since \(y_*\) ranges over a compact interval and all the constants involved vary continuously in \(y_*\), we may choose the constant C above uniformly in \(y_*\in [y_f(\gamma ),y_F(\gamma )]\). We conclude by induction on N. \(\square \)
Theorem 2.15
Let \(\gamma \in (1,\frac{4}{3})\) be given and for any \(y_*\in [y_f(\gamma ),y_F(\gamma )]\) consider the sequence \((\rho _N,\omega _N)\), \(N\in {\mathbb {N}}\) which corresponds to the formal Taylor coefficients associated with an LPH-type solution. Then there exists a \(\nu >0\) independent of \(y_*\) such that the series
converge absolutely and the functions \((\rho (\cdot ;y_*),\omega (\cdot ;y_*))\) are real analytic solutions to (1.13) on the interval \((y_*-\nu ,y_*+\nu )\). Moreover, \(y_*\) is a sonic point for the flow, there are no other sonic points on the interval, and the solutions are continuous with respect to \(y_*\in [y_f,y_F]\).
Proof
Let \(\alpha \in (1,2)\) be fixed. By Lemma 2.14 there exists a constant \(C=C(\gamma ,\alpha )\) such that
and therefore the formal power series \(\sum _{N=0}^\infty \rho _N (y-y_*)^N\) converges absolutely as long as \(|y-y_*|<\nu \), for any \(0<\nu <\frac{1}{C}\). Similarly, the power series \(\sum _{N=0}^\infty \omega _N (y-y_*)^N\) also converges absolutely as long as \(|y-y_*|<\nu \) and therefore the function defined by the power series is in fact real analytic. Recalling (1.19) we have
where we have used the sonic condition \(G(y_*,\rho ,\omega )=0\) in the second and the third line, and the notation \((R_1,W_1)\), see Lemma 2.8. Now observe that \(\omega _0>0\) by Lemma 2.2, and \(R_1<0\), \(W_1\ge 0\) by Proposition 2.9. Therefore \((\gamma -1)\omega _0 R_1 - 2 - 2W_1 <0\) and therefore, upon possibly choosing a smaller \(\nu >0\), it follows that \(G(y;\rho ,\omega )\) is strictly positive for \(y\in (y_*-\nu ,y_*)\) and strictly negative for \(y\in (y_*,y_*+\nu )\). In particular, the right-hand side of (1.13) is well-defined and it is straightforward to verify that \((\rho ,\omega )\) is a solution to (1.13). \(\square \)
In the final proposition of this section, we collect some remaining facts concerning the LPH Taylor expansions.
Proposition 2.16
Let \(\gamma \in (1,\frac{4}{3})\). For \(y_*\in [y_f(\gamma ),y_F(\gamma )]\), the following properties hold at the sonic point:
-
(i)
The branch \((R_1,W_1)\) that we take for the re-scaled first derivatives at the sonic point \(y_*\) satisfies \((R_1,W_1)(y_f)=(-\frac{2}{2-\gamma },0)\), \(W_1(y_*)>0\) for all \(y_*\in (y_f,y_F]\).
-
(ii)
The local LPH-type solution obtained by Theorem 2.15 with \(y_*=y_f\) is exactly the far-field solution
$$\begin{aligned} (\rho (y;y_f),\omega (y;y_f))\equiv (\rho _f(y),\omega _f(y))=(ky^{-\frac{2}{2-\gamma }},2-\gamma ). \end{aligned}$$ -
(iii)
The local LPH-type solution obtained by Theorem 2.15 with \(y_*=y_F\) is not the Friedmann solution: \((\rho (\cdot ;y_F),\omega (\cdot ;y_F))\ne (\rho _F,\omega _F)\).
Proof
(i) By Lemma 2.2, we know \(\omega _0(y_*)\in [\frac{4-3\gamma }{3},2-\gamma ]\). Then, by Proposition 2.9, we have \(W_1(\omega _0)\ge 0\) for all \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\) with equality if and only if \(\omega _0=2-\gamma \). In addition, \(R_1(2-\gamma )=-\frac{2}{2-\gamma }\) by direct computation from (2.54).
(ii) To see that the solution obtained at \(y_f\) is the far-field solution, it is enough to note that \(\rho _0\) is uniquely determined by \(y_*\) also through the relation \(\rho _0=f_1(\omega _0(y_*))\), and hence we have that \(\omega _0(y_f)=2-\gamma =\omega _f(y_f)\) and \(\rho _0(y_f)=\rho _f({y}_f)\). Thus the solution locally around the sonic point is determined entirely by the choice of the branch \((R_1,W_1)\) for the first order terms in the Taylor expansion. As \(W_1=0\), \(R_1=-\frac{2}{2-\gamma }\) are equal to the corresponding values for the far-field solution, the Taylor expansions of the solution derived from the choice \(y_*=y_f\) and the far-field solution are equal. Thus the solutions are locally equal (as both are analytic functions) and, by uniqueness theory for the ODE system away from the sonic point and \(y=0\), therefore globally equal on all of \((0,\infty )\).
(iii) As in item (i), we know that \(W_1(y_F)>0\) by Proposition 2.9, hence \(\omega _1(y_F)>0\) also. As the Friedmann solution satisfies \(\omega _F'(y)\equiv 0\) for all y, the two solutions are not equal. \(\square \)
2.5 Local Theory Around \(y=0\)
We now explain how to construct a local solution starting from \(y=0\) to the right, again via Taylor expansion. To that end, we write the formal power series
and derive the hierarchy of recurrence relations for the coefficients, by analogy to Lemmas 2.3 and 2.6 . We continue to use the notation (2.10) and by analogy to (2.14) we have the formal expansion
where, recalling (2.12) we have by the Faa di Bruno formula
Lemma 2.17
Suppose the pair \(({\bar{\rho }},{\bar{\omega }})\) is an analytic solution of system (1.13) such that \({\bar{\omega }}_0={\bar{\omega }}(0)=\frac{4-3\gamma }{3}\) and \({\bar{\rho }}_0>0\). Then the coefficients \(({\bar{\rho }}_N,{\bar{\omega }}_N)\) satisfy the following recurrence relations
where for any \(N\ge 1\) we have
Proof
The proof is a routine exercise. We simply substitute the formal expansion (2.85) into (2.7)–(2.8) and regroup the coefficients to isolate the terms in front of \(y^{N-1}\) by analogy to Lemma 2.3. \(\square \)
Remark 2.18
We observe that the expressions \(\overline{{\mathcal {F}}}_N,\overline{{\mathcal {G}}}_N\) depend only on the first \(N-1\) coefficients \(({\bar{\rho }}_k,{\bar{\omega }}_k)\), \(0\le k\le N-1\), and therefore the infinite sequence \(({\bar{\rho }}_N,{\bar{\omega }}_N)_{N\in {\mathbb {N}}}\) is well-defined.
The main result of this subsection is the local-in-y well-posedness result in a small right neighbourhood of the origin.
Theorem 2.19
Let \(\gamma \in (1,\frac{4}{3})\), \({\bar{\omega }}_0=\frac{4-3\gamma }{3}\) be given, and for any \({\bar{\rho }}_0>0\) consider the sequence \(({\bar{\rho }}_N,{\bar{\omega }}_N)\), \(N\in \mathbb N\) which is obtained as the solution of the recurrence relations (2.88)–(2.91). Then there exists a \(\nu >0\) such that the series
converge absolutely and the functions \(({\bar{\rho }}(\cdot ;{\bar{\rho }}_0),{\bar{\omega }}(\cdot ;{\bar{\rho }}_0))\) are real analytic solutions to (1.13) on the interval \([0,\nu )\).
Proof
The proof is similar, yet simpler than the proof of Theorem 2.15. One can show using induction, in full analogy to the proof of Lemma 2.14, that there exists a constants \(C>1\) and \(\alpha \in (1,2)\) such that the bounds \( \left| {\bar{\rho }}_N\right| \le \frac{C^{N-\alpha }}{N^3} \) and \( \left| {\bar{\omega }}_N\right| \le \frac{C^{N-\alpha }}{N^3} \) hold for all \(N\ge 2\). This in return gives the desired convergence of the infinite series in the statement of the theorem. \(\square \)
Proposition 2.20
Let \(\gamma \in (1,\frac{4}{3})\), \({\bar{\rho }}_0\ge \frac{1}{6\pi }\) be given and suppose that \((\rho _1,\omega _1)\) and \((\rho _2,\omega _2)\) are two \(C^1\) solutions to (1.13) on an interval \([0,\nu ]\) with initial condition \(\rho _1(0)=\rho _2(0)={\bar{\rho }}_0\) and \(\omega _1(0)=\omega _2(0)=\frac{4-3\gamma }{3}\). Suppose moreover that \(\rho _j\ge c_0>0\) and \(\gamma \rho _j^{\gamma -1}-y^2\omega _j^2\ge c_0>0\) on \([0,\nu ]\) for both \(j=1,2\). Then \((\rho _1,\omega _1)=(\rho _2,\omega _2)\) on \([0,\nu ]\).
Proof
Recalling (1.19) and (1.20) we first note that the function
is locally Lipschitz for \((\rho ,\omega )\) in bounded sets such that \(\rho \ge c_0>0\) and uniformly for \(y\in [0,\nu ]\). Thus, as we have uniform bounds on \(\rho _j\) and \(\omega _j\) by continuity on the closed interval \([0,\nu ]\), we may obtain upper bounds:
We now take the difference of the ODE system (1.13) for \((\rho _1,\omega _1)\) and for \((\rho _2,\omega _2)\) and see
Multiplying the first equation by \((\rho _1-\rho _2)\) and the second equation by \((\omega _1-\omega _2)\) and summing, we obtain
where we have applied the local Lipschitz bounds (2.92) and the Cauchy-Young inequality. As \((\rho _1-\rho _2)(0)=(\omega _1-\omega _2)(0)=0\), we conclude by Gronwall’s inequality that \((\rho _1,\omega _1)\equiv (\omega _1,\omega _2)\) on \([0,\nu ]\). \(\square \)
3 Solution to the Right of the Sonic Point
Now that we have established the existence of a local solution to (1.13) around each choice of sonic point \(y_*\in [y_f,y_F]\), we show in this section that the local solution can be extended to the right on the whole interval \((y_*,\infty )\) while remaining strictly supersonic and satisfying suitable asymptotics. For \(y_*=y_f\), we know from Proposition 2.16 the obtained solution is simply the far-field solution \((\rho _f,\omega _f)\) which is globally defined and supersonic for all \(y>y_f\). We will therefore restrict in the sequel to the case \(y_*\in (y_f,y_F]\).
The strategy of the section is to identify certain inequalities that propagate along the flow to the right and provide qualitative control on the solutions. Because the system (1.13) is non-autonomous, we cannot argue simply from a fixed phase plane analysis, but instead we make use of dynamical arguments that prevent the crossing of certain critical values by particular quantities fundamental to the flow. After a number of technical lemmas, we prove the key continuation estimates in Proposition 3.5. We then demonstrate that the flow remains strictly supersonic to the right and so deduce that it exists globally on \((y_*,\infty )\) in Lemma 3.8. Finally, in Lemmas 3.9 and 3.10, we study the asymptotics and monotonicity of the solution.
For each \(y_*\in [y_f(\gamma ),y_F(\gamma )]\), let \((\rho ,\omega )=(\rho (\cdot ;y_*),\omega (\cdot ;y_*))\) be the local LPH-type solution of Theorem 2.15. We define the maximal extension time to the right as
where we recall the definition of supersonicity from Definition 1.4.
The first lemma in this section states and proves the basic estimates that we will use to propagate the solution and verifies that they hold in a small neighbourhood of the sonic point.
Lemma 3.1
(Initial inequalities) Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in (y_f,y_F]\) (recall that we suppress the dependence of \(y_f\), \(y_F\) on \(\gamma \) where clear) and let \((\rho ,\omega )\) be the unique LPH-type solution to (1.13) to the right of \(y_*\) given by Theorem 2.15. Then there exists \({{\bar{\nu }}}>0\) (depending on \(y_*\)) such that for \(y\in (y_*,y_*+{{\bar{\nu }}})\), the strictly supersonic flow satisfies also the inequalities
Proof
By Theorem 2.15, the existence of \(\nu >0\) such that the solution remains supersonic on \((y_*,y_*+\nu )\) is clear. Moreover, by Lemma 2.2, we know that if \(y_*\in (y_f,y_F)\), we have \(\frac{4-3\gamma }{3}<\omega (y_*)<2-\gamma \), and hence, as \(\omega \) is continuous on \([y_*,y_*+\nu ]\), there exists \({{\bar{\nu }}}\in (0,\nu )\) such that
On the other hand, if \(y_*=y_F\), then \(\omega (y_*)=\frac{4-3\gamma }{3}\) and, by Proposition 2.9, \(\omega '(y_*)>0\), hence by possibly shrinking \({{\bar{\nu }}}\), we again have the claimed estimate.
Similarly, by Proposition 2.9 and smoothness of the flow, by possibly shrinking \({{\bar{\nu }}}\), we retain the final inequality of (3.2)
Finally, we check the second condition in (3.2) through the following observation:
for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma )\), where we have used \(\rho _0=f_1(\omega _0)\) (compare (2.2)) in the second line to eliminate \(\rho _0\), and observe that the quadratic function of \(\omega _0\) in the parentheses factorises as
to deduce the sign. By again exploiting continuity of the flow and possibly shrinking \({{\bar{\nu }}}\), we conclude. \(\square \)
We will also need the following two lemmas.
Lemma 3.2
Let \(\gamma \in (1,\frac{4}{3})\). For any \(C^1\) solution \((\rho ,\omega )\) of (1.13), the following identities hold along the flow at any point \(y>0\) such that y is not a sonic point:
Proof
Identity (3.4) is a trivial consequence of (1.21). Identity (3.5) follows from using (3.4) in the following:
and grouping the \(\omega \) terms.
To obtain (3.6), we again apply (3.4) to find
and group terms. The proof of (3.7) is similar. \(\square \)
Lemma 3.3
Let \(\gamma \in (1,\frac{4}{3})\), let \((\rho ,\omega )\) be a \(C^1\) solution of (1.13) and suppose that \(y>0\) is not a sonic point of the flow.
-
(i)
For any \(m\ge 0\), the derivative of \(\rho \) may be expressed through the following relation:
$$\begin{aligned} \frac{\rho 'y}{\rho }+\frac{m}{2-\gamma }=y^{-\frac{2(\gamma -1)}{2-\gamma }}\frac{P_m(y,\rho ,\omega )}{y^2\omega ^2-\gamma \rho ^{\gamma -1}}, \end{aligned}$$(3.8)where
$$\begin{aligned} \begin{aligned} P_m(y,\rho ,\omega )&= -\frac{4-m-2\gamma }{2-\gamma }y^{\frac{2}{2-\gamma }}\omega ^2-(\gamma -1)y^{\frac{2}{2-\gamma }}\big (\omega +(2-\gamma )\big )\\&\quad -\frac{m}{2-\gamma }\gamma \big (y^{\frac{2}{2-\gamma }}\rho \big )^{\gamma -1}+\frac{4\pi y^{\frac{2}{2-\gamma }}\omega \rho }{4-3\gamma }. \end{aligned}\end{aligned}$$(3.9)We usually suppress the explicit dependence of \(P_m\) on \((\rho ,\omega )\), writing instead \(P_m(y)=P_m(y,\rho (y),\omega (y))\) where clear.
-
(ii)
At any point \(y_1\) at which the flow is smooth and not sonic and where \(P_m(y_1)=0\), the derivative of \(P_m\) satisfies the identity
$$\begin{aligned} \begin{aligned} {P}_m'(y_1)=\frac{y_1^{\frac{2}{2-\gamma }}}{y_1\omega (y_1)}Q_m\Bigg (\omega (y_1),\frac{\gamma \rho (y_1)^{\gamma -1}}{y_1^2}\Bigg ), \end{aligned}\end{aligned}$$(3.10)where
$$\begin{aligned} \begin{aligned} Q_m(\omega , {\mathcal {R}})&=\Bigg ( \bigg (1-\frac{\omega }{2-\gamma }\bigg )\Bigg (-\frac{4-m-2\gamma }{2-\gamma }(4-3\gamma )\omega ^2+(\gamma -1)(4-3\gamma )(2-\gamma )\Bigg )\\ {}&\quad \ \ \ -\frac{2(4-m-2\gamma )(m-1)\omega ^3}{(2-\gamma )^2}-\frac{m(\gamma -1)}{2-\gamma }\omega ^2-2(\gamma -1)\omega \\ {}&\quad \ \ \ +{\mathcal {R}}\frac{m}{(2-\gamma )^2}\bigg ((4-3\gamma )(2-\gamma )-\omega \big (4-3\gamma +(\gamma -1)(2-m)\big )\bigg )\Bigg )\Bigg |_{y_1}. \end{aligned} \end{aligned}$$(3.11)
Proof
(i) To show (3.8), we let \(m\ge 0\). Then, rearranging the first equation of (1.13), we find
and pulling out a factor of \(y^{-\frac{2(\gamma -1)}{2-\gamma }}\) leaves us with the claimed identity.
(ii) By (3.5)–(3.7), as the flow is smooth at \(y_1\),
From the identity \(P_m(y_1)=0\), we rearrange to find
where all functions are evaluated at \(y_1\). In addition, by (3.8), as \(P_m(y_1)=0\) we also have \(\frac{\rho 'y}{\rho }=-\frac{m}{2-\gamma }\).
Substituting (3.14) and \(\frac{\rho 'y}{\rho }=-\frac{m}{2-\gamma }\) into (3.13), we have
which yields the required inequality after factoring out \(\omega ^{-1}\). \(\square \)
With these identities, we will show that as long as the flow remains strictly supersonic, the inequalities of Lemma 3.1 above also hold strictly. For the proof, we will require also the following technical lemma containing properties of the functions \(Q_m\).
Lemma 3.4
Define the functions
where we recall the definition of \(Q_m\) from Lemma 3.3. Then, for any \(\gamma \in (1,\frac{4}{3})\), there exists \(\delta _0>0\) such that for all \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\), we have
The proof is deferred to Appendix C.3.
We are now able to state and prove the continuation estimates for the extension of the LPH-type solutions on their maximal supersonic interval of existence, \((y_*,y_{\max }(y_*))\).
Proposition 3.5
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\), and let \((\rho ,\omega )\) be the extension of the unique LPH-type solution obtained from Theorem 2.15 to \((y_*,y_{\max }(y_*))\). Then the following strict inequalities hold on the whole interval \((y_*,y_{\max }(y_*))\):
Moreover, on this interval, we retain \(\rho >0\).
Proof
We begin the proof by observing that the upper and lower bounds on \(\rho '\) of (3.18) guarantee that as long as the flow lives to the right of \(y_*\) and satisfies the weak forms of these inequalities, we always retain \(|(\log \rho )'|\le C\), and hence \(\rho >0\). Thus we assume this throughout the following.
By (3.2), we know that all of the inequalities (3.18) hold on the interval \((y_*,y_*+{{\bar{\nu }}})\). By the smoothness and extendability of the flow guaranteed by Proposition A.1 and Theorem 2.15, the set
is clearly relatively open in \((y_*,y_{\max })\).
We therefore work to show that \({\mathfrak {Y}}\) is also relatively closed and hence deduce that, as \((y_*,y_{\max })\) is connected, we must have \({\mathfrak {Y}}=(y_*,y_{\max })\), as required. We therefore suppose we have a sequence \(y^{(n)}\rightarrow y_1\) with \(y^{(n)}\in {\mathfrak {Y}}\) for all n. By construction of \({\mathfrak {Y}}\), it is clear that, for each n, we have \((y_*,y^{(n)}]\subset {\mathfrak {Y}}\), and hence we deduce \((y_*,y_1)\subset {\mathfrak {Y}}\), that is, we assume that (3.18) holds on the interval \((y_*,y_1)\) with \(y_1< y_{\max }\). Showing that (3.18) holds strictly at \(y_1\) also is then sufficient to conclude that \(y_1\in {\mathfrak {Y}}\) so that \({\mathfrak {Y}}\) is relatively closed and hence conclude the proof.
Clearly the weak versions of (3.18) hold on \((y_*,y_1]\) in the sense that
and the flow is strictly supersonic on this whole interval. As we have guaranteed already that \(\rho _0>\rho (y_1)>0\) and \(\omega (y_1)\) is bounded, we may apply again the local existence theorem, Proposition A.1, to deduce that the flow can be smoothly extended past \(y_1\), and hence is smooth at \(y_1\) itself.
From (3.4), we see that as \(\rho '\le 0\) and \(\omega \ge \frac{4-3\gamma }{3}>0\), then
and hence
leading to
for all \(y\in [y_*,y_1]\). Clearly then \(\omega (y_1)>\frac{4-3\gamma }{3}\) also, as required.
To close the upper bound on \(\omega \), we first rearrange the first equation of (1.13) as
Note that, by assumption, on \([y_*+{{\bar{\nu }}},y_1]\), \(y^2\omega ^2-\gamma \rho ^{\gamma -1}>0\). We apply also (3.4) to calculate
Defining
we have
As \(\frac{4\pi y^2\rho \omega }{4-3\gamma }-\frac{2}{2-\gamma }\gamma \rho ^{\gamma -1}\ge 0\) on \([y_*+{{\bar{\nu }}},y_1]\), we have
and hence
Turning now to \(\frac{4\pi y^2\rho \omega }{4-3\gamma }-\frac{2}{2-\gamma }\gamma \rho ^{\gamma -1}\), we suppose for a contradiction that
From (3.20), at \(y_1\), we therefore have
due to \(\omega <2-\gamma \). Note now the simple scaled identity
Differentiating the term in the bracket, we use (3.5) to see
where we have used (3.23) in the first inequality on the last line and \(\omega (y_1)<2-\gamma \) in the second. But this contradicts the assumption that \(y_1\) is the first point at which \(\frac{4\pi y^2\rho \omega }{4-3\gamma }-\frac{2}{2-\gamma }\gamma \rho ^{\gamma -1}=0\), hence the derivative must be non-positive. So
Next, we consider the quantity
Applying (3.8) in the case \(m=1\), we get
where we recall from (3.9) that
By assumption, we have \(P_1(y)<0\) for all \(y\in (y_*,y_1)\). By Proposition 3.5 and Proposition A.1, as the flow is assumed supersonic, the flow may be extended smoothly to the right of \(y_1\), and hence is smooth at \(y_1\). Suppose now that at \(y_1\), \(\frac{\rho 'y}{\rho }=-\frac{1}{2-\gamma }\) for the first time (otherwise we are done). Then we must also have that \(P_1'(y_1)\ge 0\), \(P_1(y_1)=0\), and hence, at \(y_1\), by (3.10),
Note that \(Q_m(\omega ,{\mathcal {R}})\) is linear in \({\mathcal {R}}\) and that, as the flow is supersonic, we have always \(0\le \frac{\gamma \rho ^{\gamma -1}}{y^2}\le \omega ^2\). Thus,
by Lemma 3.4. Thus \(P'(y_1)<0\), contradicting \(P'(y_1)\ge 0\). So we obtain
To conclude the final inequality, the lower bound for \(\frac{\rho 'y}{\rho }\), we let \(m=\frac{4}{4-3\gamma }\) and apply again (3.8) to find
If \(y_1\) is the first point where \(\frac{\rho 'y}{\rho }=-\frac{4}{(4-3\gamma )(2-\gamma )}\), then \(P_m(y_1)=0\), \(P_m'(y_1)\le 0\) and so, at \(y_1\), by (3.10), we have
Again, as \(Q_m(\omega ,{\mathcal {R}})\) is linear in \({\mathcal {R}}\) and \(0\le \frac{\gamma \rho ^{\gamma -1}}{y^2}\le \omega ^2\), we have
by Lemma 3.4. This contradicts the assumption \(P_m(y_1)=0\), and hence we have
\(\square \)
To show that the flow remains supersonic to the right, and hence the global existence to the right, we need a slightly sharper upper bound on the derivative of the density, provided by the following lemma.
Lemma 3.6
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and define \(R_1=\frac{\rho _1 y_*}{\rho _0}\) as in Proposition 2.9. Let \((\rho ,\omega )\) be the extension of the unique LPH-type solution obtained from Theorem 2.15 to \((y_*,y_{\max }(y_*))\). Then there exists \(\delta >0\) such that, for any \(R>\max \{R_1,-\frac{2\gamma }{(2-\gamma )(\gamma +1)}-\delta \}\), we retain the inequality \(\frac{\rho 'y}{\rho }<R\) on the whole of \((y_*,y_{\max })\).
Remark 3.7
In effect, this says that if \(\frac{\rho _1y_*}{\rho _0}<-\frac{2\gamma }{(2-\gamma )(\gamma +1)}\), then we retain \(\frac{\rho 'y}{\rho }<-\frac{2\gamma }{(2-\gamma )(\gamma +1)}\) as long as the flow stays supersonic. If, on the other hand, we only have \(\frac{\rho _1y_*}{\rho _0}\ge -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\), then we will at least keep \(\frac{\rho ' y}{\rho }\le \frac{\rho _1y_*}{\rho _0}\) as long as the flow stays supersonic.
Proof
Choose \(\delta >0\) such that \(\delta (2-\gamma )<\delta _0\) with \(\delta _0\) the constant defined in Lemma 3.4 and let \(m\in (1,\frac{2\gamma }{\gamma +1}+\delta (2-\gamma ))\) be such that \(R_1<-\frac{m}{2-\gamma }\). Applying again (3.8), we find
where
Suppose now that at \(y_1\), \(\frac{\rho 'y}{\rho }=-\frac{m}{2-\gamma }\) for the first time, so that \({P_m}(y)<0\) for all \(y\in (y_*,y_1)\). By Proposition 3.5 and Proposition A.1, as the flow is assumed supersonic, the flow may be extended smoothly to the right of \(y_1\), and hence is smooth at \(y_1\). Suppose now that at \(y_1\), \(\frac{\rho 'y}{\rho }=-\frac{m}{2-\gamma }\) for the first time (otherwise we are done). Then we must also have that \(P_m'(y_1)\ge 0\), \(P_m(y_1)=0\), and hence, at \(y_1\), by (3.10),
Note that \(Q_m(\omega ,{\mathcal {R}})\) is linear in \({\mathcal {R}}\) and that, as the flow is supersonic, we have always \(0\le \frac{\gamma \rho ^{\gamma -1}}{y^2}\le \omega ^2\). Then,
Applying Lemma 3.4, for \(m\in [1,\frac{2\gamma }{\gamma +1}+\delta (2-\gamma )]\), \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\) this is strictly negative, leading to the desired contradiction. \(\square \)
With this, we may prove that the flow remains supersonic to the right for all \(y>y_*\), concluding the proof of existence to the right.
Lemma 3.8
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\). Then \(y_{\max }(y_*)=\infty \), that is the unique LPH-type solution \((\rho ,\omega )\) to the right of \(y_*\) obtained from Theorem 2.15 extends smoothly as a strictly supersonic solution of (1.13) to the whole of \((y_*,\infty )\).
Proof
Let now
By Theorem 2.15, there exists \(\delta >0\) such that \(S>0\) on \((y_*,y_*+\delta ]\).
By Proposition 3.5 and the local existence and uniqueness Proposition A.1, the only obstruction to continuing the solution to the right is if strict supersonicity fails.
Suppose for a contradiction that \(y_{\max }(y_*)<\infty \). Then there exists \(y_0\in (y_*,y_{\max }]\) such that \(\liminf _{y\rightarrow y_0^-}S(y)=0\) where \(S(y)>0\) on \((y_*,y_0)\). The flow is then smooth on \((y_*,y_0)\), but may not extend smoothly up to \(y_0\).
A simple calculation using (3.5)–(3.7) shows that, for all \(y\in (y_*,y_0)\),
Rearranging this identity, we obtain
where
As the flow is smooth (analytic) through \(y_*\) by construction, then this identity also holds at \(y_*\), where \(S(y_*)=0\). In particular, this gives us the inequality
where we have defined, as usual, \(R_1=\frac{\rho _1 y_*}{\rho _0}\). We distinguish now two cases: \(R_1<-\frac{2\gamma }{(2-\gamma )(\gamma +1)}\) and \(R_1\ge -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\).
Case 1: Suppose that \(R_1<-\frac{2\gamma }{(2-\gamma )(\gamma +1)}\). Then, by Lemma 3.6, there exists \(\delta >0\) such that
Thus as we have also \(\frac{4-3\gamma }{3}<\omega <2-\gamma \), we obtain
By the estimates of Proposition 3.5, there exists \(M>0\), depending only on \(y_*\), \(y_0\) and \(\gamma \), such that, for all \(y\in (y_*,y_0)\),
Thus, if \(S(y)\le \frac{{{\tilde{\delta }}}}{2M}\), we obtain from (3.28) \(S'(y)>0\), contradicting \(\liminf _{y\rightarrow y_0}S(y)=0\).
Case 2: Suppose now that \(R_1\ge -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\). By Proposition 2.9, this forces \(\gamma \le \frac{10}{9}\). As \(\rho '<0\) by Proposition 3.5, we know that on \((y_*+{{\bar{\nu }}},y_0)\) (\({{\bar{\nu }}}\) taken as in Lemma 3.1), we have \(\rho <\rho _0-\delta \) for some small \(\delta >0\). By Lemma 2.1 (compare also Fig. 3), there exists \({{\bar{\varepsilon }}}>0\), depending on \(\delta \), \(\rho _0\) and \(\gamma \le \frac{10}{9}\), such that if \(0\le h(\rho ,\omega )<{{\bar{\varepsilon }}}\), \(\omega >\frac{4-3\gamma }{3}\) and \(\rho <\rho _0-\delta \), then \(\omega <\omega _0\). Here \(h(\rho ,\omega )\) is as defined above in (1.20).
By Proposition 3.5, we have a bound \(M>0\), depending only on \(y_*\), \(y_0\) and \(\gamma \), such that
Let \(\varepsilon >0\) be such that \(\varepsilon M<\min \{\delta ^*,{{\bar{\varepsilon }}}\}\). As S is differentiable on \((y_*,y_0)\), there exists \(y_1\in (y_*,y_0)\) such that
From the first equation of (1.21), we obtain
Thus, by construction of \({{\bar{\varepsilon }}}\), we also obtain \(\omega (y_1)<\omega _0\).
We use Lemma 3.6 to see that \(\frac{\rho ' y}{\rho }\le R_1\) on \((y_*,y_0)\) and so, noting that \(\frac{\partial }{\partial R}F(\omega ,R)<0\), we have \(F(\omega (y_1),\frac{\rho '(y_1)y_1}{\rho (y_1)})\ge F(\omega (y_1),R_1)\). Now as \(R_1\ge -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\), it is clear from the definition of F that \(\frac{\partial }{\partial \omega }F(\omega ,R_1)<0\), and so, as \(\omega (y_1)<\omega _0\), we obtain
and so, using (3.30) and \(\varepsilon M<\delta ^*\) in (3.28), we find \(S'(y_1)>0\), a contradiction to the definition of \(y_1\). \(\square \)
Lemma 3.9
(Asymptotics) Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\). Then the local LPH-type solution \((\rho ,\omega )\) obtained from Theorem 2.15 may be extended to the right as a Yahil-type solution of (1.13) on the whole interval \([y_*,\infty )\).
Moreover, as \(y\rightarrow \infty \), the asymptotics of \((\rho ,\omega )\) are as follows. There exist constants \({\bar{k}}_1>0\) and \({\bar{k}}_2>0\) such that
Proof
The global existence to the right follows from Proposition 3.5 and Lemma 3.8, while the negativity of u(y) follows directly from the bounds \(\frac{4-3\gamma }{3}<\omega (y)<2-\gamma \).
We begin by showing the asymptotics for \(\omega \). Recall from (3.21) the identity
From Lemma 3.6 and the initial estimate \(\frac{y_*\rho _1}{\rho _0}<-\frac{1}{2-\gamma }\), we see that there exists \(\varepsilon >0\) such that \(\rho '\le \big (-\frac{1}{2-\gamma }-\varepsilon \big )\frac{\rho }{y}\). As also \(\rho >0\), we easily see that
and so, for y large, we may estimate
We re-write the middle term of (3.31) as
Thus, we find
leading to the desired estimate
as claimed. With this quantitative decay established, it is easier to see that this decay is also sharp by using this estimate to treat the quadratic term in \((2-\gamma -\omega )\) as higher order and so obtain a lower bound of the same form: \(2-\gamma -\omega \ge cy^{-\frac{1}{2-\gamma }}\). Indeed, we easily see that the quantity \(\big (y^{\frac{1}{2-\gamma }}(2-\gamma -\omega )\big )'\) is integrable as \(y\rightarrow \infty \), giving the existence of \({\bar{k}}_1\) as claimed.
Treating now \(\rho \), we see from (3.20) that
and the asymptotics just obtained for \(2-\gamma -\omega \) and \(\rho \) immediately yield that \(y^{\frac{2}{2-\gamma }}\rho \) remains bounded as \(y\rightarrow \infty \). In particular, the right hand side of this identity is integrable as \(y\rightarrow \infty \), giving the claimed convergence of \(y^{\frac{2}{2-\gamma }}\rho \). \(\square \)
Lemma 3.10
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\), and let \((\rho ,\omega )\) be the global Yahil-type solution to the right of (1.13) obtained as the extension of the LPH-type solution from Theorem 2.15. Then the solution remains monotone (strictly monotone for \(y_*>y_f\)) in both \(\rho \) and \(\omega \).
Proof
In the case \(y_*=y_f\), we know that the solution to the right is exactly the far-field solution \((\rho _f,\omega _f)=(ky^{-\frac{2}{2-\gamma }},2-\gamma )\). We therefore need only to consider the case \(y_*>y_f\) for which \(\omega '(y_*)>0\). Moreover, by the estimate \(\rho '<-\frac{1}{2-\gamma }\frac{y}{\rho }\) of Proposition 3.5 above, we have \(\rho '<0\) for all \(y>y_*\). It remains only to show that we retain also \(\omega '(y)>0\).
Suppose now that there exists a point \(y_0>y_*\) such that \(\omega '(y_0)=0\). Then, from (1.13), we have
Differentiating \(h(\rho ,\omega )\), we obtain
Thus, at \(y_0\),
Arguing directly, we differentiate G to obtain
Thus, at \(y_0\),
We now further differentiate the second equation of (1.21) to obtain
Hence, at \(y_0\), we find
where we have used (3.32) in the second equality. Substituting (3.34) into the second term and (3.35) into the third term, we get
where we have used that \(h>0\) (from \(\rho '<0\)) to obtain \(\frac{4\pi }{4-3\gamma }\rho \omega >2\omega ^2+(\gamma -1)\omega +(\gamma -1)(2-\gamma )\). Grouping terms, we then find
where we have used that \(\gamma \rho ^{\gamma -1}<y^2\omega ^2\) and \(-2+(\gamma -1)\frac{4-3\gamma -3\omega }{\omega }<0\) for \(\omega \in (\frac{4-3\gamma }{3},2-\gamma )\). Thus,
for all \(\omega \in (\frac{4-3\gamma }{3},2-\gamma )\) (indeed, one easily checks that the roots of the quadratic on the right are \(-\frac{1}{3}\) and \(2-\gamma \) while the coefficient of the quadratic term is negative), a contradiction to \(\omega '(y_0)=0\). \(\square \)
4 Solution to the Left of the Sonic Point
To construct a global solution to (1.13), we now need to solve to the left of the sonic point. This is the core of the construction of the global self-similar solution and is the most challenging part of the proof analytically. We develop an ad hoc shooting method, varying the sonic time \(y_*\) as our shooting parameter, to find a critical \({\bar{y}}_*\) for which the associated, local, LPH-type solution given by Theorem 2.15 can be extended smoothly up to the origin without meeting a second sonic point.
To proceed with this shooting argument, we partition the set of sonic times into three parts, defined by the relation of the associated \(\omega (y;y_*)\) to the Friedmann solution \(\omega _F\equiv \frac{4-3\gamma }{3}\). The key set of values \(y_*\) is those for which \(\omega (\cdot ;y_*)\) intersects \(\omega _F\) before a second sonic point occurs, which we call \({\mathcal {Y}}\) (see definition below). As we expect a global solution to agree with the Friedmann solution only at the origin, we find the critical \({\bar{y}}_*\) which leads to the global solution as the infimum of a connected component of \({\mathcal {Y}}\).
Throughout the section, the functions \((\rho (\cdot ;y_*),\omega (\cdot ;y_*))\) will be taken to refer to the extension of the unique LPH-type solution obtained from Theorem 2.15 as a solution of (1.13).
Following the strategy of [12], we can first define the sonic time and then partition the set \([y_f,y_F]\) as follows.
Definition 4.1
(Sonic time, \({\mathcal {X}}, {\mathcal {Y}}, {\mathcal {Z}}\))
and then the following sets:
as well as the fundamental set
Finally, we define the value
Note that \(y_f\in {\mathcal {X}}\) as \((\rho (\cdot ;y_f),\omega (\cdot ;y_f))=(\rho _f,\omega _f)\).
Remark 4.2
The unique extension of the local, unique LPH-type solution onto \((s(y_*),y_*)\) can be thought of as a maximal extension of the solution obtained by Theorem 2.15, and for the rest of this section, we will take the solution \((\rho (\cdot ;y_*),\omega (\cdot ;y_*))\) of (1.13) to be defined on this maximal interval.
To show that the solution associated to \({\bar{y}}_*\) can be extended to the origin to give a global solution, we require a number of further properties. First, we will show various continuity properties along the flow, a priori bounds away from the sonic time, upper semi-continuity of the sonic time and the openness of \({\mathcal {Y}}\). Next, we will demonstrate some basic invariant regions that hold as y decreases. The key insight that will allow us to show the global existence of the solution is that, for \(y_*\in Y\), the solution \(\omega (\cdot ;y_*)\) must remain monotone as y decreases until \(\omega \) meets the Friedmann value \(\frac{4-3\gamma }{3}\). By propagating this property along Y to \({\bar{y}}_*\) in the key Proposition 4.14, we are able to show that no second sonic point forms in the solution from \({\bar{y}}_*\), and hence the solution may be extended to the origin. In the final part of this section, we also conclude that the global solution indeed takes the value \(\omega (0)=\frac{4-3\gamma }{3}\) at the origin and that the density remains bounded globally.
4.1 Continuity Properties
We first show the simple positivity of the density to the left of the sonic point.
Lemma 4.3
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). Then \(\rho (y)>0\) for all \(y\in (s(y_*),y_*)\).
Proof
From the first equation of (1.21), we rearrange to find
For any \(y_1\in (s(y_*),y_*-\nu )\), where \(\nu \) is as in Theorem 2.15, we know that as the solution exists, is continuous, and \(G>0\) on the closed interval \([y_1,y_*-\nu ]\), we have a bound
where C may depend on \(y_1\), \(y_*\) etc., and so, integrating, we see that on \([y_1,y_*-\nu ]\), \(\log \rho \) remains bounded, and hence \(\rho >0\). As \(y_1\in (s(y_*),y_*-\nu )\) was arbitrary, we conclude that \(\rho >0\) holds on the whole interval \((s(y_*),y_*)\). \(\square \)
Lemma 4.4
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\) Then, if there exists \(y_0\in (s(y_*),y_*)\) such that \(\omega (y_0)=0\), we have that
Proof
For any \(y_0\in (s(y_*),y_*)\) such that \(\omega (y_0)=0\), the second equation of (1.21) gives \(\omega '(y_0)=\frac{4-3\gamma }{y}>0\), which is only possible if \(\omega >0\) on an interval to the right of \(y_0\). On the other hand, if there exists \(y_0\in (s(y_*),y_*)\) such that \(\omega (y_0)=0\), then as \(\omega (y)<0\) for all \(y\in (s(y_*),y_0)\), we obtain for all such y that
where we have used that the quadratic function \(2\omega ^2+(\gamma -1)\omega +(\gamma -1)(2-\gamma )>0\) for all \(\omega \in {\mathbb {R}}\) and \(\rho >0\). Thus, from the first equation of (1.21), we have \(\rho '>0\) on \((s(y_*),y_0)\) and so \(\rho (y)<\rho (y_0)\) on the whole interval. \(\square \)
We begin by establishing some a priori estimates on the solution to the left as long as it remains subsonic, that is, as long as we remain on the interval \((s(y_*),y_*)\).
Lemma 4.5
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). Let \(\alpha>\frac{4-3\gamma }{\gamma -1}>0\). Then there exists \(C>0\), depending on \(\gamma \) and \(\alpha \) but independent of \(y_*\in [y_f,y_F]\), such that the solution \((\rho ,\omega )\) satisfies the a priori bounds
Proof
Throughout the proof, constants will appear depending continuously on \(\rho _0\), \(\omega _0\) and \(y_*\). We will use the continuous dependence with respect to \(y_*\in [y_f,y_F]\) of these parameters to make the dependence on \(\gamma \) only.
Step 1: Prove (4.7) assuming (4.6).
To prove the a priori bounds on \(\omega \), we observe that it suffices to prove the claimed upper bound (4.6) for \(\rho \) on \((s(y_*),y_*)\) as the condition \(G(y;\rho ,\omega )>0\) then yields the simple bound
which gives the claimed bound for \(\omega \) of (4.7).
Step 2: Prove (4.6) in the region \(\{\omega \le 0\}\).
We first note that
which follows easily from (3.4). From here we see that for any \(y\in (s(y_*),y_*)\), we have
where we have used Lemma 4.3. We easily deduce \((y^3\rho \omega )'>0\) and thus
By Lemma 4.4, the region \(\{\omega \le 0\}\) is invariant under the dynamics of the flow to the left and, if there exists \(y_1\in (s(y_*),y_*)\) such that \(\omega (y_1)=0\), then \(\rho (y)<\rho (y_1)\) on the whole interval \((s(y_*),y_1)\). It is therefore sufficient to prove that (4.6) holds on the interval \([y_0,y_*-\nu ]\), where
Step 3: Conclude the bound (4.6) for \(\rho \) on the remaining region, \(\{\omega >0\}\).
Let \(\delta \in (0,\frac{4-3\gamma }{3})\) be fixed (and small). Then on the set \(\{\omega \ge \delta y^\alpha \}\), where \(\delta \) and \(\alpha >0\) are to be chosen later, we have from (4.9)
By continuity of the flow away from the sonic point, the set
is an open subset of \((y_0,y_*)\). If A is empty, we are done. Suppose A is not empty. It may therefore be written as a (possibly countable) union of disjoint, non-empty, open intervals. Taking such an interval, \((y_1,y_2)\), note that by the invariance of the set \(\{\omega \le 0\}\), we cannot have \(\omega (y_2)=0\). We must therefore have either \(\omega (y_2)=\delta y_2^\alpha \) (in which case (4.10) applies) or \(\rho (y_2)=\frac{1}{2} \frac{C_*}{\delta }y_2^{-(3+\alpha )}\) and hence, in either case,
For \(\delta \) sufficiently small, depending only on \(\gamma \) and \(\alpha \), on \((y_1,y_2)\), we have
Therefore, from the first equation of (1.21), we have the lower bound
Rearranging and integrating this differential inequality leads to
Note now that, by (4.11), \(\rho (y_2)\) satisfies
for some constants \(C_1\), \(C_2>0\) depending only on \(\gamma \) (where we have used that the constant \(C_*\) depends continuously on \(y_*\in [y_f,y_F]\) to remove dependence on \(y_*\)). Noting that \(2-\gamma <1\) so that \(\delta \ll \delta ^{2-\gamma }\) for \(\delta \ll 1\), we now choose \(\alpha>\frac{4-3\gamma }{\gamma -1}>0\) so that \((3+\alpha )(2-\gamma )<2+\alpha \), and hence, provided \(\delta \) was chosen small (depending on \(\gamma \), \(\alpha \)), we have
Thus, returning to (4.12), we obtain, for all \(y\in (y_1,y_2)\),
which yields the desired claim as the obtained estimate is independent of the choice of component \((y_1,y_2)\) and C depends on \(\gamma \) and \(\alpha \) only. \(\square \)
The following lemma allows us to extend any solution further to the left from a point \(y_0\in (0,y_*)\) provided the solution is uniformly subsonic, that is, \(G(y;\rho ,\omega )\ge \eta >0\). Moreover, the time that we may extend by depends only on \(y_0\) and \(\eta \).
Lemma 4.6
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). Suppose that, for some \(y_0\in (s(y_*),y_*-\nu )\), we have \(G(y;\rho ,\omega )\ge \eta >0\) for all \(y\in [y_0,y_*-\nu ]\). Then there exists \(\tau >0\), depending only on \(\gamma \), \(y_0\) and \(\eta \), such that the solution may be extended onto the interval \([y_0-\tau ,y_*]\) while remaining subsonic, that is, \(s(y_*)\le y_0-\tau \). Moreover, on the extended region, \([y_0-\tau ,y_0]\), we retain the inequalities
where \(C_\eta \) and M depend only on \(\gamma \), \(y_0\) and \(\eta \).
Proof
By Lemma 4.5, we have a constant \(M>0\), depending only on \(\gamma \) and \(y_0\) such that
As \(G(y;\rho ,\omega )\ge \eta \) on the whole interval, we make the trivial estimate
where \(C_\eta \) depends only on \(\gamma \) and \(\eta \).
We are therefore in the situation of Proposition A.1 with constant M having only the dependence claimed in the statement of the lemma. All of the estimates then follow from Proposition A.1. \(\square \)
Before we can continue, we need some continuity properties both of the sonic time, and of the flow with respect to \(y_*\) away from sonic points.
Proposition 4.7
Let \(\gamma \in (1,\frac{4}{3})\) and \(y_*\in [y_f,y_F]\). Then the following hold.
-
(i)
The sonic time is upper semi-continuous:
$$\begin{aligned} \limsup _{{{\tilde{y}}}_*\rightarrow y_*}s({{\tilde{y}}}_*)\le s(y_*). \end{aligned}$$ -
(ii)
Suppose \((y_*^n)_{n=1}^\infty \subset [y_f,y_F]\) converge \(y_*^n\rightarrow y_*\). Suppose further that there exist \(y_0\in (0,y_*-\nu )\) and \(\eta >0\) such that \(s(y_*^n)<y_0\) for all n, \(\rho (y;y_*^n)\) and \(\omega (y;y_*^n)\) are uniformly bounded on \([y_0,y_*]\), and
$$\begin{aligned} G(y;\rho (y;y_*^n),\omega (y;y_*^n))\ge \eta \quad \text { for all }n\in {\mathbb {N}},\,y\in [y_0,y_*-\nu ]. \end{aligned}$$Then there exists \(\tau =\tau (\eta ,y_0)>0\) such that
$$\begin{aligned} s(y_*)<y_0-\tau ,\quad s(y_*^n)<y_0-\tau \text { for all }n\in {\mathbb {N}}. \end{aligned}$$ -
(iii)
Suppose that \(s(y_*)<y_0\). Then for any \(\varepsilon >0\), there exist \(\delta >0\) and \(\tau >0\) such that for all \({{\tilde{y}}}_*\in [y_f,y_F]\) satisfying \(|{{\tilde{y}}}_*-y_*|<\delta \), the estimate
$$\begin{aligned} \big |(\rho (y;{{\tilde{y}}}_*),\omega (y;{{\tilde{y}}}_*))-(\rho (y;y_*),\omega (y;y_*))\big |<\varepsilon \end{aligned}$$holds uniformly in y on \([y_0-\tau ,y_*-\nu ]\).
Proof
As the proof of this Proposition is substantially similar to the proof of [12, Proposition 4.5], we defer the details to Appendix D. \(\square \)
4.2 Invariant Structures
Definition 4.8
We define the critical time
Lemma 4.9
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). Suppose that \(y_0\in (s(y_*),y_*)\) is such that on \((y_0,y_*)\), we have \(h(\rho ,\omega )<0\) and \(\omega >\frac{4-3\gamma }{3}\). Then the following hold.
-
(i)
At most one of the conditions \(h(\rho ,\omega )=0\) and \(\omega =\frac{4-3\gamma }{3}\) can occur at \(y_0\).
-
(ii)
If \(h(\rho ,\omega )=0\) at \(y_0\), then \(\inf _{y\in (s(y_*),y_*)}\omega >\frac{4-3\gamma }{3}\).
-
(iii)
If there exists \(y_1\in [y_c(y_*),y_*]\) such that \(y_1>0\) and \(\lim _{y\searrow y_1}\omega (y)=\frac{4-3\gamma }{3}\), then we must have \(y_1>s(y_*)\).
Thus if \(\inf _{y\in (s(y_*),y_*)}\omega \le \frac{4-3\gamma }{3}\), we must have that \(h<0\) on \((y_c(y_*),y_*)\).
Remark 4.10
Recalling the notation of Definition 4.1, (i) if \(y_*\in {\mathcal {Y}}\cup {\mathcal {Z}}\) then \(h<0\) on \((y_c(y_*),y_*)\); (ii) if \(y_*\in [y_f,y_F]\setminus {\mathcal {Y}}\) and \(y_c(y_*)=s(y_*)>0\), then
Proof
(i) Suppose that at \(y_0\) both \(h=0\) and \(\omega =\frac{4-3\gamma }{3}\). Solving the condition \(h(\rho ,\frac{4-3\gamma }{3})=0\) leads directly to \(\rho =\frac{1}{6\pi }\). Using the local existence and uniqueness of the ODE system around a non-sonic (and non-zero) point \(y_0\) from Proposition A.1, we therefore get that the solution is locally, and hence also globally, the Friedmann solution, \(\omega _F\equiv \frac{4-3\gamma }{3}\), \(\rho _F\equiv \frac{1}{6\pi }\). In particular, at the sonic point \(y_*\) we must also have \((\rho _0,\omega _0)=(\frac{1}{6\pi },\frac{4-3\gamma }{3})\) and hence \(y_*=y_F\). But this is a contradiction as the Friedmann solution is not of LPH-type by Proposition 2.16(iii).
(ii) Suppose that \(h(\rho ,\omega )=0\) at \(y_0\) (for short, we will write \(h(y_0)=0\)). As \(h<0\) on \((y_0,y_*)\), we must have \(h'(y_0)\le 0\). Note also that, by part (i), we have \(\omega (y_0)>\frac{4-3\gamma }{3}\). As \(y_0\) is not a sonic point and \(h(y_0)=0\), we have that \(\rho '(y_0)=0\) also. Thus, at \(y_0\), from (3.33), we have
where we have again used that \(h=0\) in the \(\omega '\) equation of (1.21). Clearly as \(\omega (y_0)>\frac{4-3\gamma }{3}\), the second bracket is strictly negative (and \(\omega >0\)). The first bracket satisfies
where we recall \(\omega _*=\sqrt{\frac{(\gamma -1)(2-\gamma )}{2}}\) from Lemma 2.1.
Case 1: \(\omega (y_0)\in (\frac{4-3\gamma }{3},\omega _*)\). In this case, we arrive at a contradiction to \(h'(y_0)\le 0\).
(recall from Lemma 2.1 that \(\omega _*\ge \frac{4-3\gamma }{3}\) only for \(\gamma >\frac{10}{9}\) with equality at \(\gamma =\frac{10}{9}\).)
Case 2: \(\omega (y_0)\ge \omega _*\). In this case, we break the proof into several steps.
Step 1: We first show that there exists \(\delta >0\) such that for \(y\in (y_0-\delta ,y_0)\), we have \(h>0\).
We treat this in two sub-cases. First, suppose that \(\omega (y_0)>\omega _*\). Then we have \(h'(y_0)<0\), and hence the existence of such a \(\delta >0\) is clear.
If, on the other hand, \(\omega (y_0)=\omega _*\), we have that \(h'(y_0)=h(y_0)=0\). By part (i), we must have \(\omega _*>\frac{4-3\gamma }{3}\) (and hence we have \(\gamma >\frac{10}{9}\)). Recall from (1.21) that
So
Thus also \(\rho ''(y_0)=\rho '(y_0)=0\).
Differentiating the middle line of (3.33) further, we use again \(h(y_0)=h'(y_0)=0\) to see
where we have used \(\omega (y_0)=\omega _*\) in the second line and \(\omega '(y_0)<0\). But this forces h to have a minimum at \(y_0\), contradicting \(h(y_0)=0\) and \(h(y)<0\) for \(y>y_0\).
Step 2: Conclude the invariance of the region \(\{h>0\}\).
Now for \(y\in (y_0-\delta ,y_0)\), as \(h>0\), we must have \(\rho '>0\) and \(\omega '<0\) as we also have \(\omega >\frac{4-3\gamma }{3}\). Thus, as we decrease y, we are in an invariant region as \(\rho \) decreases and \(\omega \) increases, taking us further away from the level set \(\{h=0\}\). Compare Fig. 3. Thus as long as the flow exists, we will retain in particular for \(y\in (s(y_*),y_0)\) the inequality \(\omega (y)>\omega _*>\frac{4-3\gamma }{3}\).
(iii) Suppose \(\limsup _{y\searrow y_1}\omega (y_1)=\frac{4-3\gamma }{3}\). Then we must have, for y close to \(y_1\),
where we have used that \(\omega _0>\frac{4-3\gamma }{3}\) and also \(\rho '<0\) on \((y_c(y_*),y_*)\) by part (ii). Thus the flow is still uniformly subsonic at \(y_1\) and hence either \(y_1=0\) or \(s(y_*)<y_1\). \(\square \)
4.3 Properties of the Fundamental Set Y
We begin by proving a basic topological property of \({\mathcal {Y}}\), and hence of Y: that the set is open.
Lemma 4.11
Let \(\gamma \in (1,\frac{4}{3})\). The set \({\mathcal {Y}}\) is open. Therefore also Y is the open interval \(({\bar{y}}_*,y_F)\).
Proof
Let \(y_*\in {\mathcal {Y}}\). As \(h(\cdot ;y_*)<0\) on \([y_c(y_*),y_*-\nu ]\) by Lemma 4.9, we must have at \(y_c(y_*)\) that \(\omega '(y_c(y_*);y_*)>0\), and so there exists \(\tau >0\) such that \(\omega (y;y_*)<\frac{4-3\gamma }{3}\) for \(y\in (y_c(y_*)-2\tau ,y_c(y_*))\) and \(s(y_*)<y_c(y_*)-2\tau \) (by definition of \({\mathcal {Y}}\), \(y_c(y_*)>s(y_*)\), so this may be achieved by taking \(\tau \) smaller if necessary). Let \(\varepsilon >0\) be sufficiently small. By parts (i) and (iii) of Proposition 4.7, there exists \(\delta >0\) such that for all \({{\tilde{y}}}_*\in [y_f,y_F]\) satisfying \(|\tilde{y}_*-y_*|<\delta \), we have \(s({{\tilde{y}}}_*)<y_c(y_*)-\frac{3}{2}\tau \) and
for all \(y\in [y_c(y_*)-\tau ,y_*-\nu ]\). By taking \(\varepsilon <\frac{4-3\gamma }{3}-\omega (y_c(y_*)-\tau ;y_*)\), we get that for all \({{\tilde{y}}}\) satisfying \(|{{\tilde{y}}}_*-y_*|<\delta \),
and hence \({{\tilde{y}}}_*\in {\mathcal {Y}}\) also. We have shown that \({\mathcal {Y}}\) is open.
To show the claim for Y, we note that clearly Y is a connected component of \({\mathcal {Y}}\). As \({\mathcal {Y}}\) is open, Y is therefore an open interval. Moreover, by Lemma 2.8 and the continuity with respect to both y and \(y_*\) of Theorem 2.15, we have that there exist \(\delta _1>0\) and \(\varepsilon >0\) such that, for \(y_F-\delta _1\le y_*\le y_F\) and \(y\in [y_*-\nu ,y_*]\) we have \(\omega '(y)\ge \varepsilon \). A simple continuity argument then reveals, as \(\omega (y_F;y_F)=\frac{4-3\gamma }{3}\), there exists \(\delta >0\) such that \((y_F-\delta ,y_F)\subset {\mathcal {Y}}\). Thus Y is non-empty and we have
\(\square \)
We wish to prove that the LPH-type solution associated to \({\bar{y}}_*\) exists on all of \((0,{\bar{y}}_*)\), that is, that \(s({\bar{y}}_*)=0\). To prove this, we show the stronger property that, for all \(y_*\in Y\), the function \(\omega (\cdot ;y_*)\) remains strictly monotone on the set \([y_c(y_*),y_*]\). This is not simply a technical observation but is a key stage in constructing a globally defined LPH-type solution. In providing the additional qualitative information of monotonicity for \(\omega \), this represents a significant advance over earlier work in the isothermal case. We therefore make the following definition.
Definition 4.12
Let \(\gamma \in (1,\frac{4}{3})\). The set of \(y_*\in Y\) for which the relative velocity \(\omega \) remains strictly monotone to the right of the critical time \(y_c(y_*)\) is defined to be
Note that if \(y_*\) is close to \(y_F\), then the monotonicity holds on \([y_c(y_*),y_*]\) and \(y_*\in {\mathcal {S}}\).
The key property that we will now prove is that \({\mathcal {S}}=Y\). In addition to giving the monotonicity of \(\omega (\cdot ;y_*)\) for all \(y_*\in Y\), this also guarantees a uniform lower bound on the function G, and hence ensures that the flow remains strictly subsonic. Before stating and proving this result, we first note a technical lemma that will be essential for the proof.
Lemma 4.13
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). Suppose that at a point \(y_0\in (s(y_*),y_*)\) such that \(\omega (y_0)\in (\frac{4-3\gamma }{3},2-\gamma )\), we have that \(\omega '(y_0)=\omega ''(y_0)=0\). Then \(\omega ^{(3)}(y_0)<0\).
The proof of this lemma is delayed until after Corollary 4.15 and the proof of Proposition 4.14 further below.
Proposition 4.14
Let \(\gamma \in (1,\frac{4}{3})\). Then, for all \(y_*\in Y\), the solution \((\rho (\cdot ;y_*),\omega (\cdot ;y_*))\) defined by Theorem 2.15 and extended to the interval \((s(y_*),y_*)\) satisfies \(\omega '(y;{y}_*)>0\text { for all }y\in [y_c({y}_*),{y}_*]\), and so
We note the following important corollary.
Corollary 4.15
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). There exists \(\eta >0\) such that, for all \(y_*\in Y\),
Proof
By continuity properties at the sonic point \(y_*\) (from Theorem 2.15), there exist \(\nu >0\) and \(\eta >0\) (independent of \(y_*\)) such that \(G(y_*-\nu ;y_*)\ge \eta >0\) for all \(y_*\in [y_f,y_F]\). Then, for any \(y_*\in {\mathcal {S}}\), as \(\omega '>0\) and \(\rho '<0\) on \([y_c(y_*),y_*]\), we retain \(G(y;y_*)\ge \eta \) on \([y_c(y_*),y_*-\nu ]\) as
Thus we have a uniform lower bound on G for \(y_*\in {\mathcal {S}}\) and, as \({\mathcal {S}}=Y\) by Proposition 4.14, we conclude. \(\square \)
Proof
(Proof of Proposition 4.14) We note by the proof of Corollary 4.15 above that for \(y_*\in {\mathcal {S}}\) we have a uniform lower bound \(G(y;y_*)\ge \eta \) on \([y_c(y_*),y_*-\nu ]\) for \(y_*\in {\mathcal {S}}\).
Note in addition that (1.21) gives that \(\omega '={\mathcal {W}}(y,\omega ,\rho )\) for some continuous function \({\mathcal {W}}\) away from sonic points. Continuity (respectively uniform continuity) of \(\omega \), \(\rho \) etc with respect to y or \(y_*\) then leads to continuity (respectively uniform continuity) of \(\omega '\).
To conclude the proof of the Proposition, we will proceed in several steps to show that \({\mathcal {S}}\) is both open and relatively closed in Y.
Step 1: We first show that \({\mathcal {S}}\) is open.
Take \(y_*\in {\mathcal {S}}\). Then we have the lower bounds \(G\ge \eta \), \(\omega '\ge c_1\), \(-h\ge c_2\) on \([y_c(y_*),y_*-\nu ]\) for some \(c_1,c_2>0\). By Lemma 4.6, we can therefore extend the solution onto an interval \([y_c-\tau ,y_*]\), where \(\tau =\tau (\eta ,y_c)>0\), and retain the inequality \(\omega '\ge \frac{1}{2} c_1>0\). By upper semi-continuity of the sonic time, there exists \(\delta >0\) such that if \(|{\tilde{y}}_*-y_*|<\delta \), we have
Using that \({\mathcal {S}}\subset Y\) and open-ness of Y, by possibly shrinking \(\delta >0\), we may assume that if \(|{\tilde{y}}_*-y_*|<\delta \), then \({\tilde{y}}_*\in Y\) and that, by the uniform continuity property of Proposition 4.7(iii), \(y_c({\tilde{y}}_*)\ge y_c(y_*)-\frac{\tau }{4}\) and, as \(\omega '\) is a continuous function of \((y,\rho ,\omega )\), also \(\omega '(\cdot ;y_*)>\frac{c_1}{4}\) on \([y_c(y_*)-\frac{\tau }{4},{\tilde{y}}_*]\), in particular, \({\tilde{y}}_*\in {\mathcal {S}}\).
Step 2: We collect properties associated to a sequence of \(y_*^n\in {\mathcal {S}}\) with \(y_*^n\rightarrow y_*\in Y\).
To show \({\mathcal {S}}\) is relatively closed in Y, first suppose \(y_*^n\in {\mathcal {S}}\) are such that \(y_*^n\rightarrow y_*\in Y\). Clearly if any of the \(y_*^n\le y_*\), then also \(y_*\in {\mathcal {S}}\). It therefore suffices to suppose that \(y_*^n\) decreases monotonically to \(y_*\). Suppose for a contradiction that there exists \(y_0\in [y_c(y_*),y_*]\) such that \(\omega '(y_0;y_*)=0\). Clearly, as \(h<0\) on \([y_c(y_*),y_*-\nu ]\) and \(\omega '(y_*-\nu ;y_*)>0\), we must have \(y_0\in (y_c(y_*),y_*-\nu )\) (and we suppose without loss of generality that we are working with the largest such \(y_0\)). Moreover, as each of the \(y_*^n\in {\mathcal {S}}\), we have the uniform lower bound \(G(y;y_*^n)\ge \eta \) on \([y_c(y_*^n),y_*-\nu ]\) (we have used the monotonicity of \(y_*^n\) to replace the upper limit on the interval with \(y_*-\nu \) rather than \(y_*^n-\nu \)).
Note that, by assumption, \(y_*\in Y\). Therefore \(y_c(y_*)>s(y_*)\).
Step 3: We show that there exists \(\tau >0\) such that \(\omega '(y;y_*)<0\) on \((y_0-\tau ,y_0)\) and \(y_0-\tau >y_c(y_*)+\tau \).
By definition of \(y_0\), we must have \(\omega ''(y_0;y_*)\ge 0\). If \(\omega ''(y_0;y_*)>0\), the claim easily follows. On the other hand, as \(y_*\in (y_f,y_F)\), then \(\omega (y_*;y_*)\in (\frac{4-3\gamma }{3},2-\gamma )\) and, by definition of \(y_0\in (y_c(y_*),y_*)\), we see that \(\omega '(y;y_*)>0\) on \((y_0,y_*)\), leading to \(\frac{4-3\gamma }{3}<\omega (y_0;y_*)<\omega (y_*;y_*)<2-\gamma \). Thus, by Lemma 4.13, if \(\omega '(y_0;y_*)=\omega ''(y_0;y_*)=0\), we have \(\omega ^{(3)}(y_0;y_*)<0\). This then forces \(\omega '(\cdot ;y_*)<0\) on a punctured interval centred at \(y_0\), a contradiction. The existence of the claimed \(\tau \) is proved.
Step 4: Apply uniform convergence to obtain a contradiction and deduce \({\mathcal {S}}\) is relatively closed.
Upper semi-continuity of the sonic time from Proposition 4.7 again gives that, for n sufficiently large, \(s(y_*^n)<s(y_*)+\frac{\tau }{2}<y_c(y_*)+\frac{\tau }{2}<y_0-\frac{3\tau }{2}\).
Suppose for a contradiction that \(\limsup _{n\rightarrow \infty }y_c(y_*^n)={\bar{y}}_c> y_0-\tau \). Without loss of generality, we take a further subsequence \(y_*^n\) such that \(y_c(y_*^n)\rightarrow {\bar{y}}_c\). By Lemma 4.6, there exists \(T=T(\eta ,{\bar{y}}_c)\in (0,\tau )\) such that
Therefore, applying the uniform convergence of Proposition 4.7(iii), we obtain
a contradiction to \(y_c(y_*)<y_0-2\tau \) as \({\bar{y}}_c>y_0-\tau \) and \(T<\tau \).
Thus, for n sufficiently large, we obtain that \(y_c(y_*^n)\le y_0-\frac{\tau }{2}\) and hence \(\omega '(y;y_*^n)>0\) on \((y_0-\frac{\tau }{2},y_0)\) as well as \(G(y;\rho (y;y_*^n),\omega (y;y_*^n))\ge \eta \) on \([y_0-\frac{\tau }{2},y_*-\nu ]\). But this gives a contradiction to the convergence
Thus \(y_*\in {\mathcal {S}}\) and so \({\mathcal {S}}\) is relatively closed in Y.
As \({\mathcal {S}}\) is relatively open and closed in Y and Y is connected, we must therefore have \({\mathcal {S}}=Y\). \(\square \)
Proof
(Proof of Lemma 4.13) Step 1: Derive identities for \(\omega (y_0)\), \(h'(y_0)\) and \(G'(y_0)\).
We begin by recalling from (3.32) and (3.34) the identities
Also, from (3.33), we recall that
Arguing directly, we differentiate G to obtain
Thus, at \(y_0\),
Step 2: Derive identities for \(\omega ''(y_0)\) and solve for \(\rho (y_0)\), \(G(y_0)\) and \(h(y_0)\).
We now further differentiate the ODE for \(\omega \) to obtain
Hence, at \(y_0\), we find
where we have used (4.17) in the second equality. Recalling that at \(y_0\) we have \(\omega ''(y_0)=0\), this gives the identity
Applying (4.17), (4.19) and (4.20) to expand the left hand side, we find at \(y_0\)
Simplifying, we find
which we rearrange to solve for \(G(y_0)\) as
so that
Note therefore that
and, from (4.17),
Therefore also
Step 3: Collect necessary identities for \(h''(y_0)\) and \(G''(y_0)\).
To compute \(\omega ^{(3)}(y_0)\), we first need \(h''(y_0)\) and \(G''(y_0)\). Clearly, from (3.33), we have
where we have used (4.22) in the middle line and (4.17) repeatedly.
Similarly, we compute \(G''(y_0)\) as
where we have again used (4.22) in the middle line and (4.24) in the last line.
Step 4: Conclude an identity for \(\omega ^{(3)}(y_0)\) and prove the sign condition.
Finally, we compute \(\omega ^{(3)}(y_0)\):
by using again (4.22). Substituting in the identities for \(h''(y_0)\), \(G''(y_0)\), we get
By inserting (4.23) for \(G(y_0)\), (4.25) for \(h(y_0)\), and (4.26) for \(\rho (y_0)\), this becomes a polynomial in \(\omega \) with coefficients depending on \(y_0\). Taking it term-by-term, we substitute (4.23) into the second term to find
For the third term, we use (4.25) and (4.26) to get
For the last term, we again substitute (4.23) to get
Substituting in all of these identities and simplifying, we find
It is simple to verify that the roots of the cubic in \(\omega \) on the right hand side are
and so, as \(\frac{(4-3\gamma )(\gamma -1)}{3\gamma -1}<\frac{4-3\gamma }{3}\) for all \(\gamma \in (1,\frac{4}{3})\), we easily see that for \(\omega \in (\frac{4-3\gamma }{3},2-\gamma )\), the right hand side of this formula is strictly positive. As \(4-3\gamma -3\omega (y_0)<0\), this yields \(\omega ^{(3)}(y_0)<0\), as required. \(\square \)
Remark 4.16
The arguments of Proposition 4.14 may be extended also to the isothermal case, \(\gamma =1\), treated previously in [12], to show that the obtained Larson–Penston solution satisfies the inequality
This can be seen by following the proof of Lemma 4.13 with \(\gamma =1\). It can be seen that it is impossible to have \(\omega (y_0)\in (\frac{1}{3},1)\) and \(\omega '(y_0)=\omega ''(y_0)=0\) simultaneously. Indeed, computing as far as (4.22) and making the necessary substitutions as in the following equation, the fact that G is independent of \(\rho \) when \(\gamma =1\) allows us to solve directly for \(\omega (y_0)\) and find either \(\omega (y_0)=\frac{1}{3}\) or \(\omega (y_0)=1\). We then follow the proof of Proposition 4.14 to obtain the monotonicity of \(\omega \) in the isothermal case \(\gamma =1\).
The next key result in this section is to show that the LPH-type solution associated to the critical value \({\bar{y}}_*\) exists on the whole of \((0,{\bar{y}}_*)\) and hence is a global solution of (1.13). This is the content of the following proposition.
Proposition 4.17
Let \(\gamma \in (1,\frac{4}{3})\). The sonic time and critical time associated to \({\bar{y}}_*\) satisfy \(s({\bar{y}}_*)=y_c({\bar{y}}_*)=0\).
Proof
As in [12, Proposition 4.12], there are 3 cases.
Case 1: \(y_c({\bar{y}}_*)=0\). Then we are done as, by definition, \(s({\bar{y}}_*)\le y_c({\bar{y}}_*)\).
Case 2: \(y_c({\bar{y}}_*)>s({\bar{y}}_*)\ge 0\). Then by continuity of the solution, we must have \(\omega (y_c({\bar{y}}_*);{\bar{y}}_*)=\frac{4-3\gamma }{3}\), and hence \({\bar{y}}_*\in Y\), a contradiction to \(Y=({\bar{y}}_*,y_F)\).
Case 3: \(y_c({\bar{y}}_*)=s({\bar{y}}_*)>0\). Now take a sequence \(y_*^n\rightarrow {\bar{y}}_*\) such that all \(y_*^n\in Y\). Then by definition of Y, \(y_c(y_*^n)>s(y_*^n)\) for all \(n\in {\mathbb {N}}\). We define
Without relabelling, we take a subsequence such that \(y_c(y_*^n)\rightarrow {\bar{y}}_c\). Then from Lemma 4.6 and Proposition 4.14, we know that there exist \(\eta >0\) and \(\tau =\tau (\eta ,{\bar{y}}_c)>0\) such that for all n sufficiently large
From Proposition 4.7(ii), we therefore find that, possibly shrinking \(\tau \), we have \(s({\bar{y}}_*),s(y_*^n)<\bar{y}_c-\tau \) for all n. Therefore, using the uniform convergence of Proposition 4.7(iii) on the interval \([\bar{y}_c-\tau ,y_*-\nu ]\), we find that the limit
and thus \(y_c({\bar{y}}_*)\ge {\bar{y}}_c>s({\bar{y}}_*)\), a contradiction to the assumption \(y_c({\bar{y}}_*)=s({\bar{y}}_*)\). \(\square \)
4.4 Asymptotics at the Scaling Origin, \(y=0\)
It is straightforward to exploit the uniform convergence property of Proposition 4.7 to obtain the weak monotonicity of \(\omega (\cdot ;{\bar{y}}_*)\). However, in order to obtain the strict monotonicity and the correct boundary value at the origin, \(y=0\), we must rule out the possibility that \({\bar{y}}_*=y_f\).
Lemma 4.18
Let \(\gamma \in (1,\frac{4}{3})\). The critical sonic point \({\bar{y}}_*\) is not equal to \(y_f\). In particular, the global solution \((\rho (\cdot ;{\bar{y}}_*),\omega (\cdot ;{\bar{y}}_*))\) is not the far-field solution \((\rho _f,\omega _f)\), defined in (1.23).
Before presenting the proof of this lemma, we collect some identities for an important auxiliary function.
Lemma 4.19
Let \(\gamma \in (1,\frac{4}{3})\), \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )\) be the associated unique LPH-type solution on \((s(y_*),y_*)\). We define a function
Then the following identity holds for f(y):
Remark 4.20
The principal utility of the function f is in comparing the density of an LPH-type solution to the density of the far-field solution, \(\rho _f\). Indeed, by construction (compare (1.23)),
Moreover, for \(y_*\in (y_f,y_F]\), we have \(f(y_*)>0\) by (3.3).
Proof
Let \(y_*\in [y_f,y_F]\) and let \((\rho ,\omega )=(\rho (\cdot ;y_*),\omega (\cdot ;y_*))\). Direct differentiation yields
Next, we rearrange the equation for \(f'\). We expand
Note that
Therefore, substituting this into (4.32), we have
that is, (4.31). \(\square \)
Proof
(Proof of Lemma 4.18) Step 1: Setup for a contradiction argument.
Suppose for a contradiction that \({\bar{y}}_*=y_f\), so that \(Y=(y_f,y_F)\). We will use the fact that for any \(y_*\in (y_f,y_F)\), we have \(\omega '(\cdot ;y_*)\ge 0\) on \([y_c(y_*),y_*]\) by Proposition 4.14, and so on this interval, \(2-\gamma -\omega (\cdot ;y_*)>0\). Along with (4.31), we also note
which is a reformulation of (3.21).
Step 2: Collect initial estimates for f and \(2-\gamma -\omega \) and define the basic set for a continuity argument to propagate the estimates.
Let \(\varepsilon >0\), \(\alpha >0\) and \(y_0>0\) be sufficiently small (to be fixed later), then by Proposition 4.7 there exists \(\delta >0\) such that if \(y_*-y_f<\delta \), we have
where \(A>\max \{\frac{(2-\gamma )^2}{\gamma -1},1\}\) is a fixed, \(\gamma \)-dependent constant and M is assumed sufficiently large so that \(\rho (y_0)>M\) and \(\omega (y_0)\in (0,2-\gamma )\) implies \(\frac{1}{G(y_0)}<\alpha \). Moreover, by upper semi-continuity of the sonic time \(s(y_*)\) from Proposition 4.7(i), as \(s(y_f)=0\), we may take \(|y_*-y_f|<\delta \) with \(\delta \) sufficiently small so that \(s(y_*)\le \frac{y_0}{8}\). Using now the uniform continuity from Proposition 4.7(iii) for \(y\ge \frac{y_0}{4}\), we may take \(\delta \) smaller if necessary to ensure \(|\omega (y;y_*)-(2-\gamma )|\) is small enough that \(\omega (y;y_*)>\frac{4-3\gamma }{3}\) for \(y\in [\frac{y_0}{4},y_*]\) and hence also \(y_c(y_*)<\frac{y_0}{2}\) giving, in total,
where the first inequality follows from \(y_*\in Y\) (so that \(y_c(y_*)>s(y_*)\)).
We take \(y_0\) small enough (depending only on \(\gamma \)) so that in all of the (finitely many) positive constants \(C=C(\gamma )\) below depending only on \(\gamma \), \(y_0<C\).
Let the set F be defined as
where \(C_1>C_0>1\) depend only on \(\gamma \) (and are to be chosen later). By taking \(C_0>1\) and \(C_1>\frac{1}{A}\), we have by (4.34) that \(y_0\in F\), so that F is clearly non-empty and relatively closed.
We will assume \(\varepsilon >0\) is small enough so that \(2-\gamma -C_0\varepsilon>\frac{3}{4}(2-\gamma )>\frac{4-3\gamma }{3}\). Note that if \(y\in F\), then as \(y_*\in Y\) and \(\omega (y)>\frac{4-3\gamma }{3}\), we must have \(\rho (y)>\rho (y_0)\) by Lemma 4.9, and so also \(\frac{1}{G(y)}<\alpha \).
Our goal is to prove that \(F=(s(y_*),y_0]\) (by showing that F is relatively open in \((s(y_*),y_0]\)). This then gives \(\inf _{(s(y_*),y_*)}\omega (\cdot ;y_*)\ge 2-\gamma -C_0\varepsilon >\frac{4-3\gamma }{3}\), a contradiction to \(y_*\in Y\).
Step 3: Show that \(f<0\) is an invariant property as y decreases and partition the set F.
Now for any \({\bar{y}}\in F\) such that \(0\le f({\bar{y}})<\varepsilon \), we use (4.31) along with the uniform bound on \(\omega \) and the estimate \(G^{-1}<\alpha \) to see that
as \(1 -(\gamma -1)\frac{2}{2-\gamma }=\frac{4-3\gamma }{2-\gamma }>0\), \(|f(\bar{y})|<\varepsilon \) and \(0<{\bar{y}}\le y_0\) is small. Thus the region \(\{f(y)<0\}\) is an invariant region in F.
In particular, we may define a point \(y_1\) such that \(\inf F\le y_1\le y_0\) as follows:
If \(f(y_0)>0\), we therefore have (by the invariance of \(\{f(y)<0\}\)) that \(f(y)< 0\) for \(y\in [\inf F,y_1)\), \(f(y)> 0\) for \(y\in (y_1,y_0]\). On the other hand, if \(f(y_0)\le 0\), then \(f(y)<0\) for all \(y\in F\setminus \{y_0\}\).
In addition, we conclude that F is not a singleton set as follows: if \(f(y_0)\ge 0\), then we have from the inequality just shown for \(f'(y_0)\) that there is an interval to the left of \(y_0\) such that \(f(y)<f(y_0)\) and the other defining inequalities of F follow from simple continuity considerations. If \(f(y_0)< 0\), then the upper bound \(f(y)<|f(y_0)|\) follows trivially on an open neighbourhood of \(y_0\), while the other defining estimates for F likewise follow from simple continuity considerations on an open neighbourhood of \(y_0\). This yields in particular that
Step 4: Obtain a uniform lower bound \(f(y)>-C_1\varepsilon \) on F.
We note the identity
and then use (4.33) along with \(G>0\) and \(\omega '>0\) (as \(y_*\in Y=S\) by Proposition 4.14 gives \(\omega '>0\) on \([y_c(y_*),y_*]\) which contains \(\overline{F}\)) to see
Using now that \(\omega (y)\in (\frac{3}{4}(2-\gamma ),2-\gamma )\) and \(G>0\), if \(f(y)<0\), then this estimate yields
while if \(f(y)\ge 0\), then this estimate holds trivially (as the right hand side is negative due to \(\omega (y)<2-\gamma \)). Thus, we have obtained
where \(C_2\) depends only on \(\gamma \) as we have assumed the estimate \(\omega \ge \frac{3(2-\gamma )}{4}\), and \(C_1\) was chosen originally so that \(C_1>C_2C_0\).
Step 5: Obtain the uniform bound \(2-\gamma -\omega (y)<\varepsilon \) on \([y_1,y_0]\).
If \(f(y_0)\le 0\), then, by definition of \(y_1\), we have \(y_1=y_0\) and the inequality follows trivially.
Suppose that \(f(y_0)>0\). Then \(y_1\in [\inf F,y_0)\). We then have from (4.35) that for all \(y\in [y_1,y_0]\), \(f'(y)> 0\), and so \(0\le f(y)< f(y_0)<\varepsilon \) for all \(y\in [y_1,y_0)\cap F\).
We recall the constant \(A>\max \{\frac{(2-\gamma )^2}{\gamma -1},1\}\) is a fixed, \(\gamma \)-dependent constant and consider the quantity
Using (4.31), (4.33), and (4.37) we get
By writing \(\omega ^{-1}=\frac{1}{2-\gamma }+O(|2-\gamma -\omega |)\), we treat terms that are quadratic in f(y) and \(2-\gamma -\omega (y)\) as higher order and recall \(0<\omega <2-\gamma \), \(G^{-1}<\alpha \) where \(\alpha \) is small to rearrange this as
For \(y\in [y_1,y_0]\cap F\), as \(f(y)\ge 0\) and \(A>\frac{(2-\gamma )^2}{\gamma -1}\), this gives us \(g_A'(y)\ge 0\) (using both \(|f(y)|+|2-\gamma -\omega |\le C\varepsilon \) and \(y_0\) small relative to \(\gamma \)), and hence \(g(y)\le g(y_0)\) on this interval. In particular, we obtain
and so clearly \([y_1,y_0]\subset F\) (using also (4.40)).
If \(y_1=\inf F\), the strict inequality, along with (4.40) (recall \(C_1>C_2C_0\) by definition), shows that F is also relatively open in \((s(y_*),y_0]\), that is, \(F=(s(y_*),y_0]\), and hence we conclude \(y_c(y_*)=s(y_*)\) and \(\inf _{(s(y_*),y_0)} \omega >\frac{4-3\gamma }{3}\), a contradiction to \(y_*\in Y\).
Step 6: Obtain the final remaining estimate \(2-\gamma -\omega (y)<4\varepsilon \) on \([\inf F,y_1]\).
We now suppose that \(y_1>\inf F\) (as we are already done by Step 5 if not) and work with either the case \(f(y_0)>0\) or the alternative, \(f(y_0)\le 0\). Then the interval \([\inf F,y_1]\cap F\) is non-empty and non-singleton.
By definition of \(y_1\), for \(y\in [\inf F,y_1)\), we trivially have the estimate \(f(y)< 0\le |f(y_0)|\).
Choosing \({{\tilde{A}}}=\frac{(2-\gamma )^2}{2}+a\), where \(a>0\) will be taken small depending only on \(\gamma \), we obtain from (4.42) that
on F, where we have used that \(f<0\) on \([\inf F,y_1)\) and \(2-\gamma -\omega >0\).
Thus, for \(y\in [\inf F,y_1)\),
where we have used the first bound in (4.40). Noting that the coefficient \(\big (\frac{(2-\gamma )^2}{2}+a\big )\frac{4-3\gamma }{2-\gamma }\frac{1}{\omega }\le \frac{3}{4}\) provided \(\omega >\frac{3(2-\gamma )}{4}\) and a is small, depending only on \(\gamma \), we absorb the last term on the right onto the left and conclude that
where the last estimate follows from (4.43) in the case \(y_1<y_0\) and (4.34) in the case \(y_1=y_0\). So provided \(C_0>4\) initially, we obtain that F is open. Applying again (4.40), we obtain the estimate \(0>f(y)>-C_2C_0\varepsilon >-C_1\varepsilon \), and hence we again find F is relatively open, leading to a contradiction as before. \(\square \)
We are now able to give a proof of the strict monotonicity of \(\omega (\cdot ;{\bar{y}}_*)\) and the correct boundary value at the origin, \(\omega (0;{\bar{y}}_*)=\frac{4-3\gamma }{3}\). These two properties are proved in the following two lemmas.
Lemma 4.21
Let \(\gamma \in (1,\frac{4}{3})\). Then the global solution \((\rho (\cdot ;\bar{y}_*),\omega (\cdot ;{\bar{y}}_*))\) satisfies \(\omega '(y;{\bar{y}}_*)>0\) for all \(y\in (0,{\bar{y}}_*)\).
Proof
For each \(y\in (0,{\bar{y}}_*)\), by the convergence with respect to \(y_*\) of \(\omega '(y;y_*)\) from Proposition 4.7, as \(\omega '(y,y_*)>0\) for all \(y_*\in Y\), we easily obtain \(\omega '(y;\bar{y}_*)\ge 0\). If we then suppose for a contradiction that \(\omega '(y;\bar{y}_*)=0\), y is a local minimum of \(\omega '\), and hence \(\omega ''(y;\bar{y}_*)=0\). By Lemma 4.18, we have that \({\bar{y}}_*\ne y_f\), and hence \(\omega ({\bar{y}}_*;{\bar{y}}_*)<2-\gamma \). By the weak monotonicity, this yields moreover that \(\omega (y;{\bar{y}}_*)<2-\gamma \) for all \(y\in (0;{\bar{y}}_*)\). In addition, from \(y_c({\bar{y}}_*)=0\) from Proposition 4.17, we obtain that, for all \(y\in (0,\bar{y}_*)\), \(\omega (y;{\bar{y}}_*)>\frac{4-3\gamma }{3}\) and so we may apply Lemma 4.13 to obtain \(\omega ^{(3)}(y;{\bar{y}}_*)<0\), a contradiction. \(\square \)
We therefore obtain that \(\omega \) is strictly monotone decreasing as we decrease y towards the origin.
Proposition 4.22
Let \(\gamma \in (1,\frac{4}{3})\) and consider the global solution \((\rho ,\omega )=(\rho (\cdot ;{\bar{y}}_*),\omega (\cdot ;{\bar{y}}_*))\). The relative velocity \(\omega \) extends continuously up to the origin and satisfies the limit
Proof
Suppose that \(\lim _{y\rightarrow 0^+}\omega (y;{\bar{y}}_*)\ne \frac{4-3\gamma }{3}\). We will derive a contradiction. Recall first of all that, by construction and Lemma 4.18, we have \(\omega (\bar{y}_*)<2-\gamma \), and thus \(\omega (y;{\bar{y}}_*)\in (\frac{4-3\gamma }{3},2-\gamma )\) for all \(y\in (0,{\bar{y}}_*)\), where the strict lower bound comes from the fact that \(y_c({\bar{y}}_*)=0\), proved in Proposition 4.17.
Define
(Note that the limit exists by monotonicity of \(\omega \) and that \({{\bar{\alpha }}}>0\).) One easily sees that the function
is monotone increasing on \((\frac{4-3\gamma }{3},2-\gamma )\) and achieves its maximum value \(\alpha _{\max }=\frac{2}{2-\gamma }\) at \(\omega =2-\gamma \). We therefore have the crucial inequality
Now from the inequality \(\omega '\ge 0\) from Lemma 4.21, we derive
where we have again used the monotonicity of \(A(\omega )\) to see \(-A(\omega (y))\le -A(\omega (0))=-{{\bar{\alpha }}}\) by the monotonicity of \(\omega \). Thus
and so, using now the equation for \(\rho \) from (1.21), we find that
Thus, for y sufficiently small, we must have
Recalling the definitions (1.20) and (1.19) of h and G respectively, this then yields that, for some possibly different constant \({\tilde{c}}_1>0\), for y sufficiently small, we must have
We recall (3.33):
Using the upper bound for h and lower bound for G just obtained, given \(\delta >0\) (to be chosen later), we may take y sufficiently small so that
This allows us to get the complementary bound
Thus we may make the estimate, for y sufficiently small,
Recall from (4.45) that, by construction, \({{\bar{\alpha }}}<\frac{2}{2-\gamma }\). We take \(\delta >0\) such that
Then the exponent here is such that \( 1-{{\bar{\alpha }}}(1+\delta )+(\gamma -1){{\bar{\alpha }}}>-1\). Thus, again taking y sufficiently small once more,
a contradiction to the fact that \(\omega '\ge 0\) for all \(y\in (0,\bar{y}_*)\). Thus \(\lim _{y\rightarrow 0^+}\omega (y)=\frac{4-3\gamma }{3}\). \(\square \)
Lemma 4.23
Let \(\gamma \in (1,\frac{4}{3})\) and consider the global solution \((\rho ,\omega )=(\rho (\cdot ;{\bar{y}}_*),\omega (\cdot ;{\bar{y}}_*))\). The density \(\rho \) remains bounded and monotone as \(y\rightarrow 0\), that is \(\rho \) converges monotonically to some \(\rho (0)>\frac{1}{6\pi }\).
Proof
The monotonicity of \(\rho \) follows from the inequality \(\rho '(y;y_*)<0\) for all \(y\in [y_c(y_*),y_*]\) for all \(y_*\in Y\) (by Lemma 4.9) and the strong convergence \(\rho '(y;y_*)\rightarrow \rho '(y;{\bar{y}}_*)\) for all \(y\in (0,{\bar{y}}_*)\) as \(y_*\rightarrow {\bar{y}}_*\) given by Proposition 4.7(iii).
To show that \(\rho \) stays bounded, suppose for a contradiction that it is not. Note that as \(\omega \) is bounded (away from 0) and convergent as \(y\rightarrow 0\), in this limit,
Moreover, we clearly also have the asymptotic form
So, given \(\delta >0\) the ODE for \(\rho \) in (1.21) becomes, for y sufficiently small,
The solution to an ODE of the form
Thus solving this pair of ordinary differential inequalities lead to exactly two possibilities: either \(\rho \) remains bounded up to the origin, a contradiction to the assumption that it is unbounded, or \(\rho = \kappa y^{-\frac{2}{2-\gamma }}\big (1+o(1)\big )\) as \(y\rightarrow 0\). To see this, choose \(y\ll 1\) and rearrange the differential inequalities to yield
Thus, for \({{\tilde{y}}}\in (0,y)\), we have first from the lower bound, integrating from \({{\tilde{y}}}\) to y,
Using that \(\rho >0\) and sending \({{\tilde{y}}}\rightarrow 0\) (as \(\rho (\tilde{y})\rightarrow \infty \), we have \(\rho ({{\tilde{y}}})^{\gamma -2}\rightarrow 0\)), this easily gives
On the other hand, from the upper bound for \((\rho ^{\gamma -2})'\), we get the inequality
and hence
else \(\rho ({{\tilde{y}}})\) would be bounded as \({{\tilde{y}}}\rightarrow 0\). Combining these inequalities, we have obtained that
as required. We note that
We return to the ODE for \(\omega \) from (1.21) to obtain that, for y sufficiently small,
for y sufficiently small, using \(\omega \rightarrow \frac{4-3\gamma }{3}\), \(\frac{G}{\gamma \rho ^{\gamma -1}}\rightarrow 1\), \(\frac{-h}{\frac{4\pi }{3}\rho }\rightarrow 1\). But this leads to a contradiction as \(\omega \) has a finite limit at the origin.
Thus, as \(\rho \) is both monotone and bounded, it has a finite limit \(\rho (0)=\lim _{y\rightarrow 0+} \rho (y)\).
To finish the proof, suppose that \(\rho (0)\le \frac{1}{6\pi }\). As we have \(h(\rho (y),\omega (y))<0\) for all \(y\in (0,{\bar{y}}_*)\) and \(\omega (y)\rightarrow \frac{4-3\gamma }{3}\), we must have \(\rho (0)=\frac{1}{6\pi }\). In this case, we may use that \(\omega \ge \omega _F\equiv \frac{4-3\gamma }{3}\), \(\rho \le \rho _F\equiv \frac{1}{6\pi }\) to get the following:
Sending \(\delta \rightarrow 0\), and then applying a simple Gronwall argument using the the Lipschitz continuity of the expression
on bounded sets of \((\rho ,\omega )\) away from the sonic points \(y_*\) and \(y_F\), we obtain that \(\omega \equiv \omega _F\), \(\rho \equiv \rho _F\), and so conclude the contradiction as, by construction, \((\rho (\cdot ;\bar{y}_*),\omega (\cdot ;{\bar{y}}_*))\ne (\rho _F,\omega _F)\). \(\square \)
Lemma 4.24
(i) Let \(\gamma \in (1,\frac{4}{3})\) and consider the global solution \((\rho ,\omega )=(\rho (\cdot ;{\bar{y}}_*),\omega (\cdot ;{\bar{y}}_*))\). The derivatives of \(\rho \) and \(\omega \) converge to zero as \(y\rightarrow 0\) and \(\rho '(0)=\omega '(0)=0\). (ii) The solution \((\rho ,\omega )=(\rho (\cdot ;{\bar{y}}_*),\omega (\cdot ;\bar{y}_*))\) coincides with the smooth solution \(({\bar{\rho }}(\cdot ;{\bar{\rho }}_0),{\bar{\omega }}(\cdot ;{\bar{\rho }}_0))\) obtained by Taylor expansion from the origin in Theorem 2.19 with \({\bar{\rho }}_0=\rho (0;{\bar{y}}_*)\).
Proof
Now for the solution \((\rho ,\omega )\) (suppressing the dependence on \({\bar{y}}_*\)), we may use the facts that \(\omega '(y)\ge 0\) for \(y>0\) and \(\omega \ge \frac{4-3\gamma }{3}\), to find
leading to \(\lim _{y\rightarrow 0+}\omega '(y)=0\). In addition,
by the above inequalities.
Similarly,
so \(\rho '(0)=\lim _{y\rightarrow 0^+}\frac{\rho (y)-\rho (0)}{y}=\lim _{\xi \rightarrow 0^+}\rho '(\xi )=0\) by the mean value theorem.
Finally, to prove part (ii), we observe that \((\rho ,\omega )\) agrees to first order with the solution obtained by Taylor expansion from the origin and hence apply Proposition 2.20 to deduce the local (and hence global) uniqueness of the flow. \(\square \)
5 Proof of the Main Theorem
We now prove Theorem 1.3. Let \(\gamma \in (1,\frac{4}{3})\) be fixed. Consider the local real analytic solution associated with the sonic point \({\bar{y}}_*\in (y_f,y_F)\):
By Lemma 3.8 the solution extends globally to the right, and by Proposition 4.17 the solution extends to the left to the whole interval \([0,{\bar{y}}_*]\). We therefore obtain a global solution, which is real analytic at \([0,\infty )\), where we use Lemma 4.24 to infer the regularity at \(y=0\).
By Lemmas 3.10, 4.21 and 4.23 , it follows that both \(\rho (\cdot ;\bar{y}_*)\) and \(\omega (\cdot ;{\bar{y}}_*)\) are strictly monotone on \((0,\infty )\): \(\omega \) is increasing and \(\rho \) is decreasing. This proves (1.17). We now recall (1.11), which implies \(u(y)= y \omega (y)-(2-\gamma )y\). Since \(\lim _{y\rightarrow 0}\omega (y)=\frac{4-3\gamma }{3}\) by Proposition 4.22 and \(\lim _{y\rightarrow \infty }\omega (y)=2-\gamma \) by Lemma 3.9, the strict monotonicity of \(\omega \) on \((0,\infty )\) implies the second claim of (1.16). The strict positivity of \(\rho \) is obvious.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Biasi, A.: Self-similar solutions to the compressible Euler equations and their instabilities. Comm. Nonlin. Sci. Num. Sim. 103, 106014, 2021
Brenner, M.P., Witelski, T.P.: On spherically symmetric gravitational collapse. J. Stat. Phys. 93, 863–899, 1998
Castro, A., Córdoba, D., Gómez-Serrano, J.: Global smooth solutions for the inviscid SQG equation. Mem. Am. Math. Soc. 266, 66, 2020
Chandrasekhar, S.: An Introduction to the Study of Stellar Structures. University of Chicago Press, Chicago, 1938
Cohen A., Li, Z., Schlag, W.: Uniqueness of excited states to \(\Delta u+u-u^3=0\) in three dimensions, arXiv preprint, arxiv:2101.08356, 2021, to appear in Analysis & PDE.
Deng, Y., Liu, T.P., Yang, T., Yao, Z.: Solutions of Euler–Poisson equations for gaseous stars. Arch. Ration. Mech. Anal. 164, 261–285, 2002
Deng, Y., Xiang, J., Yang, T.: Blowup phenomena of solutions to Euler–Poisson equations. J. Math. Anal. Appl. 286, 295–306, 2003
Fu, C.C., Lin, S.S.: On the critical mass of the collapse of a gaseous star in spherically symmetric and isentropic motion. Jpn. J. Ind. Appl. Math. 15, 461–469, 1998
Goldreich, P., Weber, S.: Homologously collapsing stellar cores. Astrophys. J. 238, 991–997, 1980
Gómez-Serrano, J., Granero-Belinchón, R.: On turning waves for the inhomogeneous Muskat problem: a computer-assisted proof. Nonlinearity 27, 1471–1498, 2014
Gómez-Serrano, J.: Computer-assisted proofs in PDE: a survey, arXiv preprint, arxiv:1810.00745, 2018
Guo, Y., Hadžić, M., Jang, J.: Larson–Penston self-similar gravitational collapse. Comm. Math. Phys., 2021. https://doi.org/10.1007/s00220-021-04175-y.
Guo, Y., Hadžić, M., Jang, J.: Continued gravitational collapse for Newtonian stars. Arch. Ration. Mech. Anal. 239, 431–552, 2021
Hadžić, M., Jang, J.: Nonlinear stability of expanding star solutions in the radially-symmetric mass-critical Euler–Poisson system. Comm. Pure Appl. Math. 71, 827–891, 2018
Harada, T., Maeda, H., Semelin, B.: Criticality and convergence in Newtonian collapse. Phys. Rev. D 67, 084003, 2003
Hunter, C.: The Collapse of unstable isothermal spheres. Astrophys. J. 218, 834–845, 1977
Jang, J.: Nonlinear instability in gravitational Euler–Poisson system for \(\gamma =\frac{6}{5}\). Arch. Ration. Mech. Anal. 188, 265–307, 2008
Jang, J.: Nonlinear instability theory of Lane–Emden stars. Comm. Pure Appl. Math. 67, 1418–1465, 2014
Krantz, S., Parks, H.: A Primer of Real Analytic Functions. Birkhäuser, 2002
Larson, R.B.: Numerical calculations of the dynamics of a collapsing protostar. Mon. Not. R. Astron. Soc. 145, 271–295, 1969
Maeda, H., Harada, T.: Critical phenomena in Newtonian gravity. Phys. Rev. D 64, 124024, 2001
Makino, T.: Blowing up solutions of the Euler-Poisson equation for the evolution of gaseous stars. Transp. Theory Stat. Phys. 21, 615–624, 1992
Merle, F., Raphaël, P., Rodnianski, I., Szeftel, J.: On the implosion of a compressible fluid I: Smooth self-similar inviscid profiles. Ann. of Math. 196 (2), 567–778, 2022
Merle, F., Raphaël, P., Rodnianski, I., Szeftel, J.: On the implosion of a compressible fluid II: Singularity formation. Ann. of Math. 196 (2), 779–889, 2022
Ori, A., Piran, T.: A simple stability criterion for isothermal spherical self-similar flow. Mon. Not. R. Astron. Soc. 234, 821–829, 1988
Penston, M.V.: Dynamics of self-gravitating spheres III. Mon. Not. R. Astron. Soc. 144, 425–448, 1969
Rein, G.: Non-linear stability of gaseous stars. Arch. Ration. Mech. Anal. 168(2), 115–130, 2003
Shu, F.H.: Self-similar collapse of spheres and star formation. Astrophys. J. 214, 488–497, 1977
Whitworth, A., Summers, D.: Self-similar condensation of spherically symmetric self-gravitating isothermal gas clouds. Mon. Not. R. Astron. Soc. 214, 1–25, 1985
Yahil, A.: Self-similar stellar collapse. Astrophys. J. 265, 1047–1055, 1983
Acknowledgements
Y. Guo’s research is supported in part by NSF DMS-Grant 2106650. M. Hadžić’s and M. Schrecker’s research is supported by the EPSRC Early Career Fellowship EP/S02218X/1. J. Jang’s research is supported by the NSF DMS-Grant 2009458 and the Simons Fellowship (Grant Number 616364).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by N. Masmoudi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Well-Posedness Away from Singular Points
At several points throughout the paper, we make use of the following straightforward local existence and uniqueness theorem for (1.21) provided the solution is away from both the singularities \(y=0\) and any sonic points. Although the proof is essentially standard, we include it here to make explicit the dependence of the time of existence on the uniform subsonicity or supersonicity. This is made precise in the following proposition.
Proposition A.1
Suppose that \(y_0>0\) and \(({{\bar{\rho }}},{{\bar{\omega }}})\) are given such that \({{\bar{\rho }}}>\frac{1}{M}\), \(|{{\bar{\rho }}}|+|{{\bar{\omega }}}|\le M\) and \(\big |G(y_0,{{\bar{\rho }}},{{\bar{\omega }}})\big |\ge \eta >0\). Then there exists \(\delta >0\), depending on y, M and \(\eta \), such that the flow (1.21) has a local, unique solution on the interval \([y_0-\delta ,y_0+\delta ]\). Moreover, on \([y_0-\delta ,y_0+\delta ]\), we have the estimates
Proof
This follows directly from the usual existence and uniqueness theory for ODEs with a locally Lipschitz right hand side. However, for the convenience of the reader and to emphasise the dependence on M, \(\eta \) and y, we provide a proof.
By the local Lipschitz continuity of the map \(y\mapsto G(y;\rho ,\omega )\) on the set \(\{|\rho |+|\omega |\le 2M,\, \rho \ge \frac{1}{2M}\}\), there exists \(\delta _1>0\) such that \(G(y,{{\bar{\rho }}},{{\bar{\omega }}})\ge \frac{\eta }{2}\) for all \(y\in [y_0-\delta _1,y_0+\delta _1]\). For any \({{\tilde{\eta }}},{\tilde{M}},{{\tilde{\delta }}}>0\), we define the set
Clearly by definition we have \(({{\bar{\rho }}},{{\bar{\omega }}})\in \Omega _{M,\eta /2,\delta _1}\).
For notational convenience, we define two new functions,
Then for given constants M, \(\eta \), there exist constants \(N>0\), \(L>0\) and \(l>0\), depending also on \(y_0\), such that
for all \(y\in [y_0-\delta _1,y_0+\delta _1]\), \((\rho _i,\omega _i)\in \Omega _{2M,\eta /4,\delta _1}\), \(i=1,2\).
We define a Picard operator via
We fix \(\delta \in (0,\delta _1)\) such that
Then for any \((\rho ,\omega )\in C([y_0-\delta ,y_0+\delta ];\Omega _{2M,\eta /4,\delta })\), we let \(({{\tilde{\rho }}},{{\tilde{\omega }}})={\mathcal {T}}[\rho ,\omega ]\) and see that for any \(y\in [y_0-\delta ,y_0+\delta ]\) we have
Moreover, estimating \({{\tilde{\rho }}}(y)\), we have
In addition, for all \(y\in [y_0-\delta ,y_0+\delta ]\) such that \(({{\tilde{\rho }}},{{\tilde{\omega }}})(y)\in \Omega _{2M,\eta /4,\delta }\) (note that this set is non-empty and open by construction of \({\mathcal {T}}\) and continuity of G away from sonic points), we have that
so that as \(G(y,{{\bar{\rho }}},{{\bar{\omega }}})\ge \frac{\eta }{2}\) for every such y (as \(\delta <\delta _1\)), a simple continuity argument shows that \(({{\tilde{\rho }}},{{\tilde{\omega }}})(y)\in \Omega _{2M,\eta /4,\delta }\) for all \(y\in [y_0-\delta ,y_0+\delta ]\). Thus we have shown
We equip \(C\big ([y_0-\delta ,y_0+\delta ];\Omega _{2M,\eta /4,\delta }\big )\) with the norm \(\Vert (\rho ,\omega )\Vert _{X}=\Vert \rho \Vert _{C^0}+\Vert \omega \Vert _{C^0}\) and observe that it is a complete metric space. To see \({\mathcal {T}}\) is a contraction, take \((\rho _1,\omega _1),(\rho _2,\omega _2)\in C([y_0-\delta ,y_0+\delta ];\Omega _{2M,\eta /4,\delta })\), write \({\mathcal {T}}[\rho _j,\omega _j]=({{\tilde{\rho }}}_j,{{\tilde{\omega }}}_j)\) for \(j=1,2\), and observe
as required. Thus there is a fixed point of the operator \({\mathcal {T}}\), \((\rho ,\omega )\in C([y_0-\delta ,y_0+\delta ];\Omega _{2M,\eta /4,\delta })\) satisfying the ODE system and the claimed estimates. \(\square \)
Combinatorial Bootstrap—Convergence of the Series at the Sonic Point
The central outcome of this section is Lemma B.6, which establishes that key N-dependent growth bounds for the coefficients in the formal Taylor expansion (2.9) around the sonic point can be bootstrapped. This is the key ingredient of the induction argument used in Lemma 2.14. Our arguments are combinatorial in nature and we first prove some technical lemmas. In the following, \(\lfloor \alpha \rfloor \) is the usual floor function, denoting the greatest integer not bigger than \(\alpha \), for any \(\alpha \in {\mathbb {R}}\).
Lemma B.1
There exists a universal constant \(c>0\) such that for all \(N\in {\mathbb {N}}\), the following holds
Proof
The first bound (B.1) follows from
The second bound (B.2) is entirely analogous. The third bound (B.3) follows from
For (B.4),
where we have used (B.1) twice.
For (B.5), using (B.1) and (B.3), we have
This finishes the proof. \(\square \)
Define the set
An element of \(\pi (n,m)\) encodes the partitions of the first n numbers into \(\lambda _i\) classes of cardinality i for \(i\in \{1,\dots ,m\}\). Observe that by necessity \(\lambda _j=0\) for any \(n-m+2\le j\le n\). With this partition set, the coefficient \(P_N\) of Taylor series for \(\rho ^{\gamma -1}=\sum _{N=0}^\infty P_N(y-y_*)^N\) in (2.86) can be written as
where \((\gamma -1)_m = \prod _{j=1}^m(\gamma -j)\).
To obtain bounds of \(P_N\) in terms of the coefficients \(\rho _j\), we will make use of the following combinatorial identities and inequalities. For any \(\alpha \in {\mathbb {R}}\), we let
Lemma B.2
Recall the set \(\pi (n,m)\) defined in (B.6).
-
1.
For each \(n\in {\mathbb {N}}\),
$$\begin{aligned} \sum _{m=1}^n\sum _{\begin{array}{c} \pi (n,m) \end{array} } \frac{(-1)^m m! }{ \lambda _1 ! \dots \lambda _n!} \left( {\begin{array}{c}\frac{1}{2}\\ 1\end{array}}\right) ^{\lambda _1} \cdots \left( {\begin{array}{c}\frac{1}{2}\\ n\end{array}}\right) ^{\lambda _n} = 2 (n+1)\left( {\begin{array}{c}\frac{1}{2}\\ n+1\end{array}}\right) \end{aligned}$$(B.8)holds.
-
2.
There exist universal constants \(c_1,c_2>0\) such that
$$\begin{aligned} c_1 \frac{1}{n^\frac{3}{2}}\le (-1)^{n-1} \left( {\begin{array}{c}\frac{1}{2}\\ n\end{array}}\right) \le c_2 \frac{1}{n^\frac{3}{2}}, \quad n\in {\mathbb {N}}. \end{aligned}$$(B.9)
Proof
The first statement follows from Lemma 1.5.2 of [19].
For the second statement, (B.9) is trivial for \(n=1\). Let \(n\ge 2\). Then
To estimate the last fraction, we invoke Stirling’s formula \( n! \sim \sqrt{2\pi n}\left( \frac{n}{e}\right) ^n, \ \ n \gg 1\). We will use the following version with upper and lower bounds valid for all n:
Then we have
Hence, combining this with (B.10), we have (B.9). \(\square \)
Lemma B.3
Let \(p>0\) be a given positive number. Let \((\lambda _1,\dots , \lambda _l ) \in \pi (l ,m)\) where \(1\le m\le l \) and \(l\ge 2\) be given.
-
1.
If \(1\le m\le \lfloor \tfrac{\sqrt{l}}{\sqrt{3}}\rfloor \), there exists a constant \(c_3=c_3(p)>0\) such that
$$\begin{aligned} \prod _{n=1}^l \left( \frac{1}{n^{\lambda _n}}\right) ^p \le \frac{c_3}{l^{p}}. \end{aligned}$$(B.13) -
2.
There exist \(c_4=c_4(p)>0\) and \(L_0=L_0(p)>1\) such that, if \(L\ge L_0\), the following holds:
$$\begin{aligned} \frac{1}{L^{m-1}}\prod _{n=1}^l \left( \frac{1}{n^{\lambda _n}} \right) ^p \le \frac{c_4}{l^{p}} \text { for all } 1\le m \le l. \end{aligned}$$(B.14) -
3.
Let \(l \ge 3\). Then there exists \(c_5=c_5(p)>0\) such that, if \(L\ge L_0\), the following holds:
$$\begin{aligned} \frac{1}{L^{m-2}}\prod _{n=1}^l \left( \frac{1}{n^{\lambda _n}} \right) ^p \le \frac{c_5}{l^{p}} \text { for all } 2\le m \le l. \end{aligned}$$(B.15)
Proof
Proof of (B.13). Let \( {\overline{m}}:= \lfloor \tfrac{\sqrt{l}}{\sqrt{3}}\rfloor \). We first claim that there exists at least one \(\lambda _j \ge 1\) for \(j \ge {\overline{m}}\). If not, \(\lambda _j =0\) for all \(j \ge {\overline{m}} \). Then we would have for \(1\le m\le {\overline{m}}\)
which is a contradiction.
We are now ready to prove (B.13). Consider two cases.
Case 1. Suppose there exists exactly one \(\lambda _{j_0} \ge 1\) for \(j_0\ge {\overline{m}}\). If \(\lambda _{j_0} = 1\), we must have \(j_0 \ge \frac{l}{2}\), for otherwise we would have
which leads to a contradiction. Therefore, we have
If \(\lambda _{j_0}\ge 2\), then \(j_0^{\lambda _{j_0}} \ge j_0^2 \ge {\overline{m}}^2\), which leads to
Case 2. Suppose there exist at least two \(\lambda _{j_1}, \lambda _{j_2} \ge 1\) for \(j_1, j_2\ge \overline{m}\). Then \(j_1^{\lambda _{j_1}} j_2^{\lambda _{j_2}} \ge j_1 j_2\ge {\overline{m}}^2\), which gives
This finishes the proof of (B.13).
Proof of (B.14). If \(1\le m\le \lfloor \tfrac{\sqrt{l}}{\sqrt{3}}\rfloor \), then by (B.13), for all \(L>1\),
If \(\lfloor \tfrac{\sqrt{l}}{\sqrt{3}}\rfloor +1\le m \le l\), note
Now letting \(L_0= e^{2p}\), it is easy to see that \((\frac{\sqrt{l}}{\sqrt{3}} -1) \log L - p \log l + p\log 3\ge 0\) for all \(l \ge 3\) and \(L\ge L_0\). Hence we obtain
for all \(l \ge 2\) and \(L\ge L_0=e^{2p}\).
Proof of (B.15). The proof is analogous to (B.14). We omit the details. \(\square \)
Let \(M>0\) be a fixed upper bound of \(|\rho _0|, \ |\omega _0|, \ |\rho _1|, \ |\omega _1|\) such that
Note that such an M may be taken to depend only on \(\gamma \) by continuity of these values as functions of \(y_*\in [y_f,y_F]\) and the uniform lower bound on \(\rho _0\) given by Lemma 2.2.
Lemma B.4
Let \(\alpha \in (1,2)\) be given. Assume that
for some \(C\ge 1\) and \(N\ge 3\). Then there exists a constant \(D=D(M)>0\) such that
Proof
We first prove the bounds for \(|(\omega ^2)_l|\), \(l\ge 0\). The bounds \(|(\omega ^2)_0|\le M^2\) and \(|(\omega ^2)_1|\le 2M^2\) are obvious from (B.16). Clearly
where we have used \(C^{2-\alpha }\ge 1\). If \(l\ge 3\) we then have
for some constant \({{\tilde{C}}}\). It is now clear that the estimates for \((\rho \omega )_l\) and \((\rho ^2)_l\), \(l\ge 0\) follow in the same way, as the only estimates we have used are (B.16) and the inductive assumptions (B.17)–(B.17), which both depend only on the index and are symmetric with respect to \(\rho \) and \(\omega \). The bound (B.20) can be obtained analogously. \(\square \)
Lemma B.5
Let \(\alpha \in (1,2)\) be given. Assume that (B.17) and (B.18) hold for \(N\ge 3\) and some large enough \(C>1\) satisfying
where \(c_1\) and \(L_0=L_0(\frac{3}{2})\) are universal constants in (B.9) and Lemma B.3. Then there exists a constant \(D=D(M, \gamma )>0\) such that
where we recall (B.7).
Proof
The bound of \(P_1\) immediately follows by recalling \(P_1= (\gamma -1)\rho _0^{\gamma -2}\rho _1\). For \(P_2\), observe that
from which we deduce
Now let \(l \ge 3\) and split \(P_l\) into two parts, \(m=1\) and \(m\ge 2\):
where we note \(\pi =\{(0,\dots ,0,1) \}\). By (B.17), it is clear that
for some constant \(D>0\) depending only on M and \(\gamma \). Next we claim that there exists \(D>0\) such that
To prove the claim, using (B.17) and Lemma B.2, we first observe
where we have used \((\alpha -1)\lambda _1\le (\alpha -1)m\) in the third line since \(\alpha >1\) and \( \lambda _1\le m\). Hence, using \(|(\gamma -1)_m| \le (\gamma -1) (m-1)! \) for \(1<\gamma <\frac{4}{3}\), we have
Now recalling \(P_{l,2}\) from (B.25) and using Lemma B.2 and Lemma B.3 with \(p=\frac{3}{2}\), we have
where C is large enough so that (B.23) holds. This proves (B.27) and (B.24). \(\square \)
We are now ready to estimate the source terms \({\mathcal {F}}_N\) and \({\mathcal {G}}_N\).
Lemma B.6
Let \(\alpha \in (1,2)\) be given. Then there exists a constant \(C_*=C_*(y_*)>0\) such that if \(C>C_*\) and for any \(N\ge 3\), the following assumptions hold
then we have
for some constant \(\beta =\beta (y_*, \gamma )>0\).
Proof
We start with (B.32). Recall \({\mathcal {F}}_N={\mathcal {F}}_N^{II} - {\mathcal {F}}_N^I\) where
and
For the first term of (B.34), we use (B.16), (B.31), and (B.1)
For the last two terms of (B.34), we have from (B.19)
The first term of (B.35) can be estimated as follows. By (B.30), (B.24), (B.3) and (B.2),
where we have used \(\alpha <2\) at the last step. The rest of (B.35) can be bounded by \(\frac{C^{N+1-2\alpha }}{N^2}\) similarly by using (B.19) in place of (B.24).
For (B.36), we first note that \(\lambda _N=0\) and hence it does not depend on \(\rho _N\). The estimation is identical to the estimation of \(P_{N,2}\) in (B.25). Therefore, as in (B.27) we have
For (B.37), by (B.30), (B.19) and the same argument as in (B.39), we see that
Next we claim
It suffices to verify the bound for the first term of (B.38), while (B.20) gives the desired bound for the second and fourth terms. We rewrite the sum as
Using the induction assumptions and (B.1), (B.4), we have
which shows the desired bound. Combining all the bounds above, we obtain (B.32).
Next, we recall \({\mathcal {G}}_N={\mathcal {G}}_N^{II} - {\mathcal {G}}_N^I \), where
and
and
Note that the structure of \({\mathcal {G}}_N^I\) and \({\mathcal {G}}_N^{II}\) is similar structure to the structure of \({\mathcal {F}}_N^I\) and \({\mathcal {F}}_N^{II}\) except for the second and third lines of (B.46). Hence we focus on the second and third lines of (B.46).
We may take \(C>0\) sufficiently large if necessary to ensure
Now for the first term in the second line of (B.46), we split indices into \(j=0,1\) and \(j\ge 2\) and use (B.24) and (B.47) to deduce
This yields the desired bound. The remaining terms in the second line can be estimated in the same way by using (B.19) in place of (B.24).
We may proceed analogously for the third line and use (B.47). We present the details for the first term in the third line of (B.46). First, we split indices as
For \(S_1\), using (B.31), (B.47), and (B.3), we have
The estimation of \(S_2\) is entirely analogous, while for \(S_3\) we split the indices further to deduce
Other terms in the third line of (B.46) can be estimated in the same way. This finishes the proof of (B.33). \(\square \)
Interval Arithmetic
Interval arithmetic is a numerical technique that allows for the rigorous proof of inequalities and estimates through replacing real numbers by closed intervals with end-points representable as floating point numbers. A survey of some of the uses of interval arithmetic in PDE theory may be found in [11]. For our purposes, we require only a very basic level of application of this method in order to estimate the signs of somewhat complicated polynomials in two variables over rectangular domains, and so we use the straightforward interval arithmetic packages available in the Julia computing language.

In this section of the appendix, we give the proofs of Proposition 2.9, Lemma 3.4 and inequalities (2.64)–(2.66). In each proof, we will insert the relevant Julia commands and state the outputs at the relevant point in the proof.
Maximisation or minimisation at ech step is taken either over a fixed interval of \(\gamma \) or a vector v=(v[1],v[2])\(=(\omega +\gamma ,\gamma )\). This ensures that the domain of v[1] is a fixed numerical interval (for example, the full range \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\) becomes v[1]\(\in [\frac{4}{3},2]\)). The two principal ranges over which we will work are then defined by

When defining functions of \(\omega \) and \(\gamma \), we use the characters w and g respectively for \(\omega \) and \(\gamma \).
1.1 Proofs of \(s(\omega _0)>0\) and Proposition 2.9
Before verifying the claimed inequalities on \(R_1\) stated in Proposition 2.9, we first complete the proof of Lemma 2.8 to show that \(R_1\) and \(R_2\) are well-defined functions of \(\omega _0\) and \(\gamma \), that is, that the square root of \(s(\omega _0)\) in the definitions (2.54) and (2.55) always yields a real number.
Proof
(Proof of Lemma 2.8, continued) Consider the definitions of \(R_1\) and \(R_2\) stated in (2.54) and (2.55). The argument of the square root is \(\omega _0^3s(\omega _0)\), and so to show that these are well-defined functions, it suffices to prove that \(s(\omega _0,\gamma )>0\) for all \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\) where we now make explicit the dependence on \(\gamma \), so that
We verify with interval arithmetic that \(s(\omega _0,\gamma )>0\) for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\), \(\gamma \in (1,\frac{4}{3})\) as follows:
First, we note that when \(\gamma =1\), \(s(\omega _0,1)=4\omega _0(2\omega _0-1)^2\), which is non-negative on the domain. Next, we differentiate with respect to \(\gamma \) to find
For \(\omega _0\in [1.42-\gamma ,2-\gamma ]\), we find that this is strictly positive by

which gives the minimum in [1.06209, 1.26472], hence for \(\omega _0\ge 1.42-\gamma \), \(\gamma \in (1,\frac{4}{3})\), \(s(\omega _0,\gamma )>0\). Next, for \(\gamma \in (1,1.1]\) and \(\omega _0\in [\frac{4}{3}-\gamma ,1.42-\gamma ]\), we check that \(s(\omega _0,\gamma )>0\) by

which gives the minimum in [0.0334093, 0.0431525]. Finally, for \(\gamma \in [1.1,\frac{4}{3})\), we check first that
and then
is uniformly positive by

which puts the minimum in [0.336312, 2.0698], and hence \(s(\omega _0,\gamma )\) is strictly increasing with respect to \(\omega _0\). \(\square \)
Proof
(Proof of Proposition 2.9) We will first show that for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\), we have \(R_1<-\frac{1}{2-\gamma }\) for all \(\gamma \in (1,\frac{4}{3})\), while for \(\omega _0\ge \frac{4-3\gamma }{3}\) and \(\gamma \ge \frac{10}{9}\), we have \(R_1\le -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\) with strict inequalities when either \(\gamma >\frac{10}{9}\) or \(\omega _0>\frac{4-3\gamma }{3}\).
To check the claimed inequalities on \(R_1\), we use the following method:
Step 1: We prove \(R_1<-\frac{1}{2-\gamma }\).
First,
It is therefore sufficient to check the sign of the numerator. When the terms in the numerator on the first line are negative, as the contribution of the square root is negative, we are clearly done. We claim
for all \(\omega _0\in [\frac{4}{3}-\gamma ,2-\gamma ]\), \(\gamma \in (1,\frac{4}{3})\). This implies the claimed inequality as, in the remaining case that the first terms are positive, this establishes that the contribution of the square root is strictly larger, and hence the difference is negative. To verify this claim, we first cancel a factor of \(\omega _0^3\) and consider instead
Eliminating the strictly positive factor \(4(\gamma ^2-1)\), we check that at \(\omega _0=\frac{4-3\gamma }{3}\), the remainder satisfies
We then take a derivative with respect to \(\omega _0\) to arrive at
for all \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\) and \(\gamma \in [1,\frac{4}{3}]\) by interval arithmetic:

with output in the closed interval \([-0.910166, -0.627474]\), thus finishing the proof that \(R_1<-\frac{1}{2-\gamma }\).
Step 2: Prove \(R_1\le -\frac{2\gamma }{(2-\gamma )(\gamma +1)}\) for \(\gamma \ge \frac{10}{9}\) with equality only for \(\gamma =\frac{10}{9}\) and \(\omega _0=\frac{4-3\gamma }{3}\).
We argue similarly to Step 1. First, we apply (2.54) to find
We again need only to compare the quantities in the numerator, and so we will prove that
with equality only when both \(\gamma =\frac{10}{9}\) and \(\omega _0=\frac{4-3\gamma }{3}\). Simplifying, we find that this expression is equal to \(4(\gamma -1)(\gamma +1)^2\omega _0^3r_2(\omega _0)\), where
Considering only \(r_2(\omega _0)\) (as the remaining factors are positive), we check
with equality only for \(\gamma =\frac{10}{9}\). Moreover, differentiating with respect to \(\omega _0\) yields
for all \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\) and \(\gamma \ge \frac{10}{9}\) (actually all \(\gamma \in [1,\frac{4}{3}]\)) by interval arithmetic:

with output in \([-2.12454, -1.63927]\), concluding the proof.
Step 3: Prove \(R_1>-\frac{4}{(4-3\gamma )(2-\gamma )}\).
The only remaining estimate for \(R_1\) is the lower bound, and again we follow the above approach. We first group
One easily sees that
provided \(\omega _0>{{\bar{\omega }}}=\frac{ (2-\gamma )(4-3\gamma )(9-7\gamma )}{8(3\gamma ^2-11\gamma +7)}\). As this value is always less than \(\frac{4-3\gamma }{3}\) (indeed, \(\frac{4-3\gamma }{3}-{{\bar{\omega }}}=\frac{(4-3\gamma )(3\gamma ^2-19\gamma +2)}{24 (3\gamma ^2-11\gamma +7)}>0\)), we conclude that the quantity is positive always.
It is therefore sufficient to compare the sizes of the squares of the terms in the numerator of (C.2). We therefore consider
where
As usual, we evaluate at \(\omega _0=\frac{4-3\gamma }{3}\) and find
as \(\gamma ^2-5\gamma +2<0\) for \(\gamma \in (1,\frac{4}{3})\). The derivative with respect to \(\omega _0\) is then
This is strictly positive as, at \(\omega _0=\frac{4-3\gamma }{3}\), we have
as the quartic in \(\gamma \) is uniformly positive:

gives lower bound in the interval [17.4556, 18.0143]. Moreover, the further \(\omega _0\) derivative is
where we have used \(\omega _0\ge \frac{4-3\gamma }{3}\) in the second line and that \(9\gamma ^4-60\gamma ^3+132\gamma ^2-104\gamma +24>0\) by

which gives the minimum in [0.827639, 1.00486]. We then further apply interval arithmetic to show the positivity of the last quantity:

gives lower bound in the interval [21.7206, 24.0462] which concludes the proof of the estimates for \(R_1\).
Step 4: Prove the lower bound \(W_1\ge 0\) with equality only for \(y_*=y_f\).
The final step is the lower bound for \(W_1\). We first rearrange (2.58) to see
where we note that, as \(R_1<-\frac{1}{2-\gamma }\), the denominator satisfies
It is therefore sufficient to verify that \(\omega _0^2 R_1+(\omega _0+2-\gamma )\ge 0\) with strict equality for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma )\) (equivalently \(y_*\in (y_f,y_F]\)). At the end-point \(y_*=y_f\), equivalently \(\omega _0=2-\gamma \), a direct computation reveals \(R_1=-\frac{2}{2-\gamma }\) and \(W_1=0\).
To prove the lower bound, we substitute \(R_1\) from (2.54) and rearrange to find
It is a simple exercise to check that the quadratic
and so it suffices to show that
for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma )\).
We first obtain the lower bound for \(\omega _0\in [\frac{4-3\gamma }{3},1.8-\gamma ]\) by interval arithmetic:

which gives that the minimum lies in [8.32454, 9.37091].
On the remaining region, we recall that \(W_1(2-\gamma )=0\) and hence \(L(2-\gamma )=0\). A direct computation shows that
and further interval arithmetic shows that this is strictly negative for \(\omega _0\in [1.8-\gamma ,2-\gamma ]\) by

which gives that the maximum lies in \([-33.9807, -33.5971]\). Hence \(L(\omega _0)>0\) for \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma )\) as required. \(\square \)
1.2 Proof of (2.64)–(2.66)
(i) The easiest of the inequalities to show is inequality (2.64) for \(A_2\). Indeed, we recall that \(R<0\) and \(W\ge 0\) for all \(\gamma \in (1,\frac{4}{3})\) and \(\omega _0\in [\frac{4-3\gamma }{3},2-\gamma ]\) and consider the coefficient of the \(\omega _0^2R\) term:
where the inequality comes from interval arithmetic:

which gives an upper bound in the range \([-0.445382, -0.442693]\). As the contributions from W and the remainder are both non-negative, we conclude \(A_2>0\).
(ii) Next, we show the inequality (2.66), \(4A_2+A_1>0\). This is more complicated than before and requires us to consider the coefficients on separate parts of the domain. We first simplify the expression for this sum as
Again, the coefficient of \(\omega _0^2R\) is negative on the whole region of interest by interval arithmetic:

which gives an upper bound in the range \([-2.22671, -2.21346]\). We therefore focus on the other two coefficients. The coefficient of \(\omega _0W\) is clearly positive when \(\omega _0>\frac{7-5\gamma }{20}\) and negative otherwise (for \(\omega _0>0\)). One also checks easily that \(\frac{7-5\gamma }{20}\ge \frac{4-3\gamma }{3}\) is equivalent to \(\gamma \ge \frac{59}{45}\) (and \(\frac{59}{45}<\frac{4}{3}\)).
Moreover, the final coefficient is
Note that \(\frac{7-5\gamma }{10}\ge \frac{4-3\gamma }{3}\) only for \(\gamma \ge \frac{19}{15}\).
In the region \(\omega _0\ge \frac{7-5\gamma }{10}\), we therefore have \(4A_2+A_1>0\), as required (and in particular, this holds for the whole region when \(\gamma \le \frac{19}{15}\)). For \(\gamma \in (\frac{19}{15},\frac{4}{3})\), we consider
so the coefficient of \(\omega _0W\) is positive for all \(\omega _0\) of interest. Recalling also that the coefficient of \(\omega _0^2R\) is negative and that \(R<-\frac{1}{2-\gamma }\), we therefore bound \(4A_2+A_1\) below by
where we check the sign of the final quadratic using

which gives a lower bound in the range [2.49842, 2.51321] (actually for all \(\omega _0\in (\frac{4-3\gamma }{3},2-\gamma )\) and \(\gamma \in (1,\frac{4}{3})\).
Finally, for \(\gamma \in (\frac{59}{45},\frac{4}{3})\) and \(\omega _0\in (\frac{4-3\gamma }{3},\frac{7-5\gamma }{20})\), we compare \(\omega _0W\) to \(\omega _0^2R\) using the formula
Differentiation of \(B(R,\omega _0)\) with respect to R reveals that
for all \(\omega _0\in (\frac{4-3\gamma }{3},2-\gamma )\), \(\gamma \in (1,\frac{4}{3})\), so B is a decreasing function with respect to R. Hence, recalling again that \(R\le -\frac{1}{2-\gamma }\), we have that
for \(\omega _0\in (\frac{4-3\gamma }{3},\frac{7-5\gamma }{20})\) (where we are using that \(\frac{7-5\gamma }{20}<\frac{2-\gamma }{3}\)). We therefore use the fact that the coefficient of \(\omega _0W\) is negative on this region to make the lower bound
We may check that the coefficient of \(\omega _0^2R\) is still negative:

which gives an upper bound in \([-2.56641, -2.55714]\). We therefore bound \(4A_2+A_1\) below on this region by taking \(R=-\frac{1}{2-\gamma }\) in (C.6). This leaves us with
which we check is again positive for \(\omega _0\in (\frac{4-3\gamma }{3},\frac{7-5\gamma }{20})\) (in fact it is uniformly positive for all \(\omega _0\in (\frac{4}{3}-\gamma ,2-\gamma )\) and \(\gamma \in (1,\frac{4}{3})\) by interval arithmetic):

with the minimum in [2.54864, 2.55882], concluding the proof of (ii).
(iii) A similar strategy holds again for showing (2.65) for the last quantity, \(4A_2+2A_1+A_0\). In fact, grouping terms again, we find
the coefficient of \(\omega _0^2R\) is always negative again:

gives an upper bound in the interval \([-2.67263, -2.65602]\). Next, we see that there exists
such that the coefficient of \(\omega _0W\) is non-negative for \(\omega _0\ge \omega _*(\gamma )\) and negative for \(\omega _0\in (0,\omega _*(\gamma ))\).
For \(\omega _0\in (\max \{\frac{4-3\gamma }{3},\omega _*(\gamma )\},2-\gamma )\), we check then that
by using interval arithmetic to estimate the final quadratic by

and obtaining the minimum is in [2.34889, 2.35904].
There is a \(\gamma _*\approx 1.148\) such that \(\omega _*(\gamma )\le \frac{4-3\gamma }{3}\) if \(\gamma <\gamma _*\) and reverse inequality otherwise. In the former case, we are already done. However, \(\omega _*(\gamma )<\frac{2-\gamma }{3}\) for all \(\gamma \in (1,\frac{4}{3})\) by using

which gives a maximum in \([-0.0134389, -0.0127184]\). Hence, for \(\gamma \ge \gamma _*\) and \(\omega _0\in (\frac{4-3\gamma }{3},\omega _*(\gamma ))\), we again get \(\frac{\omega _0W}{\omega _0^2R}\le -1\) by the same argument as that leading to (C.5). Therefore, for \(\omega _0\) in this region, replacing \(\omega _0W\) with \(-\omega _0^2R\) and combining terms, we obtain
where we have also dropped the first order term in \(\omega _0\) in the last line. The new coefficient of R is again seen to be negative as

gives a maximum in \([-2.62435, -2.59568]\). Thus it is enough to obtain a lower bound by using \(R<-\frac{1}{2-\gamma }\) and factoring out \(\omega _0^2\) from the remainder. We arrive at the lower bound
We verify that the quadratic in \(\omega _0\) in parentheses is always positive on \((\frac{4-3\gamma }{3},\omega _*(\gamma ))\) for \(\gamma >\gamma _*\) (in fact the sign holds on all \(\omega _0\in (\frac{4-3\gamma }{3},2-\gamma )\) and \(\gamma \in (1,\frac{4}{3})\)) by the following interval arithmetic:

shows a minimum in the range [1.5754, 1.58222], concluding the proof.
1.3 Proof of Lemma 3.4
Step 1: We prove (3.16) in the case \(m=1\).
Recall
Considering first \(Q_1^+\), we check that
We then check using interval arithmetic that
-
(i)
\(Q_1^+(\omega )<0\) for all \(\omega \in [\frac{4}{3}-\gamma ,2-\gamma ]\), for \(\gamma \in [1.02,1.15]\),
-
(ii)
\(Q_1^+(\omega )<0\) for all \(\omega \in [\frac{4}{3}-\gamma ,1.8-\gamma ]\), for \(\gamma \in [1,1.02]\),
-
(iii)
\(\partial _\omega Q_1^+(\omega )<0\) for all \(\omega \in [\frac{4}{3}-\gamma ,2-\gamma ]\), for \(\gamma \in [1.15,\frac{4}{3}]\),
-
(iv)
\(\partial _\omega Q_1^+(\omega )>0\) for all \(\omega \in [1.8-\gamma ,2-\gamma ]\), for \(\gamma \in [1,1.02]\),
all of which combine to prove that \(Q_1^+(\omega )<0\) for all \(\omega \in (\frac{4}{3}-\gamma ,2-\gamma )\), for \(\gamma \in (1,\frac{4}{3})\).
These are checked with the following Julia code (removing line breaks in the definition of functions):

Property (i) then follows from

which gives \(\max _{V_2} p_1\in [-0.0178999, -0.0177931]\). Property (ii) follows from

which gives \(\max _{V_3} p_1\in [-0.0638237, -0.0622099]\). Property (iii) follows from

giving \(\max _{V_5} p2\in [-0.321421, -0.231604]\). Finally,

yields \(\min _{V_4}p_2\in [0.178011, 0.190886]\), as required.
To prove the negativity of \(Q_1^-\), it is enough to observe that
and, moreover, by interval arithmetic, \(\partial _\omega Q_1^-(\omega )<0\) always. To check this last property, we cancel the factor \(\gamma -1\) to define a function Q1min\(=\frac{Q_1^-}{\gamma -1}\) and then find the maximum:

This yields \(\max _V p_4\in [-2.003, -1.99999]\), so that, for all \(\gamma \in (1,\frac{4}{3})\), we have \(\partial _\omega Q_1^-<0\).
Step 2: We prove the estimate (3.16) for \(Q_m\) for \(m\in [1,\frac{2\gamma }{\gamma +1}]\).
To extend the estimates for \(Q_m\) from \(m=1\) to \(m\in [1,\frac{2\gamma }{\gamma +1}]\), we proceed as follows. We first define a new variable k so that \(m-1=\frac{\gamma -1}{\gamma +1}k\), to ensure \(k\in [0,1]\) when \(m\in [1,\frac{2\gamma }{\gamma +1}]\). m is then recovered from k by

We create two new functions
Note that when \(m=1\), these are just \(Q_1^+\) and \(Q_1^-\) from above. We then compute the derivative with respect to m to get
It is then straightforward to see that for \(m\in [1,\frac{2\gamma }{\gamma +1}]\), the coefficient of the \(\omega ^3\) term is negative. Note also that \(\partial _m Q_5<0\) for \(\omega >\omega _*=\frac{(2-\gamma )(5-4\gamma )}{14-7\gamma -4m}\). We check by interval arithmetic that for all \(m\in [1,\frac{2\gamma }{\gamma +1}]\), all \(\gamma \in (1,\frac{4}{3})\), we have \(\omega _*<\frac{4}{3}-\gamma +0.1\):

The maximum lies in \([-0.154379, -0.153729]\), hence is negative. Thus, for \(\omega >\frac{4}{3}-\gamma +0.1\), we have \(Q_5(\omega ,m)\le Q_1^+(\omega )<0\). On the other hand, for \(\omega \in (\frac{4}{3}-\gamma ,\frac{4}{3}-\gamma +0.1)\), we have from interval arithmetic that \(\partial _\omega Q_1<-0.29\):

The output is in \([-0.304395, -0.297167]\).
We check that
provided \(\omega >\frac{2}{3}\omega _*\). We check that \(\frac{2}{3} \omega _*<\frac{4}{3}-\gamma \) always:

with output \([-0.0363685, -0.0358193]\). Thus, we retain \(\partial _\omega Q_5<0\) on \(\omega \in (\frac{4}{3}-\gamma ,\frac{4}{3}-\gamma +0.1)\) for all m and \(\gamma \) in the range we require. Thus, using the fact that, at \(\omega =\frac{4}{3}-\gamma \), we have
by using

with minimum in the range [0.483905, 0.681199], we conclude \(Q_5<0\) for all suitable \(\gamma \) and m.
To handle \(Q_6\), we compare it to \(Q_1^-\) above. We write
exploiting the definition of k to introduce factors of \(\gamma -1\) wherever we find \(m-1\). In particular, we have
Factoring out \(\gamma -1\), we differentiate and find
Interval arithmetic then yields
by working without the common factor of \((\gamma -1)\):

giving a maximum in the range \([-2.03123, -1.99999]\). This establishes inequality (3.16) for \(m\in \big [1,\frac{2\gamma }{\gamma +1}\big ]\).
Step 3: We extend to cover the full range \(m\in \big [1,\frac{2\gamma }{\gamma +1}+\delta \big ]\).
To extend (3.16) to \(m\in \big [1,\frac{2\gamma }{\gamma +1}+\delta \big ]\), we argue directly by continuity with respect to m, uniformly with respect to \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\) for each \(\gamma \in (1,\frac{4}{3})\). As \(Q_{\frac{2\gamma }{\gamma +1}}(\omega )<0\) for all \(\omega \in [\frac{4-3\gamma }{3},2-\gamma ]\), for each \(\gamma \in (1,\frac{4}{3})\), we obtain the existence of such a claimed \(\delta >0\).
Step 4: Prove (3.17).
To check (3.17) rigorously, we follow the following procedure: Define
We need to prove the positivity of both \(Q_3\) and \(Q_4\). To show the positivity of \(Q_3\), we note the following four facts:
-
\(Q_3\big (\frac{4}{3}-\gamma \big )=\frac{-2(4-3\gamma )(21\gamma ^2-71\gamma +42)}{27(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_3'\big (\frac{4}{3}-\gamma \big )=\frac{27 \gamma ^4-183 \gamma ^3+ 402 \gamma ^2 - 312 \gamma +80}{3(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_3^{(2)}\big (\frac{4}{3}-\gamma \big )=\frac{4(18\gamma ^4-120\gamma ^3+261\gamma ^2-203\gamma +50)}{(4-3\gamma )(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_3^{(3)}(\omega )=\frac{12(3\gamma ^2-10\gamma +6)(9\gamma ^2-30\gamma +16)}{(4-3\gamma )^2(2-\gamma )^2}>0\) for all \(\omega \in (\frac{4}{3}-\gamma ,2-\gamma )\), \(\gamma \in (1,\frac{4}{3})\).
Each of these is proved by interval arithmetic. We scale out the factors of \((4-3\gamma )^{-1}\) and \((4-3\gamma )^{-2}\) in the second and third derivatives of \(Q_3\) before computing to ensure the computations remain bounded.

yielding \(\min _G g_5\in [15.2996, 15.3379], \min _G g_6\in [29.4466, 30.2343], \min _G g_7\in [14.8603, 15.7849], \min _G g_8\in [15.9016, 16.0085]]]\).
Similarly,
-
\(Q_4(\frac{4}{3}-\gamma )=\frac{-2(4-3\gamma )(3\gamma ^2-13\gamma +6)}{9(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_4'(\frac{4}{3}-\gamma )=\frac{9\gamma ^4-61\gamma ^3+138\gamma ^2-112\gamma +32}{(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_4^{(2)}(\frac{4}{3}-\gamma )=\frac{12(6\gamma ^4-40\gamma ^3+87\gamma ^2-65\gamma +14)}{(4-3\gamma )(2-\gamma )^2}>0\) for \(\gamma \in (1,\frac{4}{3})\),
-
\(Q_4^{(3)}(\omega )=\frac{36(9\gamma ^4-60\gamma ^3+132\gamma ^2-104\gamma +24)}{(4-3\gamma )^2(2-\gamma )^2}>0\) for all \(\omega \in (\frac{4}{3}-\gamma ,2-\gamma )\), \(\gamma \in (1,\frac{4}{3})\).

yielding \(\min _G g_9\in [5.99518, 6.00151], \min _G g_{10}\in [11.5885, 11.8567], \min _G g_{11}\in [5.98055, 6.15133], \min _G g_{12} \in [5.96691, 6.22624]\).
Proof of Proposition 4.7
Before we prove the proposition, it is convenient to rescale the sonic point to a fixed value so that some of the continuity properties are easier to prove. We let
The system (1.21) takes the form
where
Moreover, the sonic time \(s(y_*)\) scales naturally into
so that the interval \((S(y_*),1)\) comprises all the z-values in the interval (0, 1) for which the unique LPH-type solution exists and \({\mathcal {G}}>0\). By analogy to (A.1)–(A.2) we introduce the abbreviations
Proof
We work with the formulation (D.2)–(D.3) for convenience. From there, it is easy to recover all the statements in the original \((\rho (y),\omega (y))\) variables.
Proof of part (i). We fix an \(y_*\in [y_f,y_F]\) and an arbitrary \(\mathring{z}\in (S(y_*),1-\nu )\). In the following all generic constants will depend on \(\mathring{z}\) unless specified otherwise. Since \(\mathring{z}>S(y_*)\) there exists an \(\eta >0\) such that
It follows in particular that
where
Moreover, by Lemma 4.5 it is clear that there exists a constant \(C = C(\mathring{z})\) such that for any \(\tilde{y}_*\in [y_f,y_F]\)
Let \(0<\delta \ll 1\) be a control constant to be fixed later and consider the set of \({{\tilde{y}}}_*\in [y_f,y_F]\) such that \(|\tilde{y}_*-y_*|<\delta \). For any such \({{\tilde{y}}}_*\) let \((\tilde{r}(\cdot ;{{\tilde{y}}}_*),{{\tilde{w}}}(\cdot ;{{\tilde{y}}}_*))\) be the unique LPH-type solution given by Theorem 2.15. Let
and define the control function
where \({{\tilde{\nu }}}\) is a \(y_*\)-independent positive constant whose existence follows from the existence of \(\nu >0\) in Theorem 2.15. It is straightforward to check that
where we used the shorthand \(\tilde{{\mathcal {G}}} = {\mathcal {G}}(\tilde{y}_*,{{\tilde{r}}},{{\tilde{w}}})\) and similarly for \({{\tilde{h}}}\). Note that
and also
where we have used the mean value theorem in the second line above. Note that by (D.10) and (D.7) \( \frac{|\tilde{r} - r|}{r} \le \frac{g(z)}{C_\gamma \eta ^\beta }\) and therefore since \(\gamma -2<0\)
Moreover, by (D.9) it is easy to see that
Together with (D.12) and (D.14) this gives
where
A simple consequence of (D.16) is a lower bound for \(\tilde{{\mathcal {G}}}\),
From the definition of h(r, w) and the a priori bounds (D.9) it is straightforward to obtain the bound
Using (D.9), (D.16), (D.18), and (D.19) in (D.11) we conclude
The same proof also yields the bound
where we recall (D.6).
Clearly, for \(\delta >0\) and \(|1-\nu -z|\) sufficiently small, we have from (D.16) and (D.17) by continuity
where \({{\bar{\eta }}}(z)\) is defined in (D.18). Let
where \(C_\gamma >0\) is defined in (D.8). The bound \(g(z)<\frac{C_\gamma \eta ^\beta }{2}\) ensures that
Integrating over \([z,1-{{\tilde{\nu }}}]\) it follows from (D.2)–(D.3) and the bounds (D.20)–(D.21) that
where we recall (D.17) and (D.23). We now apply the Grönwall inequality to conclude
We note that for any given \(\delta '>0\), there exists a \(\delta >0\) such that \(g(1-{{\tilde{\nu }}})<\delta '\) for all \(|y_*-\tilde{y}_*|<\delta \). Therefore, for any given \(\varepsilon >0\) we can choose a \(\delta =\delta (\eta ,\varepsilon )\) sufficiently small so that for all \(|y_*-{{\tilde{y}}}_*|<\delta \) we have the bound
In particular, with \(0<\varepsilon \ll 1\) chosen sufficiently small we have \(g(z)<\frac{{{\tilde{C}}}\eta ^\beta }{3}\) on \(({\bar{Z}}, 1-{{\tilde{\nu }}}]\) and therefore \( K(\eta ,g(z)) < K_\eta \) on \([{\bar{Z}},1-{{\tilde{\nu }}}]\). This in turn implies
for \(0<\delta \ll 1\) sufficiently small. This implies \({\bar{Z}} = Z\) and provides a uniform lower bound for \({\mathcal {G}}\) on \((Z,1-{{\tilde{\nu }}}]\) thus implying \(S({{\tilde{y}}}_*)<Z\). Therefore \(Z=\mathring{z}\) and since \(\mathring{z}>S(y_*)\) is chosen arbitrarily, this implies the upper semi-continuity.
Proof of part (ii). By Lemma 4.6 it is clear that there exists a \({{\tilde{\tau }}}={{\tilde{\tau }}}(\mathring{y}, \eta )\) such that \(S(y_*^n)<\mathring{y}-{{\tilde{\tau }}}\) for all \(n\in {\mathbb {N}}\). We now use the lower bounds (D.18) and (D.26) applied to the sequence \(\{y^n_*\}_{n\in {\mathbb {N}}}\) to conclude that \(S(y_*) < \frac{\mathring{y}}{y_*}-{{\tilde{\tau }}}\) for a possibly smaller \({{\tilde{\tau }}}>0\), which again depends only on \(\mathring{y}\) and \(\eta \).
Proof of part (iii). By the proof of part (i) it follows that there exists a \(\delta >0\) sufficiently small so that \(S({{\tilde{y}}}_*)<S(y_*)+ \frac{1}{2}\left( \frac{y_0}{{{\tilde{y}}}_*} - S(y_*)\right) \) for all \(|{{\tilde{y}}}_*-y_*|<\delta \). The claim now follows from the arguments in part (i) using in particular the uniform-in-\({{\tilde{y}}}_*\) upper bound (D.25) for the distance function g(z). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, Y., Hadžić, M., Jang, J. et al. Gravitational Collapse for Polytropic Gaseous Stars: Self-Similar Solutions. Arch Rational Mech Anal 246, 957–1066 (2022). https://doi.org/10.1007/s00205-022-01827-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-022-01827-8