A new semi-analytical approach for self and mutual inductance calculation of hexagonal spiral coil used in wireless power transfer systems

Abstract

Several methods have been proposed in the literature for the calculation of self and mutual inductance. These methods include the use of complex integral analysis, the necessity of having primary and secondary coils with the same dimensions and the limitations of the ratio of the coil dimension to the distance between the coils. To overcome these restrictions, a new semi-analytical estimation method has been proposed in this paper. Calculation the self and mutual inductance by using the same basic formula which is based on Biot Savart Law prevents the formation of complex integrals and helps create a simple solution method. In order to verify the results obtained with the analytical approach, two hexagonal coils with 10 and 20 cm outer side lengths were produced by using litz wire with a conductive cross section of 1.78 mm². The results obtained with the new approach are compared with the finite element analysis, other work presented in the literature and experimental results in order to prove the accuracy of the proposed method.

Appendix

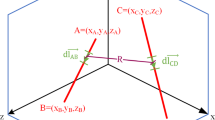
Magnetic flux density equation can be written by the Biot-Savart Law,

$$ \vec{B} = \frac{{\mu_{0} I}}{4\pi }\frac{1}{r} \cdot \left[ {\frac{z + k}{{\sqrt {\left( {z + k} \right)^{2} + r^{2} } }} - \frac{z - k}{{\sqrt {\left( {z - k} \right)^{2} + r^{2} } }}} \right] \cdot \hat{\varphi } $$

(25)

The total magnetic flux equation for calculating the triangle areas which are divided into rectangles, depending on the side length of the hexagon and the division parameters n and i is can be obtained as follows,

$$ \varphi_{\text{AB}} = \frac{{\mu_{0} I}}{4\pi }\int_{{\frac{k\sqrt 3 i}{n}}}^{{\frac{{k\sqrt 3 \left( {2n - i} \right)}}{n}}} {\int_{{\frac{{k\left( {n + i - 1} \right)}}{n}}}^{{\frac{{k\left( {n + i - 1} \right)}}{n}}} {\frac{z + k}{{\sqrt {\left( {z + k} \right)^{2} + r^{2} } }} - \frac{z - k}{{\sqrt {\left( {z - k} \right)^{2} + r^{2} } }} \cdot {\text{d}}z \cdot {\text{d}}r} } $$

(26)

$$ \begin{aligned} \varphi_{\text{AB}} = & \frac{{\mu_{0} I}}{4\pi }\int\limits_{{\frac{k\sqrt 3 i}{n}}}^{{\frac{{k\sqrt 3 \left( {2n - i} \right)}}{n}}} {\frac{1}{r} \cdot \left[ {\sqrt {\left( {\frac{k(2n + i)}{n}} \right)^{2} + r^{2} } - \sqrt {\left( {\frac{ki}{n}} \right)^{2} + r^{2} } } \right.} \\ & \left. { - \,\sqrt {\left( {\frac{k(2n + i - 1)}{n}} \right)^{2} + r^{2} } + \sqrt {\left( {\frac{k(i - 1)}{n}} \right)^{2} + r^{2} } } \right] \cdot {\text{d}}r \\ \end{aligned} $$

(27)

In order to simplify this complicated integration equation, we can divide it in four pieces and solve each part of it. As an example, only the solution of part A₁ is given and the other parts can be solved by the same approach.

$$ \varphi_{{{\text{AB}},\Delta }} = \frac{{\mu_{0} I}}{4\pi }\left( {A_{1} - A_{2} - A_{3} + A_{4} } \right) $$

(28)

$$ \begin{aligned} A_{1} = & \sqrt {\left( {\frac{k(2n + i)}{n}} \right)^{2} + \left( {\frac{{k\sqrt 3 \left( {2n - i} \right)}}{n}} \right)^{2} } \\ & - \,k\left( {\frac{(2n + i)}{n}} \right)\ln \left[ {\frac{{\sqrt {\left( {\frac{k(2n + i)}{n}} \right)^{2} + \left( {\frac{{k\sqrt 3 \left( {2n - i} \right)}}{n}} \right)^{2} } + \left( {\frac{k(2n + i)}{n}} \right)}}{{\left( {\frac{k(2n + i)}{n}} \right)}}} \right] \\ \end{aligned} $$

(29)

Since there are two symmetrical triangles within the hexagonal area, the sum of the total flux formed by the AB length is equal to the sum of the two triangular areas. Thus, the total flux equation of the triangles is,

$$ \begin{aligned} \varphi_{{{\text{T}},{\text{AB}},\Delta }} = & 2\frac{{\mu_{0} I}}{4\pi }\left( {A_{1} - A_{2} - A_{3} + A_{4} } \right) \\ = & \frac{{\mu_{0} I}}{2\pi }\left( {A_{1} - A_{2} - A_{3} + A_{4} } \right) \\ \end{aligned} $$

(30)

Finally, the large rectangular area needs to be calculated. With the same approach, the total flux equation can be obtained if the integral boundaries are re-determined,

$$ \varphi_{\text{AB,rectangular}} = \frac{{\mu_{0} I}}{4\pi }\int_{{r_{\text{w}} }}^{{2k\sqrt 3 - r_{\text{w}} }} {\frac{1}{r} \cdot \left[ {\int_{ - k}^{k} {\frac{z + k}{{\sqrt {\left( {z + k} \right)^{2} + r^{2} } }} \cdot {\text{d}}z - \int_{ - k}^{k} {\frac{z - k}{{\sqrt {\left( {z - k} \right)^{2} + r^{2} } }} \cdot {\text{d}}z} } } \right]} \cdot {\text{d}}r $$

(31)

After simplification of the equations for calculating the self-inductance of a hexagonal coil, the total flux is,

$$ \varphi_{\text{AB,total}} = 6\left( {\varphi_{{{\text{T}},{\text{AB}},\Delta }} + \varphi_{\text{AB,rectangular}} } \right) $$

(32)

By using this equation, the self-inductance for a hexagonal coil for any size and wire radius is given by,

$$ L_{\text{hexagon}} = \frac{{6N^{2} \left( {2\varphi_{{{\text{AB}},\Delta }} + \varphi_{\text{AB,rectangular}} } \right)}}{I} $$

(33)