1 Introduction

Vernier reluctance motor was invented more than 50 years ago; however, the permanent magnet Vernier machine was first presented about 20 years ago [1]. In industrial applications, such as wind power generations, in-wheel motors, and traction applications, electrical machines have been used with mechanical gear to generate power at relatively low speed [2]. In recent years, more attention has been paid to PMVMs because they have high torque and low speed intrinsically [3]. PMVMs are also a right candidate for direct-drive applications due to the magnetic gearing effects [4]. Besides, they have low pulsating torque owing to their more sinusoidal EMF waveform than other PM electrical machines [5]. Also, the PMVMs are divided into two types by the flux modulation method for the gearing effects in the air gap: one is split-pole, which has flux modulation poles on the stator and the PMs that are mounted on the rotor surface [6]. The second one is called the hybrid Vernier machine; the PMs are placed on the stator teeth surface modulating the flux from the stator coils, and the rotor has only teeth [7]. Fractional-slot concentrated-winding PMVMs are becoming attractive in many applications due to winding harmonic reduction [8]. Since the split-pole PMVM is first presented, researches on novel topologies focus on concentrated winding in [8] and high-torque-density PM Vernier machine with multiple working harmonics in [9]. Wolfgang Gruber, Richard Remplbauer, Elisabeth, and Gubel designed new bearingless PMV slice motor with external rotor [10]. A new method to design a Vernier generator for wind turbine applications and its basic formulas are proposed in [11]. Chen and Ding proposed a dual-stator Vernier machine for in-wheel applications to improve the power factor [12]. Also, new topologies for increasing torque density and power factor such as dual stator and spoke type have been proposed and analyzed [13, 14]. Also, using spoke magnet array type for improving power factor and increasing torque is presented in [15]. Xu and Jian compare both concentrated and distributed winding for Vernier in [16]. Li and Chau compare harmonic analysis between the Vernier machine and magnet gearing effect in [17]. Besides, pole number and slot shape have a direct influence on cogging torque and these impact research by Zhu [18]. A novel controllable Vernier machine with DC field in order to increase high torque at low speed and control flux weakening at high speed is proposed [19]. A wide speed range to increase efficiency in three-phase mode and improve performance is presented in [20]. Meanwhile, the comparison among different topologies of the split-pole stator has been carried out, and some characteristics, such as back-EMF, torque, cogging torque, power factor, flux density, and efficiency, have been analyzed.

2 Operation principles and torque derivation

Vernier machine operation is similar to magnetic gear; thus:

$$ N_{\text{r}} = N_{\text{s}} \pm p. $$
(1)

For split pole, Vernier machine Ns is satisfied by:

$$ N_{\text{s}} = Z_{\text{s}} \cdot N_{\text{f}} . $$
(2)

The stable torque in the synchronous motor is pulled out when the synchronous speed is:

$$ n = \frac{{60f_{s} }}{{N_{\text{r}} }}. $$
(3)

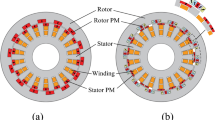
In PMVM, when the rotor has a small movement, the flux changes, which in turn leads to generating high torque. The magnetic flux density distribution produced in the air gap is shown in Fig. 1 with the bold black line. Once the current phase A is maximized, the stator slot creates the magnetic permeance wave, which modulates the magnetic flux density. The slot opening increases the magnetic permeance in the air gap; however, the surface of the tooth tip decreases it. Consequently, the magnetic flux density distribution in the air gap involves the fundamentals with fifth and seventh space harmonic waves [21].

Fig. 1
figure 1

Operation principle of surface PM Vernier machine [21]

Full size image

Also, the general torque is derived through magnetomotive force (MMF) and the flux density in the air gap. The following are the assumptions for the analysis.

  1. 1.

    The saturation effect of steel is neglected.

  2. 2.

    The relative permeability of the PM is one.

  3. 3.

    The flux density, MMF, and permeance in the air gap vary only with the circumferential direction and are uniform in the radial and axial directions [22].

A rotating magnetic field is produced in the air gap when the winding of stator PMVM is excited by balanced three-phase current (Fig. 2):

Fig. 2
figure 2

Definitions of critical axes and angles

Full size image
$$ \begin{aligned} I_{a} & = \sqrt 2 \cdot I_{\text{rms}} \cos (\omega t) \\ I_{b} & = \sqrt 2 \cdot I_{\text{rms}} \cos (\omega t - 2\pi /3) \\ I_{c} & = \sqrt 2 \cdot I_{\text{rms}} \cos (\omega t + 2\pi /3) \\ \end{aligned} $$
(4)

Hence, the air-gap MMF due to the coil current is given via:

$$ \begin{aligned} F_{\text{c}} (\theta_{1} ,t)& = \sum\limits_{n = 1,7,13, \ldots } {\frac{{K_{{{\text{d}}n}} \cdot K_{{{\text{p}}n}} }}{n}} \cos (\omega t - np\theta_{1} ) \\ &\qquad + \sum\limits_{n = 5,11,17, \ldots } {\frac{{K_{{{\text{d}}n}} \cdot K_{{{\text{p}}n}} }}{n}} \cos (\omega t + np\theta_{1} )\\ &= \frac{{3F_{{{\text{c}}1}} }}{2}\left\{ \left[ {\cos (\omega t - p\theta_{1} )} \right] - \frac{1}{7}\left[ {\cos (\omega t - 7p\theta_{1} } \right] \right.\\ &\qquad\qquad\quad \left. + \frac{1}{13}\left[ {\cos (\omega t - 13p\theta_{1} } \right] - \frac{1}{19} \cdots \right\} \\ & = \frac{{3F_{{{\text{c}}1}} }}{2}\left\{ \frac{1}{5}\left[ {\cos (\omega t + 5p\theta_{1} )} \right] - \frac{1}{11}\left[ {\cos (\omega t + 11p\theta_{1} } \right] \right.\\ &\qquad\qquad\quad \left. + \frac{1}{17}\left[ {\cos (\omega t + 17p\theta_{1} } \right] - \frac{1}{23} \cdots \right\} \\ \end{aligned} $$
(5)

where

$$ F_{{{\text{c}}1}} = \frac{0.9NI}{P}\;[23] $$
(6)
$$ \begin{aligned} K_{{{\text{d}}n}} & = \frac{\sin (n\pi /6)}{q\sin (n\pi /6q)} \\ K_{{{\text{p}}n}} & = \sin (n\gamma \pi /2)\;[24]. \\ \end{aligned} $$
(7)

When the rotor is inert, MMF is created by PM rotor. The MMF is given as:

$$ \begin{aligned} F_{\text{PM}} (\theta_{1} ) & = \sum\limits_{{n;{\text{odd}}}}^{\infty } {\frac{{F_{{{\text{PM}}1}} }}{n}} \cos (nN_{\text{r}} \theta_{2} ) \\ & = \sum\limits_{{n;{\text{odd}}}}^{\infty } {\frac{{F_{{{\text{PM}}1}} }}{n}} \cos \left\{ {nN_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} \\ & = F_{{{\text{PM}}1}} \cos \left\{ {N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} + \frac{{F_{{{\text{PM}}1}} }}{3}\cos \left\{ {3N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} + \frac{{F_{{{\text{PM}}1}} }}{5}\cos \left\{ {5N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} + \cdots \\ \end{aligned} $$
(8)

The motor permeance in the air gap can be expressed by:

$$ \begin{aligned} P\left( {\theta_{1} } \right) & = P_{0} + \sum\limits_{m = 1}^{\infty } {P_{m} \cos (mN_{\text{s}} \theta_{1} )} \\ & = P_{0} + P_{1} \cos \left( {N_{\text{s}} \theta_{1} } \right) + P_{1} \cos \left( {2N_{\text{s}} \theta_{1} } \right). \\ \end{aligned} $$
(9)

The air-gap flux density is obtained by multiple \( F_{\text{PM}} \) and P. In considering the significant component and neglecting the redundant part, the air-gap flux density can be expressed as:

$$ \begin{aligned} B_{\text{PM}} & \approx \left[ {F_{{{\text{PM}}1}} \cos \left\{ {N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\}} \right]\left[ {P_{0} + P_{1} \cos \left( {N_{\text{s}} \theta_{1} } \right)} \right] \\ & = F_{{{\text{PM}}1}} \cdot P_{0} \cos \left\{ {N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} + \frac{{F_{{{\text{PM}}1}} \cdot P_{0} }}{2}\cos \left[ {\theta_{1} \left( {N_{\text{s}} + N_{\text{r}} } \right) - N_{\text{r}} \theta_{\text{m}} } \right] \\ & \quad + \;\frac{{F_{{{\text{PM}}1}} \cdot P_{0} }}{2}\cos \left[ {\theta_{1} \left( {N_{\text{r}} - N_{\text{s}} } \right) - N_{\text{r}} \theta_{\text{m}} } \right] \\ & = F_{{{\text{PM}}1}} \cdot P_{0} \cos \left\{ {N_{\text{r}} (\theta_{1} - \theta_{\text{m}} )} \right\} + \frac{{F_{{{\text{PM}}1}} \cdot P_{0} }}{2}\cos \left[ {\theta_{1} \left( {N_{\text{s}} + N_{\text{r}} } \right) - N_{\text{r}} \theta_{\text{m}} } \right] \\ & \quad + \;\frac{{F_{{{\text{PM}}1}} \cdot P_{0} }}{2}\cos \left[ {\theta_{1} \left( {N_{\text{s}} - N_{\text{r}} } \right) + N_{\text{r}} \theta_{\text{m}} } \right]. \\ \end{aligned} $$
(10)

If the entire field energy is stored in the air gap and the virtual air gap (PM), the net torque will be expressed by:

$$ \begin{aligned} T_{e} & = \frac{p\lambda l}{\pi }\int\limits_{0}^{2\pi } {\left\{ {\frac{\partial }{{\partial \theta_{\text{m}} }}\left( {\frac{1}{2}BF} \right)} \right\}} {\text{d}}\theta_{1} \\ & = \frac{p\lambda l}{\pi }\int\limits_{0}^{2\pi } {\left\{ {P(F_{\text{c}} + F_{\text{PM}} )\frac{{\partial F_{\text{PM}} }}{{\partial \theta_{\text{m}} }}} \right\}} {\text{d}}\theta_{1} . \\ \end{aligned} $$
(11)

If all equations are combined, the net torque will be obtained as:

$$ T_{e} = \frac{1}{2}p\lambda lN_{\text{r}} K_{{{\text{d}}1}} K_{{{\text{p}}1}} F_{{{\text{c}}1}} \left( {\frac{{F_{{{\text{PM}}1}} \cdot P_{1} }}{2} \mp \frac{{F_{{{\text{PM}}1}} \cdot P_{0} }}{{N_{\text{r}} /P}}} \right) \cdot \left( {\sin \left( {\omega t \mp N_{\text{r}} \theta_{\text{m}} } \right)} \right). $$
(12)

The harmonic coupling has a significant impact on torque generation as the slot harmonic component is much higher than the fundamental one [22].

3 Theoretical analysis of PMVM with different stator tooth topologies

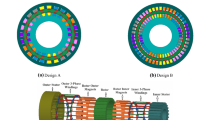
The auxiliary teeth in split-pole PMVM modulate flux in the air gap. Due to the small design space and the inner stator, it is beneficial to use a stator with a low number of poles to achieve the right balance between the stator tooth width and the slot area. Also, the number of winding poles should be small for obtaining a high torque [25]; the number of pole pairs, therefore, is selected as 2. A high number of rotor poles allow reducing the rotor yoke height as the flux distribution over the yoke is superior as compared to a low number of rotor poles. Besides, a low rotor yoke height reduces the rotor inertia [26]. Accordingly, the number of rotor pole pairs is selected as 16. In previous studies, several combinations of Zs and Nf have been proposed. However, in the present paper, the combination is fixed; α, β, and θ will be changed, and certain features will be analyzed. The stator key parameters are shown in Fig. 3. The stator has a main tooth, slot width, auxiliary tooth width, and groove depth. The width of teeth and slots on stator can be evaluated with the corresponding angles α, β, and θ due to the circumferential distribution of the teeth and slots. For a simple analysis, it is assumed that the auxiliary teeth and grooves are all with rectangular geometry (Figs. 4, 5).

Fig. 3
figure 3

Critical parameters of stator teeth geometrical shapes

Full size image
Fig. 4
figure 4

Proposed machine. a 2D geometric. b Explode geometric (3D)

Full size image
Fig. 5
figure 5

Different states for designing the stator

Full size image

The angles of α, β, and θ are satisfied as

$$ \left( {N_{\text{f}} - 1} \right)\alpha + N_{\text{f}} \beta + \theta = \frac{2\pi }{{Z_{\text{s}} }}. $$
(13)

To reveal the quantitative relationship of the three types of angles α, β, and θ, a parameter K, flux modulation pole ratio, is introduced to evaluate the specific relationship among them, where K can be defined as:

$$ K = \frac{{K_{\text{AT}} + 2}}{{K_{\text{AT}} + K_{\text{AS}} }} $$
(14)

where

$$ K_{\text{AT}} = \frac{\beta }{\theta },\;K_{\text{AS}} = \frac{\alpha }{\theta }. $$
(15)

In split-pole-type PMVM, the angle between two adjacent auxiliary teeth changes with the auxiliary tooth width angle as well as K. The optimal value of K for this combination (18/16) is 0.75 [22] (Table 1).

Table 1 Machine model parameters
Full size table

There are four states for designing split-pole stator:

  1. a.

    α = β = θ

In this state, the K parameters will be K = 1.5.

  1. b.

    α = β ≠ θ

In this state, the K parameters will be \( K = \frac{1}{2} + \frac{\theta }{\alpha } = \frac{1}{2} + \frac{\theta }{\beta } \).

  1. c.

    α ≠ β = θ

In this state, the K parameters will be \( K = \frac{3\theta }{\theta + \alpha } \).

  1. d.

    α = θ ≠ β

In this state, the K parameters will be \( K = \frac{\beta + 2\theta }{\beta + \theta } = 1 + \frac{\theta }{\beta + \theta } \).

4 FEA analysis of electromagnetic performance

The above evaluation has been verified through 2-D FEA analysis. All the results were obtained under the same conditions, such as mesh amount, time step, and so on. The significant impact of the proposed motor performance will be discussed in the following.

4.1 No-load performance comparison

The back-EMF and cogging torque can be obtained via the no-load test. After optimizing the motor parameters, the analysis results are compared to the following.

4.1.1 The back-EMF

A similar approach as illustrated in [1] is taken to determine the no-load back-EMF. The back-EMF is more sinusoidal than the other PM machines due to the large rotor poles, few slots, and harmonic couple effects [3]. The magnitude of the fundamental of average torque and the induced voltage is increased by the flux-concentrating structure located on the rotor [27]. If the leakage flux leads to great reduction in the back-EMF, the idea would be justifiable [3]. Thus, the back-EMF amplitude of traditional PM machines is much lower than that of Vernier PM machines causing high torque density in Vernier PM machines [28]. The waveform of back-EMF with corresponding value is shown in Fig. 6. The maximum amplitude for α ≠ β = θ is 46.7 V, and the minimum amplitude for α = β = θ is 38.8 V.

Fig. 6
figure 6

Back-EMF waveform

Full size image

4.1.2 The air-gap flux density

The air-gap flux density waveforms are shown in Fig. 7. According to the figure, the maximum average peak value of the proposed machine for α = θ ≠ β is 0.86 T, and the minimum average peak value for α ≠ β = θ is 0.74 T. As marked in the figure, several peaks have higher amplitudes than the others. This is because, at some points, the N or S poles appear to encounter or nearly face the FMPs on the stator, while at some other points, the PM poles are subject to the stator slots [29].

Fig. 7
figure 7

Air-gap flux density

Full size image

4.1.3 The cogging torque

An additional parameter that can be acquired from the no-load test is cogging torque; it is one of the main elements in the electrical machine. The interaction between the permanent magnet MMF harmonic and the air-gap permeance harmonic is called cogging torque. The cogging torque is dependent on the LCM (least common multiple) of Nr and Ns. The higher value of LCM leads to lower cogging torques [30]. One can describe the cogging torque period of the machines analyzed as δcog = 360°/Ncog, where Ncog represents the least common multiple between the stator teeth number and rotor poles [15]. Specific approaches have been proposed to reduce its value, such as slot or pole skewing, shifting slot, rotor shift PM, and fractional-slots concentrated winding [18]. The minimum cogging torque average for α ≠ β = θ is 1.1%, and the maximum for α = θ ≠ β is about 7.6%, which are shown in Fig. 8.

Fig. 8
figure 8

Cogging torque waveforms

Full size image

4.2 On-load performance comparison

All parameter values for four states are collected in Table 2 so that a better comparison can be made.

Table 2 Performance comparison by 2D-FEA analysis
Full size table

4.2.1 The average torque, the torque density, and torque ripple

The average torque concerning different slot openings is provided in Fig. 9. With increasing slot opening, the average torque tends to increase. Due to the higher back-EMF of Vernier machines caused by the magnetic gearing effect as explained before, they are of higher torques. Rather than using open slots, one can use semi-closed slots to limit the torque ripple. Given the increased modulation effect in the Vernier machines, the machines with open slots produce higher torques. However, for those with semi-closed slots, the torque ripple is much higher [30]. However, it should follow the optimal value of auxiliary tooth to auxiliary slot that is about 0.45 [10]. The maximum average torque for α ≠ β = θ is 9.33 N m, and the average torque for α = β ≠ θ is 9.31 N m that is a little bit lower than α ≠ β = θ, while the torque ripple for α ≠ β = θ is remarkably lower than α = β ≠ θ. The torque ripple is given as:

Fig. 9
figure 9

Torque waveforms

Full size image
$$ {\text{Ripple}} = \frac{{T_{\hbox{max} } - T_{\hbox{min} } }}{{T_{\text{ave}} }} \times 100 $$
(16)

Based on Fig. 9 and Table 2, the highest average torque and the lowest torque ripple are associated with α ≠ β = θ. It should be noted that α ≠ β = θ and α = β ≠ θ have the highest torque density than the others. Their values, according to Table 2, are about 4.1 N m/kg.

4.2.2 The core loss and the total loss

The core loss depends on the frequency; the proposed motor value is 133.33 Hz. Also, the total loss is the sum of the copper and iron losses. It is evident that a short-end winding in concentrated-winding Vernier machines results in low copper loss [31]. Copper loss is shown in Fig. 10. Highest core and total losses can be seen for α = β ≠ θ, and their values are 11.4 watts and 84.96, respectively.

Fig. 10
figure 10

Loss waveforms: a the core loss, b the total loss

Full size image

4.2.3 The self-inductance and the power factor

The power factor refers to the efficiency of the input power delivery to the output one. Thus, a high power factor is vital for excellent machine performance. It should be noted that the reactance of the concentrated winding is lower than the distributed one [31]. The power factor of concentrated winding, therefore, is better than distributed winding. Generally, because of utilizing more magnets on the rotor than traditional machines, a Vernier motor is of a high operating frequency. Also, it leads to much greater reactance. Furthermore, a Vernier motor has the same stator structure as that of the conventional PM motors. Therefore, it is of the same winding inductance as well. However, since the reactance is proportional to the operating frequency, much greater reactance is created [3]. Moreover, the power factor strongly depends on the stator leakage flux. Therefore, the reason for the oscillation is the change in the coverage of the auxiliary slot by the FMPs. The stator leakage flux will be high if the FMPs cover the auxiliary slot; therefore, the power factor is low. Nonetheless, if no FMP covers the auxiliary slot, the stator leakage flux will be low while the power factor will be high [32].

The induced voltage and injecting current are illustrated in Fig. 11. Furthermore, the self-inductance waveforms are depicted in Fig. 12. It can be seen that the lower self-inductance is 11.7 mH, α = β = θ; however, the power factor is not the highest among all. The reason for the high level of the stator flux linkage is that the FMPs cover the auxiliary slot. The power factor angle is obtained as follows:

$$ \begin{aligned} {\text{PF}} & = \cos \left( {\frac{{t_{c} - t_{0} }}{T} \times 360} \right) \\ & = \cos \left( {\frac{{t_{c} - t_{0} }}{{t_{2} - t_{1} }} \times 360} \right). \\ \end{aligned} $$
(17)
Fig. 11
figure 11

Injecting current, induced voltage, and the power factor angle

Full size image
Fig. 12
figure 12

Waveforms of self-inductance

Full size image

If t0 is near tc, the power factor will be high; as can be seen in Fig. 11, the power factor of α ≠ β = θ is higher than others because it is near them.

4.2.4 Efficiency

The last and one of the most critical parameters in the electrical machine is efficiency that is defined as:

$$ {\text{Etta}} = \frac{{P_{\text{out}} }}{{P_{\text{out}} + P_{\text{Losses}} }}. $$
(18)

According to Table 2, the highest efficiency is 85.8% for α ≠ β = θ as it has the highest torque among them and lower total loss than α = β ≠ θ.

5 Conclusion

In this paper, all of the conditions for the split-pole Vernier machine were investigated through theoretical and FEA analysis. The sizing equations and principles of operation were investigated for the proposed machine, and essential parameters were presented to be discussed. Further, all the essential parameters have been analyzed and evaluated via 2-D ANSYS Electronics. They were obtained under the same circumstances. For a particular purpose, the high power factor of the outer rotor has been due to low reactance and low flux leakage. The back-EMFs have low harmonic order due to concentrated winding; the waveform figures of back-EMF verify this claim because they have minimum distortion. As mentioned earlier, the combination of pole number and slot’s shape has an impact on cogging torque directly. In this paper, different conditions among α, β, and θ have been debated. From all figures and tables, the best state is α ≠ β = θ because it has the highest torque and torque density, power factor, efficiency, and highest output power. Also, it has the lowest cogging torque and torque ripple than the other states.