Abstract
This paper offers a comprehensive treatment of the question as to whether a binary relation can be consistent (transitive) without being decisive (complete), or decisive without being consistent, or simultaneously inconsistent or indecisive, in the presence of a continuity hypothesis that is, in principle, non-testable. It identifies topological connectedness of the (choice) set over which the continuous binary relation is defined as being crucial to this question. Referring to the two-way relationship as the Eilenberg–Sonnenschein (ES) research program, it presents four synthetic, and complete, characterizations of connectedness and its natural extensions and two consequences that stem from it. The six theorems make connections that have eluded decision theory and thereby generalize the pioneering work of Eilenberg, Sonnenschein, Schmeidler and Sen. We draw the relevance to several applied contexts, as well as to ongoing theoretical work.




Similar content being viewed by others
Notes
The first sentence is taken from p. 298, and the second from p. 367 in Sen (2017). Sen fills the ellipsis in the first by referring to Molière, and in the second, by the Aristotelian counsel that one aspire to as much precision as the subject deserves.
See, for example, Barten and Böhm (1982), a useful survey but one that misses the connections that we emphasize here. The properties of the binary relation referred to below constitute standard textbook material, as in Barten and Böhm (1982) or Sen (2017) for example, but precise definitions are spelt out for the reader’s convenience in the section to follow.
We may point out here that Sonnenschein (1965) is an elaboration of his Ph.D. dissertation that dispensed with Eilenberg’s requirement that the binary relation be antisymmetric, that preferences not be constrained by the requirement of singleton indifference sets. We return to this point in the sequel.
We return to this theorem below.
Finite-dimensional Euclidean spaces, the simplex of (objective) lotteries over a finite set and infinite-dimensional topological vector spaces are some of the most obvious examples.
This remains professional folk wisdom: see for example page 80 (last paragraph) in Gilboa (2009).
As is well known, this aspect of Eilenberg’s paper was taken up by Debreu (1954).
There is some irony in that we extend Sen’s work in a direction that he explicitly wanted to avoid. He criticizes the literature’s “ overwhelming concern with transitivity and continuity,” and referring to his results, writes how they are “derived without any assumption of continuity and related conditions as these conditions might not be very realistic for certain problems of rational choice, especially in dealing with social decisions.”
This is nothing but a loose summary sentence of the ideas explicated in the four paragraphs above. We shall reserve the term “foundational” for the results enumerated in the second paragraph above.
For a precise statement, see (a) \(\Rightarrow \) (b) in Theorem 1 and its detailed discussion encapsulated in Proposition 1 below.
We do not mean to overemphasize the novelty: a cursory reference to Wilder (1949), or to Dugundji (1966), shows that spaces with finitely many components are well known and studied extensively. The reader should beware, however, that k-connectedness is used in algebraic topology with a totally different meaning.
There is the weaker concept of a quasi-component of a topological space. In a compact Hausdorff space, the two are identical; see Wilder (1949). Even though many economic settings assume the Hausdorff separation axiom, compactness may fail, like the consumption set of a consumer in a Walrasian economy. Hence, it may be of interest to see whether the results in this paper generalize to quasi-components.
In terms of a reader’s guide, and especially for a first reading, one may read these theorems for the case \(k=1,\) and instead of the full equivalence, even limit oneself to the forward direction as in the foundational papers.
We may point out here in anticipation that our joint treatment of these foundational results has also allowed us to provide alternative proofs of the results of Eilenberg and Sonnenschein. Our method of proof is inspired by Schmeidler and is totally different compared to theirs; see this observation formally made in the paragraph preceding the proof of this theorem, and in the remark following it.
Note that the usage here differs from that of Houthakker’s concept; see Sen (2017, pp. 94, 295–298, 299).
We return to this in Sect. 4.1.
To be sure, the discussion in this paragraph assumes \(k=1;\) the foundational literature is silent on higher values of the natural number k.
We have already emphasized the first question in Footnote 8, but what is being emphasized here is the existence of the relation rather than a function, a question that is taken up in the social choice literature; see Khan and Uyanık (2018) for an exploration of this question and an elaboration of this connection. At any rate, as we shall see, it is essential to the result we present below.
The reader is again warned about the lack of a uniform terminology in the literature; see Sen (2017, p. 54).
We do not do this because Theorem 3 is primarily motivated by the transitivity claim of Eilenberg–Sonnenschein.
We present here a slightly stronger version of Sonnenschein’s theorems in order to underscore the comparison. He assumes the connectedness of \(X\backslash I\) instead of connectedness of X. It is easy to prove a version of our results under this assumption. A result similar to Sonnenschein’s theorem is provided by Rader (1963, Lemma) under a stronger connectedness assumption which requires the upper sections of the weak preference relation to be connected.
It should be noted, however, that Lorimer also shows that these conditions are not only sufficient for transitivity of a complete relation, but also necessary, and hence there is something extra and of consequent use in his paper.
We are primarily motivated by forging connections to current work; there is little doubt that results of several of the papers that we connect to can be generalized to the setting of k-connected sets for any natural number k, and thereby to reformulate the theorem presented below along the lines of Theorem 1.
These “covering” types of derived relations have important applications and implications in decision theory as well as in social choice theory. In particular, they have been used for the numerical representation of incomplete preferences; see, for example, Chateauneuf (1987) for representation of interval orders and Peleg (1970) and Galaabaatar and Karni (2013) for expected utility representation of incomplete preferences. In social choice theory, the “covering relation” has been used since mid-twentieth century; see Duggan (2013) for a comprehensive survey on covering relation.
We investigate the deconstruction of the continuity postulate elsewhere. In particular, we study the topological and behavioral implications of linear, order and differentiability structures; see Khan and Uyanık (2019).
We return to this issue in Sect. 5; see Footnote 61, and the text in footnotes.
Since we exclusively work with a topological structure, we do not investigate the implications of the added assumptions related to linear structure on the ES program. Uzawa (1960) pioneered this line of research by showing that convexity of a complete preference relation defined on a convex subset of a topological vector space with closed upper sections and a transitive asymmetric part implies that the relation itself is transitive. This result is reproduced and generalized by Sonnenschein (1965, Theorems 5 and 6) and picked up by Neuefeind and Trockel (1995) and Galaabaatar et al. (2019).
Note that to say that the symmetric part of a relation is complete renders the relation trivial, whereas to say that the asymmetric part is complete furnishes the contradiction that an element of the space is preferred to itself. In Sen (1969),
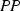 is the crucial transitivity condition and he found it convenient to give it a more usable name: “quasi-transitivity.” In this connection, also see the subject index in Sen (2017) for additional discussion of his named concept.
is the crucial transitivity condition and he found it convenient to give it a more usable name: “quasi-transitivity.” In this connection, also see the subject index in Sen (2017) for additional discussion of his named concept.For example, to see
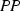 and
and  imply T from Fig. 3b, simply note that
imply T from Fig. 3b, simply note that 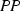 and
and 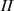 imply
imply 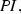 which combined with
which combined with  then implies T. And so on for the other implications.
then implies T. And so on for the other implications.There is a rich philosophical literature on the discussion of non-transitivity, already referred to in Footnote 35. One may add that Tullock (1964) defends transitivity by using simple logical arguments and criticizes the experiments which argue evidence against transitivity. Anand (1993) criticizes Tullock for not considering ternary relation; also see also Luce (1956), Fishburn (1970) and Gilboa and Lapson (1995).
We warn the reader of the difference in terminology; see Footnote 18 above.
As we shall have occasion to see below, all this supports the quotation from Wakker in the next section about the importance of judging the conditions in combination.
See Sonnenschein (1965, Footnote 4 and Theorem 7A) where the alternative proof of the special case is justified on the grounds of furnishing “an interesting technique.”
See, in particular, (Wilder 1949, Theorems 4:12 and 9.3); also Dickman (1984), Brown (2006), Brown and Camarena (2015) and their references for modern work on the property. Note that the PBP is not a strengthening of the connectedness assumption since any space with the discrete topology satisfies it, but rather a different separation property.
In a connected and locally connected space, path-connectedness of the sections of a complete relation R implies that I has connected sections. Moreover, connectedness of the sections of I in a connected space implies that R has connected sections, which is weaker than path-connectedness. See Wilder (1949, Theorem 4.5 on p. 49 and Theorem 9.9 on p. 20) for the proofs.
Gerasimou (2015) shows that reflexive, transitive and additive binary relation with closed upper sections has a closed graph, and hence, convexity of a relation has implications on its continuity; see Footnote 32 for further references and discussion on convexity.
A celebrated example of the former is Malinvaud (1952); also see Footnote 48. An example of the latter is a reconsideration of Shafer’s non-transitive consumer that we present in Sect. 4.2, and of Schmeidler’s existence theorem in Sect. 4.3; also see Footnote 22. What we do not mean by the word hiddenness is the sense that is given to it by Tourky and Yannelis (2000). Their usage is orthogonal to ours, and perhaps also to redundancy: they refer to an assumption being “hidden” as one that is explicit but essential in the sense that eliminating it would require additional hypotheses to obtain the same consequences.
Gorno (2018, Proposition 10) presents a result that Schmeidler’s theorem as a special case, but rather than the necessity and sufficiency of the property, resets it on maximal \(\succeq \)-domains, maximal on which the relation is complete.
As Kim–Richter also note, McKenzie (1981) raises a similar point and writes “Whether the preference relation \(\succcurlyeq _i\) is complete seems to be a matter of definition, since x incomparable with y can be replaced harmlessly by x indifferent to y in the absence of transitivity.”
This claim is based on the use of the convexity assumption as in Shafer. There is little doubt that the thrust of the claim also holds in a modified form with the weaker convexity assumption that Kim–Richter rely on.
We summarize the assumptions of the version of Debreu’s theorem restated in Arrow and Debreu (1954, Lemma).
Note that without non-triviality, the existence of an equilibrium is triviality, and hence the non-triviality assumption is non-restrictive.
See Assumptions 2.1 (excluding (e) and (f)), 2.6, 2.7 and 2.8 in Broome (1972).
Note that Eilenberg (1941, 2.1) observes the hiddenness of transitivity. Moreover, our insertion of non-triviality in the statement of Eilenberg’s theorem does not do violence to his original statement because of the consideration emphasized in Footnote 20 and in the text it footnotes.
While Peleg’s representation provides only froward direction representation result for incomplete preferences, Majumdar–Sen’s approach provides both directions.
This literature stems from the classic work of Herstein and Milnor (1953), where the topological structure is restricted to that on the unit interval, and the overall thrust is algebraic. We also single out in this connection, Moldau (1996, Proposition 1) and Neuefeind and Trockel (1995). Moldau asserts that transitivity on every closed interval of a preference ration defined on a linear space follows from a weak convexity assumption, and as such, hidden by the convexity postulate. Neuefeind–Trockel show that completeness and transitivity of a relation defined on a topological vector space follow from a convexity postulate under suitable consistency and continuity postulates. Since we are limiting ourselves to the topological register, we hope to engage this claim elsewhere; also see footnote 32 for further references and discussion regarding the convexity assumption.
Note that the implication (a) \(\Rightarrow \) (d) in Theorem 4 does not require the topological space to be quasi-ordered and hence is true for any topological space.
See Bernheim and Rangel (2009, pp. 75–76); also their Theorem 7 which they see as following directly from standard results of Fon, Mandler, Otani, Rigotti and Shannon.
See also Ioannides (2006) for a topological investigation of social interactions.
In some sense, we have kept doing versions that approach such a portmanteau theorem.
The reader is referred to the counterexample a little above the statement of Theorem 3.
As already pointed out in Footnote 3 in the context of the mathematical literature, Ward (1954) and Bridges and Mehta (1995) are important references subsequent to Nachbin’s pioneering monograph on “Topology and Order;” and McGehee (1992) for application to dynamical systems. The philosophical literature is immense but Anand (1987, 1993) furnishes an admirable entry into issues concerning the rationality or the irrationality of transitivity and completeness; in addition to the references in Sen (2017) and Temkin, see Tullock (1964). To be sure, any sharp lines to differentiate between the substantive and the technical eventually leads to sterility.
All this is now so much part of the folklore that detailed references are hardly necessary. But the reader can do no worse than beginning with Fishburn (1972) and Gilboa (2009) on the one hand, and Mehta (1998) and Bridges and Mehta (1995) on the other. For current activity in the field, in addition to the three references with which we began Sect. 4, we refer the reader to Gerasimou (2017) and Strzalecki (2013) and their references.
Note that we can choose this connected subset as the component C of I(z) which contains \(I_z\). This follows from the fact that if a set is connected in a subspace Y of a topological space, then it is also connected in any subspace containing Y. In order to see this, note that it follows from \(I_z\) separates x and y that there exist distinct components \(C_x\) and \(C_y\) of \(X\backslash I_z\) such that \(x\in C_x\) and \(y\in C_y\). Assume that x and y are contained in the same component \(C_{xy}\) of \(X\backslash C.\) Since C contains \(I_z,\) \(X\backslash C\subset X\backslash I_z.\) Hence, \(C_{xy}\) is connected in \(X\backslash I_z.\) Then, \(x\in C_x\cap C_{xy}\) and \(y\in C_y\cap C_{xy}\) contradict \(C_x\) and \(C_y\) being distinct components of \(X\backslash I_z.\) Therefore, x and y are contained in distinct components of \(X\backslash C,\) i.e., C separates x and y. Since any component of a space is connected, the requirement that the subset \(I_z\) is closed in the definition of the Phragmen–Brouwer property in Wilder (1949, Property V\('\), p. 50) is not restrictive. However, our version requires the separation property holds only for open sets.
Gerasimou (2013, Corollary 3) showed that this statement is true provided that the space is connected and R is reflexive. However, the statement is true without the reflexivity assumption and the construction in his proof directly follows. Hence, we drop reflexivity.
A similar result for antisymmetric binary relations is provided by Eilenberg (1941, 1.4).
References
Alcantud, J., Gutiérrez, J.: Preference through indifference: a topological approach. J. Math. Econ. 31(4), 543–551 (1999)
Anand, P.: Are the preference axioms really rational? Theory Decis. 23(2), 189–214 (1987)
Anand, P.: The philosophy of intransitive preference. Econ. J. 103(417), 337–346 (1993)
Arrow, K.J., Debreu, G.: Existence of an equilibrium for a competitive economy. Econometrica 22(3), 265–290 (1954)
Arrow, K.J., Sen, A.K., Suzumura, K.: Social Choice Re-examined. vol. 1 and 2. St. Martin’s Press, New York (1995, 1996)
Arrow, K.J., Sen, A.K., Suzumura, K.: Handbook of Social Choice and Welfare. vol. 1 and 2. Elsevier, North Holland (2002, 2011)
Asheim, G.B., Bossert, W., Sprumont, Y., Suzumura, K.: Infinite-horizon choice functions. Econ. Theory 43(1), 1–21 (2010). https://doi.org/10.1007/s00199-008-0423-z
Balasko, Y., Tvede, M.: General equilibrium without utility functions: how far to go? Econ. Theory 45(1–2), 201–225 (2010). https://doi.org/10.1007/s00199-009-0496-3
Barten, A.P., Böhm, V.: Consumer theory. In: Arrow, K., Intriligator, M. D. (eds.) Handbook of Mathematical Economics, vol. 2, pp. 381–429. North Holland (1982)
Bergstrom, T.C., Parks, R.P., Rader, T.: Preferences which have open graphs. J. Math. Econ. 3(3), 265–268 (1976)
Bernheim, B.D., Rangel, A.: Beyond revealed preference: choice-theoretic foundations for behavioral welfare economics. Q. J. Econ. 124(1), 51–104 (2009)
Bleichrodt, H., Li, C., Moscati, I., Wakker, P.P.: Nash was a first to axiomatize expected utility. Theory Decis. 81(3), 309–312 (2016)
Bridges, D.S., Mehta, G.B.: Representations of Preference Orderings. Springer, Berlin (1995)
Broome, J.: Approximate equilibrium in economies with indivisible commodities. J. Econ. Theory 5(2), 224–249 (1972)
Brown, R.: Groupoids, the Phragmen–Brouwer property, and the Jordan curve theorem. J. Homotopy Relat. Struct. 1(1), 175–183 (2006)
Brown, R., Camarena, O.A.: Erratum to: Groupoids, the Phragmen–Brouwer property, and the Jordan curve theorem. J. Homotopy Relat. Struct. 10(3), 669–672 (2015)
Carbonell-Nicolau, O., McLean, R.P.: Nash and Bayes–Nash equilibria in strategic-form games with intransitivities. Econ. Theory (2018). https://doi.org/10.1007/s00199-018-1151-7
Carmona, G.: Symposium on: existence of Nash equilibria in discontinuous games. Econ. Theory 48(1), 1–4 (2011). https://doi.org/10.1007/s00199-010-0576-4
Cerreia-Vioglio, S., Giarlotta, A., Greco, S., Maccheroni, F., Marinacci, M.: Rational preference and rationalizable choice. Econ. Theory (2018). https://doi.org/10.1007/s00199-018-1157-1
Chateauneuf, A.: Continuous representation of a preference relation on a connected topological space. J. Math. Econ. 16(2), 139–146 (1987)
Dasgupta, P., Maskin, E.: The existence of equilibrium in discontinuous economic games, I: theory, II: applications. Rev. Econ. Stud. 53(1), 1–41 (1986)
Debreu, G.: A social equilibrium existence theorem. Proc. Natl. Acad. Sci. 38(10), 886–893 (1952)
Debreu, G.: Chapter 11: Representation of a preference ordering by a numerical function. In: Thrall, M., Davis, R., Coombs, C. (eds.) Decision Processes, pp. 159–165. Wiley, New York (1954)
Debreu, G.: Topological methods in cardinal utility theory. In: Arrow, K., Karlin, S., Suppes, P. (eds.) Mathematical Methods in the Social Sciences, pp. 16–26. Stanford University Press, California (1960)
Debreu, G.: Existence of competitive equilibrium. In: Arrow, K., Intriligator, M. D. (eds.) Handbook of Mathematical Economics, vol. 2, pp. 697–743. North Holland (1982)
Dickman Jr., R.F.: A strong form of the Phragmen–Brouwer theorem. Proc. Am. Math. Soc. 90(2), 333–337 (1984)
Dierker, E.: Equilibrium analysis of exchange economies with indivisible commodities. Econometrica 39(6), 997–1008 (1971)
Dubra, J.: Continuity and completeness under risk. Math. Soc. Sci. 61(1), 80–81 (2011)
Dubra, J., Maccheroni, F., Ok, E.A.: Expected utility theory without the completeness axiom. J. Econ. Theory 115(1), 118–133 (2004)
Duggan, J.: Uncovered sets. Soc. Choice Welf. 41(3), 489–535 (2013)
Dugundji, J.: Topology. Allyn and Bacon, Boston (1966)
Edelman, P.H., Jamison, R.E.: The theory of convex geometries. Geom. Dedic. 19(3), 247–270 (1985)
Eilenberg, S.: Ordered topological spaces. Am. J. Math. 63(1), 39–45 (1941)
Evren, Ö.: On the existence of expected multi-utility representations. Econ. Theory 35(3), 575–592 (2008). https://doi.org/10.1007/s00199-007-0252-5
Evren, Ö.: Scalarization methods and expected multi-utility representations. J. Econ. Theory 151, 30–63 (2014)
Fishburn, P.C.: Utility theory. Manag. Sci. 14(5), 335–378 (1968)
Fishburn, P.C.: Intransitive indifference in preference theory: a survey. Oper. Res. 18(2), 207–228 (1970)
Fishburn, P.C.: Mathematics of Decision Theory. Mouton, The Hauge (1972)
Fleurbaey, M., Blanchet, D.: Beyond GDP: Measuring Welfare and Assessing Sustainability. Oxford University Press, Oxford (2013)
Fleurbaey, M., Salles, M., Weymark, J.: Justice, Political Liberalism, and Utilitarianism. Oxford University Press, Oxford (2006)
Galaabaatar, T., Karni, E.: Subjective expected utility with incomplete preferences. Econometrica 81(1), 255–284 (2013)
Galaabaatar, T., Khan, M.A., Uyanık, M.: Completeness and transitivity of preferences on mixture sets. Math. Soc. Sci. 99, 49–62 (2019)
Gerasimou, G.: Consumer theory with bounded rational preferences. J. Math. Econ. 46(5), 708–714 (2010)
Gerasimou, G.: On continuity of incomplete preferences. Soc. Choice Welf. 41(1), 157–167 (2013)
Gerasimou, G.: (Hemi) continuity of additive preference preorders. J. Math. Econ. 58, 79–81 (2015)
Gerasimou, G.: Partially dominant choice. Econ. Theory 61(1), 127–145 (2016). https://doi.org/10.1007/s00199-015-0869-8
Gerasimou, G.: Indecisiveness, undesirability and overload revealed through rational choice deferral. Econ. J. 128, 2450–2479 (2017)
Gerasimou, G.: Dominance solvable multicriteria games with incomplete preferences. Econ. Theory Bull. (2018). https://doi.org/10.1007/s40505-018-0159-2
Gilboa, I.: Theory of Decision Under Uncertainty. Cambridge University Press, Cambridge (2009)
Gilboa, I., Lapson, R.: Aggregation of semiorders: intransitive indifference makes a difference. Econ. Theory 5(1), 109–126 (1995). https://doi.org/10.1007/BF01213647
Gorman, W.M.: The structure of utility functions. Rev. Econ. Stud. 35(4), 367–390 (1968)
Gorno, L.: The structure of incomplete preferences. Econ. Theory 66(1), 159–185 (2018). https://doi.org/10.1007/s00199-017-1057-9
Harsanyi, J.C.: Cardinal welfare, individualistic ethics, and interpersonal comparisons of utility. J. Political Econ. 63(4), 309–321 (1955)
He, W., Yannelis, N.C.: Existence of Walrasian equilibria with discontinuous, non-ordered, interdependent and price-dependent preferences. Econ. Theory 61(3), 497–513 (2016). https://doi.org/10.1007/s00199-015-0875-x
Herstein, I.N., Milnor, J.: An axiomatic approach to measurable utility. Econometrica 21(2), 291–297 (1953)
Hervés-Beloso, C., del Valle-Inclán Cruces, H.: Continuous preference orderings representable by utility functions. J. Econ. Surv. 33(1), 179–194 (2019)
Ioannides, Y.M.: Topologies of social interactions. Econ. Theory 28(3), 559–584 (2006). https://doi.org/10.1007/s00199-005-0646-1
Jackson, M.O.: Socal and Economic Networks. Princeton University Press, Princeton (2008)
Karni, E.: Axiomatic foundations of expected utility and subjective probability. In: Machina, M., Viscusi, K. (eds.) Handbook of the Economics of Risk and Uncertainty, vol. 1, pp. 1–39. Elsevier (2014)
Khan, M.A., Sun, Y.: On a reformulation of Cournot–Nash equilibria. J. Math. Anal. Appl 146(2), 442–460 (1990)
Khan, M.A., Sun, Y.: Non-cooperative games with many players. In: Aumann, R., Hart, S. (eds.) Handbook of Game Theory with Economic Applications, vol. 3, pp. 1761–1808. North Holland (2002)
Khan, M.A., Uyanık, M.: On the existence of continuous binary relations on a topological space. mimeo (2018)
Khan, M.A., Uyanık, M.: The continuity postulate in economic theory: a deconstruction and an integration. mimeo (2019)
Khan, M.A., Yamazaki, A.: On the cores of economies with indivisible commodities and a continuum of traders. J. Econ. Theory 24(2), 218–225 (1981)
Kim, T., Richter, M.K.: Nontransitive-nontotal consumer theory. J. Econ. Theory 38(2), 324–363 (1986)
Lorimer, P.: A note on orderings. Econometrica 35(3–4), 537–539 (1967)
Luce, R.D.: Semiorders and a theory of utility discrimination. Econometrica 24(2), 178–191 (1956)
Magyarkuti, G.: Revealed preferences: a topological approach. J. Math. Econ. 46(3), 320–325 (2010)
Majumdar, M., Sen, A.: A note on representing partial orderings. Rev. Econ. Stud. 43(3), 543–545 (1976)
Malinvaud, E.: Note on von Neumann–Morgenstern’s strong independence axiom. Econometrica 20(4), 679 (1952)
Marschak, J.: Rational behavior, uncertain prospects, and measurable utility. Econometrica 18(2), 111–141 (1950)
Mas-Colell, A.: An equilibrium existence theorem without complete or transitive preferences. J. Math. Econ. 1(3), 237–246 (1974)
Mas-Colell, A.: A model of equilibrium with differentiated commodities. J. Math. Econ. 2(2), 263–295 (1975)
Mas-Colell, A.: Indivisible commodities and general equilibrium theory. J. Econ. Theory 16(2), 443–456 (1977)
Mas-Colell, A., Zame, W.R.: Equilibrium theory in infinite dimensional spaces. In: Hildenbrand, W., Sonnenschein, H. (eds.) Handbook of Mathematical Economics, vol. 4, pp. 1835–1898 (1991)
McGehee, R.: Attractors for closed relations on compact Hausdorff spaces. Indiana Univ. Math. J. 41(4), 1165–1209 (1992)
McKenzie, L.W.: The classical theorem on existence of competitive equilibrium. Econometrica 49(4), 819–841 (1981)
McKenzie, L.W.: Classical General Equilibrium Theory, vol. 1. The MIT Press, Cambridge (2005)
Mehta, G.B.: Preference and utility. In: Barbera, S., Hammond, P. J., Seidl, C. (eds.) Handbook of Utility Theory: Principles, vol. 1, pp. 1–47. Kluwer Academic Publishers (1998)
Moldau, J.H.: A simple existence proof of demand functions without standard transitivity. J. Math. Econ. 25(3), 325–333 (1996)
Narens, L.: Abstract Measurement Theory. MIT Press, Cambridge (1985)
Nash, J.F.: The bargaining problem. Econometrica 18(2), 155–162 (1950a)
Nash, J.F.: Equilibrium points in n-person games. Proc. Natl. Acad. Sci. 36(1), 48–49 (1950b)
Neuefeind, W., Trockel, W.: Continuous linear representability of binary relations. Econ. Theory 6(2), 351–356 (1995). https://doi.org/10.1007/BF01212495
Newman, M.E.J.: Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 103(23), 8577–8582 (2006)
Peleg, B.: Utility functions for partially ordered topological spaces. Econometrica 38(1), 93–96 (1970)
Pfanzagl, J.: Theory of Measurement. Springer, Berlin (1971)
Qin, D.: Partially dominant choice with transitive preferences. Econ. Theory Bull. 5(2), 191–198 (2017)
Quah, J.K.: Weak axiomatic demand theory. Econ. Theory 29(3), 677–699 (2006). https://doi.org/10.1007/s00199-005-0017-y
Rader, T.: The existence of a utility function to represent preferences. Rev. Econ. Stud. 30(3), 229–232 (1963)
Rébillé, Y.: Continuous utility on connected separable topological spaces. Econ. Theory Bull. 7, 147–153 (2019)
Reny, P.J.: On the existence of pure and mixed strategy Nash equilibria in discontinuous games. Econometrica 67(5), 1029–1056 (1999)
Reny, P.J.: Introduction to the symposium on discontinuous games. Econ. Theory 61(3), 423–429 (2016). https://doi.org/10.1007/s00199-016-0962-7
Richter, M., Rubinstein, A.: Back to fundamentals: Equilibrium in abstract economies. Am. Econ. Rev. 105(8), 2570–94 (2015)
Riella, G.: On the representation of incomplete preferences under uncertainty with indecisiveness in tastes and beliefs. Econ. Theory 58(3), 571–600 (2015). https://doi.org/10.1007/s00199-015-0860-4
Samuelson, P.A.: Bergsonian welfare economics. In: Rosefields, S. (ed.) Economic welfare and the economics of Soviet socialism: essays in honor of Abram Bergson, pp. 223–266. Cambridge University Press, New York (1981)
Schmeidler, D.: Competitive equilibria in markets with a continuum of traders and incomplete preferences. Econometrica 37(4), 578–585 (1969)
Schmeidler, D.: A condition for the completeness of partial preference relations. Econometrica 39(2), 403–404 (1971)
Sen, A.: Quasi-transitivity, rational choice and collective decisions. Rev. Econ. Stud. 36(3), 381–393 (1969)
Sen, A.: Internal consistency of choice. Econometrica 61(3), 495–521 (1993)
Sen, A.: Collective Choice and Social Welfare: An Expanded Edition. Harvard University Press, Massachusetts (2017)
Shafer, W.: The nontransitive consumer. Econometrica 42(5), 913–919 (1974)
Shafer, W., Sonnenschein, H.: Equilibrium in abstract economies without ordered preferences. J. Math. Econ. 2(3), 345–348 (1975)
Sonnenschein, H.: The relationship between transitive preference and the structure of the choice space. Econometrica 33(3), 624–634 (1965)
Sonnenschein, H.: Reply to “A note on orderings”. Econometrica 35(3, 4), 540 (1967)
Sonnenschein, H.: Demand theory without transitive indifference with applications to the theory of competitive equilibrium. In: Chipman, J., Hurwicz, L., Richter, M., Sonenschein, H. (eds.) Preferences, Utility and Demand: A Minnesota Symposium, pp. 215–234. Harcourt Brace Jovanovich, New York (1971)
Strzalecki, T.: Temporal resolution of uncertainty and recursive models of ambiguity aversion. Econometrica 81(3), 1039–1074 (2013)
Suzumura, K.: Choice, Preferences and Procedures. Harvard University Press, Cambridge (2016)
Temkin, L.S.: Rethinking the Good: Moral Ideals and the Nature of Practical Reasoning. Oxford University Press, Oxford (2015)
Thomson, W.: Fair allocation rules. In: Arrow, K., Sen, A., Suzumura, K. (eds.) Handbook of Social Choice and Welfare, vol. 2, pp. 393–506. Elsevier (2011)
Tourky, R., Yannelis, N.C.: Markets with many more agents than commodities: Aumann’s “hidden” assumption. J. Econ. Theory 101(1), 189–221 (2000)
Tullock, G.: The irrationality of intransitivity. Oxf. Econ. Pap. 16(3), 401–406 (1964)
Ullman-Margalit, E., Morgenbesser, S.: Picking and choosing. Soc. Res. 44(4), 757–785 (1977)
Uyanık, M.: Maximality in games and economies. Unpublished manuscript (2014)
Uzawa, H.: Preference and Rational Choice in the Theory of Consumption. Stanford University Press, Palo Alto (1960)
Vilkas, É.: Utility theory. J. Sov. Math. 13(4), 532–550 (1980)
Vind, K.: Independence, Additivity, Uncertainty. With Contributions by B. Grodal. Springer, Berlin (2003)
von Neumann, J., Morgenstern, O.: Theory of Games and Economic Behavior, 2nd edn. Princeton University Press, New Jersey (1947)
Wakker, P.: The algebraic versus the topological approach to additive representations. J. Math. Psychol. 32(4), 421–435 (1988a)
Wakker, P.: Continuity of preference relations for separable topologies. Int. Econ. Rev. 29(1), 105–110 (1988b)
Wakker, P.P.: Additive Representations of Preferences: A New Foundation of Decision Analysis. Kluwer Academic Publishers, Boston (1989)
Ward, L.: Partially ordered topological spaces. Proc. Am. Math. Soc. 5(1), 144–161 (1954)
Wilder, R.L.: Topology of Manifolds. American Mathematical Society Colloquium Publications XXXII, Berlin (1949)
Yannelis, N.C., Prabhakar, N.D.: Existence of maximal elements and equilibria in linear topological spaces. J. Math. Econ. 12(3), 233–245 (1983)
Yannelis, N.C., Zame, W.R.: Equilibria in Banach lattices without ordered preferences. J. Math. Econ. 15(2), 85–110 (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A previous version of this paper was completed while Uyanık was a post-doctoral fellow at the Allen Wallis Institute of Political Economy at the University of Rochester; earlier versions were presented at Rutgers University (April 19, 2017), the University of Rochester (May 4, 2017), the 17th SAET Conference in Faro (June 25–30, 2017), Positivity IX Conference in Edmonton (July 17–21, 2017), the 36th Australasian Economic Theory Workshop in Canberra (February 8, 2018) and the University of Queensland (August 8, 2018). We are grateful to Rich McLean for the SAET invitation, and thank him for detailed and indispensable advice on the presentation of our results. We also thank Max Amarante, Paul Anand, Han Bleichrodt, Ying Chen, John Duggan, Hülya Eraslan, Yorgos Gerasimou, Filippo Massari, Andy McLennan, Onur Ozgur, John Quah, Eddie Schlee and Rajiv Vohra for stimulating conversation. Finally, we thank four anonymous referees for their erudition and sympathetic reading.
Rights and permissions
About this article
Cite this article
Khan, M.A., Uyanık, M. Topological connectedness and behavioral assumptions on preferences: a two-way relationship. Econ Theory 71, 411–460 (2021). https://doi.org/10.1007/s00199-019-01206-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-019-01206-7



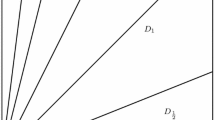

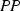 is the crucial transitivity condition and he found it convenient to give it a more usable name: “quasi-transitivity.” In this connection, also see the subject index in Sen (
is the crucial transitivity condition and he found it convenient to give it a more usable name: “quasi-transitivity.” In this connection, also see the subject index in Sen (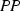 and
and  imply T from Fig.
imply T from Fig. 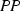 and
and 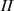 imply
imply 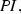 which combined with
which combined with  then implies T. And so on for the other implications.
then implies T. And so on for the other implications.