Abstract
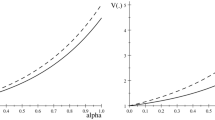
We assume that the ex post utility of a regret-sensitive agent facing a menu of lotteries depends upon the payoff of the chosen lottery in the realized state together with the forgone best payoff available in the menu in that state. If two lotteries in the menu have the same distribution of payoffs, the one whose payoff is less statistically concordant with the best alternative yields a larger risk of regret, which should be rejected by regret-risk-averse individuals. This means that regret-risk aversion is equivalent to the supermodularity of the bivariate utility function. We define regret-risk aversion in the small and in the large. We also show that regret-risk aversion tends to induce a bias in favor of the risky act in any one-risky-one-safe menu, in particular when the payoff of the risky choice is highly positively skewed. This is compatible with the “possibility effect” that is well documented in prospect theory. Symmetrically, we define the aversion to rejoicing-risk that can prevail when the ex post utility is alternatively sensitive to the forgone worst payoff. We show that rejoicing-risk-seeking is compatible with the “certainty effect”. We finally show that regret-risk-averse and rejoicing-risk-seeking people behave as if they had rank-dependent utility preferences with an inverse-S shaped probability weighting function that reproduces estimates existing in the literature.






Similar content being viewed by others
Notes
The original theory proposed by Bell (1982, 1983), Loomes and Sugden (1982, 1987a, b) and Loomes (1988) was limited to menus with only two lotteries, and allowed for rejoice (or “negative regret”) when the chosen lottery generated the largest payoff. In order to generalize the theory to menus containing more than two lotteries, and considering that people focus more on regret than on rejoice, Quiggin (1994) introduced an additional assumption into the model by claiming that statewise dominated alternatives should be irrelevant. This supports the theory of regret that has been used by economists since then, and that is used in the first part of this paper.
More precisely, it may be possible to obtain that \(x_1\) is preferred to \(x_2\) in menu \(\{x_1,x_2\}\), \(x_2\) is preferred to \(x_3\) in menu \(\{x_2,x_3\}\), but \(x_3\) is preferred to \(x_1\) in menu \(\{x_1,x_3\}\). For more on intransitivity with regret-sensitive preferences, see Bikhchandani and Segal (2011).
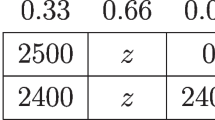
Indeed, in state H, \(x_1\) generates a payoff of \(x=0\), whereas selecting lottery \(x_2\) would have generated a payoff of \(y=1\). This yields a regret of \(r=y-x=1\). In state T, the payoff of lottery \(x_1\) is \(x=1\), but playing lottery \(x_3\) would have generated \(y=2\), thereby yielding a regret of \(r=2-1=1\).
Quiggin (1994) is an exception.
Savage (1951), who first introduced the notion of regret in economics, took the extreme view that a useful decision rule under uncertainty is the “minmax regret” criterion, which is a special case of our model in which the aversion to the risk of regret tends to infinity.
This can be seen by considering another menu in which the probability of the W state is \(p=1/2\), and the gain of the risky choice in that state is 1. In this alternative menu, the two choices generate the same distribution of regret.
See also Golec and Tamarkin (1998), Garrett and Sobel (1999), Harvey and Siddique (2000), Bhattacharya and Garrett (2008), and Eichner and Wagener (2011). By showing that adding low-probability macroeconomic catastrophes into the beliefs of the representative agent can explain the equity premium puzzle, Barro (2006, 2009) is in line with the idea that investors particularly dislike negatively skewed returns.
This formulation encompasses a wide variety of choice problems, such as the problem of choosing a portfolio of assets, or of selecting the best insurance coverage of an insurable risk.
This result implies in particular that an increase in risk of regret reduces the covariance between x and y. For a formal definition and some economic applications of the concept of supermodularity, see Milgrom and Shannon (1994).
Because y is a bad under regret aversion, the aversion to risk of regret can also be interpreted as a preference for mixing good (x) with bad (y), a common property of individual preferences first suggested by Eeckhoudt and Schlesinger (2006). These authors examined the special case of a univariate utility function. Eeckhoudt et al. (2007) extended this analysis to the case of a multivariate utility function.
References
Abdellaoui, M.: Parameter-free elicitation of utility and probability weighting functions. Manag. Sci. 46, 1497–1512 (2000)
Abdellaoui, M., L’Haridon, O., Zank, H.: Separating curvature and elevation: a parametric probability weighting function. J. Risk Uncertain. 41, 39–65 (2010)
Ali, M.M.: Probability and utility estimates for racetrack bettors. J. Polit. Econ. 85, 803–815 (1977)
Amir, R., Lazzati, N.: Endogenous information acquisition in Bayesian games with strategic complementarities. J. Econ. Theory 163, 684–698 (2016). https://doi.org/10.1016/j.jet.2016.03.005
Atkinson, A., Bourguignon, F.: The comparison of multi-dimensioned distributions of economic status. Rev. Econ. Stud. 49, 183–201 (1982)
Barro, R.: Rare disasters and asset markets in the twentieth century. Q. J. Econ. 121, 823–866 (2006)
Barro, R.: Rare disasters, asset prices, and welfare costs. Am. Econ. Rev. 99, 243–264 (2009)
Bell, D.E.: Regret in decision making under uncertainty. Oper. Res. 30, 961–981 (1982)
Bell, D.E.: Risk premiums for decision regret. Manag. Sci. 29, 1156–1166 (1983)
Bhattacharya, N., Garrett, T.: Why people choose negative expected return assets—an empirical examination of a utility theoretic explanation. Appl. Econ. 40, 27–34 (2008)
Bikhchandani, S., Segal, U.: Transitive regret. Theor. Econ. 6, 95–108 (2011)
Bleichrodt, H., Wakker, P.: Regret theory: a bold alternative to the alternatives. Econ. J. 125, 493–532 (2015)
Braun, M., Muermann, A.: The impact of regret on the demand for insurance. J. Risk Insur. 71, 737–767 (2004)
Brehaut, J.C., O’Connor, A., Wood, T., Hack, T., Siminoff, L., Gordon, E., Feldman-Stewart, D.: Validation of a decision regret scale. Med. Decis. Mak. 23, 281–292 (2003)
Camille, N., Coricelli, G., Sallet, J., Pradat-Diehl, P., Duhamel, J., Sirigu, A.: The involvement of the orbitofrontal cortex in the experience of regret. Science 304, 1167–1170 (2004)
Chabi-Yo, F., Leisen, D., Renault, E.: Aggregation of preferences for skewed asset returns. J. Econ. Theory 154, 453–489 (2014). https://doi.org/10.1016/j.jet.2014.09.020
Chapman, G., Coups, E.: Emotions and preventive health behavior: worry, regret, and influenza vaccination. Health Psychol. 25, 82–90 (2006)
Drèze, J.H.: Decision theory with moral hazard and state-dependent preferences. In: Essays on Economic Decisions Under Uncertainty. Cambridge University Press, Cambridge, UK (1987)
Eeckhoudt, L., Rey, B., Schlesinger, H.: A good sign for multivariate risk taking. Manag. Sci. 53, 117–124 (2007)
Eeckhoudt, L., Schlesinger, H.: Putting risk in its proper place. Am. Econ. Rev. 96, 280–289 (2006)
Eichner, T., Wagener, A.: Increases in skewness and three-moment preferences. Math. Soc. Sci. 61, 109–113 (2011)
Epstein, L., Tanny, S.: Increasing generalized correlation: a definition and some economic consequences. Can. J. Econ. 13, 16–34 (1980)
Filiz, E., Ozbay, E.: Auctions with anticipated regret: theory and experiment. Am. Econ. Rev. 97, 1407–1418 (2007)
Garrett, T., Sobel, R.: Gamblers favor skewness, not risk: further evidence from United States\(^{\prime }\) lottery games. Econ. Lett. 63, 85–90 (1999)
Gee, C.: A behavioral model of regret aversion. Unpublished manuscript (2012)
Gilovich, T., Medvec, V.: The experience of regret: what, when, and why. Psychol. Rev. 102, 379–395 (1995)
Golec, J., Tamarkin, M.: Bettors love skewness, not risk, at the horse track. J. Polit. Econ. 106, 205–225 (1998)
Gollier, C., Salanié, B.: Individual Decisions Under Risk, Risk Sharing and Asset Prices with Regret. Toulouse School of Economics, Toulouse (2012)
Harvey, C., Siddique, A.: Conditional skewness in asset pricing tests. J. Finance 55, 1263–1295 (2000)
Huang, R.J., Muermann, A., Tzeng, L.Y.: Regret and regulation. Geneva Risk Insur. Rev. 39, 65–89 (2014)
Inman, J.J., McAlister, L.: Do coupon expiration dates affect consumer behavior? J. Mark. Res. 16, 423–428 (1994)
Jullien, B., Salanié, B.: Extimating preferences under risk: the case of racetrack bettors. J. Polit. Econ. 108, 503–530 (2000)
Karni, E., Schmeidler, D., Vind, K.: On state-dependent preferences and subjective probabilities. Econometrica 51, 1021–1032 (1983)
Kimball, M.: Precautionary savings in the small and in the large. Econometrica 58, 53–73 (1990)
Loomes, G.: Further evidence of the impact of regret and disappointment in choice under uncertainty. Economica 55, 47–62 (1988)
Loomes, G., Sugden, R.: Regret theory: an alternative theory of rational choice under uncertainty. Econ. J. 92, 805–824 (1982)
Loomes, G., Sugden, R.: Some implications of a general form of regret theory. J. Econ. Theory 41, 270–287 (1987a). https://doi.org/10.1016/0022-0531(87)90020-2
Loomes, G., Sugden, R.: Testing for regret and disappointment in choice under uncertainty. Econ. J. 97, 118–129 (1987b)
March, J.G.: Learning to be risk-averse. Psychol. Rev. 103, 309–319 (1996)
Meyer, M., Strulovici, B.: Increasing interdependence of multivariate distributions. J. Econ. Theory 147, 1460–1489 (2012). https://doi.org/10.1016/j.jet.2011.09.001
Meyer, M., Strulovici, B.: Beyond Correlation: Measuring Interdependence Through Complementarities. Oxford University, Oxford (2015)
Michenaud, S., Solnik, B.: Applying regret theory to investment choices: currency hedging decisions. J. Int. Money Finance 27, 677–694 (2008)
Milgrom, P., Shannon, C.: Monotone comparative statics. Econometrica 62, 157–180 (1994)
Muermann, A., Mitchell, O., Volkman, J.: Regret, portfolio choice, and guarantees in defined contribution schemes. Insur. Math. Econ. 39, 219–229 (2006)
Quiggin, J.: Regret theory with general choices. J. Risk Uncertain. 8, 153–165 (1994)
Rothschild, M., Stiglitz, J.: Increasing risk: I. A definition. J. Econ. Theory 2, 225–243 (1970). https://doi.org/10.1016/0022-0531(70)90038-4
Sarver, T.: Anticipating regret: why fewer options may be better. Econometrica 76, 263–305 (2008)
Savage, L.: The theory of statistical decision. J. Am. Stat. Assoc. 46, 55–67 (1951)
Somasundaram, J., Diecidue, E.: Regret theory and risk attitude. J. Risk Uncertain. 55, 147–176 (2017)
Stalnaker, T., Cooch, N.K., Schoenbaum, G.: What the orbitofrontal cortex does not do. Nat. Neurosci. 18, 620–627 (2015)
Tchen, A.: Inequalities for distributions with given marginals. Ann. Probab. 8, 814–827 (1980)
Thaler, R.H., Ziemba, W.T.: Parimutuel betting markets: racetracks and lotteries. J. Econ. Perspect. 2, 161–174 (1988)
Tversky, A., Kahneman, D.: Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323 (1992)
Wakker, P.: Prospect Theory: For Risk and Ambiguity. Cambridge University Press, Cambridge (2010)
Wu, G., Gonzalez, R.: Curvature of the probability weighting function. Manag. Sci. 42, 1676–1690 (1996)
Zeelenberg, M., Pieters, R.: Consequences of regret aversion in real life: the case of the Dutch postcode lottery. Organ. Behav. Hum. Decis. Process. 93, 155–168 (2004)
Zeelenberg, M., Pieters, R.: A theory of regret regulation 1.0. J. Consum. Psychol. 17, 3–18 (2007)
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was completed while the author was Wesley Clair Mitchell Visiting Research Professor at the Economics Department of Columbia University, whose hospitality is gratefully acknowledged. I want to thank Mohammed Abdellaoui, Alain Chateauneuf, Keith Crocker, Thomas Epper, Helga Fehr-Duda, Yoram Halevi, Glenn Harrison, Johannes Jaspersen, Thomas Mariotti, Chuck Mason, Pietro Ortoleva, John Quiggin, Klaus Waelde, and Peter Wakker for particularly helpful comments. We also thank seminar participants at the Risk Theory Society meeting, RUD conference, HEC-Paris, Frankfurt workshop in Behavioural Economics, and at CESifo for their comments. The research leading to these results has received funding from the Chairs “Risk Markets and Value Creation” and “Sustainable Finance and Responsible Investments” at TSE.
Appendices
Appendix 1: Proof of Proposition 5
Eliminating w from (27)–(28) yields
We have that
and
Because F is continuous, there must exists a real \(c\in [x_-,x_+]\) such that \(F(c)=0\). This must be the solution of system (27)–(28). Because c is less than \(x_+\), its is immediate from (28) that \(w(p_+)\) is larger than \(p_+\) if v is increasing.
We now examine the shape of the probability weighting function. To do this, we fully differentiate system (27)–(28) with respect to \(p_-\). It yields (we simplify the notation by replacing \(p_+=p\))
and
Let us first examine the case \(p=1\). The above equations imply that \(c=x_+\) and \(w=1\), and \(w'(1)=1\). Moreover, differentiating the above equation around \(p=1\) yields
Let us alternatively consider the case \(p=0\), which implies that \(c=x_-\), \(w=0\), \(c'(0)=(u(x_-)-u(x_+)v(x_+)/u'(x_-)v(x_-)\) and \(w'(0)=v(x_+)/v(x_-)\). Finally, differentiating equation (40) in the neighborhood of \(p=0\) yields
This concludes the proof of Proposition 5. \(\square \)
Appendix 2: Proof of Lemma 2
Without loss of generality, let \(\mu \) be zero. Let \(S=m+n\), and let the risky lottery \(x_1\) in menu M be
with \(a_1^-<\cdots<a_m^-< 0<a_1^+<\cdots <a_n^+\), \(p_i^->0\), \(i=1,\ldots ,m\), \(p_j^+>0\), \(j=1,\ldots ,n\), and \(\sum _{i=1}^m p_i^- + \sum _{j=1}^n p_j^+ =1\). Assume that \(Ex_1=0\). Define \(p_{ij}\) as
Define lottery \(x_{ij}\sim (a_j^+,p_{ij};a_i^-,1-p_{ij})\). By construction, \(Ex_{ij}=0\). Initialize the probability vector \(Q=(q_1^{0-},\ldots ,q_m^{0-},q_1^{0+},\ldots ,q_n{0+})\) such that for all i, \(q_i^{0,-}=p_i^-\) and for all j, \(q_j^{0+}=p_j^+\). We also initialize two sets \(I=J=\{\emptyset \}\).
We consider the following \(n+m-2\) iterations. At the beginning of iteration k, \(I\cup J\) contains the \(k-1\) states of nature whose lottery’s initial payoff has been replaced by a binary zero-mean lottery.
Iteration k: Take an arbitrary pair (i, j), \(i\in \{1,\ldots ,m\}/I\), \(j\in \{1,\ldots ,n\}/J\). Consider two cases.
Case 1: Suppose that \(q_i^{k-1-}<-q_j^{k-1+}a_j^+/a_i^-\). Then, define \(\pi ^k=q_i^{k-1-}(a_j^+-a_i^-)/a_j^+\). Perform the following two operations on lottery \(x^{k-1}\):
-
Replace the atom \(a_i^-\) by lottery \(x_{ij}\), and raises the associated probability \(q_i^{k-1-}\) up to \(q_i^{k-}=\pi ^k\).
-
Reduce the probability associated with \(a_j^+\) from \(q_j^{k-1+}\) to \(q_j^{k+}=q_j^{k-1+}+(q_i^{k-1-}a_i^-/a_j^+)>0\).
Moreover, append state i into the set of negative states whose initial payoff \(a_i^-\) as been replaced by a binary zero-mean lottery \(x_{ij}\): \(I^k=I^{k-1}\cup {i}\).
Case 2: Suppose that \(q_i^{k-1-}\ge -q_j^{k-1+}a_j^+/a_i^-\). Then, define \(\pi ^k=-q_j^{k-1+}(a_j^+-a_i^-)/a_i^-\). Perform the following two operations on lottery \(x^{k-1}\):
-
Replace the atom \(a_j^+\) by lottery \(x_{ij}\), and raises the associated probability \(q_j^{k-1+}\) up to \(q_j^{k+}=\pi ^k\).
-
Reduce the probability associated with \(a_i^-\) from \(q_i^{k-1-}\) to \(q_i^{k-}=q_i^{k-1-}+(q_j^{k-1+}a_j^+/a_i^-)\ge 0\).
Moreover, append state j into the set of positive states whose initial payoff \(a_j^+\) as been replaced by a binary zero-mean lottery \(x_{ij}\): \(J^k=J^{k-1}\cup {j}\).
In both cases, this procedure yields a new lottery \(x^k\) that has the same distribution of payoffs, but in which one payoff has been replaced by a binary zero-mean lottery. After \(m+n-2\) iterations, all payoffs have replaced by such lotteries, expect two of them. By construction, since the \(Ex^k=0\), the remaining two atoms \((a_i^-,a_j^+)\) must be opposite in sign and have remaining probabilities \(q_i^{m+n-2-}\) and \(q_j^{m+n-2+}\) such that
This concludes the proof of Lemma 2. \(\square \)
Rights and permissions
About this article
Cite this article
Gollier, C. Aversion to risk of regret and preference for positively skewed risks. Econ Theory 70, 913–941 (2020). https://doi.org/10.1007/s00199-018-1154-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-018-1154-4
Keywords
- Longshot bias
- Certainty effect
- Possibility effect
- Probability weighting
- Risk-seeking
- Prospect theory
- Rejoicing-risk-seeking