Combination and SLR validation of IGS Repro3 orbits for ITRF2020

Abstract

In preparation for the International Terrestrial Reference Frame 2020, the International GNSS Service analysis centers released the results of the third reprocessing campaign (IGS Repro 3) of all the GNSS network solutions backwards starting from 1994. For the first time, the IGS reprocessing products included not just GPS and GLONASS, but also the Galileo constellation. In this study, we describe the methodology and results of the orbit combination provided by the IGS Analysis Center Coordinator (IGS ACC) at Geoscience Australia. The quality of the combined orbit products was cross-checked with the individual IGS Repro3 Analysis Center (AC) contributions. The internal consistency of the individual Analysis Center (AC) solutions with the combined orbits was assessed based on the root mean square of the 3D orbit differences. In 2020, the mean consistency of the combination is at the level of 9, 23, and 15 mm for GPS, GLONASS, and Galileo, respectively. The external validation of the orbits was performed using Satellite Laser Ranging (SLR). We proposed a novel approach to handling detector-specific biases in the results of SLR validation, which reduced the standard deviation of SLR residuals by up to 13% for Galileo FOC satellites. This method is based on bias aligning the offsets to single-photon SLR stations that were treated as a reference. The proposed approach increased the internal consistency of the SLR dataset, facilitating the detection of orbit modeling issues. The standard deviation of SLR residuals of the best individual solution versus the combined solution equals 13/13, 15/17, 17/17, 18/19 mm for Galileo-FOC, -IOV, GLONASS-K1B, -M, respectively. Therefore, the combined solution can be considered equal in quality compared to the best individual AC solutions. Searching for patterns in SLR residuals for different satellite-Sun-Earth geometries revealed that some orbit modeling issues are not fully diminished for individual ACs. Eventually, our findings suggest that the delivered combined orbit product may be considered the best solution overall, as it benefits from the best individual solutions for each satellite type.

1 Introduction

The International GNSS Service (IGS) analysis centers (ACs) conducted the third reprocessing campaign, IGS Repro3, which included processing of all GNSS network solutions from 01/01/1994 to 31/12/2020. The main objective of the IGS reprocessing campaigns is to standardize the entire history of IGS products and maintain internal consistency, utilizing the most current analysis models and processing methods. The Repro3 products provided the IGS contribution to the latest International Terrestrial Reference Frame 2020 (ITRF2020,¹ Altamimi et al. 2023). Unlike the previous reprocessing campaigns, the IGS Repro3 includes, for the first time, not only GPS and GLONASS but also the Galileo constellation. In total, eleven IGS ACs contributed to the IGS Repro3 initiative by providing their multi-GNSS products, including the Center for Orbit Determination in Europe (COD; Selmke et al. 2020; Dach et al. 2021), European Space Agency (ESA; Schoenemann et al. 2021), GeoForschungsZentrum (GFZ; Männel et al. 2021, 2023), Groupe de Recherche en Géodésie Spatiale (GRG; Michel et al. 2021), Jet Propulsion Laboratory (JPL; Blewitt et al. 2019), Massachusetts Institute of Technology (MIT; Herring et al. 2018), National Geodetic Survey (NGS; Damiani et al. 2019), Natural Resources Canada (NRCan, EMR), Graz University of Technology (TUG; Strasser and Mayer-Gürr 2021), Université de la Rochelle (ULR; Gravelle et al. 2023) and Wuhan University (WHU; Guo et al. 2016). Figure 1 illustrates the timeline of IGS Repro3 contributions and the progress of including subsequent constellations by individual ACs.

Fig. 1

Timeline of IGS Repro3 contributions of individual ACs

The SINEX solutions, including receiver coordinates, Earth Rotation Parameters and geocenter coordinates, provided by each of the ACs were combined using a similar strategy to the one employed in the previous IGS reprocessing campaign (IGS repro2; Rebischung et al. 2016), with a few minor modifications. The detailed description of IGS repro3 SINEX combination strategy can be found in Rebischung (2021a). On the other hand, the combination of the orbit products constituted a separate task. In IGS, the Analysis Center Coordinator (ACC) is responsible for the generation of the official combined products. In essence, a combined orbit product provides higher reliability and precision compared to the individual AC orbits. Secondly, the combination itself allows for evaluating the consistency between ACs. The general combination methodology implemented for official IGS products is based on an iterative weighted averaging designed by Beutler et al. (1995) in the interest of GPS orbit solutions. The combined IGS GLONASS orbits are generated with the same procedure but in a separate process, which is not optimal in terms of system interoperability. In line with the IGS Multi-GNSS Pilot Project (MGEX; Montenbruck et al. 2017) and with the increasing trend in the availability of multi-GNSS products through different ACs, the IGS ACC trialed an experimental MGEX orbit combination by adapting the existing combination software (Sośnica et al. 2020). The IGS ACC is also now trialing a three-constellation (GPS, Galileo and GLONASS) multi-GNSS combination similar to the Repro3 combinations as experimental operational products for the ultra-rapid, rapid and final types of product, and intends to make these experimental products available on a routine basis. In parallel to the official IGS ACC activities, GFZ initiated the independent orbit combination action (Mansur et al. 2020, 2022; Sakic et al. 2022). The combination methodology proposed by Mansur et al. (2022) relies on the least-squares variance component estimation (LSVCE), originally developed by Teunissen (1988). Chen et al. (2023) also reported the preliminary results of the multi-GNSS orbit combination actions performed at Wuhan University. Their combination strategy is mostly based on the legacy workflow of the IGS combination, however, considering all the available systems. The authors discussed the impact of the change in the processing strategies for individual ACs, which is a unique feature of the IGS MGEX products, in terms of constellation-specific transformation parameters. Nonetheless, none of the multi-GNSS orbit combinations is considered to be the final product at the moment. However, in July 2022, the IGS invited interested experts to form a new task force dedicated to the advancement of IGS product combinations in a multi-GNSS context.

This study describes a novel approach for combining multi-GNSS orbits and presents the results of the combination of the IGS Repro3 orbits. The quality of the combined orbit products is cross-checked with the individual contributions from the IGS Repro3 ACs. The presented orbit combination activity was conducted concurrently with a separate multi-GNSS orbit combination effort by GFZ (Sakic et al. 2022), who independently worked on the combination of the IGS Repro3 orbits.

Firstly, we describe the orbit combination input dataset, focusing on the orbit modeling details which have been adopted by the individual ACs. Secondly, we explain the orbit combination processing method. Eventually, we assess the internal and external quality of the Repro3 orbit products. The internal consistency of the individual AC solutions with the combined orbits is assessed based on the RMS of the 3D orbit differences. The external validation of both the solutions provided by the individual ACs and the developed combined orbit products is performed using Satellite Laser Ranging (SLR) observations.

2 Individual IGS AC orbit contributions

In total, eleven IGS ACs contributed to the IGS Repro3 initiative by providing their GNSS products. However, the ULR and EMR products were excluded from the analysis in this study because they did not contain the orbit products. Reprocessing products should follow the latest models and methodology standards drawn from the long-term experience and recommendations of the scientific community. The main findings and guidelines concerning the IGS Repro3 processing standards were put together during the IGS Analysis Center Workshop 2019 in Potsdam (Germany) and published on the dedicated ACC webpage.² However, some processing details differentiate the individual ACs, which directly translates into the quality of the provided products, including orbits. The experience with the previous IGS reprocessing campaigns highlighted that any derogations from the common set of analysis models lead to reduced internal precision and complicated interpretations of the combination results (Griffiths 2019). Regarding the orbit modeling, the individual AC contributions vary in terms of included GNSS constellations, observable types, and approaches for handling solar radiation pressure (SRP). In total, six of the nine IGS Repro3 contributors included Galileo in their solutions, namely COD, ESA, GFZ, GRG, MIT and TUG. WHU provided a GPS + GLONASS-only solution, whereas JPL and NGS processed GPS standalone. Table 1 summarizes the key differences between the Repro3 contributors, particularly their processing strategies for the orbit modeling. Unfortunately, the details of the NGS processing strategy are not available from any source, so they are not included in the table. Each AC uses its in-house developed software packages, namely, Bernese GNSS Software v5.3, NAPEOS 4.6, EPOS.P8, GINS/DYNAMO, GIPSYX-1.3/1.4, GAMIT/GLOBK 10.71, PANDA, and GROOPS. Most of the ACs use either undifferenced (ESA, GFZ, GRG, JPL) or double-differenced (COD, MIT) ionospheric-free linear combinations (L3) of two selected frequencies. TUG is the only AC that uses raw (undifferenced and uncombined) observables from all available signal frequencies (Strasser et al. 2019). The orbital arc/data span for the orbit determination is typically 24 h, but COD favors a long-arc solution over three days, whereas JPL and GRG process 30 h to obtain 6 h of overlaps surrounding the day (3 h on each side). The SRP model applied by the AC is usually dependent upon the constellation, and satellite block or type being processed. COD (for Galileo only), ESA, GRG, and TUG use the box-wing model as the a priori SRP model. MIT uses the a priori SRP model to compute only the constant direct radiation pressure acting on the satellites. The JPL products rely on the in-house developed GSPM13b model (Sakamura et al. 2017) as the a priori model, which is supported by additionally estimated solar scale and Y-bias coefficients. All the ACs estimate the empirical parameters accounting for SRP forces acting on the satellites; however, different sets of these coefficients are determined by different ACs.

Table 1 Processing strategy of the IGS Repro3 contributors that include GLONASS/Galileo in their solutions

ACs typically apply the 7-parameter extended Empirical CODE Orbit Model (ECOM; Arnold et al. 2015) with constant coefficients in the D, Y and B directions, once-per-revolution sine and cosine terms in the B direction (B1S, B1C), and twice-per-revolution sine and cosine terms in the D direction (D2S, D2C). Here, D represents the Sun-satellite axis, Y is the axis along solar panels, and B is perpendicular to D and Y, completing the right-handed orthogonal frame. COD takes a unique approach by deactivating empirical parameters during eclipses; however, for Galileo FOC satellite eclipses (when |β|< 12), they estimate additional parameters, namely once-per-revolution sine and cosine terms in the D direction (D1S, D1C) and Y-bias. GFZ and MIT estimate additional fourth-per-revolution sine and cosine terms in the D direction (D4S, D4C). The MIT solutions exploit a special constraining scheme for ECOM parameters and select the estimated coefficients based on obit overlaps and the analysis of other solution estimates. ESA does not estimate periodic terms in the D direction but incorporates additional once-per-revolution empirical parameters in the along-track direction (A1S, A1C). Finally, GRG does not estimate the constant empirical term in the D direction. In addition to the empirical orbit parameters, some ACs fit stochastic parameters to handle orbit modeling deficiencies. GRG, TUG and GFZ estimate additional stochastic parameters every noon in radial, along-track and cross-track directions. It should be noted that GRG, unlike TUG and GFZ, estimates stochastic parameters only in satellite eclipses. For Repro3 products, COD developed a novel approach to estimating pseudo-stochastic parameters as opposed to the operational processing chain at CODE. Instead of simply estimating them every 12 h, they are now estimated at orbit midnight with different intervals for GPS, GLONASS, and Galileo. Dach et al. (2021) reported that the rescheduling itself reduces the size of orbit misclosures by 10% for GPS and 15% for Galileo. All the differences listed above may have various implications for combination products, depending on the weighting of the potentially included AC products. For instance, different approaches in SRP modeling may lead to orbital differences in the radial direction of up to a few centimeters (Bury et al. 2019a, 2020).

3 Methodology of combination

The current operational IGS ACC combination software, known as the legacy combination software, has provided combined orbits and clocks since 1993 based on the algorithm described by Beutler et al. (1995). It has consistently produced robust combined orbits, with the IGS final GPS orbit solutions from different contributing ACs differing by less than 20 mm RMS from each other since 2014, and with consistency below 15 mm for most of the ACs. The legacy combination software uses a robust technique that minimizes the absolute deviations of individual orbits with respect to a weighted mean of the orbits by estimating the seven Helmert transformation parameters between individual orbit solutions and the weighted mean solution. The absolute deviation of the individual solutions with respect to the mean solution, also known as the L1-norm or robust estimator, is used instead of the L2-norm for the weighting of the AC satellite orbit solutions and for calculating the Helmert transformation parameters because it is less sensitive to outliers, i.e. poorly modeled satellite orbits. However, the legacy combination software is limited to GPS-only (and GLONASS-only) solutions.

To combine the multi-GNSS orbits of the Repro3 campaign, a new orbit combination software was developed by the IGS ACC at Geoscience Australia based on similar algorithms to the current software, but with added flexibility to handle the inclusion of multi-GNSS orbits. The multi-GNSS constellation comprises multiple distinct systems, each necessitating individual treatment due to the unique characteristics differentiating each constituent (Montenbruck et al. 2017). The constituent constellations employ diverse processing strategies (refer to Sect. 2), leading to potential variations in the quality of orbit solutions across different GNSS constellations. Initially, one might consider adopting constellation-specific weighting factors for the orbit solutions. However, significant disparities in the quality of orbit solutions were observed even within individual constellations, particularly in the case of GLONASS due to malfunctioning satellites (Bury et al. 2022). Similar circumstances are expected to arise with the BeiDou constellation within the multi-GNSS combination, as it encompasses various types of orbits (i.e., medium Earth, inclined geosynchronous, and geostationary), and literature demonstrates considerable variability in the orbit quality of individual MEO satellites as well (Zajdel et al. 2022). Hence, instead of relying solely on constellation-specific weighting factors, a novel approach incorporating satellite-specific weighting factors was introduced to the combination algorithm. The satellite-specific weighting factors contribute to superior results, particularly when considering the resilience against the adverse effects caused by malfunctioning satellites within a constellation (Masoumi and Moore 2021).

Comparisons of the combined GPS orbits from the multi-GNSS combinations using the satellite-specific AC weighting approach against the GPS orbits combined by the legacy software using the global AC weighting showed root-mean-square (RMS) differences of consistently around only 1 mm since 2004, with a median of only 1.4 mm over the whole 1994–2020 period (Villiger and Dach 2022). Preliminary precise point positioning (PPP) tests also showed no significant differences between the PPP solutions derived using the satellite-specific weighted combined orbits and the legacy combined orbits.

The orbit combination strategy, as also described in Sośnica et al. (2020), determines the combined orbits as weighted averages over all the AC orbit solutions. An iterative algorithm is used for the orbit combination, which is shown in the flowchart of Fig. 2, and further detailed in the following Subsects. 3.1–3.6. This algorithm mainly follows the same robust estimation algorithm used by the legacy software, with the exception of the satellite-specific weighting approach.

Fig. 2

Flow chart of the orbit combination software used for the IGS Repro3. Different colors denote different components of the software, as labeled in the figure

3.1 Pre-alignment of the individual AC orbit solutions

In the first step, an initial pre-alignment of the orbits is conducted using rotations derived from the AC terrestrial reference frame solution combination. The objective is to ensure the orbits are transformed to a consistent common reference frame, aligned with the terrestrial reference frame. this transformation is achieved by the OrbitPrep module in the combination software. These pre-aligned orbits serve as the basis for the combination algorithm, and undergo multiple realignments during the combination process to maintain a shared frame.

3.2 Simple mean and Helmert transformation of the individual AC orbits to a common frame

In the next step, within the Weight module of the combination software, a simple mean of the orbits from different ACs is calculated for each satellite:

$$ \widehat{x}_{0,j}^{X,Y,Z} \left( t \right) = \frac{1}{n}\mathop \sum \limits_{k = 1}^n x_{k,j}^{X,Y,Z} \left( t \right) $$

(1)

where $x_k$ is the orbit solution of the AC $k$ for each $X, Y, Z$ orbital component of the satellite j at the epoch $t$, and $n$ is the total number of ACs providing orbit solution for the satellite.

Then, seven Helmert transformation parameters (translations, rotations, and scale) are estimated between each individual orbit and the above mean orbit. To achieve this, first, an L2-norm estimation of Helmert parameters is conducted to form the initial values of the seven transformation parameters. Then an L1-norm minimization is performed to minimize the mean absolute deviation (MAD) of the position components between the individual AC orbit and the mean orbit. The L1 norm minimization uses a bracketing and bisection algorithm to determine the root of the derivative for the robust function (here the MAD), as outlined by Press et al. (2007). Only the common satellites between all the AC solutions are used for calculating the Helmert transformation parameters; in the case of the Repro3, this means that only the GPS constellation is used for calculating the Helmert transformation parameters.

It is important to note that apart from initializing the Helmert parameters, the L2 norm (RMS) is not employed anywhere during the Helmert estimation, given it is highly sensitive to extreme values due to the squaring operation which may potentially result in biased estimated values, particularly if no outlier detection has been done before or if there are still outliers or extreme values that remain unidentified. The L1 norm is consistently applied throughout all iterations of the Helmert estimation, ensuring any undetected gross errors (in this case, poorly modeled satellites) do not detrimentally influence the estimation of the Helmert parameters. This mirrors the methodology of the current legacy software providing the IGS operational combined products, and is necessary to ensure the parameter estimations are robust and are unaffected by inadequately modeled satellites. Since we only use GPS satellites to estimate the Helmert parameters, we can assume that most satellites are of comparable quality, and therefore a satellite-specific weighting is not necessary for the estimation of the Helmert parameters, and that an L1 norm minimization, in addition to the outlier removal process described in the Subsect. 3.5, are sufficient to minimize the influence of a few poorly modelled GPS satellites in the combination (Beutler et al. 1995).

For each of the AC orbit solutions, a set of seven transformation parameters between that AC orbit and the mean orbit is estimated as described above. These estimated parameters are then used to transform each of the AC orbits to the frame of the mean orbit. This ensures that all the individual orbits share a common frame before going through the combination, i.e. taking a weighted mean of the orbits.

3.3 Calculation of satellite-specific AC weights for the combination

After the individual AC orbits are all transformed into a common frame (i.e. the frame of the mean orbit), the next step is to assign weights to each AC orbit solution, so that a weighted mean of the AC orbits can be performed. To diminish the influence of the AC solutions that are inconsistent with the majority of the AC orbits, the AC weights are calculated based on the absolute deviations of the AC orbits with respect to the mean orbit. However, a major difference between the strategy used for the Repro3 combination and the one used in the operational combination software as well as that of the combinations described in Sośnica et al. (2020) is in how these L1-norm-based AC weights are calculated. Traditionally, each AC was given a weight based on the absolute deviations of the original AC orbit and the mean orbit, hereby referred to as a global AC weighting approach. For Repro3, however, a satellite-specific AC weighting approach was implemented to account for the different qualities of modelled orbits for different constellations as well as different satellites within each constellation. This was necessary as the quality of the AC solutions for different constellations differ between each AC. The GPS orbits of an AC may be very consistent with the majority of the AC solutions; however, the GLONASS or Galileo solutions of the same AC may not necessarily show similar consistencies with the other ACs. This was also observed between individual satellites of the same constellation, in particular for GLONASS. Therefore, instead of calculating a single weight for each AC orbit for a given day, a weight is calculated for each AC per each satellite for that day, based on the mean absolute deviation between the mean orbit and the AC orbit after transforming the AC orbit to the frame of the mean orbit:

$$ w_{k,j} = \left( {\frac{1}{{{\text{MAD}}_{k,j} }}} \right)^2 $$

(2)

Here, ${\text{MAD}}_{k,j}$ is the mean absolute deviation between the 3-dimensional orbit solution of the AC $k$ transformed to the reference frame of the mean orbit, and the mean orbit for satellite $j$.

3.4 Weighted mean orbit

In the next step, a weighted mean of the original AC orbits, which have the AC terrestrial frame solution combination rotations applied but otherwise not re-aligned, is determined using the satellite-specific weights calculated by Eq. (2) in the previous step:

$$ \widehat{x}_{1,j}^{X,Y,Z} (t) = \frac{1}{{\sum_{k = 1}^n w_{k,j} }}\mathop \sum \limits_{k = 1}^n w_{k,j} x_{k,j}^{X,Y,Z} (t) $$

(3)

This step is executed by the Combine module within the orbit combination software.

3.5 Outlier detection and removal

Once a weighted mean of the AC orbits is calculated, another set of seven Helmert transformation parameters is estimated between the weighted mean orbit of Eq. (3) and each AC orbit using the L1-norm minimization over the common satellites between all the ACs (i.e. GPS satellites in the case of the Repro3), using the same approach as taken in Subsect. 3.2 for the estimation of the Helmert parameters. Alongside absolute deviations (L1 norm), RMS differences are also calculated between the weighted mean orbit and each AC solution transformed to the frame of the weighted mean orbit. These RMS differences are used as criteria for outlier identification and removal process. As previously stated, the L2 norm (RMS) is not employed anywhere during the estimation of the Helmert parameters nor during the orbit weighting and weighted mean computations due to its vulnerability to outliers (poorly modelled/misbehaving satellites in case of the Helmert estimation and poorly modelled satellite orbits by an individual or a small number of ACs in case of the weighted mean). However, the RMS was selected as the criteria for detecting the outliers by setting thresholds outside of which an AC/satellite solution is identified as an outlier and thus excluded from the combination in the next iteration. One could use the absolute deviations to highlight and detect the outliers as well. However, the RMS was chosen for the Repro3 campaign to remain consistent with the outlier detection/removal process of the legacy software and to facilitate comparison and validation with the legacy combinations. RMS statistics are also used as indicators of the consistency of the AC solutions in IGS combination reports, e.g. the published IGS combination summary files.

Certain criteria are used to exclude a satellite or AC solution from the combination of a particular day. Most of the criteria used for the Repro3 analysis were based on those used in the current operational IGS combination, which have been set empirically. If the RMS of a satellite orbit solution for an AC is at least 4.7 times higher than the mean RMS of the constellation that satellite is part of, then that satellite solution is excluded from the combination. If at least 5 satellites of an AC solution are excluded from the combination due to high satellite RMS, then that AC orbit solution is fully excluded from the combination. Also, if a translation or rotation transformation parameter for a particular AC is larger than $0.95*\sqrt {3n} *\sqrt {{{\text{MEAN}}(h^2 )}}$ where n is the number of AC solutions and ${\text{MEAN}}(h^2 )$ is the mean of the corresponding Helmert parameter ($h$), or if the scale is larger than $0.98*\sqrt {n} *\sqrt {{{\text{MEAN}}(h^2 )}}$, then that particular AC solution is fully excluded from the combination.

The outlier detection and removal process is conducted within the Assess module of the combination software. When an outlier is detected, the relevant satellite or AC solution is excluded from the combination, and then the entire weighting and outlier removal process is repeated. One satellite/AC solution is excluded at a time, and the processes of simple mean, Helmert estimation and transformation, satellite-specific weighting, weighted mean calculation, and outlier removal are re-iterated until there is no outlier identified (Fig. 2).

3.6 Final weighted mean

After completing all outlier removal iterations (with no further outliers detected), each pre-aligned AC orbit (aligned based on terrestrial reference frame combination) is re-aligned to the weighted mean orbit of Eq. (3) using the last set of Helmert transformation parameters calculated in the previous step. The final combined orbit is then determined by taking a weighted mean of the transformed orbits $x_k^T$ using the previously calculated satellite-specific weights, based on the mean absolute deviations, as in Eq. (2):

$$ \widehat{x}_j ^{X,Y,Z} (t) = \frac{1}{{\sum _{k = 1}^n w_{k,j} }}\mathop \sum \limits_{k = 1}^n w_{k,j} x_{k,j}^{T,X,Y,Z} (t) $$

(4)

This final weighted mean is conducted in the Combine module of the combination software, and provides the IGS combined orbits.

4 Results

This section evaluates the internal and external quality of the Repro3 orbit products. The internal consistency of the individual AC solutions with the combined orbits is assessed based on the RMS of the 3D orbit differences. The RMS statistic is computed according to Kouba et al. (1995), which allows for a direct comparison with legacy orbit combination activities (Griffiths 2019). The external validation of the individual and combined orbit products is performed using SLR observations. The satellites of different systems and types differ in various aspects that determine the achievable orbit quality, i.e., orbital parameters, satellite construction, antenna power, integrated clock devices, and availability of supporting information in form of publicly available metadata. Therefore, in both internal and external validation, satellites are grouped by subsets, which correspond with the GPS blocks (I, II, IIA, IIF, IIR-A, IIR-B, IIIA), GLONASS types (M, M+, K1A, K1B), and Galileo types (1—IOV, 2—FOC and FOCe satellites that have been accidentally launched on the eccentric orbit). In this section, the satellites are uniquely identified using their Satellite Vehicle Numbers (SVN). The assignment of SVN to satellite types and time variable slots within the system constellation, which are identified by the Pseudo Random Noise (PRN) number as most commonly used in navigation, is provided in the IGS satellite metadata file³; thus, not elaborated here.

4.1 Internal consistency between individual solutions and the combined orbit

The final combined solution is compared against each individual AC product via 3D differences after aligning the orbits to the common frame using Helmert transformation parameters (rotation, translation, scale). Figure 3 illustrates the time series of weighted RMS for different types of satellites. For the full time range of the GPS orbits, the RMS agreement of the input solutions and combined product decreases approximately exponentially and ranges from 10 to 70 in the early years up to 5–15 mm after about 2005, when considering the inner 90% range including all values between the 5 and 95th percentiles. For GLONASS, the residuals range from 15–50 mm to 5–30 mm, for -M and -K1B satellites, respectively.

Fig. 3

RMS of 3D differences between the individual AC orbits and the combined solution grouped by satellite types smoothed using moving averages with a 30-day window

Unfortunately, the orbits of the GLONASS first generation satellites and the only GLONASS-K1A satellite (SVN 801) were mainly provided by one AC – COD. The remaining ACs provided their orbits in up to 9% of the possible epochs of these GLONASS satellites, thus, were considered meaningless for the discussion. In the early years of the Galileo orbits, the consistency of the products with the combined orbit ranged from 10 to 100 mm. It is worth noting that only TUG, GFZ and COD delivered orbits in the first 2 years of Galileo contribution (2013–2014). However, when the system became mature enough after 2016, the RMS range decreased to only 8–25 mm. Table 2 summarizes the mean RMS values for the respective satellite groups in the whole period and in 2020 only. The GPS orbit products delivered by individual ACs are more consistent with each other than with GLONASS and Galileo orbit products, as reflected in the range between the minimum and maximum mean RMS in each group (Table 2). In 2020, the mean RMS value ranged between 6 and 11 mm (TUG–GRG; GPS IIR-M), 7–11 mm (TUG–GFZ; GPS IIF), 21–44 mm (COD–TUG; GLO-M), 16–25 mm (COD–GRG; GLO-M+), 13–26 mm (ESA–GRG; GLO–K1B), 8–24 mm (TUG–GRG; GAL-1), and 12–22 mm (COD–GRG; GAL-2). Therefore, the inconsistencies in the processing strategies of individual ACs in Galileo and GLONASS precise orbit determination have dramatic consequences for orbit quality. One may also draw the general conclusion that the combined products are most consistent with COD and TUG for GLONASS and GPS/Galileo, respectively.

Table 2 Mean of 3D RMS differences between the individual AC orbits and the combined solution grouped by satellite types in the whole period and in 2020 only

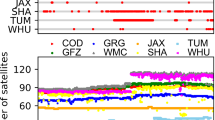
The consistency of orbit products, measured by RMS of the 3D orbit differences, directly reflects the weights of the individual products in the combination. In essence, the smaller the RMS, the higher the weight of a contribution in the combination. Figure 4 shows the distribution of weights among the ACs for satellites representing all respective groups. To enhance readability, Fig. 5 illustrates only the last year of available data in the IGS Repro3 in the form of time series and aggregated mean weight values for each AC. For GPS, the weight values for different ACs are equitably the same, indicating that each of the nine ACs contributes with a weight of several percentages. However, for GLONASS-M/M+, the differences in weights are more unevenly spread.

Fig. 4

Time series of weights for specific satellites representing different satellite types

Fig. 5

Time series of weights of individual ACs in the combined orbit product for specific satellites representing different satellite types (a) and mean weights for different satellite types in the last year of available products (b) in %

The COD and TUG solutions have the largest weights of approximately 20–26%, whereas the ESA products provide the input with the largest weight for GLONASS-K1B. For Galileo, the discrepancies between the ACs are similar to those for GLONASS, and the weights range from 7 (GRG) to 27% (COD) for GAL-1 and from 10 (GRG) to 26% (TUG) for GAL-2. Interestingly, there is not much difference in either RMS or weights of individual ACs when comparing normal GAL-2 FOC and FOCe satellites.

The weights of individual ACs are generally stable over time, with some short-term periodic fluctuations that reflect differences in efficiency of orbit modeling approaches in various Sun-Earth-satellite geometries, e.g., orbit eclipses. Figure 6 shows the percentages of epochs for each of the AC products that were included in the combination with the highest weight, grouped by satellite types. The dataset was divided into two time spans by setting the cut-off date at 01-01-2009. Focusing on the period after 2009, GPS products were most often prevailed by TUG (25–57%). For the remaining epochs, the products of either MIT, COD or ESA were included with the greatest weights. For GLONASS-M/M+/K1B, the AC with the highest weight varied between COD, ESA, TUG and less frequently GFZ. For Galileo-2 FOC, COD delivered solutions with the greatest weight 50% of the time, while swapping with MIT and TUG in approximately 25% and 15% of the remaining epochs, respectively. Finally, for GAL-1 IOV, TUG products were included with the highest weight in 49% of epochs, with the remaining epochs shifting between COD, ESA and GFZ.

Fig. 6

Rounded percentages of solutions for which the particular ACs have the largest weights

4.2 External validation using SLR

SLR can be used as a stand-alone method for verifying the accuracy of microwave-based GNSS orbits (Zajdel et al. 2017). In the so-called SLR validation, the orbit quality is assessed based on the analysis of the SLR residuals, which are the discrepancies between the direct SLR range measurements and the station-satellite vector calculated based on the SLR station positions and the evaluated orbits in Earth-fixed reference frame. The direct SLR measurements are corrected by considering factors such as tropospheric delay models (Mendes and Pavlis 2004), general relativity effects (Petit and Luzum 2010), satellite eccentricities,⁴ and laser retroreflector array (LRA) offset corrections provided by mission operators. The SLR station coordinates are provided in the International Laser Ranging Service (ILRS; Pearlman et al. 2019) version of the International Terrestrial Reference Frame, SLRF2014. The processing methods are the same as that employed by the ILRS Associated Analysis Center at UPWr (Zajdel et al. 2017) utilizing a modified version of the Bernese GNSS Software (Dach et al. 2015). For the external validation using SLR, we processed data from the last 8 years, starting in 2013, as Galileo and GLONASS are of main interest here.

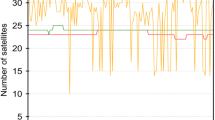
While SLR validation is the only external and independent method for validating microwave-based GNSS orbits, it is important to keep in mind its limitations. GNSS satellites are not uniformly observed by the ILRS stations, and the number of SLR normal points varies over time and between satellites. The number of normal points for individual satellites depends on the prioritization of the specific satellites by ILRS, which publishes a recommended priority list for the laser station operators. In general, the priority decreases opposite to orbital altitude and orbital inclination (at a given altitude). Therefore, Low Earth Orbiters (LEOs) are given the highest tracking priority among all spacecraft supported by ILRS because of their low altitude and short passage through the sky. Only a number of high-priority GNSS satellites are included in the priority list. Figure 7 illustrates the changes in the number of GNSS satellites on the ILRS tracking priority list over the last 20 years. For GLONASS, only up to 6 satellites were prioritized for tracking. For Galileo, this number reached 18 satellites in 2018. The freshly launched Galileo satellites were also automatically included in the priority list of the ILRS. In 2019, ILRS decided to identify four GNSS satellites per each global constellation (Galileo, GLONASS, and BeiDou) for intensive tracking, with three sectors (at least 2 normal points each) spaced widely apart over the pass. These satellites are BeiDou3 M2, M3, M9, and M10, Galileo SVNs 102, 202, 209, 210, and GLONASS SVNs 747, 802, 756, and 757. The remaining GNSS satellites can be tracked by the stations as time allows, based on the data yield of the specific station. In practice, stations adjust priorities to their special program interests. Thus, discrepancies between the ILRS recommendations and station target selection may occur (Zajdel et al. 2018). Furthermore, the priority of selected satellites may be increased to intensify support as requested by the scientific community. In 2015, the ILRS began a series of time-bound campaigns that greatly increased the number of SLR observations to GNSS satellites (Bury et al. 2019b). Figure 8 illustrates the heatmap of the number of normal points collected by the ILRS network for individual satellites in each month starting from January 2013. On average, the analysis of the GNSS orbit quality using SLR is based on about 210 ± 70 (Galileo) and 270 ± 190 (GLONASS) observations (normal points) per each satellite/month.

Fig. 7

Number of GNSS satellites in the ILRS priority list for laser stations

Fig. 8

Number of normal points (given in thousands) collected by the ILRS network for specific satellites in each month between 2013 and 2020. The individual satelltes are identified by satellite vehicle number (x axis). The satellite type groups are labeled below the figure

The quality of SLR measurements depends on the station equipment. One of the most critical factors is the type of precise photon detector, which is responsible for detecting a weak return signal of a few or single photons from a satellite. SLR stations typically employ one of three different detector types and the modifications thereof: Compensated Single-Photon Avalanche Diode (CSPAD), Micro-Channel Plate (MCP), and Photo-Multiplier Tube (PMT). The distinction between the systems is essential in understanding the outcomes of SLR measurements. In essence, the CSPAD detectors were designed to be operated at the "single to multi-photon" level by reducing the time-walk effect of SPAD (Kirchner et al. 1998). For GNSS ranging, it can be assumed that the correctly maintained and operated CSPAD stations work in single-photon mode. In this mode, the likelihood of detecting multiple photoelectron events is very low (< 0.5%). Thus the probability of biasing the detections towards the leading edge of the returned pulses is reduced, which becomes more likely as the return rate increases (Rodríguez et al. 2019). Stations that use PMT or MCP detectors, which were commonly used in older SLR systems, usually do not reduce the signal strength to low levels, but instead, aim to achieve high return rates. Different studies demonstrated the varying performance of SLR stations caused by the detector-specific issues, including problems specific to tracking LEO satellites (Strugarek et al. 2021), estimating centre-of-mass corrections for spherical geodetic satellites (Otsubo et al. 2015; Rodríguez et al. 2019), and analyzing the effect of satellite signatures on GNSS satellites (Otsubo et al. 2001; Sośnica et al. 2015, 2018). GNSS carry flat retroreflectors which increase the SLR signature effect for multi-photon PMT and MCP detectors. However, handling detector-specific issues in the validation of GNSS orbits has always been omitted, as yet.

4.2.1 Handling detector-specific issues in SLR validation of GNSS orbits

The quality of SLR data is the product of many factors, one of which, as mentioned in the previous section, is the type of the detector. Therefore, the distinction between detector types should provide the most straightforward a priori information about the clusters in the SLR dataset. Most European SLR stations, including Herstmonceux, Zimmerwald, Graz, Potsdam, Grasse, San Fernando, and Mount Stromlo in Australia, use CSPAD detectors. The Chinese stations Changchun, Beijing, Shanghai, and Kunming also use CSPAD; however, they have been classified as a separate group (CSPAD*) due to differences in system operation compared to the European CSPAD systems, e.g., issues with power control, adjustment of time walk compensation in conjunction with pulse length for single- to multi-photon use (Strugarek et al. 2021). Most of the NASA SLR stations, such as Monument Peak, Greenbelt, Yarragadee, Haleakala, as well as Matera and Wettzell, use high-energy MCP detectors. PMT detectors are used at the stations based on the Russian systems, such as Arkhyz, Svetloe, Badary, Zelechukskaya, Altay, Komsomolsk, Irkutsk, Simeiz, Kazively, and some other stations such as Brasilia or Hartebeesthoek. The multi-photon stations suffer from the so-called satellite signature effect, which should be visible in the dataset of SLR residuals as a dependence between the angle of incidence (nadir angle) and the measurement range (Sośnica et al. 2015). One should keep in mind that an ideal single-photon station and an ideal multi-photon station will not see any difference when they are perpendicular to a flat target (i.e., the angle of incidence = 0), while their measurements will be different when the angle of incidence > 0. Thus, the ideal single-photon station and the ideal multi-photon station will not see any difference when they are perpendicular to a flat target (i.e., the angle of incidence = 0).

Figure 9 shows the coefficients of the linear dependence between nadir angle and SLR residuals (left column), the mean offset in the SLR residuals for the raw data set (middle column), the mean offset in the SLR residuals after reduction of the nadir angle dependence (right column). The statistics are grouped by station and satellite type. This information was used to perform the initial clustering of the stations. The station labels on the y-axis include the station group identifier, the detector type group, the ILRS station identifier, and the percentage of SLR residuals provided in the dataset. There are five groups that can be specified: (1) GR_1 contains European CSPAD stations, i.e., Zimmerwald (7810), Wettzell (7827), Graz (7839), Herstmonceux (7840), and Mount Stromlo CSPAD station (7825); (2) GR_2 includes MCP stations at Greenbelt (7105), Monument Peak (7110), Matera (7941), and two PMT stations at Brasilia (7407), Hartebeesthoek (7501); GR_3 includes two CSPAD and two MCP stations, which together give consistent results, but slightly different from the stations in GR_1 and GR_2 Potsdam (7841), Grasse (7845), Yarragadee (7090), and Wettzell (8834); GR_4 consists of Chinese CSPAD stations, which show significant nadir angle dependencies and large offsets in the SLR residuals: Changchun (7237), Beijing (7249), Kunming (7819), Shanghai (7821); GR_5 includes Russian PMT stations, which also show significant nadir dependencies and unexpected offsets in the SLR residuals: Komsomolsk-na-Amure (1868), Altay (1879), Arkhyz (1886), Baikonur (1887). The linear dependence between SLR residuals and nadir angle is mostly below 1 mm/deg for the stations in GR_1, GR_2 and GR_3, which translates into a maximum difference of 10–15 mm between low and high (10–15 degrees) nadir angles. For the stations in groups GR_1, GR_2, and GR_3, the reduction of the nadir angle dependence changes the offset by up to a few millimeters. Looking at the stations in groups GR_1 and GR_2, the mean offsets in the SLR residuals are also mostly consistent and vary in the range of single millimeters. The offsets are slightly different for the stations in group GR_3 compared to GR_1 and GR_2. It should be noted that this group includes very productive stations such as Wettzell (8834) and Yarragadee (7090), which in our case provide about 20% of the total SLR residuals. Let us now concentrate on the remaining stations, i.e. GR_4 and GR_5. It is difficult to find internal consistency in these groups. The nadir angle dependence in the SLR residuals is significant, and reducing the linear dependence changes the mean offset in the SLR residuals by up to 4 cm. The problem for these stations is more complex than just a satellite signature effect. The post-fit reduction of the linear dependency in the nadir angle can eliminate not only the satellite signature effect, but all the observation elevation angle and distance dependent errors, which are mainly tropospheric biases, station specific hardware issues, coordinate errors, and most importantly here, orbit modeling errors. At this point, eliminating the satellite signature effect using the simple linear model of nadir angle dependence is not sufficient and actually causes more problems, and is therefore not applied in this study. The modeling of the satellite signature effect in the SLR validation of GNSS satellites should be the subject of a separate study. For the next analyses, the groups GR_4 and GR_5 have been excluded because of a high inconsistency compared to GR_1, GR_2 and GR_3.

Fig. 9

Coefficients of linear dependency between nadir angle and SLR residuals (left column), mean offset in SLR residuals for raw dataset (middle column), mean offset in SLR residuals after reducing the nadir angle dependency (right column). The statistics are grouped by stations and satellite types. The station labels on the y-axis include the station group identifier, detector type group, ILRS station identifier and percent of provided SLR residuals in the dataset

Figure 10 shows the descriptive statistics of SLR residuals for different station and satellite groups. The differences in the mean offset of SLR residuals between different groups of stations can reach up to several centimeters, see Fig. 10. As an example, when comparing the SLR residuals from the GR_1 and GR_3 stations for the Galileo FOC satellites, the difference in the mean offset equals 16 mm. One may also notice that the general pattern of differences between the station groups within the subsets of satellites is quite similar, which confirms that the offset originates from the station-specific issues in the SLR residuals and does not reflect the orbit mismodeling. Therefore, the SLR stations are affected by a kind of equipment-specific effect, which inherently biases the validation results. To prevent this, we propose to include an additional correction to each satellite-type-detector pair taking the most stable stations equipped with CSPAD detectors as a reference, i.e., GR_1. The SLR stations from the group GR-1 provide approximately 40–50% of the total SLR residuals in the validation dataset (see Fig. 10). Previous studies indicated that CSPAD-equipped stations are the most reliable systems providing SLR observations of the highest precision (Rodríguez et al. 2019). Table 3 summarizes the offsets for each satellite-type-station-group pair, based on the validation of the IGS Repro3 combined orbits.

Fig. 10

SLR validation results for different satellite types and SLR station groups. The boxes range from 1st to the 3rd quartile. A vertical line inside the box reflects the median. The whiskers go from each quartile to the minimum and maximum value, excluding outliers, which are outside 1.5 times the interquartile range above the upper quartile and below the lower quartile. The bottom subplot shows the involvement of each group in providing SLR residuals

Table 3 Corrections to the SLR measurements referred to the specific satellite-type-detector pairs

Table 4 demonstrates the effect of reducing the dataset of stations and eliminating the biases for each group in the validation of individual satellite types using the corrections from Table 3. After excluding the stations from the GR_4 and GR_5 the standard deviation of SLR resiuals decreases by up to 30%. Figure 11 illustrates the distribution of SLR stations by distinguishing the detector-type systems. Excluding the Russian PMT and CSPAD* stations from orbit validation results in a loss of SLR measurements over a large area above Asia. Because of the high productivity of Chinese stations in providing SLR measurements, about 20% of observations had to be excluded. This demonstrates the urgency of improving the precision of SLR observations so as to obtain a more consistent set of observations from across the ILRS network, thereby improving the reliability of SLR orbit validation.

Table 4 Statistics of SLR residuals of IGS Repro3 combined orbits grouped by different satellite types with and without removing detector-specific bias

Fig. 11

Distribution of SLR stations with distinguishing the detector-type systems

After applying the station group corrections from Table 3, the standard deviation of SLR residuals decreases by up to 13% for Galileo FOC satellites. The lowest standard deviation (STD) of SLR residuals is visible for GPS and equals 13 mm. However, one should remember that the only GPS satellites available for SLR tracking were available till 04/2013 (SVN 35) and 03/2014 (SVN 36). Apart from GPS, the lowest STD of SLR residuals is visible for the Galileo satellites with 14, 14, and 20 mm for Galileo FOC, FOCe, and IOV, respectively. For GLONASS, the STD of SLR residuals is 19, 15, 16 mm for GLONASS-M, -M+  and -K1B. Interestingly, there is a different offset in SLR residuals for each satellite type, which reaches 16, 20, −4, 15, 2, 38, −4 mm for Galileo-FOC, -FOCe, -IOV, GLONASS–K1B, -M, -M+, and GPS, respectively.

In the next sections, the selection of stations will be limited to the station belonging to the GR_1, GR_2 and GR_3 groups, removing the station-group specific biases aligning the offsets in the SLR residuals to the most stable C-SPAD stations (Table 3). Despite its shortcomings, this approach is considered the most optimal for maintaining the self-consistency of the SLR datasets.

4.2.2 The mean offset in SLR residuals of the individual and combined solutions

There are some factors, which may affect the mean offset of the SLR residuals, thus, the bias itself should be interpreted carefully. Firstly, one should notice that the way of handling detector-specific biases changed the mean offset in SLR residuals by almost ten milimeters in some cases. Secondly, the orbit of the IGS Repro3 solutions is represented in the terrestrial frame from the third IGS reprocessing campaign—IGSR3. For the first time, the IGS Repro3 solutions have an ITRF-independent, Galileo-based terrestrial scale. The scale of the frame is inherited from the Galileo-based igsR3.atx satellite antenna phase center offset (z-PCO). Therefore, there is a certain scale inconsistency between the reference frame of the laser stations and the validated orbits, resulting in an observed bias in the radial direction of SLR residuals. Last but not least, the orbit modeling inconsistencies between the ACs (see Table 1) change the orbit in the radial direction (Bury et al. 2019a, 2022).

Figure 12 provides the offsets of SLR residuals for different satellite types from all the individual AC solutions and the combined IGS solution, after eliminating the detector-specific bias using the corrections from Table 3. The individual AC solutions were not aligned to a common frame, therefore, each reflects a raw product as delivered by ACs. We limited the SLR validation of the individual AC solutions to the last 2 years of products (2019–2021). It is important to note that the mean offset in SLR residuals varies within a specific group of satellites between individual ACs by up to a centimeter level magnitude, particularly for Galileo-FOC. These results are consistent and complementary with the conclusions from recent studies. Rebischung (2021b) reported ± 1 mm inter-AC disagreement on a terrestrial scale of the individual IGSR3 AC contributions. Dach and Springer (2022) analysed the orbit differences in the radial direction as a function of the Sun elevation angle above the orbital plane and the satellite argument of latitude between individual ACs products delivered in the frame of the IGS Repro3 campaign. The authors indicated the differences between the Galileo FOC orbits reaching up to ± 30 mm, depending on the AC. On the other hand, the orbit consistency for Galileo-IOV satellites was much better. The analysis of SLR residuals produced a similar outcome. In the extreme case, the mean offset of GFZ and GRG Galileo-FOC satellites varies by 43 mm, which is consistent with the result provided by Sakic et al. (2022). It is important to note that there are two groups of Galileo-FOC solutions that are quite consistent in terms of the mean offset of SLR residuals: (1) COD, ESA and GFZ, with a mean offset of 0–10 mm; (2) GRG and TUG, with a mean offset of about 30–40 mm. Therefore, the mean offset of about 18 mm for the combined solution results inherently from the inconsistency of the individual products.

Unfortunately, despite being aware of the differences in orbit modeling of the individual ACs (Table 1), it is hard to find the one linking factor that makes some solutions more consistent with one than another. The large positive bias of the GRG products for Galileo orbits may arise from the lack of the D0 parameter in the estimated ECOM model. The magnitude of the D0 estimates should be overwhelmingly compensated by the use of the a priori box-wing model; however, the residual accelerations driven by the box-wing deficiencies should be accounted for with the ECOM parameters, especially D0. Bury et al. (2019a, b) demonstrated that the box-wing model can absorb up to 97% of the direct SRP, whereas the rest can be compensated by a set of estimated empirical parameters. On the other hand, this does not explain the similar bias appearing in the TUG Galileo-FOC orbits because TUG employs the a priori box-wing model with the estimation of empirical orbit parameters from the new ECOM model. This aspect needs further investigation.

Bearing in mind the potential contribution of the GNSS-based scale to the next releases of the ITRF, it is essential to maintain the inter-AC scale consistency, thus, limiting the differences of the orbit solutions in the radial direction. The mean offset of the GLONASS-M is close to − 1 mm and consistent at the level of a single mm between the individual ACs. For GLONASS-M+ , the solutions are also consistent but with a significant offset of about 36–40 mm, which is coherent with other studies (Sośnica et al. 2020; Bury et al. 2022; Mansur et al. 2022).

Fig. 12

Mean offset of SLR residuals for individual ACs and combined IGS Repro3 orbit. Values in mm

4.2.3 The standard deviation of SLR residuals of the individual and combined solutions

Figure 13 illustrates the standard deviation of SLR residuals for different satellite types from all the individual AC solutions and the combined IGS solution. The same as for the previous analysis, we limited the SLR validation of the individual AC solutions to the last 2 years of products, i.e., 2019–2021.

Fig. 13

Standard deviation of SLR residuals grouped by different satellite types and station detector groups from individual AC solutions and the combined IGS Repro3 solution

When limiting the set of stations to GR_1, GR_2 and GR_3 and applying the station-group-satellite-type corrections from Table 3, the lowest standard deviation of SLR residuals is reduced to 13, 12, 15, 17, 18, 15 for Galileo-FOC, -FOCe, -IOV, GLONASS-K1B, -M, and -M+, respectively. Due to the much larger contribution of PMT stations (mostly operated by the Russian Federation) in tracking GLONASS than Galileo (Zajdel et al. 2018), the statistics of SLR residuals for GLONASS are more affected. Either using the best CSPAD and MCP or all stations with removing the detector-specific biases lead to consistent conclusions regarding the identification of the best solutions. The difference in the magnitude of the scatter of SLR residuals when considering all the stations in the analysis arises from the decreased internal precision of measurement from some stations. On the other hand, reducing the set of stations in the SLR validation by selecting only particular detector types limits the global coverage of observed satellite flybys.

Among all the individual solutions, the ESA orbit products seem to deliver the most accurate products for most of the satellite groups. The TUG products are almost equal in terms of STD of SLR residuals for the Galileo-FOC orbits. Finally, COD delivers the best GLONASS-K1B orbits, however, the difference between the ESA and TUG products is marginal. The IGS combined orbits are never worse than 10% compared to the best individual solution. Moreover, for GAL-FOCe and GLONASS-K1B, the combined solution is the best of all available.

4.2.4 SLR validation of the individual satellites

Aiming to get more insight into the quality of the orbit solutions for individual satellites, Fig. 14 shows the results of the SLR validation for each satellite separately based on the combined solutions and full-time range of 8 years. In addition, Fig. 15 shows the time series of SLR residuals of the selected satellites together with the rolling standard deviation of residuals using one month window. The rolling standard deviation of residuals reflects the change in the orbit quality in time.

Fig. 14

SLR residuals for each satellite based on the combined IGS Repro3 orbit products. The individual satelltes are identified by satellite vehicle number (x axis). The satellite type groups are labeled above the figure. The boxes range from 1st to the 3rd quartile. A vertical line inside the box reflects the median. The whiskers go from each quartile to the minimum and maximum value, excluding outliers, which are outside 1.5 times the interquartile range above the upper quartile and below the lower quartile

Fig. 15

Time series of SLR residuals (left y-axis) for the combined IGS Repro3 orbits. The standard deviation of SLR residuals in each month is given with an orange solid line (right y-axis). The grey line refers to the elevation of the elevation angle of the Sun above the orbital plane of the satellite (right y-axis)

The Galileo-FOC satellites are self-consistent in both offset and standard deviation of SLR residuals. One Galileo satellite, SVN 204, was affected by the failure of both hydrogen masers and was removed from active service on 2017-12-08, until further notice. However, this had no visible effect on the quality of SLR residuals. For the Galileo-IOV satellites, it should be noted that there is an increased STD of SLR residuals for SVN 103 and 104. In the case of SVN 104, the satellite was unavailable since 2014-05-27, and the orbit quality decreased because of the satellite issues.

A comparison of the time series of SLR residuals for Galileo IOV SVN 102 and 103, as shown in Fig. 14, reveals that the SLR residuals of SVN 103 are much more β-dependent than the SVN 102. The SLR residuals for SVN 103 decrease significantly for high absolute β angles. However, this difference can be attributed to the characteristics of the orbital plane, where the maximum β angle values are ± 52° and ± 77° for SVN 102 and 103, respectively. Bury et al. (2020) reported that Galileo-IOV satellites suffer from acceleration in the direction B0, which is dependent on the β angle and insensitive to the SRP modeling strategy.

Interestingly, the STD of SLR residuals does not show a significant long-term change, despite the development of the GNSS tracking network over time. The fluctuations in the SLR residuals are more β-dependent, suggesting that orbit modeling issues during eclipsing periods are not yet fully mitigated. For GLONASS-M, there are some old satellites with markedly worse SLR residual statistics, e.g., SVN714, 715, 719, 728, 730, 732, 851. These are expected due to ageing of these GLONASS spacecraft (Zajdel et al. 2017; Prange et al. 2017, 2020). However, apart from these exceptions, all the remaining GLONASS satellites are consistent in terms of the offset and STD of SLR residuals to the level of single milimeters. Interestingly, compared to the study of Dach et al. (2019), the SLR residuals of some satellites which were identified as misbehaving, do not show the characteristic time-varying increase in the scatter in SLR residuals in their last years of functioning (see SVN737 in Fig. 15).

4.2.5 Signatures in the SLR residuals of the combined and individual orbit solutions

In this section, we will examine the SLR residuals to identify patterns in different Sun-Earth-satellite geometries, aiming to investigate the strengths and weaknesses of individual solutions and how their signatures affect the combined orbit. The SLR residuals will be analysed as a function of the satellite–Sun elongation angle ε and the satellite latitude Δu w.r.t. the Sun-Earth-satellite angles as defined in Fig. 16. Firstly, we will focus on the Galileo satellites and then proceed to the GLONASS satellites. The GPS orbit solutions were excluded from this analysis because of the limited number of SLR observations (see Fig. 6) and the lack of significant signatures that could be discussed.

Fig. 16

Sun-Earth-satellite geometry. β—elevation of the Sun above the orbital plane; Δu—satellite argument of latitude with respect to the latitude of the Sun; ε—the satellite elongation angle with respect to the position of the Sun. The definition of axes in different satellite-specific frames was defined, including the local orbital frame (radial—R, along-track—S, and cross-track—W), sun-oriented frame (DYB), and body-fixed satellite frame (XYZ)

Figure 17 illustrates the SLR residuals plotted as a function of the Sun elevation angle above the orbital plane (absolute value of β) and the satellite argument of latitude with respect to the latitude of the Sun (Δu) both for the individual and combined orbit solutions. Some of the Galileo IOV and FOC products reveal a distinctive pattern in SLR residuals shifted toward negative values for Δu close to 180°. This pattern is particularly prominent for the ECOM solutions, but almost eliminated when using the a priori box-wing model based on Galileo metadata with ECOM (Bury et al. 2019a). Therefore, the pattern is dominant in COD, GFZ, and MIT solutions, but is mostly diminished in IGS combined, ESA and TUG solutions. One may also notice that in contrast to COD and GFZ, the SLR residuals from the MIT solution for Δu close to 180° and low β angles are positive. Despite COD asserting using the a priori box-wing in the SRP model, the appearance of these signals suggests possible issues with box-wing coefficients in COD products. Interestingly, the dominant signatures for nominal Galileo-FOC satellites are significantly reduced for Galileo-FOC satellites on eccentric orbits. Galileo IOVs show large negative residuals exceeding − 50 mm for maximum |β| angles when the Sun is almost perpendicular to the orbital plane. The bias for high |β| of Galileo-IOV is most pronounced in MIT, GRG and TUG solutions, making it challenging to attribute the signature to any SRP modeling feature. The highest maximum |β| angles of 76° occur currently only for the Galileo C-plane, meaning the signature applies only to SVN 103. The pattern is not fully mitigated by any of the ACs.

Fig. 17

SLR residuals in millimeters as a function of the Sun elevation angle above the orbital plane (absolute value of β) and the satellite argument of latitude with respect to the latitude of the Sun (Δu) based on the individual AC solutions and combined IGS solution for Galileo-2 FOC (top panel), Galileo-2 FOCe (middle panel) and Galileo-1 IOV (bottom panel)

Bury et al. (2021) showed that combining SLR and GNSS observations in orbit determination can significantly reduce the spurious signal in SLR residuals for Galileo-IOV satellites. Adding SLR measurements stabilizes the radial component of the orbit, thereby reducing the variations in the B0 ECOM parameter for high β angles, which appears to be responsible for the signature in the GNSS-only solution. Apart from the issues with the high |β| angles, the MIT, COD, and GFZ solutions exhibit some signatures similar to those visible in the Galileo-FOC orbit products, which can be attributed to problems with the proper use of the a priori box-wing model. The GRG solution for Galileo-IOV also suffers from orbit mismodeling which is different from any other solution, possibly arising from the omission of the D0 parameter in the ECOM model. Apart from the mean offset of the TUG Galileo-FOC products, the Galileo orbit solutions delivered by ESA and TUG exhibit almost no signatures in SLR residuals. The combined solution is also almost free of any signatures, thanks mostly to the contribution of ESA and TUG, which receive the highest weights in the combination (see Sect. 4.1). Unfortunately, the errors of the other solutions affect the combined solution to some extent.

Figure 18 shows the dependencies of the SLR residuals as a function of satellite elongation angle with respect to the Sun. For Galileo FOC, the linear trend of SLR residuals ranges from < 0.02 (TUG, ESA, MIT solutions) to − 0.396 mm/° (GFZ), which translates into the differences of 3.5 and 79.5 mm between the extreme elongations of ε = 0° and 180°, respectively. For Galileo IOV and Galileo FOC on eccentric orbits, the linear trend does not exceed ≈ 0.2 mm/° for either of the solutions. Again, the combined IGS solution is nearly equivalent to the best individual AC solutions.

Fig. 18

SLR residuals as a function of satellite elongation angle with respect to the Sun position based on the individual AC solutions and combined IGS solution for Galileo-2 FOC (top panel), Galileo-2 FOCe (middle panel) and Galileo-1 IOV (bottom panel)

Now, let us move on to the GLONASS orbit solutions. Figures 19 and 20 illustrate the SLR residuals from GLONASS orbit solutions plotted as a function of β, Δu, and ε angles in analogy to Figs. 17 and 18, respectively. Figure 19 demonstrates that the individual GLONASS orbit solutions are more consistent that those of the Galileo satellites. For GLONASS-M satellites, the solutions provided by COD, ESA and TUG are exempt from any signatures in SLR residuals. Some issues occur for GRG and WHU orbit solutions, however, these are much lower in magnitude when compared to the Galileo FOC products. Interestingly, for low β angles, the sign of the SLR residuals is positive close to Δu = 180° and negative close to Δu = 0°, which is opposite to the pattern visible for the Galileo-FOC satellites. Both Galileo-FOC and GLONASS-M/-M+ satellites have the elongated shape of the satellite buses; however, in different directions. The unique pattern of positive SLR residuals for the high β angles is visible for the GLONASS-M orbit solutions delivered by GFZ. The signature is similar to those already noticed for the Galileo-IOV satellites, but with the opposite sign. Concerning the GLONASS-K1B satellites, the SLR residuals are the smoothest for the COD and TUG solutions, however, with a noticeable strip of positive SLR residuals close to the Δu = 180°. The pattern is amplified in the remaining solutions, which in turn affects the combined solution.

Fig. 19

SLR residuals in millimeters as a function of the Sun elevation angle above the orbital plane (absolute value of β) and the satellite argument of latitude with respect to the latitude of the Sun (Δu) based on the individual AC solutions and combined IGS solution for GLONASS-M (top panel), -M+ (middle panel) and -K1B (bottom panel)

Fig. 20

SLR residuals as a function of satellite elongation angle with respect to the Sun position based on the individual AC solutions and combined IGS solution for GLONASS-M (top panel), -M+ FOCe (middle panel) and -K1B (bottom panel)

The slope of the SLR residuals from GLONASS-M/-M+ orbit solutions analysed as a function of the satellite elongation angle ranges from − 0.02 (COD) to ≈ 0.15–0.18 mm/° (GFZ, TUG, WHU) (see Fig. 19). Unlike the remaining solutions, the slope is positive for the WHU solution with coefficients of 0.18 and 0.12 mm/° for GLONASS-M, -M+, respectively.

5 Conclusions and discussion

In preparation for the release of ITRF2020, the IGS ACs released the results of the third reprocessing campaign—IGS Repro3—of all the GNSS network solutions backwards starting from 1994. Unlike the previous reprocessing campaigns, the IGS Repro3 includes, for the first time, not only GPS and GLONASS but also the Galileo constellation. The individual IGS Repro3 contributions have been combined using the IGS ACC combination software using a satellite-based weighting approach to account for the varying quality of GNSS orbits provided by different IGS ACs.

The internal precision of the combination was evaluated based on the RMS of the 3D orbit differences between the individual and the combined solutions. In 2020, the range of mean RMS values was 6–11 mm (TUG–GRG; GPS IIR-M), 7–11 mm (TUG–GFZ; GPS IIF), 21–44 mm (COD–TUG; GLO-M), 16–25 mm (COD–GRG; GLO-M +), 13–26 mm (ESA–GRG; GLO-K1B), 8–24 mm (TUG–GRG; GAL-1), and 12–22 mm (COD–GRG; GAL-2). The analysis of orbit differences reveals that the combined GLONASS products are most consistent with COD, while the GPS/Galileo products are most consistent with TUG. The presented results are comparable with a complementary orbit combination study carried out by Sakic et al. (2022), which reported internal precisions of 10, 30 and 16 mm for GPS, GLONASS and Galileo, respectively, at the end of the reprocessed period (2020-12-31).

The SLR validation was performed to provide external validation of the individual and combined orbit products. To maintain the highest quality, we proposed a novel approach for handling detector-specific biases in the SLR validation. Thanks to the reduction of detector-specific biases in the dataset, the standard deviation of SLR residuals decreased by up to 15% for Galileo FOC satellites. Moreover, the SLR dataset became more internally consistent, facilitating the detection of orbit modeling issues.

The mean offset in SLR residuals varies within specific groups of satellites between individual ACs with a centimeter level magnitude, especially for Galileo-FOC. In the extreme case, the mean offset of GFZ and GRG Galileo-FOC satellites varies by 43 mm, which is consistent with the result presented by Sakic et al. (2022) and may be caused by orbit modeling differences, which strongly affects the radial component of the orbit. The standard deviation of SLR residuals for the best individual solution versus the combined solution is 13/13, 13/12, 15/17, 17/17, 18/19, 15/16 for Galileo-FOC, -FOCe, -IOV, GLONASS-K1B, -M, and -M+, respectively. Therefore, the combined solution can be considered equal in quality compared to the best individual AC solutions, proving the superb efficiency of the orbit combination methodology. Unfortunately, the SLR validation results cannot be cross-compared with the values provided by Sakic et al. (2022), who provided the validation statistics based on the daily averaged SLR residuals preceded by outlier threshold criteria that are different fom those used in this study. On the other hand, the presented SLR validation results are slightly better than those reported on the official webpage of the IGS multi-GNSS Pilot Project⁵ for MGEX products.

Aiming to expose the strengths and weaknesses of the individual solutions and how the signatures of the individual solutions affect the combined orbit, we decomposed the SLR residuals in different Sun-Earth-satellite geometries. The results show that spurious signatures occur in the SLR residuals of the individual ACs due to differences in orbit modelling. The consistency of orbit quality is expected to improve, particularly for Galileo solutions. The solutions provided by ESA and TUG demonstrate that Galileo orbits can be modelled with exceptional quality and almost without signatures in the SLR residuals. However, the orbit modeling issues present in some individual solutions affect the combined orbit product to some extent.

The analysis of the SLR validation results reveals that the ESA orbit products are the most precise among all the individual solutions for most of the satellite groups. The TUG products are almost as good as the ESA products in terms of the standard deviation of SLR residuals for the Galileo-FOC orbits. COD provided the best GLONASS-K1B orbits; however, the difference between the ESA and TUG products is marginal. The IGS combined orbits are never worse than 10% compared to the best individual solution. Moreover, for GAL-FOCe and GLONASS-K1B, the combined solution is the best among all available solutions. Eventually, the combined orbit product should be considered the best solution overall since it benefits from the best individual solutions for each satellite type.

The SLR validation of the individual AC solutions confirms some beneficial findings about the orbit modelling aspects. The hybrid approach for Galileo, which incorporates the box-wing model and a limited set of estimated empirical parameters, significantly reduces fluctuations in SLR residuals, particularly for low Sun elevation angles (β) during orbit eclipses. ESA incorporates additional once-per-revolution parameters in the along-track direction, which seems to be also beneficial, given the superb quality of their products. However, none of the ACs mitigates the pattern of large negative SLR residuals for high β angles for the Galileo-IOV orbits. A consistent orbit determination based on the combined SLR and GNSS observations has been proposed to solve this problem, but the methodology of this approach is still a topic of scientific discussion and has not been implemented operationally by any AC (Dilssner et al. 2020, 2022; Bury et al. 2021, 2022). For GLONASS, the box-wing model does not play a key role. The consistency of the GLONASS orbit products delivered by individual ACs is higher than for Galileo, despite the different approaches used to handle non-gravitational forces. The impact of selecting observables in the processing between forming DD, ZD, or processing RAW observations on the orbit products is challenging to evaluate in this study. The expected magnitude is too small to separate from the other factors such as SRP modeling, so the latter should be investigated individually with a dedicated testbed.

Interestingly, there is a slight discrepancy between the weights of individual ACs in the combination and the quality of the individual AC products, as assessed externally by SLR. For instance, taking the Galileo-FOC satellites as an example, COD delivered 50% of the solutions with the greatest weight, swapping with MIT and TUG in approximately 25% and 15% of the remaining epochs, respectively. On the other hand, the SLR analysis revealed that the ESA product was the most accurate in terms of orbit modeling, as measured by the number of artificial signatures in SLR residuals decomposed in different Sun-Earth-satellite geometries. The weights of the individual products in the combination are determined based on the consistency (RMS) of the individual product with the mean model, i.e., the smaller the RMS, the higher the weight of the contribution in the combination. Unfortunately, any combination software is currently blind to the systematic effects, such as patterns in SLR residuals, that are visible in the external validation results. In the future development of combination methodology, it should be considered to include the SLR validation results as an additional factor in the combination.

The IGS combined product is particularly useful for ACs to assess their processing and identify any potential weaknesses. The present work can also support the orbit combination currently performed by the other groups for cross-comparison and validation of, e.g., independent multi-GNSS orbit combinations at GFZ (Sakic et al. 2022; Mansur et al. 2022) and Wuhan (Chen et al. 2023).