1 Introduction

The International GNSS Service (IGS, Johnston et al. 2017) publishes on a regular basis GPS and GLONASS orbit and clock offset products with an accuracy of around \(2\,\textrm{cm}\) and \(75\,\textrm{ps}\) \(\textrm{RMS}\), respectively. These final products result from a combination using the orbits and clock offsets determined by the IGS Analysis Centers (ACs) as input. The motivation for a combination remains the same since the early years of the IGS: to smooth the errors and fill the possible gaps made by ACs during their independent processing, and thus provide a reliable, accurate, and unique product to the users (Springer and Beutler 1993; Beutler et al. 1995). Such combination is also a suitable way to have a reference for the comparison and validation of the ACs’ individual results (e.g., Griffiths 2019).

The method to perform the combination was developed by Springer and Beutler (1993) and described in detail by Kouba et al. (1995). Some updates were made over the years mainly to improve the clock combination and the alignment with the current ITRF (Kouba and Springer 2001). The complete history of changes in the combination strategy is described in the header of the combination summary files.

Within the IGS, the Multi-GNSS Experiment and Pilot Project (MGEX, Montenbruck et al. 2017) is working on the extension of its services regarding new systems. This project has gained attention since more receivers are capable of tracking new signals, and more constellations were declared operational in the last years, e.g., Galileo in 2016 (ESA 2016) or BeiDou in 2018 (CSNO 2018). Several ACs have recently been extending their products and provide the new constellations in their solutions.

However, so far no official combination for the new constellations is available. The IGS Analysis Center Coordinator (ACC) proposes an experimental combined MGEX solutionFootnote 1 since September 2019 based on an adaptation of the legacy strategy (Sośnica et al. 2020). The GFZ IGS team has been putting efforts to study and provide a dedicated and entirely consistent orbit and clock combination using the solutions provided by the ACs contributing to the MGEX project. Previous studies were made adapting the IGS combination software (Fritsche 2016; Mansur et al. 2020; Sakic et al. 2020), and have shown that significant modifications are needed to combine MGEX products, including an improved weighting strategy adapted to the different constellations. In the current software, the combination for GPS and GLONASS is done completely independent for each constellation, which is not ideal in terms of interoperability. A simple adaptation of the existing software may therefore not be suited to handle the different constellations with different quality of their orbit solutions.

To this end, we propose a unified multi-GNSS orbit combination approach based on variance component estimation (VCE). VCE has been extensively used in different applications in geodesy over the years. Some noticeable examples can be found in Koch and Kusche (2002), where VCE is used for geopotential regularization, and in Kusche (2003) within the weight determination for GOCE (Gravity Field and Steady-State Ocean Circulation Explorer) gravity recovery solutions. In the context of combining Terrestrial Reference Frames (TRF), Bähr et al. (2007) presents a comparison between three VCE methods, and more recently Kobel et al. (2019) implemented a VCE approach to combine the orbits of the Low Earth Orbit (LEO) satellite Sentinel-3. In this contribution, we make use of least-squares variance component estimation (LSVCE), originally developed by Teunissen (1988). The method is derived and described in detail in Amiri-Simkooei (2007) and Teunissen and Amiri-Simkooei (2008). Applications of LSVCE for GPS data processing are provided in Amiri-Simkooei et al. (2009) and Amiri-Simkooei et al. (2013). The method is flexible and relies on the well-known least-squares theory. We present the application of LSVCE to an orbit combination, where we study two different models: (1) Considering AC-specific orbit variances and (2) introducing AC plus constellation-specific orbit variances. The final combined orbits are derived as a weighted mean of the Helmert-transformed orbits of the ACS, where the weights are the normalized inverse estimated variance components, so that the sum of the weights equals one.

The overall structure of this manuscript contains five sections. Section 2 provides a brief explanation of the steps implemented to combine the orbits, whereas in Sect. 3 the mathematical least-squares framework of our orbit combination is introduced. Section 4 summarizes the experiments, compares the two methods, and shows a validation of the combined orbits using satellite laser ranging (SLR) and precise point positioning (PPP). A summary and conclusions are given in Sect. 5.

2 Combination steps

The task of the orbit combination is to transform the orbit products of different ACs to a single combined orbit product. In short, the current IGS combination procedure is as follows. It starts with a simple mean of the orbit solutions from all ACs. Then, seven parameter Helmert transformations between the individual orbits and the mean orbit are performed, and the ACs’ orbits are aligned to the mean via these transformations. A weight is derived for each AC from the differences of these transformed orbits and the mean orbit, and a new weighted mean orbit is computed. The same steps are repeated once, starting with the weighted mean orbit, finally yielding the combined orbit product.

In this contribution, we present a combination approach that is based on the least-squares principle. The combined orbits are then again a weighted mean of the orbits of the ACs, where the weights are proportional to the inverse variances of the ACs’ solutions. These unknown variances are estimated by means of LSVCE (Amiri-Simkooei 2007).

The orbit combination process is implemented in Python within the framework of the GeodeZYX toolbox (Sakic et al. 2019). The five main combination steps listed below are illustrated in Fig. 1. Detailed mathematical derivations are provided in Sect. 3.

  1. (1)

    We start with a pre-check to identify and exclude satellites that appear in only one of the ACs’ solutions or satellites with missing epochs. A first rough exclusion procedure is performed, in which the satellite coordinates are compared between ACs. If one AC provides an orbit for a satellite that is very far from the other ACs (e.g., threshold set at \(500\,\textrm{m}\)), this solution is already excluded at this stage. A mean orbit is computed using the pre-checked orbits.

  2. (2)

    The second step consists of a Helmert transformation between this mean orbit and the ACs’ solutions, which provides the seven parameters per AC that are used to align the orbits.

  3. (3)

    In the third step, a set of core satellites is defined. The idea is to select a subset of the orbits that are used for the VCE. The set of core satellites ensures that the satellites for computing the variance components are the same for all ACs and that outliers are detected and excluded to get proper estimates of the weights. The outlier detection is done by applying the Modified Z-Score (Iglewicz and Hoaglin 1993) to the radial, along-track, and cross-track (RAC) components of each set of AC coordinates for all satellites. If one of the components is identified as an outlier for a satellite, this satellite is excluded from the set of core satellites. The detection threshold is chosen less strict for BeiDou and QZSS since the quality of the ACs’ orbits for these systems is still not on the level of GPS, GLONASS, and Galileo.

  4. (4)

    The fourth step is the estimation of the variance components as described in Sect. 3.3, using only the above defined set of core satellites.

  5. (5)

    With the variance components determined, the final step is the orbit combination. As described in Eq. (12) in Sect. 3.2, the inverse variances are normalized and then applied as weights to the ACs’ orbits. The orbit combination is also provided for satellites that are not in the set of core satellites, where, if a solution is missing or excluded for one or more ACs for a specific satellite, the normalization is based only on the variances of the ACs that are included.

This process is repeated as mentioned at the end of Sect. 3.1, starting with the Helmert transformation that is computed with respect to the combined orbits of the previous iteration. The iteration is terminated once the 3D-RMS difference of the orbits of two subsequent iterations is below a threshold of \(1 \,\textrm{mm}\).

Fig. 1
figure 1

The flowchart represents the algorithm implemented to compute the orbit combination

Full size image

During the processing, we can define three groups of satellite orbits. (1) The first group contains the ACs’ orbits of the core satellites that pass the outlier detection and are common among all ACs. They are the ones defining the weights of the combination. With constellation-specific weighting (cf. Sect. 3.4), the set of core satellites is defined per constellation, so that ACs which provide only some constellations can still be considered. ACs with too few common satellites can be excluded in order to have enough core satellites. (2) The second group is used to compute the Helmert transformations. It includes the orbits of the core satellites of group (1), but also of the satellites that are not available at all ACs. Satellites that are excluded as outliers for some of the ACs when defining the set of core satellites are also included for the remaining ACs. (3) The third group of satellite orbits is the largest group, which is used to compute the combined orbits. In addition to the second group, it also contains orbits of satellites that are detected as outliers for all ACs. These satellites are included in order to keep the combined solution as complete as possible.

3 Mathematical framework

In this section, the mathematics for the combination framework of Sect. 2 are derived. In short, it is the solution to the problem of a joint least-squares estimation of the combined orbits and variance components for the input orbits.

3.1 System model

The input of the orbit combination is the orbits of the ACs. Let the Earth-fixed coordinates of satellite \(s \in \{ 1,\dots , S\}\) provided by AC \(r \in \{1, ..., R\}\) at the time t be given by \({\underline{x}}_{r}^{s}(t) \in {\mathbb {R}}^{3}\). We define

$$\begin{aligned} {\underline{x}}_{r}(t) = \left[ {\underline{x}}_{r}^{1}(t)^{\textrm{T}} \dots {\underline{x}}_{r}^{S}(t)^{\textrm{T}} \right] ^{\textrm{T}} \in {\mathbb {R}}^{3S} \end{aligned}$$
(1)

and

$$\begin{aligned} {\underline{x}}_{r} = \left[ {\underline{x}}_{r}(t_{1})^{\textrm{T}} \dots {\underline{x}}_{r}(t_{P})^{\textrm{T}} \right] ^{\textrm{T}} \in {\mathbb {R}}^{3SP}, \end{aligned}$$
(2)

with \(t_p\), \(p \in \{1, ..., P\}\), the time at epoch p. The unknown combined orbit vector \({\underline{x}}_{\textrm{c}} \in {\mathbb {R}}^{3SP}\) is defined according to \({\underline{x}}_{r}\). The relation between the ACs’ orbits and the combined orbits can be described by means of a linearized Helmert transformation (Watson 2006) as

$$\begin{aligned} {\underline{x}}_{r}^{s}(t) = {H}_{r} {\underline{x}}_{\textrm{c}}^{s}(t) + \varDelta {\underline{x}}_r + {\underline{\varepsilon }}_r^s(t), \end{aligned}$$
(3)

where the AC-specific Helmert transformation matrices \({H}_{r}\) are in the form of

$$\begin{aligned} {H} = \begin{bmatrix} \mu &{}\quad \theta _{z}\mu &{}\quad -\theta _{y}\mu \\ -\theta _{z}\mu &{}\quad \mu &{}\quad \theta _{x}\mu \\ \theta _{y}\mu &{}\quad -\theta _{x}\mu &{}\quad \mu \end{bmatrix} \end{aligned}$$
(4)

with \(\theta _x\), \(\theta _y\), \(\theta _z\), and \(\mu \) the rotation and scale parameters, and \(\varDelta {\underline{x}}_r\) the translation parameters, that align the ACs’ orbits and the combined orbits, and \({\underline{\varepsilon }}_r^s(t) \in {\mathbb {R}}^{3}\) an additive noise term. Analogous to Eq. (2), \({\underline{\varepsilon }}_r \in {\mathbb {R}}^{3SP}\) is composed of all \({\underline{\varepsilon }}_r^s(t_p)\). In order to facilitate our derivations, we apply the following invertible transformation to the input orbits \({\underline{x}}_{r}^{s}\left( t \right) \):

$$\begin{aligned} \bar{{\underline{x}}}_{r}^{s}\left( t \right) = {H}_{r}^{-1}\left( {\underline{x}}_{r}^{s}\left( t \right) - \varDelta {\underline{x}}_{r} \right) . \end{aligned}$$
(5)

Note that all information is kept through this transformation, so that the transformed orbits \(\bar{{\underline{x}}}_{r}^{s}\left( t \right) \) can equivalently be used instead of the original orbits. The final system model can now simply be written as

$$\begin{aligned} \underbrace{ \begin{bmatrix} \bar{{\underline{x}}}_{1} \\ \vdots \\ \bar{{\underline{x}}}_{R} \end{bmatrix}}_{\bar{{\underline{x}}}} = \underbrace{\left[ {\underline{1}}_{R} \otimes I_{3SP} \right] }_A \cdot {\underline{x}}_{\textrm{c}} + \underbrace{ \begin{bmatrix} \bar{{\underline{\varepsilon }}}_1 \\ \vdots \\ \bar{{\underline{\varepsilon }}}_R \end{bmatrix}}_{\bar{{\underline{\varepsilon }}}}, \end{aligned}$$
(6)

where \({\underline{1}}_{R}\) is an R-vector of ones, \(I_{3SP}\) an identity matrix of size 3SP, \(\otimes \) the Kronecker product, and \(\bar{{\underline{\varepsilon }}}_r\) are the transformed versions of \({\underline{\varepsilon }}_r\).

For the stochastic model, we assume that

$$\begin{aligned} \bar{{\underline{\varepsilon }}}_r \sim {\mathcal {N}} \left( {\underline{0}},\sigma _r^2 I_{3SP} \right) , \end{aligned}$$
(7)

i.e., there is an AC-specific variance \(\sigma _r^2\) that is common for all coordinates. This assumption is a simplification, since, for instance, the positions of each satellite are derived from the same set of orbital parameters within each AC, and the orbits of different satellites are connected through the receiver clock parameters in a network solution. Including such information would, however, require the covariance matrices of the ACs’ orbit estimation, which are not accessible. Assuming uncorrelated solutions between ACs, we therefore have

$$\begin{aligned} \bar{{\underline{\varepsilon }}} \simeq {\mathcal {N}}\left( {\underline{0}}, Q \right) \quad \text {with} \quad Q = \sum _{r=1}^{R} \sigma _{r}^2 Q_{r}, \end{aligned}$$
(8)

where \(\sum _{r=1}^{R} \sigma _{r}^2 Q_{r}\) is positive definite, \(\sigma _r^2\) are the variance components, and \(Q_{r} = \textrm{diag}({\underline{c}}_r) \otimes I_{3SP}\) is a known sparse block matrix, with \({\underline{c}}_r\) the rth canonical unit vector in \({\mathbb {R}}^R\). These AC-specific variance components \(\sigma _r^2\) lead to AC-specific weights for the orbit combination, cf. Sect. 3.2. An extension allowing for AC plus constellation-specific weights is presented in Sect. 3.4.

We can now solve the system model as described in (6) and (8) for the unknown combined orbits \({\underline{x}}_{\textrm{c}}\) and the variance components \(\sigma _r^2\), \(r\in \{1\dots ,R\}\). The estimation follows the LSVCE framework presented in Amiri-Simkooei (2007) and Teunissen and Amiri-Simkooei (2008). It is noted that for the computation of the Helmert transformation parameters in Eqs. (3)–(5), the unknown combined orbits \({\underline{x}}_{\textrm{c}}\) are required so that the above estimation problem is solved iteratively, where the combined orbits can be initialized with a simple mean and then updated in each iteration.

3.2 Combined orbit solution

We recall from Eqs. (6)–(8) that our system is of the form \(\bar{{\underline{x}}}=A{\underline{x}}_c + \bar{{\underline{\varepsilon }}}\), so that the weighted least-squares solution \(\hat{{\underline{x}}}_{c}\) for the combined orbit is given by

$$\begin{aligned} \hat{{\underline{x}}}_{\textrm{c}} = \left( {A}^{\textrm{T}}{Q}^{-1}{A} \right) {^{-1}A}^{\textrm{T}}Q^{-1} \bar{{\underline{x}}}. \end{aligned}$$
(9)

Using the mixed-product property of the Kronecker product and that the transposition is distributive on the Kronecker product (properties recalled by Teunissen and Amiri-Simkooei 2008 and proven by, e.g., Rao 1973), we have

$$\begin{aligned} \begin{aligned} {A}^{\textrm{T}}{Q}^{-1}&= \left( {\underline{1}}_{R}^{\textrm{T}} \otimes I_{3SP} \right) \sum _{r=1}^{R}\left( \textrm{diag} \left( {\underline{c}}_{r} \right) \otimes I_{3SP} \frac{1}{\sigma _{r}^{2}} \right) \\&= \sum _{r=1}^{R}{\underline{c}}_{r}^{\textrm{T}} \otimes I_{3SP} \frac{1}{\sigma _{r}^{2}} \end{aligned} \end{aligned}$$
(10)

and

$$\begin{aligned} \begin{aligned} {A}^{\textrm{T}}{Q}^{-1}{A}&= \left[ \sum _{r=1}^{R} \frac{1}{\sigma _{r}^{2}}\left( {\underline{c}}_{r}^{\textrm{T}} \otimes I_{3SP} \right) \right] \left( {\underline{1}}_{R}^{\textrm{T}} \otimes I_{3SP} \right) \\&= \left( \sum _{r=1}^{R} \frac{1}{\sigma _{r}^{2}} \right) I_{3SP}. \end{aligned} \end{aligned}$$
(11)

With Eqs. (10) and (11), the combined orbit solution from Eq. (9) can be rewritten as

$$\begin{aligned} \hat{{\underline{x}}}_{\textrm{c}} = \frac{1}{ \sum _{r=1}^{R}\frac{1}{\sigma _{r}^{2}}} \cdot \sum _{r=1}^{R}\frac{1}{\sigma _{r}^{2}} \cdot \bar{{\underline{x}}}_{r}, \end{aligned}$$
(12)

which shows that the combined orbits are indeed a weighted mean of the ACs’ orbits. The estimation of the variance components \(\sigma _r^2\) is shown in the next section.

3.3 Variance component solution

Following the LSVCE theory presented by Amiri-Simkooei (2007) and Teunissen and Amiri-Simkooei (2008), let B be a matrix whose columns span the null space of \(A^\textrm{T}\) so that \(A^\textrm{T}B = 0\). It follows that the random vector of misclosures \({\underline{t}}=B^{T} \bar{{\underline{x}}}\) is zero mean and uncorrelated with \(\hat{{\underline{x}}}_\textrm{c}\). There is a one-to-one correspondence between \(\left[ \hat{{\underline{x}}}_\textrm{c}^\textrm{T}, {\underline{t}}^\textrm{T} \right] ^\textrm{T}\) and \(\underline{\bar{x}}\), cf. Eq. (3) in Teunissen and Amiri-Simkooei (2008), so that instead of \(\underline{\bar{x}}\) we can equivalently use \(\hat{{\underline{x}}}_\textrm{c}\) and \({\underline{t}}\) to estimate the unknowns. As \(\hat{{\underline{x}}}_\textrm{c}\) is already the least-squares estimate of the parameter vector \({\underline{x}}_\textrm{c}\) and does not leave any redundancy, and as it is uncorrelated with \({\underline{t}}\), the variance components \(\sigma ^2_r\) are estimated only from \({\underline{t}}\). With \({\underline{t}}\) zero mean, the covariance matrix of \({\underline{t}}\) is given by \(\textrm{E}\left\{ {\underline{t}}{\underline{t}}^\textrm{T} \right\} = B^\textrm{T} Q B = \sum _{r=1}^R \sigma _r^2 B^\textrm{T}Q_r B\), which can be considered as a matrix observation equation for estimating \(\sigma _r^2\). Using the half-vectorization operator \(\textrm{vh}(\cdot )\) on \({\underline{t}}{\underline{t}}^\textrm{T}\) that transforms a matrix into a vector whose components are the \(\frac{n(n+1)}{2}\) entries on and below the main diagonal (Turkington 2005), thereby eliminating the duplicate entries of a symmetric matrix, a standard linear observation model is obtained as

$$\begin{aligned} \textrm{E}\left\{ \textrm{vh}\left( {\underline{t}}{\underline{t}}^\textrm{T} \right) \right\} = A_\textrm{vh} {\underline{\sigma }} \end{aligned}$$
(13)

with \({\underline{\sigma }}=\left[ \sigma _1^2,\dots ,\sigma _R^2 \right] ^\textrm{T}\) and \(A_\textrm{vh} = \left[ \textrm{vh}\left( B^\textrm{T}Q_1 B\right) ,\dots ,\textrm{vh} \left( B^\textrm{T} Q_R B \right) \right] \). The solution of the variance components \(\hat{{\underline{\sigma }}}\) defining the weights in Eq. (12) is given by

$$\begin{aligned} \hat{{\underline{\sigma }}}=\left( {A}_{\textrm{vh}}^{\textrm{T}} W_{\textrm{vh}} {A}_{\textrm{vh}}\right) ^{-1} {A}_{\textrm{vh}}^{\textrm{T}} W_{\textrm{vh}} \textrm{vh}\left( {\underline{t}} {\underline{t}}^{\textrm{T}}\right) , \end{aligned}$$
(14)

where \(W_{\textrm{vh}}\) is a weight matrix. With \(N={A}_{\textrm{vh}}^{\textrm{T}} W_{\textrm{vh}} {A}_{\textrm{vh}}\) and \({\underline{l}}={A}_{\textrm{vh}}^{\textrm{T}} W_{\textrm{vh}} \textrm{vh}\left( {\underline{t}} {\underline{t}}^{\textrm{T}}\right) \), we can write

$$\begin{aligned} \hat{{\underline{\sigma }}}= N^{-1} {\underline{l}}. \end{aligned}$$
(15)

Using the inverse covariance matrix \(Q_\textrm{vh}\) of \(\textrm{vh}\left( {\underline{t}} {\underline{t}}^{\textrm{T}}\right) \) as weight matrix, the elements of the normal-matrix N and the vector \({\underline{l}}\) are derived as (cf. Eqns. 4.85 and 4.86 in Amiri-Simkooei 2007)

$$\begin{aligned} n_{r, l}&=\frac{1}{2} {\text {tr}}\left( B^{\textrm{T}} Q_{r} B Q_{t}^{-1} B^{\textrm{T}} Q_{l} B Q_{t}^{-1}\right) \end{aligned}$$
(16)
$$\begin{aligned} l_{r}&=\frac{1}{2} {\underline{t}}^{\textrm{T}} Q_{t}^{-1} B^{\textrm{T}} Q_{r} B Q_{t}^{-1} {\underline{t}}, \end{aligned}$$
(17)

with \(Q_{t}=B^{\textrm{T}} Q B\) and \({\text {tr}}(\cdot )\) the trace operator. Since \(Q_t\) depends on the variance components \({\underline{\sigma }}\), (15) is again solved iteratively within each iteration of solving Eq. (6), where \(Q_t\) is computed with the estimates of the variance components \(\sigma _r^2\) from the previous iteration.

In order to solve Eq. (15), we therefore need to find a matrix B, whose columns are a basis of the null space of \(A^\textrm{T}\) such that \(A^\textrm{T}B = 0\), as already mentioned. There are infinitely many choices for B, all of which will lead to the same result \(\hat{{\underline{\sigma }}}\). Our goal is to find a matrix B that leads to an efficient implementation avoiding large scale matrices that could be obtained for daily combinations with many satellites and ACs. With \(A=\left[ {\underline{1}}_{R} \otimes I_{3SP} \right] \), one solution for B is given by

$$\begin{aligned} B = {D}\otimes {I}_{3SP} \end{aligned}$$
(18)

with the differencing operator

$$\begin{aligned} {D} = \begin{bmatrix} -{\underline{1}}_{R-1}^{\textrm{T}}\\ {I}_{R-1} \end{bmatrix}. \end{aligned}$$
(19)

The property \(A^\textrm{T}B = 0\) follows from \(D^\textrm{T}{\underline{1}}_R = {\underline{0}}\) and the mixed-product property of the Kronecker product. The vector of misclosures \({\underline{t}}=B^{\textrm{T}} \bar{{\underline{x}}}\) in Eq. (17) contains the between AC differenced orbits \({\underline{x}}_r - {\underline{x}}_1\), \(r \in \lbrace 2,\dots ,R \rbrace \), and \(\hat{{\underline{\sigma }}}\) is a function of only those differences.

With \(Q_r = \textrm{diag}({\underline{c}}_r) \otimes I_{3SP}\), we have

$$\begin{aligned} B^\textrm{T}Q_r B = \left( {D}^{\textrm{T}} {\text {diag}} \left( {\underline{c}}_{r} \right) {D} \right) \otimes {I}_{3SP}, \end{aligned}$$
(20)

and matrix \(Q_t = B^\textrm{T} Q B\) required in Eqs. (16) and (17) can be rewritten as

$$\begin{aligned} {Q}_{t} = \left( \sum _{r=1}^{R} \sigma _{r}^2 {D}^{\textrm{T}} {\text {diag}} \left( {\underline{c}}_{r} \right) {D} \right) \otimes {I}_{3SP}. \end{aligned}$$
(21)

Consequently, Eqs. (16) and (17) are given by

$$\begin{aligned}&n_{r, l}=\frac{3SP}{2} {\text {tr}} \Bigg [ {D}^{\textrm{T}} {\text {diag}} \left( {\underline{c}}_{r} \right) {D} \bigg ( \sum _{q=1}^{R} \sigma _{q}^2 {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{q} \right) {D} \bigg )^{-1} \nonumber \\&\quad {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{l} \right) {D} \bigg ( \sum _{q=1}^{R} \sigma _{q}^2 {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{q} \right) {D} \bigg )^{-1} \Bigg ] \end{aligned}$$
(22)
$$\begin{aligned}&l_{r}= \frac{1}{2}{\underline{t}}^{\textrm{T}} \Bigg \{ \Bigg [ \bigg ( \sum _{q=1}^{R} \sigma _{q}^2 {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{q} \right) {D} \bigg )^{-1} {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{r} \right) {D} \nonumber \\&\quad \bigg ( \sum _{q=1}^{R} \sigma _{q}^2 {D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{q} \right) {D} \bigg )^{-1} \Bigg ] \otimes {I}_{3SP} \Bigg \} {\underline{t}}. \end{aligned}$$
(23)

The blocks \({D}^{\textrm{T}} {\text {diag}}\left( {\underline{c}}_{r} \right) {D}\) used in this representation are only of dimension \(R-1 \times R-1\) and therefore suitable for an efficient implementation. Using Eqs. (22) and (23), the variance components \({\underline{\sigma }}\) are estimated, cf. Eq. (15), and used to compute the combined orbits, cf. Eq. (12).

3.4 Introducing constellation-specific weights

So far, we assumed that there is one variance component for each AC, see Eqs. (7) and (8), which translates into a weight per AC in the orbit combination in Eq. (12). However, this assumption might be too simple for a multi-GNSS solution, in which the orbits of different constellations might be of different quality. We can therefore extend the above model by introducing a variance component \(_g\sigma _{r}^2\), \(g\in \{ 1,\dots , G\}\), for each AC and constellation, with G the number of constellations. We define \(_g\bar{{\underline{x}}} \in {\mathbb {R}}^{3S_gPR}\) as a vector similar to \(\bar{{\underline{x}}}\) in Eq. (6) that only contains all coordinates of a specific constellation with \(S_g\) satellites. The system model then reads

$$\begin{aligned} \begin{bmatrix} _1\bar{{\underline{x}}} \\ \vdots \\ _G\bar{{\underline{x}}} \end{bmatrix}= & {} \begin{bmatrix} {\underline{1}}_R \otimes I_{3S_1P} &{}\quad &{}\quad \\ {} &{}\quad \ddots &{}\quad \\ {} &{}\quad &{}\quad {\underline{1}}_R \otimes I_{3S_GP} \end{bmatrix} \begin{bmatrix} _1{\underline{x}}_{\textrm{c}} \\ \vdots \\ _G{\underline{x}}_{\textrm{c}} \end{bmatrix}\nonumber \\ {}{} & {} + \begin{bmatrix} _1\bar{{\underline{\varepsilon }}} \\ \vdots \\ _G\bar{{\underline{\varepsilon }}} \end{bmatrix}, \end{aligned}$$
(24)

where \(_g{\underline{x}}_\textrm{c}\) and \(_g\bar{{\underline{\varepsilon }}}\) are the constellation-specific versions of \({\underline{x}}_\textrm{c}\) and \(\bar{{\underline{\varepsilon }}}\). Assuming no correlations between different constellations, which is a natural consequence of the assumption in Sect. 3.1 that no correlations are present between the coordinates of different satellites, the covariance matrix Q of the noise vector \(\left[ _1\bar{{\underline{\varepsilon }}}^\textrm{T}, \dots , _G\bar{{\underline{\varepsilon }}}^\textrm{T} \right] ^\textrm{T}\) is blockdiagonal

$$\begin{aligned} Q = \begin{bmatrix} _1Q &{}\quad &{}\quad \\ {} &{}\quad \ddots &{}\quad \\ {} &{} \quad &{} _GQ \end{bmatrix}, \end{aligned}$$
(25)

where \(_gQ\) only depends on \(_g\sigma _r^2\), with \(r\in \{1,\dots ,R\}\). Therefore, the sets of parameters \(_g{\underline{x}}_\textrm{c}\) and the variance components \(_g\sigma _r^2\) are mutually exclusive between the constellations, and the measurements \(_g\bar{{\underline{x}}}\) are uncorrelated so that the joint orbit combination and LSVCE can be computed separately for each constellation. It is important to note that this is only true within each iteration of the combination process and that the constellations are still connected through the common Helmert transformation in Eq. (3).

Table 1 List of IGS ACs that provide orbit products to the legacy and MGEX lines
Full size table
Fig. 2
figure 2

Constellation-specific RMS differences between the individual AC orbits and the combined solution for AC plus constellation weighting

Full size image
Fig. 3
figure 3

Comparison of the two combination approaches by means of the average RMS orbit differences between the AC orbits and the combined solution. The dark colors represent the ACs only weighting, and the light colors the AC plus constellation weighting

Full size image

4 Results

The two weighting approaches described in Sect. 3 are tested using products that are provided to the IGS by the ACs. We divide these products into two categories:

  • LegacyFootnote 2: GPS and GLONASS products provided by the ACs within the regular IGS operational processing, for which the IGS provides a separate combination (Kouba 2009; Johnston et al. 2017)

  • MGEXFootnote 3: products provided by the ACs to the Multi-GNSS Experiment and Pilot Project (Montenbruck et al. 2017)

Table 1 shows the ACs that contribute to the two processing lines and the constellations contained in the solutions. Some ACs provide both legacy and MGEX solutions. Except for GRG, these solutions are based on different processing setups and are therefore not identical. More information is provided in Mansur et al. (2020).

Two periods of processing are used for our analysis. For MGEX, we use orbit products between GPS week 1982 (January 2018) and GPS week 2116 (July 2020). GPS week 1930 (January 2017) until GPS week 2116 (August 2020) is considered for the legacy products.

4.1 Differences between individual AC orbit solutions and combined orbits

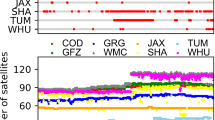
The results from the MGEX orbit combination are compared to the ACs’ individual solutions. Figure 2 shows the time series of the RMS orbit differences with the AC plus constellation weighting approach. The RMS values are computed based on the formula in Kouba et al. (1995). The smallest RMS values are obtained for GPS, and they are better than \(25\,\textrm{mm}\) for all ACs. QZSS shows the highest RMS values, which can reach around \(80\,\textrm{mm}\). This behavior is also noted by Sakic et al. (2020) who used an adaptation of the IGS legacy software to combine the MGEX orbits. Similar results are provided by the ACC where another adaptation of the legacy software is usedFootnote 4. Moreover, for QZSS, especially in 2018, there are days without a combined solution due to missing data or high discrepancy between the satellite coordinates provided by the ACs yielding solutions with high RMS values. These discrepancies can be related to the incomplete solar radiation models applied by the ACs to this constellation (Montenbruck et al. 2013). The days without a solution or with unreasonably high RMS values are not presented. One can note the gaps in Fig. 2. The RMS analysis shows similar characteristics for some ACs for certain constellations, see, for example, the RMS values of GLONASS for GRG and CODE, or for GFZ and WHU from 2018 until early 2019. TUM has the most discrepant RMS values. Similar results are obtained with the AC-only weighting approach, where the largest difference is obtained for QZSS with RMS values of around \(90\,\textrm{mm}\) instead of \(80\,\textrm{mm}\) (not shown).

Figure 3 shows the average of the daily RMS results per AC over the entire test period for both approaches. It is noted that TUM is excluded from the AC-only weighting approach. As described in Sect. 2, our algorithm defines a list of core satellites (satellite group 1), which are satellites provided by the majority of the ACs. Since TUM products do not contain GPS and GLONASS, this AC is excluded from the combination. However, a comparison of the TUM orbits with the combination is still provided. Comparing both strategies, only slight differences at the millimeter level are noted. The most significant differences are observed for QZSS with 13, 11, and \(8\,\textrm{mm}\) for CODE, WHU, and TUM, respectively. The differences are less than \(5\,\textrm{mm}\) for GPS, followed by GLONASS, BeiDou, and Galileo.

Given that the Helmert transformation connects the orbits across constellations, as shown in Eq. (3), we ensure small differences between the seven parameters obtained by our two strategies. On average, there are only differences in the millimeter level. These differences are related to the weighting scheme since, within both approaches, distinct mean orbits are computed and are used in the Helmert transformation.

4.2 Weights

Figures 4 and 5 show the weights used in the combination for the two approaches, and we can observe changes and trends of the ACs’ weights over time. For the AC plus constellation weighting in Fig. 4, GPS has the most consistent AC weights over the test period, followed by GLONASS and Galileo, while the weights for BeiDou and QZSS vary between the ACs. We might attribute this behavior to the number of satellites in the newer system, the different orbit types, or changes in the ACs’ processing routines. We note that in our processing we only consider the MEO satellites of the BeiDou constellation.

Fig. 4
figure 4

Constellation-specific weights used in the orbit combination for the AC plus constellation weighting strategy

Full size image
Fig. 5
figure 5

Weights used in the orbit combination for the AC-only weighting strategy

Full size image
Fig. 6
figure 6

RMS orbit differences compared to the combined solution for the GPS-only legacy processing. The IGS rapid (igr) and final (igs) solutions are included for validation

Full size image
Fig. 7
figure 7

SLR Residuals of the combined orbits with AC plus constellation-specific weighting. The black lines correspond to the medians, the boxes represent the Q1 to the Q3 quartile values, and the whiskers extend to 1.5 times the Q3–Q1 interquartile range

Full size image

For the GPS constellation, WHU has the largest weight, followed by GFZ, with an average of \(28\%\) and \(21\%\), respectively. We observe that since May 2020, CODE’s weight has increased by \(5\%\). Similarly, for GLONASS the most dominating weights are obtained for GFZ and WHU, and again CODE’s weight increased at the end of the test period. For Galileo, we can see an increase in the GRG weight at the end of 2018. We relate this to the time when GRG activated ambiguity fixing in their solution (Loyer et al. 2018). In addition, for this constellation, CODE is the most stable AC in the years 2018 and 2019, but with a larger change in 2020, reducing the average weight of around \(40\%\) to \(25\%\). As mentioned before, BeiDou and QZSS have overall larger variations in the weights. For the Chinese system, the values are more or less evenly distributed among the ACs at the beginning of 2018. From April 2018, SHA had a big increase until January of 2019. In 2020, GFZ reaches an average weight of \(50\%\) while WHU and SHA’s weights decreased. From June 2020, CODE’s BeiDou orbits are excluded from the combination. As mentioned before, our algorithm defines a set of core satellites commonly available at the majority of the ACs, on which the computation of the weights is based. At this period, other ACs also provide BeiDou-3 solutions, which allows for a bigger set of core satellites without CODE; therefore, the CODE BeiDou-2 only solutions were not used. For QZSS, CODE got the major weight, with on average of more than \(30\%\), followed by GFZ. Until July 2018, TUM had a significant weight, decreasing after this period while WHU’s weights are more stable in 2019 and diminishing at the beginning of 2020. Generally, an increase of the weight of an AC goes along with a reduction of the RMS, see Figure 2, for example, for GRG and the Galileo constellation in the end of 2018.

The AC-only weights shown in Fig. 5 reveal that the values are more evenly distributed over the time of processing, but with clear advantages for GFZ and WHU. There is an increase of around \(5\%\) for CODE and GRG, especially in the first half of 2020. However, one has to keep in mind that the weights are defined mainly based on GPS, GLONASS, and Galileo, since the satellites of these constellations are most represented in the core set. For both strategies, the number of iterations needed to achieve the convergence is generally small. For the ACs only weighting, where satellites of different constellations are used in the core, it takes no longer than four iterations on average, whereas for the AC plus constellation weighting on average three iterations are needed for GPS, GLONASS and Galileo, and four for BeiDou and QZSS. The weight differences are small after the second iteration, varying around \(1\%\).

4.3 Validation

To provide a validation of our combination, three different validation steps have been performed. Firstly, we combine the orbit products provided within the IGS legacy chain using the AC-only weighting approach and compare the results to the official IGS combination. Further, the MGEX-based combined orbit solutions with both weighting strategies are validated using the SLR technique, and finally the consistency of the combined orbits is verified by looking at the phase residuals of a PPP analysis.

4.3.1 Combination of IGS legacy products

Since only the constellations GPS or GLONASS are processed, we choose the AC-only weighting approach. Figure 6 shows the GPS-only RMS orbit differences between our combined solution, the ACs’ orbits, and also the legacy IGS rapid and final orbits as reference. Similar to the ACC’s official IGS results (Villiger and Dach 2020), an agreement of around \(15\,\textrm{mm}\) is shown in our solution. Compared to the IGS rapid and final orbits, the RMS is \(6\,\textrm{mm}\) and \(4\,\textrm{mm}\), respectively, showing a very good agreement. Regarding the weights, CODE, on average, has the highest weight of \(15\%\), followed by NGS with \(12\%\) and JPL with \(11\%\). In addition, we observe that MIT’s influence increased in 2020 when their weight raised from around \(6\%\) in 2019 to \(15\%\) in 2020, which can be related to the new release of the GAMIT/GLOBK 10.71, that follows the recommendations for the IGS’s repro3 (MIT 2020). For GLONASS, the RMS difference to the IGS final solution is around \(12\,\textrm{mm}\). The weights are more evenly distributed at the beginning of 2019, when ESA’s weight decreased from an average of \(55\%\) to \(30\%\), while CODE and GRG show an increase of \(10\%\) each.

4.3.2 SLR-based validation

SLR measurements to the GNSS satellites provided by the International Laser Ranging Service (ILRS) establish an independent external validation of their orbits (Pearlman et al. 2019). It is a tracking technique that depends on short laser pulses not susceptible to ionospheric delays, ambiguities, and other effects like tropospheric delays caused by water vapor that introduce errors in the observations. The SLR residuals are directly obtained from the difference between the geometric distance that comes from the GNSS orbits and the ITRF station coordinates and the SLR measurements, after applying proper corrections (Sośnica et al. 2015; Dach et al. 2019). Currently, the satellites of Galileo, QZSS, GLONASS, and BeiDou are equipped with retro-reflectors and tracked by the ILRS. The number of SLR observations depends on the constellation and the ILRS priority list, with GLONASS and Galileo having in general more measurements than BeiDou and QZSS (Sośnica et al. 2020).

The SLR residuals are computed using GFZ’s EPOS.P8 software (Gendt et al. 1998; Uhlemann et al. 2015) and confirm the similarity between both strategies, as the differences in the SLR residuals between both combination strategies are at the millimeter level. We show the results per space vehicle number (SVN) from the AC plus constellation weighting approach in Fig. 7. The constellation with the smallest standard deviation (STD) of the SLR residuals is Galileo with an average STD of \(20 \pm 6\,\textrm{mm}\), followed by GLONASS with \(28 \pm 8 \,\textrm{mm}\), whereas \(68 \pm 35\,\textrm{mm}\) and \(131 \pm 34 \,\textrm{mm}\) are obtained for BeiDou and QZSS, respectively.

In general, the offsets of Galileo are at the millimeter level, and the highest values are for the in-orbit validation (IOV) satellite group with negative offsets. However, the satellites with the minimum STD of \(14\,\textrm{mm}\) are E102 (IOV) and E209 from the full operational capability (FOC) satellite group. The highest values of the STD are obtained for the satellites E201 and E202 with eccentric orbits with 45 and \(35\,\textrm{mm}\). For GLONASS, large positive offsets are observed for R855, R856, R858 of the block M+ with 36, 27, and \(33\,\textrm{mm}\), and for block M satellite R857 with \(39\,\textrm{mm}\). This behavior can also be noted in the preliminary GFZ repro3 results presented in Männel et al. (2020a) and the analysis of the experimental ACC combination shown in Sośnica et al. (2020). Meanwhile, the lowest value of the standard deviation for GLONASS is obtained for R802 (K1B) with \(15\,\textrm{mm}\) and the highest for R730 (M) with \(47\,\textrm{mm}\). Unlike the other systems, for BeiDou, the smallest offsets and STDs are observed using the AC-only weighting approach. Using this strategy, the lowest offsets are for the satellites from BeiDou-3 with \(7\,\textrm{mm}\) for C207 (MEO) and \(1\,\textrm{mm}\) for C208 (MEO). Comparing the STD for these two satellites, the values are \(80\,\textrm{mm}\) and \(125\,\textrm{mm}\) for C207 and C208 when using the AC plus constellation weighting, whereas they are \(49\,\textrm{mm}\) and \(34\,\textrm{mm}\) when using the AC-only weighting. The QZSS constellation has the most significant differences between both strategies. For all the satellites of this constellation, the AC plus constellation weighting approach results in smaller offset and STD values. The minimum STD is observed for J001 (IQ) with \(98\,\textrm{mm}\) and the maximum for J003 (IIG) with \(178\,\textrm{mm}\). We note that for J002 (IIQ), we have the biggest difference of the STDs between both strategies with \(41\,\textrm{mm}\). The smallest offset is observed for J002 with \(23\,\textrm{mm}\), and the only satellite with negative offset values is J001.

Fig. 8
figure 8

Mean SLR residuals of the ACs’ orbits and the combined orbits with AC plus constellation-specific weighting. Note that for QZSS the limits of the plot are increased to \(100 \,\textrm{mm}\) instead of \(50 \,\textrm{mm}\)

Full size image
Fig. 9
figure 9

Average daily RMS residuals of the ionosphere-free phase combination from ten stations (IISC, KOKB, MKEA, PIE1, POL2, RIO2, SANT, STHL, STJO, YELL) during GPS week 2096 (March 2020)

Full size image

In Fig. 8, we compare the mean value of the SLR residuals of our combination (CMG) with the ACs’ orbits. This evaluation is done using the same set of satellites for all ACs during the same period, which is why the results can differ significantly from Fig. 7, in particular for QZSS. The constellation with the lowest residuals is Galileo, where the CMG mean value is \(-3\,\textrm{mm}\) with an STD of \(6\,\textrm{mm}\) and the AC with the smallest value is WHU with a mean of \(1\,\textrm{mm}\) and an STD of \(6\,\textrm{mm}\). For Galileo, the STD values are similar for all ACs, where only SHA has a bigger absolute value of the mean with around \(-34\,\textrm{mm}\). For GLONASS, our combination has a mean of \(6\,\textrm{mm}\) and an STD of \(14\,\textrm{mm}\), and SHA has the lowest absolute value of the mean with \(1\,\textrm{mm}\) and an STD of \(15\,\textrm{mm}\). For BeiDou, the best AC is WHU with \(-8\,\textrm{mm}\) mean and \(19\,\textrm{mm}\) STD. The highest absolute values of the mean SLR residuals are obtained for QZSS, where the combination has a mean of \(-31\,\textrm{mm}\) and an STD of \(12\,\textrm{mm}\). For this constellation, JAX has the lowest values with a mean of \(-3\,\textrm{mm}\) and an STD of \(38\,\textrm{mm}\). We note that the STDs of the ACs and the combination are similar. Moreover, the combination does not have the lowest residuals for any of the constellations, which is what one would expect as the weighted mean of the ACs’ orbits should average out the orbital errors. Due to potential systematic errors, it is, however, possible that the orbits of one AC are more accurate than the combined orbits. The purpose of the combination should therefore also be seen in terms of providing the most complete and stable solutions and not necessarily always the solution with the highest accuracy.

4.3.3 PPP validation

The primary purpose of the combined GNSS orbits lies in the field of high precision GNSS applications. A main technique in this context is PPP (Zumberge et al. 1997), which can provide sub-centimeter level positioning information and is used in various fields in academia and industry (Bisnath and Gao 2009). Most important, the PPP quality relies on the availability and consistency of precise satellite orbit and clock solutions.

We perform a PPP analysis using GFZ’s EPOS.P8 software. In order to provide a fair comparison, the same constellations are used for all ACs. We therefore focus on GPS, Galileo, and GLONASS so that five ACs can be compared. Daily coordinates are computed using the ACs’ orbit and clock products. The combined orbits are used together with combined clocks that are also based on the above described VCE procedure.

The average daily RMS residuals of the ionosphere-free phase combination using ten IGS stations during GPS week 2096 (March 2020) are shown in Fig. 9 for each constellation. The averaged residuals of COD, GRG, SHA, and WHU are all below \(10\,\textrm{mm}\). The GLONASS residuals are slightly larger than the ones of GPS and Galileo, which agrees with the SLR analysis (cf. Fig. 8). Residuals derived from the GFZ products are clearly larger due to problems with their inter-system clock biases (solved on day of the year 161 of 2021). The GFZ clock products are therefore excluded from the clock combination. The phase residuals with the combined CMG products are on the same level as the individual ACs with values of less than \(10\,\textrm{mm}\).

Furthermore, a PPP processing is performed using our combined solution from Sect. 4.3.1 and the IGS final products, for GPS only. The residuals of the ionosphere-free phase combination in both cases are on the same level with an RMS value of \(8\,\textrm{mm}\). In addition, Fig. 10 shows the comparison of the RMS coordinate differences between the PPP results using IGS and CMG and the final IGS combined station coordinates for four stations, where we can see that the two solutions have similar values for the three components.

Fig. 10
figure 10

Average daily RMS coordinate differences with respect to the IGS combined station coordinates during the year 2020

Full size image

The PPP analysis demonstrates that the combined products are suitable for high precision GNSS applications and that the assumption of constant inter-system biases is not violated with the constellation-specific weights.

5 Conclusions

In this study, we present and compare two approaches developed to combine GNSS orbits, where AC or AC and constellation-specific weights are used. Section 3 describes the assumed functional and stochastic models, based on which a least-squares framework is formulated that jointly estimates the combined orbits and the weights used in the combination. Aiming for a reduced computational load, Eqs. (5) and (8) are derived to be easily implemented. Among the models’ derivations, one important aspect is to find a basis matrix B for the null space of \(A^\textrm{T}\). Given the large dimensions of the matrices when considering daily solutions with many satellites and several ACs, a direct computation may require heavy usage of the computer memory. Therefore, simplifications are needed for operational usage. With the Helmert transformation applied in Eq. (5), a simple and structured form of the system matrix A is found, enabling a closed form solution for B. The structure of this matrix B again allows for an efficient implementation of the least-squares estimator of the variance components, which define the weights in the orbit combination, in which only matrices of small dimension have to be handled, see Eqs. (16) and (17). The method is initially derived for an AC-only weighting. It was shown that the AC plus constellation weighting scheme can effectively be reduced to the methods of the AC-only scheme. In this AC plus constellation weighting strategy, the weights and combined orbits can be solved individually for each constellation and are only connected by a common Helmert transformation in each iteration. Another important topic of the proposed combination approach is the definition of a set of common core satellites, which are used to compute the weights of the combination. We propose a method based on the Modified Z-Score test that only selects satellites without outliers in the RAC components.

Both combination methods are tested using the MGEX ACs’ orbits for a test period from January 2018 until August 2020. The analysis shows that using AC-only or AC plus constellation weighting leads mostly to similar results where a significant RMS difference can be found only for QZSS. As expected, GPS has the smallest RMS with less than \(25\,\textrm{mm}\), while GLONASS and Galileo are below \(50\,\textrm{mm}\). For BeiDou and QZSS, the RMS reaches \(80\,\textrm{mm}\). Concerning the weights determined by the procedures, the AC plus constellation weighting scheme shows interesting results where one can notice the different behavior of the ACs for each system over time. For example, in the Galileo weights, there are significant changes for GRGS, CODE, and GFZ. Not just for the European system but likewise for BeiDou and QZSS, significant weight variations are observed, especially for WHU, GFZ, and CODE.

A validation using products from the legacy IGS chain is performed. The RMS difference between the GPS-only combined orbit and the official IGS final and rapid orbits show an agreement of better than \(4\,\textrm{mm}\) and \(6\,\textrm{mm}\). These small differences for the standard GPS-only case confirm the validity of the new combination method. As an external validation, the orbits generated by the two approaches are tested using SLR, assessing if the combined orbits can adequately represent the satellites’ positions. Within the SLR validation, Galileo showed the smallest offsets, while QZSS has more discrepant values. When comparing the SLR residuals of each individual AC and the combination, the result shows that the combination adapts the dispersion of the ACs’ solutions, and, therefore, is not the solution with the lowest residuals. A PPP validation using the combined orbits results in sub-centimeter GNSS phase residuals, which demonstrates the consistency of the combined orbit product and its suitability for high precision GNSS applications.

The results support the application of LSVCE to determine the weights for an orbit combination. The implementation of the presented algorithm is sufficiently efficient to generate products on an operational basis, with a preliminary computational time of around ten minutes for daily solutionsFootnote 5. Judging the two strategies, even if the results are mostly similar, the AC plus constellation weighting reveals more information about the behavior of the ACs’ solutions through the distribution of the weights for each constellation, so that, for instance, problems and changes in the processing of each AC are easier visible. With more constellations becoming fully operational, several ACs are adapting their software to handle the new systems. It is therefore important to verify that an adaptation done for one system does not affect the others. Generally, from the experiments, one can see that the MGEX solutions submitted to the IGS are getting more stable over the years, and the ACs are putting efforts into providing products, including all constellations available. So far, the alignment with the ITRF is not implemented in the algorithm since there are no SINEX files provided by the ACs. A future addition will include the reference frame alignment approach from Mansur et al. (2020) in the combination. The application of the VCE-based orbit combination to the third reprocessing campaign of the IGS (repro3) is presented in Sakic et al. (2022). Summarizing, the presented combination approach was shown to be suitable to provide reliable and accurate combined multi-GNSS orbits on a regular basis, which are an important product for GNSS users.