A partition-enhanced least-squares collocation approach (PE-LSC)

Abstract

We present a partition-enhanced least-squares collocation (PE-LSC) which comprises several modifications to the classical LSC method. It is our goal to circumvent various problems of the practical application of LSC. While these investigations are focused on the modeling of the exterior gravity field the elaborated methods can also be used in other applications. One of the main drawbacks and current limitations of LSC is its high computational cost which grows cubically with the number of observation points. A common way to mitigate this problem is to tile the target area into sub-regions and solve each tile individually. This procedure assumes a certain locality of the LSC kernel functions which is generally not given and, therefore, results in fringe effects. To avoid this, it is proposed to localize the LSC kernels such that locality is preserved, and the estimated variances are not notably increased in comparison with the classical LSC method. Using global covariance models involves the calculation of a large number of Legendre polynomials which is usually a time-consuming task. Hence, to accelerate the creation of the covariance matrices, as an intermediate step we pre-calculate the covariance function on a two-dimensional grid of isotropic coordinates. Based on this grid, and under the assumption that the covariances are sufficiently smooth, the final covariance matrices are then obtained by a simple and fast interpolation algorithm. Applying the generalized multi-variate chain rule, also cross-covariance matrices among arbitrary linear spherical harmonic functionals can be obtained by this technique. Together with some further minor alterations these modifications are implemented in the PE-LSC method. The new PE-LSC is tested using selected data sets in Antarctica where altogether more than 800,000 observations are available for processing. In this case, PE-LSC yields a speed-up of computation time by a factor of about 55 (i.e., the computation needs only hours instead of weeks) in comparison with the classical unpartitioned LSC. Likewise, the memory requirement is reduced by a factor of about 360 (i.e., allocating memory in the order of GB instead of TB).

1 Introduction

Least-squares collocation (LSC) is a commonly used technique in local or regional gravity field modeling (Moritz 1980; Krarup 1969). This method is very popular because it allows to predict gravity field-related quantities at arbitrary locations. At the same time, the desired functionals can be inferred from different input functionals (e.g., geoid heights from gravity anomalies). Eventually, LSC yields an optimal solution in the stochastic sense as it minimizes the prediction error using a priori covariance information of the observation and estimation points. From this perspective, LSC also allows to consider the full variance–covariance information and an appropriate propagation in the sense of a Gaussian process.

There are also some disadvantages of LSC. The computational cost is proportional to the cubic power of the number of observation points, while memory requirements are proportional to the quadratic power. This limits the practical application of the method to a certain maximum number of observation points. Even if this number can be reasonably handled, in the general application, some sort of tiling strategy (Reguzzoni and Tselfes 2009) must be applied to comply with computational limits. However, this strategy introduces the problem of fringe effects caused by the forced locality assumption. Another disadvantage of regional LSC is that it requires the input values at the observation points to have a zero mean. In practice, there may be several reasons why a residual (nonzero) mean exists, e.g., due to datum offsets, systematic effects induced by the measurement set-up, errors in the observations or reduction models or just due to the spatial limitation of the region under consideration. In general, it is not trivial to backtrack the source of the residual mean value and, therefore, it is often not justified to preventively remove it as it is usually done. In any case, a residual mean (or unexpected long-wavelength signal) causes a severe problem to the classical LSC, which ultimately culminates in unnatural oscillations and long-wavelength compensation attempts.

In the field of gravity field modeling, the (homogeneous-isotropic) covariance function used in LSC is commonly derived from spherical harmonic degree variances using covariance propagation (Moritz 1980). Since this calculation step involves the evaluation of Legendre polynomials for spherical distances of every pair of data points (i.e., observation and estimation points), the computation of covariance matrices becomes computationally demanding. Especially when a tiling approach is applied and identical point pairs must be evaluated several times (due to the overlap between tiles), the efficiency of the covariance matrix calculation deteriorates.

Tackling these challenges, a number of practical modifications to the original LSC approach was realized resulting in the so-called partition-enhanced least-squares collocation (short PE-LSC). Among these modifications, there are several innovative aspects such as a 2D gridding approach for a fast set-up of the covariances, the use of exponential estimators, and the filtering of the transfer function to achieve improved localization characteristics. From a practical point of view, the most important aspect is a significant acceleration of the run-time, which is primarily achieved by an optimal partitioning strategy of the study area. While the investigations are focused on the geodetic modeling of the gravity field, the usability of the presented methods may be extended to any harmonic functional defined on spherical or near-spherical surfaces (e.g., spheroids with small eccentricities).

The presented investigations are motivated by the IAG Subcommission 2.4f “Gravity and Geoid in Antarctica” (AntGG) where we aim to compile a refined grid of terrestrial gravity data in Antarctica as a major update to the data set published by Scheinert et al. (2016). For this, an optimum combination of a satellite-based global model (accounting for long-wavelength signal parts) and the terrestrial (ground-based or airborne) data is sought for. From the perspective of data processing, this paper is a logical succession to the study by Zingerle et al. (2019) who discussed data reduction and validation making use of a high-resolution gravity field model based on satellite and topography data. While the present paper focusses on the treatment of methodological aspects, resulting final products with respect to the regional gravity field in Antarctica will be subject to a separate paper.

Section 2 recapitulates the basics of the theory of LSC and introduces the notation. In Sect. 3, we explain in detail the different modifications to finally end up with PE-LSC. In Sect. 4, we examine and validate these modifications. All examples and validations presented in Sects. 3 and 4 are based on selected data sets from the AntGG project. Finally, Sect. 5 concludes the discussion by investigating the computational effort when using PE-LSC in real-world scenarios and gives a brief outlook to further research on the topic of LSC.

2 Theory and notation

This section provides a brief overview of the LSC theory and specifies the notation which will be used in this publication. Since we present only the very basics, the reader is referred to Moritz (1980) for a more complete and elaborated treatment of this topic.

2.1 The LSC method

LSC is a statistically optimal method for estimating (predicting) quantities $\underline{s}$ (the underscore below items tags vectors) from observations $\underline {l}$ based on their stochastic relation:

$$ \hat{\underline {s} } = C_{SL} \left( {C_{LL} + C_{NN} } \right)^{ - 1} \underline {l} = \tilde{A}_{S}^{L} \underline {l} ,\quad {\text{with}}\quad \tilde{A}_{S}^{L} := C_{SL} \left( {C_{LL} + C_{NN} } \right)^{ - 1} . $$

(1)

Here, $\hat{\underline {s} }$ denotes the estimates for $\underline {s}$ as result of the collocation, whereby ${\mathrm{C}}_{SL}$ is the cross-covariance matrix between the estimates and observation, ${\mathrm{C}}_{LL}$ the covariance matrix of the observations and ${\mathrm{C}}_{NN}$ additive noise covariance matrix. $\tilde{A}_{S}^{L}$ is defined to be the so-called estimator or kernel of the collocation. It is useful to interpret ${\mathrm{C}}_{SL}$ and ${\mathrm{C}}_{LL}$ to origin from a common (signal) covariance matrix${C}_{VV}$, belonging to the common ‘signal’ $\underline{v}$:

$$ \underline {v} := \left( {\begin{array}{*{20}c} {\underline {s} } \\ {\underline {l} } \\ \end{array} } \right) \leftrightarrow C_{VV} := \left[ {{\text{cov}} \left( {v_{i} ,v_{k} } \right)} \right] = \left( {\begin{array}{*{20}c} {C_{LL} } & {C_{LS} } \\ {C_{SL} } & {C_{SS} } \\ \end{array} } \right). $$

(2)

In the context of this publication, the observations $\underline{l}$ are measurements of the Earth’s gravity field and $\hat{\underline{s}}$ are estimates of the gravity field signal on possibly other locations and in terms of other gravity field functionals.

2.2 LSC with a priori reduction

One major limitation of LSC is that it requires the signal $\underline{v}$ to be centered, meaning that the expectation of $\underline{v}$ shall be zero. This implies that collocating a signal that is not centered probably yields an unfavorable result. For instance, if one tries to collocate gravity observations $\underline{l}$ directly on a regional scale, $\underline{l}$ is generally not centered since it still contains longer-wavelength signal components. Thus, it is advantageous to remove such signal parts beforehand. This can be achieved through prior information ${\underline{v}}_{0}$ of the signal which can be used to reduce the actual signal $\underline{v}$ before the collocation and restore it afterward (known as remove-compute-restore technique, RCR, see Forsberg and Tscherning 1981). To reuse the previous notation, $\underline {v}$ can be replaced by ${\Delta }\underline {v}$ through the relation:

$$ \Delta \underline {v} := \underline {v} - \underline {v}_{0} = \left( {\begin{array}{*{20}c} {\Delta \underline {s} } \\ {\Delta \underline {l} } \\ \end{array} } \right) $$

(3)

In this scenario, it is effective to substitute ${\text{C}}_{VV}$ from Sect. 2.1 with the error covariance ${\text{C}}_{VV}^{e} := \left[ {{\text{cov}} \left( {{\Delta }v_{i} ,{\Delta }v_{k} } \right)} \right]$ of $\underline {v}_{0}$ (which is the same as the signal covariance of ${\Delta }\underline {v}$). Consequently, $\underline {v}$ is assumed to be error free in this context (despite the noise covariance ${\text{C}}_{NN}$, see Willberg et al. 2019). Together with the restore step, the modified LSC equation, based on residuals, reads:

$$ \begin{aligned} \Delta \hat{\underline {s} } & = \tilde{A}_{S}^{L} \Delta \underline {l} \to \\ \hat{\underline {s} } & = \underline {s}_{0} + \Delta \hat{\underline {s} } = \underline {s}_{0} + \tilde{A}_{S}^{L} \left( {\underline {l} - \underline {l}_{0} } \right) \\ \end{aligned} $$

(4)

with

$$ \tilde{A}_{S}^{L} = C_{SL}^{e} \left( {C_{LL}^{e} + C_{NN} } \right)^{ - 1} . $$

(5)

An appropriate covariance propagation yields the error covariance for the restored estimate $\hat{\underline {s} }$:

$$ C_{{\hat{S}\hat{S}}}^{e} = C_{SS}^{e} - C_{SL}^{e} \left( {C_{LL}^{e} + C_{NN} } \right)^{ - 1} C_{SL}^{e\prime } . $$

(6)

In gravity field modeling, the needed a priori information can be derived, e.g., from satellite-based global gravity field models and topographic models, respectively.

2.3 The covariance function

One crucial point for LSC is finding an adequate, ideally analytical, expression for the needed covariances ${\mathrm{C}}_{VV}^{e}$. In gravity field modeling, it is useful to exploit the harmonic character of the gravity field in the absence of masses (in the exterior space). Doing so leads to the spherical harmonic representation $\underline{h}$ (i.e., Stokes coefficients, see Moritz 1980) of the gravity field, with the relation ${\mathrm{A}}_{V}^{H}$ to the spatial gravity signal $\underline{v}$ in form of:

$$ \underline {v} = A_{V}^{H} \underline {h} $$

(7)

Assuming the covariance $C_{HH}^{e}$ related to $\underline {h}$ in the spherical harmonic domain is known, the covariance $C_{VV}^{e}$ in the spatial domain can be obtained by covariance propagation:

$$ C_{VV}^{e} = A_{V}^{H} C_{HH}^{e} A_{V}^{H\prime } . $$

(8)

In the classical application $C_{HH}^{e}$ is modeled by degree variances yielding a homogeneous-isotropic covariance function in the spatial domain (e.g., see Tscherning and Rapp 1974). In modern approaches also the full covariance information from global gravity field models is sometimes used (see Willberg et al. 2019), resulting in arbitrary, but still harmonic, covariance functions.

3 Methodology

Several modifications of the classical approach are introduced to increase the numerical efficiency and stability of RCR-LSC (cf. Sect. 2.2). In most of the strategies, the basic assumption is that a single observation $\Delta l_{i}$ has a certain localized influence on the estimates $\Delta \hat{\underline {s} }$. Generally speaking, assuming a localized influence is justified if the covariances ${\text{cov}} \left( {\Delta l_{i} , \Delta s_{k} } \right)$ become sufficiently small beyond a certain distance from the observation point. As arbitrary covariance functions do not necessarily show this behavior, their application must be restricted to the class of locally dominated covariance functions. For the ease of use this class is further constrained to (locally dominated) homogeneous-isotropic covariance functions. Since this paper deals with functionals that are harmonic and defined on or close to a sphere, the most natural and most general way of describing this class of covariance functions is by using spherical harmonic degree variances (cf. Moritz 1980 and Sect. 3.1). Consequently, they will be used to construct all covariances throughout the rest of this paper. In order to obtain the desired local character of the covariance function, it is required that within the RCR-LSC, the long-wavelength components are reduced beforehand (e.g., see Zingerle et al. 2019). Since the presented methods could theoretically also be applied to a non-reduced LSC (even if not recommended), in the following, each subsection describes a specific modification of the classical (RCR-)LSC method. Together, they form the basis for the PE-LSC approach which is evaluated in Sect. 4.

3.1 Accelerated covariance calculation

As explained in Sect. 2.3, the calculation of the covariance $C_{VV}^{e}$ from spherical harmonics theoretically requires the calculation of the transformation matrix $A_{V}^{H}$ and the evaluation of the (matrix) product $A_{V}^{H} C_{HH}^{e} A_{V}^{H\prime }$. For the special case of degree variances, this calculation can be simplified to the homogeneous-isotropic form (see Moritz 1980):

$$ \begin{aligned} c_{ik} &:= {\text{cov}} \left( {\Delta v_{i} ,\Delta v_{k} } \right) = c\left( {t_{ik} ,u_{ik} } \right) \\ &= \mathop \sum \limits_{n = 0}^{{n_{\max } }} u_{ik}^{l + 1} P_{n} \left( {t_{ik} } \right) c_{H}^{n} := \left\langle {\underline {q}_{ik}^{H} ,\underline {c}_{H} } \right\rangle \\ \end{aligned} $$

(9)

where

$$ \begin{aligned} t_{ik} &:= \left\langle {{\varvec{e}}_{i} ,{\varvec{e}}_{k} } \right\rangle \left[ { = \cos \theta_{ik} } \right],\quad {\varvec{e}}_{i} := \frac{{{\varvec{x}}_{i} }}{{r_{i} }}, \\ u_{ik} &:= \overline{u}_{i} \overline{u}_{k} ,\quad \overline{u}_{i} := \frac{R}{{r_{i} }},\quad r_{i} := \left\| {{\varvec{x}}_{i} } \right\|. \\ \end{aligned} $$

(10)

Herein, $c_{H}^{n}$ denotes the (error) degree variances and P_n the Legendre polynomial of degree n, and R is the radius of the reference sphere chosen for the degree variances. $n_{\max }$ is the maximum degree that is considered in the modeling of $c_{ik}$. x_i describes the location in form of geocentric coordinates a single signal element v_i refers to. The parameterization via t (cosine of spherical distance $\theta$) and u (product of length ratios to reference radius) is chosen so that a covariance matrix may be efficiently derived by outer (Cartesian) products regarding $\Delta \underline {v} \times \Delta \underline {v}$. For a better readability in figures (see Fig. 1), t is substituted by $\theta$ and u by the so-called equivalent height h_eq which is defined by

$$ h_{eq} := R\left( {\frac{1}{\sqrt u } - 1} \right). $$

(11)

h_eq describes the actual height of a pair of points in case that both points are located at the same height. The evaluation of the simplified Eq. 9 is still time-consuming since it involves the calculation of numerous Legendre polynomials for every element of the resulting covariance matrices. Therefore, to avoid the need to do this calculation for every element, it is proposed to introduce an intermediate regular grid $\Omega_{G} = \underline {t}_{G} \times \underline {u}_{G}$ on which the covariance values $\underline {c}_{G} = c\left( {\Omega_{G} } \right)$ are pre-calculated. Assuming a certain smoothness of the covariance function, the final elements are then simply obtained by applying a (gridded) two-dimensional interpolator (i.e., the interpolation matrix) $I^{G}$ to the pre-calculated values $\underline {c}_{G}$:

$$ c_{ik} = I^{G} \left( {\Omega_{G} \to \left( {t_{ik} ,u_{ik} } \right)} \right) \underline {c}_{G} $$

(12)

Fig. 1

Covariances in terms of gravity disturbances in the ${\Omega }_{G}$ domain. a Empirical covariances computed from reduced Antarctic gravity data (see Sect. 4). b Estimated covariance function derived from estimated degree variances (see Fig. 2). c Difference between empirical and estimated covariances. d The same covariances as in figure a-c, averaged over dimension $u$. Black: empirical covariance. Red: estimated covariances. Blue: difference between empirical and estimated covariances. Magenta: number of samples per bin for the calculation of the empirical covariances. Results shown are calculated by applying the spherical approximation to the coordinates (see Sect. 3.3)

This interpolation can be evaluated very efficiently for large numbers of point pairs avoiding the need of evaluating sums of Legendre polynomials every time. Naturally, the grid vectors ${\underline{t}}_{G}$ and ${\underline{u}}_{G}$ should be chosen such that all occurring ${t}_{ik}$ and ${u}_{ik}$ are within the limits of the appropriate grid vector. The sampling of the grid vectors shall also be adapted to the smoothness of the intermediate covariance function $c\left(t,u\right)$ and the overall accuracy requirements for the calculation of the covariance functions. The accuracy can also be controlled by the appropriate choice of the interpolation method (e.g., linear, cubic, spline, etc.).

It is even possible to calculate arbitrary derivatives of the covariance function regarding local frame coordinates (e.g., gravity disturbances, gradients, deflection of vertical, etc.) based on a generalized chain rule. Since this generalized chain rule (also known as multivariate version of Faà di Bruno’s formula, see Hardy 2006) is fairly complicated to state and even more complicated to prove, the reader is referred to the appropriate literature (e.g., Hardy 2006). In summary, the generalized chain rule consists of a linear combination of products of partial derivatives. For the commonly used local spherical east-north-up (ENU) frame, the partial derivatives are given in appendix (A.1). Since the number of summands within the generalized chain rule increases rapidly with the order of the derivative, the computation is practically limited to lower orders (i.e., below ten). In practice, this is only a minor limitation as higher-order derivatives are rarely used (at least in the scope of gravity field modeling).

3.2 Estimation of degree variances

Having a set of reduced observations $\Delta \underline {l}$ , one can estimate an empirical covariance function $\tilde{\underline {c} }_{G}$ on the regular grid $\Omega_{G}$ by binning the individual covariance estimates $\tilde{c}_{ik} := \Delta {l}_{i} \Delta {l}_{k}$ into the 2D classes defined by $\underline {t}_{G} \times \underline {u}_{G}$ (see Fig. 1a). In this context, $\Delta \underline {l}$ is assumed to be centered.

Theoretically, by inverting the linear relation of Eq. 9 it would be possible to derive empirical degree variances $\underline {c}_{H}$ from $\tilde{\underline {c} }_{G}$. In practice, there are two major obstacles that prevent us from performing this inversion: firstly, the degree variances $\underline {c}_{H}$ are defined to be only positive; hence, the relation is not linear as Eq. 9 could suggest. Secondly, in general this inversion is highly instable due to the high dynamic range of the estimates and partially high insensitivity of $\underline {c}_{H}$ to $\tilde{\underline {c} }_{G}$. Nevertheless, a solution is possible when altering the functional model and including a reasonable regularization: to force positive values and to reduce the dynamic range, it is proposed to translate the estimates into the logarithmic domain (hence losing linearity). In order to tackle the instability issue, it is further proposed to introduce cubic basis splines (B-splines, e.g., de Boor 1978) as representation for the degree variances $\underline {c}_{H}$ assuming a certain smoothness of the degree variance curve. Obviously, to acquire smoothness the number of B-spline control points must be chosen to be significantly lower than the number of degree variances to estimate. Modifying Eq. 9 accordingly yields the nonlinear relation (with ${\text{Q}}_{G}^{H}$ being the matrix extension of $\underline {q}_{ik}^{H}$ to all grid locations of $\Omega_{G}$):

$$ \underline {c}_{G} := Q_{G}^{H} \underline {c}_{H} =: Q_{G}^{H} \exp \left( {B^{SP} \underline {x}_{SP} } \right),\quad \frac{{\partial \underline {c}_{G} }}{{\partial \underline {x}_{SP} }} =: A_{G}^{SP} = Q_{G}^{H} \,{\text{diag}} \left( {\exp \left( {B^{SP} \underline {x}_{SP} } \right)} \right)B^{SP} $$

(13)

where ${\mathrm{B}}^{SP}$ denotes the linear B-spline synthesis matrix (i.e., the matrix containing the spline basis functions, transforming from the spline function space to the logarithmic degree variance space). ${\mathrm{B}}^{SP}$ might be obtained efficiently by the Cox de Boor recursion formula (see de Boor 1978). The vector ${\underline{x}}_{SP}$ contains the appropriate spline parameters to estimate. $\mathrm{exp}\left(\dots \right)$ denotes the element-wise exponential function and $\mathrm{diag}\left(\dots \right)$ indicates the vector to diagonal square matrix transform. Using the linearization ${\mathrm{A}}_{G}^{SP}$, ${\underline{x}}_{SP}$ can be obtained by an iterative LSA approach

$$ \Delta \underline {x}_{SP} = \left( {A_{G}^{SP\prime } C_{GG}^{ - 1} A_{G}^{SP} + P_{REG} } \right)^{ - 1} \left( {A_{G}^{SP\prime } \left( {\underline {c}_{G} - Q_{G}^{H} \exp \left( {B^{SP} \underline{{\tilde{x}}}_{SP} } \right)} \right) + \underline {q}_{REG} } \right) $$

(14)

starting with some initial guess ${\underline{\tilde{x}}}_{SP}$ for ${\underline{x}}_{SP}$ (and iteratively improving ${\underline{\tilde{x}}}_{SP}$ by $\Delta {\underline{x}}_{SP}$). ${C}_{GG}$ denotes the covariance of ${\underline{c}}_{G}$ which can also be derived empirically or can simply be approximated as, e.g., diagonal matrix with the diagonals (variances) as inverse of the number of samples of the appropriate bin. ${\mathrm{P}}_{REG}$ and ${\underline{q}}_{REG}$ are regularization terms that may help to further improve the result. As an example, one may add additional smoothing constraints (e.g., second derivative set to be zero), add a tie to a baseline value (e.g., zero) or force the slope to be flat (e.g., first derivative set to be zero). The appropriate weights to the regularization terms may be derived empirically such that the iterative LSA converges and yields a good fit as well as a realistic result. Figure 2 (in combination with Fig. 1) exemplarily shows the functionality of this method.

Fig. 2

Estimated degree amplitudes (i.e., square root of degree variances ${\underline{c}}_{H}$) from empirical covariances (${\underline{\tilde{c}}}_{G},$ cf. Eq. 13, Fig. 1a) in terms of gravity disturbances. Blue: degree amplitude. Red: cumulative amplitude, i.e., the aggregated total power from the maximum degree downward (from right). Black: control points of the B-spline used for estimating the degree variances (see Eq. 13, equally spaced in the logarithmic domain)

3.3 Spherical approximations

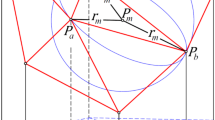
In the following, it is assumed that the reduced signal $\Delta \underline{v}$ describes some harmonic functional in the exterior of a spheroidal-shaped body (e.g., Earth’s gravity or magnetic field). When the region ${\Omega }_{V}$ of ${\Delta }\underline {v}$ is large and covers a certain latitude range, the use of covariance functions derived by spherical harmonic degree variances introduces artificial latitude-dependent systematics. This is obvious as the quantity u in Eq. 10 depends on the observation’s (body-centric) radii which vice versa depend on the latitude if ${\Delta }\underline {v}$ resides near the surface (see Fig. 3). Apparently, such a latitude-dependent influence cannot be physically explained, especially when the signal ${\Delta }\underline {v}$ was reduced beforehand for the long-wavelength signal part. Theoretically, these systematics can be avoided by using spheroidal harmonic degree variances instead of spherical harmonic degree variances, as the height-dependent item $u$ would then vanish for the signal on the surface of the spheroid (see Moritz 1980). However, spheroidal harmonic degree variances become difficult to handle when the height is not zero, as it involves the parametric latitude and Legendre polynomials of the second kind. Therefore, they are rarely used in LSC. Hence, a different approach is proposed where once again the locality assumptions are considered: in a local (or regional) setting the curvature of a spheroid (with small eccentricity) can be approximated by a sphere with the curvature radius $\overline{R}$, averaged over the region ${\Omega }_{V}$ (see also Willberg 2020). Consequently, the oblateness in the geometry can be eliminated by a spherical modification of the coordinates:

(15)

$h_{i}^{ell}$ denotes the ellipsoidal height of point x_i. Evidently, the modified geometry in preserves local relations of adjacent points to a large extent while removing the latitude dependency. When applying this geometry, also the empirical degree variances (see Sect. 3.2) should be derived using the modified coordinates (cf. Eq. 10) in order to preserve consistency. Consequently, results shown in Figs. 1 and 2 are also calculated by using the modified geometry.

Fig. 3

A priori standard deviations (i.e., square root of variance entries in $C_{SS}^{\Omega }$, see, e.g., Eq. 9) calculated from spherical degree variances (cf. Fig. 2) evaluated on the surface of Antarctica (using a polar-stereographic projection). a Standard deviations calculated using the original coordinates. b Same standard deviations calculated using the modified coordinates (Eq. 15). As the geocentric radii of the original coordinate decrease toward the pole due to the oblateness of the Earth, the a priori variances systematically increase (cf. Fig. 1b). Variations in (b) are solely correlated to varying surface heights (topography)

3.4 Localization of the LSC estimator

Even though the covariance ${\text{cov}} \left( {{\Delta }l_{i} , {\Delta }s_{k} } \right)$ between an estimate’s signal ${\Delta }s_{k}$ and observation’s signal ${\Delta }l_{i}$ is zero (or close to zero), the appropriate element $\tilde{a}_{ik}$ in the LSC estimator $\tilde{A}_{S}^{L}$ does not necessarily have to be zero (or even close to zero). This is counterintuitive because one would assume that the estimate does not depend on observations that are statistically uncorrelated. Nevertheless, due to the inversion of $C_{LL}^{e} + C_{NN}$ (cf. Eq. 5) rather large nonzero elements may pop up especially when the system has a high sensitivity to small changes. This emerging correlation among observations over rather large distances is considered to be undesirable as it destroys all previously made locality assumptions. Consequently, this behavior is mainly responsible for fringe effects when partitioning the region $\Omega$ to accelerate the collocation (see Sect. 4.2). Making a non-critical compromise in terms of optimality (cf. Sect. 4.1), this behavior can be avoided when $\tilde{a}_{ik}$ is down-weighted by applying a distance-dependent weighting function $w_{ik}$. For PE-LSC the distance measure $1 - t_{ik}$ is used for this weighting (see Eq. 16). Alternatively, also the spherical distance $\theta_{ik} := {\text{acos}}\left( {t_{ik} } \right)$ may be chosen as distance measure. The weighting function $w_{ik}$ should be (1) smooth, and (2) strongly attenuate beyond a certain distance $\theta^{\max }$, but (3) should not influence the LSC estimator $\tilde{A}_{S}^{L}$ in close proximity (i.e., when $\theta_{ik}$ is small). Although there might be many functions that satisfy these requirements, a very simple and effective one is found when applying a slightly modified Gaussian bell curve to $t_{ik}$

$$ w_{ik}^{G} := \exp \left( { - \left( {\frac{{t_{ik} - 1}}{{\cos \left( {\theta^{\max } } \right) - 1}}} \right)^{2} } \right). $$

(16)

Figure 4 exemplarily shows the behavior of $w_{ik}^{G}$. It should be noticed that using $t_{ik} := \cos \left( {\theta_{ik} } \right)$ (instead of $\theta_{ik}$) as parameter in Eq. 16 narrows down the transition width of the function and hence contributes to the requirements (2) and (3) as stated above. While this weighting approach allows for an efficient reduction of fringe effects, it does not guarantee to fully eliminate them (cf. Sect. 4.2 and discussion above).

Fig. 4

Modified Gaussian bell attenuation function $w_{ik}^{G}$ (cf. Eq. 16) and its exemplary influence to the covariance function. Blue: original covariance function in terms of gravity disturbances (cf. Fig. 1d). Red: attenuated covariance function. Green: attenuation function $w_{ik}^{G}$ ($\theta^{\max } = 1.5^\circ$). Dashed black: attenuation parameter $\theta^{\max }$ ($1\sigma$, cf. Fig. 5a). Vertical red: buffer distance $r = 5/3 \theta^{\max }$ (cf. Fig. 5a). Covariance function is evaluated on the ellipsoid

3.5 Optimal partitioning and corresponding reduction of numerical effort

The main aim of the forced localization introduced in the previous section is to enable the partitioning of the collocation region $\Omega_{S} \subseteq \Omega_{V}$ (where the estimates are located in) into smaller subregions $\Omega_{i}^{P}$. Dividing $\Omega_{S}$ into independent subregions allows a significant reduction of the overall computation time $t_{c}$ as well as of memory requirements. To perform this separation correctly every partition must include the necessary surrounding $\delta \Omega_{i}^{P}$ (buffer) to $\Omega_{i}^{P}$ (according to the localization criterion, e.g., $\theta^{\max }$) and subsequently introduces a certain amount of overhead (see Fig. 5a). As this additional overhead is introduced with every partition, the overall overhead grows linearly with the number of partitions and at a certain point becomes larger than the acquired gain. Consequently, when implementing an appropriate algorithm, it is favorable to determine an optimal partition size that allows maximizing the overall gain (i.e., to minimize $t_{c}$): from a computational perspective, evaluating the LSC estimator $\tilde{A}_{S}^{L}$ requires a matrix inversion as well as matrix multiplication (cf. Eq. 5). In general, matrix inversion as well as multiplication has a computational cost of ${\mathcal{O}}\left( {n^{3} } \right) \approx k n^{3}$, where n is the number of elements of the random vector (that is the number of observation resp. evaluation points) and k is a constant factor depending on the algorithm used. For the following considerations it is assumed that the points are evenly distributed on a sufficiently large 2D surface (region $\Omega$) with a constant (point) density of $\rho$. Dividing this surface into m identical partitions, each including n points, the needed computation time is given by:

$$ t_{c} = m k n^{3} $$

(17)

Fig. 5

a Scheme of the partitioning items. Blue hatched: central area of a partition with edge length d. Orange hatched: extended area with buffer distance r. Light green: central and buffer area of an adjacent partition. Solid red curve: 1D visualization of the attenuation function (Eq. 16) for an evaluation point located on the right edge of the partition. Dashed red line: visualization of the parameter $\theta^{\max }$ ($1\sigma$, see Fig. 4) for the attenuation function. b Normalized computation time as function of the normalized partition edge length (see Eq. 19)

Assuming the subregions $\Omega_{i}^{P}$ to be squares, their size can be characterized by their edge length d. Having an initial number of partitions m₀ corresponding to an initial edge length d₀ the actual number of partitions can be calculated (in the 2D case) by:

$$ m\left( d \right) = m_{0} \left( {\frac{{d_{0} }}{d}} \right)^{2} $$

(18)

As mentioned above, the overall size of the partition must include its surrounding $\delta \Omega_{i}^{P}$. This shall be taken into account by a buffer distance r (presumably depending on $\theta^{\max }$), yielding the edge length of the extended partition $d_{e} = 2r + d$. As a rule of thumb, choosing $r = 5/3 \theta^{\max }$ seems to yield a good trade-off between omission error and buffer distance when applying Eq. 16 as weighting function (see Fig. 4). For the sake of simplicity, $\delta \Omega_{i}^{P}$ shall also be a square (omitting the roundings of the buffer, cf. Fig. 5a); hence, the area of the extended partition is $d_{e}^{2}$, and with that the number of (observation) points per partition $n = \rho d_{e}^{2}$. By inserting n and m into Eq. 17 one finds:

$$ t_{c} \left( d \right) = \overbrace {{k m_{0} d_{0}^{2} \rho^{3} }}^{{\overline{k}}} \frac{{d_{e}^{6} }}{{d^{2} }} = \overline{k}\frac{{\left( {2r + d} \right)^{6} }}{{d^{2} }} $$

(19)

The minimum of this equation is obtained by setting the derivative $\frac{{\partial t_{c} }}{\partial d}$ to zero:

(20)

Hence, the optimal edge length is obviously the chosen buffer distance itself. Naturally, this is only valid under the assumed simplified conditions, where particularly the special treatment of fringe partitions was neglected. Nevertheless, for larger regions, this assessment should be sufficient in most cases, and for smaller regions, reaching the perfect optimum should not be important anyway. Be aware that in this derivation, n is primarily related to the number of observation points $\left\{ {\underline {L}_{i}^{P} \in \Omega_{i}^{P} ,\delta \underline {L}_{i}^{P} \in \delta \Omega_{i}^{P} } \right\}$ and not to the number of estimation points $\underline {S}_{i}^{P} \in \Omega_{i}^{P}$. If the number of the latter is significantly larger than the number of the former (i.e., $\ge n^{2}$), the optimum can be missed by this estimate, generally favoring smaller partitions (hence making the matrix multiplication less expensive).

From Eq. 19, one can further discern the most expensive parts within the LSC, which are represented by (1) the buffer distance r (resp. $\theta^{\max }$) that increases the cost by the power of six, and (2) the point density that increases the cost by the power of three. Consequently, if computation time is still problematic after partitioning, one should primarily try to further reduce the correlation length (e.g., by improved reductions) and/or to decrease the observation point density (e.g., by thinning the data). Additionally, even if the optimality criterion as stated above is met for a sub-region, in practice one might be forced to further partition it, as the system memory might not be sufficient (e.g., if the local point density is high). This is critical, as the overall computation time (Eq. 19) increases significantly for $d < r/2$ (see Fig. 3). Therefore, having enough system memory available might be crucial in such cases. In order to be able to dynamically adapt the partition size when the density is too high, it is proposed to use a divide and conquer approach. In the reference implementation the divide and conquer algorithm works recursively in the 3D Cartesian space, always dividing a partition along the dimension with the largest extent until all criteria are met (i.e., max. extents or number of points, e.g., see Fig. 9). Obviously, this algorithm tends to create partitions to be smaller than optimal regarding the chosen maximum extents. Hence, choosing these maximum extents to be slightly larger than the buffer distance r might help to better reach the optimum (i.e., r) on average. As shown in Fig. 3, choosing larger extents is less problematic than choosing them too small in terms of computation time penalty.

4 Validation

Most of the modifications described in Sect. 3 are simple to validate. For instance, the validation of the accelerated covariance calculation (Sect. 3.1) is performed by cross-comparison to the rigorous calculation method. It has been found that one can approximate the rigorous result to any desired accuracy level by increasing the grid sampling or using more elaborate interpolation algorithms. The correct estimation of the degree variances (Sect. 3.2) is verified by inspecting the fit to the empirical covariance function where the residuals are small and do not show any systematics (Fig. 1c, d). The improvement by using the modified coordinates (Sect. 3.3) is also directly discernible by inspecting the a priori variances (Fig. 3).

The validation becomes more difficult when studying the modification of the LSC estimator (Sect. 3.4) as this alteration directly influences the outcome of the LSC especially in combination with the partitioning approach (Sect. 3.5). Hence, an in-depth validation of this topic is performed focusing on the behavior of the LSC estimator (Sect. 4.1) and the impact of the localization regarding the result and the partitioning (Sect. 4.2). Note that all investigations within this section are performed using gravity observations in selected regions of Antarctica, which already served as input to the 2016 AntGG grid (Scheinert et al. 2016). In particular, we are making use of gravity disturbances resulting from airborne gravimetry in West Antarctica (Bell et al. 1999; Studinger et al. 2002) and over a transect from the Transantarctic Mts. to the South Pole (Studinger et al. 2006). The data is reduced beforehand by a high-resolution gravity model combining satellite and topographic information (see Zingerle et al. 2019 for the model, Sect. 2.2 for the RCR-LSC theory). The obtained observation residuals fit to the empirical covariance function and degree variances as shown in Figs. 1 and 2. For the localization of the LSC estimator and the partitioning, the parameters $r = d = 2.5^\circ$ and $\theta^{\max } = 1.5^\circ$ are chosen if not stated otherwise (cf. Sects. 3.4, 3.5, Figs. 4, 5, 6, 7, 8). Gravity disturbances on or near the ice surface form also the output functional in the estimation. Insights found by the following evaluations do not necessarily hold for other setups (i.e., other combinations of input/output functionals, estimates with extensive upward or downward continuation or different covariance functions), as the shape of the LSC estimator might strongly vary between different scenarios. Nevertheless, it can be stated that the following conclusions shall be valid in all cases where the pattern of the LSC estimator is locally dominated (cf. Sect. 4.1, Fig. 6).

Fig. 6

Influence of the localization of the LSC estimator $\tilde{A}_{S}^{L}$ (Eq. 5) for two different evaluation sites in Antarctica: site A is located within a densely measured area (a-c), while site B is located in an area where no observations are present (d-f). a, d Original LSC estimator. b, e Localized LSC estimator (see Sect. 3.4, Fig. 4). c, f Difference between original and localized estimator. For visualization, the individual weights of the LSC estimator are normalized regarding the appropriate largest weight. As a reference, the applied weighting parameter $\theta^{\max }$ (1.5° black dashed circle) and appropriate buffer distance r (2.5°, red circle) are shown. For $\tilde{A}_{S}^{L}$ , the covariance function chosen is according to Fig. 1 using degree variances as of Fig. 2. Reference points are located on an ellipsoidal height of 5 km (slightly above the ice layer). The figure’s background is shaded in gray (where no observations are present). Grid coordinates refer to a polar stereographic projection where the positive y-axis coincides with the Greenwich meridian. The disparity $\Delta_{i}^{\ker }$(see Eq. 21, Fig. 7b) between original and localized kernel is 0.16% for point A and 58.49% for point B

Fig. 7

Impact of the localized kernel on the estimation result (i.e., a 5 km regular polar stereographic grid of reduced gravity disturbances on the surface). The localization is identical to Figs. 4, 6 (i.e., $\theta^{\max } = 1.5^\circ$). a Estimation difference between original and localized kernel. b Kernel disparity $\Delta_{i}^{\ker }$ (see Eq. 21) on the estimation grid (logarithmic scale). c Formal error of the estimation with the original kernel (see Eq. 6). d Formal error increase when localizing the kernel (regarding the original result, see (c))

Fig. 8

Fringe effects on partition boundaries with and without kernel localization in a peripheral area of Antarctica (same setup as in Fig. 7). Partition boundaries are highlighted in red using $d = r = 2.5^\circ$ as partitioning parameters (see Fig. 5a). a Collocated residuals obtained by the original kernel (gravity disturbances). b Collocated residuals obtained by the localized kernel. c Numerical derivative of a (with original kernel) in y-direction. d Numerical derivative of b (with localized kernel) in y-direction

4.1 Behavior of the localized LSC estimator

Without explicitly calculating the LSC estimator (Eq. 5), its behavior is generally hard to predict as it involves matrix inversion and thus may produce highly variable results even when just slightly altering the input configuration. Nevertheless, when inspecting the LSC estimator (i.e., the kernel) for different locations (see Fig. 6), at least one general rule of thumb could be derived, which is valid in most cases (when the covariance function is decreasing with increasing distance). The better the observation coverage (i.e., density and quality) surrounding an estimation point, the smaller the effective influence radius of the kernel (cf. Fig. 6a, point A). Vice versa, when the nearby observation coverage is poor this influence radius can significantly increase in size (cf. Fig. 6d, point B). As a direct consequence, the kernel of estimates within good coverage (e.g., point A) can be considered to be already localized, while the kernel of estimates within poor coverage (e.g., point B) does not show this property. Subsequently, localizing the kernel (cf. Sect. 3.4) for points within good coverage has barely any influence (cf. Fig. 6b, c) while localizing those within poor coverage significantly alters the kernel (cf. Fig. 6e, f). To have an objective measure of how strongly the kernel is modified by the localization, a kernel disparity measure $\Delta_{i}^{\ker }$ is introduced for an estimate i as:

$$ \Delta_{i}^{\ker } = \sqrt {\frac{{\mathop \sum \nolimits_{k} \left( {\tilde{a}_{ik} \left( {1 - w_{ik}^{G} } \right)} \right)^{2} }}{{\mathop \sum \nolimits_{k} \tilde{a}_{ik}^{2} }}} = \sqrt {\frac{{\mathop \sum \nolimits_{k} \left( {\tilde{a}_{ik} - \tilde{a}_{ik}^{loc} } \right)^{2} }}{{\mathop \sum \nolimits_{k} \tilde{a}_{ik}^{2} }}} $$

(21)

where $\tilde{a}_{ik}$ denotes the elements of the original kernel matrix $\tilde{A}_{S}^{L}$, and $\tilde{a}_{ik}^{loc}$ the elements of the localized kernel. Since the relation $0$$\le w_{ik}^{G} \le 1$ holds for all weighting coefficients (cf. Eq. 16, Fig. 4), $\Delta_{i}^{\ker }$ ranges between zero and one. A value of 0 means that the localized kernel is identical to the original kernel, and a value of 1 indicates a completely different kernel (cf. Fig. 7b). Therefore, as the weighting function always attenuates kernel elements toward zero with increasing distance, the appropriate estimate will also be attenuated toward zero in comparison with the estimate derived from the unmodified kernel (see also Sect. 4.2, Fig. 8). Ultimately, the weighting function ensures that the further away the closest observation is located from the estimation point, the more the corresponding estimate is attenuated toward zero. In the context of RCR-LSC (Sect. 2.2.b), this behavior can be considered as desirable, as it is unlikely that the LSC is able to significantly improve such estimates in comparison with the a priori reductions (e.g., see Fig. 7). In fact, the unmodified LSC kernel tends to unnaturally overshoot (the estimate) in such locations, especially when the observations contain long-wavelength errors. This becomes obvious when examining the incisive long-range patterns of the original kernel function in such locations (cf. Fig. 6b): signals that are in the same wavelength range as the extents of the areas with positive or negative weights are able to strongly amplify the estimate due to possible resonances with the kernel.

In summary, one can conclude that the localization of the LSC estimator is probably beneficial in any situation (see Fig. 7): in areas with good coverage the original LSC estimate is widely preserved, while in areas with poor coverage the estimate is attenuated and thus prevents the previously mentioned overshooting. A further strong indication that the localization does not negatively impact the estimate is given when inspecting the increase in the formal error (Eq. 6) when applying the localized kernel: obviously, this increase (Fig. 7d) is negligible compared to the formal error amplitude (Fig. 7c).

4.2 Influence of the localization to the partitioning

Even though the localization of the LSC estimator already benefits from the classical LSC method (see Sect. 4.1), the primary reason for introducing the localization is to enable the partitioning of the collocation domain. As explained in Sect. 4.1, this localization limits the influence of the LSC estimator (i.e., kernel function) according to the chosen localization criterion (e.g., $\theta^{\max }$), and with this also to the buffer distance r (cf. Fig. 6). Obviously, applying a partitioning with buffer distance r to the collocation domain (cf. Fig. 5a) prevents the LSC estimator from including observations outside this region (e.g., see Fig. 6d, elements outside the red circle). Hence, it may be concluded that the partitioning itself directly impacts the collocation result in case that the kernel relies on observations beyond the buffer distance r. Albeit those alterations of the result mostly preserve the overall quality of the outcome, they introduce disparities between adjacent partitions, which manifest as fringe effects. In agreement with the findings in Sect. 4.1, these effects can be large especially in regions with sparse observation coverage where the LSC estimator tends to have a wide pattern (see Figs. 6d, 8a). There, the discontinuities on transitions between partitions might be problematic particularly when evaluating numerical derivatives of the result (cf. Fig. 8c) or predicting higher-order gravity functionals. As explained in Sect. 3.4, an adequate localization of the LSC estimator can prevent most of these fringe effects since correlations of the kernel beyond the buffer distance are removed in the first place (see Fig. 6e). In practical applications, residual fringe effects become virtually untraceable when using an appropriate kernel localization (cf. Fig. 8b, d).

As already mentioned in Sect. 3.4, despite the obvious large reduction in fringe effects due to the localized kernel, there is no mathematical guarantee of continuity between estimates of adjacent partitions (due to matrix inversion). Nevertheless, one can ask if there is at least convergence of the result when increasing the buffer distance r. In theory, when the buffer includes the whole collocation domain (i.e., an infinite buffer), fringe effects are again impossible (since the matrix to be inverted would always be the same in this case). Convergence is also desirable, as it indicates ‘how stable’ an obtained solution is when adding additional far-distance observations to the estimator. It is finally expected, the better the convergence, the better the fit to a result obtained by an infinite buffer and hence to a rigorous solution without partitioning. For evaluating the convergence behavior, LSC estimates are calculated for two different buffer distances r (and hence partition edge lengths d) while the localization parameter $\theta^{\max }$ is preserved. The difference between these two results can then be interpreted as a convergence resp. stability measure (see Fig. 9). As expected, the convergence is strongly improved when using the localized kernel (Fig. 9b) instead of the original one (Fig. 9a).

Fig. 9

Difference between LSC estimates when increasing the buffer distance r as well as the edge length d from 2.5° (red lines) to 3.0° (green lines). The rest of the setup is identical to Fig. 7. a Differences when using the original kernel. b Differences when using the localized kernel (with $\theta^{\max } = {\text{const}}{.} = 1.5^\circ$)

4.3 Statistical evaluation

As last validation, the behavior of the localization is inspected from a statistical perspective over the whole collocation area (see Fig. 3) by examining frequency distributions regarding the non-localized LSC solution (cf. Fig. 10). Comparing the convergence when increasing the buffer distance (see Fig. 10a) as in Sect. 4b, the localized kernel shows a much higher consistency with a 99% percentile of just about ± $10\;\upmu {\text{Gal}}$ (in contrast to $\pm 320\;\upmu {\text{Gal}}$ when using the original kernel). This improved consistency by a factor of about 30 is also in good agreement with the amplitudes of the deviations shown in Fig. 9. The findings from Sect. 4.1 are statistically substantiated in Fig. 10b where estimates in proximity to observations (<10 km) show just small differences to the original kernel with a 99% percentile of about ±0.3 mGal (cf. also Fig. 7a). These differences are getting gradually larger with the increasing distance to the nearest observation and become as large as about ±3 mGal (99% quantile) for far off estimates (>20km). Together with the evaluations in Sects. 4.1 and 4.2, this is the final evidence that the LSC kernel localization works as expected and produces stable results, where residual fringe effects are strongly reduced and can be further minimized by increasing the buffer distance r.

Fig. 10

Statistical comparison between the original and the localized kernel over the entire collocation area (see Fig. 3), covering the entire Antarctica from 60° to 90°S (for estimates on the same grid as in Fig. 7). The frequency distribution shown are generated by computing histograms from the deviations between different solutions using a bin size on a µGal level. A logarithmic scale was chosen to enable the visualization of frequency distributions of a broader range. a Frequency distribution of the deviation between the solution with $r = d = 3.0^\circ$ and the solution with $r = d = 2.5^\circ$ ($\theta^{\max } = {\text{const}}{.} = 1.5^\circ$, cf. Fig. 9) for the localized kernel (solid blue line) and the original kernel (solid red line). b Frequency distribution of the deviation between the solution using the localized kernel $(\theta^{\max } = 1.5^\circ )$ and the solution using the original kernel ($r = d = 3.0^\circ$ for both solutions, cf. Fig. 7). Solid blue line: frequency distribution for the set of estimation points where the nearest observation is less than 10 km away. Solid red line: frequency distribution for the set where nearest observation is 10 to 20 km away. Solid yellow line: frequency distribution for the set where the nearest observation is 20 to 400 km away. The dashed lines in figure (a) and (b) depict the appropriate 99% percentiles (two sided, > 0.5% and > 99.5%)

5 Discussion

In this last section, we briefly discuss the impact of PE-LSC to actual application scenarios regarding the feasibility and the computational effort, and we compare it to other LSA techniques commonly used in this field of study (Sect. 5.1). Subsequently, we conclude the paper by summarizing the benefits of PE-LSC and by discussing remaining disadvantages. Finally, we present some ideas of how to possibly overcome those drawbacks which might be subject of future investigations (Sect. 5.2).

5.1 Consequences for the computational effort

In geodesy, large-scale gravity field modeling using scattered observations is usually performed either applying spectral methods like Fourier analysis, spherical harmonic analysis or statistical approaches such as LSC. In the scattered case, the spectral methods need to be solved using a general least squares adjustment (LSA) approach, since in this case no orthogonality assumptions can be used to accelerate these methods. Comparing classical LSC and LSA it is discernible that both methods are in the same order of magnitude of computational cost (in terms of effort and memory requirements) as both require matrix multiplication and inversion. As mentioned in Sect. 1, the computational effort of those operations is in the cubic order, and memory requirements are in the quadratic order (regarding the number of observation). Solving them becomes numerically expensive with an increasing number of observations (see Fig. 11). In practice, the available memory usually poses a hard limit on the computing feasibility because conventional linear algebra routines cannot exceed the RAM limit of the system (or just with a large penalty in terms of computation time). Therefore, even current-generation high-performance computing (HPC) systems, having, e.g., about 256 TB of memory, are limited to approximately 5 million observations. Their computation would take an infeasible time of ~400 years (single core, cf. Fig. 11, dashed blue and dotted green line).

Fig. 11

Computational requirements regarding the number of observations to process (extrapolated) of the classical LSC or LSA approach (unpartitioned) in comparison with the PE-LSC method (partitioned). Single-core CPU times are scaled to the Intel Skylake-SP processor family with AVX512 enabled (using double precision). For the partitioning, a point density of $1/16 \;{\text{obs}}{\text{./km}}^{2}$ is assumed (i.e., a regular $4 \times 4\;{\text{km}}\;{\text{grid}}$) with the partition parameters $r = d = 2.5^\circ \approx 278\;{\text{km}}$. It is assumed that the number of estimates is in the same order as the number of observations. Solid blue: single-core CPU times for the partitioned approach (PE-LSC). Dashed blue: single-core CPU times for the unpartitioned approaches (LSC, LSA). Solid red: memory requirements (RAM) for the partitioned approach (PE-LSC). Dotted red: memory requirements (RAM) for the unpartitioned approaches (LSC, LSA). Dashed green: typical memory limit (RAM) of current-gen. workstation PCs (128 GB). Dotted green: typical memory limit (RAM) of current-gen. high-performance computers (256 TB)

On the other hand, PE-LSC is typically not limited by the system memory when using the partitioning approach and would accomplish the computation of the same 5 million observations in about 2 months (single core, cf. Fig. 11, solid blue line). Having a multi-core workstation CPU (e.g., 64 cores, assuming an ideal linear scale-up) available this task can be performed within a reasonable timeframe of 1–2 days. In the appropriate partitioning scenario, an exemplary but realistic point density of a 4 × 4 km grid is assumed, where 5 million observations would correspond to a covered area of $8 \cdot 10^{7} \;{\text{km}}^{2}$ which is roughly the area of Asia and Africa together. Extending this scenario further to a global scale ($\sim5 \cdot 10^{8} \;{\text{km}}^{2}$), it would include about 6 times as many points (~30 mio.) and hence, would just need about 6 times as much time to finish for the PE-LSC method, which still yields a reasonable timeframe of 1–2 weeks (on a 64 core workstation CPU). Currently, the same calculation would not be feasible with the classical approach (~100,000 years of single-core computation time and ~8PB of memory required). This leads to the conclusion, that for general high-resolution and large-scale gravity field modeling only a partitioned LSC approach is suited to perform this task (for scattered observations). With PE-LSC, such an approach is given which not only enables the optimal partitioning, but also tries to minimize fringe effect (cf. Fig. 8) caused by the partitioning. Using PE-LSC in the actual scenario of the AntGG project where more than 800,000 observations must be processed, a solution with approx. 1.4 Mio. estimates can be obtained within a few hours (on a 56 core CPU).

5.2 Conclusion and outlook

We elaborated a partition-enhanced LSC method (PE-LSC) to improve the stability and computational efficiency. The discussed modifications, i.e., the accelerated calculation of covariance matrices and the partitioning strategy together with the kernel localization make it feasible to conduct collocations on large scales with relatively low computational effort (see Sect. 5.1 and Fig. 11) while minimizing fringe effects. In fact, with the shown advancements the effort only increases linearly with the size of the study area, which makes it even possible to think of applying LSC to scattered data on a global scale (cf. Fig. 11).

Although practical limits are not left for PE-LSC (at least not in the shown scenario), there is still one major inherent shortcoming of the (PE-)LSC method to consider, which is the modeling of the covariance function. By now, for PE-LSC there is no practical alternative to homogeneous-isotropic covariance functions, since (1) the information of the actual (‘true’) covariance function is not available, and (2) there are usually not enough observations present to empirically derive general covariance functions comprehensively. (3) Even if such a general covariance function might be derived empirically, without a spectral or closed-form representation, deriving cross-covariances among different functionals would also be problematic. Using homogeneous-isotropic covariance functions means to disregard the local and directional variations of the investigated physical quantity. In gravity field modeling, for example, even if it is common knowledge that in mountainous regions the expected variation in the gravity field signal is larger, by now this fact is not considered within PE-LSC. This deficiency becomes even more prominent with increasing size of the collocation area as it can be expected that the covered terrain also becomes more heterogeneous (mountains, plains, sea, ice, etc.).

Therefore, for future work in the field of LSC, overcoming this issue is considered as the most important task to make (PE-)LSC a feasible stand-alone alternative even for global gravity field modeling. Darbeheshti (2009) provides a comprehensive overview of studies already performed on this subject. Unfortunately, none of these seems fully appropriate for PE-LSC as every method has its own limitations. A promising approach for the application in PE-LSC might be the classification of the collocation area into classes of similar behavior (e.g., mountains, hills, plains, ocean, ice, etc.) and a separate estimation of ‘local’ degree variances (see Sect. 3.2) for each class. A non-homogeneous and non-isotropic covariance function might then be derived by some sort of interpolation between the covariance functions derived from the different degree variances and based on the actual point locations (regarding the previous classification, similar as proposed by Tscherning 1999).

Until such a technique becomes available, the shortcoming of the suboptimal covariance modeling might be overcome by combining (PE-)LSC with the aforementioned spectral methods (as discussed, e.g., by Reguzzoni and Tselfes 2009). While those methods are rigorous in the way they describe the gravity field, they require the observations usually to be given on regular grids in order to be applicable efficiently (not as in the example above, e.g., see Sneeuw 1994). At this point, (PE-)LSC can help by pre-calculating the observations beforehand on the required grid and, thus, producing a best guess of what to expect on those locations. Subsequently, this best guess can be used by the spectral methods to derive the final spectral representation of the gravity field (e.g., cf. Zingerle et al. 2020). If needed, the obtained gravity field model can be further improved iteratively by recalculating reductions for the RCR-LSC from the newly derived model and by restarting the whole procedure anew using the improved (narrowed) reductions.

Appendices

Appendix

Partial derivatives of homogeneous-isotropic covariances regarding a local ENU-frame

Evaluation of the generalized chain rule (see Sect. 3.1) requires the partial derivatives of the covariance c (cf. Eq. 9) with respect to the chosen local (reference) frame coordinates. In case of gravity field modeling, which usually assumes the chosen local frame to be an ENU-frame (east, north, up) tangential to the sphere, the partial derivatives needed are:

$$ c_{ik}^{n,m} := \frac{{\partial^{{\left( {m + n} \right)}} c_{ik} }}{{\partial t^{m} \partial u^{n} }} = \mathop \sum \limits_{l = 0}^{{l_{\max } }} c_{l} \frac{{\left( {l + 1} \right)!}}{{\left( {l - n + 1} \right)!}} u_{ik}^{{\left( {l - n + 1} \right)}} P_{lm} \left( {t_{ik} } \right) $$

(22)

in terms of intermediate frame coordinates,

$$ \frac{{\partial^{m} \overline{u}_{i} }}{{\partial x_{Ui}^{m} }} = \frac{{\left( { - 1} \right)^{m} m!R}}{{r_{i}^{m + 1} }} , \,\frac{{\partial^{{\left( {m + n} \right)}} u_{ik} }}{{\partial x_{Ui}^{m} \partial x_{Uk}^{n} }} = \frac{{\partial^{m} \overline{u}_{i} }}{{\partial x_{Ui}^{m} }}\frac{{\partial^{n} \overline{u}_{k} }}{{\partial x_{Uk}^{n} }} $$

(23)

for the up component (x_U) and

$$ \frac{{\partial^{{\left( {m + n} \right)}} {\varvec{e}}_{i} }}{{\partial x_{Ei}^{m} \partial x_{Ni}^{n} }} = \left( {\begin{array}{*{20}c} {\frac{{\partial^{m} \cos \lambda_{i} }}{{\partial \lambda_{i}^{m} }} \frac{{\partial^{n} \cos \varphi_{i} }}{{\partial \varphi_{i}^{n} }}} \\ {\frac{{\partial^{m} \sin \lambda_{i} }}{{\partial \lambda_{i}^{m} }} \frac{{\partial^{n} \cos \varphi_{i} }}{{\partial \varphi_{i}^{n} }}} \\ {\frac{{\partial^{m} \left( 1 \right)}}{{\partial \lambda_{i}^{m} }} \frac{{\partial^{n} \sin \varphi_{i} }}{{\partial \varphi_{i}^{n} }}} \\ \end{array} } \right)\frac{1}{{r_{i}^{n} \left( {r_{i} \cos \varphi_{i} } \right)^{m} }}, $$

(24)

$$ \frac{{\partial^{{\left( {m + n + o + q} \right)}} t_{ik} }}{{\partial x_{Ei}^{m} \partial x_{Ni}^{n} \partial x_{Ek}^{o} \partial x_{Nk}^{q} }} = \left\langle {\frac{{\partial^{{\left( {m + n} \right)}} {\varvec{e}}_{i} }}{{\partial x_{Ei}^{m} \partial x_{Ni}^{n} }}, \frac{{\partial^{{\left( {o + q} \right)}} {\varvec{e}}_{k} }}{{\partial x_{Ek}^{o} \partial x_{Nk}^{q} }}} \right\rangle $$

for the east component and north component (x_E and x_N). Here, $P_{lm} \left( {t_{ik} } \right)$ denotes the mth derivate of $P_{l} \left( {t_{ik} } \right)$ regarding t_ik (not to confuse with the associated Legendre function which is defined slightly different), $\left( {\lambda_{i} ,\varphi_{i} } \right)$ are the appropriate spherical coordinates (longitude and latitude) of v_i. In Eq. 22, in opposition to Eq. 9, the letter n for the spherical-harmonic degree was exchanged with the letter l to reuse n for the order of derivative of u_ik. Again, it is noteworthy that also partial derivatives are expressible as outer (Cartesian) products of $\underline {v} \times \underline {v}$ which allows for efficient evaluation of all pairs over indices i, k. For the sake of performance and accuracy, it is advisable to pre-calculate all the necessary derivatives $\underline {c}_{G}^{n,m}$ of the intermediate grid $\underline {c}_{G}$ (see Eq. 9, in the same fashion as $\underline {c}_{G}$ is calculated). With some additional programming effort, also linear out-of-scheme quantities (i.e., quantities that are not directly expressible as derivative such as, e.g., gravity anomalies) can be implemented.